Косинус двойного угла формула: Формулы двойного аргумента (базовый уровень) — урок. Алгебра, 10 класс.

Формулы двойного аргумента 10 класс онлайн-подготовка на Ростелеком Лицей

 

 

Тема: Преобразование тригонометрических выражений

 

Урок: Формулы двойного аргумента

 

1. Введение. Вывод формул для синуса и косинуса двойного аргумента

 

 

На уроке выводятся формулы двойного аргумента синуса и косинуса из формул синуса и косинуса суммы аргументов и  формула для тангенса двойного аргумента двумя способами, анализируется ее область допустимых значений. Решается несколько задач на упрощение, вычисление и решение уравнений с помощью формул двойного аргумента.

 

Доказать:

Доказательство:

при  имеем:

.

Аналогично доказывается формула косинуса двойного аргумента.

 

2. Вывод формулы для тангенса двойного аргумента

 

 

 

Доказательство (1-й способ):

При получается

Вывод формулы вторым способом подчеркивает особенность формулы, то есть сужение ОДЗ.

Доказательство (2-й способ):

при  .

 

3. Анализ формулы

 

 

 

1) Область определения левой части

Иллюстрация полученного множества допустимых значений приведена на рис.1.

Рис. 1.

2) Область определения правой части

Иллюстрация полученного множества приведена на рис.2.

Рис. 2.

Происходит сужение области определения – результат анализа формулы.

Пример на ОДЗ.

существует при

не существует при так как не существует

 

4. Формулы двойного аргумента для других углов

 

 

Применяя формулы двойного аргумента для угла :

 

то  и формулы примут вид:

Аналогично, можно применить формулы для аргумента .

sin4x = sin(2·2x) = 2sin2x·cos2x

 

5. Примеры применения формул

 

 

1.    Вычислить:

 

1) 

2) 

3) 

 

6. Решение задач

 

 

2. Дано:

 

Найти:   а)      б)

Решение:

а)

Учитывая, что , то

    Ответ:

б)

Ответ:

 

7. Задачи на упрощение

 

 

3. Упростить:

 

а) б)

Решение:

а) 

    Ответ: .

б) 

Ответ:

 

8. Решение уравнений

 

 

4.   Решить уравнение:

 

Решение:

или  

                                                                                       

Ответ:

 

9. Итог  урока

 

 

На уроке рассматривались формулы двойного аргумента и их использование при решении задач.

 

На следующем уроке будут рассмотрены формулы понижения степени.

 

Список рекомендованной литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.

8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983

 

Дополнительные веб-ресурсы

1. Интернет-портал Mathematics.ru (Источник). 

2. Портал Естественных Наук (Источник). 

3. Интернет-портал exponenta.ru (Источник).

 

Сделай дома

№№ 21.3(а, б), 21.4(а, б), 21.6(а) (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)

 

Урок 22. Формулы двойных и тройных углов (аргументов)

Косинус двойного угла равен квадрату косинуса данного угла минус квадрат  синуса того же угла.Для получения косинуса двойного угла воспользуемся формулой

соs (α + β) = соs α cos β – sin α sin β

и положим в ней  α = β.

Получим:

соs (α + α) = соs α cos α – sin α sin α,

или

соs 2α = соs²α – sin²α.

ПРИМЕР:Если в формуле

соs 2α = соs²α – sin²α

заменить

соs²α  на  1 – sin²α

или

sin²α  на  1 – соs²α,

то получим ещё две формулы для  соs 2α:

соs 2α =1 – 2 sin²α,

соs 2α = 2 соs²α – 1.

ПРИМЕР:

Упростить выражение:

tg x – ctg x.

РЕШЕНИЕ:Для преобразования числителя дроби воспользуемся следующей формулой:

соs²α – sin²α = соs 2α

но сначала вынесем знак минус за скобки

sin²х – соs²х =

–(соs²х – sin²х) = – соs 2х.

Для преобразования знаменателя дроби воспользуемся следующей формулой:

2 sin α cos α = sin 2α

sin x cos x = ¹/₂ sin 2x.

В результате получим:

ОТВЕТ:  –2 ctg 2x

ПРИМЕР:

Доказать тождество:

РЕШЕНИЕ:

Знаменатель правой части преобразуем по следующей формуле:

соs 2α = соs²α – sin²α

сos х = cos^2х/₂ – sin^2х/₂ =

cos^2х/₂ – (1 – cos^2х/₂) =

2 cos^2х/₂ – 1.

1 + сos х = 2 cos^2х/₂.

Числитель правой части преобразуем по следующей формуле:

sin 2α = 2 sin α cos α.

sin х = 2 sin ^х/₂ cos ^х/₂.

В результате получим

:

Тангенс двойного угла равен удвоенному тангенсу данного угла, деленному на разность между единицей и квадратом тангенса данного угла.Выведем формулу для  tg 2α.
Полагая в формуле

получим:

или

Эта формула имеет место для всех значений  α, кроме

α = ^π/₂ + kπ,

α = ^π/₄ + 2kπ,

где  k – целое число, так как при таких значениях α   не определён (не существует) или  tg α  или  tg 2α.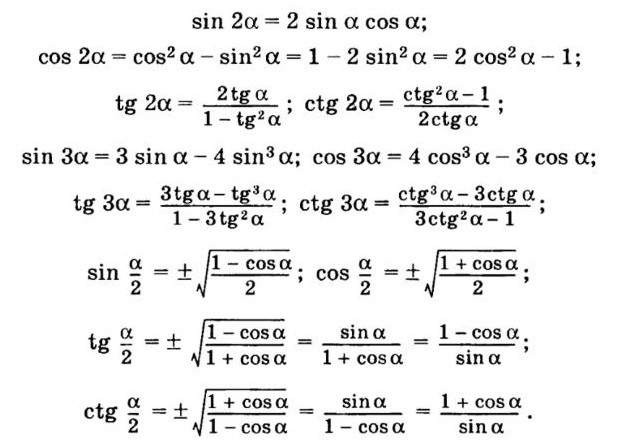

Эта формула может быть получена и в результате почленного деления формулы

sin 2α = 2 sin α cos α

на формулу

соs 2α = соs²α – sin²α

 и последующих простых преобразований.

ПРИМЕР:

Дано:  tg α = ³/₄.

Найти  tg 2α.

РЕШЕНИЕ:

Имеем:

ПРИМЕР:

Вычислите  tg x,

если  tg 2x = 2,

^3π/₂ < x < 2π.

РЕШЕНИЕ:

Так как по условию 

^3π/₂ < x < 2π, то 

tg 2x < 0. Имеем:

Делаем замену  t = tg x  и получаем уравнение

t² + t – 1 = 0,

корни которого следующие:

Так как  tg x < 0, то нас интересует только отрицательный корень. Следовательно:

ОТВЕТ:Котангенс двойного угла равен разности квадрата котангенса и единицы, делённой на удвоенный котангенс данного угла.С помощью этих формул можно выразить синус, косинус, тангенс, котангенс любого (допустимого) аргумента через тригонометрические функции вдвое меньшого аргумента.

Формула

sin 2α = 2 sin α cos α

связывает синус любого угла с синусом и косинусом угла, вдвое меньшего.

ПРИМЕР:

sin x = sin 2 ∙ ^x/₂ = 2 sin ^x/₂ cos ^x/₂,

sin 5x

= sin 2 ∙ ^5x/₂ = 2 sin ^5x/₂ cos ^5x/₂,

sin ^x/₂ = 2 sin ^x/₄ cos ^x/₄.

Формула

соs 2α = соs² α – sin² α

связывает косинус любого угла с синусом и косинусом угла, вдвое меньшего. На основании её можно, например, выражения

cos 6α, соs α, соs ^x/₂

представить следующим образом:

ПРИМЕР:

cos 6α = cos² 3α – sin² 3α,

соs α = cos^2α/₂ – sin²

^α/₂,

соs ^x/₂ = cos^2x/₄ – sin^2x/₄.

Пользуясь формулой тангенса двойного угла, можно тангенс любого угла выразить через тангенс угла вдвое меньшего.

ПРИМЕР:Путём последовательного применения формул сложения аргументов тригонометрических функций можно получить формулы для  3α, 4α  и так далее. Приведём формулы для тройных углов:

sin 3α = sin (α + 2α) =

= sin α cos 2α + sin 2α cos α =

= sin α (соs²α – sin²α) + cos α 2 sin α cos α =

= sin α (1 – 2 sin²α) + 2 sin α (1 – sin²

α) =

= sin α  – 2 sin³α + 2 sin α – 2 sin³α =

= 3 sin α – 4 sin³ α,

cos 3α = соs (α + 2α) =

= cos α cos 2α – sin α sin 2α =

= соs α (соs²α – sin²α) – sin α 2 sin α cos α =

= соs α (2 соs²α – 1) – 2 соs α (1 – соs²α) =

= 2 соs³α – соs α – 2 соs α + 2 соs³α =

= 4 cos³ α – 3 cos α,

ПРИМЕР:

Вычислить  sin 18°.

РЕШЕНИЕ:

Воспользуемся тождеством 

sin 36° = cos 54°.

Обозначим  18° = α, находим, что в данном случае 

sin 2α = cos 3α, или 

2 sin α cos α = 4 cos³α – 3 cos α.

Так как  cos α ≠ 0, то, после сокращения на  cos α, имеем

2 sin α = 4 cos² α – 3 = 4(1 – sin² α) – 3,

откуда

4 sin² α + 2 sin α – 1 = 0.

Решая это уравнение относительно  sin α, найдёмТак как в первом квадранте  sin α ˃ 0, то второе значение не подходит.

Формула двойного угла Cos — Изучите формулу для расчета двойного угла Cos

Тригонометрия — это раздел математики, который занимается изучением отношений между углами и сторонами прямоугольного треугольника.

Косинус — это одно из основных тригонометрических соотношений, которое помогает вычислить соотношение основания и гипотенузы. Таким образом, cos можно определить как отношение длины основания к длине гипотенузы в прямоугольном треугольнике.

Давайте изучим формулу двойного угла cos с ее выводом и несколько примеров решения.

Мы будем использовать формулу cos(A + B) для вывода формулы двойного угла cos.

Формула 1:

Двойная угловая идентичность cos x может быть получена с помощью формулы суммы cos (A + B).

Имеем cos (A + B) = cos A cos B — sin A sin B                              — (1)

Подставьте x вместо A и B в уравнении (1).

cos (A + B) = cos A cos B — sin A sin B

cos (x + x) = cos x cos x- sin x sin x

cos (2x) = cos ² x — sin ² x

cos (2x) = cos ² x — sin ² x

Формула 2:

Теперь воспользуемся тригонометрическим тождеством cos 2 9 x 7 0 + 2 sin 90928 чтобы вывести другую формулу двойного угла cos.

Замена 1 — cos ² x вместо sin ² x в формуле 1.

cos (2x) = cos ² x — sin ² x

= cos ² x — (1 — cos ² x)

= 2cos ² x — 1

cos ( 2x) = 2cos ² x — 1

Формула 3:

Снова воспользуемся тригонометрическим тождеством cos ² x + sin ² x = 1, чтобы вывести еще одну формулу двойного угла cos.

Замена 1 — sin ² x для cos ² x в формуле 1.

cos (2x) = cos ² x — sin ² x

= 1 — sin ² x — sin ² x

= 1 — 2Sin ² x

Cos (2x) = 1 — 2sin ² x

 

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.

No related posts.