Современные способы измерения объема жидкости
Содержание:
- 1. Первый способ измерения объема жидкости: вычисление высоты
- 2. Точность измерения давления, производимого датчиком
- 3. Второй способ вычисления: аппроксимация
Одной из важнейших задач молочной промышленности всегда был учет объема продукта: поступившего на обработку, расходуемого в течение технологического процесса, полученного на выходе. Причем эти измерения требуются как для технологических задач, так и для экономического учета.
О современных способах произведения этих измерений и пойдет речь.Существует несколько подходов к измерению объема жидкости, находящейся в емкости. Все они, однако, имеют одну общую исходную величину, требуемую для расчета. Эта величина – высота столба жидкости.Известна формула, устанавливающая математическую связь между плотностью жидкости, высотой ее столба относительно точки измерения, ускорением свободного падения и давлением, оказываемым на дно и стенки сосуда:
P=ρ×g×hP= %rho times g times h
где Р – давление, ρ – плотность жидкости, h – высота столба жидкости, g – ускорение свободного падения (9,8 м/c2).
Итак, зная давление и плотность жидкости, нетрудно рассчитать высоту, до которой она доходит относительно точки измерения. Такой способ измерения называется гидростатическим.Для того, чтобы узнать давление жидкости используются соответствующие датчики. В пищевой промышленности, как правило, это датчики с мембраной, имеющие относительно большую плоскость контакта со средой, что позволяет легко отмывать их от остатков продукта.
Среди датчиков давления наиболее распространены датчики с выходным сигналом 4…20 мА, являющимся общемировым стандартом в системах автоматического управления. Например, интеллектуальный датчик давления 4000-SAN.Сам чувствительный элемент датчика обычно представляет собой тензорезистор – элемент, изменяющий свое сопротивление в зависимости от приложенного к нему усилия. Зависимость сопротивления этих элементов от давления известна. Далее изменение сопротивления электроника датчика приводит к сигналу 4…20 мА.Современные датчики давления часто делаются цифровыми – то есть роль преобразователя играет микроконтроллер, встроенный в датчик.
Такие датчики легче настраивать, они обладают более высокой точностью и могут оснащаться дисплеями, модулями коммуникации и дополнительными функциональными возможностями.
Итак, после того, как получено значение высоты, можно переходить к расчету объема жидкости. Выделяются два основных практических подхода:
- геометрическое вычисление;
- аппроксимация линейными отрезками.
1. Первый способ измерения объема жидкости: вычисление высоты
Рисунок 1 — Цилиндрическая емкость с коническим дномПервый способ подразумевает возможность выражения зависимости высота – объем известной формулой. Он актуален для емкостей, имеющих несложную форму и построенных из таких стандартных геометрических фигур, как, например, полусфера, конус и цилиндр. Например, для широко распространенных емкостей в форме цилиндра с коническим дном (Рисунок 2), вычисление будет производиться следующим образом: до тех пор, пока жидкость не достигла края конуса зависимость ее объема от высоты такова:
V=13×π×Hж×((R2+K×H)2+(R2+K×H)×R2+R22)V= {1} over {3} times %pi times Hж times ( ( R_{2} + K times H )^{2} + ( R_{2} + K times H ) times R _{2} + R_{2} ^{2})
Где V – объем, Нж – высота столба жидкости, K – конусность
K=R1−R2h2K= { R_{1} — R_{2} } over {H_{1}}
как только высота жидкости достигает края конуса и начинает заполнять цилиндр достаточно взять заранее вычисленный полный объем конической части:
Vk=13×π×h2×(R12+R1×R2+R22) Vk= {1} over {3} times %pi times H_{1} times ( R^{2}_{1} + R_{1} times R_{2} + R^{2}_{2} )
и прибавлять к нему объем жидкости, находящейся в цилиндрической части:
Vц=π×R12×(Нж−h2)Vц= %pi times R_{1}^{2} times ( Нж — H_{1} )
С учетом степени развития микроконтроллеров, подобный алгоритм возможно реализовать непосредственно в датчике.
{3}
или 47,1 литров.
Достаточно большое значение, с учетом того, что в течение рабочего дня могут производиться десятки циклов наполнения/опустошения емкости. При этом данное значение не учитывает дополнительную погрешность, вызываемую перепадами температуры.Именно поэтому датчики для решения задач вычисления объема обычно имеют погрешность не более 0,1 %. При тех же условиях, такой датчик даст ошибку измерения всего в 9,42 литра, то есть в 5 раз меньшую.
3. Второй способ вычисления: аппроксимация
Рисунок 2 — Емкость под угломНа практике часто встречаются емкости, имеющие искажения формы внутренней поверхности, к которым неприменим геометрический метод вычисления объема емкости.Например, для емкости, установленной под углом (Рисунок 2), наклон в 2…3 градуса, кажущийся незначительным, сильно нарушит точность измерений – в горизонтальной емкости поверхность жидкости вместо прямоугольника будет иметь гораздо более сложную форму, что значительно меняет зависимость объема от уровня.
Емкость может иметь утопленный в стенку люк. В этом случае нужно производить вычисления уже по трем разным формулам, вместо двух. К тому же, зависимость объема на участке с люком будет куда более сложной, чем для прямого цилиндра. Также, геометрический метод на практике неприменим к емкостям, в которых производится перемешивание продукта.
Массивное устройство внутри емкости значительно исказит результаты вычислений – датчик будет показывать объем, больший, чем реальный. Предусмотреть готовые алгоритмы для каждой подобной ситуации и внести их в
датчик – задача практически невыполнимая. Тут на помощь приходит более трудоемкий, но и значительно более гибкий способ измерения. Если начать заливать в емкость, допустим, по 100 литров жидкости и при этом на каждом шаге отмечать высоту, соответствующую залитому объему, мы получим так называемую «тарировочную таблицу». Суть в следующем: нестандартная форма емкости моделируется с использованием некоторого количества прямых отрезков. Чем их больше, тем точнее будут производиться вычисления.
Если жидкость, например, находится посередине между двумя точками, то и объем вычисляется, как среднее значение объемов в этих точках (Рисунок 3). Очевидно, что от количества точек, используемых при тарировании,
значительно зависит точность результата. Если для участка с линейной зависимостью объем/высота достаточно двух точек, до для нелинейных участков их требуется гораздо больше. Тарирование на нелинейном участке можно производить шагами, в два раза большими, чем допустимая погрешность на данном участке. Например, если в конусной части емкости необходимо получить точность не ниже 20 литров, шаги тарирования должны быть не более 40 литров. Тут следует помнить простое правило – чем меньше шаги и больше точек, тем выше итоговая точность работы. Недостаток метода в том, что датчик, перенесенный на другую емкость, снова потребует тарирования.
Это значит, что можно произвести тарирование с использованием обычной воды, а затем, предварительно поменяв значение плотности жидкости в памяти датчика, заливать продукт, имеющий плотность, отличную от плотности воды. Таким образом, мы получаем гибкий и точный метод, позволяющий работать с емкостями любой формы и жидкостями любой плотности.
Инженер отдела проектирования ООО «КИП-Сервис»
Горбоносов М.А.
Как вычислить объем тела неправильной формы. Geometry Calculator – расчет геометрических фигур Объем геометрических фигур
Убедитесь, что тело является водонепроницаемым, так как описанный метод подразумевает погружение тела в воду.
Если тело полое или в него может проникнуть вода, то вы не сможете точно определить его объем, используя этот метод.
Если тело поглощает воду, убедитесь, что вода не повредит его. Не погружайте в воду электрические или электронные предметы, так как это может привести к поражению электрическим током и/или к повреждению самого предмета.
- Если возможно, запечатайте тело в водонепроницаемый пластиковый пакет (предварительно выпустив из него воздух). В этом случае вы вычислите довольно точное значение объема тела, так как объем пластикового пакета, скорее всего, будет небольшим (по сравнению с объемом тела).
Найдите емкость, в которой помещается тело, объем которого вы вычисляете. Если вы измеряете объем небольшого предмета, воспользуйтесь мерным стаканом с нанесенной градуировкой (шкалой) объема. В противном случае найдите емкость, объем которой можно легко вычислить, например, емкость в форме прямоугольного параллелепипеда, куба или цилиндра (стакан тоже можно рассматривать как емкость цилиндрической формы).
- Возьмите сухое полотенце, чтобы положить на него тело, вытащенное из воды.
Отметьте уровень воды. Если емкость с водой прозрачная, отметьте ее уровень с внешней стороны емкости при помощи водостойкого маркера. В противном случае отметьте уровень воды с внутренней стороны емкости, используя цветную клейкую ленту.
Погрузите тело полностью в воду. Если оно поглощает воду, подождите по крайней мере тридцать секунд, а затем вытащите тело из воды. Уровень воды должен опуститься, так как часть воды находится в теле. Удалите отметки (маркер или клейкую ленту) о предыдущем уровне воды и отметьте новый уровень. Затем еще раз погрузите тело в воду и оставьте его там.
Если тело плавает, прикрепите к нему тяжелый предмет (в качестве грузила) и продолжите вычисления с ним. После этого повторите вычисления исключительно с грузилом, чтобы найти его объем. Затем вычтите объем грузила из объема тела с прикрепленным грузилом и вы найдете объем тела.
- При вычислении объема грузила прикрепите к нему то, чем вы крепили грузило к рассматриваемому телу (например, ленту или булавки).
Отметьте уровень воды с погруженным в нее телом. Если вы используете мерный стакан, запишите уровень воды согласно шкале на стакане. Теперь вы можете вытащить тело из воды. Вероятно, не стоит оставлять предмет под водой более чем на пару минут, поскольку в противном случае вода может негативно сказаться на нем.
Знайте, почему этот метод работает. Изменение объема воды равно объему тела неправильной формы. Способ измерения объема тела с помощью емкости с водой основан на том, что при погружении тела в жидкость объем жидкости с погруженным в нее телом увеличивается на величину объема тела (то есть тело вытесняет объем воды, равный объему этого тела).
Найдите объем, используя мерную шкалу стакана. Если вы использовали емкость с мерной шкалой, то у вас уже должны быть записаны два значения уровня воды (ее объема). В этом случае из значения объема воды с погруженным в нее телом вычтите значение объема воды до погружения тела. Вы получите объем тела.
Найдите объем, используя емкость прямоугольной формы. Если вы использовали емкость в форме прямоугольного параллелепипеда, измерьте расстояние между двумя метками (уровень воды до погружения тела и уровень воды после погружения тела), а также длину и ширину емкости с водой. Объем вытесненной воды найдите посредством перемножения длины и ширины емкости, а также расстояния между двумя метками (то есть вы вычисляете объем небольшого прямоугольного параллелепипеда). Вы получите объем тела.
- Не измеряйте высоту емкости с водой. Измерьте только расстояние между двумя метками.
- Используйте
Измерьте только расстояние между двумя метками.– бесплатный геометрический калькулятор поможет вам в два клика подсчитать площадь или объем относительно простых геометрических фигур. Не нужно заниматься поиском нужных формул и производить расчеты на листочке. Работа с программой очень проста, для начала нужно выбрать, что нужно подсчитать: площадь фигуры, площадь полной поверхности или же объем. Выбранная фигура отображается рядом в окошке, и рядом с ней будет показана формула для подсчета искомой величины. Изначально все результаты округляются до целой части, но есть возможность изменить и выбрать необходимую точность, с которой следует выводить результаты. Для этого доступны варианты от одного до десяти знаков после запятой.
Что можно рассчитать?
- Круг – находим длину окружности по известному радиусу, и диаметр по известной окружности.
- Находим площадь – круга, сектора круга, элипса, квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, тора.
- Площадь поверхности – куба, призмы, пирамиды, цилиндра, сферы, конуса, тора.
- Объём фигур – куб, кубоид, призма, пирамида, цилиндр, сферы, конуса, тор, усечённый конус, бочка.
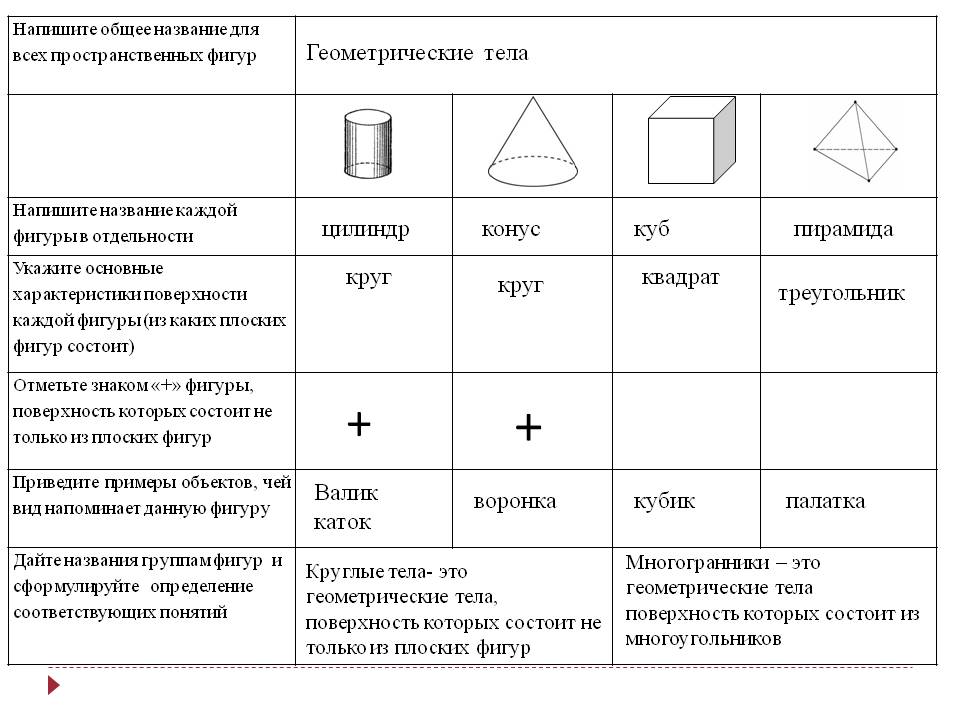
Геометрические фигуры — это замкнутые множества точек на плоскости или в пространстве, которые ограничены конечным числом линий. Они могут быть линейными (1D), плоскими (2D) или пространственными (3D).
Любое тело, имеющее форму, представляет собой совокупность геометрических фигур.
Любую фигуру можно описать математической формулой различной степени сложности. Начиная от простого математического выражения до суммы рядов математических выражений.
Основными математическими параметрами геометрических фигур являются радиусы, длины сторон или граней и углы между ними.
Ниже представлены основные геометрические фигуры, наиболее часто используемые в прикладных расчетах, формулы и ссылки на расчетные программы.
Линейные геометрические фигуры
1.
Точка
Точка — это базовый объект измерения. Основной и единственной математической характеристикой точки является её координата.
2. Линия
Линия — это тонкий пространственный объект имеющий конечную длину и представляющий собой цепь связанных друг с другом точек. Основной математической характеристикой линии является длина.
Луч — это тонкий пространственный объект имеющий бесконечную длину и представляющий собой цепь связанных друг с другом точек. Основными математическими характеристиками луча являются координата его начала и направление.
Плоские геометрические фигуры
1. Круг
Круг — это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга. Основной математической характеристикой круга является радиус.
2. Квадрат
Квадрат — это четырёхугольник, у которого все углы и все стороны равны. Основной математической характеристикой квадрата является длина его стороны.
3. Прямоугольник
Прямоугольник — это четырехугольник, у которого все углы равны 90 градусам (прямые). Основными математичскими характеристиками прямоугольника являются длины его сторон.
4. Треугольник
Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Основными математическими характеристиками треугольника являются длины сторон и высота.
5. Трапеция
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Основными математическими характеристиками трапеции являются длины сторон и высота.
6. Параллелограмм
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Основными математическими характеристиками параллелограмма являются длины его сторон и высота.
Ромб — это четырехугольник, у которого все стороны, а углы его вершин не равны 90 градусам.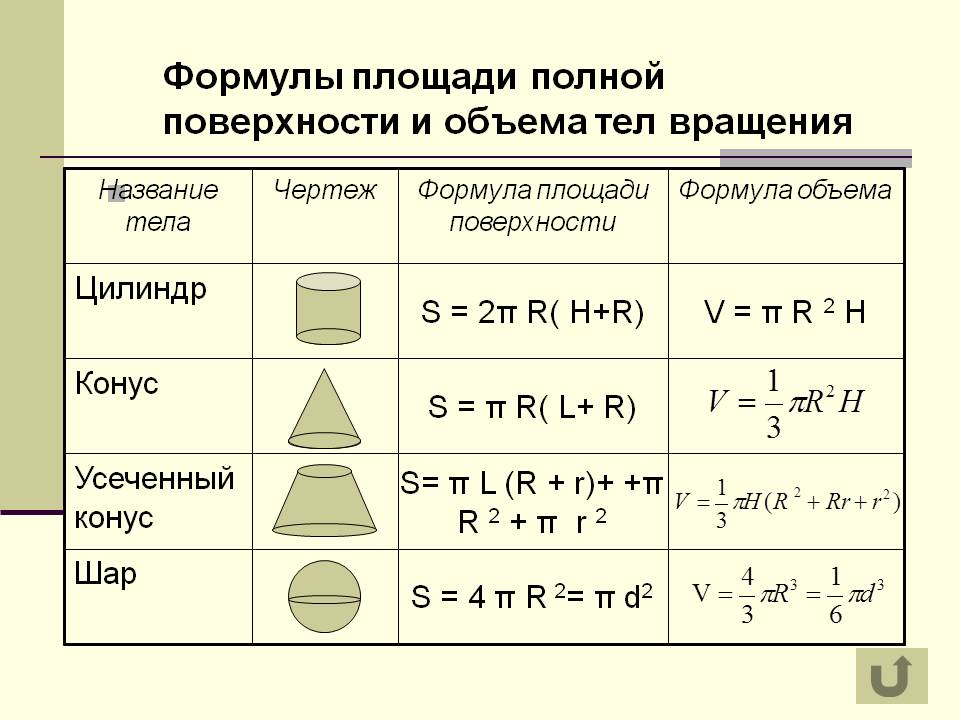
Основными математическими характеристиками ромба являются длина его стороны и высота.
8. Эллипс
Эллипс — это замкнутая кривая на плоскости, которая может быть представлена как ортогональная проекция сечения окружности цилиндра на плоскость. Основными математическими характеристиками окружности являются длина его полуосей.
Объемные геометрические фигуры
1. Шар
Шар — это геометрическое тело, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой шара является его радиус.
Сфера — это оболочка геометрического тела, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой сферы является её радиус.
Куб — это геометрическое тело, представляющее собой правильный многогранник, каждая грань которого представляет собой квадрат.
Основной математической характеристикой куба является длина его ребра.
4. Параллелепипед
Параллелепипед — это геометрическое тело, представляющее собой многогранник, у которого шесть граней и каждая из них прямоугольник. Основными математическими характеристиками параллелепипеда являются длины его ребер.
5. Призма
Призма — это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани параллелограммами, имеющими общие стороны с этими многоугольниками. Основными математическими характеристиками призмы являются площадь основания и высота.
Конус — это геометрическая фигура, полученная объединением всех лучей, исходящих из одной вершины конуса и проходящих через плоскую поверхность. Основными математическими характеристиками конуса являются радиус основания и высота.
7. Пирамида
Пирамида — это многогранник, основанием которого является произвольный многоугольник, а боковые грани являются треугольниками, имеющие общую вершину.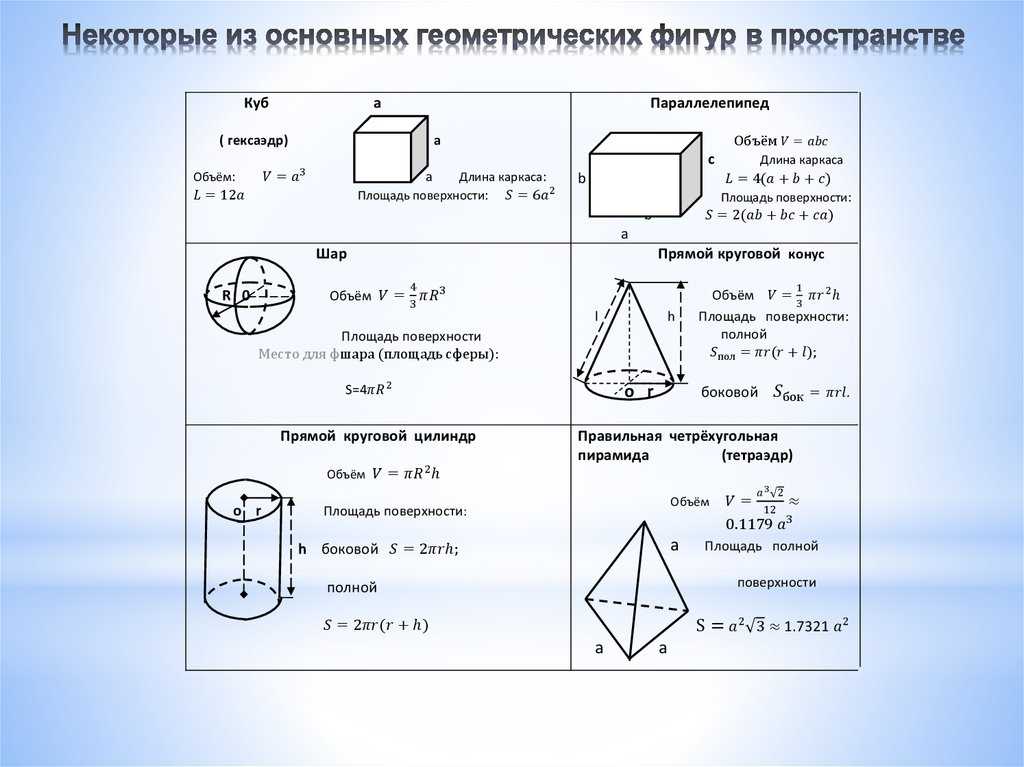
Основными математическими характеристиками пирамиды являются площадь основания и высота.
8. Цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются радиус основания и высота.
Быстро выполнить эти простейшие математические операции можно с помощью наших онлайн программ. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлены все геометрические фигуры, которые наиболее часто встречаются в геометрии для представления объекта или его части на плоскости или в пространстве.
Формула объема необходима для вычисления параметров и характеристик геометрической фигуры.
Объем фигуры — это количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т.
е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
| Фигура | Формула | Чертеж |
|---|---|---|
Параллелепипед . Объем прямоугольного параллелепипеда | ||
Цилиндр . Объем цилиндра равен произведению площади основания на высоту. Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту. | ||
Пирамида . Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS). | ||
Правильная пирамида — это пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание. | ||
Правильная треугольная пирамида — это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники. | ||
Правильная четырехугольная пирамида — это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники. | ||
Тетраэдр — это пирамида, у которой все грани — равносторонние треугольники. | V = (a 3 √2)/12 | |
Усеченная пирамида . Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S 1 (abcde), нижнего основания усеченной пирамиды S 2 (ABCDE) и средней пропорциональной между ними. | V= 1/3 h (S 1 + √S 1 S 2 + S 2) | |
Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. | ||
Конус — это тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. | ||
Усеченный конус получится, если в конусе провести сечение, параллельное основанию. | V = 1/3 πh (R 2 + Rr + r 2) | |
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра. | ||
Призма . Объем призмы равен произведению площади основания призмы, на высоту. |
Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 .Как научить детей геометрическому объему
Обновлено 24 апреля 2017 г.
Автор: Tabitha Burgtorf
Геометрический объем — это объем пространства внутри объемной формы. Чтобы научить геометрическому объему, сначала дайте своим ученикам конкретный опыт работы с манипуляторами, чтобы они могли полностью понять концепцию объема.
Затем направьте их, чтобы они открыли взаимосвязь между площадью поверхности и объемом, чтобы они могли предсказать формулу объема. Затем дайте им решить реальные проблемы.
Discover Volume
Попросите ваших учеников построить прямоугольную призму, соединяющую кубы. Длина должна быть шесть кубов, ширина четыре куба и высота один куб. Помогите им использовать то, что они знают о формуле площади поверхности, чтобы предсказать, сколько кубов они использовали, а затем попросите их посчитать кубы, чтобы убедиться, что их предсказание верно. Ответ должен быть 24 кубика.
Затем, , попросите их сохранить длину и ширину одинаковыми, но построить призму высотой в два куба. Они должны снова предсказать, сколько кубиков у них есть, и посчитать, чтобы убедиться, что они верны. Ответ должен быть 48 кубиков.
Продолжайте с тремя кубами высоты. Помогите им найти формулу объема призмы, которая равна длине х ширине х высоте или д х ш х в.
Дайте учащимся размеры нескольких прямоугольных призм, чтобы они могли попрактиковаться в нахождении объема.
Объем цилиндра
Покажите учащимся цилиндр и спросите их, сколько кубов в него поместится. Помогите им, когда они обнаружат, что объем цилиндра трудно измерить кубами, потому что кубы не вписаться в круглое пространство. 92 х час.
Дайте им несколько примеров, в которых есть измерение радиуса, и помогите им, когда они будут практиковаться.
Объем пирамиды
Покажите ученикам пирамиду. Спросите их, что сложного в предсказании объема пирамиды. Поскольку стороны пирамиды наклонены, вы не можете просто умножить площадь основания на высоту. Формула для объема пирамиды равна одной трети произведения основания на высоту или 1/3 ш х в. Покажите учащимся разницу между высотой, расстоянием по прямой от основания до точки и наклонной длиной.
Применение в реальной жизни
Учащиеся гораздо лучше запомнят, как решать геометрический объем, если увидят его применение в реальной жизни. Принесите мешок с горшечной почвой, на которой указан объем в кубических футах, и цилиндрический цветочный горшок. Спросите учащихся, как они могут вычислить, сколько цветочных горшков может заполнить мешок с горшечной почвой.
Во-первых, попросите их составить план, используя имеющиеся у них знания об объеме. Объясните, что оценка допустима, если цветочный горшок слегка наклонен. Обеспечьте их необходимыми инструментами, такими как измерительная лента и калькуляторы.
После составили план, пусть сами делают замеры и открытия. Ключевым здесь является процесс, а не получение точного правильного ответа. Для дополнительного занятия предоставьте им размеры садового ящика и посмотрите, сколько мешков с горшечной почвой им нужно, чтобы заполнить ящик.
определение объема+(геометрия) по The Free Dictionary
Объем+(геометрия) — определение объема+(геометрия) по The Free DictionaryОбъем+(геометрия) — определение объема+(геометрия) по The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
Возможно, Вы имели в виду:
Пожалуйста, попробуйте слова отдельно:
объем геометрия
Некоторые статьи, соответствующие вашему запросу:
Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.
Полный браузер ?
- ▲
- Том второй (EP)
- Объем под поверхностью
- Уникальный ключ тома
- единица объема
- единица объема
- единица объема
- единица объема
- единица объема
- единица объема
- единица объема
- метр единицы измерения объема
- метр единицы измерения объема
- Единицы объема, используемые в нефтяной инженерии
- Индекс изменчивости объема
- объемная скорость
- Объемная скорость коронарного кровотока
- объемный вентилятор
- объем против массы
- Объемная вязкость
- Средневзвешенная цена по объему
- Средневзвешенная цена по объему
- Средневзвешенные цены по объему
- Гиполимнетический кислород, взвешенный по объему
- Объемно-взвешенная скользящая средняя
- объемная доходность
- объемная доходность
- объемная доходность
- объемная доходность
- объемная доходность
- объемная доходность
- объем+(геометрия)
- Объем, площадь, двугранный угол
- Громкость, вкл.
