| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.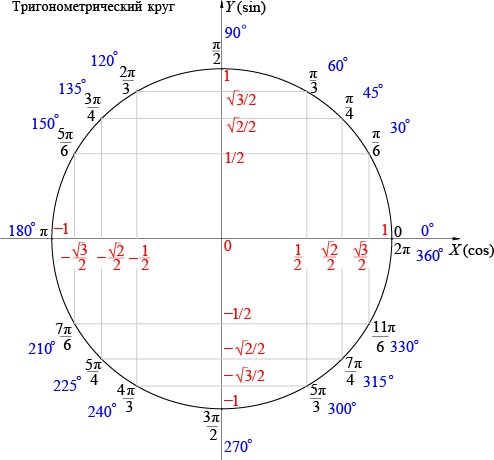 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.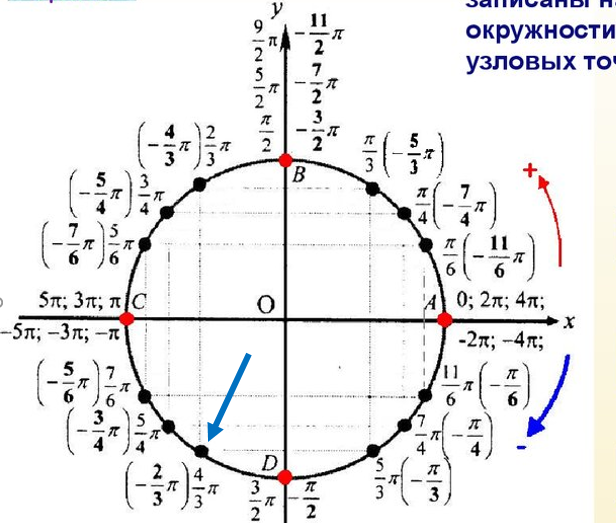 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.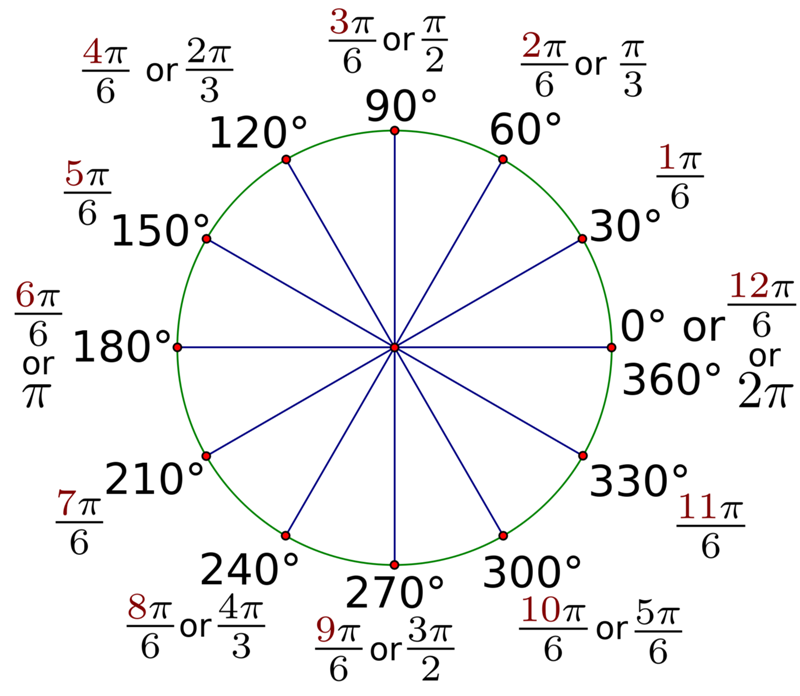 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.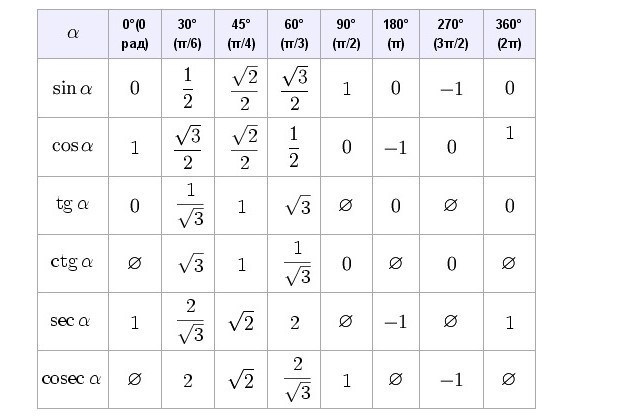 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.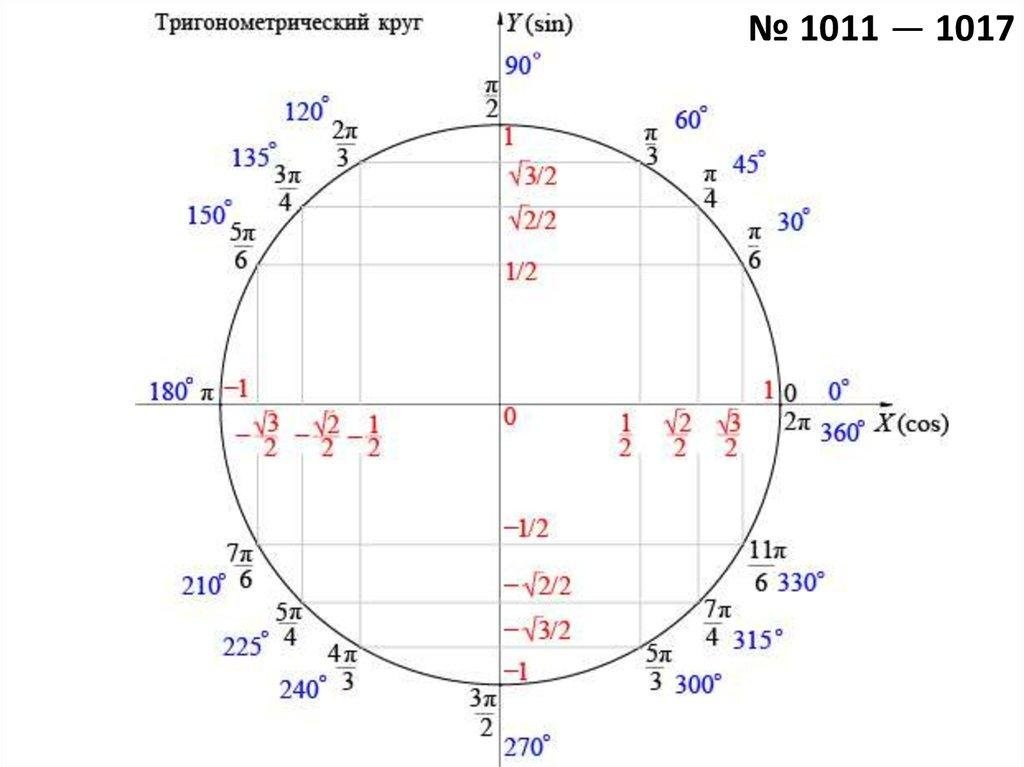 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Что такое число Пи 3 14?
Что такое число Пи 3 14?
Число Пи – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,.. Обозначается греческой буквой — π. Некоторые могут подумать, раз это отношение обозначается греческой буквой, стало быть, его вывел некий греческий математик.
Некоторые могут подумать, раз это отношение обозначается греческой буквой, стало быть, его вывел некий греческий математик.
Для чего используется число Пи?
Со школьной скамьи все помнят о числе Пи, которое обозначается греческой буквой π и используется в геометрических формулах – например для вычисления длины окружности. Число π – самая часто используемая постоянная величина в мире, обозначающая отношение длины круга к длине его диаметра.
Как получилось число Пи?
воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году. Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.
Что такое пи равно 3 14?
Число пи выражает отношение длины окружности к диаметру и приблизительно равно 3,14. Впервые его обозначил греческой буквой π англичанин Уильям Джонс в труде «Обозрение достижений математики», напечатанном в 1706 году.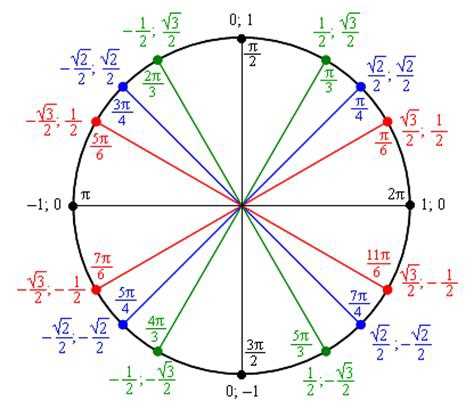 … То, что отношение длины окружности к ее диаметру — число постоянное, известно с незапамятных времен.
… То, что отношение длины окружности к ее диаметру — число постоянное, известно с незапамятных времен.
Что больше 3124 или 3 14?
Число Пи = 3, cliffffy4h и 6 других пользователей посчитали ответ полезным!
Что такое число Пи полностью?
Число Пи – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,.. Обозначается греческой буквой — π.
Как еще называют число Пи?
Сегодня она называется числом «пи» и обозначается греческой буквой π. Сейчас известно, что это число приблизительно равно 3,
Какой конец у числа Пи?
Число пи иррационально, то есть его значение не может быть точно выражено в виде дроби m/n, где m и n — целые числа. Его десятичное представление никогда не заканчивается и не является периодическим. Кроме того, это трансцендентное число, то есть оно не может быть корнем какого-либо многочлена с целыми коэффициентами.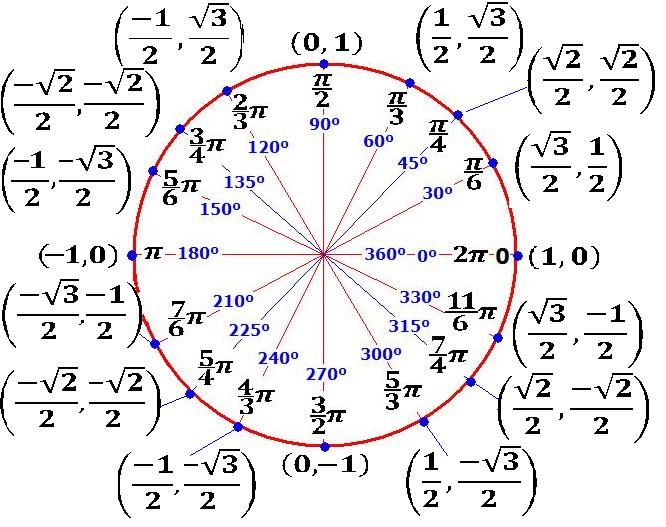
Какая последняя цифра числа Пи?
Последняя цифра числа Пи — двойка.
Кто первый открыл число Пи?
Леонарда Эйлера
Что такое число Пи в физике?
π Число «Пи» – математическая константа, выражающая отношение длины окружности к длине ее диаметра. В цифровом выражении Пи начинается как 3,141592… и имеет бесконечную математическую продолжительность.
Чему равен синус числа Пи?
| значение угла α (градусов) | значение угла α в радианах (через число пи) | sin (синус) |
|---|---|---|
| 180 | π | 0 |
| 210 | 7π/6 | -1/2 |
| 240 | 4π/3 | -√3/2 |
| 270 | 3π/2 | -1 |
Чему равен синус 40 градусов?
Таблица СИНУСОВ для углов от 0° до 360° градусов
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | грех(пи/6) | ||
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.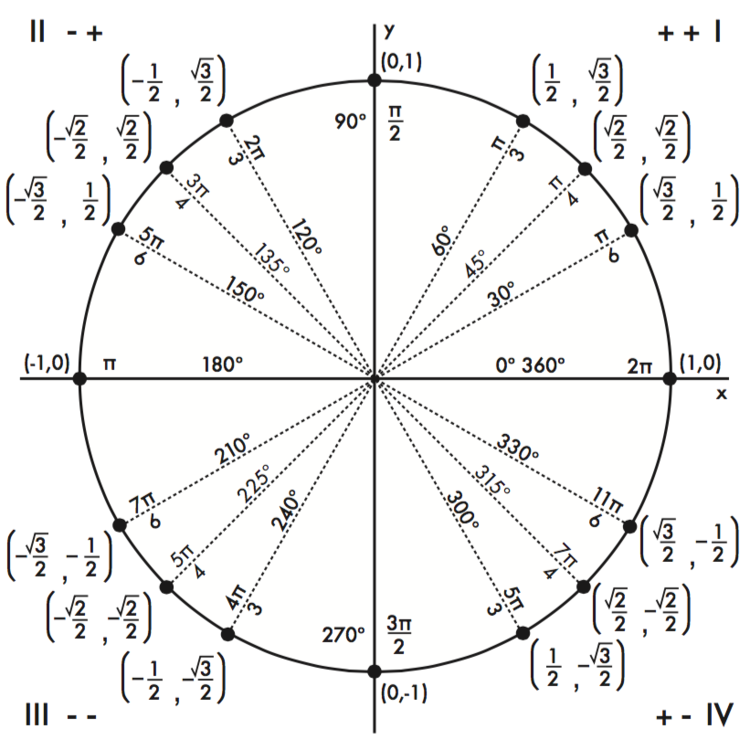 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| Ср, 15 марта 2006 г.  Почему пи равно 3 Саймон [Козенс] также спросил меня, почему получилось число около 3, а не чем около 5 или 57, и там я был в гораздо более шатком положении. Я сделал у меня не было никаких умных идей, и все, что я мог сделать, это перечислить кучу вещей, которые, казалось, имели отношение к этому вопросу. Вероятно, оно появится здесь в будущей статье.1. Самый очевидный факт, который я придумал, заключался в следующем: Впишите правильный шестиугольник в единичную окружность. Такой шестиугольник очевидно, имеет периметр 6. Окружность проходит через те же шесть точек, но вместо того, чтобы идти прямым путем между ними, маршрут окольный, поэтому его периметр чуть больше 6. Следовательно, число пи немного больше 3,9.0910 Несколько человек написали мне, чтобы указать на это, и никто не указал на что-то другое, что, я думаю, подтверждает мое утверждение что это наиболее очевидный из имеющихся фактов.  Также, как я ответил М. Козенсу: Я не знаю, как вычислить периметр круга не рассматривая его как предельный случай многоугольника с множеством очень коротких сторон, поэтому я думаю, что любое исследование того, почему число пи равно 3,14 и не что-то другое должно будет начаться здесь.Если вы описываете шестиугольник вокруг круга, немного основного геометрия показывает верхнюю границу: π < 2√3. С помощью полигонов чем больше сторон, тем лучше оценки. С квадратом вы получите только что 2√2 < π < 4, например; шестиугольник улучшает это до 3 < π < 2√3. Около 2200 лет назад Архимед сделал расчет для 96-угольников и получил правильное значение до двух знаков после запятой места: 3 + 10/71 < π < 3 + 1/7. (Здесь возникает интересный вопрос: с 96-угольником можно было бы ожидать
границы включают такие вещи, как √3, как это делает шестиугольник.
Откуда берутся странные дроби 10/71 и 1/7? Ответ: граница
типа 2√3 имел ограниченное применение у греков, потому что
заменяет плохо понятное число π другим
плохо понятное число √3. Во всяком случае, другие предметы, которые я отправил М. Козенсу, были: . 2. Кратчайшая кривая, которая может охватывать единицу площади, имеет длину 2π. (Или наоборот, наибольшая площадь, которую может охватить единица путь равен 1/4π.)Это снова будет сильно зависеть от евклидовой метрики. я не знаю, как расширить общую метрику, чтобы получить меру площади; на самом деле, я еще не уверен в разумном способе задать вопрос. я надо подумать. (Да, я уверен, что кто-то уже изучил это, и я мог бы просто посмотреть это, но я получу намного больше от ответ, если я сам подумаю над вопросом какое-то время перед заглянув в конец книги. 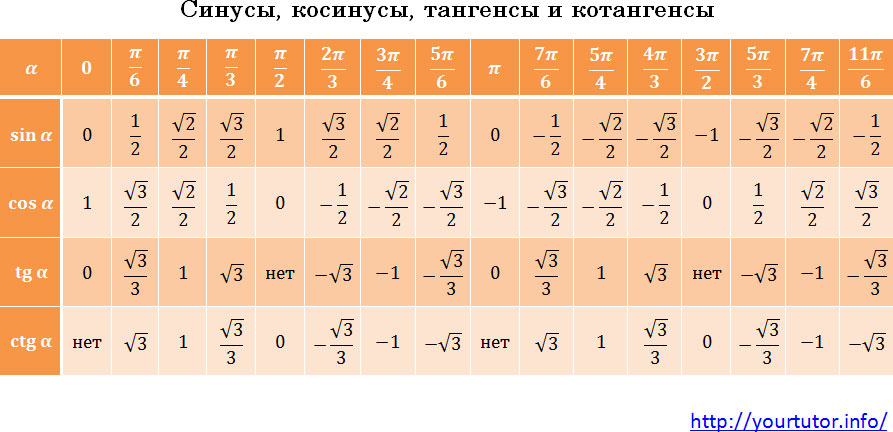 Нет, как говорится, царской дороги
к геометрии.) Нет, как говорится, царской дороги
к геометрии.)«Бессловесное» доказательство теоремы Пифагора показывает, что у меня будет быть очень осторожным в расширении от длины к площади в Манхэттен: (Подробнее о метриках, включая манхэттенскую метрику, см. мою статью о метрические пространства.)Независимый метрики, это доказательство показывает, что две маленькие белые штуковины слева имеют ту же площадь, что и большая белая штуковина справа. В евклидовом пространстве это равенство устанавливает теорема Пифагора. На Манхэттене этого лучше не делать, потому что теорема Пифагора неверна на Манхэттене; на диаграмме, c не равно √( a 2 + б 2 ), но к а + б . Кажется, я убедил себя, что квадрат со стороной s в
Площадь Манхэттена по-прежнему составляет s 2 . И я уверен
что эти две белые штуковины слева — квадраты, и поэтому
районы а 2 и б 2 соответственно. Но это означает, что большая белая вещь справа имеет площадь a 2 + b 2 , и поэтому не квадрат и не имеет площади c 2 как помечены, потому что c = a + b , и c 2 не равно a 2 + б 2 . Квадраты на Манхэттене должны иметь ребра, параллельные оси координат. Я думаю. Я не знаю, куда идти дальше; может быть Я разберусь с этим сегодня по пути домой с работы. Следующий пункт мой второй любимый, после наблюдение о вписанном шестиугольнике: 3. Если положить на стол копейку, то можно получить максимум шесть другие пенни, чтобы коснуться его в то же время. Это тесно связано с тем, что 6 — это наибольшее целое число, меньшее 2π. Аналогичные результаты справедливы и в более высоких измерениях. Площадь сферы равно 4π или примерно 12,5; вы можете получить 12 сфер, чтобы коснуться другой сферы одновременно, но не 13.Это дело сфер, соприкасающихся с центральной сферой, известно как «проблема с номером поцелуев»; мы говорим, что «поцелуи число в два измерения» равно 6, а «число поцелуев в трех измерениях» равно 12. После этого пункта я был в значительной степени вне круга связанных с ним фактов. Так что я сменил тактику и попытался взглянуть на вещи, которые казались совершенно не связанные с кругами: 4. &pi удовлетворяет уравнению:М. Козенс заметил, что вы можете получить π, используя интегральное исчисление для вычислить площадь единичного круга: Но он жаловался (я думаю, справедливо), что это не дает вам никакого понимания сути дела.x — x 3 /6 + x 5 /120 — x 7 /5040 + … = 0Это было единственное, что я мог придумать, что казалось одновременно и довольно элементарный, и в то же время хороший способ получить π не вставив его для начала. 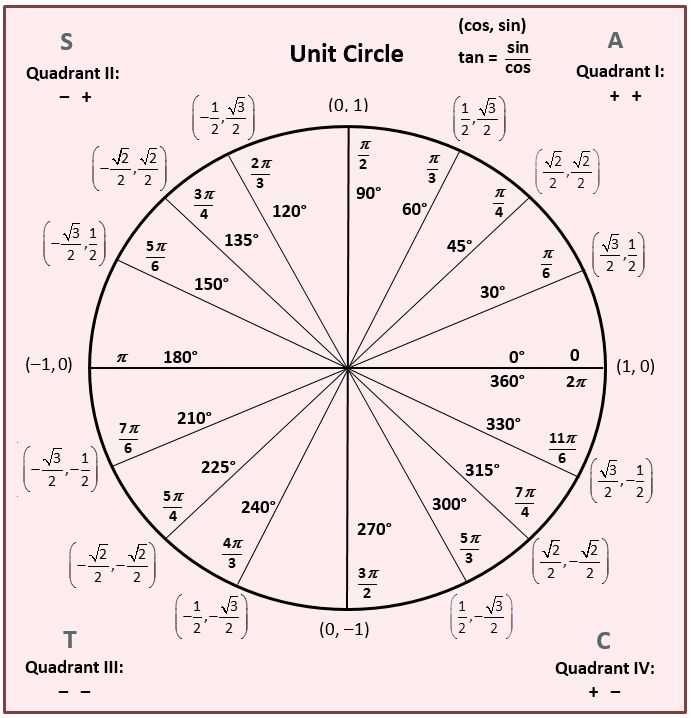 все, что касается того, откуда берется π, потому что π прокрадывается как
arccos(1) при подстановке триггера. А так как π было
один из основных ингредиентов рецепта функции косинуса
начнем с того, что все, что произошло, это то, что вы получили то, что вы положили
дюймов. (Функция косинуса связывает длину дуги окружности с
длина связанного прямого отрезка. π попадает туда, потому что
отрезок имеет длину 0, когда дуга имеет длину π/2. Но тогда ты
вернемся к загадке, почему полная дуга окружности имеет длину
2π.) Интеграл получает π из функции косинуса, и
функция косинуса получила его непосредственно из длины
длина окружности. все, что касается того, откуда берется π, потому что π прокрадывается как
arccos(1) при подстановке триггера. А так как π было
один из основных ингредиентов рецепта функции косинуса
начнем с того, что все, что произошло, это то, что вы получили то, что вы положили
дюймов. (Функция косинуса связывает длину дуги окружности с
длина связанного прямого отрезка. π попадает туда, потому что
отрезок имеет длину 0, когда дуга имеет длину π/2. Но тогда ты
вернемся к загадке, почему полная дуга окружности имеет длину
2π.) Интеграл получает π из функции косинуса, и
функция косинуса получила его непосредственно из длины
длина окружности.Так что я начал пытаться придумать способы получить π, которые, казалось бы, ничего общего с кругами. Бесконечный многочлен был первым вещь, которую я придумал. Это может быть связано с круги, но не легко, что я считаю преимуществом. Тебе нужно чтобы иметь возможность связать его с кругами, иначе он не говорит вам что-нибудь о том, почему периметр круга пи.Я просто знаю, что какой-то умный человек жаждет указать что полином — это просто разложение Маклорена для sin (π), и конечно, я так придумал. (Что, вы думали, что это было просто удачная догадка?) А вот если бы вы не знали про Маклорена серии, вы можете быть весьма шокированы, обнаружив, что π было нулем это выражение. Сроки уже начинают уменьшаться время, когда вы доберетесь до π 9 /362880, поэтому, несмотря на трансцендентности π мы имеем 9полином й степени которого почти нуль, многочлен, основанный на элементарных понятиях, в в котором нет явного круга. Пункт 5 была проблема с иглой Бюффона, но я сказал что появление π там оказалось очевидным следствием того, что он выглядит как периметр единичного круга, так что давайте перейдем к к следующему. 6. Вероятность того, что два
случайно выбранные целые числа взаимно просты
6/π 2 . Это выводит π, никуда его не вставляя очевидно, но не кажется мне элементарным. И как ты можно связать это с кругом, я понятия не имею.Но теперь отношения с кругами кажутся мне несколько яснее. Вы можете превратить это в геометрическую задачу следующим образом: Вы стоите у истоков, глядя на бесконечный яблоневый сад. Существует дерево в ( a , b ) для каждой пары целые числа. Деревья имеют нулевую ширину, но когда одно дерево прямо за другим деревом оно заблокировано и его не видно. какая часть деревьев видна? Существует одно видимое дерево для каждого (рационального) направления, в котором вы можете смотреть в. Таким образом, между точками на окружности есть связь и видимые деревья. (Отступление: если деревья имеют положительный диаметр, то только конечное число
видны из начала. Если диаметр d , пусть
количество видимых деревьев равно v ( d ). Оценка против . я
думаю, что эта проблема все еще открыта. 7. Следующим пунктом, который я упомянул, был что 1 + 1/4 + 1/9 + … = π 2 /6. Это, вероятно, как-то связано с садом. Может случиться так, что хорошее понимание этой идентичности приведет к к хорошему пониманию того, почему π немного больше 3. Это может также быть, что он имеет некоторые отношения с кругом. Но я сказал М. Козенс, если бы он хотел, чтобы кто-то понял это, «вам действительно нужно поговорить с кем-то, кто имеет опыт в аналитической теории чисел, а не мне». Я буду настаивать на этом. 8.
Наконец, я указал, что π появляется не только в кругах; Это
также появляется в сферах. Например, объем единичного шара равен
4π/3. К этому времени я чистил ствол. Симпатично
очевидно, что π попадет в сферы, потому что сферы
просто стопки кругов, а число π уже находится в кругах. Добавление
вместе кучу отрезков, которые не имеют отношения больше
сложно, чем квадратный корень, это одно; удивительно видеть
π выйти из этого. Но сложив вместе кучу кругов, которые
все включают π, и получить что-то, что снова включает π,
не удивительно. |

 Итак, Архимед заменил сурд на
рациональные приближения; например, вначале он заменяет √3
с рациональным приближением 265/153. (См. Др.
Подробное объяснение расчета Архимеда, данное Чаком Линдси, и мое объяснение того, откуда берется число 265/153.)
Я хотел бы пройти через это
и посмотреть, что он придумал бы, если бы он сделал точную
расчет, но это займет у меня некоторое время.)
Итак, Архимед заменил сурд на
рациональные приближения; например, вначале он заменяет √3
с рациональным приближением 265/153. (См. Др.
Подробное объяснение расчета Архимеда, данное Чаком Линдси, и мое объяснение того, откуда берется число 265/153.)
Я хотел бы пройти через это
и посмотреть, что он придумал бы, если бы он сделал точную
расчет, но это займет у меня некоторое время.)
 Но это
не должны быть слишком тесно связаны, потому что я думаю, что пункты 1-3
наверное исчерпывают то, что можно получить прямо с кругов.
Но это
не должны быть слишком тесно связаны, потому что я думаю, что пункты 1-3
наверное исчерпывают то, что можно получить прямо с кругов.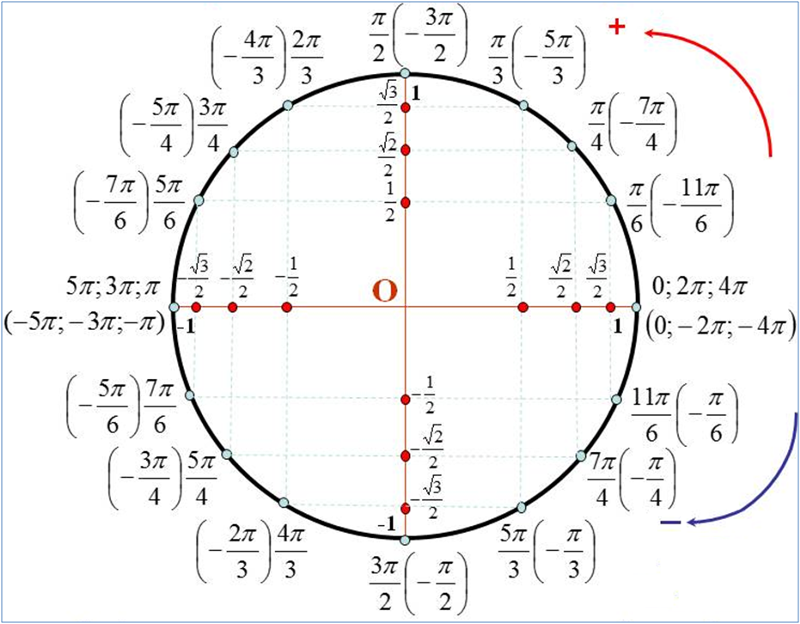 Я сказал:
Я сказал: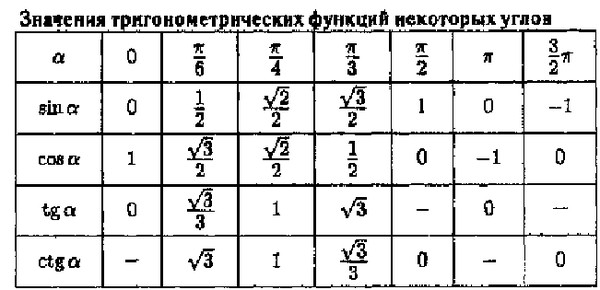 )
)