Геометрия параллелограмм решение задач: Решение основных задач по теме «Параллелограмм»

Содержание

Задачи по геометрии параллелограмм. | Геометрия

Добрый день, дорогие друзья!

Сегодня мы продолжим решение задач из сборника под редакцией М.И. Сканави.
И на этот раз мы будем решать задачи по геометрии параллелограмма.
Понятно, что прежде, чем приступать к решению таких задач, надо понимать, что такое параллелограмм и какие у него есть свойства.
Параллелограмм — выпуклый четырёхугольник, у которого противоположные стороны попарно параллельны.
У параллелограмма противоположные стороны и противоположные углы равны;
диагонали его делят параллелограмм на 2 равных треугольника,
а сами диагонали точкой пересечения делятся пополам.
И сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
Вот в основном те свойства, которые в первую очередь необходимы для понимания и решения задач по геометрии параллелограмма. А теперь задачи.
Задача 1. Периметр параллелограмма равен 90 см, а его острый угол равен 60°.
Диагональ параллелограмма делит его тупой угол на части в отношении 1:3.

Найти стороны параллелограмма.
Решение: Если угол А равен 60°, то угол В, лежащий рядом с ним , будет равен 180-60=120°.
Но диагональ BD делит его в соотношении 1:3, или на 4 равные части.
Получается, что одной части принадлежит 120:4 = 30°.
Следовательно, диагональ BD делит угол В на 2 угла 30° и 90°.
По рисунку угол 1 — прямой. Треугольник ABD — прямоугольный.
И угол 2 в треугольнике равен 30º, как накрест лежащий при параллельных прямых AB и CD и секущей BD.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы. Получается, что АВ=1/2 AD.
Теперь составляем уравнение для периметра.
AB+BC+CD+AD=90
1/2AD+AD+1/2AD+AD= 90
3AD=90 AD=30 AB=1/2*30 = 15.
Ответ: стороны параллелограмма равны 30 см и 15 см.

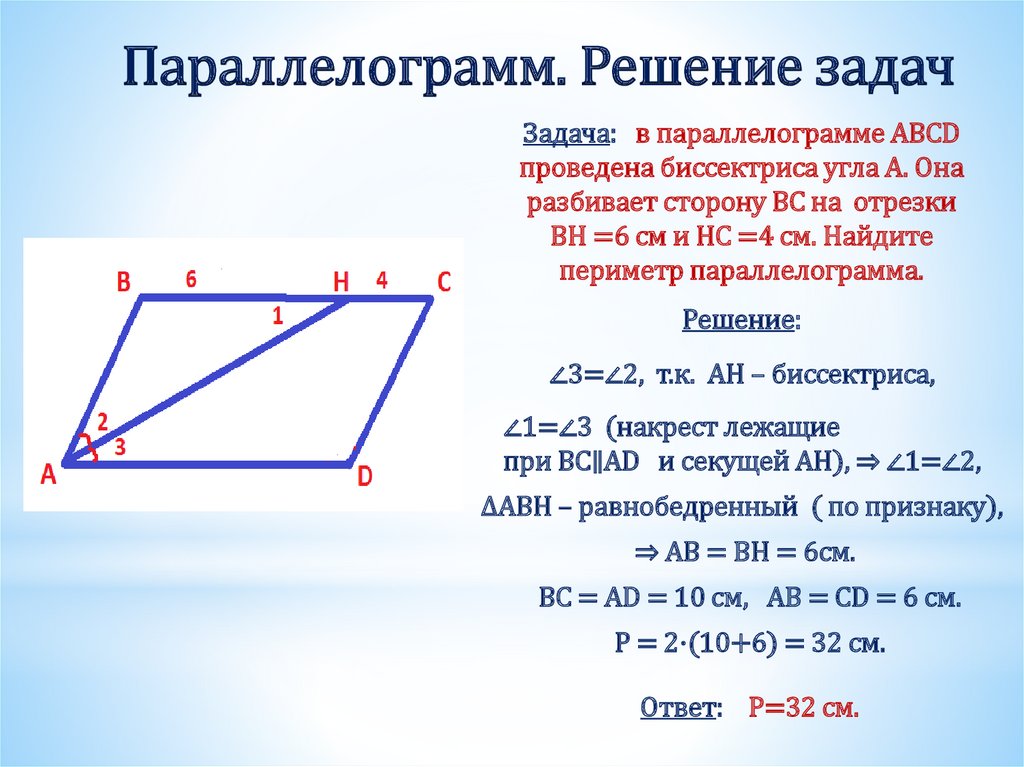
Задача 2. Биссектриса острого угла параллелограмма делит его диагональ на отрезки длиной 3,2 см и 8,8 см.

Найти стороны параллелограмма, если его периметр равен 30 см.
Решение: Мы знаем, что биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные сторонам угла.

А именно, AB:AD = BO:OD, но BO и OD равны соответственно 3,2 см и 8,8 см.
Поэтому, можно принять, что АВ = 3,2х, а AD равно 8,8х.
Противоположные стороны параллелограмма равны.
Периметр это есть сумма всех сторон параллелограмма.
Составляем уравнение: 3,2х+8,8х+3,2х+8,8х = 30 24х = 30 х = 30/24 = 5/4.
Мы нашли коэффициент пропорциональности Х=5/4.
Отсюда, сторона АВ = 3,2х = 3,2 * 5/4 = 4 см.
Сторона AD равна 8,8х = 8,8 * 5/4 = 11 см.
Ответ: стороны параллелограмма равны 4 см, 4 см, 11 см, 11 см.

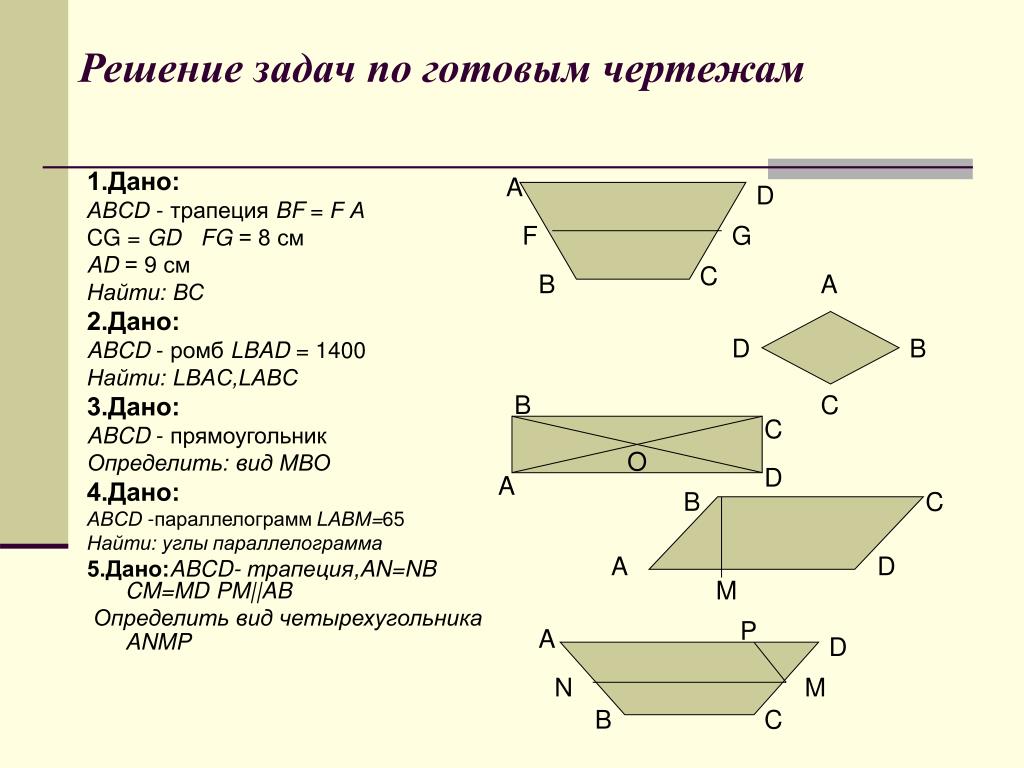
Задача 3. Параллелограмм с периметром 44 см разделён диагоналями на 4 треугольника.

Разность между периметрами двух смежных треугольников равна 6 см.
Найти стороны параллелограмма.
Решение: Рассмотрим два треугольника, лежащих выше диагонали d.
Периметр первого равен b+c+d.
Периметр второго равен a+c+d.
Разность периметров двух треугольников равна 6 см.
Составляем уравнение:
a+c+d — (b+c+d) = a+c+d-b-c-d = a-b = 6.

Получилось, что разность двух сторон параллелограмма равна 6 см.
Второе уравнение составляем из свойства периметра параллелограмма:
a+b+a+b = 44
2a+2b=44
a+b=22.
Получили систему двух уравнений с двумя неизвестными:
a — b = 6
a + b = 22             Решим её методом сложения. Сложим левые и правые части уравнений. Получим:
a — b + a + b = 6 + 22     2a = 28    a = 14.
a — b = 6   b = a — 6 = 14 — 6 = 8.
Ответ: Стороны параллелограмма равны 14 см, 14 см, 8 см, 8 см.

Задача 4. Перпендикуляр, опущенный из вершины параллелограмма на его диагональ, делит эту диагональ на отрезки АМ и МС длиной 6 см и 15 см соответственно.

Разность сторон параллелограмма равна 7 см.
Найти длины сторон и диагонали параллелограмма.
Решение: Примем сторону AB за a, сторону BC за  b.
Из двух прямоугольных треугольников АВМ и ВМС выразим равный для них катет ВМ по теореме Пифагора.
АВ² — АМ² = ВС² — МС².
Подставляем вместо сторон известные выражения:
а² — 6² = b² — 15² или   15² — 6² = b² — а²   (b — а) (b + а) = (15 — 6) (15 + 6),
но b — а = 7
7 (b + а) = 9 * 21   b + a = 9 * 3 = 27.

Имеем систему двух уравнений с двумя неизвестными, как в задаче 3.
b + a = 27
b — а = 7 Отсюда получаем 2b = 34 b = 17, a = 27 — 17 = 10.
Теперь, зная стороны параллелограмма, мы можем найти высоту ВМ.
ВМ² = 10² — 6² = 64. Отсюда ВМ = 8 см.
А теперь, из прямоугольного треугольника ВМО находим ВО.
ВМ = 8 см,
МО = АО — АМ = АС/2 — АМ = (6+15)/2 — 6 = 21/2 — 6 = 10,5 — 6 = 4,5 см.
По теореме Пифагора находим ВО.
ВО² = 8² + 4,5² = 64 + (9/2)² = 64 + 81/4 = 337/4. Или ВО = √337/2.
Поскольку BD в 2 раза больше, чем ВО, то её длина будет равна √337.
Ответ: Длины сторон параллелограмма 17 см, 17 см, 10 см, 10 см. Длина диагонали √337.

На сегодня всё. В следующий раз мы продолжим решение задач по геометрии из «Сборника для поступающих во ВТУЗы». Успехов!

Презентация к уроку решения задач «Свойства и признаки параллелогрмма»

Свойства и признаки параллелограмма.

(решение задач)

Свойства параллелограмма используем, если известно, что четырехугольник-параллелограмм.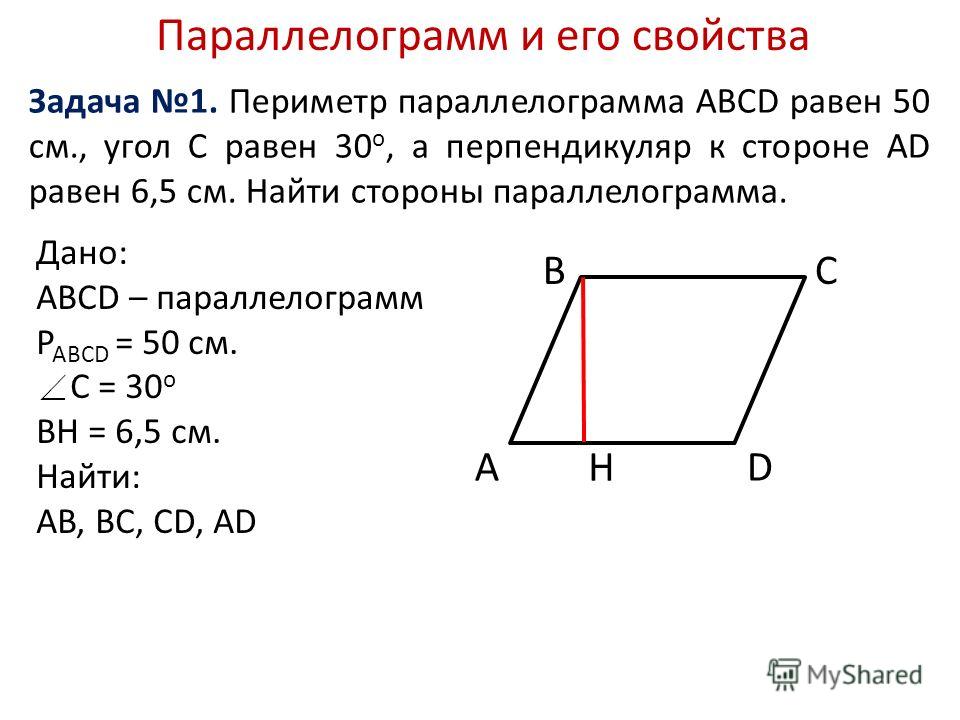

Признаки параллелограмма используем, если доказываем, что четырехугольник –параллелограмм.

У параллелограмма : 1.противолежащие стороны равны;

2.противолежащие углы равны;

Четырехугольник-параллелограмм , если: 1.противолежащие стороны равны;

2.противолежащие углы равны;

3.диагонали пересекаются и точкой пересечения делятся пополам

3.диагонали пересекаются и точкой пересечения делятся пополам;

4.противолежащая пара сторон одновременно параллельна и равна

Задача № 1

Дано: ABCD – параллелограмм

Найди: С, В, D,

AB, BC

19м

51 °

15м

Задача № 2

Дано: BCEF – параллелограмм

Найди : E, F

34°

Задача № 3

30°

11см

7см

Дано: CDEK – параллелограмм, DF-

высота

Найди: СК, ЕК

Задача № 4

Дано: DEKN — параллелограмм

Доказать: EF = ON

Задача № 5

⁽

Дано: АО=ОС,

Доказать: АВСD–

параллелограмм

⁾

Задача № 6

Дано: ABDE – параллелограмм

Доказать: АСDF — параллелограмм

Задача №7

Дано: ABCD – параллелограмм

Доказать: EBF D — параллелограмм

Самостоятельная работа

Вариант 1

Вариант 2

1. Периметр параллелограмма равен 46 см. Найдите стороны параллелограмма, если сумма трех его сторон равна 42 см.

1. Периметр параллелограмма равен 56 см. Найдите стороны параллелограмма, если сумма двух его сторон равна 20 см.

2. Сумма двух углов параллелограмма равна 84 °. Найдите углы параллелограмма.

2. Сумма трех углов параллелограмма равна 254 °. Найдите углы параллелограмма.

Автор шаблона и презентации Конева Н. А., учитель математики МБОУ БГО СОШ №4

г. Борисоглебск

Свойства параллелограмма

Свойства параллелограмма перечислены ниже. Мы будем использовать параллелограмм ABCD, чтобы показать эти свойства.

Свойство №1

Противоположные стороны параллелограмма равны.

Длина AB равна длине DC.
Длина BC равна длине AD.

Свойство №2

Противоположные углы параллелограмма равны.

Угол А равен углу С
Угол B = угол D

Свойство №3

Диагонали параллелограмма делят друг друга пополам.

Диагональ AC (красная линия) пересекает и делит пополам диагональ BD (красная линия) в точке E.

Свойство №4

Смежные углы являются дополнительными или в сумме составляют 180 градусов.

Угол A + угол B = 180 градусов
Угол B + угол C = 180 градусов
Угол C + угол D = 180 градусов
Угол D + угол A = 180 градусов

Свойство №5

Каждая диагональ параллелограмма превращает параллелограмм в 2 конгруэнтных треугольника.

Треугольник ABC равен или идентичен треугольнику ADC.
Треугольник BCD равен или идентичен треугольнику BAD.

Использование свойств параллелограмма для решения математических задач

Пример #1 : Используйте приведенный ниже параллелограмм, чтобы найти длину отрезка BC и отрезка AD.

Так как противоположные стороны параллелограмма равны, длина отрезка BC равна длине отрезка AD.

4x — 10 = 3x + 5.

Вычесть 3x с каждой стороны

4x — 3x — 10 = 3x — 3x + 5

Упростить каждую сторону

x — 10 = 5

Прибавить 100 к обеим сторонам 900 уравнение.

x — 10 + 10 = 5 + 10

Упрощение

x = 15

BC = AD = 4x — 10 = 4 x 15 — 10 = 60 — 10 = 50

50 Пример 6 параллелограмм ниже, чтобы найти длину отрезка AC и отрезка BD.

Так как диагонали параллелограмма делят друг друга пополам, мы получаем следующие результаты:

Длина отрезка AI равна длине отрезка CI

Длина отрезка BI равна длине отрезка DI

Это приводит к решению системы линейных уравнений

2y — 4 = 4x

y = x + 4

Подставить x + 4 вместо y в 2y — 4 = 4x

2(x + 4) — 4 = 4x

Распределить

2x + 8 — 90 3x 4x Упростить

2x + 4 = 4x

Вычесть 2x с каждой стороны

2x — 2x + 4 = 4x — 2x

Упрощение

4 = 2x

x = 4/2 = 2

y = x + 4 = 2 + 4 = 6

AC = AI — 4 + 4x = 2×6 — 4 + 4×2 = 12 — 4 + 8 = 16

BD = BI + DI = x + 4 + y = 2 + 4 + 6 = 12

Почему важна геометрия? (И как вы можете извлечь пользу?)
16, 22 декабря 08:47
Почему важна геометрия? Геометрия — это не только рисование фигур. Его практическое применение безгранично. Посмотрите, как геометрия может помочь улучшить вашу жизнь.
Подробнее
Что такое единичный круг? Определение и тригонометрические значения
10, 22 декабря 18:21
Определение единичной окружности и важных тригонометрических функций. Используйте единичный круг для получения важных тригонометрических значений.
Подробнее

Урок КАК РЕШАТЬ задачи на углы параллелограмма

Этот урок (КАК РЕШАТЬ задачи на углы параллелограмма — Примеры) был создан пользователем ikleyn(46846) : Посмотреть исходный код, Показать
Об ikleyn :

В этом уроке вы найдете решения некоторых типичных задач на углы параллелограмма.

Для решения такого рода задач используйте основные свойства параллелограмма:
— противоположные углы параллелограмма равны
(см.

урок Противоположные углы параллелограмма по теме Параллелограммы раздела Геометрия на этом сайте), а
— сумма последовательных углов параллелограмма равна 180
(см. урок Последовательные углы параллелограмма в той же теме того же раздела на этом сайте).

Проблема 1
В параллелограмме один угол имеет градусную меру 73. Найдите другие углы параллелограмма.

Раствор
Так как сумма последовательных углов параллелограмма равна 180, два других последовательных угла параллелограмма имеют угловую меру
180- 73 = 107.

Так как противоположные углы параллелограмма равны, то угол, противоположный данному углу 73, также имеет угловую меру 73.

Ответить . Остальные углы параллелограмма имеют угловую меру 107 (последний угол), 73 (противоположный угол) и 107 (второй последовательный угол).

Проблема 2
В параллелограмме один угол в 28 раз больше другого.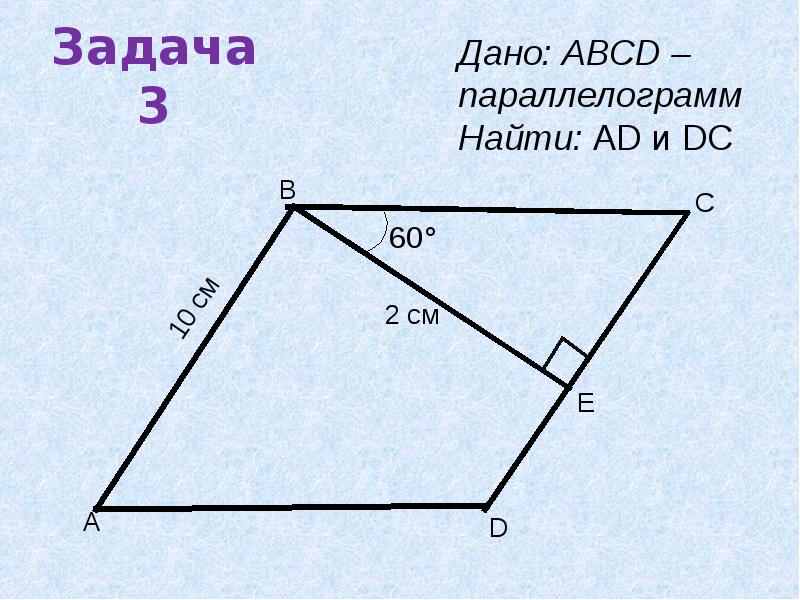
Найдите углы параллелограмма.

Решение
Пусть x будет угловой мерой (в градусах) первого из двух заданных углов.
Тогда угловая мера второго угла равна x — 28 в соответствии с условием задачи.

Поскольку данные два угла параллелограмма не равны, они не противоположны. Следовательно, они последовательные.

Следовательно, вы можете написать уравнение
x + (x-28) = 180
, говорящее, что сумма последовательных углов параллелограмма равна 180.

Упростите и решите это уравнение:
2x — 28 = 180,
2x = 180 + 28,
2x = 208,
x = 104.

Таким образом, первый угол имеет угловую меру 104.
Тогда два последовательных угла равны 180 — 104 = 76.
Можно проверить, что первый угол на 28 больше, чем последующие, так как это утверждается условием :
104 — 76 = 28.

Ответ . Углы параллелограмма равны 108, 76, 108 и 76.

Проблема 3
В параллелограмме один угол в четыре раза больше другого.
Найдите углы параллелограмма.

Раствор
Пусть x будет угловой мерой (в градусах) меньшего из двух заданных углов.
Тогда мера большего угла равна 4x в соответствии с условием задачи.

Следовательно, вы можете написать уравнение
x + 4x = 180
, говорящее, что сумма последовательных углов параллелограмма равна 180.

Упростите и решите это уравнение:
5x = 180,
x = 36.

Таким образом, меньший угол имеет угловую меру 36.
Тогда больший угол имеет угловую меру 4*36 = 144 в соответствии с условием задачи.
Вы можете проверить, что сумма этих двух последовательных углов равна 180:
36 + 144 = 180.

Ответить . Углы параллелограмма равны 36, 144, 36 и 144.

Мои другие уроки по параллелограммам на этом сайте
— В параллелограмме каждая диагональ делит его на два равных треугольника.