Гиперболическая функция ее свойства и график: The page cannot be found

23. Свойства (четность, периодичность, монотонность, ограниченность) и графики функций.

1 . Функция , определенная на множестве , называется четной, если выполняются условия и нечетной, если выполняются условия и .

График четной функции симметричен относительно оси , а нечетной – относительно начала координат.

Например, четные функции; а нечетные функции; функции общего вида, т.е. не четные и не нечетные.

2 . Функция , определенная на множестве , называется периодической на этом множестве, если существует такое число , что при каждом значение и При этом число называется периодом функции. Если — период функции, то ее периодами будут также числа , где Так, для периодами будут числа Основной период (наименьший положительный) – это период . Вообще обычно за основной период берут наименьшее положительное число , удовлетворяющее равенству

3. Функция y=f(x) называется

возрастающей на некотором интервале если для любых х из этого интервала большему значению аргумента соответствует большее значение функции, т.е. при имеет место неравенство f(x1)<f(x2) .

Функция y=f(x) называется невозрастающей, если на некотором интервале имеет место неравенство f(x1)≥f(x2) .

Функцияy=f(x) называется убывающей на некотором интервале, если для любых х из этого интервала большему значению аргумента соответствует меньшее значение функции, т.е. при имеет место неравенство f(x1)>f(x2) .

Функция y=f(x) называется неубывающей, если на некотором интервале имеет место неравенство f(x1)≤f(x2) .

Функции только убывающие или только возрастающие называются монотонными.

4. Функцию , определенную на множестве , называют ограниченной на этом множестве, если существует такое число , что для всех выполняется неравенство (короткая запись: , , называется ограниченной на , если ).

Отсюда следует, что график ограниченной функции лежит между прямыми и .

24. Гиперболические функции, их свойства и графики.

К ним относятся:

— гиперболический косинус и

— гиперболический синус.

С помощью этих функций можно определить еще 2 функции:

— гиперболический тангенс и

— гиперболический котангенс.

Функции определены, очевидно, для всех значений . Функция же определена всюду, за исключением точки .

Из определения функций и следуют соотношения, аналогичные соотношениям между соответствующими тригонометрическими функциями:

Название «гиперболические функции» объясняется тем, что функции и играют ту же роль для параметрического представления гиперболы

какую тригонометрические функции и — для параметрического представления окружности

Производные гиперболических функций определяются формулами:

25.

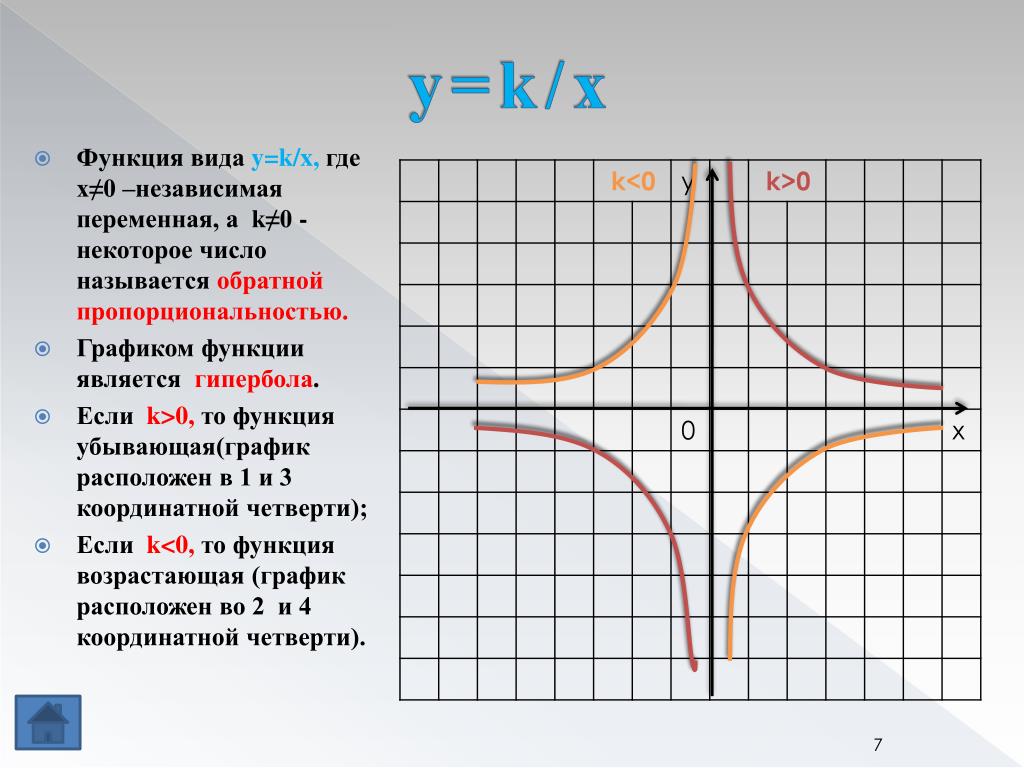Числовые последовательности. Предел числовой последовательности.

Определение. Если каждому натуральному числу n поставлено в соответствие число х_n, то говорят, что задана последовательность

x_1, х₂, …, х_n= {x_n}

Общий элемент последовательности является функцией от n.

x_n = f(n)

Таким образом последовательность может рассматриваться как функция порядкового номера элемента.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Пример. {x_n

} = {(-1)ⁿ} или {x_n} = -1; 1; -1; 1; …

{x_n} = {sinn/2} или {x_n} = 1; 0; 1; 0; …

Для последовательностей можно определить следующие операции:

1. Умножение последовательности на число m: m{x_n} = {mx_n}, т. е. mx₁, mx₂, …

2. Сложение (вычитание) последовательностей: {x_n}  {y_n} = {x_n  y_n}.

3. Произведение последовательностей: {x_n}{y_n} = {x_ny_n}.

4. Частное последовательностей: при {y_n}  0.

43. Показательные и логарифмические выражения. Показательная функция, гиперболические функции

Показательной функцией Называется функция

где

Основные свойства показательной функции

1. Область определения:

2. Множество значений:

3. Четность и нечетность: не обладает свойством четности.

4. Периодичность: непериодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства: Функция положительна для

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: если функция возрастает для всех если – убывает для

9. Точки пересечения с осями координат: пересекает ось Оу в точке ось Ох не пересекает.

10. Асимптоты: прямая Y = 0 (ось Ох) является горизонтальной асимптотой.

11. График функции для A > 1 изображен на рис. 6.1, для – на рис. 6.2.

 

Рис. 6.1 Рис. 6.2

Из свойств функции следует: неравенство равносильно неравенствам:

1) если

2) если

Показательная функция с основанием Е, где Е – иррациональное число Е = 2,718281…, называется Экспонентой, пишут или

Через показательные выражения с основанием Е определяются Гиперболические функции.

Гиперболическим синусом называется функция

Основные свойства гиперболического синуса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: нечетная.

4. Периодичность: непериодическая.

5. Нули функции:

6. Промежутки знакопостоянства: Функция отрицательна для положительна – для

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция возрастает для всех

9. Точки пересечения с осями координат:

10. Асимптоты: асимптот не имеет.

11. График функции изображен на рис. 6.3.

Гиперболическим косинусом называется функция

Основные свойства гиперболического косинуса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: четная.

4. Периодичность: непериодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства: Функция положительна для

7.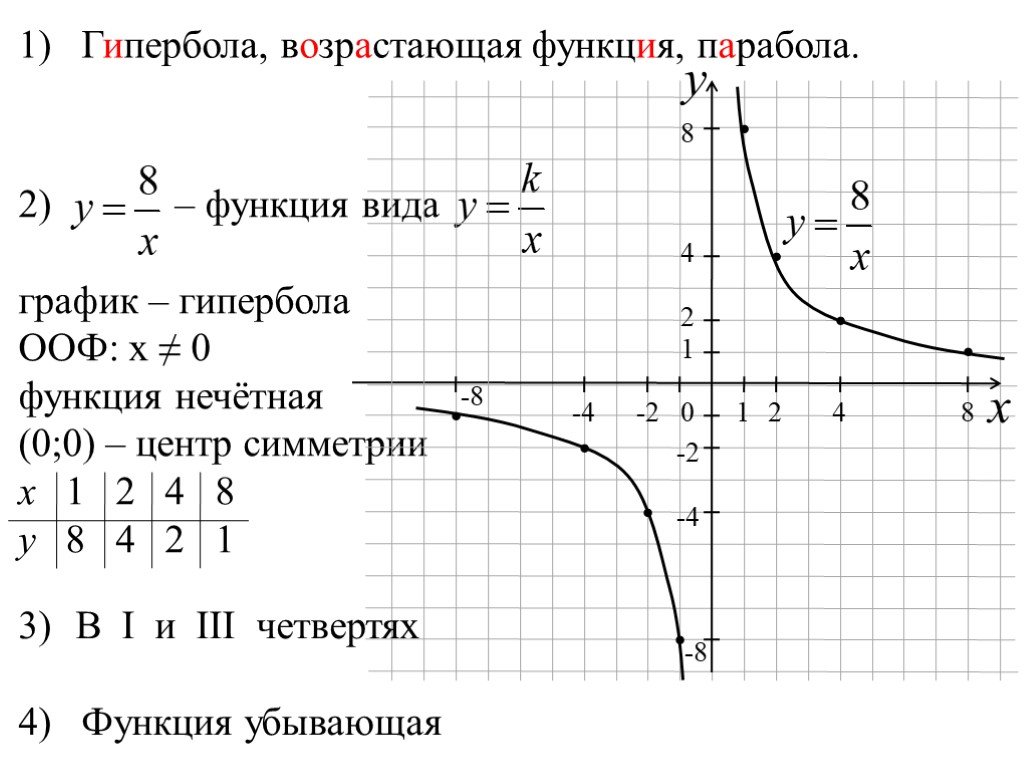 Наибольшее и наименьшее значения: наименьшее значение, равное 1, функция принимает при

8. Промежутки возрастания и убывания: функция убывает при возрастает при

9. Точки пересечения с осями координат: пересекает ось Оу в точке ось Ох не пересекает.

10. Асимптоты: асимптот не имеет.

11. График функции изображен на рис. 6.4.

 

Рис. 6.3 Рис. 6.4

Гиперболические тангенс и котангенс определяются через отношение гиперболических синуса и косинуса.

Гиперболическим тангенсом Называется функция

т. е.

Основные свойства гиперболического тангенса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: нечетная.

4. Периодичность: непериодическая.

5. Нули функции:

6. Промежутки знакопостоянства:

Функция отрицательна для положительна для

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция возрастает для

9. Точки пересечения с осями координат:

10. Асимптоты: имеет горизонтальные асимптоты и

11. График функции изображен на рис. 6.5.

 

Рис. 6.5

Гиперболический котангенсом называется функция

т. е.

Основные свойства гиперболического котангенса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: нечетная.

4. Периодичность: непериодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства: Функция отрицательна для положительна для

7.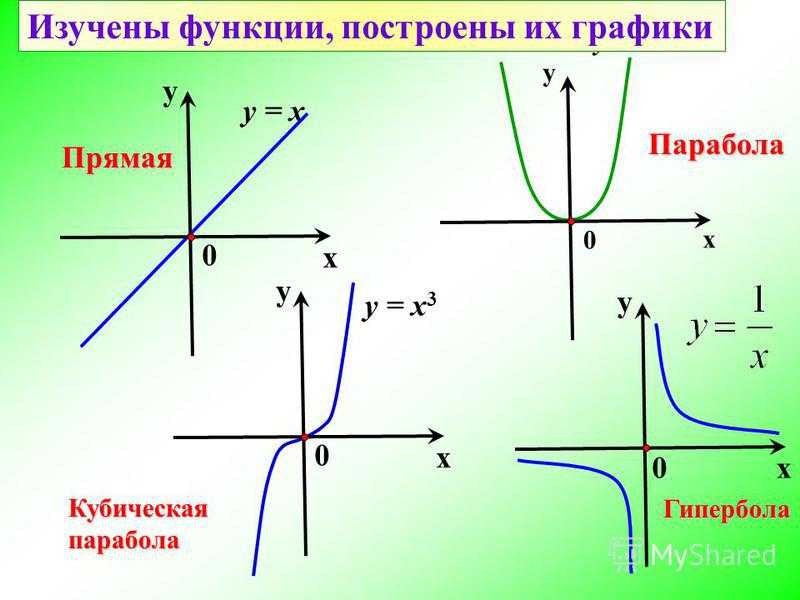 Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция убывает для

9. Точки пересечения с осями координат: нет.

10. Асимптоты: имеет горизонтальные асимптоты и

11. График функции изображен на рис. 6.6.

 

Рис. 6.6

Пример 1. Сравнить числа:

1) и 2) и

3) и

Решение. 1) Преобразуем числа к одному основанию:

Так как и функция монотонно возрастает, то следовательно,

2) Преобразуем числа:

Так как и функция монотонно убывает, то следовательно,

3) Преобразуем числа:

Так как и функция монотонно возрастает, то тогда и

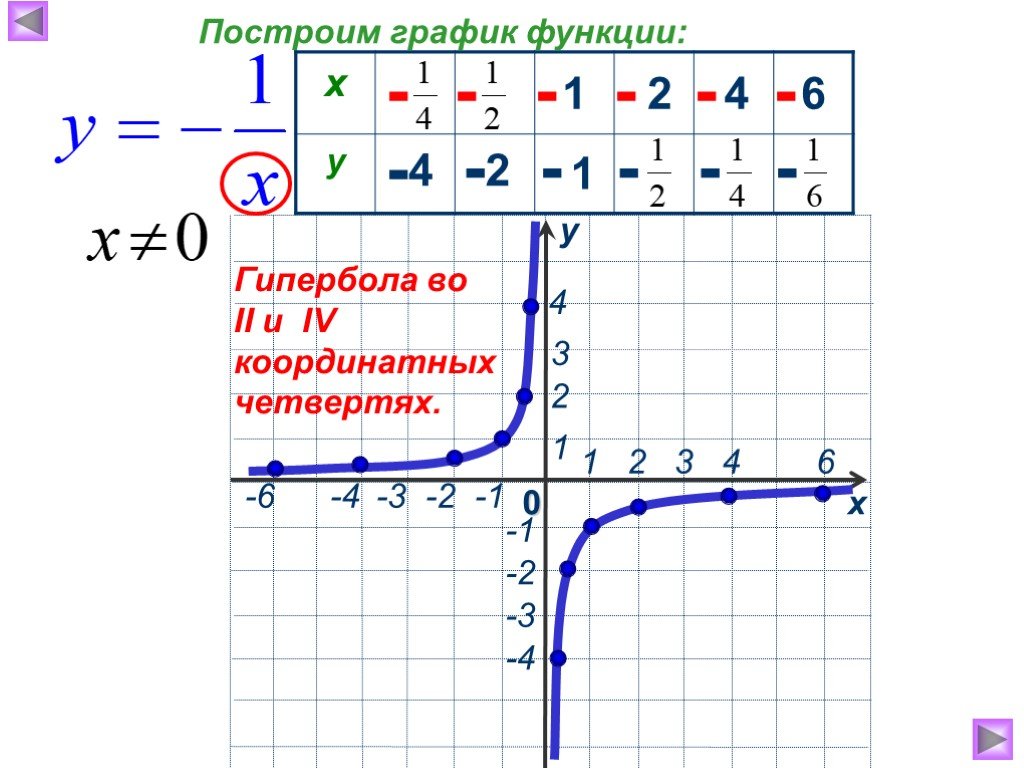
Пример 2. Построить график функции:

1) 2)

Решение.

1) Строим график функции

График функции получаем из предыдущего путем смещения его на 3 единицы влево по оси Ох и на 4 единицы вниз по оси Оу.

Для построения графика заданной функции оставляем ту часть графика функции которая лежит над осью Ох и на оси Ох. Ту часть графика, которая расположена ниже оси Ох, отображаем в верхнюю полуплоскость симметрично относительно оси Ох (рис. 6.7).

Рис. 6.7

2) Строим график функции (см. рис. 6.5).

График функции получаем из предыдущего путем смещения его на 2 единицы вниз вдоль оси Оу.

Для построения графика заданной функции оставляем ту часть графика функции которая лежит правее оси Оу и на оси Оу. Часть графика, которая лежит левее оси Оу, отбрасываем, а оставшуюся часть отображаем в левую полуплоскость симметрично оси Оу (рис. 6.8).

Рис. 6.8

Пример 3. Доказать тождество

Решение.

< Предыдущая		Следующая >

Гиперболические функции — свойства, производные, графики и формулы

В математике гиперболические функции аналогичны тригонометрическим функциям, но определяются с помощью гиперболы, а не окружности.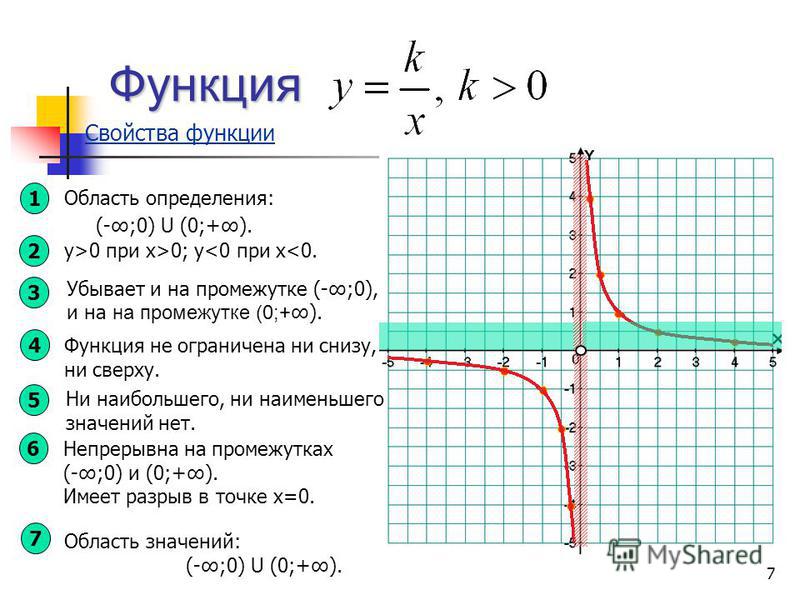 Точно так же, как точки (sin t, cost t) в тригонометрии образуют единичный круг с радиусом, точки (sin t, ch t) образуют правую половину единичной параболы.

Кроме того, производные sin(t) и cos(t) в тригонометрии равны cos(t) и -sin(t) соответственно, производные sinh(t) и ch(t) в гиперболических функциях равны ch (t) + sh(t).

Гиперболические функции проявляются при вычислении углов и расстояний в гиперболической геометрии. Они также проявляются в решениях многих линейных дифференциальных уравнений, кубических уравнений и уравнений Лапласа в декартовых координатах.

Здесь мы обсудим гиперболические тригонометрические функции, гиперболические тригонометрические формулы, гиперболические тригонометрические тождества, свойства гиперболических функций, производные гиперболических функций, интегрирование гиперболических функций и т. д. |

Свойства гиперболических функций

Свойства гиперболических функций аналогичны свойствам тригонометрических функций. Ниже приведены важные свойства гиперболических функций.

Cosh 2y = ch²y + sh² y

Гиперболические функции также могут быть получены из тригонометрических функций с комплексными аргументами. 9{2}г}\]

Интегрирование гиперболических функций

Поскольку гиперболические функции определяются через eˣ и e⁻ˣ, мы можем легко вывести правила их интегрирования. Ниже приведены все шесть интеграций гиперболических функций:

• ∫ Coshy DY = Sinh Y + C

• ∫ Sinhy DY = Cosh Y + C

• ∫ SECH²Y DY = TANH Y + C

• ∫ SECH²Y = TANH Y + C

• ∫ SECH²Y = TANH Y + C

• ∫ SECH²Y = TANH Y + C

• ∫ SECH²Y = TANH Y + C

• ∫ SECH²Y. ∫ csch²y dy = — cth y + C

• ∫ sech y tanh y dy = — sech y + C

• ∫ csch y cth y dy = — csch y + C

Графики гиперболической функции

Гипролические графики функции приведены ниже:

Гиперболическая синусная функция (SINH X)

Домен: R

Диапазон: R

Функция гиперболической косицирации (COSH X)

Domain: R

Функция (Cosh X)

: R

.

Диапазон: (1 + ∞)

Функция гиперболического тангенса (Tanh x)

Домен: R

Диапазон:   (-1 + 1)

Гиперболический котангенс x

Домен: (- ∞, 0) U (0 + ∞)

Диапазон:   (- ∞ — 1)(1 + ∞)

Гиперболическая секущая x

Домен: R

Диапазон:   ( 0, 1)

Гиперболический косеканс x

Область: ( -∞ , 0) U (0 + ∞)

Диапазон:   ( -∞ , 0)(0 + -∞)

Гиперболические тригонометрические функции

Гиперболическая идея тригонометрических функций параметрических уравнений для единичного круга (x = стоимость y и y = sin t) к параметрическому уравнению гиперболы, которое дает следующие два уравнения гиперболы: 9{-a}}{2}\]

Очень важный факт, который следует учитывать, заключается в том, что гиперболические тригонометрические функции рассматривают площадь в качестве своего аргумента (известного как «гиперболический угол»), как показано ниже: 

Гиперболический тригонометрический Формулы

Основные гиперболические тригонометрические формулы для sh x и ch x определяются показательной функцией eˣ и ее обратной показательной функцией e⁻ˣ.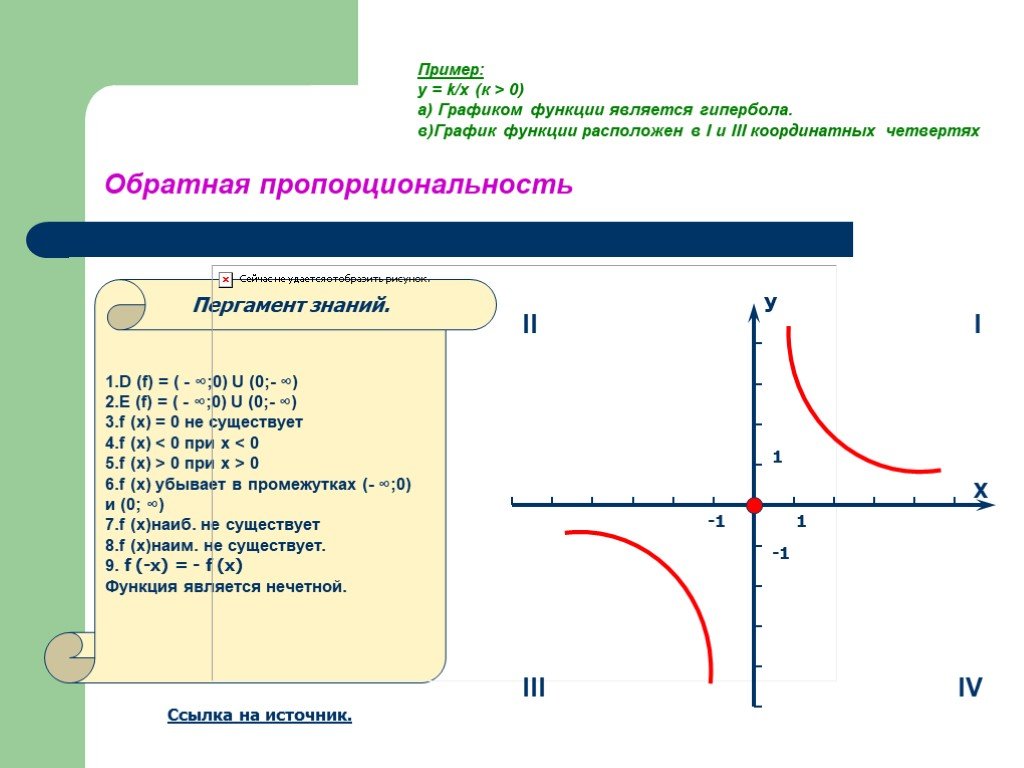 Здесь e — постоянная Эйлера. Давайте разберемся с гиперболическими тригонометрическими формулами одну за другой. 9{-a}}\]

4. Гиперболическая секущая функция

Гиперболическая функция f(x) = sech x определяется как:

Sech (x) = \[\frac{1}{cosh x}\]

5. Функция гиперболического косеканса

Гиперболическая функция f(x) = csch x определяется как:

Csch (x) = \[\frac{1}{sinh x}\ ]

6. Функция гиперболического котангенса

Гиперболическая функция f(x) = cth x определяется как: 9{-а}}\]

Гиперболические тригонометрические тождества

Гиперболические тригонометрические тождества аналогичны стандартным тригонометрическим тождествам и могут быть поняты из уравнений, приведенных ниже: )

Tanh y = -tanh(-y)

Sech y = sech(-y)

Coth y = -coth(-y)

у)

Sinh (α + λ) = sh α ch λ + ch a sinh λ

Sinh (α — λ) = sh α ch b — ch sh λ

Cosh (α + λ) = ch α ch λ + ch sh λ

ch (α — λ) = ch α ch λ — ch ch λ

Sinh ² y = \[\frac{-1+cosh(2y)}{2} \]

Sinh (2y) = 2 sinh ² y ch ² y

Cosh ² y = \[\frac{1+cosh(2y]

COSH (2Y) = COS ² Y + SIN ² Y

COSH ² (Y) — SINH ² (Y) = 1

66. HANH 2

66. 269 26 29 29 29 29 29 29 29. ) + Сч ² (у) = 1

Кот ² (у) — Ксч ² (у) =1

Применение гиперболических функций

Существует множество приложений гиперболических функций;

Например, компания планирует построить висячий мост, который протянется между баскетбольной ареной и бейсбольным стадионом до другой стороны железнодорожной линии в определенном городе. Центр этого моста будет подвешен между двумя бетонными опорами, которые находятся на расстоянии 280 футов друг от друга и имеют высоту 80 футов. Трос, удерживающий мост, должен находиться ровно в 30 футах над железнодорожными путями и посередине моста, то есть должен провисать ровно на 50 футов.

Готфрид Лейбниц и Кристиан Гюйгенс в 1691 году вычислили, что любой кабель, который висит под действием гравитационной силы, должен иметь форму графика

y(x) = a ch (x/a) + b

Эта форма стали называть контактной сетью. Здесь параметр a представляет собой отношение натяжения троса к плотности троса. Параметр здесь используется для представления смещения по вертикали, если это необходимо.

В этой ситуации могут возникнуть два вопроса. Во-первых, какими значениями должны обладать параметры a и b, чтобы контактная сеть соответствовала ограничениям, заданным размещением бетонных опор и нижней точкой троса.

Чтобы найти значения a и b, нам придется рассмотреть два разных вопроса. Как мы уже знаем, y(0) = 30. Это гарантирует наличие достаточного зазора над железнодорожными путями. Нам также дан тот факт, что y(140) = 80, так как трос прикреплен к столбу высотой 80 футов и находится на расстоянии 140 футов от самой нижней точки, то есть от центра. Таким образом,

30= a ch (0/a) + b

80 = a ch (140/a) +b

Поскольку ch(0)= , мы можем легко упростить первое уравнение как 30= a + b . Подставляя это новое производное уравнение во второе уравнение, мы получаем 80 = а(140/а) + 30-а.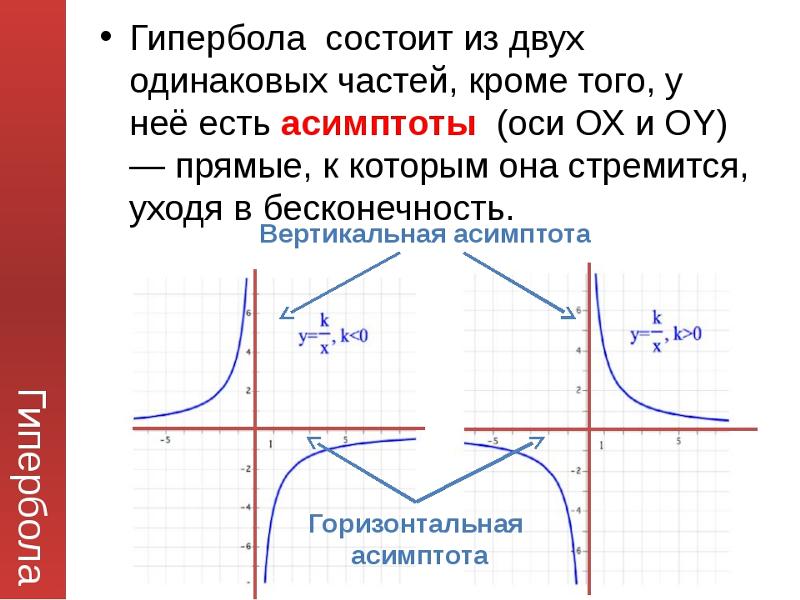 9{-x}}{2}\]

Cosh x — Sinh x = e⁻ˣ       (2)

Объединяя уравнение (1) и уравнение (2), получаем

e±x  =  ch x ± sh x

Что эквивалентно формуле Эйлера гиперболической функции.

6.9: Расчет гиперболических функций

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

10838

• OpenStax
• OpenStax

Цели обучения

• Применять формулы для производных и интегралов гиперболических функций.
• Применить формулы для производных обратных гиперболических функций и связанных с ними интегралов.
• Опишите общие прикладные условия контактной кривой. 9{−x}] \\[4pt] &=\cosh x. \end{align*} \nonumber \]

  Аналогично,

  \[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]

  Мы суммируем формулы дифференцирования для гиперболических функций в таблице \(\PageIndex{1}\).

  Таблица \(\PageIndex{1}\): производные гиперболических функций

  \(f(x)\)	\(\dfrac{d}{dx}f(x)\)
  \(\шп х\) 92\, х\)
  \(\text{sech} х\)	\(−\text{sech}\, x \tanh x\)
  \(\text{csch} х\)	\(−\text{csch}\, x \coth x\)

  Давайте сравним производные гиперболических функций с производными стандартных тригонометрических функций. Сходства много, но и различий тоже. Например, производные функций синуса совпадают:

  \[\dfrac{d}{dx} \sin x=\cos x \nonumber \]

  и

  \[\dfrac{d}{dx} \sinx x=\cosh x. \nonumber \]

  Производные функций косинуса, однако, отличаются знаком:

  \[\dfrac{d}{dx} \cos x=-\sin x, \nonumber \]

  но

  \ [\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]

  Продолжая изучение гиперболических функций, мы должны помнить об их сходствах и различиях со стандартными тригонометрическими функциями. Эти формулы дифференцирования гиперболических функций непосредственно приводят к следующим интегральным формулам. 92)+С. \end{выравнивание*}\]

  б. Пусть \(u=\ch x\). Затем \(du=\sinh x\,dx\) и

  \[\begin{align*} \int \tanh x \,dx &=\int \dfrac{\sinh x}{\cosh x}\ ,dx \\[4pt] &=\int \dfrac{1}{u}du \\[4pt] &=\ln|u|+C \\[4pt] &= \ln|\cosh x|+C .\end{align*}\]

  Обратите внимание, что \(\cosh x>0\) для всех \(x\), поэтому мы можем исключить знаки абсолютного значения и получить

  \[\int \tanh x \ ,dx=\ln(\cosh x)+C. \nonumber \]

  Упражнение \(\PageIndex{2}\)

  Вычислите следующие интегралы: 92(3x) \, dx=\dfrac{\tanh(3x)}{3}+C\)

  Исчисление обратных гиперболических функций

  Глядя на графики гиперболических функций, мы видим, что при соответствующих ограничениях диапазона все они имеют обратные функции. Большинство необходимых ограничений диапазона можно различить при внимательном рассмотрении графиков. Области и диапазоны обратных гиперболических функций приведены в таблице \(\PageIndex{2}\).

  Таблица \(\PageIndex{2}\): домены и области значений обратных гиперболических функций 9х)+С\)

  Приложения

  Одно из физических применений гиперболических функций включает подвесные кабели. Если кабель одинаковой плотности подвешен между двумя опорами без какой-либо нагрузки, кроме собственного веса, кабель образует кривую, называемую контактной сетью . Высоковольтные линии электропередач, цепи, висящие между двумя столбами, и нити паутины образуют контактную сеть. На следующем рисунке показаны цепи, свисающие с ряда столбов.

  Рисунок \(\PageIndex{3}\): Цепи между этими столбами имеют форму контактной сети. (кредит: модификация работы OKFoundryCompany, Flickr)

  Гиперболические функции можно использовать для моделирования контактных сетей. В частности, функции вида \(y=a\cdot \cosh(x/a)\) являются цепными. На рисунке \(\PageIndex{4}\) показан график \(y=2\cosh(x/2)\).

  Рисунок \(\PageIndex{4}\): Функция гиперболического косинуса образует контактную цепь.

  Пример \(\PageIndex{5}\): использование контактной сети для определения длины кабеля ≤15\), где \(x\) измеряется в футах. Определите длину кабеля (в футах). 9{15}_{−15}\\[4pt] &=10\left[\sinh\left(\dfrac{3}{2}\right)-\sinh\left(-\dfrac{3}{2} \right)\right]\\[4pt] &=20\sinh \left(\dfrac{3}{2}\right) \\[4pt] &≈42,586\,\text{ft.} \end{align *}\]

  Упражнение \(\PageIndex{5}\):

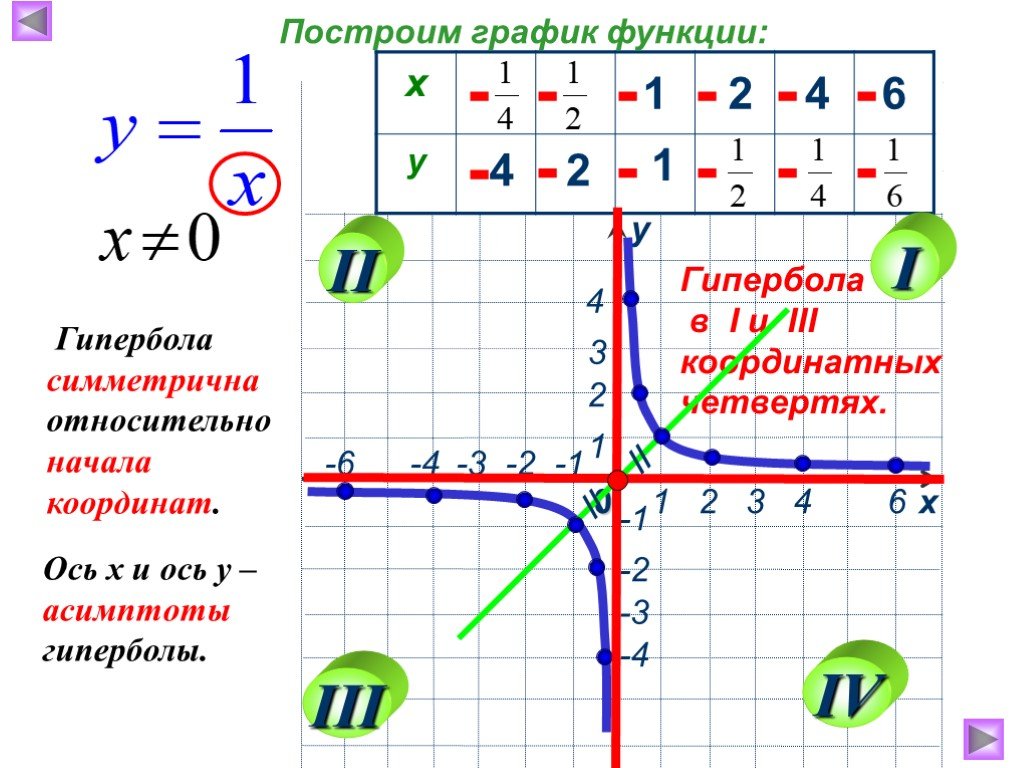
  Предположим, что подвесной трос имеет форму \(15 \cosh (x/15)\) для \(−20≤x≤20\). Определите длину кабеля (в футах).

  No related posts.

  Добавить комментарий Отменить ответ

  Ваш адрес email не будет опубликован. Обязательные поля помечены *

  Комментарий *

  Имя *

  Email *

  Сайт