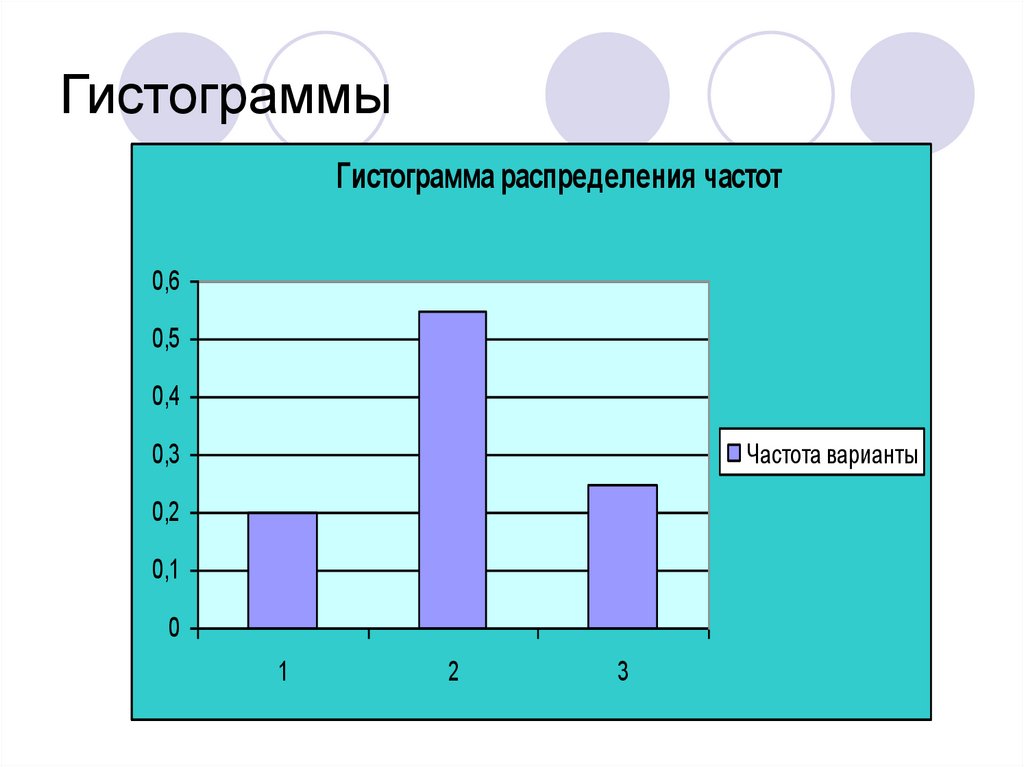
Полигон и гистограмма частот и частостей (относительных частот). Кумулятивная кривая (кумулята). Огива. Теория вероятностей и математическая статистика
Для наглядности строят различные графики статистического распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
Полигон
Полигоном частот называют ломаную, отрезки которой соединяют точки . Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты . Такие точки соединяют отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Такие точки
соединяют
отрезками прямых и получают полигон частот.
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Пример 1
Построить полигон частот и полигон относительных частот (частостей):
| 2 | 7 | 8 | 15 | 16 | 17 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим относительные частоты (частости):
| Относительные частоты, | ||
| 2 | 15 |
0. 075 075
|
| 7 | 35 | 0.175 |
| 8 | 64 | 0.320 |
| 15 | 55 | 0.275 |
| 16 | 21 | 0.105 |
| 17 | 10 | 0.050 |
| Итого | 200 | 1.000 |
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.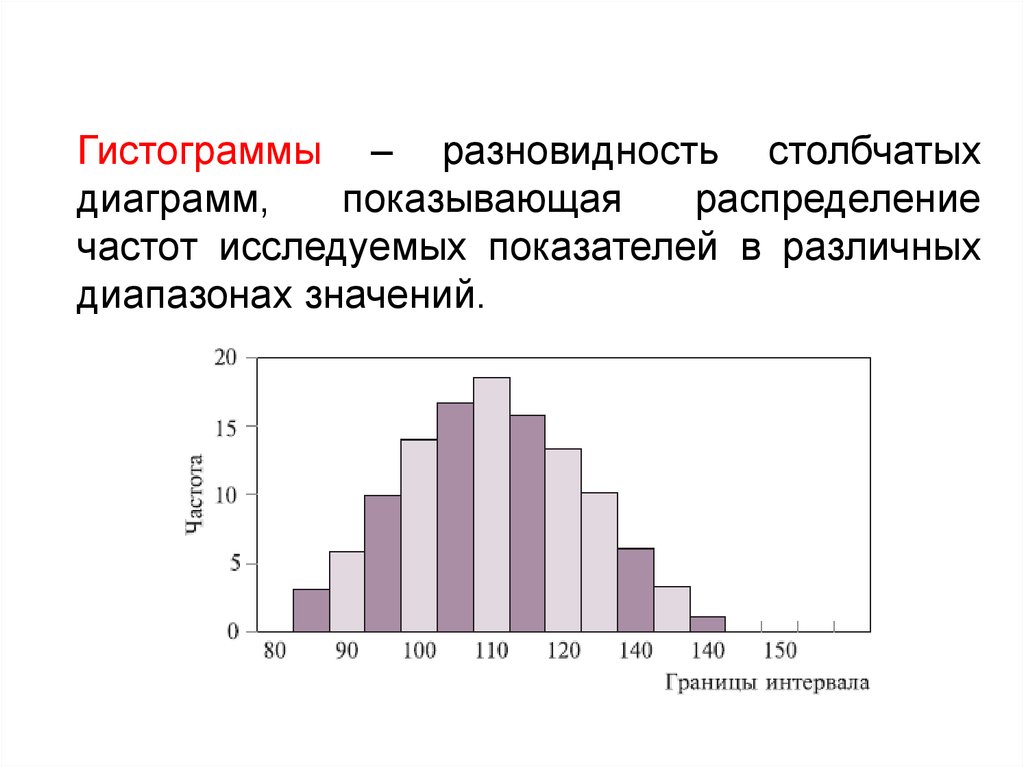
Гистограмма
В случае интервального статистического распределения целесообразно построить гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты (в случае равных интервалов) должны быть пропорциональны частотам. При построении гистограммы с неравными интервалами по оси ординат наносят не частоты, а плотность частоты . Это необходимо сделать для устранения влияния величины интервала на распределение и иметь возможность сравнивать частоты.
В случае построения гистограммы относительных частот (гистограммы частостей) высоты в случае равных интегралов должны быть пропорциональны относительной частоте , а в случае неравных интервалов высота равна плотности относительной частоты .
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Я буду работать с вами, над вашей проблемой, пока она не решится.
Пример 2
Построить гистограмму частот и относительных частот (частостей)
| 2-5 | 5-8 | 8-11 | 11-14 | 14-17 | 17-20 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим относительные частоты:
| Интервалы, | Относительные частоты, | |
| 2 – 5 | 15 |
0. 075 075
|
| 5 – 8 | 35 | 0.175 |
| 8 – 11 | 64 | 0.320 |
| 11 – 14 | 0.275 | |
| 14 – 17 | 21 | 0.105 |
| 17 – 20 | 10 | 0.050 |
| Итого | 200 | 1.000 |
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).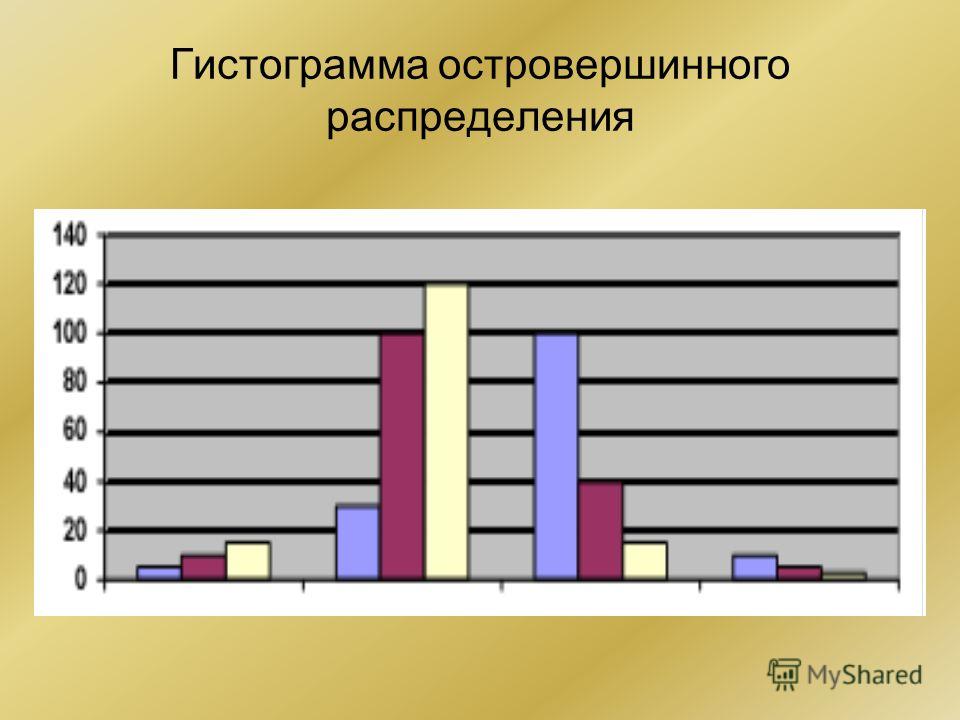
| 2-4 | 4-8 | 8-13 | 13-15 | 15-17 | 17-20 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим плотности частоты:
| Интервалы, | Длина интервала, | Плотность частоты, | |
| 2 – 4 | 15 | 2 |
7. 500 500
|
| 4 – 8 | 35 | 4 | 8.750 |
| 8 – 13 | 64 | 5 | 12.800 |
| 13 – 15 | 55 | 2 | 27.500 |
| 15 – 17 | 21 | 2 | 10.500 |
| 17 – 20 | 10 | 3 |
3. 333 333
|
| Итого | 200 | — | — |
Гистограмма частот
Кроме этой задачи на другой странице сайта есть пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов.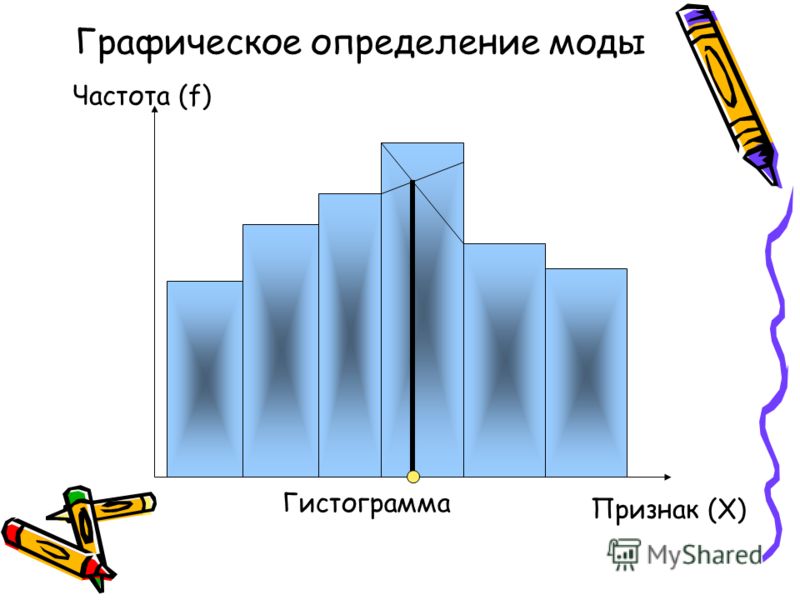
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.
Пример 4
Построить кумулятивную кривую:
| 2 | 5 | 8 | 11 | 14 | 17 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим накопленные частоты:
| Накопленные частоты, | ||
| 2 | 15 | 15 |
| 7 | 35 | 50 |
| 8 | 64 | 114 |
| 15 | 55 | 169 |
| 16 | 21 | 190 |
| 17 | 10 | 200 |
| Итого | 200 | — |
Кумулятивная кривая
как построить, гистограмма частот для выборки
Содержание:
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Содержание
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
Определение
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2),…, (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2),…, (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(W_i=\frac{n_i}n\)
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Определение
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.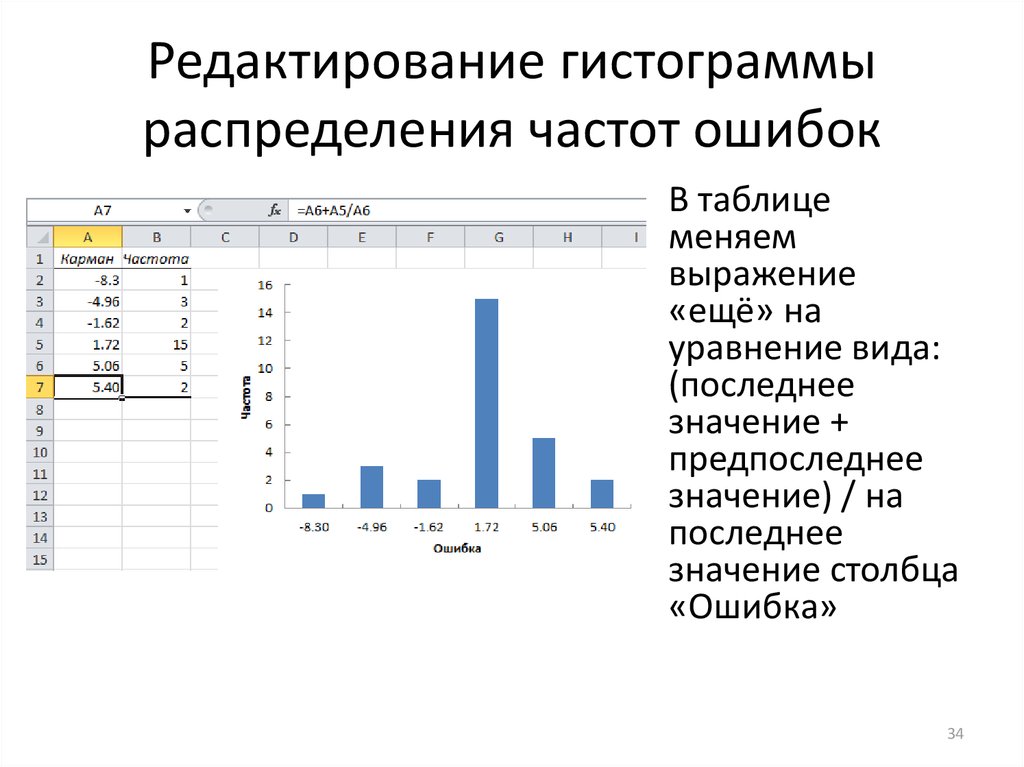
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
ni 1, 2, 2, 3, 1, 1.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.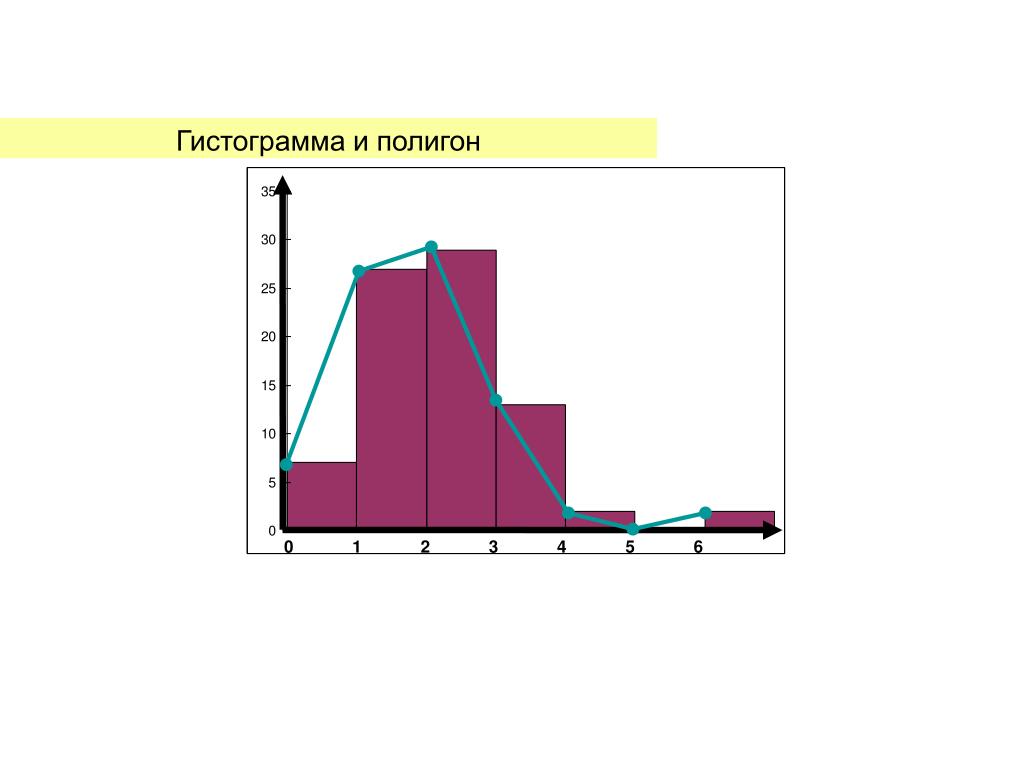
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
\(\frac{n_ih}h=n_i\)
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Насколько полезной была для вас статья?
Рейтинг: 1.38 (Голосов: 24)
Поиск по содержимому
Полигон и гистограмма — Студопедия
Поделись
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.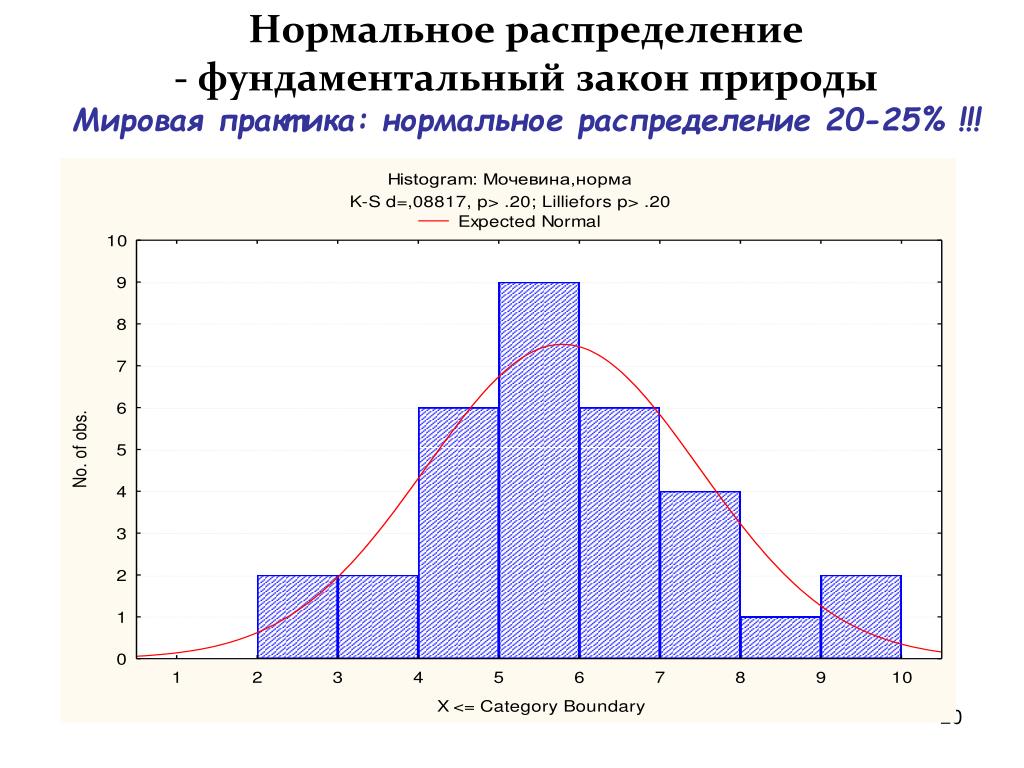
Определение. Полигоном частот называют ломаную, отрезки которой соединяют точки (x1, n1), (x2, n2), (xk, nk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni. Точки (xi, ni) соединяют отрезками прямых и получают полигон частот.
Определение. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1, w1), (x2, w2), (xk, wk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат wi. Точки (xi, wi) соединяют отрезками прямых и получают полигон относительных частот.
На рисунке изображен полигон относительных частот следующего распределения:
| x | 1,5 | 3,5 | 5,5 | 7,5 |
| w | 0,1 | 0,2 | 0,4 | 0,3 |
Рис. 6. Полигон относительных частот.
6. Полигон относительных частот.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-ый интервал.
Определение. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность частоты).
Рис. 7. Гистограмма частот.
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс, на расстоянии .
Площадь i-го частичного прямоугольника равна = — сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, то есть объему выборки n.
На рисунке 2 изображена гистограмма частот распределения объема n =100, приведенного в таблице 1.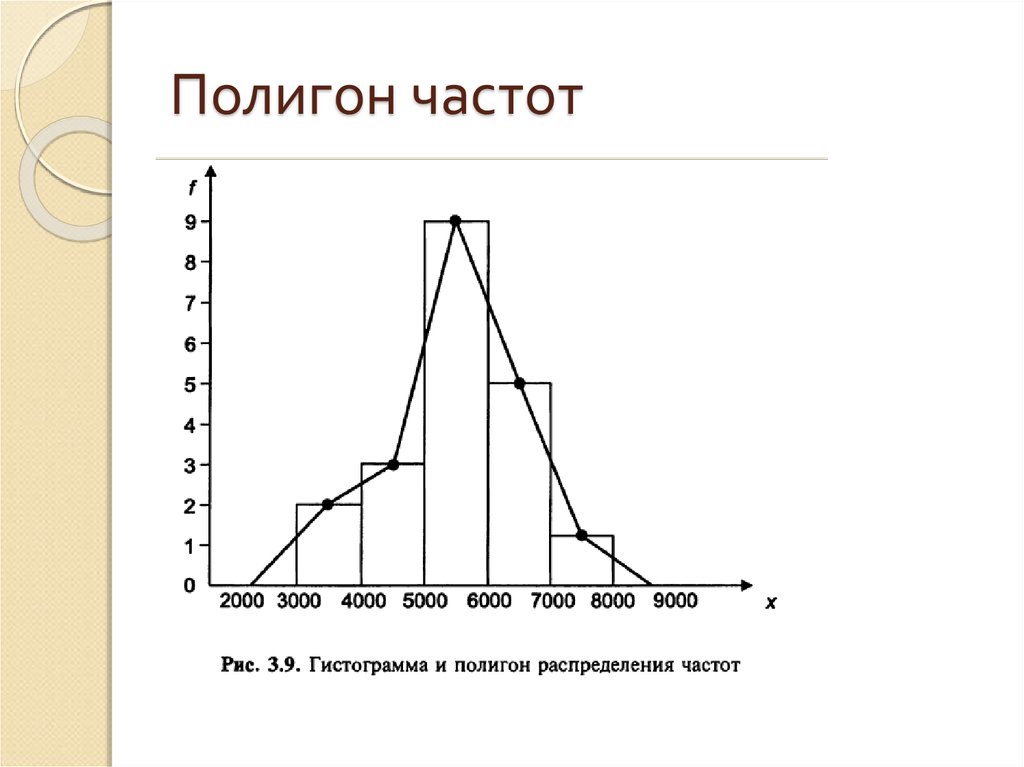
| Частичный интервал, длиною h=5 | Сумма частот вариант частичного интервала | Плотность частоты |
| 5 – 10 | 0,8 | |
| 10 – 15 | 1,2 | |
| 15 – 20 | 3,2 | |
| 20 – 25 | 7,2 | |
| 25 – 30 | 4,8 | |
| 30 – 35 | 2,0 | |
| 34 – 40 | 0,8 |
Определение. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длинною h, а высоты равны отношению (плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь i-го частичного прямоугольника равна = — относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.
Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.
Примеры.
1. В результате выборки получена следующая таблица распределения частот.
Построить полигоны частот и относительных частот распределения.
Для начала построим полигон частот.
Рис. 8. Полигон частот.
Чтобы построить полигон относительных частот найдем относительные частоты, для чего разделим частоты на объем выборки n.
n = 3 + 10 + 7 = 20.
.
Получаем
| 0,15 | 0,50 | 0,35 |
Построим полигон относительных частот.
Рис. 9. Полигон относительных частот.
2. Построить гистограммы частот и относительных частот распределения.
Найдем плотность частоты :
| Частичный интервал, длиною h = 3 | Сумма частот вариант частичного интервала | Плотность частоты |
| 2 – 5 | ||
| 5 – 8 | 3,3 | |
| 8 – 11 | 8,3 | |
| 11 – 14 |
Построим гистограмму частот.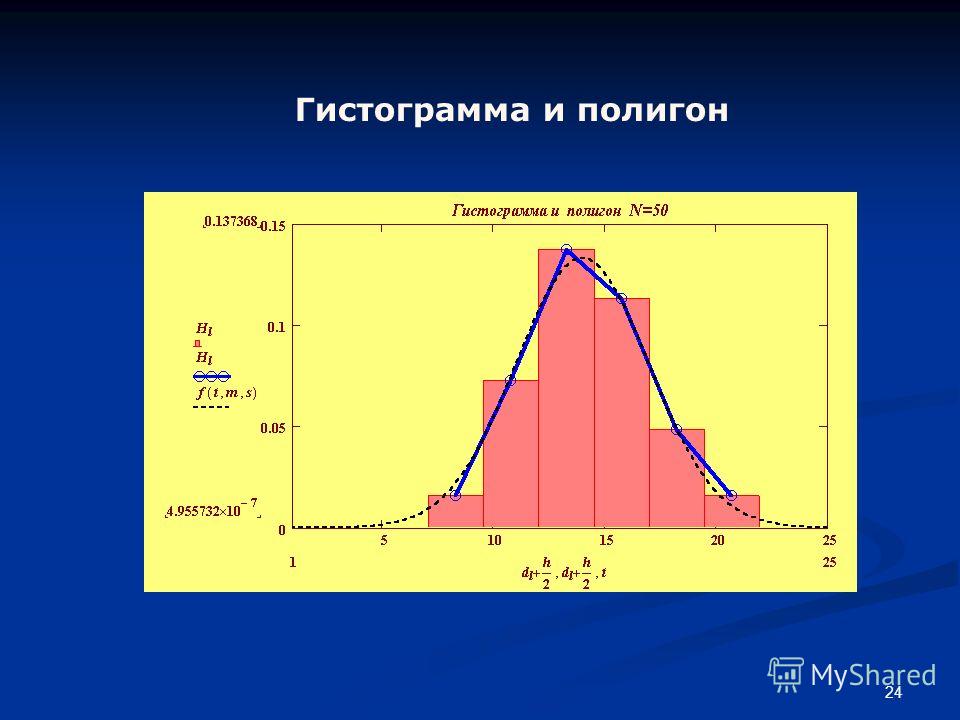
Рис. 10. Гистограмма частот.
Чтобы построить гистограмму относительных частот, нужно найти относительные частоты. Для этого найдем объем выборки n.
.
Теперь найдем относительные частоты :
Получим:
| Частичный интервал | Сумма относительных частот | Плотность частоты |
| 2 – 5 | 0,18 | 0,06 |
| 5 – 8 | 0,2 | 0,07 |
| 8 – 11 | 0,5 | 0,16 |
| 11 – 14 | 0,12 | 0,04 |
Плотности частот нужно вычислить. При этом h = 3.
Построим гистограмму относительных частот.
Рис.11. Гистограмма относительных частот.
Что такое гистограммы? Анализ и частотное распределение
- Дом /
- Качественные ресурсы /
- Гистограмма
Ищете более качественные инструменты?
Попробуйте Plan-Do-Study-Act (PDSA) Plus QTools™ Training:
- Контрольный лист
- Диаграмма Парето
- QTools TM Комплект
- Plan-Do-Study-Act плюс QTools TM
Глоссарий качества Определение: гистограмма
Распределение частоты показывает, как часто встречается каждое отдельное значение в наборе данных. Гистограмма является наиболее часто используемым графиком для отображения распределения частот. Она очень похожа на гистограмму, но между ними есть важные отличия. Этот полезный инструмент для сбора и анализа данных считается одним из семи основных инструментов обеспечения качества.
Гистограмма является наиболее часто используемым графиком для отображения распределения частот. Она очень похожа на гистограмму, но между ними есть важные отличия. Этот полезный инструмент для сбора и анализа данных считается одним из семи основных инструментов обеспечения качества.
Когда использовать гистограмму
Использовать гистограмму, когда:
- Данные числовые
- Вы хотите увидеть форму распределения данных, особенно при определении того, распределяются ли выходные данные процесса примерно нормально
- Анализ того, может ли процесс удовлетворить требования клиента
- Анализ того, как выглядит результат процесса поставщика
- Проверка того, произошло ли изменение процесса от одного периода времени к другому
- Определение того, отличаются ли выходные данные двух или более процессов
- Вы хотите быстро и легко передать распространение данных другим
Пример гистограммы
Как создать гистограмму
- Соберите не менее 50 последовательных точек данных из процесса.

- Используйте рабочий лист гистограммы для настройки гистограммы. Это поможет вам определить количество баров, диапазон чисел, которые входят в каждый бар, и метки для краев баров. После расчета W на шаге 2 рабочего листа, используйте свое суждение, чтобы настроить его на удобное число. Например, вы можете решить округлить 0,9 до четного 1,0. Значение для W не должно иметь больше десятичных разрядов, чем числа, которые вы будете отображать на графике.
- Нарисуйте оси x и y на миллиметровой бумаге. Отметьте и пометьте ось Y для подсчета значений данных. Отметьте и пометьте ось x значениями L из рабочего листа. Пробелы между этими числами будут столбцами гистограммы. Не допускайте промежутков между стержнями.
- Для каждой точки данных отметьте один счет над соответствующей полосой знаком X или заштрихуйте эту часть полосы.
Анализ гистограммы
- Прежде чем делать какие-либо выводы из гистограммы, убедитесь, что процесс работал нормально в течение изучаемого периода времени.
 Если какие-либо необычные события повлияли на процесс в течение периода времени гистограммы, ваш анализ формы гистограммы, вероятно, не может быть распространен на все периоды времени.
Если какие-либо необычные события повлияли на процесс в течение периода времени гистограммы, ваш анализ формы гистограммы, вероятно, не может быть распространен на все периоды времени. - Проанализируйте значение формы вашей гистограммы. Типичные формы гистограмм и их значение описаны ниже.
Инструменты и шаблоны гистограмм
Шаблон гистограммы (Excel) Анализируйте частотное распределение до 200 точек данных с помощью этого простого, но мощного инструмента для создания гистограмм.
Шаблон контрольного листа (Excel) Анализ количества дефектов за каждый день недели. Начните с отслеживания дефектов в контрольном листе. Инструмент создаст гистограмму, используя введенные вами данные.
Нормальное распределение
Распространенным паттерном является колоколообразная кривая, известная как «нормальное распределение». В нормальном или «типичном» распределении точки с такой же вероятностью могут появиться как по одну сторону от среднего, так и по другую.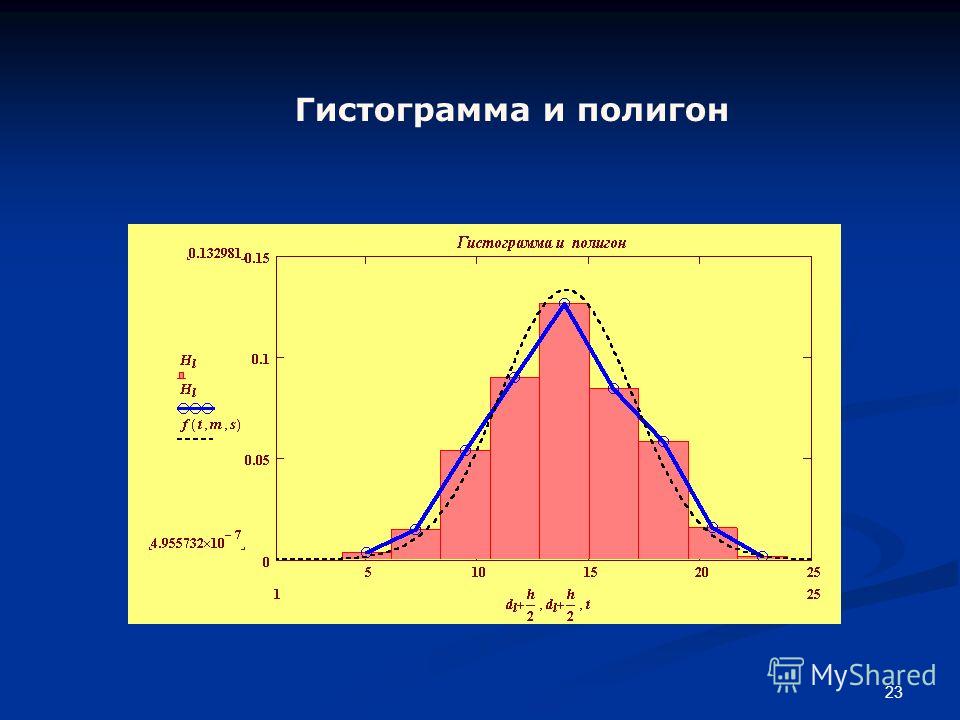 Обратите внимание, что другие распределения похожи на нормальное распределение. Для доказательства нормального распределения необходимо использовать статистические расчеты.
Обратите внимание, что другие распределения похожи на нормальное распределение. Для доказательства нормального распределения необходимо использовать статистические расчеты.
Важно отметить, что «нормальный» относится к типичному распределению для конкретного процесса. Например, многие процессы имеют естественное ограничение с одной стороны и приводят к асимметричным распределениям. Это нормально — то есть типично — для этих процессов, даже если распределение не считается «нормальным».
Распределение с перекосом
Распределение с перекосом является асимметричным, поскольку естественный предел предотвращает результаты с одной стороны. Пик распределения смещен от центра к пределу, а от него тянется хвост. Например, распределение анализов очень чистого продукта будет искажено, потому что продукт не может быть более чем на 100 процентов чистым. Другими примерами естественных ограничений являются отверстия, которые не могут быть меньше диаметра сверла, или время обработки вызовов, которое не может быть меньше нуля. Эти распределения называются правыми или левыми в зависимости от направления хвоста.
Эти распределения называются правыми или левыми в зависимости от направления хвоста.
Двухвершинное или бимодальное
Бимодальное распределение похоже на спину двугорбого верблюда. Результаты двух процессов с разными распределениями объединяются в один набор данных. Например, распределение производственных данных при работе в две смены может быть бимодальным, если каждая смена дает разное распределение результатов. Стратификация часто выявляет эту проблему.
Плато или мультимодальное распределение
Плато можно назвать «мультимодальным распределением». Комбинируются несколько процессов с нормальными распределениями. Поскольку много пиков расположены близко друг к другу, вершина распределения напоминает плато.
Распределение пиков краев
Распределение пиков краев похоже на нормальное распределение, за исключением того, что оно имеет большой пик на одном конце. Обычно это вызвано неправильным построением гистограммы, когда данные объединены в группу с пометкой «больше».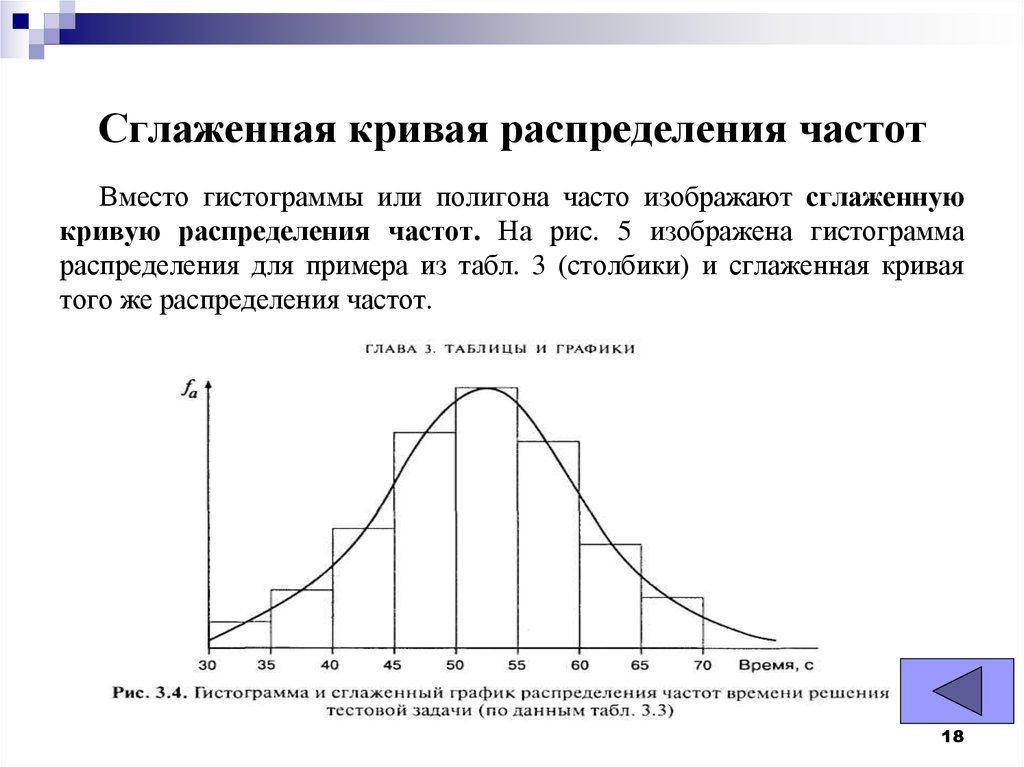
Гребенчатое распределение
В гребенчатом распределении стержни чередуются высокие и короткие. Такое распределение часто является результатом округления данных и/или неправильно построенной гистограммы. Например, данные о температуре, округленные до ближайших 0,2 градуса, будут иметь форму гребенки, если ширина столбца гистограммы будет равна 0,1 градуса.
Усеченное или вырезанное из сердец распределение
Усеченное распределение выглядит как нормальное распределение с обрезанными хвостами. Поставщик может производить нормальное распределение материала, а затем полагаться на проверку, чтобы отделить то, что находится в пределах спецификации, от того, что не соответствует спецификации. В результате отгрузки заказчику внутри спецификаций являются сердцевиной.
Раздача корма для собак
В раздаче корма для собак чего-то не хватает — результаты близки к среднему. Если покупатель получает такую раздачу, кто-то другой получает отрезанное сердце, а покупатель остается с «собачьей едой» — мелочью, оставшейся после трапезы хозяина.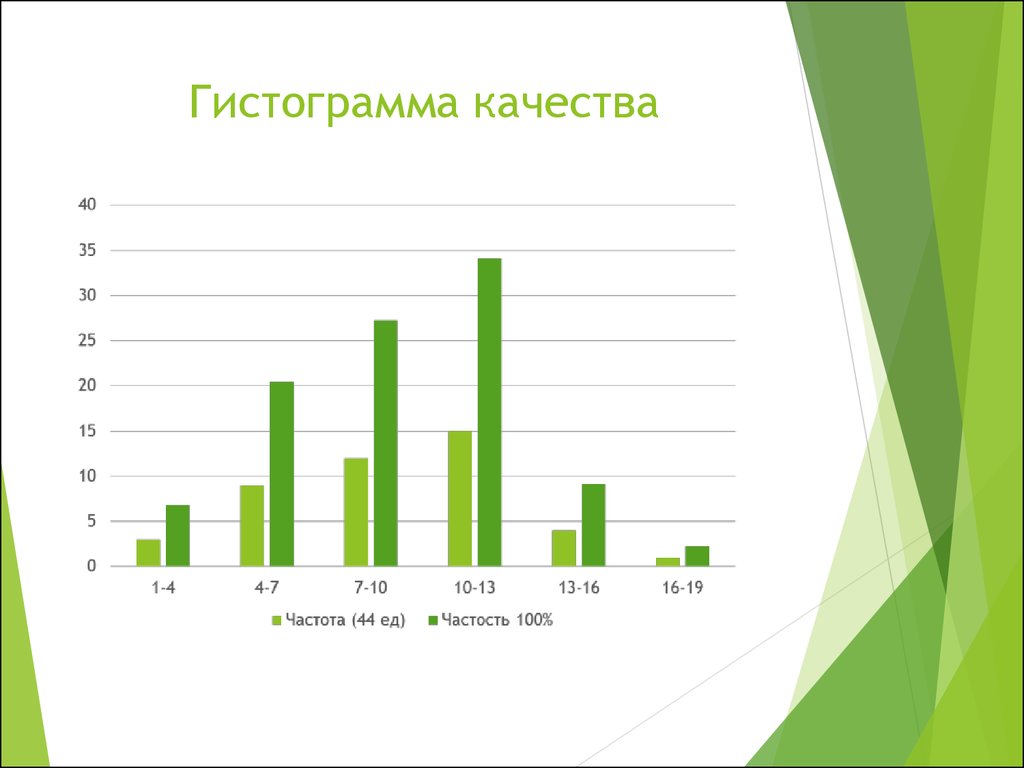 Несмотря на то, что то, что получает покупатель, соответствует спецификациям, продукт распадается на две группы: одна ближе к верхнему пределу спецификации, а другая — к нижнему пределу спецификации. Это изменение часто вызывает проблемы в процессе клиента.
Несмотря на то, что то, что получает покупатель, соответствует спецификациям, продукт распадается на две группы: одна ближе к верхнему пределу спецификации, а другая — к нижнему пределу спецификации. Это изменение часто вызывает проблемы в процессе клиента.
Адаптировано из The Quality Toolbox, Second Edition , ASQ Quality Press.
Избранные рекламодатели
Создание частотных распределений и гистограмм вручную
Как правило, статистики (и любой здравомыслящий человек) будут использовать какую-либо статистическую программу, такую как R или minitab, для построения своих статистических графиков. Тем не менее, до сих пор на удивление часто можно увидеть, как в учебниках все делается вручную, и, в конце концов, научиться составлять гистограмму вручную — это отличный способ научиться лучше читать их и выяснять, в чем проблема, когда компьютер или калькулятор дает вы чего-то не ожидаете. В этом уроке мы рассмотрим пошаговый процесс построения частотного распределения и гистограммы.
реклама
Чтобы показать вам, как это сделать, мы будем использовать набор данных ниже. Я пошел дальше и расположил числа по порядку , что сделает все намного проще.
| 12 14 14 14 16 | 18 20 20 21 23 | 27 27 27 29 31 | 31 32 32 34 36 | 40 40 40 40 40 | 42 51 56 60 65 |
Чтобы построить гистограмму вручную, мы должны сначала найти частотное распределение . Идея частотного распределения состоит в том, чтобы разбить данные на группы (называемые классами или бинами), чтобы мы могли лучше видеть закономерности. Это похоже на разницу между вопросом о вашем возрасте и вопросом о том, вам от 20 до 25 лет. Во втором вопросе я группирую возраст. Таким образом, если у меня есть ОГРОМНЫЙ набор данных (как у многих), я могу увидеть шаблоны (например, большинство людей старше или моложе) намного проще, чем если бы я просто пытался расшифровать большой список чисел.
Этапы создания частотного распределения
Шаг 1: Расчет диапазона набора данных
Диапазон представляет собой разницу между наибольшим и наименьшим значениями. Нам это нужно, чтобы понять, сколько «пространства» нам нужно разделить на группы. В этом примере:
\(\text{Диапазон}=65-12=53\)
Шаг 2: Разделите диапазон на количество групп, которые вы хотите, а затем округлите
Это позволит нам выяснить, насколько велика каждая группа. Как будто мы собираемся разрезать доску на равные части. На шаге 1 мы измерили длину доски, а теперь решаем, насколько большой будет каждая часть.
Хммм… но сколько групп иметь? Слишком много, и наши графики и таблицы будут не намного лучше, чем список чисел. Слишком мало, и узор будет скрыт слишком маленькими деталями. Часто хорошим числом групп является 5 или 6, хотя есть некоторые правила, которые люди используют для решения этого . БОЛЕЕ ЧАЩЕ люди позволяют компьютеру решать, а затем приспосабливаются, если они хотят, в то время как учебники говорят вам, сколько групп использовать. Но если вы работаете с набором данных самостоятельно, вам нужно будет увидеть, как выглядит график, прежде чем вы сможете быть уверены, что выбрали правильное число.
Но если вы работаете с набором данных самостоятельно, вам нужно будет увидеть, как выглядит график, прежде чем вы сможете быть уверены, что выбрали правильное число.
Допустим, мы выбрали 6 групп. Если мы сделаем это, то:
\(\dfrac{53}{6}=8,8\)
Число, которое мы только что нашли, обычно называют шириной класса . Мы округлим до 9 просто потому, что так проще работать. Компьютер, вероятно, сохранит 8,8, поэтому имейте в виду, что иногда вы будете видеть это число как десятичное. ПРИМЕЧАНИЕ. В общем, люди, которые делают это вручную, всегда округляют, даже если это было 8.1!
Шаг 3. Используйте ширину класса для создания групп
Я начну с наименьшего числа, которое у нас есть, то есть 12, и буду считать до 9, пока не получу свои 6 групп. Например, моя первая группа будет от 12 до 21, так как 12+9=21. Моя следующая группа будет 21-30, так как 21+9=30… и так далее. Я положу их в таблицу и обозначу как «классы». Также добавлю в таблицу «частота». :
:
| Классы | Частота |
|---|---|
| 12 – 21 | |
| 21 – 30 | |
| 30 – 39 | |
| 39 – 48 | |
| 48 – 57 | |
| 57 – 66 |
Шаг 4: Найдите частоту для каждой группы
Эта часть, вероятно, самая утомительная и основная причина, по которой нереально вручную построить частотное распределение или гистограмму для очень большого набора данных. Мы собираемся подсчитать, сколько очков в каждой группе. Давайте начнем с нашей первой группы: 12 – 21. Мы хотим подсчитать, сколько очков находится между 12 и 21, НЕ ВКЛЮЧАЯ 21. Вы видите совпадение между группами, верно? Это для учета десятичных знаков, и мы сохраняем их, даже если у нас их нет. Правая конечная точка любой группы не включена в эту группу. Он идет в следующей группе. Это означает, что 21 будет во второй группе, а любые 30, которые у нас есть, будут засчитаны в третью группу.
Вернуться к первой группе: 12-21. Я обвел кружком точки, которые будут включены в эту группу:
Хорошо, теперь я обновлю таблицу этой информацией!
| Классы | Частота |
|---|---|
| 12 – 21 | 8 |
| 21 – 30 | |
| 30 – 39 | |
| 39 – 48 | |
| 48 – 57 | |
| 57 – 66 |
Продолжая этот узор (каждая группа разного цвета!):
| Классы | Частота |
|---|---|
| 12 – 21 | 8 |
| 21 – 30 | 6 |
| 30 – 39 | 6 |
| 39 – 48 | 6 |
| 48 – 57 | 2 |
| 57 – 66 | 2 |
Последняя таблица — это наше частотное распределение! Чтобы сделать из этого гистограмму, мы будем использовать группы по горизонтальной оси и частоту по вертикальной оси. Наконец, мы будем использовать столбцы для представления частоты каждой отдельной группы. С этими данными готовая гистограмма будет выглядеть так, как показано ниже.
Наконец, мы будем использовать столбцы для представления частоты каждой отдельной группы. С этими данными готовая гистограмма будет выглядеть так, как показано ниже.
Еще один пример того, как это делается, вы можете увидеть на видео ниже.
реклама
Пример видео
В этом примере мы пройдем тот же процесс с другим набором данных.
Что изучать дальше
Как только вы научитесь рисовать гистограммы, вы должны научиться их читать и интерпретировать общие формы, общие формы и закономерности. Наконец, вы также можете увидеть, как создавать гистограммы на калькуляторе TI-83.
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и наборы задач.
Подпишитесь, чтобы время от времени получать электронные письма (раз в пару или три недели), сообщающие вам о новинках!
Гистограмма — график, определение, свойства, примеры
Гистограмма может быть определена как набор прямоугольников с основаниями и интервалами между границами классов. Каждая прямоугольная полоса отображает какие-то данные, и все прямоугольники являются смежными. Высоты прямоугольников пропорциональны соответствующим частотам как подобных, так и разных классов. Давайте узнаем о гистограммах более подробно.
| 1. | Что такое гистограмма? |
| 2. | График гистограммы |
| 3. | Как сделать гистограмму? |
| 4. | Частотная гистограмма |
| 5. | Формы гистограммы |
| 6. | Гистограмма в форме колокола |
| 7. | Бимодальная гистограмма |
8. | Гистограмма с перекосом вправо |
| 9. | Гистограмма с перекосом влево |
| 10. | Единая гистограмма |
| 11. | Разница между гистограммой и гистограммой |
| 12. | Калькулятор гистограммы |
| 13. | Часто задаваемые вопросы о гистограмме |
Что такое гистограмма?
Гистограмма — это графическое представление данных, где данные сгруппированы в непрерывные диапазоны чисел, и каждый диапазон соответствует вертикальной черте.
- По горизонтальной оси отображается диапазон чисел.
- Вертикальная ось (частота) представляет количество данных, присутствующих в каждом диапазоне.
Диапазоны номеров зависят от используемых данных.
График гистограммы
Гистограмма представляет собой столбчатую диаграмму данных.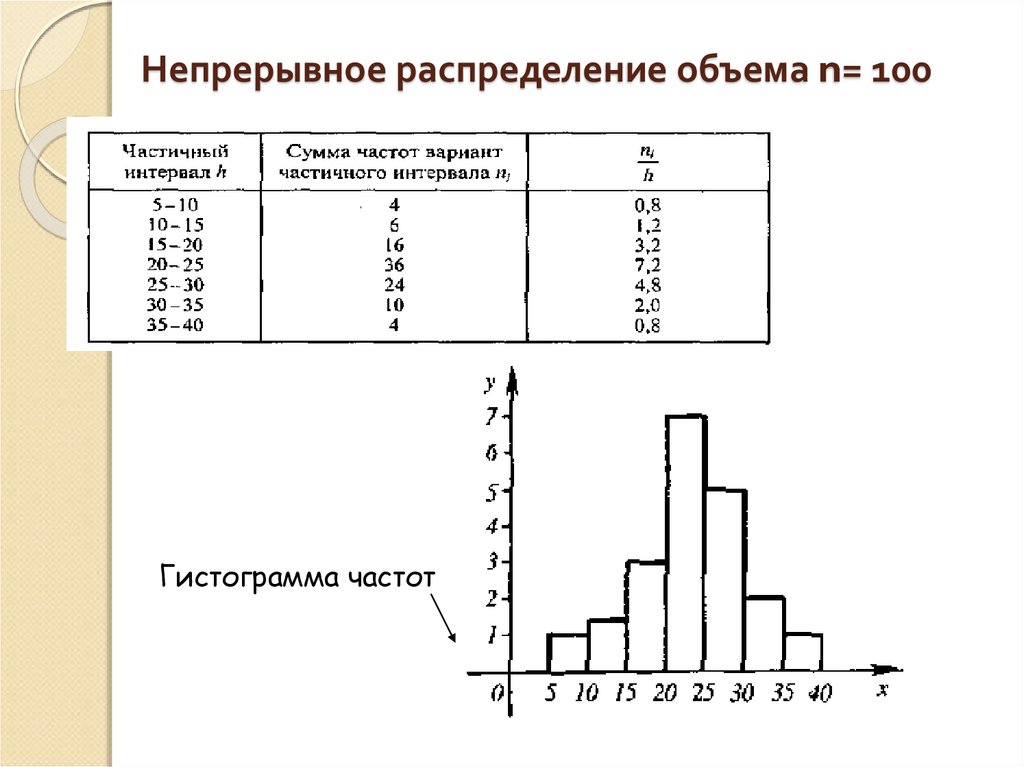 Это представление диапазона результатов в виде столбцов по оси x. на той же гистограмме число или несколько вхождений в данных для каждого столбца представлены по оси Y. Это самый простой способ, который можно использовать для визуализации распределения данных. Давайте разберемся график гистограммы , построив его для приведенного ниже примера.
Это представление диапазона результатов в виде столбцов по оси x. на той же гистограмме число или несколько вхождений в данных для каждого столбца представлены по оси Y. Это самый простой способ, который можно использовать для визуализации распределения данных. Давайте разберемся график гистограммы , построив его для приведенного ниже примера.
У дяди Бруно есть сад с 30 деревьями черной вишни. Каждое дерево разной высоты. Высота деревьев (в дюймах): 61, 63, 64, 66, 68, 69, 71, 71,5, 72, 72,5, 73, 73,5, 74, 74,5, 76, 76,2, 76,5, 77, 77,5, 78, 78,5, 79, 79,2, 80, 81, 82, 83, 84, 85, 87. Мы можем сгруппировать данные следующим образом в таблице распределения частот, установив диапазон:
| Диапазон высот (футы) | Количество деревьев (частота) |
|---|---|
| 60 — 75 | 3 |
| 66 — 70 | 3 |
| 71 — 75 | 8 |
| 76 — 80 | 10 |
| 81 — 85 | 5 |
| 86 — 90 | 1 |
Теперь эти данные можно отобразить в виде гистограммы. Нам нужно убедиться, что при построении гистограммы между барами не должно быть промежутков.
Нам нужно убедиться, что при построении гистограммы между барами не должно быть промежутков.
Как сделать гистограмму?
Ниже описан процесс построения гистограммы с использованием заданных данных:
- Шаг 1: Выберите подходящий масштаб для представления весов на горизонтальной оси.
- Шаг 2: Выберите подходящий масштаб для представления частот по вертикальной оси.
- Шаг 3: Затем нарисуйте столбцы, соответствующие каждому из заданных весов, используя их частоты.
Пример: Постройте гистограмму для следующей таблицы распределения частот, которая описывает частоты весов 25 учеников в классе.
| Вес (в фунтах) | Частота (Количество студентов) |
|---|---|
| 65 — 70 | 4 |
| 70 — 75 | 10 |
| 75 — 80 | 8 |
| 80 — 85 | 4 |
Шаги построения гистограммы:
- Шаг 1: По горизонтальной оси можно выбрать масштаб 1 единица = 11 фунтов.
 0, мы даем излом/изгиб по оси X.
0, мы даем излом/изгиб по оси X. - Шаг 2: По вертикальной оси частоты варьируются от 4 до 10. Таким образом, мы выбираем масштаб 1 единица = 2,
- Шаг 3: Затем нарисуйте столбцы, соответствующие каждому из заданных весов, используя их частоты.
Частотная гистограмма
Гистограмма частот — это гистограмма, показывающая частоты (количество вхождений) заданных элементов данных. Например, в больнице находятся 20 новорожденных детей, возраст которых в порядке возрастания выглядит следующим образом: 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3. , 3, 3, 4, 4, 5. Эту информацию можно отобразить в таблице распределения частот следующим образом:
| Возраст (в днях) | Частота |
|---|---|
| 1 | 4 |
| 2 | 5 |
| 3 | 8 |
| 4 | 2 |
| 5 | 1 |
Теперь эти данные можно отобразить с помощью частотной гистограммы.
Формы гистограммы
Гистограммы можно разделить на различные типы в зависимости от частотного распределения данных. Существуют различные типы распределений, такие как нормальное распределение, асимметричное распределение, бимодальное распределение, мультимодальное распределение, гребенчатое распределение, распределение краевых пиков, распределение собачьего корма, распределение сердцевины и так далее. Гистограмму можно использовать для представления этих различных типов распределений. У нас есть в основном 5 типов форм гистограммы. Они перечислены ниже:
- Гистограмма в форме колокола
- Бимодальная гистограмма
- Гистограмма с перекосом вправо
- Гистограмма с перекосом влево
- Единая гистограмма
Давайте подробно обсудим вышеупомянутые типы гистограмм или формы гистограмм с помощью практических иллюстраций.
Колоколообразная гистограмма
Колоколообразная гистограмма имеет один пик. Гистограмма имеет только один пик на этом временном интервале и, следовательно, это колоколообразная гистограмма . Например, , следующая гистограмма показывает количество детей, посещающих парк в разные промежутки времени. Эта гистограмма имеет только один пик. Максимальное количество детей, посещающих парк, с 17:30 до 18:00.
Гистограмма имеет только один пик на этом временном интервале и, следовательно, это колоколообразная гистограмма . Например, , следующая гистограмма показывает количество детей, посещающих парк в разные промежутки времени. Эта гистограмма имеет только один пик. Максимальное количество детей, посещающих парк, с 17:30 до 18:00.
Бимодальная гистограмма
Бимодальная гистограмма имеет два пика и выглядит как график, приведенный ниже. Например, на следующей гистограмме показаны оценки, полученные 48 учениками 8-го класса школы Святой Марии. Максимальное количество студентов, набравших от 40 до 50 баллов ИЛИ от 60 до 70 баллов. Эта гистограмма имеет два пика (между 40 и 50 и между 60 и 70), и, следовательно, это бимодальная гистограмма .
Гистограмма с перекосом вправо
Гистограмма с перекосом вправо — это гистограмма, перекошенная вправо. На этой гистограмме столбцы гистограммы скошены вправо, поэтому она называется скошенной вправо гистограммой .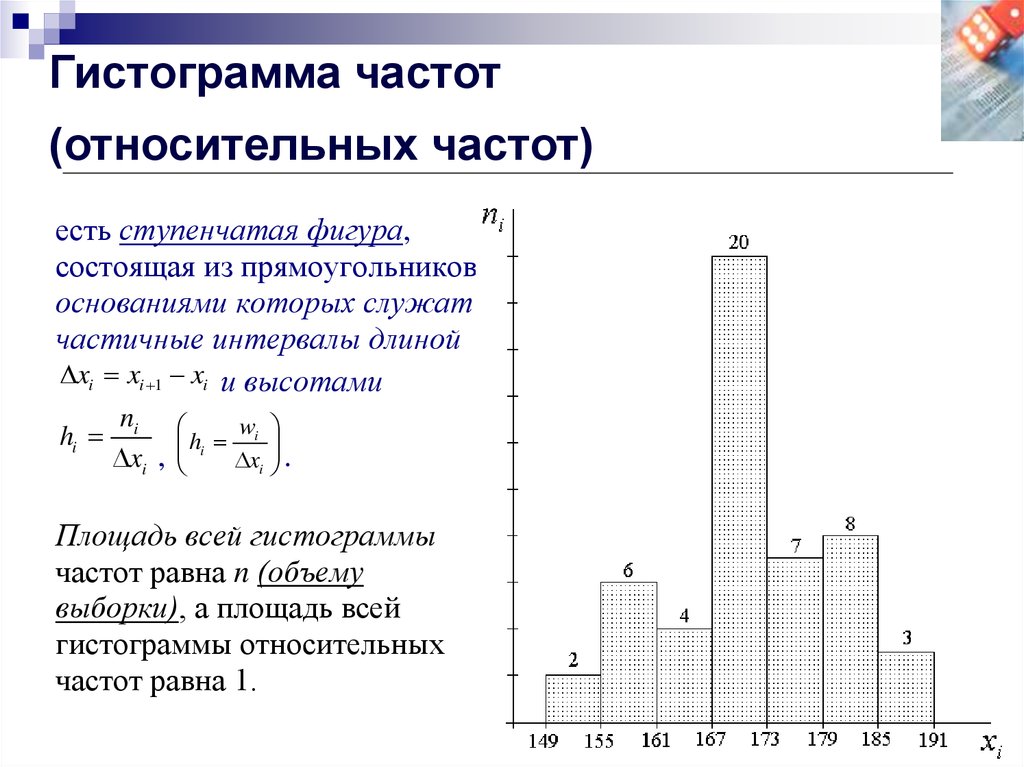 Например, следующая гистограмма показывает количество людей, соответствующих разным диапазонам заработной платы. Гистограмма скошена вправо. На максимальное количество человек заработная плата колебалась в пределах 10-20(тыс.)
Например, следующая гистограмма показывает количество людей, соответствующих разным диапазонам заработной платы. Гистограмма скошена вправо. На максимальное количество человек заработная плата колебалась в пределах 10-20(тыс.)
Гистограмма с перекосом влево
Гистограмма с перекосом влево — это гистограмма с перекосом влево. В этой гистограмме столбцы гистограммы смещены влево, поэтому гистограмма называется смещенной влево. Например, следующая гистограмма показывает количество учеников 10-го класса средней школы Гринвуда в зависимости от количества времени, которое они ежедневно тратят на учебу. Максимальное количество студентов занимается 4,5-5 (часов) ежедневно.
Единая гистограмма
Равномерная гистограмма — это гистограмма, в которой все столбцы имеют более или менее одинаковую высоту. На этой гистограмме длины всех столбцов более или менее одинаковы. Следовательно, это равномерная гистограмма. Например, мэм Люси, директор школы Little Lilly Playschool, хотела записать рост своих учеников.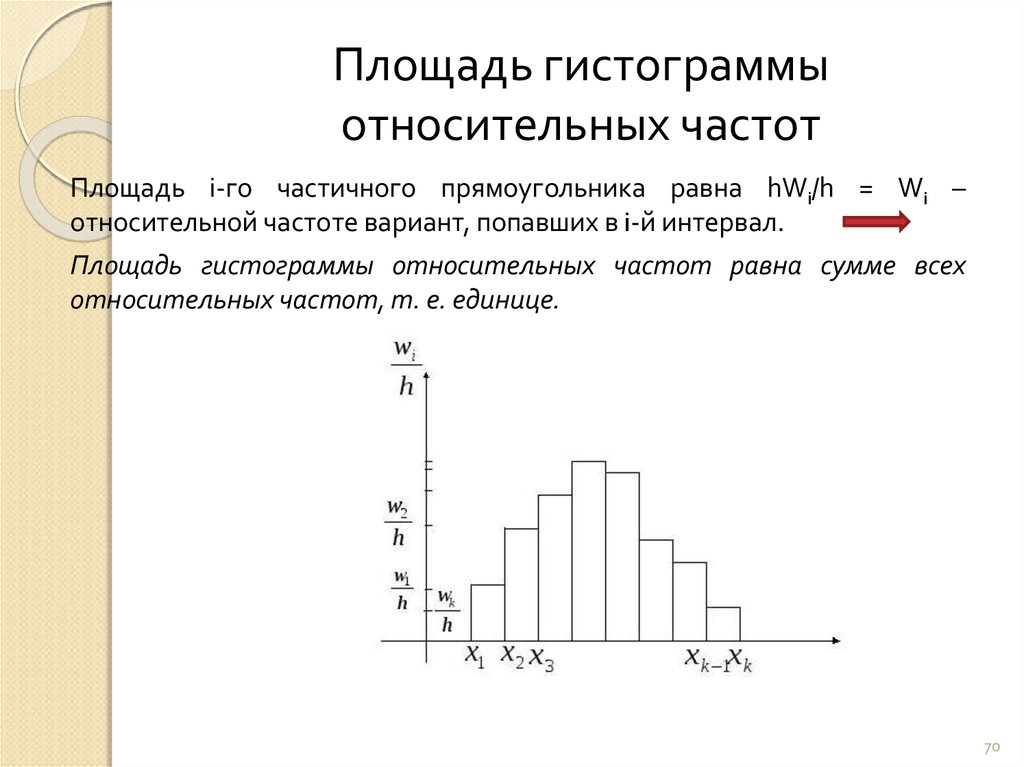 На следующей гистограмме показано количество учащихся и их разный рост. Рост учеников колеблется от 30 до 50 дюймов.
На следующей гистограмме показано количество учащихся и их разный рост. Рост учеников колеблется от 30 до 50 дюймов.
Разница между гистограммой и гистограммой
Фундаментальное различие между гистограммами и гистограммами с визуальной точки зрения заключается в том, что столбцы гистограммы не примыкают друг к другу.
- Гистограмма — это графическое представление категорийных данных с использованием прямоугольных столбцов, где длина каждого столбца пропорциональна значению, которое они представляют.
- Гистограмма — это графическое представление данных, где данные сгруппированы в непрерывные диапазоны чисел, и каждый диапазон соответствует вертикальной черте.
Основные различия между гистограммой и гистограммой заключаются в следующем:
| Гистограмма | Гистограмма |
|---|---|
Одинаковое расстояние между каждыми двумя последовательными штрихами.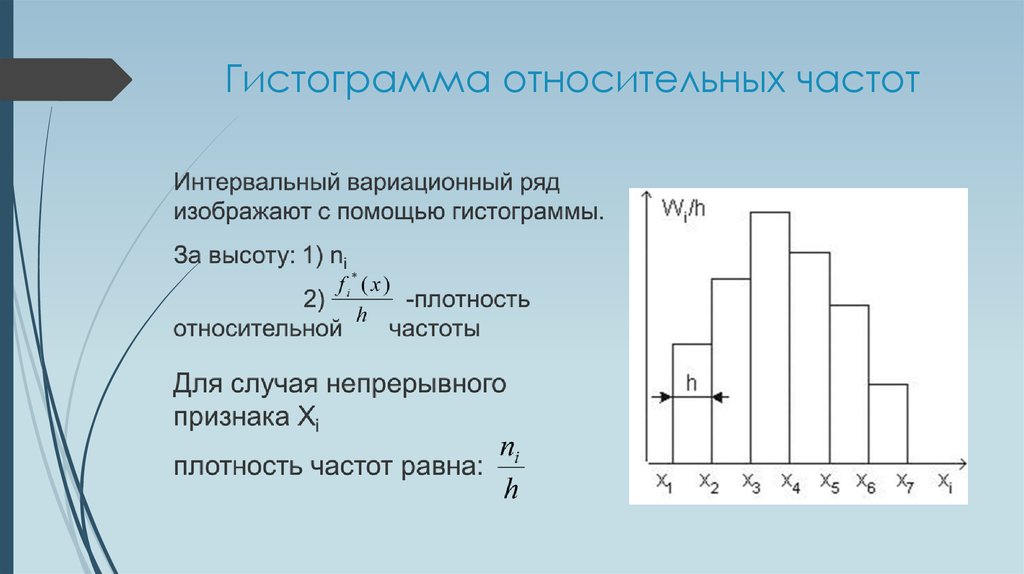 | Нет пробела между двумя последовательными стержнями. Они должны быть прикреплены друг к другу. |
| Ось X может представлять что угодно. | Ось X должна представлять только непрерывные данные в виде чисел. |
Но на обоих графиках ось Y представляет только числа. Мы можем понять эти различия из следующего рисунка:
Калькулятор гистограммы
Калькулятор гистограммы — это бесплатный онлайн-инструмент, который строит гистограмму для заданных данных. В этом калькуляторе вы можете ввести интервалы и частоту, указанные в данных, и гистограмма для этих данных будет отображаться в течение нескольких секунд. Вот калькулятор гистограммы Cuemath, где вы можете ввести список значений данных, и он сгенерирует соответствующую гистограмму. Попробуй.
Советы и рекомендации по гистограмме
Ниже приведены несколько важных советов и рекомендаций, о которых следует помнить при визуализации любых данных с помощью гистограммы.
- Выберите масштаб по вертикальной оси при построении гистограммы, проверьте наибольшее число, которое делит все частоты. Если такого числа не существует, то проверьте наибольшее число, которое делит большинство частот.
- Гистограмма — это график, используемый для суммирования непрерывных данных.
- Гистограмма дает визуальную интерпретацию непрерывных данных.
- Шкалы горизонтальной и вертикальной осей не обязательно должны начинаться с 0.
- Между столбцами гистограммы не должно быть промежутков.
Часто задаваемые вопросы о гистограмме
Что такое гистограмма в статистике?
Гистограмма в статистике — сплошная фигура или диаграмма, состоящая из прямоугольных столбцов. Это одна из основных форм гистограммы, которая используется для визуализации любых заданных числовых данных с практичным подходом.
Для чего используется гистограмма?
Гистограмма используется для отображения частоты различных данных.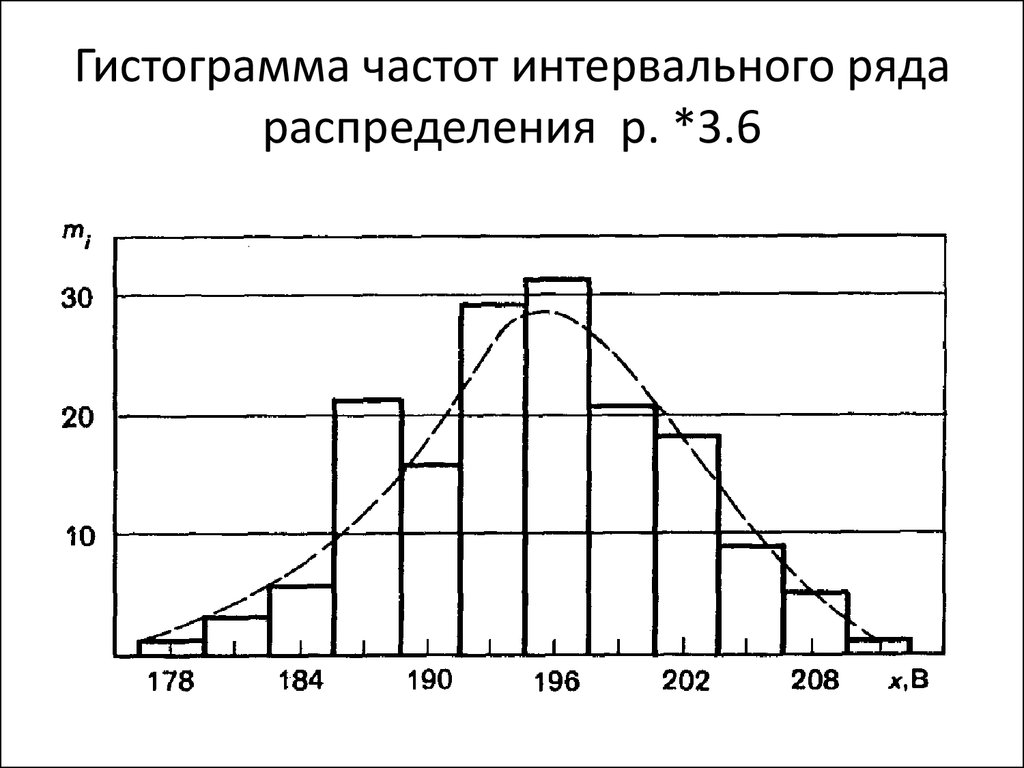 Это графическое представление данных, в котором данные сгруппированы в непрерывные диапазоны чисел, и каждый диапазон соответствует вертикальной черте.
Это графическое представление данных, в котором данные сгруппированы в непрерывные диапазоны чисел, и каждый диапазон соответствует вертикальной черте.
☛ Прочтите основы гистограммы здесь:
- Данные
- Гистограммы
Что такое гистограмма?
Гистограмма — это тип графика для графического представления данных. Эти данные сгруппированы в числовые диапазоны, и каждый диапазон соответствует вертикальной полосе.
☛ Также проверьте:
- Пиктограммы
- Линейные графики
- Круговые диаграммы
Как построить гистограмму?
Шаги построения гистограммы следующие:
- Шаг 1: Размещаем интервалы по горизонтальной оси, выбирая подходящий масштаб.
- Шаг 2: Размещаем частоты по вертикальной оси, выбирая подходящий масштаб.
- Шаг 3: Строим вертикальные полосы по заданным частотам.
В чем разница между гистограммой и гистограммой?
Фундаментальное различие между гистограммами и гистограммами с визуальной точки зрения заключается в том, что столбцы гистограммы не примыкают друг к другу.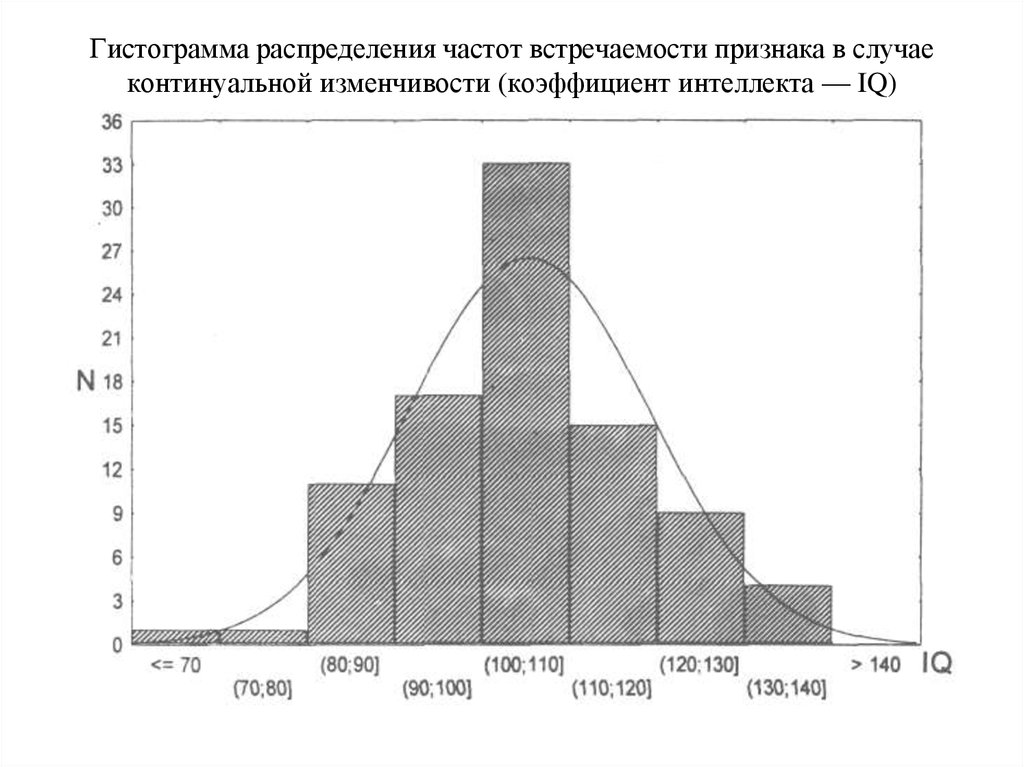 Гистограмма имеет одинаковое расстояние между каждыми двумя последовательными столбцами, а ось X может представлять что угодно. С другой стороны, на гистограмме нет пробелов между двумя последовательными барами. Они должны быть связаны друг с другом, а ось X должна представлять только непрерывные данные в виде чисел.
Гистограмма имеет одинаковое расстояние между каждыми двумя последовательными столбцами, а ось X может представлять что угодно. С другой стороны, на гистограмме нет пробелов между двумя последовательными барами. Они должны быть связаны друг с другом, а ось X должна представлять только непрерывные данные в виде чисел.
Что такое гистограмма относительной частоты?
Гистограмма относительной частоты представляет собой вид графического представления, в котором используется та же информация, что и в гистограмме частоты. Они сравнивают каждый интервал класса с общим количеством элементов.
☛ Подробнее о:
- Относительная частота
- Формула относительной частоты
Как используются гистограммы?
Гистограмма — это тип гистограммы, который используется только для отображения изменений непрерывных данных, таких как время, вес, размер или температура. Гистограмма помогает распознавать и анализировать закономерности в данных, которые не очевидны, просто глядя на таблицу данных или находя среднее значение или медиану.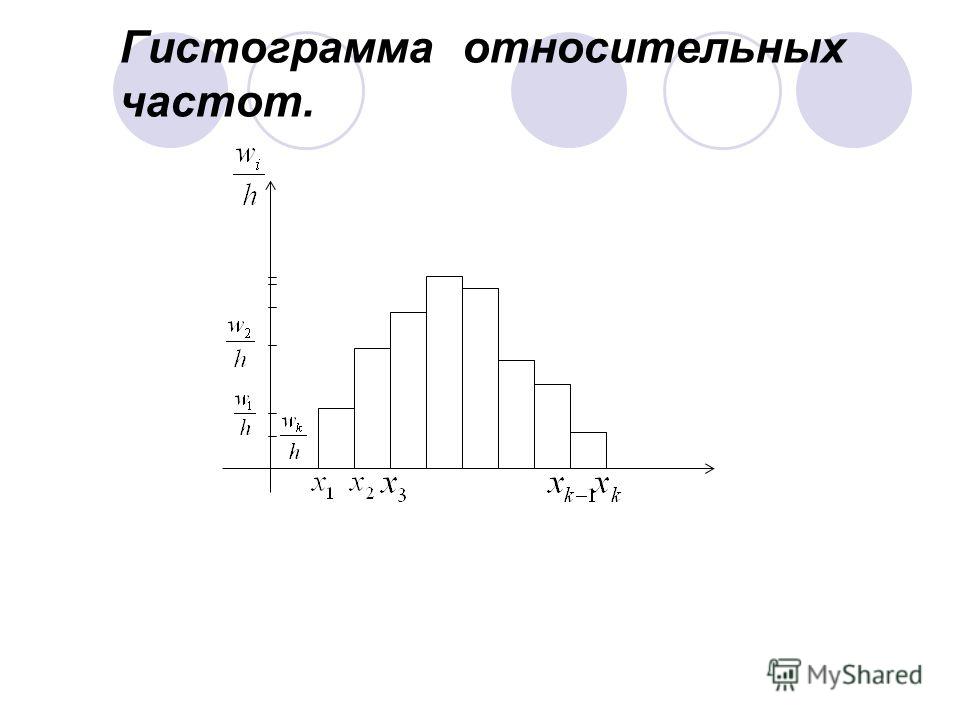
☛ Узнайте больше о следующих терминах:
- Медиана
- Режим
- Среднее
Как гистограмма представляет данные?
Гистограмма — это графическое отображение данных с столбцами разной высоты, где числа в каждом столбце группируются в диапазоны. Чем выше столбцы, тем больше данные попадают в этот диапазон. Он отображает форму, а также распространение данных непрерывной выборки.
Почему мы используем перегибы в гистограммах?
Перегиб используется для обозначения или представления разрыва на оси гистограммы. В некоторых случаях, когда данные имеют огромные цифры или числовые значения, для представления таких данных через гистограмму мы используем символ зигзага, известный как излом. Этот изгиб помогает визуализировать данные, разбивая их.
Почему гистограмма двумерная?
Гистограмма — это визуальное представление данных, двухмерный график, в котором используется набор вертикальных прямоугольников (с акцентом на длину и ширину прямоугольников) для представления частот классов данного распределения.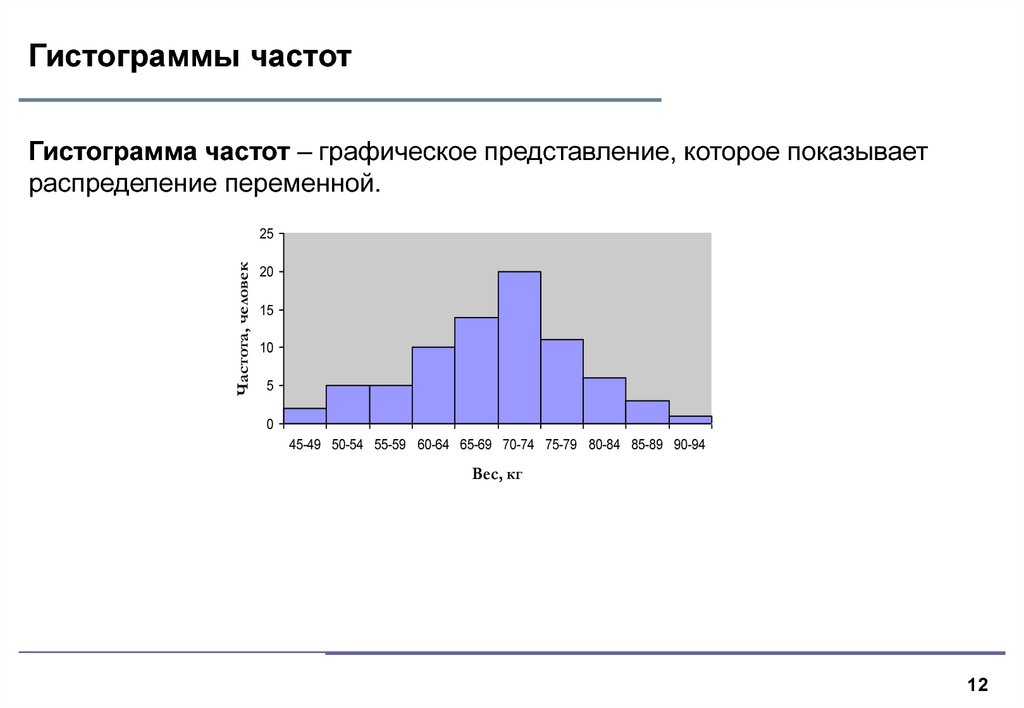

 Если какие-либо необычные события повлияли на процесс в течение периода времени гистограммы, ваш анализ формы гистограммы, вероятно, не может быть распространен на все периоды времени.
Если какие-либо необычные события повлияли на процесс в течение периода времени гистограммы, ваш анализ формы гистограммы, вероятно, не может быть распространен на все периоды времени.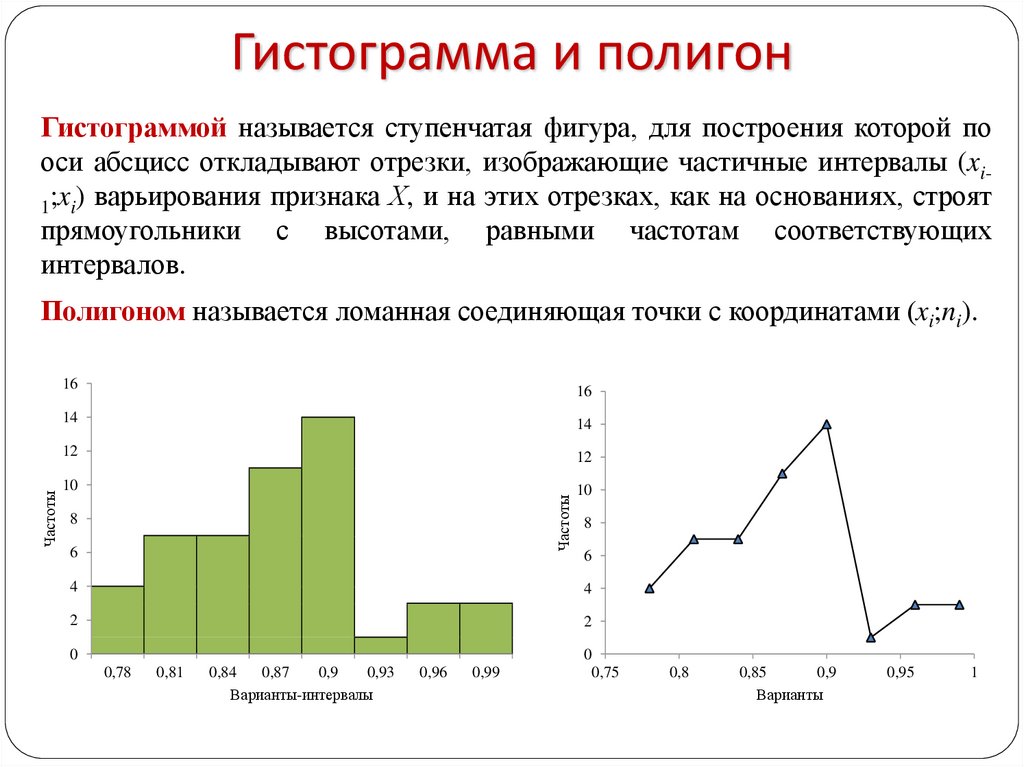 0, мы даем излом/изгиб по оси X.
0, мы даем излом/изгиб по оси X.