Полигон ⚠️ относительных частот: определение, как найти, примеры
Содержание:
- Что такое полигон относительных частот
- Построение полигона частот
- Гистограмма относительных частот, описание
- Площадь прямоугольников гистограммы
- Примеры решения задач
Содержание
- Что такое полигон относительных частот
- Построение полигона частот
- Гистограмма относительных частот, описание
- Площадь прямоугольников гистограммы
- Примеры решения задач
Что такое полигон относительных частот
Схематическое изображение статистического ряда распределения может быть представлено полигоном и гистограммой частот. Также выделяют понятия полигон относительных частот и гистограмма относительных частот
Также выделяют понятия полигон относительных частот и гистограмма относительных частот
Определение
Полигон относительных частот – это ломаная, состоящая из отрезков, соединяющих точки с координатами (xi, ωi
).Построение полигона частот
Алгоритм составления полигона относительных частот: на оси OX отмечают варианты xi, на оси OY откладывают значения ωi. Затем точки с координатами (xi, ωi) соединяют прямыми отрезками. Ломаная, образованная в результате, является полигоном относительных частот.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Пример
Полигон частот для ряда распределения:
xi: 1,5; 3,5; 5,5; 7,5.
ωi: 0,1; 0,2; 0,4; 0,3.
Гистограмма относительных частот, описание
Определение
Гистограмма относительных частот – это фигура ступенчатого вида, в составе которой имеются прямоугольники.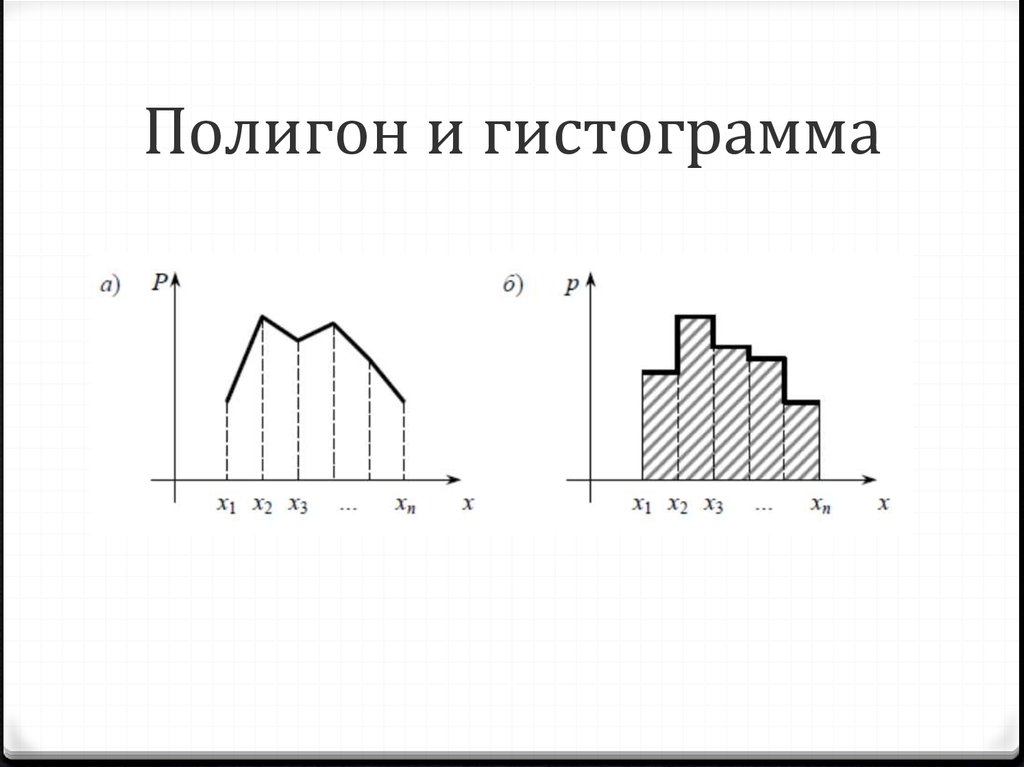
Строить гистограмму следует, соблюдая следующий порядок. На оси абсцисс указывают частичные интервалы. Над ними на расстоянии, равном плотности относительной частоты (ωi/h), отмечают отрезки, параллельные оси OX.
Пример
Интервалы, xi: 2–5, 5–8, 8–11, 11–14, 14–17, 17–20.
Частота вариант, ni: 15, 35, 64, 55, 21, 10 (всего 200).
Относительные частоты, ωi: 0,075; 0,175; 0,320; 0,275; 0,105; 0,050 (всего 1,000).
Гистограмма данного ряда распределения имеет вид:
Площадь прямоугольников гистограммы
Площадь одного прямоугольника, входящего в состав гистограммы относительных частот, равна относительной частоте вариант и вычисляется по формуле:
\(h\frac{\omega_i}h=\omega_i\)
Для вычисления площади всей гистограммы необходимо сложить площади всех прямоугольников, составляющих ступенчатую фигуру. Следовательно, искомая величина будет равна единице.
Следовательно, искомая величина будет равна единице.
Примеры решения задач
Задача 1
Постройте полигон относительных частот для следующего вариационного ряда:
xi: 2, 7, 8, 15, 16, 17.
ni: 15, 35, 64, 55, 21, 10.
Решение
Для начала необходимо вычислить относительные частоты:
xi: 2, 7, 8, 15, 16, 17.
ni: 15, 35, 64, 55, 21, 10 (итого 200).
ωi: 0,075; 0,175; 0,320; 0,275; 0,105; 0,050 (итого 1,000).
Построим искомую ломаную:
Задача 2
Построить гистограмму относительных частот распределения, имея следующие данные:
Частичный интервал при длине h, равной 3: 2–5, 5–8, 8–11, 11–14.
ni: 9, 10, 25, 6.
Решение
Сначала определим относительные частоты. Для этого установим объем выборочной совокупности n:
n=Σni=50.
Затем найдем ωi:
ω1= 9/50=0,18
ω2= 10/50=0,2
ω3= 25/50=0,5
ω4= 6/50=0,12
Далее вычислим ωi/h, то есть плотность частоты:
0,18/3=0,06
0,2/3=0.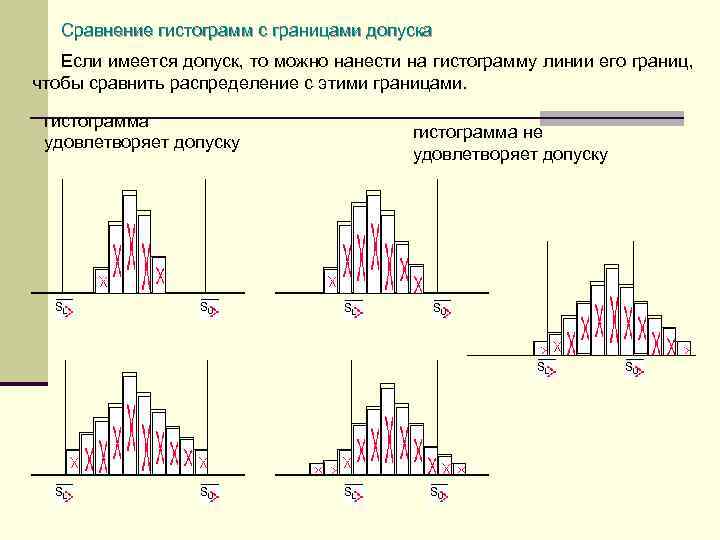 07
07
0,5/3=0,16
0,12/3=0,04
Образуются следующие данные:
Частичный интервал: 2–5, 5–8, 8–11, 11–14.
Сумма относительных частот: 0,18; 0,2; 0,5; 0,12.
Плотность частоты: 0,06; 0,07; 0,16; 0,04.
Насколько полезной была для вас статья?Рейтинг: 5.00 (Голосов: 1)
Поиск по содержимому
Часть 2. Математическая статистика. Задание 1.Рассчитать и построить гистограмму относительных частот по сгруппированным данным (смотри таблицу 1)
Поделись
Задание 1.Рассчитать и построить гистограмму относительных частот по сгруппированным данным (смотри таблицу 1), где n i – частота попадания вариант в промежуток (xi,, xi + 1].
| i | n i | |
| 7 — 9 | ||
| 9 — 11 | ||
| 11 — 13 | ||
| 13 — 15 | ||
| 15 — 17 |
Решение.
Объем выборки n=5+4+8+12+11=40.
Построим группированный статистический ряд относительных частот wi=mi/n
| i | wi | |
| 7 — 9 | 0,125 | |
| 9 — 11 | 0,1 | |
| 11 — 13 | 0,2 | |
| 13 — 15 | 0,3 | |
| 15 — 17 | 0,275 |
Построим гистограмму относительных частот
Задание 2.Найти несмещенную выборочную дисперсию на основании данного распределения выборки.
| xi | 0,01 | 0,04 | 0,08 | 0,14 |
| ni |
Решение.
Объем выборки n=19+28+31+22=100.
Составим расчетную таблицу
| xi | 0,01 | 0,04 | 0,08 | 0,14 | |
| ni | |||||
| xi ni | 0,19 | 1,12 | 2,48 | 3,08 | 6,87 |
| ∙ ni | 0,0019 | 0,0448 | 0,1984 | 0,4312 | 0,6763 |
Вычислим выборочную среднюю по формуле:
Выборочную дисперсиювычислим по формуле:
= .
Найдем исправленную выборочную дисперсию
.
Т.к. объем выборки большой, исправленная выборочная дисперсиянезначительно отличается от выборочной дисперсии.
Ответ: 0,002064.
Задание 3.Проверить нулевую гипотезу о том, что заданное значение а0 =58 является математическим ожиданием нормально распределенной случайной величины при 5% уровне значимости для двусторонней критической области, если в результате обработки выборки объема n = 10 получено выборочное среднее =56, а выборочное среднее квадратичное отклонение равно s =4
Решение.
Сформулируем гипотезы.
Н0 : — математическое ожидание нормально распределенной случайной величины равно а0 =58;
Н1: — математическое ожидание не равно 58.
Поскольку дисперсия генеральной совокупности неизвестна, для проверки основной гипотезы воспользуемся критерием Стьюдента:
,
где n = 10, а0 =58, =56, s =4.
Найдем наблюдаемое значение критерия
.
Т.к. альтернативная гипотеза имеет вид: Н1 : 58, то критическая область двухсторонняя.
По таблице критических точек распределения Стьюдента при заданном уровне значимости a = 0,05 и числу степеней свободы находим Ткр (a,k)= Ткр (0,05;9)= 2,26. Т.к. кр, то нет оснований отвергнуть нулевую гипотезу, т.е. можно считать, что математическое ожидание нормально распределенной случайной величины равно а0 =58.
Ответ: Т=-1,58; Ткр =2,26, гипотеза Н0
Задание 4.При уровне значимости α = 0,1 проверить гипотезу
H0: о равенстве дисперсий двух нормально распределенных случайных величин X и Y на основе выборочных данных при альтернативной гипотезе H1: .
| xi | ni | yi | mi |
Решение.
По данным выборкам найдем исправленные выборочные дисперсии:
для Х
| xi | ni | xi ∙ ni | ∙ ni |
Объем выборки n=15.
Вычислим выборочную среднюю по формуле:
Выборочную дисперсиювычислим по формуле:
= .
Найдем исправленную выборочную дисперсию
.
для Y
| yi | mi | уi mi | ∙ mi |
Аналогично, найдем числовые характеристики для Y.
Объем выборки n=26.
Выборочная средняя:
Выборочная дисперсия:
= .
Исправленная выборочная дисперсия:
.
Найдём наблюдаемое значение критерия Фишера
.
где в числителе стоит большая дисперсия.
Т.к. , nх = 15, 1,98; nу = 26, 3,28.
то наблюдаемое значение критерия равно
.
k1 = n1 – 1 = 26 – 1 = 25 и k2 = n2 – 1 = 15 – 1 = 14 (числа степеней свободы).
С помощью встроенной функции EXCEL FPACПОБРпри уровне значимости a = 0,1 и данным числам степеней свободы находим
Tкр (0.1; 25; 14) = .1,93. Т.к. Т < Ткр, то нет оснований отвергать нулевую гипотезу (т.е. можно считать, что дисперсии двух выборок равны).
Ответ: Т=1,66; Ткр =1,93, гипотеза Н0 принимается.
Приложение 1
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
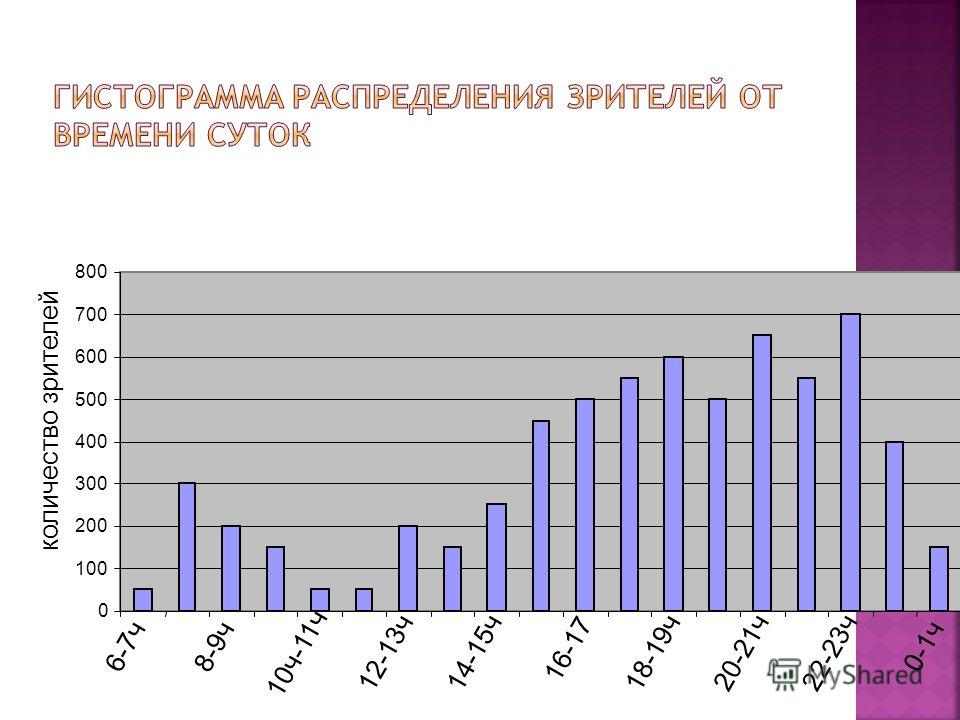
⇐ ПредыдущаяСтр 12 из 20Следующая ⇒ Для наглядности в статистике часто пользуются геометрической интер-претацией статистического распределения выборки, строя, так называемые, полигон и гистограмму частот (или относительных частот). Для построения полигона частот (или относительных частот) при дискретном распределении признака по оси абсцисс откладывают значения признака х i , а по оси ординат – частоты ni (или соответственно относительные частоты Wi). Точки с координатами (xi , ni) (или (xi , Wi)) соединяют отрезками прямых. Полигон частот дает представление о том, насколько часто встречаются те или иные значения исследуемого признака. Пример. Для распределения
полигон относительных частот имеет вид, показанный на рисунке. Полигон относительных частот – это статистический аналог многоугольника распределения дискретной случайной величины в теории вероятностей. Если исследуемый признак – непрерывная случайная величина, то целесообразно строить гистограмму частот. Для этого интервал, в котором заключены все наблюдавшиеся значения признака, делят на ряд частичных интервалов одинаковой длины ∆. Далее находят ni— сумму частот значений признака, попавших в i — ый частичный интервал, и строят ступенчатую фигуру из прямоугольников с основанием, равным ∆, и площадью, равной ni. Если значения признака совпадают с границей интервала, то их включают в сумму частот значений признака, принадлежащих соседним интервалам с частотами, равными половине частоты этого признака. Полученный график называется гистограммой частот. Площадь гистограммы частот равна сумме частот всех наблюдавшихся значений признака, то есть объему выборки. Гистограмма относительных частот строится точно также, отличаясь от гистограммы частот лишь масштабом по оси ординат, а именно, по оси ординат откладывается плотность относительной частоты . Число интервалов r гистограммы определяют приближенно по формуле Старджесса для выборки объема n (округляя r до ближайшего целого значения):
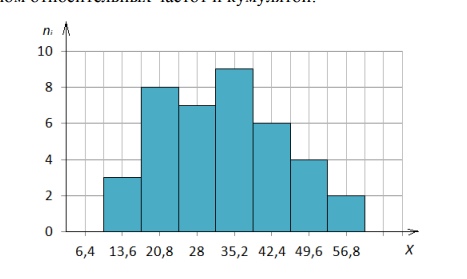
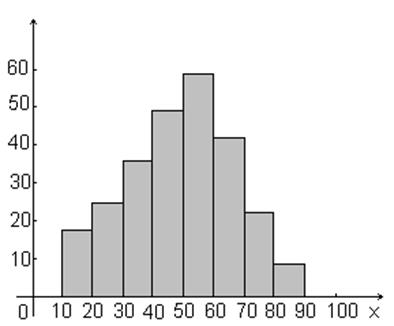
Пример. Произведено 100 измерений диаметров валиков, результаты которых представлены в таблице 4. Таблица 4
Построить гистограммы частот и относительных частот этого распределения. Как видно из таблицы, наименьшее значение диаметра-15,20 мм, наи-большее-15,60 мм, длина этого промежутка — 0,4 мм. Число частичных интервалов принимаем по правилу Старджесса, равным восьми. Подсчитываем число значений признака, попадавших в каждый интервал. Для построения гистограмм частот (и относительных частот) составим таблицу 5. Таблица 5
Соответствующие гистограммы изображены на рисунке.
При увеличении объема выборочной совокупности гистограмма относительных частот приближается к дифференциальному закону распределения признака в генеральной совокупности, то есть гистограмма относительных частот является статистическим аналогом плотности вероятностей f ( x ) непрерывной случайной величины. ⇐ Предыдущая78910111213141516Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Гистограмма относительной частоты: определение и как ее составить
Описательная статистика > Как построить гистограмму относительной частоты
Содержание (нажмите, чтобы перейти к этому разделу):
- Что такое относительная частота?
- Изготовление стола
- Гистограмма относительной частоты
- Как построить гистограмму относительной частоты: шаги
Относительная частота — это то, как часто что-то происходит, деленное на все возможные исходы. Формула относительной частоты:
Посмотрите видео, в котором объясняется, как построить гистограмму относительной частоты:
Как сделать гистограмму относительной частоты
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Пример
Например, вы играете в компьютерную игру 50 раз со своим другом Солом.
Вы выиграли 15 раз, Сол выиграл 30 раз, и вы сыграли вничью 5 раз.
На данный момент Сол выиграл 30 игр из 50. Вы можете записать это в виде дроби, то есть 30/50 = 3/5. Относительная частота выигрыша Солнца составляет 3/5.
Вы можете использовать относительную частоту как оценку вероятности выигрыша Солнца в будущем (вероятность 3/5).
Вернуться к началу
Таблица относительной частоты показывает, как часто что-то происходит по сравнению с другими событиями. Например, в следующей таблице показана частота продажи книг в том или ином книжном магазине. Другими словами, он показывает вам , сколько книг было продано :
| Цена | Частота |
| от 1 до 10 долларов | 100 |
| от 11 до 20 долларов | 160 |
| от 21 до 30 долларов | 100 |
| Более 30 долларов США | 40 |
В этой таблице показаны те же данные. Добавлен второй столбец для относительной частоты. Например, книги по цене от 1 до 10 долларов составляют 0,25 (25%) от общего объема продаж.
Добавлен второй столбец для относительной частоты. Например, книги по цене от 1 до 10 долларов составляют 0,25 (25%) от общего объема продаж.
| Цена | Частота | Относительная частота |
| от 1 до 10 долларов | 100 | .25 |
| от 11 до 20 долларов | 160 | .40 |
| от 21 до 30 долларов | 100 | .25 |
| Более 30 долларов США | 40 | .25 |
Наверх
Обычная гистограмма для приведенных выше данных будет показывать количество проданных книг. Например, в первом столбце показано, что в самой низкой ценовой группе (до 10 долларов США) было продано 100 книг.
Гистограмма, показывающая фактическое количество проданных книг. Гистограмма относительной частоты будет показывать относительную частоту проданных книг. Например, эта гистограмма показывает, что первая категория составляет 25% от общего объема продаж книг.
Что такое гистограмма относительной частоты?
Гистограмма относительной частоты — это тип графика, который показывает, как часто что-то происходит, в процентах. На следующей гистограмме относительной частоты показаны продажи книг за определенный день. Цены категорий («ячейки») отложены по горизонтальной оси (ось x), а относительные частоты (в процентах от общего числа) показаны в вертикальном столбце (ось y).
Гистограммы относительной частоты аналогичны круговым диаграммам тем, что они показывают проценты от целого. Общее количество продаж книг в таблице выше = 0,25 (25%) + 0,4 (40%) + 0,25 (25%) + 0,10 (10%) = 1 (100%). Вот круговая диаграмма, соответствующая приведенной выше гистограмме относительной частоты:
В этих шагах я собираюсь показать вам, используя частотную диаграмму для обобщения ваших данных. Это необязательный , но он действительно поможет вам отслеживать ваши данные, чтобы ваша диаграмма была правильной!
Шаг 1: Создайте частотную диаграмму ваших данных. Частотная диаграмма — это просто список того, сколько раз что-то происходило. Для приведенной выше гистограммы относительной частоты это будет количество книг, проданных по каждой цене:
Частотная диаграмма — это просто список того, сколько раз что-то происходило. Для приведенной выше гистограммы относительной частоты это будет количество книг, проданных по каждой цене:
| Ценовой диапазон | Номер продан | |
| $5-10 | 75 | |
| $11-15 | 120 | |
| $16-20 | 75 | |
| $21-$25 | 30 |
Шаг 2: Подсчитайте общее количество предметов. Для примера задачи было продано 75 + 120 + 75 + 30 = 300 книг.
Шаг 3: Определите относительную частоту, разделив количество в каждой категории на общее количество.
75/300 = 0,25
120/300 = 0,40
75/300 = 0,25
30/300 = 0,10
Добавьте эту информацию в новый столбец на диаграмме относительной частоты.
| Диапазон цен | Номер продан | ||
| $5-10 | 75 | . 25 25 | |
| $11-15 | 120 | .40 | |
| $16-20 | 75 | .25 | |
| $21-$25 | 30 | .10 |
Шаг 4: Создайте гистограмму с информацией из вашей диаграммы частот. Вы могли бы просто набросать его вручную — отложив относительные частоты по вертикальной оси, а цены по горизонтальной оси (см.: Как построить гистограмму). Тем не менее, вы также можете использовать технологии. См.: Как сделать гистограмму в Excel.
Вот и все!
Вернуться к началу
Посетите наш канал на YouTube, чтобы получить дополнительную справку по статистике и советы!
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Гистограмма относительной частоты: определение и как ее составить» от StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/relative-frequency-histogram-2/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Статистика и гистограммы – макеты
Гистограмма представляет собой гистограмму, созданную для количественных данных. Поскольку данные являются числовыми, вы делите их на группы, не оставляя пробелов между ними (таким образом столбцы соединяются). Y 9Ось 0046 — показывает либо частоты (числа), либо относительные частоты (проценты) данных, попадающих в каждую группу.Как создать гистограмму
Чтобы построить гистограмму, вы сначала делите свои данные на разумное количество групп одинаковой длины. Подсчитайте количество значений в наборе данных, попадающих в каждую группу (другими словами, составьте таблицу частот). Если точка данных попадает на границу, примите решение о том, в какую группу ее поместить, убедившись, что вы остаетесь последовательным (всегда помещайте ее в более высокую из двух или всегда помещайте ее в более низкую из двух). Составьте гистограмму, используя группы и их частоты — частотная гистограмма.
Составьте гистограмму, используя группы и их частоты — частотная гистограмма. Если вы разделите частоты на общий размер выборки, вы получите процент, который попадает в каждую группу. Таблица, которая показывает группы и их проценты, является таблицей относительной частоты. Соответствующая гистограмма представляет собой гистограмму относительной частоты .
Вы можете использовать Minitab или другой программный пакет для создания гистограмм, или вы можете сделать свои гистограммы вручную. В любом случае выбранная вами ширина интервала (называемая бинами в компьютерных пакетах) может отличаться от той, что показана на рисунках, и это нормально, если вы выглядите одинаково. И они будут, если вы не используете необычно малое или большое количество полос, и ваши полосы имеют одинаковую ширину.
Вы также можете выбрать разные точки начала/конца для каждого интервала, и это тоже нормально. Просто убедитесь, что все четко помечено, чтобы ваш инструктор мог видеть, что вы пытаетесь сделать. И будьте последовательны в отношении ценностей, которые заканчиваются прямо на границе; всегда помещайте их в нижнюю группу или всегда помещайте их в верхнюю группу. Однако, если у вас есть выбор, создавайте свои гистограммы с помощью компьютерного пакета, такого как Minitab. Это значительно облегчает вашу задачу.
И будьте последовательны в отношении ценностей, которые заканчиваются прямо на границе; всегда помещайте их в нижнюю группу или всегда помещайте их в верхнюю группу. Однако, если у вас есть выбор, создавайте свои гистограммы с помощью компьютерного пакета, такого как Minitab. Это значительно облегчает вашу задачу.Ниже приведен пример создания двух типов гистограмм.
Результаты тестов для класса из 30 учащихся показаны в следующей таблице.
| Баллы | Частота |
| 70–79 | 8 |
| 80–89 | 16 |
| 90–99 | 6 |
Гистограмма частоты для данных оценок показана на следующем рисунке.
Вы можете найти относительные частоты, взяв каждую частоту и разделив ее на 30 (общий размер выборки). Относительные частоты для этих трех групп составляют 8/30 = 0,27 или 27%; 16/30 = 0,53 или 53%; и 6/30 = 0,20 или 20% соответственно.
Относительные частоты для этих трех групп составляют 8/30 = 0,27 или 27%; 16/30 = 0,53 или 53%; и 6/30 = 0,20 или 20% соответственно.
Гистограмма, основанная на относительных частотах, выглядит так же, как гистограмма (тех же данных). Единственное отличие — метка на оси Y.
Понимание гистограмм
Гистограмма дает вам общую информацию о трех основных характеристиках ваших количественных (числовых) данных: форме, центре и разбросе.Форма гистограммы показана ее общей структурой. Возможны многие шаблоны, и некоторые из них являются общими, в том числе следующие:
- Колокольчик: Выглядит как колокольчик — большая шишка посередине и хвосты, которые с каждой стороны опускаются примерно с одинаковой скоростью. (Рисунок а)
- Перекос вправо: Большая часть данных смещена влево, а несколько более крупных наблюдений отстают вправо. (Рисунок б)
- Перекос влево: Большая часть данных смещается вправо, а несколько меньших наблюдений отстают влево.
 (Рисунок в)
(Рисунок в) - Униформа: Все стержни имеют одинаковую высоту. (Рисунок г)
- Бимодальный: Два пика или (рис. e)
- U-образный: Бимодальный с двумя пиками на нижнем и верхнем концах, с меньшим количеством данных в середине. (См. Рисунок 4-1 (Рисунок f)
- Симметричный: Выглядит одинаково с обеих сторон, если разделить его посередине; колоколообразные, однородные и U-образные гистограммы — все это примеры симметричных данных. (Рисунки а, г и е)
Гистограммы имеют несколько общих шаблонов.
Вы можете просмотреть центр гистограммы двумя способами. Одной из них является точка на оси x , где график балансируется с учетом фактических значений данных. Эта точка называется средней , , и вы можете найти ее, найдя точку балансировки (представьте, что данные качаются). Другой способ увидеть центр — найти линию на гистограмме, где 50 процентов данных лежат по обе стороны. Линия называется медиана, и представляет собой физическую середину набора данных. Представьте, что вы разрезаете гистограмму пополам так, чтобы половина области лежала по обе стороны от линии.
Линия называется медиана, и представляет собой физическую середину набора данных. Представьте, что вы разрезаете гистограмму пополам так, чтобы половина области лежала по обе стороны от линии.
Разброс относится к расстоянию между данными либо относительно друг друга, либо относительно некоторой центральной точки. Одним из грубых способов измерения спреда является определение диапазона , или расстояния между наибольшим значением и наименьшим значением. Другой способ — искать среднее расстояние от середины, также известное как 9.0046 стандартное отклонение. Стандартное отклонение трудно определить, просто взглянув на гистограмму, но вы можете получить приблизительное представление, если возьмете диапазон, разделенный на 6. Если высота столбцов, близких к середине, кажется очень высокой, это означает, что большинство значений близки к среднему, что указывает на небольшое стандартное отклонение. Если столбцы кажутся короткими, у вас может быть большее стандартное отклонение.
Вы можете использовать фактическую сводную статистику для расчета количественных данных, но гистограмма может дать вам общее направление для нахождения этих вех. И подобно круговым диаграммам и столбчатым диаграммам, не все гистограммы являются достоверными, полными и точными. Вы должны знать, что искать, чтобы оценить их.
Как исправить искаженные данные с помощью гистограмм
Вам необходимо обратить особое внимание на искаженные наборы данных с точки зрения того, какую статистику лучше всего использовать и когда. Вы также должны знать, что использование неправильных статистических данных может привести к вводящим в заблуждение ответам.Вы можете связать среднее значение и медиану, чтобы узнать о форме ваших данных. Если среднее значение и медиана близки к равным, это создаст примерно симметричную форму
На среднее значение влияют выбросы в данных, а на медиану — нет. Если среднее значение и медиана близки друг к другу, данные не искажены и, вероятно, не содержат выбросов с одной или другой стороны. Это означает, что данные выглядят примерно одинаково по обе стороны от середины, что является определением симметричных данных (см. a, d или f на предыдущем рисунке).
Это означает, что данные выглядят примерно одинаково по обе стороны от середины, что является определением симметричных данных (см. a, d или f на предыдущем рисунке).
Тот факт, что среднее значение и медиана близки друг к другу, говорит о том, что данные примерно симметричны, может быть использован в тестовом вопросе другого типа. Предположим, кто-то спрашивает вас, симметричны ли данные, и у вас нет гистограммы, но есть среднее значение и медиана. Сравните два значения среднего и медианы, и если они близки, данные симметричны. Если это не так, данные несимметричны.
Как обнаружить вводящую в заблуждение гистограмму
Читатели могут быть введены в заблуждение гистограммой так, как это невозможно сделать с гистограммой. Помните, что гистограмма имеет дело с числовыми данными, а не с категориальными данными, а это означает, что вы должны определить, как вы хотите, чтобы числовые данные, разбитые на группы, отображались на горизонтальной оси. И то, как вы определяете эти группы, может привести к тому, что график будет выглядеть совсем по-другому. Следите за гистограммами, которые используют масштаб, чтобы ввести читателей в заблуждение. Как и в случае с гистограммами, вы можете преувеличить различия, используя меньший масштаб на вертикальной оси гистограммы, и вы можете преуменьшить различия, используя больший масштаб.
Следите за гистограммами, которые используют масштаб, чтобы ввести читателей в заблуждение. Как и в случае с гистограммами, вы можете преувеличить различия, используя меньший масштаб на вертикальной оси гистограммы, и вы можете преуменьшить различия, используя больший масштаб.2.2: Гистограммы, огивы и частотные полигоны
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10921
- Кэтрин Козак
- Общественный колледж Коконино
В большинстве работ по этой книге вы будете использовать гистограмму для отображения данных. Одним из преимуществ гистограммы является то, что она может легко отображать большие наборы данных. Эмпирическое правило заключается в использовании гистограммы, когда набор данных состоит из 100 или более значений.
Эмпирическое правило заключается в использовании гистограммы, когда набор данных состоит из 100 или более значений.
Гистограмма состоит из смежных (примыкающих) прямоугольников. Он имеет как горизонтальную ось, так и вертикальную ось. Горизонтальная ось помечена тем, что представляют данные (например, расстояние от вашего дома до школы). Вертикальная ось отмечена либо частотой, либо относительной частотой (или частотой в процентах, либо вероятностью). График будет иметь одинаковую форму с любой меткой. Гистограмма (как и stemplot) может дать вам форму данных, центр и разброс данных.
График количественных данных похож на гистограмму, за исключением некоторых существенных отличий. Во-первых, на гистограмме категории могут располагаться в любом порядке по горизонтальной оси. Для этих значений данных нет установленного порядка. Вы не можете сказать, как данные распределяются на основе формы, поскольку форма может измениться, просто если расположить категории в другом порядке. В случае с количественными данными данные располагаются в определенном порядке, поскольку вы имеете дело с числами. С количественными данными вы можете говорить о распределении, поскольку форма меняется лишь немного в зависимости от того, сколько категорий вы настроили. это называется частотное распределение .
В случае с количественными данными данные располагаются в определенном порядке, поскольку вы имеете дело с числами. С количественными данными вы можете говорить о распределении, поскольку форма меняется лишь немного в зависимости от того, сколько категорий вы настроили. это называется частотное распределение .
Это приводит ко второму отличию от гистограмм. На гистограмме категории, которые вы сделали в таблице частот, были определены вами. В количественных данных категории являются числовыми категориями, а числа определяются тем, сколько категорий (или так называемых классов) вы выбираете. Если два человека имеют одинаковое количество категорий, то они будут иметь одинаковое частотное распределение. В то время как в качественных данных может быть много разных категорий в зависимости от точки зрения автора.
Третье отличие состоит в том, что категории соприкасаются с количественными данными, и в графике не будет пробелов. Причина, по которой гистограммы имеют пробелы, состоит в том, чтобы показать, что категории не продолжаются, как в количественных данных. Поскольку график для количественных данных отличается от качественных данных, ему дается новое имя. Название графика — гистограмма . Чтобы создать гистограмму, вы должны сначала создать частотное распределение. Идея частотного распределения состоит в том, чтобы взять интервал, охватываемый данными, и разделить его на равные подинтервалы, называемые классами.
Поскольку график для количественных данных отличается от качественных данных, ему дается новое имя. Название графика — гистограмма . Чтобы создать гистограмму, вы должны сначала создать частотное распределение. Идея частотного распределения состоит в том, чтобы взять интервал, охватываемый данными, и разделить его на равные подинтервалы, называемые классами.
Краткое изложение шагов, необходимых для создания частотного распределения:
- Найти диапазон = наибольшее значение – наименьшее значение
- Выберите количество классов для использования. Обычно количество классов составляет от пяти до двадцати. Пять классов используются, если имеется небольшое количество точек данных, и двадцать классов, если имеется большое количество точек данных (более 1000 точек данных). (Примечание: отныне категории будут называться классами.)
- Ширина класса = \(\frac{\text {диапазон}}{\# \text {классы}}\) Всегда округляйте до следующего целого числа (даже если ответ уже является целым числом, переходите к следующему целому числу).
 Если вы этого не сделаете, ваш последний класс не будет содержать самое большое значение данных, и вам придется добавить еще один класс только для него. Если вы округлите, то ваше самое большое значение данных попадет в последний класс, и проблем не будет.
Если вы этого не сделаете, ваш последний класс не будет содержать самое большое значение данных, и вам придется добавить еще один класс только для него. Если вы округлите, то ваше самое большое значение данных попадет в последний класс, и проблем не будет. - Создайте классы. Каждый класс имеет ограничения, которые определяют, какие значения попадают в каждый класс. Чтобы найти ограничения класса, установите наименьшее значение в качестве нижнего предела класса для первого класса. Затем добавьте ширину класса к нижнему пределу класса, чтобы получить следующий нижний предел класса. Повторяйте, пока не получите все классы. Верхний предел класса для класса на единицу меньше нижнего предела для следующего класса.
- Чтобы классы действительно соприкасались, один класс должен начинаться там, где заканчивается предыдущий. Это известно как граница класса. Чтобы найти границы класса, вычтите 0,5 из нижнего предела класса и прибавьте 0,5 к верхнему пределу класса.
- Иногда полезно найти среднюю точку класса.
 Процесс
Процесс
Середина \(=\frac{\text {нижний предел +верхний предел}}}{2}\) - Чтобы определить количество точек данных, попадающих в каждый класс, просмотрите каждое значение данных и посмотрите, между какими границами класса оно находится. Использование подсчетных меток может быть полезным при подсчете значений данных. Частота для класса — это количество значений данных, попадающих в класс.
Примечание
Приведенное выше описание относится к значениям данных, которые являются целыми числами. Если значение ваших данных имеет десятичные знаки, то ширина вашего класса должна быть округлена до ближайшего значения с тем же количеством десятичных знаков, что и исходные данные. Кроме того, границы вашего класса должны иметь на один десятичный знак больше, чем исходные данные. Например, если ваши данные имеют один десятичный разряд, то ширина класса будет иметь один десятичный разряд, а границы класса формируются путем прибавления и вычитания 0,05 из каждого предела класса.
Пример \(\PageIndex{1}\) создания таблицы частот
Таблица 2.2.1 содержит сумму арендной платы, ежемесячно выплачиваемой 24 студентам курса статистики. Сделайте распределение относительной частоты, используя 7 классов.
| 1500 | 1350 | 350 | 1200 | 850 | 900 |
| 1500 | 1150 | 1500 | 900 | 1400 | 1100 |
| 1250 | 600 | 610 | 960 | 890 | 1325 |
| 900 | 800 | 2550 | 495 | 1200 | 690 |
Таблица 2. 2.1 : Данные ежемесячной арендной платы
2.1 : Данные ежемесячной арендной платы
Решение :
- Найти диапазон:
Самое большое значение — наименьшее значение \ (= 2550-350 = 2200 \) - Выберите количество классов:
Указания сказать, чтобы использовать 7 классов. - Найдите ширину класса:
ширина \(=\frac{\text {диапазон}}{7}=\frac{2200}{7} \примерно 314,286\)
Округлить до 315
Всегда округлять до следующее целое число, даже если ширина уже является целым числом. - Найдите ограничения класса:
Начните с наименьшего значения. Это нижний предел класса для первого класса. Добавьте ширину, чтобы получить нижний предел следующего класса. Продолжайте добавлять ширину, чтобы получить все нижние пределы.
\(350+315=665,665+315=980,980+315=1295 \rightleftharpoons\),
Верхний предел на единицу меньше следующего нижнего предела: таким образом, для первого класса верхний предел класса будет \(665-1 =664\).
Когда у вас есть все 7 классов, убедитесь, что последнее число, в данном случае 2550, не меньше наибольшего значения в данных. Если нет, то вы где-то ошиблись. - Найдите границы класса:
Вычтите 0,5 из нижнего предела класса, чтобы получить границы класса. Добавьте 0,5 к верхнему пределу класса для последней границы класса.
\(350-0,5=349,5, \quad 665-0,5=664,5,\quad 980-0,5=979,5, \quad 1295-0,5=1294,5 \rightleftharpoons\)
Каждое значение в данных должно попадать ровно в один из классов . Никакие значения данных не должны попадать прямо на границу двух классов. - Найдите средние точки класса:
средняя точка \(=\frac{\text {нижний предел}+\text {верхний предел}}{2}\)
\(\frac{350+664}{2}=507, \frac{665+979}{2}=822, \rightleftharpoons\) - Подсчитайте и найдите частоту данных:
Просмотрите данные и поставьте отметку в соответствующем классе для каждой части данных, посмотрев, между какими границами класса находится значение данных. Заполните частоту, изменив каждый из подсчетов на число.
Заполните частоту, изменив каждый из подсчетов на число.
| Ограничения класса | Границы класса | Середина класса | Подсчет | Частота |
|---|---|---|---|---|
| 350-664 | 349,5-664,5 | 507 | |||| | 4 |
| 665-979 | 664,5-979,5 | 822 | \(\отмена{||||}\) ||| | 8 |
| 980-1294 | 979. 5-1294.5 5-1294.5 | 1137 | \(\отмена{||||}\) | 5 |
| 1295-1609 | 1294,5-1609,5 | 1452 | \(\отмена{||||}\) | | 6 |
| 16:10-19:24 | 1609.5-1924.5 | 1767 | 0 | |
| 1925-2239 | 1924.5-2239.5 | 2082 | 0 | |
| 2240-2554 | 2239. 5-2554.5 5-2554.5 | 2397 | | | 1 |
Таблица 2.2.2 : Распределение частоты для ежемесячной арендной платы
Убедитесь, что общее количество частот совпадает с количеством точек данных.
Трудно определить основную форму распределения, глядя на частотное распределение. Легче было бы посмотреть на график. График распределения частот для количественных данных называется частотной гистограммой или просто гистограммой для краткости.
Определение \(\PageIndex{1}\)
Гистограмма : график частот по вертикальной оси и границ классов по горизонтальной оси. Для каждого класса рисуются прямоугольники, где высота — это частота, а ширина — ширина класса.
Пример \(\PageIndex{2}\) рисования гистограммы
Рисование гистограммы для распределения из Пример 2.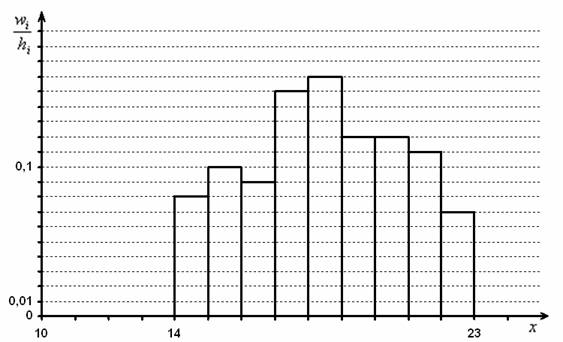 2.1 .
2.1 .
Решение :
Границы классов отложены по горизонтальной оси, а частоты отложены по вертикальной оси. Вы можете нанести средние точки классов вместо границ классов. График 2.2.1 был создан с использованием средних точек, потому что это было проще сделать с помощью программного обеспечения, создавшего график.
График 2.2.1 : Гистограмма месячной арендной платы
Обратите внимание, что на графике оси помечены, деления отмечены на каждой оси, и есть заголовок. Важно, чтобы ваши графики (все графики) были четко обозначены.
Просмотрев график, вы можете увидеть, что большинство студентов платят около 750 долларов в месяц за аренду жилья, при этом около 1500 долларов являются другой распространенной стоимостью. Из графика видно, что большинство студентов платят за аренду от 600 до 1600 долларов в месяц. Конечно, эти значения являются лишь оценками из графика. Существует большой разрыв между классом в 1500 долларов и самым высоким значением данных. Кажется, это говорит о том, что один студент платит гораздо больше, чем все остальные. Это значение можно считать выбросом. выброс — это значение данных, которое далеко от остальных значений. Это может быть необычное значение или ошибка. Это значение данных, которое следует исследовать. В данном случае студент живет в очень дорогом районе города, поэтому значение не является ошибкой, а просто очень необычно. Есть и другие аспекты, которые можно обсудить, но сначала необходимо ввести некоторые другие понятия.
Существует большой разрыв между классом в 1500 долларов и самым высоким значением данных. Кажется, это говорит о том, что один студент платит гораздо больше, чем все остальные. Это значение можно считать выбросом. выброс — это значение данных, которое далеко от остальных значений. Это может быть необычное значение или ошибка. Это значение данных, которое следует исследовать. В данном случае студент живет в очень дорогом районе города, поэтому значение не является ошибкой, а просто очень необычно. Есть и другие аспекты, которые можно обсудить, но сначала необходимо ввести некоторые другие понятия.
Частоты полезны, но понимание относительного размера каждого класса по отношению к сумме также полезно. Чтобы найти это, вы можете разделить частоту на сумму, чтобы создать относительную частоту. Если у вас есть относительные частоты для всех классов, то у вас есть относительное распределение частот.
Определение \(\PageIndex{2}\)
Распределение относительной частоты
Вариация распределения частоты — это распределение относительной частоты. Вместо того, чтобы давать частоты для каждого класса, рассчитываются относительные частоты.
Вместо того, чтобы давать частоты для каждого класса, рассчитываются относительные частоты.
Относительная частота \(=\frac{\text { частота }}{\# \text { точек данных }}\)
Это дает вам процент данных, попадающих в каждый класс.
Пример \(\PageIndex{3}\) создания таблицы относительной частоты
Найдите относительную частоту данных оценки.
Решение :
Из примера 2.2.1 частотное распределение воспроизводится в таблице 2.2.2 .
| Ограничения класса | Границы класса | Середина класса | Частота |
|---|---|---|---|
| 350-664 | 349,5-664,5 | 507 | 4 |
| 665-979 | 664,5-979,5 | 822 | 8 |
| 980-1294 | 979,5-1294,5 | 1127 | 5 |
| 1295-1609 | 1294,5-1609,5 | 1452 | 6 |
| 16:10-19:24 | 1609. 5-1924.5 5-1924.5 | 1767 | 0 |
| 1925-2239 | 1924.5-2239.5 | 2082 | 0 |
| 2240-2554 | 2239.5-2554.5 | 2397 | 1 |
Таблица 2.2.2 : Распределение частоты ежемесячной арендной платы
Разделите каждую частоту на количество точек данных.
\(\frac{4}{24}=0,17, \frac{8}{24}=0,33, \frac{5}{24}=0,21, \rightleftharpoons\)
| Ограничения класса | Границы класса | Середина класса | Частота | Относительная частота |
|---|---|---|---|---|
| 350-664 | 349,5-664,5 | 507 | 4 | 0,17 |
| 665-979 | 664,5-979,5 | 822 | 8 | 0,33 |
| 980-1294 | 979,5-1294,5 | 1127 | 5 | 0,21 |
| 1295-1609 | 1294,5-1609,5 | 1452 | 6 | 0,25 |
| 16:10-19:24 | 1609.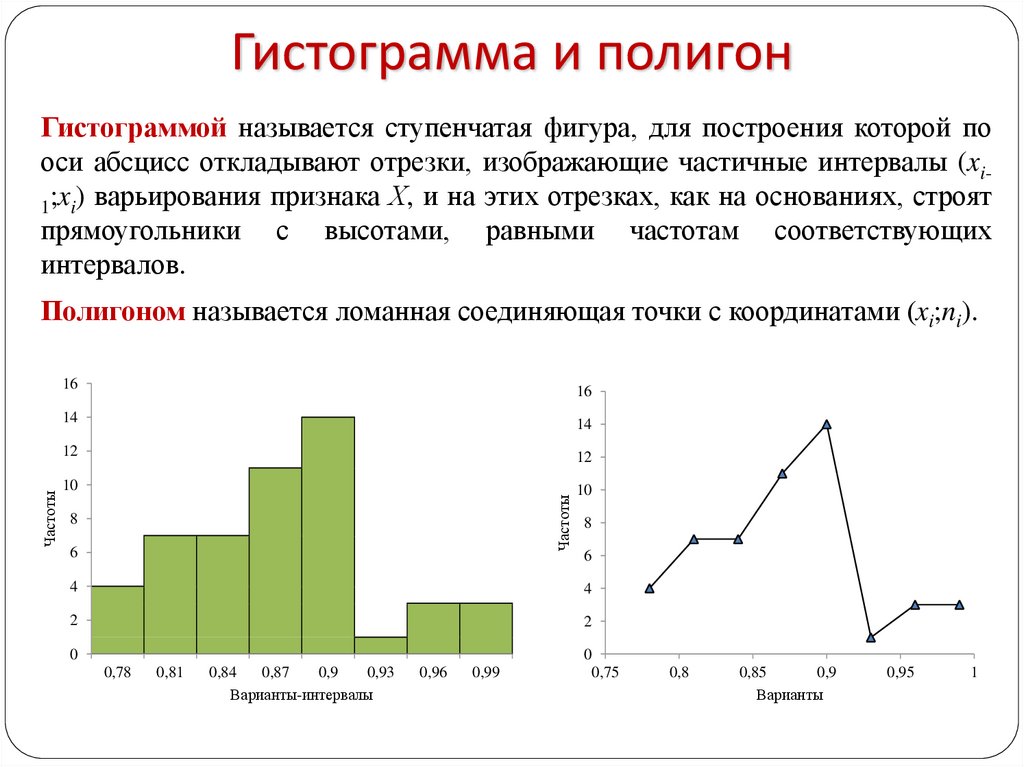 5-1924.5 5-1924.5 | 1767 | 0 | 0 |
| 1925-2239 | 1924.5-2239.5 | 2082 | 0 | 0 |
| 2240-2554 | 2239,5-2554,5 | 2397 | 1 | 0,04 |
| Всего | 24 | 1 |
Таблица 2. 2.3 : Распределение относительной частоты для ежемесячной арендной платы
2.3 : Распределение относительной частоты для ежемесячной арендной платы
Сумма относительных частот должна составлять 1 или 100%. (Это может быть немного не так из-за ошибок округления.)
График относительной частоты известен как гистограмма относительной частоты. Она выглядит идентично частотной гистограмме, но по вертикальной оси отложена относительная частота, а не просто частота.
Пример \(\PageIndex{4}\) построения гистограммы относительной частоты
Построение гистограммы относительной частоты распределения оценок из Пример 2.2.1 .
Решение :
Границы классов отложены по горизонтальной оси, а относительные частоты отложены по вертикальной оси. (Это непросто сделать в R, поэтому используйте другую технологию для построения гистограммы относительной частоты.)
График 2.2.2 : Гистограмма относительной частоты для месячной арендной платы
Обратите внимание, что форма совпадает с распределением частоты.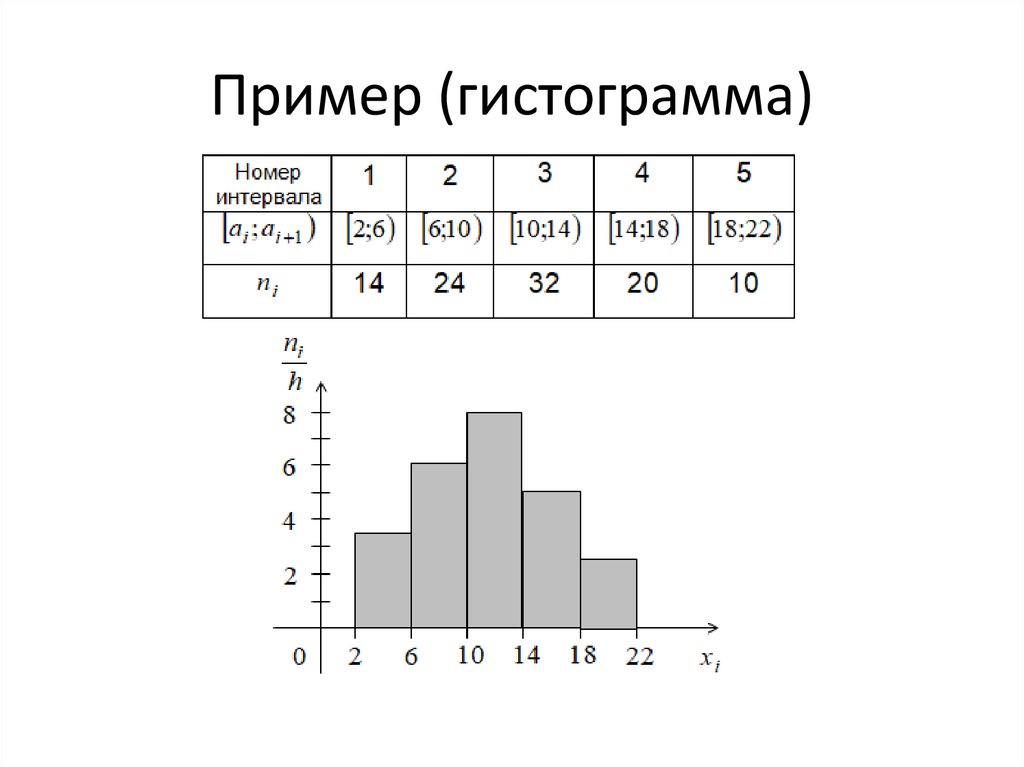
Другой полезной информацией является количество точек данных, находящихся ниже границы определенного класса. Например, учитель может захотеть узнать, сколько учеников получили показатели ниже 80%, врач может захотеть узнать, у скольких взрослых уровень холестерина ниже 160, или менеджер может захотеть узнать, сколько магазинов имеет валовой доход менее 2000 долларов в день. Это известно как кумулятивная частота . Если вы хотите знать, какой процент данных находится ниже определенной границы класса, то это будет кумулятивная относительная частота . Для кумулятивных частот вы определяете, сколько значений данных падает ниже верхнего предела класса.
Чтобы создать кумулятивное частотное распределение , подсчитайте количество точек данных, которые находятся ниже верхней границы класса, начиная с первого класса и дойдя до высшего класса. Последняя граница верхнего класса должна иметь все точки данных ниже нее. Также включите количество точек данных ниже нижней границы класса, которая равна нулю.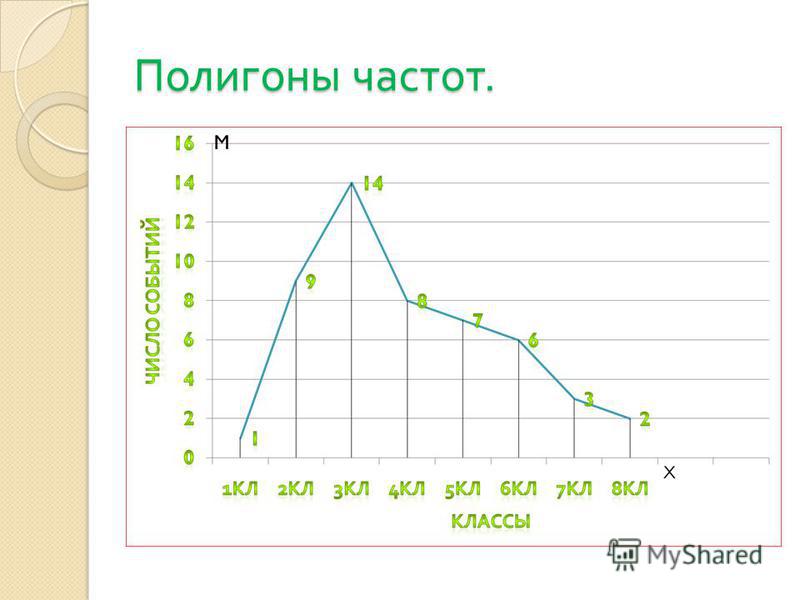
Пример \(\PageIndex{5}\) создания кумулятивного частотного распределения
Создание кумулятивного частотного распределения для данных в Пример 2.2.1 .
Решение :
Частотное распределение данных приведено в таблице 2.2.2 .
| Ограничения класса | Границы класса | Середина класса | Частота |
|---|---|---|---|
| 350-664 | 349,5-664,5 | 507 | 4 |
| 665-979 | 664,5-979,5 | 822 | 8 |
| 980-1294 | 979,5-1294,5 | 1127 | 5 |
| 1295-1609 | 1294,5-1609,5 | 1452 | 6 |
| 16:10-19:24 | 1609.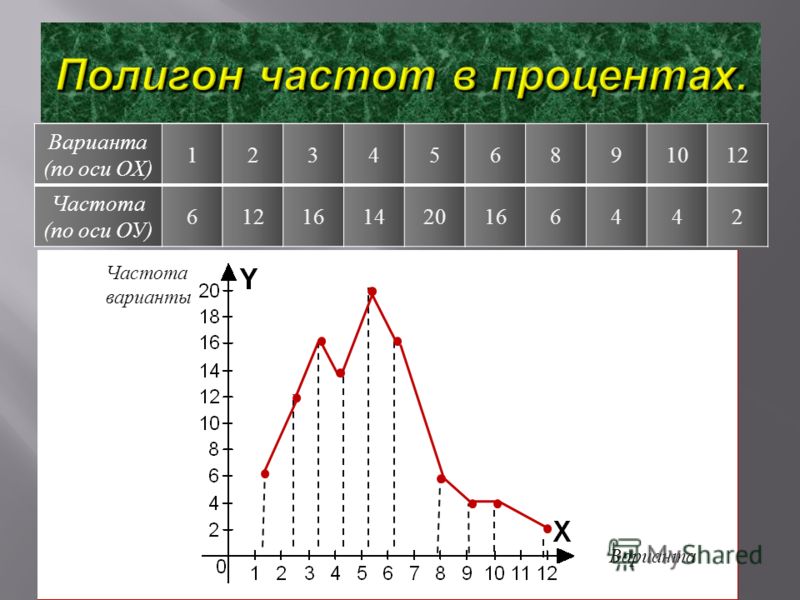 5-1924.5 5-1924.5 | 1767 | 0 |
| 1925-2239 | 1924.5-2239.5 | 2082 | 0 |
| 2240-2554 | 2239.5-2554.5 | 2397 | 1 |
Таблица 2.2.2 : Частотное распределение месячной арендной платы
Теперь спросите себя, сколько точек данных находится ниже границы каждого класса. Ниже 349,5 имеется 0 точек данных. Ниже 664,5 есть 4 точки данных, ниже 979,5 есть 4 + 8 = 12 точек данных, ниже 1294,5 есть 4 + 8 + 5 = 17 точек данных, и продолжайте этот процесс, пока не достигнете верхней границы класса. Это обобщено в таблице 2.2.4 .
Это обобщено в таблице 2.2.4 .
| Ограничения класса | Границы класса | Середина класса | Частота | Суммарная частота |
|---|---|---|---|---|
| 350-664 | 349,5-664,5 | 507 | 4 | 4 |
| 665-979 | 664,5-979,5 | 822 | 8 | 12 |
| 980-1294 | 979,5-1294,5 | 1127 | 5 | 17 |
| 1295-1609 | 1294,5-1609,5 | 1452 | 6 | 23 |
| 16:10-19:24 | 1609.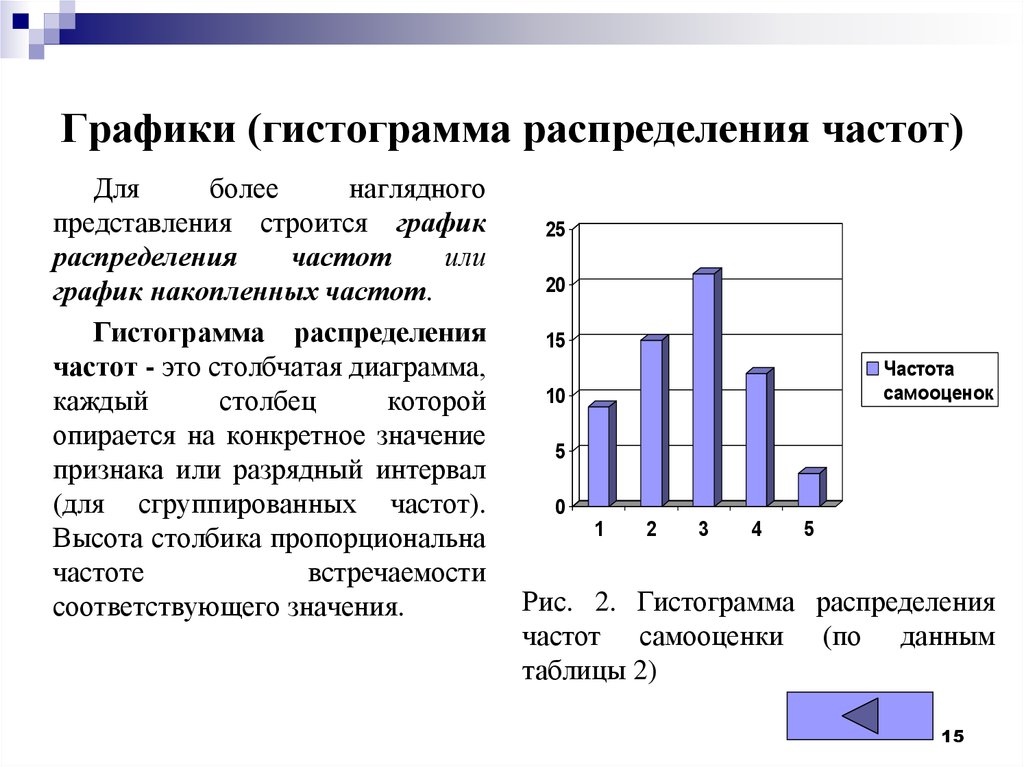 5-1924.5 5-1924.5 | 1767 | 0 | 23 |
| 1925-2239 | 1924.5-2239.5 | 2082 | 0 | 23 |
| 2240-2554 | 2239.5-2554.5 | 2397 | 1 | 24 |
Таблица 2.2.4 : Совокупное распределение ежемесячной арендной платы
Опять же, трудно смотреть на данные такими, какие они есть. График был бы полезен. График кумулятивной частоты называется ogive (o-jive). Чтобы создать оживу, сначала создайте масштаб по горизонтальной и вертикальной осям, который будет соответствовать данным. Затем нанесите точки границы высшего класса в зависимости от кумулятивной частоты. Убедитесь, что вы включили точку с самой низкой границей класса и кумулятивной частотой 0. Затем просто соедините точки.
Чтобы создать оживу, сначала создайте масштаб по горизонтальной и вертикальной осям, который будет соответствовать данным. Затем нанесите точки границы высшего класса в зависимости от кумулятивной частоты. Убедитесь, что вы включили точку с самой низкой границей класса и кумулятивной частотой 0. Затем просто соедините точки.
Пример \(\PageIndex{6}\) рисования оживы
Нарисуйте ожив для данных в Пример 2.2.1 .
Решение :
Используя верхнюю границу класса и соответствующую ей кумулятивную частоту, нанесите точки на оси в виде упорядоченных пар. Затем соедините точки. У вас должен получиться линейный график, который поднимается при движении слева направо.
Диаграмма 2.2.3 : Ожива для ежемесячной арендной платы арендную плату оплачивает определенное количество студентов. В качестве примера предположим, что вы хотите узнать, сколько студентов платят менее 1500 долларов в месяц за аренду, затем вы можете подняться от 1500 долларов до тех пор, пока не попадете на график, а затем вы перейдете к осям кумулятивной частоты, чтобы увидеть, какое значение соответствует это значение. Оказывается, около 20 студентов платят менее 1500 долларов. (см. График 2.2.4 .)
Оказывается, около 20 студентов платят менее 1500 долларов. (см. График 2.2.4 .)
График 2.2.4 : Ogive for Monthly Rent with Example
на 15 по вертикальной оси, а затем перейти к графику и вниз к горизонтальной оси, где линия пересекает график. Вы можете видеть, что 15 студентов платят менее 1200 долларов в месяц. (См. График 2.2.5 .)
График 2.2.5 : Ogive for Monthly Rent with Example
Если вы нарисуете кумулятивную относительную частоту, то сможете узнать, какой процент ниже определенного числа, а не просто количество людей ниже определенного значения.
Формы распределения:
Когда вы смотрите на распределение, смотрите на основную форму. Есть несколько основных форм, которые видны на гистограммах. Поймите, однако, что некоторые распределения не имеют формы. Общие формы симметричны, перекошены и однородны. Другой интерес заключается в том, сколько пиков может иметь график. Это известно как модальное.
Это известно как модальное.
Симметричный означает, что вы можете сложить график пополам посередине, и две стороны выровняются. Вы можете думать о двух сторонах как о зеркальных отражениях друг друга. Перекос означает, что один «хвост» графика длиннее другого. График перекошен в сторону более длинного хвоста (назад от ожидаемого). У однородного графа все столбцы одинаковой высоты.
Модальный относится к количеству пиков. Унимодальный имеет один пик, а бимодальный имеет два пика. Обычно, если на графике больше двух пиков, модальная информация уже не представляет интереса.
Другими важными особенностями, которые следует учитывать, являются промежутки между столбцами, повторяющийся шаблон, распределение данных и расположение центра графика.
Примеры графиков
:Этот график является примерно симметричным и унимодальным:
График 2.2.6 : Symmetric, Unimodal Graph
. График 2. 2.7 : Симметричный, бимодальный график
2.7 : Симметричный, бимодальный график
Этот график искажен вправо:
График 2.2.8 : Правый график. 2.2.9 : искаженный левый график
Этот график равномерный, так как все стержни та же высота:
График 2.2.10 : универсальный график
Пример \ (\ Pageindex \ (\ {7}\) создание частотного распределения, гистограммы и оживала
Следующие данные представляют процентное изменение уровня платы за обучение в государственных четырехгодичных колледжах (с поправкой на инфляцию) с 2008 по 2013 год (Weissmann, 2013). Создайте частотное распределение, гистограмму и оживу для данных.
| 19,5% | 40,8% | 57,0% | 15,1% | 17,4% | 5,2% | 13,0% |
| 15,6% | 51,5% | 15,6% | 14,5% | 22,4% | 19,5% | 31,3% |
| 21,7% | 27,0% | 13,1% | 26,8% | 24,3% | 38,0% | 21,1% |
| 9,3% | 46,7% | 14,5% | 78,4% | 67,3% | 21,1% | 22,4% |
| 5,3% | 17,3% | 17,5% | 36,6% | 72,0% | 63,2% | 15,1% |
| 2,2% | 17,5% | 36,7% | 2,8% | 16,2% | 20,5% | 17,8% |
| 30,1% | 63,6% | 17,8% | 23,2% | 25,3% | 21,4% | 28,5% |
| 9,4% | ||||||
Таблица 2. 2.5 : Данные об уровнях обучения в государственных четырехлетних колледжах
2.5 : Данные об уровнях обучения в государственных четырехлетних колледжах
Решение :
- Найдите диапазон:
наибольшее значение — наименьшее значение = \(78,4\)% \(-2,2\)% \(=76,2\)% - Выберите количество классов:
Поскольку имеется 50 точек данных, следует использовать от 6 до 8 классов. Давайте использовать 8. - Найдите ширину класса:
ширина \(=\frac{\text {диапазон}}{8}=\frac{76,2 \%}{8} \приблизительно 9,525 \%\)
Поскольку данные имеют один десятичный знак, тогда ширина класса должна округляться до одного десятичного знака. Убедитесь, что вы округлить.
ширина \(=9.6\)% - Найти ограничения класса:
\(2,2\%+9,6\%=11,8\%, 11,8\%+9,6 \%=21,4\%, 21,4\%+9,6 \%=31,0\%, \leftrightharpoons\) - Найдите границы класса:
Поскольку данные имеют один десятичный знак, границы класса должны иметь два десятичных знака, поэтому вычтите 0,05 из нижнего предела класса, чтобы получить границы класса. Добавьте 0,05 к верхнему пределу класса для границы последнего класса.
Добавьте 0,05 к верхнему пределу класса для границы последнего класса.
\(2,2-0,05=2,15 \%, 11,8-0,05=11,75 \%, 21,4-0,05=21,35 \% \левый-правыйгарпуны\)
Каждое значение в данных должно относиться ровно к одному из классов. Никакие значения данных не должны попадать прямо на границу двух классов. - Найдите средние точки класса:
средняя точка \(=\frac{\text {нижний предел}+\text {верхний предел}}{2}\)
\(\frac{2,2+11,7}{2}=6,95 \% , \frac{11,8+21,3}{2}=16,55 \%, \leftrightharpoons\) - Подсчитайте и найдите частоту данных:
| Ограничения класса | Границы класса | Середина класса | Подсчет | Частота | Относительная частота | Суммарная частота |
|---|---|---|---|---|---|---|
| 2,2-11,7 | 2,15-11,75 | 6,95 | \(\отмена{||||} |\) | 6 | 0,12 | 6 |
| 11,8-21,3 | 11. 75-21.35 75-21.35 | 16,55 | \(\cancel{||||} \cancel{||||} \cancel{||||} \cancel{||||}\) | 20 | 0,40 | 26 |
| 21,4-30,9 | 21.35-30.95 | 26.15 | \(\отмена{||||} \отмена{||||} |\) | 11 | 0,22 | 37 |
| 31,0-45,0 | 30,95-40,55 | 35,75 | \( |||| \) | 4 | 0,08 | 41 |
| 40,6-50,1 | 40,55-50,15 | 45,35 | \( || \) | 2 | 0,04 | 43 |
| 50,2-59,7 | 50,15-59,75 | 54,95 | \( || \) | 2 | 0,04 | 45 |
| 59,8-69,3 | 59,75-69,35 | 64,55 | \( ||| \) | 3 | 0,06 | 48 |
| 69,4-78,9 | 69.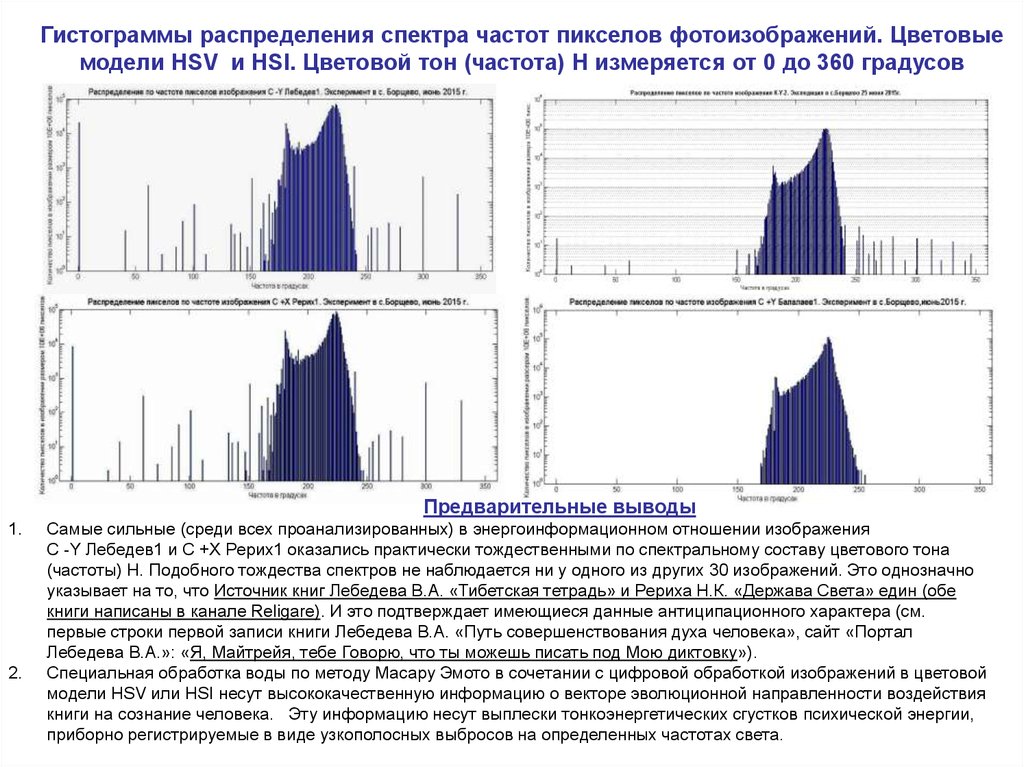 35-78.95 35-78.95 | 74,15 | \( || \) | 2 | 0,04 | 50 |
Таблица 2.2.6 : Распределение частоты для уровней обучения в государственных, четырехлетних колледжах
Убедитесь, что общее количество частот совпадает с количеством точек данных.
График 2.2.11 : Гистограмма уровней обучения в государственных колледжах с четырехгодичным обучением
Этот график смещен вправо, без пробелов. Это говорит о том, что в большинстве случаев увеличение платы за обучение составило около 16,55%, при этом в очень немногих штатах процентное увеличение составило более 45,35%.
Диаграмма 2.2.12 : Ogive для уровней обучения в государственных колледжах с четырехгодичным обучением
Глядя на ожив, вы можете видеть, что в 30 штатах процентное изменение уровня обучения составило около 25%. или менее.
или менее.
В некоторых случаях пределы классов в частотном распределении заранее определены. Пример 2.2.8 демонстрирует эту ситуацию.
Пример \(\PageIndex{8}\) создания частотного распределения и гистограммы
Ниже приведены процентные оценки 25 учащихся по курсу статистики. Составьте частотное распределение и гистограмму.
| 62 | 87 | 81 | 69 | 87 | 62 | 45 | 95 | 76 | 76 |
| 62 | 71 | 65 | 67 | 72 | 80 | 40 | 77 | 87 | 58 |
| 84 | 73 | 93 | 64 | 89 |
Таблица 2. 2.7 : Данные тестовых оценок
2.7 : Данные тестовых оценок
Решение :
обычно 9от 0 до 100 %, от 80 до 90 % и так далее. Легче не использовать границы класса, а вместо этого использовать ограничения класса и думать, что верхний предел класса соответствует нижнему пределу следующего класса, но не включает его. Например, класс 80–90 означает оценку от 80% до 90%, но не включая ее. Студент с 89,9% будет в классе 80-90.
| Ограничение класса | Середина класса | Подсчет | Частота |
|---|---|---|---|
| 40-50 | 45 | \( || \) | 2 |
| 50-60 | 55 | \( | \) | 1 |
| 60-70 | 65 | \( \отмена{||||} || \) | 7 |
| 70-80 | 75 | \( \отмена{||||} | \) | 6 |
| 80-90 | 85 | \( \отмена{||||} || \) | 7 |
| 90-100 | 95 | \( || \) | 2 |
Таблица 2.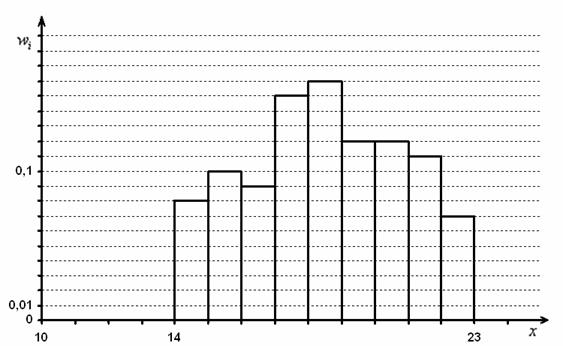

 Все правила по сольфеджио
Все правила по сольфеджио
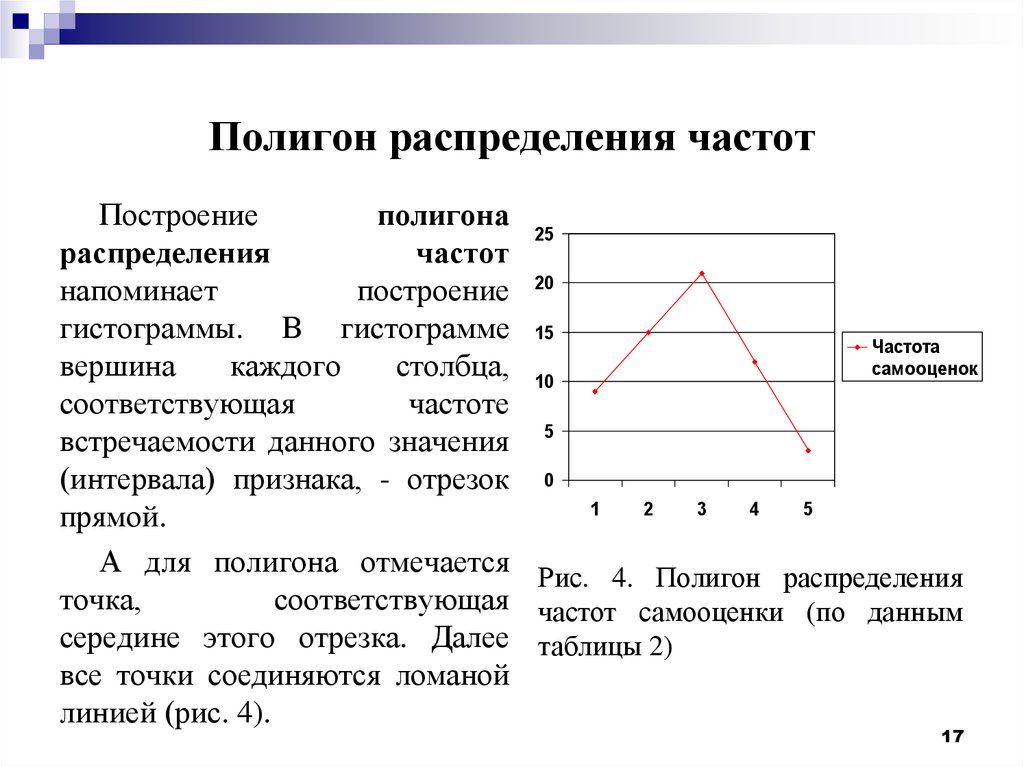
 Поэтому площадь i –го прямоугольника будет равна Wi – относительной частоте значений признака, попавших в i – ый интервал, а площадь гистограммы относительных частот будет равна сумме всех Wi, то есть единице.
Поэтому площадь i –го прямоугольника будет равна Wi – относительной частоте значений признака, попавших в i – ый интервал, а площадь гистограммы относительных частот будет равна сумме всех Wi, то есть единице.
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)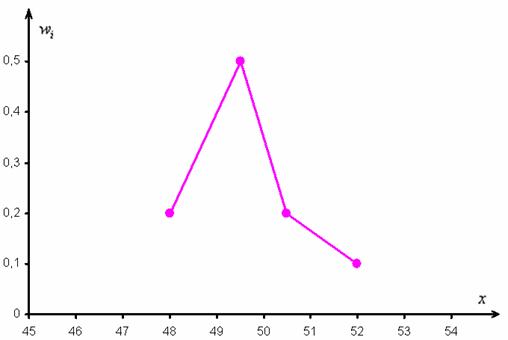 (Рисунок в)
(Рисунок в)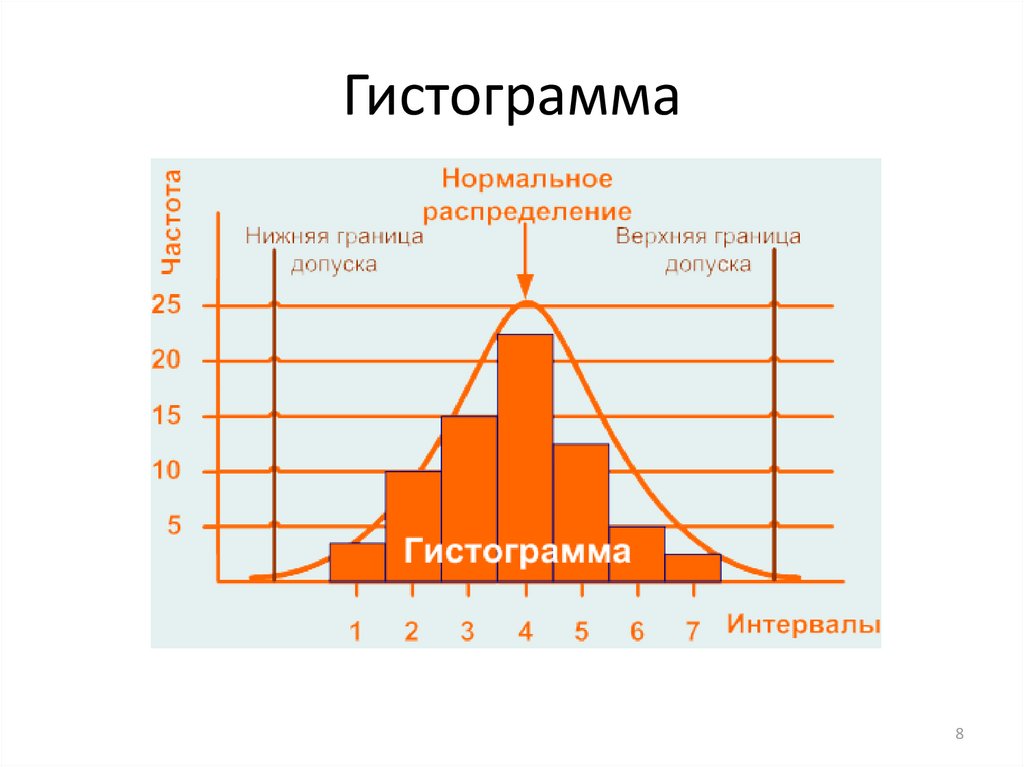 Если вы этого не сделаете, ваш последний класс не будет содержать самое большое значение данных, и вам придется добавить еще один класс только для него. Если вы округлите, то ваше самое большое значение данных попадет в последний класс, и проблем не будет.
Если вы этого не сделаете, ваш последний класс не будет содержать самое большое значение данных, и вам придется добавить еще один класс только для него. Если вы округлите, то ваше самое большое значение данных попадет в последний класс, и проблем не будет.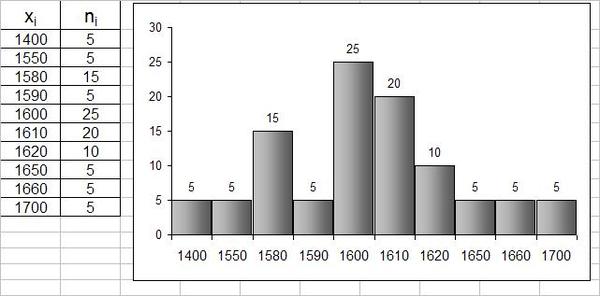 Процесс
Процесс 
 Заполните частоту, изменив каждый из подсчетов на число.
Заполните частоту, изменив каждый из подсчетов на число.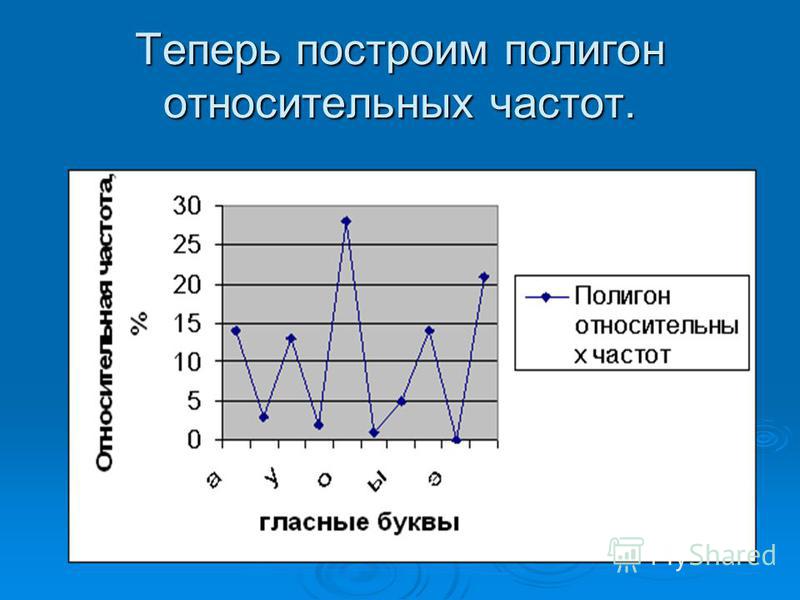 Добавьте 0,05 к верхнему пределу класса для границы последнего класса.
Добавьте 0,05 к верхнему пределу класса для границы последнего класса.