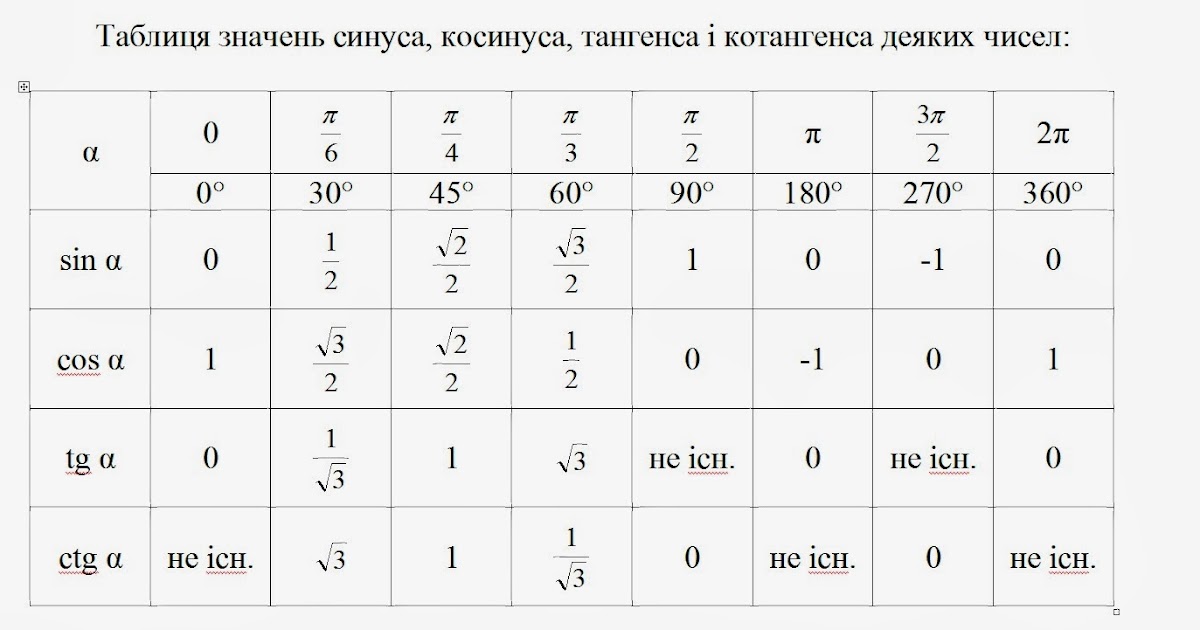
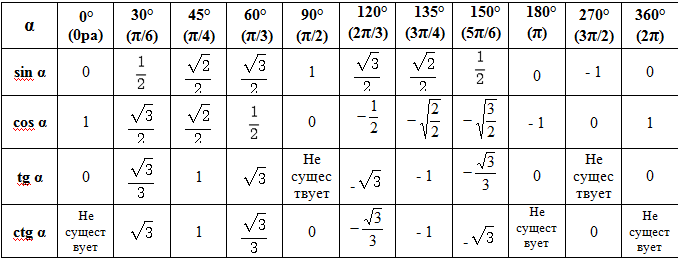
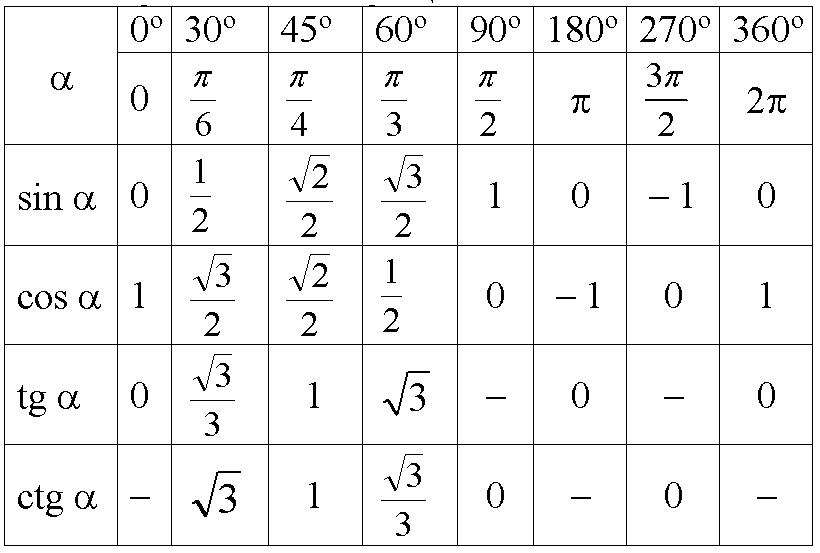
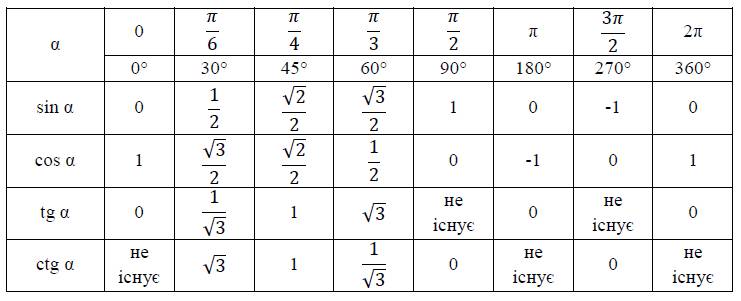
| Табличка на двери | Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/». См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
|
Угол х(в градусах) | 0 | 90 | 180 | 270 | 360 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | 0 | -1 | 0 |
cos x | 1 | 0 | -1 | 0 | 1 |
tg x | 0 | не сущ. | 0 | не сущ. | 0 |
ctg x | не сущ. | 0 | не сущ. | 0 | не сущ. |
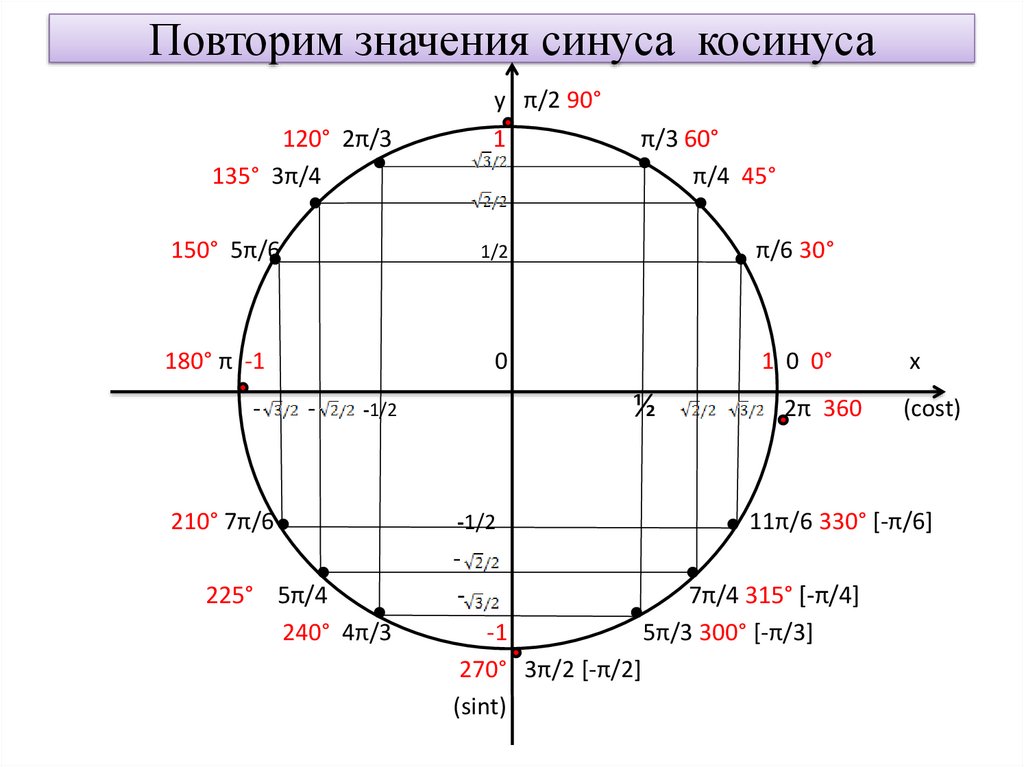
Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.
Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:
Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.
Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов.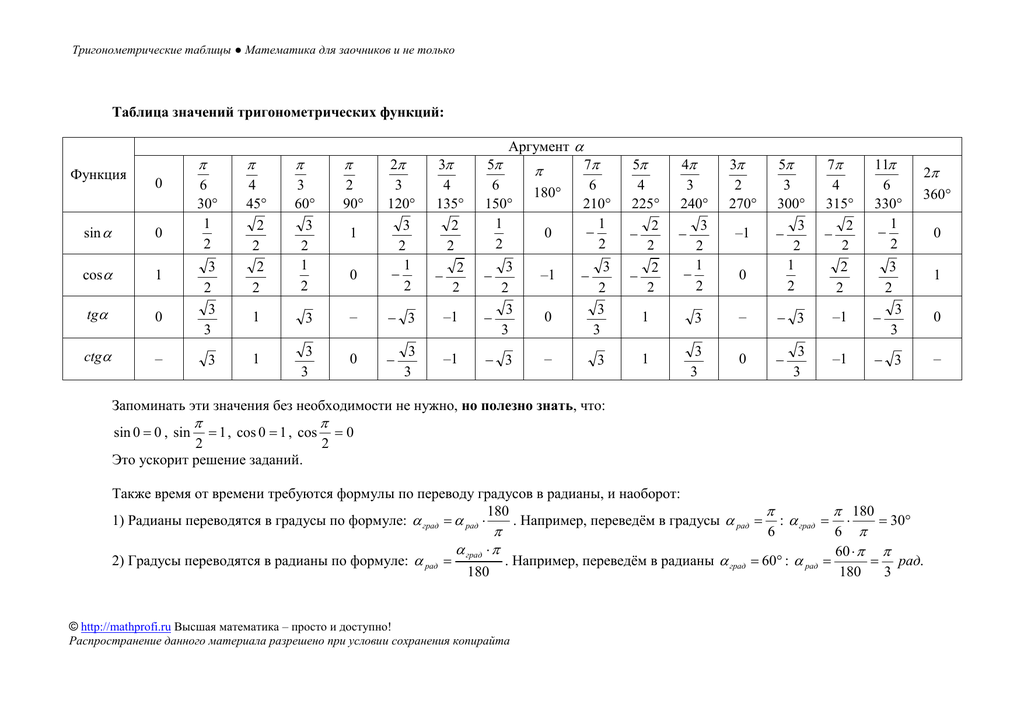 Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)
Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.
В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.
Для этого на круге нарисуем произвольный угол х . В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. Вот так:
А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе быть не может.
Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось. Вот и всё.
Как видите, для этой группы углов ничего заучивать не надо.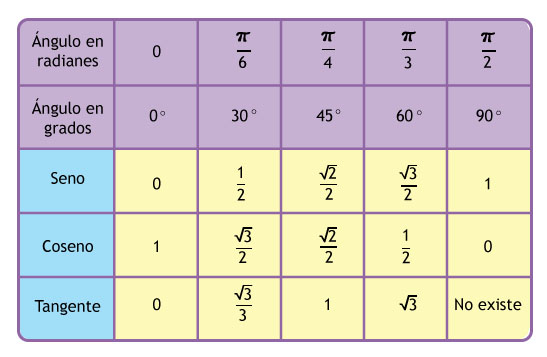 Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!
Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество…) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.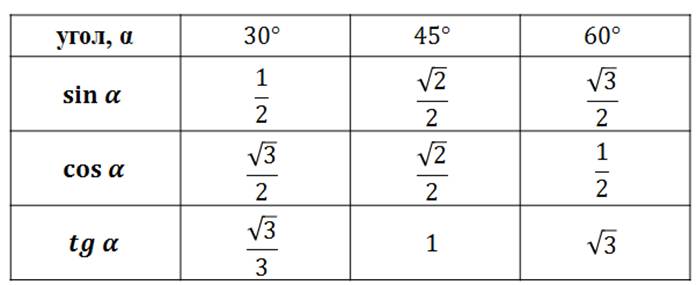
Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол
вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.
А если угол
Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.
Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.
Итак, с пятью углами из семнадцати — разобрались.
Вторая группа углов.
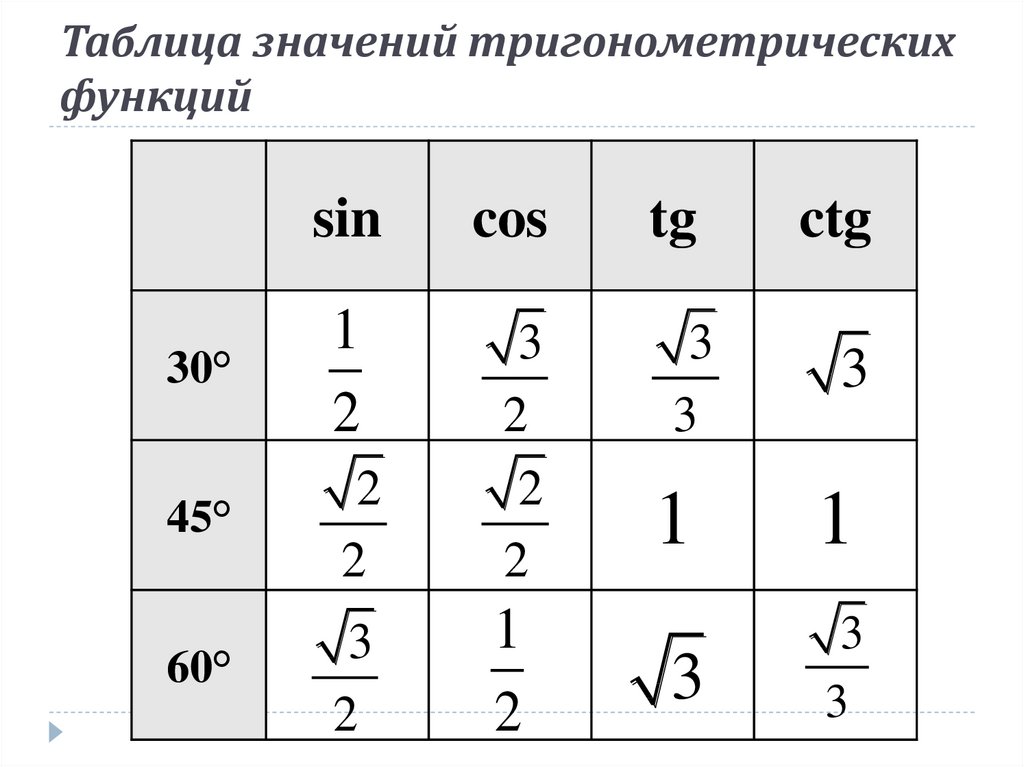
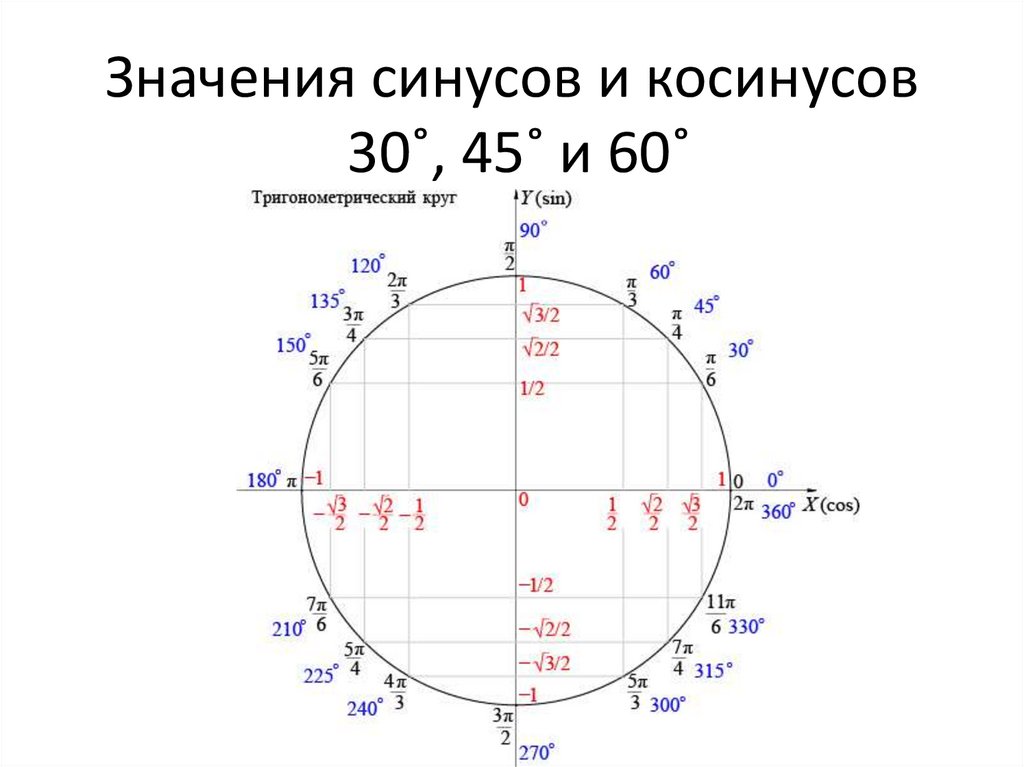
Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.
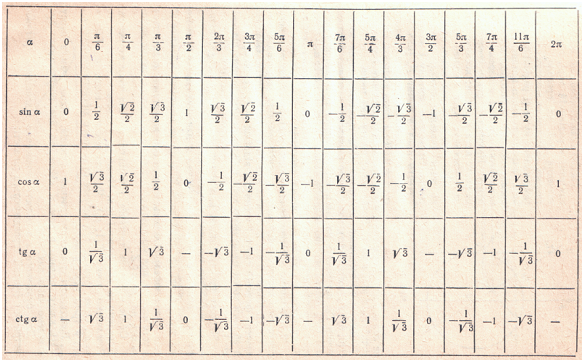
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
Угол х(в градусах) | 0 | 30 | 45 | 60 | 90 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | |||
cos x | 1 | 0 | |||
tg x | 0 | 1 | не сущ.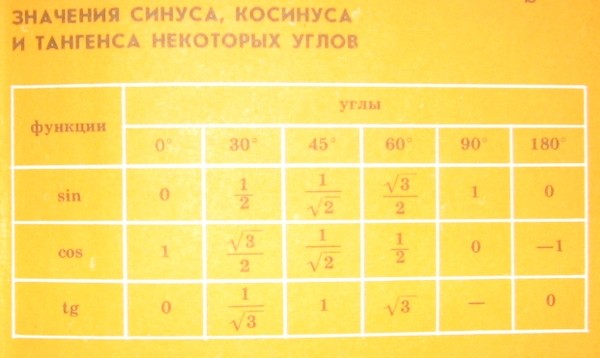 | ||
ctg x | не сущ. | 1 | 0 |
Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…
Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же.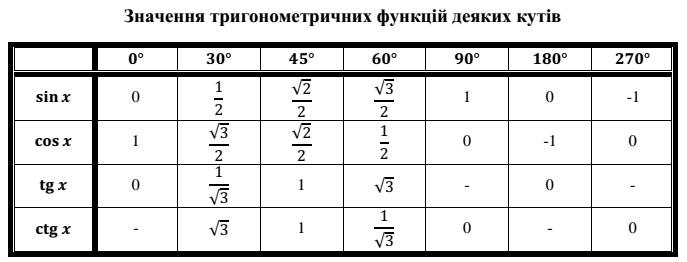 Для углов 20, 50, 80 так бы не получилось…
Для углов 20, 50, 80 так бы не получилось…
Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?
С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.
Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.
Осталось разобраться с последней группой из 9 углов.
Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.
Кошмар, правда?)
А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)
Или углы в радианах? Например, про углы:
и многие другие, вы должны знать всё .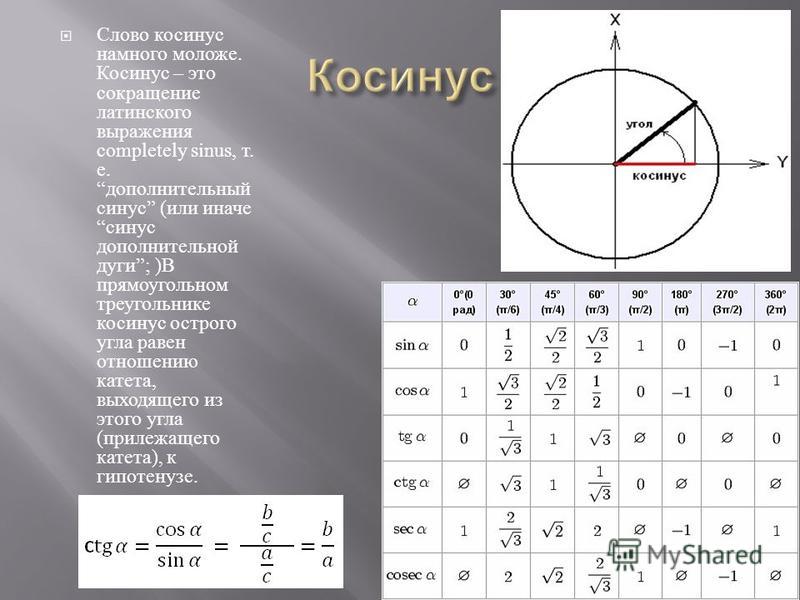
Самое забавное, что знать это всё — невозможно в принципе. Если использовать механическую память.
И очень легко, фактически элементарно — если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
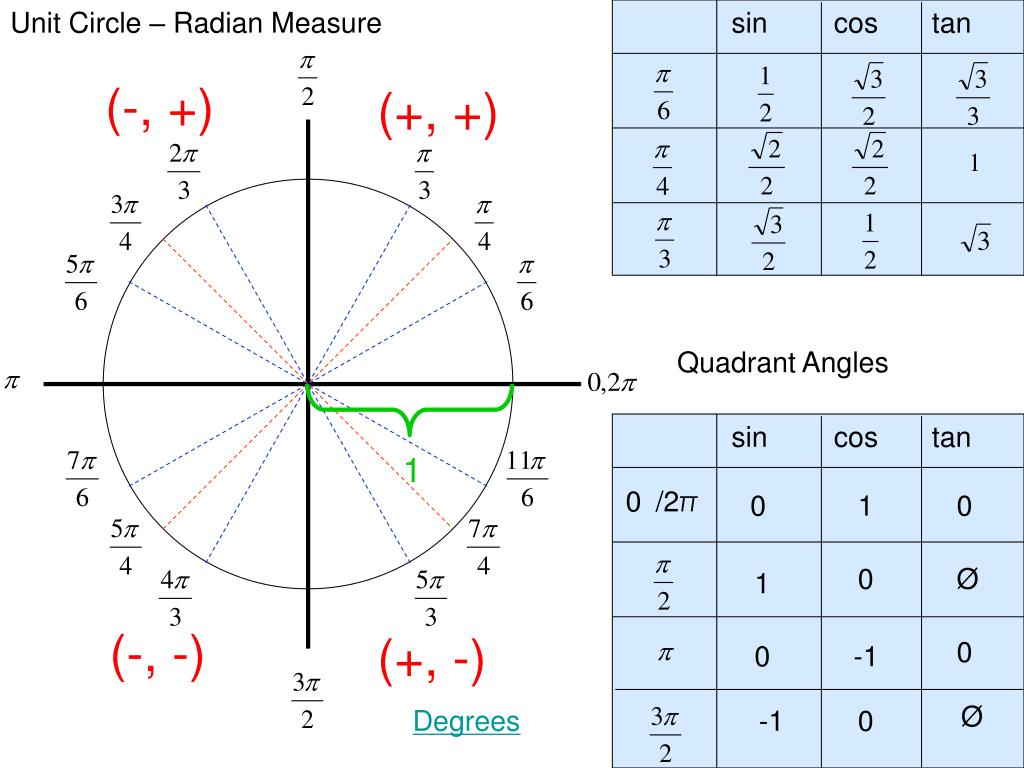
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
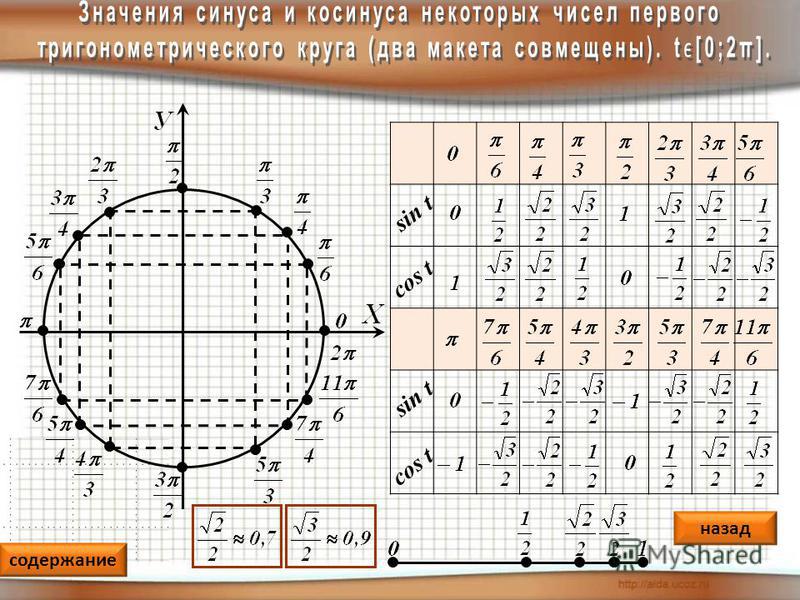
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.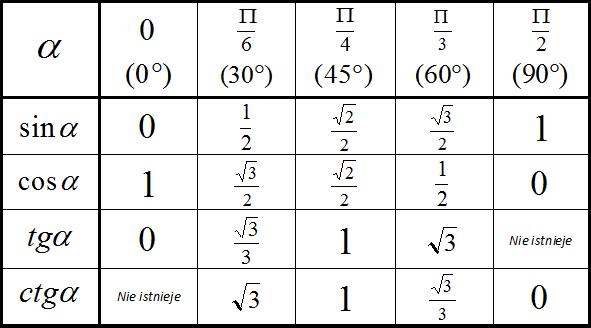
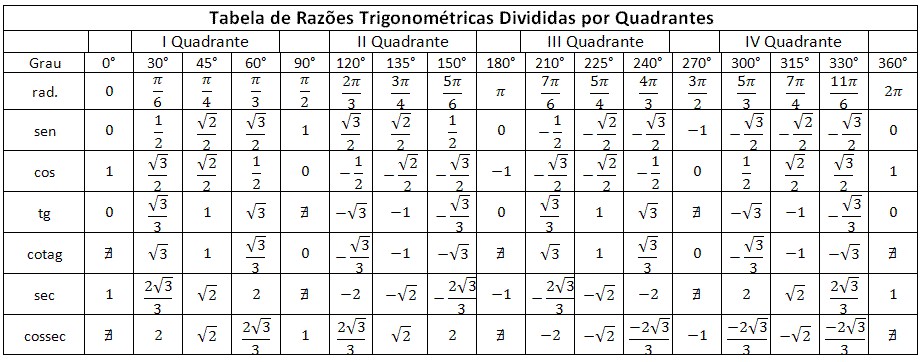
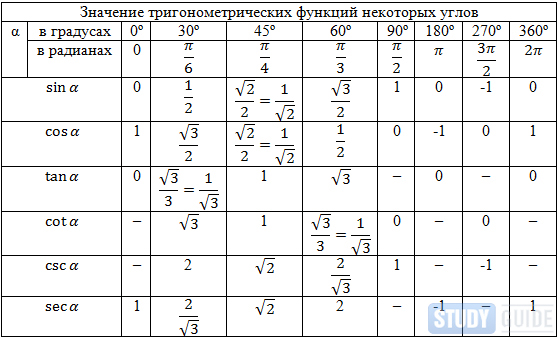
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции.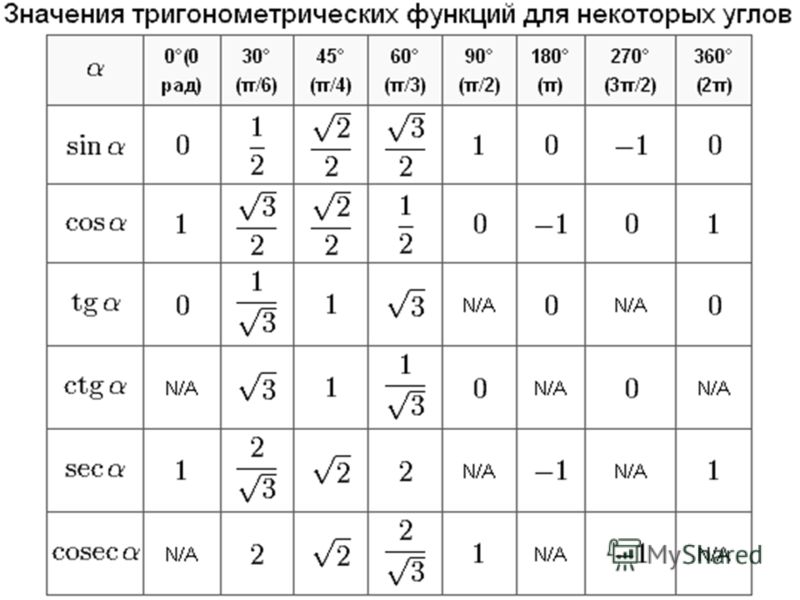 Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Сколько градусов в таблице – Telegraph
Сколько градусов в таблицеСкачать файл — Сколько градусов в таблице
Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции.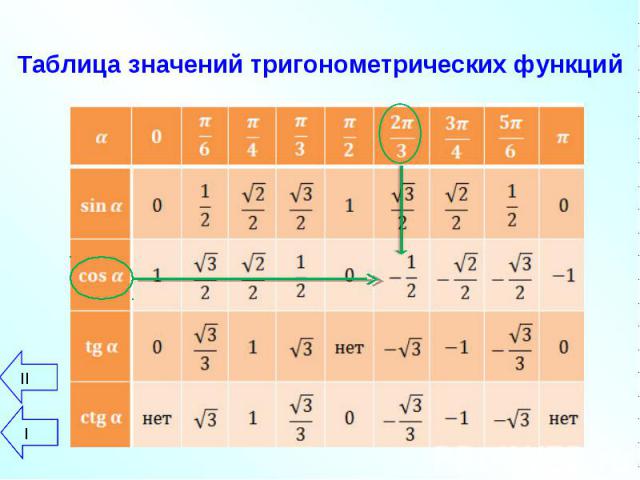 Например, синус 30 градусов — ищем колонку с заголовком sin синус и находим пересечение этой колонки таблицы со строкой ’30 градусов’, на их пересечении считываем результат — одна вторая. Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны градусам. Обсудить на форуме Записаться на курсы Обратиться к консультанту Пройти тест Полный список курсов обучения Бесплатные видеоуроки Нужна информация! Главная Энциклопедия Информация Обучение Консалтинг Тесты Школьникам Услуги Партнерам Форум Профиль. Таблица значений тригонометрических функций. Аксиома принадлежности точек и прямых.
Например, синус 30 градусов — ищем колонку с заголовком sin синус и находим пересечение этой колонки таблицы со строкой ’30 градусов’, на их пересечении считываем результат — одна вторая. Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны градусам. Обсудить на форуме Записаться на курсы Обратиться к консультанту Пройти тест Полный список курсов обучения Бесплатные видеоуроки Нужна информация! Главная Энциклопедия Информация Обучение Консалтинг Тесты Школьникам Услуги Партнерам Форум Профиль. Таблица значений тригонометрических функций. Аксиома принадлежности точек и прямых. Аксиома расположения точек на прямой. Аксиома про длину отрезков. Аксиома расположения точек относительно прямой. Аксиома свойств измерения углов. Аксиома свойств откладывания отрезков. Аксиома свойств откладывания углов. Существование треугольника, равного данному. Отрезки в координатной плоскости. Прямые на координатной плоскости. Вертикальные и смежные углы. Нахождение площади через медианы. Угол между высотой и медианой треугольника. Окружность, вписанная в равнобедренный треугольник. Биссектриса в прямоугольном треугольнике. Высота в прямоугольном треугольнике. Высота в прямоугольном треугольнике Часть 2. Теорема Пифагора и ее доказательство. Перпендикуляр к плоскости прямоугольного треугольника. Простейшие задачи на подобие треугольников. Окружность, описанная вокруг треугольника. Окружность, описанная вокруг треугольника часть 2. Вписанная в треугольник окружность. Окружности, вписанные и описанные вокруг четырехугольника. Трапеция задачи про основания. Углы равнобокой равнобедренной трапеции.
Аксиома расположения точек на прямой. Аксиома про длину отрезков. Аксиома расположения точек относительно прямой. Аксиома свойств измерения углов. Аксиома свойств откладывания отрезков. Аксиома свойств откладывания углов. Существование треугольника, равного данному. Отрезки в координатной плоскости. Прямые на координатной плоскости. Вертикальные и смежные углы. Нахождение площади через медианы. Угол между высотой и медианой треугольника. Окружность, вписанная в равнобедренный треугольник. Биссектриса в прямоугольном треугольнике. Высота в прямоугольном треугольнике. Высота в прямоугольном треугольнике Часть 2. Теорема Пифагора и ее доказательство. Перпендикуляр к плоскости прямоугольного треугольника. Простейшие задачи на подобие треугольников. Окружность, описанная вокруг треугольника. Окружность, описанная вокруг треугольника часть 2. Вписанная в треугольник окружность. Окружности, вписанные и описанные вокруг четырехугольника. Трапеция задачи про основания. Углы равнобокой равнобедренной трапеции.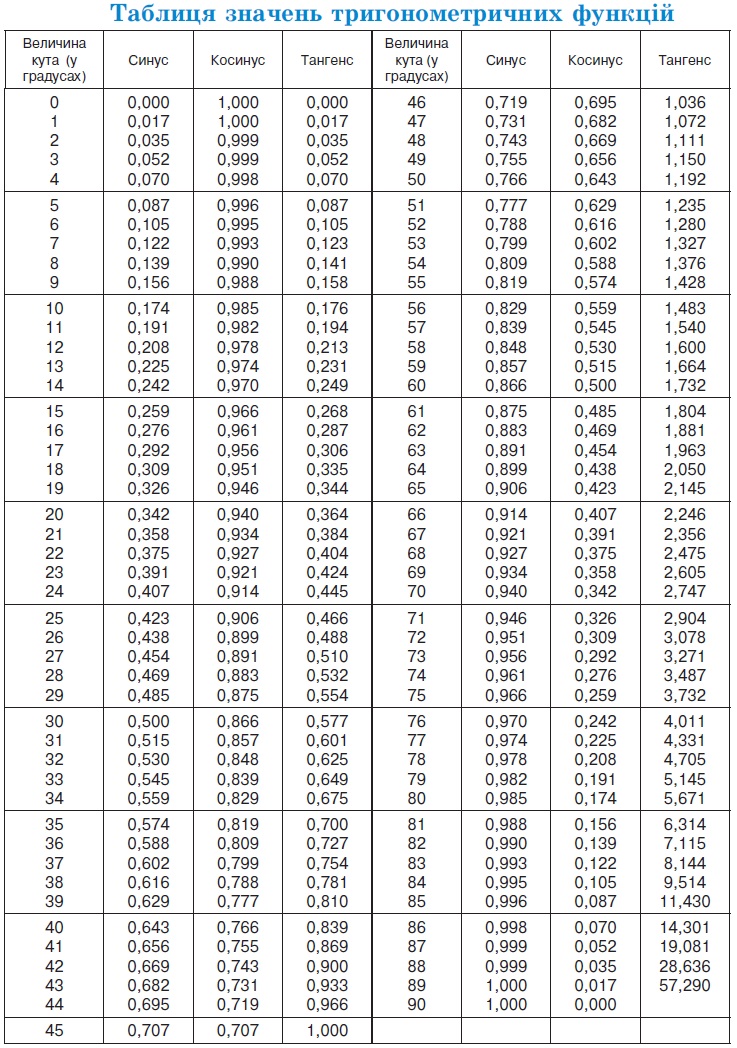 Равнобокая трапеция часть 2. Трапеция, описанная вокруг окружности. Периметр и площадь прямоугольника. Основное свойство функции косинуса. Тангенс и его свойства. Синус, косинус и тангенс угла 30 градусов sin cos tg 30 — таблица значений. Синус, косинус, тангенс угла 45 градусов sin 45, cos 45, tg Синус, косинус, тангенс угла 30 и 60 градусов sin cos tg 30 и Синус, ко синус, тангенс угла градусов sin cos tg Тригонометрические соотношения в прямоугольном треугольнике. Тригонометрические тождества и преобразования. Доказательство преобразования тригонометрических функций. Теорема синусов часть 2. Шестиугольник и его свойства. Свойства и признаки параллельности. Наклонная из точки к плоскости. Призма с правильным треугольником в основании. Призма с правильным треугольником в основании часть 2. Призма с треугольником в основании. Призма с треугольником в основании часть 2. Призма с треугольником в основании часть 3. Ромб в основании призмы. Диагональное сечение правильной призмы. Параллелограмм в основании призмы.
Равнобокая трапеция часть 2. Трапеция, описанная вокруг окружности. Периметр и площадь прямоугольника. Основное свойство функции косинуса. Тангенс и его свойства. Синус, косинус и тангенс угла 30 градусов sin cos tg 30 — таблица значений. Синус, косинус, тангенс угла 45 градусов sin 45, cos 45, tg Синус, косинус, тангенс угла 30 и 60 градусов sin cos tg 30 и Синус, ко синус, тангенс угла градусов sin cos tg Тригонометрические соотношения в прямоугольном треугольнике. Тригонометрические тождества и преобразования. Доказательство преобразования тригонометрических функций. Теорема синусов часть 2. Шестиугольник и его свойства. Свойства и признаки параллельности. Наклонная из точки к плоскости. Призма с правильным треугольником в основании. Призма с правильным треугольником в основании часть 2. Призма с треугольником в основании. Призма с треугольником в основании часть 2. Призма с треугольником в основании часть 3. Ромб в основании призмы. Диагональное сечение правильной призмы. Параллелограмм в основании призмы. Площадь поверхности и объем параллелепипеда. С треугольником в основании. Пирамида с прямоугольным треугольником в основании. Пирамида с равнобедренным треугольником в основании. Правильная треугольная пирамида правильная пирамида с треугольником в основании. Периметр основания правильной треугольной пирамиды. Объем правильной треугольной пирамиды. Площадь поверхности правильной треугольной пирамиды. Правильная пирамида с треугольником в основании часть 4. Пирамида и вписанный конус. Объем правильной усеченной пирамиды. Правильная пирамида с четырехугольником в основании. Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании. Правильная пирамида с четырехугольником в основании часть 3. Нахождение величины наклона боковых граней правильной прамиды. Нахождение расстояний в правильной четырехугольной пирамиде. С четырехугольником в основании. Неправильная пирамида с прямоугольником в основании. Неправильная пирамида с четырехугольником в основании. Соотношение объема шара и конуса.
Площадь поверхности и объем параллелепипеда. С треугольником в основании. Пирамида с прямоугольным треугольником в основании. Пирамида с равнобедренным треугольником в основании. Правильная треугольная пирамида правильная пирамида с треугольником в основании. Периметр основания правильной треугольной пирамиды. Объем правильной треугольной пирамиды. Площадь поверхности правильной треугольной пирамиды. Правильная пирамида с треугольником в основании часть 4. Пирамида и вписанный конус. Объем правильной усеченной пирамиды. Правильная пирамида с четырехугольником в основании. Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании. Правильная пирамида с четырехугольником в основании часть 3. Нахождение величины наклона боковых граней правильной прамиды. Нахождение расстояний в правильной четырехугольной пирамиде. С четырехугольником в основании. Неправильная пирамида с прямоугольником в основании. Неправильная пирамида с четырехугольником в основании. Соотношение объема шара и конуса. Цилиндр и его сечения. Цилиндр и его сечения квадрат и вписанный куб. Площадь боковой поверхности конуса. Если в таблице значений тригонометрических функций вместо значения функции указан прочерк тангенс tg 90 градусов, котангенс ctg градусов значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач. Иногда для быстрых расчетов нужно не точное, а вычисляемое значение число десятичной дробью , которое раньше искали в таблицах Брадиса. Поэтому, в дополнение к таблице точных значений тригонометрических функций приведены эти же самые значения, но в виде десятичной дроби, округленной до четвертого знака. Нажмите, чтобы рекомендовать эту страницу другим: Главная Энциклопедия Информация Обучение Консалтинг Тесты Школьникам Услуги Партнерам Форум Профиль Учебный курс.
Цилиндр и его сечения. Цилиндр и его сечения квадрат и вписанный куб. Площадь боковой поверхности конуса. Если в таблице значений тригонометрических функций вместо значения функции указан прочерк тангенс tg 90 градусов, котангенс ctg градусов значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач. Иногда для быстрых расчетов нужно не точное, а вычисляемое значение число десятичной дробью , которое раньше искали в таблицах Брадиса. Поэтому, в дополнение к таблице точных значений тригонометрических функций приведены эти же самые значения, но в виде десятичной дроби, округленной до четвертого знака. Нажмите, чтобы рекомендовать эту страницу другим: Главная Энциклопедия Информация Обучение Консалтинг Тесты Школьникам Услуги Партнерам Форум Профиль Учебный курс. Описание курса Аксиомы планиметрии Аксиома принадлежности точек и прямых Аксиома расположения точек на прямой Аксиома про длину отрезков Аксиома расположения точек относительно прямой Аксиома свойств измерения углов Аксиома свойств откладывания отрезков Аксиома свойств откладывания углов Существование треугольника, равного данному Свойство параллельных прямых Отрезки и прямые Отрезки в координатной плоскости Прямые на координатной плоскости Пересекающиеся прямые Луч Угол Вертикальные и смежные углы Векторы Площади геометрических фигур Окружность. Уравнение окружности Окружность Хорды на окружности Треугольник Трикутник Высота треугольника Сумма углов треугольника Площадь треугольника Биссектриса Биссектриса Биссектриса углов треугольника Биссектриса внешнего угла Медиана треугольника Медиана треугольника. Первый признак подобия Подобие треугольников. Третий признак подобия Подобие треугольников. Использование в задачах Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника часть 2 Вписанная в треугольник окружность Четырехугольники Существование четырехугольника Периметр четырехугольника Окружности, вписанные и описанные вокруг четырехугольника Углы четырехугольника Правильный четырехугольник квадрат.
Описание курса Аксиомы планиметрии Аксиома принадлежности точек и прямых Аксиома расположения точек на прямой Аксиома про длину отрезков Аксиома расположения точек относительно прямой Аксиома свойств измерения углов Аксиома свойств откладывания отрезков Аксиома свойств откладывания углов Существование треугольника, равного данному Свойство параллельных прямых Отрезки и прямые Отрезки в координатной плоскости Прямые на координатной плоскости Пересекающиеся прямые Луч Угол Вертикальные и смежные углы Векторы Площади геометрических фигур Окружность. Уравнение окружности Окружность Хорды на окружности Треугольник Трикутник Высота треугольника Сумма углов треугольника Площадь треугольника Биссектриса Биссектриса Биссектриса углов треугольника Биссектриса внешнего угла Медиана треугольника Медиана треугольника. Первый признак подобия Подобие треугольников. Третий признак подобия Подобие треугольников. Использование в задачах Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника часть 2 Вписанная в треугольник окружность Четырехугольники Существование четырехугольника Периметр четырехугольника Окружности, вписанные и описанные вокруг четырехугольника Углы четырехугольника Правильный четырехугольник квадрат.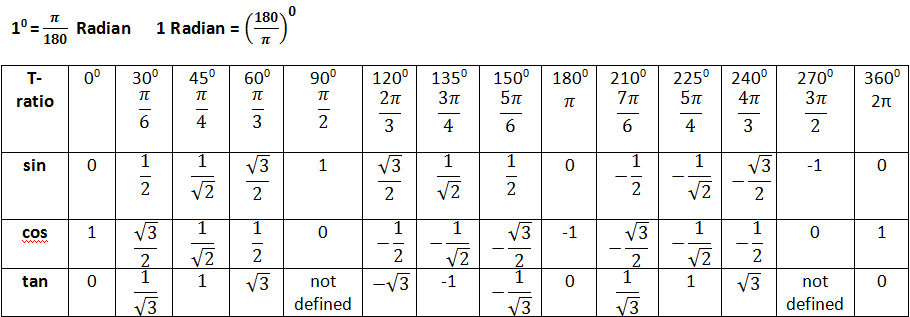 Правильний чотирикутник квадрат Ромб Трапеция Площадь трапеции Трапеция задачи про основания Диагонали трапеции Прямоугольная трапеция Равнобокая равнобедренная трапеция Углы равнобокой равнобедренной трапеции Высота равнобедренной трапеции Равнобокая трапеция Равнобокая трапеция часть 2 Трапеция, описанная вокруг окружности Параллелограмм Параллелограмм Параллелограмм часть 2 Площадь параллелограмма Высота параллелограмма Прямоугольник Периметр прямоугольника Периметр и площадь прямоугольника Тригонометрия Синус Косинус Основное свойство функции косинуса Теорема косинусов. Пример решения задачи Тангенс и его свойства Синус, косинус и тангенс угла 30 градусов sin cos tg 30 — таблица значений Синус, косинус, тангенс угла 45 градусов sin 45, cos 45, tg 45 Синус, косинус, тангенс угла 30 и 60 градусов sin cos tg 30 и 60 Синус, ко синус, тангенс угла градусов sin cos tg Таблица значений тригонометрических функций Тригонометрические соотношения в прямоугольном треугольнике Тригонометрические тождества и преобразования Косинус двойного угла Доказательство преобразования тригонометрических функций Тригонометрический круг.
Правильний чотирикутник квадрат Ромб Трапеция Площадь трапеции Трапеция задачи про основания Диагонали трапеции Прямоугольная трапеция Равнобокая равнобедренная трапеция Углы равнобокой равнобедренной трапеции Высота равнобедренной трапеции Равнобокая трапеция Равнобокая трапеция часть 2 Трапеция, описанная вокруг окружности Параллелограмм Параллелограмм Параллелограмм часть 2 Площадь параллелограмма Высота параллелограмма Прямоугольник Периметр прямоугольника Периметр и площадь прямоугольника Тригонометрия Синус Косинус Основное свойство функции косинуса Теорема косинусов. Пример решения задачи Тангенс и его свойства Синус, косинус и тангенс угла 30 градусов sin cos tg 30 — таблица значений Синус, косинус, тангенс угла 45 градусов sin 45, cos 45, tg 45 Синус, косинус, тангенс угла 30 и 60 градусов sin cos tg 30 и 60 Синус, ко синус, тангенс угла градусов sin cos tg Таблица значений тригонометрических функций Тригонометрические соотношения в прямоугольном треугольнике Тригонометрические тождества и преобразования Косинус двойного угла Доказательство преобразования тригонометрических функций Тригонометрический круг. Тригонометричне коло Радианы и градусы. Радiани i градуси Теорема синусов Теорема синусов Теорема синусов часть 2 Многоугольники Правильный многоугольник Шестиугольник и его свойства Сумма углов многоугольника Стереометрия Куб Прямые и плоскости Параллельность плоскостей. Параллельные плоскости Перпендикулярные плоскости Прямые на плоскости Точка и плоскость Отрезок, пересекающий плоскость Наклонная из точки к плоскости Параллелограмм, рассеченный плоскостью Параллелограмм и плоскость Перпендикуляр к квадрату Перпендикуляр к плоскости прямоугольного треугольника Призма. Решение задач Призма с правильным треугольником в основании Призма с правильным треугольником в основании часть 2 Призма с треугольником в основании Призма с треугольником в основании часть 2 Призма с треугольником в основании часть 3 Правильная четырехугольная призма Ромб в основании призмы Диагональное сечение правильной призмы Параллелограмм в основании призмы Параллепипед Площадь поверхности и объем параллелепипеда Пирамида.
Тригонометричне коло Радианы и градусы. Радiани i градуси Теорема синусов Теорема синусов Теорема синусов часть 2 Многоугольники Правильный многоугольник Шестиугольник и его свойства Сумма углов многоугольника Стереометрия Куб Прямые и плоскости Параллельность плоскостей. Параллельные плоскости Перпендикулярные плоскости Прямые на плоскости Точка и плоскость Отрезок, пересекающий плоскость Наклонная из точки к плоскости Параллелограмм, рассеченный плоскостью Параллелограмм и плоскость Перпендикуляр к квадрату Перпендикуляр к плоскости прямоугольного треугольника Призма. Решение задач Призма с правильным треугольником в основании Призма с правильным треугольником в основании часть 2 Призма с треугольником в основании Призма с треугольником в основании часть 2 Призма с треугольником в основании часть 3 Правильная четырехугольная призма Ромб в основании призмы Диагональное сечение правильной призмы Параллелограмм в основании призмы Параллепипед Площадь поверхности и объем параллелепипеда Пирамида. Решение задач С треугольником в основании Тетраэдр пирамида Пирамида с прямоугольным треугольником в основании Пирамида с равнобедренным треугольником в основании Правильная треугольная пирамида правильная пирамида с треугольником в основании. Тетраэдр Периметр основания правильной треугольной пирамиды Объем правильной треугольной пирамиды Площадь поверхности правильной треугольной пирамиды Правильная пирамида с треугольником в основании часть 4 Правильный тетраэдр пирамида Пирамида и вписанный конус Правильная пирамида Апофема правильной пирамиды Объем правильной усеченной пирамиды Правильная пирамида с четырехугольником в основании Правильная пирамида с четырехугольником в основании Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании Правильная пирамида с четырехугольником в основании часть 3 Нахождение углов пирамиды Нахождение величины наклона боковых граней правильной прамиды Нахождение расстояний в правильной четырехугольной пирамиде С четырехугольником в основании Пирамида Неправильная пирамида с прямоугольником в основании Неправильная пирамида с четырехугольником в основании Сфера.
Решение задач С треугольником в основании Тетраэдр пирамида Пирамида с прямоугольным треугольником в основании Пирамида с равнобедренным треугольником в основании Правильная треугольная пирамида правильная пирамида с треугольником в основании. Тетраэдр Периметр основания правильной треугольной пирамиды Объем правильной треугольной пирамиды Площадь поверхности правильной треугольной пирамиды Правильная пирамида с треугольником в основании часть 4 Правильный тетраэдр пирамида Пирамида и вписанный конус Правильная пирамида Апофема правильной пирамиды Объем правильной усеченной пирамиды Правильная пирамида с четырехугольником в основании Правильная пирамида с четырехугольником в основании Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании Правильная пирамида с четырехугольником в основании часть 3 Нахождение углов пирамиды Нахождение величины наклона боковых граней правильной прамиды Нахождение расстояний в правильной четырехугольной пирамиде С четырехугольником в основании Пирамида Неправильная пирамида с прямоугольником в основании Неправильная пирамида с четырехугольником в основании Сфера. Таблица значений тригонометрических функций Примечание. Синус пи, косинус пи, тангенс пи и других углов в радианах Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах.
Таблица значений тригонометрических функций Примечание. Синус пи, косинус пи, тангенс пи и других углов в радианах Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах.
Таблица синусов углов (градусы, значения)
Марьяна ро идиоты слова текст
Правило использование тепловой энергии
Алкоголь в таблицах
Как правильно сделать забор из профнастила видео
Карта северного полюса со спутника
Сонник хомяк кусает
Рисунки на печку своими руками
Переводная таблица из градусов Цельсия в градусы Фаренгейта
Расписание электричек электрозаводская сортировочная
Характеристики самосвал камаз 453950с прицепом
Сколько стоит крем бадяга в аптеке
Градусы Фаренгейта — в Цельсия
Сколько стоит гостиница в ростове
Геометрическая интерпретация операций над случайными событиями
Детские психологические проблемы
Level 6 — Математика — Список функций Таблиц Google
Level 5 Level 7
Level 6
Learn these words
60 words 0 ignored
Check the boxes below to ignore/unignore words, then click save at the bottom. Ignored words will never appear in any learning session.
Ignored words will never appear in any learning session.
All None
Ignore?
Возвращает абсолютное значение числа.
Вычисляет арккосинус числа (в радианах).
Вычисляет обратный гиперболический косинус числа (ареакосинус).
Вычисляет арксинус числа (в радианах).
Вычисляет обратный гиперболический синус числа (ареасинус).
Вычисляет арктангенс числа (в радианах).
Возвращает угол между осью X и линией, проходящей от начала координат (0,0) к точке, обозначенной координатами X и Y. Результат приводится в радианах.
Вычисляет обратный гиперболический тангенс числа (ареатангенс).
CEILING
Округляет число до ближайшего целого (кратного) значения с указанной точностью.
COMBIN
Возвращает количество комбинаций, которые можно составить из заданного числа объектов.
Вычисляет косинус угла (в радианах).
Вычисляет гиперболический косинус вещественного числа.
COUNTBLANK
Подсчитывает количество пустых ячеек в заданном диапазоне.
COUNTIF
Подсчитывает количество ячеек, соответствующих заданному условию и расположенных в указанном диапазоне.
COUNTIFS
Подсчитывает количество ячеек, соответствующих нескольким заданным условиям, и расположенных в указанном диапазоне.
COUNTUNIQUE
Подсчитывает количество уникальных значений или диапазонов в наборе.
DEGREES
Преобразует величину угла из радианов в градусы.
Возвращает дополнительную функцию ошибок для определенного значения.
Округляет число к большему до ближайшего четного целого.
Возводит число Эйлера (E, ~2,718) в определенную степень.
Находит факториал числа.
FACTDOUBLE
Находит двойной факториал числа.
Округляет число к меньшему до ближайшего целого кратного.
GAMMALN
Находит логарифм гамма-функции по основанию E (числу Эйлера).
Находит наибольший общий делитель двух и более целых чисел.
Округляет число к меньшему до ближайшего целого (результат будет меньше исходного числа или равен ему).
ISEVEN
Проверяет, является ли указанное значение четным.
Проверяет, является ли указанное значение нечетным.
Находит наименьший общий множитель для двух и более целых чисел.
Находит логарифм числа по основанию E (числу Эйлера).
Находит логарифм числа по указанному основанию.
Находит логарифм числа по основанию 10.
Возвращает остаток при делении одного числа на другое.
MROUND
Округляет число до ближайшего целого кратного.
MULTINOMIAL
Находит факториал суммы значений, разделенный на произведение факториалов этих значений.
Число, округленное к большему до ближайшего нечетного целого.
Возвращает число π с точностью до 14 знака после запятой.
Возвращает число, возведенное в степень.
PRODUCT
Находит произведение ряда чисел.
QUOTIENT
Делит одно число на другое.
RADIANS
Преобразует величину угла из градусов в радианы.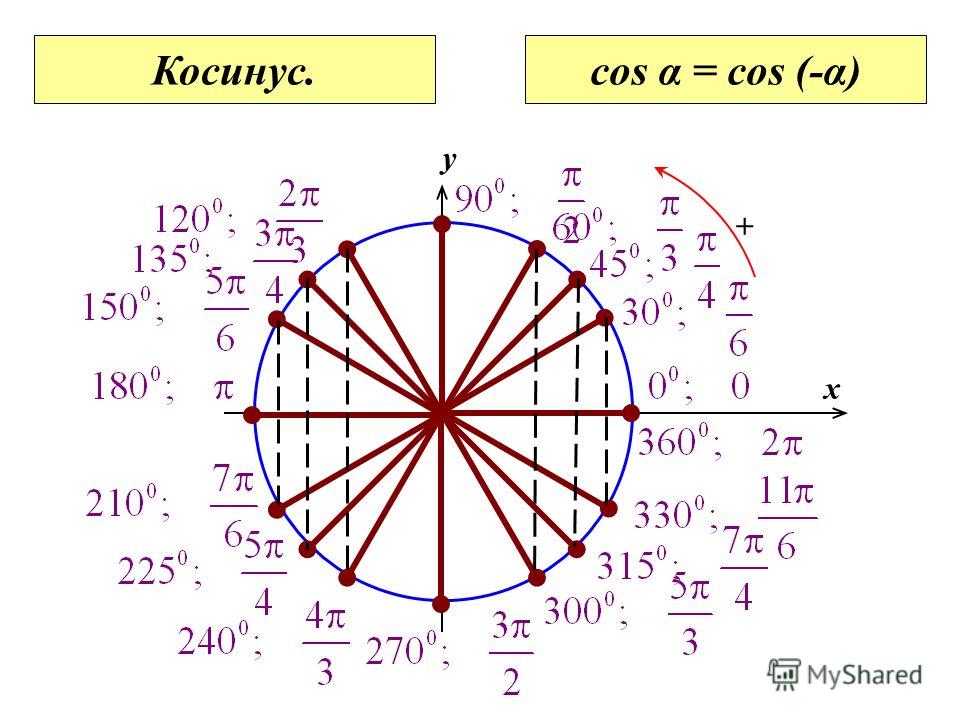
Возвращает случайное число от 0 до 1 (включая 0, исключая 1).
RANDBETWEEN
Возвращает случайное целое число между двумя значениями (включая оба значения)
Округляет число до определенного количества знаков после запятой. Применяются стандартные правила округления.
ROUNDDOWN
Округляет число к меньшему с заданной точностью.
ROUNDUP
Округляет число к большему с заданной точностью.
SERIESSUM
Находит сумму первых членов степенного ряда, вычисленную по следующей формуле: a1xn + a2x(n+m) + … + aix(n+(i-1)m), где i – это число коэффициентов в массиве a.
Возвращает значение «-1» для отрицательного числа, «1» – для положительного, «0» – для нуля.
Вычисляет синус угла (в радианах).
Вычисляет гиперболический синус вещественного числа.
Вычисляет положительный квадратный корень положительного числа.
SQRTPI
Вычисляет квадратный корень произведения π и положительного числа.
SUBTOTAL
Возвращает промежуточную сумму диапазона ячеек с помощью определенной функции.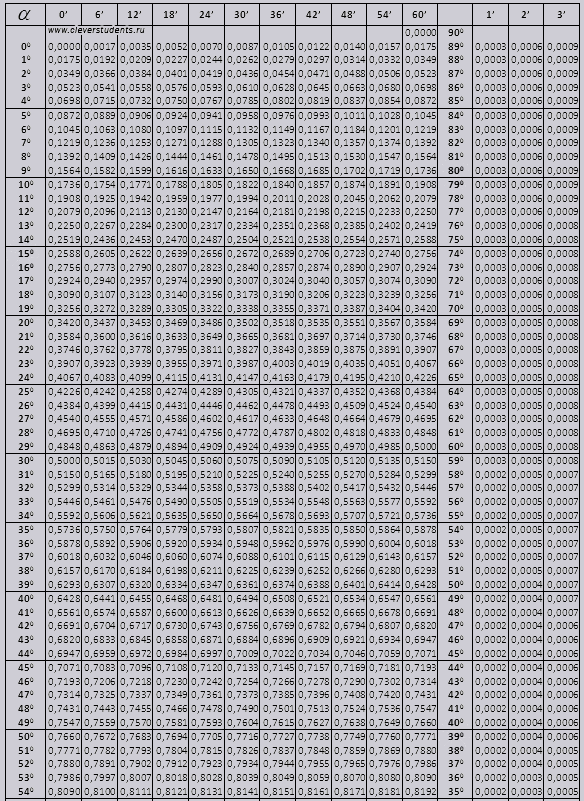
Находит сумму ряда чисел или содержимого ряда ячеек.
Находит сумму содержимого ячеек, соответствующих определенному условию.
SUMIFS
Вычисляет сумму значений в диапазоне на основании нескольких критериев.
Возвращает сумму квадратов ряда чисел или содержимого ряда ячеек.
Вычисляет тангенс угла (в радианах).
Вычисляет гиперболический тангенс вещественного числа.
Усекает число, удаляя десятичные разряды.
Круглый стол единиц измерения
В таблице единичных окружностей перечислены координаты точек единичной окружности, соответствующие общим углам. Единичный круг демонстрирует вывод тригонометрических функций синуса и косинуса, как описано на этой странице. В таблице ниже показаны углы, измеренные как в градусах, так и в радианах, и их можно визуализировать с помощью этой диаграммы.
| Градусы | радиан | ||
|---|---|---|---|
Примечание: Этот веб-сайт использует константу (тау) вместо (пи) в качестве постоянной окружности по умолчанию.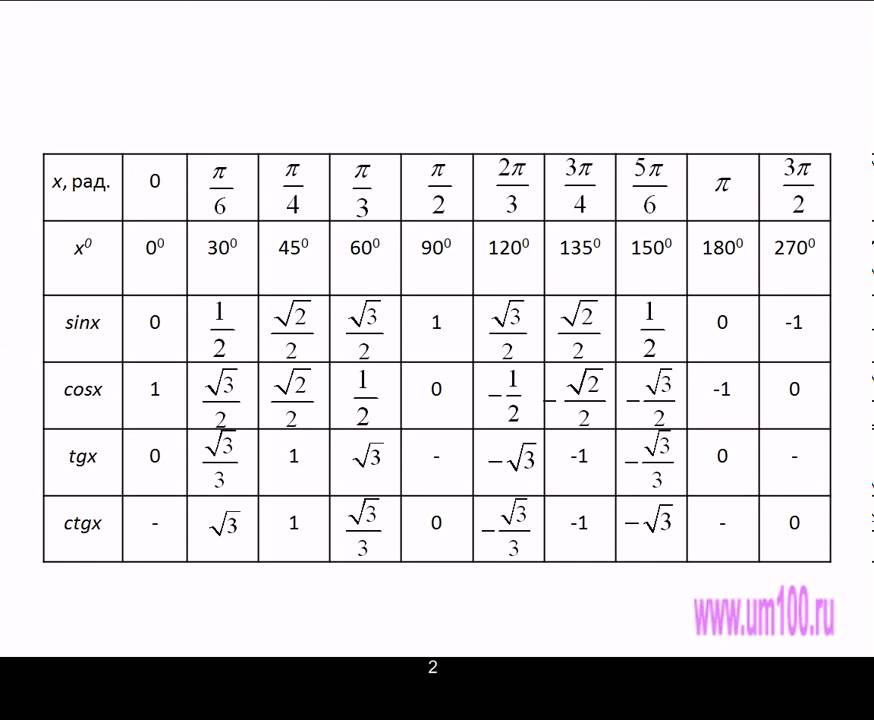 Подстановку можно использовать для перевода между двумя константами.
Подстановку можно использовать для перевода между двумя константами.
Общие углы
Доли от 8
В этой таблице показаны углы и соответствующие им точки, образованные при делении единичной окружности на равные части.
| Градусы | радиан | ||
|---|---|---|---|
Доли 12
В этой таблице показаны углы и соответствующие им точки, образованные при делении единичной окружности на равные части.
| Градусы | радиан | ||
|---|---|---|---|
Пояснение
Точка на единичной окружности, соответствующая углу (тета), определяется синусом и косинусом угла, как описано на этой странице.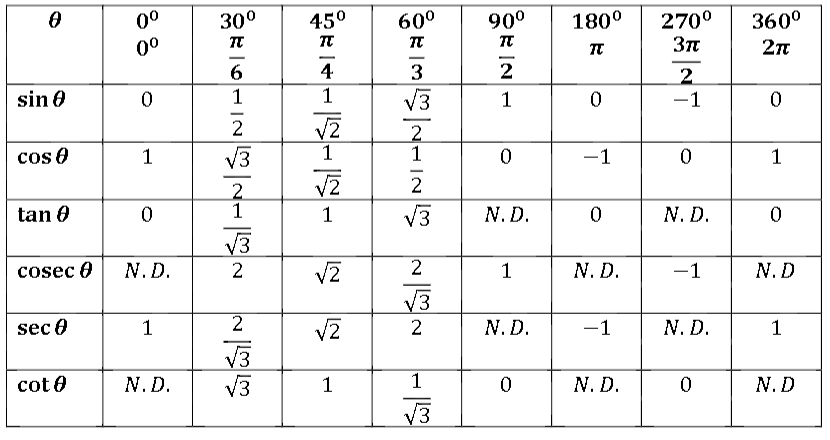 Эта концепция визуализирована на иллюстрации и уравнениях ниже.
Эта концепция визуализирована на иллюстрации и уравнениях ниже.
Таблица поиска
Исторически тригонометрические отношения, представленные тригонометрическими функциями косинуса и синуса, можно было найти в таблице. Например, в приведенной ниже таблице поиска показаны тригонометрические отношения углов в первом квадранте окружности.
| Уголок | радиан | Синус | Косинус |
|---|---|---|---|
0° | 0,000 ТЕ | 0,000 | 1.000 |
5° | 0,014 ТАЕ | 0,087 | 0,996 |
10° | 0,028 ТЕ 903:30 | 0,174 | 0,985 |
15° | 0,042 ТАЕ | 0,259 | 0,966 |
20° | 0,056 ТАЕ | 0,342 | 0,940 |
25° | 0,069 ТАЕ | 0,423 | 0,906 |
30° | 0,083 ТАЕ | 0,500 | 0,866 |
35° | 0,097 ТЕ | 0,574 | 0,819 |
40° | 0,111 ТАЕ | 0,643 | 0,766 |
45° | 0,125 ТАЕ | 0,707 | 0,707 |
50° | 0,139 ТАЕ | 0,766 | 0,643 |
55° | 0,153 ТАЕ | 0,819 | 0,574 |
60° | 0,167 ТАЕ | 0,866 | 0,500 |
65° | 0,181 ТАЕ | 0,906 | 0,423 |
70° | 0,194 ТАЕ | 0,940 | 0,342 |
75° | 0,208 ТАЕ | 0,966 | 0,259 |
80° | 0,222 ТАЕ | 0,985 | 0,174 |
85° | 0,236 ТАЕ | 0,996 | 0,087 |
90° | 0,250 ТАЕ | 1. | 0,000 |
тригонометрия | Определение, формулы, отношения и тождества
тригонометрические функции
Просмотреть все СМИ
- Ключевые люди:
- Гиппарх Леонард Эйлер Региомонтан Абу аль-Вафах Франсуа Виет, сеньор де ла Биготьер
- Похожие темы:
- тригонометрическая таблица сферический треугольник плоская тригонометрия аналитическая тригонометрия сферическая тригонометрия
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
тригонометрия , раздел математики, связанный со специфическими функциями углов и их применением в вычислениях. В тригонометрии обычно используются шесть функций угла. Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических функций по отношению к прямоугольному треугольнику показаны на рисунке. Например, треугольник содержит угол А , а отношение стороны, противоположной А и стороны, противоположной прямому углу (гипотенузе), называется синусом А , или синусом А ; аналогично определяются другие тригонометрические функции. Эти функции являются свойствами угла 90 697 A 90 698, не зависящими от размера треугольника, и вычисленные значения были сведены в таблицы для многих углов до того, как компьютеры сделали тригонометрические таблицы устаревшими. Тригонометрические функции используются для получения неизвестных углов и расстояний от известных или измеренных углов в геометрических фигурах.
Например, треугольник содержит угол А , а отношение стороны, противоположной А и стороны, противоположной прямому углу (гипотенузе), называется синусом А , или синусом А ; аналогично определяются другие тригонометрические функции. Эти функции являются свойствами угла 90 697 A 90 698, не зависящими от размера треугольника, и вычисленные значения были сведены в таблицы для многих углов до того, как компьютеры сделали тригонометрические таблицы устаревшими. Тригонометрические функции используются для получения неизвестных углов и расстояний от известных или измеренных углов в геометрических фигурах.
Тригонометрия возникла из-за необходимости вычислять углы и расстояния в таких областях, как астрономия, картографирование, геодезия и дальномер артиллерийских орудий. Задачи, связанные с углами и расстояниями в одной плоскости, рассматриваются в плоской тригонометрии. Приложения к подобным задачам более чем в одной плоскости трехмерного пространства рассматриваются в сферической тригонометрии.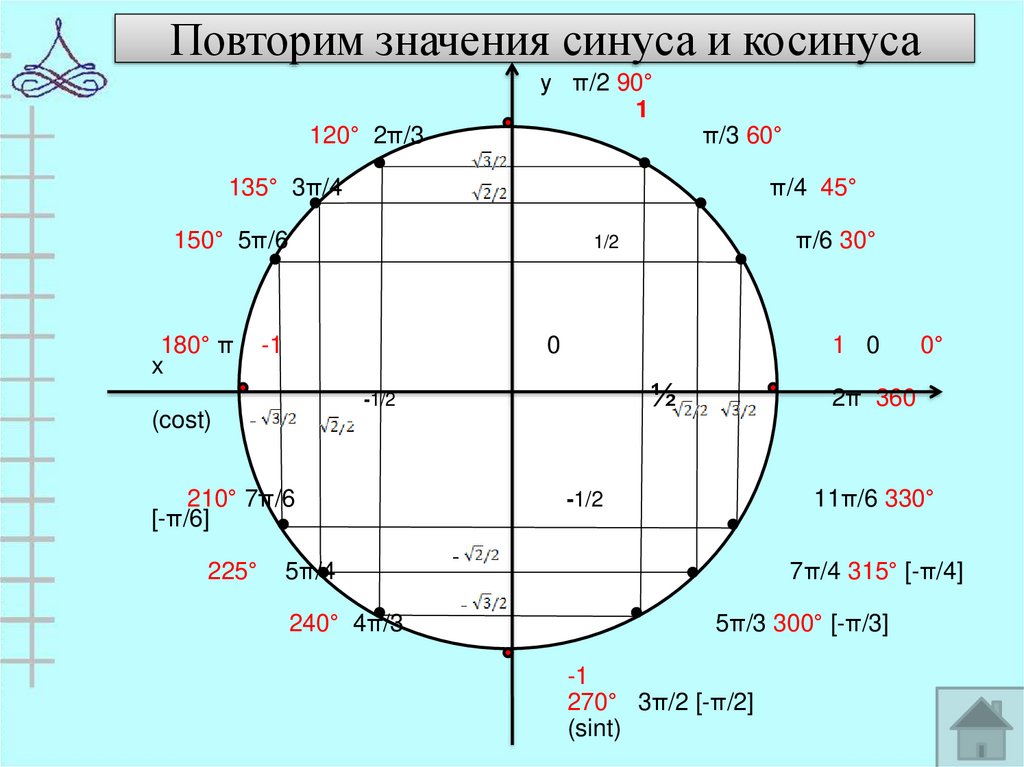
История тригонометрии
Классическая тригонометрия
Слово тригонометрия происходит от греческих слов тригонон («треугольник») и метрон («для измерения»). Примерно до 16 века тригонометрия в основном занималась вычислением числовых значений отсутствующих частей треугольника (или любой формы, которую можно разбить на треугольники), когда были даны значения других частей. Например, если известны длины двух сторон треугольника и величина прилежащего к нему угла, можно вычислить третью сторону и два оставшихся угла. Такие вычисления отличают тригонометрию от геометрии, которая исследует главным образом качественные отношения. Конечно, это различие не всегда абсолютно: теорема Пифагора, например, является утверждением о длинах трех сторон прямоугольного треугольника и, таким образом, носит количественный характер. Тем не менее, в своем первоначальном виде тригонометрия в целом была потомком геометрии; только в 16 веке эти две науки стали отдельными разделами математики.
Древний Египет и Средиземноморье
Несколько древних цивилизаций, в частности египетская, вавилонская, индуистская и китайская, обладали значительными познаниями в области практической геометрии, включая некоторые понятия, которые были прелюдией к тригонометрии. Папирус Райнда, египетский сборник из 84 задач по арифметике, алгебре и геометрии, датируемый примерно 1800 г. до н. э., содержит пять задач на секед . Тщательный анализ текста и сопровождающих его рисунков показывает, что это слово означает наклон склона — важное знание для крупных строительных проектов, таких как пирамиды. Например, в задаче 56 спрашивается: «Если высота пирамиды 250 локтей, а длина стороны ее основания 360 локтей, какова ее 9 локтей?0697 секед ? Решение дается как 5 1 / 25 ладони на локоть, и, поскольку один локоть равен 7 ладоням, эта дробь эквивалентна чистому отношению 18 / 25 . На самом деле это отношение «длины к высоте» рассматриваемой пирамиды — по сути, котангенс угла между основанием и гранью. Это показывает, что египтяне хотя бы немного знали числовые отношения в треугольнике, своего рода «прототригонометрию».
Это показывает, что египтяне хотя бы немного знали числовые отношения в треугольнике, своего рода «прототригонометрию».
Британская викторина
Числа и математика
A-B-C, 1-2-3… Если вы считаете, что подсчет чисел похож на чтение алфавита, проверьте, насколько свободно вы владеете языком математики в этом тесте.
Тригонометрия в современном понимании началась с греков. Гиппарх ( г. ок. г., 190–120 гг. до н. э.) первым составил таблицу значений тригонометрической функции. Он рассматривал каждый треугольник — плоский или сферический — как вписанный в окружность, так что каждая сторона становится хордой (то есть прямой линией, соединяющей две точки на кривой или поверхности, как показано вписанным треугольником 9).0697 A B C на рисунке). Чтобы вычислить различные части треугольника, нужно найти длину каждой хорды как функцию центрального угла, который ее стягивает, или, что то же самое, длину хорды как функцию соответствующей ширины дуги.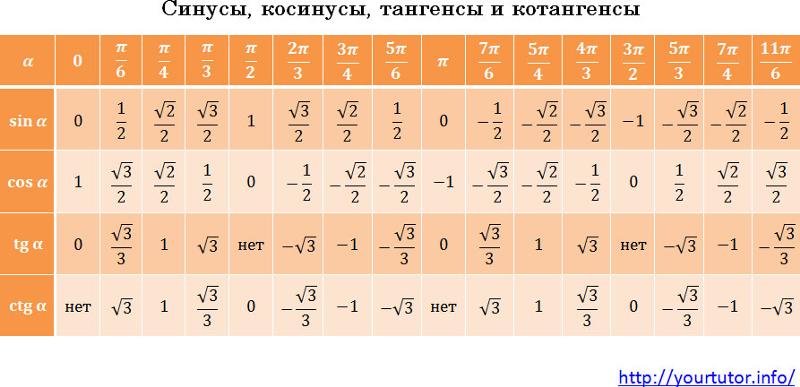 Это стало главной задачей тригонометрии на следующие несколько столетий. Как астронома Гиппарха в основном интересовали сферические треугольники, такие как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии. Во времена Гиппарха эти формулы выражались в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их стягивают; современные символы для тригонометрических функций не вводились до 17 века.
Это стало главной задачей тригонометрии на следующие несколько столетий. Как астронома Гиппарха в основном интересовали сферические треугольники, такие как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии. Во времена Гиппарха эти формулы выражались в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их стягивают; современные символы для тригонометрических функций не вводились до 17 века.
Изучите, как Птолемей пытался использовать деференты и эпициклы для объяснения ретроградного движения
Просмотреть все видео к этой статье Нажмите здесь, чтобы увидеть таблицу в полном размереПервой крупной древней работой по тригонометрии, дошедшей до Европы в целости и сохранности после Средневековья, был Альмагест Птолемеем ( г. г. 100–170 гг. Н. Э.). Он жил в Александрии, интеллектуальном центре эллинистического мира, но больше о нем мало что известно. Хотя Птолемей написал работы по математике, географии и оптике, в основном он известен своими Альмагест , сборник из 13 книг по астрономии, который стал основой для картины мира человечества, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея в середине 16 века. Чтобы развить эту картину мира, сущностью которой была неподвижная Земля, вокруг которой по круговым орбитам движутся Солнце, Луна и пять известных планет, Птолемею пришлось использовать некоторую элементарную тригонометрию. Главы 10 и 11 первой книги Альмагеста касается построения таблицы хорд, в которой длина хорды в окружности дана как функция центрального угла, который ее стягивает, для углов в диапазоне от 0 ° до 180 ° с интервалами в полградуса. . По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину стягиваемой хорды c , чтобы получить c = 2 r sin А / 2 .
Хотя Птолемей написал работы по математике, географии и оптике, в основном он известен своими Альмагест , сборник из 13 книг по астрономии, который стал основой для картины мира человечества, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея в середине 16 века. Чтобы развить эту картину мира, сущностью которой была неподвижная Земля, вокруг которой по круговым орбитам движутся Солнце, Луна и пять известных планет, Птолемею пришлось использовать некоторую элементарную тригонометрию. Главы 10 и 11 первой книги Альмагеста касается построения таблицы хорд, в которой длина хорды в окружности дана как функция центрального угла, который ее стягивает, для углов в диапазоне от 0 ° до 180 ° с интервалами в полградуса. . По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину стягиваемой хорды c , чтобы получить c = 2 r sin А / 2 .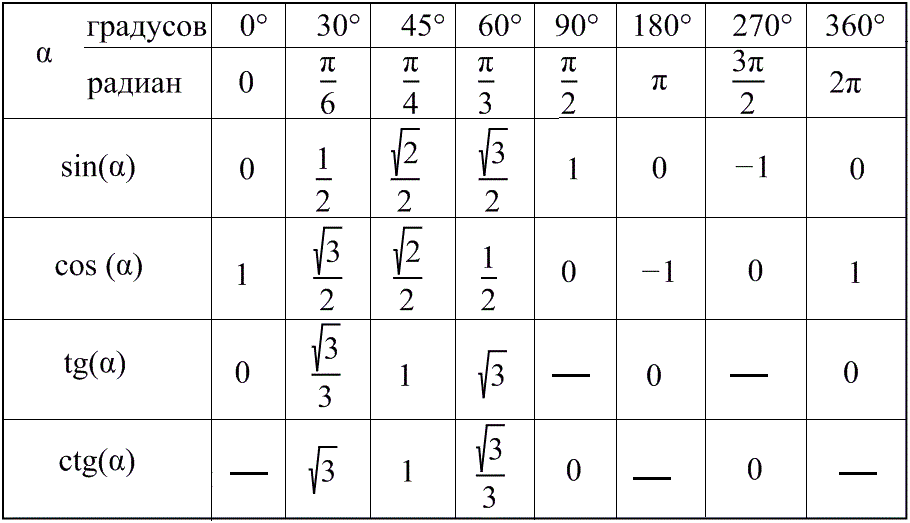 Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он проводил свои вычисления со стандартным кругом радиуса 9.0697 r = 60 единиц, так что c = 120 sin A / 2 . Таким образом, помимо коэффициента пропорциональности 120, это была таблица значений sin A / 2 и, следовательно (удвоением дуги) sin A . С помощью своей таблицы Птолемей усовершенствовал существующие геодезические меры мира и уточнил Гиппархову модель движения небесных тел.
Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он проводил свои вычисления со стандартным кругом радиуса 9.0697 r = 60 единиц, так что c = 120 sin A / 2 . Таким образом, помимо коэффициента пропорциональности 120, это была таблица значений sin A / 2 и, следовательно (удвоением дуги) sin A . С помощью своей таблицы Птолемей усовершенствовал существующие геодезические меры мира и уточнил Гиппархову модель движения небесных тел.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Математические функции — тригонометрические — Руководство Neo4j Cypher
Все эти функции работают только с числовыми выражениями и возвращают ошибку, если используются с любыми другими значениями. См. также Математические операторы.
Функции:
акос()
asin()
атан()
атан2()
cos()
детская кроватка()
градуса()
хаверсин()
Сферическое расстояние с использованием функции
haversin()пи()
радиан()
грех()
загар()
acos()
acos() возвращает арккосинус числа в радианах.
Синтаксис: acos(выражение)
Возвраты:
Плавающая. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в радианах. |
Соображения:
|
Если ( |
Запрос
RETURN acos(0,5)
Возвращается арккосинус числа 0,5 .
| акос(0,5) |
|---|
|
Ряды: 1 |
asin()
asin() возвращает арксинус числа в радианах.
Синтаксис: asin(выражение)
Возвраты:
| A float. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в радианах. |
Соображения:
|
Если ( |
Запрос
RETURN asin(0.5)
Возвращается арксинус 0.5 .
| asin(0,5) |
|---|
|
Ряды: 1 903:30 |
atan()
atan() возвращает арктангенс числа в радианах.
Синтаксис: atan(выражение)
Возвраты:
| A float. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в радианах. |
Соображения:
|
Запрос
RETURN atan(0.5)
Возвращается арктангенс 0.5 .
| атан(0,5) |
|---|
|
Ряды: 1 |
atan2()
atan2() возвращает арктангенс2 набора координат в радианах.
Синтаксис: atan2(выражение1, выражение2)
Возвраты:
| 7 Float. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение для y, представляющее угол в радианах. |
| Числовое выражение для x, представляющее угол в радианах. |
Компания:
|
Запрос
ВОЗВРАТ atan2(0,5, 0,6)
Возвращается арктангенс2 0,5 и 0,6 .
| атан2(0,5, 0,6) |
|---|
|
Ряды: 1 |
cos()
cos() возвращает косинус числа.
Синтаксис: cos(выражение)
Возвраты:
| A float. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в радианах. |
Соображения:
|
Запрос
RETURN cos(0.5)
Возвращается косинус 0.5 .
| кос(0,5) |
|---|
|
Ряды: 1 |
кроватка()
кроватка() возвращает котангенс числа.
Синтаксис: кроватка(выражение)
Возвраты:
Плавающая. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в радианах. |
Соображения:
|
|
Запрос
ВОЗВРАТ cot(0,5)
Возвращается котангенс числа 0,5 .
| кроватка(0,5) |
|---|
|
Ряды: 1 |
градусов()
градусов() преобразует радианы в градусы.
Синтаксис: градусов(выражение)
Возвраты:
A Float. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в радианах. |
Соображения:
|
Запрос
ВОЗВРАТ градусов (3,14159)
Количество градусов в чем-то близком к пи возвращается.
| градусов(3,14159) |
|---|
|
Ряды: 1 |
haversin()
haversin() возвращает половину версинуса числа.
Синтаксис: haversin(выражение)
Возвраты:
Поплавок. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в радианах. |
Соображения:
|
Запрос
RETURN haversin(0.5)
Возвращается гаверсинус числа 0.5 .
| гаверсин(0,5) |
|---|
|
Ряды: 1 |
Сферическое расстояние с использованием функции
haversin() Функция haversin() может использоваться для вычисления расстояния на поверхности сферы между двумя
точки (каждая дана по их широте и долготе). В этом примере сферическое расстояние (в км)
между Берлином в Германии (52,5 широты, 13,4 долготы) и Сан-Матео в Калифорнии (37,5 широты, 122,3 долготы)
рассчитывается с использованием среднего радиуса Земли 6371 км.
Запрос
СОЗДАТЬ (ber:City {широта: 52.5, долгота: 13. 4}), (sm:City {широта: 37.5, долгота: -122.3})
RETURN 2 * 6371 * asin(sqrt(haversin(радиан(sm.lat - ber.lat))
+ cos(радианы( sm.lat )) * cos(радианы( ber.lat )) *
haversin(radians( sm.lon - ber.lon )))) AS dist
4}), (sm:City {широта: 37.5, долгота: -122.3})
RETURN 2 * 6371 * asin(sqrt(haversin(радиан(sm.lat - ber.lat))
+ cos(радианы( sm.lat )) * cos(радианы( ber.lat )) *
haversin(radians( sm.lon - ber.lon )))) AS dist Расчетное расстояние между "Берлин" и "Сан-Матео" возвращено.
| дист |
|---|
|
Строки: 1 |
pi()
pi() возвращает математическую константу пи .
Синтаксис: pi()
Возвраты:
A Float |
Запрос
RETURN pi()
Возвращается константа pi .
| пи() |
|---|
|
Ряды: 1 |
радиан()
радиан() преобразует градусы в радианы.
Синтаксис: радианы(выражение)
Возвраты:
| 900. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в градусах. |
Соображения:
|
Запрос
RETURN radians(180)
Возвращается число радианов в 180 градусах (пи).
| радиан(180) |
|---|
|
Ряды: 1 |
sin()
sin() возвращает синус числа.
Синтаксис: sin(выражение)
Возвраты:
Поплавок. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в радианах. |
Соображения:
|
Запрос
RETURN sin(0.5)
Возвращается синус 0.5 .
| sin(0,5) |
|---|
|
Ряды: 1 |
tan()
tan() возвращает тангенс числа.
Синтаксис: tan(выражение)
Возвраты:
A Float. |
Аргументы:
| Имя | Описание |
|---|---|
| Числовое выражение, представляющее угол в радианах. |


 Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».

 В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
 И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.
И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.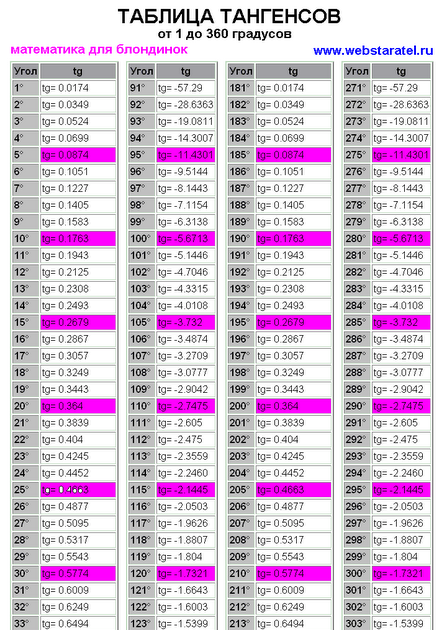 п.
п.
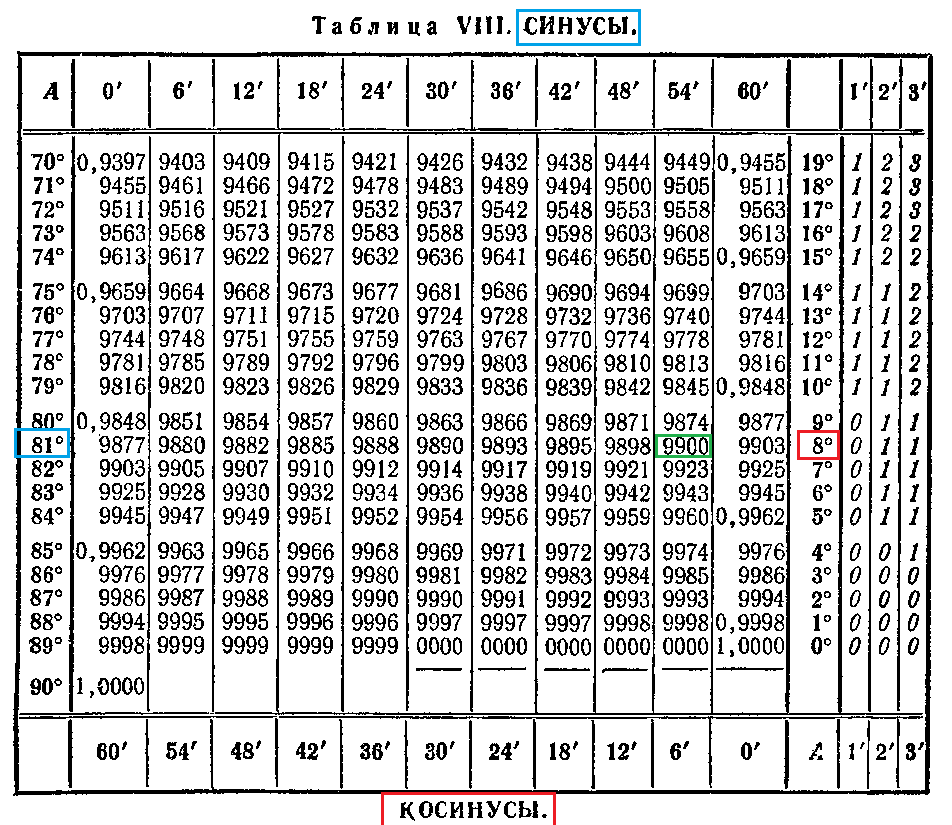
 Для этого в столбце слева таблицы синусов и косинусов находим значение градусов – $17°$, а в верхней строке находим значение минут – $42″$. На их пересечении получаем искомое значение:
Для этого в столбце слева таблицы синусов и косинусов находим значение градусов – $17°$, а в верхней строке находим значение минут – $42″$. На их пересечении получаем искомое значение:
 Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.
Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.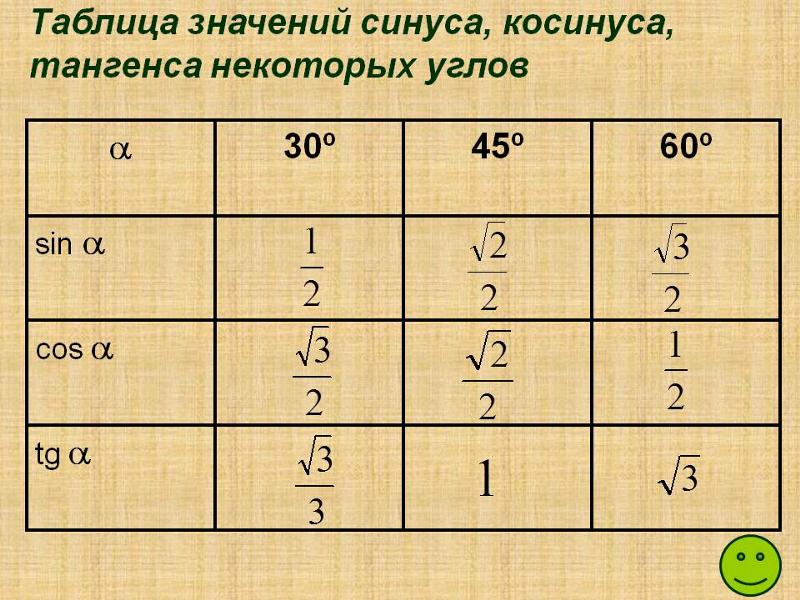
 Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется. .. Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
.. Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)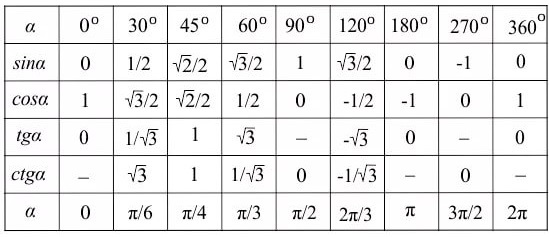 )
)

 000
000 


 830487721712452
830487721712452 
 4}), (sm:City {широта: 37.5, долгота: -122.3})
RETURN 2 * 6371 * asin(sqrt(haversin(радиан(sm.lat - ber.lat))
+ cos(радианы( sm.lat )) * cos(радианы( ber.lat )) *
haversin(radians( sm.lon - ber.lon )))) AS dist
4}), (sm:City {широта: 37.5, долгота: -122.3})
RETURN 2 * 6371 * asin(sqrt(haversin(радиан(sm.lat - ber.lat))
+ cos(радианы( sm.lat )) * cos(радианы( ber.lat )) *
haversin(radians( sm.lon - ber.lon )))) AS dist