| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.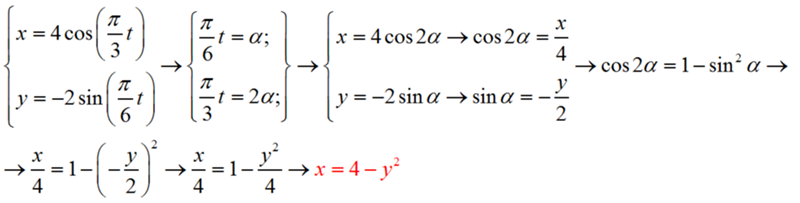 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.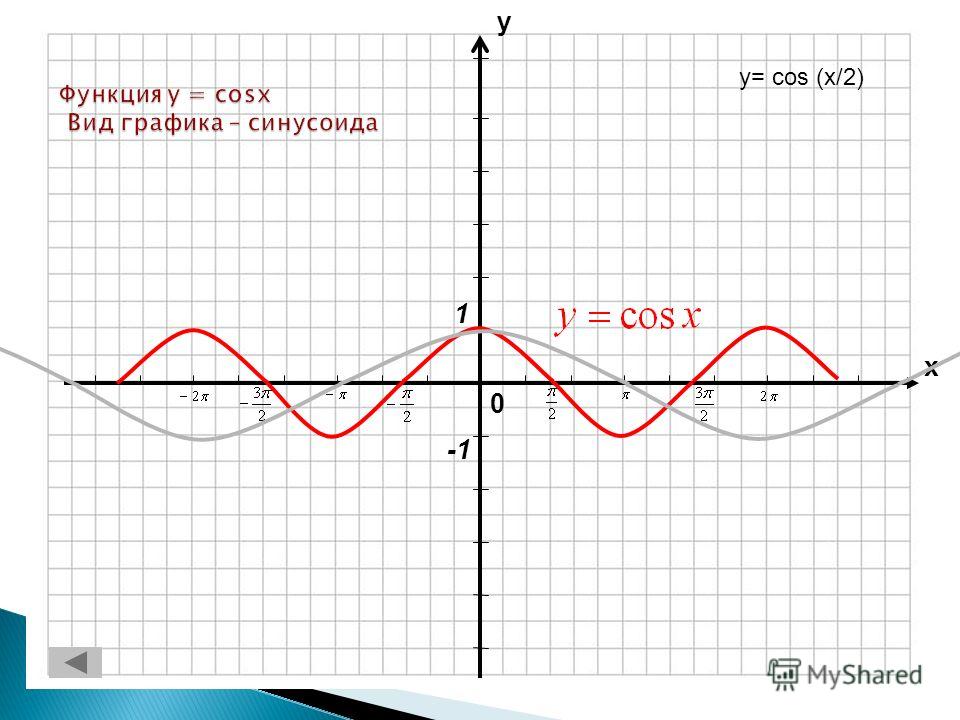 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | ||
| 95 | Найти точное значение | sin(120 град.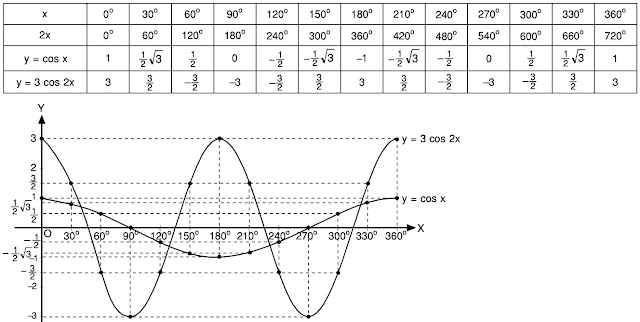 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Y cos 2x график. Функция y=cos t, её основные свойства и график
Урок и презентация на тему: «Функция y=cos(x). Определение и график функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
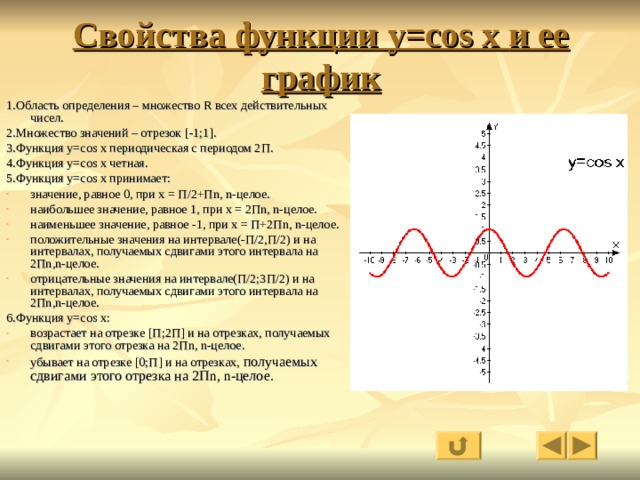
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.

- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
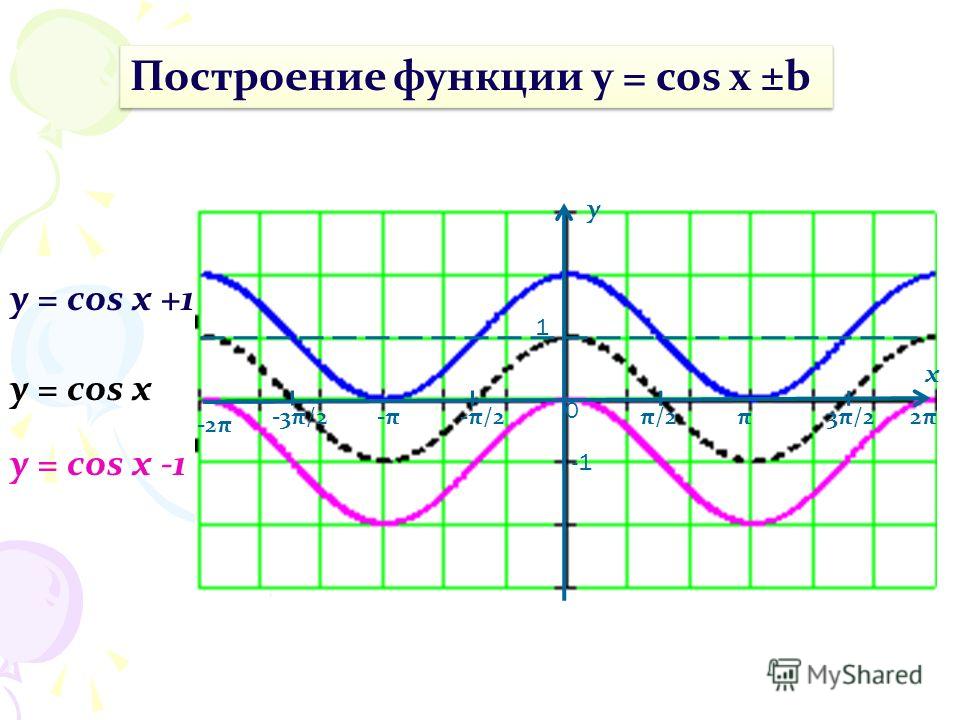
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].
На этом уроке мы подробно рассмотрим функцию у = cos х, ее основные свойства и график.В начале урока дадим определение тригонометрической функции у = cost на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=cost, её основные свойства и график
Функцией называется закон, по которому каждому значению независимого аргумента ставится в соответствие единственное значение функции.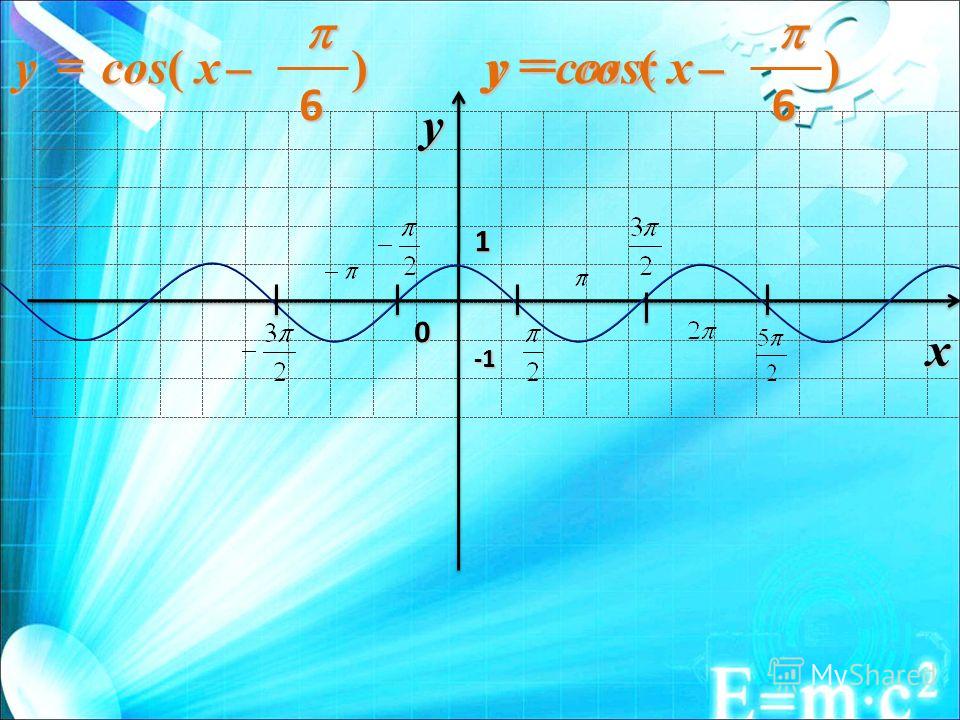
Вспомним определение функции Пусть t — любое действительное число. Ему соответствует единственная точка M на числовой окружности. У точки M есть единственная абсцисса. Она и называется косинусом числа t. Каждому значению аргумента t соответствует только одно значение функции (рис. 1).
Центральный угол численно равен величине дуги в радианах, т.е. числу Поэтому аргументом может быть и действительное число, и угол в радианах.
Если мы умеем для каждого значения определить то можем построить график функции
Можно получить график функции и другим способом. По формулам приведения поэтому график косинуса — это синусоида, сдвинутая по оси x на влево (рис.2).
Свойства функции
1) Область определения:
2) Область значений:
3) Функция четная:
4) Наименьший положительный период:
5) Координаты точек пересечения с осью абсцисс:
6) Координаты точки пересечения с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции: .
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели основные свойства и график функции Далее они будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.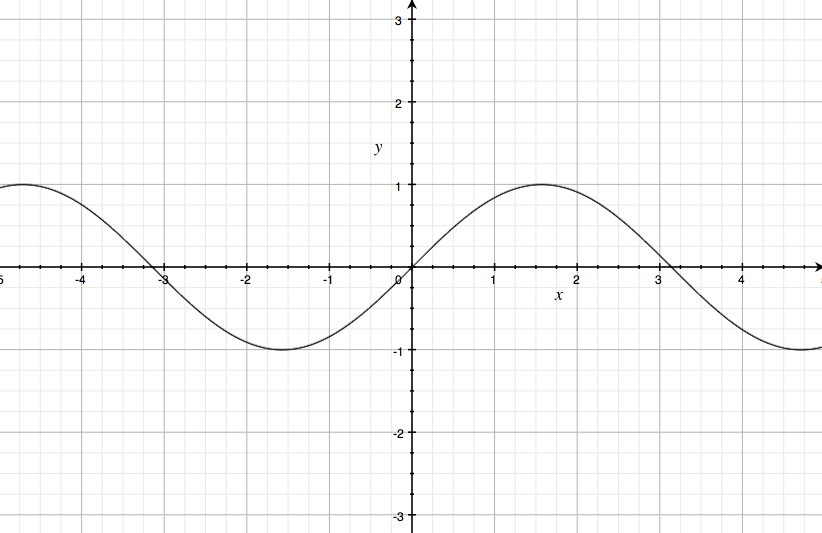
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.6, 16.7, 16.9.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.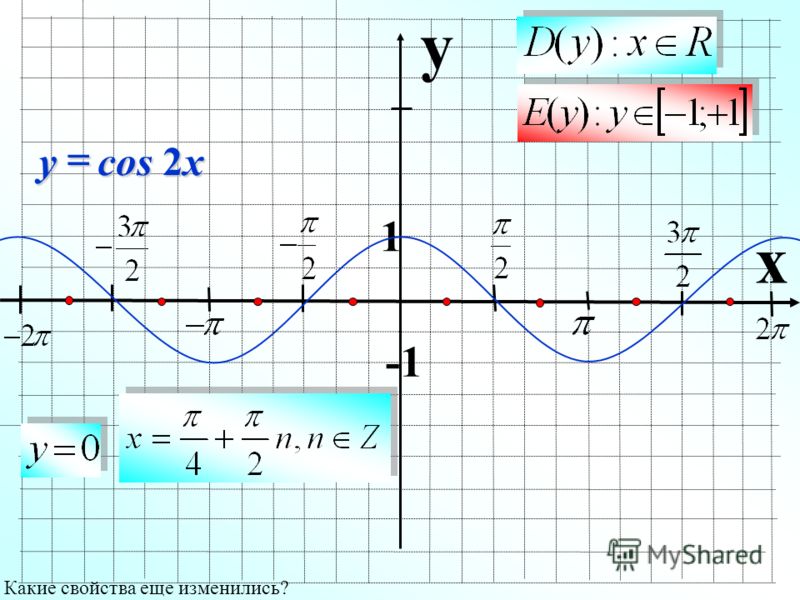
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x), y=tg(x), y=ctg(x). Рассмотрим каждую из них в отдельности.
Рассмотрим каждую из них в отдельности.
Y = sin(x)
График функции y=sin(x).
Основные свойства:
3. Функция нечетная.
Y = cos(x)
График функции y=cos(x).
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений — отрезок [-1;1].
3. Функция четная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = tg(x)
График функции y=tg(x).
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k — целое.
3. Функция нечетная.
Y = ctg(x)
График функции y=ctg(x).
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k — целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.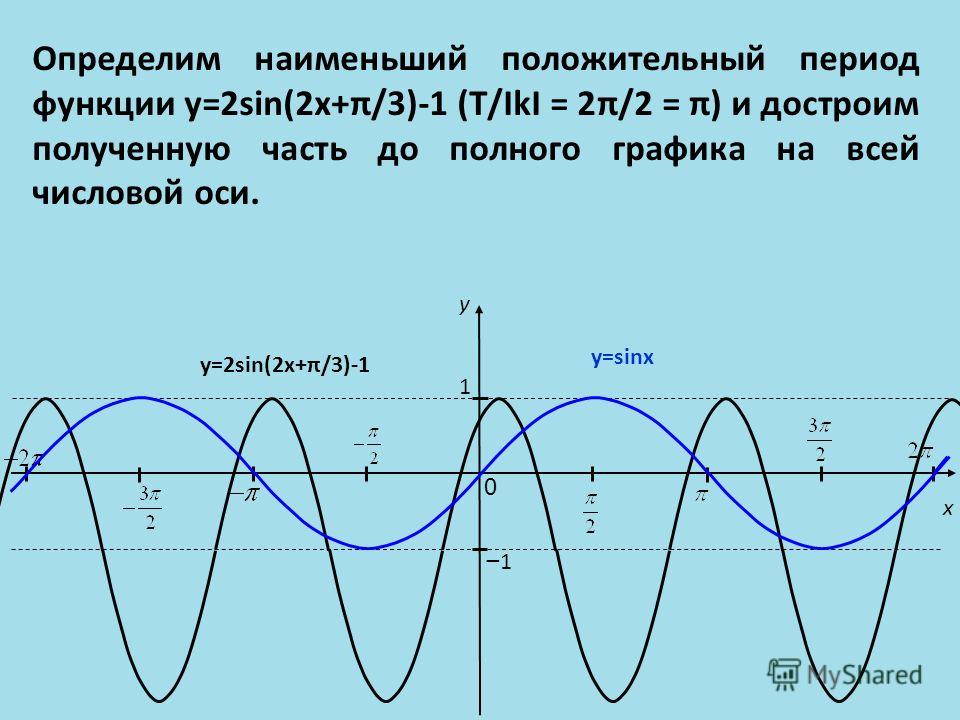
Исследование функции с помощью производной (стр. 2 из 3)
Определение: Функцию f называют периодической с периодом Т≠ 0, если для любого х из области определения значения этой функции в точках х, х-Т и х+Т равны, то есть f(x+T)=f(x)=f(x-T).
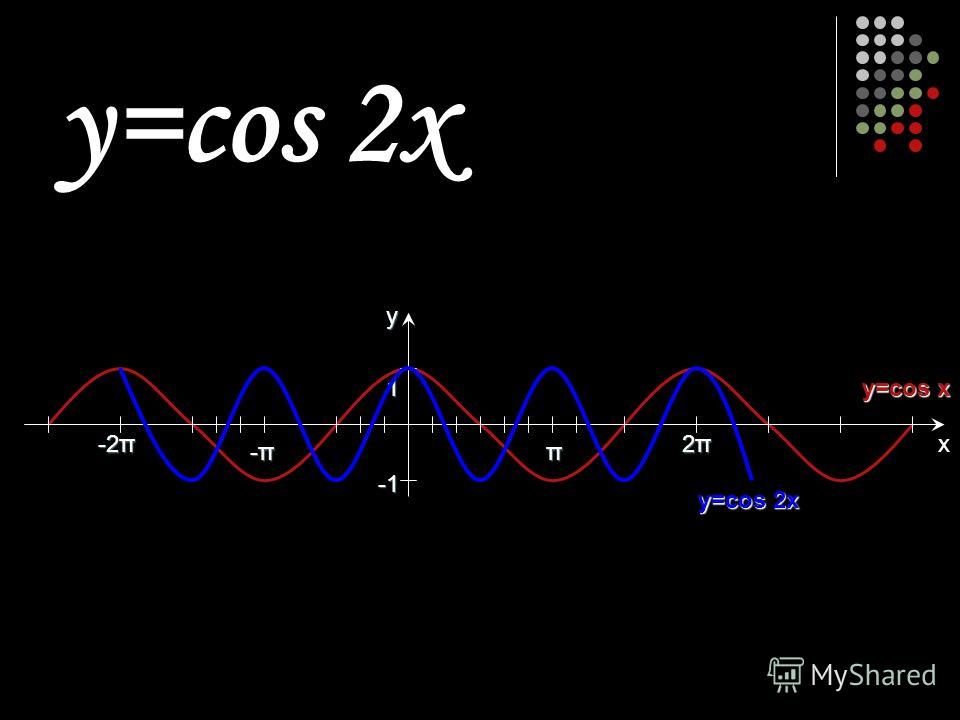
Пример 8. Определить период функции y=cos2x.
cos2x=cos2(x+T)=cos(2x+2T), где2T=2π, т.е. Т=π.
Для построения графика периодической функции с периодом Т достаточно провести построение на отрезке длиной Т и затем полученный график параллельно перенести на расстояния nT вправо и влево вдоль оси Ох.
Пример 9. Построить график периодической функции f(x)=sin2x.
f(x)=sin2x,
sin2x=sin2(x+T)=sin(2x+2T), где 2Т=2π, т.е. Т=π.
2.3. Возрастание и убывание функций. Экстремумы.
Также к свойствам функции относятся возрастание и убывание функции, экстремумы.
Функция f возрастает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2>х1 , выполнено неравенство f(x2)>f(x1).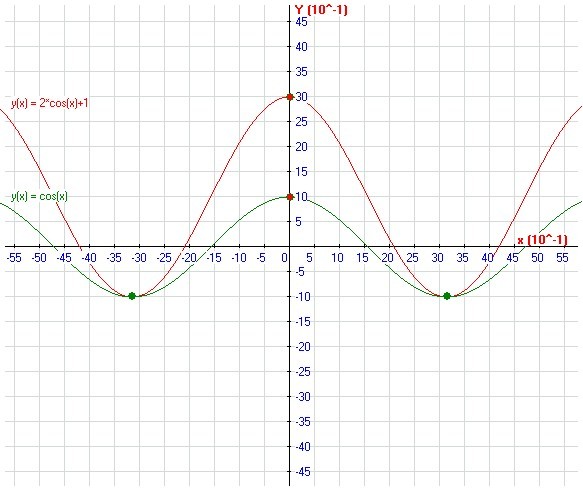
Функция fубывает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2>х1 , выполнено неравенство f(x2)<f(x1).
Иными словами, функция fназывается возрастающей на множестве Р, если большему значению аргумента из этого множества соответствует большее значение функции. Функция fназывается убывающей на множестве Р, если большему значению аргумента соответствует меньшее значение функции.
При построении графиков конкретных функций полезно предварительно найти точки минимума (xmin) и максимума (xmax).
Точка х0 называется точкой максимума функции f, если для всех х из некоторой окрестности х0 выполнено неравенство f(x) ≤f(x0).
Точка х0 называется точкой минимума функции f, если для всех х из некоторой окрестности х0 выполнено неравенство f(x)≥ f(x0).
Точки минимума и максимума принято называть точками экстремума.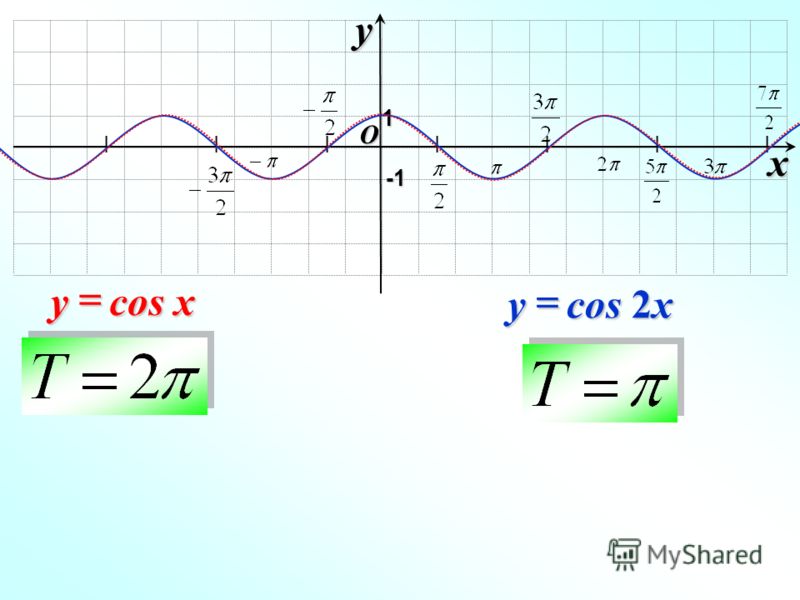
Пример 10. Найти точки экстремума, экстремумы функции y=x2+2x, и указать промежутки возрастания и убывания функции.
y=x2+2x, D(y)=R
y’=(x2+2x)’=2x+2
y’=0, т.е. 2х+2=0
2х=-2
х=-1
Исследуем знак производной справа и слева от крайней точки.
— +
-1
min
x=-2, y’=-4+2<0
x=0, y’=0+2>0
Так как производная меняет свой знак с «-» на «+», то х=-1, это точка минимума функции.
Так как функция непрерывна в точке х=-1, то функция возрастает на [-1;+∞] и убывает на [-∞;-1].
Точки экстремума: xmin= -1
Экстремумы функции: ymin=y(-1)=1-2= -1
Глава III. Исследование функций.
3.1. Общая схема исследования функций.
Исследуя функцию, нужно знать общую схему исследования:
1) D(y) – область определения (область изменения переменной х)
2) E(y) – область значения х (область изменения переменной у)
3) Вид функции: четная, нечетная, периодическая или функция общего вида.
4) Точки пересечения графика функции с осями Охи Оу (по возможности).
5) Промежутки знакопостоянства:
а) функция принимает положительное значение : f(x)>0
б) отрицательное значение : f(x)<0.
6) Промежутки монотонности функции:
а) возрастания;
б) убывания;
в) постоянства ( f=const).
7) Точки экстремума (точки минимума и максимума)
8) Экстремумы функции (значение функции в точках минимума и максимума)
9) Дополнительные точки.
Они могут быть взяты для того, чтобы более точно построить график функции.
Следует заметить, что экстремумы функции f не всегда совпадают с наибольшим и наименьшим значением функции.
3.2. Признак возрастания и убывания функций.
Если строить график функции по каким-либо произвольно выбранным его точкам, соединяя их плавной линией, то даже при очень большом числе случайно выбранных точек может оказаться, что построенный таким образом график будет сильно отличаться от графика заданной функции.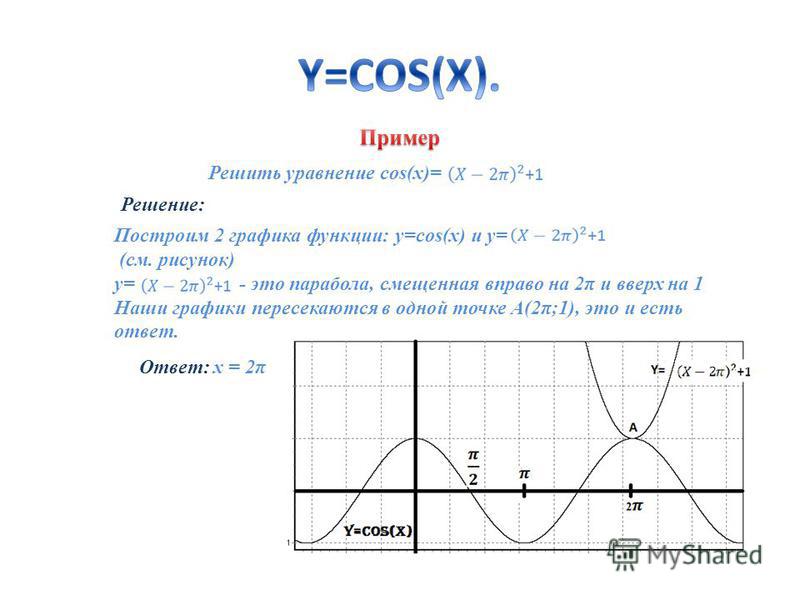
Если при исследовании функции использовать производную и найти так называемые «опорные» точки, т.е. точки разрыва, точки максимума и минимума, промежутки монотонности функции, то даже при небольшом числе таких «опорных» точек мы получим правильное представление о графике функции.
Прежде чем обратиться к примерам, приведу необходимые определения и теоремы.
Определение монотонности функции на интервале Функция y=f(x) называется возрастающей на интервале, если для любых точек х1 и х2 этого интервала из условия х1<х2 следует, что f(x1)<f(x2). Если же из условия х1<х2 следует, что f(x1)>f(x2), то функция называется убывающей на этом интервале.
Достаточный признак монотонности функции в интервале. Теорема: если функция имеет положительную (отрицательную) производную в каждой точке интервала, то функция возрастает (убывает) на этом интервале.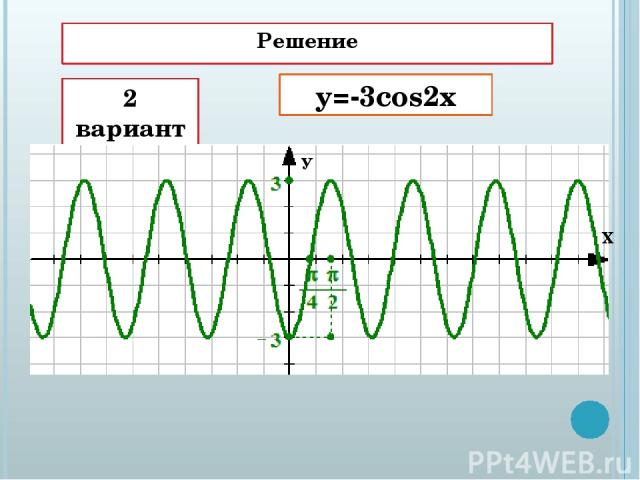
Эта теорема в школьных учебниках принимается без доказательства.
Геометрическое истолкование теоремы весьма простое, если вспомнить, что f ’(x)=tgα, α – это угловой коэффициент касательной к графику функции в заданной точке х. Если, например, f ‘ (x)>0 во всех точках некоторого интервала, то касательная к графику с осью абсцисс образуют острые углы, а значит, с ростом х возрастает и f(x). Если же f ‘ (x)<0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы.
3.3. Критические точки функции, максимумы и минимумы.
Определение точек экстремума функции. Пусть х0 – внутренняя точка из области определения функции f(x). Тогда, если существует такая δ – окрестность ] x0— δ, x0+ δ [ точки х0, что для всех х из этой окрестности выполняется неравенство f(x)≤f(x0) (неравенство f(x)≥f(x0)), точка х0 называется точкой максимума (точкой минимума) этой функции.
Точки максимума минимума являются внутренними точками области определения функции.
Необходимый признак существования экстремума дифференци-руемой функции.
Теорема Ферма.
Если х0 есть точка экстремума функции f(x) и в этой точке производная существует, то она равна нулю: f ’(x0)=0.
Эта теорема не является достаточным условием существование экстремума дифференцируемой функции: если в некоторой точке х0 производная обращается в нуль, то из этого еще не следует, что в точке х0 функция имеет экстремум.
Определение критических точек функции. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называют критическими точками функции.
Достаточные условия существования экстремума.
Теорема 1. Если функция f(x) непрерывна в точке х0, f ‘(x)>0 на интервале [a, x0] и f ‘(x)<0 на интервале [x0, b], то х0 является точкой максимума функции f(x).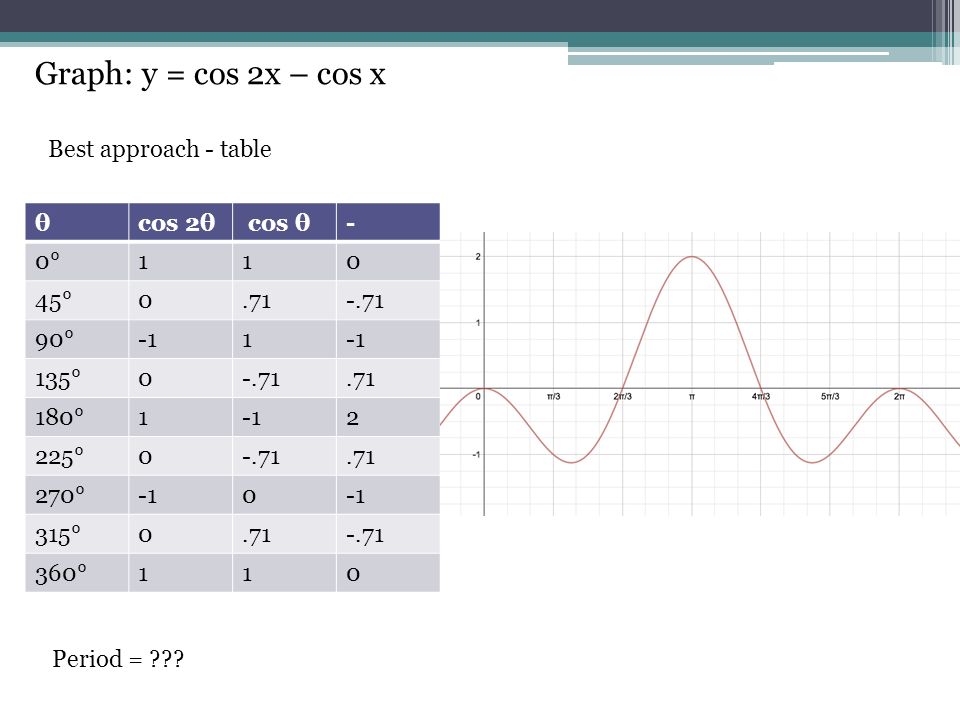
Теорема 2. Если функция f(x) непрерывна в точке х0, f ‘(x)<0 на интервале [a, x0] и f ‘(x)>0 на интервале [x0, b], то х0 является точкой минимума функции f(x).
Для отыскания экстремальных точек функции нужно найти ее критические точки и для каждой из них проверить выполнение достаточных условий экстремума.
3.4. Наибольшие и наименьшие значения функции.
Правила отыскания наибольшего и наименьшего значений функций в промежутке. Для отыскания наибольшего и наименьшего значений функции, дифференцируемой в некотором промежутке, нужно найти все критические точки, лежащие внутри промежутка, вычислить значения функции в этих точках и на концах промежутка и из всех полученных таким образом значений функции выбрать наибольшее и наименьшее.
Глава IV. Примеры применения производной к исследованию функции.
Пример 11. Исследовать функцию y=x3+6x2+9x и построить график.
y=x3+6x+9x
1) D(y)=R
2) Определим вид функции:
y(-x)=(-x)3+6(-x)2+9(-x)=-x+6x2-9x функция общего вида.
3) Найдем точки пересечения с осями:
Oy: x=0, y=0 (0;0) – точка пересечения с осью y.
Ox: y=0,
x3+6x2+9x=0
x(x2+6x+9)=0
x=0 или x2+6x+9=0
D=b2-4ac
D=36-36=0
D=0, уравнение имеет один корень.
x=(-b+D)/2a
x=-6+0/2
x=-3
(0;0) и (-3;0) – точки пересечения с осью х.
4) Найдем производную функции:
y’=(x3+6x2+9x)’=3x2+12x+9
5) Определим критические точки:
y’=0, т.е. 3x2+12x+9=0 сократим на 3
x2+4x+3=0
D=b2-4ac
D=16-12=4
D>0, уравнение имеет 2 корня.
x1,2=(-b±√D)/2a, x1=(-4+2)/2 , x2=(-4-2)/2
x1=-1 x2=-3
6) Обозначим критические точки на координатной прямой и определим знак функции:
0
-4
+ — +
-3 -1
x=-4, y’=3*16-48+9=9>0
x=-2, y’=12-24+9=-3<0
x=0, y’=0+0+9=9>0
7) Найдем xmin и xmax:
xmin=-1
xmax=-3
8) Найдем экстремумы функции:
ymin=y(-1)=-1+6-9=-4
ymax=y(-3)=-27+54-27=0
9) Построим график функции:
10) Дополнительные точки:
y(-4)=-64+96-36=-4
Пример 12.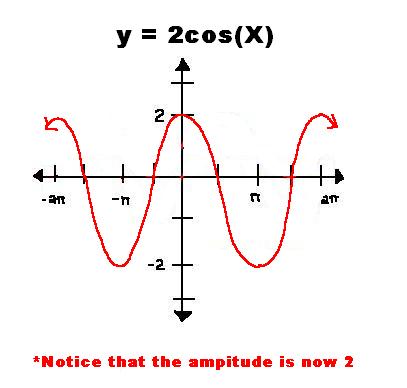 Исследовать функцию y=x2/(x-2) и построить график
Исследовать функцию y=x2/(x-2) и построить график
y=x2/(x-2)=x+2+4/(x-2)
Найдем асимптоты функции:
x≠ 2, x=2 – вертикальная асимптота
_x2 x-2
x2-2xx+2
_2x
2x-4
4
y=x+2 – наклонная асимптота, т.к.
lim 4/(x-2)=0
x→∞
Найдем область определения.
1) D(y)=R \ {2}
2)Определим вид функции.
y(-x)=(-x)2/(-x-2)=x2/(-x-2), функция общего вида.
3)Найдем точки пересечения с осями.
Oy: x=0, y=0 (0;0) – точка пересечения с осью y.
1
Первый слайд презентации
Тригонометрические функции двойного аргумента Тригонометрия
Изображение слайда
2
Слайд 2: Формулы двойного и половинного аргумента
1. sin2x = 2 sinx·cosx ;
2.cos2x = cos²x — sin²x;
3.cos2x = 1 – 2sin²x; 6.
4.cos2x = 2cos²x-1; 7.
5. ;
sin2x = 2 sinx·cosx ;
2.cos2x = cos²x — sin²x;
3.cos2x = 1 – 2sin²x; 6.
4.cos2x = 2cos²x-1; 7.
5. ;
Изображение слайда
3
Слайд 3: Основные тригонометрические тождества
1.
Изображение слайда
4
Слайд 4
. Найдите значение выражения 1) 2) 3) 4) 5) 6) cos2x = cos²x — sin²x sin2x = 2 sinx·cosx
Изображение слайда
5
Слайд 5: Задание:
Найдите если Задание:
Изображение слайда
6
Слайд 6: Функция y = cos x
Определение. Линию, служащую графиком функции y = cos x, называют косинусоидой.
Линию, служащую графиком функции y = cos x, называют косинусоидой.
Изображение слайда
7
Слайд 7: Свойства функции y = cos x
Свойство 1. D ( y ) = ( — ∞;+∞). Свойство 2. y = cos x – четная функция. Свойство 3. Функция y = cos x убывает на отрезке [ 2 π k ; π + 2 π k ] и возрастает на отрезке [π + 2 π k ; 2 π + 2 π k ], где k є Z. Свойство 4. Функция ограничена и сверху и снизу (-1 ≤ cos t ≤ 1). Свойство 5. y наим = -1; y наиб = 1. Свойство 6. Функция y = cos x периодическая, ее основной период равен 2π. Свойство 7. y = cos x – непрерывная функция. Свойство 8. E ( y ) = [-1; 1]. Свойство 9. Функция выпукла вверх на отрезке [ -0,5 π +2 π k; 0,5 π +2 π k ], выпукла вниз на отрезке [ 0,5 π +2 π k ; 1,5 π +2 π k ], где k є Z.
Изображение слайда
8
Слайд 8: Функция y = tg x
График функции
Свойства функции :
D(y) = (- π / 2 + π n ; π / 2 + π n ) ; n Z.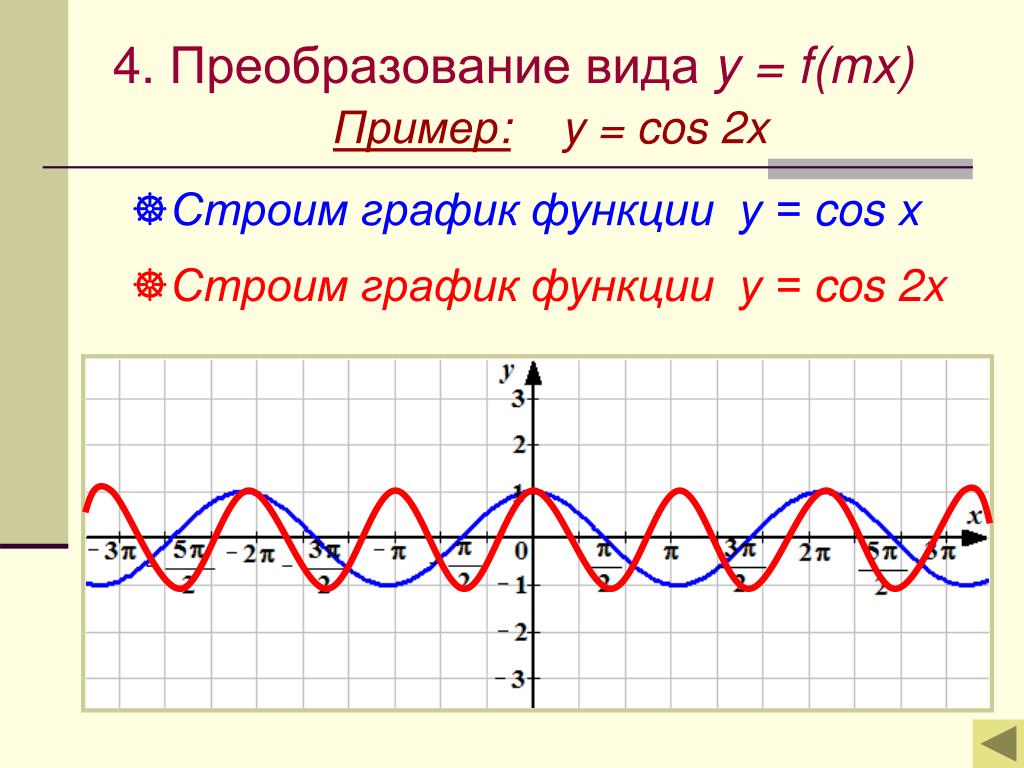 E( у ) = R.
Функция периодическая; T = π.
Функция нечетная.
5. tg x = 0 при х = π n, n Z.
Функция возрастает на
(- π / 2 + π n; π / 2 + π n ), n Z
tg x > 0
при π n < x < π / 2 + π n, n Z ;
tg x < 0
при — π / 2 + π n < x < π n, n Z.
Функция не достигает наибольшего и наименьшего значений.
Прямые π / 2 + π n, n Z, являются асимптотами графика функции.
E( у ) = R.
Функция периодическая; T = π.
Функция нечетная.
5. tg x = 0 при х = π n, n Z.
Функция возрастает на
(- π / 2 + π n; π / 2 + π n ), n Z
tg x > 0
при π n < x < π / 2 + π n, n Z ;
tg x < 0
при — π / 2 + π n < x < π n, n Z.
Функция не достигает наибольшего и наименьшего значений.
Прямые π / 2 + π n, n Z, являются асимптотами графика функции.
Изображение слайда
9
Слайд 9: Функция y = ctg x
График функции
Свойства функции:
D( у ) = ( π n ; π + π n ), n Z.
E( у ) = R
Функция периодическая; Т = π.
4. Функция нечетная.
ctg x = 0 при х = π / 2 + π n, n Z.
Функция убывает на
( π n; π + π n ), n Z.
ctg x > 0
при π n < x < π / 2 + π n, n Z ;
ctg x < 0
при π / 2 + π n < x < π + π n, n Z.
Функция не достигает наибольшего и наименьшего значений.
Прямые π n, n Z, являются асимптотами графика функции.
Изображение слайда
10
Слайд 10
y x 1 -1 π /2 — π /2 π 3 π /2 2 π — π -3 π /2 -2 π 0 y = cos (x — π/ 2) y = cos x График функции y = cos (x ± b) y = cos (x + π/ 2)
Изображение слайда
11
Слайд 11: Преобразование графиков тригонометрических функций
тригонометрические функции 11 Преобразование графиков тригонометрических функций График функции у = f (x +в) получается из графика функции у = f(x) параллельным переносом на (-в) единиц вдоль оси абсцисс График функции у = f (x )+а получается из графика функции у = f(x) параллельным переносом на (а) единиц вдоль оси ординат
Изображение слайда
12
Слайд 12: Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции 12 Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у = k f (x ) получается из графика функции у = f(x) путем его растяжения в k раз (при k>1) вдоль оси ординат График функции у = k f (x ) получается из графика функции у = f(x) путем его сжатия в k раз (при 0<k<1) вдоль оси ординат
Изображение слайда
13
Слайд 13: Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции
13
Преобразование графиков тригонометрических функций путем сжатия и растяжения
y = cos2x
y = cos 0.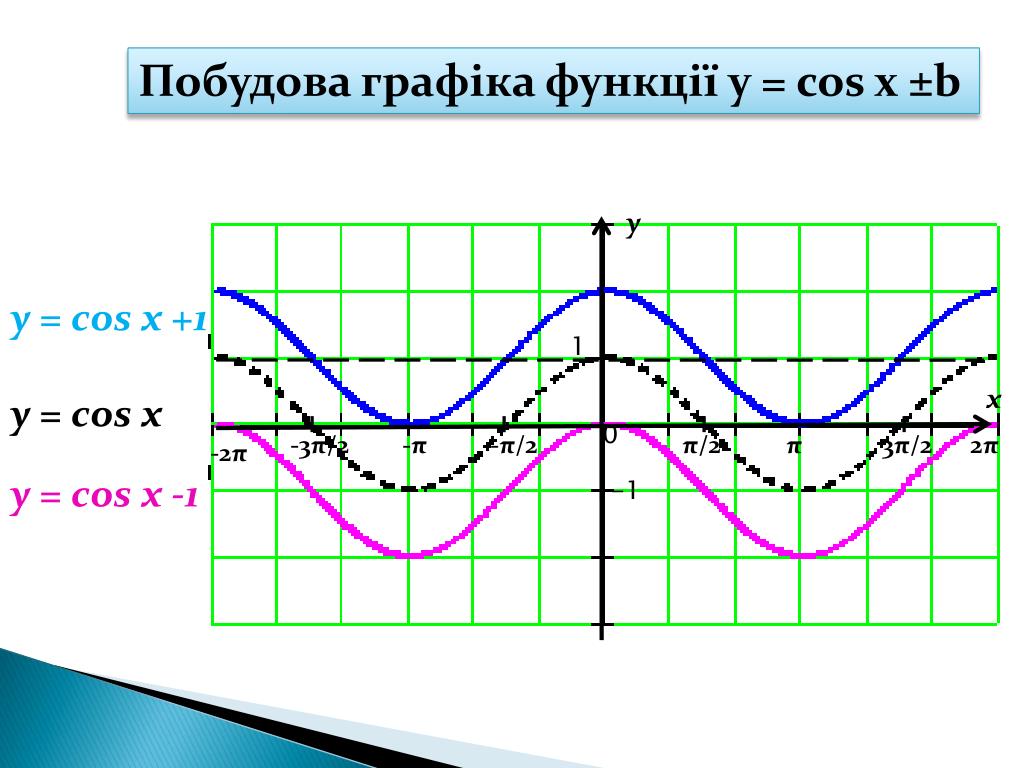 5x
5x
Изображение слайда
14
Слайд 14: Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции 14 Преобразование графиков тригонометрических функций путем сжатия и растяжения Графики функций у = -f (kx ) и у=- k f(x) получаются из графиков функций у = f(kx) и y= k f(x) соответственно путем их зеркального отображения относительно оси абсцисс синус – функция нечетная, поэтому sin(-kx) = — sin (kx) косинус –функция четная, значит cos(-kx) = cos(kx)
Изображение слайда
15
Слайд 15: Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции 15 Преобразование графиков тригонометрических функций путем сжатия и растяжения y = — sin3x y = sin3x
Изображение слайда
16
Слайд 16: Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции 16 Преобразование графиков тригонометрических функций путем сжатия и растяжения y=2cosx y=-2cosx
Изображение слайда
17
Слайд 17: Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции 17 Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у = f (kx+b ) получается из графика функции у = f(x) путем его параллельного переноса на (-в /k) единиц вдоль оси абсцисс и путем сжатия в k раз (при k>1) или растяжения в k раз ( при 0<k<1) вдоль оси абсцисс f ( kx+b) = f ( k( x+b/k))
Изображение слайда
18
Последний слайд презентации: Тригонометрические функции двойного аргумента Тригонометрия: Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции 18 Преобразование графиков тригонометрических функций путем сжатия и растяжения Y= cos(2x+ p /3) y=cos(x+ p /6) y= cos(2x+ p /3) y= cos(2(x+ p /6)) y= cos(2x+ p /3) y= cos(2(x+ p /6)) Y= cos(2x+ p /3) y=cos2x
Изображение слайда
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.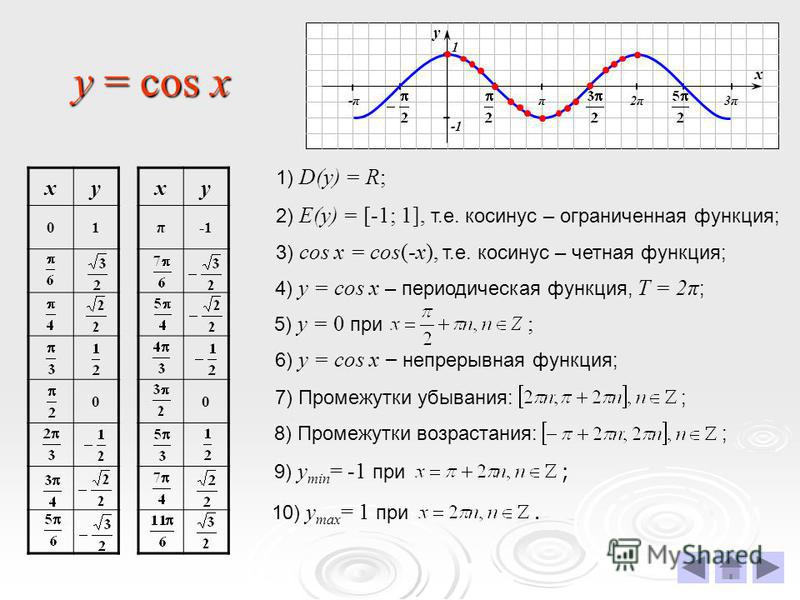 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Производное Cos 2x — формула, доказательство, примеры
Производная от cos 2x равна -2 sin 2x, что представляет собой процесс дифференцирования тригонометрической функции cos 2x относительно. угол х. Он дает скорость изменения cos 2x по отношению к углу x. Производная cos 2x может быть получена различными способами. Математически производная cos 2x записывается как d(cos 2x)/dx = (cos 2x)’ = -2sin 2x.
угол х. Он дает скорость изменения cos 2x по отношению к углу x. Производная cos 2x может быть получена различными способами. Математически производная cos 2x записывается как d(cos 2x)/dx = (cos 2x)’ = -2sin 2x.
В этой статье мы докажем производную от cos 2x, используя различные методы, включая первый принцип дифференцирования и цепное правило. Мы также сравним графики тригонометрической функции cos 2x и производной cos 2x вместе с некоторыми примерами.
| 1. | Что такое производная от Cos 2x? |
| 2. | Производная от Cos 2x с использованием цепного правила |
| 3. | Производная от Cos 2x с использованием первого принципа дифференцирования |
| 4. | График производной Cos 2x |
| 5. | Антипроизводная Cos 2x |
| 6. | Часто задаваемые вопросы о производной Cos 2x |
Что такое производная от Cos 2x?
Производная cos 2x отрицательна удвоенной тригонометрической функции sin 2x, то есть -2 sin 2x.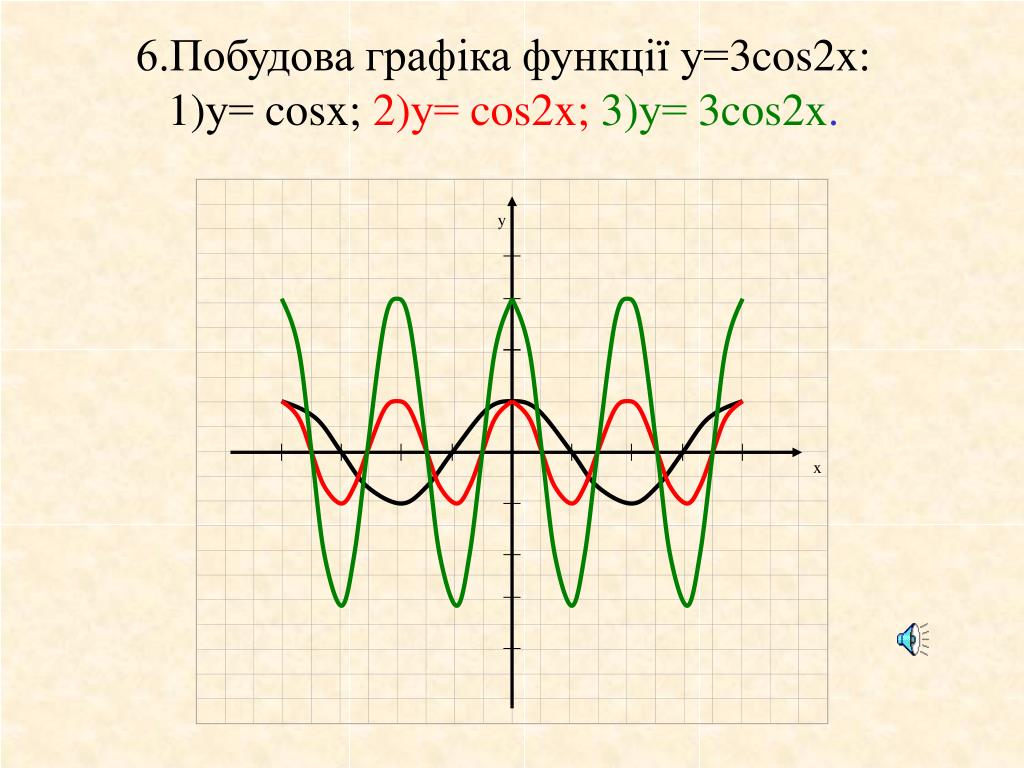 Производная от cos 2x обозначается как d(cos 2x)/dx или (cos 2x)’. Для получения производной от cos 2x используются различные тригонометрические формулы и тождества, а также некоторые правила дифференцирования. Его можно получить, используя определение пределов и цепное правило. Поскольку производная от cos 2x равна -2 sin 2x, то график производной от cos 2x будет графиком минуса от 2 sin 2x.
Производная от cos 2x обозначается как d(cos 2x)/dx или (cos 2x)’. Для получения производной от cos 2x используются различные тригонометрические формулы и тождества, а также некоторые правила дифференцирования. Его можно получить, используя определение пределов и цепное правило. Поскольку производная от cos 2x равна -2 sin 2x, то график производной от cos 2x будет графиком минуса от 2 sin 2x.
Производная формулы Cos 2x
Теперь мы математически запишем производную cos 2x. Формула производной от cos 2x:
- d(cos 2x)/dx = -2 sin 2x
- (cos 2x)’ = -2 sin 2x
Производная от Cos 2x с использованием цепного правила
Метод цепного правила для определения производных функций: (f(g(x)))’ = f’(g(x)) . г’(х). Теперь, чтобы вычислить производную от cos 2x с помощью цепного правила, мы воспользуемся некоторыми алгебраическими и тригонометрическими свойствами и тождествами, такими как:
- d(cos x)/dx = -sin x
- d(ax)/dx = a, где a — действительное число
Мы можем записать производную cos 2x по x как произведение производной cos 2x по 2x и производной 2x по x, то есть d(cos 2x)/dx = d( cos 2x)/d(2x) × d(2x)/dx. Теперь, используя приведенные выше формулы и цепное правило, мы имеем
Теперь, используя приведенные выше формулы и цепное правило, мы имеем
d(cos 2x)/dx = d(cos 2x)/d(2x) × d(2x)/dx
= -sin 2x × 2
= -2 sin 2x
Следовательно, мы получили производную от cos 2x как -2 sin 2x, используя цепное правило.
Производная от Cos 2x с использованием первого принципа дифференцирования
Теперь мы докажем, что производная от cos 2x равна — 2 sin 2x, используя определение пределов, то есть первый принцип производных. Чтобы найти производную cos 2x, мы берем предельное значение, когда x приближается к x + h. Чтобы упростить это, мы устанавливаем x = x + h и хотим взять предельное значение, когда h приближается к 0. Мы собираемся использовать определенные формулы дифференцирования и тригонометрии для определения производной cos 2x. Формулы:
- cos A — cos B = -2 sin[(A + B)/2] sin[(A — B)/2]
- \(f'(x)=\lim_{h\стрелка вправо 0}\dfrac{f(x+h)-f(x)}{h}\)
- \(\lim_{x\стрелка вправо 0} \dfrac{\sin x}{x} = 1\)
Используя приведенные выше формулы, мы имеем
\(\begin{align} \frac{\mathrm{d} \cos 2x}{\mathrm{d} x}&=\lim_{h\rightarrow 0}\dfrac {\ cos 2 (x + h) — \ cos (2x)} {h} \\ & = \ lim_ {h \ rightarrow 0} -2 \ dfrac {\ sin (\ frac {2 (x + h) + 2x) {2})\sin (\frac{2(x+h)-2x}{2})}{h}\\&=\lim_{h\rightarrow 0}-2\dfrac{\sin (2x+ h)\sin (h)}{h}\\&=-2\lim_{h\стрелка вправо 0}\sin (2x+h)\times \lim_{h\стрелка вправо 0}\dfrac{\sin h}{ h}\\&=-2 \sin 2x \times 1\\&=-2 \sin 2x\end{align}\)
Таким образом, мы получили производную от cos 2x, используя первый принцип дифференцирования.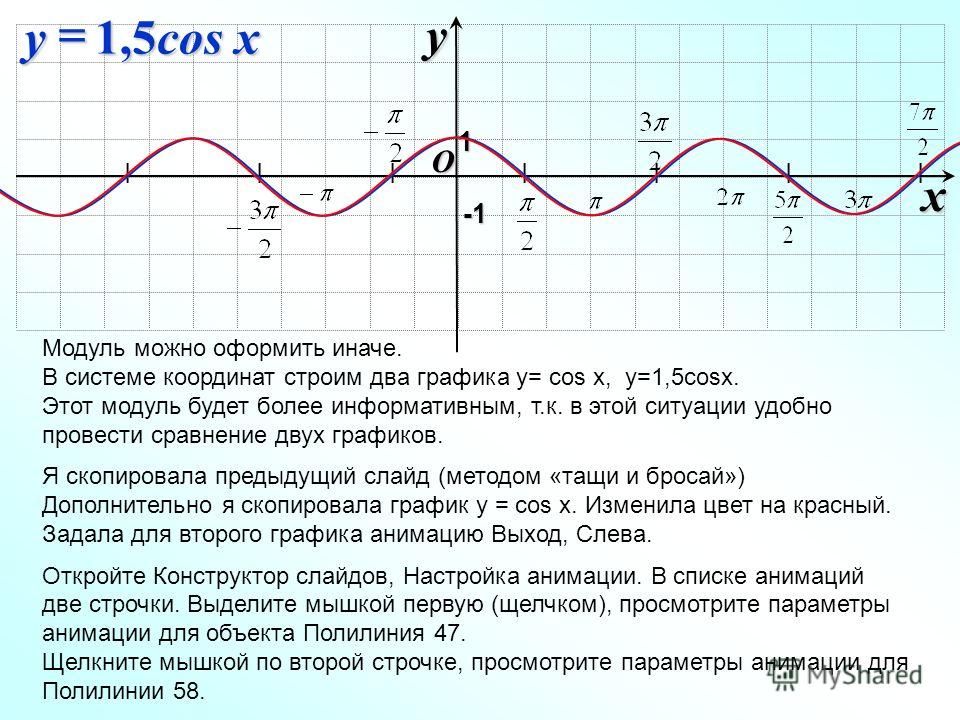
График производной Cos 2x
Мы знаем, что производная cos 2x отрицательна удвоенной тригонометрической функции sin 2x, что означает, что график производной cos 2x подобен графику тригонометрической функции sin 2x с отрицательными значениями, где sin 2x имеет положительные значения. Во-первых, давайте посмотрим, как выглядят графики cos 2x и производной от cos 2x. Поскольку sin 2x является периодической функцией, график дифференцирования cos 2x также является периодическим и его период равен π.
Антипроизводная Cos 2x
Как следует из названия, антипроизводная — это процесс, обратный дифференцировке. Антипроизводная от cos 2x есть не что иное, как интеграл от cos 2x. Мы знаем, что интеграл от cos x равен sin x + C. Используя формулу интегрирования ∫cos(ax + b) = (1/a) sin(ax + b) + C, первообразная cos 2x равна ( 1/2) sin 2x + C, где C — постоянная интегрирования. Следовательно, мы получили первообразную cos 2x как (1/2) sin 2x + C.
∫cos 2x = (1/2) sin 2x + C
Важные замечания о производной от Cos 2x
- Производная от cos 2x НЕ равна -sin 2x. Мы используем цепное правило, чтобы определить производную от cos 2x.
- Производную от cos 2x также можно определить по формуле cos 2x.
- Производные cos 2x и cos -1 2x НЕ совпадают.
Темы, относящиеся к производной от Cos 2x
- Применение производных
- Формула цепного правила
- Ограничения
- Формулы косинуса
Часто задаваемые вопросы о производной Cos 2x
Что такое производная от Cos 2x в тригонометрии?
Производная от cos 2x отрицательна удвоенной тригонометрической функции sin 2x, то есть -2 sin 2x.
Как найти производную от Cos 2x?
Мы можем найти производную от cos 2x, используя различные методы, включая первый принцип дифференцирования, формулу cos 2x и цепное правило.
Какая производная от 1 + cos 2x?
Производная от 1 + cos 2x определяется как d(1 + cos 2x)/dx = 0 — 2sin 2x = -2 sin 2x. Следовательно, производная от 1 + cos 2x равна производной от cos 2x.
Что такое антипроизводная cos 2x?
Первообразная cos 2x равна (1/2) sin 2x + C, где C — постоянная интегрирования.
Является ли производная Cos 2x такой же, как производная Cos
-1 2x?Нет, производная Cos 2x не совпадает с производной Cos -1 2x.
Собираем все вместе
Собираем все вместеВведение
Задача: Найти амплитуду, период, фазу сдвиг и вертикальный сдвиг функций синуса и косинуса; графически функции синуса и косинуса с различными амплитудами, периодами, фазами сдвиги и вертикальные сдвиги.
Ввод учителя
Отображение более двух элементов синуса или
Функция косинуса вручную может стать очень запутанной.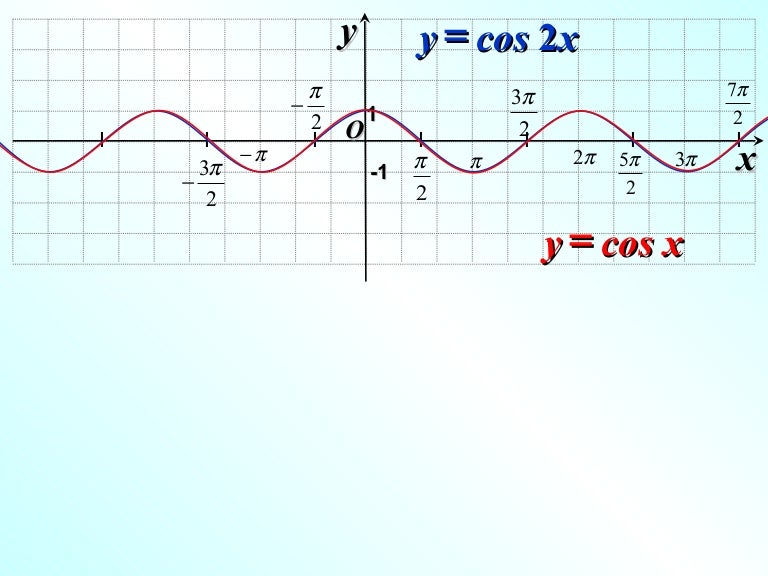 Самый легкий
способ графического отображения этих сложных уравнений состоит в том, чтобы работать поэтапно.
Самый легкий
способ графического отображения этих сложных уравнений состоит в том, чтобы работать поэтапно.
Общая форма любой функции синуса или косинуса выглядит так:
, где A влияет на амплитуду, B влияет на период, C влияет на фазовый сдвиг, а D влияет на вертикальный сдвиг.
г.Когда мы рисуем поэтапно, мы начинаем с построения графика основная функция синуса или косинуса. Тогда, если в уравнение, мы меняем базовую функцию на основе этой амплитуды (если нет A, пропустите этот шаг). Далее, если в уравнении есть B, мы меняем ПРЕДЫДУЩИЙ график на основе этого периода (если нет B, пропустить этот шаг). И так далее для C и D. Граф, созданный в последнем шаг окончательный график!
Примечание. Мы изобразим все этапы на одном и том же графике. координатная плоскость. Лучше всего графически изображать каждый шаг с разным цвета, чтобы не запутаться. Будьте осторожны, чтобы пометить или закодируйте этапы вашего графика!
г.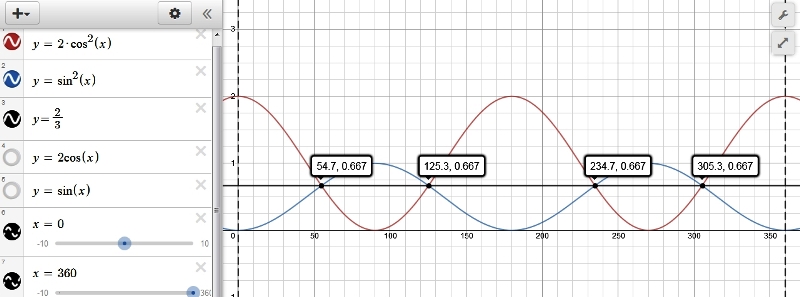
Пример 1. График y = -cos2(x — p/2) на интервале [0, 2p]
Шаг 1. График y = cosx (синий).
Шаг 2. Амплитуда не изменяется, но мы знаем, что минус перед косинусом означает график «переворачивается» вокруг оси X. Итак, график y = -cosx (зеленый).
Шаг 3. Произошла смена периода, поэтому мы теперь график y = -cos2x (бирюзовый). Период равен 2p/2 = p. Возьмем график от шаг 2 и «выжать» так, что вместо одного периода от 0 до 2p он будет иметь один период от 0 до стр.
Этап 4. Сдвиг фазы вправо на p/2 единицы. Итак, теперь мы нарисуем график y = -cos2(x — p/2) (фиолетовым цветом). Для этого просто возьмем график с шага 3 и переместите каждую точку вправо на p/2 единицы.
Шаг 5. Сдвига по вертикали нет, поэтому график из шага 4 на самом деле является окончательным графиком. Были сделаны!
г.Пример 2.
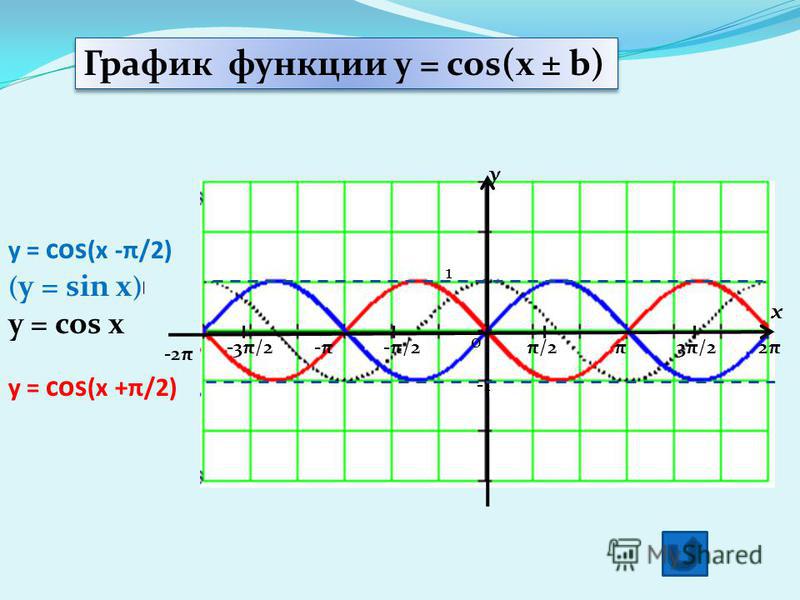 График y = 2sin0,5x + 3 на интервале [-2p, 2p]
График y = 2sin0,5x + 3 на интервале [-2p, 2p]Шаг 1. Мы всегда можем объединить шаги, если мы чувствовать себя комфортно. Например, все мы знаем, что такое график y = sinx выглядит, но мы также знаем, как выглядит график y = 2sinx похоже. Вместо того, чтобы изображать оба этих уравнения в виде двух отдельные шаги, мы можем объединить их и продолжить и построить график y = 2sinx (в красном).
Шаг 4 — фазового сдвига НЕТ, поэтому мы перейдем к вертикальному сдвигу. Есть сдвиг по вертикали от 3 единиц вверх. Итак, мы нарисуем следующий график y = 2sin0,5x + 3 (фиолетовый). К сделать это, мы просто возьмем график из шаг 2 и двигаться каждое очко вверх на 3 единицы. Это наш последний график!
Студенческая практика
1. Найти амплитуду, период, фазовый сдвиг,
и вертикальный сдвиг заданных функций.
Найти амплитуду, период, фазовый сдвиг,
и вертикальный сдвиг заданных функций.
а) у = -2sin(2x + p/2)
б) у = cos(x + p/2) — 3
в) у = 2cos(3x + p/2) + 4
г) у = 3sin(0,5x — p/2)
2. Нарисуйте график следующих функций над заданным интервалы.
а) у = -3sin(x — р/4), [0, 2р]
б) у = cos2(x + р/2) — 2, [-р, 2р]
в) y = -0,5cos0,5(x — p/4) + 1 [0, 4p]
г) у = -sin0.5x + 1, [0, 4p]
Ключ учителя для студенческой практики
1.
а) (Сначала вынесите 2: y = -2sin2(x + p/4)) amp = 2, pd = p, ps = p/4 слева, vs = 0
г.б) amp = 1, pd = 2p, ps = p/2 влево, против = 3 вниз
c) (Сначала вычтем 3: y = 2cos3(x + p/6) + 4) amp = 2, pd = 2р/3, пс = стр / 6 осталось, против = 4 вверх
d) (Сначала вычтем 0,5: y = 3sin0,5(x — р)) амп = 3, пд = 4п, пс = р справа, против = 0
2.
а)
б)
в)
г)
Возврат на домашнюю страницу Шеннон
Тригонометрические графики. Амплитуда и периодичность
Пи Хан Го, Мэй Ли, Кэлвин Лин, а также
способствовал
Содержимое
- Период тригонометрических функций
- Амплитуда тригонометрических функций
- Решение проблем — базовое
- Решение проблем — средний уровень
- Решение проблем — продвинутый уровень г.
Из определения основных тригонометрических функций как xxx- и yyy-координат точек на единичной окружности мы видим, что, обходя окружность один полный раз (((или угол 2π),2\pi), 2π), мы возвращаемся к той же точке и, следовательно, к тем же координатам xxx и yyy. Это может быть расширено для обхода круга любое кратное количество раз (((или любой угол, кратный 2π).2\pi).2π).
Изображение предоставлено: commons.wikimedia.org
Например,
0=sin(0)=sin(0+2π)=sin(0+2⋅2π)=⋯=sin(0+k⋅2π)0 = \sin(0 ) = \sin (0 + 2\pi) = \sin (0 + 2 \cdot 2\pi) = \cdots = \sin(0 + k \cdot 2\pi)0=sin(0)=sin(0 +2π)=sin(0+2⋅2π)=⋯=sin(0+k⋅2π)
для любого целого числа kkk.
Это показывает, что тригонометрические функции повторяют . Эти функции называются периодическими , а период — это минимальный интервал, необходимый для захвата интервала, который при многократном повторении дает полную функцию.
Периоды основных тригонометрических функций следующие:
FunctionPeriodsin(θ),cos(θ)2πcsc(θ),sec(θ)2πtan(θ),cot(θ)π\begin{array}{|c|c|} \hline \text{Функция} & \text{Точка}\\ \hline \sin (\theta), \cos (\theta) и 2\pi\\ \hline \csc (\тета) , \сек (\тета) и 2\пи \\ \hline \загар (\тета), \кот (\тета) и \пи\\ \hline \end{array}Functionsin(θ),cos(θ)csc(θ),sec(θ)tan(θ),cot(θ)Period2π2ππ
Как мы видели, тригонометрические функции чередуются между холмами и долинами. амплитуда тригонометрической функции равна половине расстояния от высшей точки кривой до нижней точки кривой:
(Амплитуда)=(Максимум) — (минимум)2. \text{(Амплитуда)} = \frac{ \text{(Максимум) — (минимум)} }{2}.(Амплитуда)=2(Максимум) — (минимум).
Например, если мы рассмотрим график y=sin(x)y=\sin(x)y=sin(x)
амплитуда равна (Максимум) — (минимум)2=1−(−1)2=22=1 \frac{ \text{(Максимум) — (минимум)} }{2} = \frac{ 1 — (-1)}{2} = \frac{2}{2} = 12(максимум) — (минимум)=21−(−1)=22=1.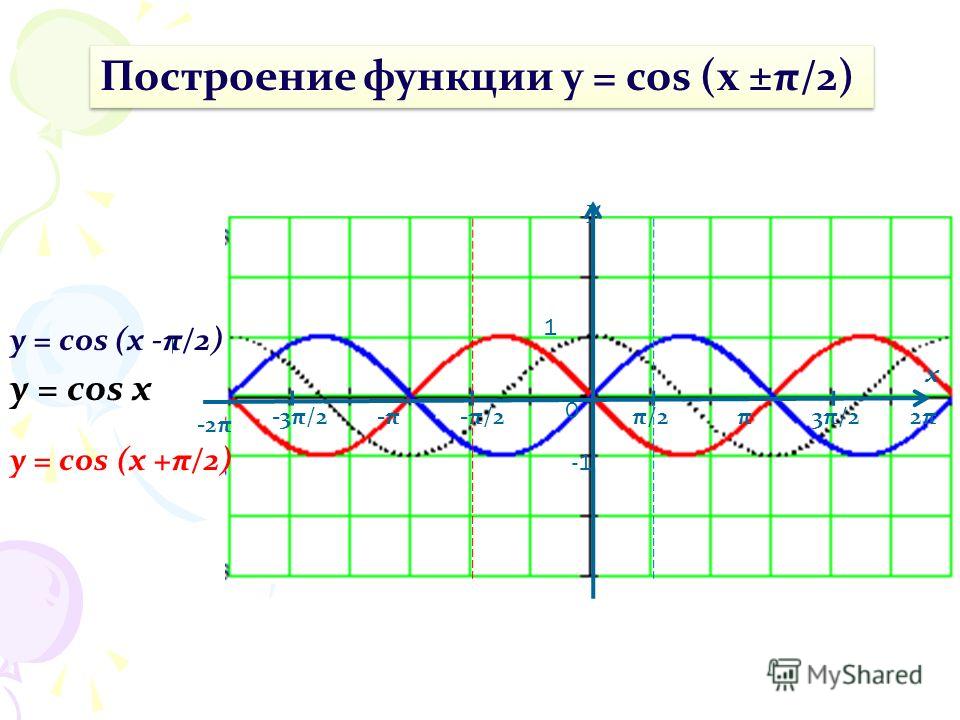 Точно так же график y=cos(x)y=\cos(x)y=cos(x) также имеет амплитуду 1,
Точно так же график y=cos(x)y=\cos(x)y=cos(x) также имеет амплитуду 1,
9\circ) = \ ?csc(750∘)= ?Амплитуды основных тригонометрических функций следующие:
Амплитуды функций in(θ),cos(θ)1csc(θ),sec(θ)N/Atan(θ),cot(θ)N/A\begin{array}{|c|c| } \hline \text{Функция} & \text{Амплитуда}\\ \hline \sin (\тета) , \cos( \тета ) &1 \\ \hline \csc (\theta) , \sec ( \theta) & \text{Н/Д} \\ \hline \tan (\theta), \cot ( \theta ) & \text{N/A} \\ \hline \end{массив}Функцииsin(θ),cos(θ)csc(θ),sec(θ)tan(θ),cot(θ)Amplitude1N/AN/A
При преобразовании тригонометрических графиков мы видим, что умножение тригонометрической функции на константу изменяет амплитуду. Например, амплитуда графика y=3sin(x)y = 3 \sin(x)y=3sin(x) равна 333.
Каковы амплитуда и период графика y=5sin(x)−2?y = 5 \sin(x) — 2?y=5sin(x)−2?
Поскольку тригонометрическая функция sin(x)\sin(x)sin(x) умножается на константу 555, амплитуда результирующего графика равна 555.
Результатом преобразования является сдвиг графика по вертикали на −2 -2−2 в направлении yyy и растянуть график по вертикали в 5,5,5 раза. Поскольку график не вытянут по горизонтали, период полученного графика совпадает с периодом функции sin(x)\sin(x)sin(x), или 2π2\pi2π. □_\квадрат□
Каковы амплитуда и период графика y=−100cos(1234π)?y=-100\cos(1234\pi)?y=−100cos(1234π)?
Не важно, будет ли это −100-100−100 или 100;100;100; в точках поворота y=±100.y = \pm100.y=±100. Таким образом, амплитуда равна 100, а основной период равен 2π1234π=1617. □ \frac{2\pi}{1234\pi} = \frac{1}{617}.\ _\square1234π2π=6171. □
Фундаментальный период синусоидальной функции fff, проходящей через начало координат, равен 3π3\pi3π, а ее амплитуда равна 5. Постройте f(x).f(x).f(x).
г.Поскольку он проходит через начало координат, он должен иметь вид f(x)=Asin(kx) f(x) = A \sin(kx) f(x)=Asin(kx) as f(0) =0f(0) = 0 f(0)=0.
{\circ}cos570∘ загар92} \sin(2x + \alpha ) = 41 \sin(2x+ \alpha) f(x)=402+92sin(2x+α)=41sin(2x+α) для некоторой константы α\alphaα, не зависящей от xxx . Таким образом, амплитуда равна 41, а основной период равен 2π2=π \frac {2\pi}2 = {\pi} 22π=π. □_\квадрат□
Каков период функции h(x)=sin(∣123x∣)?h(x) = \sin\big( |123x|\big)? ч(х)=грех(∣123x∣)?
Простой набросок графика в окрестности точки x=0x = 0 x=0 h(x)=sin(123x)={sin(123x)−sin(123x)h(x) =\sin (123x) = \begin{cases} {\sin(123x)} \\ { -\sin(123x)} \end{cases} h(x)=sin(123x)={sin(123x)−sin(123x) ) показывает, что оно не является периодическим. □_\квадрат□
π2\dfrac{\pi}{2}2π π\piπ 2π2\pi2π 4π4\pi4π g(x)g(x)g(x) не является периодическим Ничего из вышеперечисленного
g(x)=cos∣x∣+sin∣x∣\large \color{#69047E}{g(x)=\cos|x|+\sin|x|}g( x)=cos∣x∣+sin∣x∣
Найти основной период функции g(x)\color{#695(x) — 7\cos(x)?f(x)=64cos7(x)−112cos5(x)+56cos5(x)−7cos(x)?
Используя формулу двойного угла и формулу тройного угла, мы можем получить тот факт, что f(x)=cos(6x)f(x) = \cos(6x) f(x)=cos(6x). Таким образом, его амплитуда равна просто 1, а фундаментальный период равен 62π=3π \frac 6 {2\pi} = \frac3{\pi} 2π6=π3. □_\квадрат□
Таким образом, его амплитуда равна просто 1, а фундаментальный период равен 62π=3π \frac 6 {2\pi} = \frac3{\pi} 2π6=π3. □_\квадрат□
Заметим, что это можно доказать и с помощью полиномов Чебышева.
12 18 22 36 42 46 9{12} \sin (rx) = 0r=1∏12sin(rx)=0
Каково число решений xxx, удовлетворяющих приведенному выше уравнению, в интервале (0,π]?(0,\pi] ?(0,π]?
Найдите количество точек, в которых прямая 100y=x100y=x100y=x пересекает кривую y=sin(x)y=\sin(x)y=sin(x).
Эта задача входит в набор Тригонометрия
Цитировать как: Тригонометрические графики — амплитуда и периодичность. Brilliant.org .
Извлекаются из
https://brilliant. org/wiki/тригонометрические-графы-амплитуда-и-периодичность/
org/wiki/тригонометрические-графы-амплитуда-и-периодичность/
Графики тригонометрических функций — синус, косинус, тангенс и т.д.
График синуса
Чтобы легко нарисовать синусоидальную функцию, по оси х отложим значения от $-2\pi$ до $2 \pi$, а по оси y – вещественные числа.
Во-первых, кодомен синуса [-1, 1], это означает, что на вашем графике самая высокая точка по оси y будет равна 1, а самая низкая -1, проще провести линии, параллельные оси x, через -1 и 1 по оси Y, чтобы узнать, где находится ваша граница.
Далее находим нули. Нули — это точки, в которых ваш график пересекает ось x. Посмотрите на единичную линейку. Где функция синус равна нулю?
$ Sin(x) = 0$ где x – ось, пересекающая единичную прямую. Почему? Вы пытаетесь найти свои углы точно так же, как вы делали это раньше. Установите свое значение на оси y, здесь оно находится прямо в начале координат единичной окружности, и нарисуйте параллельные линии оси x. Это и есть ось х.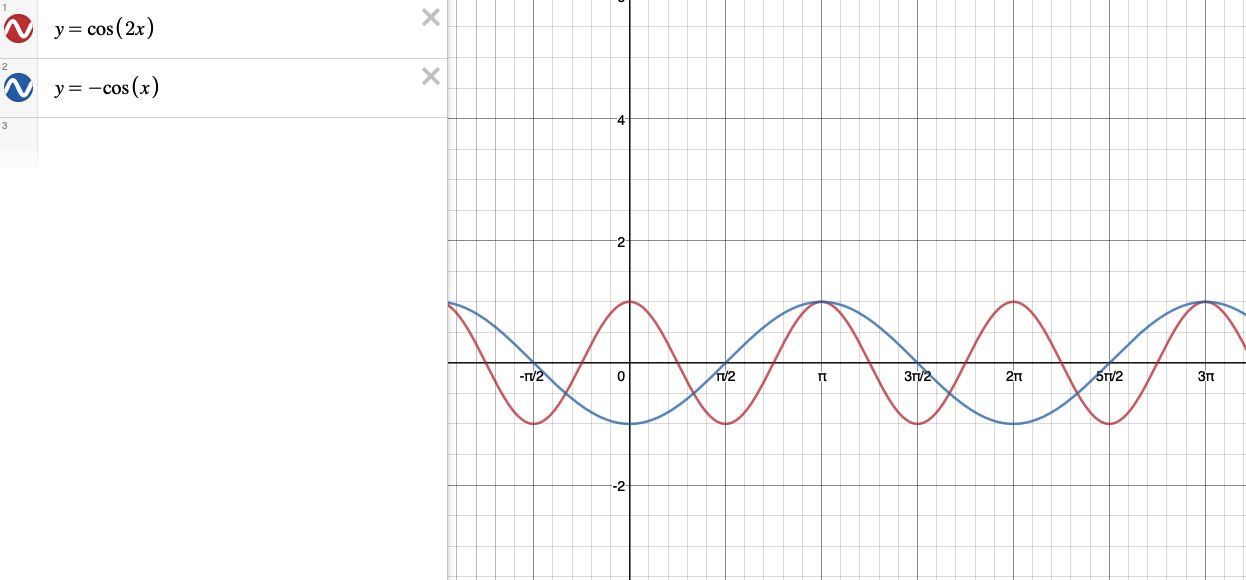
Значит, углы, значение синуса которых равно 0, равны $ 0, \pi, 2 \pi, 3 \pi, 4 \pi$ И это ваши нули, отметьте их на оси x.
Вот что у вас должно быть сейчас:
Теперь вам нужны максимальные и минимальные значения. Максимум — это точка, в которой ваш график достигает своего максимального значения, а минимум — это точка, в которой график достигает самого низкого значения в определенной области. Снова взгляните на единичную линию. Наибольшее значение равно 1, угол, при котором синус достигает этого значения, равен $\frac{\pi}{2}$, а наименьшее значение равно $-1$ в $\frac{3 \pi}{2}$. . Это также будет повторяться, поэтому наивысшими точками будут $\frac{\pi}{2}, \frac{5 \pi}{2}, \frac{9\pi}{2}$ … ($\frac{\pi}{2}$ и любой другой угол, который вы получите, когда попадете в эту точку на втором круге, третьем и т. д.), и самые низкие точки $\frac {3 \pi}{2}, \frac{7 \pi}{2}, \frac{11 \pi}{2}$ …
Так что отметьте и эти точки на графике.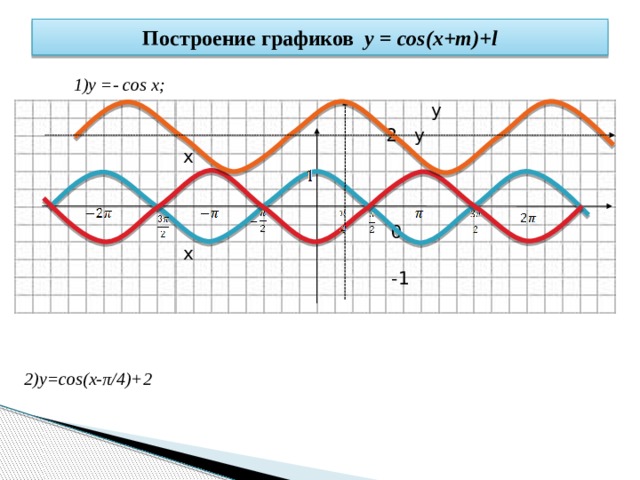
И когда вы соедините свои точки, вы должны получить что-то вроде этого:
График функции косинуса
График функции косинуса рисуется так же, как график значения синуса, с той лишь разницей, что нули.
=Взгляните еще раз на единичный круг. Где значение косинуса равно нулю? Он равен нулю там, где ось Y пересекает окружность, то есть в $ –\frac{\pi}{2}, \frac{\pi}{2}, \frac{3 \pi}{2}$ …
Просто выполните те же шаги, которые мы использовали для функции синуса.
Сначала отметьте нули. Опять же, поскольку домен косинуса равен [-1, 1], ваш график будет иметь значения только в этой области, поэтому нарисуйте линии, которые проходят через -1, 1 и параллельны оси x.
Теперь вам нужны точки, где ваша функция достигает максимума, и точки, где она достигает минимума. Снова посмотрите на единичный круг. Наибольшее значение косинуса равно 1, и он достигает его за $ 0, 2 \pi, 4 \pi$ …
Наименьшее значение косинуса равно -1, и оно достигает его в $\pi, 3 \pi, 5 \pi$ …
И когда вы соедините свои точки, вы должны получить что-то вроде этого:
Из этих графиков можно заметить одно очень важное свойство. Эти функции являются периодическими. Для функции быть периодической означает, что одна точка через определенный период снова будет иметь то же значение, а после того же периода снова будет иметь то же значение.
Эти функции являются периодическими. Для функции быть периодической означает, что одна точка через определенный период снова будет иметь то же значение, а после того же периода снова будет иметь то же значение.
Функция периодическая, если $ f(x) = f (x + p)$, где p — некоторый период.
Лучше всего это видно из крайностей. Взгляните на максимумы, они всегда имеют значение 1, а минимумы имеют значение -1, и это константа. Их период равен $2\pi$.
cos(x) = cos (x + 2 π)
Функции также могут быть нечетными или четными .
Функция четна, если $f(-x) = f(x)$
Теперь вернемся к нашим тригонометрическим функциям.
Функция синуса является нечетной функцией. Почему? Это легко увидеть из единичного круга. Чтобы узнать, является ли функция нечетной или четной, мы должны сравнить ее значение в x и –x.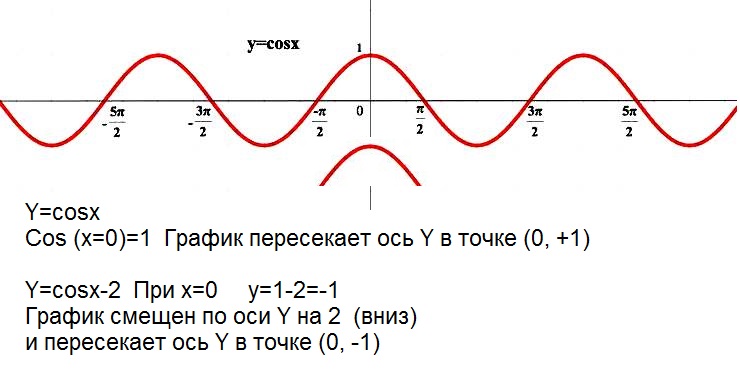
Нарисуйте любую точку, например $\frac{\pi}{4}$, а затем также нарисуйте $ – \frac{\pi}{4}$. Сейчас мы отметим это значение буквой b.
$ sin (\frac{\pi}{4}) = b \rightarrow sin (-\frac{\pi}{4}) = ?$
Из рисунка делаем вывод, что
$ Sin(-\frac{\pi}{4}) = — sin(\frac{\pi}{4})$. Это означает, что синус функции является нечетной функцией .
$ Sin(-x) = – sin(x)$.
Теперь посмотрим на значение косинуса: они равны .
Это означает, что косинус является четной функцией.
$ Cos(-x) = cos(x)$.
Тангенс и котангенс
Тангенс — это функция, полученная из функций синуса и косинуса.
Он определяется как
$tan(x) = \frac{sin(x)}{cos(x)}$
Поскольку тангенс определяется как дробь, он должен иметь особые условия относительно своей области. Знаменатель не может быть равен нулю. Это означает, что областью определения тангенса будет весь набор действительных чисел, кроме точек, где косинус достигает нуля.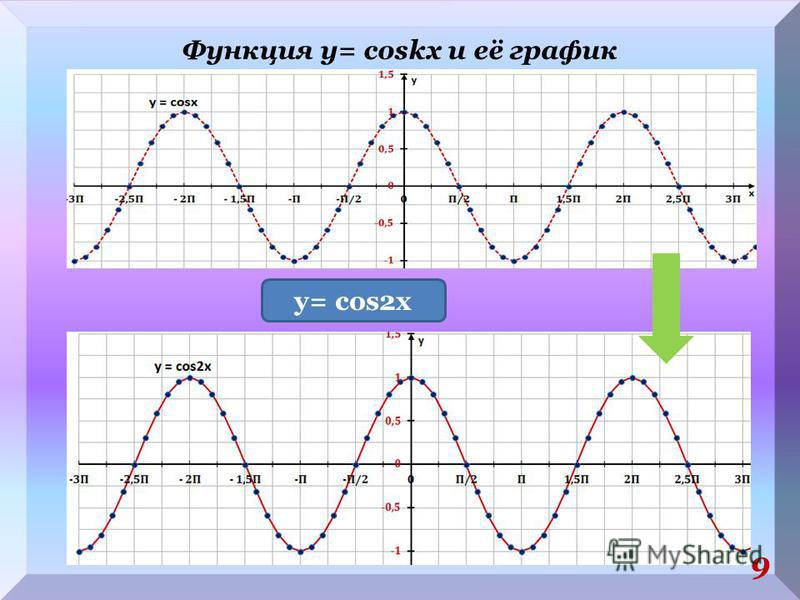 Эти точки равны $ (\frac{\pi}{2} + k \pi, k \epsilon Z)$. Что означает это обозначение? У вас есть все целые числа k. это означает $ {…-3, -2, -1, 0, 1, 2, 3…}$, когда вы умножаете это на $\pi$ и добавляете $\frac{\pi}{2}$, вы всегда будете иметь ноль для косинуса. Это означает, что к вашему первому π/2 вы прибавляете или вычитаете столько π, сколько хотите, вы всегда получите ноль.
Эти точки равны $ (\frac{\pi}{2} + k \pi, k \epsilon Z)$. Что означает это обозначение? У вас есть все целые числа k. это означает $ {…-3, -2, -1, 0, 1, 2, 3…}$, когда вы умножаете это на $\pi$ и добавляете $\frac{\pi}{2}$, вы всегда будете иметь ноль для косинуса. Это означает, что к вашему первому π/2 вы прибавляете или вычитаете столько π, сколько хотите, вы всегда получите ноль.
Это означает, что тангенс — это функция, область определения которой равна $\Re / (\frac{\pi}{2} + k \pi, k \epsilon Z)$, а область значений — $\Re$.
Снова сделайте вывод о том, как должен выглядеть график из единичного круга.
Какого значения будет достигать касательная функции в точках $\frac{\pi}{2}$ и $ -\frac{\pi}{2}$? В этих точках линия, которая сообщает нам, где находится значение касательной, теперь параллельна другой линии. Это означает, что в этих точках их значение будет равно $\pm \infty$.
Нули тангенса будут такими же, как и у синуса (просто приравниваем тангенс к нулю и решаем простое уравнение).
Линии, на которых тангенс функции уходит в бесконечность, называются асимптотами. Асимптоты — это линии, к которым функции бесконечно приближаются, но никогда не соприкасаются.
Для функции асимптотами касательной будут прямые, вертикальные по оси x, проходящие через $ (\frac{\pi}{2} + k \pi, k \epsilon Z)$.
Вот как это должно выглядеть сейчас:
Просто посмотрите, где ваша функция переходит в $ +\infty$, а где в $ -\infty$. Не забудьте помочь себе с единичным кругом. Все что нужно для графиков тригонометрических функций есть; вам просто нужно попрактиковаться в заключении из него.
И окончательный вид тангенса функции:
Изображение предоставлено пользователем Wikimedia Commons Malter
Котангенс — это функция, полученная из функций синуса и косинуса.
Котангенс определяется как
$cot (x) = \frac{cos(x)}{sin(x)}$
Котангенс также является функцией, определяемой как дробь, что означает, что областью определения котангенса будет целое множество действительных чисел без нулей функции синуса.
Домен = $ \Re / (k \pi : k \epsilon Z)$, кодовый домен $\Re$.
Нули — это точки, в которых значение косинуса равно 0, а значение, в котором график уйдет в бесконечность, находятся в нулях синуса. Также снова нарисуйте асимптоты, нули и посмотрите, где ваш график переходит в $\infty$ и $-\infty$.
Тангенс и котангенс даже не функции. Тангенс и котангенс также являются периодическими функциями с периодом π.
$ tan(-x) = – tan(x), tan(x + \pi) = tan(x)$
$cot(-x) = – cot(x), cot(x + \pi) = cot(x)$
Как и любые другие функции, тригонометрические функции также можно видоизменять, переводить и делать более «плотными» или «редкими».
Разберем эту функцию. Поскольку вы знаете, как рисовать синусоидальную функцию, это будет легко.
1. $ f(x) = 2 sin(x)$
Изучите эту функцию. Для каждого значения x его значение синуса будет удвоено, что означает, что даже эти конечные точки будут удвоены.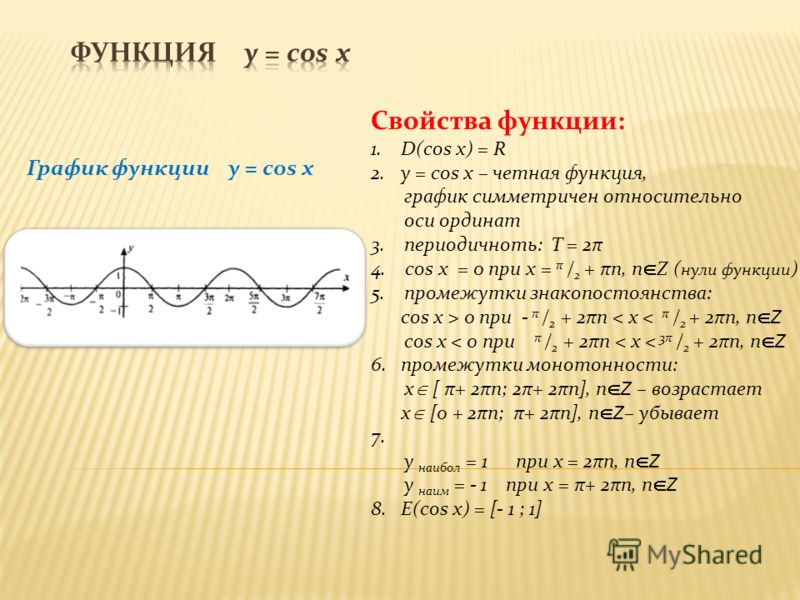 Это означает, что кодовый домен этой функции вместо [-1,1] теперь будет [-2,2]. Нули и экстремумы останутся в тех же точках.
Это означает, что кодовый домен этой функции вместо [-1,1] теперь будет [-2,2]. Нули и экстремумы останутся в тех же точках.
Если у вас есть любое число вместо 2, ваша функция будет $ f(x) = a * sin(x)$. Это означает, что кодовый домен этой функции будет [-a, a].
Аналог для $ f(x)= 3 cos(x)$
2. $ f(x) = sin(2x)$
Чем больше аргумент, тем более «плотной» будет ваша функция. Как найти нули для этой функции? Самый простой способ — использовать замену.
$ f(x) = sin(2x)$, чтобы найти нули, вы составляете уравнение $ sin(2x) = 0$ и используете замену $ t = 2x$.
Теперь у вас есть $sin(t) = 0$, и вы это знаете. $Sin(t)$ будет равен нулю, когда t равно 0 или $\pi (+2k \pi)$. Если вы вернете это в свою замену, вы получите $ 0 = 2x$ и $\pi = 2x$, что означает, что один нуль равен 0, а другой равен $\frac{\pi}{2} (+2k \ пи)$. Кодовый домен остается прежним, потому что ваш «а» равен 1. Теперь ваша функция выглядит так:
С другой стороны, когда ваше «b» меньше 1, ваша функция будет более разреженной.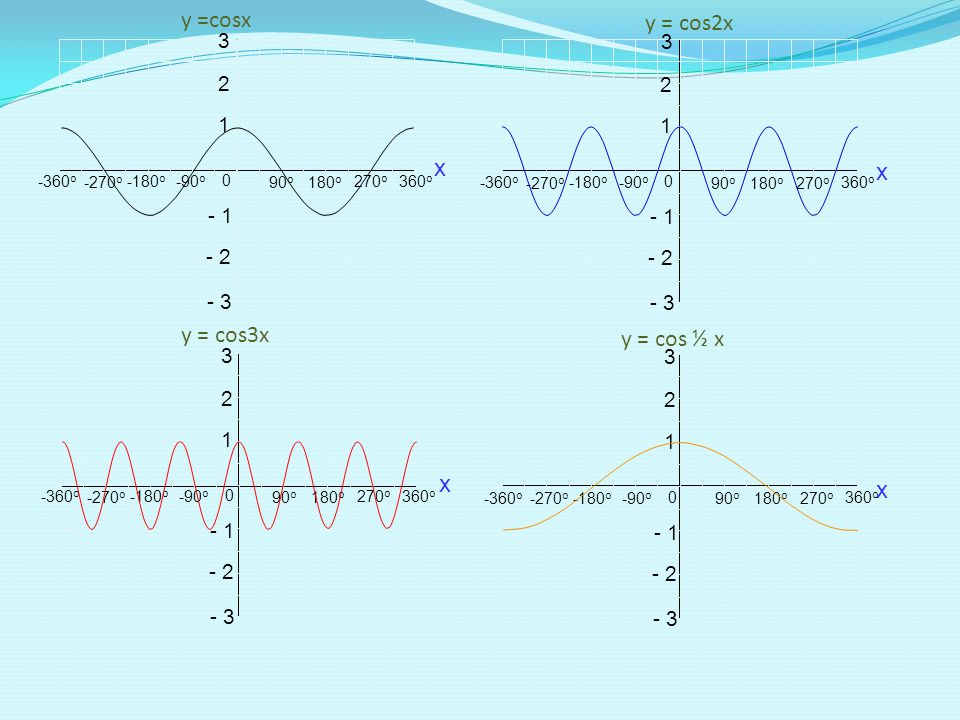
Для $ f(x) = sin(\frac{1x}{2})$
То же самое с косинусом:
$ f(x) = cos(2x)$
$ f (x) = cos(\frac{1x}{2})$
3. $ f(x) = sin(x + 2)$
расстояние, которое ваш график делает влево или вправо. Если у вас есть сложение, весь график будет сдвинут влево, а если у вас есть вычитание, то вправо.
Снова нули находятся с помощью подстановки: $sin(x + 2) = 0$, $t = x + 2$, $sin(t) = 0$ и т.д.
$ f(x)= sin(x – \pi)$
То же самое и с косинусом.
4. $ f(x) = sin(x) + 2$
Число после функции синуса представляет сдвиг по оси y. Если он положительный, то он пойдет вверх, а если отрицательный – вниз. Здесь кодомен тоже меняется, домен — это домен синуса ± это число.
Для функции $ f(x) = sin(x) + 2$ область значений синуса равна [-1, 1], если добавить 2, область значений функции $ f(x) = sin(x) + 2$ равно [1, 3]. Если не будет вариаций с аргументом функции синуса, максимумы и минимумы останутся в одних и тех же точках.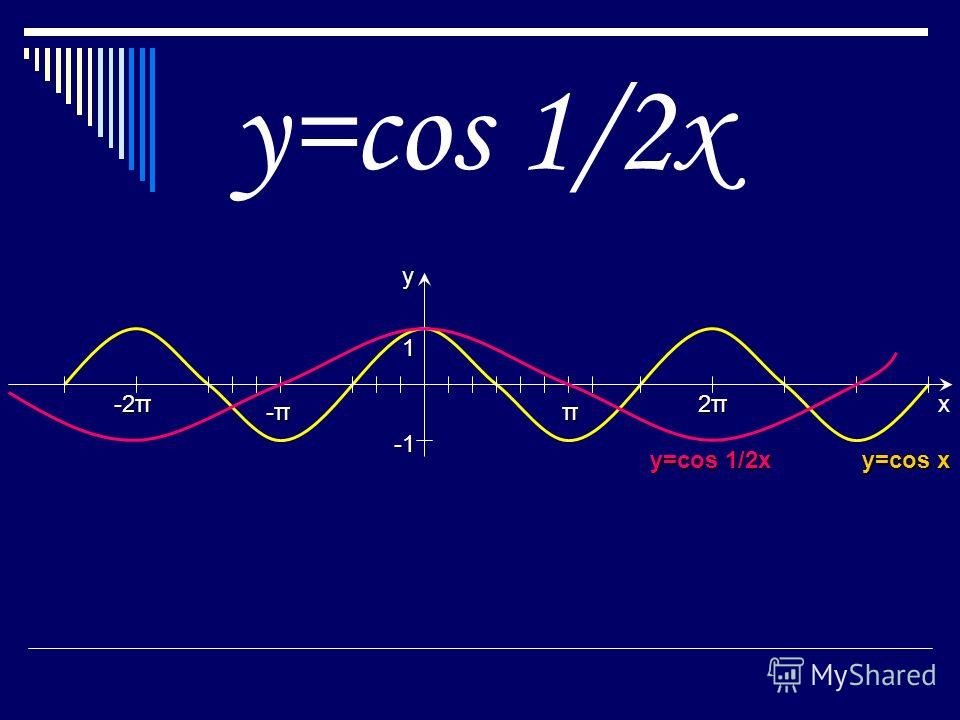
И, конечно же, чтобы было интереснее, вы можете объединить все это и получить, например:
$ f(x) = 2 sin(7x + 4) + 2$
Функция тангенса и котангенса варианты
Как только вы научитесь рисовать простые тригонометрические функции, вы изучите их все. Все, что относится к синусу и косинусу, также относится к тангенсу и котангенсу.
Опять же, вы находите свои нули, используя подстановку точно так же, как для синуса и косинуса.
1. $ f(x)= a * tan(x)$
Если «a» больше 1, функция будет быть уже, а это значит, что он будет «расти» гораздо быстрее, а если он меньше 1, то будет расти медленнее.
$ f(x) = 2 tan(x)$
$ f(x) = 0,5 tan(x)$
2. $ f(x) = tan(bx)$
In эта функция «b» изменит домен. Область определения правильного тангенса равна $\Re / (\frac{\pi}{2} + k \pi, k \epsilon Z)$, областью определения функции $f(x) = tan(bx)$ будет $\Re / (\frac{\pi}{b_2} + k \pi, k \epsilon Z)$.
Это означает, что для $ f(x) = tan(2x)$ его область определения равна $ R / (π\frac{\pi}{4} + k \pi, k \epsilon Z)$
3. $ f(x) = tan(x + c)$. «c» в этой функции изменит домен и местоположение. У вас есть два способа нарисовать эту функцию.
Во-первых, нужно найти нули и найти, где ваш график достигает асимптоты бесконечности.
Это делается с помощью замены $ t = x + c$.
Второй — нарисовать график $ f(x) = tan(x)$ и затем перевести его. Если c положительно, то график будет сдвинут влево, а если отрицательно — вправо.
$ f(x) = tan(x + 2)$
4. $ f(x) = tan(x) + d$
Как вы уже догадались, «d» будет переводить граф согласно у – ось. Если d положительное, весь граф будет сдвинут вверх, а если отрицательное вниз.
Нули изменятся, но домен останется прежним.
Те же преобразования графа применимы к котангенсу.
Графики обратных тригонометрических функций
Если мы хотим нарисовать график некоторой обратной функции, мы должны убедиться, что можем это сделать. Мы не можем потерять некоторые свойства, которые строго связаны с определением функции.
Мы не можем потерять некоторые свойства, которые строго связаны с определением функции.
Упрощенно, вы не можете найти обратную функцию функции, которая пересекает любую прямую, параллельную оси X, более чем в одной точке. Давайте сначала посмотрим на нашу синусоидальную функцию.
Если мы также нарисуем линию $ y = \frac{1}{2}$:
Эта линия разрежет нашу синусоидальную функцию во многих точках. Мы хотим ограничить нашу функцию так, чтобы любая линия, которую мы проводим параллельно оси x, пересекала синус ровно в одной точке.
Обычное ограничение на $ [-\frac{\pi}{2}, \frac{\pi}{2}]$.
Обратная функция в некотором роде заменит свойства домена и кодового домена. Это означает, что домен для Arcsin будет [-1, 1] и кодовый домен $ [-\frac{\pi}{2}, \frac{\pi}{2}]$.
Поскольку все значения будут инвертированы, этот график будет симметричен синусу с учетом прямой $ x = y$. Самый простой способ нарисовать это — нарисовать линию $ x = y$ и нарисовать конечные точки, по оси y это будут $\frac{\pi}{2}$ и $ -\frac{\pi}{2} $, а по оси y – ось.
А потом просто переводишь каждую точку. Просто будьте осторожны, чтобы не перейти с домена или кода домена.
Обратите внимание, что график никогда не пересекает -1 и 1 по оси X.
$ Arccos(x)$
Для этой функции обычным ограничением является $ [0, \pi]$
Домен арккосинуса равен [-1, 1] и кодовый домен $ [0, \pi]$.
Делаете все так же, как и для синуса. График арккосинуса симметричен графику косинуса с учетом прямой $ x = y$. сначала отметьте конечные точки и линию $ x = y $ и выполните симметричное сопоставление.
График касательной дуги получается такой же.
Его домен будет $ <-\infty, +\infty>$ и кодовый домен $ <-\frac{\pi}{2}, \frac{\pi}{2}>$. Линии $ y = -\frac{\pi}{2}$ и $y = \frac{\pi}{2}$ теперь будут горизонтальными асимптотами.
А для арккотангенса общим ограничением является домен $ <0, +\infty>$ и кодомен $ <0, +\infty>$.
$ Arcctg(x)$ определяется как $ arctan (\frac{1}{x})$ и поэтому у него будет график, аналогичный $\frac{1}{x}$, но здесь график будет пересекаться ось Y в $\frac{\pi}{2}$ и $ -\frac{\pi}{2}$.


 Результатом преобразования является сдвиг графика по вертикали на −2 -2−2 в направлении yyy и растянуть график по вертикали в 5,5,5 раза. Поскольку график не вытянут по горизонтали, период полученного графика совпадает с периодом функции sin(x)\sin(x)sin(x), или 2π2\pi2π. □_\квадрат□
Результатом преобразования является сдвиг графика по вертикали на −2 -2−2 в направлении yyy и растянуть график по вертикали в 5,5,5 раза. Поскольку график не вытянут по горизонтали, период полученного графика совпадает с периодом функции sin(x)\sin(x)sin(x), или 2π2\pi2π. □_\квадрат□ {\circ}cos570∘
загар92} \sin(2x + \alpha ) = 41 \sin(2x+ \alpha) f(x)=402+92sin(2x+α)=41sin(2x+α) для некоторой константы α\alphaα, не зависящей от xxx . Таким образом, амплитуда равна 41, а основной период равен 2π2=π \frac {2\pi}2 = {\pi} 22π=π. □_\квадрат□
{\circ}cos570∘
загар92} \sin(2x + \alpha ) = 41 \sin(2x+ \alpha) f(x)=402+92sin(2x+α)=41sin(2x+α) для некоторой константы α\alphaα, не зависящей от xxx . Таким образом, амплитуда равна 41, а основной период равен 2π2=π \frac {2\pi}2 = {\pi} 22π=π. □_\квадрат□