Вероятность выпадения: Расчет вероятности выпадения чисел — онлайн калькулятор

Содержание

Расчет вероятности выпадения чисел

Меня зовут Иван Мельников! Я – выпускник вуза НТУ «ХПИ», инженерно-физический факультет, специальность «Прикладная математика», счастливый семьянин и просто поклонник игр на удачу. С детства я увлекался лотереями. Мне всегда было интересно, по каким законам выпадают те или иные шары. С 10 лет я записываю результаты лотерей и после анализирую данные.

В моей книге «Секреты Везения или Пошаговый Алгоритм Выигрыша в Лотерее» я хочу поделиться с вами наблюдениями, накопленными годами, а также выводами, которые я смог сделать с помощью своего образования. Играйте по моей системе и уже совсем скоро вы превратите азартную игру в стабильный доход!

Математические шансы на победу

Простой расчет с факториалами

Самыми распространенными в мире лотереями являются игры на везение типа «5 из 36» и «6 из 45». Рассчитаем шанс выигрыша в лотерее банально по теории вероятности.

Пример расчета возможности получения джекпота в лотерею «5 из 36»:

Необходимо число свободных ячеек поделить на количество возможных комбинаций. То есть первую цифру можно выбрать из 36, вторую – из 35, третью – из 34 и так далее.

Следовательно, вот формула:

Количество возможных комбинаций в лотерее типа «5 из 36» = (36*35*34*33*32) / (1*2*3*4*5) = 376 992

Шанс выигрыша составляет 1 к почти 400 000.

Давайте проделаем то же самое для лотереи типа «6 к 45».

Количество возможных комбинаций = «6 из 45» = (45*44*43*42*41*40) / (1*2*3*4*5*6) = 9 774 072.

Соответственно, шанс выигрыша составляет практически 1 к 10 млн.

Немного о теории вероятности

Согласно давно уже известной теории у каждого шара в каждом следующем розыске есть абсолютно равный шанс выпасть по сравнению с другими.

Но не все так просто, даже согласно теории вероятности. Рассмотрим подробнее на примере подбрасывания монетки. Первый раз у нас выпал орел, тогда в следующий раз вероятность выпадения решки гораздо выше. Если орел выпал еще раз, то в следующий раз ожидаем решку с еще большей вероятностью.

С шарами, выходящими из лототронов, приблизительно та же история, но несколько сложнее и с более существенным количеством переменных. Если один шар выпал 3 раза, а другой – 10, то вероятность выпадения первого шара будет выше, чем у второго. Стоит отметить, что данный закон старательно нарушают организаторы некоторых лотерей, которые меняют лототроны время от времени. В каждом новом лототроне появляется новая последовательность.

Еще некоторые организаторы используют отдельный лототрон для каждого шара. Таким образом, необходимо рассчитывать вероятность выпадения каждого шара в каждом отдельном лототроне. Это с одной стороны немного облегчает задачу, с другой – усложняет.

Но это всего лишь теория вероятности, которая, как выяснилось, не очень-то и работает. Давайте посмотрим, какие есть секреты, основанные на сухой науке и статистических данных, накопленных за не одно десятилетие.

Почему не работает теория вероятности?

Неидеальные условия

Первое, о чем стоит поговорить, — это калибровка лототронов. Ни один из лототронов не откалиброван идеально.

Второй нюанс – диаметры лотерейных шаров также не являются одинаковыми. Даже отличие на малейшие доли миллиметров играют роль в частоте выпадения того или иного шара.

Третья деталь – разный вес шаров. Опять же отличие может казаться вовсе не существенным, но оно также влияет на статистику, притом, значительно.

Сумма выигрышных номеров

Если рассматривать статистику номеров, выигравших в лотерею типа «6 из 45», то можно заметить интересный факт: сумма цифр, на которые ставили игроки, колеблется между 126 и 167.

С суммой выигрышных лотерейных цифр для «5 из 36» немного другая история. Здесь выигрышные цифры составляют сумму в 83-106.

Четные или нечетные?

Как думаете, какие цифры чаще есть в выигрышных билетах? Четные? Нечетные? Скажу вам с полной уверенностью, что в лотереях «6 из 45» этих цифр поровну.

А вот как быть с «5 из 36»? Ведь нужно выбрать всего 5 шариков, четных и нечетных не может быть равное количество. Так вот. Проанализировав результаты розыгрышей лотерей данного типа четырех последних десятилетий, могу заявить, что незначительно, но все-таки чаще, в выигрышных комбинациях появляются нечетные цифры. Особенно, те, которые содержат в себе цифру 6 или 9. Например, 19, 29, 39, 69 и так далее.

Популярные группы чисел

Для лотереи типа «6 к 45» числа условно делим на 2 группы – от 1 до 22 и от 23 до 45. Следует отметить, что в выигрышных билетах отношение чисел, принадлежащих к группе, 2 к 4. То есть либо в билете будет 2 числа из группы от 1 до 22 и 4 числа из группы от 23 до 45 либо наоборот (4 числа из первой группы и 2 из второй).

Я пришел к аналогичному выводу, анализируя статистику лотерей типа «5 из 36». Только в данном случае немного иначе дробятся группы. Давайте первой обозначим группы, в которую входят цифры от 1 до 17, а второй – ту, куда помещаются оставшиеся числа от 18 до 35. Отношение цифр из первой группы ко второй в выигрышных комбинациях в 48% случаем равно 3 к 2, а в 52% случаев – наоборот, 2 к 3.

Стоит ли ставить на цифры из прошедших розыгрышей?

Доказано, что в 86% случаев в новом розыгрыше повторяется число, которое уже было в предыдущих розыгрышах. Поэтому просто необходимо следить за розыгрышами интересующей вас лотереи.

Последовательные цифры. Выбирать или не выбирать?

Шанс на то, что выпадут сразу 3 последовательные цифры, очень низок, и составляет менее 0,09%. А если вы хотите поставить сразу на 5 или 6 последовательных чисел, шанса практически нет. Поэтому выбирайте разные цифры.

Числа с единым шагом: победа или проигрыш?

Не стоит ставить на числа, которые идут в единой последовательности. Например, однозначно не нужно выбирать шаг 2 и с этим шагом делать ставку. 10, 13, 16, 19, 22 – однозначно проигрышная комбинация.

Больше одного билета: да или нет?

Лучше играть раз в 10 недель по 10 билетам, чем раз в неделю по одному. А также играйте группами. Можно выиграть большой денежный приз и разделить его между несколькими людьми.

Megamillions

Одна из самых популярных в мире лотерей проводилась по следующему принципу: необходимо выбрать 5 чисел из 56, а также 1 из 46 для так называемого золотого шара.

За 5 угаданных шаров и 1 верно названный золотой счастливчик получает джекпот.

Как рассчитать теорию вероятности в лотерее
Самые крупные выигрыши в лотереи в истории
Как выиграть в лотерею при помощи маятника

Теория и термины

В мире постоянно проводится множество лотерей с самыми различными правилами, условиями победы, призами, однако существуют общие принципы расчета вероятности выигрыша, которые можно адаптировать под условия той или иной конкретной лотереи. Но для начала желательно определиться с терминологией.

Итак, вероятность – это вычисленная оценка возможности того, что произойдет определенное событие, которая чаще всего выражается в форме отношения числа желаемых событий к общему числу исходов. Например, вероятность выпадения «орла» при подбрасывании монетки – один к двум.

Исходя из этого, очевидно, что вероятность выигрыша – это соотношение количества выигрышных комбинаций к числу всех возможных. Однако нельзя забывать, что критерии и определения понятия «выигрыш» тоже могут быть разными. К примеру, в большинстве лотерей используется такое определение как «класс выигрыша». Требования к выигрышу третьего класса ниже, чем к выигрышу первого, поэтому вероятность выигрыша первого класса самая низкая. Как правило, таким выигрышем является джек-пот.

Еще один значимый момент в расчетах заключается в том, что вероятность двух связанных событий вычисляется путем перемножения вероятностей каждого из них. Проще говоря, если вы подбросите монетку два раза, то вероятность выпадения «орла» каждый раз будет равна один к двум, но шанс, что «орел» выпадет оба раза, составит лишь один к четырем. В случае с тремя подбрасываниями шанс вообще упадет до одного к восьми.

Расчет шансов

Таким образом, для расчета шанса выигрыша джек-пота в абстрактной лотерее, где нужно верно угадать несколько выпавших значений из определенного числа шаров (например, 6 из 36), нужно рассчитать вероятность выпадения каждого из шести шаров и перемножить их между собой. Учтите, что с уменьшением числа шаров, оставшихся в барабане, вероятность выпадения нужного шара меняется. Если для первого шара вероятность того, что выпадет нужный, равна 6 к 36, то есть, 1 к 6, то для второго шанс составит 5 к 35 и так далее. В данном примере вероятность того, что билет окажется выигрышным составит 6x5x4x3x2x1 к 36x35x34x33x32x31, то есть 720 к 1402410240, что будет равно 1 к 1947792.

Несмотря на такие пугающие числа, люди регулярно выигрывают в лотереи по всему миру. Не забывайте, что даже если вы не возьмете главный приз, существуют еще выигрыши второго и третьего классов, вероятность получить которые намного выше. Кроме того, очевидно, что наилучшей стратегией является покупка нескольких билетов одного тиража, так как каждый дополнительный билет кратно увеличивает ваши шансы. Например, если купить не один билет, а два, то и вероятность победы будет в два раза больше: два из 1,95 миллиона, то есть примерно 1 к 950 тысячам.

Вероятность или шанс угадать комбинацию, развёрнутую ставку, группу чисел —
в зависимости от количества выбранных номеров, для лотерей 5 из 36, 6 из 45, 7 из 49, 6 из 49, 4 из 20, Рапидо —
смотрим по этой ссылке

Вероятности в популярных лотереях

5 из 36, 6 из 45, 7 из 49, 6 из 36, 4 из 20, Матчбол, Рапидо

На этом графике хорошо видно количество комбинаций.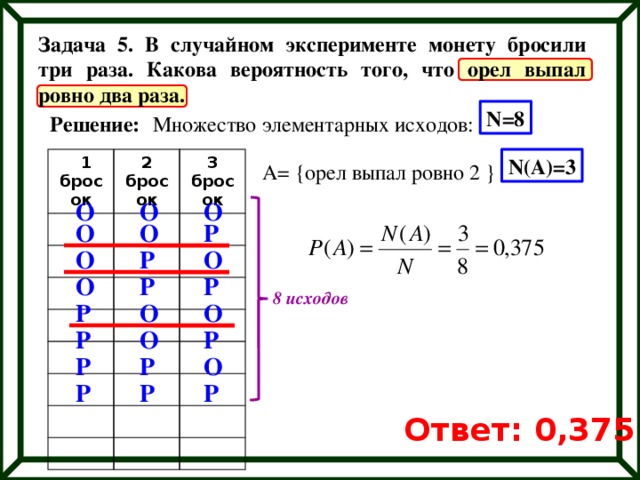 Чем меньше сектора,
тем вероятней джек пот, на одну простую комбинацию.

В лотереях 5 из 36 и Рапидо самое малое количество комбинаций — практически не видно на фоне остальных. Если учитывать призовой фонд, то в лотереях Рапидо, 4 из 20, — он самый большой (67% призового фонда), следовательно, выигрыши в низших категория будут чаще, если это можно назвать «выигрышем»… — на дистанции «слив» всё равно обеспечен, если, конечно, не «словится» суперприз! Тем не менее, чем больше возврат при длительной игре, тем больше можно ставить комбинаций, тем вероятней суперприз.

По вероятности выиграть суперприз, лотерея 5 из 36 считается лучшей из всех (без дополнительного), — сейчас «приз», который может достигать десятков миллионов. Далее по популярности у игроков следует лотерея 6 из 45, в которой шансы 1 на 8 миллионов комбинаций.
Лотерея 6 из 45 отличается ещё от остальных неплохой выплатой за приз второй категории, по такому параметру (вероятность-выплата)

Сравним популярные лотереи по вероятности выиграть приз второй категории.
Чем меньше сектора, тем вероятней выигрыш, — в игре одна простая комбинация.

При выборе лотереи желательно учитывать потенциальную выплату за приз второй категории, угадать который более реально. Для этого нужно просмотреть выплаты на сайте лотерей. Вероятность второй категории лучше не превышать 1: 100 000. В этом плане, например, лотереи 7 из 49 и 4 из 20 выглядят не очень привлекательно, у них вероятность второй категории практически сравнима с первой категорией приза лотереи 5 из 36 (1: 376 992). В какую лотерею играть, решает каждый сам!

Как определить вероятность выпадения числа

Когда бросается монета, можно сказать, что она упадет орлом вверх, или вероятность этого составляет 1/2. Конечно, это не означает того, что если монета подбрасывается 10 раз, она обязательно упадет вверх орлом 5 раз. Если монета является «честной» и если она подбрасывается много раз, то орел выпадет очень близко в половине случаев. Таким образом, существует два вида вероятностей: экспериментальная и теоретическая.

Экспериментальная и теоретическая вероятность

Если бросить монетку большое количество раз — скажем, 1000 — и посчитать, сколько раз выпадет орел, мы можем определить вероятность того, что выпадет орел. Если орел выпадет 503 раза, мы можем посчитать вероятность его выпадения:
503/1000, или 0,503.

Это экспериментальное определение вероятности. Такое определение вероятности вытекает из наблюдения и изучения данных и является довольно распространенным и очень полезным. Вот, к примеру, некоторые вероятности которые были определены экспериментально:

1. Вероятность того, что у женщины разовьется рак молочной железы составляет 1/11.

2. Если вы целуетесь, с кем-то, кто болен простудой, то вероятность того, что вы тоже заболеете простудой, составляет 0,07.

3. Человек, который только что был освобожден из тюрьмы, имеет 80% вероятности возвращения назад в тюрьму.

Если мы рассматриваем бросание монеты и беря во внимание то, что столь же вероятно, что выпадет орел или решка, мы можем вычислить вероятность выпадение орла: 1 / 2. Это теоретическое определение вероятности. Вот некоторые другие вероятности, которые были определены теоретически, с помощью математики:

1. Если находится 30 человек в комнате, вероятность того, что двое из них имеют одинаковый день рождения (исключая год), составляет 0,706.

2. Во время поездки, Вы встречаете кого-то, и в течение разговора обнаруживаете, что у вас есть общий знакомый. Типичная реакция: «Этого не может быть!». На самом деле, эта фраза не подходит, потому что вероятность такого события достаточно высока — чуть более 22%.

Таким образом, экспериментальная вероятность определяются путем наблюдения и сбора данных. Теоретические вероятности определяются путем математических рассуждений. Примеры экспериментальных и теоретических вероятностей, как например, рассмотренных выше, и особенно тех, которые мы не ожидаем, приводят нас, к ваэности изучения вероятности. Вы можете спросить: «Что такое истинная вероятность?» На самом деле, таковой нет. Экспериментально можно определить вероятности в определенных пределах. Они могут совпадать или не совпадать с вероятностями, которые мы получаем теоретически. Есть ситуации, в которых гораздо легче определить один из типов вероятности, чем другой. Например, было бы довольно найти вероятность простудиться, используя теоретическую вероятность.

Вычисление экспериментальных вероятностей

Рассмотрим сначала экспериментальное определение вероятности. Основной принцип, который мы используем для вычисления таких вероятностей, является следующим.

Принцип P (экспериментальный)

Если в опыте, в котором проводится n наблюдений, ситуация или событие Е происходит m раз за n наблюдений, то говорят, что экспериментальная вероятность события равна P (E) = m/n.

Пример 1 Социологический опрос. Было проведено экспериментальное исследование, чтобы определить количество левшей, правшей и людей, у которых обе руки развиты одинаково Результаты показаны на графике.

a) Определите вероятность того, что человек — правша.

b) Определите вероятность того, что человек — левша.

c) Определите вероятность того, что человек одинаково свободно владеет обеими руками.

d) В большинстве турниров, проводимых Профессиональной Ассоциацией Боулинга, участвуют 120 игроков. На основании данных этого эксперимента, сколько игроков могут быть левшой?

a)Число людей, являющиеся правшами, составляет 82, количество левшей составляет 17, а число тех, кто одинаково свободно владеет двумя руками — 1. Общее количество наблюдений — 100. Таким образом, вероятность того, что человек правша, есть Р
P = 82/100, или 0,82, или 82%.

b) Вероятность того, что человек левша, есть Р, где
P = 17/100, или 0,17, или 17%.

c) Вероятность того, что человек одинаково свободно владеет двумя руками составляет P, где
P = 1/100, или 0,01, или 1%.

d) 120 игроков в боулинг, и из (b) мы можем ожидать, что 17% — левши. Отсюда
17% от 120 = 0,17.120 = 20,4,
то есть мы можем ожидать, что около 20 игроков являются левшами.

Пример 2 Контроль качества. Для производителя очень важно держать качество своей продукции на высоком уровне. На самом деле, компании нанимают инспекторов контроля качества для обеспечения этого процесса. Целью является выпуск минимально возможного количества дефектных изделий. Но так как компания производит тысячи изделий каждый день, она не может позволить себе проверять каждое изделие, чтобы определить, бракованное оно или нет. Чтобы выяснить, какой процент продукции являются дефектным, компания проверяет гораздо меньше изделий.
Министерство сельского хозяйства США требует, чтобы 80% семян, которые продают производители, прорастали. Для определения качества семян, которые производит сельхозкомпания, высаживается 500 семян из тех, которые были произведены. После этого подсчитали, что 417 семян проросло.

a) Какова вероятность того, что семя прорастет?

b) Отвечают ли семена государственным стандартам?

Решение a) Мы знаем, что из 500 семян, которые были высажены, 417 проросли. Вероятность прорастания семян Р, и
P = 417/500 = 0,834, или 83. 4%.

b) Так как процент проросших семян превысил 80% по требованию, семена отвечают государственным стандартам.

Пример 3 Телевизионные рейтинги. Согласно статистических данных, в Соединенных Штатах 105 500 000 домохозяйств с телевизорами. Каждую неделю, информация о просмотре передач собирается и обрабатывается. В течение одной недели 7815000 домохозяйств были настроены на популярный комедийный сериал «Все любят Реймонда» на CBS и 8302000 домохозяйств были настроены на популярный сериал «Закон и порядок» на NBC (Источник: Nielsen Media Research). Какова вероятность того, что телевизор одного дома настроен на «Everybody Loves Raymond» в течение данной недели? на «Закон и порядок»?

Решениеn Вероятность того, что телевизор в одном домохозяйстве настроен на «Все любят Реймонда» равна Р, и
P = 7,815,000/105,500,000 ≈ 0,074 ≈ 7,4%.
Возможность, что телевизор домохозяйства был настроен на «Закон и порядок» составляет P, и
P = 8,302,000/105,500,000 ≈ 0,079 ≈ 7,9%.
Эти проценты называются рейтингами.

Теоретическая вероятность

Предположим, что мы проводим эксперимент, такие, как бросание монетки ли дротиков, вытаскивание карты из колоды, или проверка изделий на качество на сборочной линии. Каждый возможный результат такого эксперимента называется исход. Множество всех возможных исходов называется пространством исходов. Событие это множество исходов, то есть подмножество пространства исходов.

Пример 4 Бросание дротиков. Предположим, что в эксперименте «метание дротиков» дротик попадает в мишень. Найдите каждое из нижеследующих:

b) Пространство исходов

Решение
a) Исходы это: попадание в черное (Ч), попадание в красное (К) и попадание в белое (Б).

b) Пространство исходов есть <попадание в черное, попадание в красное, попадание в белое>, которое может быть записано просто как <Ч, К, Б>.

Пример 5 Бросание игральных костей. Игральная кость это куб с шестью гранями, на каждой их которых нарисовано от одной до шести точек.

Предположим, что мы бросаем игральную кость. Найдите
a) Исходы
b) Пространство исходов

Решение
a) Исходы: 1, 2, 3, 4, 5, 6.
b) Пространство исходов <1, 2, 3, 4, 5, 6>.

Мы обозначаем вероятность того, что событие Е случается в качестве Р (Е). Например, «монета упадет решкой» можно обозначать H. Тогда Р (Н) представляет собой вероятность того, монета упадет решкой. Когда все исходы эксперимента имеют одинаковую вероятность появления, говорят, что они равновероятны. Чтобы увидеть различия между событиями, которые равновероятны, и неравновероятными событиями, рассмотрим мишень, изображенную ниже.

Для мишени A, события попадания в черное, красное и белое равновероятны, так как черные, красные и белые сектора — одинаковые. Однако, для мишени B зоны с этими цветами не одинаковы, то есть попадание в них не равновероятно.

Принцип P (Теоретический)

Если событие E может случиться m путями из n возможных равновероятных исходов из пространства исходов S, тогда теоретическая вероятность события, P(E) составляет
P(E) = m/n.

Пример 6 Какая вероятность выкинуть 3, бросив игральный кубик?

Решение На игральном кубике 6 равновероятных исходов и существует только одна возможность выбрасивания цифры 3. Тогда вероятность P составит P(3) = 1/6.

Пример 7 Какая вероятность выбрасывания четной цифры на игральном кубике?

Решение Событие — это выбрасывание четной цифры. Это может случиться 3 способами (если выпадет 2, 4 или 6). Число равновероятных исходов равно 6. Тогда вероятность P(четное) = 3/6, или 1/2.

Мы будем использовать ряд примеров, связанных со стандартной колодой из 52 карт. Такая колода состоит из карт, показанных на рисунке ниже.

Пример 8 Какая вероятность вытянуть туза из хорошо перемешанной колоды карт?

Решение Существует 52 исхода (количество карт в колоде), они равновероятны (если колода хорошо перемешана), и есть 4 способа вытянуть туза, поэтому согласно принципу P, вероятность
P(вытягивания туза) = 4/52, или 1/13.

Пример 9 Предположим, что мы выбираем не глядя, один шарик из мешка с 3-мя красными шариками и 4-мя зелеными шариками. Какова вероятность выбора красного шарика?

Решение Существует 7 равновероятных исходов достать любой шарик, и так как число способов вытянуть красный шарик равно 3, получим
P(выбора красного шарика) = 3/7.

Следующие утверждения — это результаты из принципа P.

Свойства вероятности

a) Если событие E не может случиться, тогда P(E) = 0.
b) Если событие E случиться непременно тогда P(E) = 1.
c) Вероятность того, что событие Е произойдет это число от 0 до 1: 0 ≤ P(E) ≤ 1.

Например, в бросании монеты, событие, когда монета упадет на ребро имеет нулевую вероятность. Вероятность того, что монета либо на орел или решку имеет вероятность 1.

Пример 10 Предположим, что вытягиваются 2 карты из колоды с 52-мя картами. Какова вероятность того, что обе из них пики?

Решение Число путей n вытягивания 2 карт из хорошо перемешанной колоды с 52 картами есть ₅₂C₂. Так как 13 из 52 карт являются пиками, число способов m вытягивания 2-х пик есть ₁₃C₂. Тогда,
P(вытягивания 2-х пик)= m/n = ₁₃C₂/₅₂C₂ = 78/1326 = 1/17.

Пример 11 Предположим, что 3 человека выбираются случайно из группы, состоящей из 6-ти мужчин и 4-х женщин. Какова вероятность того, что будут выбраны 1 мужчина и 2 женщины?

Решение Число способов выбора троих человек из группы 10 человек ₁₀C₃. Один мужчина может быть выбран ₆C₁ способами, и 2 женщины могут быть выбраны ₄C₂ способами. Согласно фундаментальному принципу подсчета, число способов выбора 1-го мужчины и 2-х женщин ₆C₁.₄C₂. Тогда, вероятность что будет выбраны 1-го мужчины и 2-х женщин есть
P = ₆C₁.₄C₂/₁₀C₃ = 3/10.

Пример 12 Бросание игральных кубиков.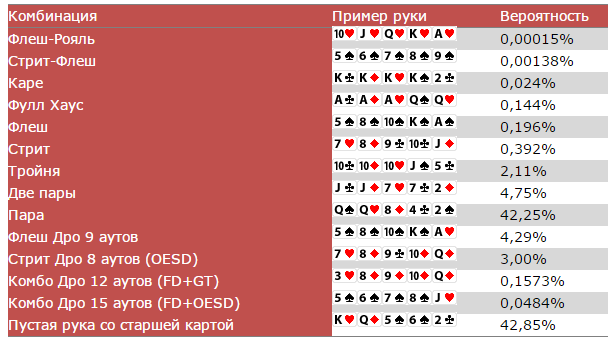 Какая вероятность выбрасывания в сумме 8 на двух игральных кубиках?

Решение На каждом игральном кубике есть 6 возможных исходов. Исходы удваиваются, то есть существует 6.6 или 36 возможных способа, в котором могут выпасть цифры на двух кубиках. (Лучше, если кубики разные, скажем один красный а второй голубой — это поможет визуализировать результат.)

Пары цифр, в сумме составляющие 8, показаны на рисунке внизу. Есть 5 возможных способов получения суммы, равной 8, отсюда вероятность равна 5/36.

Как рассчитать теорию вероятности в лотерее
Самые крупные выигрыши в лотереи в истории
Как выиграть в лотерею при помощи маятника

Теория и термины

Расчет шансов

Теория вероятностей (тервер) – раздел математики, который изучает случайные события и их свойства. Ознакомиться с ней нужно, чтобы понимать, как принимать взвешенные решения. Ведь зная статистические данные и анализируя закономерности, можно «предсказать» исход события.

Я не станут грузить вас сложными формулами – желающие углубленно заняться тервером могут сделать это по книге В. Е. Гмурмана «Теория вероятностей и математическая статистика». В статье покажу простые примеры для понимания зависимых и независимых событий, расскажу о состоянии неопределенности и интуитивном знании.

Материал полезен широкому кругу читателей.

Коротко о теории вероятностей

Вероятность в зависимых событиях

Вы решаете отправить в подарок другу балык. Знаете номер дома, подъезд, этаж. Курьер просит называть номер квартиры. С мучительными усилиями вспоминаете, что в доме по три двери на площадку, но дальше – туман. Давайте рассчитаем, сможет ли курьер попасть в нужную квартиру с первого раза.

Имеем три варианта развития событий:

Курьер звонит в первую (1) дверь.
Курьер звонит во вторую (2) дверь.
Курьер звонит в третью (3) дверь.

Но в истории участвует еще один человек: ваш друг. И событийность в его случае выглядит так:

Друг за первой (1) дверью.
Друг за второй (2) дверью.
Друг за третьей (3) дверью.

Прежде чем пойти дальше, введем определение вероятности – количество благоприятных исходов к вероятному числу событий.

Теперь соберем данные в таблицу (таблица 1). Всего — 9 исходов. Отметим положительные (курьеру откроет друг) – их 3. Получается, что вероятность с первого раза позвонить в дверь к нужному человеку – 3/9 или 1/3. Если вам нравится видеть вероятность в процентах, умножьте результат на 100%.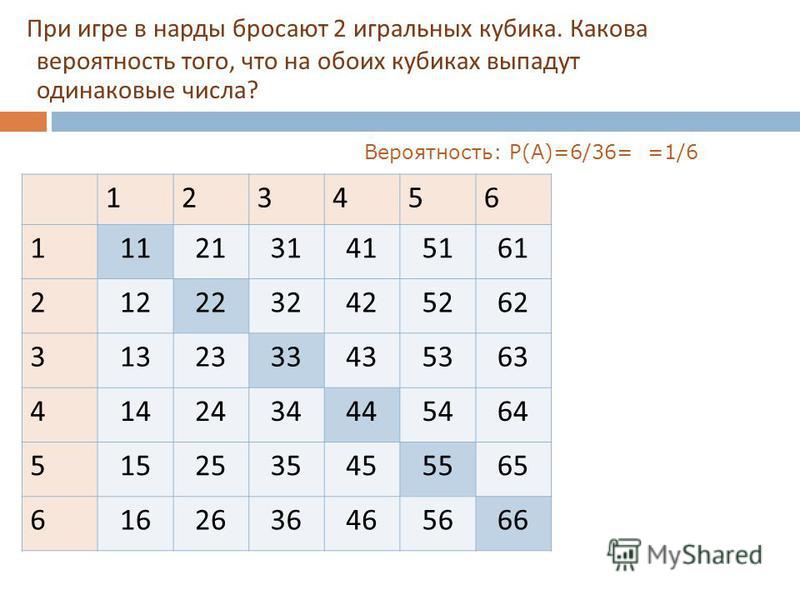

Таблица 1 – Девять исходов, три благоприятных

Представим, что курьер ошибся, и за дверью оказалась сногсшибательная блондинка в коротком халате. Для курьера исход положительный, для вас – нет. Поэтому считаем новую вероятность:

Курьер звонит в первую (1) квартиру.
Курьер звонит во вторую (2) квартиру.

То же самое с другом:

Друг ждет в первой (1) квартире.
Друг ждет во второй (2) квартире.

Теперь у нас 4 варианта и 2 – выигрышные (таблица 2). Вероятность со второго раза попасть в квартиру друга – 1/2. Она уменьшилась из-за зависимости событий: мы уже исключили неблагоприятный исход и расчёт нужно производить заново. Если курьер настолько невезуч, что промахнется во второй раз, вероятность попасть по адресу в третий раз – 100%. Опытным путем мы проверили, что за двумя предыдущими дверьми балык никто не ждет.

Таблица 2 Четыре исхода, два благоприятных

Пример с курьером — начальный уровень тервера. Он применим для бытовых нужд: предугадать вероятность побочного эффекта от антибиотиков, выбрать из разнообразия бабушкиных пирожков пирожок с повидлом и др.

На экзамене по теории вероятности советский математик и автор учебника Елена Вентцель спросила:

— Кому все понятно? Поднимите руки.

В аудитории живо взметнулся лес рук.

— Отлично! Остальные свободны, оценка – пять баллов! Поднявшие руки – останьтесь. За годы преподавания я так и не поняла большей части тервера. Рада, что вы мне все сейчас объясните.

Байка с математического факультета

Вероятность в независимых событиях

Независимые события не влияют друг на друга: количество благоприятных исходов в каждом новом событии не меняется.

Регина Тодоренко и Леся Никитюк в рамках программы «Орел и Решка» приехали в США. Обе хотят провести уик-энд «по богатому» и кидают монетку. Леся поставила на орла, Регина – на решку. Вероятность уехать на собственном авто у девушек одинакова: 1/2. На это раз повезло Лесе. Впрочем, как в следующей поездке тоже.

Регина негодует, почему тервер работает не в ее сторону

Теперь определим, могут ли независимые события происходить подряд с одним и тем же исходом. Лесе везло уже два раза и выпадал «орел». Повезет ли в третий раз? Составим список возможных исходов:

Орел, орел, орел.
Орел, орел, решка.
Орел, решка, орел.
Орел, решка, решка.
Решка, орел, орел.
Решка, орел, решка.
Решка, решка, орел.
Решка, решка, решка.

По результату видно: вероятность определенной последовательности каждый раз меньше на вероятность одного события. То есть вероятность определенной последовательности – произведение вероятностей каждого события. Если в одном событии вероятность 1/2, то в трех: 1/2*1/2*1/2=1/8.

Как человек принимает решения в состоянии неопределённости

Часть мозга, которая ответственна за оценку ситуации связана с медиаторной системой — центром мотивационных и эмоциональных процессов. Логика и эмоции часто конфликтуют между собой, поэтому решение принимается случайным образом.

У моей подруги аллергия на виноград. Но в студенчестве она не могла отказаться от бокала вина на вечеринке. Часто ее дерзость оставалась безнаказанной и организм нормально воспринимал аллерген. Реже протестовал: у подруги появлялись отеки на лице и в горле. В эти моменты ее левое полушарие отчаянно искало закономерность и просчитывало вероятность наступления аллергической реакции, правое же шептало: «Не пей, лицо распухнет!». Она могла вывести количество благоприятных исходов математическим путем и пить вино без опасений, но эмоции оказались сильней. Подруга раз и навсегда отказалась от любых продуктов с виноградом.

Хороший пример принятия решений описан в книге Млодинова «(Не) совершенная случайность». Допустим, вы отправили рассказ в четыре издательства. От каждого получили отказ. На эмоциях вы придете к мысли: рассказ ужасный! Хотя, если изучить биографии популярных писателей, может оказаться, что дело не в вас. Отказы в публикации получали Стивен Кинг, Джоан Роулинг, Виктор Франкл. Такие истории случались вовсе не из-за отсутствия у них дара: просто в одном издательстве редактор не понял тонкую философию автора, в другом – спешил домой и проставил визу не читая.

Моя бабушка считает: в Албании убивают на каждом шагу. Хотя в стране она не была и новостей о не слышала: ей так кажется интуитивно. Наверняка и вы не раз испытывали подобное чувство. Оно называется интуитивное знание – внутреннее убеждение, что собственная оценка более правдива, чем официальные источники и статистика.

Всего 127 убийств на 100 000 человек

Классическое исследование на тему интуитивного знания провели Даниэль Канеман и Амос Тверский. Они дали задание группе студентов: на основании портрета, оценить утверждения с таблицы как более (1 балл) и менее (8 баллов) вероятные (таблица 3).

Портрет выглядел так: «Линда, возраст – немного за 30. Умная, говорит, что думает. В колледже изучала философию. Тогда же выступала против социального неравенства, дискриминации и использования ядерного оружия. Не замужем».

Таблица 3

По портрету логично предположить, что Линда участвует в феминистском движении. Но студенты принимали решения интуитивно, что привело к ошибке. Вероятность, что Линда работает в банке и принимает участие в феминистском движении больше вероятности работы в банке.

Посмотрите на таблицу: вероятность работы в банке и увлечение феминистским движением – 4,1 балл. Но первое (работа в банке) и второе (феминистское движение) в сумме дают 8,3 балла. Согласно терверу, вероятность, что произойдут оба события не может быть выше, чем вероятность каждого события по отдельности. Главное утверждение (4,1 балла) содержит 2 события и является единым. В интуитивном решения правило тервера нарушено. Это доказывает — наши убеждения часто являются ложными.

В дальнейшем проводились множественные эксперименты, которые подтвердили догадку Канемана.

Вместо заключения

Теория вероятностей почти всегда разбивается о «случай», продиктованный убеждением или эмоцией отдельного человека. Поэтому использование ее в повседневной жизни может не оправдать ожиданий. Но выбирать вам! Хорошего дня!

Основы теории вероятностей для геймдизайнеров.

Часть 1 — Манжеты гейм-дизайнера

Предисловие

Большая часть данной статьи — лишь перевод статьи Джеймса Эрнеста. Огромное ему спасибо за прекрасный первоисточник! Однако я осмелился дополнить её в некоторых местах и заменить иллюстрации..

Введение

Теория вероятностей — важная часть геймдизайна. У каждого из нас есть примерное представление о теорвере, но многим новичкам не хватает инструментов для формального анализа даже самых простых систем в своих играх. Эта статья представляет собой введение в формальную теорию.

“Шел 1654 год, а у французского дворянина Антуана Гомбальда, шевалье де Мере, была проблема – он был заядлым игроком. Он раз за разом ставил на то, что при броске одного игрального кубика четыре раза подряд хотя бы один раз выпадет шестерка. На этой игре он заработал неплохие деньги, но его друзьям надоело проигрывать, и впредь они отказывались с ним играть. В поисках новых способов обобрать своих друзей шевалье изобрел еще одну игру, которая, как он считал, использовала то же правило вероятности, что и предыдущая. В новой игре он ставил на то, что при броске двух кубиков двадцать четыре раза подряд один раз выпадет двенадцать. Сначала друзья отнеслись к новой игре с подозрением, но вскоре она начала им нравиться, ведь шевалье стремительно терял свои накопления! Он не мог понять, что происходит, ведь, по его подсчетам, обе игры использовали одно и то же правило вероятности.

Запутавшийся и разоренный, он написал письмо математику Блезу Паскалю, у которого попросил совета. Паскаль нашел проблему интригующей – официальная математика не могла ответить на эти вопросы. И тогда Паскаль обратился за помощью к другу своего отца, Пьеру де Ферма. Это положило начало долгой переписке между Паскалем и Ферма, в которой они обсуждали эту и другие похожие проблемы, пытались найти методы их решения и в итоге основали новый раздел математики – теорию вероятностей“, — Джесси Шелл, Книга Линз.

Именно так из-за азартных игроков и появилась теория вероятностей.

Базовые инструменты

В теории вероятностей мы говорим о «шансах» того, что что-то случится, выраженных числом от 0% до 100% (или от 0 до 1, если мы говорим про вероятность). Если что-то имеет 100% шанс произойти, это обязательно произойдет. При 50% это с одинаковой вероятностью произойдет или не произойдет.

Если вы подбрасываете монетку, то каковы шансы падения орла? Что ж, тут необходимо немного конкретизировать. Если вы подбрасываете лишь один раз, то 50%. Если же вы будете подбрасывать монетку целый день, то орел выпадет хотя бы раз почти со 100% вероятностью.

Если вы сложите шансы всех возможных исходов случайного эксперимента, результат всегда будет 100% (или 1). Например, исключая «крайний случай», когда монета приземляется на ребро, шансы выпадения решки (50%) и орла (50%) в сумме составляют 100%.

В двух подбрасываниях есть четыре возможных результата, хотя они часто маскируются под три. Могут выпасть две решки, два орла или орел и решка. Событие “орел и решка” на самом деле происходит при двух исходах, поэтому вероятность этого события в два раза выше, чем у двух других результатов.

События:

Событие 1	Событие 2	Шанс
Р	Р	25%
Р	О	25%
О	Р	25%
О	О	25%

Таким образом, шанс выкинуть орла и решку — 50%.

Небольшое отступление

Для следующего упражнения необходимо знать одну формулу:

количество “хороших” событий / всевозможные события

Например, в сундуке есть щит, меч и броня. Игрок может вытянуть каждый предмет с одинаковой вероятностью. Каков шанс, что выпадет меч? Правильно, ~33%! Или 1/3.

Упражнение: игра в кости

Каковы шансы выпадения 6 на шестигранном кубике?

Ответ: 1/6 или 16,7%.

Как насчет вероятности выпадения любого другого числа или набора чисел на d6? Каждое индивидуальное число такое же, 1/6. Поскольку результаты исключают друг друга, вы можете сложить их вместе, так что вероятность выпадения 4 или 5 составляет 1/6 + 1/6 или 1/3.

Вы также можете найти вероятность результата, вычтя шансы противоположного результата из 1. Таким образом, вероятность выпадения чего-либо, кроме 6, будут 1 — 1/6 или 5/6.

Таким образом, мы вычитаем из 1, когда ищем противоположные события к найденному.

Упражнение: игра в пару

В игре «Пара» цель состоит в том, чтобы не поймать пару (две карты одного достоинства). Колода пар содержит одну единицу, две двойки, три тройки …, десять десяток. Других карт в колоде нет. Всего 55 карт. Возникает вопрос: если вы вытянете одну карту в руку с 9 и 10, каковы шансы получить пару?

В этом упражнении мы проигнорируем все остальные карты на руках. В колоде осталось 53 карты плюс 9 и 10 в вашей руке. Из 53 карт осталось восемь девяток и девять десяток. Получается 17 карт из 53 карт, дают вам пару. С вероятностью 17/53 (~32%) вы проиграете 🙁

Последовательные вероятности

Вероятность того, что несколько событий произойдут вместе (или последовательно), можно определить, перемножив их индивидуальные шансы. Например, вероятность выпадения двух орлов подряд составляет 25%. Это 50% для первого броска, умноженное на 50% для второго. Шанс получить три решки будет 50% * 50% * 50%, или 12,5%. Эти шансы также могут быть выражены как вероятности — 1/2, 1/4, 1/8 и так далее.

Обратите внимание, что этот тип анализа работает только с будущими событиями. Если вы уже выкинули двух орлов, вероятность того, что это произошло, составляет 1 (100%), а вероятность того, что следующий бросок также окажется орлом, составляет 1/2 (50%). Но если вы в будущем планируете получить трёх орлов подряд, то 1/8 (12,5%).

Упражнение: какова вероятность выбросить 5 или больше на каждом из 3D6?

Даже если вы бросите кубики вместе, можно подумать, что вы бросаете по одному за раз. Вероятность получить 5 или 6 на кубике — 2/6 (или 1/3). У нас три кубика, поэтому 1/3 * 1/3 * 1/3 = 1/27

Упражнение: выкинь шесть раз

Чтобы выиграть эту игру, вам нужно бросить d10 шесть раз. Каждый ход вы должны бросить больше, чем текущий номер хода. Например, на третьем ходу вы должны выбросить 4 или выше. Если выпадет меньше, вы проиграете. Какой шанс выигрыша?

На 1 ходу вы должны выбросить 2 или больше. Это событие имеет вероятность 9/10 или 90%. На втором ходу шансы уменьшаются на 10% (то есть до 80%) и так каждый ход. Шанс выиграть: (9/10) * (8/10) * (7/10) * (6/10) * (5/10) * (4/10), или около 6%.

Несовместные события

Такие события не могут произойти одновременно. Например, вы не можете получить одновременно и орла, и решку в при броске монеты. Не может сразу быть «дождя» и «без дождя» за окном.

Но как выглядят совместные события? Рассмотрим шансы на выпадение карты треф или туза. Всего 13 треф и 4 туза, поэтому, если бы эти результаты были несовместными, было бы 17 способов добиться успеха. Но одна из карт — это туз-треф, поэтому мы должны быть осторожны, чтобы не сосчитать ее дважды. Так есть только 16 способов добиться успеха в этом событии.

В таком маленьком примере легко просто подсчитать успехи и неудачи. Но в большом наборе данных не всегда удается просчитать все возможные результаты.

Небольшое отступление: основы комбинаторики

Нам часто приходится считать количество всех возможных событий или каких-то комбинаций. Например, сколько разных комбинаций может получиться при броске монеты три раза, при броске d6 дважды и так далее. Тут нам на помощь приходит формула размещений с повторениями:

n^k

n — количество возможных событий на одном шаге (например, у d6 — 6 событий)

k — количество повторений (бросков и т.п.)

Почему эта формула работает? Распишем её немного иначе. Рассмотрим случай, когда мы кидаем 3d5:

шаг 1: возможных событий — 5
шаг 2: возможных событий — 5
шаг 3: возможных событий — 5

5 * 5 * 5 = 125 = 5³

Однако стоит заметить, что это формулу мы используем, когда на каждом шаге количество событий одинаковое. Если на первом шаге будет M событий, а на втором N, то всего их будет: M * N.

В следующем упражнении предполагается, что вы без труда сможете посчитать количество комбинаций.

Упражнение: совместные события

Каковы шансы выпадения хотя бы одной 10 при броске 2d10? Фраза «хотя бы один 10» фактически включает в себя три разных набора результатов: все версии 10-X, X-10 и 10-10. Итак, всего есть 19 способов добиться успеха. Это 9 версий 10-X, 9 версий X-10 плюс один случай 10-10. Общее количество возможных бросков составляет 100 (10 *10), поэтому вероятность на успех составляют 19/100 (19%).

Другой способ решить эту задачу — выяснить, как не добиться успеха, а затем вычесть это значение из 1. Если вы проиграли, это означает, что вам не выпало 10 при первом броске (90%) и во втором броске (90%). Для достижения “успеха” в обоих случаях требуется вычислить произведение индивидуальных вероятностей, поэтому вероятность составляет 0,9 * 0,9 = 0,81. Вычитая шанс неудачи из 100%, мы получаем 19%.

Мы изучили уже довольно много, поэтому, пожалуй, сделаем остановку и дадим нашему мозгу немного передохнуть. Увидимся в следующей части!

Источник:

Probability for Game Designers

Мы принципиально не размещаем рекламу на наших страницах, чтобы она не мозолила вам глаза и существуем, только за счет поддержки читателей и членов нашего сообщества. Если вам нравится то, что мы делаем и вы считаете это важным, то вы можете поддержать нас так, как вам удобно.

Стать патроном на Patreon
Стать доном в ВК
VK Pay

Теория вероятностей: основы, примеры, задачи

Основы теории вероятностей

В этой статье мы расскажем кратко о том, что такое вероятность события. Дадим определение вероятности, введем понятия зависимых и независимых, совместных и несовместных событий. Объясним, что такое сумма событий и произведение событий.

Больше задач – в статье «Задание 2 Профильного ЕГЭ по математике. Теория вероятностей».

Случайным называется событие, которое невозможно точно предсказать заранее. Оно может либо произойти, либо нет. Теория вероятностей изучает случайные события и их закономерности, а также случайные величины и действия над ними.

Благоприятным мы называем исход, способствующий наступлению данного события.

Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.

Очевидно, что вероятность – величина положительная и не может быть больше единицы.

Например, перед экзаменом вы выучили 3 билета из 20. Вероятность вытянуть счастливый билет равна

Вот две простых задачи из вариантов ЕГЭ, где применяется определение вероятности:

1. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Иванов высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Иванову достанется удобное место, если всего в самолёте 300 мест.

В самолете 21+18=30 мест, удобных для Иванова. Всего в самолете 400 мест. Поэтому вероятность того, что пассажир Иванов получит удобное место, равна 30 : 300 = 0,1.

Просто применили определение вероятности.

2. В группе туристов 32 человека. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист К. полетит пятым рейсом вертолёта.

Каждый рейс, в том числе и пятый, перевозит 4 человек из 32. Вероятность полететь пятым рейсом:

Ответ: 0,125.

События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.

Например, вы бросаете монету. «Выпал орел» и «выпала решка» — несовместные события.

Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.
Вероятность суммы несовместных событий равна сумме их вероятностей.

Вы бросаете игральную кость. Вероятность выпадения «тройки» равна Вероятность выпадения «шестерки» также равна
Вероятность выпадения числа, которое делится на 3,

Произведение двух событий – термин, означающий, что произошло и одно, и другое событие.

События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.

Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.

3. Говорят, что в старину каждый десятый на Руси был Иван, а каждый двадцатый Петр. Если это верно, то кого было больше: Иванов Петровичей или Петров Ивановичей?

Можно по-разному решать эту задачу, и вероятностный подход здесь тоже применим. Посчитаем вероятности двух событий
Событие А. Случайно выбранного мужчину зовут Иван Петрович
Событие В. Мужчину зовут Петр Иванович.

Вероятность быть Иваном Петровичем для жившего в старину россиянина равна Мы перемножили вероятности того, что наш древнерусский житель – Иван и что его отца зовут Петр.
А вероятность оказаться Петром Ивановичем точно такая же:

4. (ЕГЭ) Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с ве-роятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Шахматист А. играет две партии, одну – белыми фигурами, другую – черными. События «выиграть белыми» и «выиграть черными фигурами» независимы. Вероятность того, что шахматист А. выиграет оба раза, равна произведению вероятностей выигрышей в каждой партии: 0,5 · 0,32 = 0,16.

5. (ЕГЭ) В классе 26 человек, среди них два друга — Андрей и Сергей. Класс случайным образом разбивают на 2 группы по 13 человек. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.

Пусть Андрей первым занял место в группе (неважно, в какой). И, кроме него, осталось еще 25 человек, среди которых его друг Сергей. Сколько у Сергея шансов оказаться в той же группе, что и Андрей? В группе должно быть 13 человек, то есть Андрей и еще 12. Значит, вероятность того, что Сергей окажется в той же группе, что и Андрей, равна , то есть 0,48.

Следующую задачу можно решить методами комбинаторики – например, с помощью формулы Бернулли. Однако в обычной школе не изучают комбинаторику, и тем не менее эта задача появилась в сборниках для подготовки к ЕГЭ.

6. Монету бросают 10 раз. Во сколько раз событие «Орел выпадет ровно 8 раз» более вероятно, чем событие «Орел выпадет ровно 9 раз»?

Начнем с числа возможных исходов. Если мы бросаем монету, возможных исходов два – орел или решка.
Бросим монету два раза (или две монеты одновременно, все равно). И вот уже 4 возможных исхода:
ОО
ОР
РО
РР
(буквой О обозначен выпавший «орел», буквой «р» — решка.
Каждый следующий бросок монеты увеличивает число возможных исходов в 2 раза (орел или решка).
Для 10 бросков монеты количество возможных исходов, очевидно, равно

По определению, вероятность равна отношению числа благоприятных исходов к общему числу исходов.

Рассмотрим случай, когда орел выпадет ровно 9 раз из 10 бросков монеты. Это значит, что решка выпала ровно 1 раз.

Это могло произойти при первом броске, при втором, при третьем… и, наконец, при десятом, всего 10 благоприятных исходов. Вероятность выпадения решки ровно 1 раз из 10 бросков

Теперь случай, когда орел выпал ровно 8 раз из 10 бросков монеты. Значит, решка выпала ровно 2 раза.

Пронумеруем броски: 1,2,3…10.

Решка могла выпасть в первый и во второй раз. Обозначим эту комбинацию 12.

Могла также выпасть в первый и третий раз, в первый и четвертый… Эти комбинации обозначаем как 13, 14…

Пронумеруем таким образом все благоприятные исходы.

12, 13, 14, 15, 16, 17, 18, 19, 1 10

23, 24, 25, 26, 27, 28, 29, 2 10

34, 35, 36, 37, 38, 39, 3 10

45, 46, 47, 48, 49, 4 10

56, 57, 58, 59, 5 10

67, 68, 69, 6 10

78, 79, 7 10

89, 8 10

9 10
Количество благоприятных исходов равно 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45.

Поделив на , получим, во сколько раз выпадение решки ровно 8 раз более вероятно, чем выпадение решки ровно 9 раз:

Ответ: 4,5.

Разберем какую-нибудь типовую задачу ЕГЭ по теме «Теория вероятностей». Такую, в которой мы рисуем «дерево» возможных исходов.

7. (ЕГЭ) Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Изобразим все возможные исходы.

По условию, купленное в магазине стекло для автомобильной фары оказалось бракованным. Как это могло получиться?

Стекло сделано либо на первой фабрике, либо на второй. Эти события несовместны.

Вероятность того, что стекло с первой фабрики, равна 0,45.

Вероятность того, что стекло сделано на второй фабрике, равна 0,55.

Первая фабрика выпускает 3% бракованных стекол. Значит, с вероятностью 0,03 стекло, произведенное на первой фабрике, бракованное.

Вторая фабрика выпускает 1% бракованных стекол. Значит, с вероятностью 0,01 сделанное на ней стекло бракованное.

Покупатель купил бракованное стекло. Оно могло быть сделано на первой фабрике и оказалось бракованным. Это означает одновременное наступление, или произведение, двух независимых случайных событий – «стекло сделано на первой фабрике» и «стекло бракованное». Вероятность произведения этих двух событий равна

Или другой случай. Стекло могло быть со второй фабрики и также бракованное. Вероятность одновременного наступления этих двух событий равна События «стекло с первой фабрики» и «стекло со второй фабрики» несовместны – они не могут случиться одновременно.
Вероятность суммы несовместных событий равна сумме вероятностей.

Значит, вероятность купить бракованное стекло равна:

Ответ: 0,019.

Следующая задача будет интересна и старшеклассникам, и студентам. В самом деле – как быть, если вы пришли на экзамен, выучив всего 20 билетов из 30? Идти отвечать первым? Или вторым? Или предпоследним? В каком случае вероятность вытянуть билет, который ты выучил, будет наибольшей?

8. Экзамен проходит по следующей схеме: если некоторый билет уже был вытянут, то после ответа экзаменатор откладывает его в сторону. Студент выучил 20 билетов из 30. Когда ему выгоднее идти, первым или вторым, чтобы вероятность вынуть выученный билет была больше?

Назовем билеты, которые студент выучил, «счастливыми».
Если студент пошел отвечать первым, вероятность вытянуть «счастливый» билет равна

Если идти отвечать вторым, возможны два случая:

1) Первый билет, который вытянул кто-то другой, был «счастливым», и тогда «счастливых» билетов теперь 19.

2) Первый билет не был «счастливым», и «счастливых» билетов так и осталось 20.

Нарисуем схему возможных исходов, как всегда делаем в подобных задачах:

Вот наш студент идет отвечать вторым. Вероятность вытянуть «счастливый» билет равна Удивительный ответ! Та же самая вероятность! Значит, неважно, первым или вторым идти отвечать, если ты выучил 20 билетов из 30.

Конечно, это были самые простые задачи по теории вероятностей. Такие, которые встречаются на ЕГЭ по математике.

Продолжение:
Задание 2 Профильного ЕГЭ по математике. Теория вероятностей
Теория вероятностей. Парадокс Монти Холла

Основы теории вероятностей для актуариев

Вероятность: основные правила

Формула полной вероятности

Формула Байеса

Случайные величины и их характеристики

Время жизни как случайная величина

Функция выживания

Характеристики продолжительности жизни

Аналитические законы смертности

Все на свете происходит детерминировано или случайно…
Аристотель

Вероятность: основные правила

Теория вероятностей вычисляет вероятности различных событий. Основным в теории вероятностей является понятие случайного события.

Например, вы бросаете монету, она случайным образом падает на герб или решку. Заранее вы не знаете, на какую сторону монета упадет. Вы заключаете договор страхования, заранее вы не знаете, будут или нет проводиться выплаты.

В актуарных расчетах нужно уметь оценивать вероятность различных событий, поэтому теория вероятностей играет ключевую роль. Ни одна другая область математики не может оперировать с вероятностями событий.

Рассмотрим более подробно подбрасывание монеты. Имеется 2 взаимно исключающих исхода: выпадение герба или выпадение решки. Исход бросания является случайным, так как наблюдатель не может проанализировать и учесть все факторы, которые влияют на результат. Какова вероятность выпадения герба? Большинство ответит ½, но почему?

Пусть формально А обозначает выпадение герба. Пусть монета бросается n раз. Тогда вероятность события А можно определить как долю тех бросков, в результате которых выпадает герб:

(1)

где n общее количество бросков, n(A) число выпадений герба.

Отношение (1) называется частотой события А в длинной серии испытаний.

Оказывается, в различных сериях испытаний соответствующая частота при больших n группируется около некоторой постоянной величины Р(А). Эта величина называется вероятностью события А и обозначается буквой Р – сокращение от английского слова probability – вероятность.

Формально имеем:

(2)

Этот закон называется законом больших чисел.

Если монета правильная (симметричная), то вероятность выпадения герба равняется вероятности выпадения решки и равняется ½.

Пусть А и В некоторые события, например, произошел или нет страховой случай. Объединением двух событий называется событие, состоящее в выполнении события А, события В, или обоих событий вместе. Пересечением двух событий А и В называется событие, состоящее в осуществлении как события А, так и события В.

Основные правила исчисления вероятностей событий следующие:

1. Вероятность любого события заключена между нулем и единицей:

2. Пусть А и В два события, тогда:

(3)

Читается так: вероятность объединения двух событий равна сумме вероятностей этих событий минус вероятность пересечения событий. Если события являются несовместными или непересекающимися, то вероятность объединения (суммы) двух событий равна сумме вероятностей. Этот закон называется законом сложения вероятностей.

Мы говорим, что события является достоверным, если его вероятность равна 1. При анализе тех или иных явлений возникает вопрос, как влияет наступление события В на наступление события А. Для этого вводится условная вероятность:

(4)

Читается так: вероятность наступления А при условии В равняется вероятности пересечения А и В, деленной на вероятность события В.
В формуле (4) предполагается, что вероятность события В больше нуля.

Формулу (4) можно записать также в виде:

(5)

Это формула умножения вероятностей.

Условную вероятность называют также апостериорной вероятностью события А – вероятность наступления А после наступления В.

В этом случае саму вероятность называют априорной вероятностью. Имеется еще несколько важных формул, которые интенсивно используются в актуарных расчетах.

Формула полной вероятности

Допустим, что проводится опыт, об условиях которого можно заранее сделать взаимно исключающие друг друга предположения (гипотезы):

Мы предполагаем, что имеет место либо гипотеза , либо … либо. Вероятности этих гипотез известны и равны:

Тогда имеет место формула полной вероятности:

(6)

Вероятность наступления события А равна сумме произведений вероятности наступления А при каждой гипотезе на вероятность этой гипотезы.

Формула Байеса

Формула Байеса позволяет пересчитывать вероятность гипотез в свете новой информации, которую дал результат А.

Формула Байеса в известном смысле является обратной к формуле полной вероятности.

(7)

Рассмотрим следующую практическую задачу.

Задача 1

Предположим, произошла авиакатастрофа и эксперты заняты исследованием ее причин. Заранее известны 4 причины, по которым произошла катастрофа: либо причина, либо , либо , либо . По имеющейся статистике эти причины имеют следующие вероятности:

При осмотре места катастрофы найдены следы воспламенения горючего, согласно статистике вероятность этого события при тех или иных причинах такая:

Вопрос: какая причина катастрофы наиболее вероятна?
Вычислим вероятности причин при условия наступления события А.

Отсюда видно, что наиболее вероятной является первая причина, так как ее вероятность максимальна.
Задача 2

Рассмотрим посадку самолета на аэродром.
При посадке погодные условия могут быть такими: низкой облачности нет (), низкая облачность есть (). В первом случае вероятность благополучной посадки равна P1. Во втором случае – Р2. Ясно, что P1>P2.
Приборы, обеспечивающие слепую посадку, имеют вероятность безотказной работы Р. Если есть низкая облачность и приборы слепой посадки отказали, вероятность удачного приземления равна Р3, причем Р3<Р2. Известно, что для данного аэродрома доля дней в году с низкой облачностью равна .
Найти вероятность благополучной посадки самолета.
Имеем:
Нужно найти вероятность .
Имеются два взаимно исключающих варианта: приборы слепой посадки действуют, приборы слепой посадки отказали, поэтому имеем:
Отсюда по формуле полной вероятности:
Задача 3

Страховая компания занимается страхованием жизни. 10% застрахованных в этой компании являются курильщиками. Если застрахованный не курит, вероятность его смерти на протяжении года равна 0.01 Если же он курильщик, то эта вероятность равна 0.05.
Какова доля курильщиков среди тех застрахованных, которые умерли в течение года?
Варианты ответов: (А) 5%, (Б) 20%, (В) 36 %, (Г) 56%, (Д) 90%.
Решение
Введём события:

= {застрахованный – курильщик}

= {застрахованный – не курильщик}

= {застрахованный умер в течение года}

Условие задачи означает, что
Кроме того, поскольку события и образуют полную группу попарно несовместимых событий, то .
Интересующая нас вероятность – это .
Используя формулу Байеса, мы имеем:
поэтому верным является вариант (В).
Задача 4

Страховая компания продаёт договора страхования жизни трёх категорий: стандартные, привилегированные и ультрапривилегированные.
50% всех застрахованных являются стандартными, 40% — привилегированными и 10% — ультрапривилегированными.
Вероятность смерти в течение года для стандартного застрахованного равна 0.010, для привилегированного – 0.005, а для ультра привилегированного – 0.001.
Чему равна вероятность того, что умерший застрахованный является ультрапривилегированным?
Решение
Введем в рассмотрение следующие события:

= {застрахованный является стандартным}

= {застрахованный является привилегированным}

= {застрахованный является ультрапривилегированным}

= {застрахованный умер в течение года}

В терминах этих событий интересующая нас вероятность – это . По условию:
Поскольку события , , образуют полную группу попарно несовместимых событий, используя формулу Байеса мы имеем:
Случайные величины и их характеристики
Пусть некоторая случайная величина, например, ущерб от пожара или величина страховых выплат.
Случайная величина полностью характеризуется своей функцией распределения.
Определение. Функция называется функцией распределения случайной величины ξ.
Определение. Если существует такая функция , что для произвольных a<b выполнено
,
то говорят, что случайная величина ξ имеет плотность распределения вероятности f(x).
Определение. Пусть . Для непрерывной функции распределения F теоретической α-квантилью называется решение уравнения .
Такое решение может быть не единственным.
Квантиль уровня ½ называется теоретической медианой, квантили уровней ¼ и ¾ — нижней и верхней квартилями соответственно.
В актуарных приложениях важную роль играет неравенство Чебышева:
при любом
— символ математического ожидания.
Читается так: вероятность того, что модуль больше меньше или равняется математическому ожиданию величины модуль , деленному на .
Время жизни как случайная величина
Неопределенность момента смерти является основным фактором риска при страховании жизни.
Относительно момента смерти отдельного человека нельзя сказать ничего определенного. Однако если мы имеем дело с большой однородной группой людей и не интересуемся судьбой отдельных людей из этой группы, то мы находимся в рамках теории вероятностей как науки о массовых случайных явлениях, обладающих свойством устойчивости частот.
Соответственно, мы можем говорить о продолжительности жизни как о случайной величине Т.
Функция выживания
В теории вероятностей описывают стохастическую природу любой случайной величины Т функцией распределения F (x), которая определяется как вероятность того, что случайная величина Т меньше, чем число x:
.
В актуарной математике приятно работать не с функцией распределения, а с дополнительной функцией распределения . Применительно к продолжительной жизни – это вероятность того, что человек доживет до возраста x лет.
Функция

называется функцией выживания (survival function):
Функция выживания обладает следующими свойствами:
убывает при ;

;

;

непрерывна.

В таблицах продолжительности жизни обычно считают, что существует некоторый предельный возраст (limiting age) (как правило, лет) и соответственно при x >.
При описании смертности аналитическими законами обычно считают, что время жизни неограниченно, однако подбирают вид и параметры законов так, чтобы вероятность жизни свыше некоторого возраста была пренебрежимо мала.
Функция выживания имеет простой статистический смысл.
Допустим, что мы наблюдаем за группой из новорожденных (как правило, ), которых мы наблюдаем и можем фиксировать моменты их смерти.
Обозначим число живых представителей этой группы в возрасте через . Тогда:
.
Символ E здесь и ниже используется для обозначения математического ожидания.
Итак, функция выживания равна средней доле доживших до возраста из некоторой фиксированной группы новорожденных.
В актуарной математике часто работают не с функцией выживания , а с только что введенной величиной (зафиксировав начальный размер группы ).
Функция выживания может быть восстановлена по плотности:
Характеристики продолжительности жизни
С практической точки зрения важны следующие характеристики:
1. Среднее время жизни
,
2. Дисперсия времени жизни
,
где
,
Корень квадратный из дисперсии называется стандартным отклонением (standard deviation). Это более удобная величина, чем дисперсия, так как имеет ту же размерность, что исходные данные.
3. Медиана времени жизни , которая определяется как корень уравнения
.
Медиана времени жизни – это возраст, до которого доживает ровно половина представителей исходной группы новорожденных.
Аналитические законы смертности
Для упрощения расчетов, теоретического анализа и т.д. естественно попытаться описать получаемые эмпирическим путем данные о функции выживания или интенсивности смертности с помощью простых аналитических формул.
Простейшее приближение было введено в 1729 году де Муавром (de Moivre), который предложил считать, что время жизни равномерно распределено на интервале , где — предельный возраст.
В модели де Муавра при 0<x<
Сравнение графиков этих функций с реальными графиками функции выживания , функции смертей , интенсивности смертности , показывает, что закон де Муавра является не очень хорошим приближением.
Например, первая формула означает, что кривая смертей является горизонтальной линией, в то время как эмпирические данные указывают на пик в районе 80 лет.
В модели, которую предложил в 1825 году Гомпертц (Gompertz), интенсивность смертности приближается показательной функцией вида , где >0 и B>0 – некоторые параметры. Соответствующая функция выживания имеет вид
,
а кривая смертей:
.
Мэйкхам (Makeham) в 1860 году обобщил предыдущую модель, приблизив интенсивность смертности функцией вида .
Постоянное слагаемое позволяет учесть риски для жизни, связанные с несчастными случаями (которые мало зависят от возраста), в то время как член учитывает влияние возраста на смертность.
В этой модели
,
.
Второй закон Мэйкхама, введенный в 1889 году, приближает интенсивность смертности функцией вида . В этой модели
,
.
Вейбулл (Weibull) в 1939 году предложил приближать интенсивность смертности более простой степенной функцией вида . В этой модели
, .
В практике страхования эти параметры неизвестны и оцениваются по реальным данным.
Связанные определения:
Вероятность события
Независимые повторные испытания Бернулли
Независимые события
В начало
Содержание портала
Вероятность выпадения комбинаций в покере. Шансы выпадения комбинаций | GipsyTeam.Ru
GipsyTeam
16.07.2021 20:35
Содержание
Что такое вероятности в покере?
Вероятности получить определенные карты на префлопе
Сравнение рук и эквити
Вероятности попадания во флоп с различными руками
Дро-руки и шансы их собрать
Какие программы считают вероятности в покере?
Покер – это азартная игра, где каждое действие игрока можно разложить по полочкам с математической точки зрения, определить, было ли принято правильное или неправильное решение.
Победа в конкретной раздаче ещё не говорит о том, что вы сыграли оптимально. Например, разномастные 72 в 12 случаях из 100 будут обыгрывать тузов при выставлении на префлопе. Однако, это не говорит о том, что игрок с АА сыграл неправильно.
Даже самая сильная комбинация против самой слабой будет проигрывать чаще одного раза из десяти
Что такое вероятности в покере?
Покер – это игра неполной информации. Каждый из участников раздачи только предполагает, какая рука у соперников. Единственное, что покеристам известно наверняка – это собственные карты и, возможно, несколько общих.
Вероятность в покере – это процентная величина, показывающая, с какой долей случится та или иная ситуация. Когда вы понимаете шансы, игра оценивается не на эмоциональном уровне, а с логической и математической точки зрения.
Например, если вам 40 раздач подряд не раздавали карманных тузов, не стоит обвинять дилера или покер-рум в мошенничестве: вероятность выпадения карманной пары тузов составляет 0,45%, так что в среднем вы должны их получать каждые 222 раздачи.
Вероятности получить определенные карты на префлопе
Префлоп — самый важный этап при игре в безлимитный техасский холдем, поскольку именно на этой улице игрок принимает решение, будет ли участвовать в борьбе за банк. Если да, то по какой стратегии.
Важно знать, с какой вероятностью вы будете получать играбельные стартеры, чтобы не отчаиваться и не строить иллюзий о борьбе за каждый банк.
Комбинация Шансы
Карманные тузы 0,45%
Карманные тузы или короли 0,90%
Любая карманная пара 5,90%
Одномастные АК 0,30%
Разномастные АК 0,90%
2 одномастные карты 24,00%
Карманные тузы, короли или АК 2,10%
Получить «монстра» на префлопе шанс совсем небольшой – чуть более 2 процентов, поэтому покеристы разыгрывают гораздо больше рук. И далеко не факт, что у соперника, который объявляет олл-ин на префлопе, вы увидите «ракеты».
Сравнение рук и эквити
Эквити – это вероятность, с которой рука покериста выиграет банк. На префлопе у любого стартера будет шанс усилиться и обыграть более сильную руку. Рассмотрим шансы на победу в раздачах, где случились типичные выставления на префлопе.
Ситуация Шансы на победу
Карманная пара против двух старших карт (55 VS AK) 54%
Старшая карманная пара против младшей (ТТ VS 88) 81%
Карманная пара против одной старшей карты (КК VS AQ) 71%
Две младшие карты против двух старших (JT VS AK) 37%
Две карты против одной старшей (JT VS A9) 45%
Две старшие карты при доминации (AK VS AQ) 74%
Первая и третья карты против второй и четвёртой (AQ VS KJ) 63%
Максимальные шансы на победу на префлопе достигаются, когда получается выставиться со старшей карманной парой против младшей. А ситуация, когда карманка (например, 88) сравнивается с оверкартами,называется монеткой, поскольку шансы на победу практически равны.
Вероятности попадания во флоп с различными руками
Торговля заканчивается олл-ином на префлопе не так часто. Профессионалы стараются минимизировать случайности, поэтому предпочитают разыгрывать свои руки на постфлопе, где у них есть перевес над новичками и любителями.
Здесь важно понимать, какие комбинации имеют больше шансов усилиться после того, как дилер откроет флоп.
Стартовая рука Готовая рука Сильное дро Эквити
Одномастный коннектор (8h9h) 5,64% 19,80% 25,50%
Дырявый одномастный коннектор (7h9h) 5,29% 17,71% 23,00%
Дырявый одномастный коннектор (6h9h) 4,97% 14,72% 19,69%
Дырявый одномастный коннектор (5h9h) 4,65% 12,06% 16,71%
Разномастный коннектор (8d9h) 4,80% 9,71% 14,51%
Дырявый разномастный коннектор (7d9h) 4,47% 7,67% 12,14%
Дырявый разномастный коннектор (6d9h) 4,!4% 4,98% 9,12%
Одномастная рука (7d2d) 4,33% 10,13% 14,46%
Разномастная рука (7d2h) 3,49% — 3,49%
Карманная пара (22) 11,75% — 11,75%
С точки зрения шансов усилиться на флопе, лучшие будут у одномастных коннекторов – рук, значения которых идут по соседству (9Т, JQ, 67 и др. ). Шансы разномастных коннекторов усилиться практически в 2 раза ниже.
Вероятность усиления карманной пары относительно небольшая – чуть менее 12%. Впрочем, она и без улучшения часто является грозным оружием и переигрывает любые не готовые руки, включая и любимую стартовую комбинацию у новичков, туз-король.
Дро-руки и шансы их собрать
Ситуации, когда игрок попадает в готовую руку на флопе, встречаются редко. В этом вы убедились из предыдущих таблиц. Гораздо чаще покеристы попадают в различные дро, и для сбора комбинаций требуется ещё одна карта. Здесь они начинают считать ауты и шансы банка, чтобы принять решение о дальнейшем ходе раздачи.
Рассмотрим вероятности попадания в различные дро, имея на префлопе две одномастные карты. Например, пиковые Т8.
Ситуация на флопе Вероятность
Готовый флеш 0,84%
Флеш-дро (2 пиковые карты и одна другой масти) 10,94%
Бэкдорное флеш-дро (1 пиковая и две других мастей) 41,60%
Готовый стрит 1,30%
Двустороннее стрит-дро 10,45%
Флеш к риверу 6,4%
С разномастной рукой шансы на усиление будут ниже. Например, с Тc7d.
Ситуация на флопе Вероятность
Флеш-дро (3 карты одной масти) 1,10%
Бэкдорное флеш-дро (две одномастные и 1 другой масти) 12,80%
Двустороннее стрит-дро 9,71%
Флеш по одной карте к риверу (выход 4 карт одной масти) 1,80%
Разыгрывать слабые разномастные руки следует гораздо осторожнее. Особенно начинающим игрокам, поскольку попав в совпадение – вы можете быть далеко позади оппонента. И вести подсчет аутов будет не соперник, а вы.
Какие программы считают вероятности в покере?
Знания о теории вероятности в покере были реализованы в различных покерных программах, которые ведут расчет шансов на победу. Есть также и онлайн-сервисы, где компьютер посчитает вероятность выигрыша одной руки против другой после того, как будут заданы все условия раздачи.
Наглядно видно, что у игрока с крестовыми 9-10 больше шансов выиграть раздачу, чем у пары двоек
Самый просто софт – это покерные калькуляторы, как на примере выше. В них задаются руки игроков, общие (если таковые имеются) карты, а программа подсчитывает вероятность каждого из стартеров на победу.
На таком флопе двойки становятся фаворитом
Есть и более сложный софт. Например, Flopzilla. Она учит мыслить не комбинациями, а диапазонами. Программа рассчитывает вероятность попадания в заданную диску различного диапазона стартовых комбинаций. Её активно используют и турнирные, и кэш-игроки.
Покерные калькуляторы
Покерные калькуляторы – это самый простой софт, который позволяет рассчитать вероятность конкретной руки на победу, исходя из складывающейся ситуации за столом.
Например, вы выставились на префлопе с карманными тройками против червовых АК. Изначально, это благоприятная ситуация для вас, поскольку вероятность победы немного выше 50 процентов.
классический коинфлип
С флопом вам не повезло: червовые QJ и пиковая четвёрка превращают в большого фаворита раздачи соперника. Любая черва даст оппоненту флеш, десятка – стрит, а попадание в туза или короля – просто старшую пару.
Тёрном спаривается четвёрка. Это хорошая карта для нас, поскольку шансы на победу увеличиваются ровно до 50 процентов.
На примере одной раздачи видно, как работают покерные калькуляторы. Сегодня они встроены в большинство покер-румов, показывая проценты на победу прямо во время раздачи. Это удобная и интересная «фишка» для любителей.
Flopzilla и другие обучающие программы
Flopzilla – программа несколько иного уровня. Если калькуляторы отображают фактическую ситуацию за столом, то Флопзилла позволяет научиться мыслить диапазонами. Это важно, когда покерист переходит играть на средние или высокие лимиты. Вы никогда не сможете «положить» соперника только на одну комбинацию. Важно анализировать каждое действие оппонента, расширяя или сужая его диапазон по принятым решениям.
Внешний вид программы
В софте есть также эквити калькулятор и инструкция по использованию программы на русском языке. 7-дневная пробная версия познакомит с возможностями ПО м двст понимание, будете вы им пользоваться сейчас или покупку пока следует отложить.
Служба поддержки GT поможет с оформлением заказа на сайте не только жителям России, а покеристам из любых стран. Также вы можете обращаться туда при любых затруднениях или сложностях со скачиванием клиента, вводом и выводом денежных средств, а также игровым проблемам.
Статистика и вероятность для рандомизированных игр (лут-шутеров, рогаликов, рогаликов и т. д.)
10.06.2020
Цель: давайте воспользуемся R и статистикой, чтобы улучшить видео с вероятностью выпадения лутер-шутера.
Игры, такие как Borderlands 1, Borderlands 2, Borderlands 3, Binding of Исаак, Dark Souls и т. д. имеют случайный шанс выпадения лута. Это означает что игрок будет случайным образом получать предметы за победу над врагом, выполнение квеста, открытие сундука или выполнение какого-либо требования. Игроки относятся к идее шанса выпадения как к частоте, с которой конкретный предмет «выпадает» из сундука или босса, именно так часто получит ли игрок этот предмет в качестве награды за определенный квест.
В Интернете есть много видео и руководств по этим играм и определенные элементы в этих играх, которые обслуживают сообщества игроков эти игры (видео о рейтинге выпадения zKarmaa). Они часто дают обзоры предметов и дают советы и ухищрения. Некоторые из этих вкладов являются полностью эмпирическими, состоящий из многочисленных повторных тестов для измерения скорости падения и другие свойства игр.
Общие вопросы, которые я вижу по адресу:
Какова вероятность выпадения предмета X из Y
Какова вероятность выпадения Каосана из Command Traunt в Borderlands 3
Биномиальные испытания / тест на пропорции
Какой шанс выпадения штурмовой винтовки Монарх из Kill-a-volt в Borderlands 3
Биномиальные испытания / тест на пропорции
Влияет ли конкретный предмет на шанс выпадения?
Влияет ли загруженный кубик в Borderlands 3 на шанс выпадения предметов из босса?
Биномиальные испытания/проверка пропорции
Критерий хи-квадрат
Какой шанс выпадения категорий предметов из Y
Какие предметы выпадают из Kill-a-volt в Borderlands 3
Критерий хи-квадрат
Вопросы, ответы на которые я не вижу, которые необходимо решить:
Сколько раз нужно повторить этот тест, чтобы оценить эффект?
Сколько раз я должен фармить этого босса, чтобы определить шанс выпадения этого предмета?
Мне очень нравятся эти эмпирические работы. Мне нравится, когда они проводят тестирование ну и поделитесь результатами своих испытаний. Я наслаждаюсь таким же обращением мирских вещей, таких как эффекты различных марок проникающих масло из таких видео от Project Farm[1][2]. Но я забочусь о статистике, и я хочу, чтобы она была хорошей.
Чего я хочу, так это лучшего статистического анализа видео игровых сервисов. В конце есть глоссарий, если какая-то терминология непонятна.
Серия Borderlands — это серия шутеров с добычей. Это означает, что когда вы побеждаете врагов и открываете сундуки, добыча обычно рандомизируется, взяты из случайной раздачи. Компьютер генерирует случайные числа, и они конвертируются в лут. Как это выглядит для игрок в том, что некоторая добыча является обычной (белое оружие), а некоторая добыча редкие (фиолетовые предметы или оранжевые легендарные предметы).
Borderlands 3 — последняя часть серии игр Borderlands. когда вы бегаете и убиваете без разбора, и каждое убийство является вытягивание игрового автомата, в результате чего может появиться случайная добыча. Вы обычно оптимизируйте синие, фиолетовые и оранжевые легендарные предметы как более высокие чем редкость, тем больше они стоят и тем больше дополнительных функций предмет имеет. Хотя некоторые легендарки того не стоят.
У многих боссов есть шанс получить добычу, а у некоторых есть специальный дроп. Например, Kaosan SMG выпадает из Commander Traunt на планета Афины. Всем нравится Kaosan, потому что это высокий огонь оцените точный SMG, который наносит вторичный урон, потому что стреляет маленькие бомбочки. Но шанс выпадения Kaosan SMG относительно низок. я 4 Kaosan SMG упали после 90 раундов победы над командиром Траунтом. Так какова вероятность выпадения Каосана из Траунта? 4/90 ~ 4,44%? А если бы мне повезло? Что, если мне повезет несколько раз? Что, если бы я был не повезло? Точно ли 4,44%? Учитывая мой опыт, что следует ли ожидать, что скорость выпадения будет?
Шанс выпадения предмета после победы над боссом
Какова фактическая вероятность выпадения определенного предмета из определенного босса?
Какова вероятность выпадения предмета X из Y
Какова вероятность выпадения Каосана из Command Traunt в Borderlands 3
Вас бы удивило, если бы я сказал, что истинная вероятность вероятно, между 1,4% и 11%? Это большой разброс. 11% означает, что я вероятно, придется взаимодействовать с командиром Траунтом всего 10–20 раз. прежде чем я получу то, что хочу. 1,4% означает, что мы должны пройти от 50 до 100 раз, 95% времени. Это огромная разница для моего времени.
Представьте, что истинная вероятность равна 4,44%. Если бы я повторил этот тест 900 раз и получил 40 каосанов, что бы разворот от моего тестирования быть? от 3,3% до 6,0%. Выполняя в 10 раз больше работы, я все еще имею большую разброс вероятности. Ну воняет. В этом и заключается загвоздка, чтобы проверить события с низкой вероятностью, нам нужно много данных, и эти стрелялки люблю иметь события с низкой вероятностью.
Как вы рассчитали этот разброс? я использовал 95% уверенности интервал, извлеченный из теста пропорций R с 1 выборкой. Это 95% доверительный интервал рассчитывается из испытаний Бернулли или биномиального испытания — испытания, которые являются успешными или неудачными с фиксированным вероятность (как подбрасывание монеты).
Что такое 95% доверительный интервал? Это диапазон значений, которые мы ожидаем извлечение в аналогичных условиях в 95% случаев, поэтому 1/20 действительно неправильно (например, выигрыш в лотерею, это может случиться). Это в этом случае это оценка пропорции (частоты пропорции) успех над неудачами.
Здесь мы делаем 1-выборочный тест пропорций против 4/90 как истинного вероятность. Тест пропорции с одной выборкой говорит, что, вероятно, p-значение равно 1,0, что превышает пороговое значение 0,1 или 0,05, это вероятно, из того же дистрибутива — это означает, что 4/90 правдоподобно, если вероятность/частота события также составляет 4/90, но мы видим 95% доверительный интервал ниже, это от 0,017 до 0,10 или от 1,7% до 11%. 95% доверительный интервал более полезен для меня, так как игрок, потому что это означает, что мой личный опыт может быть только 10 испытаний для получения оружия от 50 до 75 испытаний для достижения этого оружие. Это большой разброс. Мне может очень повезти или действительно не повезло, поэтому вы видите те посты на форуме, где игрок жалуется около 100 убийств и 0 дропов. Бывает :-(.
Здесь мы будем использовать тест пропорций с одной выборкой prop.test , и мы сообщить ему, что ожидаемая вероятность была 4/90 ( p=4/90 ), но мы также наблюдал 4 успеха, из 90 забегов. Мы хотим знать, является ли 4/90 скорее всего исходит из дистрибутива с вероятно 4/90, там написано да действительно делает. Мы также хотим знать 95% доверительный интервал вероятность p с учетом этого наблюдения.
> проп.тест(4,90,р=4/90) 1-образный тест пропорций без коррекции непрерывности данные: 4 из 90, нулевая вероятность 4/90 X-квадрат = 0, df = 1, p-значение = 1 альтернативная гипотеза: истинное p не равно 0,04444444 95-процентный доверительный интервал: 0,01741724 0,55 примерные оценки: п 0,04444444 Предупреждение: В prop.test(4, 90, p = 4/90): приближение хи-квадрат может быть неверным
Предупреждающее сообщение правильное, 4/90 не очень хорошо. Хи-квадрат хочет не менее 5 в каждом ящике. Но это другой урок.
Давайте посмотрим, что произойдет, если мы получим в 10 раз те же результаты с 40 успехов более 900 испытаний:
> проп.тест(40900,р=4/90) 1-образный тест пропорций без коррекции непрерывности данные: 40 из 900, нулевая вероятность 4/90 X-квадрат = 0, df = 1, p-значение = 1 альтернативная гипотеза: истинное p не равно 0,04444444 95-процентный доверительный интервал: 0,03280679 0,059 примерные оценки: п 0,04444444
Мы видим, что в этом случае оценка вероятности намного точнее. Больше испытаний, больше уверенности. Было ли это необходимо? Это зависит от того, что вы хотите дать вашей аудитории. Половина этих испытаний, и вы получите аналогичная оценка.
Сводка шансов выпадения
Для малых вероятностей (10 % или меньше) вам нужно гораздо больше испытаний для вероятности выпадения, чтобы получить стабильную оценку вероятности.
Для вероятности выпадения одного предмета вы можете смоделировать его как испытание Бернулли или биномиальное испытание. Каждый запуск записывается как успешный (1) или неудачный (0).
Тест пропорций с 1 выборкой ( prop.test в R) можно использовать для проверки соответствия ваших наблюдений ожидаемой вероятности
Иногда тебе просто везет (или не везет!)
Для оценки частоты выпадения следует попытаться рассчитать 95% доверительный интервал.
После победы над некоторыми боссами выпадает много легендарных предметов. некоторые падают мало. Боссы с большими выплатами довольно популярны, и люди хотят знать, чего ожидать.
Обычно статистики пытаются сопоставить то, что вы измеряете к дистрибутиву. Значения количества выпавших предметов являются добрыми странного, они неотрицательны, иногда равны нулю, а дискретный – нет 0,3 шт. Подсчеты неотрицательны целые числа. Это усложняет ситуацию, потому что статистика для такого рода данные сложные. Люди часто используют отрицательный бином. распределения и отрицательная биномиальная регрессия для моделирования этих проблемы. Я думаю, что это, вероятно, слишком много, чтобы обсуждать здесь.
Представьте, что мы не знаем основного распределения наших данных, и мы измерили это количество предметов, выпадающих за убийство босса:
элемента <- c(4,4,4,4,2,4,3,3,2,3,2,4,0,4,5)
Мы можем рассчитать некоторые сводные статистические данные, такие как среднее или среднее медиана и стандартное отклонение. Не зная базовое распределение, многие из этих мер не так уж полезны. Медиана, пожалуй, самая полезная мера: в 50 % случаев это минимальное или максимальное количество предметов, которые вы получите? Медиана посередине это значение, при котором будет выполнено 50% измерений. выше, а 50% будет ниже.
> элементы <- c(4,4,4,4,2,4,3,3,2,3,2,4,0,4,5) > среднее (предметы) [1] 3.2 > медиана (элементы) [1] 4 > резюме (элементы) Мин. 1 кв. Медиана Среднее 3-е кв. Максимум. 0,0 2,5 4,0 3,2 4,0 5,0
Мы также можем рассчитать 95%-й квартиль, который не является доверительным интервалом, который мы видели раньше, это просто то, где 95% наших измерений укладываются между ними. По сути, мы отсекаем первые 2,5% и последние 2,5%.
> # простые квантили 95% [не доверительный интервал] > квантиль(элементы,с(0,025,0,975)) 2,5% 97,5% 0,70 4,65
Самозагрузка
Мы хотим рассчитать оценку 95% доверительного интервала количество выпавших предметов.
Медиана или среднее значение служат своей цели, но зрители будут иметь разный опыт. Я бы предпочел, чтобы можно было поставить 19 из 20 зрители точное ожидание результатов. Уверенность 95% можно использовать интервал. Это раздражает, потому что R и другие языкам часто не хватает кода для их вычисления из произвольной статистики. 95-процентные доверительные интервалы хороши, потому что они дают представление о чего ожидать 19 раз из 20, как и в большинстве случаев.
Итак, приступим к начальной загрузке. Начальная загрузка это метод создания статистики из существующих измерений для получения представление об эффекте выбросов и быть немного более уверенным в наши результаты. Общая идея заключается в том, что вы снимаете свои мерки и вы сэмплируете их, вы сэмплируете из них то же количество, что и измерено. Итак, если вы измерили 20 вещей, вы выберете 20 вещей из 20 вещей, которые вы измерили. Затем вы можете вести статистику (например, вычисление среднего значения или медианы) по этим образцам. Тогда эти расчетная статистика сортируется, и вы игнорируете первые 2,5% (половину из 5%) и последние 2,5% (половина 5%), что дает вам 95% уверенности интервал.
Обычно вы злоупотребляете компьютерами и повторяете эти вычисления от 100 до От 1000 до0 раз, чтобы понять, чего ожидать. Ваш статистика улучшается как с большим количеством тестов, так и с большим количеством повторений. Это имеет тенденция исключать явные выбросы (например, выигрыш в лотерею).
Первое, что мы собираемся сделать, это произвести 10000-кратную выборку. 1 элемент из наших измерений. Это ожидание, что пользователь делает 1 попытку победить босса и должен ожидать от X до Y предметов выпасть с босса, 95% времени.
Несколько адаптировано из руководства DataCamp Quick R Bootstrapping: https://www.statmethods.net/advstats/bootstrapping.html
> # простой 95% доверительный интервал. Мы пробуем 10000 раз из нашего > # начальный набор данных, чтобы увидеть, каким будет доверительный интервал 95% > # выбранная статистика является выборкой. > N=10000 > F=функция(х) { возврат(выборка(элементы,1)) } > образцы = sapply (1: N, функция (i) { F (образец (элементы, длина (элементы), замена = ИСТИНА)) }) > квантиль(выборки,с(0,025,0,975)) 2,5% 97,5% 0 5
Таким образом, для N=10000 мы выбрали 1 элемент N раз. Срезаем верхушку и нижние значения и мы получили минимум 0 и максимум 5. Не супер полезный. В этом сценарии мы можем ожидать от 0 до 5 элементов. Не очень описательный. Но мы не описали много испытаний, возможно, если бы мы удвоив количество испытаний, мы можем получить лучшую оценку.
Более подробная информация о R-коде
sapply означает поместить/сопоставить значения от 1 до N с помощью предоставленной функции и вернуть список возвращаемых значений функции в указанном порядке. Предоставленная функция выбирает список измерений из элементов длина (шт.) длина. Образец содержит дубликаты, потому что мы выборка с заменой ( replace=TRUE ). Функция F очень простой, он выбирает 1 значение из подвыборки, как если бы вы победили босс один раз. Так эффективно мы подвыборки и подвыборки, потому что мы нужен 95% доверительный интервал подвыборок начальной загрузки.
> F=функция(х) {возврат(образец(элементы,1))} > образцы = sapply (1: N, функция (i) { F (образец (элементы, длина (элементы), замена = ИСТИНА)) })
Расчет среднего количества элементов, которые должен увидеть пользователь
Мы можем заменить нашу функцию F другой функцией, такой как среднее (среднее), и мы можем получить оценку среднего, основанную на измерение 95% тех, кто повторяет наши измерения, должны достичь в среднем от 2,5 до 3,8.
Фактически это означает, что мы сделали выборку 10000 раз, рассчитали среднее 10000 раз, а затем отсортировал результаты и нашел диапазон, который составляет 2,5% до 97,5% in — 95% доверительный интервал.
> # Теперь, если нам нужен доверительный интервал для среднего > N=10000 > F=среднее > res = sapply(1:N,function(i) { F(sample(items,length(items),replace=TRUE))}) > квантиль (рез, с (0,025, 0,975)) 2,5% 97,5% 2,533333 3,800000 >
Вероятность выпадения различных типов предметов после победы над боссом
Теперь еще одна популярная часть Borderlands — поиск боссов или квесты. которые бросают много добычи. Часто я вижу руководства и видео о фарми этих боссов и иногда получаешь подведение итогов трофея. Это кажется все очень потребительским и жадным, но если вы в игре, это довольно весело.
Часто вы хотите знать, какие типы предметов вы собираетесь получить. Некоторые квесты/боссы вознаграждают разными видами добычи, чем другие. Например, в приграничье у вас обычно есть оружие, артефакты, моды классов, моды гранат и щиты. Некоторые люди будут группироваться артефакты, классовые моды, гранатные моды и щиты вместе и лечить оружие отдельно.
Это категориальные распределения, по сути подсчеты типов. Обычно есть 3 вещи, которые нам нужны от категориальных распределений:
определить, получен ли результат из известного распределения.
мои результаты похожи на прошлые результаты?
повлияла ли обработка на предметы?
определить, влияет ли лечение на категориальные исходы
Имейте в виду, что чем больше у вас категорий, тем больше тестов вы часто должны сделать, чтобы обнаружить небольшие изменения.
Тест zKarmaa на выпадение предмета Graveward с загруженным кубиком или без него
Мы будем использовать данные из видео zKarmaa:
zKarmaa, 15 апреля 2020 г., «1000 убийств Graveward — имеет ли значение удача? Удача против No Luck Mayhem 4 Шансы выпадения! Часть 1(Borderlands 3)” https://www.youtube.com/watch?v=Nl3U6vmtzvA
zKarmaa фармит босса Graveward в Bl3 1000 раз и считает типы предметов, которые выпадают после победы над боссом. zКарма ломается это по количеству выпавших в мире легендарных предметов, мод легендарного класса, легендарные артефакты и подкатегория легендарных существ помазанник. В видео он совершает 500 убийств заряженными костями и 500 без.
Сначала представляем наши дистрибутивы:
загружен <- c(мир=658, annoit=373, класс=111, артефакт=101) контроль <- c (мир = 667, annoit = 405, класс = 113, артефакт = 130)
Тогда как мы узнаем, было ли использование загруженных костей лучше, чем нет используя загруженные кости? Наши данные являются категориальными подсчетами. Они не могут быть отрицательные, они равны 0 или больше. Мы делаем предположение, что счета масштабируются пропорционально и что вероятность каждой категории равна исправлено.
Чтобы определить, производят ли загруженные кости эффект, мы спросим у вопрос:
При таком лечении, как игра в кости, исходит ли оно от одного и того же? раздача предметов без обработки. То есть есть ли разница, использую ли я загруженные кости или нет. 2). R имеет реализацию этот тест:
> chisq.test(загружено, p=control, rescale.p=TRUE) Критерий хи-квадрат для заданных вероятностей данные: загружены X-квадрат = 5,5142, df = 3, p-значение = 0,1378
Я прошу R рассчитать критерий хи-квадрат, чтобы обработать контроль измерения как эмпирическое распределение, чтобы соответствовать и масштабировать пропорции. Он говорит мне, что у меня есть статистика X-квадрат, и степеней свободы ( 90 097 , количество категорий - 1 ) и p-значение 0,1378 . Значение p больше, чем обычно используемый порог альфа 0,05 поэтому я предполагаю, что эти дистрибутивы не статистически значимо отличаются. Это совпадает с zKarmaa претензия в его видео.
Позже он просматривает количество выпавших дробовиков Лоб, Уорд. Пожертвование Шилдса, Могилы и Мокси:
> загружен <- c (лобы = 38, варды = 36, могилы = 43, мокси = 51) > контроль <- c(лобс=43,варды=36,грейвс=43,мокси=23) > chisq. test(загружено,p=control,rescale.p=TRUE) Критерий хи-квадрат для заданных вероятностей данные: загружены X-квадрат = 26,773, df = 3, p-значение = 6,568e-06
Мы ясно видим, что p-значение ужасно маленькое. Это предполагает, что там является статистически значимой разницей между применением загруженные кости и контроль без загруженных костей.
Была ли разница исключительно из-за способностей Мокси?
> загружен <- c (лобы = 38, варды = 36, могилы = 43) > контроль <- c(лобс=43,варды=36,могилы=43) > chisq.test(загружено,p=control,rescale.p=TRUE) Критерий хи-квадрат для заданных вероятностей данные: загружены X-квадрат = 0,39257, df = 2, p-значение = 0,8218
Учитывая, что p-значение > 0,05, можно предположить, что да. Загруженные кости не кажется, многое делает для zKarmaa, кроме увеличения количества Moxxi. пожертвование.
500 много испытаний
Достаточно ли 500 попыток? Или слишком много?
Это тема для отдельного поста, но если вы хотите определить, как много прогонов/тестов, которые вы должны выполнить, чтобы определить, имеет ли лечение эффект вы можете сделать анализ мощности. Анализ мощности говорит нам, сколько испытания, которые нам нужно будет провести, чтобы ответить на нашу гипотезу в течение определенная вероятность.
Первое, что вам нужно сделать, это выбрать, сколько категорий вы хотите измерить? Так что в случае zKarmaa он измерил 4 категории, которые означает, что у нас будет тест 4-1=3 степеней свободы. Далее load-dice может быть незаметным, поэтому мы хотим искать небольшие эффекты, например разница 10%. Это приведет к размеру эффекта 0,2 для малого, 0,5 для среднего и 0,8 для большого. Но это означает, насколько лечения будет отличаться от контроля. Вот хорошее объяснение величины эффекта, если хотите: Сол Маклеод, 2019, О чем говорит размер эффекта?, https://www.simplypsychology.org/effect-size.html
Во-вторых, нам нужна сила. Насколько ты неправ? 1/20? 1/100? Это будет уровень мощности, поэтому скажем 1/20, т.е. 1-1/20 — это 0,95, что и будет нашей силой. Мы хотим быть правы на 95% время.
В-третьих, это наша альфа, которая по-прежнему равна 0,05. Это для хотя видеоигры и влияние социальных сетей, так что мы могли бы пойти еще выше до 0,10, если мы хотим.
> library(pwr) # install.packages("pwr"), если вы его пропустили > эффект = 0,2 > дф = (4-1) > знак = 0,05 > мощность = 0,95 > pwr.chisq.test(w=effect, power=power, sig.level=sig, df=df) Расчет мощности хи-квадрат ш = 0,2 N = 429,2474 дф = 3 сиг.уровень = 0,05 мощность = 0,95 ПРИМЕЧАНИЕ. N — количество наблюдений.
Итак, zKarmaa был на высоте. Если он хотел меньшего размера эффекта, то более тонкая, например, разница в 10% от контрольной, ему нужно много более.
> pwr.chisq.test(w=0.1, power=power, sig.level=sig, df=df) Расчет мощности хи-квадрат ш = 0,1 N = 1716,99 дф = 3 сиг.уровень = 0,05 мощность = 0,95 ПРИМЕЧАНИЕ. N — количество наблюдений.
Вы также можете играть с этим. Вы можете понизить свою силу до 80% и увеличьте уровень сигнала до 0,1
> pwr. chisq.test(w=0.1, power=0.8, sig.level=0.1, df=df) Расчет мощности хи-квадрат ш = 0,1 N = 879,7742 дф = 3 сиг.уровень = 0,1 мощность = 0,8 ПРИМЕЧАНИЕ. N — количество наблюдений.
Таким образом, баланс здесь будет состоять из чувствительности (величины эффекта) и того, насколько можно доверять нашему критерию хи-квадрат, плюс 20%-ная вероятность того, что мы не учли то, что было необходимо. По сути, это означает, что с 1000 образцами Grave Ward мы можем добиться значительных различий в величине эффекта.
Резюме
При сравнении количества категорий мы должны использовать распределение тесты и категориальные распределения, такие как критерий хи-квадрат.
Данные, которые являются подсчетами нескольких категорий, часто называют Категориальные данные.
Тест
хи-квадрат может сказать вам, являются ли категориальные распределения подсчета похожие или не основанные на вероятности и пропорции.
Р имеет чискв.тест
Вы можете использовать R’s pwr , чтобы определить количество тестов, которые вы необходимо определить категориальное различие
Чтобы использовать хи-квадрат, вам нужно как минимум 5 в каждой категории.
Для большего количества категорий потребуется больше образцов
В заключение стримерам и участникам игрового сообщества не трудно обеспечить более надежные (вероятностные) оценки вероятности отбрасывания в своих любимых играх. Стримеры, которые проводят такого рода тестирование, как до тех пор, пока их тесты непротиворечивы, должны сообщать цифры, которые они запись, чтобы позволить своим фанатам провести статистический анализ. Тем не менее, с немного R можно вычислить эти оценки довольно быстро и успешно.
Пожалуйста, сообщите:
Подсчеты и испытания
95% доверительные интервалы
Результаты пропорциональных тестов
Категориальная разбивка
Необработанный, за прогон считается
Ферма — чтобы повторить квест или сразиться с боссом, чтобы получить предмет.
игровой сервис — предоставление услуги сообществу геймеров в игре путем повторного выполнения чего-либо, чтобы помочь информировать игроков.
stats - статистика и измерения по тестированию
Тестирование
- несколько испытаний (возможно, фермерство), где для анализа записываются успехи и/или подсчеты.
drop-rate - частота выпадения предметов игроку за действие (победа над боссом, выполнение квеста и т.д.)
выделенный дроп — предмет больше связан с выпадением с босса или только с босса.
босс - большой враг с плохим концом квеста / миссии, которого вы должны победить.
NPC - неигровой персонаж - управляемые компьютером персонажи в игре.
враг - обычно управляемый компьютером NPC, враждебный игроку.
дроп - предмет, который выпадает из
частота - количество успехов/количество испытаний (4 монарха за 100 убийств боссов это 4/100 или 0,04 или 4%)
Категория
- дана награда, что это за награда? Категории — это способы взять что-то вроде элементов и классифицировать их по разным типам. Категория — это вид или тип.
лечение - при повторных испытаниях с определенным предметом или эффектом или без них. Например, увеличивает ли этот предмет шанс выпадения, все испытания с этим предметом — это 1 лечение, все испытания с альтернативным предметом — это лечение, а контрольные испытания — это лечение.
контроль - испытания без лечения
проба - тест, 1 прогон. Например. 1 убийство босса, 1 выполнение квеста.
лут - предметы, которые вы хотите
среднее - среднее обычно представляет собой сумму значений, деленную на количество значений
неотрицательный - 0 или более
дискретный - без промежуточных чисел, как целые числа.
p-значение — «При проверке статистической гипотезы p-значение [примечание 1] или значение вероятности — это вероятность получения результатов теста, по крайней мере столь же экстремальных, как фактически наблюдаемые результаты, при условии, что нулевая гипотеза верна». - Википедия, p-значение, получено 07 июля 2020 г. , https://en.wikipedia.org/wiki/P-value 9.0020
нулевая гипотеза - значение теста по умолчанию, обычно для тестов хи-квадрат это означает, что нет разницы между пропорциями категорий, для теста пропорций это означает, что ожидается разница в пропорциях.
отклоняет нулевую гипотезу — это означает, что нулевая гипотеза (по умолчанию), вероятно, неверна, поэтому это может означать, что распределения различаются — в зависимости от теста.
Drops — Minecraft Wiki
Эта статья о предметах, которые выпадают из сущностей и блоков. Чтобы узнать о падениях, см. Ущерб § Урон от падения.
«Добыча» перенаправляется сюда. Чтобы узнать о команде, см. Команды/лут. Таблицу JSON см. в таблице Loot. Чтобы узнать о чарах, см. Мародерство.
Выпадает со скелета: сферы опыта, стрелы, кость и лук.
Дроп — это предметы, которые появляются, когда мобы и некоторые другие существа умирают или когда ломаются большинство типов блоков.
Содержимое
1 Типы капель
1. 1 Обычные капли
1.1.1 Мародерство
1.2 Редкие дропы
1.3 Оснащенные элементы
1.4 Сферы опыта
2 капли мобов
2.1 Пассивные мобы
2.2 Нейтральные мобы
2.3 Враждебные мобы
3 капли сущности
3.1 Снаряды
3.2 Стационарный
3.3 Транспортные средства
4 падающих блока
4.1 Материалы и строительные блоки
4.2 Руды
4.3 Растения
4.4 Другое
5 Видео
6 История
7 выпусков
8 См. также
Типы дропов[]
Обычные дропы[]
Обычные дропы могут появиться на локации моба в момент получения им фатального урона. У большинства мобов есть определенные предметы, которые могут выпасть при убийстве. Некоторые распространенные предметы, такие как кожа, выпадают не всегда, но имеют большой шанс (не менее 50%, в зависимости от диапазона выпадения) выпасть. Некоторые обычные дропы, такие как огненные стержни, вообще не падают, если моб не был убит игроком.
Каждый из этих предметов имеет диапазон выпадения, который представляет собой случайное равномерное распределение количества выпадающих предметов. Например, из коровы выпадает 0–2 предмета из кожи и 1–3 предмета из сырой говядины. Поскольку диапазон для кожи включает 0, существует вероятность ¹ ⁄ ₃, что кожа не выпадет.
Детеныш животного после смерти не роняет обычные капли.
Добыча[]
На некоторые обычные и необычные дропы действуют чары "Добыча". В лучшем случае выпадает количество дополнительных предметов, равное уровню зачарования.
В частности, игра генерирует дробное число от 0 до уровня мародерства, которое затем округляется до ближайшего целого числа. Это приводит к тому, что числа в середине диапазона выпадения встречаются в два раза чаще. Вероятности следующие:
Добыча дополнительных предметов
Уровень мародерства Нет элементов 1 шт. 2 шт. 3 шт.
Мародерство I ¹ ⁄ ₂ ¹ ⁄ ₂ -- --
Мародерство II ¹ ⁄ ₄ ¹ ⁄ ₂ ¹ ⁄ ₄ --
Мародерство III ¹ ⁄ ₆ ¹ ⁄ ₃ ¹ ⁄ ₃ ¹ ⁄ ₆
Стрела Бродяги с наконечником — это особый случай: в то время как мародерство может попытаться увеличить количество выпадающих стрел, окончательное количество выпадающих стрел ограничено 1. Таким образом, мародерство эффективно увеличивает шансы выпадения стрел, вплоть до ¹¹ ⁄ ₁₂ с мародерством III.
Редкие дропа[]
Редкие дропа обычно появляются, если монстр убит игроком, хотя некоторые редкие дропа можно получить и другими способами. Редкие предметы всегда представляют собой отдельный предмет, но могут появляться в сочетании с другими обычными предметами. Дроп считается редким, если он сопровождается random_chance_with_looting условие в таблице лута моба.
Редкие предметы обычно имеют шанс выпадения 2,5%, плюс 1 процентное очко за каждый уровень грабежа используемого оружия (максимум 5,5 % в мародерстве III). Исключением является то, что из кролика выпадает кроличья лапка с вероятностью 10% плюс 3 процентных пункта за уровень мародерства (максимум 19% с мародерством III). в Bedrock Edition есть и другие исключения: из скелета-иссушителя выпадает череп-иссушитель с вероятностью 2,5% плюс 2 процентных пункта за уровень добычи (максимум 8,5% в Looting III), а из утопленника выпадает медный слиток с шансом 11. % шанса плюс 2 процентных пункта за уровень грабежа (максимум 17 % с мародерством III).
Обратите внимание, что в случае нескольких редких падений (типы стражей и зомби) шанс 2,5% делится между ними, а не для каждого предмета.
Оболочка шалкера технически также является редким дропом, выпадающим из шалкеров только в одиночном разряде, хотя они не требуют убийства игрока, имеют базовый шанс 50% и увеличиваются на 6,25% за уровень добычи.‌ ^{[ Java Только издание ]}
Экипированные предметы[]
Зачарованный лук, получаемый из дропа со скелета.
Когда монстр убит игроком или прирученным волком, он может сбросить снаряжение и доспехи, с которыми он появился. Каждое снаряжение, с которым был создан монстр, выпадает с вероятностью 8,5%‌ ^{[ Только для Java Edition ]} или с шансом 25%‌ ^{[ Только для Bedrock Edition ]} , ^[1] кроме тыквы, черт возьми фонари и железный меч Векса с шансом 0%. Это значение определяется HandDropChances моба и ArmorDropChances 9.0098 теги. Зачарование «Добыча» увеличивает этот шанс на 1 % за уровень (до 11,5 % для «Добычи III» и до 3 % для тыкв, фонарей из тыквы и упомянутого меча)‌ ^{[ Только для Java Edition ]} или 5 % за уровень в некоторых случаях‌ ^{[ Bedrock Edition только ]}. Шанс выпадает для каждого предмета снаряжения, поэтому после смерти монстра может выпасть более одного предмета снаряжения.
Есть также некоторые экипированные предметы, которые гарантированно выпадут:
Все предметы, которые моб подбирает после появления, всегда выпадают, даже если он не убит игроком и даже если это младенец-зомби. Это касается только враждебных мобов, но не жителей деревни.
Зловещее знамя всегда падает с разбойников, носящих его.
Лошади, ослы, мулы, ламы и свиньи, а также бродяги сбрасывают любые предметы, которыми их наделили игроки, такие как седла, ковер или сундуки.
Опустошители роняют седла.
Раковины наутилуса утонувшей капли появляются в левой руке.
Сферы опыта[]
Основная статья: Сферы опыта
Сферы опыта выпадают только в том случае, если моб умирает менее чем через три секунды после атаки (ближний бой, лук, снежки, яйца и зелья, наносящие мгновенный урон) со стороны игроком или домашним волком игрока, но не активируемым игроком раздатчиком. Их общая стоимость - это определенное количество опыта, полученного за убийство этого моба. Они также выпадают из брошенной бутылки чар. Собранный опыт накапливается в уровнях, которые можно использовать для зачарования или ремонта.
В отличие от других выпадающих предметов, таких как предметы, сферы опыта появляются на месте трупа моба в тот момент, когда он исчезает в клубе дыма.‌ ^{[ Только для Bedrock Edition ]} Сферы опыта перемещаются к любым ближайшим игрокам.
Дроп с мобов[]
Пассивные мобы[]
Моб опыт Обычные капли Редкие капли Снаряженные и изношенные предметы Примечания Поражено чарами мародерства
Агент, летучая мышь, NPC 0 Нет Нет Нет Н/Д
Аллей 0 Нет Нет Нет Также бросьте удерживающий предмет. Нет
Кошка 1-3 0-2 Строка Нет Нет Прирученный кот также может дарить игроку подарок утром после сна:
Перо
Фантомная мембрана
Лапка кролика
Шкура кролика
Гнилая плоть
Сырой цыпленок
Строка
Да
Курица 1–3 0–2 пера
1 сырой цыпленок или 1 вареный цыпленок Нет Нет Мясо готовится, если его убить в огне.
Падение перьев и мяса зависит от мародерства.
Также откладывает яйцо каждые 5–10 минут. Да
Код 1–3 1 сырая треска или 1 приготовленная треска‌ ^{[ только Java Edition ]} 0-2 Кость (25%) ‌ ^{[ только BE ]}
Костная мука (5%) ‌ ^{[ только JE ]} Нет Рыба будет приготовлена, если ее убить в огне. ‌ ^{[ Только Java Edition ]} Только капли костей и костной муки
Корова 1–3 0–2 Кожа
1–3 Сырая говядина или 1–3 Стейк Нет Нет Мясо готовится, если его убить в огне.
Дает молоко при нажатии на пустое ведро. Да
Осел
Мул 1–3 0–2 Кожа Нет 1 Седло при наличии седла
1 Сундук при наличии Также выпадает все содержимое сундука. Да
Лиса 1–2 ‌ ^{[ Только Java Edition ]}
1–3 ‌ ^{[ Только Bedrock Edition ]} Нет Нет

Яйцо
Изумруд
Перо
Кожа
Кроличья шкура
Кроличья лапка
Пшеница
Все естественно созданные предметы имеют 8,5%‌ ^{[ только JE ]} или 100%‌ ^{[ BE только ]} выпадения, за исключением приготовленной свинины, которую могут съесть лисы. Увеличивает шанс выпадения‌ ^{[ только Java Edition ]}
Лягушка, головастик 1-3 Нет Нет Нет Н/Д
Лошадь 1–3 0–2 Кожа Нет 1 Седло , если оседлан
1 Конский доспех , если экипирован Да
Грибной гриб 1–3 0–2 Кожа
1–3 Сырая говядина или 1–3 Стейк Нет Нет Мясо готовится, если его убить в огне.
Стрижка роняет 5 соответствующих грибов, превращая их в обычную корову, процесс, который нельзя отменить.
Дает молоко при использовании пустого ведра.
Дает грибную похлёбку при использовании с пустой миской.
если коричневый гриб покормить цветком, то при доении из чаши получается подозрительная похлебка, но только один раз . Да
Оцелот 1–3 Нет Нет Нет Н/Д
Попугай 1–3 1–2 перо Нет Нет Да
Свинья 1–3 1–3 сырых свиных отбивных или 1–3 приготовленных свиных отбивных Нет 1 Седло при наличии седла Мясо приготовлено, если умерло в огне. Да
Иглобрюх 1–3 1 рыба-фугу 1-2 Кость (25%) ‌ ^{[ BE только ]}
Костная мука (5%) ‌ ^{[ JE только ]} Нет Нет Только капли костей и костной муки
Кролик 1–3 0–1 Сырой кролик или 0–1 Приготовленный кролик
0–1 Шкура кролика Кроличья лапка (10%) Нет Мясо приготовлено, если умерло в огне. Да
Лосось 1–3 1 сырой лосось или 1 приготовленный лосось‌ ^{[ только Java Edition ]} 0-2 Кости (25%) ‌ ^{[ только BE ]}
Костная мука (5%) ‌ ^{[ JE только ]} Нет Из мелкого и обычного лосося выпадает 0–2 кости, а из крупного лосося — 1–2 кости.‌ ^{[ Только Bedrock Edition ]}
Рыба готовится, если она погибла во время пожара.‌ ^{[ Только Java Edition ]} Только капли костей и костной муки
Овцы 1–3 1 Шерсть , если не стричь
1–2 Сырая баранина или 1–2 Вареная баранина Нет Нет Стригущие капли 1-3 Шерсть.
Шерсть окрашена, если овца была порождена цветной или окрашенной.
Мясо готовится, если умерло в огне. Только мясная капля
Лошадь-скелет 1–3 0–2 Кость Нет Нет Да
Снежный голем 0 0–15 Снежок Нет Нет Стрижка снежного голема у резной тыквы дроп 1 Резная тыква Нет
Кальмар 1–3 1–3 чернильный мешок Нет Нет Да
Страйдер 1–2 0–5 Строка Нет 1 Седло при наличии седла Нет Да
Тропическая рыба 1-3 1 Тропическая рыба 1-2 Кость (25%) ‌ ^{[ BE только ]}
Костная мука (5%) ‌ ^{[ JE только ]} Нет Только капли костей и костной муки
Черепаха 1-3 0-2 Seagrass
1 миска, если убит молнией. Нет Нет Сбрасывает один щиток, когда становится взрослым. Да
Селянин 0 Нет Нет Нет Житель деревни может бросать еду другим жителям деревни при обмене, которую можно подобрать:
Хлеб, Морковь, Картофель, Свекла
Также в Java Edition жители деревни дают игроку подарок после прохождения рейдов с возможными дропами в зависимости от профессии
оружейник:
Кольчужный шлем
Кольчужный нагрудник
Кольчужные поножи
Кольчужные сапоги
мясник:
Вареная курица
Вареная баранина
Приготовленная свинина
Приготовленный кролик
Стейк
картограф:
Бумага
Пустая карта
священник:
Лазурит
Пыль красного камня
фермер:
Хлеб
Печенье
Тыквенный пирог
Рыбак:
Сырая треска
Сырой лосось
fletcher:
Стрелка
Стрела сопротивления огню
Стрела вреда
Стрела исцеления
Стрела невидимости
Стрела прыжка
Стрела ночного видения
Стрела яда
Стрела регенерации
Стрела медлительности
Стрела силы
Стрела скорости
Стрела водного дыхания
Стрела Слабости
Кожевник:
Кожа
библиотекарь:
Книга
каменщик:
Глина
пастух:
Шерсть
Мастер по инструментам:
Каменный топор
Каменная мотыга
Каменная кирка
Каменная лопата
Оружейник:
Каменный топор
Железный топор
Золотой топор
ребенок:
Мак
придурок:
Семена пшеницы
безработные:
Семена пшеницы
Нет
Странствующий торговец 0 1 Зелье невидимости или Молоко‌ ^{[ Только для Java Edition ]} если выпить после смерти Нет Зелье невидимости
Молоко‌ ^{[ Только для Java Edition ]}
вероятность его выпадения составляет 8,5%. Зелье невидимости и молоко можно получить, только убив странствующего торговца, пока он пьет зелье или молоко.
Также выпадает 2 свинца, когда его убивают или отделяют от ламы-торговца. Увеличивает шанс выпадения
Лошадь-зомби 1–3 0–2 Гнилая плоть Нет Нет Да
Нейтральные мобы[]
Моб опыт Обычные капли Редкие капли Снаряженные и изношенные предметы Примечания Поражено чарами мародерства
Пчела 1–3 Нет Нет Нет Н/Д
Пещерный паук
Паук 5 0–2 Строка
0–1 Глаз паука , если убит игроком Нет Нет Да
Дельфин 0 0–1 Сырая треска или 0–1 Приготовленная треска Нет Нет Рыба готовится, если погибла в огне. Да
Эндермен 5 0–1 Жемчуг Эндера Нет Нет Также сбрасывает удерживаемый блок. Да
Коза 1–3 Нет Нет 1 козий рог если они врезаются в сплошные блоки «Обдумывать», «Поть», «Искать» и «Чувствовать» для обычного козла.
"Восхищаться", "Зов", "Жаждать" и "Мечтать" за кричащего козла. Н/Д
Железный голем 0 3–5 Железный слиток
0–2 Мак Нет Нет Нет
Лама
Лама торговца 1–3 0–2 Кожа Нет 1 Ковер при наличии
1 Сундук при наличии Также выпадает все содержимое сундука. Да
Панда 1-3 0-2 Bamboo‌ ^{[ Только Bedrock Edition ]}
1 Bamboo‌ ^{[ Только Java Edition ]} Нет Нет Слабый и маленький панда может чихнуть, из которого выпадает комок слизи Да
Пиглин 5 + 1–3, если есть снаряжение Нет Нет Золотой меч
Арбалет
Золотая броня Н/Д
Белый медведь 1–3 0–2 Сырая треска или 0–2 Приготовленная треска (³ ⁄ ₄ шанс)
0–2 Сырой лосось или 0–2 Приготовленный лосось (¹ ⁄ ₄ шанс) Нет Нет Рыба готовится, если погибла в огне. ^{[ нужна дополнительная информация ]} Да
Зомбированный поросенок 5
+ 1–3 если есть оборудование
+ 7 если ребенок 0–1 Гнилая плоть
0–1 Золотой самородок Золотой слиток (2,5%) , если убит игроком Золотой меч
Резная тыква‌ ^{[ Только Java Edition ]}
Фонарь Джека‌ ^{[ Только Java Edition ]} Золотой меч можно зачаровать. Да
Волк 1–3 Нет Нет Нет Н/Д
Враждебные мобы[]
Оружие, инструменты и доспехи, сброшенные мобами, имеют оставшуюся прочность не менее 25, что также является наиболее распространенным. Менее поврежденные предметы встречаются все реже.
За исключением золотых мечей и инструментов, предметы всегда получают не менее 26 единиц урона. Золотые предметы могут быть выброшены целыми и невредимыми.
Моб. опыт Обычные капли Редкие капли Снаряженные и изношенные предметы Примечания Поражено чарами мародерства
Пламя 10 0–1 Blaze Rod , если убит игроком Нет Нет Да
Куриный жокей 10 (курица)
12 + 1–3 если есть снаряжение (зомби) 0–2 пера
1 сырая курица
1 вареная курица , если убит в огне
0–2 гнилая плоть
1 голова зомби , если убит взрывом заряженного крипера 2,5% шанс выпадения;
Железный слиток или
Морковь или
Картофель (Печеный картофель, если погибнет от огня) Железная лопата (в Bedrock Edition зомби-житель никогда не появляется с железной лопатой)
Железный меч (в Bedrock Edition зомби-житель никогда не появляется с железным мечом)
Случайная броня (в Bedrock Edition зомби-житель никогда не появляется с доспехами)
Резная тыква‌ ^{[ Только Java Edition ]}
Фонарь Джека‌ ^{[ Только Java Edition ]} Снаряжение можно зачаровывать (кроме тыквы и тыквы). Жокей состоит из двух мобов, которые двигаются как один. Каждая часть сбрасывает предметы отдельно, когда она побеждена. Да
Крипер 5 0–2 пороха
1 музыкальный диск если убит скелетом или бродягой
1 голова крипера если убит взрывом заряженного крипера Нет Нет Да
Утонул 5
+ 1–3 если есть оборудование
+ 7 если ребенок 0–2 Гнилая плоть 11% шанс выпадения:
Медный слиток Трезубец
Удочка
Раковина наутилуса (только для левой руки)
Случайная броня Случайная броня выпадает только при преобразовании из зомби.
Всегда бросайте раковину наутилуса в руки. Да
Старейшина-хранитель 10 0–2 Осколок призмарина
0–1 Кристаллы призмарина (¹ ⁄ ₃ шанс)
0–1 Сырая треска (¹ ⁄ ₂ шанс) или
0-1 Приготовленная треска ( ¹ ⁄ ₂ шанс) если погибнет от огня Сырая треска (60%) или
Приготовленная треска (¹ ⁄ ₂ шанс) если погибнет от огня ‌ ^{[ Только Java Edition ]}
Сырой лосось (25%) или Приготовленный лосось (25%), если убить огнем‌ ^{[ только для Java Edition ]}
Иглобрюх (13%)
Тропическая рыба (2%) если убит игроком
Нет Призмариновые кристаллы выпадают, только если сырая треска терпит неудачу.
Сырая треска — это как обычная, так и редкая добыча.
Обычная капля сырой трески готовится, если она погибла в огне.‌ ^{[ Только Java Edition ]} Все, кроме губки
Эндер Дракон 12 000 или 500 Нет Нет Нет Опыт выпадает 10 раз по 1000 опыта и один раз по 2000 опыта если это первый раз .
Активирует портал в выходном портале:
Генерирует 4 факела, 16 краеугольных камней в выходном портале и
1 яйцо дракона , если это первый раз .
В последующие разы выпадает только 500 опыта.
Генерирует конечный шлюз , если это первые 20 эндер-драконов . Н/Д
Эндермит 3 Нет Нет Нет Н/Д
Вызыватель 10 Тотем бессмертия
0-1 Изумруд, если убит игроком Нет 1 Зловещее знамя , если капитан рейда ‌ ^{[ Только Java Edition ]} Тотем бессмертия всегда выпадает из вызывающих, когда их убивают.
При убийстве призывателя всегда падает зловещее знамя, но только если он капитан рейда. Только изумруды
Гаст 5 0–1 Слеза Гаста
0–2 Порох Нет Нет Да
Хранитель 10 0–2 Призмариновый осколок
0–1 Призмариновые кристаллы (² ⁄ ₅ шанс)
0–1 Сырая треска ( ² ⁄ ₅ шанс) или
0-1 Приготовленная треска (² ⁄ ₅ шанс) , если убит пожаром ‌ ^{[). Джав. EDITIA игрок} Сырая треска (60%) или
Приготовленная треска (¹ ⁄ ₂ шанс) если погибнет от огня ‌ ^{[ Только Java Edition ]}
Сырой лосось (25%) или Приготовленный лосось (25%), если убить огнем‌ ^{[ Только Java Edition ]}
Иглобрюх (13%)
Тропическая рыба (2%) если убит игроком
Нет Призмариновые кристаллы выпадают только в том случае, если сырая рыба терпит неудачу.
Сырая треска — это как обычная, так и редкая добыча.
Обычная капля сырой трески готовится, если она погибла в огне.‌ ^{[ Только Java Edition ]} Да
Хоглин 5 2–4 Сырая или вареная свинина
0–2 Кожа Мясо приготовлено, если умерло в огне. Нет Да
Иллюзионер
‌ ^{[ Только Java Edition ]} 5 Нет Нет Лук
Зловещее знамя если капитан рейда Зловещее знамя всегда выпадает из иллюзиониста при убийстве, но только если он рейд-капитан. Увеличивает шанс выпадения только лука
Магматический куб 1, 2 или 4 0–1 Magma Cream, если размер > 1
1 Froglights если убит лягушкой Нет Нет Да
Фантом 5 0-1 Фантомная мембрана если убит игроком Нет Нет Да
Разбойник 5
+ 1–3 при наличии оборудования 0-2 Стрела‌ ^{[ Только Bedrock Edition ]} Нет Арбалет
1 Зловещее знамя если капитан рейда Арбалет можно зачаровать.
Зловещее знамя всегда падает с грабителя при убийстве, но только если он рейдовый капитан.
Зачарование мародерства увеличивает шанс выпадения арбалета на 12% за уровень.
В Bedrock Edition спавн разбойников из рейдов может выпасть:
0-1 Изумруд
И дополнительно выпадение зависит от сложности, 65% шанс выпадения на легком и нормальном уровне, а 80% шанс выпадения на сложном;
0-1 Изумруд ( ¹⁰ ⁄ ₃₉ шанс)
2-3 Изумруд ( ⁵ ⁄ ₃₉ шанс)
4-5 Изумруд ( ² ⁄ ₃₉ шанс)
1 Зачарованная книга ( ² ⁄ ₃₉ шанс)
1 железный топор (⁵ ⁄ ₇₈ шанс)
1 железная лопата (⁵ ⁄ ₇₈ шанс)
1 железный меч ( ⁵ ⁄ ₇₈ шанс)
1 Железный шлем (⁵ ⁄ ₇₈ шанс)
1 железный нагрудник (⁵ ⁄ ₇₈ шанс)
1 Железные поножи ( ⁵ ⁄ ₇₈ шанс)
1 Железные сапоги ( ⁵ ⁄ ₇₈ шанс)
Железное снаряжение из рейдерского дропа имеет 50% шанс быть зачарованным случайным зачарованием, и всегда сильно повреждено. Изумруд — это как обычная рейдерская добыча, так и дополнительная рейдерская добыча. Мародерство увеличивает количество изумрудов или шанс выпадения снаряжения. Дополнительный изумруд выпадает только в том случае, если выпадает зачарованная книга или железное снаряжение.
Все, включая выпадение рейдеров‌ ^{[ только Bedrock Edition ]}, но не для зловещего баннера
Опустошитель 20 1 Седло если убит игроком Нет Нет Н/Д
Шалкер 5 0–1 Шалкер Шелл Нет Нет Да
Чешуйница 5 Нет Нет Нет Н/Д
Скелет
Бродяга 5
+ 1–3 при наличии оборудования 0–2 Стрела
0–2 Кость
1 Череп скелета , если убит взрывом заряженного крипера (только обычный скелет)
0–1 Стрела замедления , если заблудший Нет Лук
Случайная броня
Резная тыква‌ ^{[ Только для Java Edition ]}
Светильник Джека‌ ^{[ Только для Java Edition ]} Снаряжение можно зачаровывать (кроме тыквы и тыквы). Да
Всадник-скелет 5 (скелет) + 1–3 при наличии снаряжения + 1-3 (лошадь-скелет) 0–2 Стрела
0–2 Кость (как всадника, так и животного)
1 Череп-скелет , если убит взрывом заряженного крипера Нет Лук
Случайная броня
Резная тыква‌ ^{[ Только для Java Edition ]}
Фонарь Джека‌ ^{[ Только для Java Edition ]} Снаряжение можно зачаровывать (кроме тыквы и тыквы). Жокей состоит из двух мобов, которые двигаются как один. Каждая часть сбрасывает предметы отдельно, когда она побеждена. Да
Слизь 1, 2 или 4 0–2 Комок слизи , если размер = 1 Нет Нет Да
Паук-жокей 5 (паук)
5+ 1–3 при наличии снаряжения (скелет) 0–2 Нить
0–1 Глаз паука , если убит игроком
0–2 Стрела
0–2 Кость
1 Череп скелета , если убит взрывом заряженного крипера (только обычный скелет)
0-1 Стрела медлительности если заблудший Нет Лук
Случайная броня
Резная тыква‌ ^{[ Только для Java Edition ]}
Фонарь Джека‌ ^{[ Только для Java Edition ]} Снаряжение можно зачаровывать (кроме тыквы и тыквы). Жокей состоит из двух мобов, которые двигаются как один. Каждая часть сбрасывает предметы отдельно, когда она побеждена. Да
Векс 5
+ 1–3 при наличии оборудования Нет Нет Железный меч Железный меч можно зачаровать.
Базовый шанс выпадения железного меча равен 0%, но шанс увеличивается на 1% с каждым уровнем чар «Добыча», как обычно. Увеличивает шанс выпадения
Воздаятель 5
+ 1–3 при наличии оборудования 0-1 Изумруд Нет Железный топор
Зловещее знамя если капитан рейда Выпадает добыча только в случае убийства игроком.
Железный топор можно зачаровать.
Зловещее знамя всегда выпадает из воздаятеля, когда он убит, но только если он рейдовый капитан.
В Bedrock Edition поборники появляются из рейдов, могут выпасть:
0-1 Изумруд
И дополнительно дроп зависит от сложности, 65% шанс выпадения на легком и обычном уровне, а 80% шанс выпадения на сложном;
0-1 Изумруд ( ¹⁰ ⁄ ₃₉ шанс)
2-3 Изумруд ( ⁵ ⁄ ₃₉ шанс)
4-5 Изумруд ( ² ⁄ ₃₉ шанс)
1 Зачарованная книга (² ⁄ ₃₉ шанс)
1 железный топор (⁵ ⁄ ₇₈ шанс)
1 железная лопата (⁵ ⁄ ₇₈ шанс)
1 железный меч ( ⁵ ⁄ ₇₈ шанс)
1 железный шлем (⁵ ⁄ ₇₈ шанс)
1 железный нагрудник (⁵ ⁄ ₇₈ шанс)
1 Железные поножи ( ⁵ ⁄ ₇₈ шанс)
1 Железные сапоги ( ⁵ ⁄ ₇₈ шанс)
Железное снаряжение из рейдерского дропа с вероятностью 50% может быть зачаровано случайным зачарованием и всегда сильно повреждено. Мародерство увеличивает количество изумрудов или шанс выпадения снаряжения. Изумруд — это как обычный рейдерский дроп, так и дополнительный. Дополнительные изумруды выпадают только в том случае, если выпадение зачарованной книги или железного снаряжения не удалось. С воздаятеля может выпасть 2 железных топора, один из природного снаряжения и один из дополнительного рейдерского дропа.
Все, включая выпадение рейдеров‌ ^{[ только Bedrock Edition ]}, но не для зловещего баннера
Смотритель 5 1 Катализатор Скалка Нет Нет Нет
Ведьма 5
+ 1–3 при наличии оборудования 0–6 Стеклянная бутылка
0–6 Пыль светящегося камня
0–6 Порох
0–6 Красный камень
0–6 Глаз паука
0–6 Палка
0–6 Сахар
1 Зелье , если выпить после смерти Нет Зелье исцеления
Зелье сопротивления огню
Зелье скорости
Зелье водного дыхания
шанс выпадения у них составляет 8,5%. После смерти ведьмы выпадают 1–3 типа предметов, каждый 0–2 раза. Один и тот же тип можно выбирать несколько раз, поэтому можно получить 6 предметов из одного предмета. Палки выпадают в два раза чаще, чем другие обычные предметы. Зелья можно получить, только убив ведьму, пока она пьет зелье. Да
Увядание 50 1 Звезда Нижнего мира Нет Нет Нет
Скелет-иссушитель 5
+ 1–3 при наличии оборудования 0–1 Уголь
0–2 Bone Wither Skeleton Skull , если убит взрывом заряженного крипера Череп скелета-иссушителя (2,5%) если убит игроком Каменный меч
Резная тыква‌ ^{[ Только для Java Edition ]}
Фонарь Джека‌ ^{[ Только для Java Edition ]} Да
Зоглин 5 1–3 Гнилая плоть Нет Да
Зомби
Зомби Житель
Оболочка 5
+ 1–3 при наличии оборудования
+ 7 если ребенок 0–2 Гнилая плоть
1 голова зомби если убит взрывом заряженного крипера
(только обычные зомби)
2,5% шанс выпадения;
Железный слиток или
Морковь или
Картофель (Печеный картофель, если погибнет от огня) Железная лопата (в Bedrock Edition зомби-житель никогда не появляется с железной лопатой)
Железный меч (в Bedrock Edition зомби-житель никогда не появляется с железным мечом)
Случайная броня (в Bedrock Edition зомби-житель никогда не появляется с доспехами)
Резная тыква‌ ^{[ Только Java Edition ]}
Светильник Джека‌ ^{[ Только Java Edition ]} Снаряжение можно зачаровывать (кроме тыквы и тыквы). Да
Снаряды[]
Сущность Капли Примечания
Чарующая бутылка 3–11 Опыт
Яйцо 0–4 Цыпленок породил Яйца имеют ¹ ⁄ ₈ шанс породить одного цыпленка. Если это произойдет, то есть дополнительная ¹ ⁄ ₃₂ вероятность появления четырех цыплят вместо одного.
Жемчуг Края 0–1 Эндермит Жемчуг Эндера имеет 5% шанс породить эндермита.
Стационарный[]
Объект Капли Примечания
Подставка для брони 0-1 Стойка для брони Выпадает сам, доспехи, которые он носит, и предмет, который он держит. В Bedrock Edition, если он уничтожен огнем, лавой, костром или статусным эффектом «Мгновенное повреждение» или «Иссушение», он не дает предмета для стойки для брони, а любые экипированные предметы считаются «естественно созданным снаряжением» и имеют 8,5% шанс выпадения. экипированный предмет является оружием, инструментом или доспехом, он сильно поврежден. ^[2]
Крайний кристалл Нет Создает взрыв при разрушении, на 50% мощнее тротила.
Рамка элемента
‌ ^{[ Только Java Edition ]} 1 шт. Рамка Выпадает сам и содержащийся в нем предмет.
Светящаяся рамка
‌ ^{[ только Java Edition ]} 1 Светящаяся рамка для предмета Выпадает сам и содержащийся в нем предмет.
Окраска 1 Картина
Транспортные средства[]
Организация Капли Примечания
Лодка 1 Лодка соответствующего типа
Лодка с сундуком (1 Лодка соответствующего типа
1 Сундук‌ ^{[ BE только ]})
1 Лодка соответствующего типа‌ ^{[ JE только ]} Также выпадает все содержимое сундука.
Вагонетка 1 вагонетка
Вагонетка с сундуком 1 Вагонетка с сундуком Также выпадает все содержимое сундука.
Вагонетка с командным блоком 1 вагонетка
Вагонетка с печью
‌ ^{[ только Java Edition ]} 1 Вагонетка с печью
Вагонетка с бункером 1 Вагонетка с бункером Также сбрасывает все свое содержимое.
Вагонетка с генератором
‌ ^{[ Только Java Edition ]} 1 вагонетка
Вагонетка с тротилом 1 Вагонетка с тротилом Ничего не выпадает при активации или уничтожении взрывом.
Выпадение блоков[]
В этом разделе отсутствует информация о некоторых блоках.
Пожалуйста, разверните раздел, чтобы включить эту информацию. Более подробная информация может существовать на странице обсуждения.
Большинство блоков падают при разрушении. Все особые дропа из блоков перечислены ниже. В столбце «Доступно с помощью Шелкового прикосновения» указано, можно ли собрать блок с помощью чар «Шелковое прикосновение». См. Silk Touch # Список блоков, доступных с помощью Silk Touch для получения дополнительной информации.
Материалы и строительные блоки[]
Блок опыт Обычные капли Можно получить с помощью Шелкового прикосновения Под влиянием чар удачи Примечания
Бутон аметиста — Нет Да Нет
Гроздь аметиста — 4 Осколок аметиста с киркой
2 Осколок аметиста с ручным или другим инструментом
Да Да
Книжная полка — 3 Книга Да Нет
Расцветающий аметист — Нет Нет Нет
Костер — 2 Древесный уголь Да Нет Также бросайте еду на костер
Свеча — 1-4 свечи Нет Нет 1 свеча на свечу
Глина — 4 Глина Да Нет
Паутина — 1 Нить, если ее сломать мечом,
Сам, если сломать ножницами
Частично Нет
Компостер — 1 компостер +
1 костная мука, если уровень = 8 компостер Нет Нет
Deepslate ^T — 1 Мощеный сланец Да Нет
Двойная плита ^T ^{[примечание 1]} — 2 Плита Нет Нет
Сельхозугодья — 1 Грязь Нет Нет
Стекло — Нет Да Н/Д
Стекло — Нет Да Н/Д
Светящийся камень — 2–4 Пыль светящегося камня Да Да, максимум 4
Куст травы
Мицелий
Подзол — 1 Грязь Да Нет
Грунтовая дорога — 1 Грязь Нет Нет
Да‌ ^{[ только Bedrock Edition ]} Нет
Гравий — 1 Гравий или 1 Кремень Да Увеличивает шанс выпадения кремня вместо гравия. Кремень выпадает с шансом 10% без учета удачи.
Зачарование "Удача" увеличивает этот шанс до 14% при удаче I, 25% при удаче II и 100% при удаче III.
Используя Silk Touch, вы получаете 100% выпадения гравия.
Пчелиное гнездо — 0-3 Пчела Да Н/Д
Улей — 1 улей + 0-3 пчелы Да Н/Д
Нилиум ^Т — 1 Скважина Пустоты Да Нет
Лед — Нет Да Н/Д Если непосредственно под ледяным блоком находится другой блок (твердый или жидкий), лед при разрушении превращается в воду. Это не работает в Нижнем мире.
Упакованный лед
Синий лед — Нет Да Н/Д
Морозный лед — Нет Нет Н/Д Если непосредственно под ледяным блоком находится другой блок (твердый или жидкий), лед при разрушении превращается в воду. Это не работает в Нижнем мире.
Усиленный сланец — Нет Нет Нет
Череп 1 Нет Да Нет
Катализатор Скалка 5 Нет Да Нет
Скулк Визгун 5 Нет Нет Нет
Сенсор скрытности 5 Нет Да Нет
Скулк Вейн — Нет Да Нет Использование инструментов шелкового прикосновения на вене черепа даст по вене черепа с каждой стороны ^{[примечание 2]}
Морской фонарь — 2-3 кристалла призмарина Да Да Зачарование Fortune увеличивает максимум на 1 за уровень до максимума 5, а Fortune III увеличивает шанс выпадения большего количества.
Снежная глыба ^T — 4 Снежок Да Нет
Снег ^Т — 1–8 Снежок Да Нет 1 Snowball на каждый слой без Silk Touch.
1 Снег на слои в слоях 1-7 с Silk Touch.
1 Снежный блок в 8 слоях с технологией Silk Touch.
Костер души — 1 Почва души Да Нет Также бросайте еду на костер
Камень ^Т — 1 Булыжник Да Нет
Руды[]
Блок опыт Обычные капли Можно получить с помощью Silk
Touch Под влиянием чар удачи Примечания
Угольная руда ^T 0–2 1 Уголь Да Да
Медная руда ^T — 2-5 Необработанная медь Да Да
Алмазная руда ^Т 3–7 1 бриллиант Да Да
Изумрудная руда ^T 3–7 1 Изумруд Да Да
Железная руда ^Т — 1 Сырое железо Да Да
Позолоченный черный камень ^T — 1 Позолоченный черный камень или 2-5 Золотой самородок Да Увеличивает шанс выпадения золотого самородка Золотой самородок выпадает с шансом 10% без учета удачи.
Чары Fortune увеличивают этот шанс до 14,29% для Fortune I, 25% для Fortune II и 100% для Fortune III.
Использование Silk Touch дает 100% шанс выпадения позолоченного черного камня.
Золотая руда ^T — 1 Сырое золото Да Да
Лазуритовая руда ^T 2–5 4–8 Лазурит Да Да
Кварцевая руда Нижнего мира ^T 2–5 1 кварц Нижнего мира Да Да
Золотая руда Пустоты ^T — 2-6 Золотой самородок Да Да
Руда красного камня ^T 1–5 4–5 Красная пыль Да Да
Растения[]
Блок опыт Обычные капли Можно получить с помощью Шелкового прикосновения Под влиянием чар удачи Примечания
Свекла — 1 Семена свеклы если преждевременные
0–3 Семена свеклы , если полностью созрели
1 Свекла , если полностью созрели Нет Влияет на семена, только если они полностью выращены
Морковь — 1 морковь если недоношенная
1–4 моркови если полностью созрела Нет Действует, только если полностью вырос
Пещерные лозы — 1 Светящиеся ягоды, если есть ягоды Да‌ ^{[ только Bedrock Edition ]} Нет Также нажмите на пещерные лозы или урожай лисы, чтобы получить такое же количество.
В Bedrock Edition использование инструмента с шелковым касанием на пещерных лозах всегда дает светящуюся ягоду, даже если лоза выглядит пустой.
Завод Хоруса — 0–1 Фрукт хоруса Нет Нет
Какао — 1 Какао-бобы если недоношенные
3 какао-боба если полностью выращенные Нет Нет
Коралл — Нет Да Нет Падает сам, если его сломать ножницами.
Коралловые блоки — 1 Мертвые коралловые блоки Да Нет
Коралловые вентиляторы — Нет Да Нет Падает сам, если его сломать ножницами.
Мертвый куст — 0-2 Палка Нет Нет Оригинальный блок выпадает при разрушении ножницами.
Мертвый коралл — Нет Да Нет Падает сам, если его сломать ножницами.
Мертвые коралловые веера — Нет Да Нет Падает сам, если его сломать ножницами.
Светящийся лишайник — 0–6 Светящийся лишайник, если его сломать ножницами ^{[примечание 3]} Нет Нет 1 светящийся лишайник с каждой стороны
Трава
Высокая трава
Папоротник
Большой папоротник — 0–1 семена Нет Да Вместо этого при разрушении с помощью ножниц выпадает оригинальный блок.
Семена выпадают с вероятностью 12,5%.
Удача увеличивает падение на 2 за уровень.
Грибные блоки — 0–2 Гриб Частично Нет Вероятность того, что не выпадет ни один гриб, составляет 80%, а вероятность выпадения одного и двух грибов составляет 10%. В среднем это дает 0,3 гриба на блок.
Silk Touch выбрасывает блок со всеми сторонами, имеющими стандартную грибовидную поверхность, красную с пятнами или коричневую.
Стебель гриба — Нет Частично Нет Silk Touch роняет блок со всеми сторонами, имеющими стандартную поверхность грибовидного стебля.
Листья — 0–1 Саженец
0–1 Азалия
0–2 Палочка
0–1 Яблоня из дуба и темных дубовых листьев Да Да При разрушении с помощью ножниц исходный блок падает вместе с обычным падением. 907:40 Саженец джунглей выпадает с шансом 2,5%; все остальные саженцы и азалии выпадают с шансом 5%.
Яблоко выпадает с вероятностью 0,5%.
Дыня — 9 Дыня при поломке ножницами ‌ ^{[ Только Bedrock Edition ]}
3–7 Дыня иначе Да Да, максимум 9
Стебель дыни — 0–3 Семена дыни Нет Нет Каждое из трех возможных семян выпадает с шансом, зависящим от стадии роста, от 7% (только что посаженные) до 53% (полностью выросшие).
Адский нарост — 1 адский нарост , если недоношенный
3 адский нарост , если полностью вырос Нет Действует, только если полностью вырос
Картофель — 1 Картофель если недоношенный
1–4 Картофель если полностью выращенный
0–1 Ядовитый картофель если полностью выращенный Нет Действует, только если полностью вырос
Ядовитый картофель выпадает с шансом 2%.
Стебель тыквы — 0–3 тыквенных семечка Нет Да Каждое из трех возможных семян выпадает с шансом, зависящим от стадии роста, от 7% (только что посаженные) до 53% (полностью выросшие).
Морской огурец — 1-4 Морской огурец Нет Нет 1 морской огурец на огурец
Сладкие ягоды — 1-2 сладких ягоды, если вырастет третья
1-3 сладких ягоды, если вырастет полностью Нет Действует, только если третий или полностью вырос Также нажмите на урожай сладкой ягоды или лисы, чтобы получить такое же количество.
Каждый уровень Fortune может увеличить количество выпадающих предметов на 1.
Виноградная лоза — 1 Лозы, сломанные ножницами ^{[примечание 4]} Нет Нет
Вьющиеся лозы — 0-1 Вьющиеся лозы Да Увеличивает шанс выпадения Вьющихся лоз Вьющиеся лозы выпадают с шансом 33% без удачи.
Чары Fortune увеличивают шанс до 55% для Fortune I, 77% для Fortune II и 100% для Fortune III.
Разрушение с помощью Silk Touch или ножниц дает 100% шанс выпадения.
Плачущие лозы — 0-1 Плачущие лозы Да Увеличивает шанс выпадения плачущих лоз Плачущие лозы выпадают с шансом 33% без удачи.
Чары Fortune увеличивают шанс до 55% для Fortune I, 77% для Fortune II и 100% для Fortune III.
Разбивание с помощью Silk Touch или ножниц дает 100% шанс выпадения.
Пшеница — 1 Семена если преждевременные
0–4 Семена если полностью созрели
1 Пшеница если полностью созрели Нет Влияет на семена, только если они полностью выращены
Другое[]
Блок опыт Обычные капли Можно получить с помощью Шелкового прикосновения Под влиянием чар удачи Примечания
Торт — Нет Нет Нет
Торт со свечами — 1 свеча Нет Нет
Сундук Края ^T — 8 Обсидиан Да Нет Не роняет содержимое при поломке.
Огонь
Огонь Души — Нет Нет Н/Д
Зараженные блоки — 1 Серебряная рыбка Частично Нет Когда зараженный блок уничтожается инструментом с зачарованием «Шелковое касание», из него выпадает тип блока, под которым замаскирован зараженный блок (например, камень, булыжник, каменный кирпич. ..), и чешуйницы не появляются.
Перевернутый датчик дневного света — 1 Датчик дневного света Нет Нет
Снежный порошок — Нет Нет Нет Можно наполнить только ведром
Спаунер ^Т 15–43 Нет Нет Н/Д
Яйцо черепахи — Нет Да Н/Д
↑ Из двойных деревянных плит выпадает 2 деревянные плиты при добыче вручную или другими инструментами, кроме кирки.
↑ С помощью командного или отладочного джойстика можно получить вену без боковых сторон, она не роняет ничего, даже сломанного инструментами шелкового прикосновения.
↑ С помощью командной или отладочной палочки можно получить светящийся лишайник без боковых сторон, из него ничего не падает, даже сломанного ножницами.
↑ Из лозы всегда падает 1 лоза, если ее сломать ножницами, даже если сломать лозу, не имеющую боковых сторон, или 5 боковых лоз.
Примечания:
Блоки, отмеченные буквой «Т», нужно разбивать специальным инструментом, чтобы выпало что-либо (включая опыт). Зачарование Шелковое прикосновение не снимает этого требования.
Если указано, Fortune может увеличить количество выпадающих предметов или умножить его. Повышение просто дает дополнительные предметы 0-lvl. Умножение происходит со следующими шансами: Fortune I: 33% * 2 (в среднем на 33% больше) Fortune II: 25% * 2, 25% * 3 (в среднем на 75% больше) Fortune III: 20% * 2, 20% * 3, 20% * 4 (в среднем на 120% больше)
Контейнерные блоки (доменные печи, варочные стенды, сундуки, диспенсеры, капельницы, цветочные горшки, печи, светящиеся рамки‌ ^{[ BE только ]}, бункеры, рамы предметов‌ ^{[ BE только ]}, музыкальные автоматы, коптильни и сундуки-ловушки) выпадают при разрушении вместе с содержимым.
Все блоки, не указанные в таблице выше, падают при разрушении. Фортуна не влияет на их падение.
Видео[]
История[] 9047. Java Edition Classic 0.25 ТЕСТ НА ВЫЖИВАНИЕ Свиньи падают грибы При убийстве скелетов падают стрелы. 25 октября 2009 г. Показана овца, из которой выпадает красная ткань и грибы. Java Edition Indev 20 Овцы ничего не роняют. Свиньи бросают свиные отбивные вместо грибов. Криперс сбрасывает порох. Веревка с пауками. Из зомби выпадают перья. Java Edition Alpha v1.1.0 Овцы теперь падают между 1–3, вместо того, чтобы всегда падать 2. Java Edition Beta Java Edition Beta Java Edition Beta . Новые серые, светло-серые и черные овцы. Бросьте шерсть соответствующего цвета. Добавлен кальмар, из которого выпадает новый чернильный мешок. 1.5 Свиньи, которые умирают от сжигания, теперь после смерти дают приготовленные свиные отбивные. 1.7 Из овец больше не выпадает шерсть при ударе. Овец теперь нужно стричь ножницами или убивать, чтобы получить шерсть. 1.8 Пре-релиз Из зомби вместо перьев выпадает гнилая плоть. Из мобов, убитых игроками, выпадают крошечные мигающие сферы опыта, которые увеличивают вашу шкалу опыта. Добавлены жемчужины Края вместе с людьми Края. Java Edition 1.0.0 Beta 1.9 Prerelease Огненные стержни добавлены в качестве добычи из пламени. Добавлены слезы гаста, которые выпадают из гаста. Золотые самородки добавлены в качестве дропа с зомби-свинолюдей. Добавлены снежные големы, из которых выпадают снежки. Beta 1.9 Prerelease 2 Теперь из пауков выпадают паучьи глаза. Beta 1.9 Prerelease 4 Добавлены чары Looting, Fortune и Silk Touch, увеличивающие количество выпадающих при убийстве мобов, разрушении блоков или выпадении самого блока соответственно. 1.1 11w50a Все музыкальные диски, кроме 11 , можно получить, если скелет убьет крипера. До этого было просто 13 и кат . выпуск Кубы магмы теперь могут оставлять сливки магмы при смерти. 1.2.1 12w06a Зомби имеют редкий шанс выбросить железный слиток, железный шлем, железную лопату или железный меч. Из скелетов с редкой вероятностью выпадает лук, который можно зачаровать. Зомби-свинолюди имеют редкий шанс получить золотой шлем, золотой слиток или золотой меч, который можно зачаровать. 12w08a Добавлены железные големы, из которых выпадают железные слитки и розы. 1.3.1 12w25a Из свиней теперь выпадает 1–3 свиных отбивных вместо 0–2. 1.4.2 12w32a Новая команда /gamerule doMobLoot [<значение>] переключает, сбрасывают ли мобы добычу. Зомби, скелеты и зомби-свинолюди иногда могут носить броню, которая имеет редкий шанс выпадения. 12w34a Из зомби может выпасть морковь и картофель. 12w36a Иссушитель роняет звезду Нижнего мира после смерти. Добавлены скелеты-иссушители, из которых выпадают кости, уголь и редко каменные мечи, а также черепа-иссушители, когда их убивают игроки. Оседланные свиньи теперь всегда роняют седла при смерти. 12w38a Добавлены ведьмы, из которых редко выпадают зелья мгновенного здоровья и сопротивления огню. 12w38b Ведьмы теперь могут сбрасывать ингредиенты для зелий, палочки и иметь шанс сбросить то, что они держат в момент смерти. 1.4.4 1.4.3-pre Музыкальный диск 11 теперь выпадает Creepers так же, как и другие диски. 1.8 14w04a Зачарование «Добыча» теперь увеличивает шанс выпадения редких предметов на 1% за уровень вместо 0,5%. 14w25a Добавлены стражи и старшие стражи, из которых выпадают осколки призмарина и кристаллы призмарина, а также редко выпадают рыба и мокрые губки. 14w27a Добавлены кролики, из которых может выпасть кроличья шкура, сырой кролик (приготовленный кролик на огне) и редко кроличьи лапки. Из овец теперь выпадает сырая баранина при смерти (приготовленная баранина, если горит) вместе с шерстью. 1.9 15w47a Шалкеры теперь дают опыт. 1.10 16w20a Добавлены белые медведи, из которых выпадает сырая рыба и сырой лосось. Добавлены бродяги. В дополнение к обычным дропам со скелетами, из бродяг с вероятностью 50% выпадает стрела Медлительности с наконечником. 1.11 16w39a Добавлены ламы, из которых выпадает кожа и все, что они экипировали. Добавлены поборники, из которых редко выпадают изумруды, а иногда и их железный топор. Добавлены эвокеры, из которых всегда выпадает тотем бессмертия и редко изумруды. Добавлены досадники, у которых есть небольшой шанс выпадения своего железного меча, если игрок использует зачарование "Мародёрство". 1.12 17w13a Добавлены попугаи, из которых выпадает 1 или 2 пера. 17w16a Добавлен иллюзор, у которого есть небольшой шанс выпадения лука. 1,13 18w07a Добавлены черепахи, с которых после смерти сбрасывается водоросль, а также сбрасывается щиток, когда ребенок становится взрослым. Добавлены фантомы, из которых после смерти выпадает кожа. 18w08b Добавлено 4 рыбных моба: треска, лосось, рыба-фугу и тропическая рыба. После смерти из них выпадает сырая треска, сырой лосось, рыба-фугу и тропическая рыба соответственно. 18w14a Фантомы теперь могут сбрасывать фантомную мембрану после смерти и больше не сбрасывают кожу. 18w15a Добавлены дельфины, из которых после смерти может выпасть сырая треска. 1. 14 18w43a Добавлены панды, из которых после смерти выпадает бамбук. Добавлены грабители, из которых после смерти выпадают арбалеты и изумруды. Добавлены опустошители, из которых после смерти выпадает седло. Из криперов теперь выпадают музыкальные диски, когда их убивают бродяги. 18w46a Из грабителей больше не выпадают изумруды. 19w05a Добавлены бродячие торговцы, у которых есть шанс выронить ведро с молоком или зелье невидимости, если их убить во время удержания или до того, как выпили. 1.16 20w06a Добавлены хоглины, из которых после смерти выпадает гнилая плоть. 20w07a Хоглины теперь после смерти падают с сырой свинины и кожи. Добавлены пиглины, из которых после смерти может выпасть естественно появляющееся снаряжение, включая золотой меч, арбалет и случайную золотую броню. 20w13a Добавлены страйдеры, из которых выпадает веревка после смерти. 1.16.2 20w27a Добавлены громилы-свиньи, из которых после смерти может выпасть золотой топор. 1.17 21w03a Добавлены светящиеся кальмары, из которых после смерти выпадают мешочки со светящимися чернилами. 21w05a Из утопленников теперь выпадают медные слитки вместо золотых. 21w13a Добавлены козлы, с которых ничего не падает. Зомби теперь бросают печеный картофель, когда горят. 1. 19 Deep Dark Experimental Snapshot 1 Добавлены надзиратели, из которых ничего не выпадает. 22w11a Удалены надзиратели. Магматические кубы теперь оставляют лягушачьи фонари, если их убивает лягушка. 22w12a Передобавлены надзиратели, все равно ничего не падает. 22w17a Стражи теперь сбрасывают катализаторы скрытности после смерти. Из коз теперь выпадают козлиные рога, если они врезаются в угольную руду, изумрудную руду, железную руду, бревна, уплотненный лед или камень. Предварительная версия 2 Рога козла теперь выпадают, когда козы врезаются в медную руду. Сообщайте о проблемах там. См. также[] Предмет (сущность) Добыча из сундука Геймплей Посмотреть по адресу: Template:Gameplay/content [edit] ↑ https://bugs. mojang.com/browse/MCPE-80504 ↑ MCPE-24341 Высота падения | Вероятностные планы: литература и прогнозная обработка Фильтр поиска панели навигации Oxford Academic Вероятностные расчеты: литература и прогнозная обработкаТеория литературы и культурологияКнигиЖурналы Термин поиска мобильного микросайта Закрыть Фильтр поиска панели навигации Oxford Academic Вероятностные расчеты: литература и прогнозная обработкаТеория литературы и культурологияКнигиЖурналы Термин поиска на микросайте Расширенный поиск Иконка Цитировать Цитировать Разрешения Делиться Твиттер Подробнее Cite Кукконен, Карин, 'Высота падения' , Дизайн вероятности: литература и прогнозная обработка , познание и поэтика ( New York, 2020; Online Edn, Oxford Academan , 1 онлайн Edn, Oxford Academic , 1 . декабрь 2019 г. ), https://doi.org/10.1093/oso/ 955.003.0004, , по состоянию на 20 сентября 2022 г. Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks) Закрыть Фильтр поиска панели навигации Oxford Academic Вероятностные расчеты: литература и прогнозная обработкаТеория литературы и культурологияКнигиЖурналы Термин поиска мобильного микросайта Закрыть Фильтр поиска панели навигации Oxford Academic Вероятностные расчеты: литература и прогнозная обработкаТеория литературы и культурологияКнигиЖурналы Термин поиска на микросайте Advanced Search Abstract В этой главе подробно описывается, как вероятностные схемы создают восприятие совпадения и неожиданности, создавая «высоту падения» перед сюжетными событиями. Он более подробно исследует роль читателя. Восприятие вероятности того или иного предсказания манипулируется с помощью ряда текстовых приемов, которые обсуждаются на примере сцены Джейн Остин в Пемберли в «Гордость и предубеждение» . Утверждается, что эти манипуляции с точностью (то есть предполагаемой надежностью ошибок предсказания) также способствуют формированию у читателей (иллюзорного) чувства свободы действий и их исследовательским умственным движениям. Пока читатели следуют вероятностному плану, они активно настраивают предсказания повествования, связанные с такими явлениями, как аномальное напряжение и парадокс трагедии. Ключевые слова: неожиданность, предсказательная обработка, точность, аномальная неопределенность, нарративное совпадение Предмет Теория литературы и культурология В настоящее время у вас нет доступа к этой главе. Войти Получить помощь с доступом Получить помощь с доступом Доступ для учреждений Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов: Доступ на основе IP Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией. Войдите через свое учреждение Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic. Нажмите Войти через свое учреждение. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа. Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic. После успешного входа вы вернетесь в Oxford Academic. Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору. Войти с помощью читательского билета Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю. Члены общества Доступ члена общества к журналу достигается одним из следующих способов: Войти через сайт сообщества Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале: Щелкните Войти через сайт сообщества. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic. После успешного входа вы вернетесь в Oxford Academic. Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество. Вход через личный кабинет Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже. Личный кабинет Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок. Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Просмотр учетных записей, вошедших в систему Щелкните значок учетной записи в правом верхнем углу, чтобы: Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью. Просмотр институциональных учетных записей, предоставляющих доступ. Выполнен вход, но нет доступа к содержимому Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю. Ведение счетов организаций Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д. Покупка Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях. Информация о закупках Что такое вероятность выпадения? [Решено] (2022) Просто , разделив количество успешных сбросов на количество сбросов , вы получите пропорцию. Например, 20 успешных выпадений из 100 — это 20% шанс получить успешный дроп. Это примерная пропорция.... читать дальше › Шанс выпадения может означать: Шанс выпадения (видеоигры), Вероятность получения случайного предмета . Packet drop rate, скорость, с которой пакеты теряются в сетевом соединении.... читать дальше › Если вы надеетесь получить редкого маунта Поводья коня смерти, например, у барона Ривендера, мы знаем, что шанс его выпадения составляет 1%. Это означает, что каждый раз, когда вы убиваете Черного барона, у вас есть 1% шанс получить маунта . 1% за первое убийство и 1% за 100-е убийство.... подробнее › Кольцо Элдена — получить редкие предметы ЛЕГЧЕ! Увеличение шанса выпадения. .. - YouTube... подробнее › Mathematical relations odds (ratio) 1:0 ∞ 100% 2:1 2 67% 1:2 0.5 33% 4:1 4 80% 8 больше строк 903s › Из боссов будут выпадать специальные предметы в два раза чаще !... подробнее › Swords Drops Акула Пила. Акулья пила — это редкий меч, выпадающий из рейдового босса 100 уровня, Пила, с шансом выпадения ~ 10%. ... Трезубец. Трезубец — это редкий меч, выпадающий из Босса-Лорда-Рыбака. ... Сабля V1. Сэйбер — легендарный меч, выпадающий из Мастера сабли. ... Полюс 1 кл. ... Бизенто V2. ... Длинный меч. ... Гравитационная трость. ... Джитте. Еще товары... ... продолжить чтение › Вероятность выпадения увеличивает шанс получения трофеев в режиме приключений. Шанс выпадения работает следующим образом: у каждого дропа есть определенный шанс выпадения (помимо того, что вам нужно убить что-то, из чего он выпадает, конечно) . Шанс выпадения только увеличивает этот шанс.... читать дальше › Bestiary Mob Drop Chances Odds Drop Chance Uncommon Loot 1. 01%-30% Rare Loot 0.11%-1% Legendary Loot 0,02%-0,1% RNGesus Loot <= 0,01% еще 1 ряд ... подробнее › Максимальное количество открытий, которое вы можете получить, составляет 199, если ваш Аркан равен 99 . Это идеальная ситуация, но это верно для билдов с Арканом, поскольку они полагаются на Аркан. Если вы не можете инвестировать в Arcane, не беспокойтесь, есть и другие способы увеличить шанс выпадения предметов в Elden Ring.... посмотреть подробности › Чтобы повысить скорость обнаружения предметов в Elden Ring, используйте маски и талисманы, которые ускоряют обнаружение предметов, и инвестируйте в Arcane . Примеры предметов, улучшающих обнаружение предметов, включают: Серебряную слезоточивую маску, Серебряный скарабей, Серебряную птичью лапку, Маску Марэ, Корону из блестящего камня ведьмы, Маску уверенности или Маску альбинавра.... подробнее › Дискавери — базовая характеристика в Elden Ring. ... Discovery Тип Базовые статистики Эффект Определение. Как часто дефект .0003 ... читать дальше › Подумайте о ярмарке обычных игральных костей. Чтобы найти вероятность выпадения 4, возьмите количество возможных способов выпадения 4 и разделите его на общее количество возможных исходов . Существует один способ выпадения 4 и шесть возможных исходов, поэтому вероятность выпадения 4 на кубике равна .... подробнее › Диаграмма дерева вероятностей — это удобный визуальный инструмент, который можно использовать для расчета вероятностей как зависимых, так и независимых событий. Чтобы рассчитать вероятность исходов, умножьте значения вероятности связанных ветвей . Чтобы вычислить вероятность нескольких исходов, сложите вероятности вместе.... подробнее › Информация о статье Автор: Тиш Хааг Последнее обновление: 29.09.2022 Просмотров: 6456 Рейтинг: 4.7 / 5 (67 проголосовало) Отзывы: 90% читателей считают эту страницу полезной. 4215847628708 Профессия: Инженер-консультант Хобби: катание на роликах, катание на роликах, каякинг, полеты, граффити, охота за привидениями, альбом для вырезок Введение: Меня зовут Тиш Хааг, я взволнованный, восхитительный, любопытный, красивый, приятный , очаровательный, модный человек, который любит писать и хочет поделиться своими знаниями и пониманием с вами. Mario Kart 8 распределений вероятностей предметов Взято из Super Mario Wiki, энциклопедии Mario Перейти к навигацииПерейти к поиску Следующие дистрибутивы используются версией 4.1 Mario Kart 8 для определения вероятности получения определенного предмета при открытии ящика с предметами. ^[1] Таблицы имеют ту же структуру, что и в Mario Kart 7 , с одинаковым номером столбца каждого элемента для предметов, представленных в обеих играх, и вероятностью, закодированной как процент, умноженный на два. Содержание 1 Экран заголовка ( ST ) 2 расы ( S2 ) 2.1 Гонки Гран-при 2.2 Противостояние гонок 2.2.1 Все позиции 2.2.2 Только грибы 2.2.3 Только корпуса 2.2.4 Только бананы 2. 2.5 Только боб-омбы 2.2.6 Дополнительные комплекты 2.2.7 Безумный режим 3 Специальное назначение ( S3 ) 4 Боевой режим ( S4 ) 4.1 Все позиции 4.2 Только грибы 4.3 Только корпуса 4.4 Только бананы Только боб-омбы 4,5 4.6 Дополнительные комплекты 4.7 Безумный режим 5 См. также 6 Каталожные номера Титульный экран ( ST ) Эти распределения вероятности элементов используются в демонстрации игрового процесса, которые показаны на титульном экране. Хотя для них определено 20 наборов, фактически только второй, третий и четвертый содержат хотя бы значение вероятности, отличное от нуля. Распределения вероятностей элементов (титульный экран, второй набор) Распределение 1 100 60 10 30 2 40 50 70 20 10 10 3 30 50 50 20 20 10 20 4 30 50 30 40 10 20 20 5 30 40 10 60 30 20 10 6 30 40 70 40 10 10 7 30 40 70 50 10 8 30 30 80 60 9 30 30 80 60 10 30 20 80 70 11 30 20 70 80 12 30 20 60 90 Распределения вероятностей элементов (титульный экран, третий и четвертый наборы) Распределение 1 200 2 200 3 200 4 200 5 200 6 200 7 200 8 200 9 200 10 200 11 200 12 200 Гонки ( S2 ) Во время гонок каждое распределение вероятности выбирается в зависимости от расстояния до лидера в момент открытия ящика с предметами. Сообщаемое расстояние — это расстояние, на котором происходит переключение на следующее распределение. В гонках Versus есть пять дополнительных наборов раздач, все раздачи которых сделаны для получения определенного предмета и цель которых неясна. Большинство из них сообщается без расстояния, так как не установлено, используются ли они драйверами, управляемыми игроками, или программным обеспечением. Гонки Гран-при 9 Распределения вероятностей элементов (гонки Гран-при, водители, управляемые игроками) Расстояние (ед.) 400 65 50 5 5 5 70 1000 20 25 50 20 10 10 10 5 5 15 15 10 5 2000 10 20 30 25 15 15 10 15 5 10 5 10 10 15 5 3300 15 20 50 5 5 60 5 5 10 10 10 5 5500 10 30 5 5 85 25 10 25 5 8000 10 5 65 40 30 5 40 5 13000 5 35 35 60 10 55 26000 10 30 85 15 60 9 30 40 70 60 30 40 70 60 9 Распределение вероятностей элементов (гонки Гран-при, драйверы, управляемые программным обеспечением) Расстояние (ед. ) 300 50 40 15 10 5 70 10 700 25 30 60 15 5 5 10 5 5 20 10 10 1300 30 35 30 25 10 10 10 5 10 15 10 10 2600 30 35 15 45 10 5 25 5 5 5 5 15 4500 30 35 5 50 5 3 47 10 10 5 7000 15 20 50 4 58 20 10 3 20 13000 10 10 30 57 30 30 3 30 26000 10 10 10 42 30 55 3 40 9 30 60 30 50 30 30 60 30 50 30 Versus Races Все предметы 9 Распределение вероятностей предметов (Versus Races, Все предметы, водители, управляемые игроками) Расстояние (ед. ) 400 60 50 5 5 80 1000 15 25 45 20 10 5 10 10 10 5 20 10 10 5 2000 5 15 35 30 10 25 10 15 5 10 5 10 10 10 5 3300 15 18 50 5 2 65 10 5 5 10 10 5 5500 25 10 5 85 33 10 2 25 5 8000 10 5 65 40 30 5 40 5 13000 2 40 30 65 8 55 26000 20 25 90 10 55 9 40 30 70 60 40 30 70 60 9 Распределение вероятностей элементов (Versus Races, Все элементы, драйверы, управляемые программным обеспечением) Расстояние (ед. ) 300 60 45 15 5 75 700 30 35 55 10 5 5 10 10 5 20 10 5 1300 30 35 30 20 15 10 10 5 5 10 10 10 10 2600 30 40 15 40 10 10 20 5 5 5 5 15 4500 30 40 50 10 5 40 10 10 5 7000 15 30 55 5 40 20 10 5 20 13000 10 10 40 45 30 30 5 30 26000 10 10 20 30 30 55 5 40 9 30 60 30 50 30 30 60 30 50 30 Только грибы 9 Распределение вероятности предметов (гонки против, только грибы, водители, управляемые игроками) Расстояние (ед. ) 400 100 100 1000 100 50 50 2000 100 85 15 3300 70 130 5500 30 130 40 8000 120 80 13000 80 120 26000 40 160 9 100 100 100 100 9 Распределение вероятностей элементов (против рас, только грибы, драйверы, управляемые программным обеспечением) Расстояние (ед. ) 300 120 80 700 120 40 40 1300 110 80 10 2600 110 90 4500 90 80 30 7000 70 70 60 13000 50 60 90 26000 50 60 90 9 50 110 40 50 110 40 Только снаряды 9 Распределение вероятности предметов (против рас, только снаряды, водители, управляемые игроками) Расстояние (ед. ) 400 100 100 1000 90 30 40 30 10 2000 60 60 10 40 30 3300 40 65 5 50 40 5500 20 70 10 50 50 8000 60 10 50 80 13000 50 10 50 90 26000 50 10 50 90 9 200 200 9 Распределение вероятности предметов (Versus Races, Только снаряды, драйверы, управляемые программным обеспечением) Расстояние (ед. ) 300 120 80 700 90 50 40 20 1300 80 70 10 40 2600 70 65 5 60 4500 60 55 5 80 7000 45 50 5 100 13000 35 40 5 120 26000 25 30 5 140 9 200 200 Только бананы 9 Распределение вероятности предметов (гонки против, только бананы, водители, управляемые игроками) Расстояние (ед. ) 400 100 100 1000 115 50 35 2000 120 15 65 3300 110 90 5500 80 120 8000 50 150 13000 20 180 26000 20 180 9 200 200 9 Распределение вероятностей элементов (гонки против, только бананы, драйверы управляются программным обеспечением) Расстояние (ед. ) 300 120 80 700 130 40 30 1300 140 10 50 2600 130 70 4500 110 90 7000 90 110 13000 70 130 26000 70 130 9 200 200 Только боб-омбы 9 Распределение вероятности предметов (гонки против, только боб-омбы, водители контролируются игроками) Расстояние (ед. ) 400 100 100 1000 130 70 2000 160 40 3300 180 20 5500 190 10 8000 200 13000 200 26000 200 9 200 200 9 Распределение вероятностей элементов (только гонки против боб-омбов, драйверы управляются программным обеспечением) Расстояние (ед. ) 300 120 80 700 150 50 1300 170 30 2600 190 10 4500 190 10 7000 200 13000 200 26000 200 9 200 200 Дополнительные наборы 9 Распределения вероятностей предметов (гонки Versus, дополнительные распределения только грибов, водители, управляемые игроками) Расстояние (ед. ) 400 200 1000 200 2000 200 3300 200 5500 200 8000 200 13000 200 26000 200 9 200 200 9 Распределения вероятностей предметов (Расы Versus, дополнительные распределения Mushrooms Only, драйверы, управляемые программным обеспечением) Расстояние (ед. ) 300 200 700 200 1300 200 2600 200 4500 200 7000 200 13000 200 26000 200 9 200 200 Распределения вероятности предмета (расы Versus, дополнительные распределения только снарядов) Распределение 1 200 2 200 3 200 4 200 5 200 6 200 7 200 8 200 9 200 10 200 Распределения вероятностей предметов (Расы против, дополнительные распределения Только бананы) Распределение 1 200 2 200 3 200 4 200 5 200 6 200 7 200 8 200 9 200 10 200 Распределения вероятностей предметов (распределения Versus Races, дополнительные распределения Bob-ombs Only) Распределение 1 200 2 200 3 200 4 200 5 200 6 200 7 200 8 200 9 200 10 200 Распределения вероятностей предметов (Расы Versus, второй набор дополнительных распределений Только грибы) Распределение 1 200 2 200 3 200 4 200 5 200 6 200 7 200 8 200 9 200 10 200 Безумный режим 9 Распределение вероятности предметов (Противостояние гонок, Безумный режим, водители, управляемые игроками) Расстояние (ед. ) 400 30 25 10 25 10 45 30 25 1000 5 5 30 20 15 10 15 15 15 15 5 20 20 10 2000 10 10 15 5 5 25 15 15 20 15 15 10 15 20 5 3300 5 10 10 45 40 15 20 5 5 5 5 10 15 10 5500 10 45 55 30 5 40 10 5 8000 5 35 55 45 5 50 5 13000 25 40 65 10 60 26000 10 30 85 10 65 9 30 40 70 60 30 40 70 60 9 Распределение вероятностей элементов (гонки Versus, режим Frantic Mode, драйверы, управляемые программным обеспечением) Расстояние (ед. ) 300 35 35 20 15 5 60 15 15 700 15 20 45 15 10 10 10 10 10 10 10 15 20 1300 15 20 25 20 15 30 10 10 10 5 10 10 20 2600 15 20 10 25 10 10 5 40 20 10 5 5 5 5 15 4500 15 20 25 10 5 40 30 15 5 30 5 7000 10 10 20 10 35 40 30 5 40 13000 5 5 15 5 30 35 50 5 50 26000 5 5 10 25 30 60 5 60 9 20 30 30 60 60 20 30 30 60 60 Специальное назначение ( S3 ) Эти пять дистрибутивов используются для выпадения специальных предметов, таких как предметы, выпадающие из сломанных ящиков. Распределения вероятностей элементов (специального назначения) Распределение 1 70 70 60 2 200 3 70 70 60 4 200 5 200 Боевой режим ( S4 ) В боевом режиме вероятность зависит как от времени, так и от количества оставшихся шаров. Приведенные здесь условия взяты из официального руководства Prima Games. ^[2] Так же, как и в Versus Races, есть дополнительные наборы раздач, назначение которых неясно. Все предметы Распределение вероятности предметов (боевой режим, все предметы, водители, управляемые игроками) Осталось минут шаров осталось Более 2 Более 2 30 130 10 30 Более 2 2 15 110 5 15 5 50 Более 2 1 75 10 20 10 15 70 Между 2 и 1 Более 2 20 135 10 35 Между 2 и 1 2 10 100 5 5 15 10 55 Между 2 и 1 1 15 15 10 20 10 5 15 5 20 10 75 Менее 1 Более 2 20 130 10 40 Менее 1 2 95 10 5 15 5 10 60 Менее 1 1 20 10 20 10 10 15 10 15 10 80 0 100 100 Распределение вероятностей предметов (боевой режим, все предметы, драйверы, управляемые программным обеспечением) Осталось минут шаров осталось Более 2 Более 2 20 165 5 10 Более 2 2 10 140 10 10 30 Более 2 1 100 20 30 50 Между 2 и 1 Более 2 20 150 10 20 Между 2 и 1 2 10 110 10 10 20 40 Между 2 и 1 1 35 20 20 15 10 10 10 5 10 10 55 Менее 1 Более 2 20 135 5 40 Менее 1 2 10 85 20 10 20 5 50 Менее 1 1 20 30 20 10 10 10 10 10 10 10 60 0 200 Только грибы Распределение вероятности предметов (боевой режим, только грибы, водители, управляемые игроками) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 140 60 Более 2 1 100 100 Между 2 и 1 Более 2 180 20 Между 2 и 1 2 120 80 Между 2 и 1 1 70 100 30 Менее 1 Более 2 170 30 Менее 1 2 100 80 20 Менее 1 1 50 90 60 0 200 Распределение вероятности предметов (боевой режим, только грибы, драйверы управляются программным обеспечением) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 120 80 Более 2 1 80 120 Между 2 и 1 Более 2 160 40 Между 2 и 1 2 100 100 Между 2 и 1 1 40 120 40 Менее 1 Больше 2 150 50 Менее 1 2 70 100 30 Менее 1 1 20 100 80 0 200 Только снаряды Распределение вероятности предметов (боевой режим, только снаряды, водители, управляемые игроками) Осталось минут шаров осталось Более 2 Более 2 160 40 Более 2 2 140 60 Более 2 1 80 20 100 Между 2 и 1 Более 2 140 60 Между 2 и 1 2 100 20 80 Между 2 и 1 1 50 40 110 Менее 1 Более 2 130 70 Менее 1 2 70 30 100 Менее 1 1 30 50 120 0 200 Распределение вероятности предметов (боевой режим, только снаряды, драйверы управляются программным обеспечением) Осталось минут шаров осталось Более 2 Более 2 170 30 Более 2 2 140 60 Более 2 1 80 30 90 Между 2 и 1 Более 2 160 40 Между 2 и 1 2 110 20 70 Между 2 и 1 1 50 40 110 Менее 1 Более 2 150 50 Менее 1 2 90 30 80 Менее 1 1 30 60 110 0 200 Только бананы Распределение вероятности предметов (боевой режим, только бананы, водители, управляемые игроками) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 170 30 Более 2 1 130 70 Между 2 и 1 Более 2 170 30 Между 2 и 1 2 130 70 Между 2 и 1 1 80 120 Менее 1 Более 2 150 50 Менее 1 2 100 100 Менее 1 1 50 150 0 200 Распределение вероятности элементов (боевой режим, только бананы, драйверы управляются программным обеспечением) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 160 40 Более 2 1 120 80 Между 2 и 1 Более 2 160 40 Между 2 и 1 2 120 80 Между 2 и 1 1 70 130 Менее 1 Более 2 140 60 Менее 1 2 90 110 Менее 1 1 40 160 0 200 Только боб-омбы Распределение вероятности элементов (боевой режим, только боб-омбы, драйверы, управляемые игроками, и драйверы, управляемые программным обеспечением) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 200 Более 2 1 200 Между 2 и 1 Более 2 200 Между 2 и 1 2 200 Между 2 и 1 1 200 Менее 1 Более 2 200 Менее 1 2 200 Менее 1 1 200 0 200 Дополнительные наборы Распределения вероятностей предметов (боевой режим, дополнительные распределения Green Shells и Bananas Only) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 200 Более 2 1 200 Между 2 и 1 Более 2 200 Между 2 и 1 2 200 Между 2 и 1 1 200 Менее 1 Более 2 200 Менее 1 2 200 Менее 1 1 200 0 200 Распределения вероятности предмета (боевой режим, дополнительные распределения только грибов) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 200 Более 2 1 200 Между 2 и 1 Более 2 200 Между 2 и 1 2 200 Между 2 и 1 1 200 Менее 1 Более 2 200 Менее 1 2 200 Менее 1 1 200 0 200 Распределения вероятности предметов (боевой режим, дополнительные распределения только для зеленых снарядов) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 200 Более 2 1 200 Между 2 и 1 Более 2 200 Между 2 и 1 2 200 Между 2 и 1 1 200 Менее 1 Более 2 200 Менее 1 2 200 Менее 1 1 200 0 200 Распределения вероятности предметов (боевой режим, дополнительные распределения только бананов) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 200 Более 2 1 200 Между 2 и 1 Более 2 200 Между 2 и 1 2 200 Между 2 и 1 1 200 Менее 1 Более 2 200 Менее 1 2 200 Менее 1 1 200 0 200 Распределения вероятности предметов (боевой режим, дополнительные распределения только боб-омбов) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 200 Более 2 1 200 Между 2 и 1 Более 2 200 Между 2 и 1 2 200 Между 2 и 1 1 200 Менее 1 Более 2 200 Менее 1 2 200 Менее 1 1 200 0 200 Распределения вероятности предметов (боевой режим, дополнительные распределения только зеленых ракушек и бананов) Осталось минут шаров осталось Более 2 Более 2 200 Более 2 2 200 Более 2 1 200 Между 2 и 1 Более 2 200 Между 2 и 1 2 200 Между 2 и 1 1 200 Менее 1 Более 2 200 Менее 1 2 200 Менее 1 1 200 0 200 Безумный режим Распределение вероятности предметов (Боевой режим, Безумный режим, водители, управляемые игроками) Осталось минут шаров осталось Более 2 Более 2 20 50 10 30 20 20 50 Более 2 2 10 30 10 30 20 10 20 10 60 Более 2 1 5 10 10 25 10 5 20 15 15 15 70 Между 2 и 1 Более 2 10 40 10 30 20 10 20 10 50 Между 2 и 1 2 20 10 10 25 5 20 20 20 10 60 Между 2 и 1 1 20 5 20 10 10 20 20 15 10 70 Менее 1 Более 2 40 10 30 20 15 20 15 50 Менее 1 2 20 15 5 20 10 20 20 20 10 60 Менее 1 1 30 5 10 10 20 20 20 15 5 65 0 90 80 30 9 Муса, Александр. Mario Kart 8 Официальное руководство по игре PRIMA. Раздел «Вероятность боевого предмета » на стр. 19. Распределение вероятности элементов (боевой режим, безумный режим, драйверы, управляемые программным обеспечением) Осталось минут шаров осталось Более 2 Более 2 35 55 10 25 15 20 40 Более 2 2 15 45 5 10 25 15 5 20 10 50 Более 2 1 20 10 10 25 10 10 15 10 20 10 60 Между 2 и 1 Более 2 25 50 10 25 15 5 20 10 40 Между 2 и 1 2 10 25 15 10 20 10 15 10 20 10 55 Между 2 и 1 1 10 25 10 15 10 15 15 15 15 10 60 Менее 1 Более 2 15 50 10 25 15 10 20 15 40 Менее 1 2 15 20 10 20 15 20 15 20 10 55 Менее 1 1 30 10 15 5 20 20 20 15 5 60 0 100 70 30 [Изменить] Mario Kart 8 / Mario Kart 8 Deluxe Гонщики Легкий вес Малыш Марио • Малыш Луиджи • Малыш Пич • Малыш Дейзи • Малыш Розалина • Лемми Купа • Сухие кости Светлый Жаба • Купа Тропа • Застенчивый парень (Голубой* · Черный* · Зеленый* · Желтый* · Белый* · Синий* · Розовый* · Оранжевый*) • Лакиту • Тоадетта • Ларри Купа • Венди О. Купа • Кэт Пич* • Житель деревни (женщина)* • Изабель* • Баузер-младший • Инклинг-девочка Средний Принцесса Пич • Принцесса Дейзи • Йоши (Голубой* · Черный* · Красный* · Желтый* · Белый* · Синий* · Розовый* · Оранжевый*) • Марио • Луиджи • Игги Купа • Людвиг фон Купа • Тануки Марио* • Житель деревни (мужчина)* • Инклинг-мальчик Крейсер Розалина • Металлический Марио (золото) • Розовый золотой персик • Донки Конг • Валуиджи • Рой Купа • Линк* • Кинг Бу Тяжелый Боузер • Варио • Мортон Купа младший • Сухой боузер* Любой Мии Автозапчасти Кузова Карты Стандартный карт • Трубчатая рама • 8 Махов • Steel Driver • Cat Cruiser • Специальный трек • Tri-Speeder • Badwagon • Prancer • Biddybuggy • Landship • Sneeker • Спортивное купе • Gold Standard • GLA* • W 25 Silver Arrow* • 300 SL Родстер* • Blue Falcon* • Tanooki Kart* • B Dasher* • Streetle* • P-Wing* • Koopa Clown Стандартные велосипеды Стандартный велосипед • The Duke • Flame Rider • Varmint • Mr. Scooty • City Tripper* • Master Cycle Zero ** Спортивные велосипеды Comet • Спортивный велосипед • Реактивный велосипед • Йоши-байк • Мастер-цикл* Вездеходы Стандартный квадроцикл • Wild Wiggler • Teddy Buggy • Bone Rattler* • Inkstriker • Splat Buggy Шины Standard • Monster • Roller • Slim • Slick • Metal • Button • Off-Road • Sponge • Wood • Cushion • Blue Standard • Hot Monster • Azure Roller • Crimson Slim • Cyber Slick • Retro Off-Road • Gold Tyres • GLA Tyres * • Шины Triforce* • Шины Leaf* • Шины Ancient ** Планеры Суперплан • Облачный планер • Крыло Wario • Крыло Waddle • Персиковый зонтик • Парашют • Параплан • Flower Glider • Bowser Kite • Plane Glider • MKTV Parafoil • Gold Glider • Hylian Kite* • Paper Glider* • Paraglider ** Курсы Новые курсы Чашка с грибами Стадион Mario Kart • Аквапарк • Sweet Sweet Canyon • Руины Thwomp Цветочная чашка Mario Circuit • Toad Harbour • Twisted Mansion • Shy Guy Falls Звездный кубок Аэропорт Саншайн • Дельфин Шолс • Электродром • Гора Варио Специальная чашка Круиз на облачной вершине • Сухие дюны • Замок Боузера • Радужная дорога Классические курсы Чашка из ракушек Wii Moo Moo Meadows • GBA Mario Circuit • DS Cheep Cheep Beach • N64 Toad’s Turnpike Банановая чашка GCN Dry Dry Desert • SNES Donut Plains 3 • N64 Royal Raceway • 3DS DK Jungle Чашка для листьев DS Wario Stadium • GCN Sherbet Land • 3DS Music Park • N64 Yoshi Valley Кубок молнии DS Часы Tick-Tock • 3DS Горка с растениями-пираньями • Wii Grumble Volcano • N64 Rainbow Road Курсы DLC Подставка для яиц* GCN Трасса Йоши • Excitebike Arena • Dragon Driftway • Mute City Кубок Triforce* Wii Золотая шахта Варио • SNES Радужная дорога • Ледяная застава льда • Трасса Хайрула Переходная чашка* GCN Baby Park • GBA Cheese Land • Wild Woods • Animal Crossing Кубок с колокольчиком* 3DS Neo Bowser City • GBA Ribbon Road • Super Bell Subway • Big Blue Кубок Золотой Дэш *** Tour Paris Promenade • 3DS Toad Circuit • N64 Choco Mountain • Wii Coconut Mall Чашка Lucky Cat *** Tour Tokyo Blur • DS Shroom Ridge • GBA Sky Garden • Ninja Hideaway Чашка репы *** Tour New York Minute • SNES Mario Circuit 3 • N64 Пустыня Калимари • DS Валуиджи Пинбол Чашка пропеллера *** Tour Sydney Sprint • GBA Snow Land • Wii Mushroom Gorge • Sky-High Sundae Волна 3 *** Веселая гора • DS Персиковые сады Боевые курсы Wii U Wii 2 Moo Moo Meadows • GCN Сухая сухая пустыня • SNES ДОНТ -ПЛАНИЯ 3 • N64 TOAD'S Turnpike • Mario Circuit • GCN SHERBET • 77777777777777777777777777. ВАДСКОЙ СПАС. Переключатель 3DS Город Уху • GCN Особняк Луиджи • SNES Поле битвы 1 • Подземный переход Ерчин • Дворец Дракона • Стадион битвы • Сладкое, сладкое королевство • Лунная колония Другое Предметы Банан • Блупер • Бу • Цветок-бумеранг • Купюра-пуля • Монета • Безумная восьмерка • Огненный цветок • Золотой гриб • Зеленая раковина • Молния • Гриб • Растение-пиранья • Красная раковина • Колючая раковина • Суперрог • Тройные бананы • Тройные зеленые раковины • Тройные грибы • Тройные красные раковины Объекты курса Антигравитационная панель • Поле для стрел *** • Бочка • Колокол* • Доска • Валун • Статуя Боузера • Автобус • Пушка • Автомобиль • Грузовой автомобиль • Деньги • Монета • Ящик • Ток • Приборная панель • Приборная панель рампы грузовика • Водосточная труба • Перо • Огненный стержень • Огненная цепь • Планерная рампа • Воздушный шар • Полутруба *** • Ящик с предметами • Лавовый гейзер • Куча листьев* • Жернов • Шахтная тележка* • Нефтяное пятно • Яма* • Кольцо • Рупия* • Доска для серфинга • Снеговик* • Снеговик • Спиннер • Штамп • Подводная лодка • Поезд* • Вулканические обломки Враги и виды Костяное растение-пиранья • Бу • Прыгающая записка • Памятник Боузеру • Цепное чавканье • Чип-чип • Деку-баба* • Дельфин • Огненный змей • Рыбья кость • Фризи • Лягушка • Призрак • Гумба • Башня Гумба • Рыцарь-молот • Медузный луч • Киз* • Лакиту • Маленькая птичка • Манта • Меха Чип • Мехакупа • Мини-жаба • Монти Крот • Му Му • Мистер Ресетти* • Ноки • Пингвин *** • Пианта • Растение-пиранья • Поки • Бредящее растение-пиранья • Кричащий столб • Обходчик • Катание на коньках Shy Guy • Super Thwomp* • Swoop • Thwomp • Tiki Goon • Unagi Методы Антигравитация • Дрифт • Гравитация • Highlight Reel • Hop • Mini-Turbo • Rocket Start • Slipstream • Spin Boost • Spin Turn • Trick • U-turn Разное Эндрю Трего • Animal Crossing × Mario Kart 8 * • Дом на дереве DK • Эмблема • Финишная черта • Из ямы • Highlight Reel • Внутриигровая статистика ( Deluxe ) • Распределение вероятности предметов • The Legend of Зельда × Mario Kart 8 * • Mario Kart 8 Deluxe – Пропуск на курс Booster *** • Mario Kart Band • Mario Kart TV • Mercedes-Benz × Mario Kart 8 * • Miiverse • Официальные турниры • Пре-релиз и неиспользованный контент • Саундтрек • Спонсоры • Персонал ( Deluxe ) • Штампы • Стартовая сетка • Подводное вождение Связанные игры Действия Nintendo: Прокатись на одной из этих красавиц! • Участвуйте в этом опросе • Одна чашка, четыре дорожки… • Покажи это мне • Викторина «Игровые сады» • Mario Kart 8 Deluxe Memory Match-Up 7 7026 * — загружаемый контент в Mario 58 • ** — указывает на содержимое, доступное в версии 1. 6.0 Mario Kart 8 Deluxe. • *** — указывает на содержимое, доступное в Mario Kart 8 Deluxe.0558 • - Указывает на эксклюзивность для Mario Kart 8 Deluxe Бридж-вероятности для 9-карточной масти Бридж-вероятности для 9-карточной масти (Джеффри Розенталь, Марк Голдман и Гарет Робертс, май 2020 г.) Предположим, вы играете в бридж, и вы объявляете, и между разыгрывающим и манекен у вас есть 9 мастей, включая туз-король-валет. вопрос какой курс действия дает вам лучший шанс захватить ферзя ваших противников, и выиграть все трюки в этом костюме? Эта ситуация возникла в недавней игре и вызвала обсуждение. Большинство бридж-текстов дают стандартный ответ, но мне не показалось очевидным, что этот ответ был правильным, и тексты плохо объясняют свой ответ. После дальнейших размышлений я пришел к выводу, что советы в текстах во многом верны, а вот объяснения часто нет. Стандартная рекомендация восемь никогда, девять никогда, это означает, что если у вас есть только 8 мастей, вы всегда должны попробуй хитрость (выведя младшую карту из манекена, а затем сыграв Король над дамой или валет, если королева не сыграна). Но если вы держите 9костюма, то вы никогда не должны утончать, а вместо этого просто играйте на выпадение (ведя туза, а затем короля, надеясь, что Королева выпадет). Некоторые тексты сказать, что с 9 масти, ловкость имеет 50% вероятность успеха, при игре за падение имеет вероятность 53%. (А некоторые дают другие странные советы, как "Решите, какой путь лучше для вас и делать это каждый раз. Если вы колеблетесь между позициями, шансы не сработает в вашу пользу», что абсолютно не имеет силы.) На самом деле, игра на ловкость "правильным" способом имеет 56,22% шанс успех. Означает ли это, что вы должны играть на ловкость? Нет, потому что игра на выпадение "правильно" имеет 57,92% шанс успеха, как я сейчас объясню. Во избежание дополнительных осложнений предположим, что рассматриваемый костюм козыря (поэтому нет никакого способа выиграть ферзя ни козырем, ни каким-либо другим стратегия, отличная от ловкости или дропа). И, предположим, оператор объявления держит туз, король, валет и десятка, и у вас достаточно карт и входов вести от разыгрывателя и от манекена так часто, как это необходимо. Кроме того, предположим, что у вас нет никакой информации о вашем карты противников на основе их ставок или предыдущей игры. Чтобы определить, какая стратегия лучше, нам нужно рассмотреть вероятности. При отсутствии какой-либо другой информации 26 карт соперников равновероятно разделить на любые две руки по 13 карт. Итак вероятность того, что противник справа от разыгрывающего (т.е. ГУР) имеет «i» козырей дает: Prob(RHO имеет i козырей) = (4 выбирают i) * (22 выбирают 13-i) / (26 выбирают 13) , для i=0,1,2,3,4. (Здесь «n выбирает k» означает общее возможное число способов выбора k карт из n всего, то есть n!/k!(n-k)!.) Это дает следующие вероятности для числа «i» козыря карты, находящиеся в распоряжении ГУР: Вероятность (0) = 4,78%, Вероятность (1) = 24,87%, Вероятность (2) = 40,70%, Вероятность (3) = 24,87%, Вероятность (4) = 4,78%. Это позволяет нам вычислить вероятность успеха при различных стратегии: Если просто ухищрить на первом раунде, то при отсутствии любой другой информации, вероятность того, что у РО есть ферзь, равна 50%. Итак, вероятность того, что ловкость удастся, равна 50% . И, поскольку мы предполагаем, что у вас достаточно карточек и записей, чтобы повторить ловкость по мере необходимости, эта стратегия имеет 50% вероятность успеха. Напротив, если вы сделаете простую игру для дропа путем розыгрыша двух раундов с тузом и королем, затем шанс, что королева упадет, четверть из 24,87%, что RHO имеет один козырь, плюс четверть от 24,87%, что РО имеет три козыря, плюс все 40,70%, что у РО есть два козыря (делая 2-2), 24,87/4 + 24,87/4 в первом раунде, плюс 40,70% во втором раунде, всего 24,87/4 + 40,70 + 24,87/4 или 53,14% -- немного лучше. Тем не менее, есть хитроумная стратегия, из первого розыгрыша раунд, надеясь сбросить синглтона королевы, а затем искусно ловить второй раунд, если королева не падает. Это имеет вероятность успеха 24,87/4, что У RHO есть одиночная королева, плюс 24,87/4, что у LHO есть одиночная королева, плюс (100-24,87/4-24,87/4)/2, что нет синглтона Queen, кроме ловкость во втором раунде увенчалась успехом, что дает в сумме 56,22% -- даже лучше. Наконец, рассмотрим смарт-игру для дропа стратегия первого розыгрыша раунд, а затем розыгрыш второго раунда , если только LHO не показал пустоту. Если LHO показал пустоту, то в этот момент ясно, что игра туз-король последовательно не приведет к падению ферзя, поэтому вам следует переключиться к стратегии изящества, которая теперь гарантированно сработает (поскольку мы при условии, что вы можете вернуться к манекену три раза). Это имеет вероятность успеха 4,78%, что LHO недействителен, плюс 24,87/4 + 24,87/4, что у одного из соперников одиночка ферзя, плюс 40,70%, что у масть делится на 2-2, поэтому выпадение успешно, для общей вероятности успеха из 57,92% -- лучше всех! Таким образом, вероятность успеха такова: 50% за простое изящество , 53,14% для простой капли , 56,22% для более умного изящества , а также 57,92% для смарт-дропа . Итак, действительно верно, что с 9-карточной мастью и много записей, и вообще никакой информации о ваших противниках, лучше всего играть (умно) за каплю. No related posts. Навигация по записям Предыдущая статьяГрафик cos2x 1: Mathway | Популярные задачи Следующая статьяH2So4 степени окисления: СРООЧНО!!!!!!!!!!! Определите степени окисления всех элементов-H2SO4 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Найти: Рубрики Геометрия Математика Физика Химия Школьная жизнь Разное © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа» Карта сайта