Примеры использования функции СТЕПЕНЬ в Excel
Функция СТЕПЕНЬ в Excel используется для возведения чисел в степень, значение которой может являться сложным выражением, и возвращает полученное в результате числовое значение.
Функция СТЕПЕНЬ в Excel для возведения числа в указанную степень
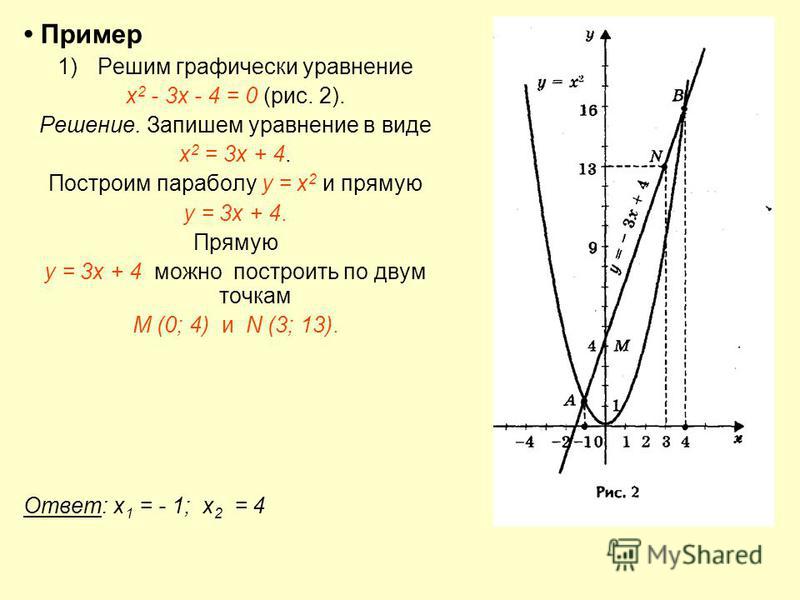
Пример 1. В таблице записана последовательность, которая представляет собой часть геометрической прогрессии. Необходимо определить: знаменатель геометрической прогрессии, значение 15-го ее члена, а также сумму первых 20 членов.
Таблица исходных данных:
Определим знаменатель из условия, что он равен частному от деления любых последующего и предыдущего соседних членов:
Для нахождения 15-го члена используем формулу:
=A2*СТЕПЕНЬ(C2;15-1)
Описание аргументов:
- A2 – ячейка, содержащая значение первого члена;
- СТЕПЕНЬ(C2;15-1) – формула, принимающая на вход значение знаменателя прогрессии, который возводится в степень, равную номеру позиции искомого члена -1.
 2+2x).
2+2x).Для построения графика будем использовать несколько точек, полученных в результате расчета значения зависимой координаты y на основе известных произвольных значениях независимой координаты x. Внесем исходные данные в таблицу:
Определим первое значение зависимой переменной:
Описание аргументов:
- 2 – число, которое необходимо возвести в степень;
- СТЕПЕНЬ(A3;2)-2*A3 – степень, полученная в результате вычисления данного выражения.
Аналогично определим второе значение для Y, выделим ячейки B3 и B4, автоматически заполним остальные ячейки растягиванием выделенной области:
Для построения графика используем точечную диаграмму с маркерами. Готовый график функций имеет следующий вид:
Депозитный калькулятор в Excel
Пример 3. В таблице Excel создан калькулятор для расчета суммы процентов прибыли по депозитным вкладам в банковскую организацию. Рассмотрим его реализацию.
Калькулятор имеет следующий вид:
Заполним шаблон депозитного калькулятора исходными данными для расчетов:
В ячейке B5 содержится следующая формула:
Описание аргументов:
- ИЛИ(B2=»»;B2<0;B3=»»;B3<0;B4=»»;B4<0) – условия для проверки, чтобы в ячейке B5 не выводилась ошибка #ЗНАЧ!, если предыдущие ячейки не заполнены или введены неверные значения.

- 0 – значение, которое выводится по умолчанию, если расчет не производится.
- B2*СТЕПЕНЬ(1+B3;B4)-B2 – формула расчета суммы процентов. Для возведения в степень используется функция СТЕПЕНЬ.
Пример использования:
Примечание: для корректной работы данного калькулятора значение процентной ставки должно являться десятичной дробью (например, значение 10% — 0,1 указано в процентном формате ячеек).
Функция СТЕПЕНЬ в Excel и особенности ее использования
Рассматриваемая функция принадлежит к классу математических функций Excel и имеет следующую синтаксическую запись:
=СТЕПЕНЬ(число; степень)
Описание аргументов:
- число – обязательный аргумент, характеризующий число, которое необходимо возвести в степень.
- степень – обязательный аргумент, характеризующий степень, в которую требуется возвести число.
Примечания:
- Функция СТЕПЕНЬ вернет код ошибки #ЗНАЧ!, если один из параметров содержит текстовые данные.
 » — символ возведения в степень. Однако запись типа =СТЕПЕНЬ(a;b) является более наглядной.
» — символ возведения в степень. Однако запись типа =СТЕПЕНЬ(a;b) является более наглядной. - С помощью рассматриваемой функции можно извлечь корень любой степени из числа. Для реализации необходимо в качестве степени ввести выражение типа (1/b), где b – корень степени b.
Первые признаки пневмонии: симптомы и причины
Пневмония или воспаление легких – это заболевание легких преимущественно инфекционного происхождения с поражением концевых участков легких – альвеол и нарушением газообмена на их уровне. Альвеолы заполняются жидкостью или гнойным материалом, вызывая кашель с мокротой, реже кровохарканье, жар, озноб и затрудненное дыхание. Пневмонию могут вызывать различные микроорганизмы, включая бактерии, вирусы и грибы.
Пневмония может варьировать от легкой до угрожающей жизни, наиболее опасное для младенцев и детей младшего возраста, людей старше 65 лет и людей с ослабленной иммунной системой.
Симптомы пневмонии
Признаки и симптомы пневмонии варьируются от легких до тяжелых, в зависимости от таких факторов, как тип микроба, вызывающего инфекцию, возраст и общее состояние здоровья.
 Легкие признаки и симптомы часто похожи на симптомы простуды или гриппа, но они длятся дольше.
Легкие признаки и симптомы часто похожи на симптомы простуды или гриппа, но они длятся дольше.Признаки и симптомы пневмонии могут включать в себя:
- Боль в груди, когда вы дышите или кашляете
- Кашель с мокротой
- Сбивчивое дыхание (одышка) при меньшей нагрузке, разговоре, в покое
- Усталость
- Температура тела ниже нормальной (у взрослых старше 65 лет и людей со слабой иммунной системой)
- Изменение настроения, аппетита, физической активности у пожилых (в сочетании с другими факторами)
- Тошнота, рвота или диарея (в редких случаях)
У новорожденных и младенцев может не быть никаких признаков инфекции. Может быть рвота, лихорадка и кашель, беспокойство, усталость и отсутствие энергии, а также проблемы с дыханием и приемом пищи.
Когда обратиться к врачу
Обратитесь к врачу, если у вас проблемы с дыханием, боль в груди, постоянная лихорадка (38.5 C) или выше, кашель, особенно если вы кашляете с мокротой.
Важно, чтобы обращались к врачу люди из групп риска:
- Взрослые старше 65 лет
- Дети младше 2 лет с признаками и симптомами
- Больные с экзогенной интоксикацией (алкоголь, наркотики)
- Люди с плохим и удовлетврительным состоянием здоровья или ослабленной иммунной системой
- Пациенты с хроническими заболеваниями, особенно в стадии декомпенсации (обструктивный бронхит, сердечная недостаточность, сахарный диабет, цирроз печени)
- Люди, получающие химиотерапию или лекарства, которые подавляют иммунную систему
- Длительно лежащие в постели
Для некоторых пожилых людей и людей с сердечной недостаточностью или хроническими заболеваниями легких пневмония может быстро стать опасным для жизни состоянием.

Причины пневмонии
Пневмонию могут вызвать многие микроорганизмы. Наиболее распространенными являются бактерии и вирусы в воздухе, которым мы дышим, особенно в воздухе помещений. иммунитет человека обычно предотвращает заражение этими микроорганизмами легких. Но иногда эти микробы могут подавить иммунную систему, даже если здоровье в целом хорошее.
Пневмония классифицируется в соответствии с типами микроорганизмов, которые ее вызывают и места возникновения инфекции.
Внебольничная пневмония
Внебольничная пневмония является наиболее распространенным типом пневмонии. Это происходит за пределами больниц или других медицинских учреждений. Это может быть вызвано:
Бактерии: Наиболее распространенной причиной бактериальной пневмонии является пневмококк (лат. Streptococcus pneumoniae). Этот тип пневмонии может возникнуть сам по себе или после того, как вы простудились или заболели гриппом. Может затронуть одну часть (долю) легкого.
Бактериоподобные организмы.
 Mycoplasma pneumoniae также может вызывать пневмонию. Обычно он вызывает более легкие симптомы, чем другие виды пневмонии. Ходячая пневмония – это неофициальное название для данного типа пневмонии, которая обычно недостаточно серьезна, чтобы требовать постельного режима.
Mycoplasma pneumoniae также может вызывать пневмонию. Обычно он вызывает более легкие симптомы, чем другие виды пневмонии. Ходячая пневмония – это неофициальное название для данного типа пневмонии, которая обычно недостаточно серьезна, чтобы требовать постельного режима.Грибы или плесень: Этот тип пневмонии чаще всего встречается у людей с хроническими проблемами со здоровьем или ослабленной иммунной системой, а также у людей, которые вдыхали большие дозы организмов. Грибки, вызывающие его, могут быть обнаружены в почве или птичьем помете и варьируются в зависимости от географического положения.
Вирусы. Некоторые вирусы, вирус гриппа, герпес-вирусы, аденовирусы вызывающие простуду, могут также вызывать пневмонию. Вирусы являются наиболее распространенной причиной пневмонии у детей младше 5 лет. Вирусная пневмония обычно легкая. Но в некоторых случаях это может стать очень серьезным.
Внутрибольничная пневмония
Некоторые люди заболевают воспалением легких во время пребывания в больнице из-за другой болезни.
 Больничная пневмония может быть серьезной, потому что бактерии, вызывающие ее, могут быть более устойчивыми к антибиотикам и потому, что люди, которые ее получают, уже больны и ослаблены. Люди, которые находятся на дыхательных аппаратах (ИВЛ), часто используемых в отделениях интенсивной терапии, подвержены более высокому риску этого типа пневмонии.
Больничная пневмония может быть серьезной, потому что бактерии, вызывающие ее, могут быть более устойчивыми к антибиотикам и потому, что люди, которые ее получают, уже больны и ослаблены. Люди, которые находятся на дыхательных аппаратах (ИВЛ), часто используемых в отделениях интенсивной терапии, подвержены более высокому риску этого типа пневмонии.Пневмония, связанная с медицинским вмешательством
Это бактериальная инфекция, которая встречается у людей, которые находятся в учреждениях длительного ухода или получают лечение в амбулаторных условиях, включая центры диализа почек. Как и внутрибольничная пневмония, может быть вызвана бактериями, которые более устойчивы к антибиотикам.
Аспирационная пневмония
Аспирационная пневмония возникает, когда пациент вдыхает пищу, питье, рвоту или слюну в легкие. Аспирация более вероятна, если что-то нарушает нормальные рвотный или кашлевый рефлексы, например, повреждение мозга, чрезмерное употребление алкоголя или наркотиков.

Факторы риска
Пневмония может повлиять на любого. Но в двух возрастных группах риск повышен:
- Дети 2 лет или младше
- Люди в возрасте 65 лет и старше
Другие факторы риска включают в себя:
- Нахождение в стационаре: повышается риск развития пневмонии, особенно в отделениях интенсивной терапии больниц, особенно при искусственной вентиляции лёгких.
- Хроническое заболевание. Риски заболеть пневмонией повышаются при бронхиальной астме, хронической обструктивной болезни легких (ХОБЛ) или хронических заболеваних сердца, сахарном диабете, циррозе печени.
- Курение. Курение нарушает естественную защиту организма от бактерий и вирусов.
- Ослабленная или подавленная иммунная система. Люди с ВИЧ/СПИДом, перенесшие пересадку органов, болеющие туберкулёзом получающие химиотерапию или длительно принимающие стероиды.
Осложнения при пневмонии
Даже при лечении некоторые люди с пневмонией, особенно в группах высокого риска, могут испытывать осложнения, в том числе:
- Бактерии в кровотоке (бактериемия).
 Бактерии, попадающие в кровь из легких, могут распространить инфекцию на другие органы, что может стать причиной нарушения функции этих органов и дальнейшего прогрессирования заболевания.
Бактерии, попадающие в кровь из легких, могут распространить инфекцию на другие органы, что может стать причиной нарушения функции этих органов и дальнейшего прогрессирования заболевания. - Затрудненное дыхание (одышка). При тяжёлых пневмониях, особенно на фоне хронических заболеваний легких, возникают проблемы с получением достаточного количества кислорода. Может потребоваться госпитализация и использование дыхательного аппарата (ИВЛ) на время лечения.
- Накопление жидкости вокруг легких (плевральный выпот). Пневмония может вызвать накопление жидкости в тонком пространстве между слоями ткани, которые выстилают легкие и грудную полость (плевру).
- Абсцесс легкого. Абсцесс возникает, если в легких образуется гной. Абсцесс обычно лечится антибиотиками. Иногда для удаления гноя требуется операция или дренаж с длинной иглой или трубкой, помещенной в абсцесс.
При подозрение на пневмонию обязательно обращение к врачу!
Не своевременное обращение, самолечение приводят к поздней диагностике, антибиотикорезистентности, различным осложнениям и даже летальному исходу.
(2)-Турито
Вопрос
- 4
- 11
- 16
Правильный ответ: 11
СТАВИТЬ: Найдите по подполковнике (-10
Hint: Найдите по подбору (-10
. ,a) и значение ‘b’ путем подстановки (a, b) в данное уравнение.
Шаг 1: подставьте (-10,a) в уравнение
Шаг 2: подставьте (a,b)[т.е. (4,b)] в уравнениеСвязанные вопросы для изучения
Общее
Математика-
Какое из следующих утверждений верно относительно приведенного выше уравнения?ПОДСКАЗКА: решите уравнение
Объяснение:
Невозможно для любого значения x.
Нет решения, потому что оно неверно для любого значения x
Какое из следующих утверждений верно относительно приведенного выше уравнения?Общая математика
СОВЕТ: решите уравнение
Объяснение:
Невозможно для любого значения x.
Нет решения, поскольку неверно ни при каком значении xОбщий
Математика-
Приведенное выше уравнение может быть представлено параболой в -плоскости. Затем парабола переводится так, чтобы вершина находилась в точке (0, 0). Что из следующего лучше всего описывает перевод?ПОДСКАЗКА: Нарисуйте график и проверьте (лучший способ и без путаницы)
Объяснение:
Пусть новые координаты будут X,Y
тогда новое сдвинутое уравнение будет Y=X 2 с (0,0) в качестве вершины
Теперь старое уравнение будет y+8 = (x+5) 2
Теперь давайте сравним новые и старые координаты x и y
При сравнении X= x+5 (т.е. сдвиг на 5 единиц в положительном направлении x)
При сравнении Y= y+8 (т.е. сдвиг на 8 единиц в положительном направлении y)
Вышеупомянутое уравнение может быть представлено параболой в -плоскости. Затем парабола переводится так, чтобы вершина находилась в точке (0, 0). Что из следующего лучше всего описывает перевод?
Что из следующего лучше всего описывает перевод?Maths-General
СОВЕТ: Нарисуйте график и проверьте (лучше всего и без путаницы)
Объяснение:
Пусть новые координаты будут X,Y
, тогда новое сдвинутое уравнение будет Y=X 2 с (0,0) в качестве вершины
Теперь старое уравнение будет y+8 = (x+5) 2
Теперь давайте сравним новые и старые координаты x и y
При сравнении X= x+5 (т.е. сдвиг на 5 единиц в положительную сторону x)
При сравнении Y= y+8 (т.е. сдвиг на 8 единиц в положительную сторону) y направление)Общий
Математика-
Каково решение данного уравнения?СОВЕТ: проверьте все условия, действительные для x, найдите условия модуля в этом диапазоне и найдите x.
Объяснение :
Если оба модуля положительны или оба модуля отрицательны, то
x+2 = x-8 (или) -(x+2) = -(x-8)
Тогда x не определен
Шаг 1 : проверка достаточных условий
|x+2| положительно, если x>-2, и отрицательно, если x<-2.
|х-8| положительно, если x>8, и отрицательно, если x<8.
Единственными возможными условиями являются x>-2 и x<8 (т.е. x
Шаг 2:
∴x = 3 является решением данного уравнения
Каково решение данного уравнения?Maths-General
СОВЕТ: проверьте все условия, действительные для x, и найдите условия модуля в этом диапазоне, и найдите x.
Объяснение :
Если оба модуля положительны или оба модуля отрицательны, то
x+2 = x-8 (или) -(x+2) = -(x-8)
Тогда x не определен
Шаг 1 : проверка достаточных условий
|x+2| положительно, если x>-2, и отрицательно, если x<-2.
|х-8| положительно, если x>8, и отрицательно, если x<8.
Единственными возможными условиями являются x>-2 и x<8 (т.е. x
Шаг 2:
∴x = 3 является решением данного уравнения показан график?ПОДСКАЗКА: График и параметры представлены в виде поиска a и b по паре точек на графике
Объяснение :
Шаг 1: Пусть график имеет вид
поиск точек на графике из наблюдения
Точки (0,2) и (1,6)
Шаг 2: Теперь подставьте точку (0,2)
∴ a = 2
Шаг 3: подставьте a = 2 и (1,6) в уравнение
Подставьте a=2 и b=3 в уравнение
Уравнение графика, показанного на рисунке.
Какое уравнение изображенного графика?Maths-General
ПОДСКАЗКА: График и параметры представлены в виде поиска a и b по паре точек на графике
Объяснение:
Шаг 1: Пусть график имеет вид
нахождение точек на графике из наблюдения
Точки (0,2) и (1,6)
Шаг 2: Теперь подставьте точку (0,2)
∴ a = 2
Шаг 3: подставьте a = 2 и (1,6) в уравнении
Подставить a=2 и b=3 в уравнение
Это уравнение графика, показанного на рисунке.Общее
Математика-
Какое выражение эквивалентно , где g и h положительны?
ПОДСКАЗКА: Измените экспоненциальную форму
Какое выражение эквивалентно , где g и h положительны?
Maths-General
ПОДСКАЗКА: Измените экспоненциальную форму
General
Maths-
Какое выражение эквивалентно ?
ПОДСКАЗКА: уравнение имеет форму 2 -2ab +b 2 и разложите уравнение дальше после получения вида (a-b) 2
Объяснение:
Шаг 1 :
Факторизация
знай это
Здесь
поэтому
Шаг 2:
Мы можем записать 9 как 3 2 , чтобы мы могли делить дальше
Мы знаем, что
Здесь
Итак,Какое выражение эквивалентно ?
Maths-General
ПОДСКАЗКА: уравнение имеет форму 2 -2ab +b 2 и разложить уравнение на множители после получения вида (a-b) 2
Объяснение:
Шаг 1 :
Факторизация
Мы знаем, что
Здесь
Итак
Шаг 2:
Мы можем записать 9 как 3 2 , чтобы мы могли делить дальше
Мы знаем, что
Здесь
Итак,Общее
Математика-
9002 треугольник DEF подобен треугольнику ABC выше, где сторона DE соответствует стороне AB, сторона DF соответствует стороне AC, а DE = AB. Чему равен угол DEF?
Чему равен угол DEF?ПОДСКАЗКА: В подобных треугольниках соответствующие углы будут равны в том же порядке подобия.
Объяснение: данный ΔDEF аналогичен ΔABC
Шаг 1: проверьте порядок подобия
Сторона DE соответствует AB (ΔDEF ~ ΔABC)
Сторона DF соответствует AC (ΔDEF ~ ΔABC)
Успешно подтверждено, что ΔDEF ~ ΔABC находятся в правильном порядке подобия, затем углы ΔABC
В ΔABC ,∠A = 90°, ∠B = 37°(даны на схеме)
Но ∠A +∠B +∠C = 180°(сумма углов треугольника)
90° + 37° +∠C =180°
∠C =180°- 90° — 37°
∴∠C =53°=∠ACB
Шаг 3:
∠DFE = ∠ACB (по подобию треугольников)
∠DFE=∠ACB= 53°
∴∠DFE = 53°
Треугольник DEF (не показан) подобен треугольнику ABC выше, где сторона DE соответствует стороне AB, сторона DF соответствует стороне AC , а DE = АБ. Чему равен угол DEF?Maths-General
ПОДСКАЗКА: В подобных треугольниках соответствующие углы будут равны в том же порядке подобия.
Объяснение: данный ΔDEF подобен ΔABC
Шаг 1: Проверьте порядок подобия
Сторона DE соответствует AB (ΔDEF ~ ΔABC)
Сторона DF соответствует AC (ΔDEF ~ ΔABC)
Успешно проверено, что ΔDEF ~ ΔABC находятся в правильном порядке подобия, затем
Шаг 2: Нахождение всех углов ΔABC
В ΔABC ,∠A = 90°, ∠B = 37°(
Но ∠A +∠B +∠C = 180°(сумма углов треугольника)
90° + 37°+∠C =180°
∠C =180°- 90° — 37°
∴∠C =53°=∠ACB
Шаг 3:
∠DFE = ∠ACB (по подобию треугольников)
∠DFE=∠ACB= 53°
∴∠DFE = 53°Общее
Математика0022
Функция моделирует пульс Джека в ударах в минуту (уд/мин) в зависимости от его скорости в километрах в час (км/ч) на велотренажере. Основываясь на модели, каким был пульс Джека в ударах в минуту, когда его скорость равнялась 0 км/ч?
Основываясь на модели, каким был пульс Джека в ударах в минуту, когда его скорость равнялась 0 км/ч?ПОДСКАЗКА: Наблюдайте за графиком скорости при скорости = 0 км/ч. Мы обнаружим, что график обрывается между 60-65. Таким образом, пульс составляет 63 в соответствии с вариантом проверки, только параметр находится между 60-65, это вариант C.
Объяснение: ЕСЛИ требуется математическое доказательство вместо проверки вариантов
Шаг 1: Нахождение любых двух точек для нахождения уравнения прямой
Прямая проходит через (3,75) и (8,95)
Шаг 2: Нахождение уравнения для прямой, проходящей через {(3.75),(8,95) }
при x = 0 ,
пульс Джека в ударах в минуту, когда он движется со скоростью 0 км/ч, составляет 63 удара в минуту.
Функция моделирует пульс Джека в ударах в минуту (уд/мин) в зависимости от его скорости в километрах в час (км/ч) на велотренажере. Основываясь на модели, каким был пульс Джека в ударах в минуту, когда его скорость равнялась 0 км/ч?Maths-General
ПОДСКАЗКА: наблюдайте за графиком при скорости = 0 км/ч, мы находим, что график обрывается между 60-65.
 Таким образом, пульс составляет 63 в соответствии с вариантом проверки только вариант находится между 60-65 это вариант C.
Таким образом, пульс составляет 63 в соответствии с вариантом проверки только вариант находится между 60-65 это вариант C.
Объяснение: ЕСЛИ вместо проверки вариантов требуется математическое доказательство
Шаг 1: Поиск любых двух точек для нахождения уравнения прямой
Линия проходит через (3,75) и (8,95)
Шаг 2: Поиск уравнения для линии, проходящей через {(3.75),(8,95)}
при x = 0,
Пульс Джека в ударах в минуту, когда он движется со скоростью 0 км/ч, составляет 63 удара в минуту.
Общее
Математика-
ka + nb = 10
Данное уравнение связывает положительные числа a, b, k и n. Что из следующего правильно выражает a через b, k и n?ПОДСКАЗКА: Измените данное уравнение
Объяснение:ka + nb = 10
Данное уравнение связывает положительные числа a, b, k и n. Что из следующего правильно выражает a через b, k и n?Maths-General
ПОДСКАЗКА: Измените данное уравнение
Объяснение:General
Maths-
Какая система линейных уравнений представлена показанными линиями?ПОДСКАЗКА: Данная прямая проходит через 2 набора точек, поэтому найдите уравнение прямых из двух точек из формы
. Объяснение: Две точки — это форма для нахождения уравнения прямой, проходящей через две точки X1, Y1 и X2. ,Y2, как показано ниже
Объяснение: Две точки — это форма для нахождения уравнения прямой, проходящей через две точки X1, Y1 и X2. ,Y2, как показано ниже
Шаг 1: Из наблюдения за данным графиком. Два набора точек: {(2,0),(0,-3)} и {(4,0),(0,-6) }
Шаг 2: Нахождение уравнения для прямой, проходящей через {(2,0),(0,-3)}
Шаг 3: Нахождение уравнения для прямой, проходящей через {(4,0),(0,-6) }
∴ и являются системой линейных уравнений, представленной на графике.
Какая система линейных уравнений представлена показанными линиями?Maths-General
ПОДСКАЗКА: Данная прямая проходит через 2 набора точек, поэтому найдите уравнение прямых из двух точек из формы
. Объяснение: Две точки — это форма для нахождения уравнения прямой, проходящей через две точки. X1 ,Y1 и X2 ,Y2, как показано ниже
Шаг 1: Наблюдение за данным графиком. 2 набора точек: {(2,0),(0,-3)} и {(4,0),(0,-6)}
Шаг 2: Нахождение уравнения для прямой, проходящей через {(2,0),(0,-3)}
Шаг 3: Нахождение уравнения для прямой, проходящей через {(4,0),(0,-6)}
∴ и – система линейных уравнений, представленная на графике.
Общий
Математика-
Какова точка пересечения по оси x графика 8x + 6y = 24 в плоскости xy?
ПОДСКАЗКА : x — точка пересечения находится в форме (a,0)(это точка пересечения прямой с осью x)
и удовлетворяет данному уравнению.
Объяснение
x-пересечение лежит в форме (a,0) и удовлетворяет заданному уравнению
Шаг 1: подставляем a,0 в данное уравнение 8x + 6y =24
8 a + 6 0 = 24
8 a = 24
a = = 3
∴ a = 3
∴ Пересечение по оси x (a,0) = (3,0)Каково пересечение по оси x графика 8x + 6y = 24 в плоскости xy?
Maths-General
ПОДСКАЗКА : x – точка пересечения имеет вид (a,0)(это точка пересечения прямой с осью x)
и удовлетворяет данному уравнению.
Объяснение
x-пересечение лежит в форме (a,0) и удовлетворяет заданному уравнению
Шаг 1: подставляем a,0 в данное уравнение 8x + 6y =24
8 a + 6 0 = 24
8 a = 24
a = = 3
∴ a = 3
∴ x-intercept (a,0) = (3,0)Общие
Математика-
Математический факультет колледжа планирует потратить 1 800 на покупку компьютеров и книг.
 Каждый компьютер стоит 300, а каждая книга — 90. Какое уравнение описывает эту ситуацию, где x — количество компьютеров, а y — количество книг, которые может купить отдел?
Каждый компьютер стоит 300, а каждая книга — 90. Какое уравнение описывает эту ситуацию, где x — количество компьютеров, а y — количество книг, которые может купить отдел?ПОДСКАЗКА: Общая сумма расходов равна сумме стоимости x компьютеров и y книг.
Объяснение :
Общая сумма расходов указана как 1800 долларов США, и эта сумма будет потрачена на книги (где стоимость каждой книги указана как 90 долларов США) и компьютер (где стоимость каждого компьютера указана как 300 долларов США) .
Общее количество компьютеров =x (дано)
Всего кол. книг =y(дано)
Шаг 1: Нахождение стоимости x компьютера = no. компьютеров стоимость каждого компьютера
= x 300 $
Нахождение стоимости y книг = кол. книг стоимость каждой книги
= y 90 долл. США
Шаг 2. Общая сумма расходов = 1 800 долл. США
стоимость x компьютеров + стоимость y книг = общая сумма расходов Математический факультет колледжа планирует потратить 1800 долл. США на покупку компьютеров и книг. Каждый компьютер стоит 300, а каждая книга — 90. Какое уравнение описывает эту ситуацию, где x — количество компьютеров, а y — количество книг, которые может купить отдел?
США на покупку компьютеров и книг. Каждый компьютер стоит 300, а каждая книга — 90. Какое уравнение описывает эту ситуацию, где x — количество компьютеров, а y — количество книг, которые может купить отдел?Общая математика
ПОДСКАЗКА: Общая сумма расходов равна сумме стоимости x компьютеров и y книг.
Объяснение :
Общая сумма расходов указана как 1800 долларов США, и эта сумма будет потрачена на книги (где стоимость каждой книги указана как 90 долларов США) и компьютер (где стоимость каждого компьютера указана как 300 долларов США) .
Общее количество компьютеров =x (дано)
Всего кол. книг =y(дано)
Шаг 1: Нахождение стоимости x компьютера = no. компьютеров стоимость каждого компьютера
= x 300 $
Нахождение стоимости y книг = кол. книг стоимость каждой книги
= y 90 долл. США
Шаг 2. Общая сумма расходов = 1 800 долл. США
стоимость x компьютеров + стоимость y книг = общая сумма расходов ОбщиеМатематика-
Что из следующего эквивалентно ?
○ В этом вопросе используется концепция сложения многочленов.

○ Расположите термины в порядке убывания их силы.
○ Чтобы добавить полиномы , просто сложите вместе любые похожие члены.
○ Подобные термины — это термины, переменные и показатели которых совпадают.- Пошаговое объяснение:
○ Приведено:
. (x 2 − x)
2x 2 — 2x + 3x 2 — 3x
○ Шаг 2:
○ Расположите члены в порядке убывания их мощности
∴ 2x
5x 2 — 5x
Следовательно, полином, эквивалентный выражению 2(x 2 — x) + 3(x 29007), равен 7(x 29007)
5x 2 — 5x.- Окончательный ответ:
Правильный вариант,
Вариант А. 5x 2 — 5x.Что из следующего эквивалентно ?
Maths-General
○ В этом вопросе используется концепция сложения многочленов.

○ Расположите термины в порядке убывания их силы.
○ Чтобы добавить полиномы , просто сложите вместе любые похожие члены.
○ Подобные термины — это термины, переменные и показатели которых совпадают.- Пошаговое объяснение:
○ Приведено:
2x 2 — 2x + 3x 2 — 3x
. (х 2 — х)
○ Шаг 2:
○ Организуйте термин в порядок уменьшения их мощности
∴ 2x 2 + 3x 2 — 2x — 3x
5x 2x 2 — 2x — 3x
5x 2x 2. — 5x
Следовательно, полином, эквивалентный выражению 2(x 2 — x) + 3(x 2 — x), равен
5x 2 — 5x.- Окончательный ответ:
Правильный вариант,
Вариант А. 5x 2 — 5x.Общие
Математика-
Каково значение x + y для приведенной выше системы уравнений?○ Концепция, используемая в вопросе, представляет собой концепцию решения линейных уравнений.

○ Данные уравнения являются линейными уравнениями с двумя переменными.○ Методы решения линейных уравнений.
- Графический метод
- Метод исключения
- Метод замены
- Метод перекрестного умножения
- Матричный метод
- Метод определителей
○ В методе исключения любой из коэффициентов сначала приравнивается и исключается. После исключения уравнения решаются, чтобы получить другое уравнение.
Дано:
2x — y = 8
x + 2y = 4
○ Шаг 1:
○ Пусть,
2x — y = 8 ——— ур. ——-eq.2
○ Шаг 2:
○ Теперь приравняйте коэффициент x
∴ умножить уравнение 2 на 2
[ x + 2y = 4 ] 2
2x + 4y = 8 ——- ур.3
○ Шаг 3:
○ Теперь вычтите уравнение ур. 3 из уравнения 1
2x — y = 8
— 2x — 4y = — 8
———————
-5y = 0
∴ y = 0
○ Шаг 4:
○ Положим y = 0 в уравнение 1
2x — y = 8
2x — 0 = 8
2x = 8
x=
x = 4
(x y 3) Поэтому ,
x + y = 4 + 0
x + y = 4- Окончательный ответ:
Правильный вариант:
Вариант C. 4.
4.
Каково значение x + y для приведенной выше системы уравнений?Maths-General
○ Концепция, используемая в вопросе, представляет собой концепцию решения линейных уравнений.
○ Данные уравнения являются линейными уравнениями с двумя переменными.○ Методы решения линейных уравнений.
- Графический метод
- Метод исключения
- Метод замены
- Метод перекрестного умножения
- Матричный метод
- Метод определителей
○ В методе исключения любой из коэффициентов сначала приравнивается и исключается. После исключения уравнения решаются, чтобы получить другое уравнение.
- Пошаговое объяснение:
Дано:
2x — y = 8
x + 2y = 4
○ Шаг 1:
○ Пусть,
2x — y = 8 ——— ур. ——-уравнение 2
○ Шаг 2:
○ Теперь приравняйте коэффициент x
∴ умножьте уравнение 2 на 2
[ x + 2y = 4 ] 2
2x + 4y = 8 —— уравнение 3
○ Теперь 0 Шаг 2 3: 0 вычесть уравнение ур. 3 из уравнения 1
3 из уравнения 1
2x — y = 8
— 2x — 4y = — 8
———————
-5y = 0
∴ y = 0
○ Шаг 4:
○ Положим y = 0 в уравнение 1
2x — y = 8
2x — 0 = 8
2x = 8
x=
x = 4
(x y 3) Поэтому ,
х + у = 4 + 0
x + y = 4- Окончательный ответ:
Правильный вариант:
Вариант C. 4.Общие
Общие
Закон Ома применим только к
Омическим проводникам
- Закон Ома применим только к омическим проводникам.
Закон Ома применим только к
GeneralGeneral
Только к омическим проводникам
- Закон Ома применим только к омическим проводникам.
В Академии Турито.
С Фондом Турито.
Получите экспертную консультацию от Turito.
Академия Турито
С Академией Турито.

Подготовка к экзаменам
С Фондом Турито.
Узнайте о графиках экспоненциальных функций
В этом видео мы рассмотрим графики экспоненциальных функций. После того, как вы закончите этот урок, просмотрите все наши уроки по алгебре 1 и практические задачи.
Пример графика экспоненциальной функции
График
становится более крутым в положительном направлении по мере увеличения значений x после построения точек, как показано на видео.
График
становится более крутым в отрицательном направлении по мере увеличения значений x после построения точек и является отражением по оси x первого графика.
График
становится круче медленнее по мере увеличения значений x после построения точек и является отражением по оси y
Пример графиков экспоненциальных функций
Пример 1
, когда тогда
Затем,
Затем,
, а затем
График будет:
Пример 2
, когда тогда:
.

затем ,
затем ,
и затем
График будет таким:
Стенограмма видеоурока
Давайте пройдемся по графикам экспоненциальных функций.
Прежде всего, что такое экспоненциальная функция?
Экспоненциальная функция имеет форму
Что-то, что должно выделиться, это то, что это любой показатель степени. А и постоянны.
Давайте сначала рассмотрим функции, которые .
Итак, решим для и .
Для демонстрации возьмем
Давайте рассмотрим некоторые из них.
Когда тогда ,
потом ,
потом ,
потом ,
потом ,
потом .Я хочу отметить, когда тогда .
Когда мы изображаем положительную экспоненту, это не будет прямая линия. Она увеличивается гораздо более высокими темпами. Он даже изгибается резко.
Когда мы наносим на график отрицательные показатели, он будет искривляться, но не будет касаться -оси.
Потому что даже если показатель степени отрицательный, он просто превращается в дробь, а не в отрицательное число.

Итак, это базовый график экспоненциальной дроби.
Это .
Посмотрим на график .
Пусть у нас будут те же точки здесь.
Тогда начнем.
Когда тогда ,
потом ,
потом ,
потом ,
потом ,
потом .Очень крутой в положительных показателях и очень низкий в отрицательных показателях.
Но все равно не коснется -оси.
Построим график .
Позвольте мне немного изменить значения.
Снова начнем с .
Когда тогда ,
когда тогда ,
и когда тогда .Если вы посмотрите на это, это зеркальное отражение нашего первого примера.
Когда тогда ,
когда тогда ,
а потом .Это будет очень близко к -оси.
Негатив будет отражен по -оси.
Посмотрим еще на один.
Пусть будет
Итак, давайте начнем снова, потому что любое число, возведенное в степень, равно .
Когда тогда ,
когда тогда ,
и когда тогда .

 2+2x).
2+2x).
 » — символ возведения в степень. Однако запись типа =СТЕПЕНЬ(a;b) является более наглядной.
» — символ возведения в степень. Однако запись типа =СТЕПЕНЬ(a;b) является более наглядной. Легкие признаки и симптомы часто похожи на симптомы простуды или гриппа, но они длятся дольше.
Легкие признаки и симптомы часто похожи на симптомы простуды или гриппа, но они длятся дольше.
 Mycoplasma pneumoniae также может вызывать пневмонию. Обычно он вызывает более легкие симптомы, чем другие виды пневмонии. Ходячая пневмония – это неофициальное название для данного типа пневмонии, которая обычно недостаточно серьезна, чтобы требовать постельного режима.
Mycoplasma pneumoniae также может вызывать пневмонию. Обычно он вызывает более легкие симптомы, чем другие виды пневмонии. Ходячая пневмония – это неофициальное название для данного типа пневмонии, которая обычно недостаточно серьезна, чтобы требовать постельного режима. Больничная пневмония может быть серьезной, потому что бактерии, вызывающие ее, могут быть более устойчивыми к антибиотикам и потому, что люди, которые ее получают, уже больны и ослаблены. Люди, которые находятся на дыхательных аппаратах (ИВЛ), часто используемых в отделениях интенсивной терапии, подвержены более высокому риску этого типа пневмонии.
Больничная пневмония может быть серьезной, потому что бактерии, вызывающие ее, могут быть более устойчивыми к антибиотикам и потому, что люди, которые ее получают, уже больны и ослаблены. Люди, которые находятся на дыхательных аппаратах (ИВЛ), часто используемых в отделениях интенсивной терапии, подвержены более высокому риску этого типа пневмонии.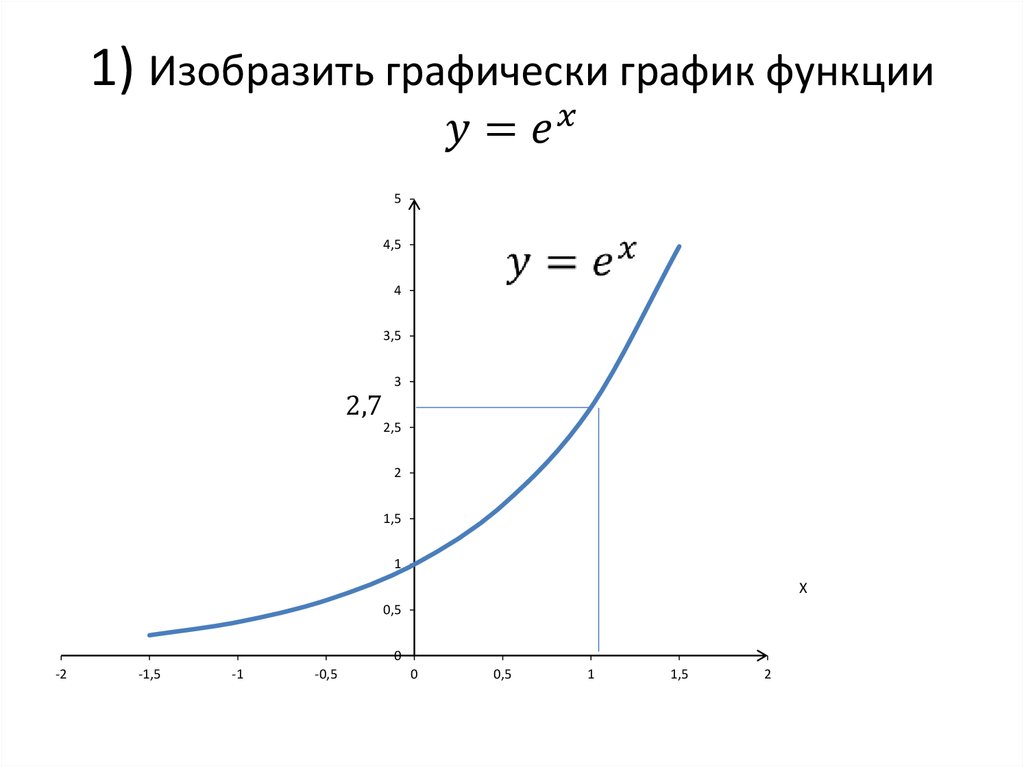
 Бактерии, попадающие в кровь из легких, могут распространить инфекцию на другие органы, что может стать причиной нарушения функции этих органов и дальнейшего прогрессирования заболевания.
Бактерии, попадающие в кровь из легких, могут распространить инфекцию на другие органы, что может стать причиной нарушения функции этих органов и дальнейшего прогрессирования заболевания.

 Что из следующего лучше всего описывает перевод?
Что из следующего лучше всего описывает перевод?
 Чему равен угол DEF?
Чему равен угол DEF?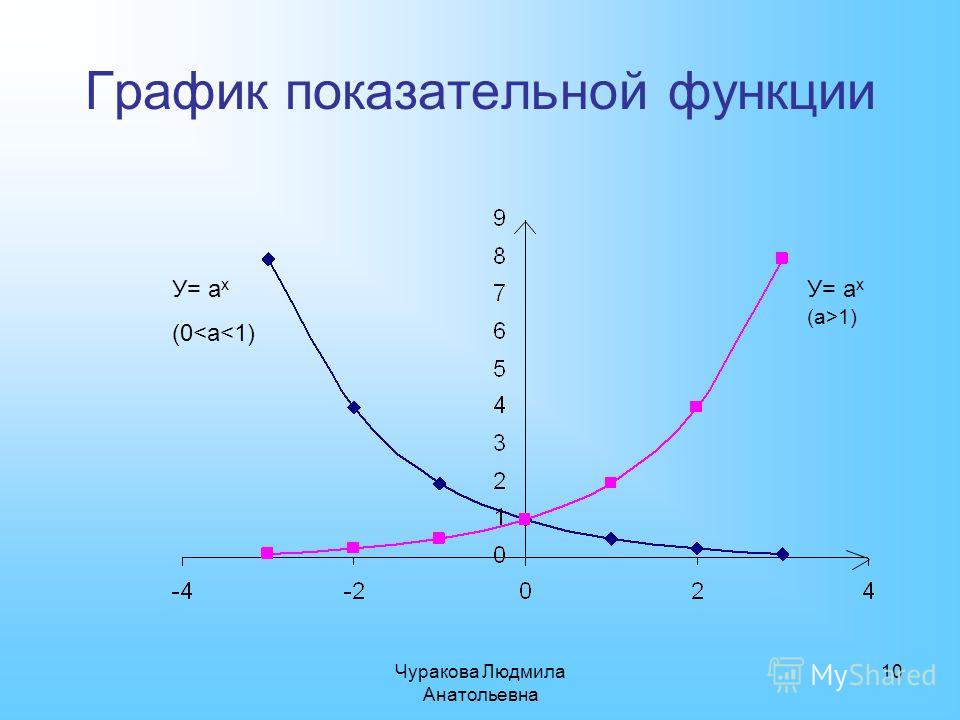 Основываясь на модели, каким был пульс Джека в ударах в минуту, когда его скорость равнялась 0 км/ч?
Основываясь на модели, каким был пульс Джека в ударах в минуту, когда его скорость равнялась 0 км/ч?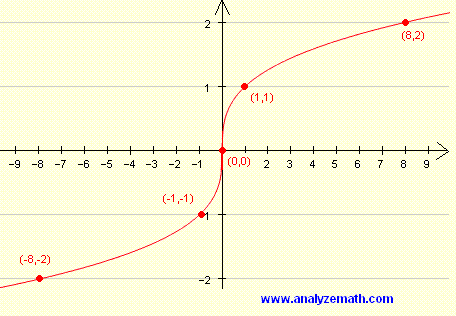 Таким образом, пульс составляет 63 в соответствии с вариантом проверки только вариант находится между 60-65 это вариант C.
Таким образом, пульс составляет 63 в соответствии с вариантом проверки только вариант находится между 60-65 это вариант C.  Объяснение: Две точки — это форма для нахождения уравнения прямой, проходящей через две точки X1, Y1 и X2. ,Y2, как показано ниже
Объяснение: Две точки — это форма для нахождения уравнения прямой, проходящей через две точки X1, Y1 и X2. ,Y2, как показано ниже 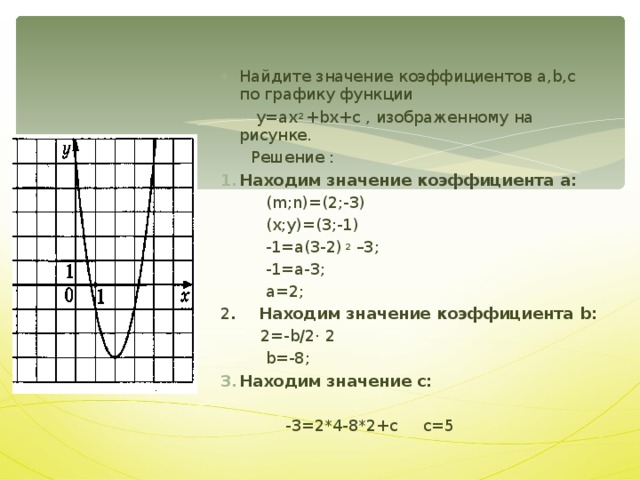
 Каждый компьютер стоит 300, а каждая книга — 90. Какое уравнение описывает эту ситуацию, где x — количество компьютеров, а y — количество книг, которые может купить отдел?
Каждый компьютер стоит 300, а каждая книга — 90. Какое уравнение описывает эту ситуацию, где x — количество компьютеров, а y — количество книг, которые может купить отдел? США на покупку компьютеров и книг. Каждый компьютер стоит 300, а каждая книга — 90. Какое уравнение описывает эту ситуацию, где x — количество компьютеров, а y — количество книг, которые может купить отдел?
США на покупку компьютеров и книг. Каждый компьютер стоит 300, а каждая книга — 90. Какое уравнение описывает эту ситуацию, где x — количество компьютеров, а y — количество книг, которые может купить отдел?
 4.
4. 3 из уравнения 1
3 из уравнения 1