График функции параметрической онлайн: Построить график функции, параметрической функции, график в полярной системе координат онлайн

grafikus.ru… Построить график функции, параметрической функции, график в …. Реформал.

Основные сведения:

Рейтинг:
Адрес: http://grafikus.ru
О сайте: Анализ данных grafikus.ru показал, что у этого домена отсутствует рейтинг Alexa и посещаемость данного сайта неизвестна. Лидирующую позицию по доле трафика занимает Россия (78,6%), а владельцем домена является Private Person.
Заголовок: Построить график функции, параметрической функции, график в полярной системе координат онлайн
Мета-описание: Сервис позволяет строить графики различных алгебраических функций. В частности, можно построить график параметрической функции и функции, заданной в полярных координатах, а также график по точкам. . Сервис Grafikus предназначен для построения графиков различных функций в двумерных и трехмерных …
Рейтинг Alexa Нет данных	Посетителей в день Нет данных	Просмотров в день Нет данных
Статус: Онлайн	Дата последней проверки: 3 Декабря 2022

Наиболее популярные страницы домена:

• Построить график функции, параметрической функции, график в полярной системе координат онлайн

  Сервис позволяет строить графики различных алгебраических функций. В частности, можно построить график параметрической функции и функции, заданной в полярных координатах, а также график по точкам.

• Помощь

  Справочный раздел сайта. Содержит список поддерживаемых функций и примеры записи формул.

Другие домены этого хостинг-провайдера (Hetzner Online GmbH):

elecgate.com

eurostroyconsult.ru

relianz.co.za

alastairbathgate.com

gisaid.org

zante-paradise.com

Географическое распределение аудитории для grafikus.ru:

Страна	Доля посетителей	Рейтинг по стране
Россия	78,6%	96 429
Украина	15,4%	61 621

Информация о домене:

Возраст домена:	11 лет
Владелец:	Private Person
Регистратор:	REGRU-RU http://www. ripn.net

Другие домены, которые могут быть вам интересны:

beta.mamsy.ru

loong.gamigo.com

hortzone.com

candystripeparty.co.uk

heatherfrendo.wordpress.com

Открытая Математика. Функции и Графики. Построение кривых, заданных параметрически

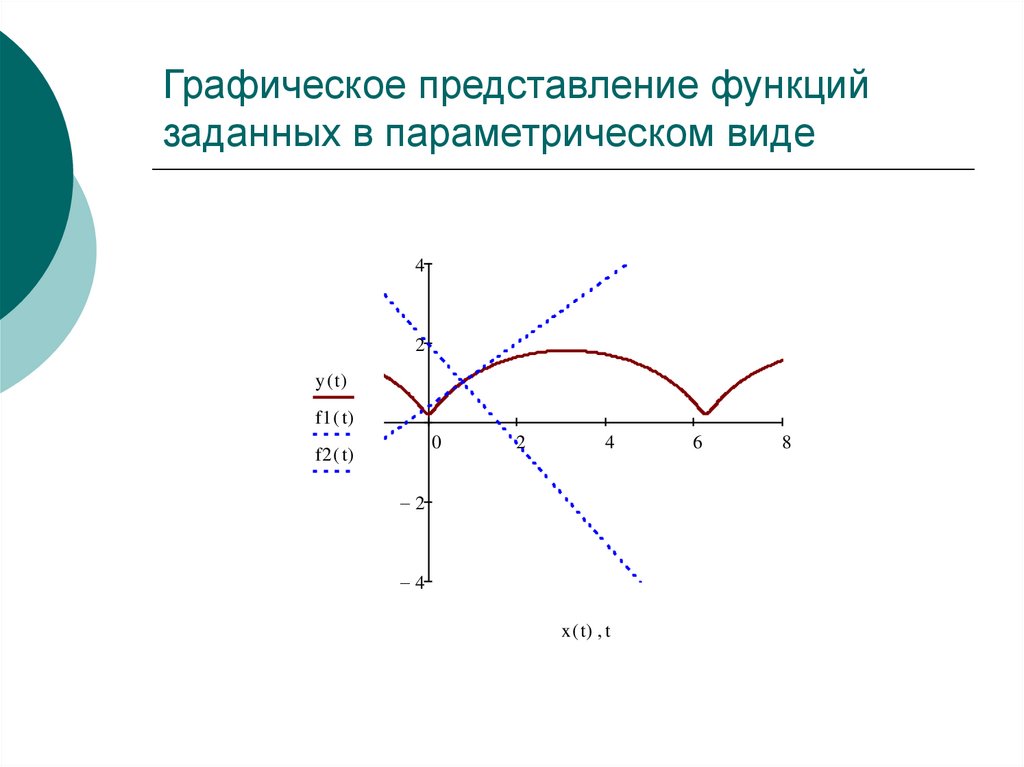
Построение кривых, заданных параметрически

При построении кривых, заданных параметрически: x = x (t), y = y (t), можно придерживаться следующего плана.

1. Найти области определения D_x (t) и D_y (t) функций x (t) и y (t).
2. Найти область определения Dt=Dxt∩Dyt функции, заданной параметрически.
3. Решив уравнения x (t) = 0, y (t) = 0, найти точки пересечения с осями координат.
4. Вычислить производные x′t и y′t.
5. Определить производную y′x=y′tx′t. Найти критические точки.
6. На каждом из интервалов, границами которых служат критические точки, определить знак производной y′x и промежутки возрастания и убывания функции y (x), заданной параметрически.
7. Определить экстремумы функции, а также точки, касательная к которым вертикальна (производная y′x в этих точках обращается в бесконечность).
8. Определить особые точки графика, в которых x′t=0 и (или) y′t=0.
9. Найти пределы limt→t0xt и limt→t0yt в точках t₀, лежащих на границах области определения.
   • Если оба предела конечны, найти касательную к кривой в точке x0=limt→t0xt,  y0=limt→t0yt.
   • Если один из пределов конечен, а второй бесконечен, то кривая имеет горизонтальную y = y₀ или вертикальную x = x₀ асимптоту.
   • Если оба предела бесконечны, то найти наклонную касательную, вычислив пределы k=limt→t0ytxt,   b=limt→t0yt-kxt. Если один из этих пределов не существует, то асимптоты нет.
10. Вычислить производную y′′xx=y′′ttx′t-y′tx′′ttx′t3 и определить точки перегиба функции и направление выпуклости на каждом из интервалов, ограниченных точками перегиба или точками, в которых вторая производная не существует.
11. Выяснить, существуют ли точки самопересечения графика функции, решив систему {xt1=xt2yt1=yt2,  t1≠t2
12. Проверить график функции на симметричность.
    • График функции симметричен относительно точки (a; b), если при любом t можно найти такое t₁, что {xt+xt1=2ayt+yt1=2b.
    • График функции симметричен относительно прямой ax + by + c = 0, если при любом t можно найти такое t₁, что {axt1+xt+byt1+yt+2c=0bxt1-xt=ayt1-yt. В частности, график функции симметричен относительно прямой y = x, если при любых t имеет решение система {xt=yt1yt=xt1.





 

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».

Исчисление II. Параметрические уравнения и кривые (практические задачи)

Онлайн-заметки Пола
Главная / Исчисление II / Параметрические уравнения и полярные координаты / Параметрические уравнения и кривые

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана (

т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 9.1: Параметрические уравнения и кривые 92}\hspace{0.5in}0 \le t \le 3\) Решение

\(\displaystyle x = \sqrt {t + 1} \hspace{0.5in}y = \frac{1}{{t + 1}} \hspace{0.5in} t > — 1\) Решение

\(x = 3\sin \left( t \right)\hspace{0.5in}y = — 4\cos \left( t \right) \hspace{0.5in} 0 \le t \le 2\pi \ ) Решение

\(x = 3\sin \left( {2t} \right)\hspace{0.5in}y = — 4\cos \left( {2t} \right) \hspace{0.5in}0 \le t \le 2\пи\) Решение

\(\ displaystyle x = 3 \ sin \ left ( {\ frac {1} {3} t} \ right) \ hspace {0.5in} y = — 4 \ cos \ left ( {\ frac {1} {3 }t} \right) \hspace{0. 5in}0 \le t \le 2\pi \) Решение

Для задач 7 – 11 путь частицы задается системой параметрических уравнений. Полностью описать путь частицы. Чтобы полностью описать путь частицы, вам потребуется предоставить следующую информацию.

1. Эскиз параметрической кривой (включая направление движения) на основе уравнения, полученного путем исключения параметра.
2. Ограничения на \(x\) и \(y\).
3. Диапазон значений \(t\) для одной трассы параметрической кривой. 92}}}{{49}} = 1\), а параметрическая кривая, полученная из параметрических уравнений, должна быть в точке \(\left( {0, — 7} \right)\), когда \(t = 0\) и кривая должна иметь вращение по часовой стрелке. Решение

Графический калькулятор

Самый совершенный в мире графический калькулятор для построения графика

из функций , уравнений (включая неявно определенных функций ), параметрических кривыхнаборы точек в декартовой и полярной системах координат . Решите для x-отрезков графика функции. Рассчитать и график производные функции и параметрические кривые . Animate полярные графики из функций и параметрические графики наиболее подходящим образом.

Графический калькулятор 92 — dx + ey — f = 0 , который может быть окружностью , эллипсом , параболой ,

гиперболой или некоторыми вырожденными графами), а также графиком кривых уровня , которые имеют форму 83 F 90 (х, у) = с .

В отличие от других графических программ, этот графический калькулятор также может строить графики в неперпендикулярных (или неортогональных ) декартовых системах координат , где оси не обязательно должны быть горизонтальными или вертикальными и могут пересекаться в любой угол. 9. Кроме того, графический калькулятор способен анимировать график параметрических уравнений как в декартовой , так и в полярной системах координат . Таким образом, декартовых и polar графический калькулятор показывает, как эти типы графиков строятся постепенно от начального значения до конечного значения в их заданной области (интервале).

Кроме того, этот графический калькулятор можно использовать для решения уравнения s для нахождения точек пересечения по оси ( нулей или корней ) заданной функции.

Кроме того, вы можете использовать этот графический калькулятор производных от до Рассчитайте производные из 1 ^ST и 2 ^nd Порядок из данного Функция или Параметрическая кривая и График Их Дерваты .

Примечание: для вычисления производных более высокого порядка, а также частных производных функций с несколькими переменными можно использовать калькулятор частных производных.

Анимация вращения оси: Икс у ► ⬛

сообщение

 

f(x) =

?

f( ) =

 

⌨

4 Десятичные разряды

График FinenessBest (медленно)+2+1Normal-1-2Fast (низко)

Label Axes ось x: ось y: Повернуть оси Ось x°: Ось Y°:

⚙

РезультатыСкрыть

Наложение Прозрачный

Функции

92-4)

Прочие графики

√(4sin(2x)) √(4cos(2x))

Функции – Polar

Линии

2csc(θ) 2сек(θ) 1/(sin(θ) — cos(θ))

Круги

1 2 6sin(θ) 8cos(θ)

Спирали

θ θ/5 дом=(0, 10π) √(θ) дом=(0, 10π) 1/θ дом=(0, 10π)

Розы

4sin(3θ) 4sin(2θ) 4sin(5θ) 4sin(4θ)

Эллипсы

1/(1-. 8cos(θ)) 1/(1-0,8sin(θ)) 1/(1+.8cos(θ)) 1/(1+.8sin(θ))

Параболы

1/(1-sin(θ)) 1/(1+cos(θ)) 1/(1+sin(θ)) 1/(1-cos(θ))

Гипербола

1/(1+2cos(θ)) 4/(1+2sin(θ)) 1/(1-2cos(θ)) 4/(1-2sin(θ))

Кардиоиды

3+3cos(θ) 2+2sin(θ) 3-3cos(θ) 2-2sin(θ)

Лимаконс

2+3cos(θ) 1+2sin(θ) 2-3cos(θ) 1-2sin(θ)

Лемнискат 92 грех (ху) = потому что (ху)

Уравнения — Polar

В настоящее время недоступно.

Параметрический

Линии

[т, 1] дом=(-5, 5) [1,t] дом=(-5, 5) [т, 2т] дом=(-5, 5)

Круги

[4sin(t), 4cos(t)] [3sin(t)+1, 3cos(t)+1]

Эллипсы

[4cos(t), 3sin(t)] [3cos(t), 4sin(t)] [4sin(t), 3cos(t)] [3sin(t), 4cos(t)]

Параболы

[т, т^2] дом=(-4, 4) [т ^ 2, т] дом = (-4, 4) 95)] дом=(0, 12π)

Параметрический – Полярный

Линии

[2csc(t), t] [2сек(т), т] [1/(sin(t) — cos(t)), t]

Круги

[1, т] [2, т] [6sin(t), t] [8cos(t), t]

Спирали

[т, т] [t/5, t] dom=(0, 10π) [√(t), t] дом=(0, 10π) [1/t, t] dom=(0, 10π)

Розы

[4sin(3t), т] [4sin(2t), т] [4sin(5t), т] [4sin(4t), т]

Эллипсы

[1/(1-. 8cos(t)), т] [1/(1-.8sin(t)), т] [1/(1+.8cos(t)), т] [1/(1+.8sin(t)), т]

Параболы

[1/(1-sin(t)), t] [1/(1+cos(t)), t] [1/(1+sin(t)), t] [1/(1-cos(t)), t]

Гипербола

[1/(1+2cos(t)), t] [4/(1+2sin(t)), t] [1/(1-2cos(t)), t] [4/(1-2sin(t)), t]

Кардиоиды

[3+3cos(t), t] [2+2sin(t), t] [3-3cos(t), t] [2-2sin(t), t]

Лимаконс

[2+3cos(t), t] [1+2sin(t), t] [2-3cos(t), t] [1-2sin(t), t]

Лемнискаты

[√(4sin(2t)), т] [√(4cos(2t)), т]

Прочие параметрические графики

[5sin(t), 4cos(t)] [5sin(t), 4cos(2t)] [5sin(t), 4cos(3t)] [5sin(2t), 4cos(t)] [5sin(2t), 4cos(3t)] [5sin(2t), 4cos(5t)] [5sin(3t), 4cos(5t)] [5sin(3t), 4cos(7t)] [5sin(5t), 4cos(7t)] [5sin(7t), 4cos(9t)]

РАД Полярный

🔍+ 1 🔍−

время построения графика (с)

Калькулятор загружается.
Пожалуйста, подождите….

Сделайте это прозрачным

Толщина графика Угловой режим РАД градус ГРД График по мере ввода (взаимодействие) Скрыть оси Скрыть сетки Показать интерфейс анимации осей

заголовок

…

Медленно Быстро

Показать угловые оси Выполнено

Отключить виртуальную клавиатуру

Чтобы скопировать или сохранить графики, щелкните правой кнопкой мыши изображение сохраненного графика ниже и выберите «Копировать изображение» или «Сохранить изображение» во всплывающем меню.

Графический калькулятор прост в использовании ; введите выражение ( функция , уравнение , параметрическое или набор точек ) в любое поле выражения. Графический калькулятор определяет тип выражения и графики, когда вы вводите (по умолчанию) в выбранных система координат . (Не беспокойтесь о том, какую переменную (x, y, t, θ) вы используете, графический калькулятор автоматически изменяет переменные в соответствии с типом выражения и выбранной системой координат .)

• В график два или более выражения в одной и той же декартовой или полярной системе координат нажмите » для отображения мультиграфической панели . Панель с несколькими графиками состоит из панели экспрессии , которые можно добавить или удалить по желанию, нажав + или × на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.
• Для удобства графический калькулятор добавляет подходящий интервал, dom = (0, 2π) или dom = (-∞, ∞) соответственно к функциям, параметрическим выражениям и графикам в указанной области. При желании можно изменить конечные точки . Конечные точки должны быть конечными для построения полярных или параметрических графиков. Графический калькулятор автоматически изменяет бесконечности, если таковые имеются, на конечные значения. Графики рисуются по мере ввода.
• Вы можете Анимировать полярный график функции или параметрические кривые (как в декартовой, так и в полярной системе координат), чтобы увидеть, как они построены.
  • Вы можете использовать эту чрезвычайно полезную функцию, нажав ► в нижней части графический калькулятор (если он скрыт, сначала нажмите кнопку Animate ).
  • Запускает анимацию процесса полярного построения графика функции или процесса параметрического построения графика параметрического выражения в фокусе . График рисуется последовательно от начального значения до конечного значения в указанной области.
  • Затем вы можете нажать || до пауза анимация или нажмите Готово до остановить это. Это также закрывает интерфейс анимации. Чтобы отобразить его снова, нажмите кнопку Animate в верхней части полярного графа.
  • Вы также можете изменить скорость из графической анимации с помощью ползунка , предоставленного
• Можно установить четкость графиков , выбрав нужный вариант из Раскрывающийся список Graph Fineness . В целом, чем выше точность, тем больше времени требуется графическому калькулятору для построения графиков.
• При построении графика с использованием декартовой системы координат этот графический калькулятор способен строить графики в неперпендикулярной декартовой системе координат путем вращения осей. Введите количество углов, на которые вы хотите повернуть оси, и нажмите Применить .
• Вы также можете пометить ось любым числом (π, π/2, 1+√2 и т. д.).
• Чтобы скопировать или сохранить графики, сначала нажмите кнопку Копировать/Сохранить график . Изображение графиков появится под графическим калькулятором . Затем вы можете использовать возможности вашего браузера, чтобы сохранить его или скопировать его в ваши документы.
• Чтобы оценить функцию или параметрическое выражение введите номер или числовое (постоянное) выражение в соответствующем поле; графический калькулятор отображает рассчитанные значения с количеством знаков после запятой, которое можно указать с помощью предоставленного ползунка.
• Графический калькулятор можно использовать в качестве решателя уравнений для нахождения пересечений по оси x ( нулей или корней ) функции. Нажмите кнопку Решить , чтобы решить уравнение f(x) = 0 .
• Кроме того, вы можете использовать графический калькулятор как калькулятор производных . Нажмите кнопку Производная , чтобы вычислить 1 ^st и 2 ^nd заказать производные функций и 70 параметрических кривых и . Затем вы можете построить график производных .

Подсказки: По мере ввода:

• пи заменяется на π ,
• inf ( бесконечность ) заменяется на ∞ и
• ..t заменяется на θ .

Для построения графика кусочно-определенных функций или кусочно-определенных параметрических кривых введите в каждом отрезке с соответствующим подынтервалом как одиночную функцию или одиночное параметрическое выражение .

Самый быстрый способ набрать dom=(0, 2π) или dom=(-∞, ∞) путем полного удаления домена, включая dom= .

---

Примечание : Поскольку значения тригонометрических функций зависят от выбранного вами углового режима, графики выражений, содержащих тригонометрических функций , как и ожидалось, будут отличаться при переходе от режима RAD (

3 по умолчанию ) в другие режимы.

---

Вращение оси, перемещение и изменение масштаба с помощью мыши

В дополнение к вводу данных вы также можете использовать мышь для выполнения некоторых функций, уникальных для этого интерактивного графического калькулятора , как описано ниже.

• Щелкните по оси (или рядом с ней) и переместите указатель мыши на , чтобы повернуть ось . график(ы) построен(ы) в неперпендикулярной декартовой системе координат или обобщенной полярной системе координат . Нажмите еще раз, чтобы освободить ось.
• Перетащите мышь на , переместите систему координат вместе с графиками.
• Дважды щелкните на холсте, чтобы переместить начало координат туда, где был сделан щелчок.
• Удерживая клавишу Alt, щелкните по оси, чтобы изменить масштаб (масштабировать в одном направлении) ; в точка, по которой был сделан щелчок, будет помечена как «1» (или «-1») и станет новой единицей измерения для этой оси.

---

Примечание : Если выбрано График по мере ввода , графики автоматически обновляются при выполнении вышеуказанных действий и вообще при любом взаимодействии с графическим калькулятором, т. е. при наборе текста, работе с мышью и нажатии кнопки. В противном случае, вы должны нажать График выбранных выражений , чтобы отразить сделанные вами изменения.

Вы можете установить следующие параметры, нажав кнопку ⚙ (шестеренка) в правом верхнем углу графического холста.

• Измените толщину графиков с помощью предоставленного ползунка.
• Выберите режим угла ( радиан — по умолчанию , градусов или градусов ).
• Если вы отмените выбор График при вводе , вам нужно будет нажать График выбранных выражений , который затем появится в нижней части калькулятора, чтобы обновлять графики всякий раз, когда вы вносите какие-либо изменения в выражения или координатную плоскость (т. е. перемещаете начало координат, вращаете оси и т. д.). .).
• При необходимости отобразите элементы управления в верхней части графического калькулятора , которые позволяют вам запустить, / приостановить и остановить вращение любой или всех осей.
• Графический калькулятор запоминает введенные вами выражения и извлекает их между посещениями. Вы можете очистить их, нажав кнопку Сброс калькулятора .

  No related posts.