 2$
2$ Функции вида $f(x)=\sin x, g(x)=\cos x, h(x)=\tan x, k(x)=\cot x$ называются тригонометрическими функциями. Область определения $f(x)=\sin x $ и $g(x)=\cos x$ это все действительные числа $\mathbb{R}$. А области определения $h(x)=\tan x $ и $k(x)=\cot x$ следующие: $h(x)=\tan x=\dfrac{\sin x}{\cos x}, \cos x=0 \rightarrow x=k\pi+\dfrac{\pi}{2} \rightarrow$
$D_h=\mathbb{R}-\lbrace x|x=k\pi+\dfrac{\pi}{2}, k \in \mathbb{Z} \rbrace$
$h(x)=\cot x=\dfrac{\cos x}{\sin x}, \sin x=0 \rightarrow x=k\pi \rightarrow$$D_k=\mathbb{R}-\lbrace x|x=k\pi, k \in \mathbb{Z} \rbrace$
Также отметим, что $-1 \leq \sin x \leq 1 $ и $ -1 \leq \cos x \leq 1$. Следовательно,$R_f=[-1,1] \,\,\,\,\,\, R_g=[-1,1]$
Множество значений of $h(x)=\tan x $ и $k(x)=\cot x$ это все действительные числа $\mathbb{R}$.Пример:
Найти область определения и множество значений $f(x)=\sin x+\cos x$.
Решение:
Область определения $\sin x $ и $\cos x$ это все действительные числа, следовательно область определения
$f(x)=\sin x+\cos x$
также все действительные числа. 4 \pi x = 0 \rightarrow \sin \pi x=0 \rightarrow \pi x=k \pi \rightarrow x=k \in \mathbb{Z}$ Значит
4 \pi x = 0 \rightarrow \sin \pi x=0 \rightarrow \pi x=k \pi \rightarrow x=k \in \mathbb{Z}$ Значит$D_f=\mathbb{Z}$
Согласно $D_f=\mathbb{Z}$, можно переписать функцию как$f(x)=\cos \pi x=\pm 1$
Теперь очевидно, что$R_f= \lbrace \pm 1 \rbrace$
Пример:
Найти область определения и множество значений $f(x)=\sin (\log (\log x))$.
Решение:
Согласно тому, что уже было сказано относительно логарифмической функции
$D_f= \lbrace x| x \in \mathbb{R}; \log x>0,x>0 \rbrace$
$= \lbrace x| x\in \mathbb{R}, x>1,x>0 \rbrace =(1,+\infty)$
Также стоит отметить, что$|\sin (\log (\log x))| \leq 1 \rightarrow |y| \leq 1 \rightarrow -1 \leq y \leq 1$
Значит$R_f=[-1,1]$
График $f$ этоОпределение:
Пусть $f$ функция, у которой область определения это $D_f$. Функция $f$ является инъективной тогда и только тогда, если для всех $x_1$ и $x_2$ в $D_f$, если $f(x_1)=f(x_2)$, то $x_1=x_2$.
 {\log x} \rightarrow y=(f \circ g)_{(x)}\,\,\, x \in (0,1) \rightarrow 0
Теперь, для того, чтобы найти множество значений $g \circ f$, отметим, что
{\log x} \rightarrow y=(f \circ g)_{(x)}\,\,\, x \in (0,1) \rightarrow 0
Теперь, для того, чтобы найти множество значений $g \circ f$, отметим, что$Z=(g\circ f)_{(x)}=x \rightarrow x=Z\in (1,+\infty) \rightarrow Z>1 \rightarrow R_{g \circ f}=(1,+\infty)$
Графиком $f$ являетсяГрафиком $g$ является
График $f \circ g$ это
График $g \circ f$ это
Пример:
Если $f(x)=x-1$ and $(f \circ g)_{(x)}=\dfrac{1}{x-1}$, то найти область определения и множество значений $g \circ f$.
Решение:
Сначала найдем $ g \circ f$
$f(x)=x-1 \rightarrow f(g(x))=g(x)-1 \rightarrow (f \circ g)_{(x)}=g(x)-1 \rightarrow \\ \dfrac{1}{x-1}=g(x)-1 \rightarrow g(x)=\dfrac{x}{x+1}$
Значит$y=(g \circ f)_{(x)}=g(f(x))=\dfrac{f(x)}{f(x)-1}=\dfrac{x-1}{x+1}$
Следовательно$D_{g \circ f}=\lbrace x|x \in \mathbb{R}, x \neq 2 \rbrace \rightarrow D_{g \circ f}=\mathbb{R}-\lbrace 2 \rbrace$
Также$y=\dfrac{x-1}{x-2} \rightarrow x=\dfrac{2y-1}{y-1}$
$R_{g \circ f}=\lbrace y | y \in \mathbb{R}, y \neq 1 \rbrace \rightarrow$
$R_{g \circ f}=\mathbb{R}-\lbrace 1 \rbrace$
График $f$ этоГрафик $f \circ g$ это
Графиком $g$ является
Графиком $g \circ f$ является
Упражнения
1) Если $f(x)=2^{\log_2 x}$ and $g(x)=\dfrac{x-1}{x^2-x}$, то найти область определения и множество значений $f \circ g$.
 2 2kx \,\,\, -1 \leq \sin 2kx \leq 1$
2 2kx \,\,\, -1 \leq \sin 2kx \leq 1$$\rightarrow \sin 2kx= \pm 1 \rightarrow y=\dfrac{1}{4} , \sin 2x=0 \rightarrow y=1$
$\rightarrow \dfrac{1}{4} \leq y \leq 1 \rightarrow R_f=[\dfrac{1}{4},1]$
Part 1
Компания КНАУФ провела обучающие курсы для студентов-первокурсников Для студентов 1 курса Новосибирского государственного архитектурно-строительного университета (Сибстрин) партнер вуза – компания КНАУФ – провела обучающие курсы. В период летней практики, с 23 июня по 2 июля, первокурсники прошли обучение по программам «Материалы и технологии КНАУФ» и «Сухие смеси». Студенты познакомились с сухими смесями на основе гипсового, цементного, а также полимерного вяжущих и необходимыми материалами для создания комплектных систем КНАУФ. Теоретические знания были закреплены на практике, в ходе которой студенты самостоятельно собрали макет перегородки с соблюдением всех необходимых рекомендаций, поработали со штукатурными и шпаклевочными растворами, после чего все успешно сдали тестирование. |
Важное направление подготовки «Природообустройство и водопользование»: много бюджетных мест Новосибирский государственный архитектурно-строительный университет (Сибстрин) ждет абитуриентов на направление подготовки «Природообустройство и водопользование», профиль «Комплексное использование и охрана водных ресурсов». В 2021 году на данное направление выделено 30 бюджетных мест. Деятельность выпускников НГАСУ (Сибстрин) по данному профилю направлена на повышение эффективности использования водных и земельных ресурсов, устойчивости и экологической безопасности, а именно: создание водохозяйственных систем комплексного назначение, охрана и восстановление водных объектов; охрана земель различного назначения, рекультивация земель, нарушенных или загрязненных в процессе природопользования; природоохранное обустройство территорий с целью защиты от воздействия природных стихий; водоснабжение сельских поселений, отвод и очистка сточных вод, обводнение территорий.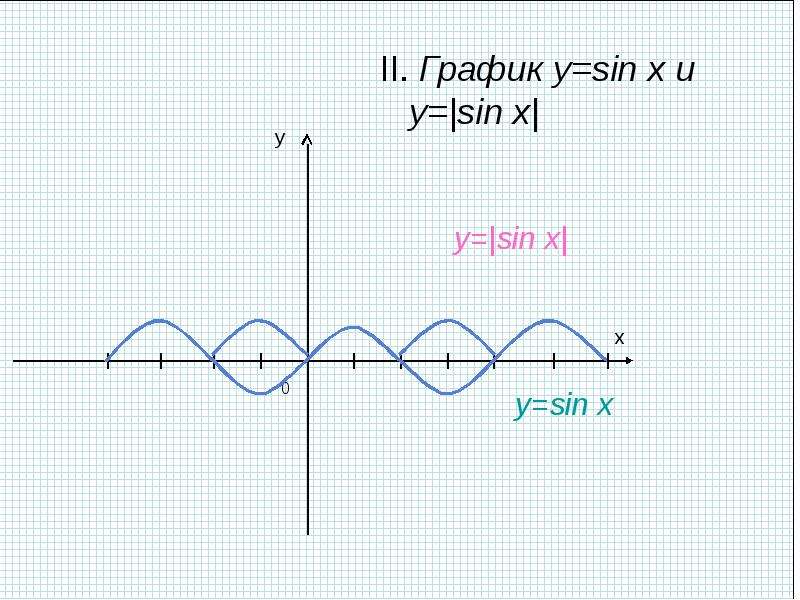 |
Профессия дорожник всегда будет востребована! Строительная специальность НГАСУ (Сибстрин) «Автомобильные дороги» Старейший вуз города – Новосибирский государственный архитектурно-строительный университет (Сибстрин) – вот уже более 90 лет занимает лидирующие позиции в обучении студентов по направлению «Строительство». С 2014 года в нашем вузе началась подготовка специалистов по профилю «Автомобильные дороги». На сегодняшний день это одно из самых актуальных направлений строительства. Национальный проект «Безопасные и качественные автомобильные дороги» предполагает приоритетное развитие транспортной инфраструктуры страны за счет средств федерального бюджета. Поэтому специалисты – строители автомобильных дорог – будут востребованы во всех регионах страны. |
Алгебра и начала анализа / КонсультантПлюс
Повторение. Решение задач с использованием свойств чисел и систем счисления, делимости, долей и частей, процентов, модулей чисел. Решение задач с использованием свойств степеней и корней, многочленов, преобразований многочленов и дробно-рациональных выражений.
Решение задач с использованием свойств степеней и корней, многочленов, преобразований многочленов и дробно-рациональных выражений.
Решение задач с использованием градусной меры угла. Модуль числа и его свойства.
Решение задач на движение и совместную работу с помощью линейных и квадратных уравнений и их систем. Решение задач с помощью числовых неравенств и систем неравенств с одной переменной, с применением изображения числовых промежутков.
Решение задач с использованием числовых функций и их графиков. Использование свойств и графиков линейных и квадратичных функций, обратной пропорциональности и функции . Графическое решение уравнений и неравенств.Тригонометрическая окружность, радианная мера угла. Синус, косинус, тангенс, котангенс произвольного угла. Основное тригонометрическое тождество и следствия из него. Значения тригонометрических функций для углов 0°, 30°, 45°, 60°, 90°, 180°, 270°. (0, , , , рад). Формулы сложения тригонометрических функций, формулы приведения, формулы двойного аргумента. .
.Нули функции, промежутки знакопостоянства, монотонность. Наибольшее и наименьшее значение функции. Периодические функции. Четность и нечетность функций. Сложные функции.
Тригонометрические функции y = cos x, y = sin x, y = tg x. Функция y = ctg x. Свойства и графики тригонометрических функций.
Арккосинус, арксинус, арктангенс числа. Арккотангенс числа. Простейшие тригонометрические уравнения. Решение тригонометрических уравнений.
Обратные тригонометрические функции, их свойства и графики. Решение простейших тригонометрических неравенств.
Степень с действительным показателем, свойства степени. Простейшие показательные уравнения и неравенства. Показательная функция и ее свойства и график.
Логарифм числа, свойства логарифма. Десятичный логарифм. Число e. Натуральный логарифм. Преобразование логарифмических выражений. Логарифмические уравнения и неравенства. Логарифмическая функция и ее свойства и график.
Степенная функция и ее свойства и график. Иррациональные уравнения.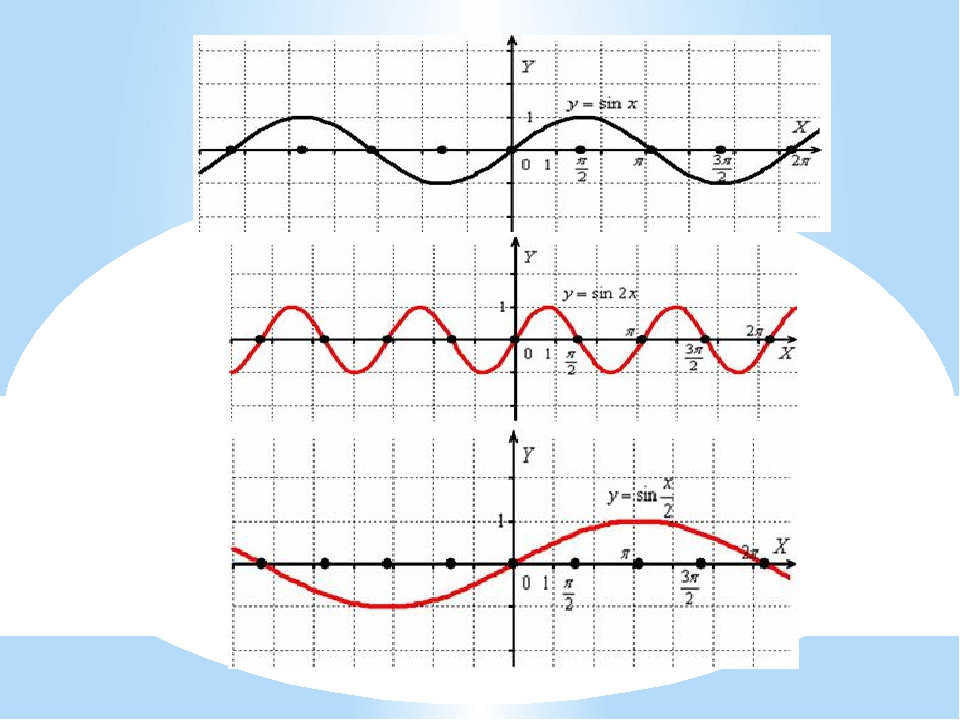
Метод интервалов для решения неравенств.
Преобразования графиков функций: сдвиг вдоль координатных осей, растяжение и сжатие, отражение относительно координатных осей. Графические методы решения уравнений и неравенств. Решение уравнений и неравенств, содержащих переменную под знаком модуля.
Системы показательных, логарифмических и иррациональных уравнений. Системы показательных, логарифмических неравенств.
Взаимно обратные функции. Графики взаимно обратных функций.
Уравнения, системы уравнений с параметром.
Производная функции в точке. Касательная к графику функции. Геометрический и физический смысл производной. Производные элементарных функций. Правила дифференцирования.
Вторая производная, ее геометрический и физический смысл.
Понятие о непрерывных функциях. Точки экстремума (максимума и минимума). Исследование элементарных функций на точки экстремума, наибольшее и наименьшее значение с помощью производной. Построение графиков функций с помощью производных. 2
2
uses
graphABC; //Подключаем графический модуль
const
W = 800; H = 500;//Размеры графического окна
function F(x: real): real;
begin
F := (sin(x)*sin(x))/ (Power(x,2)); //Функция
// F:= (cos(2*x) * Power(x,2))/2;
end;
var
x0, y0, x, y, xLeft, yLeft, xRight, yRight, n: integer;
a, b, fmin, fmax, x1, y1, mx, my, dx, dy, num: real;
i: byte;
s: string;
begin
SetWindowSize(W, H); //Устанавливаем размеры графического окна
//Координаты левой верхней границы системы координат:
xLeft := 50;
yLeft := 50;
//Координаты правой нижней границы системы координат:
xRight := W - 50;
yRight := H - 50;
//интервал по Х; a и b должно нацело делится на dx:
a := -2; b := 6; dx := 0.5;
//Интервал по Y; fmin и fmax должно нацело делится на dy:
fmin := -10; fmax := 20; dy := 2;
//Устанавливаем масштаб:
mx := (xRight - xLeft) / (b - a); //масштаб по Х
my := (yRight - yLeft) / (fmax - fmin); //масштаб по Y
//начало координат:
x0 := trunc(abs(a) * mx) + xLeft;
y0 := yRight - trunc(abs(fmin) * my);
//Рисуем оси координат:
line(xLeft, y0, xRight + 10, y0); //ось ОХ
line(x0, yLeft - 10, x0, yRight); //ось ОY
SetFontSize(12); //Размер шрифта
SetFontColor(clBlue); //Цвет шрифта
TextOut(xRight + 20, y0 - 15, 'X'); //Подписываем ось OX
TextOut(x0 - 10, yLeft - 30, 'Y'); //Подписываем ось OY
SetFontSize(8); //Размер шрифта
SetFontColor(clRed); //Цвет шрифта
{ Засечки по оси OX: }
n := round((b - a) / dx) + 1; //количество засечек по ОХ
for i := 1 to n do
begin
num := a + (i - 1) * dx; //Координата на оси ОХ
x := xLeft + trunc(mx * (num - a)); //Координата num в окне
Line(x, y0 - 3, x, y0 + 3); //рисуем засечки на оси OX
str(Num:0:1, s);
if abs(num) > 1E-15 then //Исключаем 0 на оси OX
TextOut(x - TextWidth(s) div 2, y0 + 10, s)
end;
{ Засечки на оси OY: }
n := round((fmax - fmin) / dy) + 1; //количество засечек по ОY
for i := 1 to n do
begin
num := fMin + (i - 1) * dy; //Координата на оси ОY
y := yRight - trunc(my * (num - fmin));
Line(x0 - 3, y, x0 + 3, y); //рисуем засечки на оси Oy
str(num:0:0, s);
if abs(num) > 1E-15 then //Исключаем 0 на оси OY
TextOut(x0 + 7, y - TextHeight(s) div 2, s)
end;
TextOut(x0 - 10, y0 + 10, '0'); //Нулевая точка
{ График функции строим по точкам: }
x1 := a; //Начальное значение аргумента
while x1 <= b do
begin
y1 := F(x1); //Вычисляем значение функции
x := x0 + round(x1 * mx); //Координата Х в графическом окне
y := y0 - round(y1 * my); //Координата Y в графическом окне
//Если y попадает в границы [yLeft; yRight], то ставим точку:
if (y >= yLeft) and (y <= yRight) then SetPixel(x, y, clGreen);
x1 := x1 + 0.
001 //Увеличиваем абсциссу
end
end.tg x 2 график
Вы искали tg x 2 график? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и x sin 2 x построить график функции, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «tg x 2 график».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как tg x 2 график,x sin 2 x построить график функции,y 12 x график,y 2 sin x построить график функции,y tg 2x график,y tg2x график,y tgx 2,график tg 2x,график tg x 2,график tg модуль x,период функции онлайн калькулятор,построить график функции y x 3 1.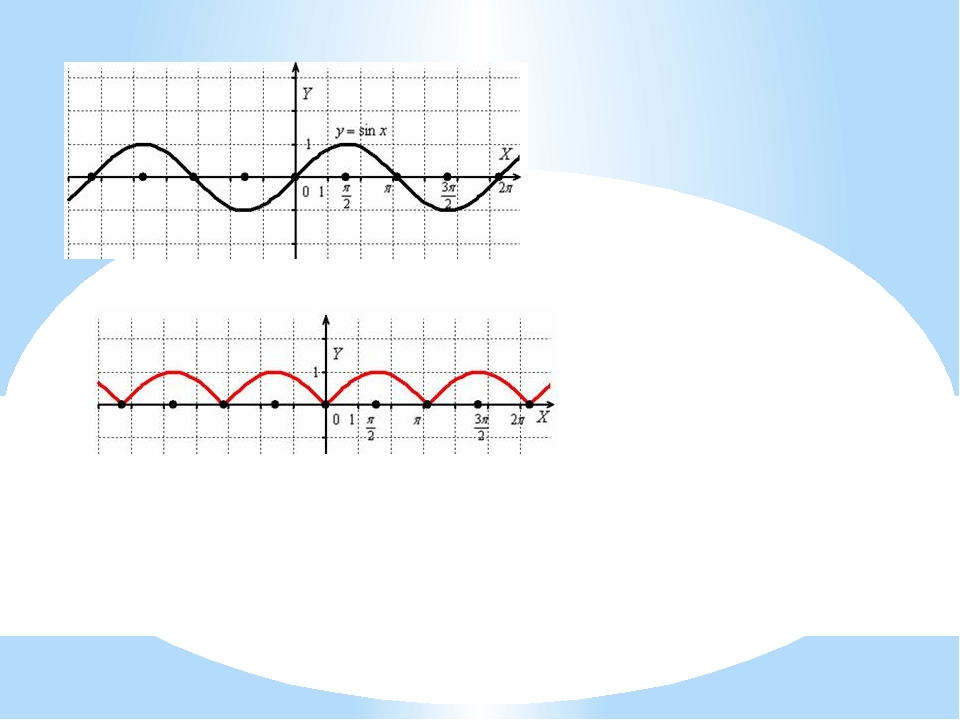
Где можно решить любую задачу по математике, а так же tg x 2 график Онлайн?
Решить задачу tg x 2 график вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Графики тригонометрических функций кратных углов. Графики тригонометрических функций кратных углов Начертить график у косинус х 2
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом. Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.
Всего в теме 25 презентаций
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
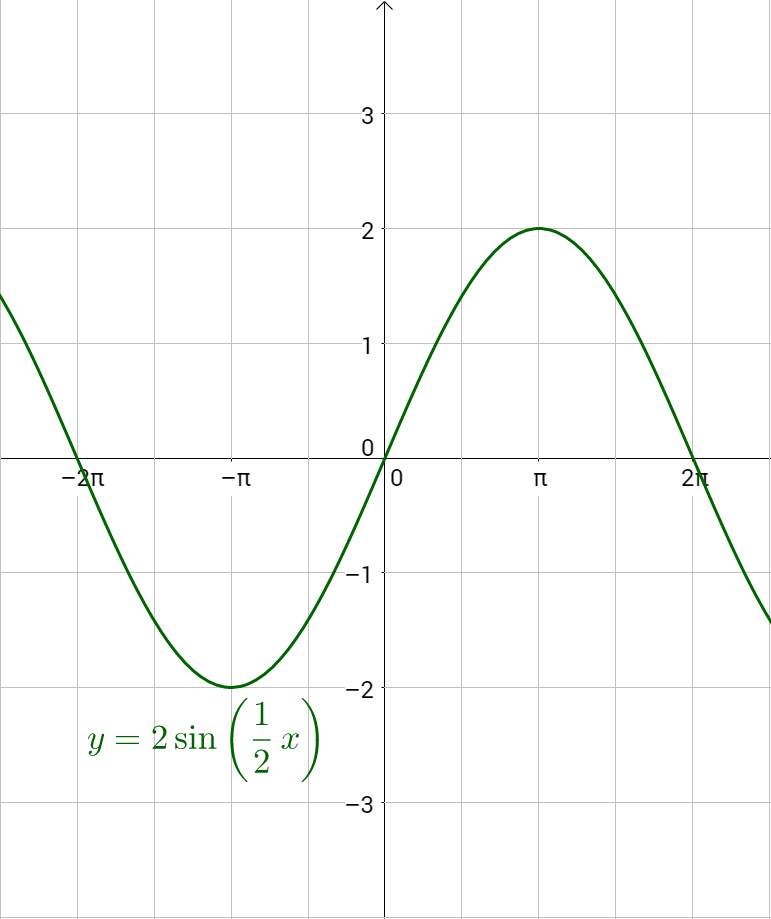
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.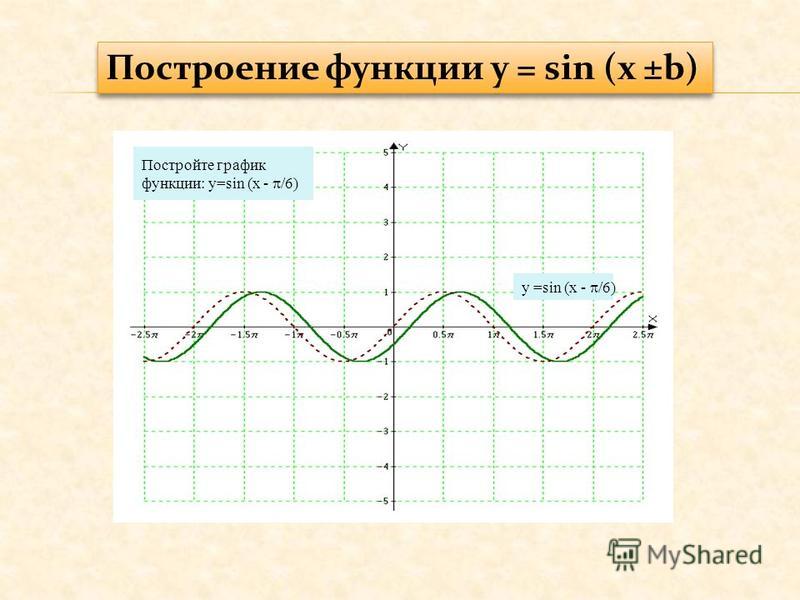
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Урок и презентация на тему: «Функция y=cos(x). Определение и график функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π].
 В этом мы можем убедиться на графике нашей функции.
В этом мы можем убедиться на графике нашей функции. - Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке [- π/6; 5π/4].
графиков функции синуса и косинуса
График изменения y = sin (x) и y = cos (x)
Напомним, что функции синуса и косинуса связывают значения действительных чисел с координатами x и y точки на единичной окружности. Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции . Мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения синусоидальной функции на единичной окружности.
| x | 0 | [латекс] \ frac {π} {6} \\ [/ латекс] | [латекс] \ frac {π} {6} \\ [/ латекс] | [латекс] \ frac {π} {3} \\ [/ латекс] | [латекс] \ frac {π} {2} \\ [/ латекс] | [латекс] \ frac {2π} {3} \\ [/ латекс] | [латекс] \ frac {3π} {4} \\ [/ латекс] | [латекс] \ frac {5π} {6} \\ [/ латекс] | π |
| sin (x) | 0 | [латекс] \ frac {1} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] | 1 | [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] \ frac {1} {2} \\ [/ латекс] | 0 |
Построение точек из таблицы по оси x дает форму синусоидальной функции.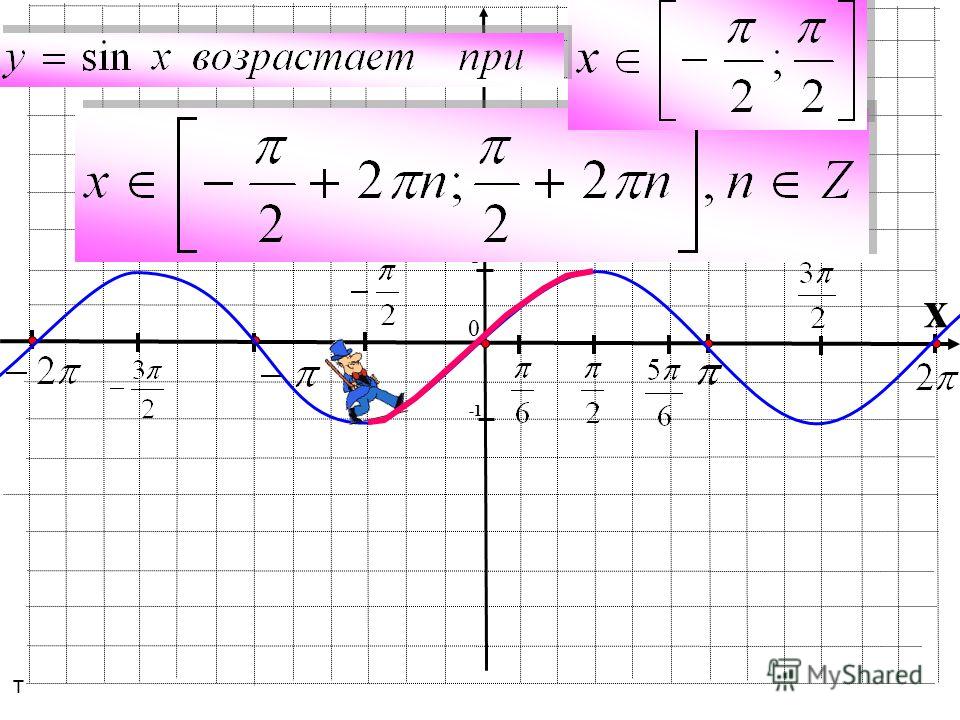 См. Рисунок 2.
См. Рисунок 2.
Рисунок 2. Синусоидальная функция
Обратите внимание, что значения синуса положительны между 0 и π, что соответствует значениям функции синуса в квадрантах I и II на единичной окружности, а значения синуса отрицательны между π и 2π, которые соответствуют значениям функция синуса в квадрантах III и IV на единичной окружности. См. Рисунок 3.
Рисунок 3. График значений синусоидальной функции
Теперь давайте аналогичным образом посмотрим на функцию косинуса .Опять же, мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения функции косинуса на единичной окружности.
| х | 0 | [латекс] \ frac {π} {6} \\ [/ латекс] | [латекс] \ frac {π} {4} \\ [/ латекс] | [латекс] \ frac {π} {3} \\ [/ латекс] | [латекс] \ frac {π} {2} \\ [/ латекс] | [латекс] \ frac {2π} {3} \\ [/ латекс] | [латекс] \ frac {3π} {4} \\ [/ латекс] | [латекс] \ frac {5π} {6} \\ [/ латекс] | π |
| cos (x) | 1 | [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] \ frac {1} {2} \\ [/ латекс] | 0 | [латекс] — \ frac {1} {2} \\ [/ latex] | [латекс] — \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] — \ frac {\ sqrt {3}} {2} \\ [/ латекс] | -1 |
Как и в случае с функцией синуса, мы можем построить точки для построения графика функции косинуса, как показано на рисунке 4.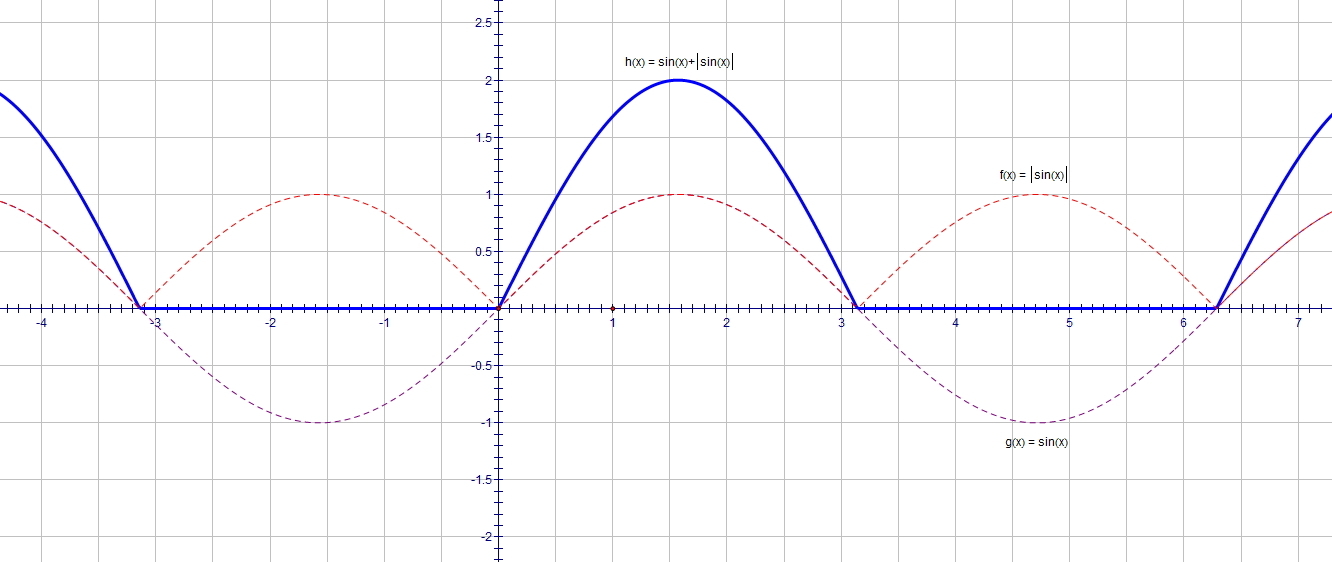
Рисунок 4. Функция косинуса
Поскольку мы можем вычислять синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Если рассматривать значения синуса и косинуса как координаты точек на единичной окружности, становится ясно, что диапазон обеих функций должен быть интервалом [-1,1].
На обоих графиках форма графика повторяется после 2π, что означает, что функции являются периодическими с периодом 2π. Периодическая функция — это функция, для которой определенный горизонтальный сдвиг , P приводит к функции, равной исходной функции: f ( x + P ) = f ( x ) для всех значений x в области f .Когда это происходит, мы называем наименьший такой горизонтальный сдвиг с P > 0 периодом функции. На рисунке 5 показаны несколько периодов функций синуса и косинуса.
Рисунок 5
Еще раз взглянув на функции синуса и косинуса в области с центром на оси y , можно выявить симметрии.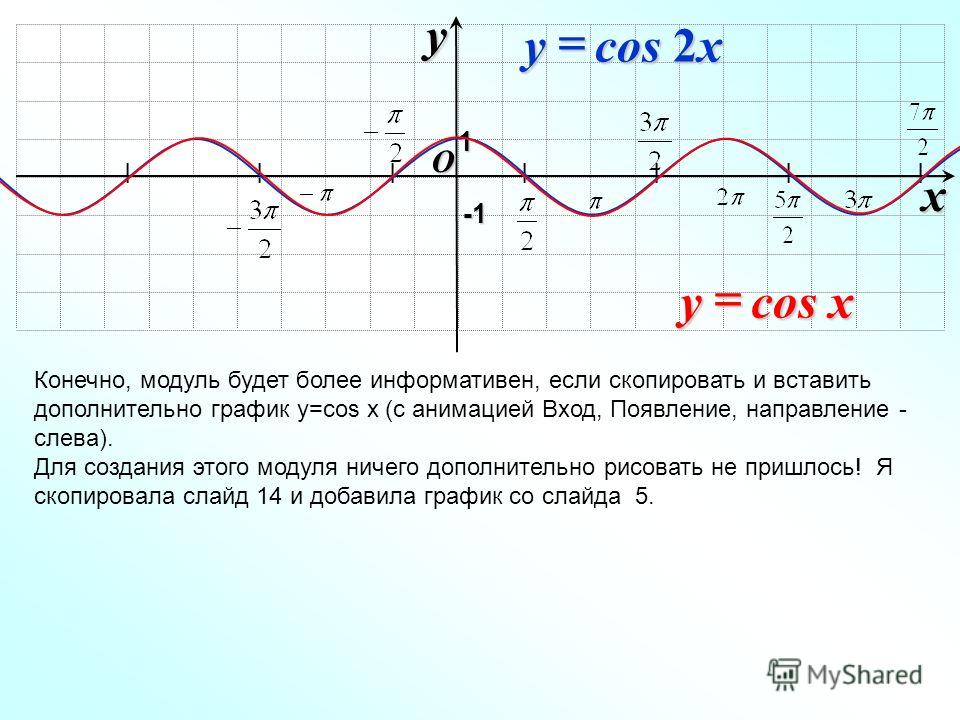 Как мы видим на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомните из «Других тригонометрических функций», что мы определили с помощью единичного круга, что синусоидальная функция является нечетной функцией, потому что [latex] sin (−x) = — sinx [/ latex].Теперь мы можем ясно видеть это свойство на графике.
Как мы видим на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомните из «Других тригонометрических функций», что мы определили с помощью единичного круга, что синусоидальная функция является нечетной функцией, потому что [latex] sin (−x) = — sinx [/ latex].Теперь мы можем ясно видеть это свойство на графике.
Рисунок 6. Нечетная симметрия синусоидальной функции
На рисунке 7 показано, что функция косинуса симметрична относительно оси y . Опять же, мы определили, что функция косинуса является четной функцией. Теперь мы можем видеть из графика, что [латекс] \ cos (−x) = \ cos x \\ [/ latex].
Рисунок 7. Четная симметрия функции косинуса
Общее примечание: Характеристики функций синуса и косинуса
Функции синуса и косинуса имеют несколько отличительных характеристик:
- Это периодические функции с периодом 2π.
- Область определения каждой функции — (−∞, ∞), а диапазон — [−1,1].

- График y = sin x симметричен относительно начала координат, потому что это нечетная функция.
- График y = cos x симметричен относительно оси y , потому что это четная функция.
Исследование синусоидальных функций
Как мы видим, функции синуса и косинуса имеют постоянный период и диапазон. Если мы увидим океанские волны или рябь на пруду, мы увидим, что они напоминают функции синуса или косинуса.Однако они не обязательно идентичны. Некоторые из них выше или длиннее других. Функция, которая имеет ту же общую форму, что и функция синуса или косинуса , известна как синусоидальная функция . Общие формы синусоидальных функций:
y = A sin ( Bx — C ) + D
и
y = A cos ( Bx — C ) + D
Определение периода синусоидальной функции
Глядя на формы синусоидальных функций, мы можем видеть, что они являются преобразованиями функций синуса и косинуса.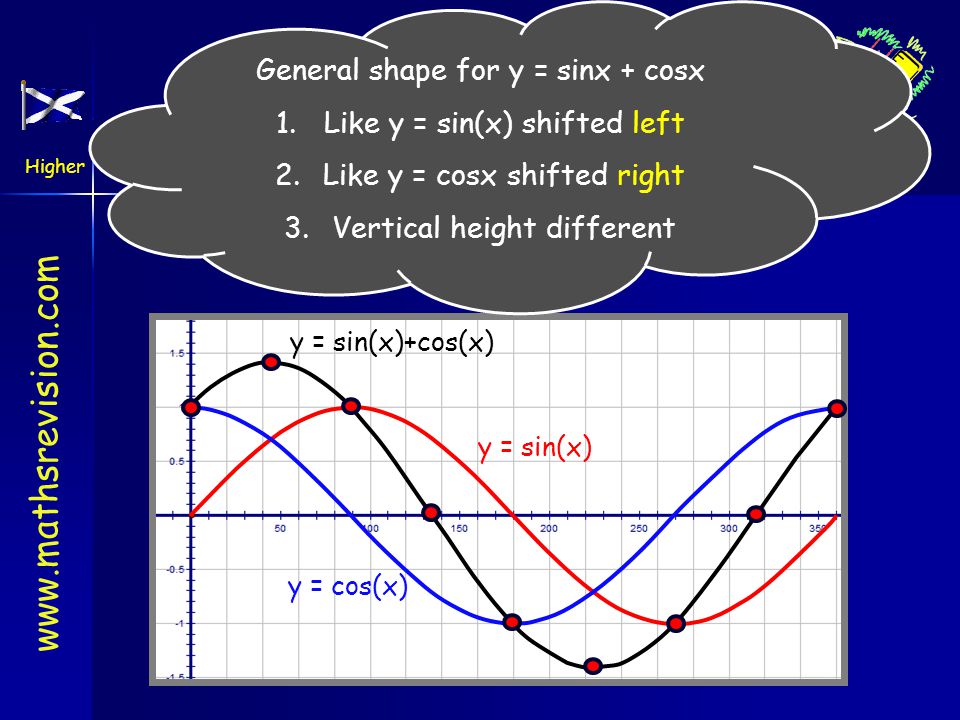 Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
В общей формуле B связано с периодом соотношением [latex] \ text {P =} \ frac {2π} {| B |} [/ latex]. Если | B | > 1, то период меньше 2π и функция испытывает сжатие по горизонтали, а если | B | <1, то период больше 2π и функция растягивается по горизонтали. Например, f ( x ) = sin ( x ), B = 1, поэтому период равен 2π, который мы знали.Если f ( x ) = sin (2 x ), то B = 2, поэтому период равен π и график сжат. Если [латекс] \ text {f (x) = sin} (\ frac {x} {2}) [/ latex], то [latex] B = \ frac {1} {2} [/ latex], поэтому период равен 4π, и график растянут. Обратите внимание на рис. 8, как период косвенно связан с | B |.
Рисунок 8
Общее примечание: период синусоидальных функций
Если положить C = 0 и D = 0 в уравнениях синуса и косинуса в общем виде, мы получим формы
Период [латекс] \ frac {2π} {| B |} [/ латекс].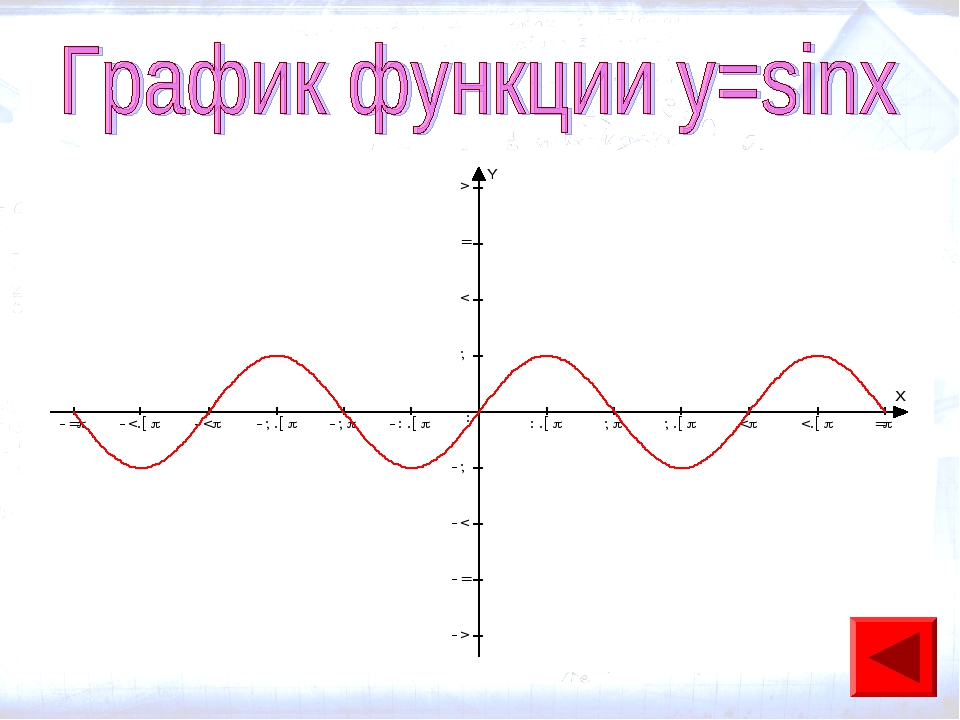
Пример 1: Определение периода функции синуса или косинуса
Определите период функции [latex] f (x) = \ sin (\ frac {π} {6} x) \\ [/ latex].
Решение
Начнем с сравнения уравнения с общей формой [latex] y = Asin (Bx) [/ latex].
В данном уравнении [latex] B = \ frac {π} {6} [/ latex], поэтому период будет
[латекс] \ begin {array} P = \ frac {\ frac {2} {\ pi}} {| B |} \ hfill \\ = \ frac {2 \ pi} {\ frac {x} {6} } \ hfill \\ = 2 \ pi \ times \ frac {6} {\ pi} \ hfill \\ = 12 \ hfill \ end {array} \\ [/ latex]
Попробуй 1
Определите период функции [latex] g (x) = \ cos (\ frac {x} {3}) \\ [/ latex].
Решение
Определение амплитуды
Возвращаясь к общей формуле синусоидальной функции, мы проанализировали, как переменная B связана с периодом. Теперь давайте обратимся к переменной A , чтобы мы могли проанализировать, как она связана с амплитудой , или наибольшим расстоянием от покоя.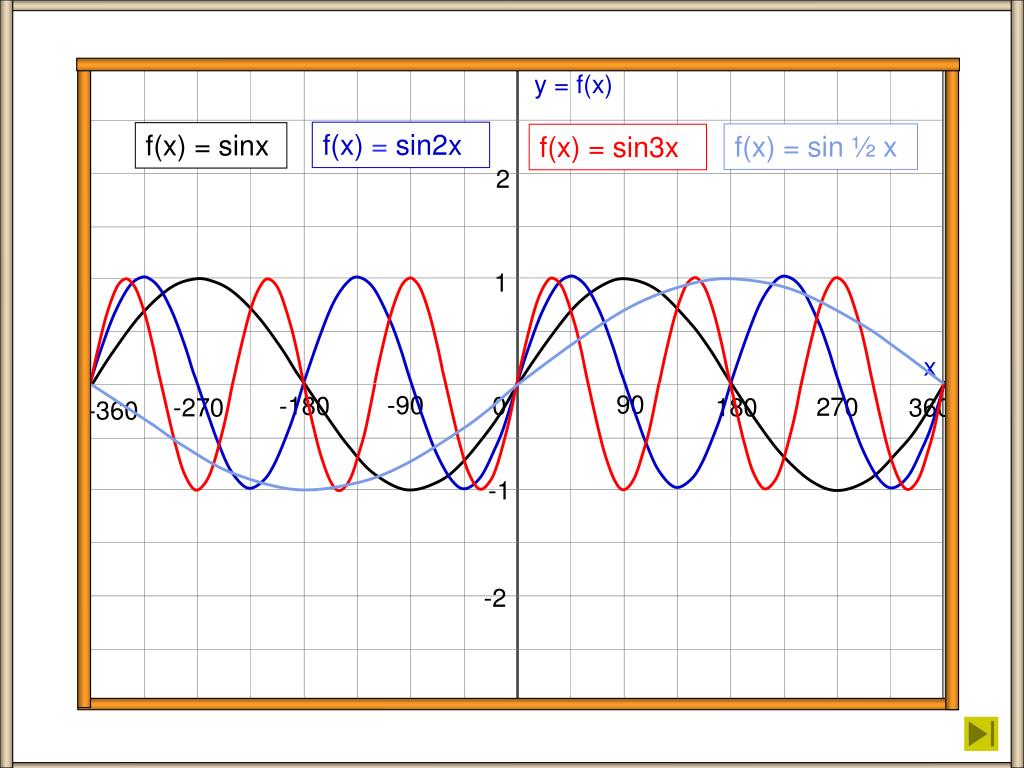 A представляет коэффициент вертикального растяжения и его абсолютное значение | A | это амплитуда. Локальные максимумы будут расстоянием | A | над вертикальной средней линией графика, которая представляет собой линию x = D ; поскольку D = 0 в этом случае, средняя линия является осью x .Локальные минимумы будут на таком же расстоянии ниже средней линии. Если | A | > 1 функция растягивается. Например, амплитуда f ( x ) = 4 sin x в два раза больше амплитуды
A представляет коэффициент вертикального растяжения и его абсолютное значение | A | это амплитуда. Локальные максимумы будут расстоянием | A | над вертикальной средней линией графика, которая представляет собой линию x = D ; поскольку D = 0 в этом случае, средняя линия является осью x .Локальные минимумы будут на таком же расстоянии ниже средней линии. Если | A | > 1 функция растягивается. Например, амплитуда f ( x ) = 4 sin x в два раза больше амплитуды
f ( x ) = 2 sin x .
Если | A | <1, функция сжимается. На рисунке 9 сравнивается несколько синусоид с разными амплитудами.
Рисунок 9
Общее примечание: амплитуда синусоидальных функций
Если положить C = 0 и D = 0 в уравнениях синуса и косинуса в общем виде, мы получим формы
[латекс] y = A \ sin (Bx) \\ [/ latex] и [латекс] y = A \ cos (Bx) \\ [/ latex]
Амплитуда равна A, а высота по вертикали от средней линии равна | A |. Кроме того, обратите внимание, что в примере
Кроме того, обратите внимание, что в примере
[латекс] | A | = \ text {амплитуда} = \ frac {1} {2} | \ text {maximum} — \ text {minimum} | \\ [/ latex]
Пример 2: Определение амплитуды функции синуса или косинуса
Какова амплитуда синусоидальной функции [латекс] f (x) = — 4 \ sin (x) \\ [/ latex]? Функция растягивается или сжимается по вертикали?
Решение
Начнем с сравнения функции с упрощенной формой y = A sin ( Bx ).
В данной функции A = −4, поэтому амплитуда | A | = | −4 | = 4. Функция растягивается.
Анализ решения
Отрицательное значение A приводит к отражению по оси x синусоидальной функции , как показано на рисунке 10.
Рисунок 10
Попробуй 2
Какова амплитуда синусоидальной функции f ( x ) = 12 sin ( x )? Функция растягивается или сжимается по вертикали?
Решение
Анализ графиков вариаций
y = sin x и y = cos x Теперь, когда мы понимаем, как A и B связаны с уравнением общей формы для функций синуса и косинуса, мы исследуем переменные C и D . Напомним общий вид:
Напомним общий вид:
[латекс] y = A \ sin (Bx-C) + D \\ [/ latex] и [латекс] y = A \ cos (Bx-C) + D \\ [/ latex]
или
[латекс] y = A \ sin (B (x− \ frac {C} {B})) + D \\ [/ latex] и [латекс] y = A \ cos (B (x− \ frac {C } {B})) + D \\ [/ latex]
Значение [latex] \ frac {C} {B} \\ [/ latex] для синусоидальной функции называется фазовым сдвигом , или горизонтальным смещением основного синуса или функцией косинуса . Если C> 0, график сдвигается вправо. Если C <0, график сдвигается влево.Чем больше значение | C |, тем больше смещен график. На рисунке 11 показано, что график [latex] f (x) = \ sin (x − π) \\ [/ latex] сдвигается вправо на π единиц, что больше, чем мы видим на графике [latex] f. (x) = \ sin (x− \ frac {π} {4}) \\ [/ latex], который сдвигается вправо на единицы [latex] \ frac {π} {4} \\ [/ latex].
Рисунок 11
В то время как C относится к горизонтальному смещению, D указывает вертикальное смещение от средней линии в общей формуле для синусоидальной функции. Функция [latex] y = \ cos (x) + D \\ [/ latex] имеет среднюю линию в [latex] y = D [/ latex].
Функция [latex] y = \ cos (x) + D \\ [/ latex] имеет среднюю линию в [latex] y = D [/ latex].
Рисунок 12
Любое значение D , кроме нуля, сдвигает график вверх или вниз. На рисунке 13 [latex] f (x) = \ sin x \\ [/ latex] сравнивается с [latex] f (x) = \ sin x + 2 \\ [/ latex], который сдвинут на 2 единицы вверх на графике. .
Рисунок 13
Общее примечание: Вариации функций синуса и косинуса
Дано уравнение в форме [латекс] f (x) = A \ sin (Bx − C) + D \\ [/ latex] или [латекс] f (x) = A \ cos (Bx − C) + D \\ [/ latex], [latex] \ frac {C} {B} \\ [/ latex] — это сдвиг фазы , а D — сдвиг по вертикали .
Пример 3: Определение фазового сдвига функции
Определите направление и величину фазового сдвига для [латекса] f (x) = \ sin (x + \ frac {π} {6}) — 2 \\ [/ latex].
Решение
Начнем с сравнения уравнения с общей формой [латекс] y = A \ sin (Bx − C) + D \\ [/ latex].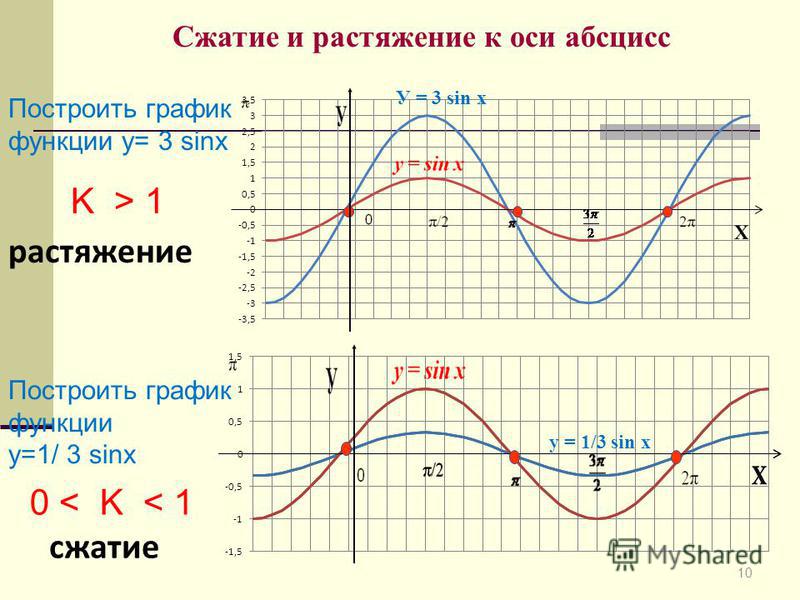
В данном уравнении обратите внимание, что B = 1 и [латекс] C = — \ frac {π} {6} \\ [/ latex]. Итак, фазовый сдвиг
[латекс] \ begin {array} \ frac {C} {B} = — \ frac {\ frac {x} {6}} {1} \ hfill \\ = — \ frac {\ pi} {6} \ hfill \ end {array} \\ [/ latex]
или [latex] \ frac {\ pi} {6} \\ [/ latex] единиц слева.
Анализ решения
Необходимо обратить внимание на знак в уравнении общего вида синусоидальной функции. Уравнение показывает знак минус перед C . Следовательно, [latex] f (x) = \ sin (x + \ frac {π} {6}) — 2 \\ [/ latex] можно переписать как [latex] f (x) = \ sin (x — (- \ гидроразрыв {π} {6})) — 2 \\ [/ latex]. Если значение C отрицательное, сдвиг влево.
Попробуй 3
Определите направление и величину фазового сдвига для [latex] f (x) = 3 \ cos (x− \ frac {\ pi} {2}) \\ [/ latex].
Решение
Пример 4: Определение вертикального сдвига функции
Определите направление и величину вертикального сдвига для [латекса] f (x) = \ cos (x) −3 \\ [/ latex].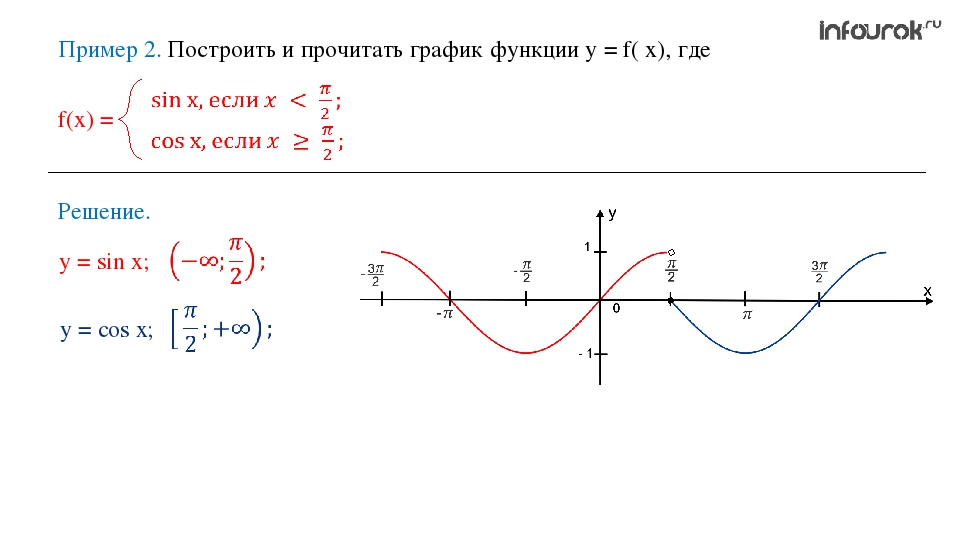
Решение
Начнем с сравнения уравнения с общей формой [латекс] y = A \ cos (Bx − C) + D \\ [/ latex]
Попробовать 4
Определите направление и величину вертикального сдвига для [латекса] f (x) = 3 \ sin (x) +2 \\ [/ latex].
Решение
Практическое руководство. Учитывая синусоидальную функцию в форме [латекс] f (x) = A \ sin (Bx − C) + D [/ latex], определите среднюю линию, амплитуду, период и фазовый сдвиг.
- Определите амплитуду как | A |.
- Определите период как [латекс] P = \ frac {2π} {| B |} \\ [/ latex].
- Определите фазовый сдвиг как [latex] \ frac {C} {B} \\ [/ latex].
- Определите среднюю линию как y = D.
Пример 5: Определение вариаций синусоидальной функции из уравнения
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции [латекс] y = 3 \ sin (2x) +1 \\ [/ latex].
Решение
Начнем с сравнения уравнения с общей формой [латекс] y = A \ sin (Bx − C) + D \\ [/ latex]. A = 3, поэтому амплитуда | A | = 3.
A = 3, поэтому амплитуда | A | = 3.
Затем B = 2, поэтому период равен [latex] \ text {P} = \ frac {2π} {| B |} = \ frac {2π} {2} = π \\ [/ latex].
В скобках нет добавленной константы, поэтому C = 0, а фазовый сдвиг равен [latex] \ frac {C} {B} = \ frac {0} {2} = 0 \\ [/ latex].
Наконец, D = 1, поэтому средняя линия составляет y = 1.
Анализ решения
Изучая график, мы можем определить, что период равен π, средняя линия равна y = 1, а амплитуда равна 3.См. Рисунок 14.
Рисунок 14
Попробуй 5
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции [латекс] y = \ frac {1} {2} \ cos (\ frac {x} {3} — \ frac {π} {3}) \ \[/латекс].
Решение
Пример 6: Определение уравнения для синусоидальной функции из графика
Определите формулу функции косинуса на рисунке 15.
Рисунок 15
Решение
[латекс] f (x) = \ sin (x) +2 \\ [/ latex]
Попробуй 6
Определите формулу синусоидальной функции на рисунке 16.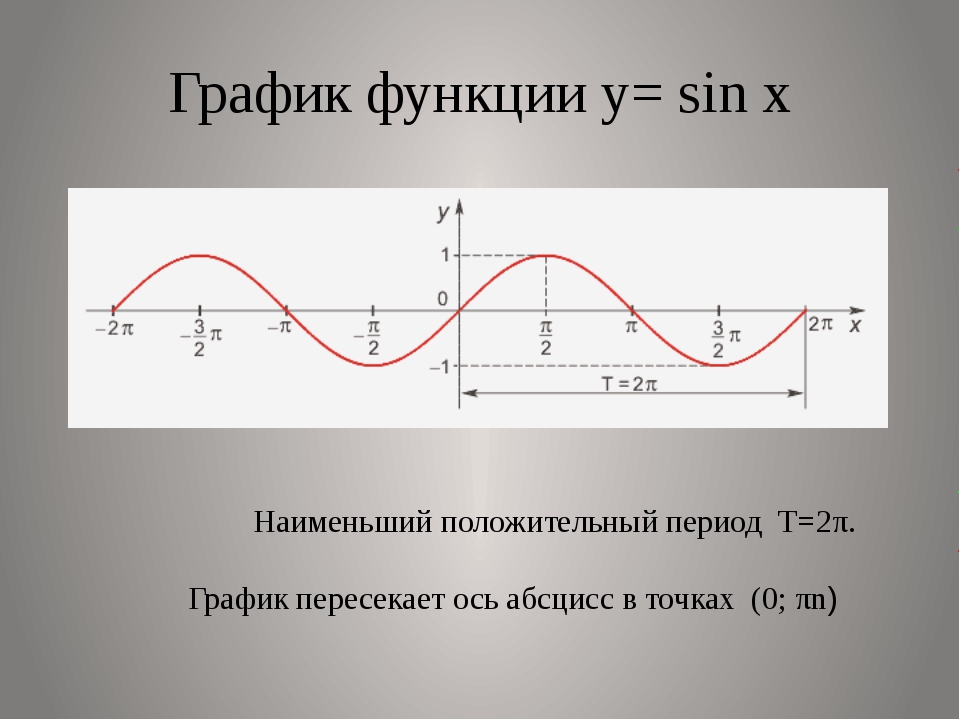
Рисунок 16
Решение
Пример 7: Определение уравнения для синусоидальной функции из графика
Определите уравнение для синусоидальной функции на рисунке 17.
Рисунок 17
Решение
При максимальном значении 1 и минимальном значении –5 средняя линия будет находиться посередине между –2. Итак, D = −2.
Расстояние от средней линии до самого высокого или самого низкого значения дает амплитуду | А | = 3.
Период графика равен 6, который может быть измерен от пика при x = 1 до следующего пика при x = 7 или от расстояния между самыми низкими точками. Следовательно, [латекс] \ text {P} = \ frac {2 \ pi} {| B |} = 6 [/ latex]. Используя положительное значение для B , находим, что
[латекс] B = \ frac {2π} {P} = \ frac {2π} {6} = \ frac {π} {3} \\ [/ latex]
Пока что наше уравнение выглядит так: [latex] y = 3 \ sin (\ frac {\ pi} {3} x − C) −2 \\ [/ latex] или [latex] y = 3 \ cos (\ frac {\ pi} {3} x − C) −2 \\ [/ латекс]. Для формы и сдвига у нас есть несколько вариантов. Мы могли бы записать это как любое из следующих:
Для формы и сдвига у нас есть несколько вариантов. Мы могли бы записать это как любое из следующих:
- косинус, смещенный вправо
- отрицательный косинус, сдвинутый влево
- синус, сдвинутый влево
- отрицательный синус смещен вправо
Хотя любой из них был бы правильным, в этом случае с косинусоидальными сдвигами работать легче, чем с синусоидальными сдвигами, поскольку они включают целочисленные значения. Итак, наша функция становится
[латекс] y = 3 \ cos (\ frac {π} {3} x− \ frac {π} {3}) — 2 \\ [/ latex] или [латекс] y = −3 \ cos (\ frac {π} {3} x + \ frac {2π} {3}) — 2 \\ [/ латекс]
Опять же, эти функции эквивалентны, поэтому обе дают один и тот же график.
Попробуй 7
Напишите формулу функции, показанной на рисунке 18.
Рисунок 18
Решение
Графические вариации
y = sin x и y = cos x В этом разделе мы узнали о типах вариаций функций синуса и косинуса и использовали эту информацию для написания уравнений из графиков. Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Вместо того, чтобы сосредоточиться на уравнениях общего вида
[латекс] y = A \ sin (Bx-C) + D \\ [/ latex] и [латекс] y = A \ cos (Bx-C) + D \\ [/ latex],
мы положим C = 0 и D = 0 и будем работать с упрощенной формой уравнений в следующих примерах.
Практическое руководство. Для функции [latex] y = Asin (Bx) \\ [/ latex] нарисуйте ее график.
- Определите амплитуду, | A |.
- Определите период, [латекс] P = \ frac {2π} {| B |} \\ [/ latex].
- Начать с начала координат, функция увеличивается вправо, если A положительно, или уменьшается, если A отрицательно.
- В [latex] x = \ frac {π} {2 | B |} \\ [/ latex] существует локальный максимум для A > 0 или минимум для A <0, с y = А .
- Кривая возвращается к оси x в точке [latex] x = \ frac {π} {| B |} \\ [/ latex].

- Существует локальный минимум для A > 0 (максимум для A <0) при [latex] x = \ frac {3π} {2 | B |} \\ [/ latex] при y = — А .
- Кривая снова возвращается к оси x в точке [latex] x = \ frac {π} {2 | B |} \\ [/ latex].
Пример 8: Построение графика функции и определение амплитуды и периода
Нарисуйте график [латекса] f (x) = — 2 \ sin (\ frac {πx} {2}) \\ [/ latex].
Решение
Давайте начнем с сравнения уравнения с формой [латекс] y = A \ sin (Bx) \\ [/ latex].
Шаг 1. Из уравнения видно, что A = −2, поэтому амплитуда равна 2.
| A | = 2
Шаг 2. Уравнение показывает, что [латекс] B = \ frac {π} {2} \\ [/ latex], поэтому период равен
[латекс] \ begin {array} \ text {P} = \ frac {2 \ pi} {\ frac {\ pi} {2}} \\ = 2 \ pi \ times \ frac {2} {\ pi} \\ = 4 \ end {array} \\ [/ latex]
Шаг 3.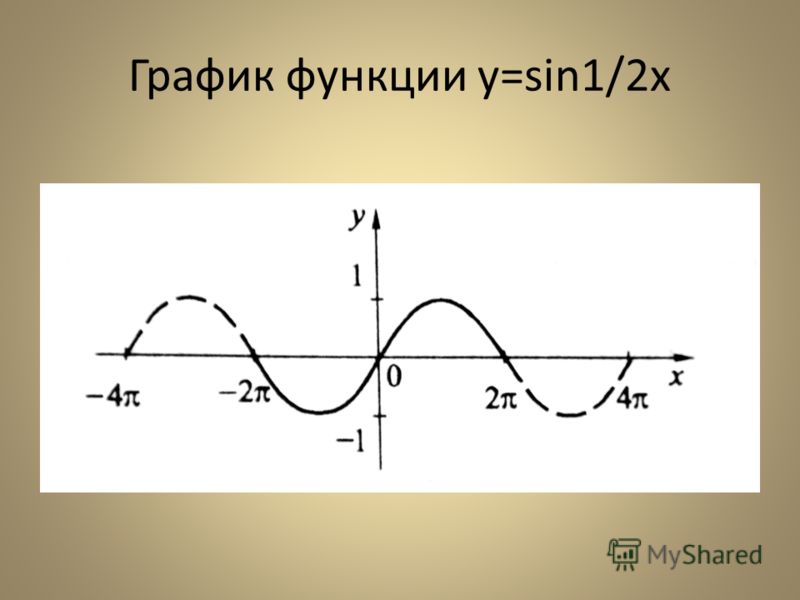 Поскольку A отрицательное значение, график опускается вниз по мере того, как мы перемещаемся вправо от начала координат.
Поскольку A отрицательное значение, график опускается вниз по мере того, как мы перемещаемся вправо от начала координат.
Шаг 4–7. x -перехватывания находятся в начале одного периода, x = 0, горизонтальные средние точки находятся на уровне x = 2 и в конце одного периода при x = 4.
Квартальные точки включают минимум x = 1 и максимум x = 3. Локальный минимум будет на 2 единицы ниже средней линии при x = 1, а локальный максимум будет на 2 единицах. над средней линией при x = 3. На рисунке 19 показан график функции.
Рисунок 19
Попробуй 8
Нарисуйте график [латекс] g (x) = — 0,8 \ cos (2x) \\ [/ latex]. Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Решение
Практическое руководство. Для синусоидальной функции со сдвигом фазы и вертикальным сдвигом нарисуйте ее график.
- Выразите функцию в общем виде [латекс] y = A \ sin (Bx − C) + D [/ latex] или [latex] y = A \ cos (Bx − C) + D \\ [/ latex] .

- Определите амплитуду, | A |.
- Определите период, [латекс] P = 2π | B | [/ латекс].
- Определите фазовый сдвиг, [latex] \ frac {C} {B} \\ [/ latex].
- Нарисуйте график [латекс] f (x) = A \ sin (Bx) \\ [/ latex], сдвинутый вправо или влево на [латекс] \ frac {C} {B} \\ [/ latex] и вверх или вниз на D .
Пример 9: Построение преобразованной синусоиды
Нарисуйте граф [латекс] f (x) = 3 \ sin (\ frac {π} {4} x− \ frac {π} {4}) \\ [/ latex].
Решение
Шаг 1. Функция уже записана в общем виде: [latex] f (x) = 3 \ sin (\ frac {π} {4} x− \ frac {π} {4}) \\ [/ латекс]. Этот график будет иметь форму синусоидальной функции , начинающейся от средней линии и увеличивающейся вправо.
Шаг 2. | А | = | 3 | = 3. Амплитуда 3.
Шаг 3. Поскольку [latex] | B | = | \ frac {π} {4} | = \ frac {π} {4} \\ [/ latex], мы определяем период следующим образом.
[латекс] \ text {P} = \ frac {2π} {| B |} = \ frac {2π} {\ frac {π} {4}} = 2π \ times \ frac {4} {π} = 8 \\ [/ латекс]
Период 8.
Шаг 4. Поскольку [latex] \ text {C} = \ frac {π} {4} \\ [/ latex], фазовый сдвиг равен
[латекс] \ frac {C} {B} = \ frac {\ frac {\ pi} {4}} {\ frac {\ pi} {4}} = 1 \\ [/ latex].
Фазовый сдвиг — 1 ед.
Шаг 5. На рисунке 20 показан график функции.
Рис. 20. Сжатая по горизонтали, растянутая по вертикали и смещенная по горизонтали синусоида
Попробуй 9
Нарисуйте график [латекс] g (x) = — 2 \ cos (\ frac {\ pi} {3} x + \ frac {\ pi} {6}) \\ [/ latex]. Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Решение
Пример 10: Определение свойств синусоидальной функции
Дано [латекс] y = −2 \ cos (\ frac {\ pi} {2} x + \ pi) +3 \\ [/ latex], определить амплитуду, период, фазовый сдвиг и горизонтальный сдвиг. Затем изобразите функцию.
Затем изобразите функцию.
Решение
Начните со сравнения уравнения с общей формой и выполните шаги, описанные в Примере 9.
[латекс] y = A \ cos (Bx − C) + D \\ [/ латекс]
Шаг 1. Функция уже написана в общем виде.
Шаг 2. Так как A = −2, амплитуда | A | = 2.
Шаг 3. [latex] | B | = \ frac {\ pi} {2} \\ [/ latex], поэтому период равен [latex] \ text {P} = \ frac {2π} {| B |} = \ frac {2 \ pi} {\ frac {\ pi} {2}} \ times2 \ pi = 4 \\ [/ latex].Период 4.
г.Шаг 4. [latex] C = — \ pi \\ [/ latex], поэтому мы вычисляем фазовый сдвиг как [latex] \ frac {C} {B} = \ frac {- \ pi} {\ frac {\ pi} {2}} = — \ pi \ times \ frac {2} {\ pi} = — 2 \\ [/ latex]. Фазовый сдвиг -2.
Шаг 5. D = 3, поэтому средняя линия составляет y = 3, а вертикальный сдвиг увеличивается 3.
Поскольку A отрицательно, график функции косинуса отражается относительно оси x .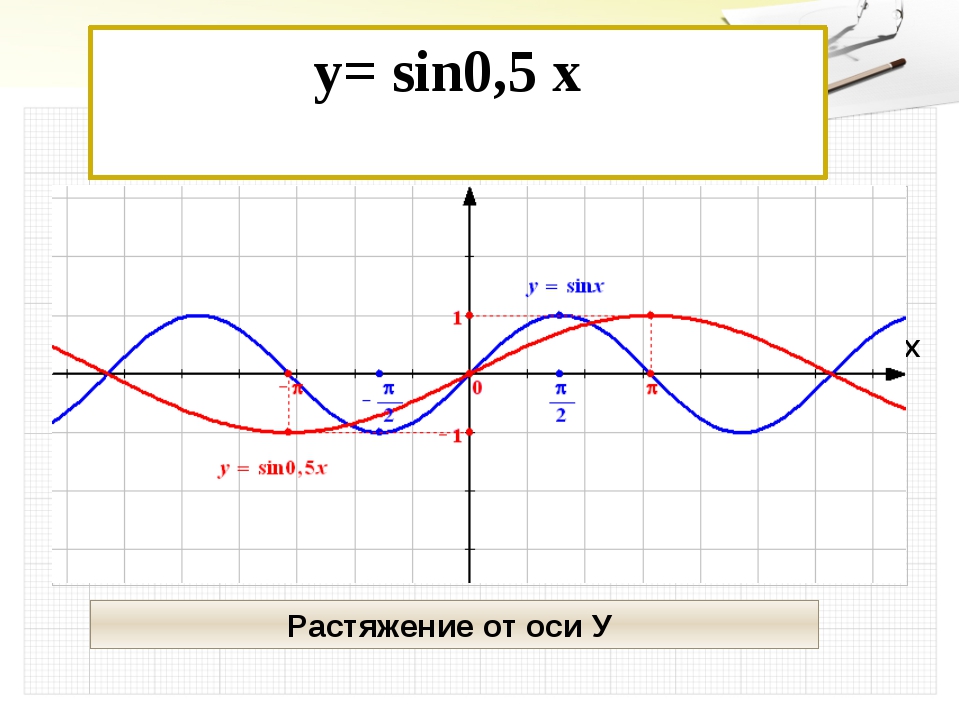
На рисунке 21 показан один цикл графика функции.
Рисунок 21
Использование преобразований функций синуса и косинуса
Мы можем использовать преобразования функций синуса и косинуса во многих приложениях. Как упоминалось в начале главы, круговое движение может быть смоделировано с использованием функции синуса или косинуса .
Пример 11: Нахождение вертикальной составляющей кругового движения
Точка вращается по окружности радиуса 3 с центром в начале координат.Нарисуйте график координаты y точки как функции угла поворота.
Решение
Напомним, что для точки на окружности радиуса r координата y точки равна [latex] y = r \ sin (x) [/ latex], поэтому в этом случае мы получаем уравнение [latex] у (х) = 3 \ грех (х) [/ латекс]. Константа 3 вызывает вертикальное растяжение значений y функции в 3 раза, что мы можем видеть на графике на рисунке 22.
Константа 3 вызывает вертикальное растяжение значений y функции в 3 раза, что мы можем видеть на графике на рисунке 22.
Рисунок 22
Анализ решения
Обратите внимание, что период функции по-прежнему равен 2π; путешествуя по кругу, мы возвращаемся в точку (3,0) для x = 2π, 4π, 6π,….Поскольку выходные данные графика теперь будут колебаться между –3 и 3, амплитуда синусоидальной волны равна 3.
Попробуй 10
Какова амплитуда функции [латекс] f (x) = 7 \ cos (x) [/ latex]? Нарисуйте график этой функции.
Решение
Пример 12: Нахождение вертикальной составляющей кругового движения
Круг радиусом 3 фута устанавливается с центром в 4 футах от земли. Ближайшая к земле точка обозначена P , как показано на рисунке 23.Нарисуйте график высоты над землей точки P при вращении окружности; затем найдите функцию, которая дает высоту через угол поворота.
Рисунок 23
Решение
Набрасывая высоту, мы отмечаем, что она начинается на высоте 1 фута над землей, затем увеличивается до 7 футов над землей и продолжает колебаться на 3 фута выше и ниже центрального значения в 4 фута, как показано на Рисунке 24.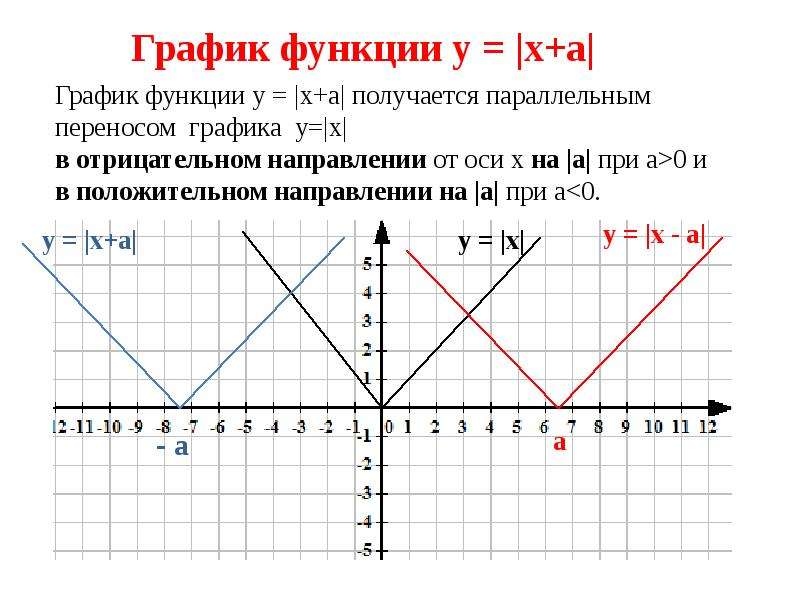
Рисунок 24
Хотя мы могли бы использовать преобразование функции синуса или косинуса, мы начнем с поиска характеристик, которые сделают использование одной функции проще, чем другой.Давайте использовать функцию косинуса, потому что она начинается с самого высокого или самого низкого значения, а функция синуса начинается со среднего значения. Стандартный косинус начинается с самого высокого значения, а этот график начинается с самого низкого значения, поэтому нам нужно включить вертикальное отражение.
Во-вторых, мы видим, что график колеблется на 3 выше и ниже центра, в то время как основной косинус имеет амплитуду 1, поэтому этот график был растянут по вертикали на 3, как в последнем примере.
Наконец, чтобы переместить центр круга на высоту 4, график был сдвинут по вертикали на 4.Объединяя эти преобразования, мы находим, что
[латекс] y = −3 \ cos (x) +4 [/ латекс]
Попробуй 11
Груз прикрепляется к пружине, которая затем подвешивается к доске, как показано на рисунке 25.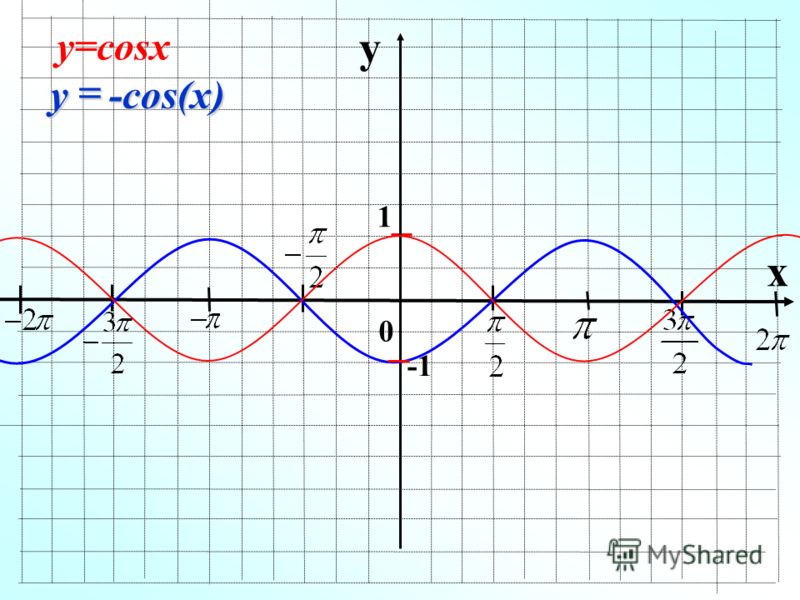 Когда пружина колеблется вверх и вниз, положение груза и относительно доски изменяется от –1 дюйма (при время x = 0) до –7 дюймов. (в момент времени x = π) под доской. Предположим, что положение y задано как синусоидальная функция x .Нарисуйте график функции, а затем найдите функцию косинуса, которая дает положение y в единицах x .
Когда пружина колеблется вверх и вниз, положение груза и относительно доски изменяется от –1 дюйма (при время x = 0) до –7 дюймов. (в момент времени x = π) под доской. Предположим, что положение y задано как синусоидальная функция x .Нарисуйте график функции, а затем найдите функцию косинуса, которая дает положение y в единицах x .
Рисунок 25
Решение
Пример 13: Определение роста всадника на колесе обозрения
Лондонский глаз — это огромное колесо обозрения диаметром 135 метров (443 фута). Он совершает один оборот каждые 30 минут. Всадники садятся на платформу на высоте 2 метров над землей. Выразите высоту всадника над землей как функцию времени в минутах.
Решение
При диаметре 135 м колесо имеет радиус 67,5 м. Высота будет колебаться с амплитудой 67,5 м выше и ниже центра.
Пассажирский борт на высоте 2 м над уровнем земли, поэтому центр колеса должен находиться на высоте 67,5 + 2 = 69,5 м над уровнем земли. Средняя линия колебания составит 69,5 м.
Средняя линия колебания составит 69,5 м.
Колесо совершает 1 оборот за 30 минут, поэтому высота будет колебаться с периодом 30 минут.
Наконец, так как райдерские борта находятся в самой нижней точке, высота будет начинаться с наименьшего значения и увеличиваться, следуя форме вертикально отраженной косинусоидальной кривой.
- Амплитуда: 67,5, поэтому A = 67,5
- Средняя линия: 69,5, поэтому D = 69,5
- Период: 30, поэтому [латекс] B = \ frac {2 \ pi} {30} = \ frac {\ pi} {15} [/ latex]
- Форма: −cos ( t )
Уравнение для роста всадника будет
[латекс] y = -67,5 \ cos (\ frac {\ pi} {15} t) +69,5 [/ латекс]
, где т, — в минутах, а y — в метрах.
Ключевые уравнения
| Синусоидальные функции | [латекс] f (x) = A \ sin (Bx-C) + D [/ латекс] |
| [латекс] f (x) = A \ cos (Bx-C) + D [/ латекс] |
- Периодические функции повторяются после заданного значения.
 Наименьшее из таких значений — период. Основные функции синуса и косинуса имеют период 2π.
Наименьшее из таких значений — период. Основные функции синуса и косинуса имеют период 2π. - Функция sin x нечетная, поэтому ее график симметричен относительно начала координат. Функция cos x четная, поэтому ее график симметричен относительно оси y .
- График синусоидальной функции имеет ту же общую форму, что и синусоидальная или косинусная функция.
- В общей формуле для синусоидальной функции период равен [latex] \ text {P} = \ frac {2 \ pi} {| B |} [/ latex].
- В общей формуле синусоидальной функции | A | представляет амплитуду. Если | A | > 1 функция растягивается, а если | A | <1, функция сжимается.
- Значение [latex] \ frac {C} {B} [/ latex] в общей формуле для синусоидальной функции указывает фазовый сдвиг.
- Значение D в общей формуле для синусоидальной функции указывает вертикальное смещение от средней линии.
- Комбинации вариаций синусоидальных функций могут быть обнаружены с помощью уравнения.

- Уравнение для синусоидальной функции может быть определено из графика.
- Функцию можно изобразить, указав ее амплитуду и период.
- Функцию также можно изобразить, указав ее амплитуду, период, фазовый сдвиг и горизонтальный сдвиг.
- Синусоидальные функции могут использоваться для решения реальных проблем.
Глоссарий
- амплитуда
- вертикальная высота функции; константа A , фигурирующая в определении синусоидальной функции
- средняя линия
- горизонтальная линия y = D , где D появляется в общем виде синусоидальной функции
- периодическая функция
- функция f ( x ), которая удовлетворяет [latex] f (x + P) = f (x) [/ latex] для определенной константы P и любого значения x
- сдвиг фазы
- горизонтальное смещение основной функции синуса или косинуса; константа [латекс] \ frac {C} {B} [/ latex]
- синусоидальная функция
- любая функция, которая может быть выражена в форме [латекс] f (x) = A \ sin (Bx − C) + D [/ latex] или [latex] f (x) = A \ cos (Bx − C) + D [/ латекс]
Упражнения по разделам
1. Почему функции синуса и косинуса называются периодическими функциями?
Почему функции синуса и косинуса называются периодическими функциями?
2. Как график [латекса] y = \ sin x [/ latex] соотносится с графиком [латекса] y = \ cos x [/ latex]? Объясните, как можно горизонтально перевести график [latex] y = \ sin x [/ latex], чтобы получить [latex] y = \ cos x [/ latex].
3. Какие константы влияют на диапазон функции и как они влияют на диапазон для уравнения [латекс] A \ cos (Bx + C) + D [/ latex]?
4. Как диапазон преобразованной синусоидальной функции соотносится с уравнением [латекс] y = A \ sin (Bx + C) + D [/ latex]?
5.Как можно использовать единичный круг для построения графика [латекса] f (t) = \ sin t [/ latex]?
6. [латекс] f (x) = 2 \ sin x [/ латекс]
7. [латекс] f (x) = \ frac {2} {3} \ cos x [/ латекс]
8. [латекс] f (x) = — 3 \ sin x [/ латекс]
9. [латекс] f (x) = 4 \ sin x [/ латекс]
10. [латекс] f (x) = 2 \ cos x [/ латекс]
11. [латекс] f (x) = \ cos (2x) [/ латекс]
12.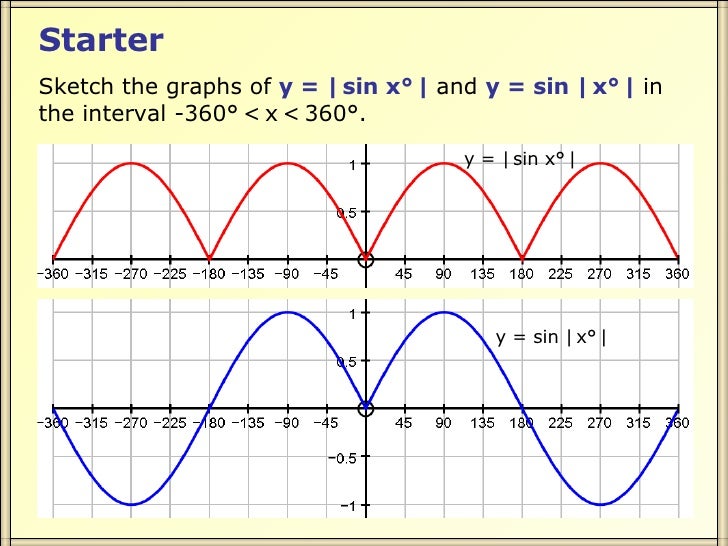 [латекс] f (x) = 2 \ sin (\ frac {1} {2} x) [/ latex]
[латекс] f (x) = 2 \ sin (\ frac {1} {2} x) [/ latex]
13. [латекс] f (x) = 4 \ cos (\ pi x) [/ латекс]
14. [латекс] f (x) = 3 \ cos (\ frac {6} {5} x) [/ latex]
15.[латекс] y = 3 \ sin (8 (x + 4)) + 5 [/ латекс]
16. [латекс] y = 2 \ sin (3x − 21) +4 [/ латекс]
17. [латекс] y = 5 \ sin (5x + 20) -2 [/ латекс]
Для следующих упражнений нарисуйте один полный период каждой функции, начиная с [latex] x = 0 [/ latex]. Для каждой функции укажите амплитуду, период и среднюю линию. Укажите максимальное и минимальное значения y и соответствующие им значения x на одном периоде для [latex] x> 0 [/ latex]. Укажите фазовый сдвиг и вертикальный сдвиг, если применимо.При необходимости округлите ответы до двух десятичных знаков.
18. [латекс] f (t) = 2 \ sin (t− \ frac {5 \ pi} {6}) [/ latex]
19. [латекс] f (t) = — \ cos (t + \ frac {\ pi} {3}) + 1 [/ latex]
20. [латекс] f (t) = 4 \ cos (2 (t + \ frac {\ pi} {4})) — 3 [/ латекс]
21. [латекс] f (t) = — \ sin (12t + \ frac {5 \ pi} {3}) [/ latex]
22. [латекс] f (x) = 4 \ sin (\ frac {\ pi} {2} (x − 3)) + 7 [/ latex]
23. Определите амплитуду, среднюю линию, период и уравнение, включающее синусоидальную функцию, для графика, показанного на рисунке 26.
Рисунок 26
24. Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 27.
Рисунок 27
25. Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 28.
Рисунок 28
26. Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на рисунке 29.
Рисунок 29
27.Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 30.
Рисунок 30
28. Определите амплитуду, период, среднюю линию и уравнение с синусом для графика, показанного на рисунке 31.
Рисунок 31
29. Определите амплитуду, период, среднюю линию и уравнение, включающее косинус, для графика, показанного на рисунке 32.
Рисунок 32
30. Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на рисунке 33.
Рисунок 33
Для следующих упражнений пусть [latex] f (x) = \ sin x [/ latex].
31. На [0,2π) решите [латекс] f (x) = \ frac {1} {2} [/ latex].
32. Вычислить [латекс] f (\ frac {\ pi} {2}) [/ latex].
33. На [0,2π), [латексе] f (x) = \ frac {\ sqrt {2}} {2} [/ latex]. Найдите все значения x .
34. На [0,2π) максимальное значение (я) функции встречается (а), при каком значении (ах) x ?
35. На [0,2π) встречается минимальное значение (я) функции, при каком значении (ах) x ?
36.Покажите, что [latex] f (−x) = — f (x) [/ latex]. Это означает, что [latex] f (x) = \ sin x [/ latex] является нечетной функцией и обладает симметрией относительно ________________ .
Для следующих упражнений пусть [latex] f (x) = \ cos x [/ latex].
37. На [0,2π) решите уравнение [латекс] f (x) = \ cos x = 0 [/ latex].
38. На [0,2π) решите [латекс] f (x) = \ frac {1} {2} [/ latex].
39. На [0,2π) найдите x -перехваты [latex] f (x) = \ cos x [/ latex].
40. На [0,2π) найдите значения x , при которых функция имеет максимальное или минимальное значение.
41. На [0,2π) решите уравнение [latex] f (x) = \ frac {\ sqrt {3}} {2} [/ latex].
42. График [латекс] h (x) = x + \ sin x \ text {on} [0,2 \ pi] [/ latex]. Объясните, почему график выглядит именно так.
43. График [латекс] h (x) = x + \ sin x [/ latex] на [−100,100]. График выглядел так, как было предсказано в предыдущем упражнении?
44. Изобразите [латекс] f (x) = x \ sin x [/ latex] на [0,2π] и вербализируйте, как график отличается от графика [латекса] f (x) = \ sin x [/ latex ].
45. Изобразите [латекс] f (x) = x \ sin x [/ latex] в окне [-10,10] и объясните, что показывает график.
46. Изобразите [латекс] f (x) = \ frac {\ sin x} {x} [/ latex] в окне [−5π, 5π] и объясните, что показывает график.
47. Колесо обозрения имеет диаметр 25 метров и поднимается на него с платформы, находящейся на высоте 1 метра над землей. Шесть часов на колесе обозрения находится на уровне погрузочной платформы. Колесо совершает 1 полный оборот за 10 минут. Функция h ( t ) дает высоту человека в метрах над землей t минут после начала поворота колеса.
а. Найдите амплитуду, среднюю линию и период ч ( т ).
г. Найдите формулу для функции высоты h ( t ).
г. Как высоко над землей окажется человек через 5 минут?
график sinx | график y = sin x
График sin x является периодической функцией с периодом 2π. Итак, мы нарисуем график y = sin (x) в интервале [0,2π]. График синуса выглядит так. Чтобы нарисовать график y = sin (x), мы будем использовать следующие шаги:1) Нарисуйте ось Y с 0,1, -1.{0} $ или 2π.
3) y = a sin (x) амплитуда ‘a’ равна 1, поэтому кривая будет до (0,1). Если y = 2 sin (x), то амплитуда будет 2, поэтому кривая будет до (0,2).
Здесь ask-math объясняет синусоидальную кривую только в радианах.
Шаг 1: Проведите ось Y и отметьте точки 0,1 и -1, так как амплитуда для графика y = sin (x) равна 1. Нарисуйте ось x от 0 и отметьте точки π, 2π, 3π. ..etc.Шаг 2: Поскольку sin (0) = 0, то синусоидальный график начинается с начала координат, или вы можете сказать, что синусоидальный график пересекает ось X в точке (0,0).
И sin (π / 2) = 1, что является максимумом для этого конкретного графика, так как амплитуда равна 1, поэтому синусоидальная кривая достигает [π / 2,1].
аналогично sin (3π / 2) = -1, который максимален вдоль отрицательной оси Y, поэтому синусоида достигает [3π / 2, -1].
Примечание: для y = 2 sin x амплитуда равна 2, а sin (π / 2) = 1, поэтому синусоидальная кривая достигает [π / 2,2] на положительной оси Y и [3π / 2, — 2] по отрицательной оси Y.
Поскольку sin x является возрастающей функцией, мы получаем график y = sin x в интервале [0, π / 2].Мы рисуем график y = sin x, используя тот факт, что sin (π- x) = sin x. Итак, наконец, мы рисуем его в интервале [π, 2π], используя тот факт, что sin (π + x) = -sin x, что означает, что график y = sin x в [π, 2π] является зеркальным отображением график y = sin x в [0, π].
Практика на графике sinx
1) Каков период y = 2 sin (x).2) Запишите амплитуду y = 3 sin (x).
3) Нарисуйте график y = 2 sin (x). Математика 11-го класса
От графика sinx к дому
Covid-19 привел мир к феноменальному переходу.
Электронное обучение — это будущее сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Что такое период синусоидальной функции?
Обновлено 30 ноября 2020 г.
Автор: Элиза Хансен
Период синусоидальной функции равен 2π , что означает, что значение функции одинаково каждые 2π единиц.
Синусоидальная функция, такая как косинус, тангенс, котангенс и многие другие тригонометрические функции, является периодической функцией , что означает, что она повторяет свои значения через равные промежутки времени или «периоды». В случае синусоидальной функции этот интервал равен 2π.
TL; DR (слишком долго; не читал)
TL; DR (слишком долго; не читал)
Период синусоидальной функции равен 2π.
Например, sin (π) = 0. Если вы прибавите 2π к значению x , вы получите sin (π + 2π), который равен sin (3π).Как и sin (π), sin (3π) = 0. Каждый раз, когда вы добавляете или вычитаете 2π из нашего значения x , решение будет таким же.
Вы можете легко увидеть период на графике как расстояние между «совпадающими» точками. Поскольку график y = sin ( x ) выглядит как единый шаблон, повторяющийся снова и снова, вы также можете думать об этом как о расстоянии по оси x перед графиком. начинает повторяться.
На единичной окружности 2π — это полный оборот по окружности.Любая величина, превышающая 2π радиан, означает, что вы продолжаете двигаться по кругу — это повторяющийся характер синусоидальной функции и еще один способ проиллюстрировать, что каждые 2π единицы значение функции будет одинаковым.
Изменение периода функции синуса
Период основной функции синуса
y = \ sin (x)
равен 2π, но если x умножить на константу, это может измениться стоимость периода.
Если x умножить на число больше 1, это «ускорит» функцию, и период будет меньше.Функция не займет много времени, чтобы начать повторяться.
y = \ sin (2x)
удваивает «скорость» функции. Период равен всего π радиан.
Но если x умножить на дробь от 0 до 1, это «замедлит» функцию, а период будет больше, потому что для повторения функции требуется больше времени.
y = \ sin \ bigg (\ frac {x} {2} \ bigg)
снижает «скорость» функции вдвое; требуется много времени (4π радиан), чтобы он завершил полный цикл и снова начал повторяться.
Найдите период синусоидальной функции
Допустим, вы хотите вычислить период модифицированной синусоидальной функции, например
y = \ sin (2x) \ text {или} y = \ sin \ bigg (\ frac { x} {2} \ bigg)
Коэффициент x является ключевым; назовем этот коэффициент B .
Итак, если у вас есть уравнение в форме y = sin ( Bx ), тогда:
\ text {Period} = \ frac {2π} {| B |}
Бары | | означает «абсолютное значение», поэтому, если B — отрицательное число, вы должны просто использовать положительную версию.Если, например, B было −3, вы бы просто выбрали 3.
Эта формула работает, даже если у вас есть сложный вариант синусоидальной функции, например
y = \ frac {1} { 3} × \ sin (4x + 3)
Коэффициент x — это все, что имеет значение для расчета периода, так что вы все равно должны:
\ text {Period} = \ frac {2π} {| 4 |} \\ \, \\ \ text {Period} = \ frac {π} {2}
Найдите период любой триггерной функции
Чтобы найти период косинуса, тангенса и других триггерных функций, вы используйте очень похожий процесс.Просто используйте стандартный период для конкретной функции, с которой вы работаете при расчетах.
Поскольку период косинуса равен 2π, то же самое, что и синус, формула для периода функции косинуса будет такой же, как и для синуса. Но для других триггерных функций с другим периодом, таких как тангенс или котангенс, мы сделаем небольшую корректировку. Например, период детской кроватки ( x ) равен π, поэтому формула для периода y = кроватка (3 x ) следующая:
\ text {Period} = \ frac {π} {| 3 |}
, где мы используем π вместо 2π.
\ text {Period} = \ frac {π} {3}
Абсолютные функции значений · Алгебра и тригонометрия
Абсолютные функции · Алгебра и тригонометрияВ этом разделе вы:
- Постройте график функции абсолютного значения.
- Решите уравнение абсолютного значения.
До 1920-х годов считалось, что так называемые спиральные туманности представляют собой облака пыли и газа в нашей галактике, находящейся на расстоянии нескольких десятков тысяч световых лет от нас.Затем астроном Эдвин Хаббл доказал, что эти объекты сами по себе являются галактиками на расстояниях в миллионы световых лет. Сегодня астрономы могут обнаруживать галактики, удаленные от нас на миллиарды световых лет. Расстояния во Вселенной можно измерить во всех направлениях. Таким образом, полезно рассматривать расстояние как функцию абсолютного значения. В этом разделе мы продолжим наше исследование функций абсолютного значения .
Понимание абсолютного значения
Напомним, что в его основной форме f (x) = \ | x \ |,
функция абсолютного значения — это одна из функций нашего инструментария.Функция абсолютного значения обычно рассматривается как обеспечивающая расстояние, на котором число находится от нуля на числовой прямой. Алгебраически, для любого входного значения, выход — это значение без учета знака. Зная это, мы можем использовать функции абсолютного значения для решения некоторых видов реальных проблем.
Функция абсолютного значения
Функция абсолютного значения может быть определена как кусочная функция
f (x) = \ | x \ | = {xifx≥0 − xifx <0
Использование абсолютного значения для определения сопротивления
Электрические детали, такие как резисторы и конденсаторы, имеют указанные значения рабочих параметров: сопротивление, емкость и т. Д.Однако из-за неточности изготовления фактические значения этих параметров несколько различаются от детали к детали, даже если они предполагаются одинаковыми. Лучшее, что могут сделать производители, — это попытаться гарантировать, что отклонения останутся в пределах указанного диапазона, часто ± 1%, ± 5%,
или ± 10%.
Предположим, у нас есть резистор номиналом 680 Ом, ± 5%.
Используйте функцию абсолютного значения, чтобы выразить диапазон возможных значений фактического сопротивления.
Мы можем найти, что 5% от 680 Ом составляет 34 Ом. Абсолютное значение разницы между фактическим и номинальным сопротивлением не должно превышать заявленную изменчивость, поэтому при сопротивлении R
Ом,
\ | R − 680 \ | ≤34
Студенты, набравшие в пределах 20 баллов из 80, пройдут тест. Запишите это как расстояние от 80, используя обозначение абсолютного значения.
с использованием переменной p
для прохождения, \ | p − 80 \ | ≤20
Построение графика функции абсолютного значения
Наиболее важной особенностью графика абсолютных значений является угловая точка, в которой график меняет направление.Эта точка показана в исходной точке в [ссылка].
[ссылка] показывает график y = 2 \ | x – 3 \ | +4.
График y = \ | x \ |
был смещен вправо на 3 единицы, растянут по вертикали в 2 раза и сдвинут на 4 единицы вверх. Это означает, что угловая точка находится в точке (3,4)
.для этой преобразованной функции.
Написание уравнения для функции абсолютного значения на основе графика
Напишите уравнение для функции, изображенной на [ссылка].
Основная функция абсолютного значения изменяет направление в начале координат, поэтому этот график сдвинут вправо на 3 единицы и на 2 единицы вниз от базовой функции инструментария. См. [Ссылка].
Мы также замечаем, что график выглядит растянутым по вертикали, потому что ширина окончательного графика на горизонтальной линии не равна двукратному расстоянию по вертикали от угла до этой линии, как это было бы для нерастянутой функции абсолютного значения.Вместо этого ширина равна 1 вертикальному расстоянию, как показано в [ссылка].
Из этой информации мы можем написать уравнение
f (x) = 2 \ | x − 3 \ | −2, рассматривая растяжение как вертикальное растяжение, или f (x) = \ | 2 (x − 3) \ | −2, рассматривая растяжение как горизонтальное сжатие.
Анализ
Обратите внимание, что эти уравнения алгебраически эквивалентны — растяжение для функции абсолютного значения может быть взаимозаменяемо записано как вертикальное или горизонтальное растяжение или сжатие.
Если бы мы не могли наблюдать растяжение функции по графикам, могли бы мы определить его алгебраически?
Да. Если мы не можем определить растяжение на основе ширины графика, мы можем вычислить коэффициент растяжения, введя известную пару значений для
xи
f (x).
е (х) = а \ | х − 3 \ | −2
Теперь подставляем в точку (1, 2)
2 = a \ | 1−3 \ | −24 = 2aa = 2
Напишите уравнение для функции абсолютного значения, которая сдвигается по горизонтали на 2 единицы влево, переворачивается по вертикали и смещается по вертикали на 3 единицы.
е (х) = — \ | х + 2 \ | +3
Всегда ли графики функций абсолютных значений пересекают вертикальную ось? Горизонтальная ось?
Да, они всегда пересекают вертикальную ось. График функции абсолютного значения будет пересекать вертикальную ось, когда вход равен нулю.
Нет, они не всегда пересекают горизонтальную ось. График может пересекать или не пересекать горизонтальную ось, в зависимости от того, как график был смещен и отражен.Функция абсолютного значения может пересекать горизонтальную ось в нуле, одной или двух точках (см. [Ссылка]).
Решение уравнения абсолютных значений
В разделе «Другой тип уравнений» мы затронули концепции уравнений абсолютных значений. Теперь, когда мы немного больше разбираемся в их графиках, мы можем еще раз взглянуть на эти типы уравнений. Теперь, когда мы можем построить график функции абсолютного значения, мы узнаем, как решить уравнение абсолютного значения.Чтобы решить такое уравнение, как 8 = \ | 2x − 6 \ |,
мы замечаем, что абсолютное значение будет равно 8, если количество внутри абсолютного значения равно 8 или -8. Это приводит к двум различным уравнениям, которые мы можем решить независимо.
2x − 6 = 8 или 2x − 6 = −82x = 142x = −2x = 7x = −1
Полезно знать, как решать задачи, связанные с функциями абсолютного значения. . Например, нам может потребоваться определить числа или точки на линии, которые находятся на заданном расстоянии от заданной контрольной точки.
Уравнение абсолютного значения — это уравнение, в котором неизвестная переменная отображается в столбцах абсолютного значения. Например,
\ | x \ | = 4, \ | 2x − 1 \ | = 3 или \ | 5x + 2 \ | −4 = 9
Решения уравнений абсолютных значений
Для вещественных чисел A
и B
, уравнение вида \ | A \ | = B,
с B≥0,
будет иметь решения, когда A = B
или A = -B.
Если B <0,
уравнение \ | A \ | = B
не имеет решения.
Учитывая формулу функции абсолютного значения, найдите горизонтальные пересечения ее графика .
- Выделите член абсолютного значения.
- Использование
\ | A \ | = B
для записи
A = Bили
−A = B,в предположении
В> 0. - Решить для Икс.
Нахождение нулей функции абсолютного значения
Для функции f (x) = \ | 4x + 1 \ | −7,
найти значения x
такой, что f (x) = 0.
0 = \ | 4x + 1 \ | −7 Заменить 0 вместо f (x). 7 = \ | 4x + 1 \ | Изолировать абсолютное значение на одной стороне уравнения. 7 = 4x + 1 или − 7 = 4x + 1 Разбить на два отдельных уравнения и решите 6 = 4x − 8 = 4xx = 64 = 1,5x = −84 = −2
Функция выводит 0, если x = 32
или x = −2.
См. [Ссылка].
Для функции f (x) = \ | 2x − 1 \ | −3,
найти значения x
такой, что f (x) = 0.
Следует ли всегда ожидать двух ответов при решении
\ | A \ | = B?
№Мы можем найти один, два или даже не найти ответов. Например, нет решения для 2+ \ | 3x − 5 \ | = 1.
Ключевые понятия
- Прикладные задачи, такие как диапазоны возможных значений, также могут быть решены с помощью функции абсолютного значения. См. [Ссылка].
- График функции абсолютного значения напоминает букву V. У него есть угловая точка, в которой график меняет направление. См. [Ссылка].
- В уравнении абсолютного значения неизвестная переменная является входом функции абсолютного значения.
- Если абсолютное значение выражения установлено равным положительному числу, ожидайте два решения для неизвестной переменной. См. [Ссылка].
Упражнения по разделам
Устный
Как решить уравнение абсолютного значения?
Выделите член абсолютного значения так, чтобы уравнение имело вид \ | A \ | = B.
Сформируйте одно уравнение, задав выражение внутри символа абсолютного значения, A,
, равное выражению на другой стороне уравнения B.
Сформируйте второе уравнение, задав A
равно величине, противоположной выражению на другой стороне уравнения, −B.
Решите каждое уравнение для переменной.
Как узнать, есть ли у функции абсолютного значения два интерцептора x , не отображая функцию в виде графика?
При решении функции абсолютного значения изолированный член абсолютного значения равен отрицательному числу. Что это говорит вам о графике функции абсолютного значения?
График функции абсолютного значения не пересекает x
-ось, поэтому график либо полностью выше, либо полностью ниже x
— ось.
Как можно использовать график функции абсолютного значения для определения значений x , для которых значения функции отрицательны?
Алгебраические
Опишите все числа x
, которые находятся на расстоянии 4 от числа 8. Выразите этот набор чисел, используя обозначение абсолютных значений.
Опишите все числа x
, которые находятся на расстоянии 12
из числа −4.Выразите этот набор чисел, используя обозначение абсолютных значений.
\ | х + 4 \ | = 12
Опишите ситуацию, в которой расстояние до этой точки x
из 10 — это минимум 15 единиц. Выразите этот набор чисел, используя обозначение абсолютных значений.
Найти все значения функции f (x)
такое, что расстояние от f (x)
до значения 8 меньше 0,03 единицы. Выразите этот набор чисел, используя обозначение абсолютных значений.
\ | f (x) −8 \ | <0,03
Для следующих упражнений найдите точки пересечения x и y графиков каждой функции.
f (x) = — 3 \ | x − 2 \ | −1
(0, −7);нет x
-перехватывает
е (х) = — 5 \ | х + 2 \ | +15
(0, 5), (1,0), (- 5,0)
f (x) = 2 \ | x − 1 \ | −6
(0, −4), (4,0), (- 2,0)
f (х) = \ | −2x + 1 \ | −13
(0, −12), (- 6,0), (7,0)
е (х) = — \ | х − 9 \ | +16
(0,7), (25,0), (- 7,0)
Графический
Для следующих упражнений постройте график функции абсолютного значения.Нарисуйте от руки не менее пяти точек для каждого графика.
y = \ | x − 1 \ |
! [График абсолютной функции с точками в точках (-1, 2), (0, 1), (1, 0), (2, 1) и (3, 2).] (/ Algebra-trigonometry-book /resources/CNX_Precalc_Figure_01_06_201.jpg)
у = \ | х \ | +1
! [График абсолютной функции с точками в точках (-2, 3), (-1, 2), (0, 1), (1, 2) и (2, 3).] (/ Алгебра-тригонометрия- book / resources / CNX_Precalc_Figure_01_06_203.jpg)
Для следующих упражнений нарисуйте данные функции вручную.
у = — \ | х \ |
! [График абсолютной функции.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_01_06_205.jpg)
у = — \ | х − 3 \ | −2
! [График абсолютной функции.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_01_06_207.jpg)
е (х) = — \ | х + 3 \ | +4
! [График абсолютной функции.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_01_06_209.jpg)
f (x) = 3 \ | x − 2 \ | +3
! [График абсолютной функции.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_01_06_211.jpg)
е (х) = \ | 3x + 9 \ | +2
! [График абсолютной функции.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_01_06_213.jpg)
е (х) = — \ | х + 4 \ | −3
! [График абсолютной функции.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_01_06_215.jpg)
Технологии
Используйте графическую утилиту для построения графика f (x) = 10 \ | x − 2 \ |
на смотровом окошке [0,4].
Определите соответствующий диапазон. Покажи график.
диапазон: [0,20]
Используйте графическую утилиту для построения графика f (x) = — 100 \ | x \ | +100
в окне просмотра [−5,5].
Определите соответствующий диапазон. Покажи график.
Для следующих упражнений нарисуйте график каждой функции с помощью графической утилиты. Укажите окно просмотра.
f (х) = — 0,1 \ | 0,1 (0,2 — х) \ | +0,3
x-перехватывает:
f (x) = 4 × 109 \ | x− (5 × 109) \ | + 2 × 109
Расширения
Для следующих упражнений решите неравенство.
Если возможно, найдите все значения
такие, что нет х-
перехватов для f (x) = 2 \ | x + 1 \ | + a.
Если возможно, найдите все значения
такое что нету
-перехватывания для f (x) = 2 \ | x + 1 \ | + a.
Нет решения для
, который не позволит функции иметь y
-перехват. Функция абсолютного значения всегда пересекает y
-перехват, когда x = 0.
Реальные приложения
Города A и B находятся на одной линии восток-запад. Предположим, что город A расположен в исходной точке. Если расстояние от города A до города B составляет не менее 100 миль и x
представляет собой расстояние от города B до города A, выразите это, используя обозначение абсолютных значений.
Истинная пропорция
р.человек, которые дают положительную оценку Конгрессу, составляют 8% с погрешностью 1,5%. Опишите это утверждение, используя уравнение абсолютного значения.
\ | p − 0,08 \ | ≤0,015
Учащиеся, набравшие в пределах 18 баллов из числа 82, пройдут определенный тест. Запишите этот оператор, используя обозначение абсолютного значения, и используйте переменную x
для оценки.
Машинист должен изготовить подшипник, диаметр которого не превышает 0,01 дюйма (5,0 дюйма). Использование x
в качестве диаметра подшипника, запишите это утверждение, используя обозначение абсолютного значения.
\ | х − 5.0 \ | ≤0.01
Допуск для шарикового подшипника 0,01. Если истинный диаметр подшипника должен составлять 2,0 дюйма, а измеренное значение диаметра составляет x
дюйма, выразите допуск, используя обозначение абсолютного значения.
Эта работа находится под международной лицензией Creative Commons Attribution 4.0.
Вы также можете бесплатно скачать по адресу http://cnx.org/contents/[email protected]
Авторство:
Период и амплитуда — тригонометрия
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
6.1 Графики функций синуса и косинуса — предварительное вычисление
Цели обучения
В этом разделе вы:
- Графические вариации y = sin (x) y = sin (x) и y = cos (x) y = cos (x).
- Используйте фазовые сдвиги синусоидальных и косинусных кривых.
Рис. 1 Свет можно разделить на цвета из-за его волнообразных свойств. (кредит: «wonderferret» / Flickr)
Белый свет, такой как свет от солнца, на самом деле совсем не белый. Вместо этого это композиция всех цветов радуги в виде волн. Отдельные цвета можно увидеть только тогда, когда белый свет проходит через оптическую призму, которая разделяет волны в соответствии с их длинами волн, образуя радугу.
Световые волны могут быть представлены графически с помощью синусоидальной функции. В главе о тригонометрических функциях мы рассмотрели тригонометрические функции, такие как синусоидальная функция. В этом разделе мы будем интерпретировать и создавать графики функций синуса и косинуса.
Графические функции синуса и косинуса
Напомним, что функции синуса и косинуса связывают значения действительных чисел с координатами x и y точки на единичной окружности. Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции.Мы можем создать таблицу значений и использовать их для построения графика. В таблице 1 перечислены некоторые значения синусоидальной функции на единичной окружности.
| xx | 00 | π6π6 | π4π4 | π3π3 | π2π2 | 2π32π3 | 3π43π4 | 5π65π6 | ππ |
| sin (x) sin (x) | 00 | 1212 | 2222 | 3232 | 11 | 3232 | 2222 | 1212 | 00 |
Таблица 1
Построение точек из таблицы и продолжение по оси x дает форму синусоидальной функции.См. Рисунок 2.
Рисунок 2 Синусоидальная функция
Обратите внимание, что значения синуса положительны между 0 и π, π, которые соответствуют значениям синусоидальной функции в квадрантах I и II на единичной окружности, а значения синуса отрицательны между ππ и 2π, 2π, которые соответствуют значениям синусоидальной функции в квадрантах III и IV на единичной окружности. См. Рисунок 3.
Рисунок 3 График значений функции синуса
Теперь давайте аналогичным образом взглянем на функцию косинуса.Опять же, мы можем создать таблицу значений и использовать их для построения графика. В таблице 2 перечислены некоторые значения функции косинуса на единичной окружности.
| хх | 00 | π6π6 | π4π4 | π3π3 | π2π2 | 2π32π3 | 3π43π4 | 5π65π6 | ππ |
| cos (x) cos (x) | 11 | 3232 | 2222 | 1212 | 00 | −12−12 | −22−22 | −32−32 | −1−1 |
Таблица 2
Как и в случае с функцией синуса, мы можем построить точки для построения графика функции косинуса, как показано на рисунке 4.
Рисунок 4 Функция косинуса
Поскольку мы можем вычислить синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Если рассматривать значения синуса и косинуса как координаты точек на единичной окружности, становится ясно, что диапазон обеих функций должен быть интервалом [-1,1]. [-1,1].
На обоих графиках форма графика повторяется после 2π, 2π, что означает, что функции являются периодическими с периодом 2π.2π. Периодическая функция — это функция, для которой определенный горизонтальный сдвиг, P , приводит к функции, равной исходной функции: f (x + P) = f (x) f (x + P) = f (x) для все значения xx в области f.f. Когда это происходит, мы называем наименьший такой горизонтальный сдвиг с P> 0P> 0 периодом функции. На рисунке 5 показаны несколько периодов функций синуса и косинуса.
Рисунок 5
Еще раз взглянув на функции синуса и косинуса в области с центром на оси y , можно выявить симметрии. Как мы видим на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомните из книги «Другие тригонометрические функции», которую мы определили по единичной окружности, что синусоидальная функция является нечетной функцией, поскольку sin (−x) = — sinx.sin (−x) = — sinx. Теперь мы можем ясно видеть это свойство на графике.
Рисунок 6 Нечетная симметрия функции синуса
Рисунок 7 показывает, что функция косинуса симметрична относительно оси y . Опять же, мы определили, что функция косинуса является четной функцией. Теперь из графика видно, что cos (−x) = cosx.cos (−x) = cosx.
Рисунок 7 Четная симметрия функции косинуса
Характеристики функций синуса и косинуса
Функции синуса и косинуса имеют несколько отличительных характеристик:
- Это периодические функции с периодом 2π.2π.
- Область определения каждой функции — (−∞, ∞) (- ∞, ∞), а диапазон — [−1,1]. [- 1,1].
- График y = sinxy = sinx симметричен относительно начала координат, потому что это нечетная функция.
- График y = cosxy = cosx симметричен относительно оси yy, потому что это четная функция.
Исследование синусоидальных функций
Как мы видим, функции синуса и косинуса имеют постоянный период и диапазон. Если мы увидим океанские волны или рябь на пруду, мы увидим, что они напоминают функции синуса или косинуса.Однако они не обязательно идентичны. Некоторые из них выше или длиннее других. Функция, имеющая ту же общую форму, что и функция синуса или косинуса, известна как синусоидальная функция. Общие формы синусоидальных функций:
y = Asin (Bx − C) + Dandy = Acos (Bx − C) + Dy = Asin (Bx − C) + Dandy = Acos (Bx − C) + DОпределение периода синусоидальной функции
Глядя на формы синусоидальных функций, мы можем видеть, что они являются преобразованиями функций синуса и косинуса. Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
В общей формуле BB связано с периодом соотношением P = 2π | B | .P = 2π | B |. Если | B |> 1, | B |> 1, то период меньше 2π2π и функция подвергается горизонтальному сжатию, тогда как если | B | <1, | B | <1, то период больше 2π2π и функция растягивается по горизонтали. Например, f (x) = sin (x), f (x) = sin (x), B = 1, B = 1, поэтому период равен 2π, 2π, что мы знали. Если f (x) = sin (2x), f (x) = sin (2x), то B = 2, B = 2, поэтому период равен ππ и график сжат. Если f (x) = sin (x2), f (x) = sin (x2), то B = 12, B = 12, поэтому период равен 4π4π и график растянут.Обратите внимание на рис. 8, как период косвенно связан с | B |. | B |.
Рисунок 8
Период синусоидальной функции
Если мы положим C = 0C = 0 и D = 0D = 0 в уравнениях общего вида для функций синуса и косинуса, мы получим формы
Период равен 2π | B | .2π | B |.
Пример 1
Определение периода функции синуса или косинуса
Определите период функции f (x) = sin (π6x). F (x) = sin (π6x).
Решение
Начнем с сравнения уравнения с общей формой y = Asin (Bx).у = Asin (Bx).
В данном уравнении B = π6, B = π6, поэтому период будет
P = 2π | B | = 2ππ6 = 2π⋅6π = 12P = 2π | B | = 2ππ6 = 2π⋅6π = 12Попробовать # 1
Определите период функции g (x) = cos (x3) .g (x) = cos (x3).
Определение амплитуды
Возвращаясь к общей формуле для синусоидальной функции, мы проанализировали, как переменная BB связана с периодом. Теперь давайте обратимся к переменной AA, чтобы мы могли проанализировать, как она связана с амплитудой , или наибольшим расстоянием от покоя.AA представляет коэффициент вертикального растяжения, а его абсолютное значение | A || A | это амплитуда. Локальными максимумами будет расстояние | A || A | выше горизонтальной средней линии графика, которая представляет собой линию y = D; y = D; поскольку в этом случае D = 0D = 0, средняя линия представляет собой ось x . Локальные минимумы будут на таком же расстоянии ниже средней линии. Если | A |> 1, | A |> 1, функция растягивается. Например, амплитуда f (x) = 4sinxf (x) = 4sinx в два раза больше амплитуды f (x) = 2sinx.f (x) = 2sinx. Если | A | <1, | A | <1, функция сжимается.На рисунке 9 сравнивается несколько синусоид с разными амплитудами.
Рисунок 9
Амплитуда синусоидальной функции
Если мы положим C = 0C = 0 и D = 0D = 0 в уравнениях общего вида для функций синуса и косинуса, мы получим формы
y = Asin (Bx) и y = Acos (Bx) y = Asin (Bx ) И y = Acos (Bx)Амплитуда равна | A |, | A |, которая представляет собой высоту по вертикали от средней линии. Кроме того, обратите внимание на пример, что
| A | = Амплитуда = 12 | максимум — минимум || A | = Амплитуда = 12 | максимум — минимум |Пример 2
Определение амплитуды функции синуса или косинуса
Какова амплитуда синусоидальной функции f (x) = — 4sin (x)? F (x) = — 4sin (x)? Функция растягивается или сжимается по вертикали?
Решение
Начнем с сравнения функции с упрощенной формой y = Asin (Bx).у = Asin (Bx).
В данной функции A = −4, A = −4, поэтому амплитуда равна | A | = | −4 | = 4. | A | = | −4 | = 4. Функция растянута.
Анализ
Отрицательное значение AA приводит к отражению по оси x синусоидальной функции, как показано на рисунке 10.
Рисунок 10
Попробуй # 2
Какова амплитуда синусоидальной функции f (x) = 12sin (x)? F (x) = 12sin (x)? Функция растягивается или сжимается по вертикали?
Анализ графиков вариаций
y = sin x и y = cos xТеперь, когда мы понимаем, как AA и BB соотносятся с уравнением общей формы для функций синуса и косинуса, мы исследуем переменные CC и D.D. Напомним общую форму:
y = Asin (Bx − C) + D и y = Acos (Bx − C) + Dory = Asin (B (x − CB)) + D и y = Acos (B (x − CB)) + Dy = Asin ( Bx − C) + D и y = Acos (Bx − C) + Dory = Asin (B (x − CB)) + D и y = Acos (B (x − CB)) + DЗначение CBCB для синусоидальной функции называется фазовым сдвигом или горизонтальным смещением основной синусоидальной или косинусоидальной функции. Если C> 0, C> 0, график сдвигается вправо. Если C <0, C <0, график сдвигается влево. Чем больше значение | C |, | C |, тем больше сдвигается график.Рисунок 11 показывает, что график f (x) = sin (x − π) f (x) = sin (x − π) сдвигается вправо на ππ единиц, что больше, чем мы видим на графике f (x ) = sin (x − π4), f (x) = sin (x − π4), который сдвигается вправо на π4π4 единиц.
Рисунок 11
В то время как CC относится к горизонтальному смещению, DD указывает вертикальное смещение от средней линии в общей формуле для синусоидальной функции. См. Рисунок 12. Функция y = cos (x) + Dy = cos (x) + D имеет среднюю линию в точке y = D.y = D.
Рисунок 12
Любое значение DD, кроме нуля, сдвигает график вверх или вниз.На рисунке 13 сравнивается f (x) = sin (x) f (x) = sin (x) с f (x) = sin (x) + 2, f (x) = sin (x) +2, которое сдвинуто на 2. единиц на графике.
Рисунок 13
Вариации функций синуса и косинуса
Дано уравнение в форме f (x) = Asin (Bx − C) + Df (x) = Asin (Bx − C) + D или f (x) = Acos (Bx − C) + D, f (x ) = Acos (Bx − C) + D, CBCB — фазовый сдвиг, DD — вертикальный сдвиг.
Пример 3
Определение фазового сдвига функции
Определите направление и величину фазового сдвига для f (x) = sin (x + π6) −2.е (х) = грех (х + π6) −2.
Решение
Начнем с сравнения уравнения с общей формой y = Asin (Bx − C) + D.y = Asin (Bx − C) + D.
Обратите внимание, что в данном уравнении B = 1B = 1 и C = −π6.C = −π6. Итак, фазовый сдвиг
CB = −π61 = −π6CB = −π61 = −π6или π6π6 единиц слева.
Анализ
Необходимо обратить внимание на знак в уравнении общего вида синусоидальной функции. Уравнение показывает знак минус перед C.C. Следовательно, f (x) = sin (x + π6) −2f (x) = sin (x + π6) −2 можно переписать как f (x) = sin (x — (- π6)) — 2.е (х) = грех (х — (- π6)) — 2. Если значение CC отрицательное, сдвиг влево.
Попробуй # 3
Определите направление и величину фазового сдвига для f (x) = 3cos (x − π2). F (x) = 3cos (x − π2).
Пример 4
Определение вертикального сдвига функции
Определите направление и величину вертикального сдвига для f (x) = cos (x) −3.f (x) = cos (x) −3.
Решение
Начнем с сравнения уравнения с общей формой y = Acos (Bx − C) + D.у = Acos (Bx − C) + D.
В данном уравнении D = −3D = −3, поэтому сдвиг составляет 3 единицы вниз.
Попробуй # 4
Определите направление и величину вертикального сдвига для f (x) = 3sin (x) + 2. f (x) = 3sin (x) +2.
Как к
Для синусоидальной функции в форме f (x) = Asin (Bx − C) + D, f (x) = Asin (Bx − C) + D, идентифицирует среднюю линию, амплитуду, период и фазовый сдвиг. .
- Определите амплитуду как | A |. | A |.
- Определите период как P = 2π | B |.P = 2π | B |.
- Определите фазовый сдвиг как CB.CB.
- Определите среднюю линию как y = D.y = D.
Пример 5
Определение вариаций синусоидальной функции из уравнения
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции y = 3sin (2x) + 1.y = 3sin (2x) +1.
Решение
Начнем с сравнения уравнения с общей формой y = Asin (Bx − C) + D.y = Asin (Bx − C) + D.
A = 3, A = 3, поэтому амплитуда | A | = 3.| А | = 3.
Далее, B = 2, B = 2, поэтому период равен P = 2π | B | = 2π2 = π.P = 2π | B | = 2π2 = π.
В скобках нет добавленной константы, поэтому C = 0C = 0, а фазовый сдвиг CB = 02 = 0. CB = 02 = 0.
Наконец, D = 1, D = 1, поэтому средняя линия y = 1.y = 1.
Анализ
Изучая график, мы можем определить, что период равен π, π, средняя линия равна y = 1, y = 1, а амплитуда равна 3. См. Рисунок 14.
Рисунок 14
Попробуй # 5
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции y = 12cos (x3 − π3).у = 12cos (х3 — π3).
Пример 6
Определение уравнения для синусоидальной функции из графика
Определите формулу функции косинуса на рисунке 15.
Рисунок 15
Решение
Чтобы определить уравнение, нам нужно идентифицировать каждое значение в общем виде синусоидальной функции.
y = Asin (Bx − C) + Dy = Acos (Bx − C) + Dy = Asin (Bx − C) + Dy = Acos (Bx − C) + DГрафик может представлять либо функцию синуса, либо функцию косинуса, которая сдвигается и / или отражается.Когда x = 0, x = 0, график имеет крайнюю точку (0,0). (0,0). Поскольку функция косинуса имеет крайнюю точку при x = 0, x = 0, давайте запишем наше уравнение в терминах функции косинуса.
Начнем со средней линии. Мы видим, что график поднимается и опускается на одинаковое расстояние выше и ниже y = 0,5.y = 0,5. Это значение, которое является средней линией, является DD в уравнении, поэтому D = 0,5, D = 0,5.
Наибольшее расстояние выше и ниже средней линии — это амплитуда. Максимумы на 0,5 единицы выше средней линии, а минимумы — на 0.На 5 единиц ниже средней линии. Итак, | A | = 0,5. | A | = 0,5. Другой способ определить амплитуду — это признать, что разница между высотой локальных максимумов и минимумов равна 1, поэтому | A | = 12 = 0,5. | A | = 12 = 0,5. Кроме того, график отображается относительно оси x , так что A = -0,5.A = -0,5.
График не растягивается и не сжимается по горизонтали, поэтому B = 1; B = 1; и график не смещен по горизонтали, поэтому C = 0.C = 0.
Собирая все вместе,
g (x) = — 0,5cos (x) + 0,5g (x) = — 0.5cos (x) +0,5Попробуй # 6
Определите формулу синусоидальной функции на рисунке 16.
Рисунок 16
Пример 7
Определение уравнения для синусоидальной функции из графика
Определите уравнение для синусоидальной функции на рисунке 17.
Рисунок 17
Решение
При максимальном значении 1 и минимальном значении −5, −5 средняя линия будет находиться на полпути между −2. − 2. Итак, D = −2.D = −2.
Расстояние от средней линии до самого высокого или самого низкого значения дает амплитуду | A | = 3. | A | = 3.
Период графика равен 6, и его можно измерить от пика при x = 1x = 1 до следующего пика при x = 7, x = 7 или от расстояния между самыми низкими точками. Следовательно, P = 2π | B | = 6. P = 2π | B | = 6. Используя положительное значение для B, B, мы находим, что
B = 2πP = 2π6 = π3B = 2πP = 2π6 = π3Пока что наше уравнение выглядит так: y = 3sin (π3x − C) −2y = 3sin (π3x − C) −2 или y = 3cos (π3x − C) — 2. у = 3cos (π3x − C) −2. Для формы и сдвига у нас есть несколько вариантов.Мы могли бы записать это как любое из следующих:
- косинус, смещенный вправо
- отрицательный косинус, сдвинутый влево
- синус, сдвинутый влево
- отрицательный синус смещен вправо
Хотя любой из них был бы правильным, в этом случае с косинусоидальными сдвигами работать легче, чем с синусоидальными сдвигами, поскольку они включают целочисленные значения. Таким образом, наша функция принимает вид
y = 3cos (π3x − π3) −2 или y = −3cos (π3x + 2π3) −2y = 3cos (π3x − π3) −2 или y = −3cos (π3x + 2π3) −2Снова , эти функции эквивалентны, поэтому обе дают один и тот же график.
Попробуй # 7
Напишите формулу функции, показанной на рисунке 18.
Рисунок 18
Графические вариации
y = sin x и y = cos xВ этом разделе мы узнали о типах вариаций функций синуса и косинуса и использовали эту информацию для написания уравнений из графиков. Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Вместо того, чтобы сосредоточиться на уравнениях общего вида
y = Asin (Bx − C) + D и y = Acos (Bx − C) + D, y = Asin (Bx − C) + D и y = Acos (Bx − C) + D,мы положим C = 0C = 0 и D = 0D = 0 и будем работать с упрощенной формой уравнений в следующих примерах.
Как добраться
Для функции y = Asin (Bx), y = Asin (Bx) нарисуйте ее график.
- Определите амплитуду, | A |. | A |.
- Определите период, P = 2π | B | .P = 2π | B |.
- Начните с начала координат, функция увеличивается вправо, если AA положительна, или уменьшается, если AA отрицательна.
- При x = π2 | B | x = π2 | B | существует локальный максимум для A> 0A> 0 или минимум для A <0, A <0, при y = A.y = A.
- Кривая возвращается к оси x при x = π | B |.х = π | B |.
- Существует локальный минимум для A> 0A> 0 (максимум для A <0A <0) при x = 3π2 | B | x = 3π2 | B | с y = –A.y = –A.
- Кривая снова возвращается к оси x при x = 2π | B | .x = 2π | B |.
Пример 8
Построение графика функции и определение амплитуды и периода
Нарисуйте график функции f (x) = — 2sin (πx2) .f (x) = — 2sin (πx2).
Решение
Давайте начнем с сравнения уравнения с формой y = Asin (Bx) .y = Asin (Bx).
- Шаг 1. Из уравнения видно, что A = −2, A = −2, поэтому амплитуда равна 2.
- Шаг 2. Уравнение показывает, что B = π2, B = π2, поэтому период равен P = 2ππ2 = 2π⋅2π = 4P = 2ππ2 = 2π⋅2π = 4
- Шаг 3. Поскольку AA отрицательно, график опускается по мере продвижения вправо от начала координат.
- Шаг 4–7. Перехваты x находятся в начале одного периода, x = 0, x = 0, горизонтальные средние точки находятся в точке x = 2x = 2 и в конце одного периода в точке x = 4.х = 4.
Четверть точки включают минимум при x = 1x = 1 и максимум при x = 3.x = 3. Локальный минимум будет на 2 единицы ниже средней линии при x = 1, x = 1, а локальный максимум будет на 2 единицы выше средней линии при x = 3.x = 3. На рисунке 19 показан график функции.
Рисунок 19
Попробуй # 8
Нарисуйте график g (x) = — 0.8cos (2x) .g (x) = — 0.8cos (2x). Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Как к
Для синусоидальной функции со сдвигом фазы и вертикальным сдвигом нарисуйте ее график.
- Выразите функцию в общем виде y = Asin (Bx − C) + D или y = Acos (Bx − C) + Dy = Asin (Bx − C) + D или y = Acos (Bx − C) + D .
- Определите амплитуду, | A |. | A |.
- Определите период, P = 2π | B | .P = 2π | B |.
- Определите фазовый сдвиг, CB.CB.
- Нарисуйте график f (x) = Asin (Bx) f (x) = Asin (Bx), сдвинутый вправо или влево на CBCB и вверх или вниз на D.D.
Пример 9
Графическое изображение преобразованной синусоиды
Нарисуйте график функции f (x) = 3sin (π4x − π4).f (x) = 3sin (π4x − π4).
Попробуй # 9
Нарисуйте график g (x) = — 2cos (π3x + π6) .g (x) = — 2cos (π3x + π6). Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Пример 10
Определение свойств синусоидальной функции
Для заданного y = −2cos (π2x + π) + 3, y = −2cos (π2x + π) +3 определите амплитуду, период, фазовый сдвиг и горизонтальный сдвиг. Затем изобразите функцию.
Решение
Начните со сравнения уравнения с общей формой и выполните шаги, описанные в Примере 9.
y = Acos (Bx − C) + Dy = Acos (Bx − C) + D- Шаг 1. Функция уже написана в общем виде.
- Шаг 2. Поскольку A = −2, A = −2, амплитуда равна | A | = 2. | A | = 2.
- Шаг 3. | B | = π2, | B | = π2, поэтому период равен P = 2π | B | = 2ππ2 = 2π⋅2π = 4. P = 2π | B | = 2ππ2 = 2π⋅2π = 4. Период 4.
- Шаг 4. C = −π, C = −π, поэтому мы вычисляем фазовый сдвиг как CB = −π, π2 = −π⋅2π = −2.CB = −π, π2 = −π⋅2π = −2. Сдвиг фазы равен -2-2.
- Шаг 5. D = 3, D = 3, поэтому средняя линия y = 3, y = 3, а вертикальный сдвиг увеличивается на 3.
Поскольку AA отрицательно, график функции косинуса отражается относительно оси x .
На рисунке 21 показан один цикл графика функции.
Рисунок 21
Использование преобразований функций синуса и косинуса
Мы можем использовать преобразования функций синуса и косинуса во многих приложениях. Как упоминалось в начале главы, круговое движение можно моделировать с помощью функции синуса или косинуса.
Пример 11
Нахождение вертикальной составляющей кругового движения
Точка вращается по окружности радиуса 3 с центром в начале координат. Нарисуйте график координаты y точки как функции угла поворота.
Решение
Напомним, что для точки на окружности радиусом r координата точки y равна y = rsin (x), y = rsin (x), так что в этом случае мы получаем уравнение y (x) = 3sin (x).у (х) = 3sin (х). Константа 3 вызывает растяжение значений функции y по вертикали в 3 раза, что мы можем видеть на графике на рисунке 22.
Рисунок 22
Анализ
Обратите внимание, что период функции по-прежнему равен 2π; 2π; путешествуя по кругу, мы возвращаемся в точку (3,0) (3,0) для x = 2π, 4π, 6π, … x = 2π, 4π, 6π, … Поскольку выходы график теперь будет колебаться между –3–3 и 3,3, амплитуда синусоидальной волны составит 3,3.
Попробуй # 10
Какова амплитуда функции f (x) = 7cos (x)? F (x) = 7cos (x)? Нарисуйте график этой функции.
Пример 12
Нахождение вертикальной составляющей кругового движения
Круг радиусом 3 фута устанавливается с центром в 4 футах от земли. Ближайшая к земле точка обозначена P , как показано на рисунке 23. Нарисуйте график высоты точки PP над землей при вращении круга; затем найдите функцию, которая дает высоту через угол поворота.
Рисунок 23
Решение
Набрасывая высоту, мы отмечаем, что она начинается на высоте 1 фута над землей, затем увеличивается до 7 футов над землей и продолжает колебаться на 3 фута выше и ниже центрального значения в 4 фута, как показано на рисунке 24.
Рисунок 24
Хотя мы могли бы использовать преобразование функции синуса или косинуса, мы начнем с поиска характеристик, которые сделают использование одной функции проще, чем другой. Давайте использовать функцию косинуса, потому что она начинается с самого высокого или самого низкого значения, а функция синуса начинается со среднего значения. Стандартный косинус начинается с самого высокого значения, а этот график начинается с самого низкого значения, поэтому нам нужно включить вертикальное отражение.
Во-вторых, мы видим, что график колеблется на 3 выше и ниже центра, в то время как основной косинус имеет амплитуду 1, поэтому этот график был растянут по вертикали на 3, как в последнем примере.
Наконец, чтобы переместить центр круга на высоту 4, график был сдвинут по вертикали на 4. Собирая эти преобразования вместе, мы находим, что
y = −3cos (x) + 4y = −3cos (x) +4Попробуй # 11
К пружине прикрепляется груз, который затем подвешивается к доске, как показано на рисунке 25. Когда пружина колеблется вверх и вниз, положение yy груза относительно доски изменяется в диапазоне от –1 до 1 дюйма (при время x = 0) x = 0) до –7–7 дюймов (в момент времени x = π) x = π) под доской.Предположим, что положение yy задано как синусоидальная функция от x.x. Нарисуйте график функции, а затем найдите функцию косинуса, которая дает положение yy через x.x.
Рисунок 25
Пример 13
Определение роста всадника на колесе обозрения
Лондонский глаз — это огромное колесо обозрения диаметром 135 метров (443 фута). Он совершает один оборот каждые 30 минут. Всадники садятся на платформу на высоте 2 метров над землей. Выразите высоту всадника над землей как функцию времени в минутах.
Решение
При диаметре 135 м колесо имеет радиус 67,5 м. Высота будет колебаться с амплитудой 67,5 м выше и ниже центра.
Пассажирский борт на высоте 2 м над уровнем земли, поэтому центр колеса должен находиться на высоте 67,5 + 2 = 69,567,5 + 2 = 69,5 м над уровнем земли. Средняя линия колебания составит 69,5 м.
Колесо совершает 1 оборот за 30 минут, поэтому высота будет колебаться с периодом 30 минут.
Наконец, поскольку райдерские борта находятся в самой нижней точке, высота будет начинаться с наименьшего значения и увеличиваться в соответствии с формой вертикально отраженной косинусоидальной кривой.
- Амплитуда: 67,5,67,5, поэтому A = 67,5A = 67,5
- Средняя линия: 69,5,69,5, поэтому D = 69,5D = 69,5
- Период: 30,30, поэтому B = 2π30 = π15B = 2π30 = π15
- Форма: −cos (t) −cos (t)
Уравнение для роста всадника будет
y = -67,5cos (π15t) + 69,5y = -67,5cos (π15t) +69,5, где tt выражается в минутах, а yy — в метрах.
6.1 Упражнения по разделам
Устные
1.Почему функции синуса и косинуса называются периодическими функциями?
2.Как график y = sinxy = sinx сравните с графиком y = cosx? y = cosx? Объясните, как можно горизонтально перевести график y = sinxy = sinx чтобы получить y = cosx.y = cosx.
3.Какие константы влияют на диапазон функции и как они влияют на диапазон для уравнения Acos (Bx + C) + D, Acos (Bx + C) + D?
4.Как диапазон преобразованной синусоидальной функции соотносится с уравнением y = Asin (Bx + C) + D? Y = Asin (Bx + C) + D?
5.Как можно использовать единичный круг для построения графика f (t) = sint? F (t) = sint?
Графический
Для следующих упражнений нарисуйте на графике два полных периода каждой функции и укажите амплитуду, период и среднюю линию. Укажите максимальное и минимальное значения y и соответствующие им значения x на одном периоде для x> 0.x> 0. При необходимости округлите ответы до двух десятичных знаков.
8.f (x) = — 3sinxf (x) = — 3sinx
12.f (x) = 2sin (12x) f (x) = 2sin (12x)
13.f (x) = 4cos (πx) f (x) = 4cos (πx).
14.f (x) = 3cos (65x) f (x) = 3cos (65x)
15.y = 3sin (8 (x + 4)) + 5y = 3sin (8 (x + 4)) + 5
16.y = 2sin (3x − 21) + 4y = 2sin (3x − 21) +4
17.y = 5sin (5x + 20) −2y = 5sin (5x + 20) −2
Для следующих упражнений нарисуйте один полный период каждой функции, начиная с x = 0.x = 0. Для каждой функции укажите амплитуду, период и среднюю линию. Укажите максимальное и минимальное значения y и их соответствующие значения x на одном периоде для x> 0.х> 0. Укажите фазовый сдвиг и вертикальный сдвиг, если применимо. При необходимости округлите ответы до двух десятичных знаков.
18.f (t) = 2sin (t − 5π6) f (t) = 2sin (t − 5π6)
19.f (t) = — cos (t + π3) + 1f (t) = — cos (t + π3) +1
20.f (t) = 4cos (2 (t + π4)) — 3f (t) = 4cos (2 (t + π4)) — 3
21.f (t) = — sin (12t + 5π3) f (t) = — sin (12t + 5π3)
22.f (x) = 4sin (π2 (x − 3)) + 7f (x) = 4sin (π2 (x − 3)) + 7
Алгебраические
Для следующих упражнений пусть f (x) = sinx.f (x) = sinx.
31.На [0,2π), [0,2π) решить f (x) = 0. f (x) = 0.
32.На [0,2π), [0,2π) решите f (x) = 12. f (x) = 12.
34.На [0,2π), f (x) = 22. [0,2π), f (x) = 22. Найдите все значения x.x.
35.На [0,2π), [0,2π), максимальное значение (я) функции встречается (я) при каком значении (ах) x ?
36.На [0,2π), [0,2π), минимальное (ые) значение (я) функции встречается (а) при каком (ых) значении (ах) x ?
37.Покажите, что f (−x) = — f (x) .f (−x) = — f (x). Это означает, что f (x) = sinxf (x) = sinx — нечетная функция и обладает симметрией относительно ________________.
Для следующих упражнений пусть f (x) = cosx.f (x) = cosx.
38.На [0,2π), [0,2π) решите уравнение f (x) = cosx = 0. f (x) = cosx = 0.
39.На [0,2π), [0,2π) решите f (x) = 12. f (x) = 12.
40.На [0,2π), [0,2π) найдите x -перехватывания f (x) = cosx.f (x) = cosx.
41.На [0,2π), [0,2π) найдите значения x , при которых функция имеет максимальное или минимальное значение.
42.На [0,2π), [0,2π) решите уравнение f (x) = 32.f (x) = 32.
Технологии
43.График h (x) = x + sinxh (x) = x + sinx на [0,2π]. [0,2π]. Объясните, почему график выглядит именно так.
44.График h (x) = x + sinxh (x) = x + sinx на [−100,100]. [- 100,100]. График выглядел так, как было предсказано в предыдущем упражнении?
45.График f (x) = xsinxf (x) = xsinx на [0,2π] [0,2π] и вербализует, как график отличается от графика f (x) = sinx.f (x) = sinx.
46. График f (x) = xsinxf (x) = xsinx в окне [−10,10] [- 10,10] и объясните, что показывает график.
47.График f (x) = sinxxf (x) = sinxx в окне [−5π, 5π] [- 5π, 5π] и объясните, что показывает график.
Реальные приложения
Как найти период синусоидальных функций — Видео и стенограмма урока
Шаги для решения
Функция называется периодической , если она постоянно повторяется в обоих направлениях. Синусоидальная функция , подобная приведенной ниже, известна как периодическая тригонометрическая функция.
Когда функция является периодической, как функция синуса, у нее есть нечто, называемое периодом.Период периодической функции — это интервал значений x , на котором возникает одна копия повторяющегося шаблона. Обратите внимание, что на графике синусоидальной функции показано, что f ( x ) = sin ( x ) имеет период 2π, потому что график от x = 0 до x = 2π повторяется навсегда в обоих случаях. направления.
Хорошо, пока все хорошо, правда? Мы видим, что основная синусоидальная функция имеет период 2π. Однако существуют разные варианты синусоидальной функции.Другими словами, функция синуса имеет вид f ( x ) = A sin ( Bx + C ) + D , где A , B , C , и D может быть любым числом. Из-за этого функция может принимать множество различных форм, и форма определяет период. Теперь, прежде чем вы отчаиваетесь, у меня хорошие новости! У нас есть действительно простой способ определить период синусоидальной функции.
Если у нас есть синусоидальная функция вида f ( x ) = A sin ( Bx + C ) + D , то период функции равен 2π / | B |.Следовательно, чтобы найти период функции f ( x ) = A sin ( Bx + C ) + D , мы выполняем следующие шаги:
- Идентифицируем B в функция f ( x ) = A sin ( Bx + C ) + D .

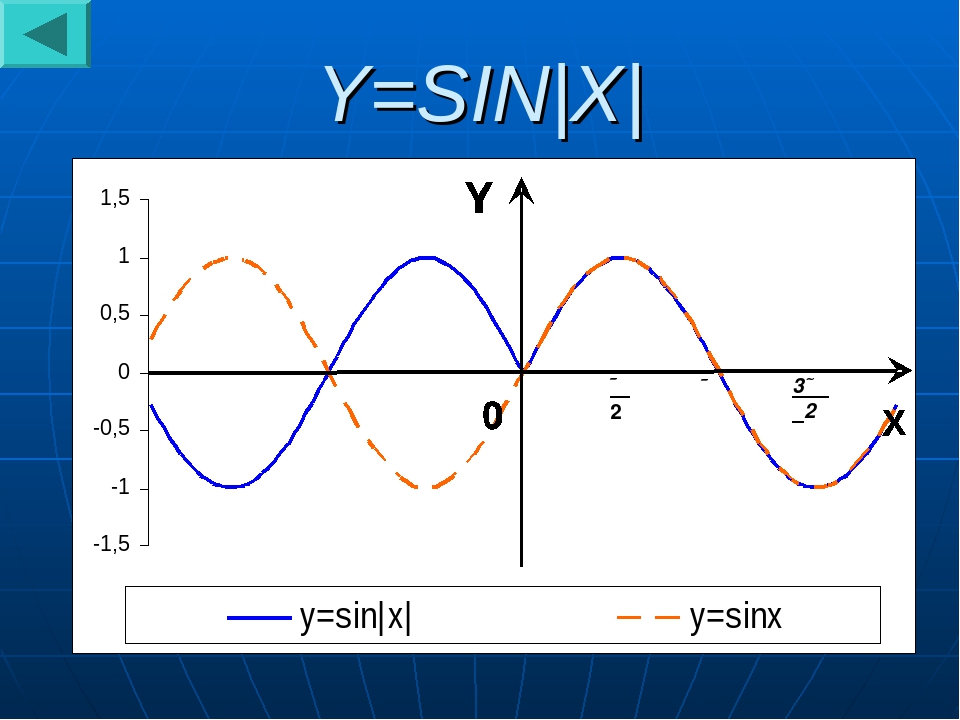
 В этом мы можем убедиться на графике нашей функции.
В этом мы можем убедиться на графике нашей функции.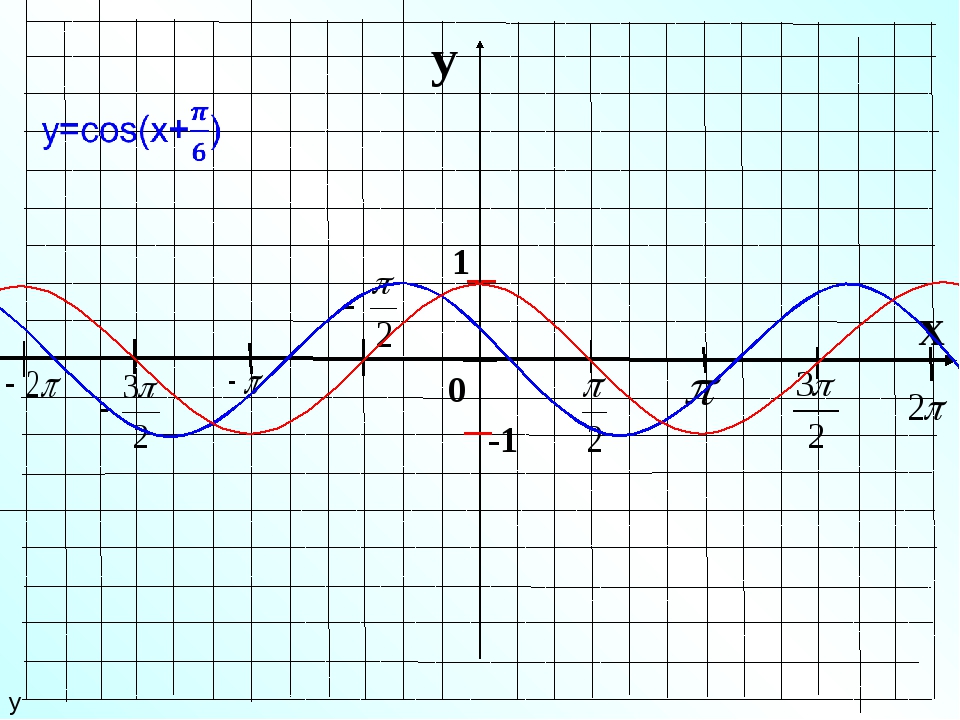
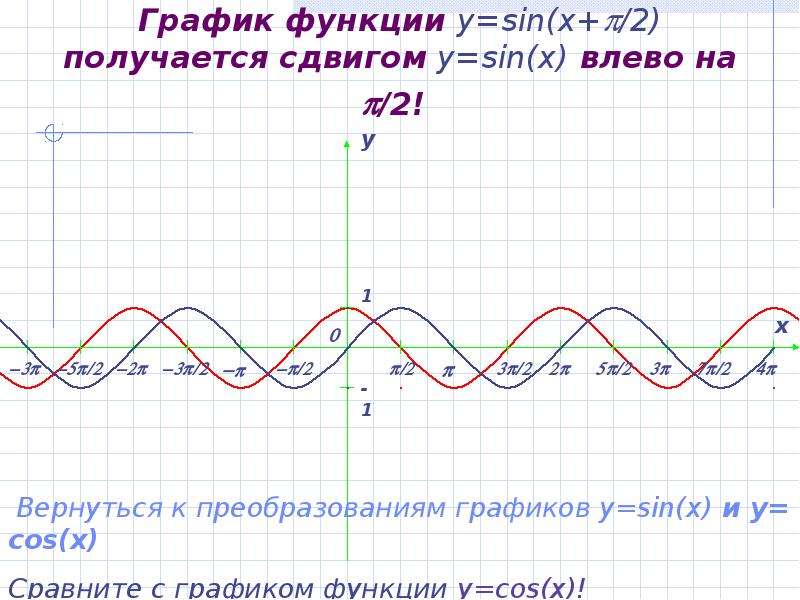
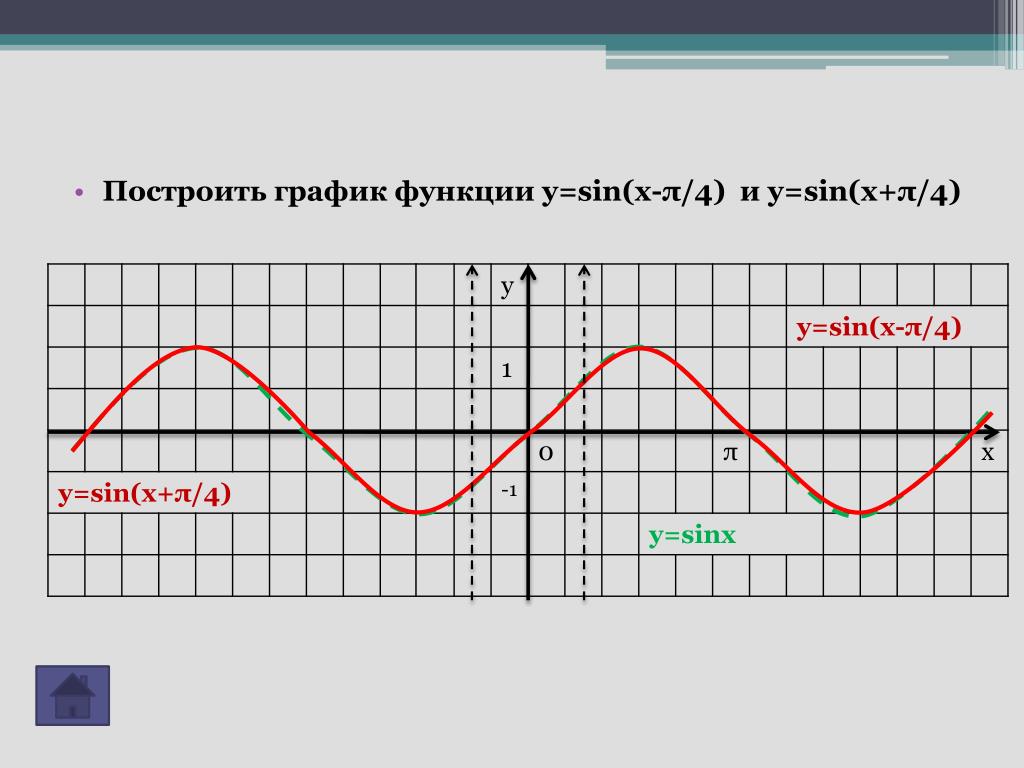
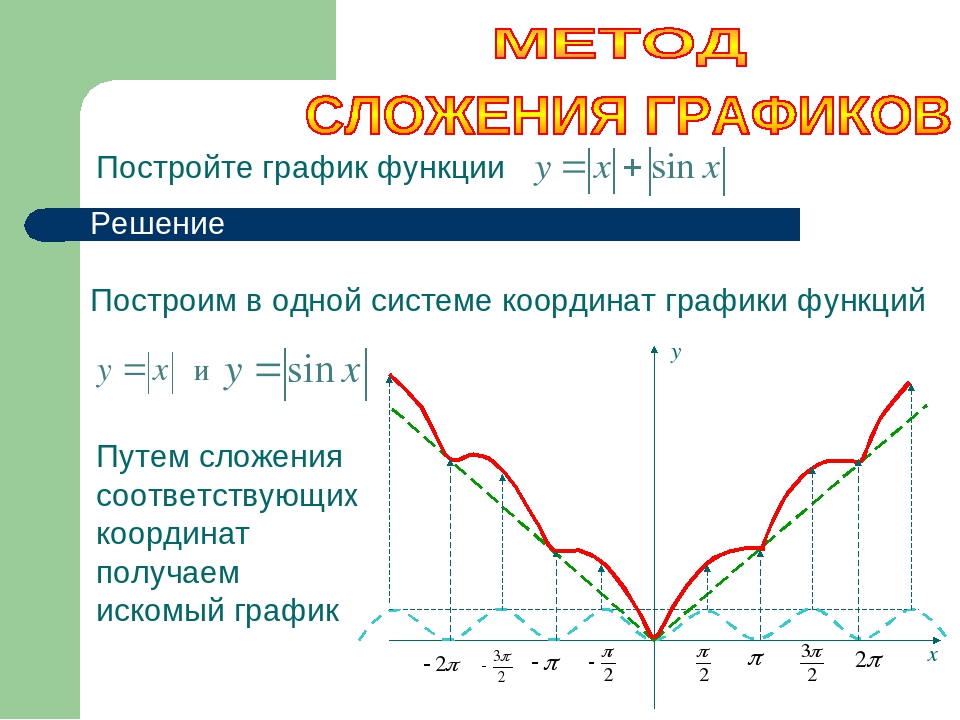 Наименьшее из таких значений — период. Основные функции синуса и косинуса имеют период 2π.
Наименьшее из таких значений — период. Основные функции синуса и косинуса имеют период 2π.