Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
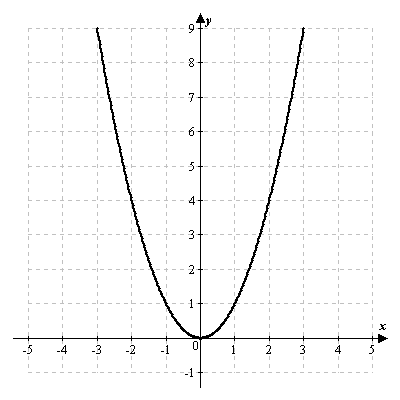
Постройте график функции игрек равно минус 2 икс в квадрате плюс один — Знания.site
Ответы 1
Функция
Графиком функции является парабола, ветви которой направлены вниз (k=-2, k<0), с вершиной в начале координат, построенная на основе функции y=x², смещённая на 1 ед. отрезок вверх по оси OY.
Таблица значений для функции y=-2x²+1:
x=0 x=1 x=2
y=1 y=-1 y=-7
Знаешь ответ? Добавь его сюда!
Последние вопросы
Алгебра
16 секунд назад
Доказать тождество: sin a +2cos² a — cos a=1.Математика
16 секунд назад
виконати дії : 17/28*(-4/51)География
5 минут назад
Атмосферний тиск біля підніжжя гори 760 мм рт. ст., а температура повітря 18 °* C . Визначити атмосферний тиск на вершині гори, якщо температура повітря на ній становить — 6°
* C
ст., а температура повітря 18 °* C . Визначити атмосферний тиск на вершині гори, якщо температура повітря на ній становить — 6°
* CБиология
5 минут назад
6.. Визначте про який клас йдеться у тексті « Шкіра суха, захищена роговими лусочками й щитками, залоз немає, органи дихання — легені» a) Головохордові в) Плазуни; б) амфібії г) хрящові рибиХимия
5 минут назад
Маса нітратної кислоти, яка необхідна для взаємодії з 4г магній оксиду, дорівнює:Экономика
10 минут назад
В чем заключается ваш материальный успех и денежный интерес?География
10 минут назад
Атмосферний тиск біля підніжжя гори 760 мм рт. ст., а температура повітря 18 ° * C . Визначити атмосферний тиск на вершині гори, якщо температура повітря на ній становить — 6° * C
ст., а температура повітря 18 ° * C . Визначити атмосферний тиск на вершині гори, якщо температура повітря на ній становить — 6° * CФизика
10 минут назад
За допомогою лінзи, фокусна відстань якої дорівнює 60 см, отримали уявне пряме зображення предмета. Висота предмета становить 1,8 м. Чому дорівнює висота Зображення, якщо предмет розташовано на відстані 1,2 м від лінзи?Химия
10 минут назад
Допишіть рівняння реакцій: а) КOH + HCI → ; б) Zn + h3SO4 → ; в) СаO + h3O → ; г) FeO + HNO3 →Химия
10 минут назад
Добудьте двома способами ферум(ІІ) хлоридИнформатика
15 минут назад
Помогите, пожалуйста, с решением задачи по информатике. Нужно вставить данные по формуле и вычислить кол-во страниц.
Нужно вставить данные по формуле и вычислить кол-во страниц.Физика
15 минут назад
На дифракційну ґратку, що має 500 штрихів на 1 мм, нормально падае монохрома- тична хвиля довжиною 450 нм. На якій відстані розташовано ґратку від екрана, якщо відстань між максимумами другого та третього порядку дорівнює 7 см? Кути дифракції вважай малимиАлгебра
20 минут назад
3. Упростить выражение: 1/(cos² а — 1) × ctg ² аединица делённая *Алгебра
20 минут назад
упростите выражения ПОЖАЛУЙСТА ПОМОГИТЕ!История
25 минут назад
ПОМОГИТЕ ПОЖАЛУЙСТА С БИЛЕТАМИ БИЛЕТЫ ПО ИСТОРИИ КЫРГЫЗСТАНА Билет №1 1. Первое упоминание этнонима «киргизы» в истории. Первая родина кыргызов (долина Енисея, бассейн Хыргыс-Нур («Кыргыз-Куль»), район Тенир-Тоо).
2. Установление советской власти в Киргизии (1917-1918 гг.).
Билет №2
1. Саки — древние степные кочевники.
2. Провозглашение и развитие независимой Кыргызской Республики.
Деятельность легендарного парламента.
Билет №3
1. Образование Усуньского племенного союза и Усуньского государства.
2. ХVIII в. во второй половине 19 века. Политическая ситуация в Кыргызстане в первом полугодии. Визит послов Кыргызстана в Россию. Атаке — герой.
Билет №4
1. Даванское государство: развитие земледелия и животноводства.
Исследовательские поездки Чжан Цяна.
2. Общественно-политическая жизнь и экономическое развитие Кыргызстана в период волюнтаристских реформ (1950-1961 гг.). Исхак Раззаков (1910–1979) — советский государственный и партийный деятель.
Билет №5
1. Памятники каменного и бронзового веков на территории Кыргызстана.
2. Солдаты-кыргызы в Великой Отечественной войне
Сын Тыная (ок.
Первое упоминание этнонима «киргизы» в истории. Первая родина кыргызов (долина Енисея, бассейн Хыргыс-Нур («Кыргыз-Куль»), район Тенир-Тоо).
2. Установление советской власти в Киргизии (1917-1918 гг.).
Билет №2
1. Саки — древние степные кочевники.
2. Провозглашение и развитие независимой Кыргызской Республики.
Деятельность легендарного парламента.
Билет №3
1. Образование Усуньского племенного союза и Усуньского государства.
2. ХVIII в. во второй половине 19 века. Политическая ситуация в Кыргызстане в первом полугодии. Визит послов Кыргызстана в Россию. Атаке — герой.
Билет №4
1. Даванское государство: развитие земледелия и животноводства.
Исследовательские поездки Чжан Цяна.
2. Общественно-политическая жизнь и экономическое развитие Кыргызстана в период волюнтаристских реформ (1950-1961 гг.). Исхак Раззаков (1910–1979) — советский государственный и партийный деятель.
Билет №5
1. Памятники каменного и бронзового веков на территории Кыргызстана.
2. Солдаты-кыргызы в Великой Отечественной войне
Сын Тыная (ок.
 Шабдан — герой. Байтик — герой.
(1901–1938) — Совнарком Киргизской АССР.
Председатели (1927–1933)
3
2. Развитие образования, науки и культуры в советской Киргизии.
Билет №12
1. Кыргызы в 1873–1876 гг. Восстание против Королевства Кокон. Исхак Асан уулу (Полот хан). Российская оккупация юга Киргизии. Алайская экспедиция.
2. Кыргызстан в период после падения монархии. Троицкое правительство в Киргизии.
Билет №13
1. Борьба кыргызского народа против завоевательной политики Кокандского ханства. Тайлак — герой.
2. Экономические реформы советской власти: «военный коммунизм», новая экономическая политика, плановая экономика.
Билет №14
1. Гунны — предки тюркских народов.
2. Усиление тоталитарного порядка. Массовые репрессии. «Отец-
Могила.
Шабдан — герой. Байтик — герой.
(1901–1938) — Совнарком Киргизской АССР.
Председатели (1927–1933)
3
2. Развитие образования, науки и культуры в советской Киргизии.
Билет №12
1. Кыргызы в 1873–1876 гг. Восстание против Королевства Кокон. Исхак Асан уулу (Полот хан). Российская оккупация юга Киргизии. Алайская экспедиция.
2. Кыргызстан в период после падения монархии. Троицкое правительство в Киргизии.
Билет №13
1. Борьба кыргызского народа против завоевательной политики Кокандского ханства. Тайлак — герой.
2. Экономические реформы советской власти: «военный коммунизм», новая экономическая политика, плановая экономика.
Билет №14
1. Гунны — предки тюркских народов.
2. Усиление тоталитарного порядка. Массовые репрессии. «Отец-
Могила.
How much to ban the user?
1 hour 1 day 100 years
3-88.
 4: Парабола — Математика LibreTexts
4: Парабола — Математика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 15099
- ОпенСтакс
- ОпенСтакс
Цели обучения
- Графические параболы с вершинами в начале координат.
- Запишите уравнения парабол в стандартной форме.
- Параболы графа с вершинами не в начале координат.
- Решение прикладных задач на параболах.
А вы знали, что олимпийский огонь зажигают за несколько месяцев до начала игр? Церемониальный метод зажжения пламени такой же, как и в древние времена. Церемония проходит в храме Геры в Олимпии, Греция, и уходит своими корнями в греческую мифологию, отдавая дань уважения Прометею, который украл огонь у Зевса, чтобы раздать его всем людям. Одна из одиннадцати действующих жриц помещает факел в фокус параболического зеркала (рис. \(\PageIndex{1}\)), которое фокусирует солнечные лучи и зажигает пламя.
Одна из одиннадцати действующих жриц помещает факел в фокус параболического зеркала (рис. \(\PageIndex{1}\)), которое фокусирует солнечные лучи и зажигает пламя.
Параболические зеркала (или отражатели) способны улавливать энергию и фокусировать ее в одной точке. О преимуществах этого свойства свидетельствует обширный список параболических объектов, которые мы используем каждый день: спутниковые тарелки, подвесные мосты, телескопы, микрофоны, прожекторы и автомобильные фары, и это лишь некоторые из них. Параболические отражатели также используются в устройствах альтернативной энергии, таких как солнечные плиты и водонагреватели, потому что они недороги в производстве и не требуют особого обслуживания. В этом разделе мы рассмотрим параболу и ее использование, в том числе недорогие и энергоэффективные солнечные конструкции.
Графическое изображение парабол с вершинами в начале координат
Ранее мы видели, что эллипс образуется, когда плоскость пересекает прямой круговой конус. Если плоскость параллельна ребру конуса, образуется неограниченная кривая. Эта кривая представляет собой параболу (рис. \(\PageIndex{2}\)).
Рисунок \(\PageIndex{2}\): ПараболаПодобно эллипсу и гиперболе, парабола также может быть определена набором точек на координатной плоскости. Парабола — это множество всех точек \((x,y)\) на плоскости, которые находятся на одинаковом расстоянии от фиксированной линии, называемой директриса , а фиксированная точка ( фокус ) не на директрисе.
Ранее мы узнали о вершине параболы и оси симметрии. Теперь мы расширим обсуждение, включив в него другие ключевые свойства параболы (рис. \(\PageIndex{3}\)). Обратите внимание, что ось симметрии проходит через фокус и вершину и перпендикулярна директрисе. Вершина — это середина между директрисой и фокусом. Отрезок, проходящий через фокус и параллельный директрисе, называется 9-м.0954 широкая прямая кишка . Концы широкой прямой кишки лежат на кривой. По определению расстояние d от фокуса до любой точки \(P\) на параболе равно расстоянию от \(P\) до директрисы.
Отрезок, проходящий через фокус и параллельный директрисе, называется 9-м.0954 широкая прямая кишка . Концы широкой прямой кишки лежат на кривой. По определению расстояние d от фокуса до любой точки \(P\) на параболе равно расстоянию от \(P\) до директрисы.
Для работы с параболами в координатной плоскости мы рассмотрим два случая: с вершиной в начале координат и с вершиной в точке . точка, отличная от исходной. Начнем с первого.
Рисунок \(\PageIndex{4}\) 92=4py\) когда ось y является осью симметрии. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.СТАНДАРТНЫЕ ФОРМЫ ПАРАБОЛ С ВЕРШИНОЙ \((0,0)\)
Таблица \(\PageIndex{1}\) и рисунок \(\PageIndex{5}\) суммируют стандартные характеристики парабол с вершиной в Происхождение.
| Ось симметрии | 92=4py\)\((0, р)\) | \(у=-р\) | \((\pm 2p, p)\) |
|---|
 (b) Когда \(p<0\) и осью симметрии является ось x, парабола открывается влево. (c) Когда \(p<0\) и осью симметрии является ось y, парабола раскрывается. (d) Когда \(p<0\) и осью симметрии является ось y, парабола открывается вниз.
(b) Когда \(p<0\) и осью симметрии является ось x, парабола открывается влево. (c) Когда \(p<0\) и осью симметрии является ось y, парабола раскрывается. (d) Когда \(p<0\) и осью симметрии является ось y, парабола открывается вниз.Ключевыми характеристиками параболы являются ее вершина, ось симметрии, фокус, директриса и широкая прямая кишка (рис. \(\PageIndex{5}\)). Получив стандартное уравнение для параболы с центром в начале координат, мы можем легко определить ключевые особенности для построения графика параболы. Прямая называется касательной к кривой, если она пересекает кривую ровно в одной точке. Если мы нарисуем линии, касающиеся параболы в конечных точках прямой кишки , эти линии пересекутся на оси симметрии, как показано на рисунке \(\PageIndex{6}\). 92=4px\), тогда
- осью симметрии является ось \(x\), \(y=0\)
- набор \(4p\) равный коэффициенту \(x\) в данном уравнении для решения для \(p\). Если \(p>0\), парабола открывается вправо.
 Если \(p<0\), парабола открывается влево.
Если \(p<0\), парабола открывается влево. - используйте \(p\) для нахождения координат фокуса, \((p,0)\)
- используйте \(p\) для нахождения уравнения направляющей, \(x=−p\)
- используйте \(p\) для нахождения концов широкой прямой кишки, \((p,\pm 2p)\). В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда
- осью симметрии является ось \(y\), \(x=0\)
- набор \(4p\) равный коэффициенту \(y\) в данном уравнении, которое нужно решить для \(p\). Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз.
- используйте \(p\) для нахождения координат фокуса, \((0,p)\)
- используйте \(p\) для нахождения уравнения направляющей, \(y=−p\)
- используйте \(p\) для нахождения концов широкой прямой кишки, \((\pm 2p,p)\) 92=4px\). Таким образом, осью симметрии является ось x .
 Отсюда следует, что:
Отсюда следует, что:- \(24=4p\), значит \(p=6\). Так как \(p>0\), парабола выходит вправо
- координаты фокуса \((p,0)=(6,0)\)
- уравнение направляющей \(x=−p=−6\)
- конечные точки широкой прямой кишки имеют одинаковые координаты x в фокусе. Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\) 9092=4py\). Таким образом, осью симметрии является ось \(у\). Отсюда следует, что:
- \(−6=4p\), поэтому \(p=−\dfrac{3}{2}\). Так как \(p<0\), парабола направлена вниз.
- координаты фокуса равны \((0,p)=(0,−\dfrac{3}{2})\)
- уравнение направляющей \(y=−p=\dfrac{3}{2}\)
- конечные точки широкой прямой кишки можно найти, подставив \(y=\dfrac{3}{2}\) в исходное уравнение, \((\pm 3,−\dfrac{3}{2})\)
- Ответить
- Фокус: \((0,2)\)
- Директриса: \(y=−2\)
- Конечные точки широкой прямой кишки: \((\pm 4,2)\).
Далее наносим фокус, директрису и 92=8у\). Определите и обозначьте фокус, направляющую и конечные точки прямой кишки latus .

Запись уравнений параболы в стандартной форме
В предыдущих примерах мы использовали уравнение стандартной формы параболы для вычисления расположения ее ключевых элементов. Мы также можем использовать вычисления в обратном порядке, чтобы написать уравнение для параболы, учитывая ее ключевые особенности. 92=4py\).
- Умножить \(4п\).
- Подставить значение из шага 2 в уравнение, полученное на шаге 1.
- использовать данное уравнение для определения \(h\) и \(k\) для вершины, \((h,k)\)
- использовать значение \(k\) для определения оси симметрии, \(y=k\)
- набор \(4p\) равный коэффициенту \((x−h)\) в данном уравнении для решения \(p\). Если \(p>0\), парабола выходит вправо. Если \(p<0\), парабола открывается влево.
- используйте \(h\), \(k\) и \(p\) , чтобы найти координаты фокуса, \((h+p, k)\) 92=4p(y−k)\), тогда:
- использовать данное уравнение для определения \(h\) и \(k\) для вершины, \((h,k)\)
- использовать значение \(h\) для определения оси симметрии, \(x=h\)
- набор \(4p\) равный коэффициенту \((y−k)\) в данном уравнении для решения \(p\). Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз.
- используйте \(h\), \(k\) и \(p\) , чтобы найти координаты фокуса, \((h, k+p)\)
- используйте \(k\) и \(p\) для нахождения уравнения направляющей, \(y=k−p\)
- используйте \(h\), \(k\) и \(p\) , чтобы найти концы широкой прямой кишки, \((h\pm 2p, k+p)\)
- Постройте вершину, ось симметрии, фокус, директрису и прямую кишку, а затем нарисуйте плавную кривую, чтобы сформировать параболу.

- вершина равна \((h,k)=(−3,1)\)
- ось симметрии \(y=k=1\)
- \(−16=4p\), поэтому \(p=−4\). Так как \(p<0\), парабола открывается влево.
- координаты фокуса равны \((h+p,k)=(−3+(−4),1)=(−7,1)\)
- уравнение направляющей \(x=h−p=−3−(−4)=1\)
- концы широкой прямой кишки равны \((h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))\), или \((−7,− 7)\) и \((−7,92=4(х-8)\). Определите и обозначьте вершину, ось симметрии, фокус, директрису и конечные точки прямой кишки latus .
- Ответить
- Вершина: \((8,−1)\)
- Ось симметрии: \(y=−1\)
- Фокус: \((9,−1)\)
- Директриса: \(x=7\)
- Концы широкой прямой кишки : \((9,−3)\) и \((9,1)\).

92&= 4⋅7⋅(y+8) \end{align*}\]- вершина \((h,k)=(4,−8)\)
- ось симметрии \(x=h=4\)
- так как \(p=7\), \(p>0\) и таким образом парабола раскрывается
- координаты фокуса равны \((h,k+p)=(4,−8+7)=(4,−1)\)
- уравнение направляющей равно \(y=k−p=−8−7=−15\)
- концы широкой прямой кишки равны \((h\pm 2p,k+p)=(4\pm 2(7),−8+7)\) или \((−10,−1)\) и \((18,−1)\) 92=−20(y−3)\). Определите и обозначьте вершину, ось симметрии, фокус, директрису и конечные точки прямой кишки latus .
- Ответить
- Вершина: \((−2,3)\)
- Ось симметрии: \(x=−2\)
- Фокус: \((−2,−2)\)
- Директриса: \(y=8\)
- Конечные точки широкой прямой кишки : \((−12,−2)\) и \((8,−2)\).
Решение прикладных задач, связанных с параболами
Как мы упоминали в начале раздела, параболы используются для проектирования многих объектов, которые мы используем каждый день, таких как телескопы, подвесные мосты, микрофоны и радиолокационное оборудование.
Рисунок \(\PageIndex{16}\): отражающее свойство парабол Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему Олимпийский огонь зажигается, когда его держат в фокусе параболического зеркала.
Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему Олимпийский огонь зажигается, когда его держат в фокусе параболического зеркала.Параболические зеркала способны фокусировать солнечную энергию в одной точке, повышая температуру на сотни градусов за считанные секунды. Таким образом, параболические зеркала используются во многих недорогих, энергоэффективных солнечных продуктах, таких как солнечные плиты, солнечные обогреватели и даже поджигатели для путешествий.
Пример \(\PageIndex{6}\): решение прикладных задач, связанных с параболами
На рисунке \(\PageIndex{17}\) показано поперечное сечение конструкции переносного солнечного пожарного пускателя. Солнечные лучи отражаются от параболического зеркала к объекту, прикрепленному к воспламенителю.
 2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6,8y\qquad \text{Подставить } 2,25 \text{ вместо } x\\ y&\ приблизительно 0,74\qquad \text{Решить для } y \end{выравнивание*}\]
2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6,8y\qquad \text{Подставить } 2,25 \text{ вместо } x\\ y&\ приблизительно 0,74\qquad \text{Решить для } y \end{выравнивание*}\]Размер блюда примерно \(0,74 \) дюймов глубиной.
Упражнение \(\PageIndex{6}\)
Солнечные плиты размером с балкон были разработаны для семей, живущих в Индии. Верх блюда имеет диаметр \(1600\) мм. Солнечные лучи отражаются от параболического зеркала в сторону «варки», расположенной \(320\) мм от основания.
- Найдите уравнение, моделирующее поперечное сечение солнечной плиты. Предположим, что вершина параболического зеркала является началом координатной плоскости и что парабола выходит вправо (т. е. имеет 92=4р(у-к)\)
Ключевые понятия
- Парабола — это множество всех точек \((x,y)\) на плоскости, находящихся на одинаковом расстоянии от фиксированной прямой, называемой направляющей, и фиксированной точки (директрисы).
 фокус) не на директрисе.
фокус) не на директрисе. - Стандартная форма параболы с вершиной \((0,0)\) и осью x в качестве оси симметрии может быть использована для построения графика параболы. Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево. См. пример \(\PageIndex{1}\).
- Стандартная форма параболы с вершиной \((0,0)\) и осью y в качестве оси симметрии может быть использована для построения графика параболы. Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{2}\).
- Зная фокус и направляющую параболы, мы можем записать ее уравнение в стандартной форме. См. пример \(\PageIndex{3}\).
- Для построения параболы можно использовать стандартную форму параболы с вершиной \((h,k)\) и осью симметрии, параллельной оси \(x\) . Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево. См. пример \(\PageIndex{4}\).
- Стандартная форма параболы с вершиной \((h,k)\) и осью симметрии, параллельной оси \(y\) может быть использована для построения параболы.
 Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\).
Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\). - Реальные ситуации можно моделировать с помощью стандартных уравнений парабол. Например, зная диаметр и фокус поперечного сечения параболического отражателя, мы можем найти уравнение, моделирующее его стороны. См. пример \(\PageIndex{6}\).
Эта страница под названием 8.4: The Parabola распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа ООР или издатель
- ОпенСтакс
- Показать страницу оглавление
- нет
- Включено
- да
- Теги
- широкая прямая кишка
- парабола
- Парабола с горизонтальной осью
- Парабола с вертикальной осью
- источник@https://openstax.

- Парабола — это множество всех точек \((x,y)\) на плоскости, находящихся на одинаковом расстоянии от фиксированной прямой, называемой направляющей, и фиксированной точки (директрисы).
Отсюда следует, что:
Пример \(\PageIndex{3}\): запись уравнения параболы в стандартной форме с учетом ее фокуса и директрисы
Какое уравнение для параболы с фокусом \((−\dfrac{1}{2} ,0)\) и направляющая \(x=\dfrac{1}{2}\)?
Решение
Фокус имеет вид \((p,0)\), поэтому уравнение будет иметь вид \(y^2=4px\). 2=4p(y−k)\) для парабол, у которых ось симметрии параллельна \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.
2=4p(y−k)\) для парабол, у которых ось симметрии параллельна \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.
СТАНДАРТНЫЕ ФОРМЫ ПАРАБОЛ С ВЕРШИНОЙ \((H, K)\)
Таблица \(\PageIndex{2}\) и рисунок \(\PageIndex{11}\) суммируют стандартные характеристики парабол с вершиной в точка \((h,k)\).
| Ось симметрии | Уравнение | Фокус | Директриса | Конечные точки широкой прямой кишки 92=4р(у-к)\) | \((ч, к+р)\) | \(у=к-р\) | \((ч\пм 2п, к+п)\) |
|---|
 2=4p(y−k)\). 92=4p(x−h)\), тогда:
2=4p(y−k)\). 92=4p(x−h)\), тогда:
 3
3 14159..
14159.. ст., а температура повітря 18 °* C . Визначити атмосферний тиск на вершині гори, якщо температура повітря на ній становить — 6°
* C
ст., а температура повітря 18 °* C . Визначити атмосферний тиск на вершині гори, якщо температура повітря на ній становить — 6°
* C ст., а температура повітря 18 ° * C . Визначити атмосферний тиск на вершині гори, якщо температура повітря на ній становить — 6° * C
ст., а температура повітря 18 ° * C . Визначити атмосферний тиск на вершині гори, якщо температура повітря на ній становить — 6° * C Нужно вставить данные по формуле и вычислить кол-во страниц.
Нужно вставить данные по формуле и вычислить кол-во страниц. Первое упоминание этнонима «киргизы» в истории. Первая родина кыргызов (долина Енисея, бассейн Хыргыс-Нур («Кыргыз-Куль»), район Тенир-Тоо).
2. Установление советской власти в Киргизии (1917-1918 гг.).
Билет №2
1. Саки — древние степные кочевники.
2. Провозглашение и развитие независимой Кыргызской Республики.
Деятельность легендарного парламента.
Билет №3
1. Образование Усуньского племенного союза и Усуньского государства.
2. ХVIII в. во второй половине 19 века. Политическая ситуация в Кыргызстане в первом полугодии. Визит послов Кыргызстана в Россию. Атаке — герой.
Билет №4
1. Даванское государство: развитие земледелия и животноводства.
Исследовательские поездки Чжан Цяна.
2. Общественно-политическая жизнь и экономическое развитие Кыргызстана в период волюнтаристских реформ (1950-1961 гг.). Исхак Раззаков (1910–1979) — советский государственный и партийный деятель.
Билет №5
1. Памятники каменного и бронзового веков на территории Кыргызстана.
2. Солдаты-кыргызы в Великой Отечественной войне
Сын Тыная (ок.
Первое упоминание этнонима «киргизы» в истории. Первая родина кыргызов (долина Енисея, бассейн Хыргыс-Нур («Кыргыз-Куль»), район Тенир-Тоо).
2. Установление советской власти в Киргизии (1917-1918 гг.).
Билет №2
1. Саки — древние степные кочевники.
2. Провозглашение и развитие независимой Кыргызской Республики.
Деятельность легендарного парламента.
Билет №3
1. Образование Усуньского племенного союза и Усуньского государства.
2. ХVIII в. во второй половине 19 века. Политическая ситуация в Кыргызстане в первом полугодии. Визит послов Кыргызстана в Россию. Атаке — герой.
Билет №4
1. Даванское государство: развитие земледелия и животноводства.
Исследовательские поездки Чжан Цяна.
2. Общественно-политическая жизнь и экономическое развитие Кыргызстана в период волюнтаристских реформ (1950-1961 гг.). Исхак Раззаков (1910–1979) — советский государственный и партийный деятель.
Билет №5
1. Памятники каменного и бронзового веков на территории Кыргызстана.
2. Солдаты-кыргызы в Великой Отечественной войне
Сын Тыная (ок.
 Шабдан — герой. Байтик — герой.
(1901–1938) — Совнарком Киргизской АССР.
Председатели (1927–1933)
3
2. Развитие образования, науки и культуры в советской Киргизии.
Билет №12
1. Кыргызы в 1873–1876 гг. Восстание против Королевства Кокон. Исхак Асан уулу (Полот хан). Российская оккупация юга Киргизии. Алайская экспедиция.
2. Кыргызстан в период после падения монархии. Троицкое правительство в Киргизии.
Билет №13
1. Борьба кыргызского народа против завоевательной политики Кокандского ханства. Тайлак — герой.
2. Экономические реформы советской власти: «военный коммунизм», новая экономическая политика, плановая экономика.
Билет №14
1. Гунны — предки тюркских народов.
2. Усиление тоталитарного порядка. Массовые репрессии. «Отец-
Могила.
Шабдан — герой. Байтик — герой.
(1901–1938) — Совнарком Киргизской АССР.
Председатели (1927–1933)
3
2. Развитие образования, науки и культуры в советской Киргизии.
Билет №12
1. Кыргызы в 1873–1876 гг. Восстание против Королевства Кокон. Исхак Асан уулу (Полот хан). Российская оккупация юга Киргизии. Алайская экспедиция.
2. Кыргызстан в период после падения монархии. Троицкое правительство в Киргизии.
Билет №13
1. Борьба кыргызского народа против завоевательной политики Кокандского ханства. Тайлак — герой.
2. Экономические реформы советской власти: «военный коммунизм», новая экономическая политика, плановая экономика.
Билет №14
1. Гунны — предки тюркских народов.
2. Усиление тоталитарного порядка. Массовые репрессии. «Отец-
Могила. Если \(p<0\), парабола открывается влево.
Если \(p<0\), парабола открывается влево. Отсюда следует, что:
Отсюда следует, что:
 Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему Олимпийский огонь зажигается, когда его держат в фокусе параболического зеркала.
Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему Олимпийский огонь зажигается, когда его держат в фокусе параболического зеркала. 2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6,8y\qquad \text{Подставить } 2,25 \text{ вместо } x\\ y&\ приблизительно 0,74\qquad \text{Решить для } y \end{выравнивание*}\]
2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6,8y\qquad \text{Подставить } 2,25 \text{ вместо } x\\ y&\ приблизительно 0,74\qquad \text{Решить для } y \end{выравнивание*}\]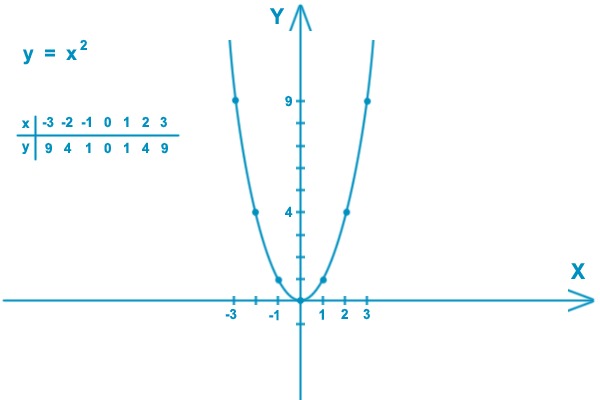 фокус) не на директрисе.
фокус) не на директрисе. Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\).
Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\).