D=9-4*(-4)=25
корень из D =5
x1 = (3+5)/2=4 ,x2=(3-5)/2=-1
рисуем ось х,отмечаем на ней 2 точки( закрашенные) -1 и 4
в промежутке [-беск.;-1] выражение будет положительным. нужно просто подставить в уравнение число из промежутка,
в [-1: 4 ] отриц
в [4: беск] полож.
=>
выбираем промежутки ,где ф-я принимает полож значение
[-беск.;-1] и [4: беск]
1) Найдите первый член и разность арифметической прогрессии (аn),если а9+а7=70,а5-а2=15 2) Найдите сумму первых 12 членов арифметической прогрессии, заданной формулой аn=7-3n. 3) В арифметической прогрессии (an) а5=-1,5, а6=3/4. Найдите а4+а7 4) Дана геометрическая прогрессия (bn). Найдите b1, q, S8 если bn=4/2в степени 3-n степени. 5) Найдите такие значения переменной х, при которых числа -20,2х,-5 образуют геометрическую прогрессию. 6) Дана геометрическая прогрессия 32;16; … Найдите сумму членов прогрессии с четвертого по седьмой включительно. 7) Найдите область определения функции у= под корнем -х2+5х+24 8) Решите систему уравнений 3х+7у=1 (х-3у)(3х+7у)=11 9) Постройте график функции у=(х+1)в кубе, что из себя представляет график функции, какое новое начало координат.
 Найдите координаты точек пересечения графика данной функции с графиком функции у=4х+4 10) Четвертый член арифметической прогрессии равен 9 а восьмой равен -7. Найдите сумму первых восьми членов прогрессии.
Найдите координаты точек пересечения графика данной функции с графиком функции у=4х+4 10) Четвертый член арифметической прогрессии равен 9 а восьмой равен -7. Найдите сумму первых восьми членов прогрессии.Решение: 1) нужно составить систему:
а₉+а₇=70
а₅-а₂=15
затем выразить а через разность:
а₁+8d+a₁+6d=70
a₁+4d-a₁+d=15
получается:
2a₁+14d=70
5d=15
откуда найдем d=3
подставим в первое уравнение 2а₁+14*3=70
а₁=14
7)√-х2+5х+24
т.к. это выражение под корнем, то можно записать так:
-х2+5х+24≥0(надеюсь, понятно почему)
затем вычисляем корни и получается х₁=-3, х₂=8
Дальше будем работать по методу интервалов: -х2+5х+24=-(х+3)(х-8), можем избавиться от минуса, умножив -(х+3)(х-8) на -1.
получается -(х+3)(х-8)≥0, т.к обе части умножили на отрицательное число, меняем знак и получаем (х+3)(х-8)≤0
Теперь на числовой прямой отмечаем точки х=-3 и х=8 и ставим знаки. Справа налево: +,-,+. Т.к. нам нужны отрицательные значения(потому что (х+3)(х-8)≤0), то ответ будет таким:
Справа налево: +,-,+. Т.к. нам нужны отрицательные значения(потому что (х+3)(х-8)≤0), то ответ будет таким:
D(y)=[-3;8]
Найдите область определения функции y=log3 (3x-2):(x2-1) Найдите значение выражения (log5 36 — log5 12) : log5 9 Решите неравенство 3в степени x-2 > 1разделить на 9 Решить уравнение log2 (3x-1)=2 Найдите площадь фигуры ограниченной линиями y=3 в степени x, y=0, x=1, x=4. Высота конуса равна 3 см, его образующая равна 5 см. Найдите объём конуса и площадь его полной поверхности.
Решение: 1)О.О.Ф.= система первая строка 3х-2>0
вторая хв квадрате-1>0 знак следования
1= 3х>2
2= х в квадрате >1 знак следования
1= х>2/3
2=х > 1
3=х>-1
Ответ: х принадлежит промежутку от 1 до плюс бесконечности, скобки круглые
2) (лог по осн 5 числа 36/12)/ (лог по основанию 5 числа 9)= (лог по основанию 5 числа 3)/ (лог по основанию 5 числа 9)=лог по основанию 9 числа 3=-2
3) 3 в степени х-2> 1/9
3 в степени х-2> 3 в степени -2
так как 3>1, то функция y=a в степени х-возрастающая
х-2>-2
x>0
х принадлежит промежутку от 0 до полюс бесконечности скобки круглые
4)
О.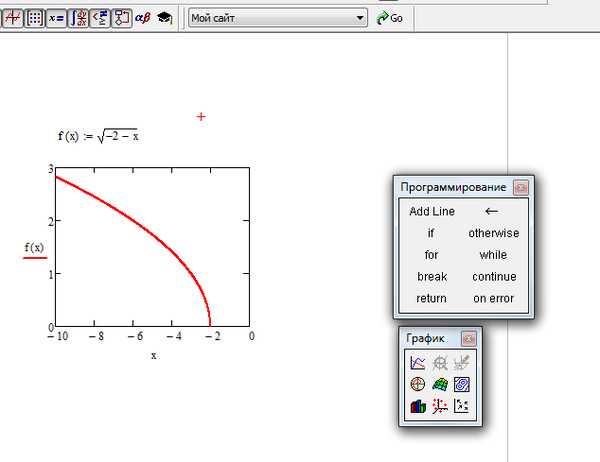 4, потом сдвигаем ее вверх по оси Оу на 4 единицы вверх, а потом сдвигаем слево по оси оХ на три единицы.
4, потом сдвигаем ее вверх по оси Оу на 4 единицы вверх, а потом сдвигаем слево по оси оХ на три единицы.
координаты вершины (-3;2)
Область определения: х — любое число
Найти область определения функции 1) y(x)=корень из х — корень из 2-х 2) y=1/2х*корень из 1-х 3) y=1/х*корень из 1-2х 4) y=3 в степени 1/x 5) y= 1/5 встепени корень из х 6) y= 2 в степени корень из х-1 7) y= 0,2 в степени 1/x в квадрате
Решение: 1) y(x)=корень из х — корень из 2-х ищем пересечение x,больше или равно0 и х меньше или равно 2 получаем от 0 до 2 обе скобки квадратные
2) 2) y=1/2х*корень из 1-х х меньше 1 xe от — бесконечности до 1, обе скобка круглые (вопрос корень в числителе или в знаменателе, если в числителе то правая скобка квадратная)
3) y=1/х*корень из 1-2х x меньше 1/2 от — бесконечности до 1/2 обе скобка круглые (вопрос корень в числителе или в знаменателе, если в числителе то правая скобка квадратная)
4) y=3 в степени 1/x x не равно 0, от — беск до о в объединении от 0 до + беск
все скобки круглые
5) y= 1/5 в степени корень из х х больше или равно 0 от 0 до + бесконечн, первая скобка квадратная, вторая круглая
6) y= 2 в степени корень из х-1 x больше или равно 1 от 1 до + беск
первая скобка квадратная, вторая круглая
Найдите область определения функцииy=log0,2(x в кубе — х в 4 степени)
Решение:
Логарифмическая функция определена на множестве положительных чисел, поэтому выражение стоящее под знаком логарифма должно быть положительным. Составляем неравенство:
Составляем неравенство:
х³-х⁴>0
Решаем методом интервалов:
х³(1-х)>0
Находим нули функции
х³(1-х)=0
х³=0 или 1-х=0
х=0 х=1
Точки х=0 и х=1 (отмечаем их пустым кружком, мы круглыми скобками) разбивают числовую прямую на три промежутка:
_______(0)___________(1)________
Находим знак на (1;+∞)
10∈(1;+∞)
10³(1-10)<0, значит на (1;+∞) ставим знак минус.
И далее знаки чередуем.
____-___(0)_____+______(1)____-____
О т в е т. D(y)=(0;1).
График функции с корнем 3 степени
Разделы: Математика
Использование на уроках современных технологий (КСО) и средств обучения (мультимедийной доски) помогают учителю планировать и проводить эффективные уроки, создавать условия ученикам для осознанного понимания, запоминания и отработки навыков.
Урок получается динамичным и интересным, если во время учебного занятия сочетать различные формы обучения.
В современной дидактике выделяют четыре общие организационные формы обучения:
- индивидуально-опосредованная;
- парная;
- групповая;
коллективная (в парах сменного состава). (Дьяченко В.К. Современная дидактика. – М.: Народное образование, 2005).
На традиционном уроке, как правило, используются только первые три, перечисленные выше, организационные формы обучения. Коллективная форма обучения (работа в парах сменного состава) практически не используется учителем. Однако эта организационная форма обучения дает возможность коллективу обучать каждого и каждому активно участвовать в обучении других. Коллективная форма обучения является ведущей в технологии КСО.
Одной из самых распространенных методик технологии коллективного способа обучения является методика “Взаимный тренаж”.
Эта “волшебная” методика хороша на любом предмете и на любом уроке. Целевое предназначение – тренировка.
Целевое предназначение – тренировка.
Тренировка – наследница самоконтроля, она помогает ученику наладить его контакт с предметом изучения, облегчая поиск правильных шагов-действий. Через тренировку в приобретении, закреплении, перегруппировке, пересмотре, применении знаний происходит развитие познавательных способностей человека . (Яновицкая Е.В. Как учить и учиться на уроке так, чтобы хотелось учиться. Альбом-справочник. – СПб: Образовательные проекты, М.: Издатель А.М. Кушнир, 2009.-С.14;131)
Она поможет быстро повторить какое-либо правило, вспомнить ответы на изученные вопросы, закрепить необходимый навык. Оптимальное время для работы по методике 5-10 минут. Как правило, работа по тренажным карточкам проводится во время устного счета, то есть в начале урока, но по усмотрению учителя она может быть проведена на любом этапе урока, в зависимости от его целей и структуры. В тренажной карточке может быть от 5 до 10 несложных примеров (вопросов, заданий). Каждый ученик класса получает карточку.
Проект урока по теме “Функция у=, ее свойства и график”
В проекте урока, тема которого: “Функция у=, ее свойства и график” представлено использование методики взаимного тренажа в сочетании с применением традиционных и мультимедийных средств обучения.
Тема урока: “Функция у=, ее свойства и график
”надпредметный уровень:
| Время | |
1. Информационный ввод учителя (ИВУ) Информационный ввод учителя (ИВУ) | 5 мин. |
| 2. Актуализация опорных знаний: работа в парах сменного состава по методике “Взаимный тренаж” | 8 мин. |
| 3. Знакомство с темой “ Функция y=, ее свойства и график”: презентация учителя | |
| 4. Закрепление вновь изученного и уже пройденного материала по теме “Функция”: использование интерактивной доски | 15 мин. |
| 5. Самоконтроль: в форме теста | 7 мин. |
| 6. Подведение итогов, запись домашнего задания. | 2 мин. |
Рекомендации к проведению урока
Раскроем подробнее содержание каждого этапа.
1. Информационный ввод учителя (ИВУ) включает в себя организационный момент; озвучивание темы, цели и плана урока; показ образца работы в паре по методике взаимного тренажа.
Демонстрация образца работы в паре учениками на этом этапе урока целесообразна для повторения алгоритма работы нужной нам методики, т.к. на следующем этапе урока по ней планируется работа всего классного коллектива. Заодно можно назвать ошибки работы по алгоритму (если они имелись), а так же оценить работу этих учащихся.
2. Актуализация опорных знаний ведется в парах сменного состава по методике взаимного тренажа.
Алгоритм методики включает в себя индивидуальную, парную (статические пары) и коллективную (пары сменного состава) организационные формы обучения.
Индивидуальная: каждый, получивший карточку, знакомится с ее содержанием (читает вопросы и ответы на оборотной стороне карточки).
Парная: первый (в роли “тренируемого”) читает задание и отвечает на вопросы карточки партнера;
Коллективная: в новой паре работают как в первой; переход в новую пару и т.д.
Количество переходов зависит от времени отведенного учителем на данный этап урока, от трудолюбия и скорости осмысления каждого учащегося и от партнеров по совместной работе.
Содержание работы учащихся представлено в комплекте карточек (приложение 1).
После работы в парах учащиеся делают отметки в листках учета, учитель проводит количественный и качественный анализ работы.
Листок учета может выглядеть следующим образом:
Иванов Петя 7 “б” класс
| Дата | Номер карточки | Количество ошибок | С кем работал |
| 20.12.09 | №7 | Сидоров К. | |
| №3 | 2 | Петрова М. | |
| №2 | 1 | Самойлова З. |
3. Знакомство с темой “ Функция y=, ее свойства и график” проводится учителем в форме презентации с использованием мультимедийных средств обучения (приложение 4). С одной стороны – это вариант наглядности, понятный современным ученикам, с другой стороны – экономия времени на объяснение нового материала.
4. Закрепление вновь изученного и уже пройденного материала по теме “Функция” организуется в двух вариантах, с использованием традиционных средств обучения (доска, учебник) и инновационных (интерактивная доска).
Сначала предлагается несколько заданий из учебника на закрепление вновь изученного материала. Используется тот учебник, по которому ведется обучение. Работа ведется одновременно со всем классом.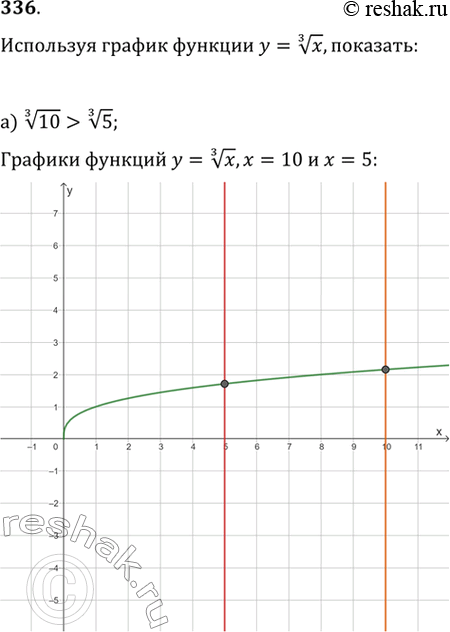 При этом один ученик выполняет задание “а” – на традиционной доске; другой – задание “б” на интерактивной доске, остальные обучающиеся записывают решения этих же заданий в тетрадь и сверяют свое решение с решением, представленным на досках. Далее учитель оценивает работу учащихся у доски.
При этом один ученик выполняет задание “а” – на традиционной доске; другой – задание “б” на интерактивной доске, остальные обучающиеся записывают решения этих же заданий в тетрадь и сверяют свое решение с решением, представленным на досках. Далее учитель оценивает работу учащихся у доски.
Затем, для более быстрого закрепления изученного материала по теме “Функция”, предлагается фронтальная работа с интерактивной доской, которую можно организовать следующим образом:
- на интерактивной доске появляется задание и график;
- ученик, желающий ответить, выходит к доске, выполняет необходимые построения и озвучивает ответ;
- на доске появляется новое задание и новый график;
- отвечать выходит другой ученик.
Содержание данной работы представлено в приложении 2.
Таким образом, за короткий промежуток времени, удается решить довольно много заданий, оценить ответы учащихся. Некоторые задания, представляющие интерес (аналогичные заданиям, из предстоящей контрольной работы), можно зафиксировать в тетрадь.
5. На этапе самоконтроля обучающимся предлагается тест с последующей самопроверкой (приложение 3).
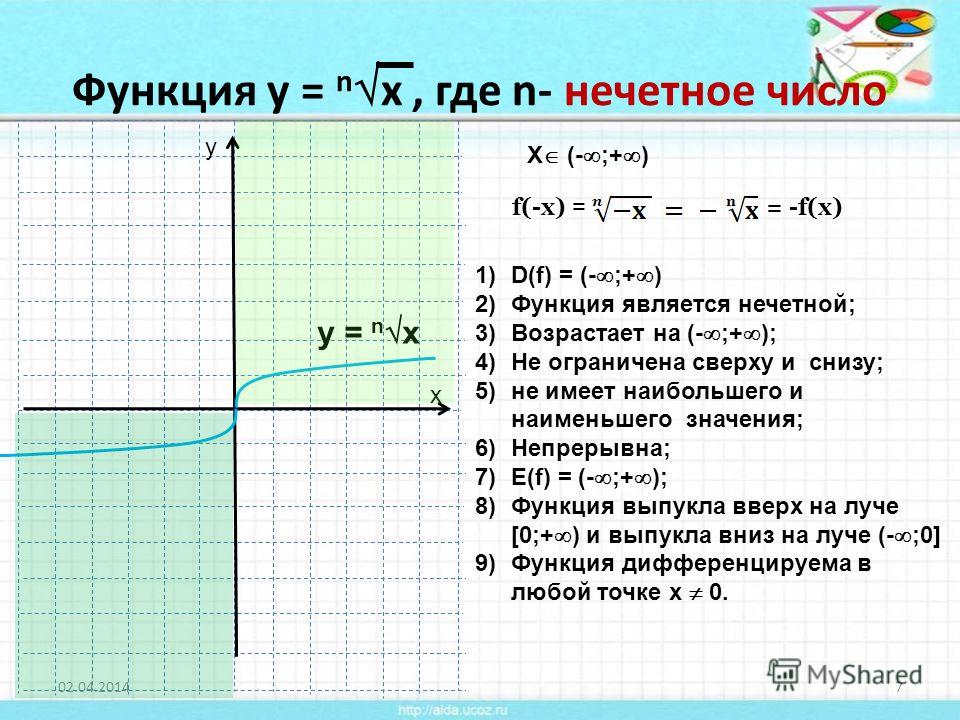
Корнем n-степени из неотрицательного числа a является такое неотрицательное число, при возведении в n-степень которого получается число a.
Корнем нечетной n-степени из отрицательного числа a называется такое отрицательное число, при возведении в n-степень которого получается число a.
Где n – это показатель корня и a – подкоренное число.
Таким образом, извлечь корень любой степени (от второй и далее) можно из любого неотрицательного числа, а из отрицательного числа извлекается только корень нечетной степени.
На [0; +∞) можно поставить каждому числу х в соответствие единственное число корень n-степени из x при любом значении n.
То есть это означает, что на множестве [0; +∞) можно говорить о функции корня:
Теперь определим свойства данной функции и построим ее график.
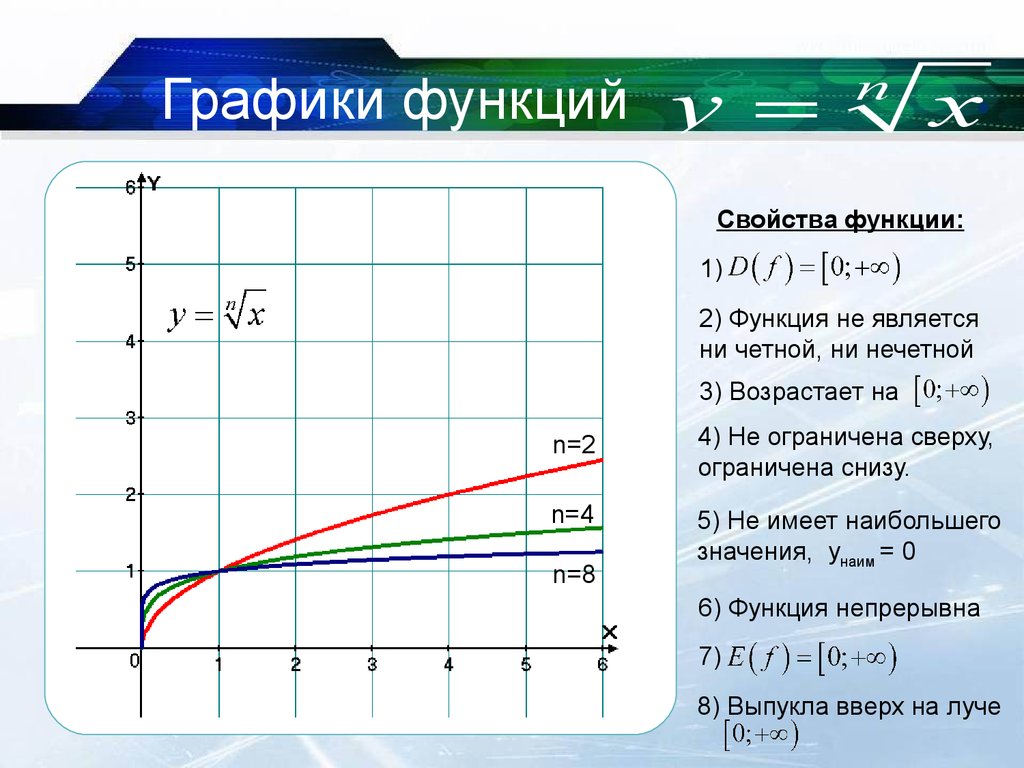
Основные свойства функции:
Промежуток [0; +∞) – является областью определения.
Так как неотрицательное число является корнем n-степени из неотрицательного числа, значит промежуток [0; +∞) будет областью значения функции.
Поскольку симметричным множеством не является область определения функции, поэтому данная функция не является ни нечетной, ни четной.
Операция по извлечению корня вводилась как обратная операция возведения в соответствующую степень.
Значит можно утверждать, что:
Теперь можно построить график функции корня.
Пользуясь графиком, можно записать оставшиеся свойства функции.
На промежутке [0; +∞) функция возрастает.
Сверху функция не ограничена, но она ограничена снизу, например, прямой у, которая = -0,5.
На всей области определения функция выпукла вверх.
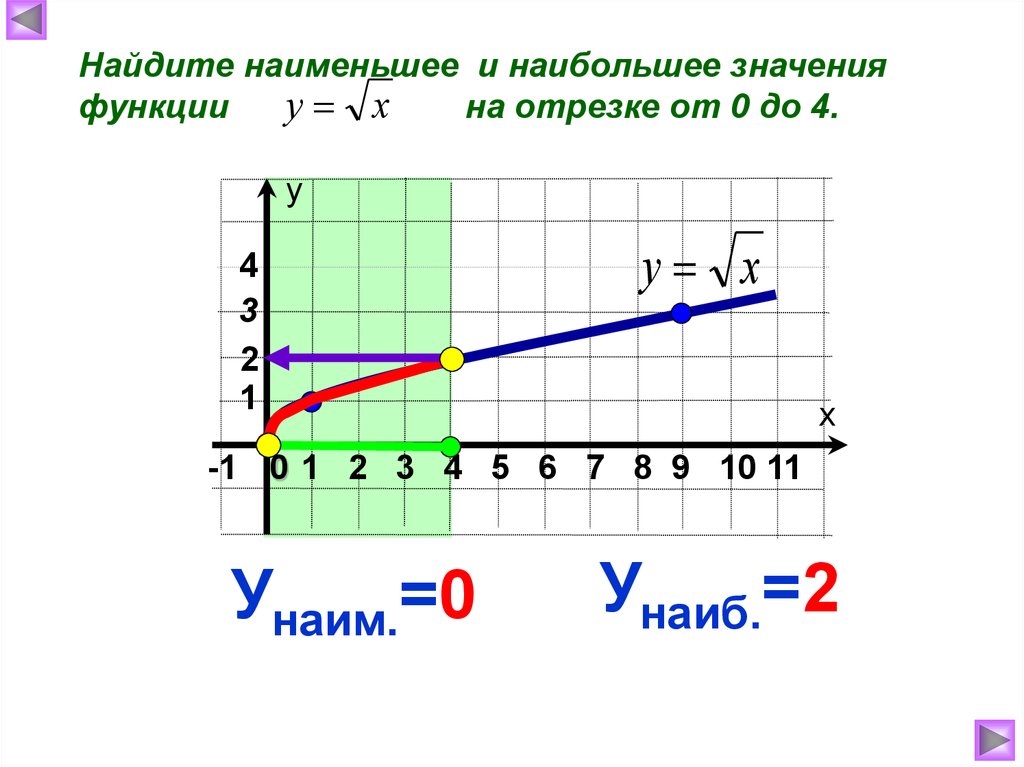
У функции наименьшим значением будет являться 0, а наибольшего значения она не имеет.
Если в каждой из точек некоторого промежутка функция дифференцируема, то это значит, что на данном промежутке она непрерывна.
В любой точке промежутка [0; +∞) существует эта производная, исключением является только точка 0. Поскольку в любой точке промежутка (0; +∞) функция имеет производную, значит на промежутке (0; +∞) функция дифференцируема.
Эти примеры касаются функции, у которой у равно корень n-степени из x, только при неотрицательных значениях аргумента.
Но если n является нечетным числом, то для отрицательных х также имеет смысл выражение корень n-степени из x. А значит, говорить можно о функции:
Запишем свойства данной функции.
Промежуток (– ∞; + ∞) является областью определения функции.
Промежуток (– ∞; + ∞) будет областью значений.
Область определения функции является симметричным множеством, значит данную функцию можно исследовать на четность:
Таким образом получаем, что функция будет нечетной при нечетном n.
Построим график функции.
Добавим к этой ветви еще ветвь, которая симметрична ей относительно начала координат, для этого воспользуемся свойством нечетности функции корня.
- Получившийся график позволяет легко записать оставшиеся свойства функции.
- На всей области определения функция возрастает.
- Ни сверху, ни снизу функция не ограничена.
- У функции нет наибольшего и наименьшего значения.
- На всей области определения функция непрерывна.
- На промежутке (– ∞; 0) функция выпукла вниз, а на промежутке (0; + ∞) она выпукла вверх.
- На всей области определения функция дифференцируема, за исключением точки 0.
Еще несколько примеров графиков функции корня.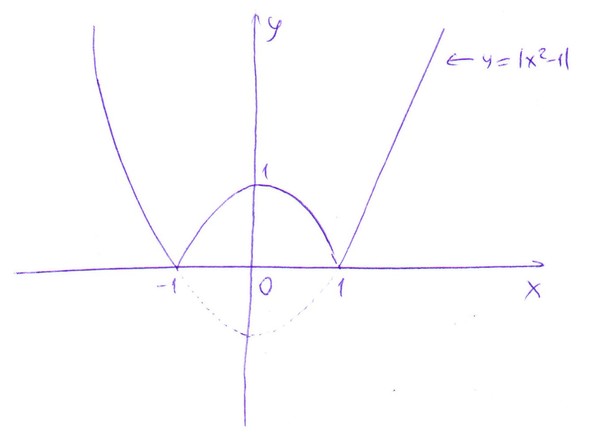
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке вы ознакомитесь с понятием кубического корня из действительного числа, также вы узнаете, что такое функция . Мы изучим различные основные ее свойства и рассмотрим график. Также решим типовые примеры по данной теме
Определение кубического корня, его запись и назначение
Практическая задача
Необходимо сконструировать кубический резервуар, объем которого равен Предположим, что ребро куба имеет длину Например: если объем равен Число Таким образом, выражения
Кубический корень из Доказательство иррациональности
Построим доказательство методом от противного. Предположим, что Подставим значение из последнего равенства в начальное:
Последнее равенство означает, что двадцать пять является делителем числа
Читайте также: Как проверить извещение почты по штрих коду
3.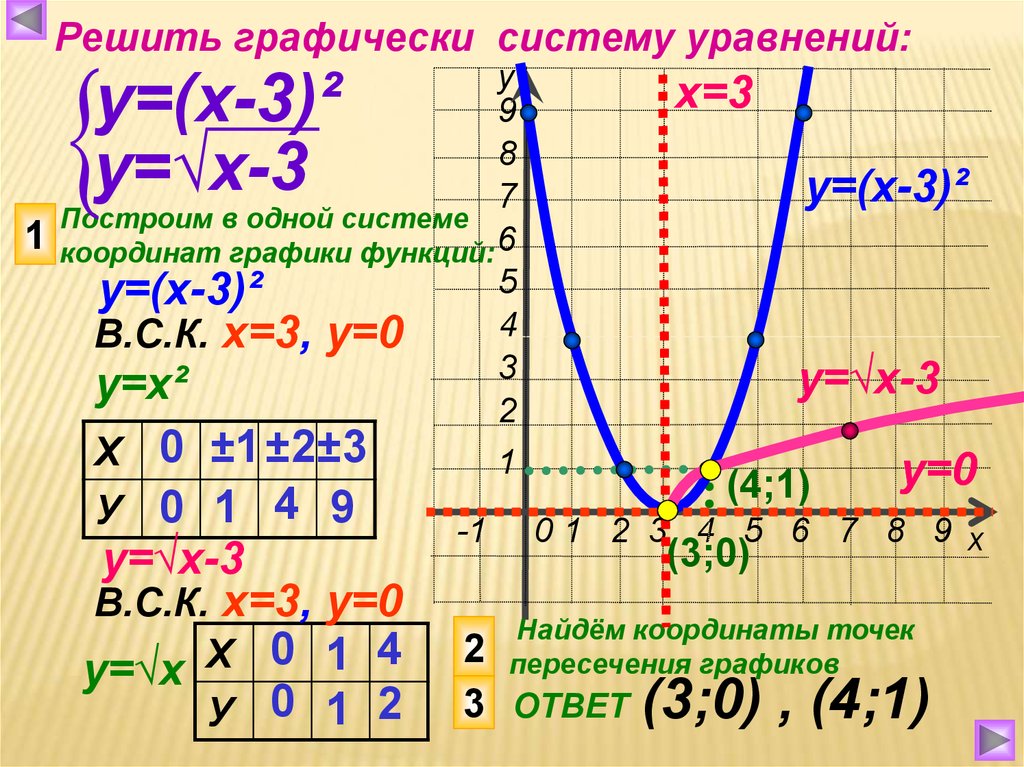 Функция возрастает на луче от нуля до плюс бесконечности (Возьмем два значения аргумента, расположенные следующим образом: Построим доказательство методом от противного. Предположим, что В силу нечетности функции, свойство можно обобщить на всю область определения (4. Функция не ограничена сверху на луче от нуля до плюс бесконечности ()
Функция возрастает на луче от нуля до плюс бесконечности (Возьмем два значения аргумента, расположенные следующим образом: Построим доказательство методом от противного. Предположим, что В силу нечетности функции, свойство можно обобщить на всю область определения (4. Функция не ограничена сверху на луче от нуля до плюс бесконечности ()
Построим доказательство методом от противного. Предположим, что существует такое положительное число Не ограничена сверху при Доказывается это аналогично приведенным доказательствам для положительной полуоси .
Построим четыре точки на координатной плоскости, координаты которых возьмем из таблицы. По данным точкам можно построить некоторую линию, которую можно построить, учитывая возрастающий характер функции и ее неограниченность сверху. Воспользовавшись нечетностью функции, добавим к приведенной линии ветвь, симметричную ей относительно начала координат (рис. 1).
С помощью этого графика и уже установленных свойств функции легко определить оставшиеся свойства функции.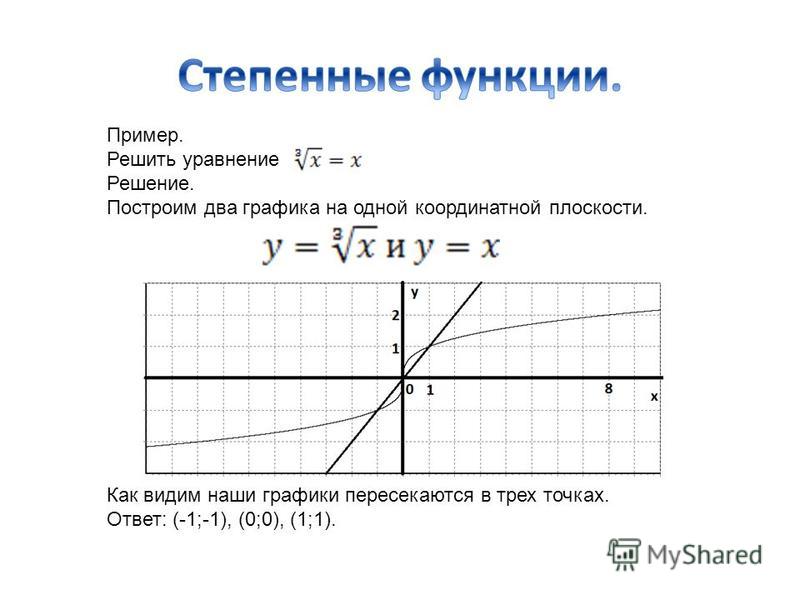
Имеется помещение кубической формы, в которое необходимо подобрать подходящий обогреватель. Теплоизоляция стен имеет фиксированную теплопроводность для всех возможных размеров помещений.
Найдем точки пересечения двух графиков. Как видно из рисунка, графики пересекаются лишь в одной точке с координатами .
Для того чтобы решить данную задачу, вспомним тему «Преобразование графиков функций».
Контрольная работа по теме степени и корни
Контрольная работа №1
Вариант 1
1. Вычислите:
а) б) в)
2. Расположите числа в порядке убывания:
3. Постройте график функции:
а) б)
4. Вычислите:
5. Найдите значение выражения: при
6. Решите уравнение:
Контрольная работа №1
Вариант 2
1. Вычислите:
а) б) в)
2. Расположите числа в порядке возрастания:
3. Постройте график функции:
Постройте график функции:
а) б)
4. Вычислите:
5. Найдите значение выражения: при
6. Решите уравнение:
Контрольная работа №1
Вариант 3
1. Вычислите:
а) б) в)
2. Расположите числа в порядке убывания:
3. Постройте график функции:
а) б)
4. Вычислите:
5. Найдите значение выражения: при
6. Решите уравнение:
Контрольная работа №1
Вариант 4
1. Вычислите:
а) б) в)
2. Расположите числа в порядке возрастания:
3. Постройте график функции:
а) б)
4. Вычислите:
5. Найдите значение выражения: при
6. Решите уравнение:
Контрольная работа №2
Вариант 1
1. Вычислите:
Вычислите:
а) б) в) г)
2. Постройте график функции: а) б)
3. Решите уравнение: а) б)
4. Решите неравенство:
5. Составьте уравнение касательной к графику функции в точке х=1.
6. Дана функция , где
а) Вычислите: f(-1), f (3).
б) Постройте график функции.
в) Найдите область значений функции.
г) Выясните, при каких значениях параметра уравнение имеет два корня.
Контрольная работа №2
Вариант 2
1. Вычислите:
а) б) в) г)
2. Постройте график функции: а) б)
3. Решите уравнение: а) б)
4. Решите неравенство:
5. Найдите наибольшее и наименьшее значения функции на отрезке [0;8].
6.
Дана функция , где а) Вычислите: f(-2), f (7).
б) Постройте график функции.
в) Найдите область значений функции.
г) Выясните, при каких значениях параметра уравнение имеет два корня.
Контрольная работа №2
Вариант 3
1. Вычислите:
а) б) в) г)
2. Постройте график функции: а) б)
3. Решите уравнение: а) б)
4. Решите неравенство:
5. Составьте уравнение касательной к графику функции в точке х=1.
6. Дана функция , где
а) Вычислите: f(-4), f (31).
б) Постройте график функции.
в) Найдите область значений функции.
г) Выясните, при каких значениях параметра уравнение имеет два корня.
Контрольная работа №2
Вариант 4
1. Вычислите:
Вычислите:
а) б) в) г)
2. Постройте график функции: а) б)
3. Решите уравнение: а) б)
4. Решите неравенство:
5. Найдите наибольшее и наименьшее значения функции на отрезке [1;9].
6. Дана функция , где
а) Вычислите: f(-1), f (4).
б) Постройте график функции.
в) Найдите область значений функции.
г) Выясните, при каких значениях параметра уравнение имеет два корня.
Контрольная работа №3
Вариант 1
1. Вычислите: а) б)
2. Постройте график функции: а) б)
3. Решите уравнение: а) б)
4. Решите неравенство:
5. Решите уравнение:
Контрольная работа №3
Вариант 2
1. Вычислите: а) б)
Вычислите: а) б)
2. Постройте график функции: а) б)
3. Решите уравнение: а) б)
4. Решите неравенство:
5. Решите уравнение:
Контрольная работа №3
Вариант 3
1. Вычислите: а) б)
2. Постройте график функции: а) б)
3. Решите уравнение: а) б)
4. Решите неравенство:
5. Решите уравнение:
Контрольная работа №3
Вариант 4
1. Вычислите: а) б)
2. Постройте график функции: а) б)
3. Решите уравнение: а) б)
4. Решите неравенство:
5. Решите уравнение:
Контрольная работа №4
Вариант 1
1. Решите неравенство:
Решите неравенство:
2. Исследуйте функцию на монотонность и экстремумы.
3. Напишите уравнение касательной к графику функции
в точке x=1.
4. Решите уравнение:
5. Решите систему уравнений
Контрольная работа №4
Вариант 2
1. Решите неравенство:
2. Исследуйте функцию на монотонность и экстремумы.
3. Напишите уравнение касательной к графику функции
в точке x=3.
4. Решите уравнение:
5. Решите систему уравнений
Контрольная работа №4
Вариант 3
1. Решите неравенство:
2. Исследуйте функцию на монотонность и экстремумы.
3. Напишите уравнение касательной к графику функции
в точке x=4.
4. Решите уравнение: 2
5. Решите систему уравнений
Контрольная работа №4
Вариант 4
1. Решите неравенство:
Решите неравенство:
2. Исследуйте функцию на монотонность и экстремумы.
3. Напишите уравнение касательной к графику функции
в точке x=2.
4. Решите уравнение:
5. Решите систему уравнений
Контрольная работа №5
Вариант 1
1. Докажите, что функция является первообразной для функции .
2. Для данной функции найдите ту первообразную, график которой проходит через заданную точку А (-π;0).
3. Вычислите интеграл: а) ; б) .
4. Вычислите площадь фигуры, ограниченной линиями .
5. Известно, что функция – первообразная для функции . Исследуйте функцию на монотонность и экстремумы.
Контрольная работа №5
Вариант 2
1. Докажите, что функция является первообраз-ной для функции .
2.
Для данной функции найдите ту первообразную, график которой проходит
через заданную точку А (-).
3. Вычислите интеграл: а) ; б) .
4. Вычислите площадь фигуры, ограниченной линиями .
5. Известно, что функция – первообразная для функции . Исследуйте функцию на монотонность и экстремумы.
Контрольная работа №5
Вариант 3
1. Докажите, что функция является первообразной для функции .
2. Для данной функции найдите ту первообразную, график которой проходит через заданную точку А ().
3. Вычислите интеграл: а) ; б) .
4. Вычислите площадь фигуры, ограниченной линиями .
5. Известно, что функция – первообразная для функции . Сравните числа F (6) и F (7).
Контрольная работа №5
Вариант 4
1. Докажите, что функция является первообразной для функции .
2.
Для данной функции найдите ту первообразную, график которой проходит
через заданную точку А ().
3. Вычислите интеграл: а) ; б) .
4. Вычислите площадь фигуры, ограниченной линиями.
5. Известно, что функция – первообразная для функции . Сравните числа F (3) и F (4).
Контрольная работа №6
Вариант 1
1. В клубе 25 спортсменов. Сколькими способами из них можно составить команду из четырёх человек для участия в четырёхэтапной эстафете с учётом порядка пробега этапов?
2. Сколько трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 0 при условии, что каждая цифра может встретиться в записи числа один раз?
3. Решите уравнение .
4. Напишите разложение степени бинома.
5. Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом карты одинаковой масти?
6. На прямой взяты шесть точек, а на параллельной ей прямой – 7 точек. Сколько существует треугольников, вершинами которых являются данные точки?
Контрольная работа №6
Вариант 2
1. Сколькими способами можно
составить трёхцветный полосатый флаг, если имеется ткань пяти различных цветов?
Сколькими способами можно
составить трёхцветный полосатый флаг, если имеется ткань пяти различных цветов?
2. Сколько различных трёхзначных чисел можно составить из цифр 1, 2, 3 при условии, что цифры могут повторяться?
3. Решите уравнение .
4. Напишите разложение степени бинома.
5. Из колоды в 36 карт вытаскивают три карты. Какова вероятность того, что все они тузы?
6. Сколько существует треугольников, вершины которых являются вершинами данного выпуклого 10-угольника?
Контрольная работа №6
Вариант 3
1. В городской думе 30 человек. Из них на общем заседании надо выбрать председателя, а также его первого, второго и третьего заместителей. Сколькими способами это можно сделать?
2. Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6 при условии, что цифры могут повторяться?
3. Решите уравнение .
4.
Напишите разложение
степени бинома.
5. В урне находятся 3 белых и 4 чёрных шара. Какова вероятность того, что вынутые из неё наудачу два шара окажутся белыми?
6. На прямой взяты 8 точек, а на параллельной ей прямой – 5 точек. Сколько существует треугольников, вершинами которых являются данные точки?
Контрольная работа №6
Вариант 4
1. В яхт-клубе состоит 9 человек. Из них на общем собрании надо выбрать председателя, заместителя, секретаря и казначея. Сколькими способами это можно сделать?
2. Сколько четырёхзначных чисел можно составить из цифр 1, 2, 3, 0 при условии, что каждая цифра может встретиться в записи числа один раз?
3. Решите уравнение .
4. Напишите разложение степени бинома.
5. В урне находятся 2 белых, 3 красных и 16 чёрных шаров. Какова вероятность того, что из вынутых наудачу двух шаров один окажется белым, а другой красным?
6. Сколько существует треугольников, вершины которых являются вершинами данного выпуклого 8-угольника, а стороны не совпадают со сторонами этого многоугольника?
Контрольная работа №7 (2 часа)
Вариант 1
1. Решите уравнение: а) б)
Решите уравнение: а) б)
в)
2. Решите неравенство: а) б)
в)
3. Решите уравнение в целых числах:
4. Решите систему уравнений:
5. Решите уравнение:
Контрольная работа №7 (2 часа)
Вариант 2
1. Решите уравнение: а) б)
в)
2. Решите неравенство: а) б)
в)
3. Решите уравнение в целых числах:
4. Решите систему уравнений:
5. Решите уравнение:
Контрольная работа №7 (2 часа)
Вариант 3
1. Решите уравнение: а) б)
в)
2. Решите неравенство: а) б)
в)
3. Решите уравнение в целых числах:
4. Решите систему уравнений:
5. Решите уравнение:
Решите уравнение:
Контрольная работа №7 (2 часа)
Вариант 4
1. Решите уравнение: а) б)
в)
2. Решите неравенство: а) б)
в)
3. Решите уравнение в целых числах:
4. Решите систему уравнений:
- Решите уравнение:
Нарисуйте пожалуйста на листе. Не понимаю как это сделать… -reshimne.ru
Новые вопросы
Ответы
Постройте график функции y=- корень 4 степени из (x+3) +5(
Похожие вопросы
Сравните величины 50 и 70см и 5000см…
Как сделать обратную задачу?…
Какие 2 цифры нужно приписать справа к числу 2017,чтобы получилась число, делящиеся на 99?. ..
..
Випишите в пустая клетки такие пропущенные числа,чтобы наравенства были верными.
7× <50 ×2000<40000
6× <500 ×5000<80000
8× <5000 ×7000<20000
9× <50000 ×8000<50000…
Пожалуйста помогите
общий знаменатель 27 и 90…
Трехзначное число которое делится на число 3 и на число 5 но не делится на число 10…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
3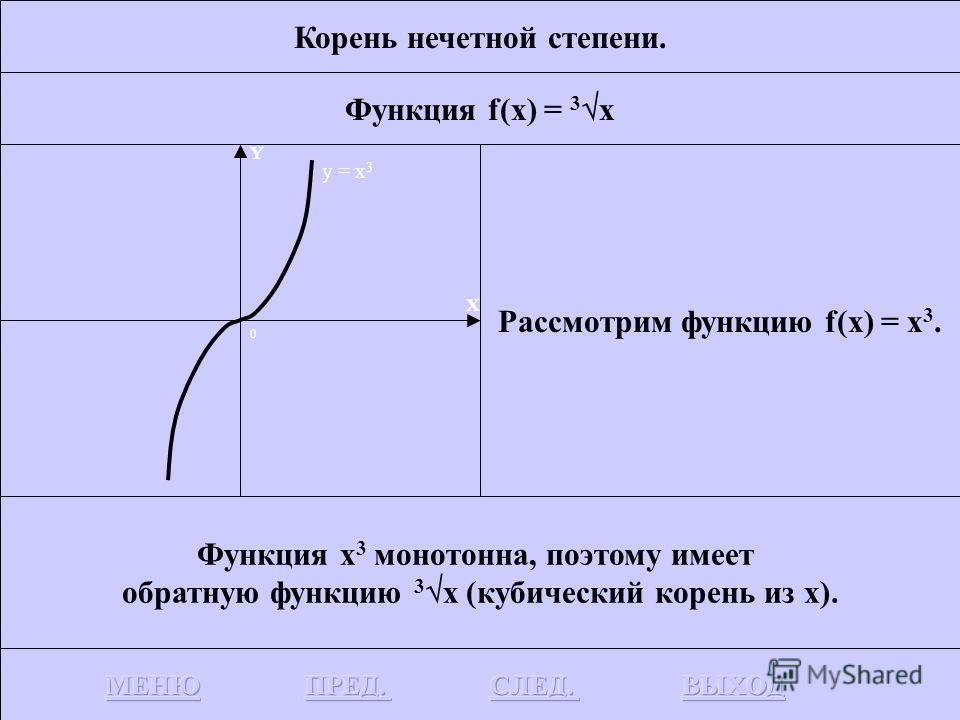
Функция кубического корня — построение графиков
Функция кубического корня использует символ кубического корня ∛ (который обозначает кубический корень), поэтому давайте вспомним кое-что об этом.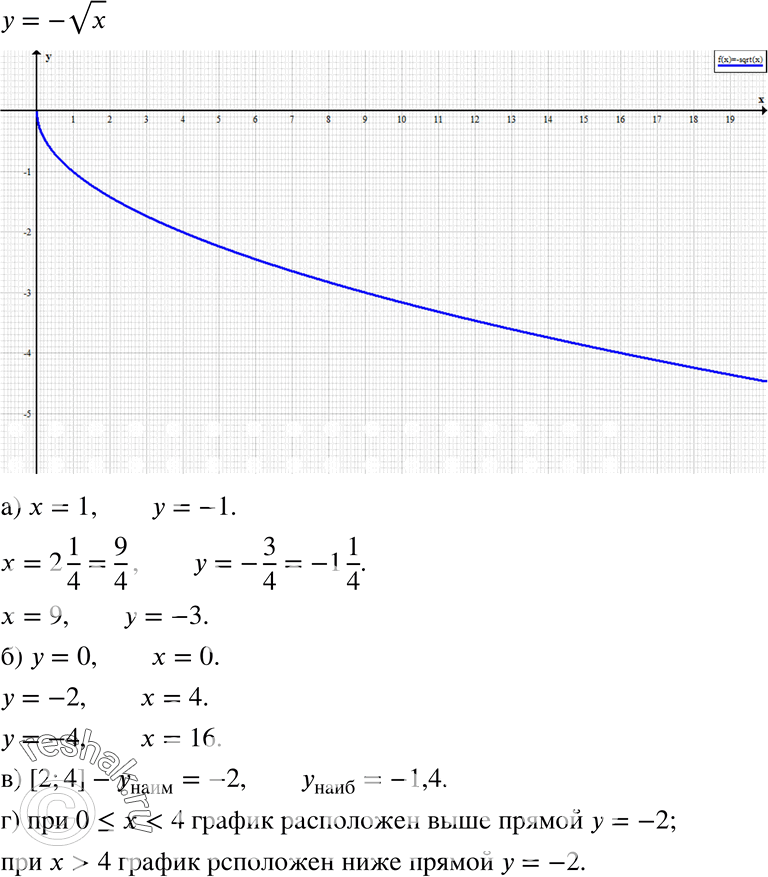 Кубический корень числа «а» — это число «b», такое что b 3 = a. т. е. если b 3 = a ⇒ b = ∛a. то есть, если «b» является кубом «a», то «a» является кубическим корнем «b». Некоторые примеры:
Кубический корень числа «а» — это число «b», такое что b 3 = a. т. е. если b 3 = a ⇒ b = ∛a. то есть, если «b» является кубом «a», то «a» является кубическим корнем «b». Некоторые примеры:
- 2 3 = 8 ⇒ ∛8 = 2
- (-2) 3 = -8 ⇒ ∛(-8) = -2
- 0 3 = 0 ⇒ ∛0 = 0
Таким образом, кубический корень из положительного числа положительный, а из отрицательного — отрицательный. Давайте воспользуемся всеми этими фактами, чтобы понять функцию кубического корня.
| 1. | Что такое функция кубического корня? |
| 2. | Домен и диапазон функции кубического корня |
| 3. | Асимптоты функции кубического корня |
| 4. | График корневой функции родительского куба |
| 5. | График кубических корневых функций |
6. | Свойства функции кубического корня |
| 7. | Часто задаваемые вопросы о функции кубического корня |
Что такое функция кубического корня?
г.Функция кубического корня является обратной кубической функцией. Мы знаем, что исходная кубическая функция имеет форму f(x) = x 3 , и эта функция возрастает, один на один и дальше. Следовательно, это биекция. Таким образом, его обратная функция, которая является функцией кубического корня, имеет вид f (x) = ∛x, также является биекцией. Мы знаем, что функция и обратная ей функция симметричны относительно прямой y = x, поэтому графики родительской кубической функции и родительской функции кубического корня выглядят так.
f(x) = ∛x — базовая/родительская функция кубического корня. Но к этой функции можно применить преобразования. Таким образом, общая форма функции кубического корня имеет вид:
- f(x) = a ∛(bx — h) + k
Здесь a, b, h и k — действительные числа, где «h» представляет горизонтальное смещение, «k» — вертикальное смещение, а «a» и «b» — расширение.
Домен и диапазон функции кубического корня
г.Мы уже видели во введении, что кубический корень определен для всех чисел (положительных, действительных и нулевых). Таким образом, для любой функции кубического корня f(x) не существует x, где f(x) не определена. Таким образом, его областью определения является множество всех действительных чисел (R). Точно так же функция кубического корня дает все числа (положительные, действительные и 0), и, следовательно, ее диапазон также является набором всех действительных чисел. Таким образом, функция кубического корня есть f(x): R → R, т. е.
- Область определения функции кубического корня есть R. г.
- Диапазон функции кубического корня составляет R.
Асимптоты функции кубического корня
Асимптоты функции — это линии, часть графика которых находится очень близко к этим линиям, но на самом деле не касается этих линий. Возьмем корневую функцию родительского куба f(x) = ∛x. Тогда
Тогда
- Поскольку x → ±∞, f(x) → ±∞ и, следовательно, оно не имеет горизонтальных асимптот.
- Не существует ‘x’, где f(x) не определена и, следовательно, не имеет вертикальных асимптот. г.
Таким образом, функция кубического корня не имеет асимптот.
График корневой функции родительского куба
Мы уже видели, что область определения и область значений функции кубического корня — это множество всех действительных чисел, и она не имеет асимптот. Давайте сначала посмотрим, как построить график родительской функции кубического корня f(x) = ∛x, а позже мы расширим этот процесс, чтобы построить график любой общей функции кубического корня. Давайте построим таблицу значений с некоторыми случайными действительными числами (поскольку домен представляет собой множество всех действительных чисел) для x (с некоторыми положительными, некоторыми отрицательными, а также 0). Подставим каждое значение в функцию f(x) = ∛x, чтобы найти соответствующее значение y.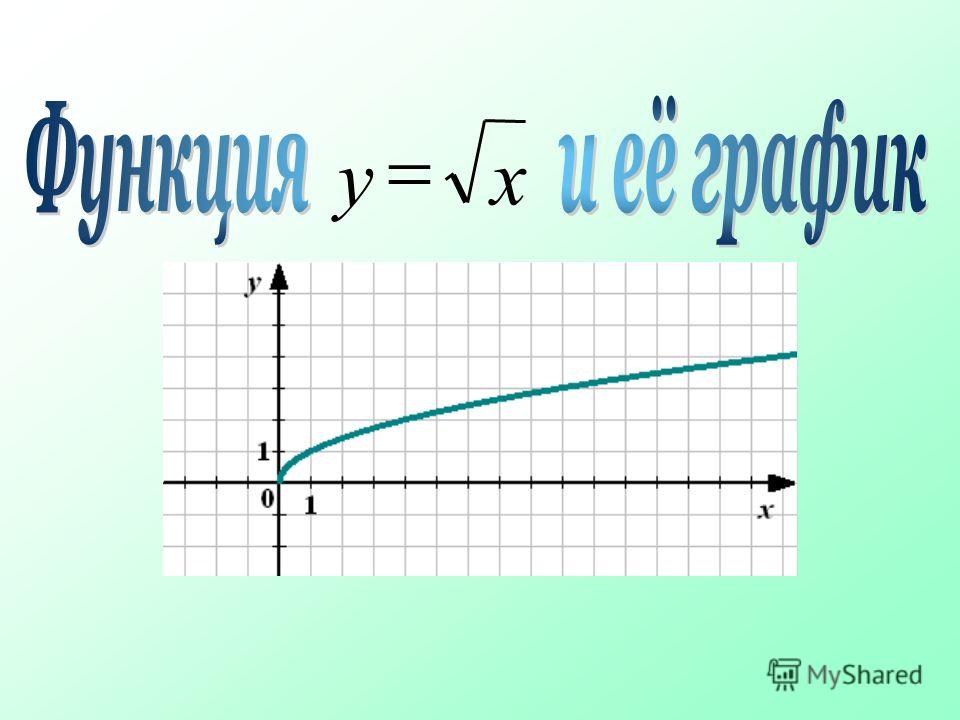
| х | и |
|---|---|
| -8 | ∛(-8) = -2 |
| -1 | ∛(-1) = -1 |
| 0 | ∛0 = 0 |
| 1 | ∛1 = 1 |
| 8 | ∛8 = 2 |
Здесь мы выбрали -8, -1, 0, 1 и 8 в качестве значений x, поскольку они являются идеальными кубами, и они помогут нам легко вычислить значения y. Теперь точки из таблицы равны (-8, -2), (-1, -1), (0, 0), (1, 1) и (8, 2). Нанесем все эти точки на лист графика и соединим их кривой, которая дает график функции кубического корня f(x) = ∛x. Также не забудьте расширить граф в обе стороны.
График корневых функций куба
Чтобы построить график любой функции кубического корня вида f(x) = a ∛(bx — h) + k, просто возьмите ту же таблицу, что и выше, и получите новые координаты x и y следующим образом в соответствии с заданной функцией:
- Чтобы получить новые координаты y, примените внешние операции знака кубического корня к координатам y из приведенной выше таблицы.

- Чтобы получить новые координаты x, установите bx — h равными каждой из старых координат x и найдите x, чтобы получить новые координаты x. г.
Вот пример.
Пример: Постройте график функции кубического корня f(x) = 2 ∛(x — 1) + 3.
Решение:
).
| х | и |
|---|---|
| -8 | -2 |
| -1 | -1 |
| 0 | 0 |
| 1 | 1 |
| 8 | 2 |
Получим новую таблицу, которая будет соответствовать заданной функции, следующим образом.
- Новые координаты x можно получить, установив x — 1 = старые координаты и найдя x.
- Новые координаты y можно получить, упростив 2(старая координата y) + 3.
| х | и |
|---|---|
| х — 1 = -8 ⇒ х = -7 | 2(-2) + 3 = -1 |
| х — 1 = -1 ⇒ х = 0 | 2(-1) + 3 = 1 |
| х — 1 = 0 ⇒ х = 1 | 2(0) + 3 = 3 |
| х — 1 = 1 ⇒ х = 2 | 2(1) + 3 = 5 |
| х — 1 = 8 ⇒ х = 9 | 2(2) + 3 = 7 |
Очки из таблицы: (-7, -1), (0, 1), (1, 3), (2, 5) и (9, 7).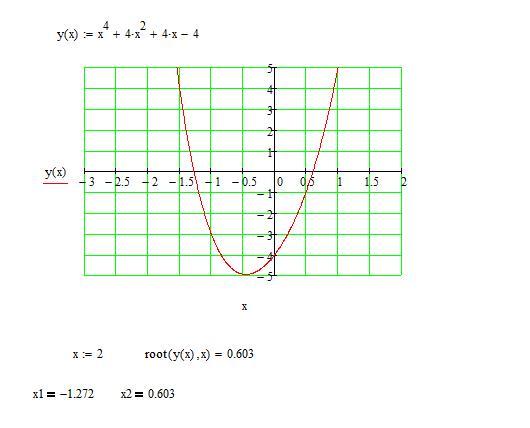 Давайте построим их, соединим их кривой и продолжим кривую.
Давайте построим их, соединим их кривой и продолжим кривую.
Свойства функции кубического корня
Вот характеристики функции кубического корня f(x) = ∛x. Мы можем посмотреть на график функции корня родительского куба, чтобы обосновать каждое из следующих свойств.
- Возрастает на (-∞, ∞). г.
- Оно положительно на (0, ∞) и отрицательно на (-∞, 0). f(x) = 0, когда x = 0.
- Таким образом, конечное поведение функции кубического корня:
f(x) → ∞ при x → ∞
f(x) → -∞ при x → -∞ - Не имеет относительного макс./мин.
- Нет глобального макс./мин.
- Не имеет асимптот.
- Его домен и диапазон равны (-∞, ∞).
☛ Связанные темы:
- Формула кубического корня г.
- Калькулятор кубического корня
- Кубический корень от 1 до 20
- Формула квадратного корня
Часто задаваемые вопросы о функции кубического корня
Что такое формула функции кубического корня?
Формула для основной (родительской) функции кубического корня такова: f(x) = ∛x.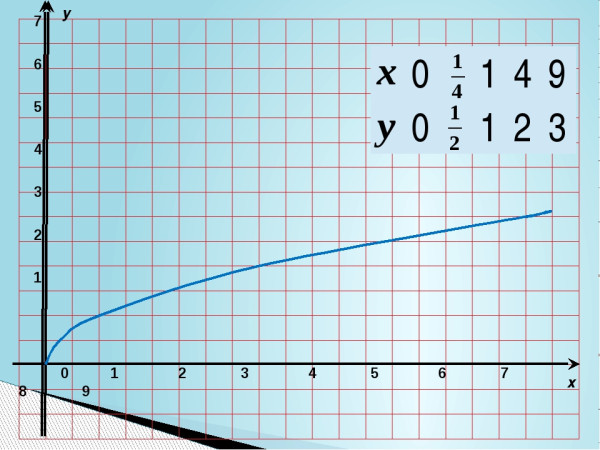 Он также может иметь вид f(x) = a ∛(bx — h) + k после преобразований. Здесь a, b, h и k — действительные числа, представляющие преобразования.
Он также может иметь вид f(x) = a ∛(bx — h) + k после преобразований. Здесь a, b, h и k — действительные числа, представляющие преобразования.
Как нарисовать график кубического корня?
Чтобы нарисовать график функции корня родительского куба f(x) = ∛x, нарисуйте таблицу значений с двумя столбцами x и y. Возьмите числа -8, -1, 0, 1 и 8 в столбце x (поскольку это идеальные кубы), вычислите кубический корень каждого из этих чисел и вставьте их в столбец с пометкой y. Тогда у нас есть 5 точек (-8, -2), (-1, -1), (0, 0), (1, 1) и (8, 2). Просто начертите их и соедините их кривой. Поскольку эта кривая не является полной, просто растяните ее с обеих сторон по всему листу графика.
В чем разница между функцией извлечения квадратного корня и кубического корня?
Вот различия между функцией извлечения квадратного и кубического корня.
| Функция извлечения квадратного корня | Функция кубического корня |
|---|---|
Основная родительская функция квадратного корня имеет вид f(x) = √x.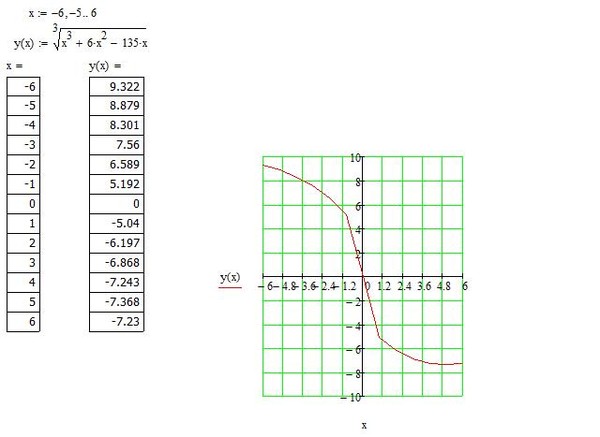 | Базовая функция корня родительского куба имеет вид f(x) = ∛x. |
| Возрастает на интервале (-∞, ∞). | Возрастает на интервале [0, ∞). |
| Оно положительно на (0, ∞) и отрицательно на (-∞, 0). | Это всегда неотрицательная функция (на [0, ∞)). |
| Абсолютный минимум равен 0, но не абсолютный максимум. | Не имеет абсолютного максимума или минимума. |
| Его домен и диапазон — это набор всех действительных чисел. | Его домен и диапазон [0, ∞). |
| Его конечное поведение: f(x) → ∞ при x → ∞ f(x) → -∞ при x → -∞ | Его конечное поведение: f(x) → ∞ при x → ∞ f(x) → 0 при x → 0 |
Как найти производную функции кубического корня?
Функция кубического корня может быть записана как f(x) = ∛x = x 1/3 . Мы можем найти его производную, используя степенное правило производных, которое гласит: d/dx (x n ) = nx н — 1 .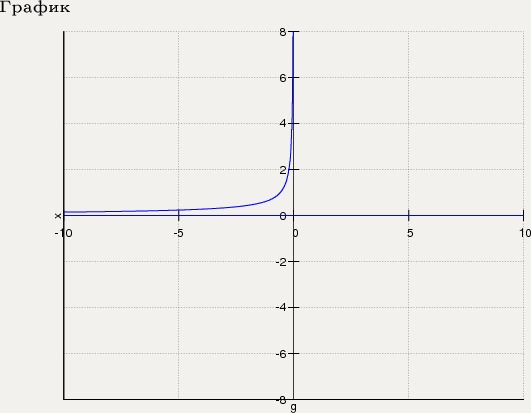 Используя это, d/dx (x 1/3 ) = (1/3) x (1/3 — 1) = (1/3) x -2/3 = 1 / (3x 2 /3 ).
Используя это, d/dx (x 1/3 ) = (1/3) x (1/3 — 1) = (1/3) x -2/3 = 1 / (3x 2 /3 ).
Как интегрировать функцию кубического корня?
Пусть f(x) =∛x. Его можно записать как x 1/3 . Его интеграл можно найти по формуле ∫ x n dx = (x n + 1 ) / (n + 1) + C. Используя эту формулу, ∫ x 1/3 dx = (x 1/ 3 + 1 ) / (1/3 + 1) + C = (3/4) x 4/3 + C.
Что такое домен и область значений функции кубического корня?
Областью определения функции кубического корня f(x) = ∛x является множество всех действительных чисел (R), поскольку ее можно вычислить для всех значений x. Его диапазон также равен набору всех действительных чисел, потому что он приведет к тому, что все действительные числа будут y-значениями. Другими словами, вся ось x и вся ось y покрываются ее графиком, и, следовательно, и домен, и диапазон равны R.
Имеет ли функция кубического корня асимптоты?
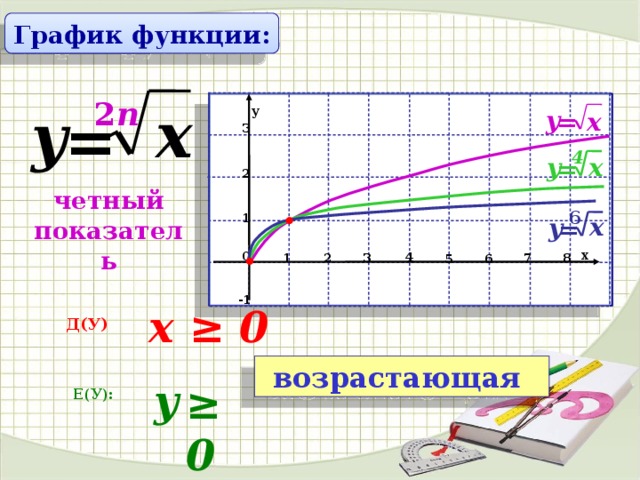
Нет, функция кубического корня f(x) = ∛x не имеет асимптот.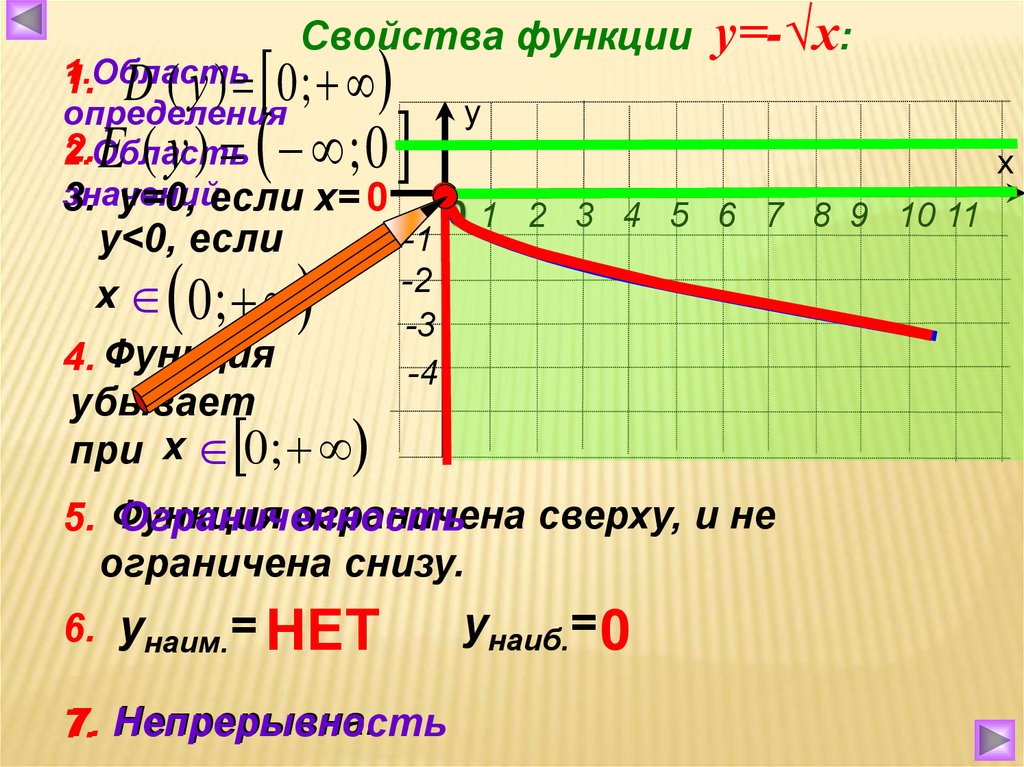 У него нет горизонтальной асимптоты, потому что он возрастает на множестве всех действительных чисел. У него нет вертикальной асимптоты, потому что он определен для всех действительных чисел. 9\frac{1}{6}=\sqrt[\leftroot{1}\uproot{2}6]{x}[/latex], которые являются четными корневыми функциями.
У него нет горизонтальной асимптоты, потому что он возрастает на множестве всех действительных чисел. У него нет вертикальной асимптоты, потому что он определен для всех действительных чисел. 9\frac{1}{6}=\sqrt[\leftroot{1}\uproot{2}6]{x}[/latex], которые являются четными корневыми функциями.
Рисунок 1
Обратите внимание, что эти графики имеют сходную форму, очень похожую на форму квадратного корня в наборе инструментов. Однако по мере увеличения значения n графики несколько круче вблизи начала координат и становятся более пологими вдали от начала координат, растущие медленнее. Перехватами [latex]x[/latex] и [latex]y[/latex] этих функций являются [latex]\left(0,0\right)[/latex]. Конечное поведение для функции четного корня имеет смысл только при неограниченном увеличении [latex]x[/latex], поскольку отрицательные значения не находятся в домене. Мы наблюдаем как [латекс]x\to\infty,\textrm{ }f\left(x\right)\to\infty[/latex]. 9\frac{1}{7}=\sqrt[\leftroot{1}\uproot{2}7]{x}[/latex], которые являются нечетными корневыми функциями.
Рисунок 2
Обратите внимание, что эти графики похожи на функцию кубического корня в наборе инструментов. Опять же, по мере увеличения значения n графики становятся более крутыми вблизи начала координат и становятся более плоскими по мере удаления от начала координат, увеличиваясь медленнее. Перехватами [latex]x[/latex] и [latex]y[/latex] этих функций являются [latex]\left(0,0\right)[/latex]. Конечное поведение для функции четного корня выражается как [latex]x\to\infty,\textrm{ }f\left(x\right)\to\infty[/latex] для больших значений [latex]x[/ латекс] и как [латекс]x\to-\infty,\textrm{ }f\left(x\right)\to-\infty[/latex] для очень отрицательных значений [latex]x.[/latex]
Преобразования корневых функций
Для преобразований четных корневых функций домен и область значений изменяются горизонтальными и вертикальными сдвигами, отражениями и растяжениями. Есть два метода, которые вы можете использовать, чтобы найти домен. Первый метод заключается в использовании алгебры и идеи о том, что даже корневые функции должны иметь неотрицательные значения под корневым символом.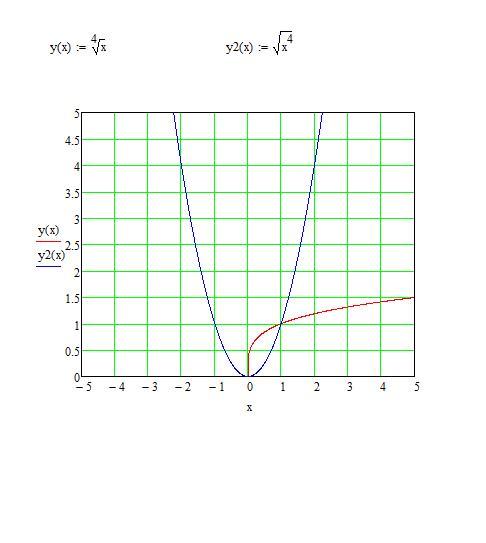 Выражение под корневым символом устанавливается большим или равным нулю, и неравенство решается для нахождения домена. В качестве альтернативы вы можете использовать свойства преобразования, указав базовую функцию и определив, куда преобразуется точка (0,0) в новой функции. Координата x будет начальной или конечной точкой домена. Если нет горизонтального отражения, домен будет от этого значения вправо, а если есть горизонтальное отражение, то домен будет идти от этого значения влево.
Выражение под корневым символом устанавливается большим или равным нулю, и неравенство решается для нахождения домена. В качестве альтернативы вы можете использовать свойства преобразования, указав базовую функцию и определив, куда преобразуется точка (0,0) в новой функции. Координата x будет начальной или конечной точкой домена. Если нет горизонтального отражения, домен будет от этого значения вправо, а если есть горизонтальное отражение, то домен будет идти от этого значения влево.
Диапазон определяется путем определения базовой функции и определения того, какое преобразование применяется для получения функции, с которой вы работаете. После применения преобразования к точке (0,0) координата y сообщает вам, где начинается или заканчивается диапазон. Если нет вертикального отражения, диапазон будет от этого значения до бесконечности, а если есть вертикальное отражение, диапазон будет от минус бесконечности до этого значения.
Как сделать
Учитывая корневую функцию, найдите домен и диапазон.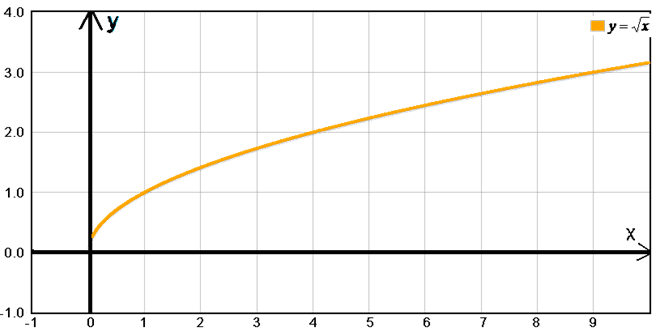
Метод предметной области 1: алгебраический
- Установите выражение под корневым символом больше или равное нулю и решите.
- Запишите решение в интервальной записи. Не забудьте использовать квадратную скобку по мере необходимости.
Домен Метод 2: Преобразования
- Определите базовую корневую функцию.
- Опишите преобразование словами, а затем определите, куда точка (0,0) отображается при этом преобразовании. г.
- Если нет вертикального отражения, домен простирается от координаты x преобразованной точки до бесконечности. Если есть вертикальное отражение, домен находится от минус бесконечности до этой координаты x.
Диапазон
- Определите основную корневую функцию.
- Опишите преобразование словами, а затем определите, куда точка (0,0) отображается при этом преобразовании.
- Координата Y указывает, где начинается или заканчивается диапазон.
 Если нет вертикального отражения, диапазон будет от этого значения до бесконечности, а если есть вертикальное отражение, диапазон будет от минус бесконечности до этого значения. г.
Если нет вертикального отражения, диапазон будет от этого значения до бесконечности, а если есть вертикальное отражение, диапазон будет от минус бесконечности до этого значения. г.
Пример 1. Область определения и диапазон функции четного корня
Найдите область определения, диапазон и точки пересечения функции квадратного корня, сдвинутые на 3 единицы влево и на 1 единицу вверх.
Показать решение
Пример 2. Домен и перехваты функций четного корня
Найдите домен и диапазон для
a. [латекс]г\влево(х\вправо)=\sqrt[\leftroot{1}\uproot{2}4]{3-2x}.[/латекс]
б. [латекс]ч\влево(х\вправо)=-3\sqrt[\leftroot{1}\uproot{2}4]{x}.[/latex]
Показать решение
Перехваты четных корневых функций
Преобразования четных корневых функций могут иметь или не иметь перехваты [latex]x[/latex] или [latex]y[/latex]. Если [latex]x = 0[/latex] находится в области определения преобразованной функции, тогда будет найдена точка пересечения с осью y путем вычисления [latex]f\left(0\right).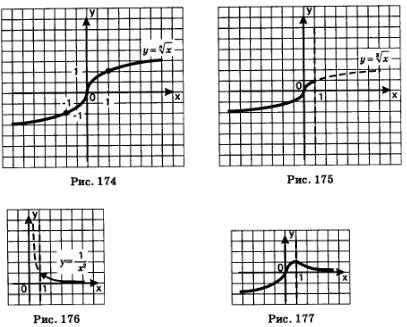 [/latex] If [latex] y=0[/latex] находится в диапазоне, то будет пересечение по оси x, и мы решаем [latex]f\left(x\right)=0.[/latex]
[/latex] If [latex] y=0[/latex] находится в диапазоне, то будет пересечение по оси x, и мы решаем [latex]f\left(x\right)=0.[/latex]
Пример 3. Перехваты преобразований Даже корневые функции
Найдите точки пересечения по осям x и y для
a. [латекс]г\влево(х\вправо)=\sqrt[\leftroot{1}\uproot{2}4]{3-2x}.[/латекс]
б. [латекс]ч\влево(х\вправо)=-3\sqrt[\leftroot{1}\uproot{2}4]{x}.[/latex]
c. [latex]f\left(x\right)=\sqrt[\leftroot{1}\uproot{2} ]{x+3}+1.[/latex]
Показать решение
Попробуйте #1
Найдите область определения, диапазон и точки пересечения четвертой корневой функции, сдвинутой на 2 единицы вправо и на 1 единицу вниз.
Показать решение
Попробуйте #2
Найдите домен, точки пересечения по оси X и оси Y для [latex]g\left(x\right)=\sqrt[\leftroot{1}\uproot{2} ]{7-0,5 x}.[/latex]
Показать решение
Конечное поведение функций с четным корнем
Последнее свойство, которое необходимо изучить для функций с четным корнем и их преобразований, — это конечное или долгосрочное поведение. Поскольку домен является только частью действительных чисел, необходимо определить только поведение влево или вправо в зависимости от того, движется ли домен к минус бесконечности или плюс бесконечности.
Поскольку домен является только частью действительных чисел, необходимо определить только поведение влево или вправо в зависимости от того, движется ли домен к минус бесконечности или плюс бесконечности.
Пример 4. Поведение конца горизонтально отраженной функции четного корня
Определите поведение конца [латекс]k\left(x\right)=\sqrt[\leftroot{1}\uproot{2}6]{2 -x}.[/latex]
Показать решение
Свойства нечетных корневых функций
Нечетные корневые функции не изменяют свои домены и диапазоны при преобразованиях, поскольку они определены на [латекс]\левый(-\infty,\infty\правый).[/латекс] Однако с горизонтальным и сдвиги по вертикали, ожидается, что точки пересечения изменятся, и если есть горизонтальное или вертикальное отражение, то может быть достигнуто конечное поведение.
Пример 5. Свойства отраженной функции нечетного корня
Определить домен, диапазон, точку пересечения по оси x, точку пересечения по оси y и конечное поведение функции [latex]f\left(x\right)=\sqrt[\leftroot {1}\uproot{2}3]{3-x}+1.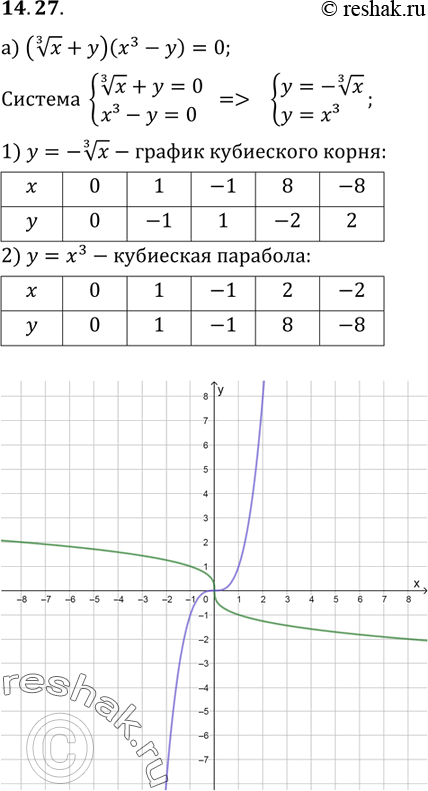 [/latex]
[/latex]
Показать решение
Ключевые понятия
- Корневые функции имеют крутой наклон вблизи начала координат, а затем медленно растут.
- Домен, диапазон, перехваты и конечное поведение могут измениться при преобразовании даже корневых функций.
- Перехваты могут не существовать для всех преобразованных четных корневых функций. г.
- Только одна сторона конечного поведения имеет смысл для трансформированных четных корневых функций.
- Домен и диапазон преобразованных функций нечетных корней остаются [latex]\left(-\infty,\infty\right)[/latex]
- Поведение перехватов и концов может измениться при преобразовании нечетных корневых функций. Тем не менее, будут перехваты и [latex]x[/latex] и [latex]y[/latex], и конечное поведение должно учитываться как справа, так и слева.
Примеры задач, 4.8
Примеры задач, 4.8 8
8Пример задачи: #8, урок 4.8
Используйте метод Ньютона, чтобы приблизить заданное число правильно до восьми знаков после запятой: | Данная задача: #8, Урок 4.8 | |||||||
| С помощью простой алгебры мы можем получить это в набор уравнений, равный нулю. | ||||||||
| Нам также нужна производная, чтобы Можно использовать метод Ньютона. | ||||||||
| Мы используем метод Ньютона, содержащийся в формуле выше. Я использовал электронную таблицу для расчета. Мы пришли к 8-значному точность, когда два последовательных значения для x согласуются все 8 цифр. Приблизительное значение: 2,682695795 |
Пример задачи, №12, урок 4.8
Используйте метод Ньютона, чтобы найти все корни уравнение правильно до восьми знаков после запятой. Для начала нарисуйте график найти начальные приближения. | Данная задача, #12, урок 4.8 |
| Упростим уравнение на умножив левую часть, а затем умножив обе части на знаменатель в правой части. | |
Строим график левой части
приведенного выше уравнения.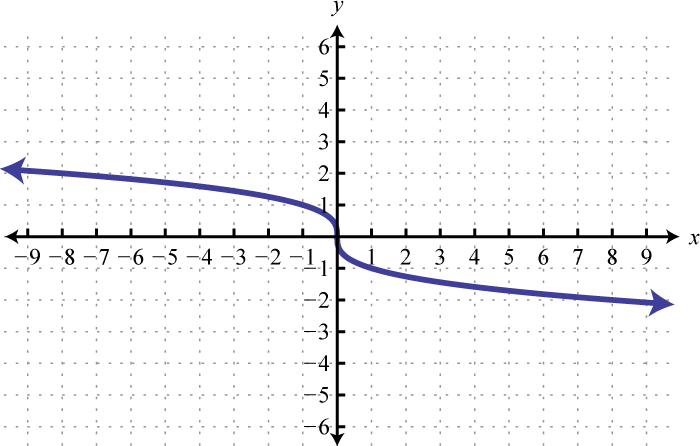 3″ nowrap=»nowrap» valign=»bottom»> 3″ nowrap=»nowrap» valign=»bottom»>-62,8224 |
Пример задачи, №18, урок 4.8
Используйте метод Ньютона, чтобы найти все корни уравнение правильно до восьми знаков после запятой. Для начала нарисуйте график найти начальные приближения. г. | Пример задачи, №18, урок 4.8 | |||||||||||||||||||||||||||||||||||||||
Переставляем члены так, чтобы решения уравнение будет x — точки пересечения на графике. Мы также вычисляем производную для использования с Ньютоном. Метод. | ||||||||||||||||||||||||||||||||||||||||
Строим график левой части приведенного выше
уравнение. Кажется, есть 2 места, где этот график имеет значение
нуль. Кажется, примерно -2 и 1,3. Заметим, что домен ограничен [-3,3]. | ||||||||||||||||||||||||||||||||||||||||
| Мы используем метод Ньютона, содержащийся в формуле выше. Я использовал электронную таблицу для расчета. Мы пришли к 8-значному точность, когда два последовательных значения для x согласуются все 8 цифр. Приближение для 1-го корня: -1,98982601 | |||||||||||||||||||||||||||||||||||||||
| Аппроксимация для 2-го корня это: 1.2208 |
1, 3, 5, 11, 17 | |
Использование радикалов в функциях — алгебра среднего уровня
Корни и радикалы
Цели обучения
К концу этого раздела вы сможете:
- Оценивать радикальную функцию
- Найдите область определения радикальной функции г.
- Радикальные функции графа
Прежде чем приступить к работе, пройдите этот тест на готовность.
- Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).
- Для оценки
Если вы пропустили эту проблему, просмотрите (рисунок).
- График Укажите область определения и область значений функции в интервальной записи.
Если вы пропустили эту проблему, просмотрите (рисунок).
Вычисление радикальной функции
В этом разделе мы продолжим нашу предыдущую работу с функциями, включив в нее радикалы. Если функция определяется подкоренным выражением, мы называем ее подкоренной функцией.
Функция квадратного корня — это
Функция кубического корня — это
Функция радикала
Функция радикала — это функция, которая определяется выражением радикала.
Чтобы вычислить радикальную функцию, мы находим значение f ( x ) для заданного значения x точно так же, как мы делали в нашей предыдущей работе с функциями.
Для функции найти ⓐ ⓑ
ⓐ
ⓑ
Поскольку квадратный корень из отрицательного числа не является действительным числом, функция не имеет значения по адресу
Для функции find ⓐ ⓑ
ⓐⓑ нет значения по адресу
Для функции find ⓐ ⓑ
ⓐ ⓑ нет значения в
Мы следуем той же процедуре для вычисления кубических корней.
для функции находки ⓐ ⓑ
ⓐ
ⓑ
Для функции Найти ⓐ ⓑ
ⓐⓑ
для функции ⓐ ⓑ
ⓐⓑ
для функции ⓐ
ⓐⓑ
для функции ⓐ
ⓐⓑ
для функции ⓐ
ⓐⓑ
.1815
ⓐ
ⓑ
Следующий пример имеет корни четвертой степени.
Для функции find ⓐ ⓑ
ⓐ
ⓑ
ⓐⓑ
Для поиска функции ⓐ ⓑ
ⓐⓑ
Найдите область определения радикальной функции
Чтобы найти область определения и область значений радикальной функции, мы используем наши свойства радикалов. Для радикала с четным индексом мы сказали, что подкоренная часть должна быть больше или равна нулю, поскольку четные корни отрицательных чисел не являются действительными числами. Для нечетного индекса подкоренной может быть любое действительное число. Мы повторяем свойства здесь для справки.
Для радикала с четным индексом мы сказали, что подкоренная часть должна быть больше или равна нулю, поскольку четные корни отрицательных чисел не являются действительными числами. Для нечетного индекса подкоренной может быть любое действительное число. Мы повторяем свойства здесь для справки.
Свойства числа
Когда n является четным числом и:
- тогда является действительным числом.
- тогда не настоящее число.
Когда n является нечетным числом , это действительное число для всех значений от до .
Итак, чтобы найти область определения радикальной функции с четным индексом, мы устанавливаем подкоренное число больше или равным нулю. Для нечетного радикала индекса подкоренной может быть любое действительное число.
Домен радикальной функции
Когда индекс радикала равен даже , подкоренное число должно быть больше или равно нулю.
Когда индекс радикала равен нечетному , подкоренным может быть любое действительное число.
Найдите область определения функции. Запишите область определения в интервальной записи.
Поскольку подкоренная часть функции имеет четный индекс с индексом 2, мы знаем, что подкоренная часть должна быть больше или равна 0. Мы устанавливаем подкоренную часть больше или равной 0, а затем решаем найти домен.
Область определения состоит из всех значений, и мы запишем ее в интервальной записи как
Найдите область определения функции, Запишите область в интервальной записи.
Найдите домен функции, Запишите домен в интервальной записи.
Найдите домен функции, Запишите домен в интервальной записи.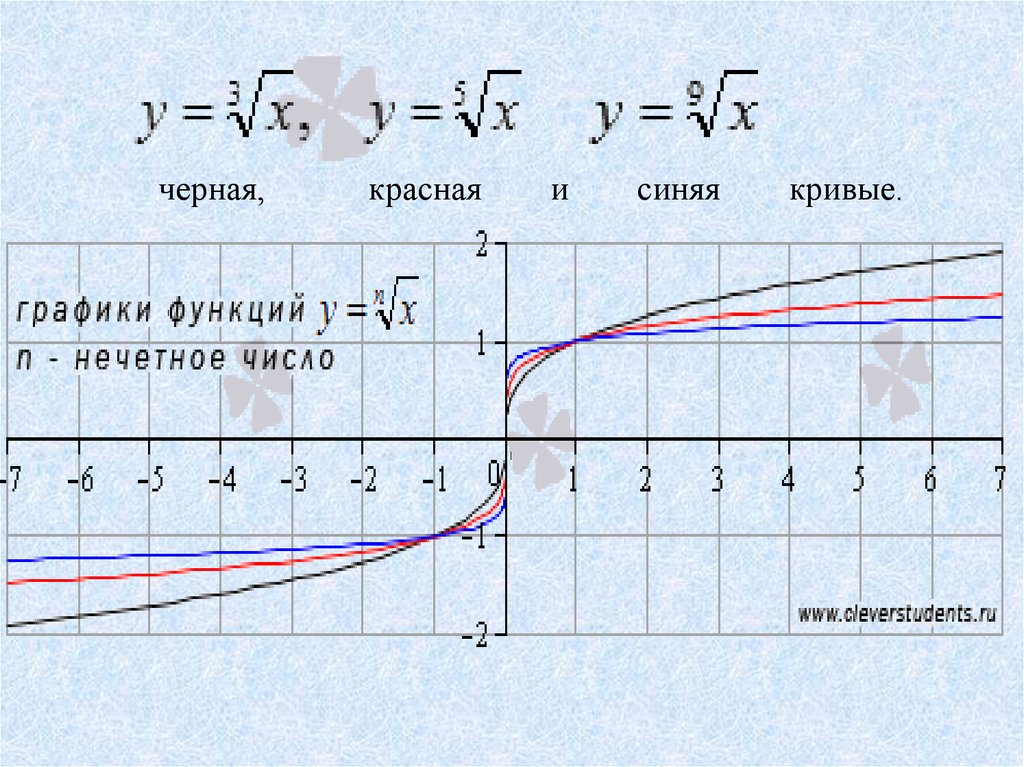
Так как функция имеет радикал с индексом 2, который является четным, мы знаем, что радикал должен быть больше или равен 0.
Подкоренное число не может быть равно нулю, так как числитель не равен нулю.
Чтобы быть больше нуля, знаменатель должен быть положительным, поскольку положительный числитель. Мы знаем, что положительное, деленное на положительное, является положительным.
Ставим и решаем.
Кроме того, поскольку подкоренное число является дробью, мы должны понимать, что знаменатель не может быть равен нулю.
Решаем найти значение, которое необходимо исключить из домена.
Объединив это, мы получим домен is и запишем его как
Найдите область определения функции. Запишите область определения в интервальной записи.
Найдите домен функции, Запишите домен в интервальной записи.
В следующем примере используется кубический корень, поэтому он потребует другого мышления.
Найдите область определения функции.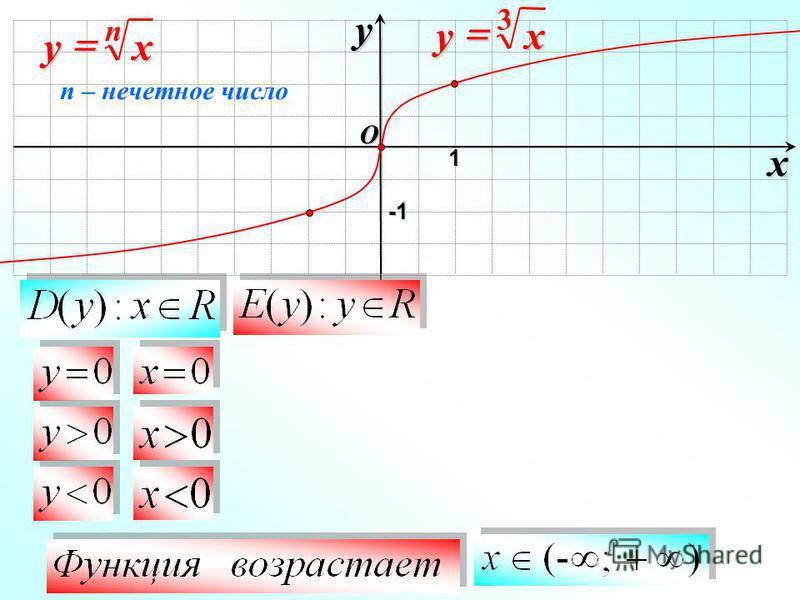 Запишите область определения в интервальной записи.
Запишите область определения в интервальной записи.
Поскольку у функции есть радикал с индексом 3, что является нечетным, мы знаем, что радикал может быть любым действительным числом. Это говорит нам, что домен представляет собой любое действительное число. В интервальных обозначениях мы пишем
Область определения состоит из всех действительных чисел, и мы запишем ее в интервальной записи как
Найдите область определения функции, Запишите область определения в интервальной записи.
Найдите домен функции, Запишите домен в интервальной записи.
График радикальной функции
Прежде чем построить график любой радикальной функции, мы сначала находим область определения функции. Для функции индекс четный, поэтому подкоренное число должно быть больше или равно 0,
Это говорит нам о домене, и мы запишем это в интервальной нотации как
Ранее мы использовали точечный график для построения графика функции. Мы выбрали значения x , подставили их и затем создали диаграмму. Обратите внимание, что мы выбрали точки, которые являются идеальными квадратами, чтобы упростить извлечение квадратного корня.
Мы выбрали значения x , подставили их и затем создали диаграмму. Обратите внимание, что мы выбрали точки, которые являются идеальными квадратами, чтобы упростить извлечение квадратного корня.
Как только мы увидим график, мы сможем найти диапазон функции. и -значения функции больше или равны нулю. Тогда диапазон равен
Для функции
ⓐ найти домен ⓑ построить график функции ⓒ использовать график для определения диапазона.
ⓐ Поскольку подкоренное число имеет индекс 2, мы знаем, что подкоренное число должно быть больше или равно нулю. Если тогда Это говорит нам, что домен состоит из всех значений и записан в виде интервала как
ⓑ Чтобы построить график функции, мы выбираем точки в интервале, которые также дадут нам подкоренное выражение, из которого будет легко извлечь квадратный корень.
ⓒ Глядя на график, мы видим y -значения функции больше или равны нулю. Тогда диапазон будет
Тогда диапазон будет
Для функции ⓐ найти домен ⓑ построить график функции ⓒ использовать график для определения диапазона.
ⓐ домен:
ⓑ
ⓒ диапазон:
Для функции ⓐ найти домен ⓑ построить график функции ⓒ использовать график для определения диапазона.
ⓐ домен:
ⓑ
ⓒ диапазон:
В нашей предыдущей работе по построению графика функций мы построили график, но не график функции. Мы сделаем это сейчас в следующем примере.
Для функции ⓐ найти домен ⓑ построить график функции ⓒ использовать график для определения диапазона.
ⓐ Так как радикал имеет индекс 3, мы знаем, что радикал может быть любым действительным числом. Это говорит нам, что домен состоит из всех действительных чисел и записан в виде интервала как
ⓑ Чтобы построить график функции, мы выбираем точки в интервале, которые также дадут нам подкоренное выражение, из которого будет легко извлечь кубический корень.
ⓒ Глядя на график, мы видим y -значения функции — все действительные числа. Тогда диапазон будет
Тогда диапазон будет
. Для функции
ⓐ найти домен ⓑ построить график функции ⓒ использовать график для определения диапазона.
ⓐ домен:
ⓑ
ⓒ диапазон:
Для функции
ⓐ найти домен ⓑ построить график функции ⓒ использовать график для определения диапазона.
ⓐ домен:
ⓑ
ⓒ диапазон:
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с радикальными функциями.
- Область радикальной функции
- Область радикальной функции 2
- Нахождение области определения радикальной функции
Основные понятия
Практика ведет к совершенству
Оценка радикальной функции
В следующих упражнениях оцените каждую функцию.
найти
ⓐ
ⓑ
ⓐⓑ нет значения в
найти
ⓐ
ⓑ 9 18015
найтиⓑ
ⓐⓑ
find
ⓐ
ⓑ
find
ⓐ
ⓑ
ⓐⓑ
find
ⓐ
ⓑ
find
ⓐ
ⓑ
ⓐ ⓑ
find
ⓐ
ⓑ
find
ⓐ
ⓑ
ⓐⓑ
find
ⓐ
ⓑ
find
ⓐ
ⓑ
ⓐⓑ
find
ⓐ
ⓑ
For the function
find
ⓐ
ⓑ
ⓐⓑ
For the function
find
ⓐ
ⓑ
For the function
find
ⓐ
ⓑ
ⓐⓑ
для функции
Найти
ⓐ
ⓑ
Найти домен в Radical Function 9184
Найти домен radical функции 9184
Найти домен radical function 9184 Найти Dradical Function 9184 . График радикальных функций В следующих упражнениях ⓐ найдите область определения функции ⓑ постройте график функции ⓒ используйте график для определения диапазона. ⓐ domain: ⓑ ⓒ ⓐ domain: ⓑ ⓒ ⓐ domain: ⓑ ⓒ ⓐ domain: ⓑ ⓒ ⓐ domain: ⓑ ⓒ ⓐ domain: ⓑ ⓒ ⓐ domain: ⓑ ⓒ ⓐ domain: ⓑ ⓒ ⓐ Домен: ⓑ ⓒ ⓐ Домен: ⓑ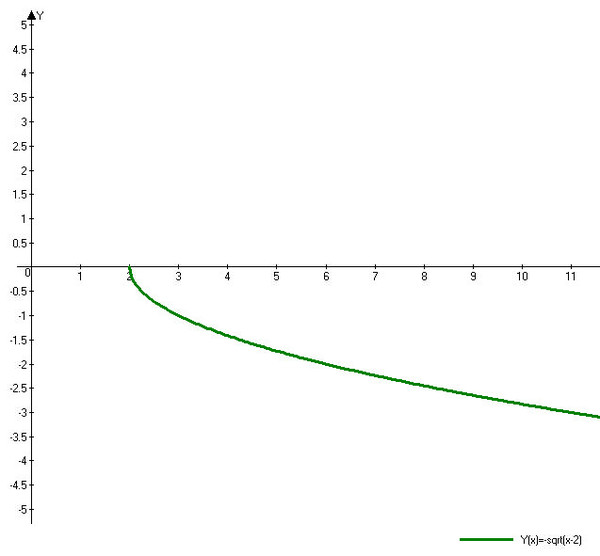 область в интервальной записи.
область в интервальной записи.
ⓑ
181815151515ⓑ
18181815151515ⓑ
1815151515
.


 Если нет вертикального отражения, диапазон будет от этого значения до бесконечности, а если есть вертикальное отражение, диапазон будет от минус бесконечности до этого значения.
Если нет вертикального отражения, диапазон будет от этого значения до бесконечности, а если есть вертикальное отражение, диапазон будет от минус бесконечности до этого значения.
 4-4″ nowrap=»nowrap» valign=»bottom»>1
4-4″ nowrap=»nowrap» valign=»bottom»>1 5Е-08
5Е-08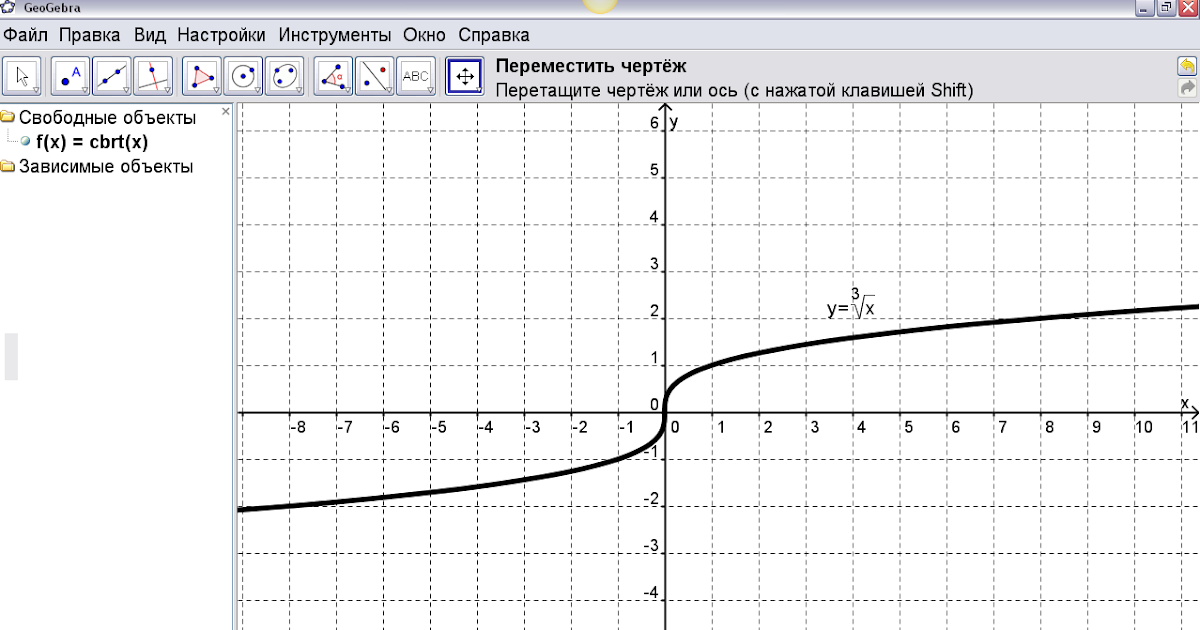 49432
49432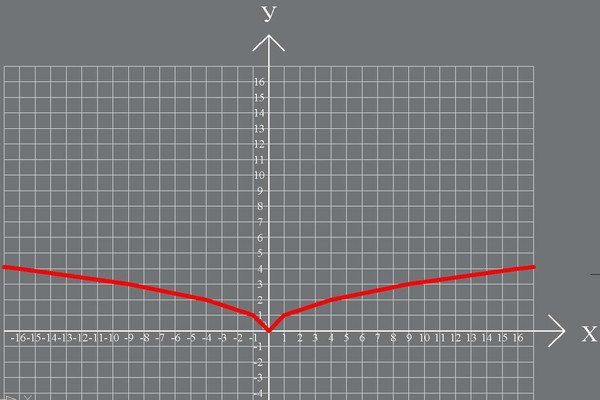 063406
063406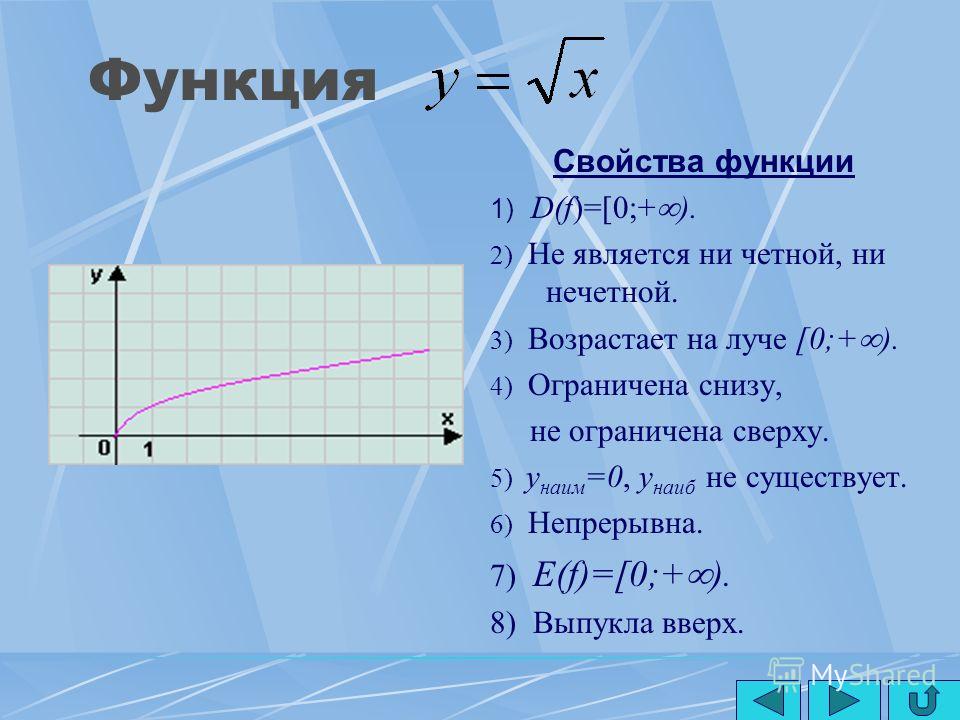 063894
063894