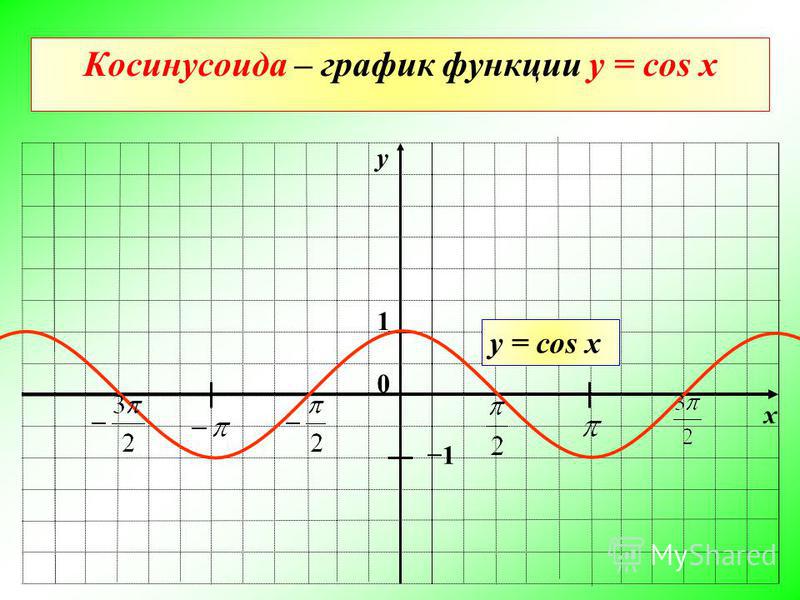
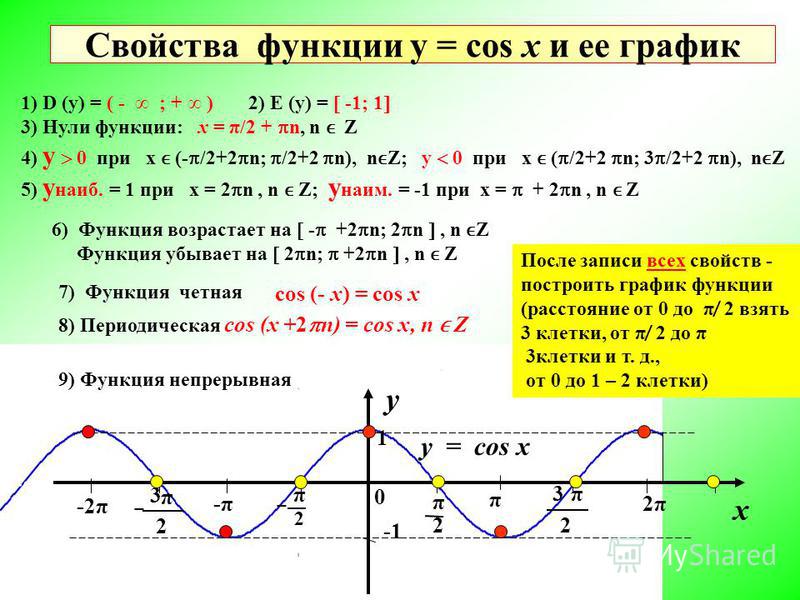
Функция y=cos х, её свойства и график
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Презентация с сайта: http://le-savchen.ucoz.ru
C
12·3
12 3
B
12·5
20 5
?
A
A
B ctg B
B tg A
B cos A
sin A
cos90°
01
sin90°
12
3
√2/2
sin(π/4)
4
cos180°
-1
5
sin270°
-1
6 3)
sin(π/
√3/2
7
√3/2
cos(π/6)
cos360°
18
9
ctg(π/6)
-1 2)
10
sin(3π/
11
cos(2π)
1
12
cos(‒π)
-1
13
tg(π/4)
1
0 2)
14
cos(-π/
15
1/2
cos(π/3)
☺
I
II
III
II
Построение графика функции y = cosx с
применением тригонометрического круга
p — шесть клеток
2p
5p 3
6
p
2
II
Ось
p
y
p
3
I
p
6
косинусов
III
-1
-5p
6 -2p
-p
3 2
1
0
IY p
-p 6
3
0
1
-p
2
-p
-5p -2p
3
6
III
p
-p
3
-p
6
IY
0
-1
p x
2
p
p
6
3
I
2p
3
5p
6
II
p
III
2
Создание шаблона графика
функции y = cosx
p
cos0 = 1
p
cos 2 = 0
cosp = -1
— +
— +
Ось
-p -1косинусов
0
-p
cos 2 = 0
0
1
-p
2
сos(-p) = -1
p — три клетки
y
-5p
2
-2π
-3p
2
-π
-p
2
1
0
p
2
π
3p
2
-1
Полный круг
2π
5p
2
x
Постройте график функции:
5p
)
№ 203.
в) y cos( x ) ; г) y cos( x 6
3
— три клетки
p
1-2
p
y cos x
-5p
2
-2π
-3p
2
-π
-p
2
y
1
0
p
2
p
3
-1
5p
6
π
3p
2
2π
5p
2
x
Постройте график функции:
1
3-4
№ 204. в) y cos x
; г) y cos x 1,5
2
— три клетки
p
y cos x
-5p
2
y
-2π
-3p
2
-π
-p
1
2 1,52
1
0
-1
p
2
π
3p
2
2π
5p
2
x
Постройте график функции:
№ 205. а) 3) y cos( x
5
2) y cos( x
1) y cos x
p
2
p
2
) 1
)
p — три клетки
y
-5p
2
-2π
-3p
2
1
-π
-p
2
1
0
-1
p
2
p
2
π
3p
2
2π
2
x
Назовите функции,
графики которых
изображены на рисунке:
1
y
4
y cos x+2
y cos x
3
2
+2
-5p
2
-2π
-3p
2
-π
-p
2
1
0
-1
-2
-3
-4
p
2
π
3p
2
2π
5p
2
x
Назовите функции,
графики которых
изображены на рисунке:
2
y
4
y sin x
3
p
y sin( x )
4
2
-5p
2
-2π
-3p
2
-π
-p
2
1
0
-1
-2
-3
-4
p
2
π
3p
2
2π
5p
2
x
Назовите функции,
графики которых
изображены на рисунке:
3
y
4
y cos x 2p )
3
(
-5p
2
-2π
-3p
2
-π
y cos x
3
2
-p
2
1
0
-1
-2
-3
-4
p
2
π
3p
2
2π
5p
2
x
Назовите функции,
графики которых
изображены на рисунке:
4
y
4
y x2
3
2
-5p
2
-2π
-3p
2
-π
-p
2
1
0
p
2
π
3p
2
2π
5p
2
-1
-2
-3
-4
2
p
y (x ) — 2
x
Назовите функции,
графики которых
изображены на рисунке:
5
y
4
3
y cos(x 2p )+3
3
2
-5p
2
-2π
-3p
2
-π
-p
2
1
0
p
2
π
3p
2
2π
5p
2
-1
-2
-3
-4
y cos x
x
Назовите функции,
графики которых
изображены на рисунке:
6
4p
y x
3
y
4
y x
3
2
-5p
2
-2π
-3p
2
-π
-p
2
1
0
p
2
π
3p
2
2π
-1
2p
y x
-3
3
-2
-3
-4
3p
y x
-4
4
5p
2
x
Назовите функции,
графики которых
изображены на рисунке.
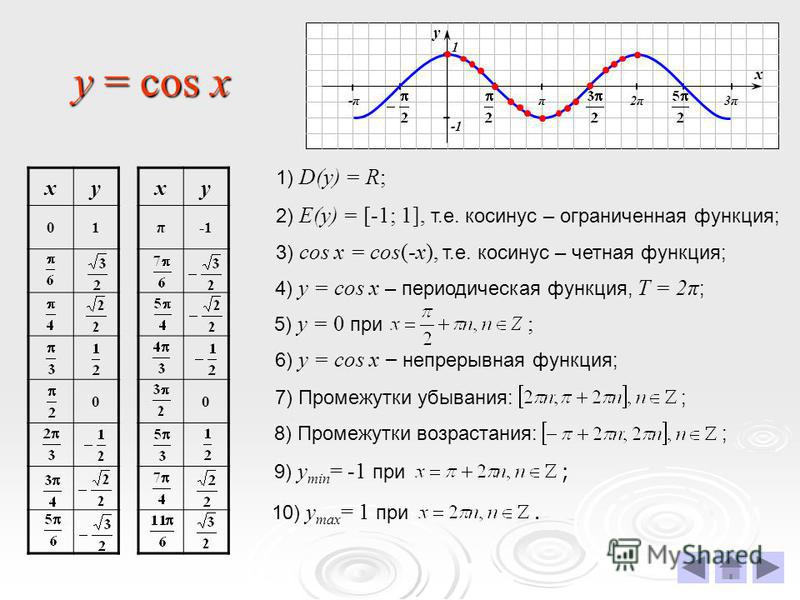
I
Графиком функции y = cosx является
p
y = cosx = sin(x+ )
y = sinx
2
p — три клетки
y
-5p
2
-2π
-3p
2
-π
-p
2
1
0
-1
p
2
π
3p
2
2π
5p
2
x
6-7
№ 206. Найдите наименьшее и наибольшее
значения функции y = cosx:
p
p 2p
а) на отрезке ; ; в) на луче ; ;
6
6 3
— шесть клеток
p
yнаиб.
-p
2
yнаим.
y
1
0
p
2
p
p
6
3
π
2p
3
3p
2
2π
3p
3
-1
p
3
p
yнаиб. y cos
.
6
2
6
Ответ.
2p
1
2p
yнаим. y cos
.
3
2
3
1
3
yнаиб.
. yнаим. .
2
2
x
№ 206. Найдите наименьшее и наибольшее
значения функции y = cosx:
6-7
p
p 2p
а) на отрезке ; ; в) на луче ; ;
6
6 3
— шесть клеток
p
yнаиб.
-p
2
y
1
p
0
yнаим.
2
π
3p
2
p
6
-1
Ответ.
yнаиб. 1.
yнаим. 1.
2π
x
ЕГЭ. Найдите наименьшее значение функции
5p
5p 17p
.
y 2 cos x
, если x ;
8
12
4 12
Решение.
Комбинированное задание с применением
свойств числовых неравенств.
Замена:
5p
t.
x
12
5p
17p
x
,
4
12
5p
,
12
5p 5p5p
5p11p17p 5p
x t ,
,
4 12 3
12 6 12 12
20
5yp = cost5pи найдем
11
22pp
Строим график функции
x
,,
123 значения,
12 если
12
6
наибольшее и наименьшее
ЕГЭ. Найдите наименьшее значение функции
5p
5p 17p
.
y 2 cos x
, если x ;
12
4 12
p
pp 5p 11p 11p
5
2p .
Решение.
2 p t t .
6
33 3 6 6
— шесть клеток
p
yнаиб.
yнаим.
-p
2
y
1
p
0
2
π
pp
3
3p
6
2π
2
5p
3
11p
6
x
ЕГЭ.
Найдите наименьшее значение функции5p
5p 17p
.
y 2 cos x
, если x ;
12
4 12
5p
11p
Решение.
t
.
3
6
По графику определили: yнаим. cost yнаиб. .
yнаим. cos 5p cos 2p p cos p 1 .
3
3 2
3
yнаиб. cos 11p cos 2p p cos p 3 .
6
6
2
6
3
1
1 2cost 3
·2
cost
2
2
Ответ: наименьшее значение функции равно 1.
Каким вопросам был посвящен урок?
Чему научились на уроке?
№39, №41, 42, 48
1. Мордкович А.Г. Алгебра и начала анализа.
10-11 класс.: В двух частях. Ч.1: Учеб. для
общеобразоват учреждений. – 3-е изд.
испр. – М.: Мнемозина, 2002.
2. Алгебра и начала анализа. 10-11 класс.:
Задачник для общеобразоват.
учреждений / А. Г. Мордкович, Л.О.
Денищева, Т.Н. Мишустина, Е.Е.
Тульчинская. – 2-е изд., испр. – М.:
Мнемозина, 2004.
3. Единый государственный экзамен: математика :
2004-2005: контрол. Измерит. Материалы / [Л.
О.Денищева, Г. К. Безрукова, Е. М. Бойченко и
др.; под ред. Г. С. Ковалевой]; М-во
образования и науки Рос. Федерации,
Федерал. служба по надзору в сфере
образования и науки. — М.: Просвещение, 2005.
Все рисунки в презентации авторские.
English Русский Правила
алгебраическое предварительное исчисление — график $y = a\cos(bx+c)+d$
Задавать вопрос
спросил
Изменено 5 лет, 5 месяцев назад
Просмотрено 223 раза
Прилагается график $y = a\cos(bx+c)+d$, где $a>0$, $b>0$ и $c>0$, а $c$ минимально возможное . Найдите $a + b + c + d$.
Мне трудно решить эту проблему.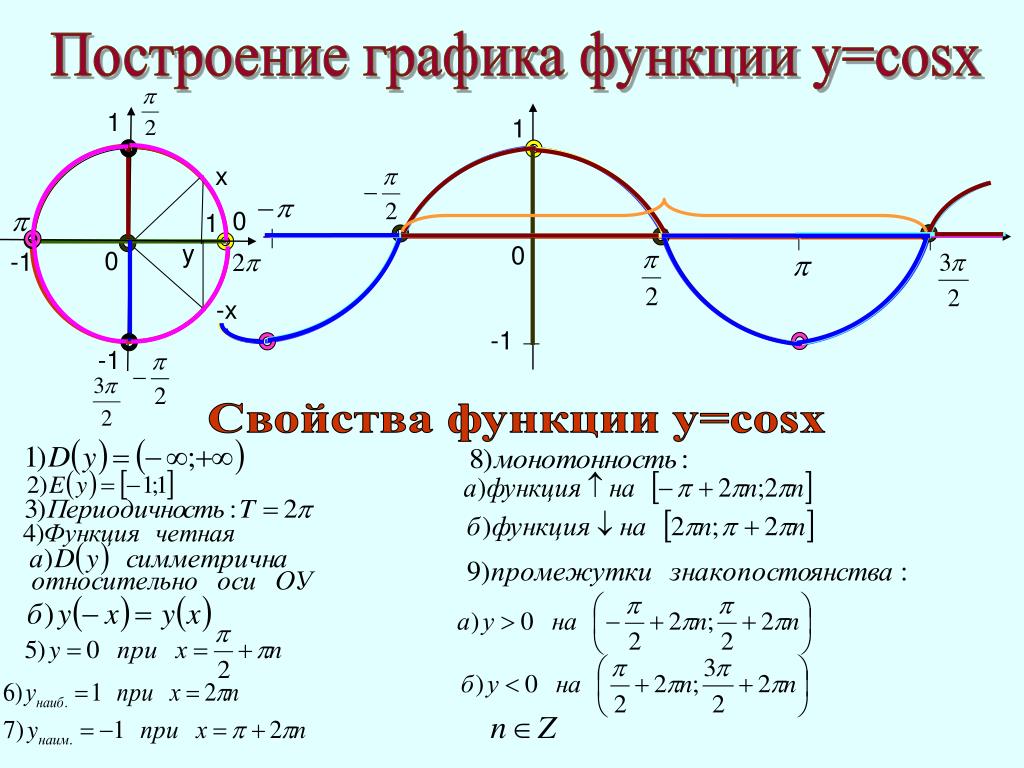
Во-первых, период кажется равным $3\pi$, а это означает, что $b=2/3$, а амплитуда, или a, равна 2 и $d=1$. Однако сдвиг косинуса по горизонтали кажется равным $3\pi/2$, что дает значение $c=9\pi/4$. Но когда я добавляю $a+b+c+d$, я получаю $11/3 + 9.\pi/4$, что не является правильным ответом. Есть ли значение c меньше, чем то, которое я нашел? Как?
- алгебра-предварительное исчисление
- тригонометрия
$\endgroup$
1
$\begingroup$
В исходный ответ внесены исправления из-за ошибок, на которые указал @zwim.
Обратите внимание, как он выглядит как «перевернутый» график косинуса, но с удвоенной амплитудой, периодом $3\pi$ вместо $2\pi$ и сдвинутым вверх на одну единицу?
Это означает, что уравнение может быть записано как
$$y=-2\cos\left(\frac{2}{3}x\right)+1\tag{1}$$
Однако это оговаривается, что $a>0$ и $c>0$, поэтому мы используем тождество
$$ \cos(\theta+\pi)=-\cos\theta $$
, чтобы переписать уравнение $(1) $ as
$$y=2\cos\left(\frac{2}{3}x+\pi\right)+1$$
Итак, решение $a=2,\,b=\frac{ 2}{3},\,c=\pi,\,d=1$.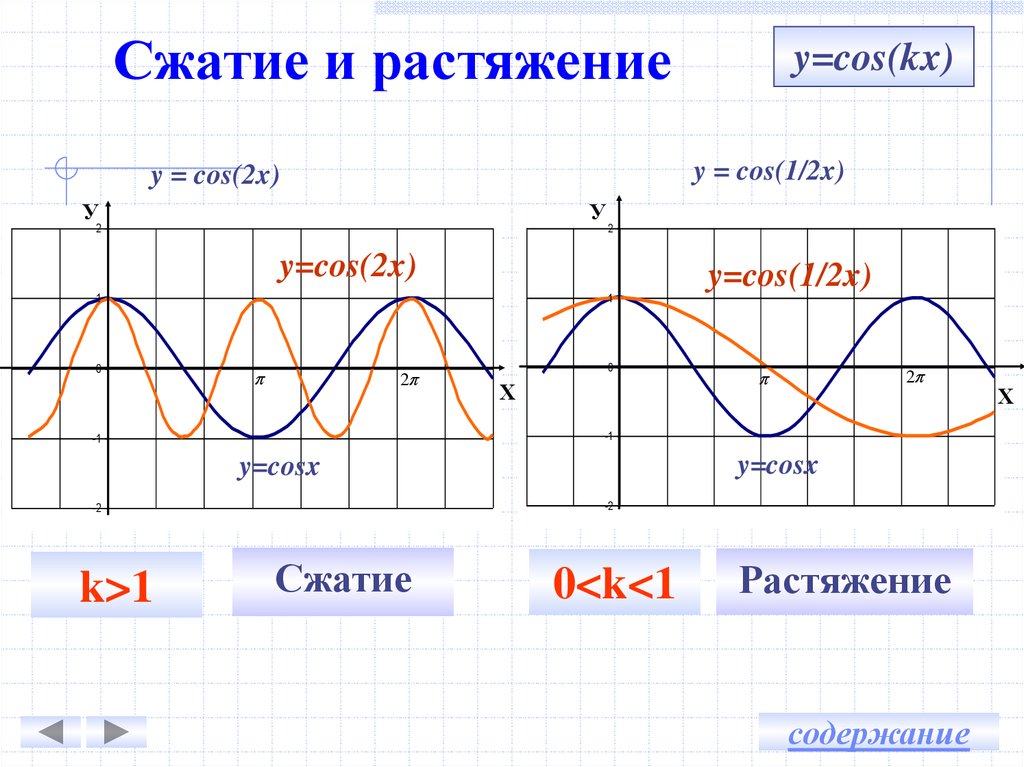
$\endgroup$
2
$\begingroup$
Сначала нам нужно найти среднюю линию графика, которая будет переменной $d$. Поскольку максимальное значение составляет $3$, а минимальное — $-1$, средняя линия равна: $$y=\frac{(3)+(-1)}{2} = \fbox{d = 1}$$
Можно также заметить, что два максимума кривой приходятся на: $-\frac {3\pi}{2}$ и $\frac{3\pi}{2}$, поэтому период функции равен $3\pi$. Что подразумевает: $$\frac{2\pi}{b}=3\pi \Longrightarrow b = \frac{2}{3} $$
Теперь возможны два следующих подхода:
1) Вы можете заметить, что график представляет собой «перевернутый» график косинуса (это приведет к тому, что $c$ будет равно $0$, что недопустимо, поскольку $c>0$).
или
2) Вы можете заметить, что график представляет собой сдвинутый график косинуса
Поскольку ближайший гребень волны находится в точке $-\frac{3\pi}{2}$, исходная функция косинуса должна была быть переместил $\frac{3\pi}{2}$ влево (до масштабирования по горизонтали на $b$).