Открытый урок на тему: «Обратные тригонометрические функции»
Тема урока: Обратные тригонометрические функции
Цель урока: знать определения арксинуса, арккосинуса, арктангенса, арккотангенса, графики этих функций, свойства аркфункций, связь с тригонометрическими функциями уметь находить значения обратных тригонометрических функций, решать простейшие уравнения, содержащие обратные тригонометрические функции графическим и функционально-графическим методом
воспитывать ответственность, аккуратность при построении графиков
развивать логическое мышление, математическую речь, умение работать в нужном темпе
Тип урока: формирования зун.
Методы ведения: Комбинированный урок.
Оборудование урока Презентация
ХОД УРОКА:
Организационный момент – 1 – 2 мин.
Приветствие учащихся.
Отметить отсутствующих.
II. Опрос по домашнему заданию
Какие тригонометрические функции вы знаете?
Какая тригонометрическая функция четная?
III.
Объяснение нового материала. Краткий конспект.
Функции y=arcsinx,y=arccosx,y=arctgx,y=arcctgx называются обратными
тригонометрическими функциями. Приставка «arc» означает обратный.
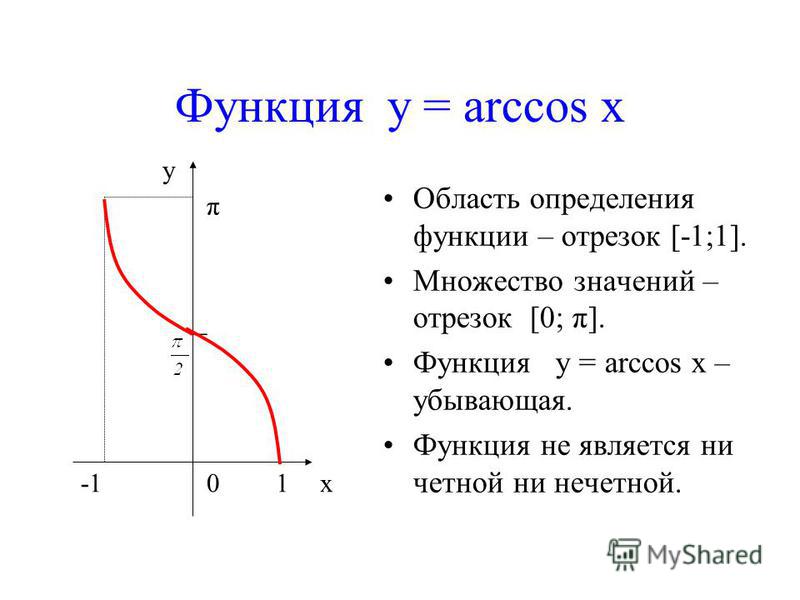
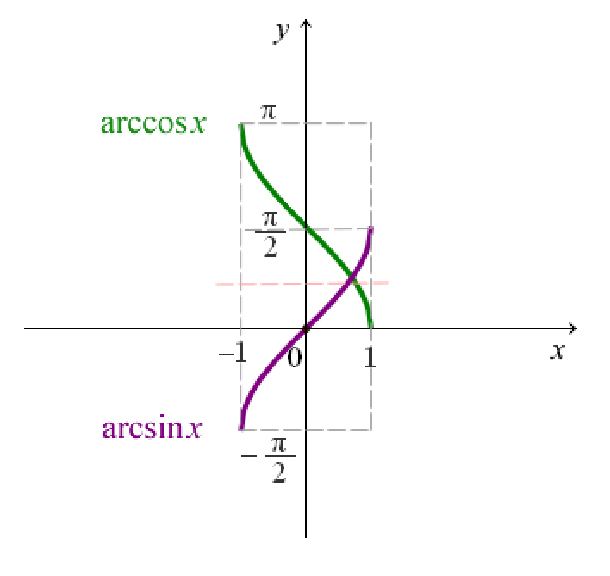
Функция y = arcsin x
По определению арксинуса числа для каждого x∈[−1;1] определено одно число y=arcsinx. Тем самым на отрезке [−1;1] задана функция y=arcsinx,−1≤x≤1
Функция y=arcsinx является обратной к функции
y=sinx, где −π/2≤x≤π/2
Поэтому свойства функции y=arcsinx можно получить из свойств функции
y=sinx
График функции y=arcsinx симметричен графику функции
y=sinx, где −π/2≤x≤π/2 относительно прямой y=x .
График функции y=arcsinx
Основные свойства функции y=arcsinx
1. Область определения — отрезок [−1;1]
2. Множество значений — отрезок [−π/2;π/2]
3. Функция y=arcsinx — возрастает.
4. Функция y=arcsinx является нечётной, так как
arcsin(−x)=−arcsinx
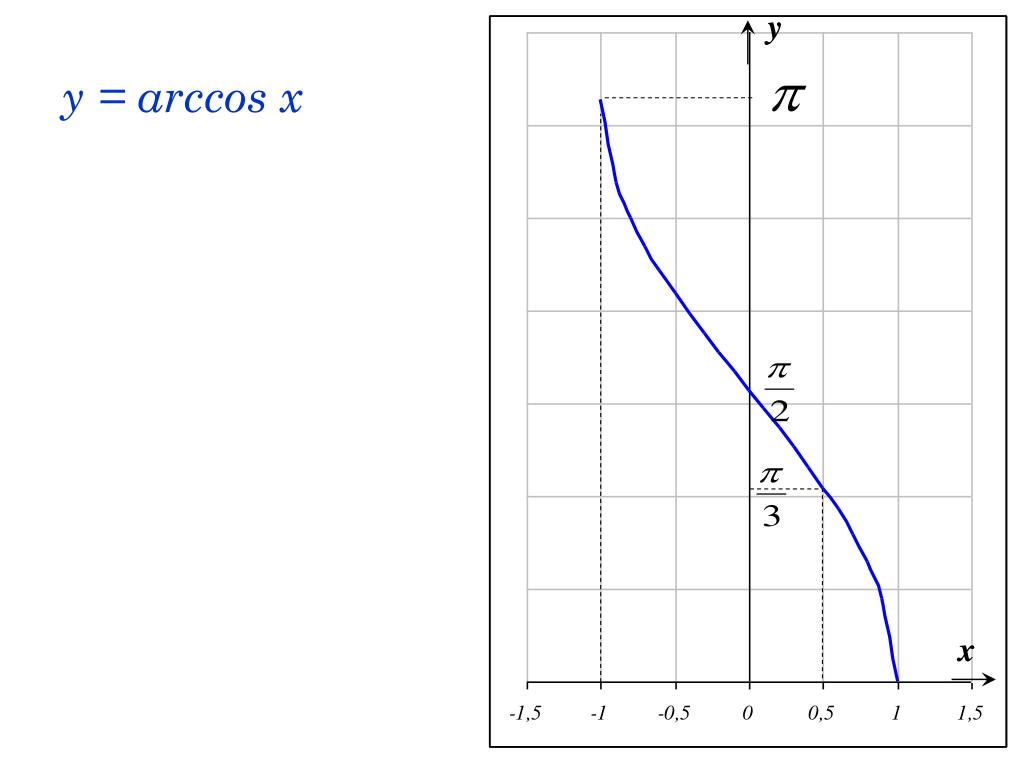
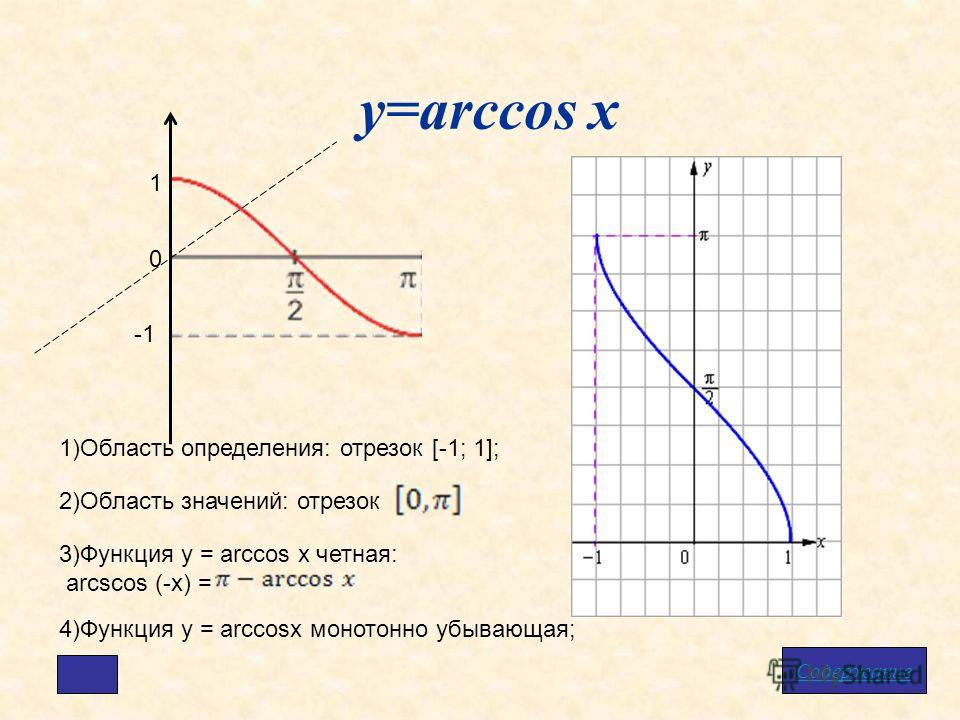
Функция y = arccos x
По определению арккосинуса числа для каждого x∈[−1;1] определено одно число y=arccosx.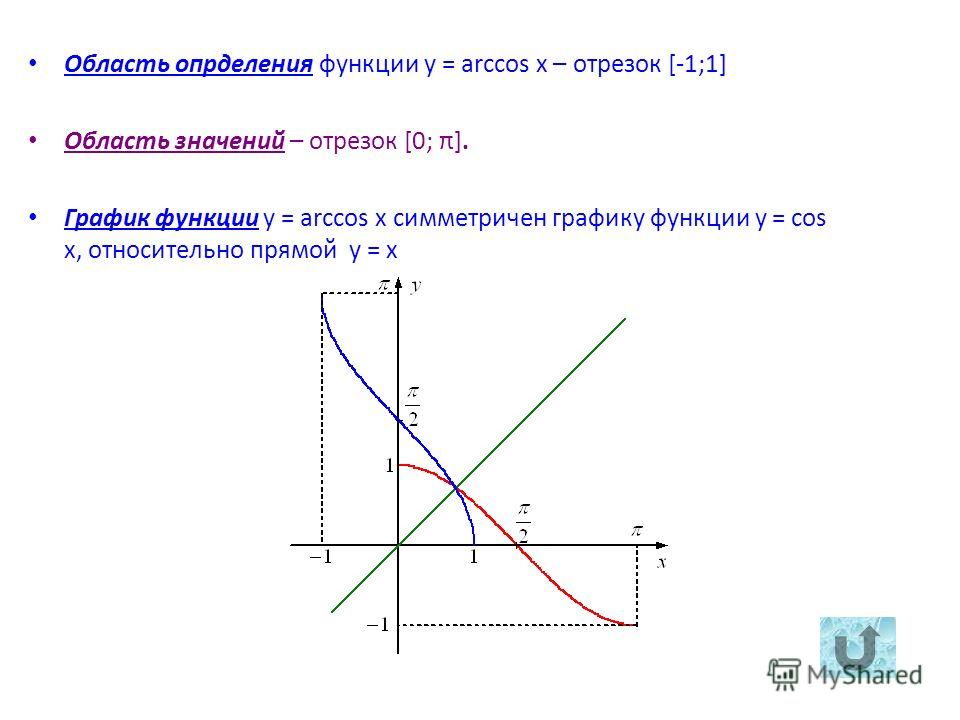
Тем самым на отрезке [−1;1] определена функция
y=arccosx,где −1≤x≤1.
Функция y=arccosx является обратной к функцииy=cosx,где 0≤x≤π
График функции y=arccosx симметричен графику функции y=cosx,где 0≤x≤π, относительно прямой y=x
Функция y=arccosx
Основные свойства функции y=arccosx
1. Область определения — отрезок [−1;1]
2. Множество значений — отрезок [0;π]
3. Функция y=arccosx убывает
Функция y = arctg x
По определению арктангенса числа для каждого действительного x определено одно число y=arctgx. Тем самым на всей числовой прямой определена функция y=arctgx,x∈R.
Эта функция y=arctgx является обратной к функции
y=tgx,где −π/2≤x≤π/2
График функции y=arctgx симметричен графику функции
y=tgx,где −π/2≤x≤π/2 относительно прямой y=x
График функции y=arctgx
Основные свойства функции y=arctgx
1. Область определения — множество R всех действительных чисел
2.
Множество значений — интервал (−π/2;π/2)
3. Функция y=arctgx возрастает.
4. Функция y=arctgx является нечётной, так как
arctg(−x)=−arctgx
Функция y=arcctgx
Поэтому, график функции y=arcctgx можно получить из графика функции
y=ctgx, x∈(0;π) с
помощью преобразования симметрии относительно прямой y=x.
Свойства функцииy=arcctgx
1. D(f)=(−∞;+∞)
2. E(f)=(0;π)
3. Функция не является ни чётной, ни нечётной, т.к. график функции не симметричен ни относительно начала координат, ни относительно оси y.
4. Функция убывает.
5. Функция непрерывна.
arcctga — это такое число из интервала (0;π), котангенс которого равен a
Итак, arcctga=t⇔{ctgt=a,0
Для арккотангенса имеет место соотношение, аналогичное для арккосинуса
arcctg(−a)=π−arcctga
1.Вычислите:
а) 2 arcsin √3/2 + arctg 1 + arccos (-√2/2) — 5π/3
б) 3 arccos √3/2+ arcctg (-1) + arcsin√3/2 — 19π/12
в) arcsin(sin /3)+ arcsin (- /2)
г)10cos(arctg( ))
2.
Вычислите:
а) sin(arcsin(-1/5))
б) sin( + arcsin 3/4)
в) 5 sin( + arcsin (-3/5)
г) cos(arccos(-2/3))
д) sin( /2+ arccos 1/3)
Рассмотреть решения примеров с обратными функциями:
Группа В
Пример 1: Найти sin(arccos ).Пусть arccos = , тогда 0≤ ≤ , соs = .
sin +cos =1. Учитывая, что 0≤ ≤ , sin = = = = .
Ответ: sin(arccos )= .
Пример 2: Вычислити
Заполнить таблицу ( проверка знания формул)
, |x| 1 | , |x| 1 |
, |x| 1 | , |x 1 |
, |x| | , |x| 1, x=/= 0 |
, |x| 1, x =/= 0 | , |x| |
, x=/= 0 | , x=/= 0 |
Закрепление нового материала:№ 85, 87, 88
Задание на дом §8№86
Литература: А.
Е. Абылкасымова и др. Алгебра и начала анализа 10, 11 классы.
Дидактический материал по алгебре и начала анализа для 10, 11 класов.
Преподаватель Бурковская Нина Дмитриевна
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
Интел и АМД — крупнейшие и наиболее известные производители центральных процессоров (ЦП) в мире. Обе компании имеют долгую историю в отрасли: Intel была основана в 1968 году, а AMD — в 1969 году. Несмотря на то, что они были основаны с разницей всего в год, эти две компании использовали очень разные подходы к проектированию и производству процессоров, что привело к разделению рынка компьютерных комплектующих на два основных направления.
Одним из наиболее очевидных различий между процессорами Интел и АМД является их архитектура. Именно она во многом влияет на то, какой будет на процессор цена, а также сложность его производства. Процессоры Intel традиционно используют архитектуру сложных вычислений с набором команд (CISC), ориентированную на повышение мощности процессоры при уменьшении потребляемой электроэнергии.
С другой стороны процессоры АМД обычно используют архитектуру вычислений с сокращенным набором команд (RISC), которая больше ориентирована на стоимость и простоту производства. Покупатели выбирают себе процессор исходя из конкретных задач, которые будут перед ним поставлены.
Главное отличие между двумя производителями
Ключевое различие между продуктами Intel и AMD заключается в их производственном процессе. Intel традиционно использует более продвинутый производственный процесс с меньшими транзисторами и более высокими тактовыми частотами. Это позволило ЦП Intel быть более энергоэффективными и быстрыми, чем варианты от AMD. Однако в последние годы AMD удалось сократить разрыв, используя более совершенный производственный процесс.
С точки зрения ценообразования товары АМД обычно считаются более доступными, чем варианты от Интел. Это связано с тем, что AMD традиционно сосредоточилась на производстве комплектующих, цена которых более доступная для среднего потребителя, в то время как Intel сосредоточилась на производстве оптимальных решений для разработчиков, графических дизайнеров.
Технические особенности
Когда дело доходит до производительности, ЦП Intel обычно считаются более быстрыми. Среди качественных отличительных особенностей:
- Более высокие тактовые частоты;
- Более совершенная архитектура;
- Большая энергоэффективность.
Такие CPU способны выполнять задачи, требующие высокого уровня вычислительной мощности, такие как игры и редактирование видео. Однако обычно считается, что процессоры AMD лучше купить для задач, требующих многозадачности и многопоточности таких, как рендеринг и научное моделирование. Среди главных преимуществ, которые можно отметить относительно ЦП AMD:
- Отличные показатели при рендеринге;
- Наличие высокопроизводительных, но доступных CPU;
- Подключение через стандартизированный сокет AM4.
Продукты обеих компаний обладают своими достоинствами. Процессоры Intel обычно считаются более быстрыми и энергоэффективными, в то время как процессоры AMD обычно считаются более доступными с точки зрения цены и лучшими для многозадачности.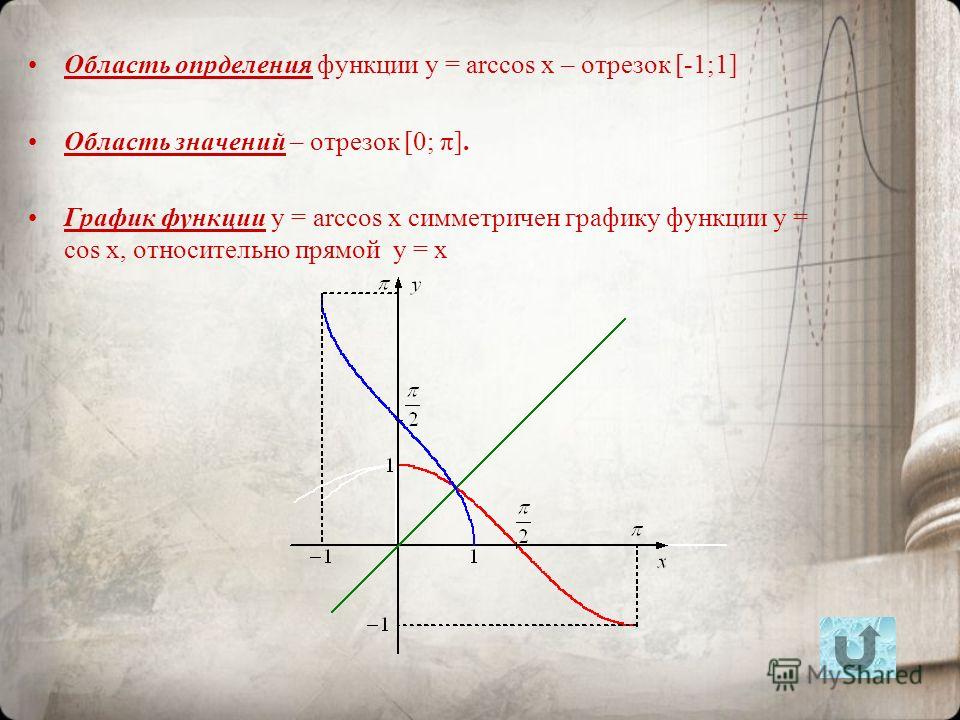
Каков правильный график sec(arccos(x))?
Недавно Шей задал вопрос на IntMath Forum:
У меня проблема с sec(arccos 5), и я понимаю, что sec является обратной величиной cos. Но если домен arccos равен [0,pi], то как это может быть 1/5?
Это выглядело интересно и напомнило мне о похожей проблеме, о которой я писал ранее, каков правильный график arccot x?.
Во-первых, я мягко поправил утверждение Шэя (указав, что диапазон arccos равен [0,pi], а не домену).
Затем я продолжил расследование вместе с ним. Вот еще информация.
Некоторый фон — арккосинус
ПРИМЕЧАНИЕ. Функция y = arccos( x ) записывается в большинстве учебников (и на вашем калькуляторе) как y = cos −1 ( x ) . Последнее обозначение мне не нравится по многим причинам (особенно потому, что студенты путают его с «обратным»), поэтому в этой статье я использую первое.
Arccos — это функция арккосинуса . То есть она работает «назад» по сравнению с функцией косинуса. Вы задаете ему отношение, и оно возвращает угол (тогда как для косинуса вы задаете угол, и он возвращает отношение).
Примеры — cos и обратный cos
cos(60°) = 0,5
arccos(0,5) = 60° , то
cos(arccos( x )) = x
и
arccos(cos( x )) = x
Но всегда ли это верно?
На самом деле нет.
График y = cos(arccos( x )) начинается с (−1,−1) и заканчивается на (1,1), как вы можете видеть ниже. Это не «полный» график, y = x , как утверждалось выше.
С другой стороны, график y = arccos(cos( x )) продолжается для всех значений x по пилообразной схеме, включающей π, следующим образом.
Очевидно, что ни один из двух приведенных выше графиков не является простой функцией y = x .
Почему это происходит?
Функция y = arccos( x ) определена только в области −1 ≤ x ≤ 1 (подробнее см. Обратные тригонометрические функции), поэтому следует, что косинус этой функции равен
y = cos(arccos( x )),
также должны быть определены только в этом домене.
Однако функция y = cos( x ) определена для всех x , поэтому, когда мы берем arccos этой функции,
он будет определен и для всех x .
Дополнительную информацию о домене функции функции см. в разделе Домен композиции (PDF), где указано:
Область определения f ◦ g — это множество всех действительных чисел x в области определения g , такое что g ( x ) находится в области определения f .
Вернемся к первоначальному вопросу.
Каков график
y = sec(arccos( x ))?Поскольку секущая функция определяется как:
, то
Выше мы узнали, что cos(arccos( x )) определяется только для −1 ≤ x ≤ 1 и имеет значение x в этом домене.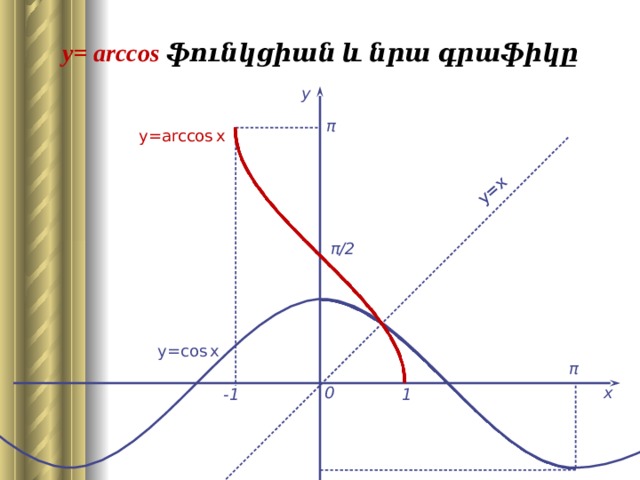
Итак, мы имеем:
для −1 ≤ x ≤ 1, за исключением x = 0.
Давайте теперь посмотрим, как это графически отображают некоторые программные пакеты.
Программные графы
y = sec(arccos( x ))Desmos ясно показывает, что домен имеет область −1 ≤ x ≤ 1, за исключением x = 0,
Это тот же результат, который дает JSXGraph:
Мой собственный Asvg-IM.js также дает тот же результат.
С другой стороны, Scientific Notebook дает нам следующее, с доменом все x , кроме x = 0. — со всеми значениями x , кроме 0, как и в Scientific Notebook.
Так какой график правильный?
В сообщении на форуме я сказал, что буду следить за этим с помощью Wolfram|Alpha. Я сделал, и они ответили:
Мы ценим ваши отзывы. После проверки наша внутренняя группа разработчиков считает, что указанный результат правильный:
.Домен arcCos дает комплексный результат всякий раз, когда x больше 1 или меньше -1, но Sec все еще может работать с комплексными числами для получения действительных значений.
Для получения дополнительной информации см. здесь.
Если вы по-прежнему не согласны, уточните, предоставив ссылки на источник конкретной информации, которую вы хотите увидеть.
(Вторая ссылка была не очень полезной.) Дело было не в том, что я был не согласен с их результатом, я был больше заинтересован в том, чтобы они сделали свой результат более ясным.
Arccos x от Wolfram|Alpha
При использовании запроса arccos x (без «sec») Wolfram|Alpha сначала выдает график с действительным знаком (с доменом −1 ≤ x ≤ 1), затем приводится следующий график, на котором показаны как действительные, так и мнимые части.
Это хорошо для тех, кто исследует функцию — дает реальный случай (тот, который чаще всего нужен студентам бакалавриата математики), затем следует воображаемый случай и ясно излагает, что происходит.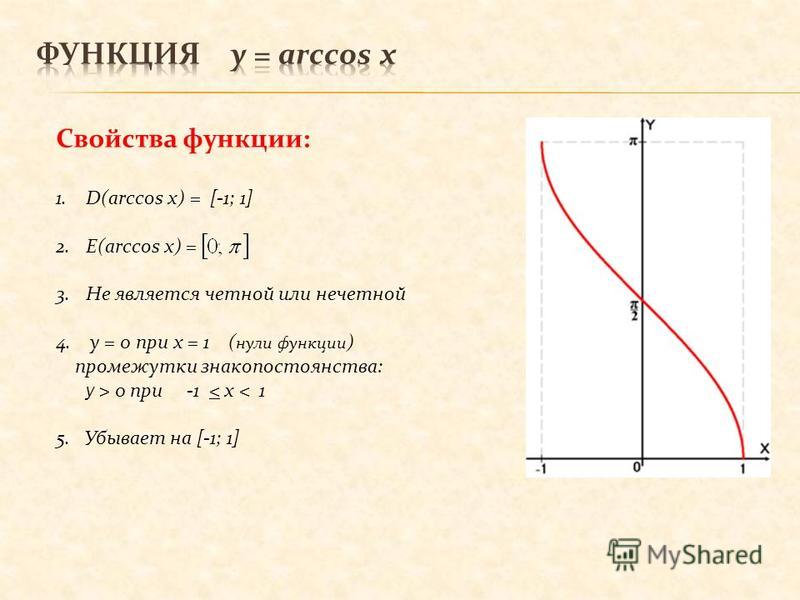
Имея это в виду, я ответил Wolfram|Alpha:
Спасибо, что обратили внимание на это — я очень ценю это.
Для результата W|A для arccos(x) реальный результат и комплексный результат четко разделены на 2 отдельных графиках.
Мне интересно, сделает ли тот же подход результат для sec(arccos(x)) более понятным. То есть, есть один график для случая, когда x является реальным (с доменом [-1,1], ≠ 0, и другой для случая, когда x является сложным (все x ≠ 0). Будет ли это по-прежнему быть математически обоснованным?
Мне ответили:
Спасибо за отзыв. Я передам это разработчикам.
До сих пор не было никаких изменений в результате для sec(arccos x).
Реальные свойства sec(arccos x)
Под графиком Wolfram|Alpha sec(arccos x) указаны некоторые «Свойства как реальная функция», а именно:
Заключение
Итак, это решение вопроса Шэя — если мы допускаем комплексные значения, областью определения sec(arccos x) является «все x , за исключением 0″ (и «правильным» графиком будет график, предоставленный Scientific Notebook и Wolfram|Alpha), но для реальных значений функция определена только для -1 ≤ x ≤ 1, за исключением x = 0 (и «правильным» графиком будет тот, который дается другими программными пакетами)
Таким образом, ответ на его первоначальный вопрос:
, предполагая, что 5 является комплексным числом (которым оно может быть — если мнимая часть равна 0), и это undefined , если функция действительна.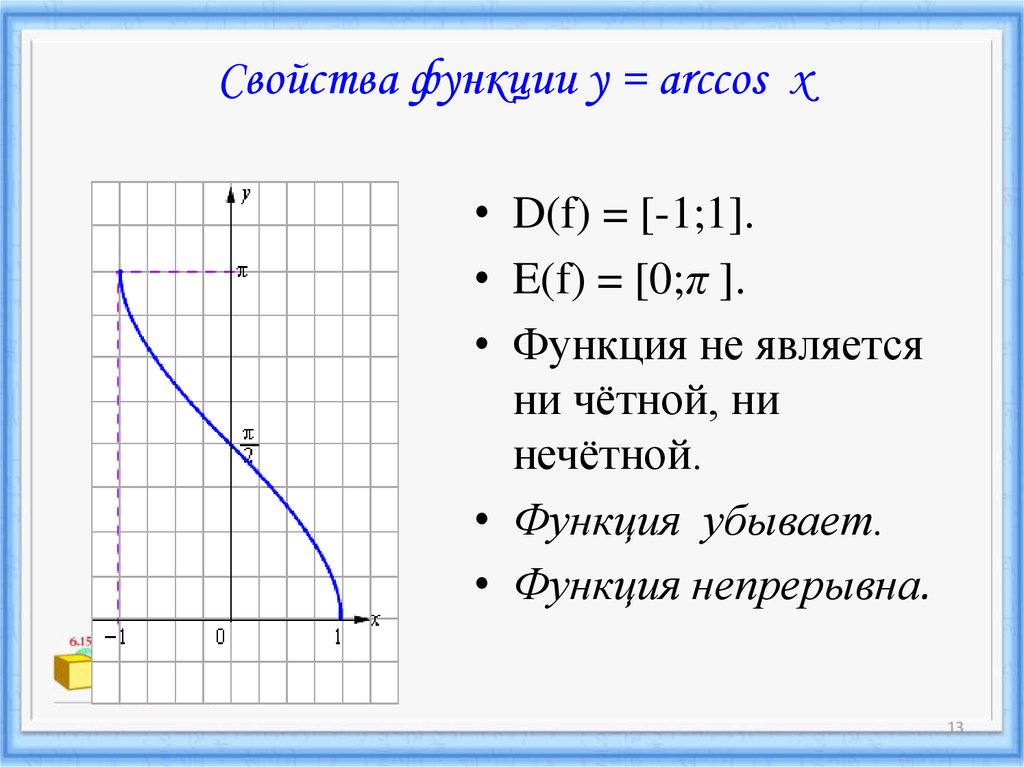
См. 9 комментариев ниже.
Нарисуй форму моего сердца. Как две простые функции образуют… | by Slawomir Chodnicki
Как две простые функции образуют красивую пиктограмму
Красивая пиктограмма сердца, построенная из основных функцийДавайте рассмотрим, как строится фигура.
Функция вида y= f (x) не может принимать два значения одновременно. Таким образом, наш сюжет должен включать более одной функции. Обратите внимание, что ось x аккуратно разделяет пиктограмму на две части, каждая из которых может быть выражено как y= f (x) .
В верхней части ищем два полукруга радиусом один каждый.
Как их получить?
Создание полукруга
Начнем с одного полукруга радиусом 1. Что мы о нем знаем? Что ж, в круге радиуса 1 мы всегда можем построить прямоугольный треугольник, самая длинная сторона которого имеет длину 1. Вспоминая Пифагора, мы знаем, что x²+y²=1 .
Давайте использовать это.
Верхний полукруг согласно теореме Пифагора: y=sqrt(1-x²) Решим для y и получим y = ±sqrt(1-x²) . Если мы выберем только положительные решения, эффективно выбрав верхнюю половину нашего круга, мы можем построить его как y=sqrt(1-x²) .
Обратите внимание, что значения x выше и ниже 1 не определены. Мы бы извлекли квадратный корень из отрицательного числа, а мы не можем сделать это с реальными числами.
Перемещение чашки
Если мы сможем сдвинуть нашу фигуру вправо на 1, мы получим половину желаемой функции. Мы хотим сдвинуть наш график таким образом, чтобы любое f(x) , которое мы получаем сейчас, возвращалось для значений x на единицу выше. По сути, нам нужно f(x-1) . Включив это в нашу функцию, мы получим y=sqrt(1-(x-1)²) .
График y=sqrt(1-(x-1)²) Отражение чашки
Теперь нам нужна еще одна чашка, точно такая же, как та, что у нас есть, но слева.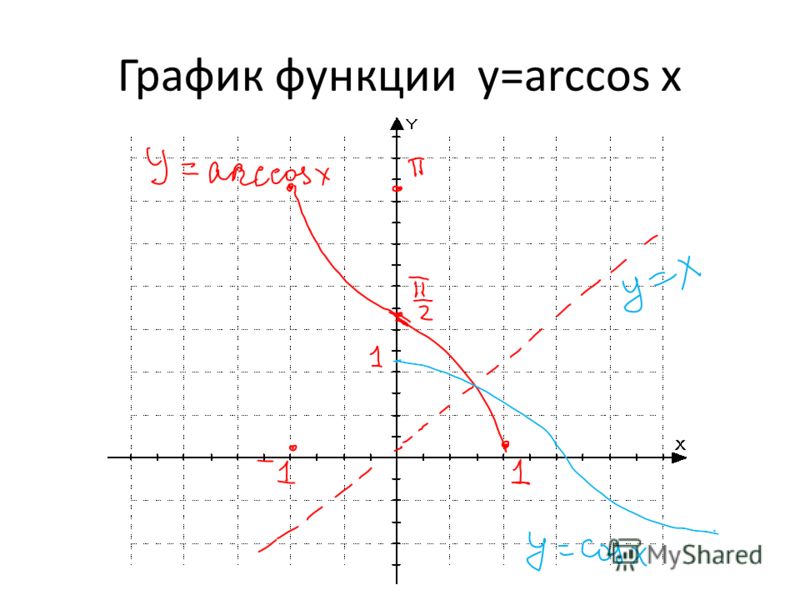
Мы видим, что наша функция определена только для положительных значений x. Если бы мы могли определить его для того же диапазона отрицательных значений, это достигло бы нашей цели. Мы хотим f(x) и f(-x) должны быть определены и давать одинаковые значения y. Другими словами, нам нужно f(|x|) . Давайте включим это в нашу функцию, и мы получим y=sqrt(1-(|x|-1)²) .
График y=sqrt(1-(|x|-1)²) Итак, верхняя часть нашего сердца готова. Перейдем к нижней части.
Для нижней части у нас также есть лево-правая симметрия. И разрыв в середине. Вспомним, как выглядит нижняя часть.
Ищем функцию для построения графика дна сердцаДавайте сначала разберемся с левой стороной.
Поиск формы
Мы ищем функцию, которая приближается к вертикали с обеих сторон, определена в диапазоне, охватывающем две единицы, и ее диапазон значений y выглядит подозрительно похожим на 3,1415… =π.
Звучит как тригонометрическая функция или одна из ее инверсий.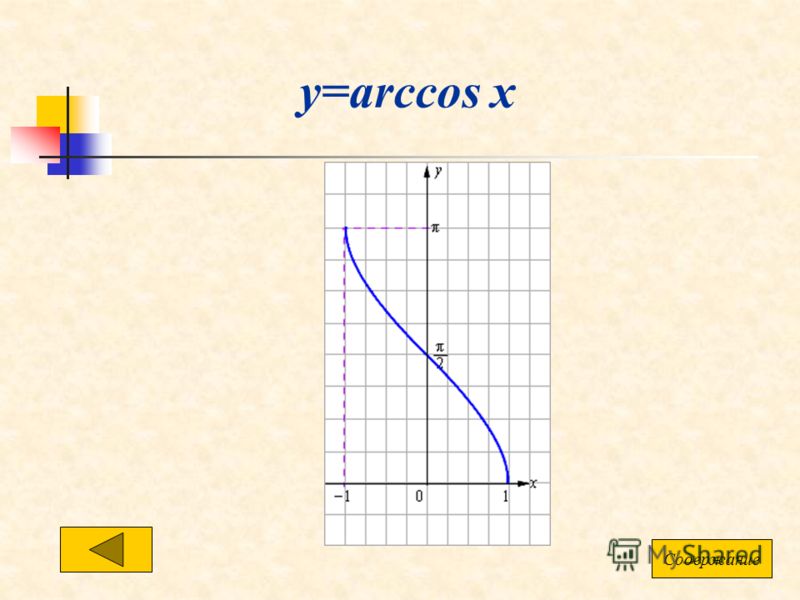
Давайте посмотрим на arccos(x)
Похоже, у нас есть хорошее совпадение. Нам нужно сдвинуть его вниз на π, чтобы график упал ниже оси x, и нам нужно преобразовать наш x влево на одну единицу.
Принимая это во внимание, мы получаем y=arccos(1+x)-π в качестве левой части.
y=arccos(1+x)-π формирует нашу левую сторону внизу Отражение формы
Обратите внимание, что наши левые значения являются результатом отрицательных значений x. Поэтому мы не можем просто расширить нашу функцию, заменив x абсолютным значением x. Это работало при зеркальном отражении правой части графика влево. Теперь это немного сложнее.
Мы ищем такое выражение, при котором arccos выдает симметричные значения.