Синус, косинус, тангенс острого угла прямоугольного треугольника
| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека▪Публикации▪Статьи
Материал опубликовал
#8 класс #Математика #Методические разработки #Урок #Все учителя #Школьное образование #УМК Л.
С. Атанасяна
Синус, косинус, тангенс острого угла прямоугольного треугольника
1.Закончи предложение: «Треугольник, у которого один угол прямой 1.Закончи предложение: «Треугольник, у которого один угол прямой называется…» А) остроугольный Б) равнобедренный В) равносторонний Г) прямоугольный Математический диктант
2. Отметь прямоугольный треугольник: 2. Отметь прямоугольный треугольник: А Б в г
3. Как называются стороны в прямоугольном треугольнике? 3. Как называются стороны в прямоугольном треугольнике? А) боковые стороны Б) основания В) катеты и гипотенуза Г) параллельные стороны
4. Один из острых углов прямоугольного треугольника равен 30°, чему равен другой острый угол? 4. Один из острых углов прямоугольного треугольника равен 30°, чему равен другой острый угол? А) 90° Б) 60° В) 30° С) 180°
5.
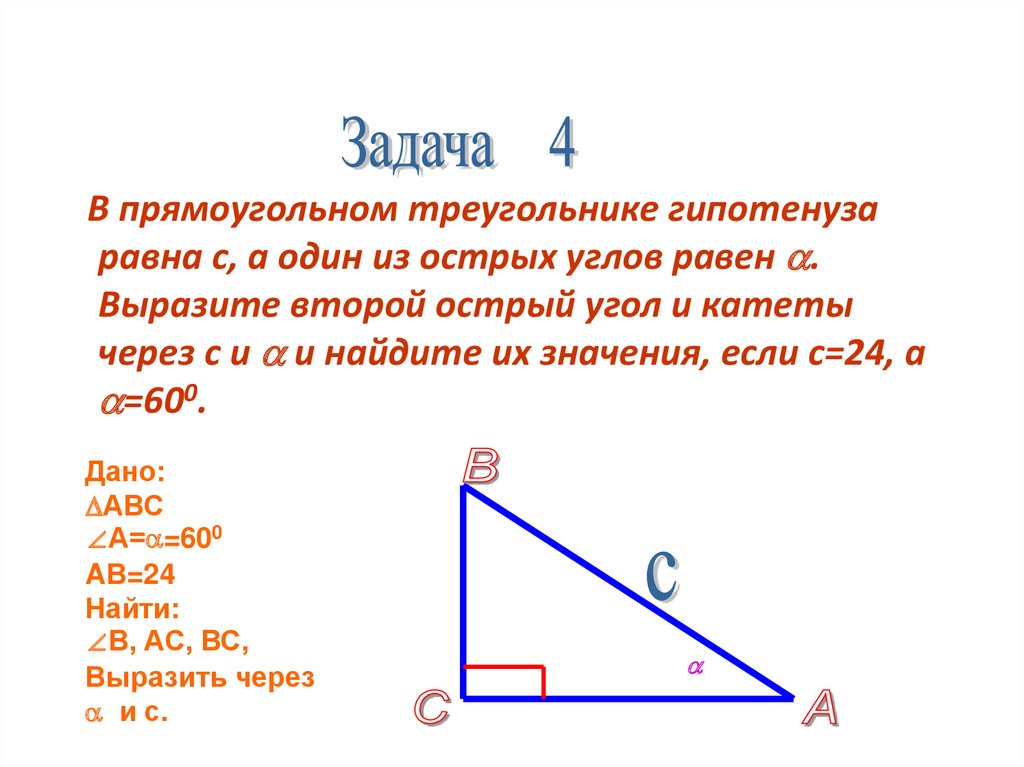Выберите формулу площади
5. Выберите формулу площади
прямоугольного треугольника:
А) S = a·b
Б) S = a·h
B) S = a·b·sin α
Г) S = ٕ√p(p-a)(p-b)(p-c)
6. Катет прямоугольного треугольника, лежащий напротив угла в 30°, равен 15см. Чему равна гипотенуза? 6. Катет прямоугольного треугольника, лежащий напротив угла в 30°, равен 15см. Чему равна гипотенуза? А) 15см Б) 7,5см В) 20см Г) 30см
Результаты: 1 2 3 4 5 6 Г Б В Б А Г
Оценка «5» — все верные ответы.
Оценка «4» — 5 верных ответов.
Оценка «3» — 4 верных ответа.
Оценка «5» — все верные ответы.
Оценка «4» — 5 верных ответов.
Оценка «3» — 4 верных ответа.
«Надо ещё повторить» — менее 4 верных ответов.
а b с катет катет гипотенуза
C B A Назвать катет, прилежащий к углу А. Назвать катет, прилежащий к углу В. Назвать катет, противолежащий углу А. Назвать катет, противолежащий углу В.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. В С А
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.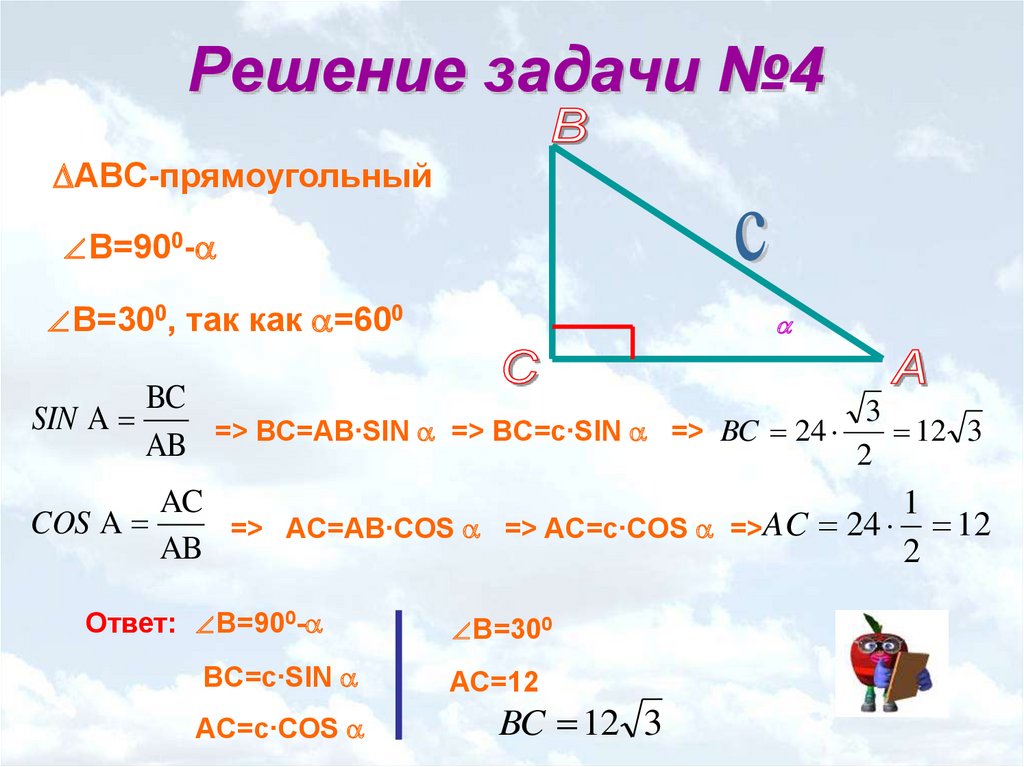
В
С
А
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. В С А
Минутная пауза Внимание на экран!
C B A
Значение косинуса острого угла прямоугольного треугольника не зависит от величины и положения прямоугольного треугольника.
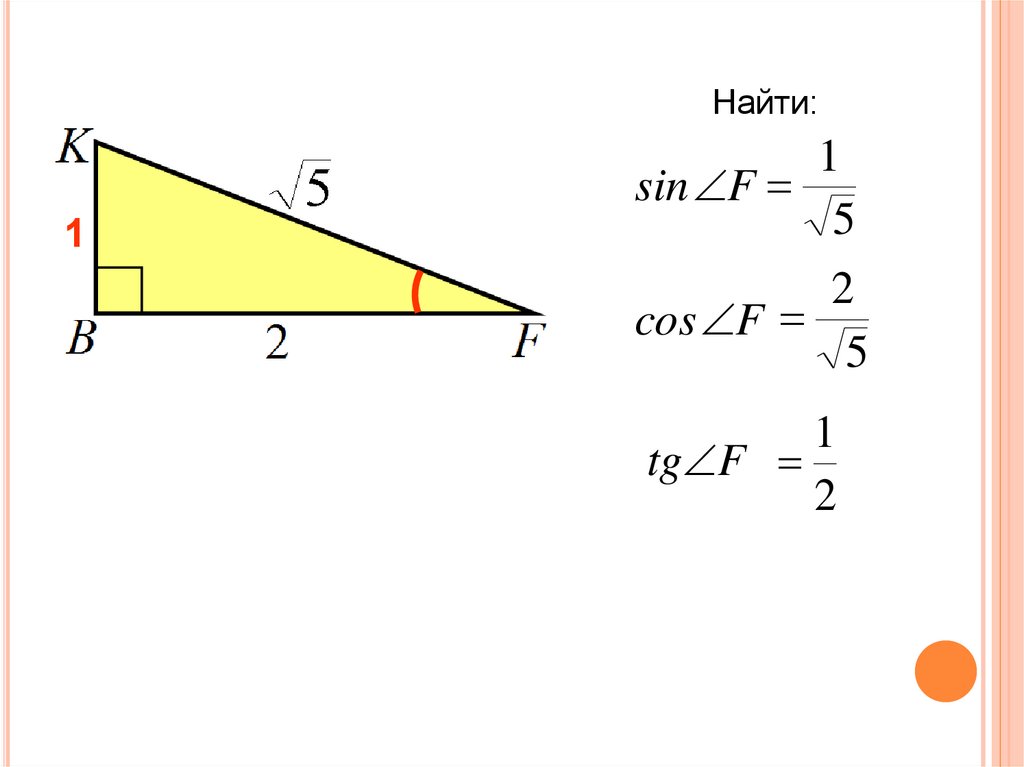
Найти: 1) sinA, 2) cоsA, 3) tg A, 4) сtg A, С А В 5см 13 см Ответ: sin A= Ответ: соsA= tg A= сtg A=
Домашнее задание:
1.
Выполнение домашнего задания начни с изучения
§ 4 пункта 66.
2. Повтори определения синуса, косинуса, тангенса и
котангенса острого угла прямоугольного
треугольника.
3. Реши следующие задачи из учебника:
№ 591(а), № 592 (а).
4. Дополнительно: выполнить тест.
Синус, косинус, тангенс острого угла прямоугольного треугольника
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1.
Синус, косинус, тангенс острого угла прямоугольного треугольника. Петрова Анна Георгиевна 451 школа1.Закончи предложение: «Треугольник, укоторого один угол прямой
называется…»
А) остроугольный
Б) равнобедренный
В) равносторонний
Г) прямоугольный
2. Отметь прямоугольный
треугольник:
3. Как называются стороны в
прямоугольном треугольнике?
А) боковые стороны
Б) основания
В) катеты и гипотенуза
Г) параллельные стороны
4. Один из острых углов прямоугольного
треугольника равен 30°, чему равен
другой острый угол?
А) 90°
Б) 60°
В) 30°
Г) 180°
Выберите формулу площади
прямоугольного треугольника:
А) S =1 a·b
2
Б) S =1 a·h
2
B) S = 1 a·b·sin α
2
Г) S = √ٕp(p-a)(p-b)(p-c)
5.
6. Катет прямоугольного треугольника,
лежащий напротив угла в 30°, равен
15см. Чему равна гипотенуза?
А) 15см
Б) 7,5см
В) 20см
Г) 30см
Оценка «5» — все верные ответы.
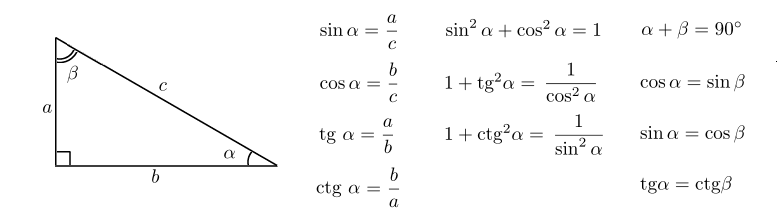
Оценка «4» — 5 верных ответов.
Оценка «3» — 4 верных ответа.
«Надо ещё повторить» — менее 4 верных
ответов.
B
Назвать катет, прилежащий к
углу А.
Назвать катет, прилежащий к
углу В.
Назвать катет,
противолежащий углу А.
Назвать катет,
противолежащий углу В.
C
A
Синусом острого
угла
прямоугольного
треугольника
называется
отношение
противолежащего
катета к
гипотенузе.
В
sin A
С
BC
AB
А
Косинусом острого
угла
прямоугольного
треугольника
называется
отношение
прилежащего
катета к
гипотенузе.
В
cos A
С
AC
AB
А
Тангенсом острого
угла
прямоугольного
треугольника
называется
отношение
противолежащего
катета к
прилежащему.
В
tg A
С
BC
AC
А
B
BC
sin A
AB
AC
cos A
AB
BC
tg A
AC
C
A
sin B ?
cos B ?
tg B ?
Найти: 1) sin A, 2) cоs A, 3) tg A, 4) сtg A,
В
Ответ:
5
13
tg
A=
sin
соs A=
сtg A=
A=
13 см
12
125
13
512
5см
С
А
17.
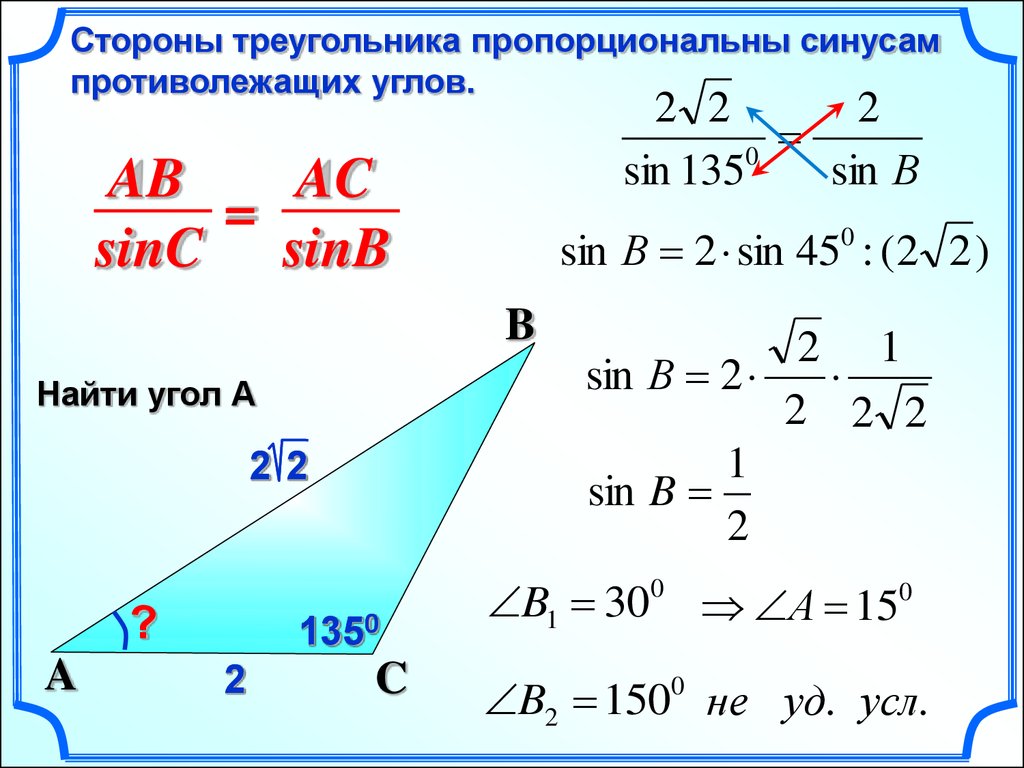Домашнее задание. 1.§4 пункт 682. Решите
следующие задачи
из учебника №
591(в,г) № 592(в,г).
за урок!
English Русский Правила
Sin a Sin b — Club Z! Tutoring
Sin A + Sin BСумма двух синусов равна произведению косинуса их разности на произведение их амплитуд. Два синуса не совпадают по фазе друг с другом, если их разность не является целым числом, кратным числу пи.
Что такое тождество SinA + SinB в тригонометрии?В тригонометрии синус угла определяется как отношение длины противоположной стороны к длине гипотенузы. Косинус угла определяется как отношение длины прилежащего катета к длине гипотенузы. Тангенс угла определяется как отношение длины противоположной стороны к длине прилежащей стороны.
Тождество sin a sin b утверждает, что:
sin(a + b) = sin a cos b + cos a sin b
Это тождество можно вывести из первых принципов, используя определение синуса и косинуса.
Это также можно проверить с помощью основных алгебраических манипуляций.
Это тождество полезно при решении задач с углами, не кратными 90 градусам. Например, рассмотрите возможность нахождения значения sin 75 градусов без использования калькулятора. Применяя тождество sin a sin b, мы можем разбить этот угол на два меньших угла: 60 градусов и 15 градусов. Мы знаем, что sin 60 градусов = 0,5 и что cos 60 градусов = 0,866, поэтому мы можем подставить эти значения в наше уравнение:0007
sin(60 + 15) = sin 60 cos 15 + cos 60 sin 15 к формуле продукта
Когда два угла в треугольнике имеют стороны, противоположные друг другу, равные по длине, такой треугольник называется равнобедренным. Сторона, противоположная общему углу, равна по длине, поэтому на изображении выше сторона AC имеет равную длину со стороной BC. Следовательно, углы А и В равны.
Мы можем обозначить эти углы буквами:
Угол A = a
Угол B = b
Общий угол C = c
Формула Sin A + Sin B Sum to Product утверждает, что:
sin(a) + sin(b ) = 2 * sin((a + b)/2) * cos((a – b)/2)
Эта формула утверждает, что синус суммы двух углов равен равно произведению синусов этих углов.
Это можно записать как: Sin(A + B) = SinA * SinB.
Эта формула полезна во многих ситуациях, например, при вычислении сторон треугольника, когда известны два угла и одна сторона. Его также можно использовать для нахождения угла, когда известны две стороны и один угол.
При использовании этой формулы необходимо помнить о нескольких вещах. Во-первых, он работает только для углов меньше 90 градусов. Во-вторых, порядок углов имеет значение. Синус A + B не обязательно совпадает с синусом B + A.
Чтобы использовать эту формулу, просто подставьте значения для A и B, а затем вычислите синус каждой стороны. Результат будет равен произведению синусов A и B.
Как применить Sin A + Sin B?Чтобы применить sin A + sin B, сначала вычислите значение sin A и sin B. Затем сложите эти значения, чтобы получить окончательный ответ.
SIN A SIN B
3D участок
Контур.
Свойства как функция
Разложение в ряд при a = 0
Производная
Неопределенный интеграл
Global Maxima
Global Minima
Альтернативные представления
серии.
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3245
- Майкл Коррал
- Колледж Скулкрафт
Рассмотрим прямоугольный треугольник \(\треугольник\,ABC\) с прямым углом \(C\) и длинами \(a\), \(b\) и \(c\), как в рисунок справа. Для острого угла \(A\) назовите катет \(\overline{BC} \) его противоположной стороной , а катет \(\overline{AC} \) назовите его соседняя сторона . Напомним, что гипотенузой треугольника является сторона \(\overline{AB} \). Отношения сторон прямоугольного треугольника достаточно часто встречаются в практических приложениях, чтобы оправдать их собственные названия, поэтому мы определяем шесть тригонометрических функций от \(A\) следующим образом:
Таблица 1.
2 Шесть тригонометрических функций \(A\)
Обычно мы будем использовать сокращенные названия функций. Обратите внимание на таблицы 1.2, что пары \(\sin A \) и \(\csc A \), \(\cos A \) и \(\sec A \), и \(\tan A \) и \( \cot A \) обратны:
Пример 1.5
Для прямоугольного треугольника \(\треугольник\,ABC\), показанного справа, найти значения всех шести тригонометрических функций острых углов \(A\) и \(B\).
Решение:
Гипотенуза \(\треугольника\,ABC\) имеет длину \(5\). Для угла \(A \) противолежащая сторона \(\overline{BC} \) имеет длину \(3 \), а прилежащая сторона \(\overline{AC} \) имеет длину \(4 \). Таким образом:
\[ \nonumber \sin A ~=~ \dfrac{\text{напротив}}{\text{гипотенуза}} ~=~ \dfrac{3}{5} \qquad\qquad
\cos A ~=~ \dfrac{\text{смежный}}{\text{гипотенуза}} ~=~ \dfrac{4}{5} \qquad\qquad
\tan A ~=~ \dfrac{\text {напротив}}{\text{смежный}} ~=~ \dfrac{3}{4} \nonumber \]
\[\nonumber \csc A ~=~ \dfrac{\text{гипотенуза}}{\text {напротив}} ~=~ \dfrac{5}{3} \qquad\qquad
\sec A ~=~ \dfrac{\text{гипотенуза}}{\text{смежный}} ~=~ \dfrac{5} {4} \qquad\qquad
Для угла \ (B \), противоположная сторона \(\overline{AC} \) имеет длину \(4 \), а примыкающая сторона \(\overline{BC} \) имеет длину \(3 \).
Таким образом:
\[\sin B ~=~ \dfrac{\text{напротив}}{\text{гипотенуза}} ~=~ \dfrac{4}{5} \qquad\qquad
\cos B ~=~ \dfrac {\text{смежный}}{\text{гипотенуза}} ~=~ \dfrac{3}{5} \qquad\qquad
\tan B ~=~ \dfrac{\text{напротив}}{\text{смежный }} ~=~ \dfrac{4}{3} \nonumber \]
\[\csc B ~=~ \dfrac{\text{гипотенуза}}{\text{напротив}} ~=~ \dfrac{5 }{4} \qquad\qquad
\sec B ~=~ \dfrac{\text{гипотенуза}}{\text{adjacent}} ~=~ \dfrac{5}{3} \qquad\qquad
\cot B ~=~ \dfrac{\text{смежный}}{\text{напротив}} ~=~ \dfrac{3}{4} \nonumber \]
Обратите внимание, что в примере 1.5 мы не указали единицы измерения длины. Это повышает вероятность того, что наши ответы зависели от треугольника определенного физического размера.
Например, предположим, что этот учебник читают два разных ученика: один в США, другой в Германии. Американский студент думает, что длины \(3\), \(4\) и \(5\) в примере 1.5 измеряются в дюймах, а немецкий студент думает, что они измеряются в сантиметрах.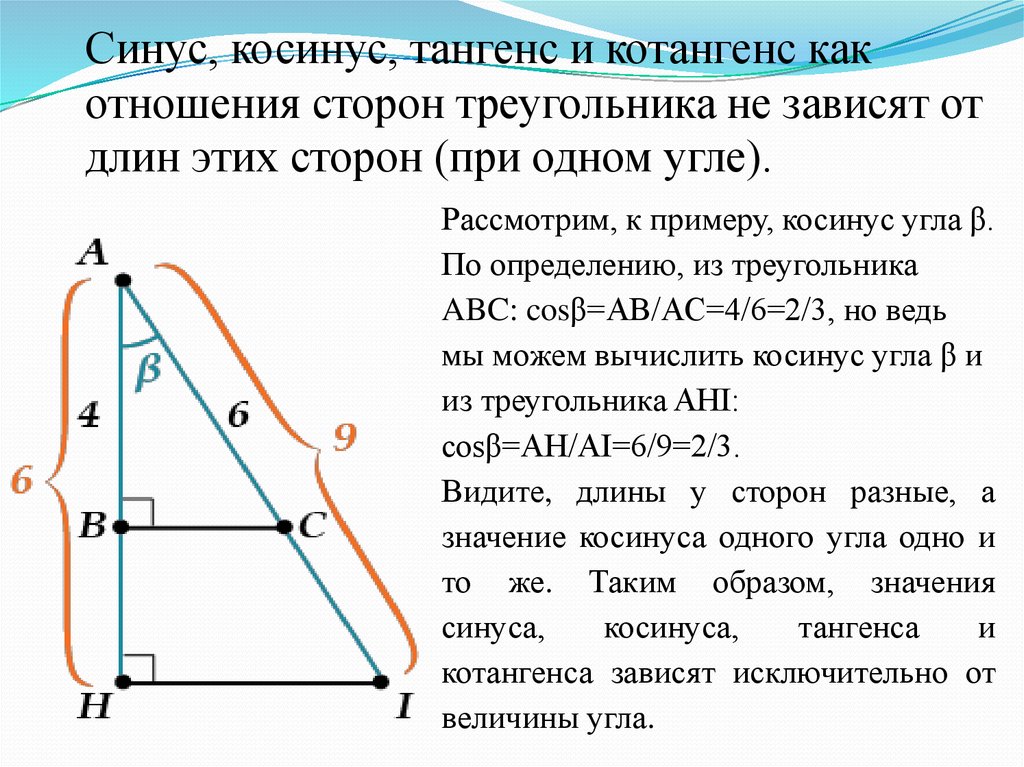
Поскольку \(1 \) в \(\приблизительно \) \(2,54 \) см, учащиеся используют треугольники разных физических размеров (см. рисунок 1.2.1 ниже, не в масштабе).
Если американский треугольник равен \(\triangle\,ABC \), а немецкий треугольник равен \(\triangle\,A’B’C ‘ \), то из рис. 1.2.1 мы видим, что \(\треугольник\,ABC\) подобен \(\треугольнику\,A’B’C’ \), а значит, соответствующие углы равны и отношения соответствующих сторон равны. На самом деле, мы знаем это обычное соотношение: стороны \(\треугольника\,ABC\) примерно в \(2,54\) раза длиннее соответствующих сторон \(\треугольника\,A’B’C’ \). Таким образом, когда американский студент вычисляет \(\sin A \), а немецкий студент вычисляет \(\sin A’ \), они получают один и тот же ответ:
\[\triangle\,ABC ~\sim~ \triangle\,A’B’C’ \quad\Стрелка вправо\quad
\dfrac{BC}{B’C’} ~=~ \dfrac{AB}{A ‘B’} \quad\Rightarrow\quad
\dfrac{BC}{AB} ~=~ \dfrac{B’C’}{A’B’} \quad\Rightarrow\quad \sin A ~=~ \sin А’ \номер \]
Точно так же другие значения тригонометрических функций \(A\) и \(A’\) одинаковы.
На самом деле наш аргумент был достаточно общим, чтобы работать с любыми подобными прямоугольными треугольниками. Это приводит нас к следующему выводу:
При вычислении тригонометрических функций острого угла \(A\) можно использовать любой прямоугольный треугольник, у которого \(A\) является одним из углов.
Поскольку мы определили тригонометрические функции в терминах отношений сторон, вы можете думать о единицах измерения этих сторон как о сокращении этих отношений. Это означает, что значения тригонометрических функций являются безразмерными числами . Таким образом, когда американский студент вычислил \(3/5\) как значение \(\sin A\) в примере 1.5, это то же самое, что и \(3/5\), вычисленный немецким студентом, несмотря на другие различия. единицы длины сторон. 9\циркуляр \;=\; \dfrac{\text{смежный}}{\text{напротив}} \;=\;
\dfrac{\sqrt{3}}{1} \;=\; \sqrt{3} \nonumber \]
Пример 1.8
\(A \) острый угол такой, что \(\sin A = \frac{2}{3} \).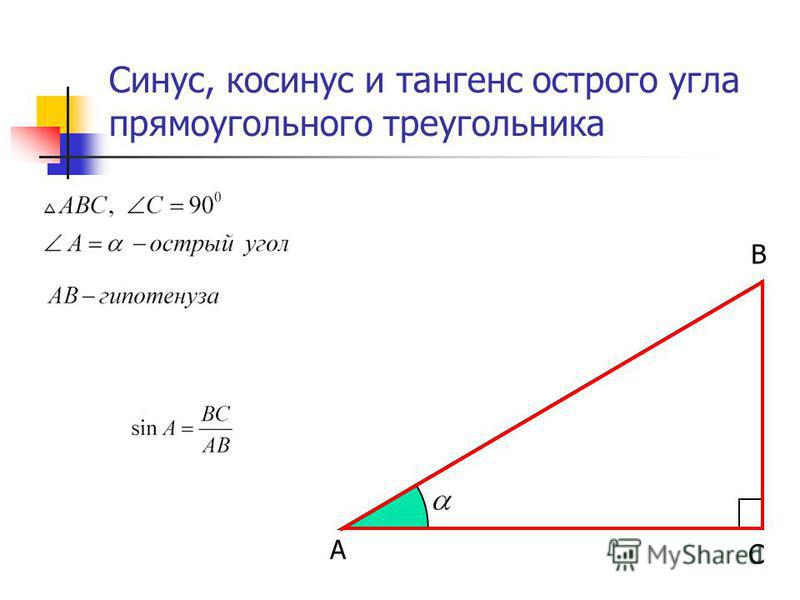
Найдите значения других тригонометрических функций \(A \).
Решение:
Обычно для решения задач такого типа помогает нарисовать прямоугольный треугольник. Причина в том, что тригонометрические функции были определены в терминах отношений сторон прямоугольного треугольника, а вам дана одна такая функция (в данном случае синус) уже в терминах отношения: \(\sin\;A = \фракция{2}{3} \). Поскольку \(\sin\;A \) определяется как \(\frac{\text{напротив}}{\text{гипотенуза}} \), используйте \(2\) как длину стороны, противоположной \(A \) и используйте \(3 \) как длину гипотенузы в прямоугольном треугольнике \(\triangle\,ABC \) (см. рисунок выше), так что \(\sin\;A = \frac{2} {3} \). Сторона, примыкающая к \(A\), имеет неизвестную длину \(b\), но мы можем использовать теорему Пифагора, чтобы найти ее: 92 ~=~ 9 ~-~ 4 ~=~ 5 \quad\Rightarrow\quad
b ~=~ \sqrt{5} \nonumber \]
Теперь мы знаем длины всех сторон треугольника \(\triangle \,ABC\), поэтому имеем:
\[ \cos\;A \;=\; \dfrac{\text{смежный}}{\text{гипотенуза}} \;=\; \dfrac{\sqrt{5}}{3} \qquad
\tan\;A \;=\; \dfrac{\text{напротив}}{\text{смежный}} \;=\;
\dfrac{2}{\sqrt{5}}\quad\quad \nonumber \]
\[ \csc\;A \;=\; \dfrac{\text{гипотенуза}}{\text{напротив}} \;=\; \dfrac{3}{2} \qquad
\sec\;A \;=\; \dfrac{\text{гипотенуза}}{\text{смежный}} \;=\; \dfrac{3}{\sqrt{5}} \qquad
\кот\;А \;=\; \dfrac{\text{смежный}}{\text{напротив}} \;=\; \dfrac{\sqrt{5}}{2} \nonumber \]
Возможно, вы заметили связь между синусом и косинусом, секансом и косекансом, а также тангенсом и котангенсом дополнительных углов в примерах 1.
5 и 1.7. Обобщая эти примеры, мы получаем следующую теорему:
Теорема 1.2 Теорема о кофункциях
Если \(A\) и \(B\) — дополнительные острые углы в прямоугольном треугольнике \(\triangle\,ABC \), то выполняются следующие соотношения:
\[\sin\;A ~=~ \cos\;B \qquad\qquad \sec\;A ~=~ \csc\;B \qquad\qquad \tan\;A ~=~ \cot\; B \nonumber \]
\[\sin\;B ~=~ \cos\;A \qquad\qquad \sec\;B ~=~ \csc\;A \qquad\qquad \tan\;B ~= ~ \cot\;A \nonumber \]
Мы говорим, что пары функций \(\lbrace\;\sin, \cos\;\rbrace \), \(\lbrace\;\sec, \csc\; \rbrace \) и \(\lbrace\;\tan, \cot\;\rbrace \) являются \(\textbf{кофункции}\).
Итак, синус и косинус являются кофункциями, секанс и косеканс являются кофункциями, а тангенс и котангенс являются кофункциями. Вот почему функции косинуса, косеканса и котангенса получили в своих названиях букву «со». Теорема о кофункциях утверждает, что любая тригонометрическая функция острого угла равна своей кофункции дополнительного угла.
\circ \), поскольку это сумма этих двух углов. Таким образом, нам нужно найти синус, косинус и тангенс \(\угол\,ДАУ\). 9\circ \), поскольку он является дополнением к \(\angle\,BDF \). Гипотенуза \(\overline{BD} \) треугольника \(\треугольник\,DFB\) имеет длину \(1\) и \(\треугольник\,DFB\) является \(45-45-90\) прямым треугольник, поэтому мы знаем, что \(DF = FB = \frac{1}{\sqrt{2}} \).
Теперь мы знаем, что \(\overline{DE} \perp \overline{AC} \) и \(\overline{BC} \perp \overline{AC} \), поэтому \(\overline{FE} \ ) и \(\overline{BC} \) параллельны. Точно так же \(\overline{FB} \) и \(\overline{EC} \) оба перпендикулярны \(\overline{DE} \) и, следовательно, \(\overline{FB} \) параллельны \( \overline{EC} \). Таким образом, \(FBCE\) — прямоугольник, так как \(\angle\,BCE \) — прямой угол. Итак, \(EC = FB = \frac{1}{\sqrt{2}}\) и \(FE = BC = \sqrt{\frac{3}{2}} \). Следовательно, 9\circ = \frac{\sqrt{6} — \sqrt{2}}{\sqrt{6} + \sqrt{2}} \).
Эта страница под названием 1.