График функции y x 2 4x 1. Исследование функции и построение графика
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
В. -1. План построения. 2) Построить ось симметрии x=-1. y.
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x).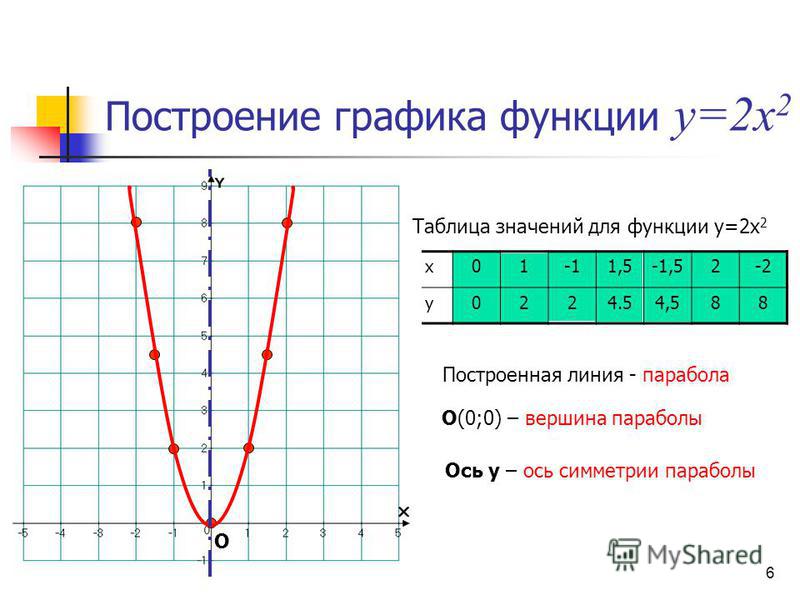 Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.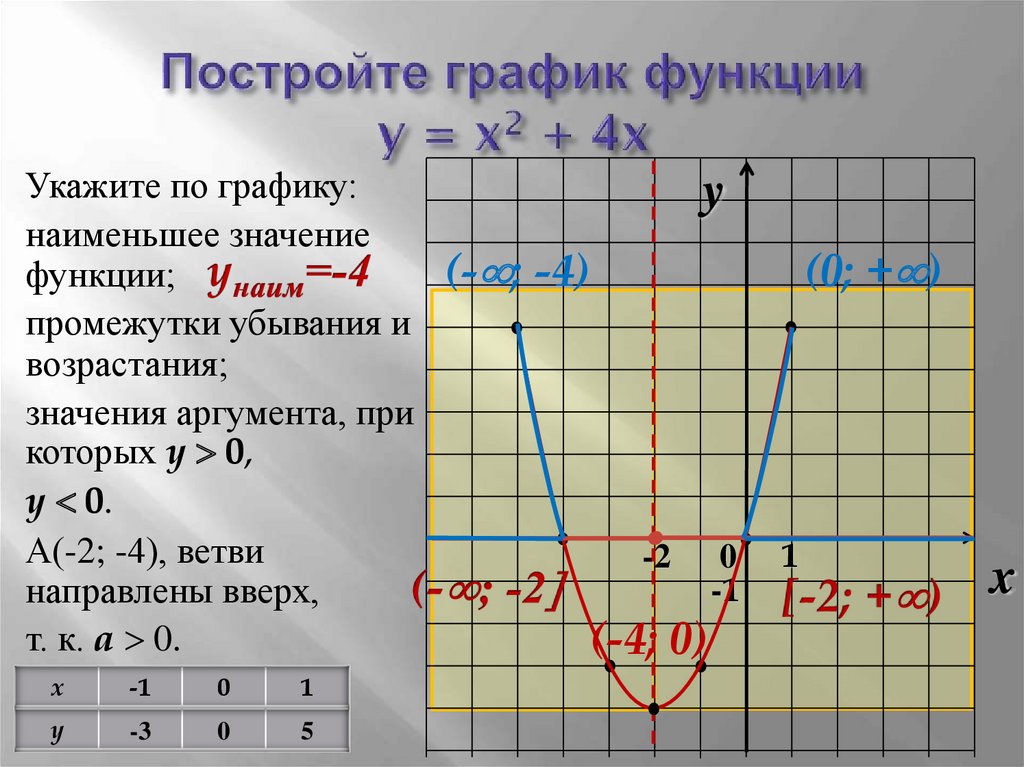
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн.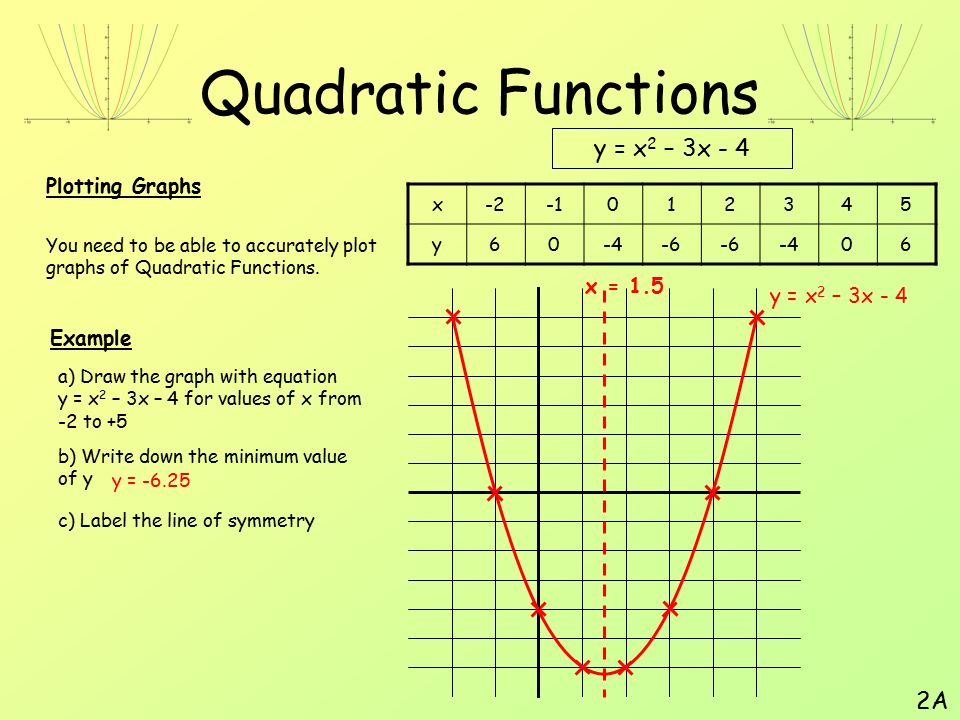 Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x).
 Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
 2} — 4\left({\frac{{ — 1 + \sqrt 5 }}{2}} \right) }
= { — \frac{1}{8}\left({1 — 3\sqrt 5 + 15 — 5\sqrt 5 } \right) + \frac{1}{2}\left({1 — 2\sqrt 5 + 5} \right) + 2\left({1 — \sqrt 5 } \right) }
= { — \cancel{2} + \cancel{\sqrt 5} + 3 — \cancel{\sqrt 5} + \cancel{2} — 2\sqrt 5 }
= {3 — 2\sqrt 5 \approx — 1,47.}
\]
Разделим ось \(t\) на \(5\) интервалов:
\[
{\left({ — \infty , — 2} \right),}\;\;
{\left({ — 2, — 1} \right),}\;\;
{\left({ — 1,\frac{1}{3}} \right),}\;\;
{\left({\frac{1}{3},\frac{2}{3}} \right),}\;\;
{\left({\frac{2}{3}, + \infty } \right).}
\]
На первом интервале \(\left({ — \infty , — 2} \right)\) значения \(x\) и \(y\) возрастают от \(-\infty\) до \(x\left({ — 2} \right) = — 2\)
и \(y\left({ — 2} \right) = 8.\) Это схематически показано на рисунке \(15b.\)
2} — 4\left({\frac{{ — 1 + \sqrt 5 }}{2}} \right) }
= { — \frac{1}{8}\left({1 — 3\sqrt 5 + 15 — 5\sqrt 5 } \right) + \frac{1}{2}\left({1 — 2\sqrt 5 + 5} \right) + 2\left({1 — \sqrt 5 } \right) }
= { — \cancel{2} + \cancel{\sqrt 5} + 3 — \cancel{\sqrt 5} + \cancel{2} — 2\sqrt 5 }
= {3 — 2\sqrt 5 \approx — 1,47.}
\]
Разделим ось \(t\) на \(5\) интервалов:
\[
{\left({ — \infty , — 2} \right),}\;\;
{\left({ — 2, — 1} \right),}\;\;
{\left({ — 1,\frac{1}{3}} \right),}\;\;
{\left({\frac{1}{3},\frac{2}{3}} \right),}\;\;
{\left({\frac{2}{3}, + \infty } \right).}
\]
На первом интервале \(\left({ — \infty , — 2} \right)\) значения \(x\) и \(y\) возрастают от \(-\infty\) до \(x\left({ — 2} \right) = — 2\)
и \(y\left({ — 2} \right) = 8.\) Это схематически показано на рисунке \(15b.\)На втором промежутке \(\left({ — 2, — 1} \right)\) переменная \(x\) возрастает от \(x\left({ — 2} \right) = — 2\) до \(x\left({ — 1} \right) = 1,\) а переменная \(y\) убывает от \(y\left({ — 2} \right) = 8\) до \(y\left({ — 1} \right) = 5.
 \) Здесь мы имеем участок убывающей кривой \(y\left(x \right).\)
Она пересекает ось ординат в точке \(\left({0,3 + 2\sqrt 5 } \right).\)
\) Здесь мы имеем участок убывающей кривой \(y\left(x \right).\)
Она пересекает ось ординат в точке \(\left({0,3 + 2\sqrt 5 } \right).\)На третьем интервале \(\left({ — 1,\large\frac{1}{3}\normalsize} \right)\) обе переменные убывают. Значение \(x\) изменяется от \(x\left({ — 1} \right) = 1\) до \(x\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{5}{{27}}\normalsize.\) Соответственно, значение \(y\) уменьшается от \(y\left({ — 1} \right) = 5\) до \(y\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{29}{{27}}\normalsize.\) Кривая \(y\left(x \right)\) при этом пересекает начало координат.
На четвертом интервале \(\left({\large\frac{1}{3}\normalsize,\large\frac{2}{3}\normalsize} \right)\) переменная \(x\) возрастает от \(x\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{5}{{27}}\normalsize\) до \(x\left({\large\frac{2}{3}\normalsize} \right) = \large\frac{2}{{27}}\normalsize,\) а переменная \(y\) убывает от \(y\left({\large\frac{1}{3}\normalsize} \right) = — \large\frac{29}{{27}}\normalsize\) до \(y\left({\large\frac{2}{3}\normalsize} \right) = — \large\frac{40}{{27}}\normalsize.
 2} + 2t — 1}} }
= {\frac{{\cancel{3}\left({t + 2} \right)\left({t — \frac{2}{3}} \right)}}{{\cancel{3}\left({t + 1} \right)\left({t — \frac{1}{3}} \right)}} }
= {\frac{{\left({t + 2} \right)\left({t — \frac{2}{3}} \right)}}{{\left({t + 1} \right)\left({t — \frac{1}{3}} \right)}}.}
\]
Изменение знака производной \(y»\left(x \right)\) показано на рисунке \(15c.\) Видно, что в точке \(t = — 2,\)
т.е. на границе \(I\)-го и \(II\)-го интервалов кривая имеет максимум, а при \(t = \large\frac{2}{3}\normalsize\)
(на границе \(IV\)-го и \(V\)-го интервалов) существует минимум. При переходе через точку \(t = \large\frac{1}{3}\normalsize\)
производная также меняет знак с плюса на минус, но в этой области кривая \(y\left(x \right)\) не является однозначной функцией. Поэтому указанная точка экстремумом
не является.
2} + 2t — 1}} }
= {\frac{{\cancel{3}\left({t + 2} \right)\left({t — \frac{2}{3}} \right)}}{{\cancel{3}\left({t + 1} \right)\left({t — \frac{1}{3}} \right)}} }
= {\frac{{\left({t + 2} \right)\left({t — \frac{2}{3}} \right)}}{{\left({t + 1} \right)\left({t — \frac{1}{3}} \right)}}.}
\]
Изменение знака производной \(y»\left(x \right)\) показано на рисунке \(15c.\) Видно, что в точке \(t = — 2,\)
т.е. на границе \(I\)-го и \(II\)-го интервалов кривая имеет максимум, а при \(t = \large\frac{2}{3}\normalsize\)
(на границе \(IV\)-го и \(V\)-го интервалов) существует минимум. При переходе через точку \(t = \large\frac{1}{3}\normalsize\)
производная также меняет знак с плюса на минус, но в этой области кривая \(y\left(x \right)\) не является однозначной функцией. Поэтому указанная точка экстремумом
не является.Исследуем также выпуклость данной кривой. Вторая производная \(y»»\left(x \right)\) имеет вид: \[ y»»\left(x \right) = {y»»_{xx}} = \frac{{{{\left({{y»_x}} \right)}»_t}}}{{{x»_t}}} = \frac{{{{\left({\frac{{3{t^2} + 4t — 4}}{{3{t^2} + 2t — 1}}} \right)}^\prime }}}{{{{\left({{t^3} + {t^2} — t} \right)}^\prime }}} = \frac{{\left({6t + 4} \right)\left({3{t^2} + 2t — 1} \right) — \left({3{t^2} + 4t — 4} \right)\left({6t + 2} \right)}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}} = \frac{{18{t^3} + 12{t^2} + 12{t^2} + 8t — 6t — 4 — \left({18{t^3} + 24{t^2} — 24t + 6{t^2} + 8t — 8} \right)}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}} = \frac{{\cancel{\color{blue}{18{t^3}}} + \color{red}{24{t^2}} + \color{green}{2t} — \color{maroon}{4} — \cancel{\color{blue}{18{t^3}}} — \color{red}{30{t^2}} + \color{green}{16t} + \color{maroon}{8}}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}} = \frac{{ — \color{red}{6{t^2}} + \color{green}{18t} + \color{maroon}{4}}}{{{{\left({3{t^2} + 2t — 1} \right)}^3}}} = \frac{{ — 6\left({t — \frac{{9 — \sqrt {105} }}{6}} \right)\left({t — \frac{{9 + \sqrt {105} }}{6}} \right)}}{{{{\left({t + 1} \right)}^3}{{\left({3t — 1} \right)}^3}}}.
 \]
Следовательно, вторая производная меняет свой знак на противоположный при переходе через следующие точки (рис.\(15с\)):
\[
{{t_1} = — 1:\;\;x\left({ — 1} \right) = 1,}\;\;
{y\left({ — 1} \right) = 5;}
\]
\[
{{t_2} = \frac{{9 — \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,24;}\;\;
{y\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,91;}
\]
\[
{{t_3} = \frac{1}{3}:}\;\;
{x\left({\frac{1}{3}} \right) = — \frac{5}{{27}},}\;\;
{y\left({\frac{1}{3}} \right) = — \frac{{29}}{{27}};}
\]
\[
{{t_4} = \frac{{9 + \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,1;}\;\;
{y\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,8.}
\]
Поэтому указанные точки представляют собой точки перегиба кривой \(y\left(x \right).\)
\]
Следовательно, вторая производная меняет свой знак на противоположный при переходе через следующие точки (рис.\(15с\)):
\[
{{t_1} = — 1:\;\;x\left({ — 1} \right) = 1,}\;\;
{y\left({ — 1} \right) = 5;}
\]
\[
{{t_2} = \frac{{9 — \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,24;}\;\;
{y\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,91;}
\]
\[
{{t_3} = \frac{1}{3}:}\;\;
{x\left({\frac{1}{3}} \right) = — \frac{5}{{27}},}\;\;
{y\left({\frac{1}{3}} \right) = — \frac{{29}}{{27}};}
\]
\[
{{t_4} = \frac{{9 + \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,1;}\;\;
{y\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,8.}
\]
Поэтому указанные точки представляют собой точки перегиба кривой \(y\left(x \right).\)Схематический график кривой \(y\left(x \right)\) показан выше на рисунке \(15b.\)
3-89 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 Мэтуэй | Популярные задачи
1 Оценка с использованием заданного значения квадратный корень из 50 2 Оценка с использованием заданного значения квадратный корень из 45 3 Оценка 5+5 4 Оценить 7*7 5 Найти простую факторизацию 24 6 Преобразование в смешанный номер 52/6 7 Преобразование в смешанный номер 93/8 8 Преобразование в смешанный номер 34/5 9 График у=х+1 10 Оценить, используя заданное значение квадратный корень из 128 11 Найдите площадь поверхности сфера (3) 12 Оценить 54-6÷2+6 13 График г=-2x 14 Оценить 8*8 15 Преобразование в десятичное число 5/9 16 Оценка с использованием заданного значения квадратный корень из 180 17 График у=2 18 Преобразование в смешанный номер 7/8 19 Оценить 9*9 20 Решите для C С=5/9*(Ф-32) 21 Упростить 1/3+1 1/12 22 График у=х+4 23 График г=-3 24 График х+у=3 25 График х=5 26 Оценить 6*6 27 Оценка 2*2 28 Оценить 4*4 29 Оценить 1/2+(2/3)÷(3/4)-(4/5*5/6) 30 Оценить 1/3+13/12 31 Оценить 5*5 32 Решить для d 2д=5в(о)-вр 33 Преобразование в смешанный номер 3/7 34 График г=-2 35 Найдите склон у=6 36 Преобразование в проценты 9 37 График у=2х+2 92+5х+6=041 Преобразование в смешанный номер 1/6 42 Преобразование в десятичное число 9% 43 Найти n 12н-24=14н+28 44 Оценить 16*4 45 Упростить кубический корень из 125 46 Преобразование в упрощенную дробь 43% 47 График х=1 48 График у=6 49 График г=-7 50 График у=4х+2 51 Найдите склон у=7 52 График у=3х+4 53 График у=х+5 54 График 92-9=058 Оценка с использованием заданного значения квадратный корень из 192 59 Оценка с использованием заданного значения квадратный корень из 25/36 60 Найти простую факторизацию 14 61 Преобразование в смешанный номер 7/10 62 Решите для (-5а)/2=75 63 Упростить х 64 Оценить 6*4 65 Оценить 6+6 66 Оценить -3-5 67 Оценить -2-2 68 Упростить квадратный корень из 1 69 Упростить квадратный корень из 4 70 Найди обратное 1/3 71 Преобразование в смешанный номер 20.  11.
11.72 Преобразование в смешанный номер 7/9 73 Найти LCM 11, 13, 5, 15, 14 , , , , 76 График 3x+4y=12 77 График 3x-2y=6 78 График у=-х-2 79 График у=3х+7 80 Определить, является ли многочлен 2x+2 81 График у=2х-6 82 График у=2х-7 83 График у=2х-2 84 График у=-2х+1 85 График у=-3х+4 86 График у=-3х+2 87 График у=х-4 88 Оценить (4/3)÷(7/2) 89 График 2x-3y=6 90 График х+2у=4 91 График х=7 92 График х-у=5 93 Решение с использованием свойства квадратного корня 92-2x-3=0 95 Найдите площадь поверхности конус (12)(9) 96 Преобразование в смешанный номер 3/10 97 Преобразование в смешанный номер 7/20 92-4x-6=0 Tiger Algebra SolverПошаговое решение :
Шаг 1 :
Попытка разложить на множители путем разделения среднего члена
1.
 1 Факторизация x 2 -4x-6 Первый член 918 918 , x 2 его коэффициент равен 1 .
1 Факторизация x 2 -4x-6 Первый член 918 918 , x 2 его коэффициент равен 1 .
Средний член равен -4x, его коэффициент равен -4.
Последний член, «константа», равен -6Шаг-1 : Умножьте коэффициент первого члена на константу 1 • -6 = -6 равен коэффициенту среднего члена, который равен -4 .
-6 + 1 = -5 -3 + 2 = -1 -2 + 3 = 1 -1 + 6 = 5
Наблюдение: Невозможно найти два таких фактора!!
Вывод: Трехчлен нельзя разложить на множителиУравнение в конце шага 1 :
x 2 - 4x - 6 = 0
Шаг 2 :
Парабола, поиск вершины :
2.
 1 Найти вершину y = x 2 -4x-6
1 Найти вершину y = x 2 -4x-6Параболы имеют наивысшую или низшую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 1 , положителен (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ax 2 +Bx+C, x координата вершины определяется как -B/(2A) .
 В нашем случае координата x составляет 2,0000
В нашем случае координата x составляет 2,0000Подключение к формуле параболы 2.0000 для x Мы можем рассчитать y -координату:
Y = 1,0 * 2,00 * 2,00 — 4,0 * 2,00 — 6,0
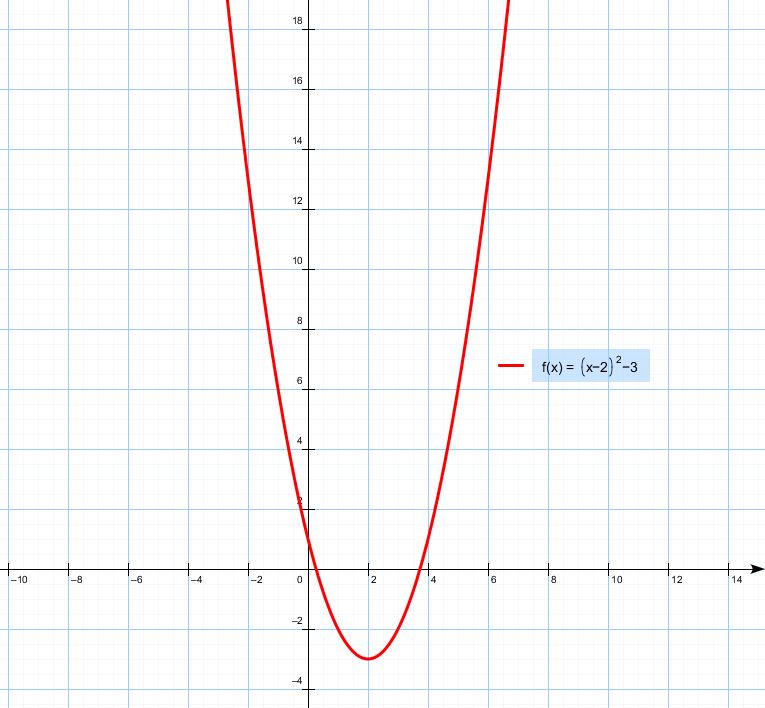
или Y = -10,000Parabola, Графическая вершина и X-перехваты:
Корневой график для: y = x 2 -4x-6
Ось симметрии (штриховая) {x}={ 2,00}
Вершина в {x,y} = { 2,00,- 10.00}
x -Перехваты (корни):
Корень 1 при {x,y} = {-1,16, 0,00}
Корень 2 при {x,y} = {5,16, 0,00}Решите квадратное уравнение, заполнив квадрат
2.2 Решение x 2 -4x-6 = 0 путем заполнения квадрата.
Прибавьте 6 к обеим частям уравнения:
x 2 -4x = 6Теперь немного хитрости: возьмем коэффициент при x, равный 4, разделим на два, получим 2, и, наконец, возведем его в квадрат, получим 4
Добавьте 4 к обеим частям уравнения:
В правой части мы имеем :
6 + 4 или (6/1)+(4/1)
Общий знаменатель двух дробей равен 1 Сложение (6/1)+(4/1) дает 10 /1
Таким образом, прибавив к обеим сторонам, мы окончательно получим :
x 2 -4x+4 = 10Добавление 4 дополнит левую часть до полного квадрата:
2
x 2 -4x+4 = 9 826 ( x-2) • (x-2) =
(x-2) 2
Вещи, равные одной и той же вещи, также равны друг другу. С
С
x 2 -4x+4 = 10 и
x 2 -4x+4 = (x-2) 2
тогда по закону транзитивности
(x-2)
10Мы будем называть это уравнение уравнением. #2.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
9 1 82x-21819 Теперь, применяя принцип квадратного корня к уравнению. #2.2.1 получаем:
(x-2) 2 равен
(x-2) 2/2 =
(x-2) 1 2
x-2 = √ 10Добавьте 2 к обеим частям, чтобы получить:
x = 2 + √ 10Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 — 4x — 6 = 0
Имеет два решения:
x = 2 + √ 10
или
x = 2 — √ 10Решение квадратичного уравнения с использованием квадратичной формулы
2.3 Решение x 2 -4x -6 = 0 по квадратичной формуле .


 3$.
3$.
 Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.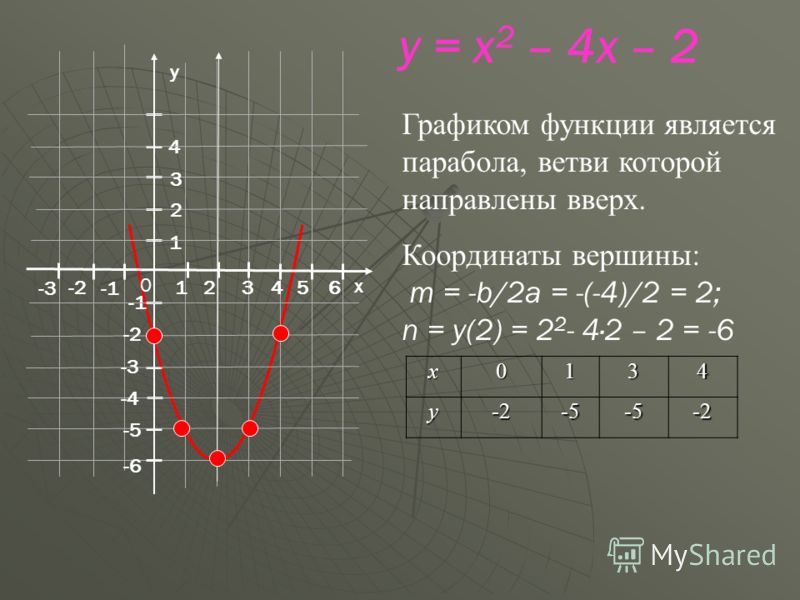

 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.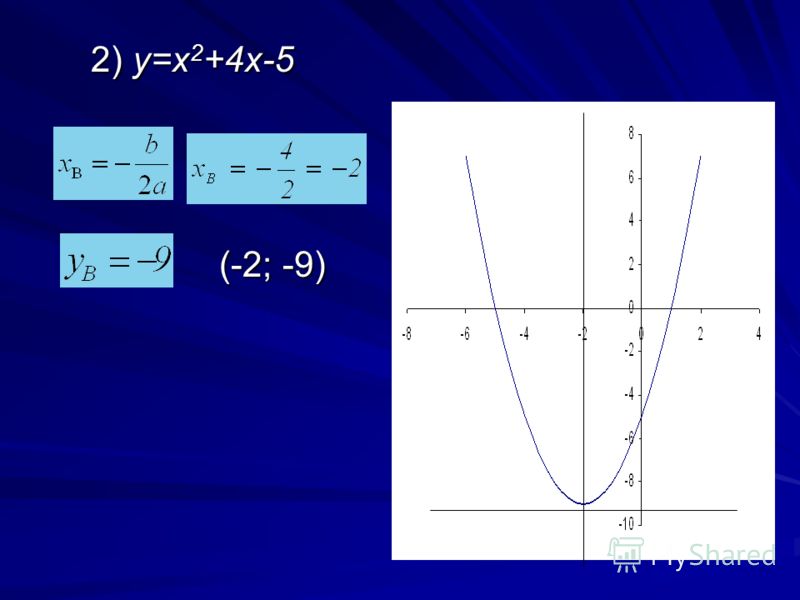 2} — 4\left({\frac{{ — 1 + \sqrt 5 }}{2}} \right) }
= { — \frac{1}{8}\left({1 — 3\sqrt 5 + 15 — 5\sqrt 5 } \right) + \frac{1}{2}\left({1 — 2\sqrt 5 + 5} \right) + 2\left({1 — \sqrt 5 } \right) }
= { — \cancel{2} + \cancel{\sqrt 5} + 3 — \cancel{\sqrt 5} + \cancel{2} — 2\sqrt 5 }
= {3 — 2\sqrt 5 \approx — 1,47.}
\]
Разделим ось \(t\) на \(5\) интервалов:
\[
{\left({ — \infty , — 2} \right),}\;\;
{\left({ — 2, — 1} \right),}\;\;
{\left({ — 1,\frac{1}{3}} \right),}\;\;
{\left({\frac{1}{3},\frac{2}{3}} \right),}\;\;
{\left({\frac{2}{3}, + \infty } \right).}
\]
На первом интервале \(\left({ — \infty , — 2} \right)\) значения \(x\) и \(y\) возрастают от \(-\infty\) до \(x\left({ — 2} \right) = — 2\)
и \(y\left({ — 2} \right) = 8.\) Это схематически показано на рисунке \(15b.\)
2} — 4\left({\frac{{ — 1 + \sqrt 5 }}{2}} \right) }
= { — \frac{1}{8}\left({1 — 3\sqrt 5 + 15 — 5\sqrt 5 } \right) + \frac{1}{2}\left({1 — 2\sqrt 5 + 5} \right) + 2\left({1 — \sqrt 5 } \right) }
= { — \cancel{2} + \cancel{\sqrt 5} + 3 — \cancel{\sqrt 5} + \cancel{2} — 2\sqrt 5 }
= {3 — 2\sqrt 5 \approx — 1,47.}
\]
Разделим ось \(t\) на \(5\) интервалов:
\[
{\left({ — \infty , — 2} \right),}\;\;
{\left({ — 2, — 1} \right),}\;\;
{\left({ — 1,\frac{1}{3}} \right),}\;\;
{\left({\frac{1}{3},\frac{2}{3}} \right),}\;\;
{\left({\frac{2}{3}, + \infty } \right).}
\]
На первом интервале \(\left({ — \infty , — 2} \right)\) значения \(x\) и \(y\) возрастают от \(-\infty\) до \(x\left({ — 2} \right) = — 2\)
и \(y\left({ — 2} \right) = 8.\) Это схематически показано на рисунке \(15b.\)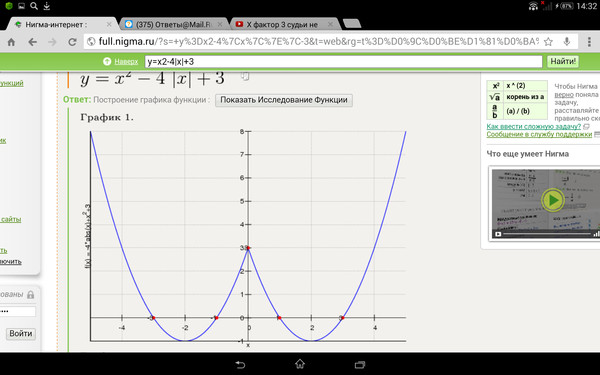 \) Здесь мы имеем участок убывающей кривой \(y\left(x \right).\)
Она пересекает ось ординат в точке \(\left({0,3 + 2\sqrt 5 } \right).\)
\) Здесь мы имеем участок убывающей кривой \(y\left(x \right).\)
Она пересекает ось ординат в точке \(\left({0,3 + 2\sqrt 5 } \right).\) 2} + 2t — 1}} }
= {\frac{{\cancel{3}\left({t + 2} \right)\left({t — \frac{2}{3}} \right)}}{{\cancel{3}\left({t + 1} \right)\left({t — \frac{1}{3}} \right)}} }
= {\frac{{\left({t + 2} \right)\left({t — \frac{2}{3}} \right)}}{{\left({t + 1} \right)\left({t — \frac{1}{3}} \right)}}.}
\]
Изменение знака производной \(y»\left(x \right)\) показано на рисунке \(15c.\) Видно, что в точке \(t = — 2,\)
т.е. на границе \(I\)-го и \(II\)-го интервалов кривая имеет максимум, а при \(t = \large\frac{2}{3}\normalsize\)
(на границе \(IV\)-го и \(V\)-го интервалов) существует минимум. При переходе через точку \(t = \large\frac{1}{3}\normalsize\)
производная также меняет знак с плюса на минус, но в этой области кривая \(y\left(x \right)\) не является однозначной функцией. Поэтому указанная точка экстремумом
не является.
2} + 2t — 1}} }
= {\frac{{\cancel{3}\left({t + 2} \right)\left({t — \frac{2}{3}} \right)}}{{\cancel{3}\left({t + 1} \right)\left({t — \frac{1}{3}} \right)}} }
= {\frac{{\left({t + 2} \right)\left({t — \frac{2}{3}} \right)}}{{\left({t + 1} \right)\left({t — \frac{1}{3}} \right)}}.}
\]
Изменение знака производной \(y»\left(x \right)\) показано на рисунке \(15c.\) Видно, что в точке \(t = — 2,\)
т.е. на границе \(I\)-го и \(II\)-го интервалов кривая имеет максимум, а при \(t = \large\frac{2}{3}\normalsize\)
(на границе \(IV\)-го и \(V\)-го интервалов) существует минимум. При переходе через точку \(t = \large\frac{1}{3}\normalsize\)
производная также меняет знак с плюса на минус, но в этой области кривая \(y\left(x \right)\) не является однозначной функцией. Поэтому указанная точка экстремумом
не является.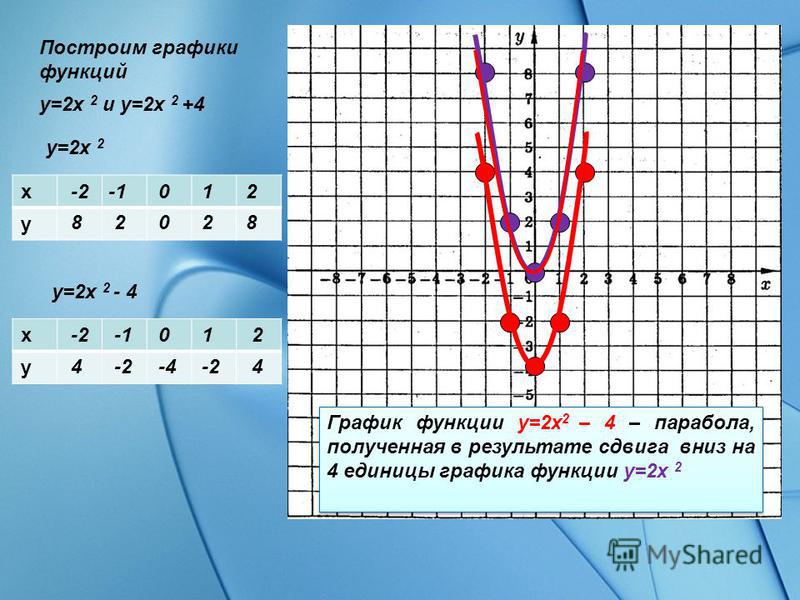 \]
Следовательно, вторая производная меняет свой знак на противоположный при переходе через следующие точки (рис.\(15с\)):
\[
{{t_1} = — 1:\;\;x\left({ — 1} \right) = 1,}\;\;
{y\left({ — 1} \right) = 5;}
\]
\[
{{t_2} = \frac{{9 — \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,24;}\;\;
{y\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,91;}
\]
\[
{{t_3} = \frac{1}{3}:}\;\;
{x\left({\frac{1}{3}} \right) = — \frac{5}{{27}},}\;\;
{y\left({\frac{1}{3}} \right) = — \frac{{29}}{{27}};}
\]
\[
{{t_4} = \frac{{9 + \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,1;}\;\;
{y\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,8.}
\]
Поэтому указанные точки представляют собой точки перегиба кривой \(y\left(x \right).\)
\]
Следовательно, вторая производная меняет свой знак на противоположный при переходе через следующие точки (рис.\(15с\)):
\[
{{t_1} = — 1:\;\;x\left({ — 1} \right) = 1,}\;\;
{y\left({ — 1} \right) = 5;}
\]
\[
{{t_2} = \frac{{9 — \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,24;}\;\;
{y\left({\frac{{9 — \sqrt {105} }}{6}} \right) \approx 0,91;}
\]
\[
{{t_3} = \frac{1}{3}:}\;\;
{x\left({\frac{1}{3}} \right) = — \frac{5}{{27}},}\;\;
{y\left({\frac{1}{3}} \right) = — \frac{{29}}{{27}};}
\]
\[
{{t_4} = \frac{{9 + \sqrt {105} }}{6}:}\;\;
{x\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,1;}\;\;
{y\left({\frac{{9 + \sqrt {105} }}{6}} \right) \approx 40,8.}
\]
Поэтому указанные точки представляют собой точки перегиба кривой \(y\left(x \right).\)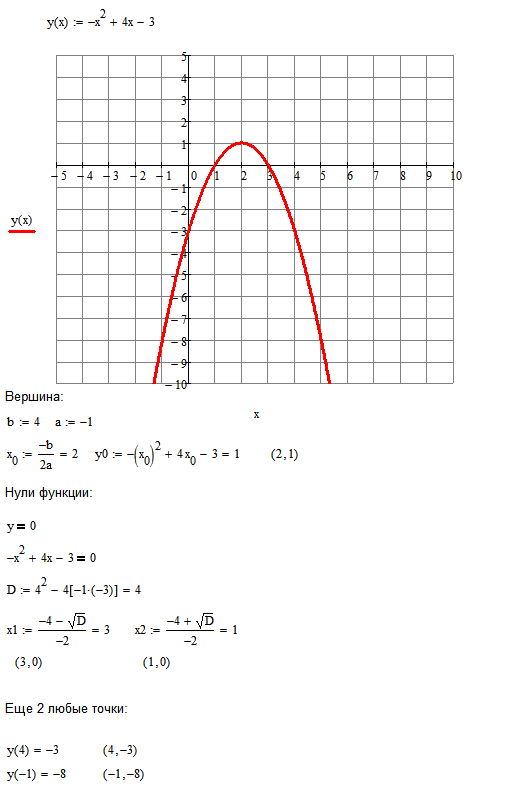 11.
11. 1 Факторизация x 2 -4x-6 Первый член 918 918 , x 2 его коэффициент равен 1 .
1 Факторизация x 2 -4x-6 Первый член 918 918 , x 2 его коэффициент равен 1 .  1 Найти вершину y = x 2 -4x-6
1 Найти вершину y = x 2 -4x-6 В нашем случае координата x составляет 2,0000
В нашем случае координата x составляет 2,0000 С
С 