Уравнение модуль х » задачи
модуль »
Найти мах целое значение параметра а при котором уравнение имеет 2 корня [x+3](x-3) разделить на а-3 =1
х+3 под знаком модуль
Решение:Запишем уравнение в виде
|x+3|(x-3)=a-3
а≠3
Строим график функции
у=|x+3|(x-3)
На (-∞;-3)
|x+3|=-x-3
cтроим график у=-х²+9
на [-3;+∞)
|x+3|=x+3
строим график у=х²-9График функции у=a-3 при разных значения а — прямые, параллельные оси ох.
Графики такого вида пересекаются с графиком у=|x+3|(x-3) в двух точка только в двух случаях
a-3=0, но по условию а≠3
или
a-3=-9 ⇒ а=-6О т в е т. при а = — 6
решить уравнения
1.5*(-1+9x)-5=-1
*- это умножить
2. x/6+x/12+x= -34/4
/- это дробь
Минус относится к полной дроби
3. (2x+5)*(8-x)=0
*- это умножить
4. x/-5= -7/9
Минус относится к 7
5. |x-3|=8
|- это модуль
Решение: 1)-5*(-1+9x)-5 = -1
5 — 45x — 5 = -1
-45x = — 1
x = 1/45
2) x/6 + x/12 + x = -34/4 (*12, Домножим все на 12)
2x + x + 12x = — 102
15x = -102
x = — 6,8
3) (2x+5)*(8-x)= 0 (нужно чтобы хотябы один из множителей = 0)=>
2x + 5 = 0 или 8-x = 0
2x = -5 -x = -8
x = -2. 2-11х-40=0 Д=21 Х1=-2,5 х2= 8 4) х/-5=-7/9 9х=35 Х=35/9 Х=3 8/9 5){х-3}=8 Х-3=8 Х=11 Или -х+3=8 -х=5 Х=-5
2-11х-40=0 Д=21 Х1=-2,5 х2= 8 4) х/-5=-7/9 9х=35 Х=35/9 Х=3 8/9 5){х-3}=8 Х-3=8 Х=11 Или -х+3=8 -х=5 Х=-5Помогите решиь тест
1) Мастер, делая по 18 деталей в час, изготовил все детали за 5 часов. Если он будет делать по 20 деталей в час, то за часов изготовит все детали
2) Сравните числа: -2/5и-3/4
3) Выполните действие:(-9,2:4 целых3/5+3целых1/4)*(-0,8)-Просто ответ
4) Тоже самое:-8*(-7+23):64-3
5) Решите уравнение 5х+2=1/2
/////-палочка
9
6) Решите уравнение (2х+3)-1,5=-0,5
7) Решите уравнение /2х+3/=19 //-Это модуль
8) Решите уравнение (3х-1)(х+4)=0
9) Представьте в виде десятичной периодической дроби число:2целых3/22
Решение: 1) 4.5 ч
2) $$ — \frac{2}{5} \ > \ — \frac{3}{4} $$
3) $$ (\frac{-9.2}{4.6} +3.25)*(-0.8)=(-2+3.25)*(-0.8)=1.25*(-0.8)=-1 $$
4) $$ \frac{-8*(-7+23)}{64} -3= -2-3=-5 $$
5) $$ 5x+2= 0.5 $$⇒$$ x= \frac{-1.5}{5} $$⇒$$ x=-0.3 $$
6) $$ (2x+3)-1.5=-0.5\\2x+3=1 \\ 2x=-2\\x=-1 $$
7) $$ \left \{ {{2x+3=19, x \geq 0} \atop {-2x+3=19, x\ 8) 3x-1=0 x+4=0
x=$$ \frac{1}{3} $$ x=-4
9) 2. 1(36)
1(36)1)18*5=90 деталей за 5 часов
90:20=4,5 часов
2)-2/5<-3/4,0,4<-0,75
3)(-9,2:4 3/5+3 1/4)*(-0,8)=-1
4)-8*(-7+23):64-3=-5
5)5х+2=1/2
5х=-1,5
х=-1,5:5
х=-0,3
6)(2х+3)-1,5=-0,5
2х=-0,5+1,5-3
2х=-2
х=-1
7)|2х+3|=19
2х=19-3
2х=16
х=16:2
х=±8
8)(3х-1)(х+4)=0
3х-1=0
3х=1
х1=1/3
х+4=0
х2=-4
Ответ: х1=1/3
9)2 3/22=47/22=2,136(36)х — 4 = модуль х-2 дробь х -2
Решите уравнение
Решение: x-4=Ix-2I/(x-2)Первый случай:
x-4=(x-2)/(x-2)
x-4=1
x=5
Второй случай:
x-4=-(x-2)/(x-2)
x-4=-1
x=3
Ответ: x=3; x=5
$$ x-4=\frac {|x-2|}{x-2}; $$
если х-2>0 т. е. x>2, то |x-2|=x-2 и уравнение принимает вид
x-4=1
x=4+1
x=5 — удовлетворяет
если х-2<0 т. е. x<2, то |x-2|=-(x-2) и уравнение принимает вид
x-4=-1
x=4-1
x=3 — не удовлетворяет
ответ: 5
( — 2 дробь 3 + 5 дробь 12) + (- 0,45)=
I I- это модуль числа
Ix — 3I=-6-сколько решений имеет это уравнение
Решение: $$ (-\frac{2}{3}+\frac{5}{12})-\frac{45}{100}=\frac{-8+5}{12}-\frac{9}{20}=\\=-\frac{3}{12}-\frac{9}{20}=-\frac{1}{4}-\frac{9}{20}=\frac{-5-9}{20}=-\frac{14}{20}=0,7 $$Ix — 3I=-6
имеет 2 решения
1) когда $$ Ix — 3I\geq0 $$ 2)Ix — 3I
тогда x-3=-6 тогда -x+3=-6
x=-6+3 -x=-6-3
x=-3 -x=-9
x=9
Сума модулей корней квадратного уравнения 4x²+kx-3=0 равно 2,
при этом модуль отрицательного корня больше от положительного. 2 \\ x_1=\frac{4-8}{2*4}=-\frac{1}{2}<0 \\ x_2=\frac{4+8}{2*4}=\frac{3}{2}>0 \\ |x_1|<|x_2| $$- не подходит
2 \\ x_1=\frac{4-8}{2*4}=-\frac{1}{2}<0 \\ x_2=\frac{4+8}{2*4}=\frac{3}{2}>0 \\ |x_1|<|x_2| $$- не подходит
ответ: k=4Как мне кажется решение будет такое
Решить уравнение
l l — модуль
X — переменная
> — знак «больше»
< — знак «меньше»
УР-Е: lxl + l2x-1l — x > 1
Решение: Уравнение выглядит так : | x | — | 2x — 1| больше x + 1
Надо снимать знак модуля. При этом учесть, что | x| = x при х ≥ 0
| x| = — x при х меньше 0
первый модуль =0 при х =0, второй модуль = 0 при х = 1/2
Вся числовая прямая разбилась на промежутки:
-∞ 0 1/2 +∞
Надо решать 3 уравнения ( относительно каждого промежутка)
а) (-∞; 0)
Снимаем знак модуля
-х -(2х — 1) больше х + 1
-х -2х +1 больше х +1
-4х больше 0
х меньше 0
б) (0; 1/2)
Снимаем знак модуля
х -(2х — 1) больше х +1
х — 2х +1 больше х +1
-2х больше 0
х меньше 0 (не подходит)
в) (1/2 ; +∞)
х + 2х -1 больше х +1
2х больше 2
х больше 1Уравнения с модулем.
 2 — 3x| = 0
2 — 3x| = 0
||x + 1| — 4| = 3
|||x — 5| — 5| — 5| = 5
|8 — |x — 2|| = 7
|x + 1| + |5 — x| = 2
|1 — x| + |x + 2| = 3
|8 + x| + |x — 7| = 10
||2x + 3| — 4| = xВалерий Волков 7 29.05.2017
Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!
Новости образования
ЕГЭ по математике
Профильный уровень
Задание 1 Задание 2
Задание 3 Задание 4
Задание 5 Задание 6
Задание 7 Задание 8
Задание 9 Задание 10
Задание 11 Задание 12
Задание 13 Задание 14
Задание 15 Задание 16
Задание 17 Задание 18
Задание 19 Задание 20
Задание 21
ГИА по математике
Задача 1 Задача 2
Задача 3 Задача 4
Задача 5 Задача 6
Задача 7 Задача 8
Задача 9 Задача 10
Задача 11 Задача 12
Задача 13 Задача 14
Задача 15 Задача 16
Задача 17 Задача 18
Задача 19 Задача 20
Задача 21 Задача 22
Задача 23 Задача 24
Задача 25 Задача 26
Демонстрационные варианты ОГЭ по математике
Математика.
 5 класс.
5 класс.Натуральные числа
Обыкновенные дроби
Десятичные дроби
Проценты
Математика. 6 класс.
Делимость чисел
Сложение и вычитание дробей с разными знаменателями
Умножение и деление обыкновенных дробей
Отношения и пропорции
Положительные и отрицательные числа
Измерение величин
Математика. 7 класс.Преобразование выражений
Многочлены
Формулы сокращенного умножения
Математика. 8 класс.
Модуль числа. Уравнения и неравенства.
Квадратные уравнения
Квадратные неравенства
Уравнения с параметром
Задачи с параметром
Математика. 9 класс.
Функции и их свойства
Прогрессии
Векторы
Комбинаторика, статистика и теория вероятностей
Математика.
 10 — 11 класс.
10 — 11 класс.Числовые функции
Тригонометрические функции
Тригонометрические уравнения
Преобразование тригонометрических выражений
Производная
Степенные функции
Показательная функция
Логарифмические функции
Первообразная и интеграл
Уравнения и неравенства
Комбинаторика
Создаёте видеоуроки?
Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.
Актуально
Физкультминутки для школьников и дошкольников
Подготовка к ЕГЭ Подготовка к ОГЭ© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
алгебраическое предварительное исчисление — Решение модульного неравенства $|x — 1| + |x — 6|\le11$ геометрически
спросил
Изменено 6 лет, 6 месяцев назад
Просмотрено 519 раз
Найдите все возможные значения $x$, для которых $x$ и для которых выполняется неравенство $$|x — 1| + |x — 6|\le11$$ верно.

Я знаю, что это можно легко решить, взяв $3$ наблюдений за $x$, а затем взяв пересечение этих $3$ наблюдений. Решение будет $-2\ge x\le9$.
Но предположим, если я интерпретирую это следующим образом:
Какое число $x$ удовлетворяет условию, что расстояние между $x$ и $6$ плюс расстояние между $x$ и $1$ меньше или равно $11$?
Мне бы лучше понять, как решать подобные задачи геометрически, интуитивно, используя числовую прямую.
- алгебра-предварительное исчисление
- геометрия
- неравенство
- абсолютное значение
5
$\begingroup$
Как вы сказали, мы ищем точки, для которых:
$$(\text{расстояние до $1$})+(\text{расстояние до $6$})\leq 11.$$ Первое, что сейчас приходит мне на ум, — это эллипс.
Сначала рассмотрим все $x\in \mathbb C$, для которых $\vert x-1\vert +\vert x-6\vert \leq 11$.
 Все точки этого «закрашенного» эллипса, лежащие на действительной оси, и есть те, которые нам нужны.
Все точки этого «закрашенного» эллипса, лежащие на действительной оси, и есть те, которые нам нужны.Нетрудно представить, что это будут за точки. Если мы находимся на реальной линии, то наша самая дальняя левая точка, $x_\ell$, будет лежать слева от $1$. Таким образом, расстояние до $6$ будет не менее пяти. Итак, у нас есть $$\vert x_\ell-1\vert+\vert x_\ell -6\vert=2\vert x_\ell-1\vert+5=11. $$ А поскольку $x_\ell $ находится слева от $1$, это означает, что $x_\ell=-2$. Аналогично получаем, что $x_r=9$.
Итак, мы нашли, что $-2\leq x\leq 9$, с помощью геометрических методов.
$\endgroup$ 91$ (действительная числовая прямая), каждая точка лежит на прямой, проходящей через точки $1$ и $6$. Таким образом, есть три возможности для $1, x$ и $6$: $x-1-6$, $1-x-6$ или $1-6-x$.
CASE: $x-1-6$
Тогда $ x \le 1 \le 6$
\begin{align} |1-х| + |х-6| &\ле 11\\ (1-x) + (6-x) &\le 11\\ -2x &\le 4\\ х&\ге-2\\ х &\в [-2,1] \end{align}
CASE: $1-x-6$
Тогда $1 \le x \le 6$ и $|1-x| + |х-6| = |1-6| = 5$
\begin{align} |1-х| + |х-6| &\ле 11\\ 5&\ле 11\ х &\в [1,6] \end{выравнивание}
CASE: $1-6-x$
Тогда $1 \le 6 \le x$
\begin{align} |1-х| + |х-6| &\ле 11\\ (х-1) + (х-6) &\le 11\ 2x &\le 18\\ х &\ле 9\\ х &\ в [6,9] \end{align}
Итак, $x \in [-2,9]$
$\endgroup$
1
$\begingroup$
Добавить графическое решение:
$$y=|x-1|+|x-6|; у=11$$ $$x \in [x_1;x_2] =[-2;9]$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
абстрактная алгебра — Разница между $\mathbb{Q}[X]/(X-1) \otimes_\mathbb{Q} \mathbb{Q}[X]/(X+1)$ и $\mathbb{Q} [X]/(X-1)\otimes_{\mathbb{Q}[X]}\mathbb{Q}[X]/(X+1)$?
спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 408 раз
$\begingroup$
Исходная задача на самом деле хочет, чтобы я нашел, какой из модулей является нулевым. Но сначала, в чем разница между $\mathbb{Q}[X]/(X-1) \otimes_\mathbb{Q} \mathbb{Q}[X]/(X+1)$ и $\mathbb{ Q}[X]/(X-1)\otimes_{\mathbb{Q}[X]}\mathbb{Q}[X]/(X+1)$? Я новичок в концепции «тензорного продукта», и мне трудно это понять.
Согласно определению, мы рассматриваем $\mathbb{Q}[X]/(X-1)$ как модуль над $\mathbb{Q}$ в первом, а его рассматриваем как модуль над $\ mathbb{Q}[X]$ во втором.
 Но как это меняет ситуацию?
Но как это меняет ситуацию?Точнее, поскольку $\gcd(X-1,X+1)=1$ в $\mathbb{Q}[X]$, значит $\mathbb{Q}[X]/(X-1)\ otimes_{\mathbb{Q}[X]}\mathbb{Q}[X]/(X+1)$ — нулевой модуль, поскольку существуют $f,g\in\mathbb{Q}[X]$ такие что $(X-1)f + (X+1)g = 1$. В результате для любого $r\otimes s=1\cdot (r\otimes s)=\left((X-1)f + (X+1)g\right)\cdot(r\otimes s)= (X-1)(fr\otimes s)+(X+1)(gr\otimes s) = 0$
Но я не знаю, как быть с другим.
- абстрактная алгебра
- тензорные произведения
$\endgroup$
1
$\begingroup$
Что вы упускаете из виду, так это то, что кольцо, которое вы тензорите, влияет на скаляры, которые вы можете перемещать слева направо в тензорном произведении. $\def\Q{\mathbb{Q}}$
Фактически, первое из ваших тензорных произведений равно $\mathbb{Q}$, а второе равно нулю.
 Сначала мы покажем второе (ваше доказательство также работает и является лучшим доказательством, потому что оно обобщает, но я хочу привести другое доказательство, подчеркивающее «скольжение»). Пусть $f$ произвольно в $\mathbb{Q}[x]/(x-1)$. Тогда $xf = f$. Для произвольного $g$ в $\mathbb{Q}[x]/(x+1)$ имеем $xg = -g$.
Сначала мы покажем второе (ваше доказательство также работает и является лучшим доказательством, потому что оно обобщает, но я хочу привести другое доказательство, подчеркивающее «скольжение»). Пусть $f$ произвольно в $\mathbb{Q}[x]/(x-1)$. Тогда $xf = f$. Для произвольного $g$ в $\mathbb{Q}[x]/(x+1)$ имеем $xg = -g$.Итак, учитывая $f \otimes g \in \Q[x]/(x-1) \otimes_{\Q[x]} \Q[x]/(x+1)$, мы имеем $f \otimes g = (xf) \otimes g = f \otimes (xg) = -(f\otimes g)$, поэтому $f \otimes g = 0$; поскольку каждый элемент тензорного произведения является суммой «простых тензоров» (имеющих вид $f \otimes g$), тензорное произведение равно нулю.
В другом примере существует $\Q$-модульный изоморфизм $\mathbb{Q}[x]/(x+1) = \mathbb{Q}$, заданный вычислением многочлена в $-1$, и аналогично для другого модуля, так что тензорное произведение равно $\Q \otimes_\Q \Q$, что естественно изоморфно $\mathbb{Q}$.
Soapbox: вы услышите много лекций о том, что лучший способ думать о тензорном произведении — это его универсальное свойство, что верно, но практический способ думать о нем как о «сумме символов $a \ otimes b$, где вы можете двигать букву r слева направо» также очень важны и их легче освоить поначалу.


 2-11х-40=0 Д=21 Х1=-2,5 х2= 8 4) х/-5=-7/9 9х=35 Х=35/9 Х=3 8/9 5){х-3}=8 Х-3=8 Х=11 Или -х+3=8 -х=5 Х=-5
2-11х-40=0 Д=21 Х1=-2,5 х2= 8 4) х/-5=-7/9 9х=35 Х=35/9 Х=3 8/9 5){х-3}=8 Х-3=8 Х=11 Или -х+3=8 -х=5 Х=-5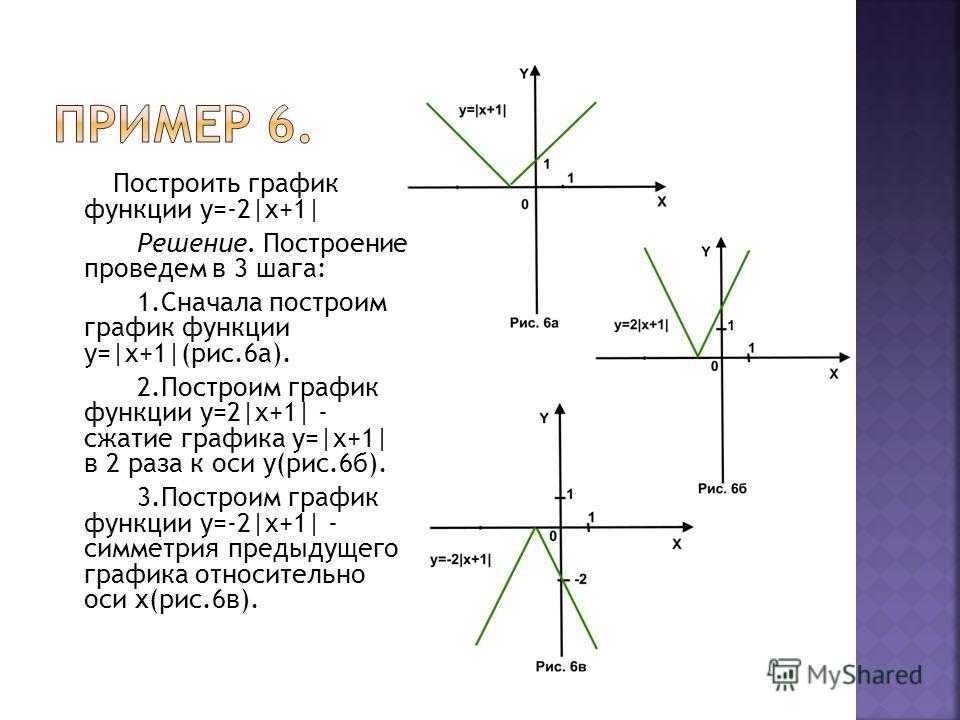 1(36)
1(36) 2 \\ x_1=\frac{4-8}{2*4}=-\frac{1}{2}<0 \\ x_2=\frac{4+8}{2*4}=\frac{3}{2}>0 \\ |x_1|<|x_2| $$- не подходит
2 \\ x_1=\frac{4-8}{2*4}=-\frac{1}{2}<0 \\ x_2=\frac{4+8}{2*4}=\frac{3}{2}>0 \\ |x_1|<|x_2| $$- не подходит 2 — 3x| = 0
2 — 3x| = 0 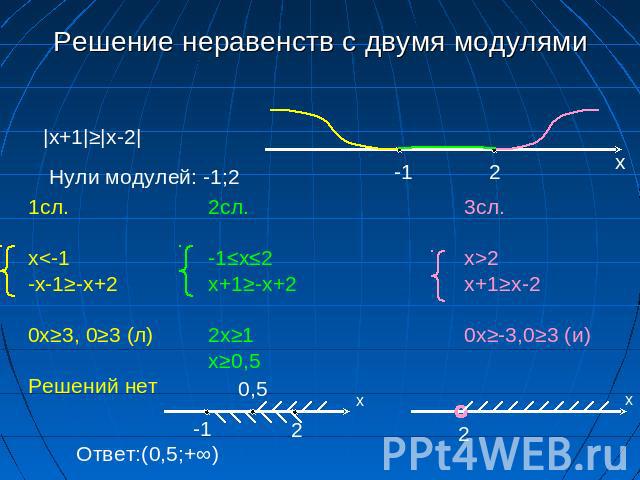 5 класс.
5 класс. 10 — 11 класс.
10 — 11 класс.

 Все точки этого «закрашенного» эллипса, лежащие на действительной оси, и есть те, которые нам нужны.
Все точки этого «закрашенного» эллипса, лежащие на действительной оси, и есть те, которые нам нужны.
 Но как это меняет ситуацию?
Но как это меняет ситуацию? Сначала мы покажем второе (ваше доказательство также работает и является лучшим доказательством, потому что оно обобщает, но я хочу привести другое доказательство, подчеркивающее «скольжение»). Пусть $f$ произвольно в $\mathbb{Q}[x]/(x-1)$. Тогда $xf = f$. Для произвольного $g$ в $\mathbb{Q}[x]/(x+1)$ имеем $xg = -g$.
Сначала мы покажем второе (ваше доказательство также работает и является лучшим доказательством, потому что оно обобщает, но я хочу привести другое доказательство, подчеркивающее «скольжение»). Пусть $f$ произвольно в $\mathbb{Q}[x]/(x-1)$. Тогда $xf = f$. Для произвольного $g$ в $\mathbb{Q}[x]/(x+1)$ имеем $xg = -g$.