Пошаговое решение:
Шаг 1 :
6
Упростить —
Икс
Уравнение в конце шага 1 :
3 6 (———— - 9) - (— + 3) = 0 (х 2 ) х
Шаг 2 :
Преобразование целого в виде эквивалентной дроби:
2. 1 Прибавление целого к дроби
1 Прибавление целого к дроби
Преобразование целого в виде дроби, используя x в качестве знаменателя:
3 3 • х
3 = — = —————
1 х
Эквивалентная дробь: полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое
Общий знаменатель: эквивалентная дробь и другая дробь, участвующая в вычислении, имеют один и тот же знаменатель
Сложение дробей, имеющих общий знаменатель:
2.2 Сложение двух эквивалентных дробей
Сложение двух эквивалентных дробей, которые теперь имеют общий знаменатель
Соедините числители, подставьте сумму или разность к общему знаменателю, затем приведите к наименьшему числу, если возможно:
6 + 3 • x 3x + 6
"="
х х
Уравнение в конце шага 2 :
3 (3x + 6) (———— - 9) — ———————— = 0 (х 2 ) хШаг 3 :
3 Упростить —— x 2
Уравнение в конце шага 3 :
3 (3x + 6) (—— - 9) — ———————— = 0 х 2 х
Шаг 4:
Переписывание целого в качестве эквивалентной фракции:
4. 1 Вычитание целого из фракции
1 Вычитание целого из фракции
Перепишите целое фракцию, используя x 2 в качестве деноминатора:
99919 2 2 2 в качестве деноминатора:9 99921 2 2 . 9 = — = —————— 1 x 2Сложение дробей с общим знаменателем:
4.2 Сложение двух эквивалентных дробей
3 - (9 • x 2 ) 3 - 9x 2
"="
x 2 x 2 Уравнение в конце шага 4 :
(3 - 9x 2 ) (3x + 6)
————————— ————————— = 0
х 2 х
Шаг 5 :
Шаг 6 :
Вытягивание одинаковых членов:
6.1 Вытягивание одинаковых факторов :
3 — 9x 2 = -3 • (3x 2 — 1)
Пыхая фактор как разница в квадратах:
6.2. Факторинг: 3x 2 — 1
. два полных квадрата, A 2 — B 2 можно разложить на (A+B)• (AB) B 2 =
A 2 — AB + AB — B 2 =
A 2 — B 2
Примечание. AB = BA — это коммутативное свойство умножения.
AB = BA — это коммутативное свойство умножения.
Примечание. — AB + AB равно нулю и поэтому исключается из выражения.
Проверить : 3 не является квадратом !!
Правило: Биномиал нельзя разложить на множители как
разность двух полных квадратов )
Расчет наименьшего распространенного множественного множественного:
7.2. Найдите наименьшее распространенное множество
Левый знаменатель: x 2
Правый знаменатель: x
| Алгебраический Множитель | Левый Знаменатель | Правый Знаменатель | L.C.M = MAX {Слева, справа} |
|---|---|---|---|
| x | 2 | 1 | 2 |
Обозначим наименьшее общее кратное через L.C.M LEATE_M = L. Right_M = L.C.M/R_DENO = X
Наименее множество:
x 2
Мноря множители для двух дробей
Обозначьте левый множитель через Left_M
Обозначьте правый множитель через Right_M
Обозначьте левый знаменатель через L_Deno
Обозначите правый множитель с помощью R_DENO C.M/L_DENO = 1
C.M/L_DENO = 1 FRCHANCE имеют одинаковое числовое значение.
Например: 1/2 и 2/4 эквивалентны, y/(y+1) 2 и (y 2
Чтобы рассчитать эквивалентную дробь, умножьте числитель каждой дроби на соответствующий множитель.
Л. Мульт. • L. Num. -3 • (3x 2 -1)
"="
L.C.M x 2
Р. Мульт. • R.Число. 3 • (х+2) • х
"="
L.C.M x 2 Складываем дроби, имеющие общий знаменатель:
7.5 Складываем две эквивалентные дроби
-3 • (3x 2 -1) - (3 • (x+2) • x) -12x 2 - 6x + 3
"="
x 2 x 2 Шаг 8:
Вытягивание, как термины:
8.1. Вытягивание, как факторы:
-12x 2 -6X + 3 = -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 • -3 •.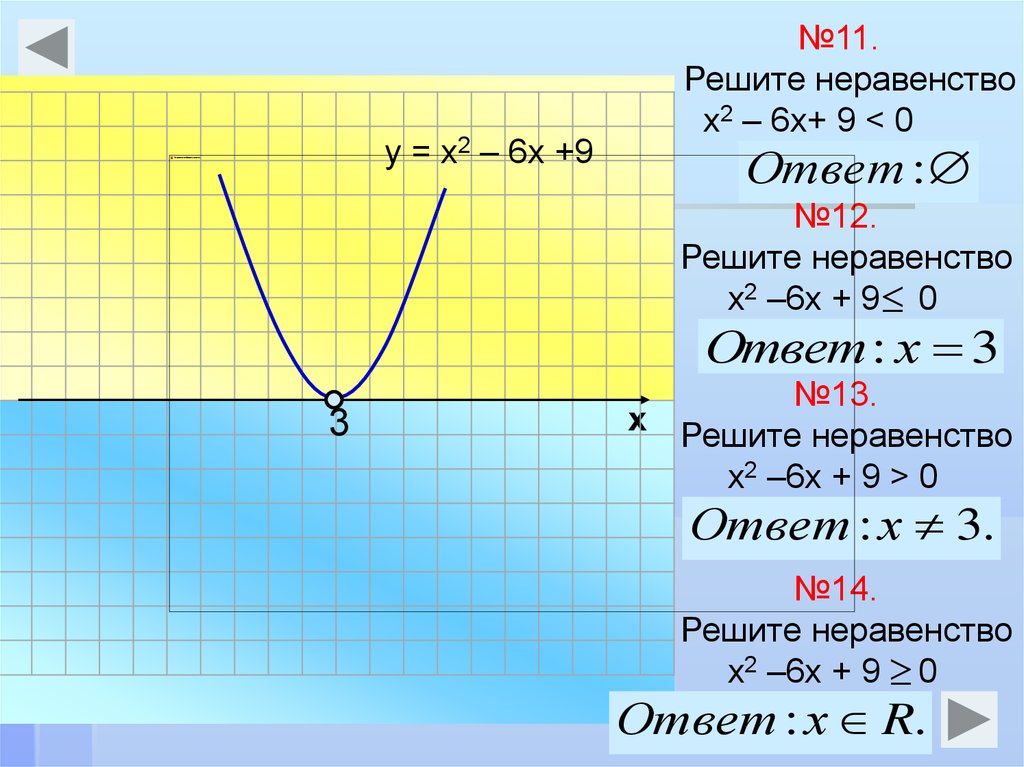 — 1)
— 1)
Попытка факторинга путем разделения среднего члена
8.2 Факторизация 4x 2 + 2x — 1
Первый член равен 4x 2 , его коэффициент равен 4 .
Средний член равен +2 x , его коэффициент равен 2 .
Последний член, «константа», равен -1
Шаг-1: умножьте коэффициент первого члена на константу 4 • -1 = -4 равен коэффициенту среднего члена, который равен 2 .
| -4 | + | 1 | = | -3 | ||
| -2 | + | 2 | = | 0 | ||
| -1 | + | 4 | = | 3 |
Наблюдение: Невозможно найти два таких фактора!!
Вывод: Трехчлен нельзя разложить на множители
Уравнение в конце шага 8 :
-3 • (4x 2 + 2x - 1)
——————————————————— = 0
x 2 Шаг 9 :
Когда дробь равна нулю :
9.1 Когда дробь равна нулю ...
Если дробь равна нулю, ее числитель, часть, которая находится над дробной чертой, должна быть равна нуль.
Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
Вот как:
-3•(4x 2 +2x-1)
———————————— • х 2 = 0 • х 2
x 2 Теперь в левой части x 2 сокращает знаменатель, а в правой части ноль, умноженный на что-либо, по-прежнему равен нулю.
Теперь уравнение принимает вид :
-3 • (4x 2 +2x-1) = 0
Уравнения, которые никогда не бывают истинными :
9.2 Решите: -3 90 = 0 0 уравнение
A ненулевая константа никогда не равна нулю.
Парабола, нахождение вершины :
9.3 Найдите вершину y = 4x 2 +2x-1
Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум).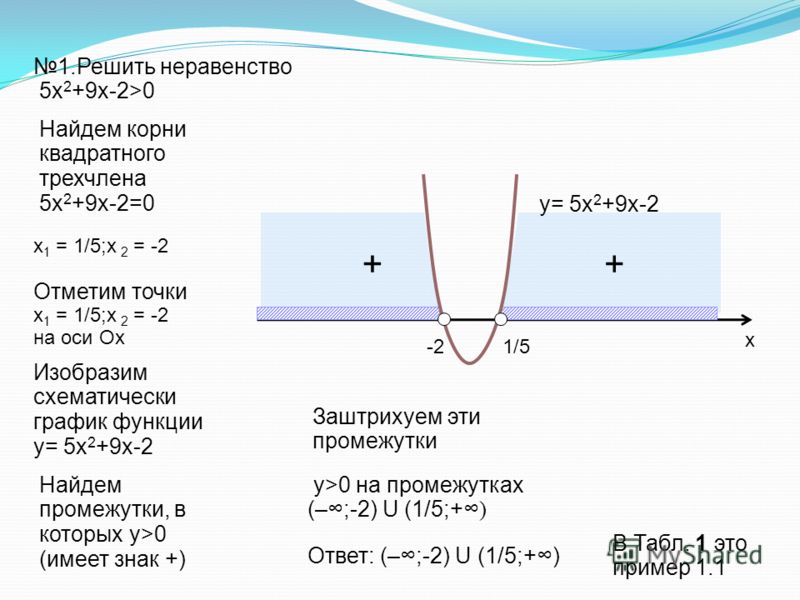 Мы знаем это еще до того, как нанесем на график «у», потому что коэффициент первого члена, 4 , положителен (больше нуля).
Мы знаем это еще до того, как нанесем на график «у», потому что коэффициент первого члена, 4 , положителен (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх, через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ax 2 +Bx+C, x-координата вершины определяется как -B/(2A) . В нашем случае координата x равна -0,2500
Подставив в формулу параболы -0,2500 вместо x, мы можем вычислить координату y:
y = 4,0 * -0,25 * -0,25 + 2,0 * -0,25 — 1,0
или y = -1,250
Vertexing Vertex and X Graphing Parabola, -Пересечения:
Корневой график для: y = 4x 2 +2x-1
Ось симметрии (пунктирная) {x}={-0,25}
Вершина в {x,y} = {-0,25,-1,25}
x -Отрезки (корни):
Корень 1 в точке {x,y} = {-0,81, 0,00}
Корень 2 в точке {x,y} = {0,31, 0,00}
Решить квадратное уравнение, заполнив квадрат
9. 4 Решение 4x 2 +2x-1 = 0, заполнив квадрат.
4 Решение 4x 2 +2x-1 = 0, заполнив квадрат.
Поделите обе части уравнения на 4, чтобы получить 1 в качестве коэффициента при первом члене:
x 2 +(1/2)x-(1/4) = 0
Прибавьте 1/4 к обеим частям уравнения:
x 2 +(1/2)x = 1/4
Теперь немного хитрости: возьмем коэффициент при x, равный 1/2, разделим на два, получим 1/4, и, наконец, возведите его в квадрат, что даст 1/16
Прибавляем 1/16 к обеим частям уравнения:
В правой части имеем:
1/4 + 1/16 Общим знаменателем двух дробей является 16 Складываем (4/16)+(1/16 ) дает 5/16
Таким образом, прибавив к обеим сторонам, мы наконец получим :
x 2 +(1/2)x+(1/16) = 5/16
полный квадрат:
x 2 +(1/2)x+(1/16) =
(x+(1/4)) • (x+(1/4)) =
(x+(1/4)) 2
То, что равно одному и тому же, равно и одно другому. Поскольку
x 2 +(1/2)x+(1/16) = 5/16 и
x 2 +(1/2)x+(1/16) = (x+(1/4)) 2
, тогда, согласно закону транзитивности,
(x+(1/4)) 2 = 5/16
Мы будем называть это уравнение уравнением #9. 4.1
4.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x+(1/4)) 2 is
(x+(1/4)) 2/2 =
(x+(1/4)) 1 =
x+(1/4)
Теперь, применяя принцип квадратного корня к уравнению. #9.4.1 получаем:
x+(1/4) = √ 5/16
Вычтем 1/4 с обеих сторон, чтобы получить:
x = -1/4 + √ 5/16
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное0941 или
x = -1/4 — √ 5/16
Обратите внимание, что √ 5/16 можно записать как
√ 5 / √ 16 , что равно √ 5 / 4
Согласно квадратичной формуле, x , решение для Ax 2 +Bx+C = 0 , где A, B и C – числа, часто называемые коэффициентами, определяется следующим образом:
-B ± √ B 2 -4AC
x = ————————
2A
В нашем случае A = 4
B = 2
C = -1
Accounlly, B2121212121212121212121212121212121212121212121211.

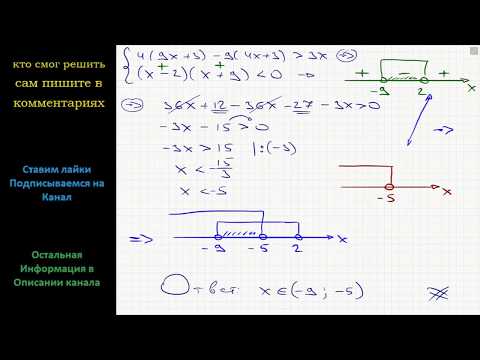 1 Когда дробь равна нулю ...
1 Когда дробь равна нулю ...