Корень в python — 6 способов извлечь квадратный корень из числа
Квадратный корень из числа — это значение, которое при умножении само на себя дает исходное число. Каждое положительное число имеет два квадратных корня (то же значение с положительным и отрицательным знаками). Ниже приводится запись квадратного корня:√25 = ±5
Для отрицательного числа результат извлечения квадратного корня включает комплексные числа, обсуждение которых выходит за рамки данной статьи.
Математическое представление квадрата числа
Все мы в детстве узнали, что, когда число умножается само на себя, мы получаем его квадрат. Также квадрат числа можно представить как многократное умножение этого числа. Попробуем разобраться в этом на примере.
Предположим, мы хотим получить квадрат 5. Если мы умножим число (в данном случае 5) на 5, мы получим квадрат этого числа. Для обозначения квадрата числа используется следующая запись:
52 = 25
При программировании на Python довольно часто возникает необходимость использовать функцию извлечения квадратного корня. Есть несколько способов найти квадратный корень числа в Python.
Есть несколько способов найти квадратный корень числа в Python.
1. Используя оператор возведения в степень
Копировать Скопировано Use a different Browser
num = 25 sqrt = num ** (0.5) print("Квадратный корень из числа "+str(num)+" это "+str(sqrt))
Вывод:
Квадратный корень из числа 25 это 5.0
Объяснение: Мы можем использовать оператор «**» в Python, чтобы получить квадратный корень. Любое число, возведенное в степень 0.5, дает нам квадратный корень из этого числа.
2. Использование math.sqrt()
Квадратный корень из числа можно получить с помощью функции sqrt() из модуля math, как показано ниже. Далее мы увидим три сценария, в которых передадим положительный, нулевой и отрицательный числовые аргументы в sqrt().
a. Использование положительного числа в качестве аргумента.
Копировать Скопировано Use a different Browser
import math num = 25 sqrt = math.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа 25 это 5.0.
b. Использование ноля в качестве аргумента.
Копировать Скопировано Use a different Browser
import math num = 0 sqrt = math.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа 0 это 0.0.
c. Использование отрицательного числа в качестве аргумента.
Копировать Скопировано Use a different Browser
import math num = -25 sqrt = math.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод:
Traceback (most recent call last):
File "C:\wb.py", line 3, in
sqrt = math.sqrt(num)
ValueError: math domain errorОбъяснение: Когда мы передаем отрицательное число в качестве аргумента, мы получаем следующую ошибку «math domain error».
sqrt() из модуля cmath.3. Использование cmath.sqrt()
Ниже приведены примеры применения cmath.sqrt().
а. Использование отрицательного числа в качестве аргумента.
Копировать Скопировано Use a different Browser
import cmath num = -25 sqrt = cmath.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа -25 это 5j.
Объяснение: Для отрицательных чисел мы должны использовать функцию sqrt() модуля cmath, которая занимается математическими вычислениями над комплексными числами.
b. Использование комплексного числа в качестве аргумента.
Копировать Скопировано Use a different Browser
import cmath num = 4 + 9j sqrt = cmath.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа (4+9j) это (2.6314309606938298+1.7100961671491028j).
Объяснение: Для нахождения квадратного корня из комплексного числа мы также можем использовать функцию cmath.sqrt().
4. Использование np.sqrt()
Копировать Скопировано Use a different Browser
import numpy as np num = -25 sqrt = np.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод:
... RuntimeWarning: invalid value encountered in sqrt Квадратный корень из числа -25 это nan
5. Использование scipy.sqrt()
Копировать Скопировано Use a different Browser
import scipy as sc num = 25 sqrt = sc.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
Вывод: Квадратный корень из числа 25 это 5.0.
Объяснение: Как и функция sqrt() модуля numpy, в scipy квадратный корень из положительных, нулевых и комплексных чисел может быть успешно вычислен, но для отрицательных возвращается nan с RunTimeWarning.
6. Использование sympy.sqrt()
Копировать Скопировано Use a different Browser
import sympy as smp num = 25 sqrt = smp.sqrt(num) print("Квадратный корень из числа "+str(num)+" это "+str(sqrt))
Вывод: Квадратный корень из числа 25 это 5.
Объяснение: sympy — это модуль Python для символьных вычислений. С помощью функции sympy.sqrt() мы можем получить квадратный корень из положительных, нулевых, отрицательных и комплексных чисел. Единственная разница между этим и другими методами заключается в том, что, если при использовании  {\frac{5}{12}}} = 1 $$
{\frac{5}{12}}} = 1 $$
Что в 9 раз больше квадратного корня из 3, упрощенно? – Обзоры Wiki
Из этого следует, что такое значение 9 корень 3? Значение корня 3 является положительным действительным числом, когда оно умножается само на себя; это дает число 3. Это не натуральное число, а дробь. Квадратный корень из 3 обозначается как u221a3.
…
Таблица квадратного корня.
| Номер | Квадратный корень (u221a) |
|---|---|
| 8 | 2,828 |
| 9 | 3.000 |
| 10 | 3.162 |
| 3,317 |
• 4 июня 2020 г.
Дополнительно Чему равен квадрат квадратного корня из 3? Точнее его называют главным квадратным корнем из 3, чтобы отличить его от отрицательного числа с тем же свойством. Квадратный корень из 3 это иррациональное число .
Квадратный корень из 3 это иррациональное число .
…
Квадратный корень из 3.
| Представления | |
|---|---|
| Десятичное число | 1,7320508075688772935… | 9 0015
| Непрерывная дробь | |
| Двоичный | 1.10111011011001111010… |
| Шестнадцатеричный | 1.BB67AE8584CAA73B… |
К каким наборам принадлежит квадратный корень из 3? Объяснение: 3 не является полным квадратом, поэтому не имеет точного квадратного корня. √3 равно иррациональное число . Ответ — бесконечное неповторяющееся десятичное число.
Сколько будет 9 в степени 3?
Ответ: 9 в степени 3 можно выразить как 9 3 = 9 × 9 × 9 = 729 .
Что такое квадратный корень из 9? Квадратный корень из 9 равен 3. Следовательно, 9 √9 = 9 × 3 = 27 .
Как написать корень 3? Квадратный корень из 3 представляется с помощью квадратного корня или подкоренного символа «√» и записывается как √3. Значение √3 приблизительно равно 1,732 . Это значение широко используется в математике. Так как корень 3 является иррациональным числом, которое нельзя представить в виде дроби.
Значение √3 приблизительно равно 1,732 . Это значение широко используется в математике. Так как корень 3 является иррациональным числом, которое нельзя представить в виде дроби.
Является ли √ 3 действительным числом?
Действительные числа — это числа, включающие как рациональные, так и иррациональные числа. Рациональные числа, такие как целые числа (-2, 0, 1), дроби (1/2, 2,5) и иррациональные числа, такие как √3, π(22/7) и т. д., равны , все действительные числа .
Также Что такое 0,01234567901 как дробь? В виде дроби 0,01234567901 можно представить как 1234567
0 000 000 000 1234567901 100 , 000 , 000 , 000 .Как делить дроби?
Деление двух дробей — это то же самое , что и умножение первой дроби на обратную величину второй дроби . Первым шагом к делению дробей является нахождение обратной дроби (поменять местами числитель и знаменатель) второй дроби. Затем умножьте два числителя. Затем умножьте два знаменателя.
Чему равно число 9 в отрицательной 3-й степени в виде дроби? 9−3=193= 1729 .
Как найти корень из 9?
Фактическое значение квадратного корня из 9 равно 3 . Если возвести в квадрат +3 или -3, результирующее значение будет равно 9. Примечание: поскольку квадратный корень из 9 дает целое число, следовательно, 9 — это полный квадрат.
Как называется √?
Радикал – Символ √, который используется для обозначения квадратного корня или корня n-й степени. Подкоренное выражение. Подкоренное выражение — это выражение, содержащее квадратный корень. Подкоренное число — число или выражение внутри подкоренного символа.
Является ли 9 квадратным числом? Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или нулевое) на само себя, полученное произведение называется квадратным числом, или полным квадратом, или просто «квадратом». Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — все квадратные числа.
Что такое куб 3? Следовательно, кубический корень из 8 равен 2, а из 27 равен 3. Кубический корень любого числа n равен числу x, например x 3 = n.
…
Как найти кубический корень из 3?
| Число (x) | Куб числа (x 3 ) |
|---|---|
| 3 | 3×3×3 = 27 |
| 4 | 4×4×4 = 64 |
| 5 | 5×5×5 = 125 |
| 6 | 6×6×6 = 216 |
Как найти квадратный корень из 3 вручную?
Что такое реальный номер?
В математике действительным числом является значение непрерывной величины, которое может представлять расстояние вдоль линии . Действительные числа включают в себя как рациональные, так и иррациональные числа. Рациональные числа, такие как целые числа (-5, 0, 9), дроби (1/2, 7/8, 2,5) и иррациональные числа, такие как √7, π и т. д., являются действительными числами.
Действительные числа включают в себя как рациональные, так и иррациональные числа. Рациональные числа, такие как целые числа (-5, 0, 9), дроби (1/2, 7/8, 2,5) и иррациональные числа, такие как √7, π и т. д., являются действительными числами.
Является ли ноль действительным числом? На самом деле реальные числа — это практически любые числа, которые только можно придумать. … Действительные числа могут быть положительными или отрицательными, и включает число ноль . Их называют действительными числами, потому что они не мнимые, а это другая система чисел.
Является ли бесконечность действительным числом?
Бесконечность — это «настоящая» и полезная концепция. Однако бесконечность не входит в математически определенный набор «действительных чисел» и, следовательно, не является числом на прямой числовой прямой.
Сколько 2 разделить на 9 как дробь? Ответ: 2 разделить на 9, так как дробь записывается как 2/9. .
Как умножать дроби?
Есть 3 простых шага, чтобы умножить дроби
- Умножьте верхние числа (числители).

- Умножьте нижние числа (знаменатели).
- При необходимости упростите дробь.
Сколько 2 разделить на 3 как дробь?
Ответ: 2 разделить на 3 как дробь 2/3 .
Делитель представлен знаменателем, т. е. 3.
Как разделить 3 дроби вместе?
Таблица квадратов и квадратных корней
Обновлено 31 января 2023 г. | Логан Чемберлен
Квадратный корень числа — это число, которое при умножении само на себя дает желаемое значение. Так, например, квадратный корень из 49 равен 7 (7×7=49). Процесс умножения числа на само себя называется 9.0244 в квадрате
Так, например, квадратный корень из 49 равен 7 (7×7=49). Процесс умножения числа на само себя называется 9.0244 в квадрате
Числа, квадратные корни которых являются целыми числами (точнее, целыми положительными числами), называются совершенными квадратными числами. Числа с десятичными знаками не являются идеальными квадратными корнями.
Все положительные числа имеют положительное число в качестве квадратного корня, называемого главным, и отрицательное число. Все эти числа известны как действительные числа.
Все отрицательные числа будут иметь комплексное число в качестве квадратного корня. Комплексное число это число умноженное на я. i — это «мнимый» квадратный корень из -1. Оно называется воображаемым, но для математиков оно существует.
Как мы выписываем квадратные корни?
Уравнение с квадратным корнем записывается с использованием подкоренного знака или подкоренного символа (). Число, из которого мы хотим получить корень, находится после или под хвостом радикала (например, 3, если мы хотим найти квадратный корень из 3).
Для чего мы используем квадратные корни?
Возможно, это сложно представить, но квадратные корни — одни из самых полезных чисел. Функции квадратного корня очень важны для физических уравнений всех видов. Они также ценны для статистики; статистики постоянно используют квадратные корни при анализе корреляции между различными точками данных.
Список идеальных квадратов
Используйте эту таблицу, чтобы найти квадраты и квадратные корни чисел из 1 до 100 .
Вы также можете использовать эту таблицу для оценки квадратных корней больших чисел.
- Например, если вы хотите найти квадратный корень из 2000 , просматривайте средний столбец , пока не найдете число, ближайшее к 2000. Число в среднем столбце, ближайшее к 2000, равно 2025. .
- Теперь посмотрите на число слева от 2025 , чтобы найти его квадратный корень.
 Квадратный корень из 2025 равен 9.0244 45 .
Квадратный корень из 2025 равен 9.0244 45 . - Следовательно, приблизительный квадратный корень из 2000 равен 45 .
Чтобы получить более точное число, вам придется использовать калькулятор (44,721 — более точный квадратный корень из 2000).
Готовитесь к длительной учебной сессии? Возможно, вас заинтересует наш список лучших рабочих стульев 2020 года.
| НОМЕР | КВАДРАТ | КВАДРАТНЫЙ КОРЕНЬ |
| 1 | 1.000 | |
| 2 | 4 | 1,414 |
| 3 | 9 | 1,732 |
| 4 | 16 | 2. 000 000 |
| 5 | 25 | 2,236 |
| 6 | 36 | 2,449 |
| 7 | 49 | 2,646 |
| 8 | 64 | 2,828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3,162 |
| 11 | 121 | 3,317 |
| 12 | 144 | 3,464 |
| 13 | 169 | 3,606 |
| 14 | 196 | 3,742 |
| 15 | 225 | |
| 16 | 256 | 4. 000 000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4.243 |
| 19 | 361 | 4,359 |
| 20 | 400 | 4,472 |
| 21 | 441 | 4,583 |
| 22 | 484 | 4,690 |
| 23 | 529 | 4,796 |
| 24 | 576 | 4,899 |
| 25 | 625 | 5. 000 000 |
| 26 | 676 | 5.099 |
| 27 | 729 | 5,196 |
| 28 | 784 | 5,292 |
| 29 | 841 | 5,385 |
| 30 | 900 | 5,477 |
| 31 | 961 | 5,568 |
| 32 | 1 024 | 5,657 |
| 33 | 1089 | 5,745 |
| 34 | 1 156 | 5,831 |
| 35 | 1 225 | 5,916 |
| 36 | 1 296 | 6. 000 000 |
| 37 | 1 369 | 6.083 |
| 38 | 1 444 | 6,164 |
| 39 | 1 521 | 6,245 |
| 40 | 1 600 | 6,325 |
| 41 | 1 681 | 6.403 |
| 42 | 1 764 | 6.481 |
| 43 | 1 849 | 6,557 |
| 44 | 1 936 | 6,633 |
| 45 | 2 025 | 6. 708 708 |
| 46 | 2 116 | 6,782 |
| 47 | 2 209 | 6,856 |
| 48 | 2 304 | 6,928 |
| 49 | 2 401 | 7.000 |
| 50 | 2 500 | 7.071 |
| 51 | 2 601 | 7.141 |
| 52 | 2 704 | 7.211 |
| 53 | 2 809 | 7,280 |
| 54 | 2 916 | 7,348 |
| 55 | 3 025 | 7,416 |
| 56 | 3 136 | 7,483 |
| 57 | 3 249 | 7,550 |
| 58 | 3 364 | 7,616 |
| 59 | 3 481 | 7. 681 681 |
| 60 | 3 600 | 7,746 |
| 61 | 3 721 | 7.810 |
| 62 | 3 844 | 7,874 |
| 63 | 3 969 | 7,937 |
| 64 | 4 096 | 8.000 |
| 65 | 4 225 | 8.062 |
| 66 | 4 356 | 8.124 |
| 67 | 4 489 | 8,185 |
| 68 | 4 624 | 8. 246 246 |
| 69 | 4 761 | 8.307 |
| 70 | 4 900 | 8,367 |
| 71 | 5 041 | 8.426 |
| 72 | 5 184 | 8.485 |
| 73 | 5 329 | 8,544 |
| 74 | 5 476 | 8.602 |
| 75 | 5 625 | 8.660 |
| 76 | 5 776 | 8,718 |
| 77 | 5 929 | 8,775 |
| 78 | 6 084 | 8,832 |
| 79 | 6 241 | 8,888 |
| 80 | 6 400 | 8,944 |
| 81 | 6 561 | 9.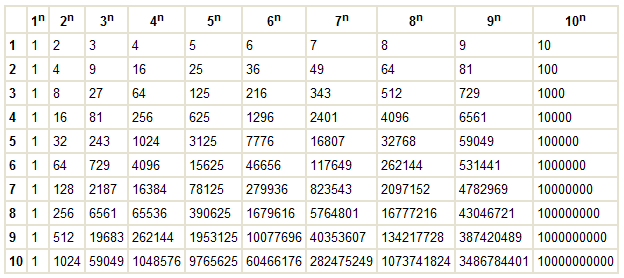 000 000 |
| 82 | 6 724 | 9.055 |
| 83 | 6 889 | 9.110 |
| 84 | 7 056 | 9,165 |
| 85 | 7 225 | 9.220 |
| 86 | 7 396 | 9,274 |
| 87 | 7 569 | 9,327 |
| 88 | 7 744 | 9.381 |
| 89 | 7 921 | 9. 434 434 |
| 90 | 8 100 | 9.487 |
| 91 | 8 281 | 9.539 |
| 92 | 8 464 | 9,592 |
| 93 | 8 649 | 9,644 |
| 94 | 8 836 | 9,695 |
| 95 | 9 025 | 9,747 |
| 96 | 9 216 | 9,798 |
| 97 | 9 409 | 9,849 |
| 98 | 9 604 | 9,899 |
| 99 | 9 801 | 9,950 |
| 100 | 10 000 | 10. |


 sqrt(num)
print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
sqrt(num)
print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
 Квадратный корень из 2025 равен 9.0244 45 .
Квадратный корень из 2025 равен 9.0244 45 .