Х под корнем х производная: Производная корня из х, sqrt(x)’

2 tg2x y= 1-cos x/ 1+sin x — Учеба и наука

Лучший ответ по мнению автора

Михаил Александров 23. 03.16 Лучший ответ по мнению автора

Андрей Андреевич от 70 p. Читать ответы

Eleonora Gabrielyan от 0 p. Читать ответы

Галина Владимировна от 50 p. Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Пользуйтесь нашим приложением

3. Корни многочленов. Теорема Безу. Формальная производная. Кратные корни

Корни многочленов

Пусть есть кольцо $A$ – коммутативное с 1 целостное кольцо.

Определение. $c \in A$ – корень многочлена $f(x)$, если $f(c)=0$.

Теорема Безу. Элемент $c \in A$ является корнем многочлена $f(x) \Leftrightarrow (x-c)$ делит $f(x)$. {k_n-1}(x).$

Замечание. Для нахождения корней $f(x)$ можно использовать соображение:

$\frac{f(x)}{НОД(f,f’)}=p_1(x)…p_n(x)$

Производная корень из 1 x 2. Решение квадратных уравнений через производные

Дети

Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.

Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:

Перейдем от квадратного уравнения к квадратичной функции:

Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.

Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант . Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!

Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.

На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение ) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.

Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:

Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.

Разве формула перемещения для РУД не является следствием решения квадратного уравнения?

Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.

Теперь осталось разобраться что есть что, и чего нам не хватает.

«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.

В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:

В таком случае составим уравнение для поиска :

[подставили в производную первого порядка ]

Корнем такого уравнения относительно будет:

А значением исходной функции при таком аргументе будет:

Теперь становится очевидно, что:

Соединим все «детали пазла» воедино:

Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).

Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.

С вами был Петр, спасибо за внимание!

Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$

Для обозначения производной часто используют символ y».

Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .

Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f»(a) \)

Поскольку \(k = tg(a) \), то верно равенство \(f»(a) = tg(a) \) .

А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \(y = f(x) \) имеет производную в конкретной точке \(x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x) $$
Это означает, что около точки х выполняется приближенное равенство \(\frac{\Delta y}{\Delta x} \approx f»(x) \), т.е. \(\Delta y \approx f»(x) \cdot \Delta x \). Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х.

2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.

Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .

Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)

Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.

Правила дифференцирования

Операция нахождения производной называется дифференцированием . При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. 2} $$

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Таблица производных простых функций

1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто
2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго
3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни.
4. Производная переменной в степени -1
5. Производная квадратного корня
6. Производная синуса
7. Производная косинуса
8. Производная тангенса
9. Производная котангенса
10. Производная арксинуса
11. Производная арккосинуса
12. Производная арктангенса
13. Производная арккотангенса
14. Производная натурального логарифма
15. Производная логарифмической функции
16. Производная экспоненты
17. Производная показательной функции

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т. е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.

Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».

Пошаговые примеры — как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

На этом занятии мы будем учиться применять формулы и правила дифференцирования.

Примеры. Найти производные функций.

1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:

y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.

2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.

y’=3∙6x 5 -2=18x 5 -2.

Применяем правило I , формулы 3, 5 и 6 и 1.

Применяем правило IV , формулы 5 и 1 .

В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.

Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.

Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.

Решим шестой пример и выведем еще одну формулу.

Используем правило IV и формулу 4 . Получившиеся дроби сократим.

Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:

Учим новые формулы!

Примеры.

1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .

Решение.

Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.

Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.

2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .

Решение.

Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.

Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .

3. Вывести формулу производной функции y=x n .

Дифференцирование — это действие нахождения производной функции.

При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .

Вот эти формулы.

Таблицу производных легче будет заучить, проговаривая словесные формулировки:

1. Производная постоянной величины равна нулю.

2. Икс штрих равен единице.

3. Постоянный множитель можно вынести за знак производной.

4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.

5. Производная корня равна единице, деленной на два таких же корня.

6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.

7. Производная синуса равна косинусу.

8. Производная косинуса равна минус синусу.

9. Производная тангенса равна единице, деленной на квадрат косинуса.

10. Производная котангенса равна минус единице, деленной на квадрат синуса.

Учим правила дифференцирования .

1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.

2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.

3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».

4. Частный случай формулы 3.

Учим вместе!

Страница 1 из 1 1

Производная кубического корня из x

Производная из x ^1/3 . В этой статье мы найдем производную кубического корня из x, применив степенное правило производных. Мы также будем использовать определение предела для вычисления производной кубического корня из x.

Содержание

Какова производная кубического корня из x?

Первый метод нахождения производной кубического корня из x: Сначала вычислим производную кубического корня x по степенному правилу производных. См. шаги ниже. 9{2/3}}$.

 

Читайте также: Производная квадратного корня из x

 

Теперь найдем производную кубического корня из $x$ по первому принципу.

Производная кубического корня из x из первого принципа

Пусть $f(x)=\sqrt{x}.$ Нам нужно найти производную $f(x).$ Из первого принципа производных мы есть

$\frac{d}{dx}(f(x)) = \lim\limits_{h \to 0}\frac{f(x+h)-f(x)}{h}$

$=\lim\limits_{h \to 0} \dfrac{\sqrt[3]{x+h}-\sqrt[3]{x}}{h}$ $\cdots (i)$ 9{2/3}}$

Таким образом, производная кубического корня из x равна 1/3x ^2/3

Производная кубического корня x с помощью логарифмического дифференцирования

Теперь найдем производную кубический корень из x с помощью логарифмической производной. {2/3}} \cdot \dfrac{d} {dx}(x+2)$ по уравнению (I) 9x]$

Вернуться на ГЛАВНУЮ СТРАНИЦУ

Часто задаваемые вопросы о производной кубического корня из x

Q1: Что такое производная кубического корня из x?

Ответ: Производная кубического корня из x равна 1/3x ^2/3 .

Q2: Как определяется кубический корень из x?

Ответ: Кубический корень из x — это число b такое, что b ³ =x. Символически кубический корень из x можно записать как $\sqrt[3]{x}$.

Найдите производную от tan sqrt x wrt x, используя математику первого класса 12 CBSE

Ответ

Проверено

198k+ просмотров

Подсказка : Чтобы решить эту проблему, мы можем использовать цепное правило и вывести его напрямую. Но нас просят найти производную, используя первый принцип, который является основным методом нахождения производной. Здесь также необходимо использовать тригонометрическую формулу для определения искомой производной.
Используемые формулы:
Первый принцип производных утверждает, что производная функции $ f\left( x \right) $ задается как $ f’\left( x \right) = \mathop {\lim }\limits_{h \ до 0} \dfrac{{f\left( {x + h} \right) — f\left( x \right)}}{h} $
 $
  \tan \left( {A — B} \right) = \dfrac{{\tan A — \tan B}}{{1 + \tan A\tan B}} \\
   \Rightarrow \tan A — \tan B = \tan \left( {A — B} \right)\left( {1 + \tan A\tan B} \right) \;
  $

Полный пошаговый ответ :
Имеем $ f\left( x \right) = \tan \sqrt x $ , поэтому $ f\left( {x + h} \right) = \tan \sqrt {x + h} $
Теперь мы знаем, что по первому принципу производная can определяется следующей формулой:
 $ f’\left( x \right) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f\left( {x + h} \right) — f\left( x \right )}}{h} $
Теперь положим $ f\left( x \right) = \tan \sqrt x $ и $ f\left( {x + h} \right) = \tan \sqrt {x +h}$ в этой формуле.
 $ \Rightarrow f’\left( x \right) = \mathop {\lim }\limits_{h \to 0} \dfrac {{\tan \sqrt {x + h} — \tan \sqrt x}}{ h} $
Мы знаем, что $ \tan A — \tan B = \tan \left( {A — B} \right)\left( {1 + \tan A\tan B} \right) $ . Мы будем использовать эту формулу для $ \tan \sqrt {x + h} — \tan \sqrt x $.
Положим $ \tan \sqrt {x + h} — \tan \sqrt x = \tan \left( {\sqrt {x + h} — \sqrt x } \right)\left( {1 + \tan \sqrt {x + h} \tan \sqrt x } \right) $
 $ \Rightarrow f’\left( x \right) = \mathop {\lim }\limits_{h \to 0} \dfrac{{\ загар \ влево ( {\ sqrt {x + h} — \ sqrt x} \ right) \ left ( {1 + \ tan \ sqrt {x + h} \ tan \ sqrt x } \ right)}} {h} $
Теперь разделим термины
 $ \Rightarrow f’\left( x \right) = \mathop {\lim }\limits_{h \to 0} \dfrac{{\tan \left( {\sqrt {x + h} — \ sqrt x } \ right)}} {h} \ mathop {\ lim } \ limit_ {h \ to 0} \ left ( {1 + \ tan \ sqrt {x + h} \ tan \ sqrt x } \справа) $
Мы сначала найдем пределы отдельно и подставим их в основное уравнение.
Сначала мы решим $ \mathop {\lim }\limits_{h \to 0} \dfrac{{\tan \left( {\sqrt {x + h} — \sqrt x} \right)}}{h } $
Мы можем написать $ h = \left( {\sqrt {x + h} — \sqrt x } \right)\left( {\sqrt {x + h} + \sqrt x} \right) $
 $
  \ mathop {\lim }\limits_{h \to 0} \dfrac{{\tan \left( {\sqrt {x + h} — \sqrt x} \right)}}{h} \\
   = \ mathop {\ lim} \ limit_ {h \ to 0} \ dfrac {{\ tan \ left ({\ sqrt {x + h} — \ sqrt x} \ right)}} {{\ left ({\ sqrt {x + h} — \sqrt x } \right)\left( {\sqrt {x + h} + \sqrt x } \right)}} \\
   = \ mathop {\lim}\limits_{h \to 0} \dfrac{{\tan \left({\sqrt {x + h} — \sqrt x} \right)}}{{\left( {\ sqrt {x + h} — \ sqrt x } \ right)}} \ mathop {\ lim} \ limit_ {h \ to 0} \ dfrac {1} {{\ left ({\ sqrt {x + h} + \ sqrt x } \right)}} \\
   = 1 \times \dfrac{1}{{2\sqrt x }} \\
   = \dfrac{1}{{2\sqrt x }} \;
  $
Теперь решим второй член \[\mathop {\lim }\limits_{h \to 0} \left( {1 + \tan \sqrt {x + h} \tan \sqrt x } \right )\]
\[
  \mathop {\lim }\limits_{h \to 0} \left( {1 + \tan \sqrt {x + h} \tan \sqrt x} \right) \\ 92}\sqrt x $

Недавно обновленные страницы

Если ab и c единичные векторы, то левое ab2 правое+bc2+ca2 математика класса 12 JEE_Main

Стержень AB длиной 4 единицы движется горизонтально, когда математика класса 11 JEE_Main

Оценить значение intlimits0pi cos 3xdx A 0 B 1 класс 12 математика JEE_Main

Что из следующего верно 1 nleft S cup T right класс 10 математика JEE_Main

Какова площадь треугольника с вершинами Aleft класс 11 математика JEE_Main

KCN легко реагирует с образованием цианида с A Этиловый спирт класса 12 химического состава JEE_Main

Если ab и c единичные векторы, то левое ab2 правое+bc2+ca2 математический класс 12 JEE_Main

Стержень AB длиной 4 единицы движется горизонтально, когда class 11 maths JEE_Main

Оценить значение intlimits0pi cos 3xdx A 0 B 1 class 12 maths JEE_Main

Что из следующего верно 1 nleft S cup T right class 10 maths JEE_Main

Какова площадь треугольника с вершинами Левый класс 11 математика JEE_Main

KCN легко реагирует с образованием цианида с этиловым спиртом класса 12 по химическому составу JEE_Main

Тенденции сомнения

Предел в бесконечности Проблемы с квадратными корнями есть

гораздо больше интерактивных способов узнать об основополагающей концепции Limits at Infinity, активно используя графические калькуляторы Desmos. Пожалуйста, посетите наш Введение в лимиты в бесконечности, чтобы начать с действительно запишите этот материал для себя. Все это бесплатно и предназначено для того, чтобы помочь вам преуспеть в вашем курсе.

Если вам сейчас просто нужно попрактиковаться с ограничениями, предыдущие ученики сочли нижеприведенную информацию очень полезной. А если у вас есть вопросы, задавайте их на нашем форуме!

Пределы на бесконечности с квадратными корнями: проблемы и решения

Для анализа задач на предел на бесконечности с квадратными корнями мы будем использовать инструменты, которые мы использовали ранее для решения задач на предел на бесконечности, ПЛЮС один дополнительный бит: это 92}$ в любой задаче, где $x \to\, -\infty$, поскольку тогда вы автоматически просматриваете отрицательные значения x .

Для более полного обсуждения этого важного вопроса, пожалуйста, посетите экран «Предел в бесконечности с квадратными корнями» в нашей главе «Пределы», посвященной этой теме. У нас также есть специально разработанные интерактивные графические калькуляторы Desmos, которые помогут вам понять, что вы делаете, когда вычисляете эти пределы.

Приведенные ниже задачи иллюстрируют, начиная с части (b) первой. 92}}}{1} \\[8px]
&= \lim_{x \to \infty} \sqrt{5 + \dfrac{2}{x}} \\[8px]
&= \sqrt{5 } \quad \cmark
\end{align*} \]

Обратите внимание, что на последнем шаге мы использовали тот факт, что $\displaystyle{\lim_{x \to \infty}\frac{2}{x} = 0}$.

Мы можем проверить результат, взглянув на график функции. Обратите внимание, что горизонтальная линия $y = \sqrt{5}$ является горизонтальной асимптотой для этого графика.

Прежде чем делать что-либо еще, давайте посмотрим на функцию и решим, ожидаем ли мы предел — 92\left( 5 + \frac{2}{x} \right)}}{x}$, числитель всегда будет положительным из-за квадратного корня. Знаменатель, с другой стороны, всегда будет отрицательным, потому что мы рассматриваем постоянно увеличивающиеся отрицательные значения для x . Следовательно, поскольку $x \to\, -\infty$, дробь всегда будет иметь отрицательное значение , и поэтому, если мы найдем число в качестве предела, мы ожидаем, что оно будет отрицательным. Это быстрое начальное рассуждение является хорошей проверкой нашего окончательного результата.

Чтобы получить этот результат, мы снова используем наш обычный «трюк» деления числителя и знаменателя на 92}}}{1} \\[8px]
&= \lim_{x \to\, -\infty} -\sqrt{5 + \dfrac{2}{x}} \\[8px]
&= -\sqrt{5} \quad \cmark
\end{align*} \]
Обратите внимание, что на последнем этапе мы использовали тот факт, что $\displaystyle{\lim_{x \to\, -\infty}\frac {2}{x} = 0}$.

Обратите внимание, что в качестве ответа мы получили отрицательное число, что соответствует нашим быстрым первоначальным рассуждениям выше.

Мы можем проверить результат, взглянув на график функции. Обратите внимание, что горизонтальная линия $y = -\sqrt{5}$ является горизонтальной асимптотой для этого графика. 92 + x} – x \\[8px]
f(10) &= \sqrt{100 + 10} – 10 \приблизительно 10,488 – 10 = 0,488 \\[8px]
f(20) &= \sqrt{400 + 20} – 20 \приблизительно 20,494 – 20 = 0,494 \\[8px]
f(100) &= \sqrt{10,000 + 100} – 100 \приблизительно 100,499 -100 = 0,499
\end{align*} \]

[свернуть]

Практическая задача №3

Эта задача предоставлена ​​по запросу учащегося. У него есть другой (тот же самый) классный, неожиданный результат.
Найдите $\displaystyle{\lim_{x \to \infty}\left(\sqrt{x + \sqrt{x}} – \sqrt{x} \right)}$.

Нажмите, чтобы просмотреть решение исчисления

По мере того, как $x$ растет и растет, как $\sqrt{x + \sqrt{x}}$, так и $\sqrt{x}$ растут и растут. Таким образом, мы не сразу знаем, в чем разница между двумя терминами. $(“\infty – \infty”$ может быть чем угодно — это «неопределенное выражение», означающее, что у нас есть еще работа.)

Чтобы продолжить, мы будем использовать тот же подход, который мы использовали ранее при оценке пределов, которые имели в них квадратные корни: мы рационализируем выражение, умножив его на сопряженное $\sqrt{x + \sqrt{x}} + \sqrt{x}$, деленное само на себя: 92}{\sqrt{x + \sqrt{x}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty} \frac{\left(x + \sqrt{x } \right) – x}{\sqrt{x + \sqrt{x}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty}\frac{\sqrt{x }}{\sqrt{x + \sqrt{x}} + \sqrt{x}} \\[8px]
\end{align*} \]
Теперь воспользуемся нашим обычным приемом деления числителя и знаменателя на самая большая степень в знаменателе . Эта мощность равна $\sqrt{x}.$
\[ \begin{align*}
&= \lim_{x \to \infty}\frac{\dfrac{\sqrt{x}}{\sqrt{x} }}{\dfrac{\sqrt{x + \sqrt{x}}+ \sqrt{x}}{\sqrt{x}}} \\[8px]
&= \lim_{x \to \infty}\frac{1}{\dfrac{\sqrt{x + \sqrt{x}}}{\sqrt{x}}+ \dfrac{\sqrt{x}} {\ sqrt {x}}} \\ [8px]
&= \ lim_ {x \ to \ infty} \ frac {1} {\ sqrt {\ dfrac {x + \ sqrt {x}} {x}} + 1} \\[8px]
&= \lim_{x \to \infty}\frac{1}{\sqrt{1 + \dfrac{1}{\sqrt{x}}}+ 1} \\[8px ]
&= \frac{1}{\sqrt{1 + \cancelto{0}{\dfrac{1}{\sqrt{x}}}}+ 1} \\[8px]
&= \frac{1 }{\sqrt{1}+ 1} \\[8px]
&= \dfrac{1}{2} \quad \cmark
\end{align*} \]

Обратите внимание, что ближе к концу мы использовали тот факт, что $\displaystyle{\lim_{x \to\, \infty}\frac{1}{\sqrt{x}} = 0}$.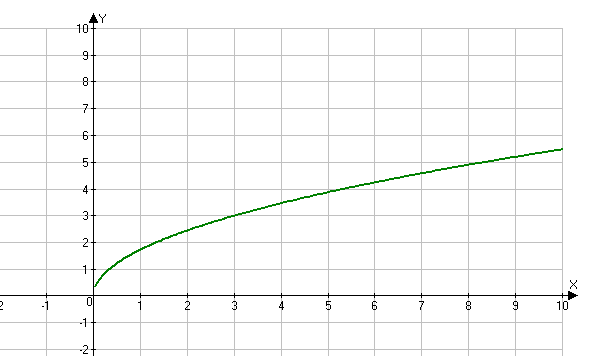

Этот предел неожиданный, по крайней мере для нас! Но вы можете проверить несколько чисел, чтобы увидеть, как это работает:
\[ \begin{align*}
f(x) &= \sqrt{x + \sqrt{x}} – \sqrt{x} \\[8px ]
f(100) &= \sqrt{100 + \sqrt{100}} – \sqrt{100} \приблизительно 10,48 – 10 = 0,48 \\[8px]
f(10000) &= \sqrt{10000 + 100 } – 100 \приблизительно 100,499 – 100 = 0,499 \\[8px]
\end{align*} \]

[свернуть]

Практическая задача № 4

Это обобщенная версия задачи № 2 выше . 92 + ax} \right) }$, где $a$ — константа.

Нажмите, чтобы просмотреть решение для расчета

При $x \to \, -\infty$ член $x$ становится все больше и больше в отрицательном направлении, а член квадратного корня становится все больше и больше в положительном направлении направление. 2 + ax}$, деленное само на себя: 92}}}\\[8px]
&= \lim_{x \to\, -\infty}\frac{-a}{1 + \sqrt{1 + \frac{a}{x}}} \\ [8px]
&= \frac{-a}{1 + \sqrt{1}} \\[8px]
&= \frac{-a}{2} \quad \cmark
\end{align*} \ ]

Обратите внимание, что в предпоследней строке мы использовали тот факт, что $\displaystyle{\lim_{x \to\, -\infty} \frac{a}{x} = 0 }.$

[ свернуть]

Практическая задача #7

Учащийся разместил этот вопрос в комментариях ниже.
Найти $\displaystyle{\lim_{x \to \infty}\big[\sqrt{x}\sqrt{x}\sqrt{x} – \sqrt{x} \big]}.$ 93}} = \infty$ и $ \displaystyle{\lim_{x \to \infty}\sqrt{x}} = \infty,$ имеем $”\infty – \infty”$, что неопределенно: мы не Мы не знаем, каков на самом деле предел, но у нас есть еще много работы.

Как это часто бывает, разложение на множители обеспечивает путь вперед: обратите внимание, что мы можем извлечь $\sqrt{x}$ из обоих членов:

\begin{align*}
\sqrt{x}\sqrt{ x}\sqrt{x} – \sqrt{x} &= \sqrt{x} \big( \sqrt{x}\sqrt{x} – 1 \big) \\[8px]
&= \sqrt{x }(х – 1)
\end{выравнивание*}
Как только мы это сделали, предел становится ясным:
\begin{align*}
\lim_{x \to \infty}\big[\sqrt{x}\sqrt{x}\sqrt{x} – \ sqrt{x} \big] &= \lim_{x \to \infty}\big[\sqrt{x}(x – 1)\big] \\[8px]
&= \big[\lim_{x \ к \infty}\sqrt{x} \big] \cdot \big[\lim_{x \to \infty}(x – 1)\big] \\[8px]
&= \infty \cdot \infty \\ [8px]
&= \infty \quad \cmark
\end{align*}

[свернуть]

Практическая задача №8

Учащийся разместил этот вопрос в комментариях ниже.
Найдите $\displaystyle{ \lim_{x \to \infty}\sqrt{x + \sqrt{x + \sqrt{x}}} – \sqrt{x} }$.

Нажмите, чтобы просмотреть решение исчисления

Есть два основных шага, чтобы найти этот предел.

Шаг 1 : Как и в предыдущих задачах, мы умножаем выражение на его сопряженное деление на себя:
\begin{align*}
\lim_{x \to \infty}\left( \sqrt{x + \sqrt{x + \sqrt{x}}} — \sqrt{x}\right) &= \lim_{x \to \infty}\left(\sqrt{x + \sqrt{x + \sqrt{x) }}} – \sqrt{x} \right)\cdot \frac{\sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x}}{\sqrt{x + \sqrt{ х + \sqrt{x}}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty} \frac{\left(\sqrt{x + \sqrt{x + \sqrt{x}}}\right)\left(\sqrt{x + \sqrt{x) + \sqrt{x}}} \right) + \cancel{\left(\sqrt{x + \sqrt{x + \sqrt{x}}} — \sqrt{x} \right)\left(\sqrt{ x} \right)} – \cancel{\left(\sqrt{x}\right)\left(\sqrt{x + \sqrt{x + \sqrt{x}}} – \sqrt{x} \right) } + \left( -\sqrt{x}\right)\left(\sqrt{x} \right) }{\sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x} }\\[8px]
&=\lim_{x \to \infty} \frac{\left(x + \sqrt{x + \sqrt{x}} \right) -x}{\sqrt{x + \ sqrt{x + \sqrt{x}}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty}\frac{\sqrt{x + \sqrt{x}}}{\sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x }}
\end{align*}
С помощью этого переписанного выражения вы могли бы взглянуть на него и увидеть, что в числителе преобладает (первый) член $\sqrt{x}$, в то время как числитель преобладает в равной степени на два множителя $\sqrt{x}$, поэтому предел будет $\dfrac{1}{2}. $

Но если вы этого не видите (потому что вы еще не сделали 10 000 такие типы задач), или вам нужно это доказать, мы переходим к нашему обычному подходу Шаг 2 : Разделите числитель и знаменатель на наибольший множитель в знаменателе, который равен $\sqrt{x}.$ Итак, давайте умножим и числитель, и знаменатель на $\dfrac{1}{\sqrt{x} } $:
\begin{align*}
\lim_{x \to \infty}\frac{\sqrt{x + \sqrt{x}}}{\sqrt{x + \sqrt{x + \sqrt{x }}} + \sqrt{x}}
&= \lim_{x \to \infty}\frac{\frac{1}{\sqrt{x}}\sqrt{x + \sqrt{x}}}{ \frac{1}{\sqrt{x}}\left( \sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x}\right)} \\[8px]
&= \ lim_ {x \ to \ infty} \ frac {\ sqrt {\ frac {x + \ sqrt {x}} {x}}} {\ sqrt {\ frac {x + \ sqrt {x + \ sqrt {x} }}{x}} + \frac{\sqrt{x}}{\sqrt{x}}}\\[8px]
&= \lim_{x \to \infty}\frac{\sqrt{1 + \frac{1}{\sqrt{x}}}}{\sqrt{1 + \frac{\sqrt{x + \sqrt {x}}}{x}}+1} \\[8px]
&= \frac{\sqrt{1 + \cancelto{0}{\left( \lim_{x \to \infty}\frac{1 }{\sqrt{x}}\right)}}}{\sqrt{1 + \cancelto{0}{\left( \lim_{x \to \infty}\frac{\sqrt{x + \sqrt{x }}}{x}\right)}}+1} \\[8px]
&= \frac{\sqrt{1}}{\sqrt{1} + 1} \\[8px]
&= \frac {1}{2} \quad \cmark
\end{align*}
Ого! : )

[свернуть]

Хотите доступ к все наших проблем исчисления и решения? Войдите бесплатно с помощью своей учетной записи Google, Facebook или Apple или с помощью специальной учетной записи Matheno (которую вы можете создать за 60 секунд). Затем посетите наш главный экран исчисления.

И если у вас есть вопрос о проблеме с ограничениями, с которыми вам может понадобиться помощь, или о ограничениях в целом, пожалуйста, зайдите на наш форум и напишите. Будем рады помочь!

---

По состоянию на сентябрь 2022 года мы используем наш форум для комментариев и обсуждения этой темы, а также для любых математических вопросов. Будем рады вас видеть и помочь! Нажмите, чтобы посетить наш форум: community.matheno.com.

Войти

Вы можете бесплатно войти в систему, чтобы получить доступ ко всем нашим материалам, с помощью своей учетной записи Facebook, Google или Apple ИЛИ с помощью специальной учетной записи Matheno. (У вас нет специальной учетной записи Matheno, но вы хотели бы ее создать? Создайте ее здесь за 60 секунд.)

3.2 Производная как функция — исчисление, том 1

Цели обучения

• 3.2.1 Определите производную функцию данной функции.
• 3.2.2 График производной функции по графику заданной функции.
• 3.2.3 Укажите связь между производными и непрерывностью.
• 3.2.4 Назовите три условия, при которых функция не имеет производной.
• 3.2.5 Объясните значение производной высшего порядка.

Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы продифференцируем функцию положения в данный момент времени, мы получим скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке даст ценную информацию о поведении функции. Однако процесс нахождения производной даже при нескольких значениях с использованием методов из предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.

Производные функции

Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная. Мы можем формально определить производную функцию следующим образом.

Определение

Пусть ff — функция. Производная функция, обозначаемая через f′,f′, представляет собой функцию, область определения которой состоит из таких значений xx, что существует следующий предел:

f′(x)=limh→0f(x+h)−f(x )h.f′(x)=limh→0f(x+h)−f(x)h.

(3.9)

Говорят, что функция f(x)f(x) дифференцируема в точке aa, если f′(a)f′(a) существует. В более общем смысле функция называется дифференцируемой на SS, если она дифференцируема в каждой точке открытого множества S, S, а дифференцируемая функция — это функция, в которой f′(x)f′(x) существует в своей области определения.

В следующих нескольких примерах мы используем уравнение 3.9 для нахождения производной функции.

Пример 3.11

Нахождение производной функции квадратного корня

Найдите производную f(x)=x.f(x)=x.

Решение

Начните непосредственно с определения производной функции. Используйте уравнение 3.1.

f′(x)=limh→0x+h−xhЗаменитьef(x+h)=x+handf(x)=xintof′(x)=limh→0f(x+h)−f(x)h.= limh→0x+h−xh·x+h+xx+h+xУмножить числитель и знаменатель наx+h+x без распределения в знаменателе.=limh→0hh(x+h+x)Умножить числители и упростить.=limh→01 (x+h+x)Отменить h.=12xВычислить предел.f′(x)=limh→0x+h−xhЗаменитьef(x+h)=x+handf(x)=xintof′(x)=limh→0f (x+h)−f(x)h.=limh→0x+h−xh·x+h+xx+h+xУмножить числитель и знаменатель наx+h+x без распределения в знаменателе.=limh→0hh(x+h +x)Умножить числители и упростить.=limh→01(x+h+x)Отменить h.=12xВычислить предел.

Пример 3.12

Нахождение производной квадратичной функции

Нахождение производной функции f(x)=x2−2x.f(x)=x2−2x.

Решение

Выполните ту же процедуру здесь, но без умножения на сопряженное.

f′(x)=limh→0((x+h)2−2(x+h))−(x2−2x)hПодставитьef(x+h)=(x+h)2−2(x+ h)иf(x)=x2−2xintof′(x)=limh→0f(x+h)−f(x)h. =limh→0x2+2xh+h3−2x−2h−x2+2xhExpand(x+h )2−2(x+h).=limh→02xh−2h+h3hУпростить.=limh→0h(2x−2+h)hМножитель hвыпадает из числителя.=limh→0(2x−2+h)Отменить общий множитель ofh.=2x−2Вычислить предел.f′(x)=limh→0((x+h)2−2(x+h))−(x2−2x)hПодставитьef(x+h)=(x+h )2−2(x+h) и f(x)=x2−2xintof′(x)=limh→0f(x+h)−f(x)h.=limh→0x2+2xh+h3−2x−2h− x2+2xhExpand(x+h)2−2(x+h).=limh→02xh−2h+h3hУпростить.=limh→0h(2x−2+h)hМножитель hиз числителя.=limh→0(2x−2 +h)Отменить общий множитель h.=2x−2Вычислить предел.

Контрольно-пропускной пункт 3,6

Найдите производную f(x)=x2.f(x)=x2.

Мы используем различные обозначения для выражения производной функции. В примере 3.12 мы показали, что если f(x)=x2−2x,f(x)=x2−2x, то f′(x)=2x−2.f′(x)=2x−2. Если бы мы представили эту функцию в виде y=x2−2x,y=x2−2x, мы могли бы выразить производную как y′=2x−2y′=2x−2 или dydx=2x−2.dydx=2x− 2. Мы могли бы передать ту же информацию, написав ddx(x2−2x)=2x−2.ddx(x2−2x)=2x−2. Таким образом, для функции y=f(x),y=f(x) каждое из следующих обозначений представляет собой производную от f(x):f(x):

f′(x),dydx,y′,ddx(f(x)). f′(x),dydx,y′,ddx(f(x)).

Вместо f′(a)f′(a) мы также можем использовать dydx|x=adydx|x=a Использование нотации dydxdydx (называемой нотацией Лейбница) довольно распространено в технике и физике. Чтобы лучше понять эти обозначения, вспомним, что производная функции в точке — это предел наклона секущих по мере приближения секущих к касательной. Наклоны этих секущих часто выражаются в виде ΔyΔxΔyΔx, где ΔyΔy — разность значений yy, соответствующая разнице значений xx, которая выражается как ΔxΔx (рис. 3.11). Таким образом, производная, которую можно рассматривать как мгновенную скорость изменения yy по отношению к x,x, выражается как

dydx=limΔx→0ΔyΔx.dydx=limΔx→0ΔyΔx.

Рисунок 3.11 Производная выражается как dydx=limΔx→0ΔyΔx.dydx=limΔx→0ΔyΔx.

График производной

Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы могли бы построить график. Учитывая оба, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку f′(x)f′(x) дает скорость изменения функции f(x)f(x) (или наклон кривой). касательная к f(x)).f(x)).

В примере 3.11 мы нашли, что для f(x)=x,f′(x)=1/2x.f(x)=x,f′(x)=1/2x. Если мы изобразим эти функции на тех же осях, как на рис. 3.12, мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями. Во-первых, мы замечаем, что f(x)f(x) возрастает по всей своей области, а это означает, что наклоны ее касательных во всех точках положительны. Следовательно, мы ожидаем, что f′(x)>0f′(x)>0 для всех значений xx в его области определения. Кроме того, по мере увеличения xx наклоны касательных линий к f(x)f(x) уменьшаются, и мы ожидаем увидеть соответствующее уменьшение f′(x).f′(x). Заметим также, что f′(0)f′(0) не определено и что limx→0+f′(x)=+∞, limx→0+f′(x)=+∞, что соответствует вертикальной касательной к f(x)f(x) при 0,0.

Рисунок 3.12 Производная f′(x)f′(x) везде положительна, поскольку функция f(x)f(x) возрастает.

В примере 3.12 мы нашли, что для f(x)=x2−2x,f′(x)=2x−2.f(x)=x2−2x,f′(x)=2x−2. Графики этих функций показаны на рис. 3.13. Обратите внимание, что f(x)f(x) убывает при x<1.x<1. Для этих же значений x,f′(x)<0.x,f′(x)<0. Для значений x>1,f(x)x>1,f(x) возрастает, а f′(x)>0.f′(x)>0. Кроме того, f(x)f(x) имеет горизонтальную касательную в точке x=1x=1 и f′(1)=0.f′(1)=0.

Рисунок 3.13 Производная f′(x)<0f′(x)<0, где функция f(x)f(x) убывающая и f′(x)>0f′(x)>0, где f(x)f(x) ) растет. Производная равна нулю там, где функция имеет горизонтальный тангенс.

Пример 3.13

Набросок производной с помощью функции

Используйте следующий график функции f(x)f(x), чтобы нарисовать график функции f′(x).f′(x).

Решение

Решение показано на следующем графике. Заметим, что f(x)f(x) возрастает и f′(x)>0f′(x)>0 на (–2,3).(–2,3). Кроме того, f(x)f(x) убывает и f′(x)<0f′(x)<0 на (−∞,−2)(−∞,−2) и на (3,+∞). (3,+∞). Также обратите внимание, что f(x)f(x) имеет горизонтальные касательные в точках –2–2 и 3,3, а также f′(−2)=0f′(−2)=0 и f′(3)=0. f ′(3)=0.

Контрольно-пропускной пункт 3,7

Нарисуйте график функции f(x)=x2−4.f(x)=x2−4. На каком интервале находится график функции f′(x)f′(x) над осью xx?

Производные и непрерывность

Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Сначала рассмотрим связь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в точке, не обязательно должна быть дифференцируемой в этой точке. На самом деле функция может быть непрерывной в точке и не быть дифференцируемой в этой точке по одной из нескольких причин.

Теорема 3.1

Дифференцируемость подразумевает непрерывность

Пусть f(x)f(x) — функция и aa — ее область определения. Если f(x)f(x) дифференцируема в точках а, а, то функция ff непрерывна в точках а.

Доказательство

Если f(x)f(x) дифференцируема в точках a,a, то f′(a)f′(a) существует и

f′(a)=limx→af(x)−f(a)x−a. f′(a)=limx→af(x)−f(a)x−a.

Мы хотим показать, что f(x)f(x) непрерывна в точке aa, показав, что limx→af(x)=f(a).limx→af(x)=f(a). Таким образом,

limx→af(x)=limx→a(f(x)−f(a)+f(a))=limx→a(f(x)−f(a)x−a·(x−a) +f(a)) Умножить и разделить f(x)−f(a)наx−a.=(limx→af(x)−f(a)x−a)·(limx→a(x−a))+ limx→af(a)=f′(a)·0+f(a)=f(a).limx→af(x)=limx→a(f(x)−f(a)+f(a) )=limx→a(f(x)−f(a)x−a·(x−a)+f(a)) Умножить и разделить f(x)−f(a)наx−a.=(limx→af (x)−f(a)x−a)·(limx→a(x−a))+limx→af(a)=f′(a)·0+f(a)=f(a).

Следовательно, поскольку f(a)f(a) определено и limx→af(x)=f(a),limx→af(x)=f(a), мы заключаем, что ff непрерывен в п.в.

□

Мы только что доказали, что дифференцируемость влечет непрерывность, но теперь мы рассмотрим, влечет ли непрерывность дифференцируемость. Чтобы найти ответ на этот вопрос, мы исследуем функцию f(x)=|x|.f(x)=|x|. Эта функция всюду непрерывна; однако f′(0)f′(0) не определено. Это наблюдение приводит нас к мысли, что непрерывность не влечет дифференцируемости. Давайте исследовать дальше. Для f(x)=|x|,f(x)=|x|,

f′(0)=limx→0f(x)−f(0)x−0=limx→0|x|−|0|x−0=limx→0|x|x.f′(0)=limx→ 0f(x)−f(0)x−0=limx→0|x|−|0|x−0=limx→0|x|x.

Это ограничение не существует, так как

limx→0−|x|x=−1и limx→0+|x|x=1.limx→0−|x|x=−1иlimx→0+|x|x=1.

См. рис. 3.14.

Рисунок 3.14 Функция f(x)=|x|f(x)=|x| непрерывна в точке 00, но не дифференцируема в точке 0,0.

Рассмотрим некоторые дополнительные ситуации, в которых непрерывная функция не может быть дифференцируемой. Рассмотрим функцию f(x)=x3:f(x)=x3:

f′(0)=limx→0x3−0x−0=limx→01×23=+∞.f′(0)=limx→0x3−0x−0=limx→01×23=+∞.

Таким образом, f′(0)f′(0) не существует. Беглый взгляд на график f(x)=x3f(x)=x3 проясняет ситуацию. Функция имеет вертикальную касательную в точке 00 (рис. 3.15).

Рисунок 3.15 Функция f(x)=x3f(x)=x3 имеет вертикальную касательную в точке x=0.x=0. Он непрерывен в точке 00, но не дифференцируем в точке 0,0.

Функция f(x)={xsin(1x)ifx≠00ifx=0f(x)={xsin(1x)ifx≠00ifx=0 также имеет производную, которая демонстрирует интересное поведение при 0,0. Мы видим, что

f′(0)=limx→0xsin(1/x)−0x−0=limx→0sin(1x).f′(0)=limx→0xsin(1/x)−0x−0=limx→0sin( 1х).

Этого предела не существует, в основном потому, что наклоны секущих постоянно меняют направление по мере приближения к нулю (рис. 3.16).

Рисунок 3.16 Функция f(x)={xsin(1x)ifx≠00ifx=0f(x)={xsin(1x)ifx≠00ifx=0 не дифференцируема при 0,0.

Итого:

1. Заметим, что если функция не непрерывна, она не может быть дифференцируемой, так как каждая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она может не быть дифференцируемой.
2. Мы видели, что f(x)=|x|f(x)=|x| не мог быть дифференцируем в 00, потому что предел наклонов касательных слева и справа не был одинаковым. Визуально это привело к появлению острого угла на графике функции в точке 0. 0. Отсюда заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке.
3. Как мы видели на примере f(x)=x3,f(x)=x3, функция не может быть дифференцируемой в точке, где есть вертикальная касательная.
4. Как мы видели с f(x)={xsin(1x)ifx≠00ifx=0f(x)={xsin(1x)ifx≠00ifx=0 функция может не быть дифференцируемой в точке и более сложными способами .

Пример 3.14

Кусочная функция, которая является непрерывной и дифференцируемой

Компания по производству игрушек хочет разработать траекторию для игрушечной машинки, которая начинается с параболической кривой, а затем переходит в прямую линию (рис. 3.17). Функция, описывающая дорожку, должна иметь вид −10, где xx и f(x)f(x) указаны в дюймах. Чтобы автомобиль двигался плавно по трассе, функция f(x)f(x) должна быть одновременно непрерывной и дифференцируемой при −10,−10. Найдите значения bb и cc, которые делают f(x)f(x) непрерывным и дифференцируемым.

Рисунок 3.17 Чтобы автомобиль двигался плавно по трассе, функция должна быть одновременно и непрерывной, и дифференцируемой.

Решение

Чтобы функция была непрерывной при x=−10,limx→−10−f(x)=f(−10).x=−10,limx→−10−f(x)=f(−10). Таким образом, поскольку

limx→−10−f(x)=110(−10)2−10b+c=10−10b+climx→−10−f(x)=110(−10)2−10b+c =10−10b+c

и f(−10)=5,f(−10)=5, мы должны иметь 10−10b+c=5,10−10b+c=5. Эквивалентно, мы имеем c=10b−5.c=10b−5.

Чтобы функция была дифференцируемой при −10, −10,

f′(-10)=limx→−10f(x)−f(−10)x+10f′(-10)=limx→−10f(x)−f(−10)x+10

обязательно существует. Поскольку f(x)f(x) определяется по разным правилам справа и слева, мы должны вычислить этот предел справа и слева, а затем приравнять их друг другу:

limx→−10−f( x)−f(−10)x+10=limx→−10−110×2+bx+c−5x+10=limx→−10−110×2+bx+(10b−5)−5x+10Substitutec=10b−5.= limx→−10−x2−100+10bx+100b10(x+10)=limx→−10−(x+10)(x−10+10b)10(x+10) Фактор по группировке. =b−2. limx→−10−f(x)−f(−10)x+10=limx→−10−110×2+bx+c−5x+10=limx→−10−110×2+bx+(10b−5)−5x+ 10Подставитьc=10b−5.=limx→−10−x2−100+10bx+100b10(x+10)=limx→−10−(x+10)(x−10+10b)10(x+10)Множитель на группировка.=b−2.

У нас также есть

limx→−10+f(x)−f(−10)x+10=limx→−10+−14x+52−5x+10=limx→−10+−(x+10 )4(x+10)=−14.limx→−10+f(x)−f(−10)x+10=limx→−10+−14x+52−5x+10=limx→−10+− (х+10)4(х+10)=-14.

Это дает нам b−2=−14.b−2=−14. Таким образом, b=74b=74 и c=10(74)−5=252.c=10(74)−5=252.

Контрольно-пропускной пункт 3,8

Найдите значения aa и bb, которые делают f(x)={ax+bifx<3x2ifx≥3f(x)={ax+bifx<3x2ifx≥3 непрерывными и дифференцируемыми в 3.3.

Производные высшего порядка

Производная функции сама по себе является функцией, поэтому мы можем найти производную производной. Например, производная функции положения — это скорость изменения положения или скорость. Производная скорости — это скорость изменения скорости, то есть ускорение. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать брать производные, чтобы получить третью производную, четвертую производную и так далее. В совокупности они называются производными более высокого порядка. Обозначение производных высшего порядка от y=f(x)y=f(x) может быть выражено в любой из следующих форм:

f″(x),f‴(x),f(4)(x),…,f(n)(x)f″(x),f‴(x),f(4)(x), …,f(n)(x)

y″(x),y‴(x),y(4)(x),…,y(n)(x)y″(x),y‴(x),y(4)(x), …,у(п)(х)

d2ydx2,d3ydx3,d4ydx4,…,dnydxn.d2ydx2,d3ydx3,d4ydx4,…,dnydxn.

Интересно отметить, что нотация для d2ydx2d2ydx2 может рассматриваться как попытка выразить ddx(dydx)ddx(dydx) более компактно. Аналогично, ddx(ddx(dydx))=ddx(d2ydx2)=d3ydx3.ddx(ddx(dydx))=ddx(d2ydx2)=d3ydx3.

Пример 3.15

Нахождение второй производной

Для f(x)=2×2−3x+1,f(x)=2×2−3x+1 найдите f″(x).f″(x).

Решение

Сначала найдите f′(x). f′(x).

f′(x)=limh→0(2(x+h)2−3(x+h)+1)−(2×2−3x+1)hПодставить f(x)=2×2−3x+1иf(x+ h)=2(x+h)2−3(x+h)+1intof′(x)=limh→0f(x+h)−f(x)h.=limh→04xh+2h3−3hhУпростим числитель. =limh→0(4x+2h−3) Вынести в числитель и сократить в знаменателе.=4x−3 Возьмем предел. f′(x)=limh→0(2(x+h)2−3(x+ h)+1)−(2×2−3x+1)hПодставитьef(x)=2×2−3x+1andf(x+h)=2(x+h)2−3(x+h)+1intof′(x)= limh→0f(x+h)−f(x)h.=limh→04xh+2h3−3hhУпростить числитель.=limh→0(4x+2h−3)Вынести из числителя в множитель и сократить в знаменателе.=4x− 3Возьмите лимит.

Затем найдите f″(x)f″(x), взяв производную от f′(x)=4x−3.f′(x)=4x−3.

f″(x)=limh→0f′(x+h)−f′(x)hUsef′(x)=limh→0f(x+h)−f(x)hс f′(x) на месте off( x).=limh→0(4(x+h)−3)−(4x−3)hПодставьте f′(x+h)=4(x+h)−3 и f′(x)=4x−3.=limh →04Упростить.=4Возьмем предел. (x) вместо off(x).=limh→0(4(x+h)−3)−(4x−3)hПодставить f′(x+h)=4(x+h)−3andf′(x)= 4x−3.=limh→04Упростить.=4Возьмем предел.

Контрольно-пропускной пункт 3,9

Найдите f″(x)f″(x) для f(x)=x2.f(x)=x2.

Пример 3.16

Определение ускорения

Положение частицы вдоль координатной оси в момент времени tt (в секундах) определяется выражением s(t)=3t2−4t+1s(t)=3t2−4t+1 (в метрах). Найдите функцию, описывающую его ускорение в момент времени t.t.

Решение

Поскольку v(t)=s′(t)v(t)=s′(t) и a(t)=v′(t)=s″(t), a(t)=v′(t) =s″(t), начнем с нахождения производной от s(t):s(t):

s′(t)=limh→0s(t+h)−s(t)h=limh→03 (t+h)2−4(t+h)+1−(3t2−4t+1)h=6t−4.s′(t)=limh→0s(t+h)−s(t)h= limh→03(t+h)2−4(t+h)+1−(3t2−4t+1)h=6t−4.

Далее,

s″(t)=limh→0s′(t+h)−s′(t)h=limh→06(t+h)−4−(6t−4)h=6.s ″(t)=limh→0s′(t+h)−s′(t)h=limh→06(t+h)−4−(6t−4)h=6.

Таким образом, a=6м/с2.a=6м/с2.

Контрольно-пропускной пункт 3.10

Для s(t)=t3,s(t)=t3 найти a(t).a(t).

Раздел 3.2 Упражнения

В следующих упражнениях используйте определение производной, чтобы найти f′(x).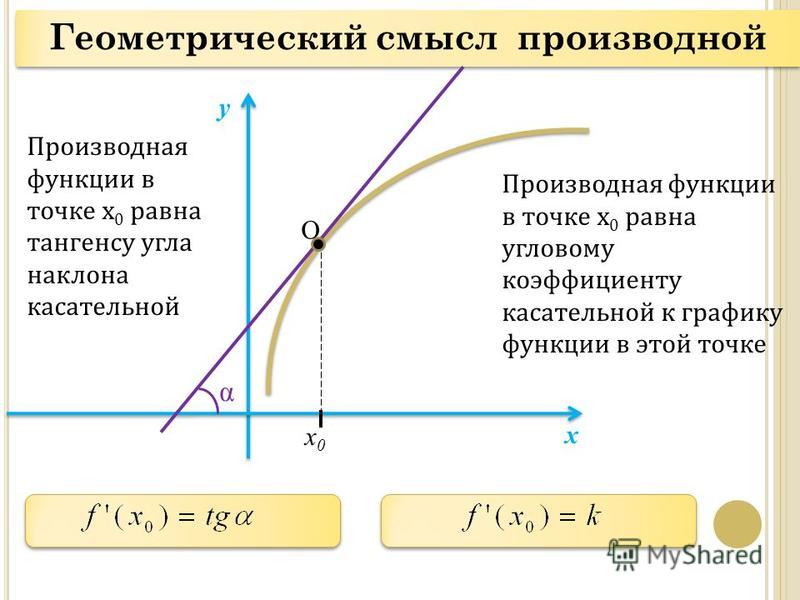 f′(x).

54.

f(x)=6f(x)=6

55.

f(x)=2−3xf(x)=2−3x

56.

f(x)=2×7+1f(x)=2×7+1

57.

f(x)=4x2f(x)=4×2

58.

f(x)=5x−x2f(x)=5x−x2

59.

f(x)=2xf(x)=2x

60.

f(x)=x−6f(x)=x−6

61.

f(x)=9xf(x)=9x

62.

f(x)=x+1xf(x)=x+1x

63.

f(x)=1xf(x)=1x

В следующих упражнениях используйте график y=f(x)y=f(x), чтобы начертить график его производной f′(x).f′(x).

64.

65.

66.

67.

Для следующих упражнений данный предел представляет собой производную функции y=f(x)y=f(x) при x=a.x=a. Найти f(x)f(x) и п.в.

68.

limh→0(1+h)2/3−1hlimh→0(1+h)2/3−1h

69.

limh→0[3(2+h)2+2]−14hlimh→0[3(2+h)2+2]−14h

70.

limh→0cos(π+h)+1hlimh→0cos(π+h)+1h

71.

limh→0(2+h)4−16hlimh→0(2+h)4−16h

72.

limh→0[2(3+h)2−(3+h)]−15hlimh→0[2(3+h)2−(3+h)]−15h

73.

limh→0eh−1hlimh→0eh−1h

Для следующих функций,

1. эскиз графика и
2. используют определение производной, чтобы показать, что функция не дифференцируема при x=1.x=1.

74.

f(x)={2x,0≤x≤13x−1,x>1f(x)={2x,0≤x≤13x−1,x>1

75.

f(x)={3,x<13x,x≥1f(x)={3,x<13x,x≥1

76.

f(x)={−x2+2,x≤1x,x>1f(x)={−x2+2,x≤1x,x>1

77.

f(x)={2x,x≤12x,x>1f(x)={2x,x≤12x,x>1

Для следующих графиков

1. определить, для каких значений x=ax=a существует limx→af(x)limx→af(x), но ff не является непрерывным при x=a,x=a, и
2. определить, при каких значениях x=ax=a функция непрерывна, но не дифференцируема при x=a.x=a.

78.

79.

80.

Используйте график для оценки a. f'(-0,5),f'(-0,5), б. f′(0),f′(0), в. f′(1),f′(1), д. f′(2),f′(2) и e. f′(3),f′(3), если он существует.

Для следующих функций используйте f″(x)=limh→0f′(x+h)−f′(x)hf″(x)=limh→0f′(x+h)−f′(x)h чтобы найти f″(x).f″(x).

81.

f(x)=2−3xf(x)=2−3x

82.

f(x)=4x2f(x)=4×2

83.

f(x)=x+1xf(x)=x+1x

В следующих упражнениях используйте калькулятор для построения графика f(x).f(x). Определите функцию f′(x),f′(x), затем используйте калькулятор для построения графика f′(x).f′(x).

84.

[Т] f(x)=−5xf(x)=−5x

85.

[Т] f(x)=3×2+2x+4.f(x)=3×2+2x+4.

86.

[Т] f(x)=x+3xf(x)=x+3x

87.

[Т] f(x)=12xf(x)=12x

88.

[Т] f(x)=1+x+1xf(x)=1+x+1x

89.

[Т] f(x)=x3+1f(x)=x3+1

В следующих упражнениях опишите, что представляют два выражения в терминах каждой из данных ситуаций.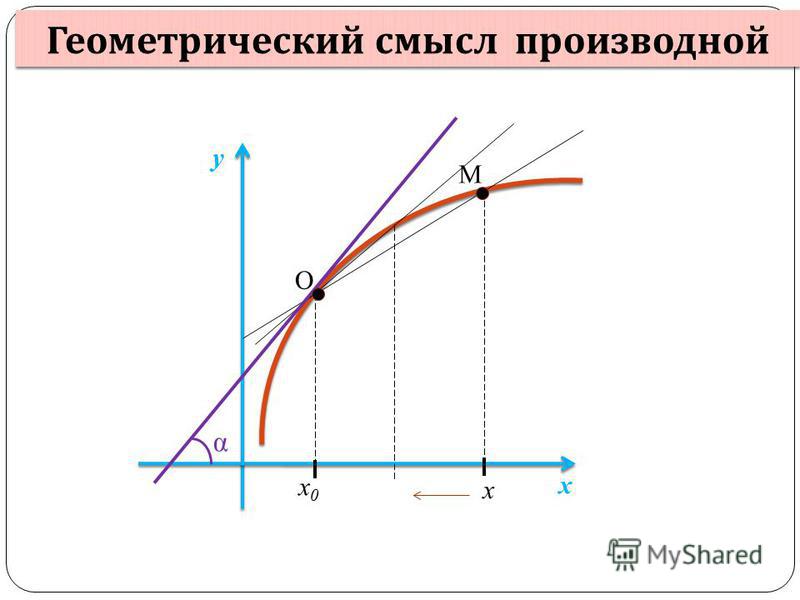 Обязательно укажите единицы измерения.

1. f(x+h)−f(x)hf(x+h)−f(x)h
2. f′(x)=limh→0f(x+h)−f(x)hf′(x)=limh→0f(x+h)−f(x)h

90.

P(x)P(x) обозначает население города в момент времени xx в годах.

91.

C(x)C(x) обозначает общую сумму денег (в тысячах долларов), потраченную на концессии xx клиентов в парке развлечений.

92.

R(x)R(x) обозначает общую стоимость (в тысячах долларов) изготовления xx радиочасов.

93.

g(x)g(x) обозначает оценку (в процентах), полученную за тест при xx часах обучения.

94.

B(x)B(x) обозначает стоимость (в долларах) учебника по социологии в университетских книжных магазинах США в xx лет, начиная с 1990.1990.

95.

p(x)p(x) обозначает атмосферное давление в торрах на высоте xx футов.

96.

Нарисуйте график функции y=f(x)y=f(x) со всеми следующими свойствами:

1. f′(x)>0f′(x)>0 для −2≤x<1−2≤x<1
2. f'(2)=0f'(2)=0
3. f′(x)>0f′(x)>0 для x>2x>2
4. f(2)=2f(2)=2 и f(0)=1f(0)=1
5. limx→−∞f(x)=0limx→−∞f(x)=0 и limx→∞f(x)=∞limx→∞f(x)=∞
6. f′(1)f′(1) не существует.

97.

Предположим, что температура TT в градусах Фаренгейта на высоте xx в футах над землей равна y=T(x).y=T(x).

1. Дайте физическую интерпретацию с единицами измерения T′(x).T′(x).
2. Если мы знаем, что T′(1000)=−0,1,T′(1000)=−0,1, объясни физический смысл.

98.

Предположим, что общая прибыль компании составляет y=P(x)y=P(x) тысяч долларов при продаже xx единиц товара.

1. Что измеряет P(b)−P(a)b−aP(b)−P(a)b−a для 0
2. Что измеряет P′(x)P′(x) и каковы единицы измерения?
3. Предположим, что P′(30)=5, P′(30)=5, как приблизительно изменится прибыль, если количество проданных товаров увеличится с 30 до 31?30 до 31?

99.

График на следующем рисунке моделирует количество людей N(t)N(t), заболевших гриппом tt недель после его первоначальной вспышки в городе с населением 50 000 50 000 жителей.

1. Опишите, что представляет собой N'(t)N'(t) и как она ведет себя при увеличении tt.
2. Что эта производная говорит нам о том, как этот город пострадал от вспышки гриппа?
   

Для следующих упражнений используйте следующую таблицу, в которой показана высота hh ракеты Saturn VV для миссии Apollo 1111 через tt секунд после запуска.

Время (секунды)	Высота (метры)
00	00
11	22
22	44
33	1313
44	2525
55	3232

100.

Каков физический смысл h'(t)?h'(t)? Что такое единицы?

101.

[T] Постройте таблицу значений для h'(t)h'(t) и отобразите h(t)h(t) и h'(t)h'(t) на одном графике. ( Подсказка: для внутренних точек оцените как левый предел, так и правый предел и усредните их. Внутренняя точка интервала I — это элемент I, который не является конечной точкой I.)

102.

[T] Наилучшая линейная аппроксимация данных дается формулой H(t)=7,229t−4,905,H(t)=7,229t−4,905, где HH — высота ракеты (в метрах) и tt — время, прошедшее с момента взлета. Из этого уравнения определите H′(t).H′(t). График H(t)H(t) с заданными данными и на отдельной координатной плоскости график H′(t).H′(t).

103.

[T] Наилучшее квадратичное соответствие данным определяется выражением G(t)=1,429t2+0,0857t−0,1429,G(t)=1,429t2+0,0857t−0,1429, где GG — высота ракеты (в метрах) и tt — время, прошедшее с момента взлета.

No related posts.