Таблица синусов и: Таблица синусов и косинусов

Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы. Таблица Брадиса

Содержание

1. Часто используемые значения косинуса
2. Таблица Брадиса – синусы и косинусы.
3. Как пользоваться таблицей Брадиса.
4. Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
5. Тригонометрия. Свойства, графики тригонометрических функций.
6. Прямые тригонометрические функции.
7. Таблица значений тригонометрических функций sin , cos , tg для наиболее популярных углов (таблица Брадиса).
8. Производные тригонометрические функции.
9. Полная таблица Брадиса
10. Другие тригонометрические функции.
11. Тригонометрия. Обратные тригонометрические функции. Арксинус.
12. Как пользоваться таблицей Брадиса косинусов или синусов
13. Таблица Брадиса – тангенсы и котангенсы.

Часто используемые значения косинуса

Косинус 0 градусов = 1

Косинус 30 градусов = 0,866025404 = {frac {sqrt{3}}{2}}

Косинус 45 градусов = 0,707106781 = {frac {sqrt{2}}{2}}

Косинус 60 градусов = 0,5 = {frac {1}{2}}

Косинус 90 градусов = 0

Косинус 120 градусов = -0,5 = {-frac {1}{2}}

Косинус 135 градусов = -0,707106781 = {-frac {sqrt{3}}{2}}

Косинус 180 градусов = -1

Таблица Брадиса – синусы и косинусы.

Прямые тригонометрические функции.

– синус (sin x)

– косинус (cos x)

Таблица значений тригонометрических функций sin , cos , tg для наиболее популярных углов (таблица Брадиса).

Таблица Брадиса – это таблица, помогающая при вычислениях в решении задач как в школе (на математике, алгебре, геометрии и физике в старших классах), так и в вузах.
Таблица Брадиса – синусы и косинусы.
	Как пользоваться таблицей Брадиса. На некоторых примерах рассмотрим, как пользоваться таблицей Брадиса. sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392. sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668. Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса. Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере: sin 3°45′=sin 3°42′+3′=0. 0645+0.0009=0.0654 либо sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654 Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный. cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо cos 80°27′=80°30′−3′=0.1650−(-0.0009)=0.1659 Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов Тригонометрические определения синуса, косинуса, тангенса и котангенса позволяют указать значения тригонометрических функций для углов 0 и 90 градусов: , а котангенс нуля градусов не определен, и , а тангенс 90 градусов не определен. В курсе геометрии из прямоугольных треугольников с углами 30, 60 и 90 градусов, а также 45, 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов: , и . Занесем указанные значения тригонометрических функций для углов 0, 30, 45, 60 и 90 градусов (0, π/6, π/4, π/3, π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса. Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120, 135, 150, 180, 210, 225, 240, 270, 300, 315, 330 и 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид. Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже. Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть, так как они очень часто используются при решении задач.   Тригонометрия. Свойства, графики тригонометрических функций.
Тригонометрия — раздел в математику, изучающий тригонометрические функции и их использование в геометрии.
Тригонометрия. Свойства, графики тригонометрических функций.

α(град)	0	15	30	45	60	75	90
α(рад)	0	π/12	π/6	π/4	π/3	5π/12	π/2
sin	0	0,259	0,5	0,707	0,866	0,966	1
cos	1	0,966	0,866	0,707	0,5	0,259	0
tg	0	0,268	0,577	1	1,732	3,732	–
ctg	–	3,732	1,732	1	0,577	0,268	0

α(град)	120	135	150	180	270	360
α(рад)	2π/3	3π/4	5π/6	π	3π/2	2π
sin	0,866	0,707	0,5	0	-1	0
cos	-0,5	-0,707	-0,866	-1	0	1
tg	-1,732	-1	-0,577	0	–	0
ctg	-0,577	-1	-1,732	–	0	–

Производные тригонометрические функции.

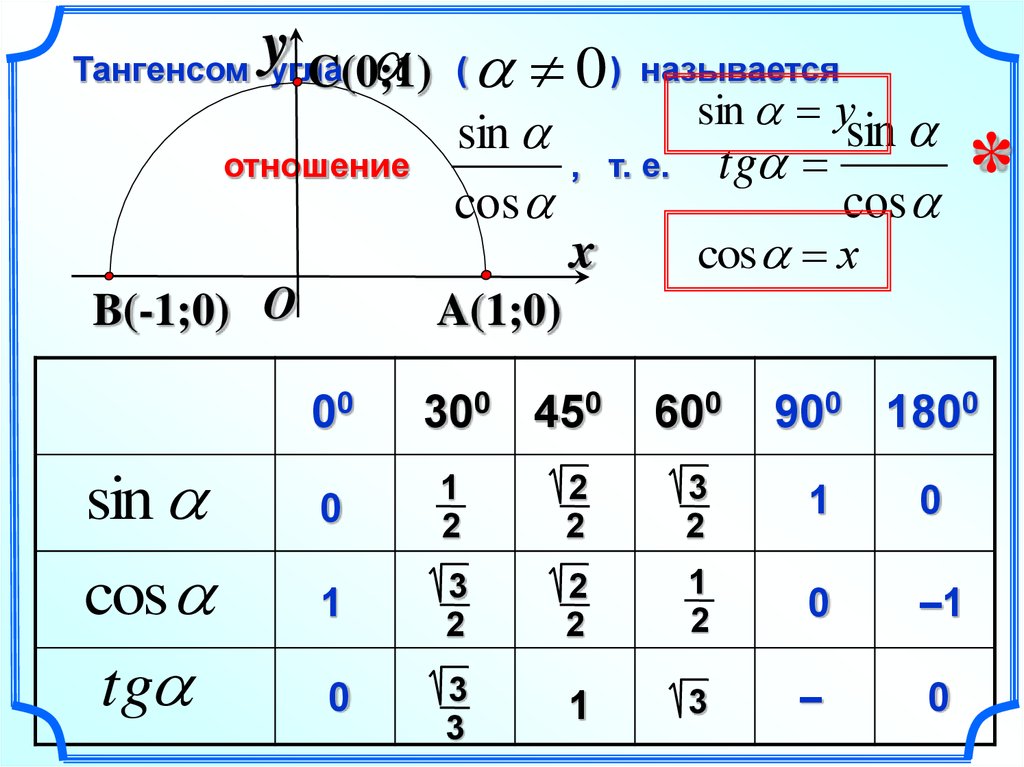
– тангенс (tg x)

– котангенс (ctg x)

Полная таблица Брадиса

sin	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	cos	± 1′	± 2′	± 3′
											0,0000	90°
0°	0,0000	0017	0035	0052	007	0087	0105	0122	014	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0366	0384	0401	0419	0436	0454	0471	0488	0506	0523	87°	3	6	9
3°	0523	0541	0558	0576	0593	061	0628	0645	0663	068	0698	86°	3	6	9
4°	0698	0715	0732	075	0767	0785	0802	0819	0837	0854	0872	85°	3	6	9
5°	0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84°	3	6	9
6°	1045	1063	108	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	134	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	153	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	165	1668	1685	1702	1719	1736	80°	3	6	9
10°	1736	1754	1771	1788	1805	1822	184	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	213	2147	2164	2181	2198	2215	2233	225	77°	3	6	9
13°	225	2267	2284	23	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	247	2487	2504	2521	2538	2554	2571	2588	75°	3	6	8
15°	2588	2605	2622	2639	2656	2672	2689	2706	2723	274	2756	74°	3	6	8
16°	2756	2773	279	2807	2823	284	2857	2874	289	2907	2924	73°	3	6	8
17°	2924	294	2957	2974	299	3007	3024	304	3057	3074	309	72°	3	6	8
18°	309	3107	3123	314	3156	3173	319	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	342	70°	3	5	8
20°	342	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	36	3616	3633	3649	3665	3681	3697	3714	373	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	421	4226	65°	3	5	8
25°	4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	454	63°	3	5	8
27°	454	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	471	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	497	4985	5	60°	3	5	8
30°	5	5015	503	5045	506	5075	509	5105	512	5135	515	59°	3	5	8
31°	515	5165	518	5195	521	5225	524	5255	527	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	549	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	565	5664	5678	5693	5707	5721	5736	55°	2	5	7
35°	5736	575	5764	5779	5793	5807	5821	5835	585	5864	5878	54°	2	5	7
36°	5878	5892	5906	592	5934	5948	5962	5976	599	6004	6018	53°	2	5	7
37°	6018	6032	6046	606	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	617	6184	6198	6211	6225	6239	6252	6266	628	6293	51°	2	5	7
39°	6293	6307	632	6334	6347	6361	6374	6388	6401	6414	6428	50°	2	4	7
40°	6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	66	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	673	6743	6756	6769	6782	6794	6807	682	47°	2	4	6
43°	682	6833	6845	6858	6871	6884	6896	6909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	7071	45°	2	4	6
45°	7071	7083	7096	7108	712	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	723	7242	7254	7266	7278	729	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	742	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	749	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	757	7581	7593	7604	7615	7627	7638	7649	766	40°	2	4	6
50°	766	7672	7683	7694	7705	7716	7727	7738	7749	776	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	788	38°	2	4	5
52°	788	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	807	808	809	36°	2	3	5
54°	809	81	8111	8121	8131	8141	8151	8161	8171	8181	8192	35°	2	3	5
55°	8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	829	34°	2	3	5
56°	829	83	831	832	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	848	32°	2	3	5
58°	848	849	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	859	8599	8607	8616	8625	8634	8643	8652	866	30°	1	3	4
60°	866	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	878	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829	8838	8846	8854	8862	887	8878	8886	8894	8902	891	27°	1	3	4
63°	891	8918	8926	8934	8942	8949	8957	8965	8973	898	8988	26°	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	9063	25°	1	3	4
65°	9063	907	9078	9085	9092	91	9107	9114	9121	9128	9135	24°	1	2	4
66°	9135	9143	915	9157	9164	9171	9178	9184	9191	9198	9205	23°	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9265	9272	22°	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	933	9336	21°	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9385	9391	9397	20°	1	2	3
70°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	9455	19°	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	95	9505	9511	18°	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17°	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16°	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	965	9655	9659	15°	1	2	2
75°	9659	9664	9668	9673	9677	9681	9686	969	9694	9699	9703	14°	1	1	2
76°	9703	9707	9711	9715	972	9724	9728	9732	9736	974	9744	13°	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	977	9774	9778	9781	12°	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	981	9813	9816	11°	1	1	2
79°	9816	982	9823	9826	9829	9833	9836	9839	9842	9845	9848	10°	1	1	2
80°	9848	9851	9854	9857	986	9863	9866	9869	9871	9874	9877	9°	0	1	1
81°	9877	988	9882	9885	9888	989	9893	9895	9898	99	9903	8°	0	1	1
82°	9903	9905	9907	991	9912	9914	9917	9919	9921	9923	9925	7°	0	1	1
83°	9925	9928	993	9932	9934	9936	9938	994	9942	9943	9945	6°	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	996	9962	5°	0	1	1
85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4°	0	0	1
86°	9976	9977	9978	9979	998	9981	9982	9983	9984	9985	9986	3°	0	0	0
87°	9986	9987	9988	9989	999	999	9991	9992	9993	9993	9994	2°	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	9998	1°	0	0	0
89°	9998	9999	9999	9999	9999	1. 0	1.0	1.0	1.0	1.0	1.0	0°	0	0	0
90°	0,0000

Другие тригонометрические функции.

– секанс (sec x)

– косеканс (cosec x)

В современном мире есть 6 базовых тригонометрических функций, которые ниже в таблице указаны вместе с уравнениями, которые связывают их.

Функция	Соотношение
sin
cos
tg или tan
ctg или cot
sec
cosec или csc

Тригонометрия.

Обратные тригонометрические функции. Арксинус.Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям .Тригонометрия. Обратные тригонометрические функции. Арксинус.

Как пользоваться таблицей Брадиса косинусов или синусов

Таблица Брадиса для синусов и косинусов даёт значение синуса любого острого угла, содержащего целое число градусов и десятых долей градуса, на пересечении строки, имеющей в заголовке (слева) соответствующее число минут. Так, sin 70° 30`=0.9426. Для получения синусов прочих углов нужна интерполяция, вводящая поправку на равность между данным углом и ближайшим табличным. Эта поправка берется из соответствующего столбца поправок справа (курсив). Она прибавляется к ближайшему меньшему значению синуса, если данный угол превосходит ближайший меньший табличный на 1,2,3 минуты, и отнимается от ближайшего большего табличного синуса в остальных случаях.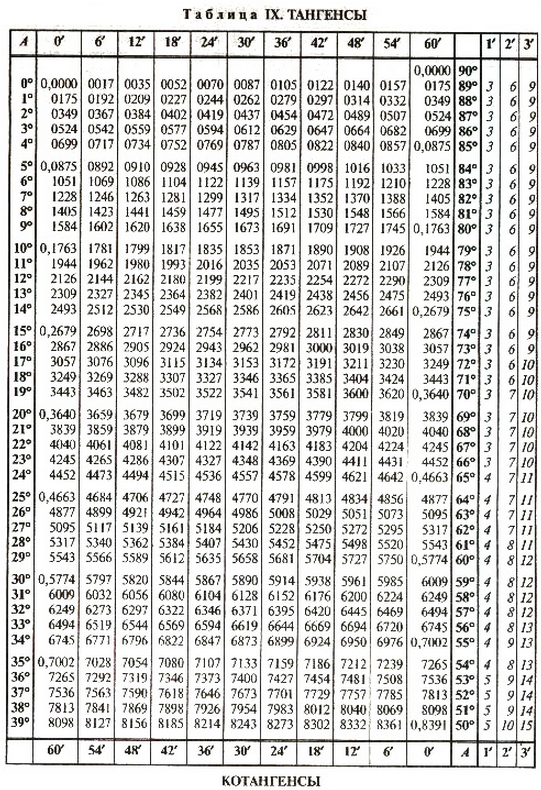 Например, sin 70° 32`=0,9428, так как 9426+2=9428, и sin 70° 34`= 0,9430, так как 9432-2=9430. Та же таблица синусов и косинусов служит для разыскания косинусов, при чем надо пользоваться нумерацией градусов справа, нумерацией минут снизу и не забывать, что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, звменяя их синусами дополнительных углов.
Значение тангенса любого острого угла, содержащего целое число градусов и минут определяется по табл. если угол заключен между 0° и 76°, и по таблице тангенсов если между 76° и 90. Работа по таблице тангенсов и котангенсов требует применения интерполяции, облегчаемой поправками, помещенными в столбцах справа (курсив) и ничем не отличается от работы таблицы sin и cos. Тангенсы углов, которые больше 76 градусов, содержащих целое число градусов и минут, табл. дает непосредственно (без интерполяции).
Таблицы Брадиса по синусам, косинусам, тангенсам и котангенсам позволяют решать и обратный вопрос, то есть находить острый угол по данному значению его синуса или тангенса.

Таблица Брадиса – тангенсы и котангенсы.

Таблица Брадиса – это таблица, помогающая при вычислениях в решении задач как в школе (на математике, алгебре, геометрии и физике в старших классах), так и в вузах.Таблица Брадиса – тангенсы и котангенсы.

Источники

• https://mnogoformul.ru/tablica-sinusov-i-kosinusov
• https://www.calc.ru/Tablitsa-Bradisa-Tangensy-I-Kotangensy.html
• https://www.calc.ru/Tablitsa-Bradisa-Sinusy-I-Kosinusy.html
• http://www.cleverstudents.ru/trigonometry/tables_of_sin_cos_tg_ctg.html
• https://www.calc.ru/Trigonometricheskiye-Funktsii-Znacheniye-Trigonometricheskik.html
• https://www.kontrolnaya-rabota.ru/s/tablica-bradisa/sinus-i-cosinus/

Таблица синусов и косинусов — сборник таблиц

Синусы и косинусы
sin	0’	6’	12’	18’	24’	30’	36’	42’	48’	54’	60’	cos	1’	2’	3’
											0	90°
0°	0	17	35	52	70	87	105	122	140	157	175	89°	3	6	9
1°	175	192	209	227	244	262	279	297	314	332	349	88°	3	6	9
2°	349	366	384	401	419	436	454	471	488	506	523	87°	3	6	9
3°	523	541	558	576	593	610	628	645	663	680	698	86°	3	6	9
4°	698	715	732	750	767	785	802	819	837	854	0,0872	85°	3	6	9
5°	0,0872	889	906	924	941	958	976	993	1011	1028	1045	84°	3	6	9
6°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0,1736	80°	3	6	9
10°	0,1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	77°	3	6	9
13°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0,2588	75°	3	6	8
15°	0,2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	74°	3	6	8
16°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	73°	3	6	8
17°	2924	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	72°	3	6	8
18°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0,342	70°	3	5	8
20°	0,342	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0,4226	65°	3	5	8
25°	0,4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	63°	3	5	8
27°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0,5	60°	3	5	8
30°	0,5	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	59°	3	5	8
31°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0,5736	55°	2	5	7
35°	0,5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0,5878	54°	2	5	7
36°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	53°	2	5	7
37°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	51°	2	5	7
39°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0,6428	50°	2	4	7
40°	0,6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	47°	2	4	6
43°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0,7071	45°	2	4	6
45°	0,7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0,766	40°	2	4	6
50°	0,766	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	38°	2	4	5
52°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	36°	2	3	5
54°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0,8192	35°	2	3	5
55°	0,8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	34°	2	3	5
56°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	32°	2	3	5
58°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0,866	30°	1	3	4
60°	0,866	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	27°	1	3	4
63°	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	26°	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0,9063	25°	1	3	4
65°	0,9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	24°	1	2	4
66°	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	23°	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	22°	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	21°	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0,9397	20°	1	2	3
70°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0,9455	19°	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	18°	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17°	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16°	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0,9659	15°	1	2	2
75°	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	14°	1	1	2
76°	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	13°	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	12°	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	11°	1	1	2
79°	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0,9848	10°	1	1	2
80°	0,9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	9°	0	1	1
81°	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	8°	0	1	1
82°	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	7°	0	1	1
83°	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	6°	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	5°	0	1	1
85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4°	0	0	1
86°	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	3°	0	0	0
87°	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	2°	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0,9998	1°	0	0	0
89°	9998	9999	9999	9999	9999	1	1	1	1	1	1	0°	0	0	0
90°	1
sin	60’	54’	48’	42’	36’	30’	24’	18’	12’	6’	0’	cos	1’	2’	3’

← Назад в раздел

Таблица синусов

\begin{align} \text{угол} \end{align}	\begin{align} 0 \end{align}	\begin{align} \frac{\pi}{6} \end{align}	\begin{align} \frac{\pi}{4} \end{align}	\begin{align} \frac{\pi}{3} \end{align}	\begin{align} \frac{\pi}{2} \end{align}	\begin{align} \frac{2\pi}{3} \end{align}	\begin{align} \frac{3\pi}{4} \end{align}	\begin{align} \frac{5\pi}{6} \end{align}	\begin{align} \pi \end{align}
\begin{align} \sin{x} \end{align}	\begin{align} \frac{\sqrt{0}}{2} \end{align}	\begin{align} \frac{\sqrt{1}}{2} \end{align}	\begin{align} \frac{\sqrt{2}}{2} \end{align}	\begin{align} \frac{\sqrt{3}}{2} \end{align}	\begin{align} \frac{\sqrt{4}}{2} \end{align}	\begin{align} \frac{\sqrt{3}}{2} \end{align}	\begin{align} \frac{\sqrt{2}}{2} \end{align}	\begin{align} \frac{\sqrt{1}}{2} \end{align}	\begin{align} \frac{\sqrt{0}}{2} \end{align}
\begin{align} \cos{x} \end{align}	\begin{align} \frac{\sqrt{4}}{2} \end{align}	\begin{align} \frac{\sqrt{3}}{2} \end{align}	\begin{align} \frac{\sqrt{2}}{2} \end{align}	\begin{align} \frac{\sqrt{1}}{2} \end{align}	\begin{align} \frac{\sqrt{0}}{2} \end{align}	\begin{align} -\frac{\sqrt{1}}{2} \end{align}	\begin{align} -\frac{\sqrt{2}}{2} \end{align}	\begin{align} -\frac{\sqrt{3}}{2} \end{align}	\begin{align} -\frac{\sqrt{4}}{2} \end{align}
\begin{align} \text{tg x} \end{align}	\begin{align} \sqrt{\frac{0}{4}} \end{align}	\begin{align} \sqrt{\frac{1}{3}} \end{align}	\begin{align} \sqrt{\frac{2}{2}} \end{align}	\begin{align} \sqrt{\frac{3}{1}} \end{align}	\begin{align} \varnothing \end{align}	\begin{align} -\sqrt{\frac{3}{1}} \end{align}	\begin{align} -\sqrt{\frac{2}{2}} \end{align}	\begin{align} -\sqrt{\frac{1}{3}} \end{align}	\begin{align} -\sqrt{\frac{0}{4}} \end{align}
\begin{align} \text{ctg x} \end{align}	\begin{align} \varnothing \end{align}	\begin{align} \sqrt{\frac{3}{1}} \end{align}	\begin{align} \sqrt{\frac{2}{2}} \end{align}	\begin{align} \sqrt{\frac{1}{3}} \end{align}	\begin{align} 0 \end{align}	\begin{align} -\sqrt{\frac{1}{3}} \end{align}	\begin{align} -\sqrt{\frac{2}{2}} \end{align}	\begin{align} -\sqrt{\frac{3}{1}} \end{align}	\begin{align} \varnothing \end{align}
\begin{align} \text{cosec x} \end{align}	\begin{align} \varnothing \end{align}	\begin{align} \frac{2}{\sqrt{1}} \end{align}	\begin{align} \frac{2}{\sqrt{2}} \end{align}	\begin{align} \frac{2}{\sqrt{3}} \end{align}	\begin{align} \frac{2}{\sqrt{4}} \end{align}	\begin{align} \frac{2}{\sqrt{3}} \end{align}	\begin{align} \frac{2}{\sqrt{2}} \end{align}	\begin{align} \frac{2}{\sqrt{1}} \end{align}	\begin{align} \varnothing \end{align}
\begin{align} \sec{x} \end{align}	\begin{align} \frac{2}{\sqrt{4}} \end{align}	\begin{align} \frac{2}{\sqrt{3}} \end{align}	\begin{align} \frac{2}{\sqrt{2}} \end{align}	\begin{align} \frac{2}{\sqrt{1}} \end{align}	\begin{align} \varnothing \end{align}	\begin{align} -\frac{2}{\sqrt{1}} \end{align}	\begin{align} -\frac{2}{\sqrt{2}} \end{align}	\begin{align} -\frac{2}{\sqrt{3}} \end{align}	\begin{align} -\frac{2}{\sqrt{4}} \end{align}

Таблица синусов.

Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.

Вычислить синус угла

sin(°) = 0

Таблица синусов в радианах

α	0	π6	π4	π3	π2	π	3π2	2π
sin α	0	12	√22	√32	1	0	-1	0

Таблица синусов углов от 0° до 180°

sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0. 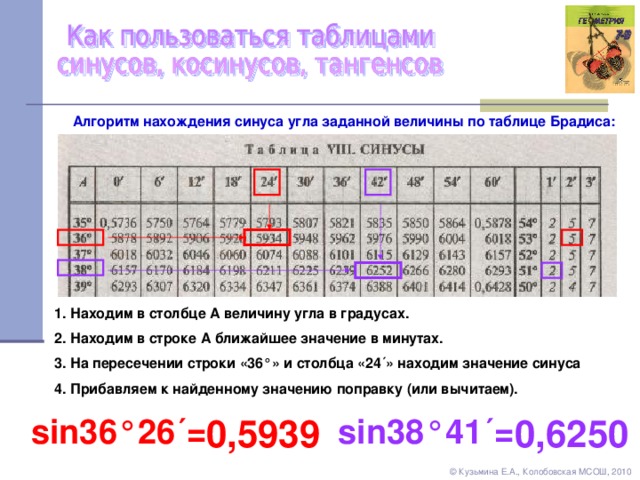207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107

sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0. 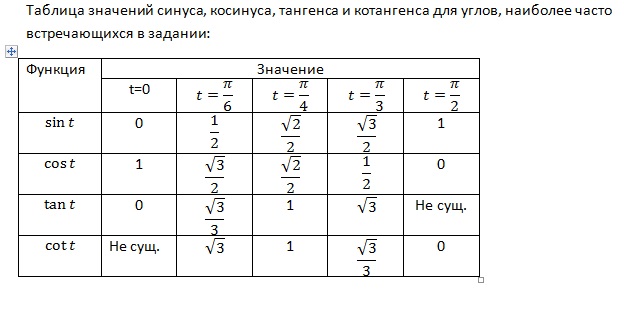809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1

sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0. 994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107

sin(136°) = 0. 694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0. 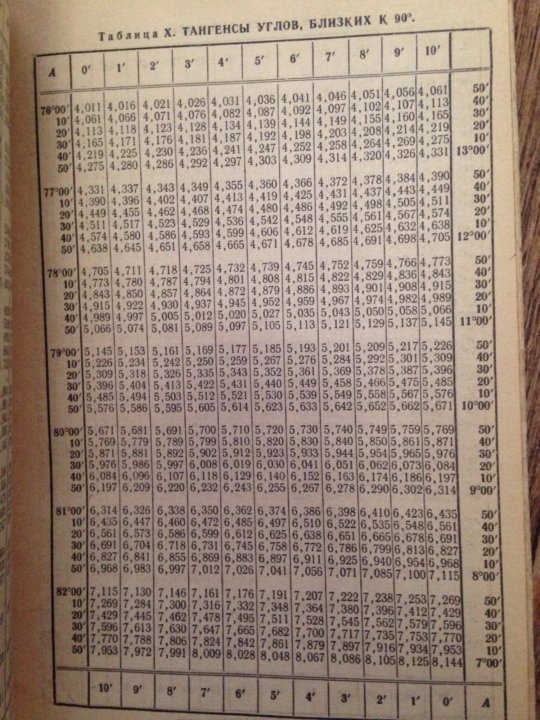052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0

Таблица синусов углов от 181° до 360°

sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0. 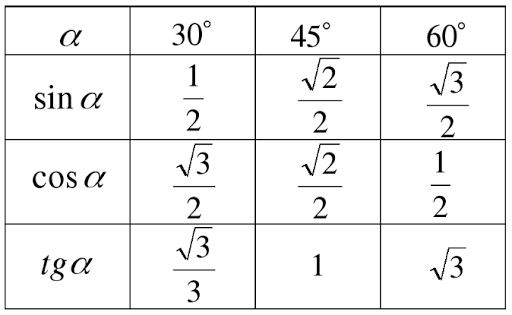544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107

sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0. 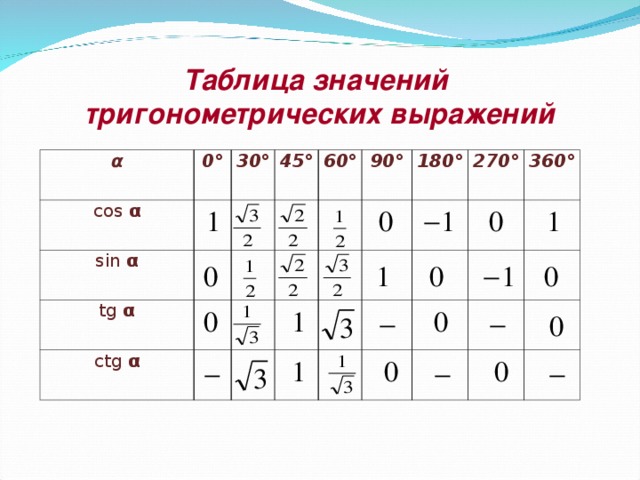951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1

sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0. 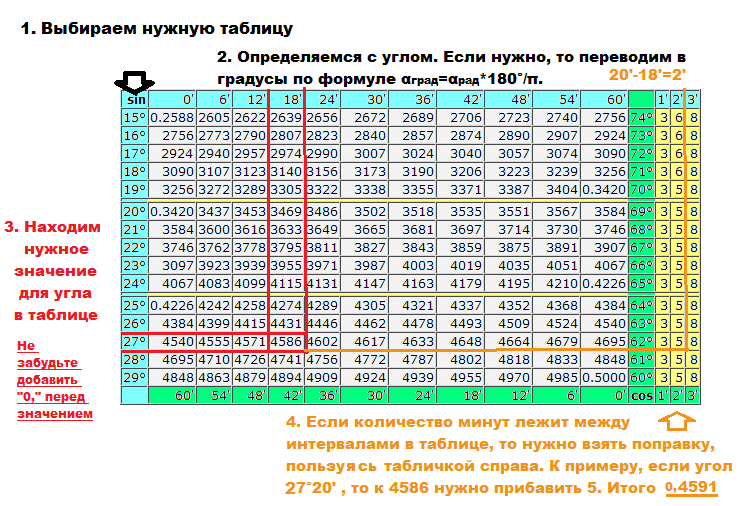93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107

sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0. 5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0

Таблицы значений тригонометрических функций Таблица косинусов Таблица тангенсов Таблица котангенсов Сводная таблица тригонометрических функций

Тригонометрические формулы

Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Синусы каких углов выражаются формулами?

В 8 классе ученики заучивают таблицу синусов и других тригонометрических функций.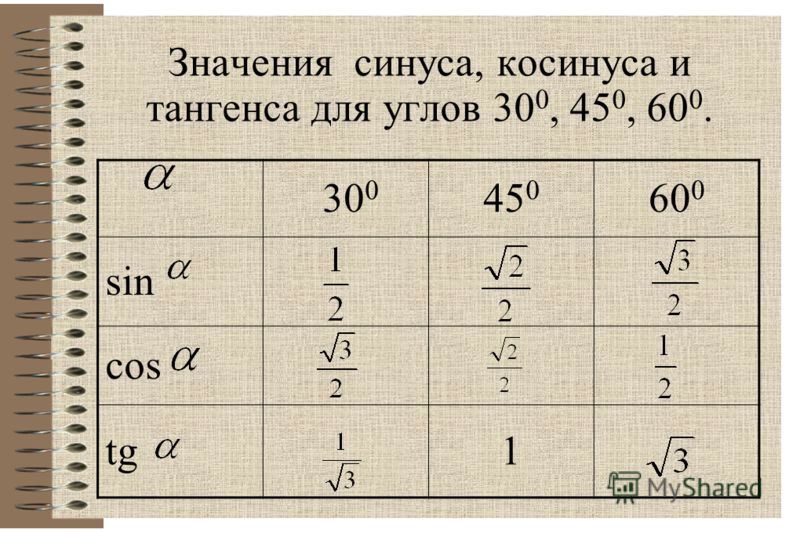 Она выглядит так:

Школьная таблица синусов, косинусов, тангенсов и котангенсов

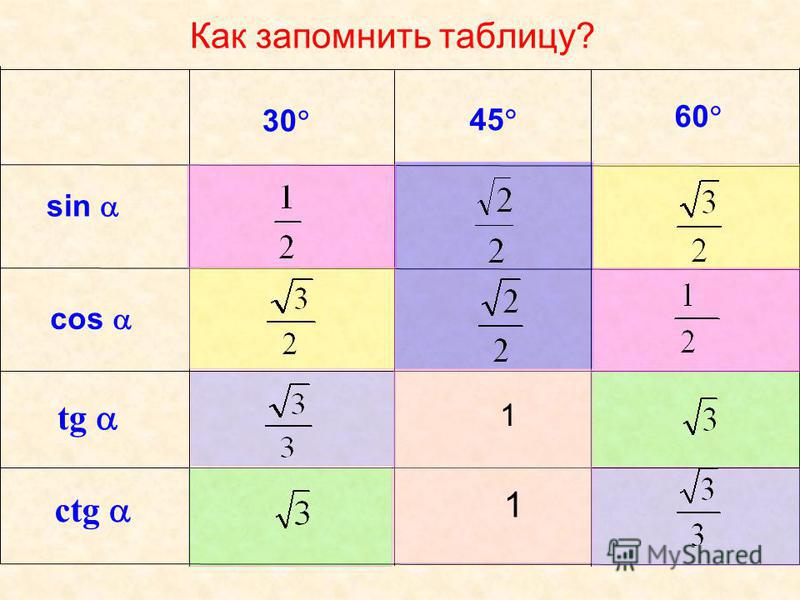
угол $\alpha$, o		30	45	60	90
sin$\alpha$		$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
cos$\alpha$	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$
tg$\alpha$		$\frac{1}{\sqrt{3}}$	1	$\sqrt{3}$	—
ctg$\alpha$	—	$\sqrt{3}$	1	$\frac{1}{\sqrt{3}}$

Есть очень хороший мнемонический приём, позволяющий запомнить значения тригонометрических функций табличных углов.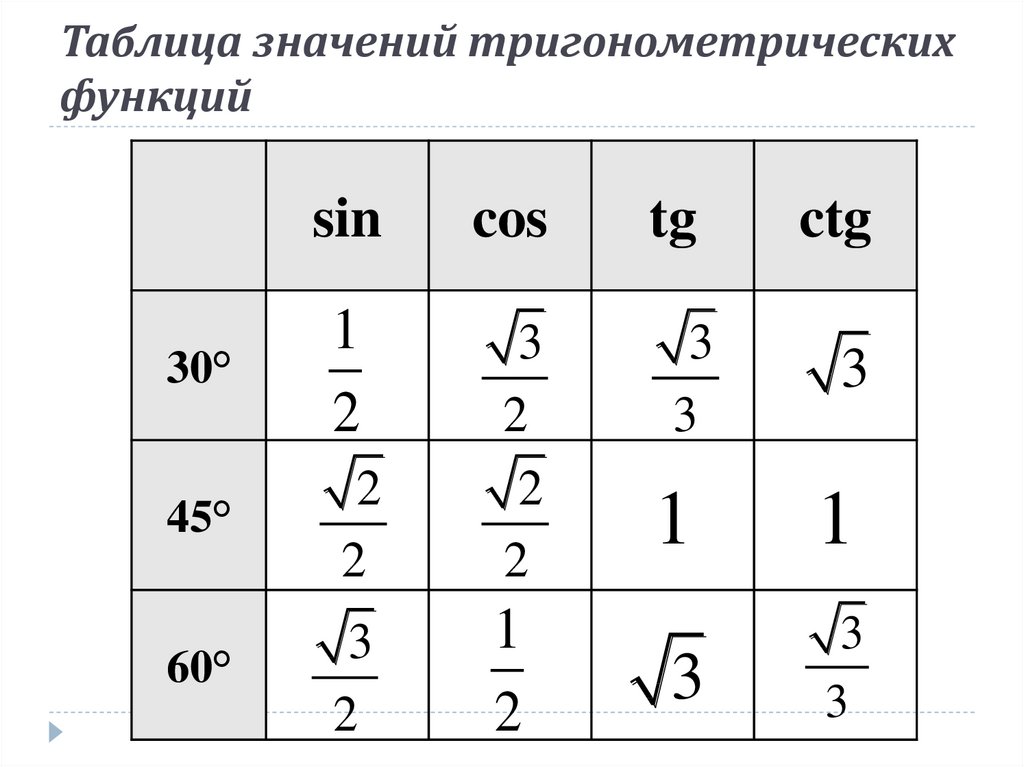 o = \frac{\sqrt{5}+1}{4}\frac{\phi}{2}$

Можно выражать с помощью форул с корнями синусы сумм и разностей углов, тригонометрические функции которых тоже выражаются формулами с корнями. Поскольку все исходные углы делятся на 3, то и точные формулы тригонометрических функций можно получить для углов, кратных тём градусам. Приведём значения значения синусов. Значения остальных фнукций углов можно получить, воспользовавшись формулами приведения и соотношениями между тригонометрическими функциями.

sin 0^o = 0
sin 3^o = $\frac{(2-\sqrt{12})\sqrt{5+\sqrt5}+(\sqrt{10}-\sqrt2)(\sqrt3+1)}{16}$ — это центральный угол правильного 60-угольника
sin 6^o = $\frac{\sqrt{30-\sqrt{180}}-\sqrt5-1}{8}$ — это центральный угол правильного 30-угольника
sin 9^o = $\tfrac{1}{8} \left[\sqrt{10}+\sqrt2-2\sqrt{5-\sqrt5}\right]$ — это центральный угол правильного 20-угольника
sin 12^o = $\tfrac{1}{8} \left[\sqrt{2(5+\sqrt5)}+\sqrt3-\sqrt{15}\right]$ — это центральный угол правильного 15-угольника
sin 15^o = $\tfrac{1}{4}(\sqrt6-\sqrt2)$
sin 18^o = $\tfrac{1}{4}\left(\sqrt5-1\right)$ — это центральный угол правильного 10-угольника
sin 21^o = $\tfrac{1}{16}\left[2(\sqrt3+1)\sqrt{5-\sqrt5}-(\sqrt6-\sqrt2)(1+\sqrt5)\right]$
sin 24^o = $\tfrac{1}{8}\left[\sqrt{15}+\sqrt3-\sqrt{2(5-\sqrt5)}\right]$
sin 27^o = $\tfrac{1}{8}\left[2\sqrt{5+\sqrt5}-\sqrt2\;(\sqrt5-1)\right]$
sin 30^o = $\frac{1}{2}$ — это центральный угол правильного 6-угольника
sin 33^o = $\tfrac{1}{16}\left[2(\sqrt3-1)\sqrt{5+\sqrt5}+\sqrt2(1+\sqrt3)(\sqrt5-1)\right]$
sin 36^o = $\frac{\sqrt{10-\sqrt{20}}}{4}$ — это центральный угол правильного 5-угольника
sin 39^o = $\tfrac1{16}[2(1-\sqrt3)\sqrt{5-\sqrt5}+\sqrt2(\sqrt3+1)(\sqrt5+1)]$
sin 42^o = $\frac{\sqrt{30+\sqrt{180}}-\sqrt5+1}{8}$
sin 45^o = $\frac{1}{\sqrt2}$ — это центральный угол правильного 4-угольника
sin 48^o = $\frac{\sqrt{15}-\sqrt3+\sqrt{10+\sqrt{20}}}{8}$
sin 51^o = $\tfrac1{16}[2(1+\sqrt3)\sqrt{5-\sqrt5}+\sqrt2(\sqrt3-1)(\sqrt5+1)]$
sin 54^o = $\frac{\sqrt5+1}{4}$
sin 57^o = $\tfrac{1}{16}\left[2(\sqrt3+1)\sqrt{5+\sqrt5}+\sqrt2(1-\sqrt3)(\sqrt5-1)\right]$
sin 60^o = $\frac{sqrt{3}}{2}$
sin 63^o = $\tfrac{1}{8}\left[2\sqrt{5+\sqrt5}+\sqrt2\;(\sqrt5-1)\right]$
sin 66^o = $\tfrac{1}{8}\left(\sqrt{6(5-\sqrt5)}+\sqrt5+1\right)$
sin 69^o = $\tfrac{1}{16}\left[2(\sqrt3-1)\sqrt{5-\sqrt5}+(\sqrt6+\sqrt2)(1+\sqrt5)\right]$
sin 72^o = $\tfrac{1}{4}\sqrt{2(5+\sqrt5)}$
sin 75^o = $\tfrac{1}{4}(\sqrt6+\sqrt2)$
sin 78^o = $\tfrac{1}{8} \left[\sqrt{6(5+\sqrt5)}+\sqrt5-1\right]$
sin 81^o = $\tfrac{1}{8} \left[\sqrt{10}+\sqrt2+2\sqrt{5-\sqrt5}\right]$
sin 84^o = $\frac{\sqrt{10-\sqrt{20}}+\sqrt3+\sqrt{15}}{8}$
sin 87^o = $\frac{(2+\sqrt{12})\sqrt{5+\sqrt5}+(\sqrt{10}-\sqrt2)(\sqrt3-1)}{16}$
sin 90^o = 1

Итак, только для этих целых углов первой четверти синусы, косинусы и им подобные функции можно выразить точно.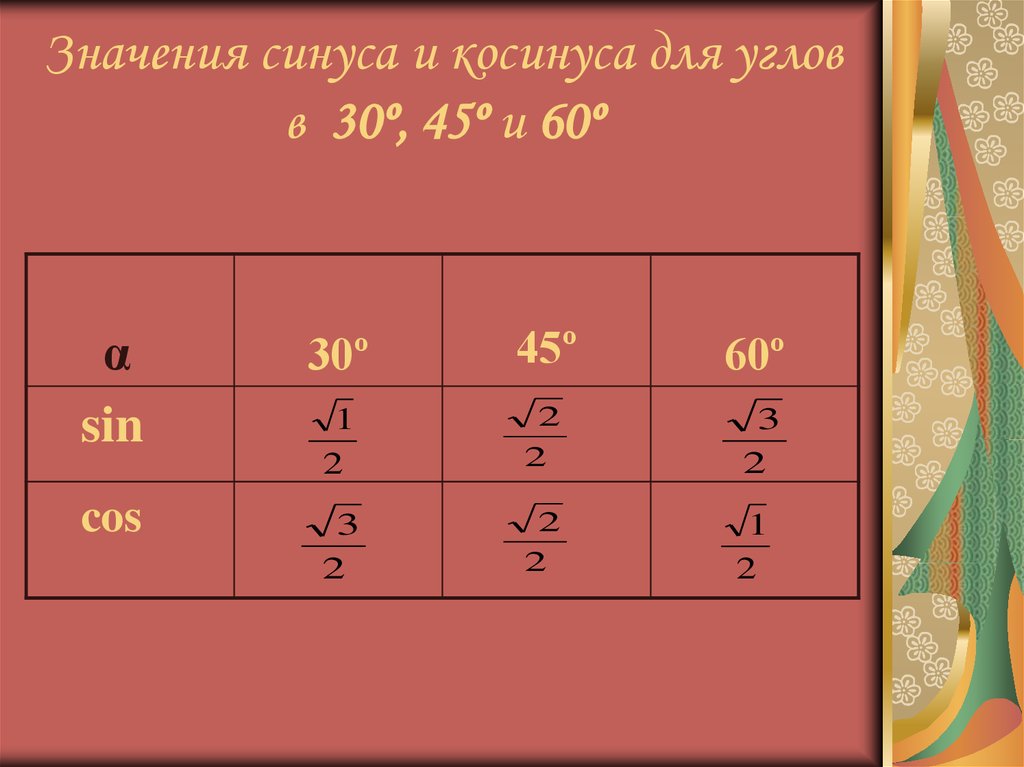 o=\frac{1}{16}(-1+\sqrt{17}+\sqrt{34-2\sqrt{17}}+ 2\sqrt{17+3\sqrt{17}- \sqrt{34-2\sqrt{17}}- 2\sqrt{34+2\sqrt{17}}})$

Также существуют методы построения для правильного 257- и 65537 угольников. Они дают точные формулы для бесконечного количества синусов рациональных углов.

Таблица синусов | Cubens

Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы можете делать вычисления, даже если под руками не будет инженерного калькулятора. Чтобы узнать значение синуса от нужного вам угла достаточно найти его в таблице.

Используя таблицу синусов вы сможете провести расчеты даже если под рукой не окажется инженерного калькулятора.

Чтобы найти значение синусанужного угла, достаточно воспользоваться данной таблицей.

Таблица синусов в радианах

α	0	π6	π4	π3	π2	π	3π2	2π
sin α

Таблица синусов— наравне с таблицей косинусов изучается в самом начале тригонометрии.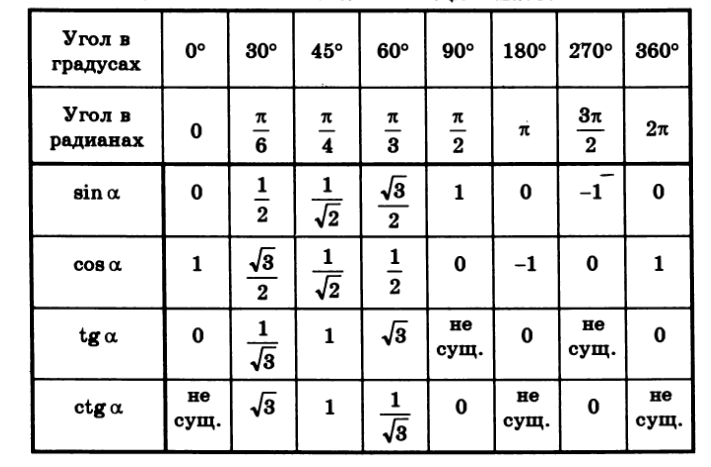 Без понимания таблицы синусов будет очень сложно изучать тригонометрию и применять тригонометрические формулы.

Тригонометрические функции имеют большое практическое значение в геометрии. Является по сути лишь показателями отношения различных сторон прямоугольного треугольника друг к другу, они способны помощь в решении большинства задач, результат которых сводится к решений прямоугольных треугольников.

Одной из основных тригонометрических функций синус. Поэтому в данной таблице синусоввы сможете найти любое значение синуса.

Таблица синусов углов от 0° до 180°

sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0. 258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107

sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0. 829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1

sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0. 992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107

sin(136°) = 0.694658 sin(137°) = 0. 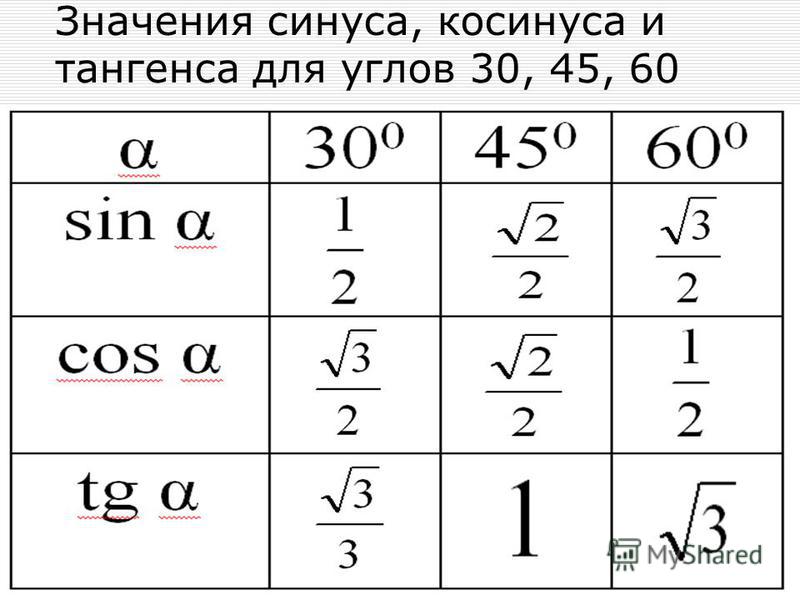681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0. 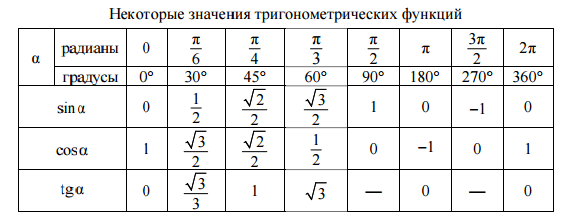034899 sin(179°) = 0.017452 sin(180°) = 0

 

Синус 0 (синус нуля)

равна (равна нулю)

Синус 1 (без единицы)

равна

Синус 3 (синус трех)

равна

Синус 90 (синус 90 градусов)

= (равен единице)

Синус 30 (синус 30 градусов)

равна

Синус 45 (синус 45 градусов)

равна

Синус 60 (синус 60 градусов)

равна

 

Таблица синусов углов от 181° до 360°

sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0. 275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107

sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0. 809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1

sin(271°) = -0.999848 sin(272°) = -0. 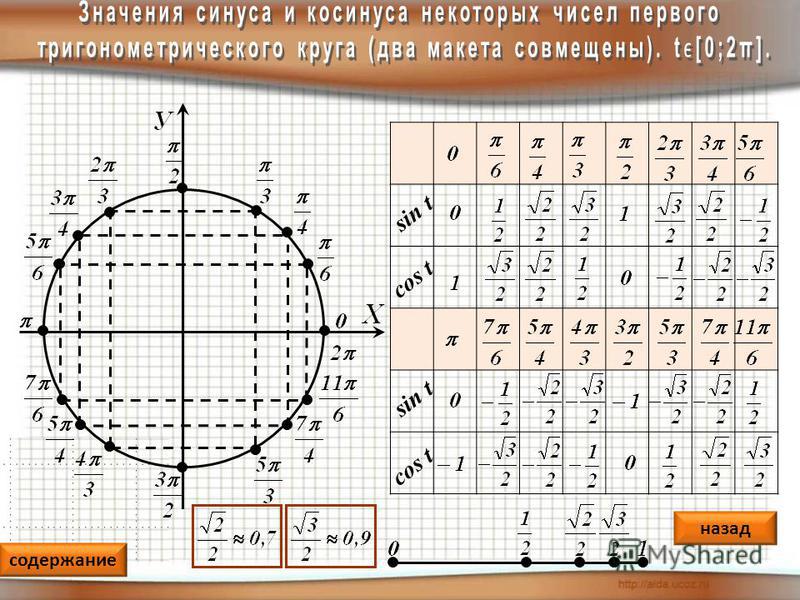999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0. 75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107

sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0. 173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0

 

Кроме таблицы синусов, на нашем сайте вы можете просмотреть таблицу косинусов, таблицу тангенсов, таблица котангенсів.

Построение таблицы синусов голыми руками | Тригонометрия: очень краткое введение

Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаКнигиЖурналы Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаКнигиЖурналы Термин поиска на микросайте

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Твиттер
  • Подробнее

CITE

Van Brummelen, Glen,

‘Здание синусоидального стола с вашими голыми руками’

,

Тригонометрия: очень короткое введение

, очень короткие введения

(

Oxford,

202020;

онлайн-издание,

Oxford Academic

, 23 января 2020 г.

), https://doi.org/10.1093/actrade/9780198814313.003.0003,

, по состоянию на 3 октября 2022 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаКнигиЖурналы Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаКнигиЖурналы Термин поиска на микросайте

Advanced Search

Abstract

Технологические достижения, столь широко распространенные почти во всех аспектах нашей современной жизни, почти мгновенно становятся для нас обыденными.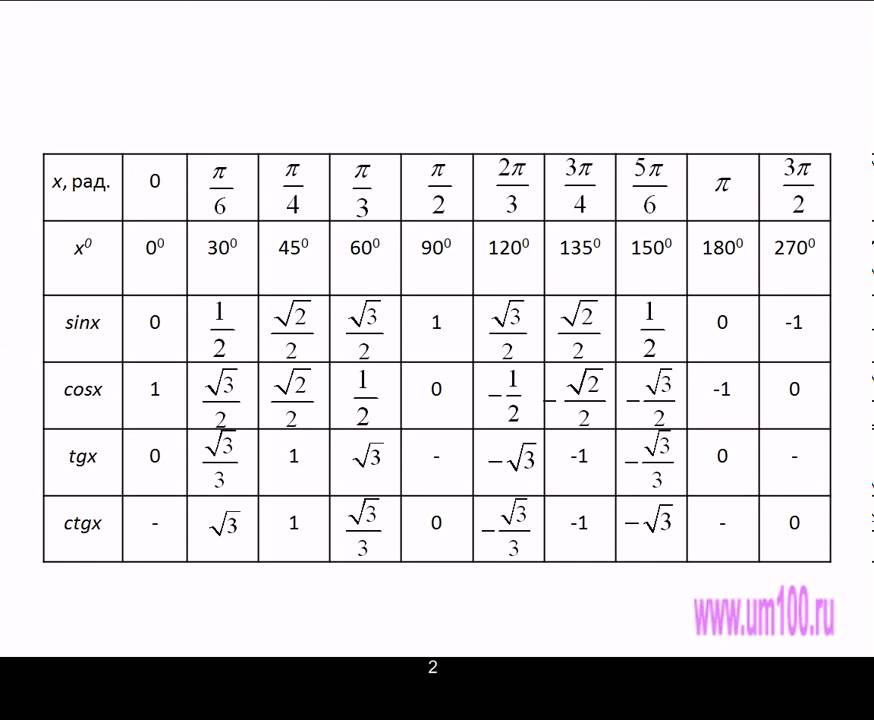 Как вычислитель, по-видимому, без особых усилий выясняет, что sin 33° = 0,5446? Внутри калькулятора не нарисованы прямоугольные треугольники, так откуда взялось это число? «Построение таблицы синуса голыми руками» показывает, как различные значения синуса вычислялись на протяжении истории без каких-либо механических вспомогательных средств. Он вводит законы суммы синусов и разностей, формулы половинного и двойного угла, золотой треугольник и одно из самых замечательных чисел во всей математике, золотое сечение, которое встречается в ослепительном множестве областей математики, естественных наук. явлений, произведений искусства и архитектуры.

Ключевые слова: угол, Генри Бриггс, круг, формула половинного угла, отношение, Региомонтан, квадрат, Франсуа Виет

Предмет

Чистая математика

Ряд

Краткие введения

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Нажмите Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Войти через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.

Информация о покупке

Простая таблица синусов Fixar | ВАЛЬМАГ

Список продуктов

Fixar — простой синусоидальный стол с постоянным патроном Neomicro, подходящий для точного углового шлифования, электроэрозионной обработки и измерения. Вы можете выбрать модель с установкой угла по продольной или по поперечной оси.

Преимущества:

• Установка продольного угла в диапазоне 0–45° (или поперечного 0–30°)
• Закаленная опорная плита для исключительной устойчивости
• Чрезвычайная точность +/- 5 угловых секунд даже после длительного использования
• Параллельность (параллельность): +/- 5 микрометров на 100 мм
• Оснащен высококачественным магнитным патроном Neomicro с точным расположением полюсов (опционально стол может быть оснащен другим патроном, например, Neomill или Electrofine)

Купить

Сопутствующие товары

Магнитный патрон Neomicro для плоского шлифования
Магнитный патрон с тонкими полюсами для точного шлифования.

Синусоидальный стол Fixar для точного углового шлифования и EDM
Составные таблицы синусов для магнитной плиты

Этот продукт можно взять напрокат. Просто создайте запрос и установите флажок аренды.

Вы не уверены, что этот продукт является правильным выбором? Отправьте нам свой запрос, и наши представители будут рады проконсультировать вас.

• Модели
• Описание
• Скачать
• Видео

Показать в виде таблицы

Каталожный номер	Размер	Высота [мм]	Наличие (приблизительно)	Цена без НДС (действительно только для ЕС)
SINES70140	70×140 мм	67.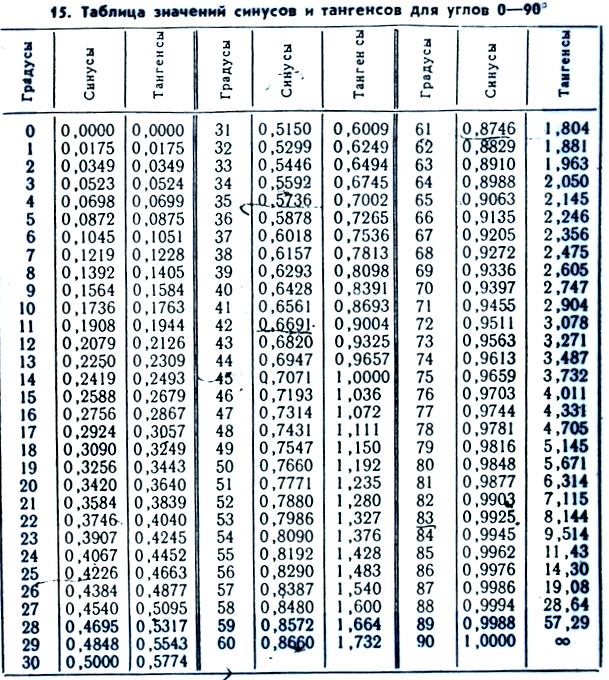 00	7 — 8 недель	По требованию
SINES130255	130×255 мм	76. 00	7 — 8 недель	По требованию
SINES150250	150×250 мм	79. 00	7 — 8 недель	По требованию
SINES150300	150×300 мм	79. 00	7 — 8 недель	По требованию
SINES150350	150×350 мм	87. 00	7 — 8 недель	По требованию
SINES150450	150×450 мм	87. 00	7 — 8 недель	По требованию
SINES200400	200×400 мм	88.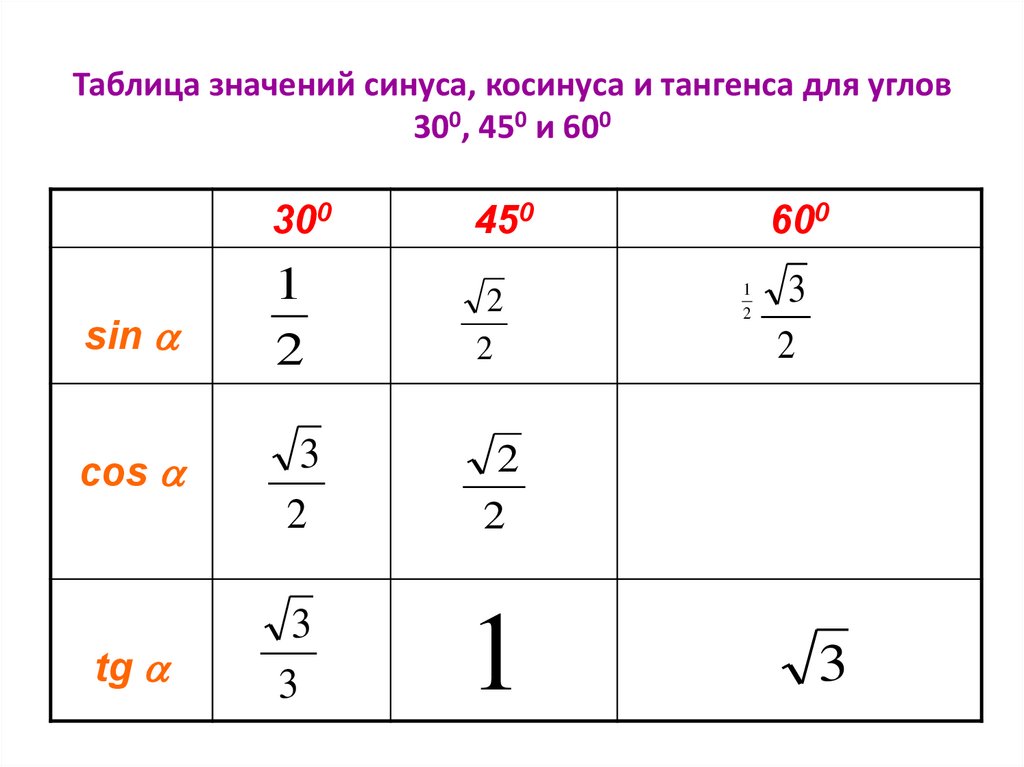 00	7 — 8 недель	По требованию
SINES300600	300×600 мм	95. 00	7 — 8 недель	По требованию

Вложить в корзину

Вы поместили выбранный товар в корзину

Как продолжить?

перейти в корзину перейти к кассе

Контактная форма

Ваш вопрос/сообщение успешно отправлено, и мы обработаем его как можно скорее.

Спасибо за проявленный интерес.

закрыть окно

Каталоги

Список каталогов Fixar простой

---

Запрос/Сообщение: Обязательная информация

Взять напрокат этот продукт

Контактная форма

Ваш вопрос/сообщение успешно отправлено, и мы обработаем его как можно скорее.

Спасибо за проявленный интерес.

закрыть окно

Составная синусоидальная таблица Fixar | ВАЛЬМАГ

Список продуктов

Составной синусоидальный стол Fixar с постоянным патроном Neomicro предназначен для точного углового шлифования. Вы получите отличную вариативность обработки при зажиме заготовки, потому что Fixar позволяет выполнять наклон по продольной и поперечной осям одновременно.

Преимущества:

• Возможен наклон по обеим осям, продольный и поперечный
• Установка углов в продольном диапазоне 0–45°, в поперечном 0–30°
• Уникальная конструкция подшипника
• Массивная закаленная опорная плита
• Превосходная точность +/- 5 угловых секунд даже после длительного использования
• Параллельность (параллельность): +/- 5 мкм на 100 мм
• Оснащен высококачественным магнитным патроном Neomicro с точным расположением полюсов (опционально стол может быть оснащен другим патроном, например, Neomill или Electrofine)

Купить

Сопутствующие товары

Магнитный патрон Neomicro для плоского шлифования
Магнитный патрон с тонкими полюсами для точного шлифования.

Простая таблица синусов Fixar для точного углового шлифования и EDM
Составные и простые таблицы синусов для магнитной плиты.

Этот продукт можно взять напрокат. Просто создайте запрос и установите флажок аренды.

Вы не уверены, что этот продукт является правильным выбором? Отправьте нам свой запрос, и наши представители будут рады проконсультировать вас.

• Модели
• Описание
• Скачать
• Видео

Показать в виде таблицы

Каталожный номер	Размер	Высота [мм]	Наличие (приблизительно)	Цена без НДС (действительно только для ЕС)
SINEC100175	100×175 мм	104. 00	7 — 8 недель	По требованию
SINEC130255	130×255 мм	120. 00	7 — 8 недель	По требованию
SINEC150300	150×300 мм	123. 00	7 — 8 недель	По требованию
SINEC150350	150×350 мм	123. 00	7 — 8 недель	По требованию
SINEC200400	200×400 мм	124. 00	7 — 8 недель	По требованию

Вложить в корзину

Вы поместили выбранный товар в корзину

Как продолжить?

перейти в корзину перейти к кассе

Контактная форма

Ваш вопрос/сообщение успешно отправлено, и мы обработаем его как можно скорее.

Спасибо за проявленный интерес.

закрыть окно

Каталоги

Список каталогов Fixar

---

Запрос/Сообщение: Обязательная информация

Взять напрокат этот продукт

Контактная форма

Ваш вопрос/сообщение успешно отправлено, и мы обработаем его как можно скорее.

Спасибо за проявленный интерес.

закрыть окно

Прецизионный синусоидальный стол без магнитного держателя, тип SS | Брайон Магнетикс | Шлифование, электроэрозионная обработка, метрология Прочная конструкция, малая высота

Области применения

Зажим

Шлифование

Плоское шлифование

Поворотные и синусоидальные столы

Прецизионный синусоидальный стол без магнитной плиты типа SS

REF 12. 03

3 . Основной корпус из прецизионно отшлифованной стали, закаленный до 58 HRC

. Поворот по длинной оси от 0° до 60°
. Оснащен резьбовыми отверстиями
Входит в комплект поставки :
— Таблица синусов

• Использование :

  • Шлифование
  • ЭДМ
  • метрология

• Угловая точность :

  • ± 5 с

• Параллельность :

  • ±0,005/100 мм

Кол-во	Продукт	Вес в кг	A	B	C	D
	12.03.175100	6,5	175	100	60	75
	12.03.150150	8,1	150	150	60	100
	12.03.300150	15,8	300	150	60	100

Индикация.

Запросить цену

Введите суммы в таблицу выше Заполните контактную форму ниже

Поля со звездочкой * не должны быть пустыми

Детали

E-mail *

Я профессионал

Компания/Учреждение *

Вежливость

РавнодушиеМадамМесье

Фамилия *

Имя

Адрес

Адрес (2)

Штат/округ/провинция

Почтовый индекс *

Город *

Country

AfghanistanAlbaniaAlgeriaAndorraAngolaAntigua and BarbudaArgentinaArmenieAustraliaAustriaAzerba?djanBahreBangladeshBarbados (It)BelgiumBelizeBenignBhutanBielorussiaBoliviaBosnia-HerzegovineBotswanaBrazilBruneiBulgariaBurkina FasoBurundiCamerounCanadaCentral African (Republic)ChadChileChinaColombiaCongoCongo (democratic Republic of)Costa RicaCroatiaCubaCyprusCzech (Republic)DenmarkDjiboutiDominican (Republic)Eastern TimorEcuadorEgyptEl SalvadorEquatorial GuineaErythrEstoniaEthiopiaFiji (Islands)FinlandFranceGabonGambiaGeorgiaGermanyGhanaGreeceGreen CapeGreenlandGrenadeGuatemalaGuineaGuinea-BissauGuyanaHaitiHondurasHungaryIcelandIndiaIndonesiaIranIraqIrelandIsraelItalyIvory CoastJamaicaJapanJordanKampucheaKazakhstanKenyaKirghizstanKiribatiKuwaitLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacedoniaMadagascarMalawiMalaysiaMaldives (Islands)MaliMaltaMarshall (Острова)Морис (Остров)МавританияМексикаМикронезияМолдавияМонакоМонголияМарокко MozambiqueMyanmar (Burma)NamibiaNauruNepalNetherlandsNew Guinea-News-GuineaNew ZealandNicaraguaNigerNigeriaNorth KoreaNorwayOmanOuzb?kistanPakistanPalau (Belau)Palestine (autonomous Territories of)PanamParaguayPeruPlain Arab EmiratesPolandPortugalPuerto RicoQatarRomaniaRussiaRwandaS?o Divide into volumes-and-Pr?ncipeSaint-Kitts and NevisSaint-Vincent and GrenadinesSainte-LucieSamoaSan MarinoSaudi ArabiaSenegalSerbia MontenegroSeychelles (Them)Sierra LeoneSingaporeSlovakiaSloveniaSolomon (Islands)SomaliaSouth AfricaSouth KoreaSpainSri LankaSudanSurinameSwazilandSwedenSwitzerlandSyriaTadjikistanTaiwanTanzaniaThailandThe BahamasThe Comoros (Them)The Philippines (Them)The United KingdomThe United States of AmericaThe VaticanThe Western SaharaTibetTogoTrinity and TobagoTunisiaTurkeyTurkm?nistanTuvaluUgandaUkraineUruguayVanuatuVenezuelaVietnamYemenZambiaZimbabwe

Телефон *

Я хочу получать по электронной почте информацию, распространяемую по номеру

Мой запрос

Intérêt principal (+) *

Aimants permanents

Coupleur

Démagnétisation

Dépression

Electro-érosion

Fraisage

Levage

OEM

Rail

Plateau presse

Rectification

Robotisation/automatisation

Турнир

Сортировка

Основная работа *

Торговый посредник

Производитель

Инженерное бюро

Ссылка (+) *

Воспользуйтесь вашим запросом

Согласно Закону №. 78-17 от 6 января 1978 г. французского закона о персональных данных (CNIL), касающихся информационных технологий, файлов и личной свободы (статья 36), обладатель права доступа может потребовать, чтобы любая информация, которая является неточной, отсутствующей или — актуальную информацию или сбор, использование, передачу или хранение которой в отношении него самого запрещено, исправлять, дополнять, уточнять, обновлять или удалять. Чтобы воспользоваться этим правом, воспользуйтесь приведенной выше формой.

индикация_tableau_dessous

Функция синуса – формула, таблица и свойства

В тригонометрии всего существует шесть тригонометрических функций: синус, кос, тангенс, секанс, косеканс и котангенс. Из всех этих шести тригонометрических функций три считаются первичными функциями, и функция синуса является одной из них. Остальные двое — загар и кос. Обычно мы определяем синус тета как отношение противоположной стороны прямоугольного треугольника к его гипотенузе. Если рассматривать треугольник с ABC как угол альфа, функция синуса будет: 

Изображение будет загружено в ближайшее время

SIN α = противоположный/ гипотенуза

Теперь мы все знаем, как это запутано, чтобы вспомнить отношения тригонометива, но, эй, у нас есть техника или, скорее сделать часть запоминания легкой и интересной. Вы можете запомнить тригонометрические функции с помощью мнемоники SOH-CAH-TOA.

Где SOH означает «синус противоположен гипотенузе», CAH означает «косинус примыкает к гипотенузе», а TOA означает «тангенс прилегает к гипотенузе».

Формула функции синуса

На приведенной ниже диаграмме показано, что Sin α = BC/AB.

Следовательно, мы можем записать формулу как: 

Sin α = a/h

Изображение будет загружено в ближайшее время

Ниже приведена таблица синусов от 0 до 360 градусов с соответствующими значениями.

SINE Value Table

SINE DEGEING 9{o}\] = 0,95       Синусоидальные тождества Существует 5 общих синусоидальных тождеств: синус (θ) = cos(π/2 − θ) = 1/cosec(θ) 100 sin θ) = θ, для −π/2 ≤ θ ≤ π/2 cos2 (θ) + sin2 (θ) = 1 Sin (2x) = 2sin (x) cos (x) Cos (2x) = cos2(x) − sin2(x) Другие тригонометрические функции: 9{2}(\theta)}}\]   Тригонометрический закон синусов Тригонометрический закон синусов установил соотношение между сторонами a, b и c, а также углами, противоположными этим сторонам A , B и C для произвольного треугольника. Вот отношения:    Изображение будет загружено в ближайшее время На диаграмме выше видно, что A, B, C — это углы, а a, b, c — длины сторон. Значит по закону синуса: \[\frac{a}{sin A}\] = \[\frac{b}{sin B}\] = \[\frac{c}{sin C}\] = d d = диаметр описанная окружность треугольника. График синусоидальной функции График синусоидальной функции, также называемый графиком синусоиды или синусоидальным графиком, представляет собой перевернутый график. Он повторяется каждые 360 с шагом 2π Изображение скоро будет загружено Обратный синус Обратный синус, также известный как арксинус, — это функция, которая помогает измерять угол прямоугольного треугольника. Его также можно обозначать как asin или sin-1. Теперь рассмотрим прямоугольный треугольник со сторонами 1, 2 и √3. Что нам нужно сделать, так это вычислить угол а. Таким образом, функция синуса может быть использована как: Изображение скоро будет загружено                                                                                   Мы можем вычислить угол A, используя функцию арксинуса. sin−1(½) = a Таким образом, мы получаем значение угла «a» как 30° Вычисление синусов По синусоидальной функции f(x) = sin(x): можно построить интеграл от sin(x), ∫f(x) dx = −cos(x) + C (C= постоянная интегрирования ) и производная от sin(x),f′(x) как cos(x). Мы можем определить значения функции синуса как положительные или отрицательные в зависимости от квадрантов. Вот таблица, где мы видим, что с одной стороны синус 270 отрицателен, а с другой стороны синус 90 положителен. В основном, для первого и второго квадранта он положительный, а для третьего и четвертого квадранта отрицательный. The four quadrants in Trigonometry diagram are shown below: Image will be uploaded soon Properties of Sine as per Quadrants Range of the degrees       Quadrant Знак функции синуса Диапазон значений синуса 0-90 1-й квадрант Positive  0 < sin(x) < 1 90-180 2nd quadrant Positive  0 < sin(x) < 1 180-270 3rd quadrant Negative -1 < sin(x) < 0 270-360 4th quadrant Отрицательный -1 < sin(x) < 0 Решенный Пример: Пример 1. Якорь длиной 30 метров привязан к якорю. гипотенуза прямоугольного треугольника. Угол между гипотенузой и дном океана составляет 39 градусов. Итак, какова будет глубина якоря?   Изображение будет загружено в ближайшее время Решение 1. Практически невозможно нырнуть полностью, чтобы измерить глубину якоря, поэтому мы воспользуемся тригонометрическим соотношением, чтобы вычислить его. Зная угол и длину троса, мы можем найти длину стороны, противоположной углу, то есть d, поэтому используем функцию синуса. sin 39 = d/30 0,63 = d/30 d = 18,9 м Таблица интегралов синуса и косинуса для аргументов от 10 до 100 Один из 8 отчетов в серии: На этом сайте доступна серия статей по прикладной математике (Вашингтон, округ Колумбия). Показаны 1-4 из 204 страницы в этом отчете. PDF-версия также доступна для скачивания. Описание Отчет, содержащий таблицы и интегралы синуса и косинуса для различных волн. Физическое описание xv, 187 стр. : диаг. ; 27 см. Информация о создании Соединенные Штаты. Национальное бюро стандартов. Вычислительная лаборатория. 1954. Контекст Этот отчет входит в состав сборника под названием: Архив технических отчетов и библиотека изображений а также предоставлено отделом государственных документов библиотек ЕНТ к Электронная библиотека ЕНТ, цифровой репозиторий, размещенный на Библиотеки ЕНТ. Его просмотрели 23001 раз, из них 280 за последний месяц. Более подробную информацию об этом отчете можно посмотреть ниже. Поиск Открытый доступ Кто Люди и организации, связанные либо с созданием этого отчета, либо с его содержанием. Автор Соединенные Штаты. Национальное бюро стандартов. Вычислительная лаборатория. Издатель Соединенные Штаты. Государственная типография. Место публикации: Вашингтон, округ Колумбия Аудитории Мы определили это отчет как первоисточник в наших коллекциях. Исследователи, преподаватели и студенты могут найти этот отчет полезным в своей работе. Предоставлено Библиотеки ЕНТ Отдел государственных документов Являясь одновременно федеральной и государственной депозитарной библиотекой, отдел государственных документов библиотек ЕНТ хранит миллионы единиц хранения в различных форматах. Департамент является членом Программы партнерства по контенту FDLP и Аффилированного архива Национального архива. О | Просмотрите этого партнера Свяжитесь с нами Исправления и проблемы Вопросы какая Описательная информация, помогающая идентифицировать этот отчет. Перейдите по ссылкам ниже, чтобы найти похожие элементы в электронной библиотеке. Титулы Основное название: Таблица синусоидальных и косинусных интегралов для аргументов от 10 до 100 Название серии: Серия прикладной математики (Вашингтон, округ Колумбия) Добавлен заголовок: Соединенные Штаты. Национальное бюро стандартов. Серия «Прикладная математика», 32 Название серии: Отчеты Национального бюро стандартов Добавлен заголовок: Серия «Прикладная математика», бюллетень 32 Описание Отчет, содержащий таблицы и интегралы синуса и косинуса для различных волн. Физическое описание xv, 187 стр. : диаг. ; 27 см. Предметы Тематические рубрики Библиотеки Конгресса Тригонометрические функции. Тригонометрия — Таблицы. Язык Английский Тип вещи Отчет Идентификатор Уникальные идентификационные номера для этого отчета в электронной библиотеке или других системах. OCLC : 852744 | Внешняя ссылка Архивный ресурсный ключ : ковчег:/67531/metadc40300 Коллекция Этот отчет является частью следующей коллекции связанных материалов. Архив технических отчетов и библиотека изображений Эта подборка материалов из Архива технических отчетов и библиотеки изображений (TRAIL) включает труднодоступные отчеты, опубликованные различными государственными учреждениями. Технические публикации содержат отчеты, изображения и технические описания исследований, выполненных для правительственных учреждений США. Темы варьируются от добычи полезных ископаемых, опреснения и радиации до более широких исследований в области физики, биологии и химии. Некоторые отчеты включают карты, раскладки, чертежи и другие материалы большого размера. О | Просмотрите эту коллекцию Какие обязанности у меня есть при использовании этого отчета? Цифровые файлы 204 файлы изображений доступны в нескольких размерах 1 файл (. pdf) API метаданных: описательные и загружаемые метаданные, доступные в других форматах Когда Даты и периоды времени, связанные с этим отчетом. Дата создания 1954 г. Добавлено в цифровую библиотеку ЕНТ 2 сентября 2011 г., 22:21 Описание Последнее обновление 3 апреля 2019 г. , 12:58 Статистика использования Когда последний раз использовался этот отчет? Вчерашний день: 14 Последние 30 дней: 280 Всего использовано: 23,001 Дополнительная статистика Взаимодействие с этим отчетом Вот несколько советов, что делать дальше. Поиск внутри Поиск Начать чтение PDF-версия также доступна для скачивания. Все форматы Цитаты, права, повторное использование Ссылаясь на этот отчет Обязанности использования Лицензирование и разрешения Связывание и встраивание Копии и репродукции Международная структура взаимодействия изображений Мы поддерживаем IIIF Презентация API Распечатать/поделиться Полезные ссылки в машиночитаемом формате. Архивный ресурсный ключ (ARK) ERC Запись: /арк:/67531/metadc40300/? Заявление о стойкости: /ark:/67531/metadc40300/?? Международная структура совместимости изображений (IIIF) IIIF Манифест: /арк:/67531/metadc40300/манифест/ Форматы метаданных УНТЛ Формат: /ark:/67531/metadc40300/metadata. untl.xml DC RDF: /ark:/67531/metadc40300/metadata.dc.rdf DC XML: /ark:/67531/metadc40300/metadata.dc.xml OAI_DC : /oai/?verb=GetRecord&metadataPrefix=oai_dc&identifier=info:ark/67531/metadc40300 МЕТС : /ark:/67531/metadc40300/metadata. mets.xml Документ OpenSearch: /ark:/67531/metadc40300/opensearch.xml Картинки Миниатюра: /ark:/67531/metadc40300/миниатюра/ Маленькое изображение: /ковчег:/67531/metadc40300/маленький/ URL-адреса В текст: /ark:/67531/metadc40300/urls. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт