Самая длинная хорда в геометрии, 7 букв
Ответ на вопрос в сканворде (кроссворде) «Самая длинная хорда в геометрии», 7 букв (первая — д, последняя — р):
диаметр
(ДИАМЕТР)
Другие определения (вопросы) к слову «диаметр» (79)
- Удвоенный радиус
- У дискеты он составляет 3,5 дюйма
- Два радиуса
- Математический калибр
- Отрезок, равный двум радиусам окружности
- В два раза больше радиуса
- Что делит круг пополам
- м. греч. поперечник, говоря о круге или шаре. Истинный диаметр светила, астроном. поперечник планеты в линейной мере; видимый диаметр, поперечник в градусах и в долях его, служащий мерою угла, под которым планета видна. Диаметральный, поперечный; поперек
- Расстояние по прямой линии между крайними точками окружности
- Линия, соединяющая две точки окружности или шара
- У всех советских сигарет он был равен 7,62 мм
- Прямая линия, проходящая через центр кривой фигуры и ограниченная её контуром
- Число «пи» — это отношение длины окружности к какому её параметру
- Поперечник любого круглого тела
- В применении к оружию он будет калибром
- Поперечник круга
- Два луча
- Характеристика окружности
- Тот же поперечник
- Калибр ствола
- Удвоенный радиус окружности
- Хорда, проходящая через центр окружности
- «Толщина» окружности
- Отрезок, соединяющий две точки окружности и проходящий через ее центр
- Отрезок прямой, соединяющий две точки окружности и проходящий через её центр
- Шапочный размер
- Калибр — это, собственно он и есть
- Отрезок прямой, соединяющий две точки окружности, проходящий через центр
- Прямая, соединяющая две точки окружности и проходящая через ее центр
- Максимальная хорда окружности
- Что он, что два радиуса
- Сумма двух радиусов
- Окружность, размер
- Отрезок между точками окружности через её центр
- «Двойной радиус» в измерении окружности
- Хорда через центр
- Два радиуса — один за одним
- Главное отличие сосиски от сардельки
- Радиус, переходящий в радиус
- Самая длинная хорда
- Радиус + радиус
- Двойной радиус
- Расстояние по прямой линии между крайними точками круга
- Два радиуса круга
- «Дважды радиус»
- Двойной радиус окружности
- Калибр нефтяной трубы
- «Калибр круга»
- Линия, делящая круг пополам
- Размер отверстия трубы
- Толщина круглоты
- Главная характеристика круга
- У дискеты он составлял 3,5 дюйма
- Максимальная из хорд
- Геометрический калибр
- Радиус плюс радиус
- Равен двум радиусам
- Радиус, умноженный на два
- Наибольшая хорда в окружности
- Размер круга
- Отрезок, разделивший круг
- Делит круг пополам
- Делит круг на половинки
- Делит окружность пополам
- Радиус, выросший вдвое
- Два радиуса окружности
- В математике: отрезок прямой линии, соединяющий две точки окружности и проходящий через её центр, а также длина этого отрезка
- Самый длинный «мост» через окружность
- Число «пи» — это отношение длины окружности к какому её параметру?
- Мера круга
- Максимальная хорда или двойной радиус
- Поперечник трубы
- Итог сложения двух радиусов
- Самая большая хорда
- Линия, проходящая через центр круга
- Два радиуса — один за одним
- Пара объединённых радиусов
- Два радиуса на одной линии
- Вобрал в себя два радиуса
- геометр.
 (геометрическое) отрезок прямой линии, соединяющий две точки окружности (сферы, гиперсферы) и проходящий через её центр || его длина ◆ Величина сферического треугольника Y равна величине противолежащего ему треугольника ABCʹ, в котором сторона АВ общая с треугольником Р, а третий угол Сʹ лежит при конечной точке диаметра сферы, идущего от С через центр сферы. Н. И. Лобачевский, «Геометрические исследования по теории параллельных линий», 1840 г. ◆ На катете прямоугольного треугольнике как на диаметре построена окружность. «Хотите стать математиком?», 2008 г. // «Наука и жизнь»
(геометрическое) отрезок прямой линии, соединяющий две точки окружности (сферы, гиперсферы) и проходящий через её центр || его длина ◆ Величина сферического треугольника Y равна величине противолежащего ему треугольника ABCʹ, в котором сторона АВ общая с треугольником Р, а третий угол Сʹ лежит при конечной точке диаметра сферы, идущего от С через центр сферы. Н. И. Лобачевский, «Геометрические исследования по теории параллельных линий», 1840 г. ◆ На катете прямоугольного треугольнике как на диаметре построена окружность. «Хотите стать математиком?», 2008 г. // «Наука и жизнь» - поперечник любого круглого или кажущегося круглым тела, вместилища, пространства ◆ Круглый бассейн имеет сажени три в диаметре. А. С. Пушкин, «Путешествие в Арзрум во время похода 1829 года», 1835 г. ◆ На спине у каждого был вшит чёрный круг, вершка два в диаметре. Ф. М. Достоевский, «Записки из мертвого дома», 1862 г.
- матем.
 (математический термин) максимальное расстояние между двумя точками множества ◆ Всякое n-мерное выпуклое тело диаметра d может быть разбито на n + 1 частей меньшего диаметра. В. Г. Болтянский, И. Ц. Гохберг, «Теоремы и задачи комбинаторной геометрии», 1965 г. (см. w:Гипотеза Борсука)
(математический термин) максимальное расстояние между двумя точками множества ◆ Всякое n-мерное выпуклое тело диаметра d может быть разбито на n + 1 частей меньшего диаметра. В. Г. Болтянский, И. Ц. Гохберг, «Теоремы и задачи комбинаторной геометрии», 1965 г. (см. w:Гипотеза Борсука)
Значение слова
ДИА́МЕТР,
-а, мужской род
Отрезок прямой, соединяющий две точки окружности и проходящий через центр (мат.).
||
Поперечник любого круглого или кажущегося круглым тела, вместилища, пространства. Ствол дерева диаметром в метр. ◆ Это круглый пруд, версты три в диаметре, с высокими берегами, защищающими от ветров. Чехов, Остров Сахалин.
[От греч. διάμετρος — поперечник]
Диа́метр (французское diamètre из лат. diametrus из древне-греческое διάμετρος — поперечник) — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Обобщённо диаметром фигуры (множества) называется максимальное расстояние между точками этой фигуры (множества), или точная верхняя грань всевозможных расстояний, если максимальное не существует.
Показать дальше
1. Значение слова диаметр. 2. Синонимы «диаметр». 3. Антонимы «диаметр». 4. Разбор по составу «диаметр». 5. Ассоциации «диаметр». 6 фонетический разбор «диаметр».
- Поиск занял 0.126 сек. Вспомните, как часто вы ищете, чем заменить слово? Добавьте sinonim.org в закладки, чтобы быстро искать синонимы, антонимы, ассоциации и предложения.
Пишите, мы рады комментариям
Вверх ↑
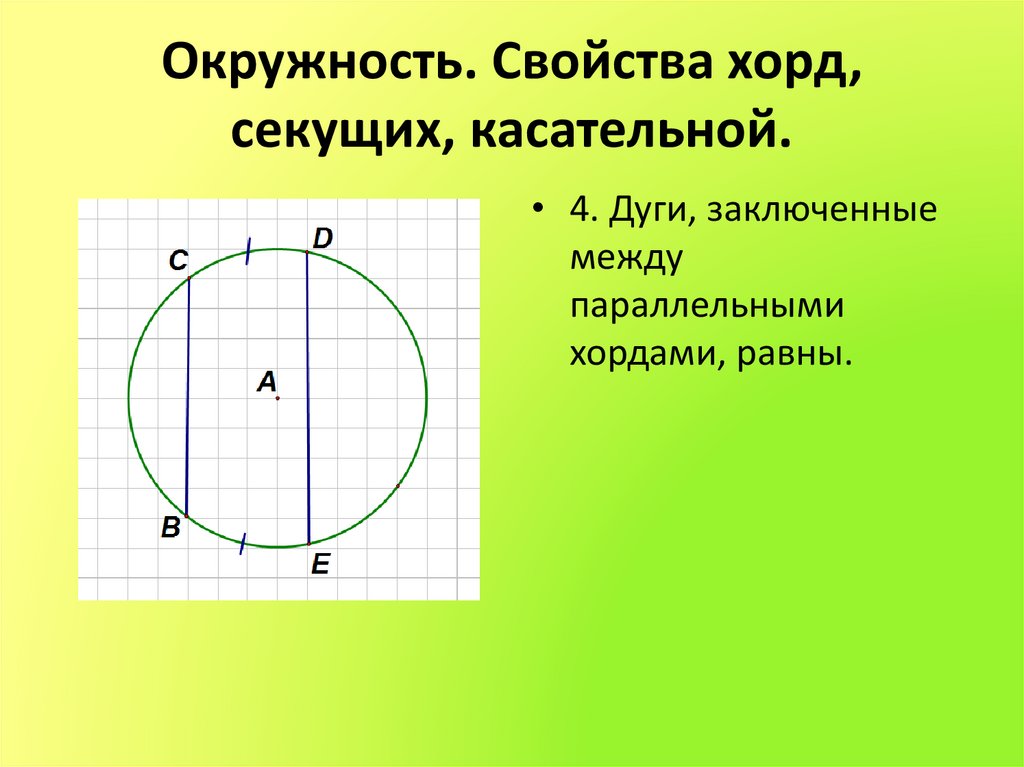
Определения: Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Расстояние (r) от точки окружности до ее центра называется радиусом окружности. Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром (d=2r).
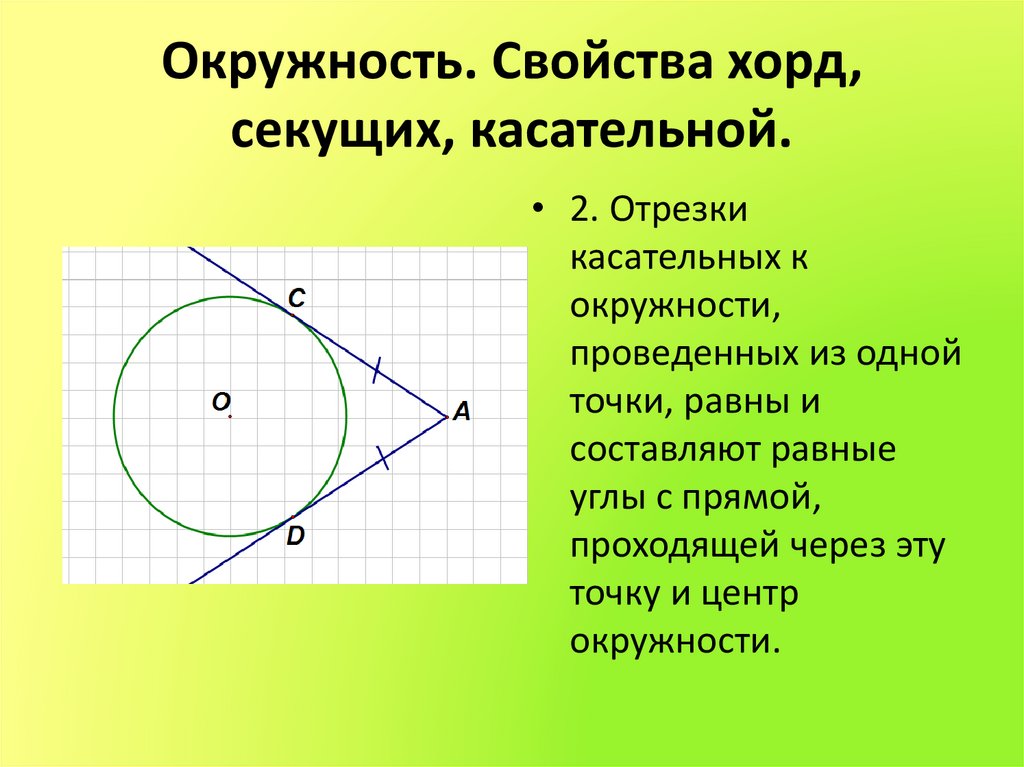
Касательная — прямая (а), проходящая через точку (А) окружности перпендикулярно к радиусу, проведенному в эту точку, называется. При этом данная точка (А) окружности называется точкой касания.
Часть плоскости, ограниченная окружностью, называется кругом. |
|
Если две хорды АВ и CD пересекаются внутри круга в точке Е, то произведение отрезков одной хорды равно произведению отрезков другой хорды, т. AЕ·ЕВ = DE·EC
| |
AB·AC=АВ1·АС1.
|
|
Теорема о квадрате касательной
МC 2 = МВ·МА |
|
Диаметр окружности, перпендикулярный хорде, проходит через ее середину. Обратно: если диаметр проходит через середину хорды, то он ей перпендикулярен. |
|
Вписанный угол Описанный угол — угол, образованный двумя касательными DM и DN (∠MDN). Центральный угол имеет ту же градусную меру, что и дуга, на которую он опирается. Вписанный угол измеряется половиной дуги, на которую он опирается.
|
|
Угол, образованный двумя хордами и опирающийся на них центральный угол связаны соотношением |
|
Длина дуги, соответствующая центральному углу в n°
|
|
Площадь кругового сектора где α — градусная мера угла, R — радиус круга. Квадрант — сектор, отсекаемый радиусами, образующими угол 90°.
|
|
Площадь сегмента, не равного полукругу где α — градусная мера центрального угла, которая содержит дугу этого кругового сегмента, Знак «−» надо брать, когда α Основание и высота сегмента | |
R, r — внешний и внутренний радиусы;
|
|
Объяснение урока: Связь между хордами и центром окружности
В этом объяснении мы узнаем, как определить связь между хорды, равные или разные по длине и центру окружности и использовать свойства хорд в конгруэнтных кругах для решения задач.
Начнем с того, что вспомним, что серединные перпендикуляры хорд проходят через центр круга. Нарисуем схему, отражающую этот факт.
На приведенной выше диаграмме отрезок синей линии перпендикулярно делит хорду пополам. 𝐴𝐵. Заметим, что эта линия проходит через центр 𝑂 и, следовательно, определяет перпендикулярное расстояние между центром и аккорд.
Определение: расстояние хорды от центра
Расстояние хорды от центра окружности измеряется длиной отрезка от центра, пересекающего перпендикулярно аккорд.
На схеме выше обозначим середину хорды
𝐴𝐵, где синяя линия
перпендикулярно пересекаются с хордой. Также мы добавим радиус
𝑂𝐴.
Также мы добавим радиус
𝑂𝐴.
Поскольку △𝑂𝐶𝐴 — прямоугольный треугольник, мы можем использовать теорема Пифагора, чтобы найти длину 𝐴𝐶 из радиуса 𝐴𝑂 и расстояние 𝑂𝐶. Так как 𝐶 является серединой хорды 𝐴𝐵, мы знаем, что 𝐴𝐵=2𝐴𝐶. Следовательно, если нам дан радиус окружности и расстояние хорды от центра круга, мы можем использовать этот метод для найти длину хорды. Вместо того, чтобы явно писать это вычисления, мы сосредоточимся на качественной связи между длинами хорд и их расстояние от центра круга в этом объяснителе.
Рассмотрим две разные хорды в одном круге, как на диаграмме ниже.
С 𝑂𝐴 и
𝑂𝐷 — это радиусы одной окружности, они имеют
одинаковая длина. Мы хотим знать соотношение между длинами хорд
𝐴𝐵 и
𝐷𝐸 если мы это знаем
𝐷𝐸 находится дальше от центра, чем
𝐴𝐵. Другими словами, мы предполагаем
𝑂𝐶𝑂𝐹. Вместо того, чтобы сравнивать полные длины
два аккорда, мы можем сравнить полуаккорды
𝐴𝐶 и
𝐷𝐹.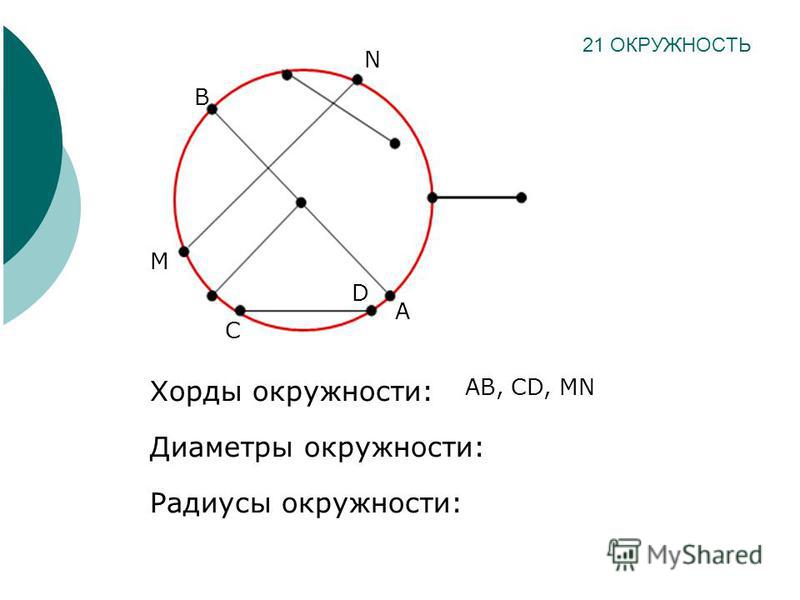
Мы знаем, что 𝑂𝐴=𝑂𝐷, поэтому левые части обоих уравнений должны быть равны друг другу: 𝐴𝐶+𝑂𝐶=𝐷𝐹+𝑂𝐹.
Это уравнение можно преобразовать, чтобы сказать 𝐴𝐶−𝐷𝐹=𝑂𝐹−𝑂𝐶.
Наше предположение, что 𝑂𝐹>𝑂𝐶, приводит к 𝑂𝐹−𝑂𝐶>0, поэтому левая часть этого уравнения должна быть положительной. Это означает 𝐴𝐶−𝐷𝐹>0,𝐴𝐶>𝐷𝐹.что приводит к
Поскольку 𝐴𝐶 и 𝐷𝐹 положительные длины, мы можем извлечь квадратный корень из обеих частей неравенства, чтобы получить 𝐴𝐶>
Теорема: связь между длинами хорд и их расстоянием от центра
Рассмотрим две хорды в одном круге, расстояние от центра которых равно разные. Хорда, расположенная ближе к центру окружности, имеет большую длина больше, чем у другого.
Эта теорема позволяет нам сравнивать длины хорд одного и того же круга
в зависимости от их расстояния от центра круга.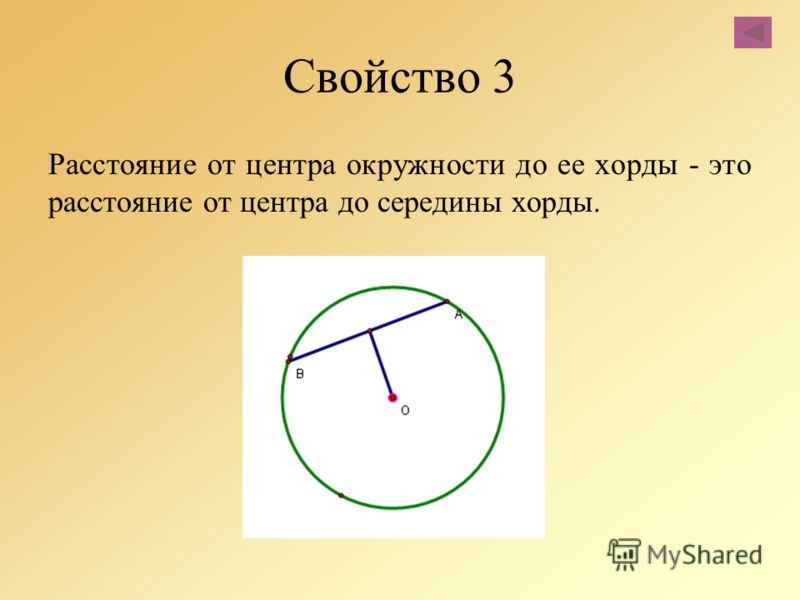 В нашем первом примере
мы применим эту теорему, чтобы получить неравенство, касающееся длин.
В нашем первом примере
мы применим эту теорему, чтобы получить неравенство, касающееся длин.
Пример 1: Сравнение длин хорд на основе их расстояний от центра
Предположим, что 𝐵𝐶=8 см и 𝐵𝐴=7см. Какие из следующих утверждений верно?
- 𝐷𝑀=𝑋𝑌
- 𝐷𝑀>𝑋𝑌
- 𝐷𝑀𝑋𝑌
Ответ
к центру окружности имеет большую длину, чем другая. Мы также известно, что расстояние хорды от центра окружности измеряется на длину отрезка от центра, пересекающего перпендикулярно хорде.
В этом примере у нас есть два аккорда
𝑋𝑌 и
𝐷𝑀. С
𝐵𝐴 пересекается перпендикулярно
хорда 𝑋𝑌, длина 𝐵𝐴
расстояние этой хорды от центра. Точно так же длина 𝐵𝐶
— расстояние хорды 𝐷𝑀 от центра. На основании приведенной информации отметим, что 𝐵𝐶>𝐵𝐴, а значит
эта хорда 𝑋𝑌 ближе к центру. Следовательно, длина хорды 𝑋𝑌
больше, чем у другой хорды.
Верным вариантом является C, который утверждает, что 𝐷𝑀𝑋𝑌.
В следующем примере мы найдем диапазон неизвестной переменной, определяющей длины, используя соотношение между хордами и центром окружности.
Пример 2. Нахождение диапазона значений неизвестного Удовлетворить заданным условиям
Если 𝑀𝐹>𝑀𝐸, найти диапазон значений 𝑥, которые удовлетворяют данным представлены.
Ответ
Напомним, что для двух хорд в одном круге та хорда, которая ближе к центру окружности имеет большую длину, чем другая. Мы также известно, что расстояние хорды от центра окружности измеряется на длину отрезка от центра, пересекающего перпендикулярно хорде.
В этом примере у нас есть два аккорда,
𝐴𝐵 и
𝐶𝐷. С
𝑀𝐸 пересекается перпендикулярно
хорда 𝐴𝐵, длина 𝑀𝐸
— расстояние этой хорды от центра. Аналогично, длина
𝑀𝐹 — расстояние хорды
𝐶𝐷 от центра. Поскольку нам дано
𝑀𝐹>𝑀𝐸, мы знаем этот аккорд
𝐴𝐵 ближе к центру. Этот
приводит к тому, что хорда 𝐴𝐵 имеет
большей длины, чем хорда 𝐶𝐷.
Поскольку нам дано
𝑀𝐹>𝑀𝐸, мы знаем этот аккорд
𝐴𝐵 ближе к центру. Этот
приводит к тому, что хорда 𝐴𝐵 имеет
большей длины, чем хорда 𝐶𝐷.
На приведенной диаграмме отметим, что 𝐴𝐵=(𝑥+4)см и 𝐶𝐷=24см. Следовательно, неравенство 𝐴𝐵>𝐶𝐷 можно записать в виде 𝑥+4>24,𝑥>20, что приводит к
Однако это дает только нижнюю границу для 𝑥. Чтобы определить верхнюю границу для 𝑥, мы должны спросить, что
максимальная длина хорды 𝐴𝐵. Поскольку длина хорды тем больше, чем ближе она к центру,
самая длинная хорда должна иметь место, когда расстояние от центра равно нулю. Если
расстояние хорды от центра равно нулю, хорда должна содержать
центр. В данном случае хорда – это диаметр окружности. С
радиус круга
33 см, его диаметр
2×33=66 см. Это говорит нам о том, что длина 𝐴𝐵 не может
превышать 66 см. Кроме того,
так как 𝐴𝐵 на данной диаграмме не содержит
центр 𝑀, мы знаем, что длина хорды
𝐴𝐵 должно быть строго меньше
66 см. Следовательно,
𝑥+466,𝑥62.что приводит к
Следовательно,
𝑥+466,𝑥62.что приводит к
Это дает нам верхнюю границу для 𝑥. Сочетание обоих нижняя и верхняя границы, мы имеем 20𝑥62.
В интервальных обозначениях это записывается как ]20,62[.
В предыдущих примерах мы рассматривали соотношение между длинами две хорды в одном круге и их расстояния от центра круга когда расстояния не равны. Напомним, что две окружности равны между собой, если меры их радиусов равны. Поскольку доказательство этого отношение использует только тот факт, что радиусы окружности равны длины, это отношение может распространяться на две хорды из двух конгруэнтных круги.
Что мы можем сказать о длинах хорд в том же круге или в равные окружности, если их расстояния от соответствующих центров равны? Нетрудно изменить предыдущее обсуждение, чтобы оно соответствовало этому конкретному случаю. Рассмотрим следующую схему.
Предположим, что хорды 𝐴𝐵 и
𝐷𝐸 равноудалены от центра,
что означает 𝑂𝐶=𝑂𝐹. Мы также знаем, что радиусы
одинаковой длины, поэтому 𝑂𝐴=𝑂𝐷. Это говорит нам о том, что
гипотенуза и другая сторона двух прямоугольных треугольников
△𝑂𝐶𝐴 и
△𝑂𝐹𝐷 равны. Так как длины
остальные стороны можно получить по теореме Пифагора,
длины третьих сторон, 𝐴𝐶 и
𝐷𝐹, также должны быть равны. Поскольку эти длины
составляют половину длины хорд, обе хорды должны иметь одинаковую длину. Этот
результат можно резюмировать следующим образом.
Мы также знаем, что радиусы
одинаковой длины, поэтому 𝑂𝐴=𝑂𝐷. Это говорит нам о том, что
гипотенуза и другая сторона двух прямоугольных треугольников
△𝑂𝐶𝐴 и
△𝑂𝐹𝐷 равны. Так как длины
остальные стороны можно получить по теореме Пифагора,
длины третьих сторон, 𝐴𝐶 и
𝐷𝐹, также должны быть равны. Поскольку эти длины
составляют половину длины хорд, обе хорды должны иметь одинаковую длину. Этот
результат можно резюмировать следующим образом.
Теорема: Эквидистантные хорды в конгруэнтных окружностях
Рассмотрим две хорды в одной и той же окружности или в конгруэнтных окружностях. Если они равноудалены от центра окружности или от соответствующих центров окружности, то их длины равны.
В следующем примере мы будем использовать это отношение, чтобы найти недостающую длину хорда на заданной схеме.
Пример 3. Нахождение недостающей длины по равноотстоящим хордам от центра круга
Учитывая, что 𝑀𝐶=𝑀𝐹=3см,
𝐴𝐶=4см,
𝑀𝐶⟂𝐴𝐵, и
𝑀𝐹⟂𝐷𝐸, найдите длину
𝐷𝐸.
Ответ
Напомним, что две хорды одной окружности равноудалены от центры окружности имеют одинаковую длину. Мы также знаем, что расстояние хорда из центра окружности измеряется длиной линии отрезок от центра, перпендикулярно пересекающийся с хордой.
В этом примере у нас есть два аккорда, 𝐴𝐵 и 𝐷𝐸. С 𝑀𝐶 пересекается перпендикулярно хорда 𝐴𝐵, длина 𝑀𝐶 — расстояние этой хорды от центра. Точно так же длина 𝑀𝐹 — это расстояние хорды 𝐷𝐸 от центра. Из данного информации, отметим, что 𝑀𝐶=𝑀𝐹, поэтому две хорды равноудалены от центра окружности. Следовательно, две хорды должны имеют одинаковую длину, 𝐷𝐸=𝐴𝐵.
На диаграмме выше дано, что 𝐴𝐶=4. Мы
Напомним, что биссектриса хорды проходит через центр
круга. Так как 𝑀𝐶
перпендикулярно хорде 𝐴𝐵 и проходит
через центр 𝑀 круга, это должно быть
Биссектриса хорды 𝐴𝐵. В частности, это означает, что 𝐶 является серединой
𝐴𝐵, что дает нам
𝐴𝐶=𝐵𝐶. Так как 𝐴𝐶=4см,
мы также знаем, что 𝐵𝐶=4см. Следовательно,
𝐴𝐵=𝐴𝐶+𝐵𝐶=4+4=8.см
В частности, это означает, что 𝐶 является серединой
𝐴𝐵, что дает нам
𝐴𝐶=𝐵𝐶. Так как 𝐴𝐶=4см,
мы также знаем, что 𝐵𝐶=4см. Следовательно,
𝐴𝐵=𝐴𝐶+𝐵𝐶=4+4=8.см
Это говорит нам о том, что длина 𝐴𝐵 составляет 8 см. С тех пор, как мы зная 𝐷𝐸=𝐴𝐵, мы заключаем, что длина 𝐷𝐸 это 8 см.
До сих пор мы обсуждали значения длин хорд в зависимости от их расстояние от центра круга. Теперь обратим внимание на обратное отношение. Точнее, если мы знаем, что два аккорда в двух конгруэнтные окружности имеют одинаковую длину, что мы можем сказать о расстоянии хорды из соответствующих центров окружностей? Давайте рассмотрим следующую схему.
Мы можем отметить середины обеих хорд, где синие линии
пересекаются с хордами перпендикулярно. Также добавляем радиусы
𝑂𝐴 и 𝑃𝐷 к схеме. Поскольку
окружности конгруэнтны, мы знаем, что длины радиусов равны,
что приводит к 𝑂𝐴=𝑃𝐷, как показано на диаграмме ниже.
Мы знаем, что 𝐸 и 𝐹 являются серединами хорд, поэтому 𝐴𝐸=12𝐴𝐵𝐷𝐹=12𝐶𝐷.и
Поскольку мы предполагаем, что хорды имеют одинаковую длину, мы знаем, что 𝐴𝐸=𝐷𝐹, как отмечено на диаграмме выше. Это говорит нам что гипотенуза и другая сторона двух прямоугольных треугольников △𝑂𝐸𝐴 и △𝑃𝐹𝐷 равны. Так как длины остальные стороны можно получить по теореме Пифагора, длины третьи стороны также должны быть равны. Это говорит нам 𝑂𝐸=𝑃𝐹.
Другими словами, расстояния хорд от соответствующих центров равны равный. Мы можем резюмировать этот результат следующим образом.
Теорема: хорды равной длины в конгруэнтных окружностях
Две хорды одинаковой длины в одной и той же окружности или в конгруэнтных окружностях равноудалены от центра окружности или соответствующих центров окружностей.
Давайте рассмотрим пример, где нам нужно использовать этот оператор вместе с
другие свойства хорд окружности, чтобы найти недостающую длину.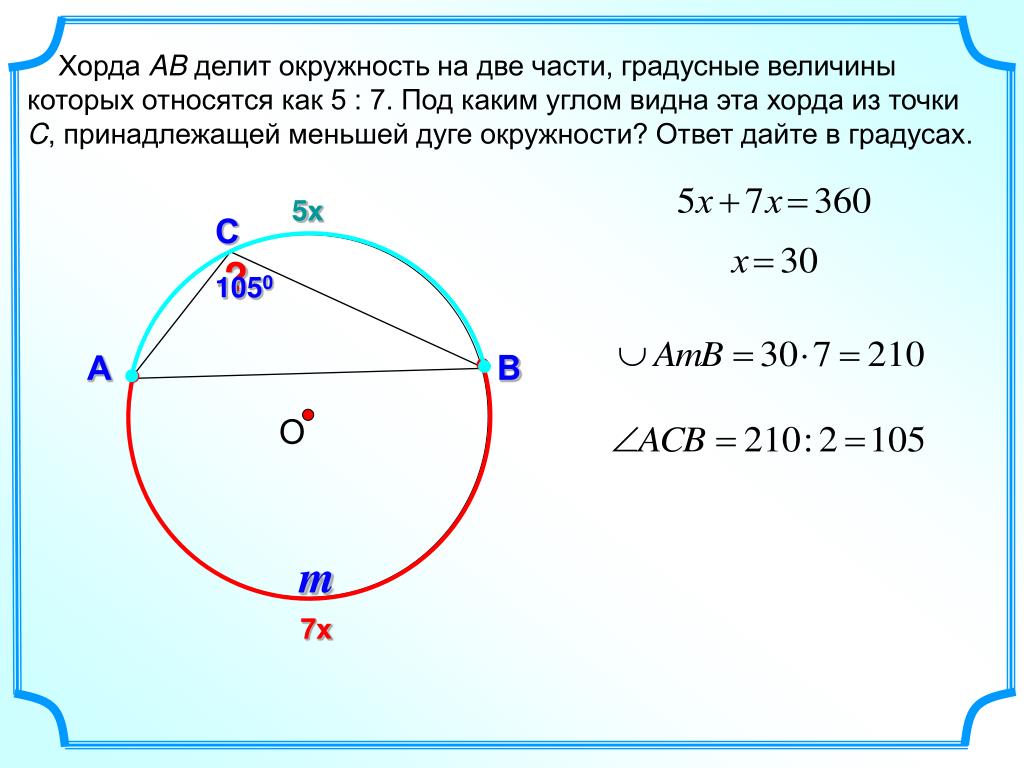
Пример 4: Поиск недостающей длины с использованием равных хорд
Учитывая, что 𝐴𝐵=𝐶𝐷, 𝑀𝐶=10 см, и 𝐷𝐹=8см, найдите длину 𝑀𝐸.
Ответ
Напомним, что две хорды одинаковой длины в одной окружности равны равноудалены от центра окружности. Мы также знаем, что расстояние хорды, проходящей через центр окружности, измеряется длиной отрезок прямой из центра, пересекающийся перпендикулярно хорде.
В этом примере у нас есть два аккорда, 𝐴𝐵 и 𝐶𝐷. С 𝑀𝐸 пересекается перпендикулярно хорда 𝐴𝐵, длина 𝑀𝐸 — расстояние этой хорды от центра. Точно так же длина 𝑀𝐹 — это расстояние хорды 𝐶𝐷 от центра. Так как мы учитывая 𝐴𝐵=𝐶𝐷, мы знаем, что хорды равны длины. Это приводит к тому, что хорды равноудалены от центр: 𝑀𝐸=𝑀𝐹.
Так как мы ищем длину 𝑀𝐸, то достаточно найти
длина 𝑀𝐹 вместо этого. Мы отмечаем, что
𝑀𝐹 — сторона прямоугольного треугольника
△𝑀𝐶𝐹, гипотенуза которого определяется выражением
𝑀𝐶=10см. Если мы можем найти длину стороны 𝐶𝐹,
то мы можем применить теорему Пифагора, чтобы найти длину третьей стороны,
𝑀𝐹.
Мы отмечаем, что
𝑀𝐹 — сторона прямоугольного треугольника
△𝑀𝐶𝐹, гипотенуза которого определяется выражением
𝑀𝐶=10см. Если мы можем найти длину стороны 𝐶𝐹,
то мы можем применить теорему Пифагора, чтобы найти длину третьей стороны,
𝑀𝐹.
Чтобы найти длину 𝐶𝐹, вспомним, что перпендикуляр биссектриса хорды проходит через центр окружности. С 𝑀𝐹 перпендикулярно пересекает хорду 𝐶𝐷 и проходит через центр 𝑀, это биссектриса хорды. Следовательно, 𝐶𝐹=𝐷𝐹. Так как 𝐷𝐹=8см, получаем 𝐶𝐹=8см.
Применение теоремы Пифагора к △𝑀𝐶𝐹, 𝑀𝐹+𝐶𝐹=𝑀𝐶.
Замена 𝑀𝐶=10см и 𝐶𝐹=8см в это уравнение, 𝑀𝐹+8=10,𝑀𝐹=100−64=36.что приводит к
Поскольку 𝑀𝐹 — положительная длина, мы можем взять квадрат корень для получения 𝑀𝐹=√36=6.cm
Помните, что, поскольку 𝑀𝐸=𝑀𝐹, мы заключаем, что длина 𝑀𝐸 это 6 см.
В нашем последнем примере мы будем использовать соотношение между длинами хорд
и их расстояния от центра круга, чтобы определить недостающий угол.
Пример 5. Нахождение меры угла в треугольнике внутри круга, две вершины которого пересекаются с хордами, а третья Центр круга
Найдите 𝑚∠𝑀𝑋𝑌.
Ответ
Напомним, что две хорды одинаковой длины в одной окружности равны равноудалены от центра окружности. Мы также знаем, что расстояние хорды, проходящей через центр окружности, измеряется длиной отрезок прямой из центра, пересекающийся перпендикулярно хорде.
В этом примере у нас есть два аккорда
𝐴𝐵 и
𝐴𝐶 одинаковой длины. Напомним, что биссектриса хорды проходит через
центр круга. Так как 𝑋 и 𝑌 являются серединами
две хорды, а 𝑀 — центр круга,
сегменты линии
𝑀𝑋 и 𝑀𝑌 должны быть
серединные перпендикуляры двух хорд. В частности, эти строки
пересекаются перпендикулярно соответствующим хордам. Это говорит нам, что
𝑀𝑋 и 𝑀𝑌 — соответствующие расстояния
аккорды
𝐴𝐵 и
𝐴𝐶 от центра круга.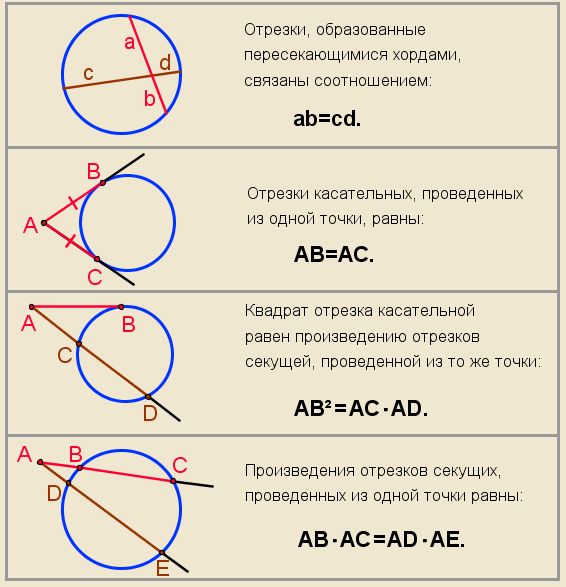
Поскольку две хорды имеют одинаковую длину, они должны быть равноудалены от центр. Это говорит нам 𝑀𝑋=𝑀𝑌.
Это также говорит нам о том, что две стороны треугольника 𝑀𝑋𝑌 имеют одинаковую длину. Другими словами, △𝑀𝑋𝑌 — равнобедренный треугольник. Следовательно, 𝑚∠𝑀𝑋𝑌=𝑚∠𝑀𝑌𝑋.
Мы также знаем, что сумма внутренних углов треугольника равна 180∘. Мы можем написать 𝑚∠𝑋𝑀𝑌+𝑚∠𝑀𝑋𝑌+𝑚∠𝑀𝑌𝑋=180.∘
Мы знаем, что 𝑚∠𝑋𝑀𝑌=102∘ и также 𝑚∠𝑀𝑋𝑌=𝑚∠𝑀𝑌𝑋. Подставляя эти выражения в приведенное выше уравнение, 102+2𝑚∠𝑀𝑋𝑌=180,2𝑚∠𝑀𝑋𝑌=180−102=78.∘∘что приводит к
Следовательно, 𝑚∠𝑀𝑋𝑌=782=39∘.
Давайте закончим повторением нескольких важных понятий из этого объяснения.
Ключевые точки
- Расстояние хорды от центра окружности измеряется длина отрезка от центра, пересекающего перпендикулярно аккорд.
- Рассмотрим две хорды в одном круге или в двух конгруэнтных кругах, чьи
расстояния от центра или соответствующих центров различны.
 Аккорд
тот, что ближе к соответствующему центру, имеет большую длину, чем другой.
Аккорд
тот, что ближе к соответствующему центру, имеет большую длину, чем другой. - Рассмотрим две хорды в одном круге или в конгруэнтных кругах. Если они равноудалены от центра окружности или от соответствующих центров окружности, их длины равны.
- Две хорды одинаковой длины в одной окружности или в конгруэнтных окружностях, равноудалены от центра окружности или соответствующих центров круги.
Chords — SAT Math
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
SAT Math Help » Геометрия » Плоская геометрия » Круги » Хорды
Две хорды окружности и пересекаются в одной точке. в два раза длиннее , , и .
Укажите длину .
Возможные ответы:
Недостаточно информации, чтобы найти длину .
Правильный ответ:
Недостаточно информации, чтобы найти длину .
Объяснение:
Обозначим длину ; то длина в два раза больше или . Цифра, указанная ниже:
Если две хорды пересекаются внутри круга, то они пересекают друг друга таким образом, что произведение длин частей одинаково для двух хорд, то есть
Подставляя соответствующие количества, затем находя:
Это утверждение точно так же верно. Следовательно, без дополнительной информации мы не можем определить значение – длину .
Сообщить об ошибке
Две хорды окружности и пересекаются в точке . на 12 единиц длиннее, чем , , и .
Укажите длину (ближайшая десятая, если применимо)
Возможные ответы:
Правильный ответ:
Объяснение:
Обозначим длину ; тогда длина равна . Цифра, указанная ниже:
Цифра, указанная ниже:
Если две хорды пересекаются внутри круга, то они пересекают друг друга таким образом, что произведение длин частей одинаково для двух хорд, то есть
Подставляем соответствующие количества, затем находим:
Это квадратное уравнение можно решить, составив квадрат; поскольку коэффициент равен 12, квадрат можно составить, прибавив
к обеим сторонам:
Переформулировать трехчлен как квадрат двучлена:
Извлечь квадратный корень из обеих сторон:
3
или
Либо
,
в этом случае
,
или
в этом случае
,
Поскольку это длина, мы отбрасываем отрицательное значение; следует, что правильная длина .
Сообщить об ошибке
Диаметр окружности перпендикулярен хорде в точке.
Каков диаметр круга?
Возможные ответы:
Недостаточно информации для ответа на вопрос.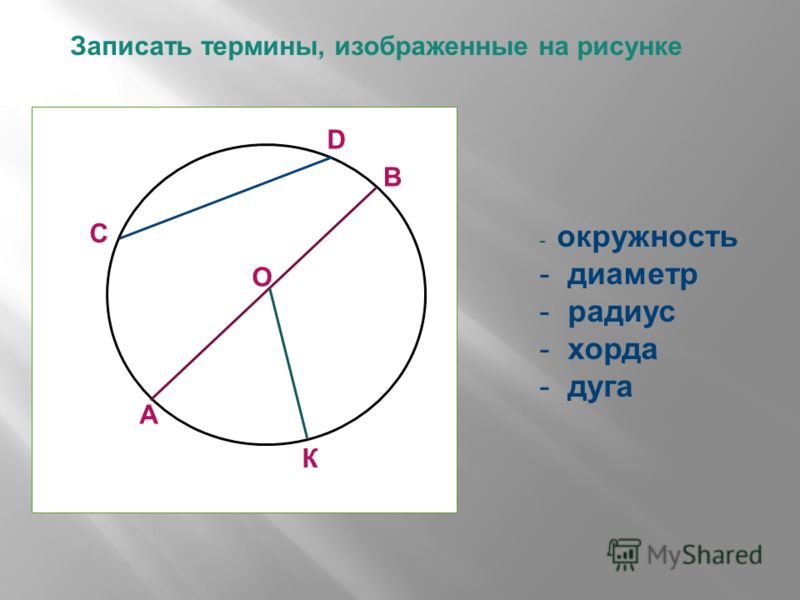
Правильный ответ:
Объяснение:
В окружности диаметр, перпендикулярный хорде, делит хорду пополам. Это делает середину ; следовательно, .
На рисунке ниже:
Если две хорды пересекаются внутри круга, то они пересекают друг друга таким образом, что произведение длин частей одинаково для двух хорд, то есть
Настройка и решение для :
,
правильную длину.
Сообщить об ошибке
Две хорды окружности и пересекаются в точке .
Укажите длину .
Возможные ответы:
Недостаточно информации для ответа на вопрос.
Правильный ответ:
Объяснение:
Пусть , в этом случае ; ссылка на рисунок ниже (не в масштабе).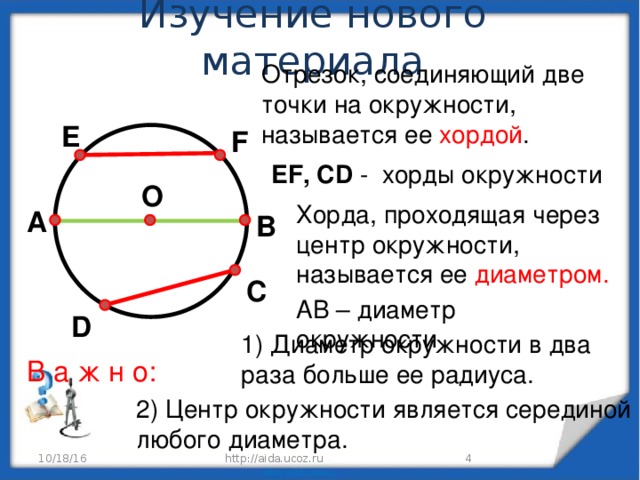
Если две хорды пересекаются внутри окружности, то они пересекают друг друга таким образом, что произведение длин частей одинаково для двух хорд, то есть
Установка .
Сообщить об ошибке
Диаметр окружности перпендикулярен хорде в точке . и . Укажите длину (ближайшую десятую, если применимо).
Возможные ответы:
недостаточно информации для определения длины .
Правильный ответ:
Объяснение:
Диаметр окружности, перпендикулярной хорде, делит хорду пополам. Таким образом, точка пересечения — это середина, а
.
Обозначим общую длину и ,
Ссылка на рисунок приведена ниже.
Если внутри окружности пересекаются две хорды, то они пересекают друг друга таким образом, что произведение длин частей одинаково для двух хорд, т.

 (геометрическое) отрезок прямой линии, соединяющий две точки окружности (сферы, гиперсферы) и проходящий через её центр || его длина ◆ Величина сферического треугольника Y равна величине противолежащего ему треугольника ABCʹ, в котором сторона АВ общая с треугольником Р, а третий угол Сʹ лежит при конечной точке диаметра сферы, идущего от С через центр сферы. Н. И. Лобачевский, «Геометрические исследования по теории параллельных линий», 1840 г. ◆ На катете прямоугольного треугольнике как на диаметре построена окружность. «Хотите стать математиком?», 2008 г. // «Наука и жизнь»
(геометрическое) отрезок прямой линии, соединяющий две точки окружности (сферы, гиперсферы) и проходящий через её центр || его длина ◆ Величина сферического треугольника Y равна величине противолежащего ему треугольника ABCʹ, в котором сторона АВ общая с треугольником Р, а третий угол Сʹ лежит при конечной точке диаметра сферы, идущего от С через центр сферы. Н. И. Лобачевский, «Геометрические исследования по теории параллельных линий», 1840 г. ◆ На катете прямоугольного треугольнике как на диаметре построена окружность. «Хотите стать математиком?», 2008 г. // «Наука и жизнь» 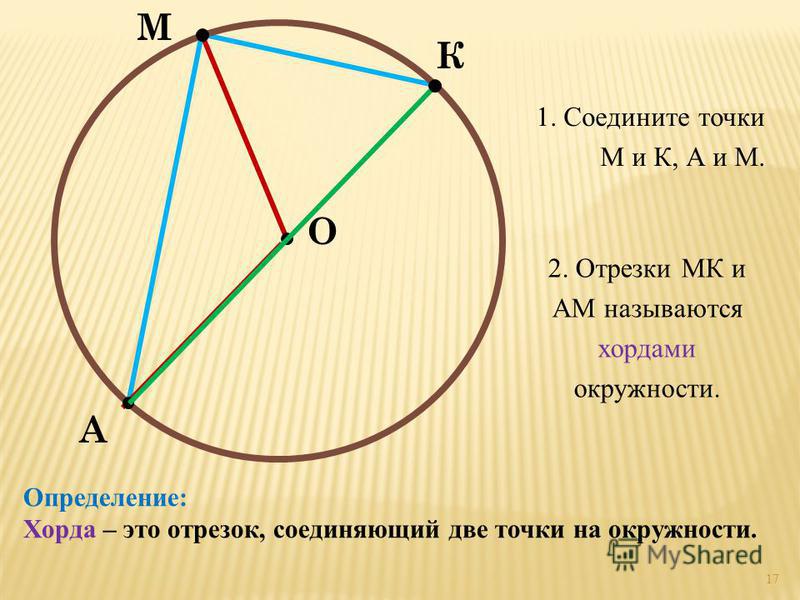 (математический термин) максимальное расстояние между двумя точками множества ◆ Всякое n-мерное выпуклое тело диаметра d может быть разбито на n + 1 частей меньшего диаметра. В. Г. Болтянский, И. Ц. Гохберг, «Теоремы и задачи комбинаторной геометрии», 1965 г. (см. w:Гипотеза Борсука)
(математический термин) максимальное расстояние между двумя точками множества ◆ Всякое n-мерное выпуклое тело диаметра d может быть разбито на n + 1 частей меньшего диаметра. В. Г. Болтянский, И. Ц. Гохберг, «Теоремы и задачи комбинаторной геометрии», 1965 г. (см. w:Гипотеза Борсука)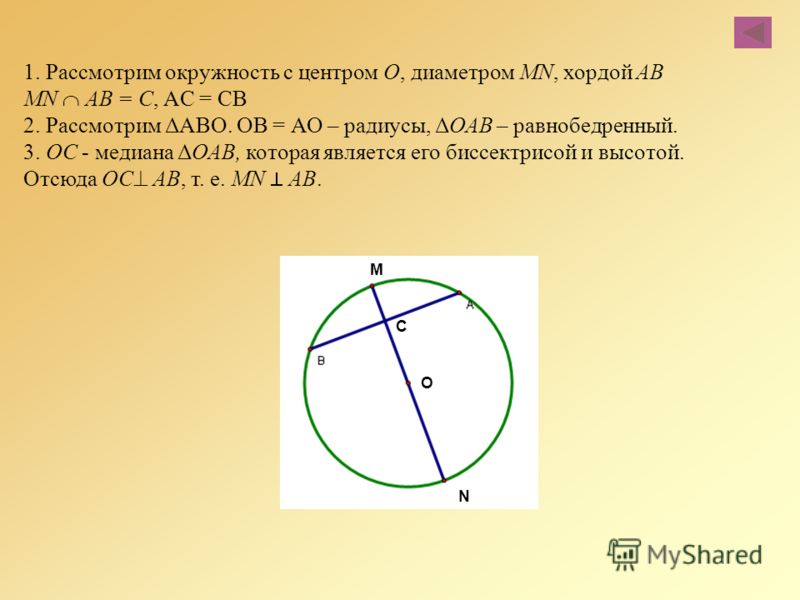
 е.
е.
 Аккорд
тот, что ближе к соответствующему центру, имеет большую длину, чем другой.
Аккорд
тот, что ближе к соответствующему центру, имеет большую длину, чем другой.