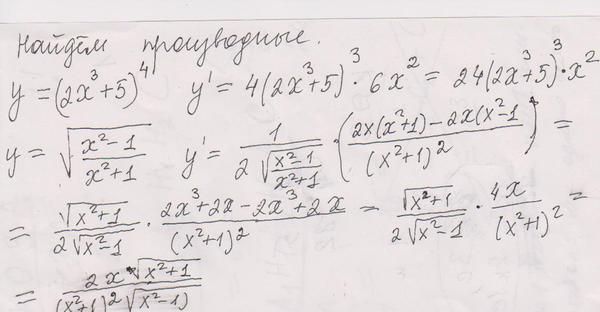| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Рассчитайте корень куба с использованием линейной аппроксимации
BY: Mark Ryan и
Обновлен: 04-14-2017
Дифференцированные уравнения.

Вот пример. Можете ли вы приблизительно
у тебя в голове? Да, ты можешь! Как?
Вот так: Бинго! 4.125.
Ну, ладно, есть еще немного . Взгляните на рисунок, а затем выполните следующие шаги, чтобы получить полную картину.
Линия, касательная к кривой в точке (64, 4), может использоваться для аппроксимации кубических корней или чисел, близких к 64.
Оценить
выполните следующие действия:
Найдите совершенный кубический корень рядом с
Вы заметили, что
почти не представляет сложности,
, что, конечно же, равно 4. Это дает вам точку (64, 4) на графике
.Найдите наклон числа
(наклон касательной) при x = 64.
Это говорит вам о том, что — для аппроксимации кубических корней около 64 — вы добавляете (или вычитаете)
на 4 за каждое увеличение (или уменьшение) единицы из 64.
. Например, кубический корень из 65 равен примерно
Например, кубический корень из 65 равен примернокубический корень из 66 равен примерно
кубический корень из 67 равен
, а кубический корень из 63 равен
.Используйте форму точка-наклон, чтобы написать уравнение касательной в точке (64, 4).
В третьей строке вышеприведенного уравнения вы поместили 4 в начало правой части уравнения (вместо крайней правой, что может показаться более естественным) по двум причинам. Во-первых, потому что это уравнение согласуется с объяснением в конце шага 2 о том, что нужно начинать с 4 и подниматься (или опускаться) оттуда по мере удаления от точки касания. А во-вторых, привести это уравнение в соответствие с объяснением в конце шага 4. Через минуту вы увидите, как все это работает.
Поскольку эта касательная проходит так близко к функции
около x = 64, вы можете использовать его для оценки кубических корней чисел около 64, например, x = 70.


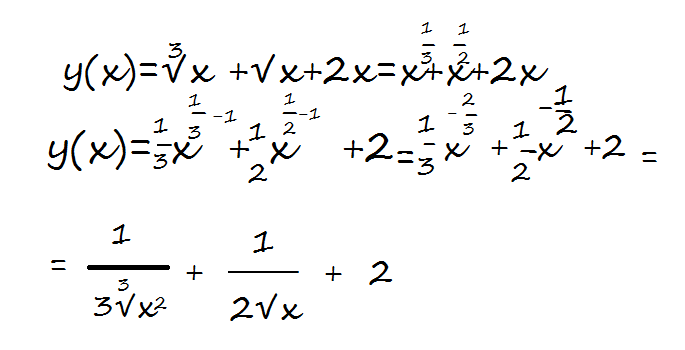 Например, кубический корень из 65 равен примерно
Например, кубический корень из 65 равен примерно