Касательные, секущие, хорды | ЕГЭ по математике (профильной)
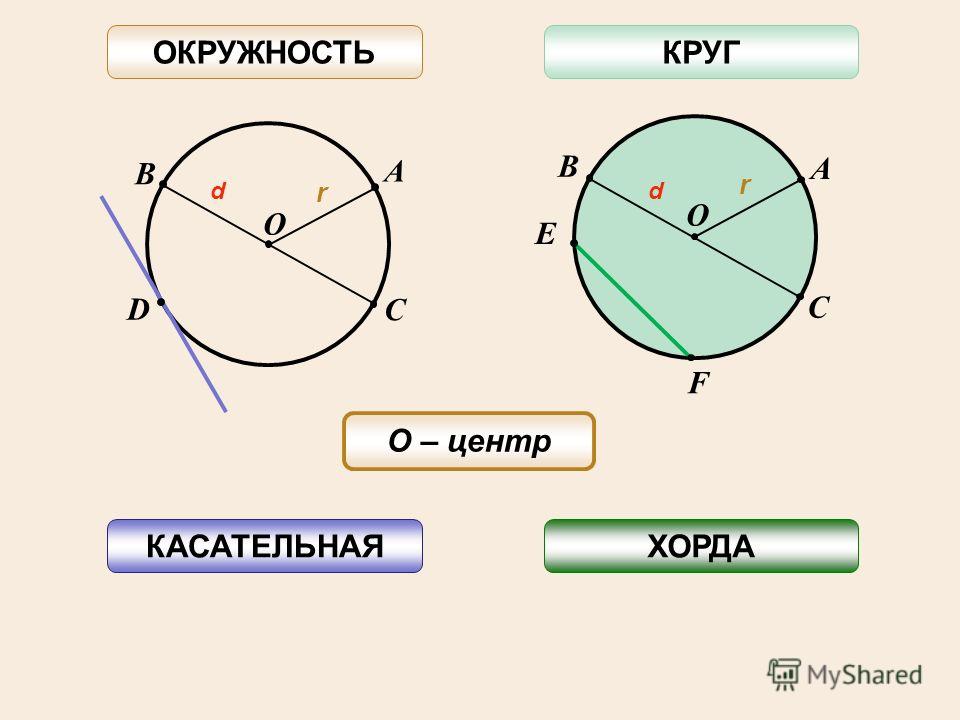
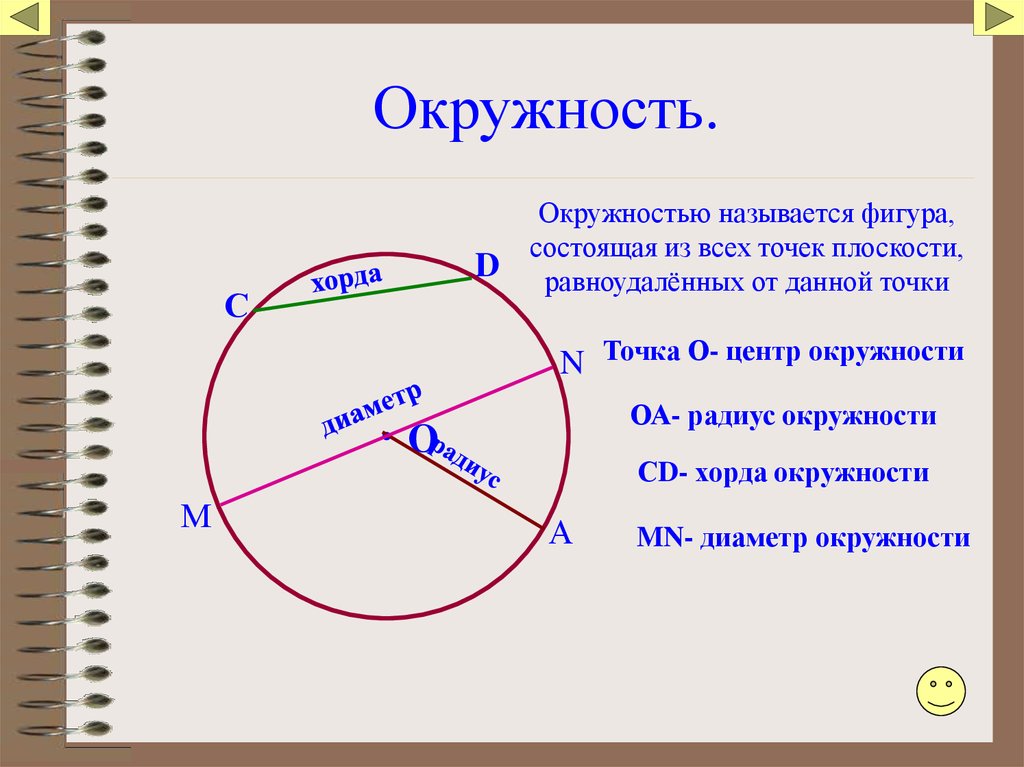
Окружность — это фигура, которая состоит из множества точек плоскости, равноудаленных от данной точки (центра).
Отрезок, соединяющий любую точку на окружности с центром окружности, называется радиусом ($R$).
$ОС=OD=OE=R.$
Отрезок, соединяющий любые две точки на окружности, называется хордой, а хорда, проходящая через центр, — диаметром ($d$).
$ВС$ – хорда
$СЕ$ — диаметр
Свойства хорды и диаметра:
1. Диаметр равен двум радиусам $d=2R; СЕ=2СО$
2. Равные хорды стягивают равные дуги
Если $AB=CD$, то $∪AB=∪CD$.
3.Вся окружность составляет $360°$. Диаметр делит окружность на две полуокружности по $180°$.
4. Хорды окружности, удаленные от центра на равные расстояния, равны.
5. Из двух хорд больше та, которая менее отдалена от центра.
Касательные и секущие:
Прямая, имеющая с окружностью только одну общую точку, называется касательной.
2$
Углы в окружности:
1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается
$∠О=∪BmA$
2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается
$∠B={∪AmC}/{2}$
Пример:
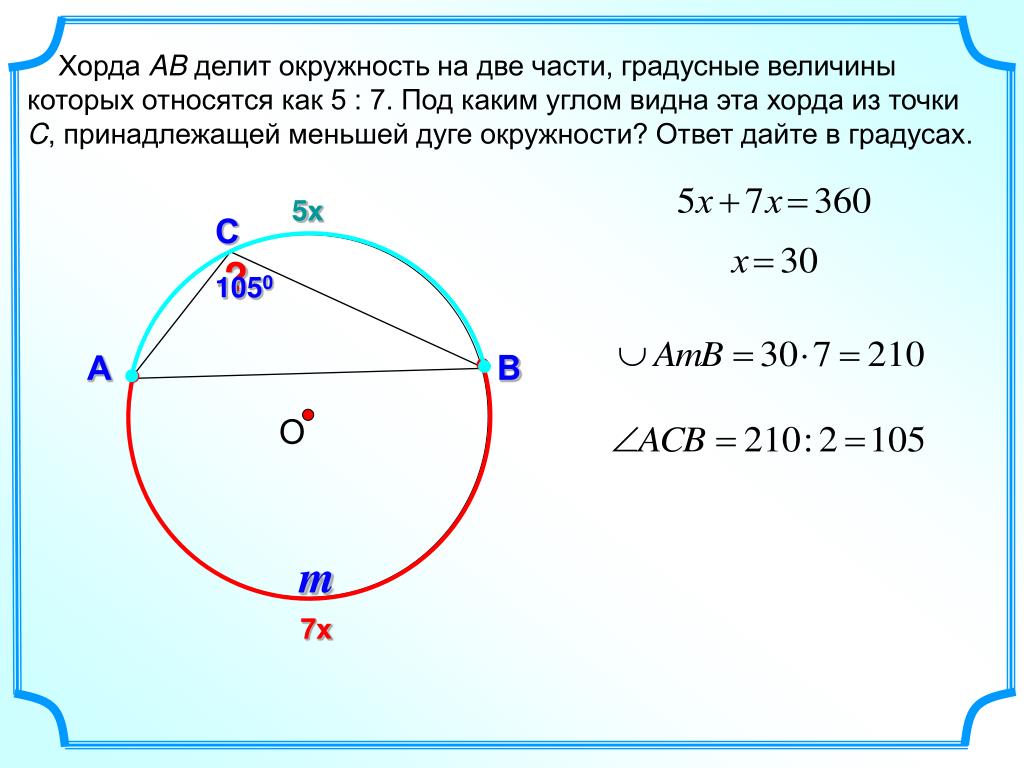
Точки $A, B, C$, расположенные на окружности, делят её на три дуги, градусные меры которых относятся как $2:3:7$. Найдите больший угол треугольника $ABC$. Ответ дайте в градусах.
Решение:
Данное условие можно рассмотреть как задачу на части:
1) Найдем общее количество частей, на которые разделили окружность.
$2+3+7=12$ (всего частей)
2) Найдем, сколько градусов приходится на одну часть
$360:12=30°$
3) $∪АВ$ составляет две части, следовательно, $∪АВ=2·30=60°$
$∪АС=3·30=90°$
$∪СВ=7·30=210°$
4) В треугольнике $АВС$ самым большим углом является $∠А$, он вписанный, опирается на дугу $СВ$ и равен ее половине.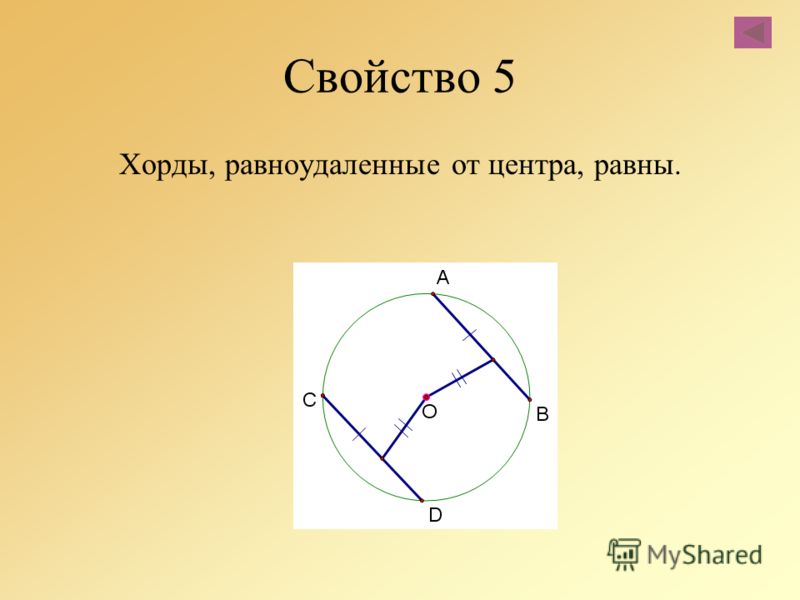
$∠А={∪СВ}/{2}={210}/{2}=105°$
Ответ: $105$
3. Угол между хордой и касательной равен половине дуги, отсекаемой хордой .
$∠B={∪BmC}/{2}$
1. Угол между хордами равен полусумме дуг, на которые этот угол опирается
$∠СND={∪CD+∪AB}/{2}$
2. Угол между двумя касательными равен полуразности дуг, заключенных внутри угла.
$∠В={∪АmC-∪AnC}/{2}$
3. Угол между двумя секущими равен полуразности дуг, заключенных внутри угла.
$∠С={∪AE-∪BD}/{2}$
4. Угол между касательной и секущей равен полуразности дуг, заключенных внутри угла.
$∠B={∪AD-∪AC}/{2}$
Практика: решай 6 задание и тренировочные варианты ЕГЭ по математике (профильной)
Математика. Задачи. Хорды, касательные и секущие.
№ 1.
Решение:
Отрезки пересекающихся хорд
связаны соотношением:
AO∙OB=CO∙OD
12 ∙8=CO ∙4, = CO=24
Ответ:24
А
D
4
12
?
О
8
B
C
№ 2.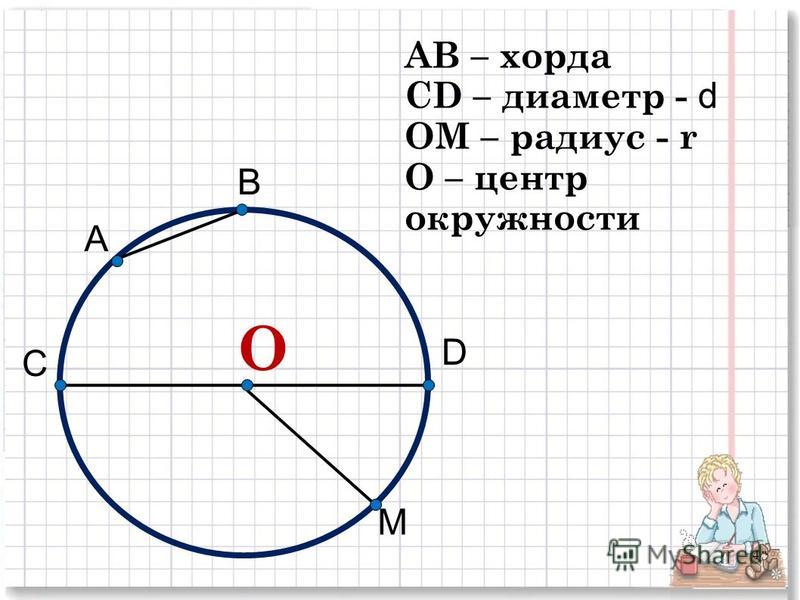
Решение:
CO∙OD=AO∙OB
CO=CD-OD=18-4=14
14 ∙4=8 ∙OB, =OB=7
Ответ:7
A
D
OB=?
4
8
О
18
B
C
№ 3.
Решение:
CO 1 ∙O 1 D=AO 1 ∙O 1 B
OD=CO(как радиус)
O 1 D=OD-OO 1 =11-7=4
O 1 C=O 1 O+OC=7+11=18
O 1 B=x, AO 1 =18-x
CO 1 ∙O 1 D=AO 1 ∙O 1 B
x ∙(18-x)=4 ∙18
x 2 -18 x+72=0, O 1 B=6,AO 1 =12
Ответ: 6 и 12
A
D
?
7
?
O 1
O
11
B
C
№ 4.
Решение:
AO∙OB=CO ∙OD AO:CO=OD:OB
4:3=x(49-x)
4(49-x)=3x
196=7x = x=28 OD=28,OB=49-28=21
Ответ: 28 и 21
A
AO:CO=4:3
OD+OB=49
D
O
B
C
A
№ 5.
Решение:
Отрезки касательных проведенных из
одной точки равны:
AB=AC
- AB=8 Ответ: 8
?
8
C
B
Решение:
AB=AC= ∆ ABC – равнобедренный№ 6.
∠ B= ∠ C=45º, ∠ B+ ∠ C=90º =
∠ A=180º-90º=90º
sin45 º=AC/BC = √2/2=AC/4√2 =
AC=4 =AB=4 Ответ: 4 и 4
A
?
?
C
45º
B
20
№ 7.
Решение:
AC 1 =AB 1 =20 AB=AC=7 =
CC 1 =BB 1 =AC 1 -AC=20-7=13
Ответ: 7 и 13
A
?
7
C
B
?
C 1
B 1
Решение:
AC=AC 1 +C 1 K+KC
AB 1 =AC 1 =7
K 1 B 1 =K 1 D 1 =3
KD 1 =KC 1 =KK 1 -K 1 D 1 =13-3=10
K 1 B=K 1 D 1 +D 1 D (1) KC 1 =KD+DD 1 (2)
AB 1 +B 1 K 1 +K 1 B=AC 1 +C 1 K+KC(3)
учитывая K 1 B 1 =K 1 D 1 , KD=KC, AB 1 =AC 1
- и (2) в (3)
AC 1 +K 1 D 1 +(K 1 D 1 +D 1 D)=AC 1 +(KD+DD 1 )+KD
2K 1 D 1 =2KD =KD=KC=3 =AC=7+10+3=20
Ответ: 20
A
№ 8.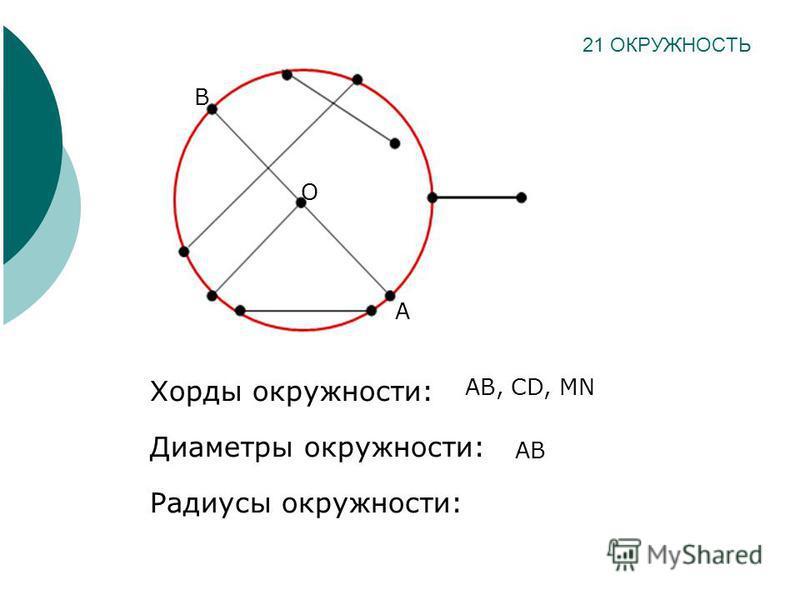
AB 1 =7
B 1 K 1 =3
KK 1 =13
AC — ?
C 1
B 1
K 1
D 1
K
D
B
C
Квадрат отрезка касательной равен
произведению отрезков секущей,
проведенной из той же точки:
AB 2 =AC∙AD AB 2 =5∙20 =AB=10
Ответ: 10
A
№ 9.
5
?
C
B
15
D
Решение:
∆ BDC, ∠ С= 90º, по т.Пифагора:
DC 2 =DB 2 -BC 2 =100-36=64 = D=8
Пусть AC=x, тогда AD=8+x
AB 2 =AC ∙AD
AB 2 =AC 2 +BC 2
AC ∙AD=AC 2 +BC 2
x(8+x)=x 2 +36
8x+x 2 =x 2 +36 =8x=36 =x=4,5
AC=4,5 AD=8+4,5=12,5
AB 2 =4,5 ∙12,5 =AB=7,5
Ответ: 7,5
A
№ 10.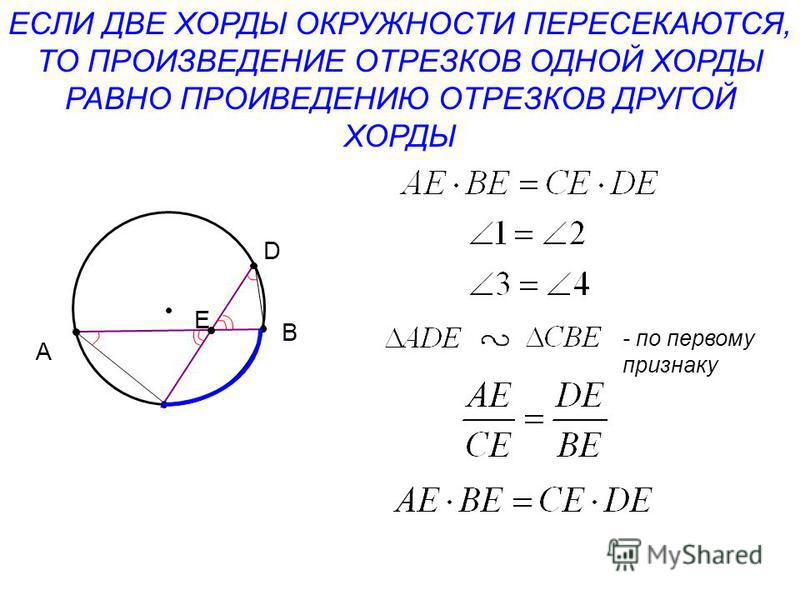
?
C
6
B
D
10
№ 11.
Решение:
AB 2 =AC∙AD =
AB/AD=AC/AB, по условию
AC/AB=3 =AD/AB=1/3
AD/AB=(AC-DC)/AB=
AC/AB — DC/AB=3-DC/AB=1/3 =
DC/AB=3-1/3=2 2 / 3 ; DC= 8 / 3 AB
Ответ: в 2 2 / 3 раза
AC=3AB
Во сколько раз
DC длиннее AB?
C
D
A
B
Решение:
C 2 D 1 =C 2 B 2 +B 2 B 1 +D 1 B 1
C 2 B 1 ∙C 2 D 1 =C 2 C 1 2 и D 1 B 2 ∙D 1 C 2 =D 1 D 2 2
Поскольку C 1 C 2 =D 1 D 2 , то C 2 B 1 =D 1 B 2 =C 2 B 2 =D 1 B 1 =3
C 2 C 1 2 =C 2 B 1 ∙C 2 D 1
B 2 B 1 =x, тогда C 2 B 1 =x+3, C 2 D 1 =x+6
√ 154=(x+3)(x+6)
154=x 2 +9x+18
x=8 = C 2 D 1 =3+8+3=14
Ответ: 14
№ 12.
C 2 D 1 — ?
C 2
3
C 1
B 2
B 1
A
D 1
D 2
№ 13.
A
Решение:
Произведения отрезков секущих
проведенных из одной точки, равны:
AB∙AC=AD∙AE
4 ∙AC=6 ∙8
AC=12 Ответ: 12
AC — ?
4
6
B
D
2
E
C
Решение:
S ∆ ABF ½AB ∙AF ∙sinA 1
S ∆ ADC ½ AD ∙AC ∙sinA 4
AF ∙AD=AB ∙AC
AB AF AB AF 1 AB 1
AD AC AD AC 4 AD 2
Ответ: 1/2
№ 14.
A
S ∆ ABF 1
S ∆ ADC 4
AB
AD
D
B
?
∙
=
C
F
Аккорд круга — GCSE Maths
Введение
Что такое хорда окружности?
Ключевые части круга
Доказательство того, что серединный перпендикуляр из центра окружности к хорде делит хорду пополам
Как найти недостающие длины с помощью хорд
Хорда окружности рабочий лист
Распространенные заблуждения
Практикуйте аккорд круга вопросы
Хорда круга Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое хорда окружности?
Ключевые части круга
Доказательство того, что серединный перпендикуляр из центра окружности к хорде делит хорду пополам
Как найти недостающие длины с помощью хорд
Хорда окружности рабочий лист
Распространенные заблуждения
Практические вопросы по аккорду круга
Хорда круга Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о теоремах о кругах, включающих хорд окружности , включая их применение, доказательство и использование для решения более сложных задач.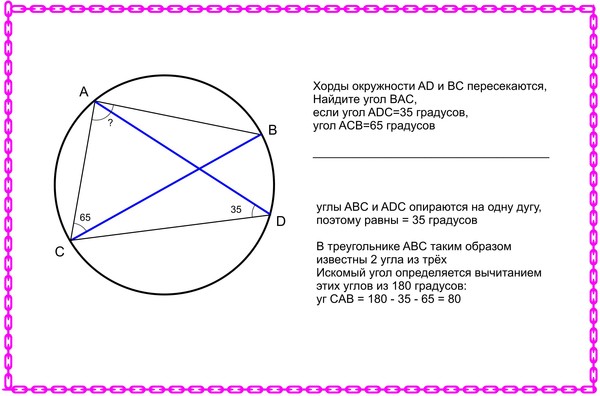
Существует также рабочих листов с теоремой о круге , основанных на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое хорда окружности?
Хорда окружности — это прямая линия, соединяющая две точки на окружности окружности. Самая длинная хорда в окружности — это диаметр окружности.
Перпендикуляр из центра окружности к хорде делит хорду пополам (разделяет хорду на две равные части).
На приведенной выше диаграмме AB — это хорда, а CE — радиус. Здесь мы видим, что радиус CE делит хорду AB пополам под углом 90 градусов, а длины AD = BD = x.
Что такое хорда окружности?
Ключевые части круга
Ниже приведена диаграмма, показывающая ключевые части круга для этой теоремы:
- Диаметр круга — это ширина круга через центр. Концы диаметра лежат на окружности окружности.
- Дуга является частью окружности.
- Большой сегмент является большей частью круга, когда он окружен хордой и большой дугой .
- Младший сегмент — это меньшая часть круга, когда он пересекается хордой и малой дугой .
- Радиус круга — это расстояние между центром круга и окружностью круга.
Стягивающие углы
Угол внутри окружности образуется двумя хордами, сходящимися в одной точке на окружности. На рисунках ниже показан вписанный угол, опирающийся на дугу AC из точки B для двух разных окружностей.
Полезный совет: слово «подтягивать» часто используется в теоремах о кругах, поэтому убедитесь, что вы знаете, что оно означает.
Доказательство того, что серединный перпендикуляр из центра окружности к хорде делит хорду пополам
Чтобы доказать эту теорему, вам не нужно знать никакие другие теоремы об окружности.
Вам просто нужно быть уверенным с углов в треугольнике и конгруэнтностью .
| Шаг | Схема | Описание |
| 1 | Начнем с окружности с центром C. Линия AB — это хорда, а CE — радиус. Прямые CE и AB пересекаются в точке D под углом 90 градусов друг к другу, потому что они перпендикулярны. | |
| 2 | Затем проводим линии AC и BC. Длина AC = BC, так как они оба являются радиусами окружности. Следовательно, треугольники ACD и BCD оба являются прямыми углами, их гипотенуза равна, а прямая CD совпадает, так как она является общей для обоих треугольников. Это означает, что треугольники конгруэнтны, поэтому отрезок BD и отрезок AD имеют одинаковую длину или BD = AD. |
Как найти недостающие длины с помощью хорд
Чтобы найти недостающие углы или длину хорды:
- Найдите ключевые части окружности для соответствующей теоремы о окружности.
- Используйте другие данные об углах, чтобы определить недостающие углы .
- Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .
Как найти недостающие длины с помощью хорд
Рабочий лист «Хорда круга»
Получите бесплатный рабочий лист «Хорда круга», содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист «Хорда круга»
Получите бесплатный рабочий лист «Хорда круга», содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
Примеры хорды окружности
Пример 1: отношение косинуса
Внизу круг с центром C . Точки А, В, С и D лежат на окружности. Хорда АВ перпендикулярна прямой CD в точке Е. Прямая AE равна 5 см, а угол ADE = 71°.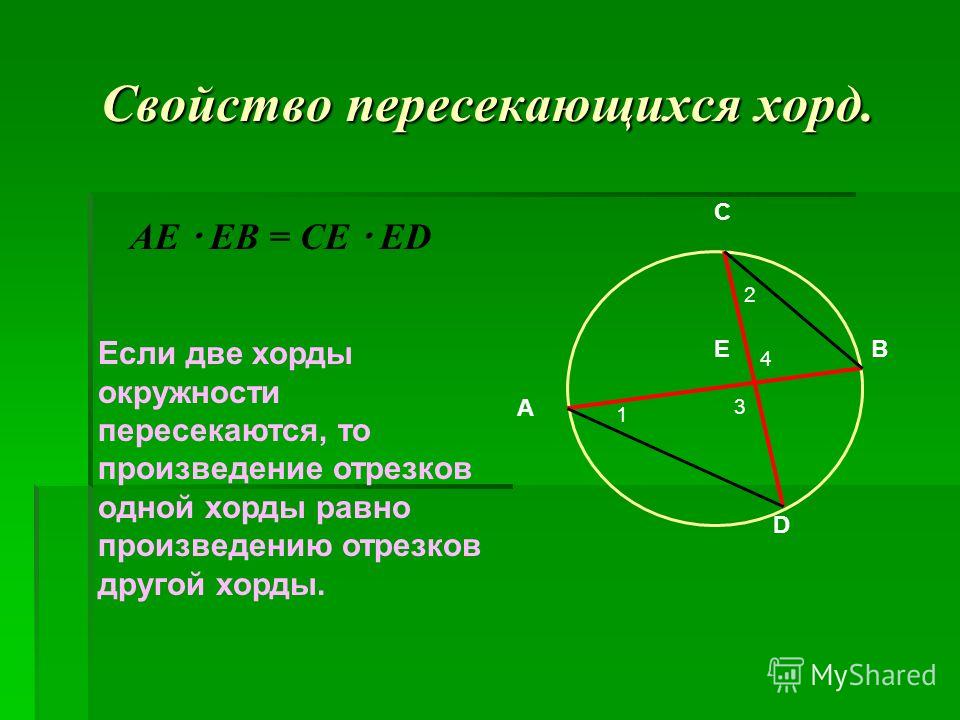
Вычислите длину прямой до н.э. с точностью до 1 знака после запятой.
- Найдите ключевые части круга для соответствующей теоремы круга .
Здесь имеем:
- CD диаметром
- AB — хорда, перпендикулярная CD
- Угол ADE = 71°
- Угол BEC = 90°
- Линия AE = 5см
- Линия ВС = х
2 Используйте другие данные об углах для определения других необходимых углов .
Поскольку углов в одном отрезке равны , угол ADE равен углу ABC, значит угол ABC = 71° . Кроме того, поскольку , перпендикулярный из центра окружности к хорде, делит пополам хорду , линия BE равна AE, поэтому BE = 5 см.
3 Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .
Чтобы вычислить длину хорды BC, нам нужно использовать тригонометрию, так как мы знаем длину одной стороны и два угла, где один угол равен 90°.
Поскольку мы знаем сторону, прилегающую к углу, и хотим вычислить гипотенузу, нам нужно использовать \cos(\theta)=\frac{A}{H} с H в качестве подлежащего.
H=\frac{A}{\cos(\theta)}
x=\frac{5}{\cos(71)}
x=15,4 см (1 дп)
Пример 2: коэффициент синуса
Ниже показана окружность с центром O . А, В, С и D лежат на окружности. AC и BD — перпендикулярные прямые. Вычислите длину AE с точностью до 1 знака после запятой.
Найдите ключевые части круга для соответствующей теоремы о круге .
Здесь имеем:
- BD диаметр
- AC — хорда, перпендикулярная BD
- Угол CDE = 35°
- Угол CED = 90°
- Линия CD = 8см
- Линия АЕ = х
Использование других фактов об углах для определения других необходимых углов .
Поскольку , перпендикулярный из центра окружности к хорде, делит пополам хорду , это означает, что длина AE равна длине CE.
Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .
Мы можем вычислить длину CE, используя прямоугольный треугольник DEC, поскольку мы знаем гипотенузу, угол и находим недостающую сторону:
\[CE=Синь\раз(\тета)\\ CE=8\times\sin(35)\\ CE=4,6 см (1dp)\]
Пример 3: отношение касательной
Ниже показана окружность с центром O. А, В, С и D лежат на окружности. AC и BD — перпендикулярные прямые. FG является касательной в точке B и параллельна прямой AC. Вычислите длину BE с точностью до 1 знака после запятой.
Найдите ключевые части круга для соответствующей теоремы о круге .
Здесь имеем:
- BD диаметр
- AC — хорда, перпендикулярная BD
- Угол ABF = 77°
- Линия СЕ = 12см
- Строка БЭ = х
Использование других фактов об углах для определения других необходимых углов .
Поскольку , перпендикулярный из центра окружности к хорде, делит пополам хорду , это означает, что длина AE равна длине CE.
Так как тангенс и радиус пересекаются в 9{\circ}\]
Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .
Мы можем рассчитать длину хорды BE, используя прямоугольный треугольник ABE, поскольку мы знаем сторону, противоположную углу ABE , угол ABE и находим отсутствующую соседнюю сторону BE :
BE=\frac{O} {\tan(\theta)}
x=\frac{12}{\tan(13)}
x=52,0 см (1dp)
Пример 4: теорема Пифагора
A, B, C и D точки на окружности с центром O . Радиус ОА = 6см, хорда АВ = 13см. Хорда BD перпендикулярна диаметру AC в точке E .
ОЕ:ОС = 1:1 . Вычислите длину BE с отметкой x.
Найдите ключевые части круга для соответствующей теоремы о круге .
Здесь имеем:
- АС это диаметр
- BD — хорда, перпендикулярная AC
- Линия АВ = 13см
- Линия ОА = 6см
- Строка БЭ = х
Использование других фактов об углах для определения других необходимых углов .
AEB равно 92=88\\ x=9.38cm (2dp)\]
Пример 5: равнобедренный треугольник
Окружность с центром O имеет перпендикулярные диаметры AC и BD . Используйте информацию на диаграмме, чтобы вычислить значение x .
Найдите ключевые части круга для соответствующей теоремы о круге .
Здесь имеем:
- AC = BD диаметр
- AC и BD перпендикулярны
- Линия ОС = 4см
- Линия АВ = х
Использование других фактов об углах для определения других необходимых углов .
OA = OB = OC = OD — это все радиусы, поэтому мы можем утверждать, что OA = OB = 4 см. AOB равен 90°, так как AC и BD перпендикулярны.
Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .
Поскольку мы знаем две стороны прямоугольного треугольника AOB , нам нужно использовать теорему Пифагора, чтобы найти значение x (длину хорды AB ).
\[х^2=4^2+4^2\\ х^2=16+16\\ х^2=32\\ х=4\квадрат{2}см\]
Пример 6: полукруг
На приведенном ниже рисунке показан полукруг.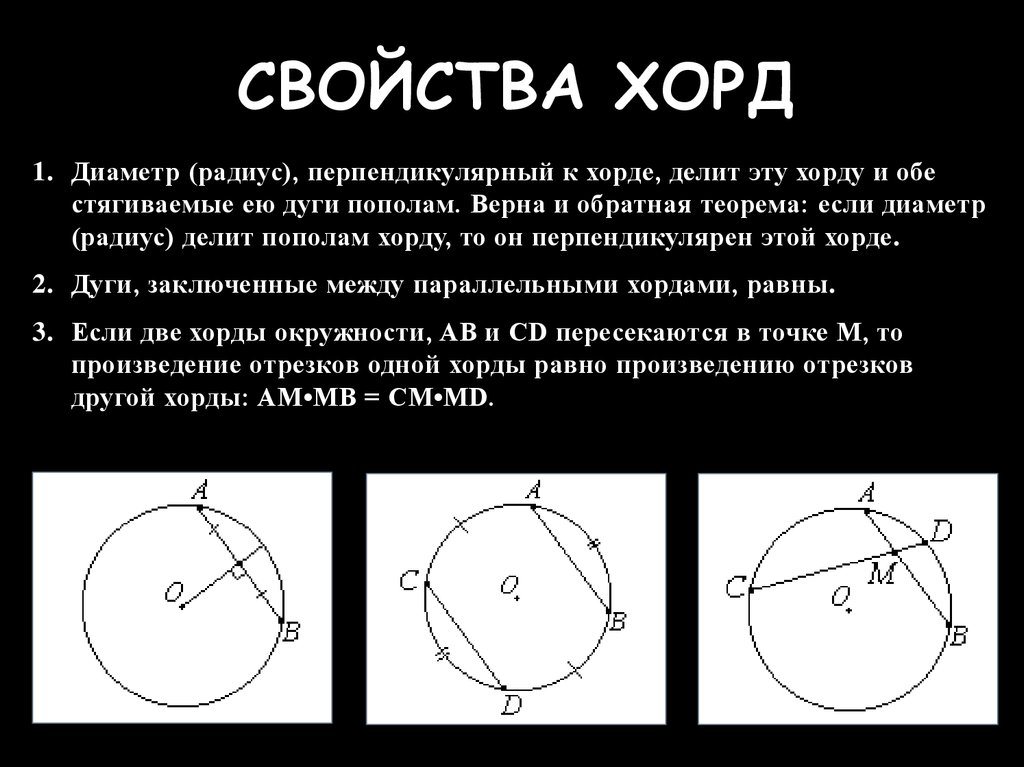
Линия BF является хордой, перпендикулярной диаметру. Вычислите длину диаметра AD.
Найдите ключевые части круга для соответствующей теоремы о круге .
Здесь имеем:
- AD диаметр
- BF — хорда, перпендикулярная AD .
- Угол BGE = 112°
- Линия DE = 3см
- Строка AD = x
Использование других фактов об углах для определения других необходимых углов .
Угол полуокружности равен 90° поэтому угол AEB = 90° . Углы на прямой составляют 180° , поэтому BGA = 180 — 112 = 68° . Поскольку угол ABG = 90°, угол BAG = 180 — (90 + 68) = 22°. Теперь мы знаем
Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .
Поскольку ADE — прямоугольный треугольник с DE = 3 см и DAE = 22°, мы можем использовать тригонометрию для вычисления стороны AD:
\[H=\frac{Opp}{\sin(\theta)}\\
H=\frac{3}{\sin(22)}\\
H=8.
0cm (1dp)\]
Распространенные заблуждения
- Недостаточная сторона теоремы Пифагора
Недостающая сторона вычисляется путем неправильного сложения квадрата гипотенузы и меньшей стороны, или путем вычитания квадрата меньшей стороны.
- Неверная тригонометрическая функция
Используется неверная тригонометрическая функция, поэтому вычисляемая сторона или угол неверны. Это также включает в себя обратные тригонометрические функции. 9{\circ} (BC перпендикулярна AF)
(1)
x=\frac{6.2}{\cos(55)}=10.8cm\quad(1dp)
(1)
2. (a) Окружность внизу имеет центр O. Диаметр BD перпендикулярен хорде AC в точке E. CE = 5,4 см, а угол AB = 8,1 см. Вычислите длину линии BE.
(b) Вычислите величину угла ABE. Запишите свой ответ с точностью до 1 знака после запятой.
(5 баллов) 9{2}}=8\sqrt{2}
(1)
AD = CD = 11 см
Масштабный коэффициент увеличения: 11\div8=1,375
(1)
AC=8\sqrt{2}\times{1,375}=11\sqrt{2}
(1)
11\кв{2}-8\кв{2}=3\кв{2} см
(1)
Учебный контрольный список
Теперь вы узнали, как:
- Применять и доказывать стандартные теоремы о окружностях, касающиеся углов, радиусов, касательных и хорд, и использовать их для доказательства связанных результатов
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.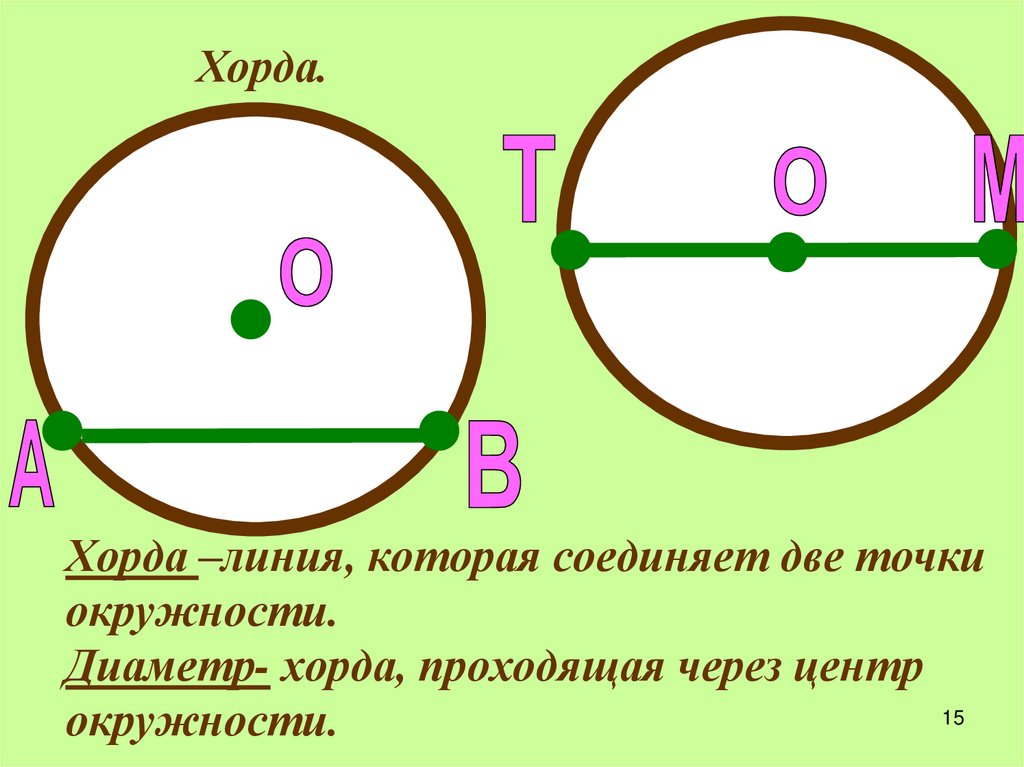
Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять или изменять ваши настройки файлов cookie. Принять
Является ли радиус хордой окружности?
Улучшить статью
Сохранить статью
Геометрия — это часть математики, изучающая свойства линий, тел, точек, измерений, углов и т. д. Ее также можно определить как визуальное изучение форм, размеров и т. д. Евклид — отец геометрии. . Некоторыми из основных типов геометрии являются алгебраическая геометрия, топология, неевклидова геометрия, комплексная геометрия, выпуклая геометрия, дифференциальная геометрия и т. д. Вот некоторые из важных геометрических терминов:
- Отрезок линии: Набор точек на линии, состоящей из двух концов, называется сегментом линии.
- Луч: Одна из частей линии состоит только из одной конечной точки.
- Линия : Прямая одномерная бесконечно тонкая фигура, которая имеет длину, но не имеет ширины/ширины.
- Координаты: Термин или адрес, который помогает найти точку в пространстве.
Что такое аккорд?
Когда две разные точки окружности соединяются отрезком, это называется хордой. Длина хорды измеряется в единицах длины, будь то сантиметр или метр.
Что такое радиус?
Радиус — это отрезок, соединяющий центр окружности с точкой окружности. Длина радиуса равна половине диаметра данной окружности. Символически радиус обозначается буквой «r».
Длина радиуса может быть определена, если диаметр известен по формуле
r = d/2
, так как диаметр в два раза больше радиуса.
Является ли радиус хордой окружности?
Ответ:
Как обсуждалось выше, любой отрезок, соединяющий две точки на окружности, называется хордой.
В то время как радиус соединяет центр окружности с точкой окружности. Следовательно, из определения обоих терминов мы можем утверждать, что радиус не является хордой.Примеры вопросов
Вопрос 1. Как можно рассчитать диаметр окружности, если известен радиус?
Ответ:
Диаметр окружности можно определить через радиус по данной формуле .
Вопрос 2. Является ли диаметр хордой?
Ответ:
Диаметр — это хорда, соединяющая две точки окружности, проходящие через ее центр. Она известна как самая длинная хорда окружности.
Вопрос 3. В чем разница между радиусом и радиусом?
Ответ:
Радиус — это форма единственного числа, которая используется для обозначения одного радиуса. В то время как радиусы — это форма множественного числа, которая указывает более одного радиуса в данном круге.
