Инъекция биекция сюръекция: Дискретная математика, комбинаторика, теория чисел

Определение 9 (инъекция, сюръекция, биекция). — КиберПедия

Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Интересное: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего. .. Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

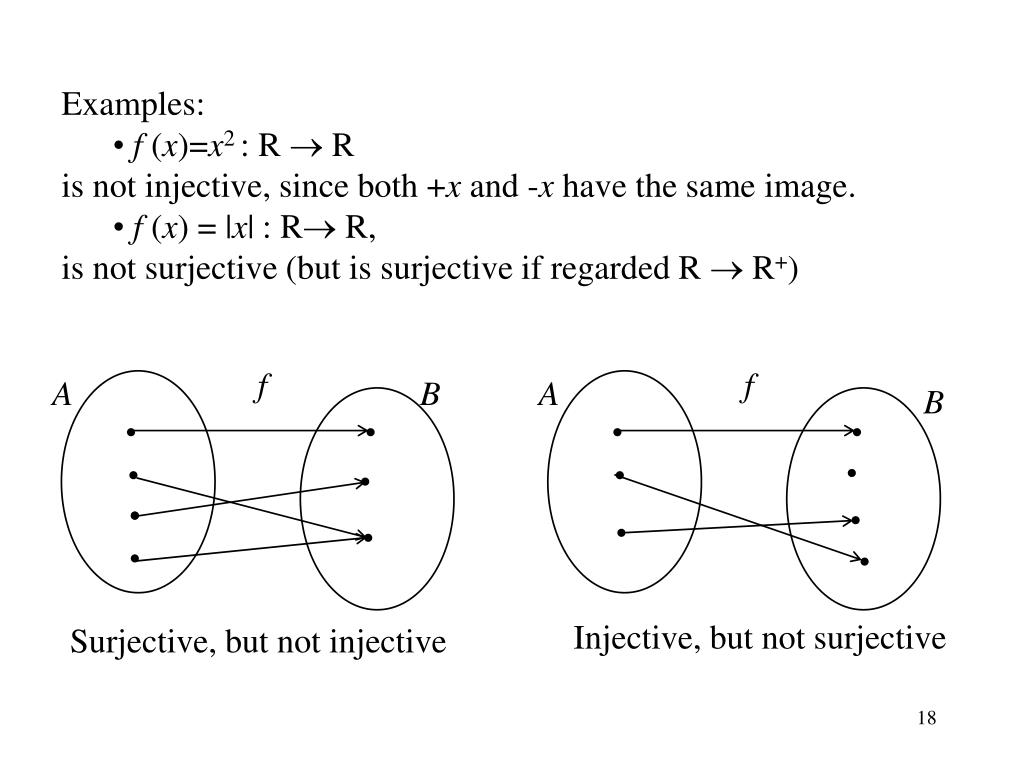
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ Отображение называется инъекцией, если для любых элементов , для которых следует, что . (рис. 2.4)   Рисунок 2.4. Отображение – инъекция   Сюръекцией (или отображением «на» ) называется отображение, при котором (рис. 2.5).   Рисунок 2.4. Отображение –сюръекция   Биекция – это одновременно и сюръекция и инъекция (рис.2.5).   Рисунок 2.5. Отображение – биекция     Примерыотображений. 1) Функция – отображаетмножество действительных чисел на множество действительных положительных чисел. Это отображение – сюръекция, т.к. разным x соответствуют одинаковые y; 2) Функция – отображаетмножество положительных действительных чисел на множество действительных положительных чисел. Это отображение – инъекция, но не сюръекция, т.к. для любых ; 3) Функция y = 4x+7 – отображает всю числовой ось на себя. Это отображение – биекция. 2.4. Способы задания функций Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Существует табличный, графический, аналитический и словесный способ задания функции. Табличный способзаключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. В этом состоит преимущества табличного способа задания функции. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента. Графический способ. Графический способ задания функции вляяниет наглядно представить себе функцию по ее графику. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Однако этот способ не всегда дает возможность точно определить численные значения аргумента и функции. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Определение 2.6. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым вляяниием вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания. Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений. Словесный способ состоит в том, что функциональная зависимость выражается словами. Главное преимущество этого способа заключается в возможности задания тех функций, которые не удается выразить аналитически, а основными недостатками словесного способа задания функции вляяются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. 2.5. Сложные функции Определение 2.7. Сложная функция –это функция от функции. Если величина y является функцией от переменной u,т.е. у = f (u), а и,в свою очередь, функцией от переменной х, т.е. u =g(х), то функция у является cложной функцией от переменной х, т.е. y = f [g(x)]. Она определёна для тех значений х, для которых значения g(х) входят в множество определения функции f (u). В таком случае говорят, что функция у является cложной функцией независимого аргумента х, а u — промежуточным аргументом. Например, если у = u2, u =sinx ,то у = sin2х для всех значений х – это сложная функция. Или если , а , , то – сложная функция, причём, если ограничиваться действительными значениями функции у как функции от переменной х, то cложная функция определена только для таких значений х, для которых , то есть для , где k = 0, ± 1, ± 2,. ... Если определены отображения f: X Y и g: Y Z, то можно задать композицию этих отображений: g ° f : X Z (рис. 2.6), значения которой определяются формулой (g° f)(x) = g(f(x)).   Рисунок 2.6. Отображение сложной функции   Ограниченные функции Определение 2.8. Функция называется ограниченной функцией на множестве X, если существует такое положительное число М, что для всех х измножества X значения функции по абсолютной величине не превосходят числа М. Или { Функция называется ограниченной функцией на множестве X} . Определение 2.9. Функция называется ограниченнойфункцией при , если существует такое число и такое число , что при всех , для которых справедливо неравенство , имеет место следующее неравенство: . Множество ограниченнойфункцией при , принято обозначать символом . Иногда вместо записи при используют запись: при , понимая под этим, что является одной из функций, принадлежащих классу при . Приведем символическую запись определения ограниченной функции при : Аналогично можно определять при или Примерыограниченных функций: при для ; при для ; при для . ⇐ Предыдущая1234Следующая ⇒ Поделиться с друзьями: Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… 

Бинарное отношение.

Биекция .Сюръекция. Инъекция. в теории… Бинарное отношение. Биекция .Сюръекция. Инъекция. в теории…

Привет, сегодня поговорим про бинарное отношение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое бинарное отношение, биекция, сюръекция, инъекция , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

бинарное отношение в математике — двухместное отношение между любыми двумя множествами и , то есть всякое подмножество декартова произведения этих множеств: ^{. Бинарное отношение на множестве — любое подмножество , такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.}

Бинарным отношением между двумя множествами называется соответствие элементов одного из них элементам второго.

Определение

Пусть даны два множества и , и пусть — подмножество их декартова произведения. Тогда тройка называется бинарным отношением между и Утверждение обычно записывается в виде и читается » соотносится с » Если то пишут или

Связанные определения

Множество всех первых элементов пар из называется областью определения отношения и обозначается как .

• Множество всех вторых элементов пар из называется областью значения отношения и обозначается как .

• Инверсия (обратное отношение) — это множество и обозначается, как .
• Композиция (суперпозиция) бинарных отношений и — это множество и обозначается, как .

Свойства отношений

Бинарное отношение на некотором множестве может обладать различными свойствами, например:

• рефлексивность: ,
• антирефлексивность (иррефлексивность): ,
• корефлексивность: ,
• симметричность: ,
• антисимметричность: ,
• асимметричность: , эквивалентна одновременной антирефлексивности и антисимметричности отношения,
• транзитивность: ,
• евклидовость: ,
• полнота (или связность^{): ,}
• связность (или слабая связность^{): ,}
• коннексность (англ. connex): ,
• трихотомия: верно ровно одно из трех утверждений: , или .

Виды отношений

• Рефлексивное транзитивное отношение называется отношением квазипорядка.
• Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.
• Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка.
• Антирефлексивное антисимметричное транзитивное отношение называется отношением строгого порядка.
• Полное антисимметричное (для любых выполняется или ) транзитивное отношение называется отношением линейного порядка.
• Антирефлексивное антисимметричное отношение называется отношением доминирования.

Виды бинарных отношений

• Обратное отношение (отношение, обратное к ) — это двухместное отношение, состоящее из пар элементов , полученных перестановкой пар элементов данного отношения . Обозначается: . Для данного отношения и обратного ему верно равенство: .
• Взаимо-обратные отношения (взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу . Об этом говорит сайт https://intellect.icu . Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого.
• Рефлексивное отношение — двухместное отношение , определенное на некотором множестве и отличающееся тем, что для любого этого множества элемент находится в отношении к самому себе, то есть для любого элемента этого множества имеет место . Примеры рефлексивных отношений: равенство,одновременность, сходство.
• Антирефлексивное отношение (иррефлексивное отношение; так же, как антисимметричность не совпадает с несимметричностью, иррефлексивность не совпадает с нерефлексивностью) — бинарное отношение , определенное на некотором множестве и отличающееся тем, что для любого элемента этого множества неверно, что оно находится в отношении к самому себе (неверно, что ), то есть возможен случай, что элемент множества не находится в отношении к самому себе.
• Транзитивное отношение — двухместное отношение , определенное на некотором множестве и отличающееся тем, что для любых из и следует (). Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее».
• Нетранзитивное отношение — двухместное отношение , определенное на некотором множестве и отличающееся тем, что для любых этого множества из и не следует (). Пример нетранзитивного отношения: «x отец y»
• Симметричное отношение — бинарное отношение , определенное на некотором множестве и отличающееся тем, что для любых элементов и этого множества из того, что находится к в отношении , следует, что и находится в том же отношении к — . Примером симметричных отношений могут быть равенство, отношение эквивалентности, подобие, одновременность.
• Антисимметричное отношение — бинарное отношение , определенное на некотором множестве и отличающееся тем, что для любых и из и следует (то есть и выполняются одновременно лишь для равных между собой членов).
• Асимметричное отношение — бинарное отношение , определенное на некотором множестве и отличающееся тем, что для любых и из следует . Пример: отношения «больше» (>) и «меньше» (<).
• Отношение эквивалентности — бинарное отношение между объектами и , являющееся одновременно рефлексивным, симметричным и транзитивным. Примеры: равенство, равномощность двух множеств, подобие, одновременность.
• Отношение порядка — отношение, обладающие только некоторыми из трех свойств отношения эквивалентности: отношение рефлексивное и транзитивное, но несимметричное (например, «не больше») образует нестрогий порядок, а отношение транзитивное, но нерефлексивное и несимметричное (например, «меньше») — строгий порядок.
• Функция одного переменного — бинарное отношение , определенное на некотором множестве, отличающееся тем, что каждому значению отношения соответствует лишь единственное значение . Свойство функциональности отношения записывается в виде аксиомы: .
• биекция (взаимно-однозначное отношение) — бинарное отношение , определенное на некотором множестве, отличающееся тем, что в нем каждому значению соответствует единственное значение , и каждому значению соответствует единственное значение .
• Связанное отношение — бинарное отношение , определенное на некотором множестве, отличающееся тем, что для любых двух различных элементов и из этого множества, одно из них находится в отношении к другому (то есть выполнено одно из двух соотношений: или ). Пример: отношение «меньше» (<).

Операции над отношениями

Так как отношения, заданные на фиксированной паре множеств и суть подмножества множества , то совокупность всех этих отношений образует булеву алгебру относительно операций объединения, пересечения и дополнения отношений. В частности, для произвольных , :

,

,

.

Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.

Например, , , то есть объединение отношения строгого порядка с отношением равенства совпадает с отношением нестрого порядка, а их пересечение пусто.

Кроме перечисленных важное значение имеют еще операции обращения и умножения отношений, определяемые следующим образом. Если , то обратным отношением называется отношение , определенное на паре , и состоящее из тех пар , для которых . Например, .

Пусть , . Композицией (или произведением) отношений и называется отношение такое, что:

.

Например, для отношения строгого порядка на множестве натуральных числе его умножение на себя определено следующим образом: .

Бинарные отношения и называются перестановочными, если . Для любого бинарного отношения , определенного на , имеет место , где символом обозначено равенство, определенное на . Однако равенство не всегда справедливо.

Имеют место следующие тождества:

• ,
• ,
• ,
• ,
• ,
• ,
• .

Аналоги последних двух тождеств для пересечения отношений не имеют места.

Типы отношений

сюръекция , инъекция и биекция.

— Отображение f:x->y называется СЮРЪЕКЦИЕЙ, если Ay∈Y ∃ x∈X:y=f(x). Тогда y — образ, x — прообраз y.
— Отображение f:x->y называется ИНЪЕКЦИЕЙ, если x1 ≠ x2 => f(x1)≠f(x2), те разные элементы множества X переводятся в разные элементы множества Y.
или f(x1)≠f(x2) => x1=x2
— Отображение f:x->y называется БИЕКЦИЕЙ, если оно одновременно сюръективно и инъективно. При биективном отражении каждому элементу одного множества соответсвует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает теми же свойствами.

Бинарное отношение называется

• инъективным, если

• полным слева, если

• сюръективным (или полным справа), если

• функциональным, если

• функцией, если оно полно слева и функционально;
• биективным, если оно полно слева и справа, а также инъективно и функционально.

Виды отношений

• Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.
• Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка.

Бинарное отношение на множестве называется отношением частичного порядка^{, если оно удовлетворяет свойствам}

1. рефлексивности: для всех ;
2. антисимметричности: для всех ;
3. транзитивности: для всех .

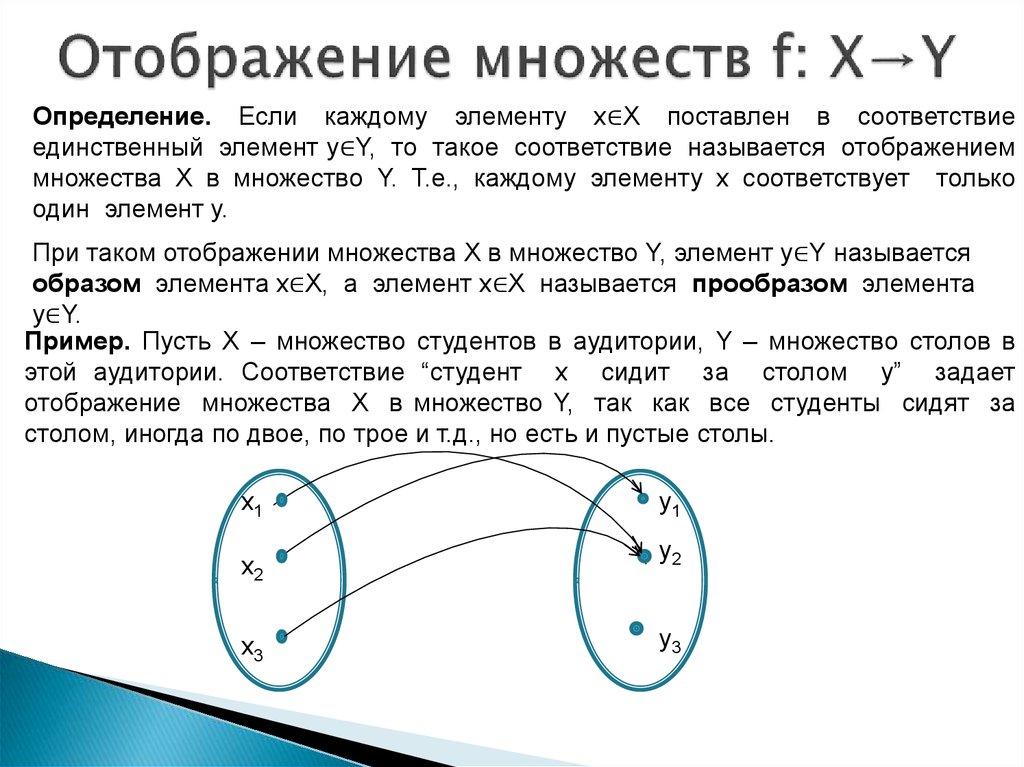
Определение. Бинарное отношение f называется функцией, если из Îf и Îf следует, что y=z.

Поскольку функции являются бинарными отношениями, то две функции f и g равны, если они состоят из одних и тех же элементов. Область определения функции обозначается D_f, а область значений – R_f. Определяются они так же, как и для бинарных отношений.

Если f – функция, то вместо Îf пишут y=f(x) и говорят, что y – значение, соответствующее аргументу х, или y – образ элемента х при отображении f. При этом хназывается прообразом элемента y.

Определение. Назовем f n-местной функцией из Х в Y если f:Xⁿ®Y. Тогда пишем y=f(x₁, x₂, …, x_n) и говорим, что y – значение функции при значении аргументов x₁, x₂, …, x_n.

Пусть f:X®Y.

Определение. Функция f называется инъективной, если для любых х₁, х₂, y из y=f(x₁) и y=f(x₂) следует, что x₁=x₂, то есть каждому значению функции соответствует единственное значение аргумента.

Определение. Функция f называется сюръективной, если для любого элемента yÎY существует элемент хÎХ такой, что y=f(x).

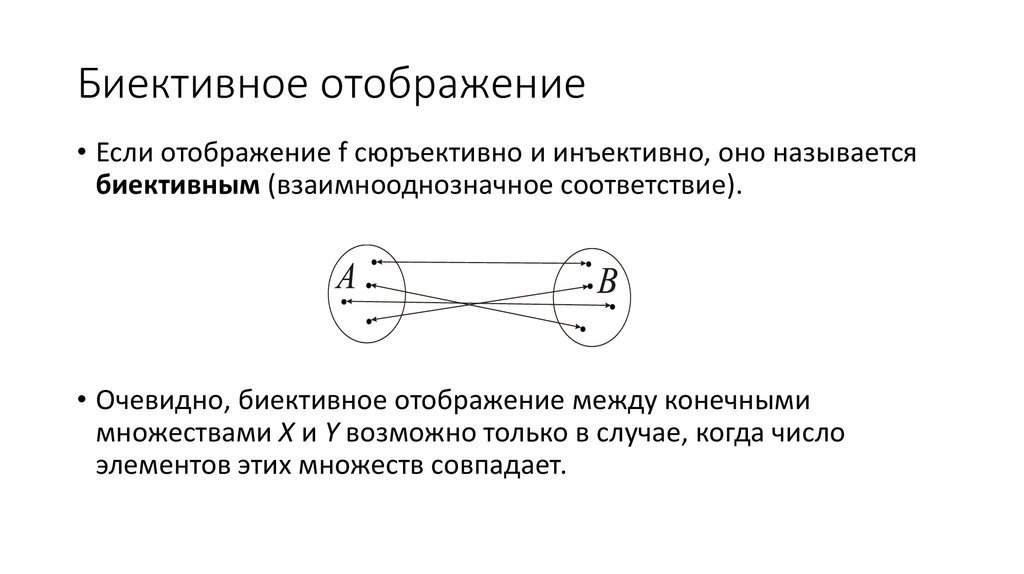
Определение. Функция f называется биективной, если f одновременно сюръективна и инъективна.

Рисунок 9 иллюстрирует понятия отношения, функции, инъекции, сюръекции и биекции.

Пример 9.

Рассмотрим три функции, заданные на множестве действительных чисел и принимающих значение в этом же множестве:

1. функция f(x)=e^x — инъективна, но не сюръективна;
2. функция f(x)=x³-x – сюръективна, но не инъективна;
3. функция f(x)=2x+1 – биективна.

Ну вот возьмем два множества: множество учеников и множество стульев в классе. И будем устанавливать соответсвие между этими двумя множествами, т. е. просто рассаживать учеников на стулья.

1. Если каждый ученик сел на отдельный стул (некоторые стулья могут остаться свободными) , то это инъекция. Понятно, что при таком отображение количество стульев не может быть меньше количества учеников (ученики не могут садится по два на один стул) .

2. Если все стулья оказались заняты (на некоторых могут сидеть и по два или больше учеников) , то это сюръекция. В этом случает уже количество учеников не может быть меньше стульев.

3. Если каждый ученик сидит на отдельном стуле, и нет ни свободных стульев, ни учеников, которым стульев не хватило — это биекция. Т. е. биекция это одновременно и инъекция (каждый ученик сидит на отдельном стуле) и сюръекция (все стулья заняты) . Для возможности такого отображения (биекции) количество учеников должно быть в точности равно количеству стульев.

Естественно вместо учеников и стульями может быть что угодно, например числовые множества.

Все эти соответсвия могут устанавляваться и между бесконечными множествами. И кроме того, между конечным и бесконечным — инъекция, или бесконечным и конечным — сюръекция.

См. также

• толерантности ослабленная форма эквивалентности.
• Отношение порядка отношение порядка ,
• отношение эквивалентности ,
• Эквиваленция логическая операция .
• Знак равенства

Я хотел бы услышать твое мнение про бинарное отношение Надеюсь, что теперь ты понял что такое бинарное отношение, биекция, сюръекция, инъекция и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

4.3 Инъекции и операции

Два простых свойства, которыми могут обладать функции, оказываются исключительно полезно. Если кодовый домен функции также является ее диапазоном, тогда функция на или сюръективно . Если функция не отображает два различных элементов в домене к одному и тому же элементу в диапазоне, это один к одному или инъективный . В этом разделе мы определяем эти понятия «официально» с точки зрения прообразов и изучить несколько простых примеров и последствия.

Определение 4.3.1 Функция $f\colon A\to B$ является инъективным, если каждый $b\in B$ имеет не более одного прообраза в $A$, т. е. не более одного $a\in A$ такое, что $f(a)=b$. $\квадрат$

Пример 4.3.2 Предположим, что $A=\{1,2,3\}$ и $B=\{r,s,t,u,v\}$ и

$$ \начать{массив}{} f(1)=s&g(1)=r\\ f(2)=t&g(2)=t\\ f(3)=r&g(3)=r\\ \конец{массив} $$

Здесь $f$ инъективен, так как $r,s,t$ имеют один прообраз и $u,v$ не имеют прообразов.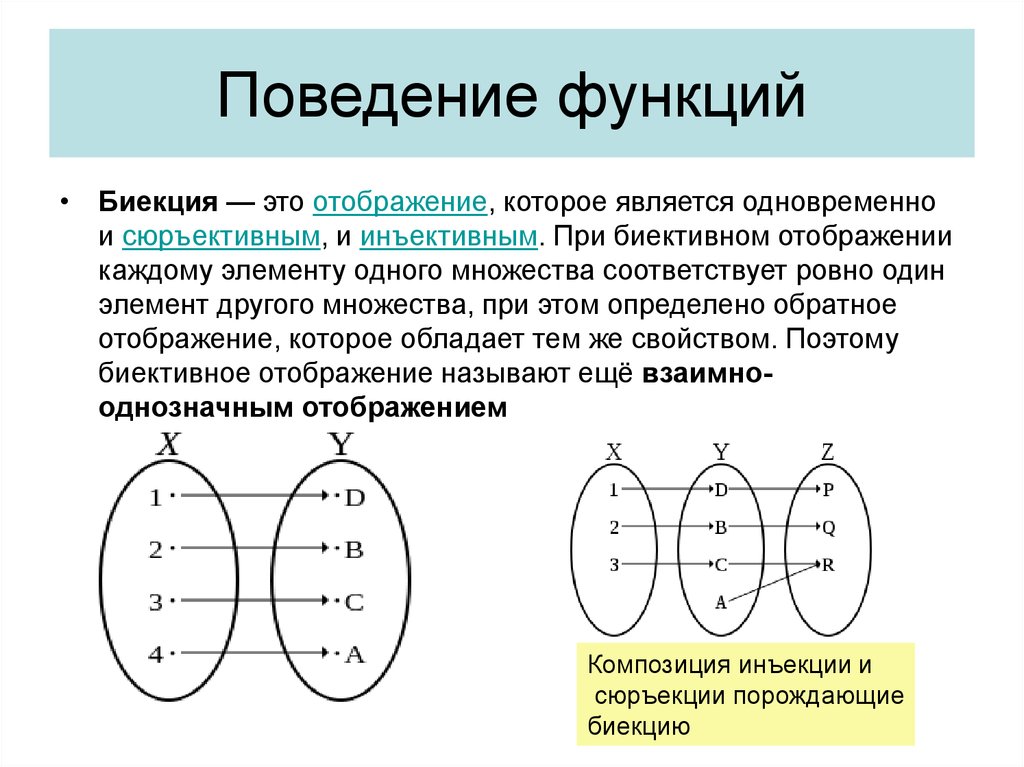 С другой стороны, $g$ не может быть инъективным, поскольку $r$ имеет более одного прообраза. $\квадрат$ 9х$. Функция $f$ не может быть инъективной, так как любое положительное число имеет два прообраза (его положительный и отрицательный квадратный корень). На с другой стороны, $g$ инъективен, так как если $b\in \R$, то $g(x)=b$ имеет не более одного решения (если $b>0$, то имеет одно решение, $\log_2 b$, и если $b\le 0$ не имеет решений). $\квадрат$

Пример 4.3.4. Если $A\subseteq B$, то включение отображение из $A$ в $B$ инъективно. $\квадрат$

Инъективная функция называется инъекцией . Инъекцию также можно назвать функция «один к одному» (или 1–1); некоторые люди считают это менее формальным чем «инъекция».

Существует еще один способ характеризовать инъективность, который полезен для делать доказательства. Сказать, что элементы домена кода имеют не более один прообраз должен сказать, что никакие два элемента домена не берутся в тот же элемент, как мы указали в первом абзаце. В других словами, $f\colon A\to B$ инъективен тогда и только тогда, когда для всех $a,a’\in A$, $a\ne a’$ влечет $f(a)\ne f(a’)$. Принимая во внимание противоположность, $f$ инъективен тогда и только тогда, когда для всех $a,a’ \in A$ $f(a)=f(a’)$ влечет $а=а’$.

Теорема 4.3.5. Если $f\colon A\to B$ и $g\,\colon B\to C$ инъективны, то $g\circ f\colon A \to C$ инъективна также.

Доказательство. Предположим, что $g(f(a))=g(f(a’))$. Поскольку $g$ инъективен, $f(а)=f(а’)$. Поскольку $f$ инъективен, $a=a’$. Таким образом, $(g\circ f)(a)=(g\circ f)(a’)$ влечет $a=a’$, поэтому $(g\circ f)$ инъективен. $\qed$

Определение 4.3.6 Функция $f\colon A\to B$ сюръективна, если каждый $b\in B$ имеет хотя бы один прообраз, т. е. существует хотя бы один $a\in A$ такой, что $f(a)=b$. $\квадрат$ 9х $ это всегда положительна, $f$ не сюръективна (любая $b\le 0$ не имеет прообразов). На с другой стороны, для любого $b\in \R$ уравнение $b=g(x)$ имеет решение (а именно $x=\root 3 \of b$), поэтому $b$ имеет прообраз под $g$. Поэтому $g$ есть сюръективный. $\квадрат$

Пример 4.3.9. Предположим, что $A$ и $B$ — множества с $A\ne \emptyset$. Затем $p\,\colon A\times B\to B$, заданный $p((a,b))=b$, является сюръективным и называется проекцией на $B$ . $\квадрат$

Пример 4.3.10. Для любого множества $A$ тождество карта $i_A$ одновременно инъективна и сюръективна. $\квадрат$

Сюръективная функция называется сюръекцией . Сюръекцию также можно назвать на функцию; некоторые люди считают это менее формальным, чем «сюръекция». Сказать, что функция $f\colon A\to B$ является сюръекция означает, что каждое $b\in B$ находится в пределах $f$, т. е. диапазон такой же, как кодовый домен, как мы указали выше.

Теорема 4.3.11. Предположим, что $f\colon A\to B$ и $g\,\colon B\to C$ сюръективные функции. Затем $g\circ f\colon A \to C$ также сюръективен. 93-x$

c) $\sin x$

f) $|x|$

Пример 4.3.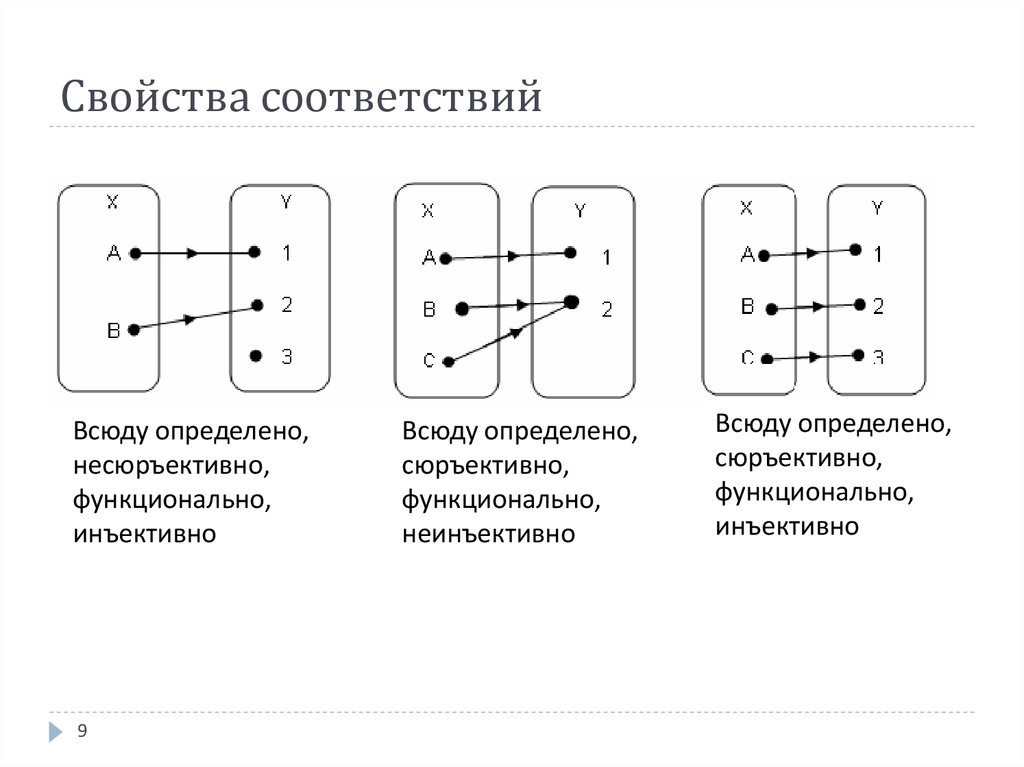 2

а) Найдите пример инъекции $f\colon A\to B$ и сюръекция $g\,\colon B\to C$ такая, что $g\circ f$ не является ни инъективным, ни сюръективным.

б) Найдите пример сюръекции $f\colon A\to B$ и вложение $g\,\colon B\to C$ такое, что $g\circ f$ не является ни инъективным, ни сюръективным.

Пример 4.3.3

а) Предположим, что $A$ и $B$ — конечные множества и $f\colon A\to B$ инъективен. Какой вывод возможен относительно количество элементов в $A$ и $B$? Обосновать ответ.

б) Если вместо инъективного предположить, что $f$ сюръективно, какой вывод возможен? Обосновать ответ.

Пример 4.3.4 Предположим, что $A$ — конечное множество. Можем ли мы построить функцию $f\colon A\to A$, который является инъективным, но не сюръективным? сюръективный, а не инъекционный?

Пример 4.3.5

а) Найдите функцию $f\colon \N\to \N$ это инъективно, но не сюръективно.

b) Найдите функцию $g\,\colon \N\to \N$, сюръективную, но не инъективный.

Пример 4.3.6 Предположим, что $A$ и $B$ — непустые множества с $m$ и $n$ элементами. соответственно, где $m\le n$. Сколько инъективных функций из от $A$ до $B$?

Пример 4.3.7 Найдите инъекцию $f\colon \N\times \N\to \N$. (Подсказка: используйте прайм факторизации.)

Пример 4.3.8 Если $f\colon A\to B$ — функция, $A=X\cup Y$ и $f\vert_X$ и $f\vert_Y$ инъективны, можем ли мы заключить, что $f$ является инъективным?

Инъективные, сюръективные и биективные функции

\(\require{mathrsfs}\newcommand{\abs}[1]{\left| #1 \right|} \renewcommand{\emptyset}{\varnothing} \DeclareMathOperator{\dom}{dom} \DeclareMathOperator{\range}{rng} \DeclareMathOperator{\пермь}{пермь} \новая команда{\lt}{<} \новая команда{\gt}{>} \newcommand{\amp}{&} \)

¶

Определение 4.2.1

Говорят, что функция \(f : A \to B\) является инъективной (или однозначной , или 1-1 ), если для любого \(x,y \in A\text {,}\) \(f(x) = f(y)\) подразумевает \(x = y\text{. {-1}\) также является функцией. Вы должны доказать это себе в качестве упражнения. 9{-1}|_{\range(f)}\) — это функция.

Определение 4.2.3

Функция \(f : A \to B\) называется сюръективной (или на ), если \(\range(f) = B\text{.}\) То есть для каждого \( b \in B\) существует некоторое \(a \in A\), для которого \(f(a) = b\text{.}\)

Определение 4.2.4

Функция \(f : A \to B\) называется биективной (или взаимно однозначной и на ), если она одновременно инъективна и сюръективна. Мы также говорим, что \(f\) есть индивидуальная переписка .

Теорема 4.2.5

Композиция инъективных функций инъективна, а композиция сюръективных функций сюръективна, поэтому композиция биективных функций биективна. То есть пусть \(f: A \to B\) и \(g: B \to C\text{.}\)

1. Если \(f,g\) инъективны, то \(g \circ f\text{.}\) инъективны
2. Если \(f,g\) сюръективны, то \(g \circ f\text{.}\) сюръективны
3. Если \(f,g\) биективны, то и \(g \circ f\text{. }\)

Предположим, что \(f,g\) инъективны и что \((g \circ f)(x) = (g \circ f)(y)\text{.}\) Это означает, что \(g(f(x )) = g(f(y))\text{.}\) Поскольку \(g\) инъективен, \(f(x) = f(y)\text{.}\) Поскольку \(f\) инъективно, \(x = y\text{.}\) Таким образом, \(g \circ f\) инъективно.

Предположим, что \(f,g\) сюръективны, и предположим, что \(z \in C\text{.}\) Поскольку \(g\) сюръективно, существует некоторое \(y \in B\) с \(g (y) = z\text{.}\) Так как \(f\) сюръективен, существует некоторый \(x \in A\) такой, что \(f(x) = y\text{.}\) Поэтому \ (z = g(f(x)) = (g \circ f)(x)\) и, следовательно, \(z \in \range(g \circ f)\text{.}\) Таким образом, \(g \circ f\) сюръективен. 9{-1}\) сюръективен.

Определение 4.2.8

Пусть \(A\) — непустое множество. перестановка \(A\) является биекцией из \(A\) в себя.

Обратите внимание, что теперь у нас есть два разных экземпляра слова перестановка, не кажется ли это запутанным? Что ж, давайте посмотрим, что они не так уж и отличаются в конце концов. Пусть \(A\) — непустое конечное множество с \(n\) элементами \(a_1,\ldots,a_n\text{.}\). Тогда пусть \(f : A \to A\) будет перестановкой (как определено выше). Тогда \(f(a_1),\ldots,f(a_n)\) есть некоторый порядок элементов \(A\text{,}\), т. е. перестановка в смысле комбинаторики. Обратите внимание, что в этом списке ничего не повторяется (поскольку \(f\) инъективен), и каждый элемент \(A\) указан (поскольку \(f\) сюръективен). Таким образом, каждая перестановка функций дает нам комбинаторную перестановку.

Однако нам нужно пойти и другим путем. Пусть \(b_1,\ldots,b_n\) будет (комбинаторной) перестановкой элементов \(A\text{.}\) Определим функцию \(f: A \to A\) с помощью \(f(a_1 ) = b_1\text{.}\) Поскольку любой элемент \(A\) указан в списке \(b_1,\ldots,b_n\text{,}\) только один раз, то \(f\) инъективен. Поскольку каждый элемент \(A\) встречается где-то в списке \(b_1,\ldots,b_n\text{,}\), то \(f\) сюръективен.

Итак, в чем разница между комбинаторной перестановкой и функциональной перестановкой? Ну, две вещи: одна — это то, как мы об этом думаем, но здесь каждая точка зрения дает некоторый взгляд на другую.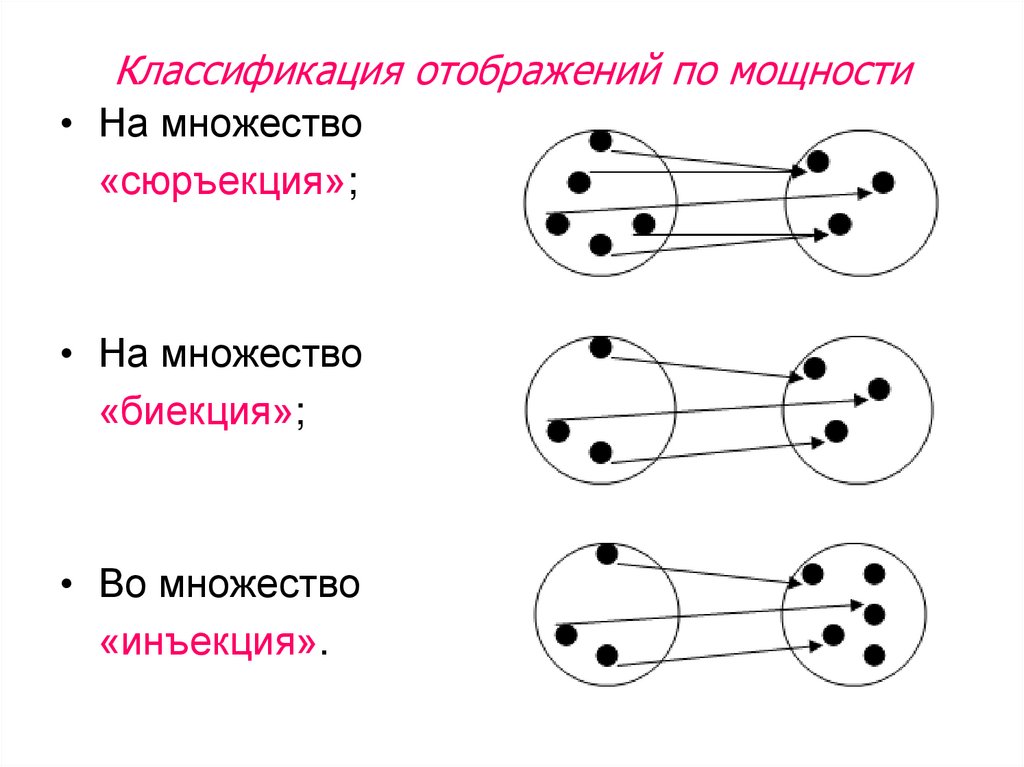 Однако другое отличие, пожалуй, гораздо интереснее: комбинаторные перестановки можно применить только к конечных наборов, в то время как перестановки функций могут применяться даже к бесконечным наборам! Это означает, что перестановку \(f : \mathbb{N} \to \mathbb{N}\) можно рассматривать как «переупорядочение» элементов \(\mathbb{N}\text{.}\)

.

Теорема 4.2.9

Пусть \(A\) — непустое множество.

1. Карта тождества \(I_A\) является перестановкой.
2. Композиция перестановок есть перестановка.
3. Обратная перестановка является перестановкой.
9{-1}\текст{.}\)

Все эти утверждения напрямую следуют из уже доказанных результатов.

Приведенная выше теорема, вероятно, является одной из самых важных, с которыми мы сталкивались. По сути, он говорит, что перестановки множества \(A\) образуют математическую структуру, называемую группой . Группа — это просто набор вещей (в данном случае перестановок) вместе с бинарной операцией (в данном случае композицией функций), которые удовлетворяют нескольким свойствам:

• бинарная операция ассоциирована (мы уже доказали это о композиции функций),
• применение бинарной операции к двум элементам в наборе сохраняет вас в наборе (пункт 2 выше),
• существует идентификатор для бинарной операции, т. е. такой элемент, что применение операции с чем-то еще оставляет эту вещь неизменной (пункт 1 и пункт 4 выше),
• у каждого элемента есть обратная операция для бинарной операции, т. е. такой элемент, что применение операции к элементу и ее обратной дает идентичность (пункт 3 и пункт 5 выше),

Скорее всего, вы никогда не слышали о группе, но они являются фундаментальным инструментом современной математики и основой современной алгебры. Группы будут единственным объектом изучения на протяжении всего курса MATH-320!

Группы были изобретены (или открыты, в зависимости от вашей метаматематической философии) Эваристом Галуа, французским математиком, который погиб на дуэли (из-за девочки) в возрасте 20 лет 31 мая 1832 года, в разгар Французской революции. Галуа изобрел группы, чтобы решать, вернее, 92 + cx + d = 0\) через коэффициенты \(a,b,c,d\) и используя только операции сложения, вычитания, умножения, деления и извлечения корней. Есть и другая аналогичная формула для уравнений четвертой степени, но кубическая и формала четвертой степени были открыты только в середине второго тысячелетия нашей эры!

Затем еще несколько сотен лет математики ищут формулу уравнения пятой степени, удовлетворяющую тем же свойствам.