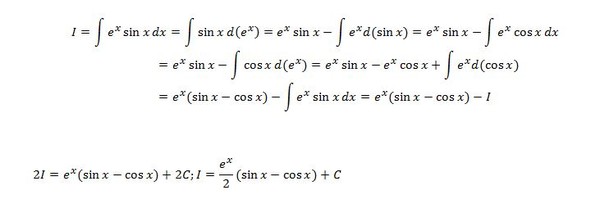Интеграл экспоненты в степени: Интеграл от экспоненты в степени, примеры решений

2

Интегралы от экспоненты, умноженной на многочлен

Общее правило: за   всегда обозначается многочлен

Пример 5

Найти неопределенный интеграл.

Решение:

Используя знакомый алгоритм, интегрируем по частям:

Если возникли трудности с интегралом  , то следует вернуться к статье Метод замены переменной в неопределенном интеграле.

Единственное, что еще можно сделать, это «причесать» ответ:

Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом   или даже 

То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.

Пример 6

Найти неопределенный интеграл.

Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что   – сложная функция.

Больше про экспоненту рассказывать особо нечего. Могу только добавить, что экспонента и натуральный логарифм взаимно-обратные функции, это я к теме занимательных графиков высшей математики =) Стоп-стоп, не волнуемся, лектор трезв.

Интегралы от тригонометрических функций, умноженных на многочлен

Общее правило: за   всегда обозначается многочлен

Пример 7

Найти неопределенный интеграл.

Интегрируем по частям:

Хммм, …и комментировать нечего.

Пример 8

Найти неопределенный интеграл

Это пример для самостоятельного решения

Пример 9

Найти неопределенный интеграл

Еще один пример с дробью. Как и в двух предыдущих примерах за   обозначается многочлен.

Интегрируем по частям:

Если возникли трудности или недопонимание с нахождением интеграла  , то рекомендую посетить урок Интегралы от тригонометрических функций.

Пример 10

Найти неопределенный интеграл

Это пример для самостоятельного решения.

Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.

Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….

Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен

Общее правило: за   всегда обозначается обратная тригонометрическая функция.

Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»

Пример 11

Найти неопределенный интеграл.

Решаем.

Интегрируем по частям:

Интеграл   найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример мы разбирали на уроке 

Метод замены переменной в неопределенном интеграле.

Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.

Пример 12

Найти неопределенный интеграл.

Это пример для самостоятельного решения

И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для маньяков желающих лучше разобраться в методе интегрирования по частям. Пример, пожалуй, будет тоже для самостоятельного решения, поскольку меня немного утомил тот логарифм в квадрате.

Пример 13

Найти неопределенный интеграл.

Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.

Решения и ответы:

Пример 3: Решение:

Пример 4: Решение:

Интегрируем по частям:

Пример 6: Решение:

Дважды интегрируем по частям:

Пример 8: Решение:

Интегрируем по частям:

Пример 10: Решение:

Интегрируем по частям:

Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла .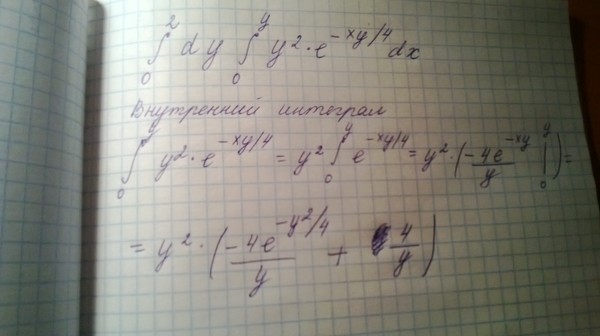 Её можно было использовать и сразу: , а  потом интегрировать по частям.

Похожим способом также решаются интегралы вроде ,  – в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул. Более подробно – см. Интегралы от тригонометрических функций.

Пример 12:

Интегрируем по частям:

Пример 13:

Интегрируем по частям:

Примечание: Если возникли трудности с интегралом

,

то следует посетить урок Интегрирование некоторых дробей.

Глава 8. Неполная гамма и родственные функции

Содержимое

1. §8. 19(i) Определение и интегральные представления
2. §8.19(ii) Графика
3. §8.19(iii) Специальные значения
4. §8.19(iv) Расширения серии
5. §8.19(v) Рекуррентное соотношение и производные
6. §8.19(vi) Связь с вырожденной гипергеометрической функцией
7. §8.19(vii) Непрерывная дробь
8. §8.19(viii) Аналитическое продолжение
9. §8.19(ix) Неравенства
10. §8.19(x) Интегралы
11. §8.19(xi) Дальнейшие обобщения

§8.19(i) Определение и интегральные представления

Для p,z∈ℂ

8.19.1		Ep⁡(z)=zp−1⁢Γ⁡(1−p,z).

Большинство свойств Ep⁡(z) непосредственно следуют из свойств Г⁡(а,г). Подробное описание E1⁡(z) см. Глава 6.

8.19.2		Ep⁡(z)=zp−1⁢∫z∞e−ttp⁢dt.

Когда путь интегрирования исключает начало координат и не пересекает отрицательная действительная ось (8. 19.2) определяет главное значение Ep⁡(z) и , если не указано иное в руководитель DLMF значения предполагаются.

Другие интегральные представления

8.19.3		Эп⁡(г)	=∫1∞e−z⁢ttp⁢dt,
|ph⁡z|<12⁢π,
8.19.4		Эп⁡(г)	=zp−1⁢e−zΓ⁡(p)⁢∫0∞tp−1⁢e−z⁢t1+t⁢dt,
|ph⁡z|<12⁢π, ℜ⁡p>0.

Интегральные представления типа Меллина–Барнса для Ep⁡(z) следуют непосредственно из (8.6.11), (8.6.12) и (8.19.1).

§8.19(ii) Графика

Рисунок 8.19.1: Ep⁡(x), 0≤x≤3, 0≤p≤8. Увеличить 3D Помощь

На рисунках 8.19.2–8.19.5 высота соответствует абсолютное значение функции и цвет фазы. См. раздел Цветовая карта.

Рисунок 8.19.2: E12⁡(x+i⁢y), −4≤x≤4, −4≤y≤4. Основное значение. Имеется ветвь, срезанная вдоль отрицательной действительной оси. Увеличить 3D Помощь Рисунок 8.19.3: E1⁡(x+i⁢y), −4≤x≤4, −4≤y≤4. Основное значение. Имеется ветвь, срезанная вдоль отрицательной действительной оси. Увеличить 3D Помощь Рисунок 8.19.4: E32⁡(x+i⁢y), −3≤x≤3, −3≤y≤3. Основное значение. Имеется ветвь, срезанная вдоль отрицательной действительной оси. Увеличить 3D Помощь Рисунок 8.19.5: E2⁡(x+i⁢y), −3≤x≤3, −3≤y≤3. Основное значение. Имеется ветвь, срезанная вдоль отрицательной действительной оси. Увеличить 3D Помощь

§8.19(iii) Специальные значения

8.19.5		E0⁡(z)=z−1⁢e−z,
г≠0,

8.19.6		Ер⁡(0)=1р-1,
ℜ⁡p>1,

8. 19.7		En⁡(z)=(−z)n−1(n−1)!⁢E1⁡(z)+e−z(n−1)!⁢∑k=0n−2(n−k−2) !⁢(−z)k,
n=2,3,….

§8.19(iv) Расширения серии

Для n=1,2,3,…,

8.19.8		En⁡(z)=(−z)n−1(n−1)!⁢(ψ⁡(n)−ln⁡z)−∑k=0k≠n−1∞(−z)kk!⁢( 1−n+k),

и

8.19.9		En⁡(z)=(−1)n⁢zn−1(n−1)!⁢ln⁡z+e−z(n−1)!⁢∑k=1n−1(−z)k−1 ⁢Γ⁡(n−k)+e−z⁢(−z)n−1(n−1)!⁢∑k=0∞zkk!⁢ψ⁡(k+1),

с |ph⁡z|≤π в обоих уравнениях. Для ψ⁡(x) см. §5.2(i).

Когда p∈ℂ

8.19.10		Ep⁡(z)=zp−1⁢Γ⁡(1−p)−∑k=0∞(−z)kk!⁢(1−p+k),

8. 19.11		Ep⁡(z)=Γ⁡(1−p)⁢(zp−1−e−z⁢∑k=0∞zkΓ⁡(2−p+k)),

снова с |ph⁡z|≤π в обоих уравнениях. Правые стороны заменены их предельными формами при p=1,2,3,….

§8.19(v) Рекуррентное соотношение и производные

8.19.12		p⁢Ep+1⁡(z)+z⁢Ep⁡(z)=e−z.

8.19.13		ddz⁡Ep⁡(z)	=-Ep-1⁡(z),
8.19.14		ddz⁡(ez⁢Ep⁡(z))	= ez⁢Ep⁡(z)⁢(1+p−1z)−1z.

p-Производные

Для j=1,2,3,…,

8.19.15		∂j⁡Ep⁡(z)∂⁡pj=(−1)j⁢∫1∞(ln⁡t)j⁢t−p⁢e−z⁢t⁢dt,
ℜ⁡z>0.

Свойства и числовые таблицы см. в Milgram (1985) , а также (при p=1) Маклеод (2002b) .

§8.19(vi) Связь с вырожденной гипергеометрической функцией

8.19.16		Ep⁡(z)=zp−1⁢e−z⁢U⁡(p,p,z).

Для U⁡(a,b,z) см. §13.2(i).

§8.19(vii) Непрерывная дробь

8.19.17		Ep⁡(z)=e−z⁢(1z+p1+1z+p+11+2z+⋯),
|ph⁡z|<π.

См. также Cuyt et al. (2008, стр. 277–285) .

§8.19(viii) Аналитическое продолжение

Общая функция Ep⁡(z) достигается расширением пути в (8,19.2) поперек отрицательной действительной оси. Если p не является неположительным целое число, Ep⁡(z) имеет точку ветвления в точке z=0. Для z ≠ 0 каждый ветвь Ep⁡(z) является целой функцией p.

8.19.18		Ep⁡(z⁢e2⁢m⁢π⁢i)=2⁢π⁢i⁢em⁢p⁢π⁢iΓ⁡(p)⁢sin⁡(m⁢p⁢π)sin⁡(p⁢π)⁢ zp−1+Ep⁡(z),
m∈ℤ, z≠0.

§8.19(ix) Неравенства

Для n=1,2,3,… и x>0,

8,19.19		n−1n⁢En⁡(x)

8.19.20		(En⁡(x))2

8.19.21		1x+n

8.19.22		ddx⁡En⁡(x)En−1⁡(x)>0.

§8.

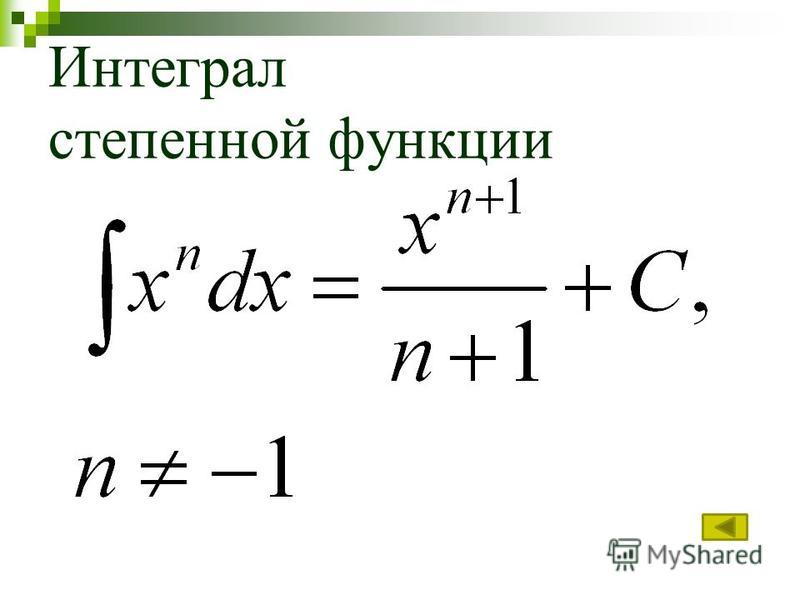19(x) Интегралы

8.19.23		∫z∞Ep−1⁡(t)⁢dt=Ep⁡(z),
|ph⁡z|<π,

8.19.24		∫0∞e−a⁢t⁢En⁡(t)⁢dt=(−1)n−1an⁢(ln⁡(1+a)+∑k=1n−1(−1)k⁢akk),
n=1,2,…, ℜ⁡a>−1,

8.19.25		∫0∞e−a⁢t⁢tb−1⁢Ep⁡(t)⁢dt=Γ⁡(b)⁢(1+a)−bp+b−1⁢F⁡(1,b;p+b ;а/(1+а)),
ℜ⁡a>−1, ℜ⁡(p+b)>1.

8.19.26		∫0∞Ep⁡(t)⁢Eq⁡(t)⁢dt=L⁡(p)+L⁡(q)p+q−1,
р>0, q>0, р+q>1,

где

19. 08.27		L⁡(p)=∫0∞e−t⁢Ep⁡(t)⁢dt=12⁢p⁢F⁡(1,1;1+p;12),
р>0.

О гипергеометрической функции F⁡(a,b;c;z) см. §15.2(i). Когда p=1,2,3,…, L⁡(p) можно также оценить с помощью (8.19.24).

Для наборов интегралов, содержащих Ep⁡(z), особенно для целое число p, см. Apelblat (1983, §§7.1–7.2) и Лекейн (1945) .

§8.19(xi) Дальнейшие обобщения

Об обобщенных экспоненциальных интегралах высшего порядка см. Мейер и Бакен (1987) и Милграм (1985) .

[PDF] Таблица интегралов экспоненциального интеграла.

Численное вычисление двух трансцендентных функций, связанных с экспоненциальным интегралом

• Д. Чипман

• Математика

• 1972

Алгоритмы вычисления двух трансцендентных функций! (Ei(t) — -n Itil) dt и f ! (Ei(t) — — in Itl) exp(-t)dt, где y — постоянная Эйлера, а Ei(t) —…

Трансцендентные функции, обобщающие экспоненциальные интегралы

• И. Абу-Шумайс

• Математика

• 1973

Новый набор обобщенных экспоненциальных интегралов, возникающих в (vm(ev), Ev(Ev) теории переноса) определены, а их асимптотики и (т) разложены в ряды. Особые случаи E (x,n),…

О некоторых границах экспоненциальной интегральной функции

В 1934 г. Хопф установил элегантное неравенство, ограничивающее экспоненциальную интегральную функцию. В 1959, Гаучи установил улучшение результатов Хопфа. В 1969 году Люк также установил два…

Использование рядов полиномов деления в обращении сложных функций по Лапласу с приложениями в исчислении дробей

В этой статье представлен аналитический метод обращения сложных функций с помощью преобразования Лапласа с помощью полиномиальных рядов Белла. Представленные результаты используются для получения точного решения…

О новых типах дробных операторов и приложениях 9{-t}}{t}\,dt,\quad x>0, $$, а другое определено…

Анализ моментов оценщика поля мозаики Делоне

• М. Лисхаут

• Математика

• 2009

Теорема Кэмпбелла–Мекке используется для получения явных выражений для среднего значения и дисперсии оценки поля мозаики Делоне Шаапа и Ван де Вейгарта. Особое внимание уделено Пуассону…

Решения экспоненциального интеграла для времени фиксации в модели Райта-Фишера с выбором

• В. Рунге, Арно Лиерманн, Полина Спинга

• Математика

• 2022

В этой работе мы выводим новые аналитические выражения для времени фиксации в модели Райта-Фишера с выбором. Рассмотрены три стандартных случая фиксации: фиксация на ноль, на единицу или на то и другое. Второй…

Явная асимптотика времен первого прохождения диффузионных процессов

Аннотация Мы вводим единую основу для решения времен первого прохождения однородных во времени диффузионных процессов. Используя теорию потенциала и теорию возмущений, мы можем вывести замкнутую форму…

Аппроксимация байесовских моделей для данных о времени до события

• Marta Catalano, A.

  No related posts.