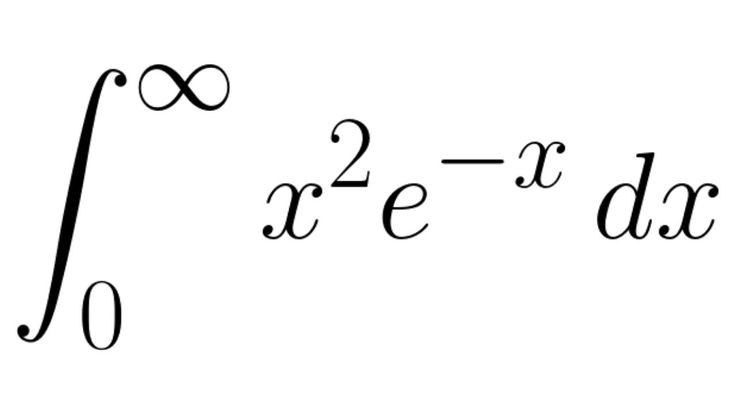Интеграл математика: простыми словами об интегрировании функций / Skillbox Media

Содержание

Интеграл — Умскул Учебник

На этой странице вы узнаете:

Как связаны Ньютон и Лейбниц?
Почему площадь криволинейной трапеции считается через интеграл?

Интеграл

В топ-5 страшилок по математике неизменно входит интеграл. Так ли он ужасен на самом деле?

Если объяснять простыми словами, интеграл — это площадь фигуры под графиком функции. Например, в геометрии есть формулы, чтобы посчитать площадь прямоугольника или треугольника, а если нужно посчитать площадь фигуры с кривой стороной, заданной функцией, поможет интеграл.

Если у функции y = f(x) есть первообразная y = F(x), тогда множество значений первообразных у = F(x) + С называют неопределенным интегралом функции y = f(x)

Записывается это следующим образом:

\(\int f(x)dx = F(x) + C\)

Какие бывают интегралы?

Интегралы бывают неопределенные и определенные.

Рассмотрим определенный интеграл. b f(x)dx = F(b) — F(a)\)

Для данного интеграла пределом является отрезок от a до b

Как связаны Ньютон и Лейбниц?

И Ньютон, и Лейбниц, бесспорно, являются великими учеными. Как и у обычных людей, у них бывают споры. Именно такой спор и послужил названию одной из формул в математике в честь этих двух замечательных ученых. Формула Ньютона-Лейбница используется для вычисления определенного интеграла. Она была выведена Ньютоном и Лейбницем независимо друг от друга. Есть мнение, что Ньютон свою версию создал раньше Лейбница, но опубликовал позже, из-за этого и случился спор, который завершился только после смерти обоих ученых.

Формула Ньютона-Лейбница

Если функция f(x) непрерывна на промежутке [a; b], то

где F(x) – первообразная для функции f(x),
a – нижний предел интегрирования,
b – верхний предел интегрирования

Данная формула применяется для вычисления определенного интеграла

Пример вычисления определенного интеграла по формуле Ньютона – Лейбница:

Интеграл для нахождения площади фигуры

Представим, что нам нужно посчитать расстояние, пройденное автомобилем с непостоянной скоростью в промежуток времени [a; b].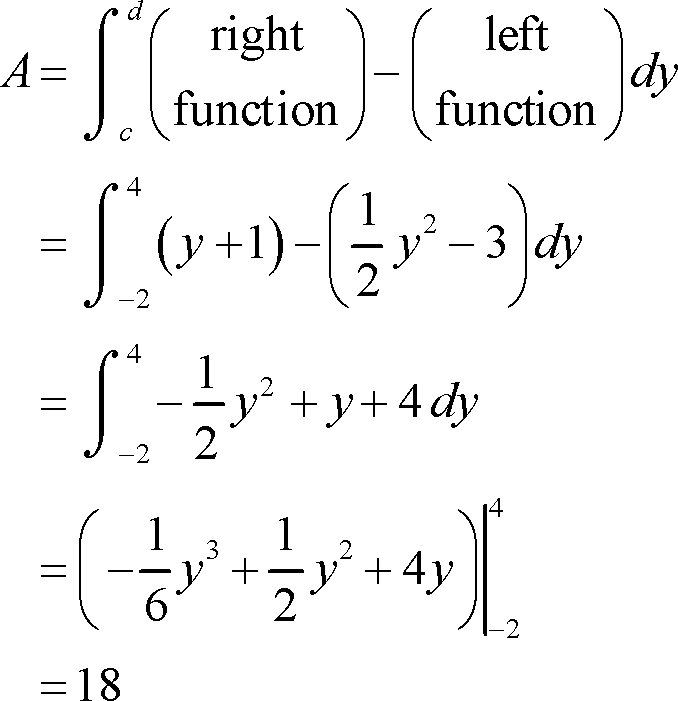 b f(x)dx\)

Почему площадь криволинейной трапеции считается через интеграл?

Чтобы понять это, разобьем фигуру на конечное число узких прямоугольных столбцов.

Найдем общую площадь, умножив высоту каждого столбика на его ширину и сложив все полученные значения, такая площадь будет приблизительной.

Если разделить данную фигуру на большее количество столбиков, только уже меньших по ширине, получим более точное значение. Повторять такое действие можно до бесконечности, следовательно, ширина будет стремиться к нулю, а количество прямоугольников — к бесконечности.

Сумму такого количества прямоугольников запишем в виде предела при количестве прямоугольников, стремящемся к бесконечности.

При таких условиях рассматриваемая сумма площадей сходится к пределу, описываемому следующим образом

, и равна какому-то числу.

А если фигура расположена под осью абсцисс, для вычисления площади фигуры нужно добавить минус к изначальной формуле.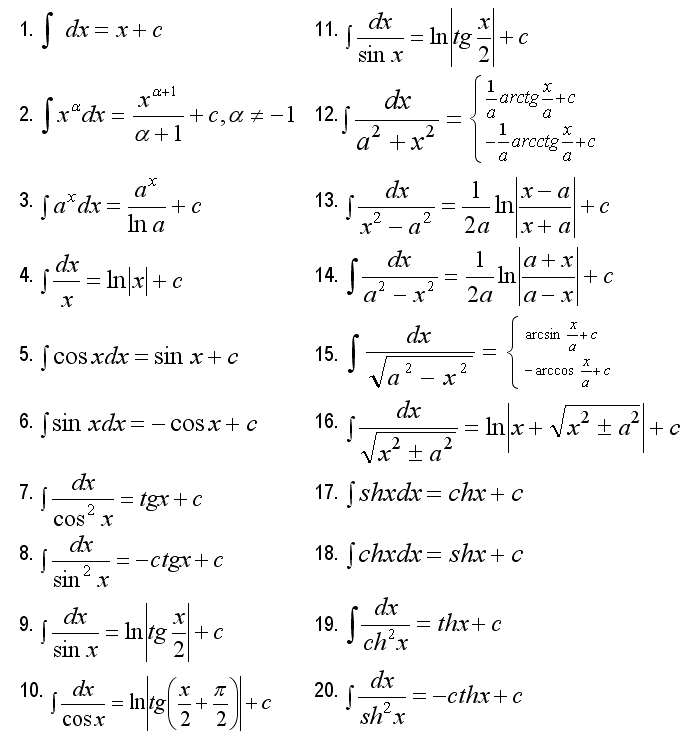 5 3dx\)

Задание 2.
Вычислите площадь фигуры ограниченной \(y = \sin x, x = 0, x = \frac{\pi}{2}\)

Задание 3.
Вычислите площадь фигуры ограниченной y = 2x²— 5, x = -1, x = 1

9
\(8\frac{2}{3}\)
\(\frac{20}{3}\)
8

Задание 4.
Вычислите площадь фигуры ограниченной y = x² — 3 и y = -2x² + 9

Ответы: 1. – 3; 2. – 1; 3. – 2; 4. – 1

Интегралы для чайников — что это, как решать, примеры

О чем статья

Почему вы не знаете, как решать интегралы

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

вычисление площади фигуры.
вычисление массы тела с неравномерной плотностью.
определение пройденного пути при движении с непостоянной скоростью.
и др.

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Объясняем понятие «Интеграл»

Процесс нахождения производной называется

дифференцированием, а нахождение первообразной – интегрированием.

Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».
Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».

Пример решения неопределенного интеграла.

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

Точки A и B на оси X – есть ограничение зоны определения интеграла

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

Пример решения определенного интеграла

Таблица интегралов для студентов (основные формулы)

Скачайте формулы интегралов, они вам еще пригодятся

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

Разложение интеграла суммы на сумму интегралов

Если поменять местами a и b, знак изменится

Можно разбить интеграл на промежутки следующим образом

Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Введение в интеграцию

Интеграция — это способ добавления фрагментов для поиска целого.

Интеграцию

можно использовать для поиска площадей, объемов, центральных точек и многих других полезных вещей. Но проще всего начать с нахождения области

между функцией и осью x следующим образом:

Какая площадь?

Срезы

Мы могли бы вычислить функцию в нескольких точках и сложить срезы шириной Δx вот так (но ответ будет не очень точным):

Мы можем сделать Δx намного меньше, а добавить много маленьких кусочков (ответ становится лучше):

И когда срезы приближаются к нулю по ширине , ответ приближается к истинному ответу . Теперь мы пишем dx , чтобы обозначить, что Δx срезов приближаются к нулю по ширине.

Столько всего!

Но складывать их не надо, так как есть «ярлык», потому что…

… найти интеграл — это обратный нахождения производной.

(Таким образом, вы должны действительно знать о деривативах, прежде чем читать дальше!)

Как здесь:

Пример: 2x

Интеграл от 2x равен x ² …

… потому что производная от x ² равна 2x

(Подробнее о «+C» позже.)

Этот простой пример можно подтвердить, вычислив площадь:

Площадь треугольника = 1 2 (основание)(высота) = 1 2 (х)(2х) = х ²

Интеграция иногда может быть такой простой!

Обозначение

Символ «Интеграл» — стильная буква «S»
(для «Суммы» — идея суммирования срезов):

После символа интеграла мы помещаем функцию, от которой мы хотим найти интеграл (называемую интегралом),

, а затем закончить с dx означает, что срезы идут в направлении x (и приближаются к нулю по ширине).

А вот как запишем ответ:

Плюс С

Мы записали ответ как x ² но почему +C ?

Это «Постоянная интегрирования». Именно там из-за все функции, производная которых 2х :

производная от x ² это 2x ,
и производная от x ² +4 тоже 2x ,
и производное от x ² +99 тоже 2x ,
и так далее!

Потому что производная константы равна нулю.

Итак, когда мы обращаем операцию (чтобы найти интеграл), мы знаем только

2x , но могла быть константа с любым значением .

Итак, мы завершаем идею, просто написав + C в конце.

Практический пример: кран и бак

Давайте воспользуемся краном, чтобы наполнить бак.

Вход (до интегрирования) расход из крана.

Мы можем интегрировать этот поток (сложить все маленькие кусочки воды), чтобы получить объем воды в резервуаре.

Представьте себе Постоянный расход из 1:

При расходе 1 объем резервуара увеличивается на x . это Интеграция !

Интеграл от 1 равен

При скорости потока 1 литр в секунду объем увеличивается на 1 литр каждую секунду, поэтому он будет увеличиваться на 10 литров через 10 секунд, на 60 литров через 60 секунд и т. д.

Скорость потока остается равной 1 , и объем увеличивается на

И наоборот:

Если объем бака увеличивается на x , то скорость потока должна быть 1.

Производная x равна 1

Это показывает, что интегралы и производные противоположны!

Сейчас для увеличения расхода

Представьте, что поток начинается с 0 и постепенно увеличивается (возможно, мотор медленно открывает кран):

По мере увеличения расхода бак наполняется все быстрее и быстрее:

Интеграция: при расходе 2x объем резервуара увеличивается на х ²
Производная: Если объем резервуара увеличивается на x ² , тогда скорость потока должна быть 2x

Запишем так:

Интеграл расхода 2x говорит нам об объеме воды:

∫2x dx = x ² + С

Производная тома

x ² +C возвращает скорость потока:

д дх (х ² + С) = 2х

И эй, мы даже получаем хорошее объяснение этого значения «C» . .. может быть, в резервуаре уже есть вода!

Поток по-прежнему увеличивает объем на ту же величину
А увеличение объема может вернуть нам скорость потока.

Что учит нас всегда помнить «+C».

Другие функции

Как интегрировать другие функции?

Если нам посчастливится найти функцию на стороне результата производной, то (зная, что производные и интегралы являются противоположностями) у нас есть ответ. Но не забудьте добавить C.

Пример: что такое ∫cos(x) dx ?

Из таблицы правил производных мы видим, что производная от sin(x) равна cos(x), поэтому:

∫cos(x) dx = sin(x) + C

Но многое из этого «реверсирования» уже сделано (см. Правила интеграции).

Пример: Что такое ∫x

³ dx ?

В правилах интегрирования есть «степенное правило», которое гласит:

∫x ⁿ dx = x ⁿ⁺¹ n+1 + C

Мы можем использовать это правило с n= 3:

∫x ³ dx = x ⁴ 4 + C

Знание того, как использовать эти правила, является ключом к успеху в интеграции.

Итак, изучите правила и побольше практики .

Изучите правила интеграции и попрактикуйтесь! Упражняться! Упражняться!
(ниже есть несколько вопросов для начала)

Определенные и неопределенные интегралы

До сих пор мы делали Неопределенные интегралы .

A Определенный интеграл имеет фактические значения для расчета между (они помещаются внизу и вверху буквы «S»):


Бессрочный Целый		Определенный Интегральный

Прочтите Определенные интегралы, чтобы узнать больше.

Главная | Интеграл

для поддержки преподавания и изучения математики

Предназначен для развития глубокого понимания математики и развития всех навыков, необходимых учащимся

Забронировать турилиПодписаться

Integral — это онлайн-среда для преподавания и обучения, которая. ..

…поддерживает учителей обширными ресурсами для использования как в классе, так и в Интернете
…помогает учащимся самостоятельно изучать математику
…позволяет учителям отслеживать успеваемость своих учеников с помощью передовых аналитических инструментов

Integral содержит все необходимое в одном месте

Integral поможет вам максимально эффективно использовать свое время, позволяя сосредоточиться на планировании, обучении и повторении.
В нашем обширном банке удобных для навигации ресурсов вы найдете тысячи обучающих и учебных материалов.
Динамические ресурсы и полезные заметки позволяют учащимся самостоятельно исследовать и практиковать новые области математики.
Отслеживайте и оценивайте успеваемость учащихся с помощью мощной аналитики.

Предыдущий Следующий

Широкий выбор различных ресурсов

Интерактивные ресурсы

Поддержка самостоятельного обучения учащихся

Последовательность действий на экране, позволяющая учащимся встречаться, исследовать и практиковать новые концепции самостоятельно. Они интерактивны и динамичны и снабжены пошаговыми инструкциями.

Примечания, примеры и важные моменты

Помощь в прояснении понимания

Тысячи страниц высококачественных и подробных заметок, услужливо написанных и доступных для всех. Они содержат полностью проработанные примеры и объясняют распространенные заблуждения.

Экранные тесты

Для отслеживания успеваемости на всем пути к экзамену

Экранные тесты для оценки уровня и глубины навыков учащихся, для отслеживания прогресса на всем пути к экзамену. Немедленная обратная связь доступна с помощью мощных аналитических инструментов.

Упражнения

Для укрепления уверенности учащихся

Три уровня упражнений:

базовая практика
стандарт экзамена
дополнительных вопросов

На все вопросы предоставляются полностью проработанные решения.

Преподавательская деятельность

Помочь вам максимально эффективно использовать свое время

Широкий выбор материалов, предлагающих идеи для уроков и занятий с соответствующими материалами для учащихся.

Предыдущий ресурс Следующий ресурс

Интерактивный
Примечания
Экранные тесты
Упражнения
Преподавательская деятельность

Высокое качество и доступная цена

Integral был разработан экспертами MEI.