11.1.7. Интегрирование тригонометрических функций-2.
Главная » 11 класс. Алгебра. » 11.1.7. Интегрирование тригонометрических функций-2
Продолжаем интегрировать тригонометрические функции по простейшим формулам 6) — 9) таблицы интегралов (лист «Интегралы«) Но вот незадача — у нас всего 4 формулы, и нужная формула не всегда сразу «видна»! Как же следует поступать в таких случаях? Нужно постараться упростить подынтегральное выражение, используя подходящие тригонометрические тождества.
Содержание
Пример 1
∫(cos²x-sin²x) dx. Такой формулы интегрирования у нас нет, но мы можем упростить подынтегральное выражение, используя тригонометрическую формулу для косинуса двойного аргумента: cos2α=cos²α-sin²α.
Решение.
∫(cos²x-sin²x) dx=∫cos2xdx=½∫cos2xd (2x)=1/2sin2x+C.
При решении мы применяем метод подведения под знак дифференциала (смотрите предыдущие занятия).
Так как мы подвели под знак дифференциала 2х и получили выражение под знаком интеграла в 2 раза больше: d (2x)=2dx, то перед знаком интеграла ставим множитель ½. Сделаем проверку.
(F (x)+C)’=(1/2sin2x+C)’=½·cos2x·2=cos2x=cos²x-sin²x=f (x).
Пример 2
∫(cos²4x-sin²4x) dx (аналогичный).
Решение.
∫(cos²4x-sin²4x) dx=∫cos8xdx=1/8∫cos8xd (8x)=1/8sin8x+C.
Пример 3
∫(cos²x/2-sin²x/2) dx.
Решение.
∫(cos²x/2-sin²x/2) dx=∫сosxdx=sinx+C.
В примерах 2 и 3 мы так же, как и в примере 1, упрощали подынтегральное выражение по формуле для косинуса двойного аргумента,
а затем применяли формулу 6): ∫cosudu=sinu+C (лист Интегралы).
Пример 4
. ∫(sin²x+cos²x) dx.
Решение.
Применяем основное тригонометрическое тождество: sin²α+cos²α=1. (*)
∫(sin²x+cos²x) dx=∫1·dx=∫dx=x+C.
Пример 5
∫2sinxcosxdx.
Решение.
Используем формулу синуса двойного аргумента: sin2α=2sinαcosα (**) и упростим подынтегральное выражение.
∫2sinxcosxdx=∫sin2xdx=½∫sin2xd (2x)=-1/2cos2x+C.
Пример 6
∫sin3xcos3xdx. Решаем аналогично примеру 5.
Решение.
∫sin3xcos3xdx=∫1/2sin6xdx=½∫sin6xdx=(½)·(1/6)∫sin6xd (6x)=- (1/12) cos6x+C.
В примерах 5 и 6 мы использовали формулу 7): ∫sinudu=-cosu+C (лист Интегралы), причем, интегрировали путем подведения под знак дифференциала.
Пример 7
∫(sinx+cosx)²dx.
Решение.
Раскроем скобки, используя формулу квадрата суммы двух выражений: (a+b)²=a²+2ab+b².
∫(sinx+cosx)²dx=∫(sin²x+2sinxcosx+cos²x) dx. Теперь в подынтегральном выражении можно увидеть сразу 2 тригонометрические формулы (*) и (**).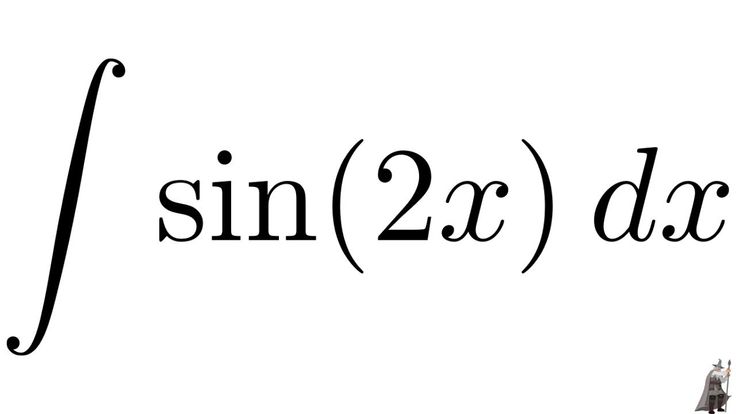
∫(sinx+cosx)²dx=∫(sin²x+2sinxcosx+cos²x) dx=∫(1+sin2x) dx=
=∫dx+∫sin2xdx=∫dx+½∫sin2xd (2x)=x-1/2cos2x+C.
Пример 8
∫2sin²xdx.
Решение.
Применим тригонометрическую формулу понижения степени для квадрата синуса данного аргумента: 2sin²α=1-cos2α.
∫2sin²xdx=∫(1-cos2x) dx=∫dx-∫cos2xdx=∫dx-½∫cos2xd (2x)=x-1/2sin2x+C.
Пример 9
∫2cos²xdx.
Решение.
Применяем формулу понижения степени для квадрата косинуса аргумента: 2cos²α=1+cos2α. Тогда:
∫2cos²xdx=∫(1+cos2x) dx=∫dx+∫cos2xdx=∫dx+½∫cos2xd (2x)=x+1/2sin2x+C.
Пример 10
Пример аналогичен примеру 8.
∫2sin²5xdx.
Решение.
∫2sin²5xdx=∫(1-cos10x) dx=∫dx- (1/10)∫cos10xd (10x)=x- (1/10) sin10x+C.
Пример 11
Пример аналогичен примеру 9.
∫2cos²(x/2) dx.
Решение.
∫2cos²(x/2) dx=∫(1+cosx) dx=∫dx+∫cosxdx=x+sinx+C.
Пример 12
∫8sinxcosxcos2xcos4xdx.
Решение.
Преобразуем подынтегральное выражение по формуле (**) — синуса двойного аргумента:
8sinxcosxcos2xcos4x=2·2·2·sinx·cosx·cos2x·cos4x=
=2sinxcosx·2·2·cos2x·cos4x=sin2x·2·2·cos2x·cos4x=
=2sin2xcos2x·2·cos4x=sin4x·2cos4x=sin8x.
Итак, ∫8sinxcosxcos2xcos4xdx=∫sin8xdx=1/8∫sin8xd (8x)=- (1/8) cos8x+C.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Определение, уравнение, формула и т.
д.Содержание
Обычно интеграл означает площадь. Это правда, что в некоторых случаях число, которое мы получаем, когда вычисляем интеграл, представляет собой площадь. Сумма Римана представляет собой общую площадь нескольких прямоугольников. Если мы увеличим количество прямоугольников, они покроют область между графиками. Однако они охватывают и горизонтальную ось. В этом случае площадь области равна пределу суммы Римана. Теперь этот предел является в точности интегралом функции по интервалу. Итак, в данном случае интервал представляет собой площадь.
Но в целом это другое. Проблемы возникают, когда функция становится отрицательной в определенных точках. Однако в точках, где функция отрицательна, соответствующие члены в сумме Римана также будут отрицательными. Однако сумма Римана представляет собой общую площадь прямоугольников над осью за вычетом общей площади прямоугольников под осью. График, горизонтальная ось и линии x= a и x= b охватывают область.
Теперь интеграл представляет собой общую площадь B части над горизонтальной осью минус площадь A части под осью. Далее Это подписанная область региона. Таким образом, фактический смысл интеграла — это площадь со знаком области, ограниченной графиком. 92x
Косинус в квадрате x равен половине единицы плюс косинус 2x. Теперь уменьшаем квадрат. Итак, мы вытащим эту половину вперед. Затем мы можем вынести константы из интегралов, и это будет первообразная единицы плюс косинус 2x. Так вот, это то, что мы действительно можем анти-вывести. У нас есть половина; первообразная одного dx — это просто x. Итак, первообразная плюс косинус есть плюс синус. Однако, если бы мы выводили, нам пришлось бы умножать на два по цепному правилу. Затем нам нужно разделить на 2. Однако это работает только тогда, когда внутри постоянное время x. Неопределенный интеграл заслуживает плюс c. 92x
- Итак, нам нужно преобразовать квадрат синуса x в 1 минус квадрат косинуса x. Далее, косинус в квадрате, умноженный на 1, является косинусом в квадрате, и это x делает косинус в четвертой степени x.
Однако мы не можем использовать u-подстановку, потому что если мы хотим, чтобы u равнялось синусу x, производная синуса x была косинусом x. Теперь у нас есть косинус во второй степени x. Теперь перепишем интеграл как интеграл от синуса x, умноженного на косинус x. Затем возведите оба этих числа во вторую степень. Потому что, когда у нас есть синус х косинус х, мы ничего не можем распознать. Теперь нам нужно разделить обе части на 2. Итак, это интеграл от ½ умножения на синус от 2x и их возведение в квадрат. Теперь у нас есть ¼ впереди, и тогда мы должны интегрировать. Далее, функциональная часть является синусоидальной, и мы должны возвести ее в квадрат. - После этого в скобках укажите 2x состояния. Теперь 2x — это постоянное кратное x, и пусть u равно 2x. Теперь мы используем формулу уменьшения мощности для квадрата синуса. Мы можем изменить квадрат синуса тета на ½ умножить на один минус косинус угла в шайрах на два умножить на тета. Затем мы можем вывести ½ вперед, и ¼ умножить на один больше двух будет один больше 8. Затем мы можем проинтегрировать один минус косинус два раза 2x, что для x. Тогда мы можем вывести ⅛ вперед и раскрыть скобки; мы получаем x и интегрируем косинус, мы получаем положительный знак. Однако входные состояния одинаковы, потому что ввод был 4x. Итак, наконец, у нас есть ⅛ x минус 1/32x синус 4x плюс c. 92x от 0 до pi
Квадрат косинуса равен ½, умноженному на один плюс косинус 2 тета, и это будет гораздо проще интегрировать. Теперь ½ будет внутри, но тогда число, которое мы можем вывести за пределы полуцелого 0, больше 2. Далее, это будет просто один плюс косинус два тета d тета, и тогда мы можем это проинтегрировать. Однако ½ находится снаружи и открывает скобки. Тогда интеграл 1 тета в мире тета плюс по синусу и внутри состояний, это два тета. Теперь нам нужно разделить его на два. Наконец, ответ равен π/4. 92
Интегрируем функцию cos2x, деленную на cos x плюс синус x, в степени два dx. Теперь мы разбиваем числительное с помощью cos2x. Однако мы знаем, что cos2x равно квадрату cos x минус квадрат синуса x.
Затем мы применяем эту формулу к числительному, и это становится кос-квадратом х минус квадрат синуса х, деленным на косинус х плюс синус х и суммой в степени два в dx. Следующим шагом мы разделим числитель по формуле (а в квадрате минус b в квадрате). Теперь это станет (cos x минус синус x) в (cos x плюс синус x) разделить на cos x плюс синус x и суммировать в степени два в dx. Затем, после отмены cos x плюс синус x, это будет cos x минус синус x, деленное на cos x плюс синус x в dx.Пусть cosx + sinx = t
(-sinx + cosx) dx= dt
После замены на t вопрос будет dt по t. Теперь интеграл функции равен логарифмическому модулю x плюс c. Далее мы интегрируем эту функцию, и это будет логарифмическая модификация t плюс c. Теперь результатом является логарифмическая модификация cos x плюс sine x плюс c.
I=∫cos2x/(sinx+cosx)2 dx
I=∫cos2x/(sinx+cosx)2dx
I=∫cos2x−sin2x/(sinx+cosx)2dx
I=∫(cosx sinx)(cosx-sinx)/(sinx+cosx)2dx
I=∫cosx−sinx/sinx+cosx dx
Пусть sinx+cosx=t Тогда (cosx−sinx)dx=dt
Тогда
I=∫dt/t
I=log|t |+c
I=log|sinx+cosx|+c
Интеграл от dx/cos(x+a)cos(x+b)- Интегрируем функцию, которая представляет собой dx по cos x плюс a и cos x плюс b.Теперь нам нужно умножить числитель и знаменатель на синус a минус b. После этого это будет синус a минус b, деленный на cos of (x+a) cos of (x+b) на dx. Теперь будем дальше манипулировать этим форматом и получим синус от (a-b). В числителе мы получим синус (a+x-b-x). И в знаменателе мы получим cos (x + a) в cos из (x + b) в dx. На следующем шаге синус (a+b) будет таким же. Но числитель и знаменатель будут синусом (x+a-x-b) и cos (x+a) в cos (x+b) в dx. Однако грех (a-b) равен sinA cosA минус cosA синус B.
- Применив эту формулу, мы получим синус (x+a) в cos из (x+b) минус cos из (x+a) в синус из (x-b), деленный на cos из (x+a) в cos из (x+b) в dx. Далее, после некоторых вычислений, это будет синус (a-b), а теперь это интеграл от тангенса (x+a) к dx минус 1/синус (a-b). Снова интеграл тангенса (x+b) от dx. Затем, после интеграла от тангенса и применения log, окончательный результат равен единице при синусе (a-b) и log total mod от cos(x+b) при cos(x+a) плюс c.
∫ 1/cos(x+a) cos(x+b) dx
= 1/sin(a-b) ∫ tan(x+a) – tan(x+a) dx
= 1/sin(a-b ) [-log|cos(x+a)| + c1 -(-log|cos(x+b)| + c2)
= 1/sin(a-b) [-log|cos(x+a)| + log|cos(x+b)|+ c1 + c2]
= 1/sin(a-b) [-log|cos(x+a)| + log|cos(x+b)|] + 1/sin(a+b) (c1+c2)
= 1/sin(a-b) [-log|cos(x+a)| + log|cos(x+b)|] + c
= 1/sin(a-b) log|cos(x+b)/cos(x+a)| + c
Некоторые часто задаваемые вопросы Что такое интеграция LOG X?X log x−x+c представляет собой интегрирование log x.
- Интегрируем функцию, которая представляет собой dx по cos x плюс a и cos x плюс b.
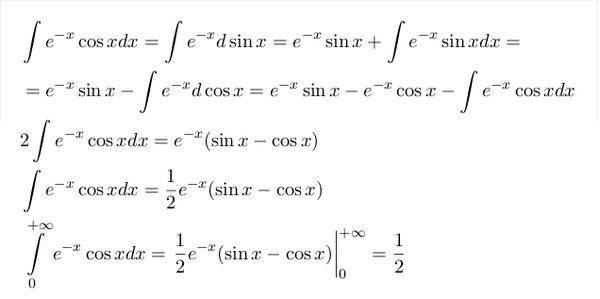Однако мы не можем использовать u-подстановку, потому что если мы хотим, чтобы u равнялось синусу x, производная синуса x была косинусом x. Теперь у нас есть косинус во второй степени x. Теперь перепишем интеграл как интеграл от синуса x, умноженного на косинус x. Затем возведите оба этих числа во вторую степень. Потому что, когда у нас есть синус х косинус х, мы ничего не можем распознать. Теперь нам нужно разделить обе части на 2. Итак, это интеграл от ½ умножения на синус от 2x и их возведение в квадрат. Теперь у нас есть ¼ впереди, и тогда мы должны интегрировать. Далее, функциональная часть является синусоидальной, и мы должны возвести ее в квадрат.
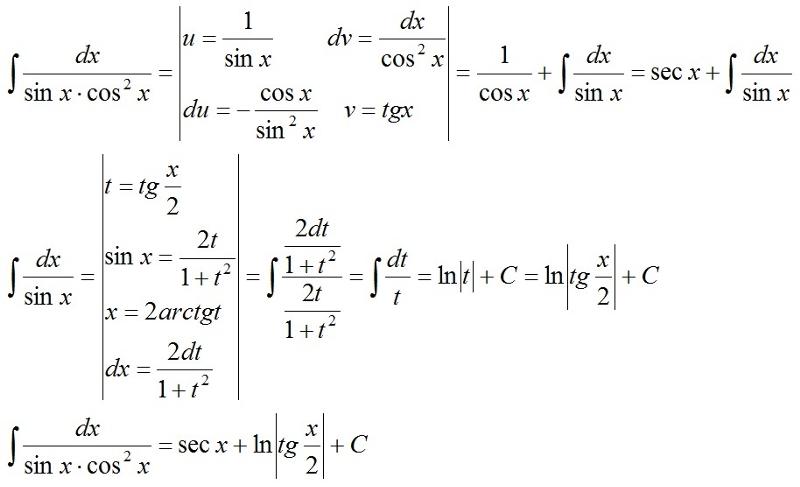Затем мы можем проинтегрировать один минус косинус два раза 2x, что для x. Тогда мы можем вывести ⅛ вперед и раскрыть скобки; мы получаем x и интегрируем косинус, мы получаем положительный знак. Однако входные состояния одинаковы, потому что ввод был 4x. Итак, наконец, у нас есть ⅛ x минус 1/32x синус 4x плюс c. 92x от 0 до pi 
Затем мы применяем эту формулу к числительному, и это становится кос-квадратом х минус квадрат синуса х, деленным на косинус х плюс синус х и суммой в степени два в dx. Следующим шагом мы разделим числитель по формуле (а в квадрате минус b в квадрате). Теперь это станет (cos x минус синус x) в (cos x плюс синус x) разделить на cos x плюс синус x и суммировать в степени два в dx. Затем, после отмены cos x плюс синус x, это будет cos x минус синус x, деленное на cos x плюс синус x в dx.
