НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ новое
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
1. Подведение под знак дифференциала, замена переменной.
2. Метод интегрирования по частям . (1)
1) Интегралы вида P(x)ekxdx, Р(х) sin kх dx, Р(х) cos kx dx, где Р(х) — многочлен, k — число. Удобно положить u = Р(х), а за dv обозначить все остальные сомножители.
2) Интегралы вида P(x) arcsin x dx, P(x) arccos x dx, Р(х) arctg x dx,P(x) arcctg x dx,P(x) ln
Удобно положить P(x) dx = dv,
а за u обозначить
остальные сомножители.3) Интегралы вида еахsin bх dx, еах cos bх dx, где а и b — числа. За u можно принять функцию u=еах, применить интегрирование по частям дважды, составить уравнение относительно искомого интеграла.
3. Интегрирование рациональных дробей.
1) Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби;
2) Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей:
Теорема. Всякую правильную
рациональную дробь, знаменатель которой разложен на множители Q(х)
= (х – x1 (х — х2.
...(х— хr…(2) (корни квадратного трехчлена комплексные), можно представить в виде
следующей суммы простейших дробей:
=++…++++…++…++ ++…++…+++…+(3)
Найти неопределенные коэффициенты.
3) Проинтегрировать многочлен и полученную сумму простейших дробей:
Интегрирование простейших рациональных дробей.
1. = A=А · ln |х – а| + С; (4)
2. = A= ; (5)
3. (6) , где знаменатель не имеет действительных корней. В знаменателе выделить полный квадрат, заменить выражение под квадратом новой переменной, разбить на сумму двух интегралов, первый из которых заменой переменной приводится к табличному (№2), второй – к табличному (№15).
4. (7), где знаменатель не имеет
действительных корне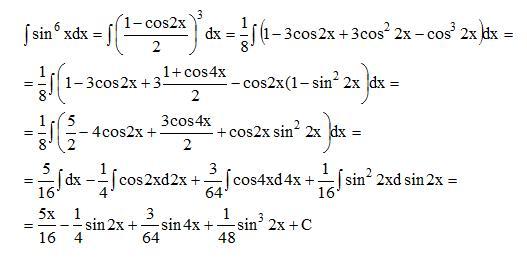й.
В знаменателе
выделить полный
квадрат, выполнить подстановку , разбить на сумму двух интегралов, первый из которых решается с помощью замены переменной, второй – с помощью рекуррентной формулы
(8) (9)
4. Интегрирование тригонометрических функций.
1) Универсальная тригонометрическая подстановка tgt, (10) sin x=, cos x=, dx =dt
подстановка cos x = t; (11) , ,
подстановка sin x = t; (12)
, ,подстановка tg x = t (13) , ,
2) Интегралы типа .
подстановка sin x = t, если n — целое положительное нечетное число;
подстановка cos x = t, если m — целое положительное нечетное число;
формулы понижения порядка: cos2x = (1 + cos 2x), sin2x = (1 – cos2x), sin x ∙ cos x =sin2x, (14) если m и n — целые неотрицательные четные числа;
подстановка tg х = t, если т + п — есть четное отрицательное целое число.
3) Использование тригонометрических преобразований. sin α cosβ = (sin(α – β) + sin(α +β)),
cos α cosβ = (cos(α —β) + cos(α +β)), sin α sinβ = (cos(α —β)—cos(α +β)). (15)
5. Интегрирование иррациональных функций.
1) Квадратичные иррациональности., , : под радикалом выделить полный квадрат и сделать подстановку х + = t. (16)
2) Интегралы типа dx, где Рn(x)—многочлен степени n, можно вычислять, пользуясь формулой
dx = Qn-1(x)+(17) где Qn-1(x) — многочлен степени (n – 1) с неопределенными коэффициентами, — также неопределенный коэффициент. Все неопределенные коэффициенты находятся из тождества, получаемого дифференцированием обеих частей равенства (14): . (18)
после чего необходимо приравнять
коэффициенты при одинаковых степенях
неизвестной х.
3) Дробно-линейная подстановка. Интегралы типа , где a, b, c, d – действительные числа, — натуральные числа, подстановка , (19) где k — наименьшее общее кратное знаменателей дробей .
4) Тригонометрическая подстановка.
Интеграл подстановка (20)
Интеграл подстановка (21)
Интеграл подстановка (22)
5) Интегрирование дифференциального бинома. Интегралы типа , где а, b — действительные числа; т, п, р — рациональные числа.
если р — целое число, то подстановка х = tk , (23) где k — наименьшее общее кратное знаменателей дробей m и n;
если — целое число, то подстановка а + bхn = ts, (24) где s —знаменатель дроби р;
если + р — целое число, то подстановка а + bхn = хn ts, (25) где s — знаменатель дроби р.
6. «Неберущиеся» интегралы.
dx — интеграл Пуассона (теория
вероятностей),
интегральный логарифм (теория чисел),
, — интегралы Френеля (физика),
dx, dx — интегральные синус и
косинус,
dx — интегральная показательная функция.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92$. И оказывается всесторонним применением многих элементарных теорем в вещественном и комплексном анализе. Рекомендуется убедиться, что вы можете вычислить и понять все тождества в этом посте самостоятельно. Также ожидается, что вы сможете вспомнить, что означают все слова, выделенные курсивом Чтобы было ясно, под преобразованием Фурье $f$ мы на самом деле подразумеваем Это вопрос удобства. Действительно, коэффициент $\frac{1}{\sqrt{2\pi}}$ лишний, но без этого коэффициента при вычислении обратного Фурье приходится писать $\frac{1}{2\pi}$ на другой стороне. Вместо того чтобы сделать обратное преобразование несбалансированным, мы постоянно пишем $\frac{1}{\sqrt{2\pi}}$ и делаем вид, что его здесь нет. 9{itz}dz$, мы видим $I_A(t)=\varphi_A(t+1)-\varphi_A(t-1)$. Удобно делить $\varphi_A$ на $\pi$, так как получается , и нас устраивает знаменатель $2\pi i$. Теперь замкнем путь $\Gamma_A$ двумя способами. Во-первых, полуокружностью от $A$ до $-Ai$ до $-A$; во-вторых, полуокружностью от $A$ до $Ai$ до $-A$. , мы видим, что остаток этой функции в точке $0$ равен $1$. По теореме о вычетах , Обратите внимание, что мы использовали формулу замены переменной так же, как и для верхней. $\operatorname{Ind}_{\Gamma_L}(0)$ обозначает номер обмотки $\Gamma_L$ около $0$, что, конечно, равно $1$. Вышеприведенное тождество подразумевает Следовательно, когда $t>0$, поскольку $\sin\theta>0$ при $0<\theta<\pi$, мы получаем 91$, мы можем легко сказать, что приведенный выше интеграл есть преобразование Фурье $h(x)$ (умноженное на $\sqrt{2\pi}$). Но по-прежнему мы используем предельную форму , где И мы по-прежнему используем контурное интегрирование, как в задаче 1 (помните $\Gamma_A$, $\Gamma_U$ и $\Gamma_L$!). |
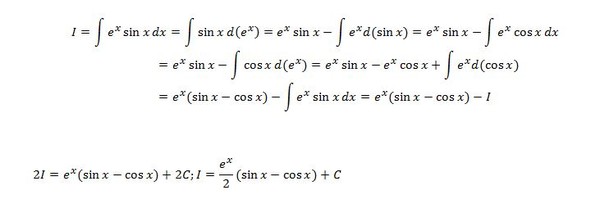
Для простоты обозначим два пути через $\Gamma_U$ и $\Gamma_L$. Опять же по теореме Коши, первый случай дает нам интеграл со значением $0$, таким образом, по теореме Коши, 9{itz}}{z}$ — мероморфная функция в $\mathbb{C}$ с простым полюсом в точке $0$. Поскольку