Неопределенный интеграл — презентация онлайн
Похожие презентации:
Неопределенный интеграл
Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл
Неопределенный интеграл и его свойства
Неопределенный интеграл
Неопределенный интеграл
Неопределенный интеграл
Неопределенный интеграл. Основные понятия и определения
Первообразная и неопределенный интеграл
Интегральное исчисление. Первообразная и неопределенный интеграл
Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов
Лекция N14
Лектор: доц. Лаптева Надежда Александровна
Тема: Неопределенный интеграл
Ранее мы по данной функции
вычисляли ее производную. Сегодня
мы поставим обратную задачу: для
данной функции f ( x) найти такую
функцию F ( x), производная
которой равнялась бы заданной
функции f ( x), т.
F ( x) f ( x).
Определение. Функция F ( x)
называется первообразной
функции f ( x), если
F ( x) f ( x).
Примеры.
(sin x) cos x F1 ( x) sin x;
(sin x 1) cos x F2 ( x) sin x 1;
Таким образом, F ( x) C — это
совокупность всех первообразных от
данной функции.
Определение 2. Пусть F ( x) — одна
из первообразных для функции f ( x).
Тогда выражение F ( x) C , где C произвольная постоянная,
называется неопределенным
интегралом и обозначается
f ( x) dx.
Здесь f ( x) называется
подынтегральной функцией, а f ( x) dx
— подынтегральным выражением.
Свойства
1) d
2)
f ( x) dx f ( x) dx
dF
(
x
)
F
(
x
)
C
3)
f
(
x
)
(
x
)
dx
f ( x) dx ( x) dx
4)
kf
(
x
)
dx
k
f
(
x
)
dx
Таблица основных интегралов
n 1
x
1) x dx
C, n 1
n 1
2) dx x C
dx
3) ln x C
x
n
Таблица основных интегралов
x
a
4) a dx
C
ln a
x
x
5) e dx e C
x
Таблица основных интегралов
6)
sin
x
dx
cos
x
C
7)
cos
x
dx
sin
x
C
Таблица основных интегралов
dx
8)
tg x C
2
cos x
dx
9) 2 ctg x C
sin x
Таблица основных интегралов
dx
1
x
10) 2
arctg C
2
a x a
a
dx
x
11)
arcsin C
2
2
a
a x
dx
2
2
12)
ln x x a C
2
2
x a
Докажем справедливость формулы 3)
dx
ln
x
C
x
Если x 0, то | x | x и ln | x | ln x.
dx
d (ln x) . Следовательно, для x 0
x
dx
ln
x
C
ln
x
C
.
x
x 0, то | x | x и ln | x | ln( x).
1
dx
d ln( x)
( 1)dx .
x
x
Следовательно, для x 0
dx
ln(
x
)
C
ln
x
C
.
x
Примеры.
1
2
2
1) x x 3 dx x dx
x 1
3
2
x dx x dx
3
1
1
2
3 1
x
x
x
C
3 1 1 3 1
2
3
3
2
x 2 2 x
x
C
3 3
2
3
x 2
1
x x 2 C.
3 3
2x
x 1
2)
dx
x
x 1
1
dx 1 dx
x
x x
dx
dx x ln | x | C.
x
dx
3)
2
2
cos x sin x
2
2
cos x sin x
dx
2
2
cos x sin x
dx
dx
2
ctg x tg x C.
2
sin x
cos x
x
6
4) 2 3 dx 6 dx
C.
ln 6
x
x
x
2 3
2 3
5)
dx
dx
x
x
x
3
3 3
x
x
x
x
2
2
1 dx dx dx
3
3
x
2
3
x C.
2
ln
3
x
x
dx
dx
1
x
6)
2
arctg C.
2
2
4 x
2 x
2
2
7)
dx
x
arcsin
C.
2
3
3 x
x
x x 1
x 1
8)
dx 2 2 2 dx
2
x
x
x
x
3
2
dx
2
x dx x dx
x
x
1
2
1
x
ln | x |
C
1 1
2
2 1
ln | x |
C.
x x
2
9)
sin x
tg
x
dx
dx
cos2 x
2
1
1 cos x
cos x
dx
dx
2
2
2
cos x
cos x cos x
2
2
dx
dx
tg
x
x
C
.
2
cos x
2
cos x
10) ctg x dx 2 dx
sin x
2
1 sin x
dx
dx
dx
2
2
sin x
sin x
2
ctg x x C.
Теорема. Любая непрерывная на
отрезке функция имеет на этом
отрезке первообразную.
Действие отыскания неопределенного
интеграла или, что то же самое,
нахождение всех первообразных от
данной функции, называется
Дифференцирование и интегрирование
являются взаимно обратными
операциями.
Геометрический смысл
неопределенного интеграла
Назовем график первообразной
функции от f ( x) интегральной кривой.
F ( x) f ( x),
y F ( x) есть
Таким образом, если
то график функции
интегральная кривая.
Неопределенный интеграл
геометрически представляется
семейством всех интегральных кривых
y
0
y F ( x) C2
y F ( x) C1
y F ( x)
x
Пример.
2
x
dx
x
C
.
2
Построить интегральные кривые.
Пусть
C 0;
y x .
y
2
C 1;
y x 1.
C 2;
y x 2.
2
2
2
1
0
x
Интегралы, не берущиеся в
элементарных функциях
В дифференциальном исчислении
производная от любой элементарной
функции есть функция элементарная.
Другое дело операция, обратная
дифференцированию, – интегрирование.
Можно привести примеры элементарных
функций, первообразные от которых хотя
и существуют, но не являются
элементарными функциями.
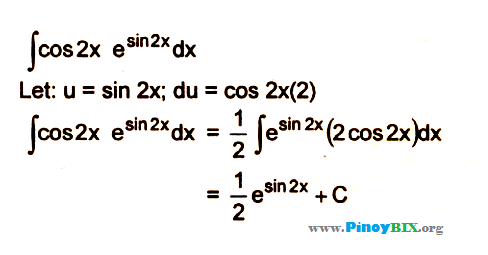Так,например, по теореме существования для
функций
e
x2
sin x cos x 1
,
,
,
x
x ln x
существуют первообразные, но они не
выражаются в элементарных функциях.
Несмотря на это, все эти первообразные
хорошо изучены и для них составлены
таблицы, помогающие практически
использовать эти функции.
Так, например, большое значение в
приложениях играет первообразная
от функции
1
e
2
x2
2
( x)
,
удовлетворяющая дополнительному
условию ( x) 0.
Эта функция встречается в теории
вероятностей и называется интегралом
Если первообразная для некоторой
функции не является элементарной
функцией, то говорят, что интеграл не
берется в элементарных функциях.
Тема: Замена переменной в
неопределенном интеграле
Введем вместо x новую
переменную t , связанную с
соотношением x (t ).
x
Тогда
f ( x) dx f (t ) (t ) dt.
Примеры.
1)
sin
ax
dx
ax t ;
d (ax) dt ;
1
a dx dt dx dt .
a
dt 1
sin t sin t dt
a a
1
1
cos t C cos ax C.
a
a
2)
tg
x
dx
.
Имеем
sin x
d (cos x)
tg
x
dx
dx
cos x
cos x
dt
ln | t | C ln | cos x | C.
t
Заметим, что
sin x dx d (cos x).
Здесь мы устно ввели под знак
интеграла функцию sin x.
3)
x
1
x
dx
.
2
1
2
Замечая, что x dx d x 1 ,
2
получаем
1
1
2
2 2
2
x
1
x
dx
1
x
d
x
1
.
2
3
3
2
2
2
2
x 1
1 x 1
C
C.
3
2
3
2
4)
Интегралы вида
sin
mx
sin
nx
dx
,
sin
mx
cos
nx
dx
,
cos
mx
cos
nx
dx
.
Эти интегралы вычисляются
методом разложения на основании
тригонометрических тождеств.
sin(m n) x sin(m n) x
sin mx cos nx
,
2
cos(m n) x cos(m n) x
sin mx sin nx
,
2
cos(m n) x cos(m n) x
cos mx cos nx
.
2
2
x
5) 3 dx
x 1
3
x 1 t;
d x 1 dt ;
3
3 x dx dt ;
2
1
x dx dt.
3
2
1 dt 1
1
3
ln | t | C ln x 1 C.
3 t 3
3
2
Можно устно внести x под знак
1
2
3
x dx d x 1 .
3
Тогда
x dx 1 d x 1 1
3
ln
x
1
C
.
3
3
x 1 3 x 1 3
2
3
6)
sin
x
cos
x
dx
.
Рассмотрим три способа.
sin x cos x dx sin x d (sin x)
2
sin x
C.
2
sin x cos x dx cos x d (cos x)
2
cos x
C.
2
1
sin
x
cos
x
dx
sin
2
x
dx
2
1 1
1
sin 2 x d (2 x) cos 2 x C.
2 2
4
Проверка.
sin x
C sin x cos x.
2
2
cos x
C sin x cos x.
2
1
1
cos 2 x C 2sin 2 x
4
4
2
1
sin 2 x sin x cos x.
2
1
7) cos x dx 1 cos2 x dx
2
1
1
x sin 2 x C.
2
4
2
8)
cos
x
dx
cos
x
cos
x
dx
3
2
(1 sin x) d (sin x)
2
d (sin x) sin x d (sin x)
2
3
sin x
sin x
C.
3
English Русский Правила
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92x Интеграл sin 2x и интеграл sin 2 x имеют разные значения. Определим разницу между интегралом sin 2x и интегралом sin 2 x, найдя их значения соответствующими методами, а также решим некоторые задачи, связанные с этими интегралами. 92x |
Чтобы найти интеграл sin 2 x, мы используем формулу cos 2x и метод подстановки, тогда как мы используем только метод подстановки, чтобы найти интеграл sin 2x.Чему равен интеграл от Sin 2x dx?
Интеграл от sin 2x обозначается ∫ sin 2x dx, а его значение равно -(cos 2x) / 2 + C , , где «C» — постоянная интегрирования. Для доказательства воспользуемся интегрированием методом подстановки. Для этого предположим, что 2x = u. Тогда 2 dx = du (или) dx = du/2. Подставляя эти значения в интеграл ∫ sin 2x dx,
∫ sin 2x dx = ∫ sin u (du/2)
= (1/2) ∫ sin u du
Мы знаем, что интеграл от sin x равен -cos x + C. Итак,
= (1/2) (-cos u) + C
Подставляя u = 2x здесь,
∫ sin 2x dx = -(cos 2x) / 2 + C
Это интеграл формулы sin 2x.
Определенный интеграл от греха 2x
Определенный интеграл — это неопределенный интеграл с некоторыми нижними и верхними границами. По основной теореме математического анализа, чтобы вычислить определенный интеграл, мы подставляем верхнюю и нижнюю границы в значение неопределенного интеграла, а затем вычитаем их в том же порядке. При вычислении определенного интеграла константой интегрирования можно пренебречь. Вычислим здесь некоторые определенные интегралы от интеграла sin 2x dx. 92x Использование формулы двойного угла для cos
Чтобы найти интеграл от sin 2 x, мы используем формулу двойного угла для cos. Одна из формул cos 2x: cos 2x = 1 — 2 sin 2 x. Решая это для sin 2 x, мы получаем sin 2 x = (1 — cos 2x) / 2. Мы используем это, чтобы найти ∫ sin 2 x dx. Тогда мы получаем
∫ sin 2 x dx = ∫ (1 — cos 2x) / 2 dx
= (1/2) ∫ (1 — cos 2x) dx
= (1/2) ∫ 1 dx — (1/2) ∫ cos 2x dx
92x Используя интегрирование по частям Мы знаем, что можем записать sin 2 x как sin x · sin x.
Чтобы найти интеграл произведения, мы можем использовать интегрирование по частям.
∫ sin 2 x dx = ∫ sin x · sin x dx = ∫ u dv
Здесь u = sin x и dv = sin x dx.
Тогда du = cos x dx и v = -cos x.
По формуле интегрирования по частям
∫ sin 2 x dx = (-1/2) (2 sin x cos x) + ∫ cos 2 x dx
По формуле двойного угла sin, 2 sin x cos x = sin 2x и тригонометрическое тождество, cos 2 x = 1 — sin 2 x. Итак,
∫ sin 2 x dx = (-1/2) sin 2x + ∫ (1 — sin 2 x) dx
∫ sin 2 x dx = (-1/2) sin 2x + ∫ 1 dx — ∫ sin 2 x dx
∫ sin 2 x dx + ∫ sin 2 x dx = (-1/2) sin 2x + x + C₁ 9{\pi}\)
= [π/2 — (sin 2π)/4] — [0 — (sin 0)/4]
= π/2 — 0/4
= π/2
Следовательно, интеграл от sin 2 x от 0 до π равен π/2.
Важные примечания, относящиеся к интегралу от Sin 2x и интегралу от Sin 2 x:
- ∫ sin 2x dx = -(cos 2x)/2 + C
- ∫ sin 2 x dx = x/2 — (sin 2x)/4 + C
Темы, относящиеся к интегралу Sin 2 x и интегралу Sin 2x: 93x дх? ∫ sin 3 x dx = ∫ sin 2 x sin x dx = ∫ (1 — cos 2 x) sin x dx.