Интегрирование рациональных функций
Рациональная функция — это дробь вида 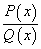 ,
числитель и знаменатель которой — многочлены или произведения многочленов.
,
числитель и знаменатель которой — многочлены или произведения многочленов.
Из урока «Интегрирование некоторых рациональных дробей и иррациональностей» известно, что рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе. В том же уроке говорилось о том, как представить неправильную дробь в виде суммы её целой части и некоторой правильной дроби.
На этом уроке будем учиться интегрировать такие рациональные функции, которые представлены в виде правильных дробей. Для этого существует метод неопределённых коэффициентов, основанный на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.
Приведённый ниже алгоритм интегирования рациональных функций будет пошагово проиллюстрирован в примерах.
Алгоритм интегрирования рациональных функций
- Шаг 1. Определить вид многочлена в знаменателе дроби (он может иметь действительные, кратные действительные, комплексные и кратные комплексные корни) и в зависимости от вида разложить дробь на простые дроби, в числителях которых — неопределённые коэффициенты, число которых равно степени знаменателя.
- Шаг 2. Определить значения неопределённых коэффициентов. Для этого потребуется решить систему уравнений, сводящуюся к системе линейных уравнений.
- Шаг 3. Найти интеграл исходной рациональной функции (дроби) как сумму интегралов полученных простых дробей, к которым применяются табличные интегралы.
Переходим к первому шагу алгоритма
Многочлен в знаменателе имеет действительные корни.
То есть, в знаменателе имеет место цепочка сомножителей вида
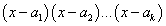 , в которой
каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых
коэффициентов будет следующим:
, в которой
каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых
коэффициентов будет следующим:
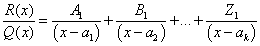
Пример 1. Шаг 1. Дан интеграл от рациональной функции
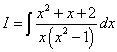 .
.
От нас требуется разложить подынтегральное выражение — правильную дробь
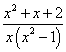 на простые дроби.
на простые дроби.
Решение. Дискриминант уравнения 
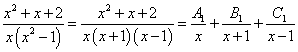 .
.
Пример 2. Шаг 1.Дан интеграл от рациональной функции
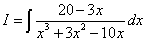 .
.
Решение. Разложим знаменатель подынтегрального выражения на множители. Сначала можно вынести за скобки x. (На сайте есть урок о вынесении общего множителя за скобки.) Получаем следующую дробь:
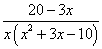 .
.
Для разложения квадратного трёхчлена в скобках решаем квадратное уравнение:
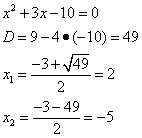
Получаем разложение знаменателя на множители в подынтегральном выражении:
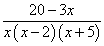 .
.
Дискриминант решённого выше квадратного уравнения положительный, то есть имеем дело со случаем, когда многочлен в знаменателе имеет действительные корни. Разложение исходной дроби подынтегрального выражения будет следующим:
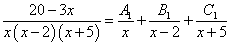 .
.
Как и в первом примере, числа, обозначенные большими буквами, пока неизвестны. Отсюда и название — метод неопределённых коэффициентов.
Многочлен в знаменателе имеет кратные действительные корни.
Этот случай имеет место, когда в цепочке сомножителей в знаменателе присутствует выражение вида
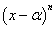 ,
то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
,
то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
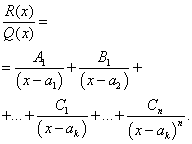
Пример 3. Шаг 1. Дан интеграл от рациональной функции
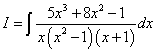 .
.
Решение. Представляем разность квадратов 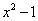 в виде произведения суммы и разности
в виде произведения суммы и разности 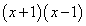 .
.
Тогда подынтегральное выражение запишется в виде
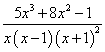 ,
,
все уравнения с многочленами которого имеют действительные корни. Это случай кратных действительных корней, так как последний сомножитель находится во второй степени. Получаем следующее разложение исходной дроби на простые дроби:
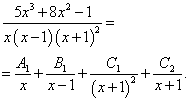
Как видим, в этом случае нужно понижать степень кратного многочлена с исходной до первой и записывать простую дробь с каждой из этих степеней в знаменатель.
Пример 4. Шаг 1. Дан интеграл от рациональной функции
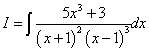 .
.
Решение. Уравнения с многочленами в знаменателе имеют действительные корни, а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее разложение исходной дроби на простые дроби:
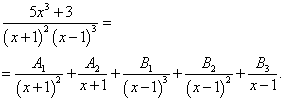 .
.
Многочлен в знаменателе имеет комплексные корни: дискриминант квадратного уравнения
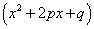
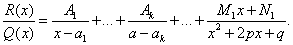
Пример 5. Шаг 1. Дан интеграл от рациональной функции
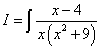 .
.
Решение. Уравнение в скобках имеет комплексные корни, а оба сомножителя присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:
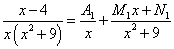 .
.
Пример 6. Шаг 1.
Дан интеграл от рациональной функции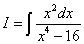 .
.Решение. Представим знаменатель дроби в подынтегральном выражении в виде следующего произведения сомножителей:
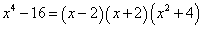 .
.
Решение. Уравнение с последним сомножителем имеет комплексные корни, а все сомножители присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:
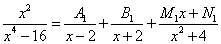
Многочлен в знаменателе имеет кратные комплексные корни:
дискриминант квадратного уравнения
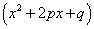 , присутствующего в
цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше.
, присутствующего в
цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше.
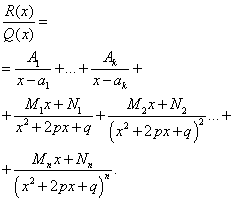
То есть в сумме простых дробей число простых дробей с линейным выражением в числителе должно быть равно степени сомножителя, имеющего комплексные корни.
Пример 7. Шаг 1. Дан интеграл от рациональной функции
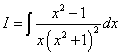 .
.
Решение. Квадратный трёхчлен 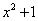 имеет
комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
имеет
комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
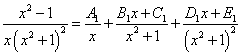 .
.
Пример 8. Шаг 1.
Дан интеграл от рациональной функции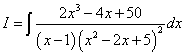 .
.Решение. Квадратный трёхчлен в знаменателе имеет комплексные корни и присутствует в подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
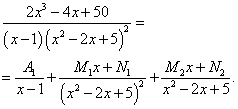 .
.
На первом шаге мы представили подынтегральные дроби в виде суммы дробей с неопределёнными коэффициентами. В начале этого шага потребуется привести полученную сумму дробей к общему знаменателю. После этого в их числителях будут произведения неопределённых коэффициентов на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях.
Полученное таким образом выражение приравнивается к числителю исходной дроби. Затем составляется система из уравнений, в которых степени икса одинаковы. Путём решения системы и находятся неопределённые коэффициенты. Для решения достаточно знать, как системы уравнений решаются
Пример 1. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
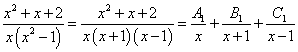 .
.
Умножаем неопределённые коэффициенты на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях:
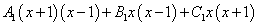 .
.
Раскрываем скобки и приравниваем полученое к полученному выражению числитель исходной подынтегральной дроби:
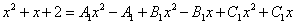 .
.
В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений:
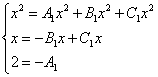 .
.
Сокращаем все иксы и получаем эквивалентную систему уравнений:
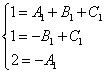 .
.
Решая систему, получаем следующие значения неопределённых коэффициентов:
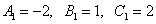 .
.
Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:
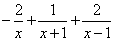 .
.
Пример 2. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
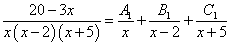 .
.
Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:
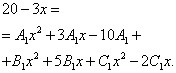
Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:
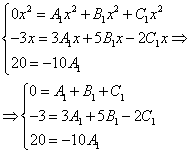
Решаем полученную систему:
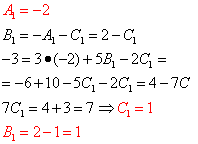
Итак, 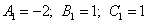 , отсюда
получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
, отсюда
получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
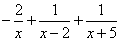 .
.
Пример 3. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
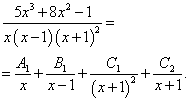
Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:
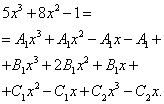
Как и в предыдущих примерах составляем систему уравнений:
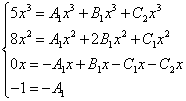
Сокращаем иксы и получаем эквивалентную систему уравнений:
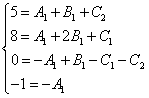
Решая систему, получаем следующие значения неопределённых коэффициентов:
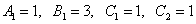 .
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
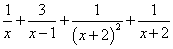 .
.
Пример 4. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
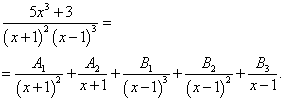 .
.
Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров. Поэтому лишь для контроля приведём получившуюся систему уравнений:
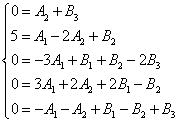
Решая систему, получаем следующие значения неопределённых коэффициентов:
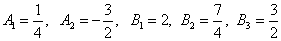 .
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
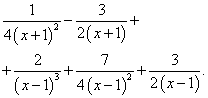
Пример 5. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
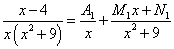 .
.
Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:
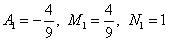 .
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
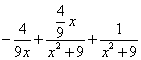 .
.
Пример 6. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
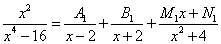
Производим с этой суммой те же действия, что и в предыдущих примерах. В результате должна получиться следующая система уравнений:
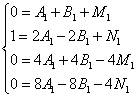
Решая систему, получаем следующие значения неопределённых коэффициентов:
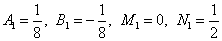 .
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
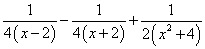 .
.
Пример 7. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
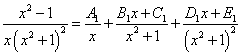 .
.
После известных действий с полученной суммой должна получиться следующая система уравнений:
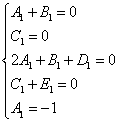
Решая систему, получаем следующие значения неопределённых коэффициентов:
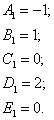 .
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
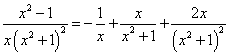 .
.
Пример 8. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
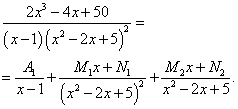 .
.
Внесём некоторые изменения в уже доведённые до автоматизма действия для получения системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения к числителю исходной дроби, получаем:
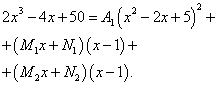
Можно заметить, что если принять за значение икса единицу, то второе и третье
слагаемые в правой части равенства обратятся в нули и нет необходимости их вычислять. Тогда получаем,
что 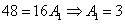 .
Далее по уже отработанной схеме получаем систему уравнений:
.
Далее по уже отработанной схеме получаем систему уравнений:
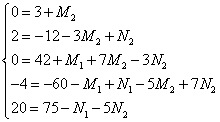
Решая систему, получаем следующие значения неопределённых коэффициентов:
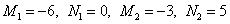 .
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
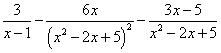 .
.
Полученные простые дроби и интегировать проще. К исходной сумме дробей применяется правило интеграла суммы (интеграл суммы равен сумме интегралов) и табличные интегралы. Чаще всего требуется применять табличные интегралы, приводящие к натуральному логарифму и арктангенсу.
Пример 1. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
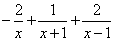 .
.
Интегрируем изначальную рациональную функцию как сумму дробей и используем табличный интеграл, приводящий к натуральному логарифму:
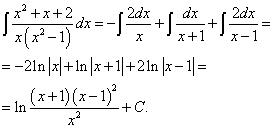
Последнее действие с натуральным логарифмом — приведение к единому выражению под логарифмом — может требоваться при выполнении работ, но требуется не всегда.
Пример 2. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
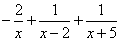 .
.
Вновь применяем табличный интеграл, приводящий к натуральному логарифму:
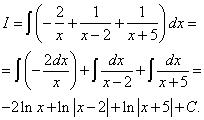
Пример 3. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
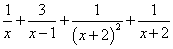 .
.
В результате интегрирования получаем сумму натуральных логарифмов и одной простой дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:
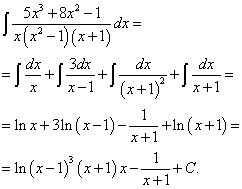
Пример 4. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
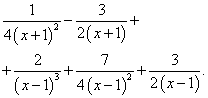
В результате интегрирования получаем сумму натуральных логарифмов и одной дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:
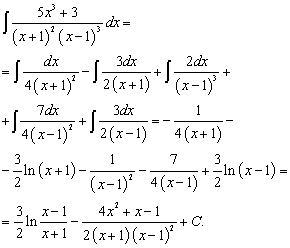
Пример 5. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
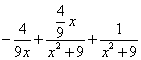 .
.
Интегрируем и получаем сумму натурального логарифма и арктангенса:
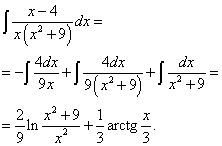
Пример 6. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
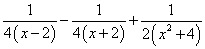 .
.
Опять получаем сумму натурального логарифма и арктангенса:
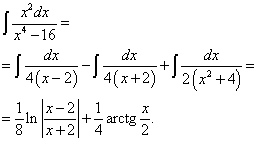
Пример 7. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
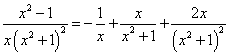 .
.
Интегрируя, получаем натуральные логарифмы и дробь:
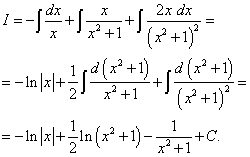
Приведение к единому логарифму попробуйте выполнить самостоятельно.
Пример 8. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
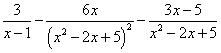 .
.
Интегрируя, получаем сумму натурального логарифма, арктангенса и дроби:
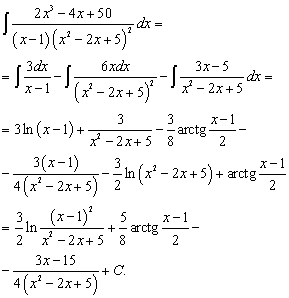

Начало темы «Интеграл»
Продолжение темы «Интеграл»
Примеры интегрирования рациональных функций (дробей)
Здесь мы приводим подробные решения трех примеров интегрирования следующих рациональных дробей:
, , .
Пример 1
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит рациональная функция, поскольку подынтегральное выражение является дробью из многочленов. Степень многочлена знаменателя (3) меньше степени многочлена числителя (4). Поэтому, вначале необходимо выделить целую часть дроби.
1. Выделим целую часть дроби. Делим x 4 на x 3 – 6x 2 + 11x – 6:
Отсюда
.
2. Разложим знаменатель дроби на множители. Для этого нужно решить кубическое уравнение:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, 3, 6, –1, –2, –3, –6.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим на x – 1:
Отсюда
.
Решаем квадратное уравнение .
.
Корни уравнения: , .
Тогда
.
3. Разложим дробь на простейшие.
.
Итак, мы нашли:
.
Интегрируем.
Ответ
.
Пример 2
Вычислить интеграл:
.
Решение
Здесь в числителе дроби – многочлен нулевой степени (1 = x 0). В знаменателе – многочлен третьей степени. Поскольку 0 < 3, то дробь правильная. Разложим ее на простейшие дроби.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение третьей степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 3 (члена без x). То есть целый корень может быть одним из чисел:
1, 3, –1, –3.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим x 3 + 2x – 3 на x – 1:
Итак,
.
Решаем квадратное уравнение:
x 2 + x + 3 = 0.
Находим дискриминант: D = 1 2 – 4·3 = –11. Поскольку D < 0, то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x – 1)(x 2 + x + 3):
(2.1) .
Подставим x = 1. Тогда x – 1 = 0,
.
Подставим в (2.1) x = 0:
1 = 3A – C;
.
Приравняем в (2.1) коэффициенты при x 2:
;
0 = A + B;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
(2.2) .
Для вычисления второго интеграла, выделим в числителе производную знаменателя и приведем знаменатель к сумме квадратов.
;
;
.
Вычисляем I2.
.
Поскольку уравнение x 2 + x + 3 = 0 не имеет действительных корней, то x 2 + x + 3 > 0. Поэтому знак модуля можно опустить.
Поставляем в (2.2):
.
Ответ
.
Пример 3
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит дробь из многочленов. Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3. Степень многочлена знаменателя дроби равна 4. Поскольку 3 < 4, то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение четвертой степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли один корень x = –1. Делим на x – (–1) = x + 1:
Итак,
.
Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли еще один корень x = –1. Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.
Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x + 1) 2(x 2 + 2):
(3.1) .
Подставим x = –1. Тогда x + 1 = 0,
.
Продифференцируем (3.1):
;
.
Подставим x = –1 и учтем, что x + 1 = 0:
;
; .
Подставим в (3.1) x = 0:
0 = 2A + 2B + D;
.
Приравняем в (3.1) коэффициенты при x 3:
;
1 = B + C;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
6.3 Интегрирование рациональных функций. — ПриМат
Рациональной функцией (или дробью) называется функция вида
$$f(x) = \displaystyle\frac{P(x)}{Q(x)},$$
где $P(x)$ и $Q(x)$ – многочлены. Если степень числителя меньше степени знаменателя, то рациональная дробь называется правильной. Ясно, что каждая рациональная дробь может быть представлена в виде
$$\displaystyle\frac{P(x)}{Q(x)} = R(x) + \displaystyle\frac{P_{1}(x)}{Q(x)},$$
где $R(x)$ – многочлен, а дробь $\displaystyle\frac{P_{1}(x)}{Q(x)}$ – правильная. Поскольку интегралы от многочленов вычисляются совсем просто, то мы будем рассматривать методы интегрирования правильных дробей.
Будем различать следующие четыре вида дробей:
- $\displaystyle\frac{A}{x-a}$, где $A$, $a$ — постоянные.
- $\displaystyle\frac{A}{(x-a)^k}$, где $A$, $a$ — постоянные, $k = 2,3 \ldots$
- $\displaystyle\frac{Mx + N}{x^2 + px + q}$, где $M$, $N$, $p$, $q$ – постоянные, квадратный трехчлен в знаменателе не имеет действительных корней.
- $\displaystyle\frac{Mx + N}{(x^2 + px + q)^k}$, где $M$, $N$, $p$, $q$ – постоянные, квадратный трехчлен в знаменателе не имеет действительных корней.
Покажем как вычисляются интегралы от каждой из этих дробей.
- $\int \displaystyle\frac{a}{x-a}dx = A\ln\left | x — a \right | + C$.
- $\int \displaystyle\frac{a}{(x-a)^k}dx = -\frac{A}{k-1}\cdot \displaystyle\frac{1}{(x-a)^{k-1}} + C$.
- $\int \displaystyle\frac{Mx + N}{x^2 + px + q}dx$. Для вычисления этого интеграла представим подынтегральное выражение в виде
$$\displaystyle\frac{Mx + N}{x^2 + px + q} = \displaystyle\frac{\frac{M}{2}(2x+p) + N — p\frac{M}{2}}{x^2 + px + q} = \displaystyle\frac{M}{2} \cdot \displaystyle\frac{2x+p}{x^2 + px + q} + \displaystyle\frac{N-p\displaystyle\frac{M}{2}}{x^2 + px + q}.$$
Для вычисления интеграла от первого слагаемого справа, очевидно, достаточно выполнить замену $t = x^2 + px + q$. Тогда получим
$$\int \displaystyle\frac{2x + p}{x^2 + px + q} = \ln(x^2 + px + q) + C.$$
Для вычисления интеграла от второго слагаемого справа выделим полный квадрат в знаменателе, т.е. представим знаменатель в виде $x^2 + px + q = (x+\displaystyle\frac{p}{2})^2 + q — \displaystyle\frac{p^2}{4}$. Поскольку квадратный трехчлен в знаменателе не имеет действительных корней, то его дискриминант $\displaystyle\frac{p^2}{4} — q < 0$. Обозначим $a^2 = q — \displaystyle\frac{p^2}{4}$. Выполняя замену $x + \displaystyle\frac{p}{2} = t$, получим
$$\int \displaystyle\frac{1}{x^2 + px + q}dx = \int \displaystyle\frac{1}{(x+\displaystyle\frac{p}{2})^2 + a^2}dx = \int \displaystyle\frac{dt}{t^2 + a^2} = \frac{1}{a^2} \int \displaystyle\frac{dt}{\displaystyle\frac{t^2}{a^2} + 1} =\\= \displaystyle\frac{1}{a} \int \displaystyle\frac{d(\displaystyle\frac{t}{a})}{(\displaystyle\frac{t}{a})^2 + 1} = \displaystyle\frac{1}{a} \text{arctg}\: \displaystyle\frac{t}{a} + C .$$
Возвращаясь теперь к старой переменной, получим исходный интеграл. - $\displaystyle\frac{Mx + N}{(x^2 + px + q)^k}$. Для вычисления этого интеграла, как и в предыдущем случае, представим подынтегральное выражение в виде
$$\displaystyle\frac{Mx + N}{(x^2 + px + q)^k} = \displaystyle\frac{\frac{M}{2}(2x + p) + N — p\displaystyle\frac{M}{2}}{(x^2 + px + q)^k} =\\=\displaystyle\frac{M}{2} \cdot \displaystyle\frac{2x+p}{(x^2 + px + q)^k} + \displaystyle\frac{N-p\frac{m}{2}}{(x^2 + px + q)^k}.$$
Для вычисления интеграла от первого слагаемого справа, очевидно, достаточно выполнить замену $t = x^2 + px + q.$ Тогда получим
$$\int \displaystyle\frac{2x + p}{(x^2 + px + q)^k}dx = \displaystyle\frac{1}{-k+1}(x^2+px+q)^{-k+1} +C.$$
Для вычисления интеграла от второго слагаемого, как и в предыдущем случае, выделим полный квадрат из квадратного трехчлена в знаменателе. Тогда после замены переменной $t = x+\displaystyle\frac{p}{2}$ он сведется к интегралу вида $\int \displaystyle\frac{dt}{(t^2+a^2)^k}$. Обозначим этот интеграл через $I_{k}$ и выведем рекуррентную формулу для вычисления этого интеграла. Будем применять формулу интегрирования по частям. Имеем
$$ I_{k} = \int \displaystyle\frac{dt}{(t^2 + a^2)^k} = \begin{bmatrix}u = \displaystyle\frac{1}{(t^2+a^2)^k}, & dv = dt \\ du = -\displaystyle\frac{2kt}{(t^2+a^2)^{k+1}}, & v = t \end{bmatrix} =\\=\displaystyle\frac{t}{(t^2 + a^2)^k} + 2k\int \displaystyle\frac{t^2}{(t^2 + a^2)^{k+1}}dt = \displaystyle\frac{t}{(t^2 + a^2)^k}+2k\int\displaystyle\frac{t^2 + a^2 — a^2}{(t^2 + a^2)^{k+1}}dt =\\= \displaystyle\frac{t}{(t^2 + a^2)^k} + 2k\int \displaystyle\frac{dt}{(t^2 + a^2)^k} — 2ka^2 \int \displaystyle\frac{dt}{(t^2 + a^2)^{k+1}} =\\= \displaystyle\frac{t}{(t^2 + a^2)^k} + 2kI_{k} — 2ka^2I_{k+1}.$$
Отсюда находим
$$I_{k+1} = \displaystyle\frac{1}{2ka^2}\begin{bmatrix} \displaystyle\frac{t}{(t^2 + a^2)^k} +(2k-1)I_k \end{bmatrix} (k = 1,2,\ldots).$$
При этом, как мы уже вычислили ранее,
$$I_{1} = \int \displaystyle\frac{dt}{t^2 + a^2} = \displaystyle\frac{1}{a} \text{arctg}\:\displaystyle\frac{t}{a} + C.$$
Итак, и в этом случае мы получили правило вычисления интеграла от дроби четвертого вида.
Из основной теоремы алгебры следует, что каждый многочлен с действительными коэффициентами может быть представлен в виде произведения конечного числа линейных сомножителей вида $x — a$ и квадратичных сомножителей вида $x^2 + px + q$, где $\displaystyle\frac{p^2}{4} — q < 0$. Именно, справедливо равенство
$$Q(x) = A(x-a_1)^{k_1}\ldots(x-a_r)^{k_r}(x^2+p_1x+q_1)^{m_1}\ldots(x^2+p_sx+q_s)^{m_s}, (1)$$
где $k_i$ и $m_i$ – целые неотрицательные числа.
С использованием этого представления можно показать, что справедлива следующая
Теорема. Пусть $\displaystyle\frac{P(x)}{Q(x)}$ – правильная дробь, знаменатель которой допускает разложение (1). Тогда эта дробь единственным образом может быть представлена в виде суммы простых дробей, т.е.
$$\displaystyle\frac{P(x)}{Q(x)} = \sum_{i=1}^{r}\sum_{j=1}^{k_i}\displaystyle\frac{A_{ij}}{(x-a_i)^j} + \sum_{i=1}^{r}\sum_{j=1}^{m_i}\displaystyle\frac{M_{ij}x + N_{ij}}{(x^2 + P_ix+q_i)^j}.$$
Выше уже показано, что интеграл от каждой простой дроби выражается через элементарные функции. Таким образом, справедлива
Теорема. Каждая рациональная дробь имеет первообразную, которая выражается через элементарные функции, а именно, с помощью рациональных функций, логарифмической функции и арктангенса.Метод Остроградского. Этот метод интегрирования рациональных дробей предназначен для выделения рациональной части из интеграла от рациональной функции. Именно, используя представление (1), интеграл от правильной дроби представляется в виде
$$\int \displaystyle\frac{P(x)}{Q(x)} =\\=\int \displaystyle\frac{P(x)}{A(x-a_1)^{k_1}\ldots(x-a_r)^{k_r}(x^2+p_1x +q_1)^{m_1}\ldots(x^2+p_sx+q_s)^{m_s}}dx =\\=\int \displaystyle\frac{R_{k_1 + \ldots + k_r + 2(m_1 + \ldots + m_s) — r — 2s — 1}(x)dx}{A(x-a_1)^{k_1-1}\ldots(x-a_r)^{k_r-1}(x^2+p_1x +q_1)^{m_1-1}\ldots(x^2+p_sx+q_s)^{m_s-1}} +\\+ \int \displaystyle\frac{S_{r+2r-1}(x)}{A(x-a_1)…(x-a_r)(x^2+p_1x +q_1)^{m_1-1}\ldots(x^2+p_sx+q_s)}dx,$$
где многочлены $R_{k_1+\ldots+k_r+2(m_1 + \ldots + m_s)-r-2s-1}(x)$ и $S_{r+2s-1}(x)$ степени $k_1+\ldots+k_r+2(m_1+\ldots+m_s)-r-2s-1$ и $r+2s-1$ соответственно имеют неопределенные коэффициенты. Эти коэффициенты находятся затем из условия равенства производных левой и правой частей записанного равенства. Таким образом, вычисление интеграла от правильной дроби сводится к вычислению интеграла от другой правильной дроби, у которой в знаменателе все множители в первой степени. Такой интеграл вычисляется, как указано выше, путем разложения подынтегрального выражения
на простые дроби. Тем самым отпадает необходимость в использовании полученной выше рекуррентной формулы для вычисления интегралов от простой дроби четвертого типа.
Примеры решения задач
- Найти неопределенный интеграл $I = \int \displaystyle\frac{2x^2 — 3x + 3}{x^3 — 2x^2 + x}dx$.
РешениеРазложим знаменатель на множители: $x^3 -2x^2 + x = x(x-1)^2$. Тогда подынтегральная функция представима в виде
$$\displaystyle\frac{2x^2-3x+3}{x(x-1)^2} = \displaystyle\frac{A}{x} + \displaystyle\frac{B}{x-1} + \displaystyle\frac{C}{(x-1)^2},$$
где $A$, $B$, $C $ – постоянные коэффициенты. Для их нахождения приведем выражение справа к общему знаменателю и, приравнивая числители полученных дробей, найдем$$2x^2-3x+3=A(x-1)^2 + Bx(x-1)+Cx.$$
Поскольку это тождество имеет место при всех $x$, кроме $x=0,x=1,$ то коэффициенты этих многочленов при одинаковых степенях $x$ равны. Приравнивая их, получаем линейную систему уравнений
$$\left.\begin{matrix}x^2 : & A+B=2\\ x : & -2A-B+C=-3\\ x^0 : & A=3\end{matrix}\right\}$$
Решая эту систему, находим $A = 3$, $B = −1$, $C = 2.$ Подставляя эти значения в разложение подынтегральной функции и вычисляя соответствующие интегралы, получаем
$$I=3\ln\left | x \right | — \ln \left | x-1 \right | — \displaystyle\frac{2}{x-1} + C = \ln \displaystyle\frac{\left | x \right |^3}{\left | x-1 \right |} — \displaystyle\frac{2}{x-1} +C.$$ - Найти неопределенный интеграл $I = \int \displaystyle\frac{x dx}{x^3 + 1}dx$.
РешениеКак и в предыдущем примере, разложим на множители знаменатель:
$$x^3 + 1 = (x+1)(x^2-x+1).$$
Раскладываем подынтегральное выражение с неопределнными коэффициентами
$$\displaystyle\frac{x}{x^3 + 1} = \displaystyle\frac{A}{x+1} + \displaystyle\frac{Mx+N}{x^2-x+1},$$
откуда $x = A(x^2−x+1)+(Mx+N)(x+1)$. Приравнивая коэффициенты при одинаковых степенях $x$, составляем линейную систему для нахождения чисел $A$, $M$, $N$:
$$\left.\begin{matrix}x^2 : & 0+A+M,\\ x : & 1=-A+M+N,\\ x^0 : & 0=A+N.\end{matrix}\right\}$$
Решая эту систему, находим $A = −\displaystyle\frac{1}{3}, M = N =\displaystyle\frac{1}{3}$. Поэтому
$$I=-\displaystyle\frac{1}{3}\ln\left | x+1 \right | + \displaystyle\frac{1}{3}\int \displaystyle\frac{x+1}{x^2-x+1}dx=\\=-\displaystyle\frac{1}{3}\ln\left | x+1 \right | + \displaystyle\frac{1}{6}\int \displaystyle\frac{2x-1}{x^2-x+1}dx + \displaystyle\frac{1}{2}\int \displaystyle\frac{dx}{x^2-x+1}=\\=-\displaystyle\frac{1}{3}\ln\left | x+1 \right | + \displaystyle\frac{1}{6}\ln(x^2-x+1) + \displaystyle\frac{1}{2} \int \displaystyle\frac{dx}{(x — \displaystyle\frac{1}{2})^2 + \displaystyle\frac{3}{4}} =\\=-\displaystyle\frac{1}{3}\ln\left | x+1 \right | + \displaystyle\frac{1}{6}\ln(x^2-x+1) + \displaystyle\frac{1}{\sqrt{3}}\text{arctg}\:\displaystyle\frac{2}{\sqrt{3}}(x-\displaystyle\frac{1}{2}) + C.$$ - Найти неопределенный интеграл $\int \displaystyle\frac{(x^2 — 19x + 6)}{(x-1)(x^2 + 5x + 6)}dx$
РешениеРазложим знаменатель на множители: $(x-1)(x^2+5x+6) = (x-1)(x-2)(x-3).$ Тогда подынтегральная функция представима в виде:
$$\displaystyle\frac{x^2-19x+6}{(x-1)(x^2+5x+6)} = \displaystyle\frac{A}{x-1} + \displaystyle\frac{B}{x+2} + \displaystyle\frac{C}{x+3}$$
Для нахождения $A, B$ и $C$ приведем выражение справа к общему знаменателю и, приравнивая числители полученных дробей, найдем
$$A(x^2 + 5x + 6) + B(x^2 + 2x — 3) + c(x^2 + x — 2) = x^2 -19x+6$$
Приравнивая коэффициенты при одинаковых степенях $x$, составляем систему линейных уравнений для нахождения чисел $A, B, C$
$$\left.\begin{matrix} x^2 : & 1=A+B+C \\ x : & -19 = 5A+2B+C \\ x^0 : & 6=6A-3B-2C \end{matrix}\right\}$$
Решаем систему, получаем значения $A = -1; B = -16; C=18$. Возвращаемся к изначальному интегралу и находим окончательное решение
$$\int (-\displaystyle\frac{1}{x-1}-\displaystyle\frac{16}{x+2}+\displaystyle\frac{18}{x+3})dx = -\ln\left | x-1 \right | — 16\ln\left | x+2 \right |+18\ln\left | x+3 \right | + C.$$ - Найти неопределенный интеграл $\int \displaystyle\frac{x^2-6x+8}{x^3+8}dx$
РешениеПо формуле суммы кубов раскладываем знаменатель на множители, используя формулу сокращенного умножения $a^3 + b^3 = (a+b)(a^2-ab+b^2)$
$$\int \displaystyle\frac{x^2-6x+8}{x^3+8}dx = \int \displaystyle\frac{x^2-6x+8}{(x+2)(x^2-2x+4)}dx.$$
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей
$$\displaystyle\frac{A}{x+2} +\displaystyle\frac{Bx+C}{x^2-2x+4} = \displaystyle\frac{x^2-6x+8}{(x+2)(x^2-2x+4)}.$$
Приводим дробь к общему знаменателю
$$A(x^2 — 2x + 4) + B(x^2 + 2x) + C(x+2) = x^2-6x+8$$
Составим и решим систему
$$\left.\begin{matrix}x^2 : & A+B=1\\ x : & -2A+2B+C=-6\\ x^0 : & 4A+2C=8\end{matrix}\right\}$$
Подставим значения $A = 2$, $B = -1$, $C = 0$ в функцию и найдем интеграл
$$\int (\displaystyle\frac{2}{x+2} — \displaystyle\frac{x}{x^2-2x+4})dx = 2\int \displaystyle\frac{dx}{x+2} + \int \displaystyle\frac{-\displaystyle\frac{1}{2}d(x^2-2x+4) — dx}{x^2 -2x +4} =\\= 2\ln \left | x+2 \right | — \displaystyle\frac{1}{2}\int\displaystyle\frac{d(x^2-2x+4)}{x^2-2x+4} — \int\displaystyle\frac{dx}{x^2-2x+1 +3} = \\= 2\ln \left | x+2 \right | — \frac{1}{2}\ln(x^2 — 2x + 4) — \int \frac{d(x-1)}{(x-1)^2 + (\sqrt{3})^2} = \\= 2\ln \left | x+2 \right | — \frac{1}{2}\ln(x^2 — 2x + 4) — \frac{1}{\sqrt{3}}\text{arctg}\:(\frac{x-1}{\sqrt{3}}) + C.$$
Литература:
Смотрите также:
Поделиться ссылкой:
Похожее
Интегрирование рациональных дробей и функций
1. Интегрирование рациональных дробей.
2. Алгоритм интегрирования рациональной дроби.
3. Примеры интегрирования рациональных функций.
Интегрирование рациональных дробей
Рациональной дробью называется дробь вида
– многочлены степени m и n соответственно. Рациональная дробь называется правильной , если степень числителя меньше степени знаменателя (m<n), в противном случае дробь называется неправильной .
Простейшими элементарными дробями называются дроби следующего вида:
Пример 1
Пример 2
Интегралы, содержащие в знаменателе квадратный трехчлен, можно вычислить, применяя прием выделения полного квадрата разности или суммы. Рассмотрим пример такого интеграла.
Пример 3.
Алгоритм интегрирования рациональной дроби
1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:
2. Знаменатель разложим на простейшие сомножители: Qn(x)
3. Представим дробь
виде суммы простейших дробей с неопределенными коэффициентами.
- Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства.
- Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях x.
- Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая равным действительным корням знаменателя.
- Подставим найденные коэффициенты A1,A2,…,Cs,Ds в разложение дроби.
- Проинтегрируем простейшие дроби.
Примеры интегрирования рациональных функций
Пример 4.
Корни знаменателя: x=1, а x2+1 = 0 не имеет действительных корней.
Тогда разложение для данной дроби имеет вид:
Приводя полученные дроби к общему знаменателю, получим тождество:
Пример 5.
Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.
Подставим найденные коэффициенты в разложение и проинтегрируем дроби.
Интегрирование дробно-рациональных функций — Студопедия
Дробно-рациональной функцией или рациональной дробью 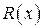 называется отношение двух многочленов:
называется отношение двух многочленов: 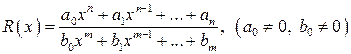 .
.
Если степень многочлена в числителе меньше степени многочлена в знаменателе, т.е. 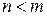 , то рациональная дробь называется правильной. В противном случае рациональная дробь называется неправильной.
, то рациональная дробь называется правильной. В противном случае рациональная дробь называется неправильной.
Интегрирование дробно-рациональной функции проводится в несколько этапов. Сначала мы перечислим эти этапы, а потом подробно поясним каждый из них на примере. Итак, для интегрирования дробно-рациональной функции 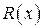 следует:
следует:
1) если рациональная дробь неправильная, то выделить из нее целую часть и правильную рациональную дробь 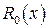 :
: 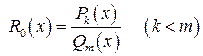 ;
;
2) знаменатель дроби 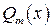 разложить на линейные множители
разложить на линейные множители 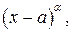
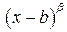 , и квадратные множители
, и квадратные множители 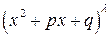 , с действительными коэффициентами;
, с действительными коэффициентами;
3) правильную рациональную дробь разложить методом неопределенных коэффициентов на простейшие дроби
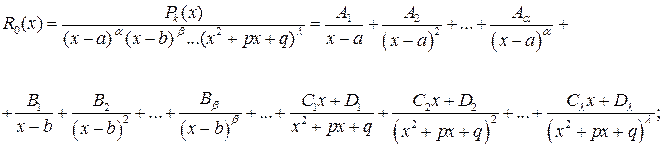
4) найти неопределенные (неизвестные пока) коэффициенты
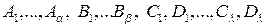 ;
;
5) найти интегралы от целой части и простейших дробей.
Поясним все сказанное на примерах.
Пример 4. Найти интеграл 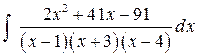 .
.
Подынтегральная функция есть правильная рациональная дробь, так как степень многочлена в числителе меньше степени многочлена в знаменателе. Кроме того, знаменатель уже разложен на линейные множители. Поэтому сразу переходим к разложению рациональной дроби на простейшие дроби с неопределенными коэффициентами:
 .
.
Умножив это равенство на 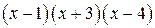 , получим:
, получим:
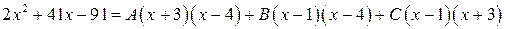 .
.
Подставив в это равенство последовательно 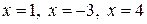 , получим
, получим 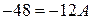 ,
, 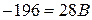 ,
, 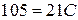 . Таким образом,
. Таким образом, 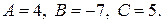
Мы нашли коэффициенты разложения 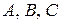 методом частных значений.
методом частных значений.
Теперь подставим найденные значения 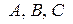 в равенство:
в равенство:
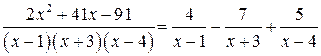 .
.
Проинтегрируем полученные простейшие дроби:
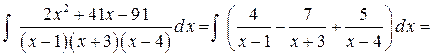

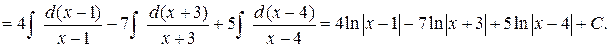
Пример 5. Найти интеграл 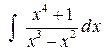 .
.
Подынтегральная функция есть неправильная рациональная дробь, так как степень многочлена в числителе больше степени многочлена в знаменателе. Поэтому выделим из неправильной дроби ее целую часть, поделив числитель на знаменатель.
В результате деления получим:
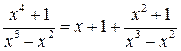 .
.
Теперь знаменатель получившейся правильной дроби разложим на множители 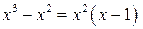 , а саму правильную дробь на простейшие дроби:
, а саму правильную дробь на простейшие дроби:
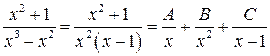 .
.
Умножив это равенство на 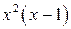 , получим:
, получим:
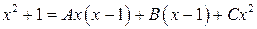 .
.
Подставив в это равенство значения 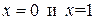 , получим
, получим 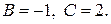
Для отыскания коэффициента 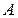 можно либо в равенстве (14.5) подставить еще одно частное значение
можно либо в равенстве (14.5) подставить еще одно частное значение 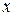 , либо в правой и левой частях равенства (14.5) приравнять коэффициенты при одинаковых степенях
, либо в правой и левой частях равенства (14.5) приравнять коэффициенты при одинаковых степенях 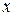 , например, при
, например, при 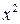 :
: 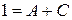 .
.
Тогда 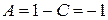 . Подставляя найденные
. Подставляя найденные 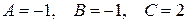 в равенство (14.4) и используя равенство (14.3), окончательно получим
в равенство (14.4) и используя равенство (14.3), окончательно получим
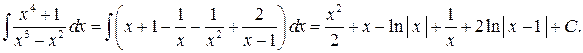
Пример 6. Найти интеграл 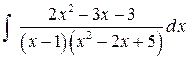 .
.
Подынтегральная функция есть правильная рациональная дробь, так как степень многочлена в числителе меньше степени многочлена в знаменателе. Квадратный трехчлен в знаменателе 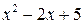 имеет отрицательный дискриминант, следовательно, он не имеет действительных корней и не разлагается на линейные множители с действительными коэффициентами. Поэтому перейдем к разложению рациональной дроби на простейшие:
имеет отрицательный дискриминант, следовательно, он не имеет действительных корней и не разлагается на линейные множители с действительными коэффициентами. Поэтому перейдем к разложению рациональной дроби на простейшие:
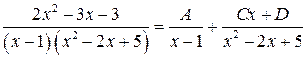 .
.
Умножив это равенство на 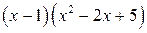 , получим
, получим
 .
.
Подставив в это равенство значения 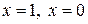 получим:
получим:
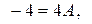
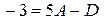 или
или 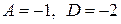 .
.
Кроме того, в правой и левой частях равенства сравним коэффициенты при 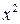 :
: 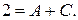 Итак,
Итак, 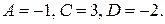 Используя равенство, получим
Используя равенство, получим
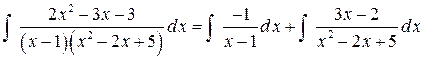 .
.
Найдем первый интеграл: 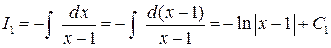 .
.
Для отыскания второго интеграла выделим в числителе производную квадратного трехчлена, стоящего в знаменателе:
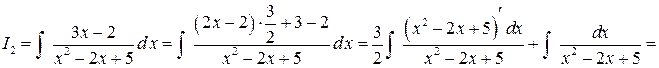
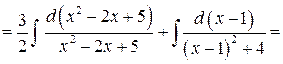
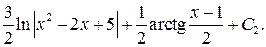
Складывая 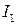 ,
, 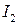 и вводя
и вводя 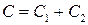 , получим искомый интеграл:
, получим искомый интеграл:
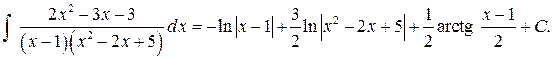
Пример 7. Найти интеграл 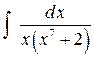 .
.
Здесь разложение знаменателя на линейные и квадратичные множители и разложение дроби на простейшие требуют громоздких выкладок. Значительно проще вынести из скобки 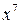 :
: 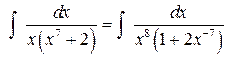
и воспользоваться тем, что 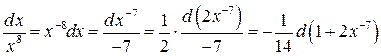 .
.
Тогда 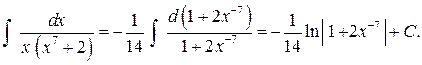
Пример 8. Найти интеграл 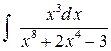 .
.
Решение. Как и в предыдущем примере, разложение знаменателя на линейные и квадратичные множители и разложение дроби на простейшие требуют громоздких выкладок. Удобнее воспользоваться тем, что 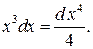 Тогда
Тогда

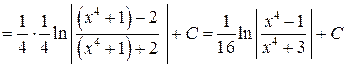 .
.
Алгоритм интегрирования рациональных функций — Студопедия.Нет
Рациональная функция — это дробь вида 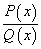 , числитель и знаменатель которой — многочлены или произведения многочленов.
, числитель и знаменатель которой — многочлены или произведения многочленов.
Из урока «Интегрирование некоторых рациональных дробей и иррациональностей» известно, что рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе. В том же уроке говорилось о том, как представить неправильную дробь в виде суммы её целой части и некоторой правильной дроби.
На этом уроке будем учиться интегрировать такие рациональные функции, которые представлены в виде правильных дробей. Для этого существует метод неопределённых коэффициентов, основанный на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.
Приведённый ниже алгоритм интегирования рациональных функций будет пошагово проиллюстрирован в примерах.
Алгоритм интегрирования рациональных функций
- Шаг 1.Определить вид многочлена в знаменателе дроби (он может иметь действительные, кратные действительные, комплексные и кратные комплексные корни) и в зависимости от вида разложить дробь на простые дроби, в числителях которых — неопределённые коэффициенты, число которых равно степени знаменателя.
- Шаг 2.Определить значения неопределённых коэффициентов. Для этого потребуется решить систему уравнений, сводящуюся к системе линейных уравнений.
- Шаг 3.Найти интеграл исходной рациональной функции (дроби) как сумму интегралов полученных простых дробей, к которым применяются табличные интегралы.
Переходим к первому шагу алгоритма
Шаг 1: разложение исходной дроби
Многочлен в знаменателе имеет действительные корни. То есть, в знаменателе имеет место цепочка сомножителей вида 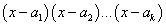 , в которой каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
, в которой каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

Пример 1.Шаг 1.Дан интеграл от рациональной функции  .
.
От нас требуется разложить подынтегральное выражение — правильную дробь 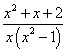 на простые дроби.
на простые дроби.
Решение. Дискриминант уравнения 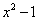 положительный, поэтому многочлен в знаменателе имеет действительные корни. Получаем следующее разложение исходной дроби на сумму простых дробей:
положительный, поэтому многочлен в знаменателе имеет действительные корни. Получаем следующее разложение исходной дроби на сумму простых дробей:
 .
.
Пример 2.Шаг 1.Дан интеграл от рациональной функции
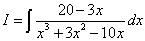 .
.
Решение. Разложим знаменатель подынтегрального выражения на множители. Сначала можно вынести за скобки x. Получаем следующую дробь:
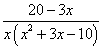 .
.
Для разложения квадратного трёхчлена в скобках решаем квадратное уравнение:
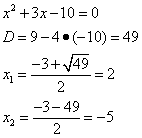
Получаем разложение знаменателя на множители в подынтегральном выражении:
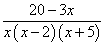 .
.
Дискриминант решённого выше квадратного уравнения положительный, то есть имеем дело со случаем, когда многочлен в знаменателе имеет действительные корни. Разложение исходной дроби подынтегрального выражения будет следующим:
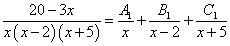 .
.
Как и в первом примере, числа, обозначенные большими буквами, пока неизвестны. Отсюда и название — метод неопределённых коэффициентов.
Многочлен в знаменателе имеет кратные действительные корни. Этот случай имеет место, когда в цепочке сомножителей в знаменателе присутствует выражение вида 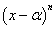 , то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
, то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
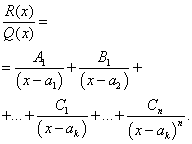
Пример 3.Шаг 1.Дан интеграл от рациональной функции 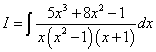 .
.
Решение. Представляем разность квадратов 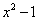 в виде произведения суммы и разности
в виде произведения суммы и разности 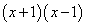 .
.
Тогда подынтегральное выражение запишется в виде
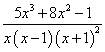 ,
,
все уравнения с многочленами которого имеют действительные корни. Это случай кратных действительных корней, так как последний сомножитель находится во второй степени. Получаем следующее разложение исходной дроби на простые дроби:
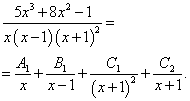
Как видим, в этом случае нужно понижать степень кратного многочлена с исходной до первой и записывать простую дробь с каждой из этих степеней в знаменатель.
Пример 4.Шаг 1.Дан интеграл от рациональной функции 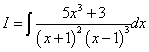 .
.
Решение. Уравнения с многочленами в знаменателе имеют действительные корни, а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее разложение исходной дроби на простые дроби:
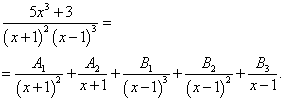 .
.
Многочлен в знаменателе имеет комплексные корни: дискриминант квадратного уравнения 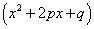 , присутствующего в цепочке сомножителей в знаменателе, меньше нуля. В этом случае при разложении дроби в простой дроби, соответствующей описанному выше сомножителю, в числителе нужно записывать линейное выражение с переменной x (это выражение — последнее в следующей записи):
, присутствующего в цепочке сомножителей в знаменателе, меньше нуля. В этом случае при разложении дроби в простой дроби, соответствующей описанному выше сомножителю, в числителе нужно записывать линейное выражение с переменной x (это выражение — последнее в следующей записи):
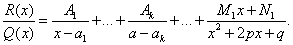
Пример 5.Шаг 1.Дан интеграл от рациональной функции 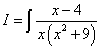 .
.
Решение. Уравнение в скобках имеет комплексные корни, а оба сомножителя присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:
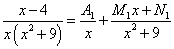 .
.
Пример 6.Шаг 1.Дан интеграл от рациональной функции 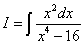 .
.
Решение. Представим знаменатель дроби в подынтегральном выражении в виде следующего произведения сомножителей:
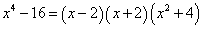 .
.
Решение. Уравнение с последним сомножителем имеет комплексные корни, а все сомножители присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:
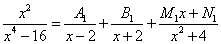
Многочлен в знаменателе имеет кратные комплексные корни: дискриминант квадратного уравнения 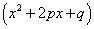 , присутствующего в цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
, присутствующего в цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
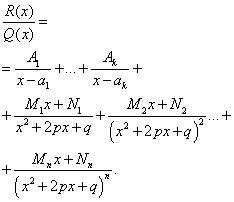
То есть в сумме простых дробей число простых дробей с линейным выражением в числителе должно быть равно степени сомножителя, имеющего комплексные корни.
Пример 7.Шаг 1.Дан интеграл от рациональной функции 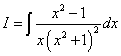 .
.
Решение. Квадратный трёхчлен 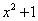 имеет комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
имеет комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
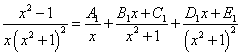 .
.
Пример 8.Шаг 1.Дан интеграл от рациональной функции  .
.
Решение. Квадратный трёхчлен в знаменателе имеет комплексные корни и присутствует в подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
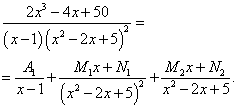 .
.
§5. Интегрирование рациональных функций.
Рациональной функцией называется функция, являющаяся отношением двух многочленов (полиномов):
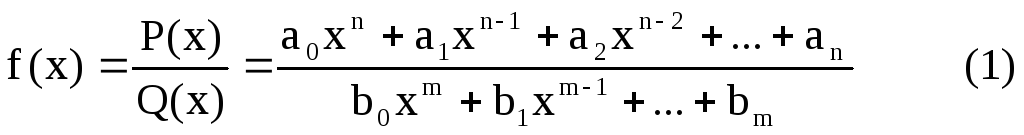
Если Q(x) ≡ 1, то f(x) = P(x) , т.е. многочлен является частным случаем рациональной функции – целая рациональная функция. Рациональную функцию (1) /Q(x)≢1/ называют дробно-рациональной функцией (или рациональной дробью).
Без ограничения общности можно считать, что многочлены P(x) и Q(x) не имеют одинаковых нулей (корней), т. к. в противном случае можно сократить дробь (1) на общие множители.
Рациональною дробь (1) называют правильной, если степень числителя ниже степени знаменателя, т. е. n < m. Если же n ≥ m, (1) называется неправильной.
Если рациональная дробь (1) неправильная, то её можно всегда представить в виде суммы целой рациональной функции (целой части) и правильной рациональной дроби. /например, деля числитель на знаменатель как два полинома/:
г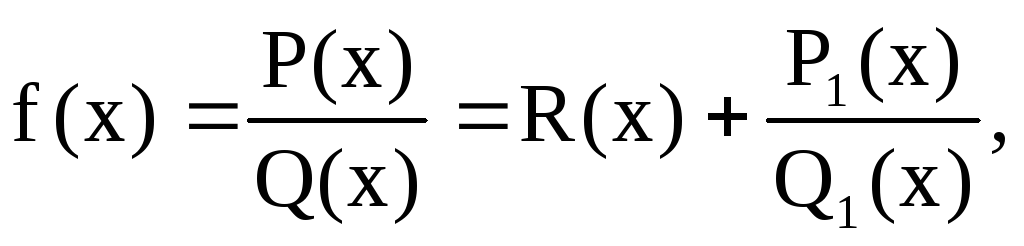 деR(x)
– полином, P1(x)/Q1(x) – правильная дробь.
деR(x)
– полином, P1(x)/Q1(x) – правильная дробь.
Интегрирование полинома не составляет труда, поэтому будем рассматривать
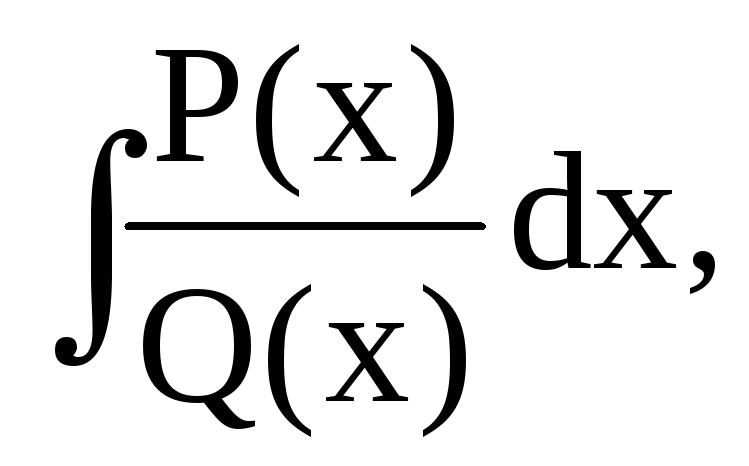
полагая P(x)/Q(x) правильной.
1. Изучим сначала интегрирование простейших (элементарных) рациональных дробей.
Определение. Правильные рациональные дроби вида
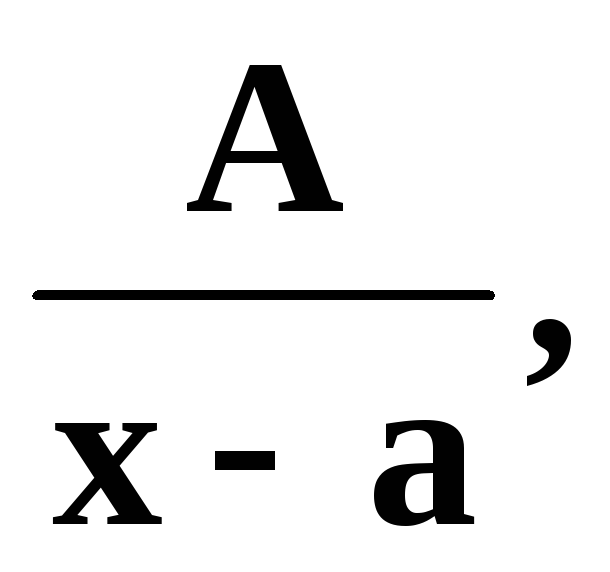
I.
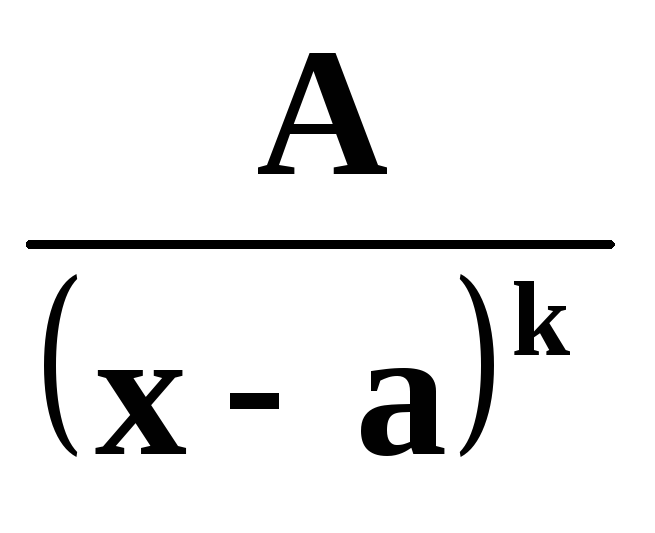
II. /k – натуральное число ≥ 2/,
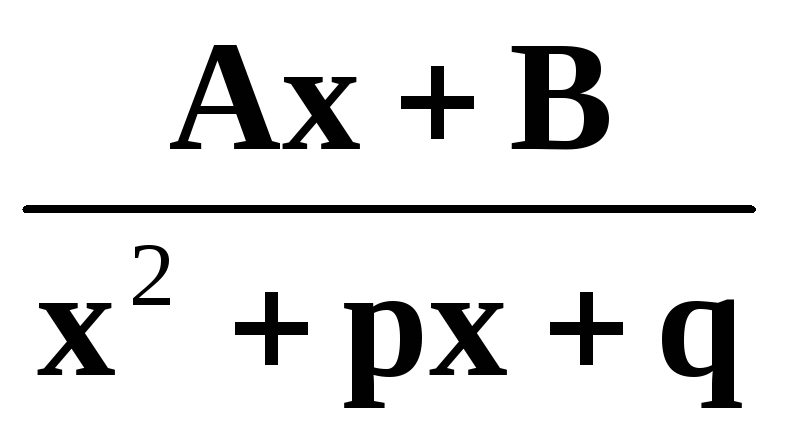
III. /знаменатель не имеет действительных корней, т. е.
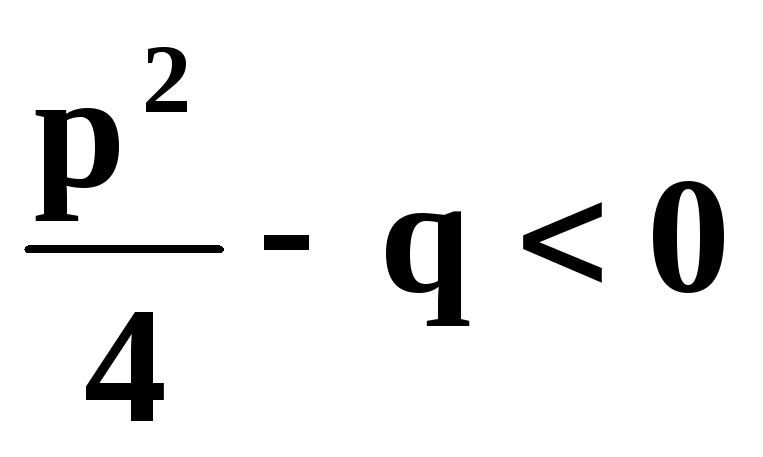
; A, B, a, p, q – действительные числа /,
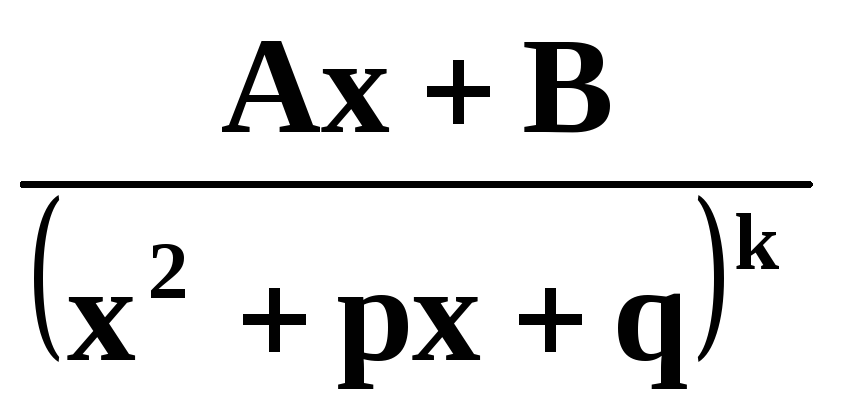
IV. /k – натуральное число ≥ 2; знаменатель не имеет действительных корней/,
называются соответсвенно простейшими рациональными дробями I, II, III и IV типов.
Интегрирование дробей первых трёх типов осуществляется просто.
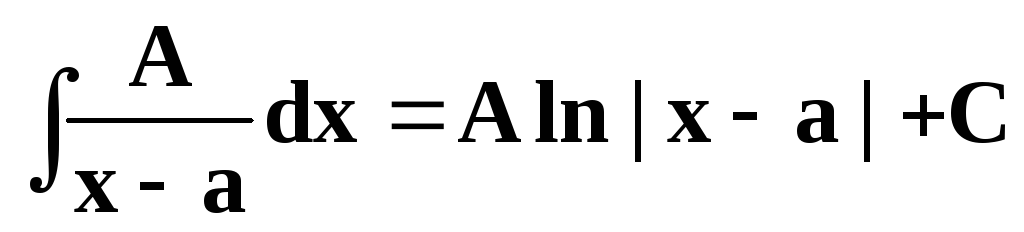
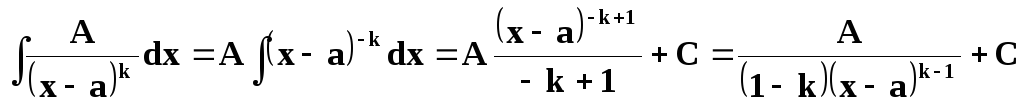
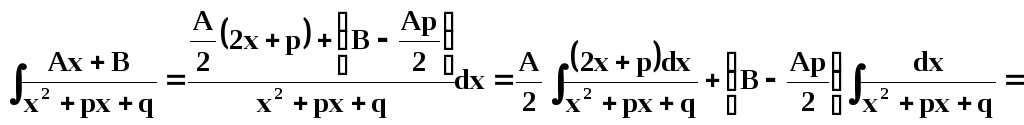
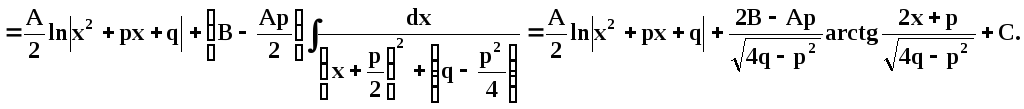
/см. §3/.
Интегрирование простейших дробей IV типа осуществляется таким же методом, но выкладки значительно сложнее. Мы в этом же параграфе рассмотрим метод Остроградского, который позволит интегрировать любые рациональные дроби, применяя интегралы только от простейших дробей первых трёх типов.
2. Разложение рациональной дроби в сумму рациональных дробей. Справедлива (доказательство опускаем) следующая
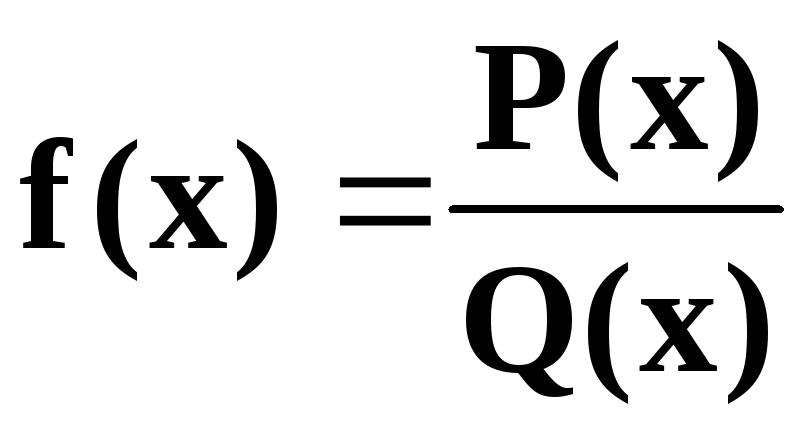
Теорема Всякая правильная несократимая рациональная дробь может
быть представлена как сумма конечного числа простейших рациональных дробей, а именно
е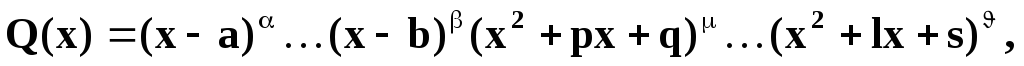 сли(2)
сли(2)
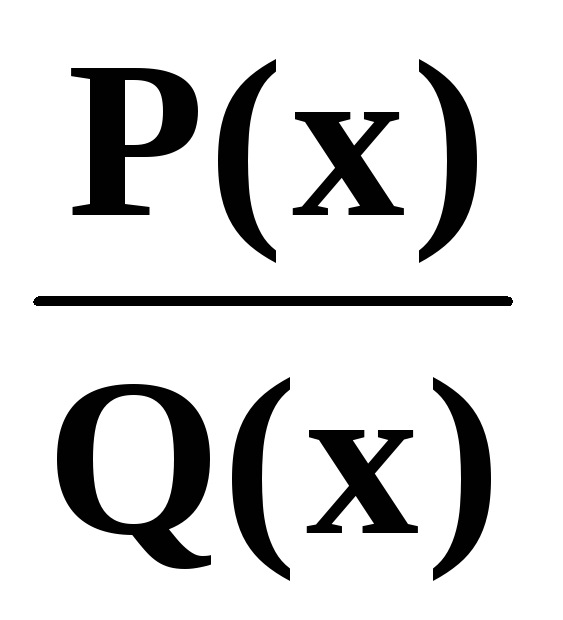
т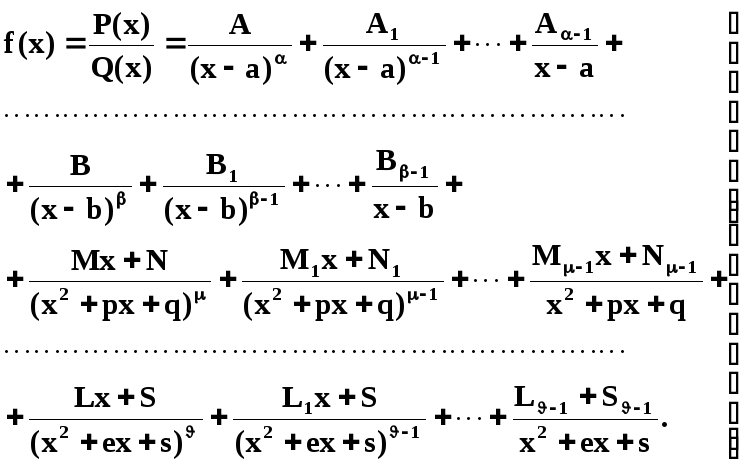 о
дробь может быть представлена
в виде:
о
дробь может быть представлена
в виде:
(3)
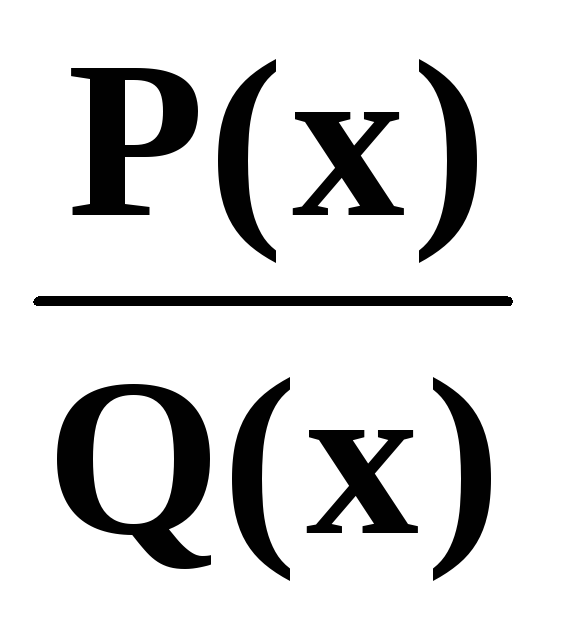 На
практике эту теорему применяют следующим
образом. Каким – либо образом знаменатель
дробиQ(x) представляют в виде (2),
причём квадратные трёхчлены имеют
дискриминанты отрицательные и потому
уже не могут разлагатся в произведение
линейных множителей с действительными
коэффициентами. Затем пишут для дроби
На
практике эту теорему применяют следующим
образом. Каким – либо образом знаменатель
дробиQ(x) представляют в виде (2),
причём квадратные трёхчлены имеют
дискриминанты отрицательные и потому
уже не могут разлагатся в произведение
линейных множителей с действительными
коэффициентами. Затем пишут для дроби
соответствующее разложение (3) с буквенными коэффициентами A,A1, … L-1,
S-1. Эти коэффициенты определяют по методу неопределённых коэффициентов. Равенство (3) есть тождество, поэтому, приведя дроби справа к наименьшему общему знаменателю (он, очевидно будет равен Q(x)), получают тождественное равенство числителей, двух многочленов – P(x) и того, который получится справа. Приравнивая коэффициенты при одинаковых степенях x, получают систему линейных уравнений относительно A, A1, A2, … L-1, S-1, из которой их и определяют.
Замечание 1. Уравнение для определения коэффициентов можно получать и другим способом. Т. к. полученное равенство числителей есть тождество, то давая x конкретные (удобные!) значения, имеют необходимые уравнения для определения этих коэффициентов (более простые, чем в описанной выше системе).
Замечание 2. Из выше изложенного следует такой вывод: неопределённый интеграл от рациональной функции всегда может быть выражен через конечное число элементарных функций.
П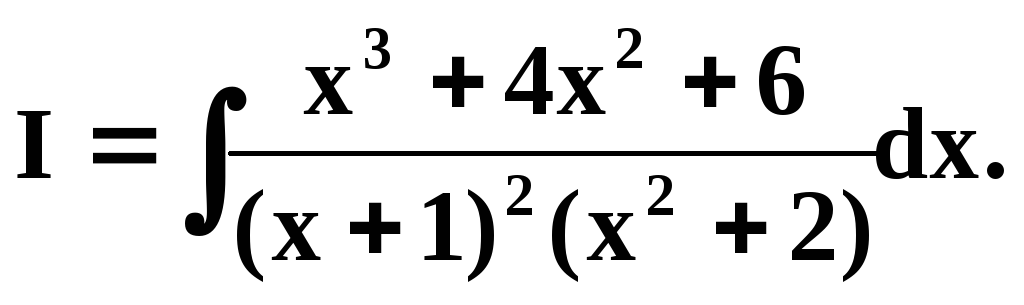 римеры
1)Вычислить
интеграл
римеры
1)Вычислить
интеграл
Подинтегральная функция f(x) является правильной рациональной дробью. Знаменатель уже разложен в произведение простых (неприводимых) множителей, т. к. x2 + 2 не имеет действительных корней /x1,2 = i 2/.
Р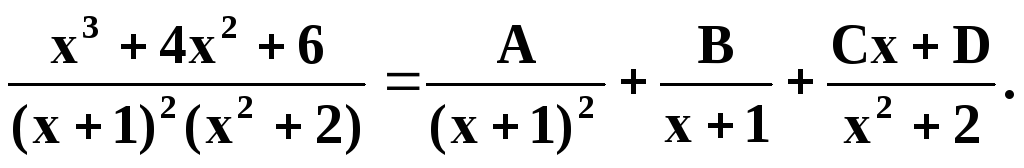 азложим
подинтегральную дробь в сумму простейших
дробей:
азложим
подинтегральную дробь в сумму простейших
дробей:
Приведём дроби справа к наименьшему общему знаменателю и приравняем числители:
x3 + 4x2 + 6 A(x2 + 2) + B(x +1)(x2 + 2) + (Cx + D)(x +1)2. (4)
или x3 + 4x2 + 6 = (B + C)x3 + (A + B + 2C +D)x2 + (2B + 2D + C)x + (2A + 2B + D).
Приравнивая коэффициенты при x3, x2, x1, x0, получим систему четырёх линейных уравнений с четырмя неизвестными A, B, C, D:
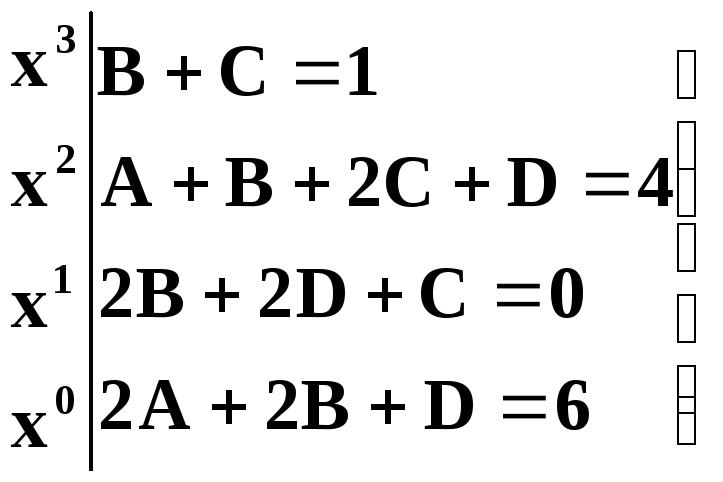
(5)
Ещё из тождества (4) при удобном значении x = – 1 получаем дополнительное простое уравнение: 3A = 9, откуда A = 3
Последующее решение системы (5) даст: B = 1/3, C =2/3, D = –2/3

Итак,
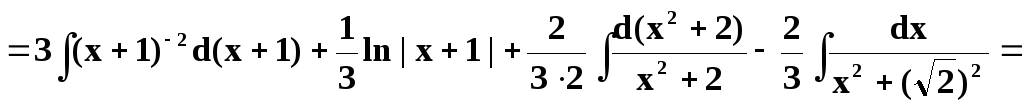
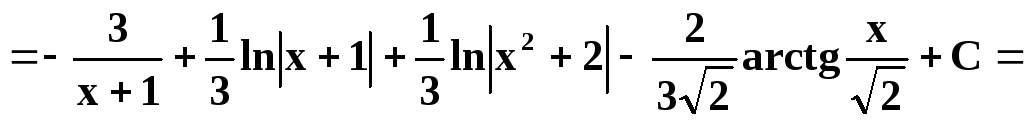
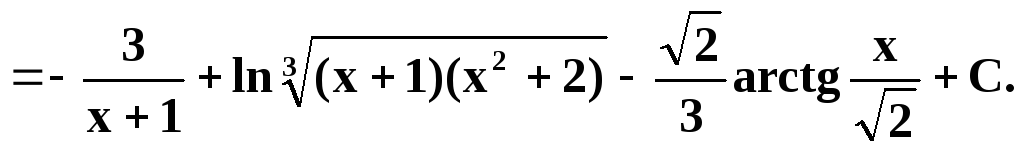
2) Вычислить самостоятельно
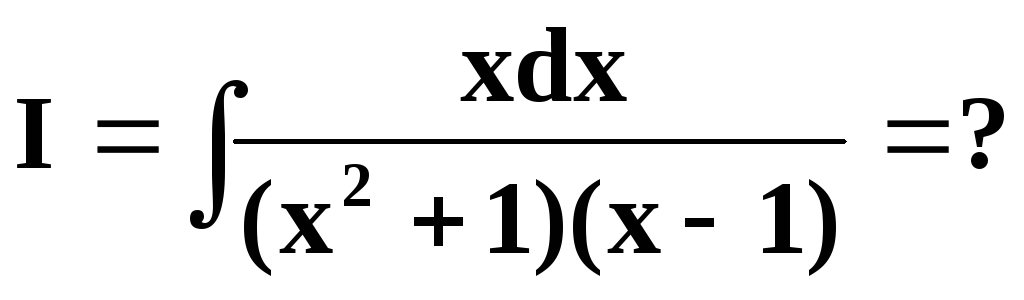
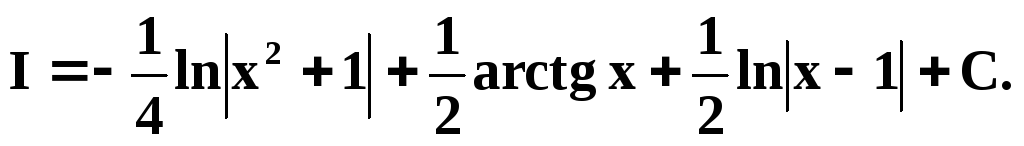
Ответ:
Интегралов от рациональных функций — Исчисление
Наука
- Анатомия и физиология
- Астрономия
- Астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- Физика
Математика
- Алгебра
Интеграция функций Rational
Интеграция функций RationalРациональная функция по определению является отношением двух многочленов. Например
все рациональные функции. Помните в определении рационального
функции, вы не увидите ни | x | для
пример. Обратите внимание, что интеграции по частям будет недостаточно, чтобы помочь
интегрировать рациональную функцию. Следовательно, нужна новая техника.
делать работу.Эта техника называется Разложение
рациональные функции в сумму дробных долей (сокращенно Частичное дробное разложение ).
Давайте подведем итог практических шагов, как интегрировать рациональное
функция:
- 1
- Если выполнить полиномиальное деление в столбик. В противном случае переходите к шагу 2.
- 2
- Разложите знаменатель Q ( x ) на неприводимые многочлены: линейные и неприводимые квадратичные многочлены.
- 3
- Найдите дробное разложение.
- 4
- Интегрируйте результат шага 3.
Замечание: Основная трудность, возникающая в Обычно при использовании этой техники речь идет о шаге 2 и шаг 3. Поэтому настоятельно рекомендуется провести серьезную проверку техника частичной декомпозиции перед тем, как приступить к интеграции дробные функции.
Следующие примеры иллюстрируют случаи в
который вам потребуется для использования техники частичного разложения на фракции:
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор: Мохамед Амин ХамсиАвторское право 1999-2020 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час .n}.
Фонд Викимедиа. 2010.
- Центральное бюро расследований
- Списки интегралов
Посмотреть другие словари:
Список статей по математике (L) — NOTOC LL (сложность) L BFGS L² когомология L функция L игра L нотация L система L теория L Анализ бесконечности Petits pour l Intelligence des Lignes Courbes L Правило Гопиталя L (R) La Géométrie Помеченный граф Теорема о маркированном перечислении Недостаток…… Wikipedia
Список тем по исчислению — Это список тем по исчислению.Примечание: порядок тем в разделах предлагается студентам. Перед исчислением (предварительное вычисление) * График функции * Линейная функция * Секанс * Наклон * Касательная * Вогнутость * Конечная разность * Радиан * Факториал…… Wikipedia
Список тем теории интеграции и меры — Это список тем теории интеграции и меры, на странице Википедии. Интуитивные основы * Длина * Площадь * Объем * Вероятность * Скользящее среднее Интеграл Римана * Сумма Римана * Интеграл Римана Стилтьеса * Ограниченный вариация * Jordan contentImproper…… Wikipedia
Список тригонометрических тождеств — Косинусы и синусы вокруг единичной окружности… Википедия
Список тем по тригонометрии — Это список тем по тригонометрии на странице Википедии.* Угол * Превышение угла * Формула интерполяции Брахмагупты * Многочлены Чебышева * Обозначение треугольника Конвея * Формула Де Муавра * Ядро Дирихле * Формула Эйлера * Точная тригонометрия…… Wikipedia
Список основных тем по тригонометрии — Для более полного списка см. Список тем по тригонометрии. Тригонометрия — это раздел математики, который имеет дело с углами, треугольниками и тригонометрическими функциями, такими как синус, косинус и тангенс. Следующая схема представлена в виде…… Wikipedia
Список реальных тем анализа — это список статей, которые считаются реальными темами анализа.Содержание 1 Общие темы 1.1 Ограничения 1.2 Последовательности и серии 1.2.1 Методы суммирования… Википедия
Список тем численного анализа — Это список тем численного анализа по страницам Википедии. Содержание 1 Общие 2 Ошибка 3 Элементарные и специальные функции 4 Числовая линейная алгебра… Wikipedia
Список математических функций — В математике несколько функций или групп функций достаточно важны, чтобы заслужить свои собственные названия.Это список указателей на статьи, в которых эти функции объясняются более подробно. Есть большая теория специальных функций…… Wikipedia
Список математических статей (D) — DD-распределение NOTOC D модуль DD Агостино критерий К-квадрата D Условие Эйлера D Оператор Аламберта D Формула Аламбера D Парадокс Аламбера D Принцип Аламберта Категория кинжала Компактная категория кинжала Симметричный моноидальный кинжал …… Википедия
интегралов рациональных функций — Скачать PDF бесплатно
Неполные дроби.(х 1) (х 2 + 1)
 Неполные дроби Добавление рациональных функций включает в себя поиск общего знаменателя, переписывание каждой дроби так, чтобы она имела этот знаменатель, а затем сложение. Например, 3x x 1 3x (x 1) (x + 1) (x 1) + 1 (x +
Неполные дроби Добавление рациональных функций включает в себя поиск общего знаменателя, переписывание каждой дроби так, чтобы она имела этот знаменатель, а затем сложение. Например, 3x x 1 3x (x 1) (x + 1) (x 1) + 1 (x +
тождественно равно x 2 + 3x +2
 Неполные дроби 3.6. Введение Часто бывает полезно разбить сложную алгебраическую дробь на сумму более простых дробей.4x + 7 Например, можно показать, что имеет то же значение, что и 1 + 3
Неполные дроби 3.6. Введение Часто бывает полезно разбить сложную алгебраическую дробь на сумму более простых дробей.4x + 7 Например, можно показать, что имеет то же значение, что и 1 + 3
Неполные дроби. р (х) д (х)
 Неполные дроби Введение в частичные дроби Для рациональной функции вида p (x) q (x), где степень p (x) меньше степени q (x), метод частичных дробей стремится разбить
Неполные дроби Введение в частичные дроби Для рациональной функции вида p (x) q (x), где степень p (x) меньше степени q (x), метод частичных дробей стремится разбить
Дифференциация и интеграция
 Этот материал является дополнением к Приложению G Стюарта.Перед этим материалом вы должны прочитать приложение, за исключением последнего раздела, посвященного комплексным показателям. Дифференциация и интеграция Предположим, у нас есть
Этот материал является дополнением к Приложению G Стюарта.Перед этим материалом вы должны прочитать приложение, за исключением последнего раздела, посвященного комплексным показателям. Дифференциация и интеграция Предположим, у нас есть
Интегрирование алгебраических дробей
 Интегрирование алгебраических дробей Иногда интеграл от алгебраической дроби можно найти, сначала вычеркнув алгебраическую дробь как сумму ее частичных дробей. В этом модуле мы проиллюстрируем
Интегрирование алгебраических дробей Иногда интеграл от алгебраической дроби можно найти, сначала вычеркнув алгебраическую дробь как сумму ее частичных дробей. В этом модуле мы проиллюстрируем
3.1. РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
 3.1. РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ РАЦИОНАЛЬНЫЕ ЧИСЛА На предыдущих курсах вы научились работать (выполнять сложение, вычитание, умножение и деление) над рациональными числами (дробями). Рациональные числа
3.1. РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ РАЦИОНАЛЬНЫЕ ЧИСЛА На предыдущих курсах вы научились работать (выполнять сложение, вычитание, умножение и деление) над рациональными числами (дробями). Рациональные числа
тождественно равно x 2 + 3x +2
 Неполные дроби.6 Введение Часто бывает полезно разбить сложную алгебраическую дробь на сумму более простых дробей.4x + 7 Например, можно показать, что имеет то же значение, что и + для любого
Неполные дроби.6 Введение Часто бывает полезно разбить сложную алгебраическую дробь на сумму более простых дробей.4x + 7 Например, можно показать, что имеет то же значение, что и + для любого
Методы интеграции
 ГЛАВА 7 Методы интеграции 7 .. Замещение Интеграция, в отличие от дифференцирования, является больше формой искусства, чем набором алгоритмов. Многие задачи прикладной математики связаны с интегрированием
ГЛАВА 7 Методы интеграции 7 .. Замещение Интеграция, в отличие от дифференцирования, является больше формой искусства, чем набором алгоритмов. Многие задачи прикладной математики связаны с интегрированием
Нули полиномиальной функции
 Нули полиномиальной функции Важным следствием теоремы о множителях является то, что нахождение нулей полинома — это то же самое, что разложение его на линейные множители.В этом разделе мы
Нули полиномиальной функции Важным следствием теоремы о множителях является то, что нахождение нулей полинома — это то же самое, что разложение его на линейные множители.В этом разделе мы
Разложение на частичные дроби
 Разложение на частичные дроби Доктор Филипп Б. Лаваль Государственный университет Кеннесо 6 августа 2008 г. Резюме В этом раздаточном материале описывается разложение на частичные дроби и то, как его можно использовать при интегрировании рациональных
Разложение на частичные дроби Доктор Филипп Б. Лаваль Государственный университет Кеннесо 6 августа 2008 г. Резюме В этом раздаточном материале описывается разложение на частичные дроби и то, как его можно использовать при интегрировании рациональных
Графическое отображение рациональных функций
 Графическое изображение рациональных функций Здесь рациональная функция определяется как функция, которая равна отношению двух многочленов p (x) / q (x), таких, что степень q (x) равна не менее 1.Примеры: это рациональная функция
Графическое изображение рациональных функций Здесь рациональная функция определяется как функция, которая равна отношению двух многочленов p (x) / q (x), таких, что степень q (x) равна не менее 1.Примеры: это рациональная функция
2 Объединение обеих сторон
 2 Интегрирование обеих сторон До сих пор единственный общий метод, который у нас есть для решения дифференциальных уравнений, включает уравнения вида y = f (x), где f (x) — любая функция от x. Решение такого уравнения
2 Интегрирование обеих сторон До сих пор единственный общий метод, который у нас есть для решения дифференциальных уравнений, включает уравнения вида y = f (x), где f (x) — любая функция от x. Решение такого уравнения
Примеры проблем. Проблемы с практикой
 Примечания к лекции Страница с частичными дробями Примеры задач Вычислите каждый из следующих интегралов.. х dx. x + x (x +) (x) (x) dx 8. xx dx … x (x +) (x +) dx x + xx dx x + xx + 6x x dx + x 6. 7. x ( х
Примечания к лекции Страница с частичными дробями Примеры задач Вычислите каждый из следующих интегралов.. х dx. x + x (x +) (x) (x) dx 8. xx dx … x (x +) (x +) dx x + xx dx x + xx + 6x x dx + x 6. 7. x ( х
7.7 Решение рациональных уравнений
 Раздел 7.7 Решение рациональных уравнений 7 7.7 Решение рациональных уравнений При упрощении полных дробей в предыдущем разделе мы увидели, что числитель и знаменатель умножаются на соответствующие
Раздел 7.7 Решение рациональных уравнений 7 7.7 Решение рациональных уравнений При упрощении полных дробей в предыдущем разделе мы увидели, что числитель и знаменатель умножаются на соответствующие
Примеры частичных дробей
 Примеры частичных дробей Частичные дроби — это название метода интегрирования, который может использоваться для интегрирования любого отношения многочленов.Отношение многочленов называется рациональной функцией.
Примеры частичных дробей Частичные дроби — это название метода интегрирования, который может использоваться для интегрирования любого отношения многочленов.Отношение многочленов называется рациональной функцией.
РЕШЕНИЕ ПОЛИНОМИАЛЬНЫХ УРАВНЕНИЙ
 C РЕШЕНИЕ ПОЛИНОМИАЛЬНЫХ УРАВНЕНИЙ В этом приложении мы предполагаем, что вы знаете, как делить многочлены с помощью деления в столбик и синтетического деления. Если вам нужно изучить эти методы, обратитесь к алгебре
C РЕШЕНИЕ ПОЛИНОМИАЛЬНЫХ УРАВНЕНИЙ В этом приложении мы предполагаем, что вы знаете, как делить многочлены с помощью деления в столбик и синтетического деления. Если вам нужно изучить эти методы, обратитесь к алгебре
1.3 Алгебраические выражения
 1.3 Алгебраические выражения Многочлен — это выражение в форме: тревога + an 1 xn 1 + … + a 2 x 2 + a 1 x + a 0 Числа a 1, a 2, …, an называются коэффициентами . Каждая из отдельных частей,
1.3 Алгебраические выражения Многочлен — это выражение в форме: тревога + an 1 xn 1 + … + a 2 x 2 + a 1 x + a 0 Числа a 1, a 2, …, an называются коэффициентами . Каждая из отдельных частей,
Нули полиномиальных функций
 Нули полиномиальных функций Цели: 1. использовать фундаментальную теорему алгебры, чтобы определить количество нулей полиномиальных функций; 2. найти рациональные нули полиномиальных функций; 3.Найти конъюгат
Нули полиномиальных функций Цели: 1. использовать фундаментальную теорему алгебры, чтобы определить количество нулей полиномиальных функций; 2. найти рациональные нули полиномиальных функций; 3.Найти конъюгат
Ограниченная оптимизация.
 Дополнительные примечания к ams / econ 11b ucsc Оптимизация с ограничениями. c 2010, Йонатан Кацнельсон 1. Ограничения Во многих проблемах оптимизации, которые возникают в экономике, существуют ограничения на значения
Дополнительные примечания к ams / econ 11b ucsc Оптимизация с ограничениями. c 2010, Йонатан Кацнельсон 1. Ограничения Во многих проблемах оптимизации, которые возникают в экономике, существуют ограничения на значения
Краткий обзор алгебры
 1.Упрощение Epressions. Решение уравнений 3. Решение проблем 4. Неравенства 5. Абсолютные значения 6. Линейные уравнения 7. Системы уравнений 8. Законы компонентов 9. Квадраты 10. Рационалы 11. Радикалы
1.Упрощение Epressions. Решение уравнений 3. Решение проблем 4. Неравенства 5. Абсолютные значения 6. Линейные уравнения 7. Системы уравнений 8. Законы компонентов 9. Квадраты 10. Рационалы 11. Радикалы
Ответы на обзор основ алгебры
 Ответы на обзор основ алгебры 1. -1.1 При сложении и вычитании следуйте правилам знаков: если числа имеют один и тот же знак, сложите их вместе и сохраните знак.Если числа имеют разные знаки, вычтите
Ответы на обзор основ алгебры 1. -1.1 При сложении и вычитании следуйте правилам знаков: если числа имеют один и тот же знак, сложите их вместе и сохраните знак.Если числа имеют разные знаки, вычтите
Математический тест общего керна
 Базовый учебный план по алгебре для старших классов Тест по математике Общий тест по математике Наш тест по алгебре для старших классов охватывает двадцать наиболее распространенных вопросов, которые, по нашему мнению, предназначены для этого уровня. Для полных тестов
Базовый учебный план по алгебре для старших классов Тест по математике Общий тест по математике Наш тест по алгебре для старших классов охватывает двадцать наиболее распространенных вопросов, которые, по нашему мнению, предназначены для этого уровня. Для полных тестов
Решение рациональных уравнений
 Урок M Урок: Результаты учащихся Учащиеся решают рациональные уравнения, наблюдая за созданием посторонних решений.Примечания к уроку На предыдущих уроках учащиеся научились складывать, вычитать, умножать
Урок M Урок: Результаты учащихся Учащиеся решают рациональные уравнения, наблюдая за созданием посторонних решений.Примечания к уроку На предыдущих уроках учащиеся научились складывать, вычитать, умножать
Решение кубических многочленов
 Решение кубических многочленов 1.1 Общее решение квадратного уравнения Есть четыре шага к нахождению нулей квадратного многочлена. 1. Сначала разделите на главный член, получив многочлен
Решение кубических многочленов 1.1 Общее решение квадратного уравнения Есть четыре шага к нахождению нулей квадратного многочлена. 1. Сначала разделите на главный член, получив многочлен
Решение квадратных уравнений
 9.3 Решение квадратных уравнений с помощью квадратной формулы 9.3 ЦЕЛИ 1. Решить квадратное уравнение с помощью квадратной формулы 2. Определить характер решений квадратного уравнения
9.3 Решение квадратных уравнений с помощью квадратной формулы 9.3 ЦЕЛИ 1. Решить квадратное уравнение с помощью квадратной формулы 2. Определить характер решений квадратного уравнения
Факторинговые полиномы
 Факторинг многочленов 4-1-2014 Факторинг — это противоположность умножению многочленов. Зачем вам факторизовать многочлен? Пусть p (x) — многочлен.p (c) = 0 эквивалентно x c делению p (x). Напомним
Факторинг многочленов 4-1-2014 Факторинг — это противоположность умножению многочленов. Зачем вам факторизовать многочлен? Пусть p (x) — многочлен.p (c) = 0 эквивалентно x c делению p (x). Напомним
ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ
 ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ Полиномиальное деление … 314 Тест рационального нуля … 317 Правило знаков Декарта … 319 Теорема об остатке … 31 Нахождение всех нулей полиномиальной функции ……. 33 Написание
ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ Полиномиальное деление … 314 Тест рационального нуля … 317 Правило знаков Декарта … 319 Теорема об остатке … 31 Нахождение всех нулей полиномиальной функции ……. 33 Написание
Факторинговые полиномы
 Факторинг полиномов Хост, Миллер, Муриека 12 сентября 2011 г. 1 Факторинг В предыдущем разделе мы обсуждали, как определить произведение двух или более членов.Рассмотрим, например, уравнения
Факторинг полиномов Хост, Миллер, Муриека 12 сентября 2011 г. 1 Факторинг В предыдущем разделе мы обсуждали, как определить произведение двух или более членов.Рассмотрим, например, уравнения
Факторинг квадратичного многочлена
 Разложение квадратичного многочлена на множители Если мы умножим два бинома вместе, в результате получится квадратичный многочлен: это умножение довольно просто, с использованием распределительного свойства умножения
Разложение квадратичного многочлена на множители Если мы умножим два бинома вместе, в результате получится квадратичный многочлен: это умножение довольно просто, с использованием распределительного свойства умножения
Полиномиальные и рациональные функции
 Полиномиальные и рациональные функции. Квадратичные функции. Обзор целей, студенты должны уметь: 1.Узнай характеристики парабол. 2. Найдите точки перехвата a. x перехватывает, решая
Полиномиальные и рациональные функции. Квадратичные функции. Обзор целей, студенты должны уметь: 1.Узнай характеристики парабол. 2. Найдите точки перехвата a. x перехватывает, решая
Базовая математика C1. Примечания к редакции
 Core Maths C Примечания к редакции Ноябрь 0 Core Maths C Алгебра … Индексы … Правила индексов … Surds … 4 Упрощение Surds … 4 Рационализация знаменателя … 4 Квадратичные функции … 4 Завершение
Core Maths C Примечания к редакции Ноябрь 0 Core Maths C Алгебра … Индексы … Правила индексов … Surds … 4 Упрощение Surds … 4 Рационализация знаменателя … 4 Квадратичные функции … 4 Завершение
ПРОСМОТРЕТЬ УПРАЖНЕНИЯ ДЭВИДА ЛОУРИ
 ПЕРЕСМОТРЕТЬ УПРАЖНЕНИЯ ДЭВИДА ДЖЛАУРИ Содержание 1.Введение 1 2. Основные функции 1 2.1. Факторинг и квадратичное решение 1 2.2. Полиномиальные неравенства 3 2.3. Рациональные функции 4 2.4. Экспоненты и
ПЕРЕСМОТРЕТЬ УПРАЖНЕНИЯ ДЭВИДА ДЖЛАУРИ Содержание 1.Введение 1 2. Основные функции 1 2.1. Факторинг и квадратичное решение 1 2.2. Полиномиальные неравенства 3 2.3. Рациональные функции 4 2.4. Экспоненты и
Системный подход к факторингу
 Системный подход к факторингу Шаг 1 Подсчитайте количество терминов. (Помните ****. Знание числа терминов позволит вам избавиться от ненужных инструментов.) Шаг 2 Есть ли наибольший общий фактор? Инструмент
Системный подход к факторингу Шаг 1 Подсчитайте количество терминов. (Помните ****. Знание числа терминов позволит вам избавиться от ненужных инструментов.) Шаг 2 Есть ли наибольший общий фактор? Инструмент
Урок 9: радикалы и конъюгаты
 Результаты учащихся Учащиеся понимают, что сумма двух квадратных корней (или двух кубических корней) не равна квадратному корню (или кубическому корню) из их суммы.Учащиеся переводят выражения в простейшую радикальную форму.
Результаты учащихся Учащиеся понимают, что сумма двух квадратных корней (или двух кубических корней) не равна квадратному корню (или кубическому корню) из их суммы.Учащиеся переводят выражения в простейшую радикальную форму.
1.6 Порядок действий
 1.6 Порядок операций Содержание: Символы группировки операций Порядок экспонентов операций и отрицательных чисел Квадратный корень отрицательного числа Квадратный корень отрицательного числа Порядок операций и отрицательный
1.6 Порядок операций Содержание: Символы группировки операций Порядок экспонентов операций и отрицательных чисел Квадратный корень отрицательного числа Квадратный корень отрицательного числа Порядок операций и отрицательный
КОЛЛЕДЖ АЛГЕБРА.Пол Докинз
 АЛГЕБРА КОЛЛЕДЖА Пол Докинз Содержание Предисловие … iii Краткое содержание … iv Предварительные сведения … Введение … Целочисленные показатели … Рациональные показатели … 9 Действительные показатели … 5 Радикалы … 6 Полиномы .. .5
АЛГЕБРА КОЛЛЕДЖА Пол Докинз Содержание Предисловие … iii Краткое содержание … iv Предварительные сведения … Введение … Целочисленные показатели … Рациональные показатели … 9 Действительные показатели … 5 Радикалы … 6 Полиномы .. .5
Основы теории полиномов
 3 Основы теории полиномов 3.1 Полиномиальные уравнения В геодезии и геоинформатике большинство наблюдений связано с неизвестными параметрами через уравнения алгебраического (полиномиального) типа.В случаях, когда
3 Основы теории полиномов 3.1 Полиномиальные уравнения В геодезии и геоинформатике большинство наблюдений связано с неизвестными параметрами через уравнения алгебраического (полиномиального) типа.В случаях, когда
Числовые и алгебраические дроби
 Числовые и алгебраические дроби Факультет математики Аквинского Подготовка к AS Maths Этот блок охватывает числовые и алгебраические дроби. На уровне A решения часто включают дроби и одно из Core
Числовые и алгебраические дроби Факультет математики Аквинского Подготовка к AS Maths Этот блок охватывает числовые и алгебраические дроби. На уровне A решения часто включают дроби и одно из Core
5 Численное дифференцирование
 Д.Леви 5 Численное дифференцирование 5. Основные понятия В этой главе рассматриваются численные приближения производных. Первый вопрос, который приходит в голову: зачем нам аппроксимировать производные
Д.Леви 5 Численное дифференцирование 5. Основные понятия В этой главе рассматриваются численные приближения производных. Первый вопрос, который приходит в голову: зачем нам аппроксимировать производные
