Интегрирование по площади: Вычисление поверхностных интегралов: теория и примеры

Содержание

Вычисление поверхностных интегралов: теория и примеры

Понятие поверхностного интеграла первого рода
Вычисление поверхностого интеграла первого рода
Понятие поверхностного интеграла второго рода
Вычисление поверхностного интеграла второго рода
Больше примеров на вычисление поверхностных интегралов

Поверхностный интеграл — обобщение понятия криволинейного интеграла на случаи, когда интегрирование происходит не по отрезку кривой, а по ограниченной поверхности. Как и криволинейные интегралы, поверхностные интегралы бывают первого рода и второго рода.

Поверхностный интеграл первого рода записывается в виде

где f(M) = f(x,y,z) – функция трёх переменных, а поверхность σ — область интегрирования этой функции. Если f(x,y,z) равна единице, то поверхностный интеграл равен площади поверхности.

Представьте себе довольно большой подсолнух с очень-очень маленькими семечками. Тогда по сумме поверхностей очень-очень маленьких семечек, расположенных на поверхности подсолнуха, можно вычислить поверхность подсолнуха — таким может быть упрощённое толкование поверхностного интеграла. Почему так?

Давайте перейдём к более формальному определению поверхностного интеграла. Поверхность σ разбита на n частей с площадями Δσ1, Δσ2, …, Δσn. Если выбрать на каждой частичной поверхности (семечке) произвольную точку Mi с координатами (ζi, ηi, ςi,), то можно составить сумму

Эта сумма называется интегральной суммой для функции f(M) по поверхности σ. Теперь будем максимально увеличивать число таких маленьких частей, а наибольший диаметр Δ

σi — наоборот, уменьшать. Если интегральная сумма при стремлении наибольшего из диаметров частей к нулю (то есть, как мы уже отмечали, все части очень маленькие) имеет предел, то этот предел и называется поверхностным интегралом первого рода от функции f(M) по поверхности σ.

Вычисление поверхностного интеграла первого рода производится сводением к двойному интегралу.

Пусть поверхность σ задана уравнением z = z(x, y), её проекцией на плоскость xOy является область Dxy, при этом функция z = z(x, y) и её частные производные и непрерывны в области Dxy.

Тогда

Это и есть формула, выражающая поверхностный интеграл первого рода через двойной интеграл по проекции поверхности

σ на плоскость xOy.

Пример 1. Вычислить поверхностный интеграл первого рода

где σ — часть плоскости в первом октанте.

Решение. Чертёж:

Из уравнения плоскости получаем выражение «зет»: .

Тогда частные производные: , и

Поверхность σ является изображённым на чертеже треугольником ABC, а его проекцией на плоскость xOy — треугольником AOB, который ограничен прямыми x = 0, y = 0 и 3x + y = 6. От поверхностного интеграла перейдём к двойному интегралу и решим его:

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Кратные и криволинейные интегралы

Прежде чем перейти к определению поверхностного интеграла второго рода, требуется познакомиться с понятиями стороны поверхностей и ориентированных поверхностей.

Пусть в пространстве дана гладкая поверхность σ. На этой поверхности выберем произвольную точку M и проведём через неё вектор нормали к поверхности. Через точку M проведём также на поверхности σ произвольный контур, не имеющий общих точек с границей поверхности σ. Точку M вместе с вектором нормали будем перемещать по контуру так, чтобы вектор нормали постоянно был перпендикулярен поверхности σ. По возвращении точки M в начальное положение возможны два случая: направление вектора нормали сохранится или же поменяется на противоположное.

Если направление вектора нормали не поменяется, то поверхность σ называется двусторонней. Если же при обходе контура направление вектора нормали поменяется на противоположное, то поверхность называется односторонней. Двусторонние поверхности называются ориентированными поверхностями, односторонние — неориентированными поверхностями.

Пример односторонней поверхности — лист Мёбиуса (на рисунке выше), который можно сделать из полоски бумаги, одна сторона которой повёрнута на 180 градусов, и затем концы склеены. И вот что здесь важно: для односторонней поверхности понятие поверхностного интеграла второго рода не вводится.

Так что будем рассматривать только двусторонние поверхности. Примеры двусторонних поверхностей — плоскости, сфера, эллипсоид, параболоид.

Положительную сторону двустороней поверхности определяет направление вектора нормали. Противоположная сторона поверхности называется отрицательной. Положительной стороной поверхности называется её верхняя сторона. Если единичные векторы нормали составляют острые углы с осью Oz, то выбрана верхняя сторона поверхности z = z(x, y), если углы тупые, то нижняя сторона поверхности.

Как и в случае поверхностного интеграла первого рода, поверхность можно разбить на n частей. При формулировке понятия поверхностного интеграла первого рода в интегральной сумме присутствовали площади каждой из частей, на которые умножаются значения функции f(Mi). В случае поверхностного интеграла второго рода берутся площади не самих частей, а площади их проекций на координатные плоскости.

А функцию трёх переменных для отличия от интеграла первого рода обозначим R(x,y,z). Тогда интегральная сумма запишется так:

где Δsi — площади упомянутых проекций частей стороны поверхности на координатную ось (пока будем считать, что на ось xOy).

При таких соглашениях и обозначениях определение поверхностного интеграла второго рода аналогично определению интеграла первого рода. А именно: поверхностным интегралом второго рода называется предел данной интегральной суммы при стремлении к нулю наибольшего из диаметров частей рассматриваемой поверхности.

Записывается он так:

В данном случае функция R(x,y,z) интегрируема по переменным x и y, так как части поверхности проецировались на плоскость xOy.

Аналогично можно записать и два других поверхностных интеграла второго рода:

(функция P(x,y,z) интегрируема по переменным y и z, так как части поверхности проецируются на плоскость yOz),

(функция Q(x,y,z) интегрируема по переменным z и x, так как части поверхности проецируются на плоскость zOx).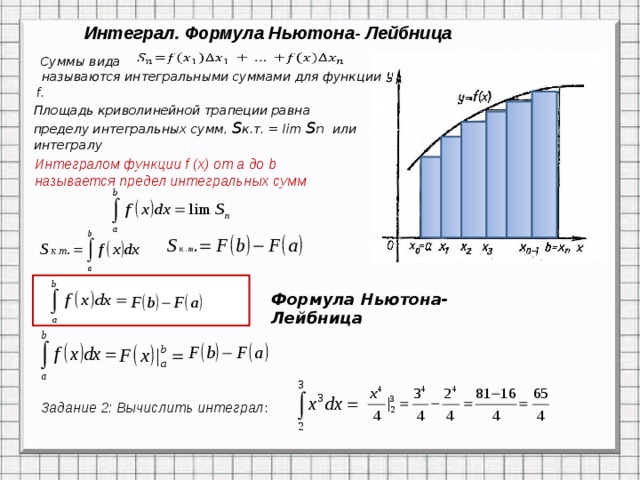

Сумма этих интегралов

называется общим поверхностным интегралом второго рода и обозначается

Поверхностный интеграл второго рода вычисляется путём разложения общего поверхностного интеграла второго рода на сумму поверхностных интегралов (см. окончание предыдущего параграфа) и сведением каждого из них к двойному интегралу.

Рассмотрим подробно вычисление интеграла

Пусть поверхность σ задана уравнением z = z(x, y). Положительную сторону поверхности обозначим , отрицателную , а проекцию на плоскость xOy — Dxy.

Таким образом, получаем формулу для вычисления поверхностного интеграла второго рода:

Если выбрана отрицательная сторона поверхности, то знак интеграла меняется:

Аналогично вычисляются два других отдельных интеграла — слагаемых общего:

Пример 2. Вычислить поверхностный интеграл второго рода

где σ — верхняя сторона части плоскости , отсечённая плоскостями y = 0 и y = 4 и находящаяся в первом октанте.

Решение. Чертёж — на рисунке сверху. По определению получаем сумму трёх двойных интегралов:

Второй интеграл равен нулю, так как плоскость σ параллельна оси Oy. Поэтому найдём первый и третий интегралы:

Остаётся лишь сложить все отдельные интегралы и получить общий поверхностный интеграл второго рода:

Если требуется вычислить поверхностный интеграл второго рода по замкнутой поверхности, можно перейти к тройному интегралу, используя формулу Остроградского. Тогда, если функции

P(x,y,z), Q(x,y,z) и R(x,y,z) и их частные производные , , — непрерывные функции в области W, которую ограничивает замкнутая поверхность σ, то при интегрировании по внешней стороне поверхности в силе равенство

Пример 3. Вычислить поверхностный интеграл второго рода

где σ — внешняя сторона поверхности конуса, образованного поверхностью и плоскостью z = 2.

Решение. Данная поверхность является поверхностью конуса с радиусом R = 2 и высотой h = 2. Это замкнутая поверхность, поэтому можно использовать формулу Остроградского. Так как P = 3x, Q = 4y, R = −z, то частные производные , , .

Переходим к тройному интегралу, который и решаем:

Пример 4. Вычислить поверхностный интеграл первого рода

где σ — боковая поверхность конуса при .

Решение. Так как частные производные , , то

Сводим данный поверхностный интеграл к двойному:

Проекцией поверхности на плоскость xOy является круг с центром в начале координат и радиусом R = 2, поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:

Получаем следующий интеграл, который окончательно и решаем:

Пример 5. Вычислить поверхностный интеграл второго рода

где σ — верхняя часть треугольника, образованного пересечением плоскости с координатными плоскостями.

Решение. Данный поверхностный интеграл разделим на сумму двух интегралов

, где

Чтобы вычислить интеграл I1, построим проекцию поверхности σ на плоскость yOz. Проекцией является треугольник OCB, который на плоскости yOz ограничивают прямые или , y = 0 и z = 0. Из уравнения плоскости выводится . Поэтому можем вычислить интеграл I1:

Чтобы вычислить интеграл I2, построим проекцию поверхности σ на плоскость zOx. Проекцией является треугольник AOC, который ограничивают прямые или , x = 0 и z = 0. Вычисляем:

Складываем два полученных интеграла и окончательно получаем данный поверхностный интеграл:

Пример 6. Вычислить поверхностный интеграл второго рода

где σ — внешняя поверхность пирамиды, образованной плоскостью и координатными плоскостями.

Решение. Данный поверхностный интеграл вычислим двумя способами

1) интегрируя по каждой грани пирамиды;

2) используя формулу Остроградского.

1) Вычисление интегрированием по каждой грани пирамиды.

а) Вычислим интеграл по треугольнику ABC. Для этого разделим интеграл на сумму трёх интегралов, которые отдельно решим:

;

Складываем и получаем:

б) Вычислим поверхностный интеграл по треугольнику AOB, который находится в плоскости z = 0. Тогда dz = 0 и, учитывая, что нормальный вектор плоскости образует с осью Oz тупой угол, получаем

в) Треугольник AOC находится в плоскости y = 0, таким образом, dy = 0 и (нормальный вектор плоскости образует с осью Oy тупой угол) получаем

г) Осталось вычислить поверхностный интеграл по треугольнику CBO находится в плоскости x = 0, таким образом, dx = 0 и получаем

В результате получаем данный поверхностный интеграл второго рода:

2) Используя формулу Остроградского, от поверхностного интеграла по замкнутой поверхности перейдём к тройному интегралу, где W — область, ограниченная поверхностью σ. Так как P = xz, Q = 1, R = 2y, то частные производные , , .

Получаем следующее решение данного поверхностного интеграла:

В последнем примере вернёмся к вычислению поверхностного интеграла первого рода.

Пример 7. Вычислить площадь поверхности параболоида во внутренней части сферы .

Решение. Определим, при каком значении z данные поверхности пересекаются:

Значение −3 не подходит, поэтому остаётся только z = 1.

Обозначим через C часть поверхности данного параболоида во внутреней стороне сферы. Проекция поверхности C (обозначим её D) на плоскость xOy является кругом с центром в начале координат и радиусом √2, так как при z = 1 получаем уравнение окружности . Решаем поверхностный интеграл первого рода:

Так как

то

Проекцией поверхности на плоскость xOy является круг, поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:

Получаем окончательное решение данного поверхностного интеграла:

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Кратные и криволинейные интегралы

Кратные и криволинейные интегралы

Вычисление двойных интегралов
Двойные интегралы в полярных координатах
Вычисление тройных интегралов
Вычисление криволинейных интегралов
Интегралы по замкнутому контуру, формула Грина
Вычисление поверхностных интегралов

Поделиться с друзьями

Поверхностный интеграл первого рода и его свойства / Поверхностный интеграл / 3dstroyproekt.

n { f(M_i )\cdot \sigma _i } $.

Если существует предел последовательности интегральных сумм при $\mathop { \max } \limits_ { i=1,2,\ldots n } diam\sigma _i \to 0$, не зависящий ни от способа разбиения поверхности $\sigma $ на части $\sigma _i (i=1,2,\ldots ,n)$, ни от выбора точек $M_i $, то функция $\mathbf { \textit { f } } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } $,$\mathbf { \textit { z } } )$ называется интегрируемой по поверхности $\sigma $, а значение этого предела называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности и обозначается $\iint\limits_\sigma { f(M)\cdot d\sigma } $.

Теорема существования Если функция $\mathbf { \textit { f } } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } $,$\mathbf { \textit { z } } )$ непрерывна на поверхности $\sigma $, то она интегрируема по этой поверхности.

Свойства поверхностного интеграла первого рода

Аналогичны по формулировке и доказательству свойствам рассмотренных ранее интегралов первого рода.

Линейность. $\iint\limits_\sigma { (\lambda \,f+ } \mu \,g)d\sigma =\lambda \iint\limits_\sigma { fd\sigma } +\mu \iint\limits_\sigma { gd\sigma } $
Аддитивность $\iint\limits_ { \sigma _1 \cup \sigma _2 } { fd\sigma } =\iint\limits_ { \sigma _1 } { fd\sigma } \iint\limits_ { \sigma _2 } { fd\sigma } $
$\iint\limits_\sigma { d\sigma } =S_\sigma -$ площадь поверхности.
Если $f(x,\,y,\,z)\geqslant g(x,\,y,\,z)$, то $\iint\limits_\sigma { fd\sigma \geqslant \iint\limits_\sigma { gd\sigma } } $ { если $f\geqslant 0$, то $\iint\limits_\sigma { fd\sigma } \geqslant 0)$,
Теорема об оценке Если $m\leqslant f\left( { x,\,y,\,z }\right)\leqslant M$, то $mS_\sigma \leqslant \iint\limits_\sigma { fd\sigma } \leqslant MS_\sigma $,
Теорема о среднем Пусть функция $f(M)=f(x,\,y,\,z)$ непрерывна на кусочно-гладкой ограниченной поверхности $\sigma $. Тогда на поверхности найдется точка С, такая что $f(C)=\frac { 1 } { S_\sigma } \iint\limits_\sigma { f\left( { x,\,y,\,z }\right)d\sigma } $

Доказательство

Первые четыре свойства доказываются аналогично подобным свойствам в двойном, тройном интегралах, криволинейном интеграле первого рода { записью соотношений в интегральных суммах и предельным переходом } . Во втором свойстве используется возможность такого разбиения поверхности на две части, чтобы ни один элемент разбиения не содержал граничные точки этих частей в качестве своих внутренних точек.

Теорема об оценке следует из свойств 3, 4.

Теорема о среднем, как и ранее, использует теоремы Вейерштрасса и Больцано-Коши для функций, непрерывных на замкнутых ограниченных множествах.

Седьмое, персональное, свойство — независимость поверхностного интеграла первого рода от выбора стороны поверхности

Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах

Класс $T_1$. Теорема о замкнутости класса $T_1$

Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина

Механические и физические приложения поверхностного интеграла первого рода

Критерий полноты {формулировка}. Лемма о немонотонной функции

Вычисление площади поверхности

Гармонические поля

Формула Грина

Теорема об аналоге СДНФ в Pk

Теорема об алгоритме распознавания полноты

Булевы функции от $n$ переменных

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Поток векторного поля через поверхность

Критерий полноты {формулировка}. Лемма о несамодвойственной функции

Теорема о заведомо полныx системаx

Огравление $\Rightarrow $

23 сентября 2016, 12:04 проектирование км, кмд, кж Поверхностный интеграл 0 13439 0

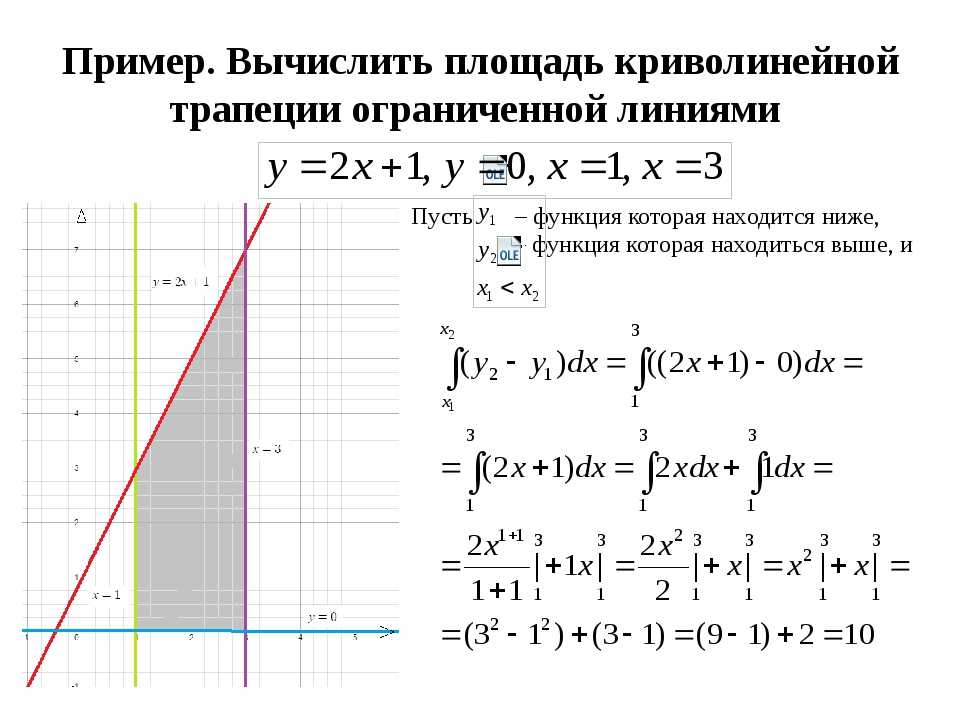
2. Площадь под кривой путем интегрирования

М. Борна

Мы встречались с областями под кривыми ранее в разделе Интеграция (см. 3. Площадь под кривой), но здесь мы развиваем концепцию дальше. (Вас также может заинтересовать Архимед и область параболического сегмента, где мы узнаем, что Архимед понял идеи, лежащие в основе исчисления, за 2000 лет до того, как это сделали Ньютон и Лейбниц!)

Перед началом важно обрисовать ситуацию.

Мы хотим найти площадь под кривой `y = f(x)` от `x = a` до `x = b`.

У нас может быть несколько ситуаций:

Случай 1: Кривые, полностью лежащие на над осью x . xf(x)abyxy = f(x)ΔОткрыть изображение на новой странице

Кривая y = f(x), полностью выше оси x. Показывает «типичный» прямоугольник, Δ x в ширину и y в высоту.

В этом случае мы находим площадь, просто находя интеграл: 9бф(х)дх`

Откуда взялась эта формула?

Видеомини-лекции

Для предыстории:

Мини-лекция по интегрированию

Разница между неопределенными и определенными интегралами

Интегрирование подстановкой

Область под кривой из первых принципов

На диаграмме выше показан «типичный прямоугольник» с шириной `Δx` и высотой `y`. Его площадь равна yΔx.

Если мы сложим все эти типичные прямоугольники, начиная с `a` и заканчивая `b`, площадь составит примерно: 92`

Случай 2: Кривые, полностью лежащие на

ниже x -оси

Мы рассматриваем случай, когда кривая находится ниже оси `x` для рассматриваемого диапазона значений `x` .

xf(x)abyxy = f(x)ΔОткрыть изображение на новой странице

Кривая y = f(x), полностью ниже оси x. Показывает «типичный» прямоугольник, Δ x в ширину и y в высоту.

В этом случае интеграл дает отрицательное число. 92`

Случай 3 : Часть кривой ниже по оси x , часть ее выше по оси x xf(x)acby = f(x)Открыть изображение на новой странице
От `a` до `c` кривая y = f(x) находится ниже оси x, а от `c` до `b` , это выше.
В этом случае мы должны суммировать индивидуальные части, взяв абсолютное значение для участка, где кривая находится ниже оси `x` (от `x = a` до `x = c`).
91`
`=(1/4-16/4)`
`=-15/4`
`=-3.25`
Это , а не правильный ответ для площади под кривой. Это — это значение интеграла, но ясно, что площадь не может быть отрицательной.
Всегда лучше набросать кривую, прежде чем искать области под кривыми.
Резюме (на данный момент)
В каждом случае 1, 2 и 3 мы суммируем элементы слева направо, например:
xf(x)abydxy = f(x)Открыть изображение на новой странице 9бф(х)дх`
(со знаками абсолютного значения, где необходимо, если кривая проходит под осью `x`).
Случай 4: некоторые кривые гораздо проще суммировать по вертикали
В некоторых случаях легче найти площадь, если взять по вертикали суммы. Иногда единственным возможным способом является суммирование по вертикали.
xydcx
dy
Лучший способ найти площадь под этой кривой — суммировать по вертикали.
В этом случае мы находим площадь как сумму прямоугольников, высот `x = f(y)` и ширины `dy`. 9df(y)dy`
Пример случая 4
Найдите площадь области, ограниченной кривой `y=sqrt(x-1)`, осью `y` и линиями `y = 1` и `y = 5`.
Ответить
Первый эскиз:
51015202530123456xy
x
крас
х = у ² + 1
Кривая x = y ² + 1, показывающая часть «под» кривой от y 95`
`=45 1/3\ текст[квадратные единицы]`
Примечание: Для этого конкретного примера мы могли бы также просуммировать его по горизонтали (интегрируя `y` и используя `dx`), но сначала нам нужно было бы разбить его на секции.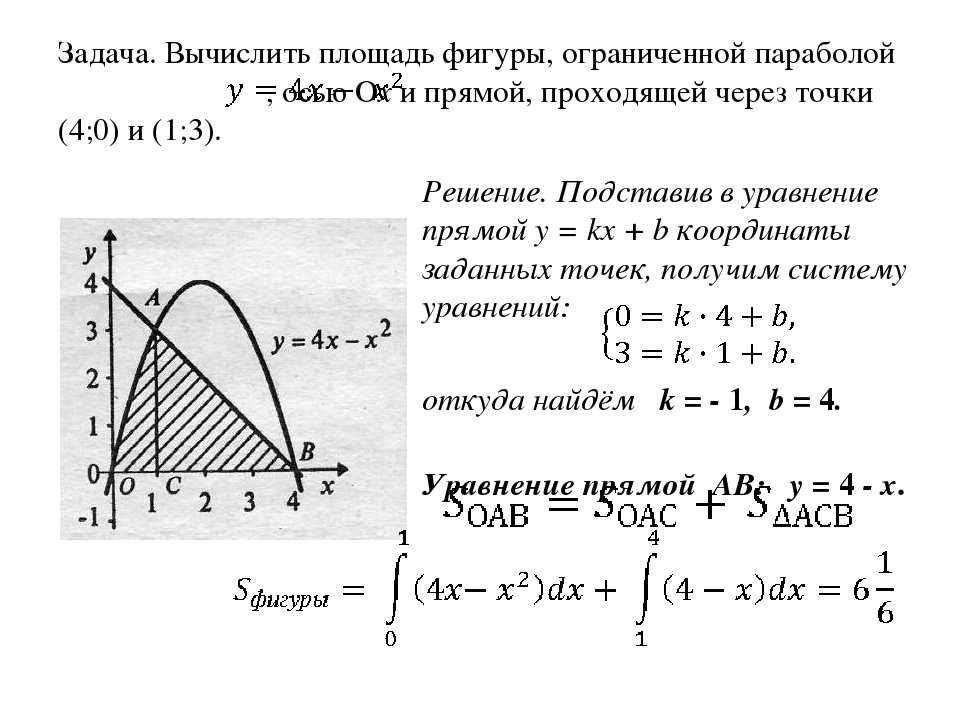
Видео: Заявки на интегрирование: площадь под кривой
Видео: Заявки на интегрирование: площадь под кривой
Ссылки на видео
Это видео находится на страницах
Список всех видео
Видео слайды
Стенограмма видео
Одним из классических применений интегрирования является его использование для определения площади под графиком функции, что часто называют нахождением площади под кривой.
Например, мы хотим найти площадь под графиком функции $f(x)$, равной $x$ плюс $e$ до $2x$ между значениями $x=-1$ и $ х=2$. Область, которую мы хотим определить, — это заштрихованная область на этом графике.
Найти площадь такой искривленной области сложно. Гораздо проще найти площади прямоугольников. Для этого разделим интервал $[-1,2]$ на два подинтервала и аппроксимируем функцию постоянной на обоих подинтервалах. Здесь мы вычисляем левостороннюю оценку, поэтому мы аппроксимируем функцию как значение с левой стороны каждого подинтервала. Представим, что функция равна 6,39в первой половине, потому что $f(-1)$ равно 6,39$, и представьте, что оно равно 0,87 во второй половине, потому что $f(0,5)$ равно 0,87. Для этой кусочно-постоянной функции, показанной двумя синими отрезками, легко вычислить площадь под ней. Площадь — это просто сумма двух прямоугольников. Ширина всего интервала от $-1$ до $2$ равна 3, поэтому ширина прямоугольника ровно вдвое меньше, что составляет $\Delta x=1.5$. Мы умножаем две высоты на 1,5, чтобы получить две площади: 9,58 для первого прямоугольника и 1,3 для второго прямоугольника. Когда мы суммируем эти две области, мы вычисляем общую площадь как 10,89.. Ну, на самом деле я получаю 10,88 при сложении этих двух чисел, но компьютер выполняет более точную работу, не округляя до конца, и получается 10,89.
Мы могли бы сделать аналогичный расчет, аппроксимировав высоту функции в каждом подинтервале ее высотой в правой части интервала, получив правостороннюю оценку. В этом случае высоты прямоугольников равны 0,87 и 2,02, их площади равны 1,3 и 3,03, а общая площадь равна 4,33.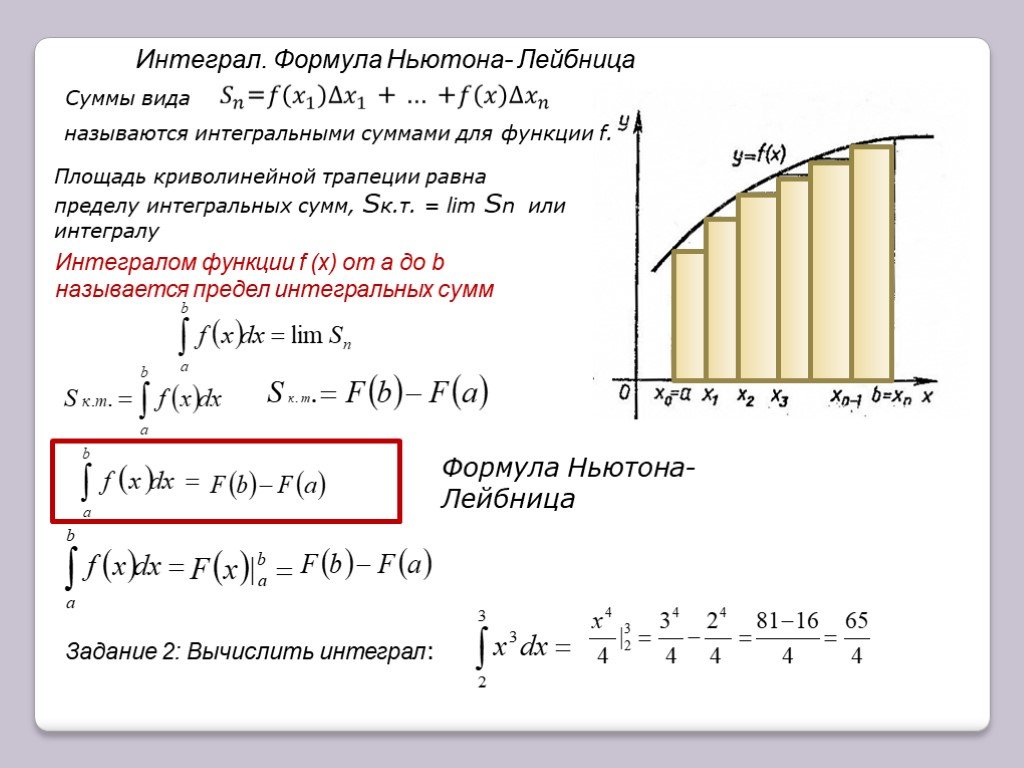 Эти две оценки 10,89 для левой оценки и 4,33 для правой оценки довольно далеки друг от друга и не слишком близки к фактической области под функцией. Для повышения точности мы можем увеличить количество подынтервалов. Для 10 подинтервалов получаем оценки для площади 5,95 для левой оценки и 4,64 для правой оценки.
Сумма, используемая для вычисления площади прямоугольников, точно соответствует сумме Римана, которую мы использовали для определения определенного интеграла. Для левой оценки мы получаем левую сумму Римана, которая является суммой от $i=1$ до $10$ $f(t_{i-1})$, которая является высотой левой части каждого подинтервал, умноженный на ширину прямоугольника $\Delta x$. Для правой суммы Римана меняется только то, что мы используем высоту правой стороны, $f(t_i)$, для высоты прямоугольника. Мы можем увеличить количество прямоугольников, чтобы улучшить оценку площади. Чтобы получить фактическую площадь под кривой, нам нужно взять предел, поскольку количество прямоугольников, $n$, стремится к бесконечности. Этот предел и есть определение определенного интеграла. Таким образом, площадь под функцией $f(x)$ для $x$ между $-1$ и $2$ представляет собой интеграл от $-1$ до $2$ от $f(x)dx$, который, поскольку наша функция $ f(x)$ равно $x$ плюс $e$ в $2x$, является интегралом от $-1$ до $2$ от $x$ плюс $e$ в $2x$ $dx$. 92$. Интеграл от экспоненты, умноженной на $-2$, является самой экспонентой, поэтому второй член равен экспоненте, умноженной на $-1/2$. Эта функция является нашей антипроизводной большой $F(x)$. Нам не нужно было добавлять здесь произвольную константу $C$, потому что мы вычисляем определенный интеграл.
Согласно основной теореме исчисления, определенный интеграл, определяющий площадь под кривой, представляет собой просто этот неопределенный интеграл $F(x)$, вычисленный при $x=2$, минус тот же $F(x)$, оцененный при $x= -1$. Мы подставляем эти числа, чтобы найти, что площадь под кривой составляет приблизительно 5,185. Как эта фактическая площадь соотносится с нашими оценками для прямоугольников? Когда у нас есть 100 прямоугольников, левая сумма Римана дает нам 5,25, а правая сумма Римана дает нам 5,12. Ответы сходились к правильному ответу 5,185. Нам потребуется намного больше, чем 100 прямоугольников, чтобы получить три правильные цифры. К счастью, мы можем избежать вычисления огромной суммы Римана и просто вычислить интеграл напрямую.
Давайте сделаем еще один пример. Вычислим площадь между графиком функции $1/x$ и осью $x$ на интервале $x$ от $-2$ до $-1$. Начнем с вычисления интеграла от $-2$ до $-1$ от $1/x$ $dx$. Антипроизводная $1/x$ — это логарифм абсолютного значения $x$, поэтому по основной теореме исчисления мы оцениваем этот логарифм при $x=-1$, а затем вычитаем логарифм при $x=- 2$. Абсолютное значение исключает отрицательные знаки, поэтому мы имеем логарифм единицы минус логарифм двойки. Логарифм единицы равен нулю, а логарифм двойки равен 0,69.3. Рассчитываем, что площадь равна $-0,693$.
Э-э, подождите минутку, это не имеет смысла. Не имеет смысла иметь отрицательную область. Должно быть, здесь что-то пошло не так. Давайте посмотрим на график функции, чтобы определить, что произошло. Поскольку $x$ отрицательна, функция $1/x$ также отрицательна. При попытке вычислить площадь мы получаем отрицательную высоту, поэтому логично, что в итоге мы получим отрицательное число. Если функция отрицательна, определенный интеграл не дает площади; это дает минус площадь. Эта проблема легко устраняется. Расстояние от оси $x$ до функции всегда будет абсолютным значением функции, которое избавляется от отрицательного знака, если функция отрицательна. Чтобы получить площадь, нам нужно проинтегрировать абсолютное значение $1/x$. Когда $x$ отрицательно, каково абсолютное значение $1/x$? Поскольку $1/x$ отрицательно, нам просто нужно умножить на $-1$, чтобы сделать его положительным. Площадь представляет собой интеграл от $-2$ до $-1$ от $-1/x$ $dx$. Нам просто нужно взять наш предыдущий ответ $-0,69.2$. Мы оцениваем его в $1$ и $-2$ и берем разницу. Число, которое мы получаем для нашего ответа, равно 9.
Чтобы увидеть, что представляет собой эта 9 с точки зрения площади, давайте построим график функции. Между $-2$ и $1$ функция бывает как положительной, так и отрицательной. Он положителен от $-2$ до $0$, а затем отрицателен от $0$ до конца нашего интеграла в $1$. Это означает, что мы складываем положительные числа для области от $-2$ до $0$, а затем объединяем это с отрицательными числами для области от $0$ до $1$. Что мы делаем, так это вычисляем площадь над осью $x$, а затем вычитаем площадь под осью $x$. Мы называем этот результат «подписанной областью». Если не брать абсолютное значение, интеграл от $f(x)$ представляет собой площадь со знаком между графиком функции и осью $x$. Это площадь над осью $x$ минус площадь под осью $x$.
Чтобы продемонстрировать этот результат более наглядно, давайте вычислим положительную и отрицательную части интеграла отдельно. Если мы вычислим интеграл от $-2$ до $0$, где функция положительна, мы получим $16$. Площадь под кривой для $x$ между $-2$ и $0$ составляет $16$. Если мы вычислим интеграл от $0$ до $1$, где функция отрицательна, мы получим $-7$. Это означает, что площадь между кривой и осью $x$ составляет $7$, но получается $-7$, потому что график находится ниже оси $x$. Площадь со знаком представляет собой сумму этих двух членов, поэтому мы получаем 9 долларов.$.
Если мы хотим рассчитать фактическую площадь, мы должны взять абсолютное значение. Абсолютное значение не меняет интеграл от $-2$ до $0$, так как там функция положительна. Однако она умножает функцию на $-1$ для $x$ между $0$ и $1$, изменяя $-7$ на $7$. Фактическая площадь под кривой составляет $16 + 7$, что составляет $23$.
Таким образом, определенный интеграл функции $f(x)$ даст вам площадь со знаком между графиком функции и осью $x$, вычитая площадь ниже оси $x$ из площади выше ось $x$. Если вам нужна фактическая площадь между графиком функции и осью $x$, вам нужно взять абсолютное значение. Это немного усложняет вычисления, потому что вам нужно выяснить, где функция отрицательна, и умножить ее на $-1$ именно в этих интервалах. Тем не менее, использование определенного интеграла — довольно изящный способ определить площадь под кривой.
No related posts.