Исследование функции и построение графика 10 класс примеры: Исследование функции и построение графика функции

Построение графиков функций — урок. Алгебра, 10 класс.

построить график функции y=x2+1×2−1.

Решение 1. Введём обозначение: f(x)=x2+1×2−1. Найдём область определения функции. Она задаётся условиями x≠1,x≠−1. Итак, D(f)=(−∞;−1)∪(−1;1)∪(1;+∞).

2. Исследуем функцию на чётность:

f(−x)=−x2+1−x2−1=x2+1×2−1=f(x).

Значит, заданная функция чётна, её график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при x≥0.

3. Найдём асимптоты. Вертикальной асимптотой является прямая \(x=1\), поскольку при этом значении \(x\) знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить limx→∞f(x):

limx→∞x2+1×2−1=limx→∞x2x2+1x2x2x2−1×2=limx→∞1+1×21−1×2=1.

 Значит, \(y=1\) — горизонтальная асимптота графика функции.

4. Найдём стационарные и критические точки, точки экстремума и промежутки монотонности функции:

y′=x2+1×2−1′=(x2+1)′⋅(x2−1)−(x2+1)⋅(x2−1)′x2−12=2x⋅(x2−1)−(x2+1)⋅2xx2−12==−4xx2−12.

Производная существует всюду в области определения функции, значит, критических точек у функции нет.

Стационарные точки найдём из соотношения y′=0. Получаем: \(-4x=0\) — откуда находим, что \(x=0\). При \(x<0\) имеем: y′>0; при \(x>0\) имеем: y′<0. Значит, \(x=0\) — точка максимума функции, причём ymax=f(0)=02+102−1=−1.

При \(x>0\) имеем: y′<0; но следует учесть наличие точки разрыва \(x=1\). Значит, вывод о промежутках монотонности будет выглядеть так: на промежутке 0;1) функция убывает, на промежутке (1;+∞) функция также убывает.

5. Составим таблицу значений функции f(x)=x2&plus;1×2−1 при x≥0:

\(x\)	\(0\)	\(0.5\)	\(2\)	\(3\)	\(4\)
\(y\)	\(-1\)	−53	53	54	1715

 

6. Отметим найденные точки на координатной плоскости, учтя при этом, что \((0;-1)\) — точка максимума, что \(y=1\) — горизонтальная асимптота, что \(x=1\) — вертикальная асимптота, построим ветви искомого графика при x≥0. Добавив ветви, симметричные построенным относительно оси ординат, получим весь график.

Полное исследование функции и построение графика, примеры решений

Задание. Исследовать функцию $y(x)=\frac{x^{2}-x-1}{x^{2}-2 x}$ и построить ее график.

Решение. 1) Область определения функции.

$D(y) : x^{2}-2 x \neq 0 \Rightarrow x_{1} \neq 0, x_{2} \neq 2 \Rightarrow$

$\Rightarrow x \in(-\infty ; 0) \cup(0 ; 2) \cup(2 ;+\infty)$

2) Четность, нечетность.

$y(-x)=\frac{(-x)^{2}-(-x)-1}{(-x)^{2}-2 \cdot(-x)}=\frac{x^{2}+x+1}{x^{2}+2 x} \neq \left\{\begin{array}{l}{y(x)} \\ {-y(x)}\end{array}\right.$

Функция общего вида.

3) Точки пересечения с осями.

а) с осью $O x : y=0$ :

$\frac{x^{2}-x-1}{x^{2}-2 x}=0 \Rightarrow x^{2}-x-1=0 \Rightarrow$

$\Rightarrow x_{1}=\frac{1+\sqrt{5}}{2}, x_{2}=\frac{1-\sqrt{5}}{2}$

то есть точки $A_{1}\left(\frac{1+\sqrt{5}}{2} ; 0\right), A_{2}\left(\frac{1-\sqrt{5}}{2} ; 0\right)$

б) с осью $O y : x=0$ : в данной точке функция неопределенна.

4) Асимптоты.

а) вертикальные: прямые $x=0$ и $x=2$ — вертикальные асимптоты.

б) горизонтальные асимптоты:

$\lim _{x \rightarrow \infty} \frac{x^{2}-x-1}{x^{2}-2 x}=1$

то есть прямая $y=1$ — горизонтальная асимптота.

в) наклонные асимптоты $y=k x+b$ :

$k=\lim _{x \rightarrow \infty} \frac{x^{2}-x-1}{x\left(x^{2}-2 x\right)}=0$

Таким образом, наклонных асимптот нет.

5) Критические точки функции, интервалы возрастания, убывания.

$y^{\prime}=\left(\frac{x^{2}-x-1}{x^{2}-2 x}\right)^{\prime}=\frac{(2 x-1)\left(x^{2}-2 x\right)-\left(x^{2}-x-1\right)(2 x-2)}{\left(x^{2}-2 x\right)^{2}}=$

$=\frac{2 x^{3}-4 x^{2}-x^{2}+2 x-\left(2 x^{3}-2 x^{2}-2 x^{2}+2 x-2 x+2\right)}{\left(x^{2}-2 x\right)^{2}}=$

$=\frac{2 x^{3}-5 x^{2}+2 x-2 x^{3}+4 x^{2}-2}{\left(x^{2}-2 x\right)^{2}}=\frac{-x^{2}+2 x-2}{\left(x^{2}-2 x\right)^{2}}$

Найдем точки, в которых первая производная равна нулю или не существует: $y^{\prime} \neq 0$ для любого $x$ из области определения функции; $y^{\prime}$ не существует при $x_{1}=0$ и $x_{2}=2$ .

Таким образом, функция убывает на всей области существования. Точек экстремума нет.

6) Точки перегиба, интервалы выпуклости, вогнутости.

$y^{\prime \prime}=\left(y^{\prime}\right)^{\prime}=\left(\frac{-x^{2}+2 x-2}{\left(x^{2}-2 x\right)^{2}}\right)^{\prime}=$

$=\frac{(-2 x+2)\left(x^{2}-2 x\right)^{2}-\left(-x^{2}+2 x-2\right) \cdot 2\left(x^{2}-2 x\right)(2 x-2)}{\left(x^{2}-2 x\right)^{4}}=$

$=\frac{(-2 x+2)\left(x^{2}-2 x\right)-\left(-x^{2}+2 x-2\right) \cdot 2(2 x-2)}{\left(x^{2}-2 x\right)^{3}}=$

$=\frac{-2 x^{3}+6 x^{2}-4 x+4 x^{3}-12 x^{2}+16 x-8}{\left(x^{2}-2 x\right)^{3}}=$

$=\frac{2 x^{3}-6 x^{2}+12 x-8}{\left(x^{2}-2 x\right)^{3}}$

Найдем точки, в которых вторая производная равна нулю или не существует: $y^{\prime \prime}=0 : x=1$ ; при $x=0$ и $x=2$ вторая производная не существует.

Таким образом, на промежутках $(0 ; 1)$ и $(2 ;+\infty)$ функция вогнута, а на промежутках $(-\infty ; 0)$ и $(1 ; 2)$ — выпукла. Так как при переходе через точку $x=1$ вторая производная поменяла знак, то эта точка является точкой перегиба.

7) Эскиз графика.

Общая схема исследования графика функции

Схема исследования функции

1. Найти область значений E(f) и область определения D(f) функции;
2. Определить четность или нечетность функции, периодичность функции;
3. Найти точки пересечения графика функции с осями координат;
4. Нахождение  вертикальной, горизонтальной и наклонной асимптоты;
5. Определение критических точек, экстремумов функции, наибольшее и наименьшее значение, интервалы монотонности функции — возрастания и убывания функции;
6. Определение интервалов вогнутости, выпуклости, точек разрыва и перегиба функции;
7. Построить график исходной функции (построить график, касательную и её производную онлайн).

---

Пример
Исследовать функцию и построить график функции

$y = \frac{{{x^2}}}{{x — 2}}$

Решение
1.

D(f)=(−∞;2)∪(2;+∞)

E(f)=(−∞;0)∪(8;+∞)

2.
Функция ни четная и ни нечётная, непериодическая

${\rm{f}}\left( { — {\rm{x}}} \right) = \frac{{{{( — x)}^2}}}{{ — x — 2}} = \frac{{{x^2}}}{{ — x — 2}}$

3.
Ox: ${\rm{y}} = \frac{{{x^2}}}{{x — 2}} = 0$, x=0 точка (0;0)
Oy: x=0, y=0 точка (0;0)
4.
Так как

$\mathop {{\rm{lim}}}\limits_{x \to + 2} \frac{{{x^2}}}{{x — 2}} = + \infty $

$\mathop {{\rm{lim}}}\limits_{x \to — 2} \frac{{{x^2}}}{{x — 2}} = — \infty $

следовательно
x = 2 — вертикальная асимптота
Уравнение наклонной асимптоты (как определить её, пример см. здесь)

y=x+2

5.
Вычисляем первую производную функции: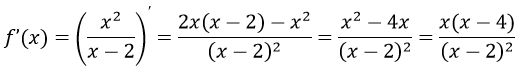

Находим критические точки:

$\frac{{x\left( {x — 4} \right)}}{{{{\left( {x — 2} \right)}^2}}} = 0$

отсюда получаем корни уравнения
x=2, x=4, x=0
Исследуем знак производной на интервалах

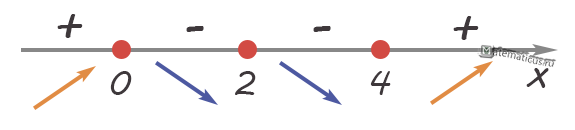
Функция возрастает при

$x∈\left( { — \infty ;0} \right)\mathop \cup \nolimits \left( {4; + \infty } \right)$

Функция  убывает при

$x∈\left( {0;2} \right)\mathop \cup \nolimits \left( {2;4} \right)$

Функция имеет максимум при f(0)=0
Функция имеет минимум при 

$f(4) = \frac{{{4^2}}}{{(4 — 2)}} = 8$

6.
Вычисляем вторую производную

${\rm{f}}\left( {\rm{x}} \right) = \left( {\frac{{{x^2} — 4x}}{{{{\left( {x — 2} \right)}^2}}}} \right){\rm{}} = \frac{{\left( {2x — 4} \right){{\left( {x — 2} \right)}^2} — \left( {{x^2} — 4x} \right)\left( {2x — 4} \right)}}{{{{\left( {x — 2} \right)}^4}}} = \frac{{4\left( {2x — 4} \right)}}{{{{\left( {x — 2} \right)}^4}}}$

Приравниваем к нулю и находим критические точки:

$\frac{{4\left( {2x — 4} \right)}}{{{{\left( {x — 2} \right)}^4}}} = 0$

x=2 точка разрыва функции
Функция выпукла вверх при x∈(−∞;2)
Функция выпукла вниз при x∈(2;+∞)
Точки перегиба нет.
7. 

Строим график функции
Онлайн график можно построить здесь.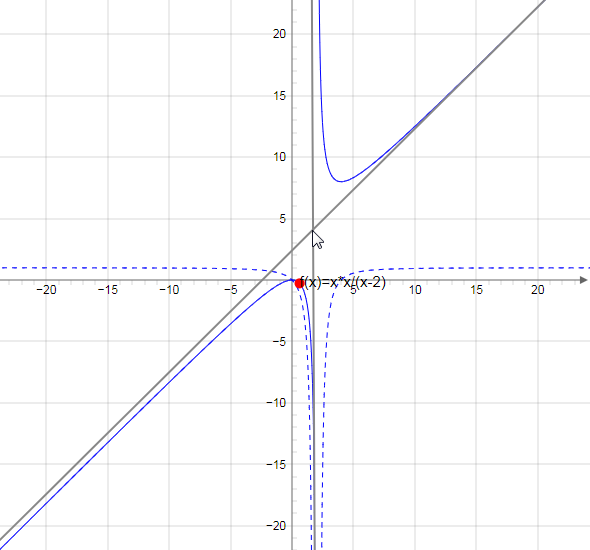

Пунктирной линией показана производная функции.

Построение графиков функции. Алгебра, 10 класс: уроки, тесты, задания.

1.	Вертикальная асимптота Сложность: лёгкое	1
2.	Горизонтальная асимптота Сложность: лёгкое	1
3.	Выпуклости графика функции Сложность: лёгкое	2
4.	Построение графика дробной функции Сложность: среднее	8
5.	Точки перегиба функции Сложность: среднее	2
6.	Доказательство выпуклости функции Сложность: среднее	4
7.	Исследование и построение графика сложной функции, содержащей квадратный корень Сложность: сложное	6
8.	Уравнение с параметром Сложность: сложное	4
9.	Определение количества корней Сложность: сложное	3

Исследование функции с помощью производной и построение графиков

Инфоурок › Алгебра ›Презентации›Исследование функции с помощью производной и построение графиков

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Исследование функции Построение графика

2 слайд Описание слайда:

Цели урока: Повторить понятия: область определения функции, четность и нечетность. Повторить алгоритм исследования функции на монотонность при помощи производной. Научиться строить графики функций.

3 слайд Описание слайда:

Найти область определения функции 0 x y 1 1 -6 8

4 слайд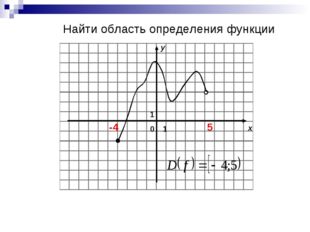 Описание слайда:

Найти область определения функции 0 x y 1 1 -4 5

5 слайд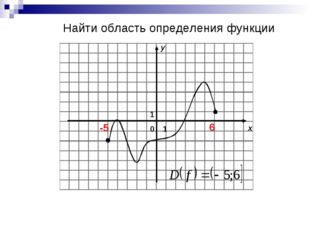 Описание слайда:

Найти область определения функции 0 x y 1 1 -5 6

6 слайд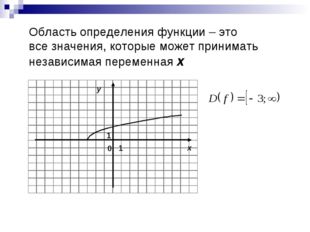 Описание слайда:

Область определения функции – это все значения, которые может принимать независимая переменная х

7 слайд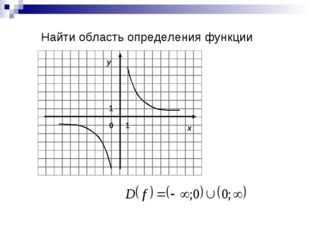 Описание слайда:

Найти область определения функции

8 слайд Описание слайда:

Найти область определения функции

9 слайд Описание слайда:

Найти область определения функции

10 слайд Описание слайда:

Четная функция Нечетная функция

11 слайд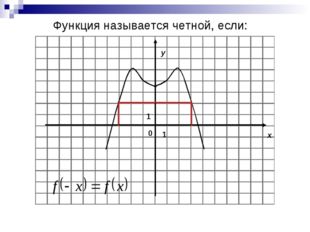 Описание слайда:

Функция называется четной, если:

12 слайд Описание слайда: 13 слайд Описание слайда: 14 слайд 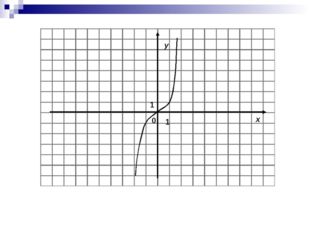Описание слайда:

0 x y 1 1

15 слайд Описание слайда: 16 слайд 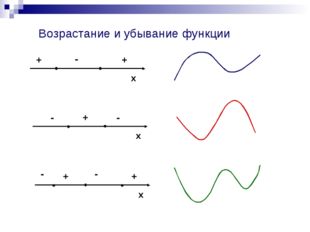Описание слайда:

Возрастание и убывание функции

17 слайд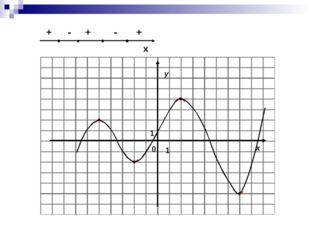 Описание слайда:

0 x y 1 1

18 слайд Описание слайда:

Исследование функции Область определения функции Точки пересечения с осями координат Четность Экстремумы и монотонность Построение графика функции.

19 слайд Описание слайда:

Исследование функции 2) Точки пересечения с осями координат 1) Область определения 3) Функция ни четная, ни нечетная 4) Экстремумы и монотонность 0 2 + + —

20 слайд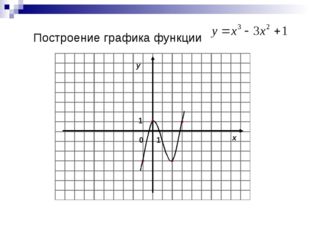 Описание слайда:

Построение графика функции 0 x y 1 1

21 слайд Описание слайда:

Исследование функции 2) Точки пересечения с осями координат 1) Область определения 3) Функция четная 4) Экстремумы и монотонность + + — — -2

22 слайд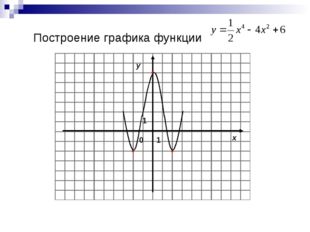 Описание слайда:

Построение графика функции 0 x y 1 1

23 слайд Описание слайда:

Домашнее задание: Выучить алгоритм исследования функции и построения графика. Построить график функции Подготовить выступление по теме: «Точки перегиба»

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики и информатики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Проверен экспертом

Общая информация

Номер материала: ДБ-1103653

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Урок 20. построение графиков функций — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №20. Построение графиков функций.

Перечень вопросов, рассматриваемых в теме

1. Исследование функций;
2. Построение графиков функций;
3. Применение производной для решения графических задач.

Глоссарий по теме

Асимптота графика функции y = f(x) – прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х₁и х₂, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Выпуклость вверх. Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка.

Выпуклость вниз. Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.

Максимум функции. Значение функции в точке максимума называют максимумом функции.

Минимум функции. Значение функции в точке минимума называют минимумом функции.

Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).

Производная второго порядка (вторая производная). Производная второго порядка есть первая производная от производной первого порядка.

Производную определяют, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к 0, если такой предел существует.

Точка максимума функции. Точку х₀называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  .

Точка минимума функции. Точку  х₀ называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  .

Точка перегиба. Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.

Точки экстремума функции. Точки минимума и максимума называют точками экстремума.

Убывание функции. Функция y=f(x) убывает на интервале X, если для любых х₁ и х₂ , из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.

Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит вышепроведенного отрезка.

Полная схема построения графика функции:

1. Найти область определения функции D(f).
2. Исследовать функцию на четность (найти f(-x)).
3. Найти асимптоты.
4. Найти стационарные и критические точки.
5. Найти промежутки монотонности.
6. Найти интервалы выпуклости вверх и выпуклости вниз.
7. Найти точки перегиба
8. Составить таблицу значений функции для некоторых точек.
9. По полученным данным построить график функции.

Примеры и разбор решения заданий тренировочного модуля

Пример 1. Постройте график функции у = х³ – 3х + 3, используя краткую схему построения. схему построения.

Решение:

1) D(y) = (-∞; +∞)

2) Функция не является ни четной, ни нечетной, т. к.

3) Асимптот нет

4) f’(x) = 3x² – 3, f’(x) = 0 при х = 1, х = -1.

х = 1, х = -1 – стационарные точки.

5) f’(x)>0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки возрастания.

f’(x)<0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки убывания.

6) Так как в точке х = -1 производная меняет знак с «+» на «-», то х = -1 – точка максимума.

Так как в точке х = 1 производная меняет знак с «-» на «+», то х = 1 – точка минимума.

7) Результаты исследования представим в виде таблицы.

x	(-∞; -1)	-1	(-1; 1)	1	(1; +∞)
f’(x)	+	0	—	0	+
f(x)		5		1
		max		min

8) Координаты некоторых точек:

9) По полученным данным строим график (рис. 1)

Рисунок 1 – график функции у = х³ – 3х + 3

Пример 2. Постройте график функции, используя подробную схему построения. схему построения.

Решение:

1)

2) Функция не является ни четной, ни нечетной, т. к.

3) х = 1 – вертикальная асимптота

4) , f’(x) = 0 при х = 2, х = 0.

х = 2, х = 0 – стационарные точки.

5) f’(x)>0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки возрастания.

f’(x)<0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки убывания.

Так как в точке х = 0 производная меняет знак с «+» на «-», то х = 0 – точка максимума.

Так как в точке х = 2 производная меняет знак с «-» на «+», то х = 2 – точка минимума.

х = 1 – не является точкой экстремума

6) Найдем интервалы выпуклости функции.

; при функция выпукла вверх.

; при функция выпукла вниз.

7) Результаты исследования представим в виде таблицы.

x	(-∞; 0)	0	(0; 1)	1	(1; 2)	2	(2; +∞)
f’(x)	+	0	—	Не сущ.	—	0	+
f’’(x)	—		—	Не сущ.	+		+
f(x)		-4		Не сущ.		0
		max				min

8) Координаты некоторых точек:

x	-1	0,5	1,5	3
f(x)	-4,5	-4,5	0,5	0,5

9) По полученным данным строим график (рис. 2)

Рисунок 2 – график функции

Построение графиков функции — методическая рекомендация. Алгебра, 10 класс.

1.	Вертикальная асимптота	1 вид — рецептивный	лёгкое	1 Б.	Нахождение вертикальной асимптоты заданной функции.
2.	Горизонтальная асимптота	1 вид — рецептивный	лёгкое	1 Б.	Нахождение горизонтальной асимптоты заданной функции.
3.	Выпуклости графика функции	2 вид — интерпретация	лёгкое	2 Б.	Нахождение промежутков выпуклости функции, используется вторая производная. Для профильного курса.
4.	Построение графика дробной функции	2 вид — интерпретация	среднее	8 Б.	Так как на портале проверка построения графика ограничена, то предлагается ответить на вопросы по заданному плану построения графика функции. Заданная функция — дробная.
5.	Точки перегиба функции	2 вид — интерпретация	среднее	2 Б.	Нахождение точек перегиба функции, используется вторая производная. Для профильного курса.
6.	Доказательство выпуклости функции	3 вид — анализ	среднее	4 Б.	Доказать выпуклость функции с использованием второй производной. Для профильного курса.
7.	Исследование и построение графика сложной функции, содержащей квадратный корень	3 вид — анализ	сложное	6 Б.	Исследование и построение графика сложной функции, содержащей квадратный корень. Так как на портале проверка построения графика ограничена, то предлагается ответить на вопросы по заданному плану построения графика функции.
8.	Уравнение с параметром	3 вид — анализ	сложное	4 Б.	В решении уравнения с параметром используется график функции.
9.	Определение количества корней	3 вид — анализ	сложное	3 Б.	По заданному уравнению определить количество корней. В решении используются свойства графика функции.

Десятый класс (10 класс) Вопросы о функциях и отношениях для тестов и рабочих листов

Вы можете создавать печатные тесты и рабочие листы из этих 10 класс Функции и отношения вопроса! Выберите один или несколько вопросов, установив флажки над каждым вопросом. Затем нажмите кнопку добавить выбранные вопросы к кнопке теста перед переходом на другую страницу.

Предыдущая Страница 1 из 10 Следующие Выбрать все вопросы Если область определения функции [math] f (x) = 5x ^ 2–3 [/ math] ограничена значениями [math] {2,4,6,8} [/ math], каков диапазон эта функция?

1. [Математика] RR [/ математика]
2. [математика] {17, 77, 177, 317} [/ математика]
3. [Математика] {2,4,6,8} [/ математика]
4. [математика] {x в RR | x> = — 3} [/ математика]

Это функция? Объясните, почему да или почему нет.

1. Да, это действительно функция, потому что все точки различны (ни одна из них не совпадает).
2. Нет, это не функция, поскольку функция не может состоять только из точек.
3. Нет, это не функция, так как не проходит тест вертикальной линии.
4. Нет, это не функция, поскольку функция состоит из многих других точек.

Предыдущая Страница 1 из 10 Следующие ,

Класс 10 Репетитор по математике, Помощь и практика в Интернете

Не видите то, что вам нужно?

Не волнуйтесь, попробуйте поискать по всем нашим темам

Искать по всему StudyPug

Что такое математика в 10 классе?

Выходя из ужасного опыта по математике в 9 классе? Неуверенный и неподготовленный к тому, что будет дальше? Позвольте нам помочь вам понять, чего ожидать дальше — StudyPug предлагает комплексную провинциальную программу обучения математике 10, которая удовлетворит все ваши потребности. Итак, идете ли вы из 10 класса по математике в Альберте, по программе математики Онтарио или готовитесь к B.C. математика 10, мы вам поможем. Изучите математику для 10-го класса и с легкостью изучите такие темы, как факторизация многочленов, линейные уравнения и квадратичные функции. Овладейте радикалами, побеждайте экспоненты и побеждайте свой страх перед тригонометрией, пока мы подробно исследуем Math 10.

Понимание математики 10 класса никогда не будет таким легким, как с StudyPug! С помощью уроков на основе примеров и круглосуточной помощи с 10 классами по математике от наших известных преподавателей вы получите новые навыки решения задач и понаблюдайте за реальным применением математических тем для 10 класса.Прикладная математика 10-го класса расширяет абстрактные математические концепции, помогая вам увидеть взаимосвязь с реальным миром. Всегда будьте готовы ответить на пресловутый вопрос «когда я когда-нибудь этим воспользуюсь?» и откройте для себя новое понимание того, насколько увлекательной может быть математика!

Это вкратце Math 10! Получите доступ ко всей нашей библиотеке уроков, вопросов по математике для 10-го класса и всегда будьте готовы к домашнему заданию, тесту или экзамену!

Сложна ли математика в 10 классе?

Нет, если ты усердно учишься! Как и любой другой предмет или уровень обучения, вопросы и материалы по математике для 10-го класса имеют разные уровни сложности.То, что некоторым из вас может показаться сверхлегким, для следующего человека может оказаться невероятно трудным. Чтобы уравнять правила игры, мы предлагаем вам лучший онлайн-курс по математике для 10-х классов в Интернете! Позвольте нам сделать тяжелую работу и снять с вас груз беспокойства.

В StudyPug мы намеренно выискивали самые сложные темы и исследовали лучшие методы обучения, чтобы мы могли предложить лучшие услуги репетиторства по математике для 10 класса ВСЕ (Да! Даже если вы чувствуете, что принадлежите к 10 классу математики для манекены).Мы разрабатываем и проводим простые, понятные, но емкие уроки; удовлетворение различных стилей обучения и уровней понимания. Мы пошагово ответим на вопросы, чтобы убедиться, что вы получаете полный обзор по математике за 10 класс. Избегайте стресса от зубрежки или обычных 30-минутных видеоуроков и просмотрите вместе с нами школьную математику!

Обеспокоены тем, насколько сложным был последний экзамен по математике в 10 классе? Не знаете, как вернуться после этой уродливой буквенной оценки? Читайте дальше, чтобы узнать больше о наших обширных советах по практике экзаменов по математике для 10 класса и стратегиях сдачи экзаменов!

Как сдать 10 класс по математике?

Прохождение 10 класса по математике поначалу может показаться неуправляемым — из-за множества тем, которые нужно рассмотреть, вы можете не знать, с чего даже начать! Мы хотим убедиться, что вы хорошо подготовлены, поэтому наша команда из StudyPug тщательно разработала наш курс математики для 10-го класса, чтобы он отражал руководство по обзору экзамена по математике для 10-го класса.Откажитесь от унылых заданий по математике для 10-го класса и присоединяйтесь к нам, чтобы весело и легко попрактиковаться в вопросах экзамена по математике!

Начните с уроков математики в 10 классе. Начните здесь, если вы чувствуете себя особенно потерянным или запутавшимся в этой теме. Просмотрите эти видео в кратчайшие сроки и изучите тысячи других уроков, которые могут вам потребоваться для понимания урока. Некоторые из этих уроков математики для 10-го класса являются сопутствующими, поэтому найдите время, чтобы изучить основные понятия, прежде чем переходить к следующему уроку. Это может быть причиной того, что вы вообще боретесь!

Чтобы дать вам представление о том, чего ожидать от теста по математике в 10 классе, мы посвящаем значительную часть наших уроков пошаговым примерам.Мы делаем это для того, чтобы вы были знакомы с вопросами, которые встретятся на вашем тесте или экзамене. Изучите методы, позволяющие решать подобные вопросы, и узнайте, как избежать глупых ошибок.

Наконец, попрактикуйтесь с нашим хранилищем из 936 практических вопросов! Это очень важная часть подготовки к экзамену по математике в 10 классе, так что не упустите его! Проверьте свои знания и понимание тем и посмотрите, насколько хорошо вы справитесь с этим пробным тестом / экзаменом. Чем больше вопросов вы зададите, тем лучше вы будете готовы успешно сдать 10 класс по математике!

В тупике во время тренировки? Мы всегда работаем круглосуточно и без выходных, поэтому вернитесь к одному из наших уроков и снова учитесь на собственном примере!

Как подготовиться к 10 классу по математике?

Начинающим студентам и любителям математики всегда рекомендуется стремиться к успеху в игре! Партнерство с StudyPug в качестве вашего репетитора — лучший способ сделать это, поскольку мы предлагаем множество курсов математики, чтобы заранее подготовить вас к будущему! Если вам кажется, что учебная программа по математике для 9 класса слишком проста, или вы ищете задачи, или, возможно, у вас достаточно рабочих листов по математике для 9 класса, StudyPug здесь, чтобы спасти вас от скуки и развить ваш потенциал.Освойте 10-й класс математики раньше времени или вернитесь назад, чтобы освежить свою память о математике для 9-го класса в любое время и в любом месте. Многие темы, изучаемые в 9-м классе, будут расширены в 10-м классе, так что не торопитесь и не стесняйтесь возвращаться назад.

StudyPug предоставляет вам мгновенный доступ ко всем нашим учебным пособиям по математике для 10-го класса, заметкам по математике для 10-го класса и многому другому! Изучайте математику 10 класса онлайн в удобном для вас темпе под руководством наших профессиональных репетиторов по математике 10 класса. Перестаньте беспокоиться о том, охватим ли мы ваш учебный план по математике для 10 класса или этот конкретный учебник по математике для 10 (мы всегда делаем!), И начните подготовку сегодня! Следите за своими успехами с помощью личного учебного плана, зарабатывайте значки, оставайтесь заинтересованными и мотивированными на протяжении наших уроков.Напомним, что наши материалы основаны друг на друге, поэтому начните с урока 1 и проработайте основы, прежде чем приступать к изучению сложных тем в математике 10 класса.

На протяжении каждого урока не забывайте посещать наш банк вопросов, чтобы помочь вам отточить свои математические навыки в 10 классе — поставьте перед собой задачу на каждом уроке выполнить все вопросы, связанные с этой главой, прежде чем двигаться дальше, поскольку это настоящий тест, чтобы увидеть, как подготовил тебя к 10 классу по математике!

.

R plot () Функция (добавление заголовков, меток, изменение цветов и наложение горшков)

В этой статье вы научитесь использовать функцию построения графика в R. Она используется для построения графиков в соответствии с типом переданного объекта.

Наиболее часто используемой функцией построения графиков в программировании на R является функция plot () . Это общая функция, то есть у нее есть много методов, которые вызываются в зависимости от типа объекта, переданного в plot () .

В простейшем случае мы можем передать вектор и получить диаграмму разброса величины и индекса.Но обычно мы передаем два вектора и строим диаграмму рассеяния этих точек.

Например, команда plot (c (1,2), c (3,5)) построит точки (1,3) и (2,5) .

Вот более конкретный пример, где мы строим график синусоидальной функции в диапазоне от -pi до pi .

  x <- seq (-pi, pi, 0,1)
сюжет (x, sin (x))
  

---

Добавление заголовков и осей надписей

Мы можем добавить заголовок к нашему графику с помощью параметра main .Точно так же xlab и ylab можно использовать для обозначения оси x и оси y соответственно.

  участок (x, sin (x),
main = "Функция синуса",
ylab = "грех (х)")
  

---

Изменение цвета и типа графика

Выше мы видим, что график состоит из круглых точек и имеет черный цвет. Это цвет по умолчанию.

Мы можем изменить тип графика с помощью аргумента типа . Он принимает следующие строки и имеет заданный эффект.

 "p" - баллов
"l" - линии
«б» - и точки, и линии
«c» - пустые точки, соединенные линиями
«o» - точки и линии, нанесенные поверх графика
«s» и «S» - ступеньки лестницы
"h" - вертикальные линии в виде гистограммы
«n» - не создает точек или линий
 

Точно так же мы можем определить цвет, используя col .

  участок (x, sin (x),
main = "Функция синуса",
ylab = "грех (х)",
TYPE = "л",
цв = «синий»)
  

---

Наложение графиков с помощью функции legend ()

Вызов plot () несколько раз приведет к построению текущего графика в том же окне, заменяющего предыдущий.

Однако иногда мы хотим наложить графики, чтобы сравнить результаты.

Это стало возможным с помощью функций линий () и точек () для добавления линий и точек соответственно к существующему графику.

  участок (x, sin (x),
main = "Наложение графиков",
ylab = "",
TYPE = "л",
цв = «синий»)
строки (x, cos (x), col = "red")
Легенда ( «верхний-левый»,
с ( "грех (х)", "сов (х)"),
заливка = с ( «синий», «красный»)
)
  

Мы использовали функцию legend () , чтобы правильно отобразить легенду.Посетите функцию legend (), чтобы узнать больше.

Также посетите функцию plot (), чтобы узнать больше о различных аргументах. Функция plot () может принимать и другие примеры.

.

стеблевых и листовых делянок: Примеры | Purplemath

Purplemath

Следующие примеры демонстрируют некоторую практику работы со схемами «стебель и лист», а также объясняют некоторые детали форматирования и показывают, как создать «ключ» для вашего графика.

• Субъекты психологического исследования были рассчитаны на время выполнения определенного задания.Завершите заговор на основе стеблей и листьев следующий список раз:

7.6, 8.1, 9.2, 6.8, 5.9, 6.2, 6.1, 5.8, 7.3, 8.1, 8.8, 7.4, 7.7, 8.2

MathHelp.com

Первое, что я сделаю, это переупорядочу этот список.Это не обязательно, но, безусловно, облегчает жизнь. Мой заказанный список:

5,8, 5,9, 6,1, 6,2, 6,8, 7,3, 7,4, 7,6, 7,7, 8,1, 8,1, 8,2, 8,8, 9,2

Эти значения имеют один десятичный знак, но диаграмма «стебель-лист» для этого не предусмотрена. На графике «стебель-лист» учитывается только последняя цифра (для листьев) и все предыдущие цифры (для стебля). Поэтому мне придется поставить «ключ» или «легенду» на этот график, чтобы показать, что я имею в виду под числами на этом графике.Единичные цифры будут значениями основы, а десятые - листьями.

---

Собственно, у каждого стеблево-листового участка должен быть ключ. Но многие этого не делают, и ваш класс может не охватить это. Если это не упоминается в вашем учебнике или на лекции, вы, вероятно, можете проигнорировать этот вопрос.

---

• Заполните диаграмму стеблей и листьев для следующих двух списков размеров классов:

Экономика 101: 9, 13, 14, 15, 16, 16, 17, 19, 20, 21, 21, 22, 25, 25, 26

Либертарианство: 14, 16, 17, 18, 18, 20, 20, 24, 29

В этом примере есть два списка значений.Поскольку значения похожи, я могу нанести их все на одном участке стебля и листа, нарисовав листья по обе стороны от стебля. Я буду использовать цифры десятков в качестве значений основы, а цифры единиц - как листья. Поскольку «9» (в списке Econ 101) не имеет разряда десятков, значение основы будет «0».

---

• Завершите построение диаграммы стеблей и листьев для следующего списка значений:

100, 110, 120, 130, 130, 150, 160, 170, 170, 190, 210, 230, 240, 260, 270, 270, 280, 290, 290

Поскольку все цифры единицы - это нули, я сделаю этот график с сотнями цифр, которые будут значениями основы, а цифры десятков - листьями.Я могу сделать сюжет так:

Но листья здесь довольно длинные, потому что значения так близко друг к другу. Чтобы немного разложить значения, я могу разбить каждый лист на два. Например, лист для класса двух сотен можно разделить на два класса с числами от 200 до 240 и числами от 250 до 290. Я также могу изменить порядок, чтобы меньшие значения находились внизу «стебель».Новый сюжет выглядит так:

---

В приведенном выше примере я разделил наборы из десяти на наборы по пять; каждый исходный лист стал двумя классами. Для очень компактных точек данных вы даже можете разделить листья на пять классов, например:

Способ разделения данных на категории будет зависеть от имеющихся данных, а также (в определенной степени) от личного вкуса.В основном вы стремитесь выглядеть «разумным» на уроках.

---

• Завершите построение диаграммы стеблей и листьев для следующего списка значений:

23,25, 24,13, 24,76, 24,81, 24,98, 25,31, 25,57, 25,89, 26,28, 26,34, 27,09

Если я попытаюсь использовать последнюю цифру, сотую цифру, для этих чисел, график «стебель-лист» будет чрезвычайно длинным, потому что эти значения сильно разбросаны.(Если первые три цифры чисел находятся в диапазоне от 232 до 270, у меня будет тридцать девять листов, большинство из которых будут пустыми.) Поэтому вместо того, чтобы работать с заданными числами, я округлю каждое из чисел до ближайшая десятая, а затем использовать эти новые значения для моего графика. Округление дает мне следующий список:

23,3, 24,1, 24,8, 24,8, 25,0, 25,3, 25,6, 25,9, 26,3, 26,3, 27,1

Тогда мой график выглядит так:

---

В последнем примере выше некоторые данные были потеряны из-за округления.Иногда приходится высказывать подобное суждение.

И, конечно же, когда вы рисуете сюжет со стволами и листьями, вы всегда должны использовать линейку, чтобы построить аккуратную таблицу, и вы должны четко обозначить все. Следующие ниже примеры демонстрируют некоторую практику работы со схемами «стебель и лист», а также объясняют некоторые детали форматирования и показывают, как создать «ключ» для вашего графика.

---

URL: https: // www.purplemath.com/modules/stemleaf2.htm

,

No related posts.