Исследование на сходимость онлайн: Необходимые и достаточные признаки сходимости числового ряда

{\infty}\frac{1}{\sqrt{n}}\arctg\frac{\pi}{\sqrt[3]{2n-1}}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=\frac{1}{\sqrt{n}}\arctg\frac{\pi}{\sqrt[3]{2n-1}}$. Для начала определим, является ли этот ряд положительным, т.е. верно ли неравенство $u_n≥ 0$. Сомножитель $\frac{1}{\sqrt{n}}> 0$, это ясно, а вот что насчёт арктангенса? С арктангесом ничего сложного: так как $\frac{\pi}{\sqrt[3]{2n-1}} >0$, то и $\arctg\frac{\pi}{\sqrt[3]{2n-1}}>0$. Вывод: наш ряд является положительным. Применим признак сравнения для исследования вопроса сходимости этого ряда.

Для начала выберем ряд, с которым станем сравнивать. Если $n\to\infty$, то $\frac{\pi}{\sqrt[3]{2n-1}}\to 0$. Следовательно, $\arctg\frac{\pi}{\sqrt[3]{2n-1}}\sim\frac{\pi}{\sqrt[3]{2n-1}}$. Почему так? Если посмотреть таблицу в конце этого документа, то мы увидим формулу $\arctg x\sim x$ при $x\to 0$. Мы эту формулу и использовали, только в нашем случае $x=\frac{\pi}{\sqrt[3]{2n-1}}$.

n}\)

Ответ: ряд сходится абсолютно.

Примеры решения задач к разделу ряды ,…

Привет, мой друг, тебе интересно узнать все про примеры решения задач к разделу ряды , тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое примеры решения задач к разделу ряды , тесты по рядам, задачи по рядам , настоятельно рекомендую прочитать все из категории Ряды. Кликните на вариант (или варианты ответов), если он правильный — то будет подсвечен зеленым цветом и вам будет зачислено пару монеток, а если неверный — то красным и будет снята монетка. Удачи в прохождении онлайн теста!

Ряд, называемый также бесконечная сумма — одно из центральных понятий математического анализа.

Пример N 1

Исследовать ряд на сходимость .

Решение.

Находим

Так как 2 > 1, то, по признаку Коши, ряд расходится.

Ответ: ряд расходится.

Пример N 2

Исследовать на сходимость ряд .

Решение.

Так как в Un присутствуют факториалы, используем признак Даламбера.

Следовательно, по признаку Даламбера ряд расходится.

Ответ: ряд расходится.

Пример N 3

Исследовать на сходимость ряд .

Решение.

Признак Коши в этом случае не работает, так как . Здесь применим необходимый признак сходимости рядов.

Следовательно, по необходимому признаку ряд расходится.

Ответ: ряд расходится.

• Пример N 4

Исследовать на сходимость ряд

Решение.

Составим ряд из модулей членов нашего ряда:

получим знакоположительный ряд.

Применим предельный признак сравнения. Составим ряд эквивалентный ряду (*):

ряды эквивалентны. Так как — расходится, то ряд (*) также расходится. Следовательно, исходный ряд не сходится абсолютно.

Исследуем на условную сходимость по признаку Лейбница:

следовательно, наш ряд сходится условно.

Ответ: ряд сходится условно.

Пример N 5

Найти интервал сходимости ряда .

Решение.

Выполнив замену , получаем ряд . Об этом говорит сайт https://intellect.icu . Находим радиус сходимости:

,

Следовательно, , выполнив обратную замену, получаем . Решаем неравенство: , .

Проверим сходимость ряда на границах интервала сходимости:

Следовательно, ряд сходится абсолютно при , во всех остальных точках он расходится.

Ответ: ряд сходится абсолютно при , во всех остальных точках он расходится.

Пример N 6

Вычислить интеграл с точностью до 0,001.

Решение.

Используя ряд Маклорена функции :

Выражаем функцию через функциональный ряд:

Так как областью сходимости данного ряда является интервал и интервал , то интегрируя полученный ряд почленно, находим:

Получен знакочередующийся ряд, следовательно, ошибка в вычислении суммы не превышает модуля первого отброшенного члена ряда. Найдем член ряда, величина которого меньше 0,001:

Следовательно, для достижения требуемой точности необходимо отбросить член ряда и все последующие:

Ответ:

Тесты по темы Ряды

1. Для исследования положительных числовых рядов на сходимость не используют признак

• сравнения
• Лейбница
• интегральный Коши
• радикальный Коши

2. Вычислить интеграл, указанный на рисунке, приближенно с точностью до 0,01 путем разложения подынтегральной функции в степенной ряд

• 0,925
• 0,813
• 0,764
• 0,547

3. С помощью степенных рядов приближенно не находят

• частные производные
• значения функций
• решения дифференциальных уравнений
• определенные интегралы

4. Частичной суммой Sn ряда называется сумма его

• первых n членов
• первых десяти членов
• . бесконечного числа членов
• произвольного конечного числа членов

5.

• R=1
• R=1/5
• R=5
• R=6

6. Признак Даламбера рассматривает сходимость

• степенных рядов
• знакопеременных числовых рядов
• чередующихся числовых рядов
• положительных числовых рядов

7. Данный числовой ряд

• Сходится абсолютно
• Расходится
• Сходится условно
• Сходится

8. Данный числовой ряд

• Сходится условно
• Расходится
• Нельзя исследовать на сходимость
• Сходится абсолютно

9. Интервал сходимости степенного ряда вычисляется с помощью теоремы

• Даламбера
• Коши интегральной
• Лейбница
• Коши радикальной

10.

• –3 ≤ x < 3
• –3 < x < 3
• –3 < x ≤ 3
• –3 ≤ x ≤ 3

См. также

• Ряды
• ряды , применение рядов , числовые ряды , функциональные ряды ,
• анализ временных рядов , временные ряды ,

Как ты считаеешь, будет ли теория про примеры решения задач к разделу ряды улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое примеры решения задач к разделу ряды , тесты по рядам, задачи по рядам и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу.

Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Ряды

Из статьи мы узнали кратко, но емко про примеры решения задач к разделу ряды

Сходимость сетки с примерами — Enterfea

Должен признаться, что я не всегда обращал внимание на размер сетки. В начале своей карьеры я просто строил свои модели и был счастлив, когда они сходились. Я смутно (имею в виду смутно!) осознавал, что размер элемента «что-то делает». Но я был абсолютно доволен любыми настройками по умолчанию! Теперь я немного поумнел и покажу вам несколько важных вещей о сходимости сетки!

Выбрать правильный размер сетки довольно сложно. Конечно, вы можете основываться на своем опыте в любом конкретном типе анализа. Но этот опыт должен откуда-то браться, верно? Наиболее точным подходом будет проверка сходимости сетки. Я покажу вам пример того, как это сделать.

Если вас интересуют общие принципы того, как это работает, вы можете прочитать мой предыдущий пост. Здесь я хочу показать вам, как применять этот метод, на простом примере (чтобы вы могли следовать ему).

Проблема, которую мы можем решить…

Признаюсь, то, что я здесь сделаю, в какой-то степени является трюком. В основном потому, что я сделаю пример, где мы действительно можем знать правильный ответ (я вычислю его позже). Я знаю, что у вас, скорее всего, не будет такой роскоши в вашей «настоящей» работе. И это тоже довольно очевидно! Если бы можно было легко рассчитать результат вручную… зачем вообще делать МКЭ?!

Мой совет: попробуйте сделать то же самое, но на другом примере. Желательно такой, который вы легко сможете решить своими руками! Может быть, даже что-то более похожее на то, что вы обычно решаете в FEA? Таким образом, вы можете сами проверить, работает ли это. Не буду скрывать, я большой поклонник подхода «сначала проверьте, работает ли» при работе с МКЭ. Так что на простых примерах в начале я учусь чему-то.

Конечно, всегда можно сказать: «Да, я видел, как это сделал Лукаш, и я уверен, что это сработает, так что давайте просто сделаем это». Я не могу (и не буду!) вас останавливать. Но я думаю, что учиться лучше всего, когда вы делаете простые примеры. В основном потому, что вы можете легко и быстро «настроить» их, просто чтобы посмотреть, «что произойдет, если…». Часть «что произойдет, если…» и просто «экспериментирование» с различными вещами научат вас больше всего!

Вот почему для нашей задачи я выбрал две простые консоли. Мы будем делать их один за другим, так как я хочу показать вам кое-что интересное!

Перво-наперво!

Первый — «классический» кантилевер с грузом на конце. Я буду использовать пластинчатые элементы для моделирования этой проблемы. По сути, это консольная пластина (0,2 х 0,5 м) толщиной всего 10 мм.

Чтобы сделать это более интересным, я буду делать элементы QUAD4 и QUAD8 (то есть 4-узловые и 8-узловые четырехъядерные элементы). Таким образом, мы можем видеть, как быстро сходится ответ в обоих случаях. Это также даст нам возможность узнать некоторые другие интересные вещи!

Модель конечно супер простая, но есть маленькая вещь, которую я сделал, чтобы облегчить себе жизнь. Видите ли, если бы я смоделировал опору «только» как закрепленную на поддерживаемом конце, распределение напряжения, которое я получил бы, выглядело бы так:

Это не то, что мы ожидали, верно? Я имею в виду, что при нагрузке на «наконечник» можно было бы ожидать приятного «плавного» увеличения напряжения по направлению к опоре. И здесь мы получаем какую-то странную «концентрацию напряжения» возле поддержки, казалось бы, без всякой причины.

Ну, конечно, есть причина, и если вы уже прошли мой замечательный тест FEA Quiz, вы уже знаете ответ! Это связано с тем, что наш кантилевер хочет изменить свою ширину и под нагрузкой (закон Гука), а вблизи опоры «не может», так как опирается. Не вдаваясь в подробности, мы можем это быстро исправить, предположив, что наша «тарелка» на самом деле «бесконечна» по ширине. Таким образом, мы получим красивое «гладкое» распределение напряжения, например:

Важное примечание:

Все стрессы, которые я покажу здесь, НЕ являются стрессами фон Мисс. Вместо этого я показываю нормальное напряжение в «направлении длины» кантилевера. Это нормальное напряжение будет «сопротивляться» изгибу! Обратите внимание, что такое напряжение обычно называют «нормальным X» или «нормальным Y» или чем-то подобным… НО это в вашей ориентации конечных элементов, поэтому оно не должно следовать «направлению глобальной системы координат».

В моем случае все конечные элементы имеют свою систему координат с осью Y «вправо» на картинке выше. Итак, я показываю «Нормальное напряжение Y». Даже если глобальная UCS предполагает, что это должно быть «X», а не «Y». Как я уже писал Это локальная ось элемента, а не глобальная ПСК, решает, какое нормальное напряжение в каком направлении!

Сначала это может показаться нелогичным, я знаю. Но представьте себе тот же кантилевер, ориентированный под углом 45 градусов между осями X и Y. Глобальная ПСК вообще не будет совмещена с элементами! но все же вы можете отобразить «нормальное напряжение» вдоль и поперек кантилевера!

С этим маленьким трюком мы готовы к бою!

Точность приседания, схождение скрытой сетки!

Когда модель уже настроена, мы наконец можем начать. Скажем так, максимальное напряжение в нашем элементе нам пока неизвестно. Итак, мы хотим ответить на вопрос: Каково максимальное нормальное напряжение в нашем элементе?

Итак, что мы можем сделать, так это смоделировать кусок, использовать автоматическое создание сетки и нажать кнопку «Рассчитать». Это именно то, что я сделал! Ниже вы можете увидеть размер сетки, который Femap автоматически принимает в зависимости от размера модели. Вот что мы получили бы для элементов QUAD4:

Как видно справа, максимальное нормальное напряжение составляет 283 МПа. В таком случае необходимо ответить на 2 вопроса:

• Считаю ли я, что ответ *достаточно* точен? Если это так, то отлично — у вас есть ответ! В начале моей карьеры у меня не было возможности самому ответить на такой вопрос. Мой ответ должен быть тогда: «Я просто не знаю». «К счастью» для меня, мне не пришло в голову задать такой вопрос, так что все было просто «хорошо»…
• Если вышесказанное верно, не слишком ли мала сетка? С этой проблемой я столкнулся много лет спустя. Видите ли, связать вашу модель с очень маленькими элементами очень просто. Но вычисление и хранение данных становятся очень большой проблемой. Таким образом, вы не только хотите быть уверены, что ответ достаточно точен. Вы также хотите знать, что вы используете как можно меньше ресурсов, чтобы получить этот приемлемый ответ! Думаю, на этот вопрос сложнее ответить…

Эти два вопроса являются краеугольным камнем конвергенции сетки. По сути, если вы уверены в своих ответах в МКЭ и знаете, что используете «оптимальный» размер сетки… тогда все готово! Однако, если у вас есть сомнения, вы находитесь в правильном месте! Давайте углубимся в эту тему вместе, чтобы найти эти ответы!

Конвергенция сетки: Возьмем 1

Мы не знаем, правильный ответ выше (из «сетки по умолчанию») или нет. Это означает, что нам нужно принять 2 вещи (сразу!) и учесть третью:

• Это может быть неверный ответ! Проще говоря, размер сетки по умолчанию может быть слишком большим, и точность в данном конкретном случае неудовлетворительна. Нам нужно проверить, получим ли мы лучший ответ с меньшими элементами!
• Возможно, это слишком точный ответ! Возможно, это правильно… но было бы так же здорово, если бы элементы были намного крупнее. В таком случае сам ответ в порядке. Но… мы будем тратить драгоценные ресурсы на вычисление и сохранение результатов для подобных задач в будущем. Следует проверить, имеет ли смысл использовать меньшую сетку!
• Возможно, другой тип элемента? Это дополнительное соображение. Каждый тип элемента будет сходиться — это супер очевидная вещь. Однако в разных ситуациях одни элементы могут быть «лучше», чем другие. Обратите внимание: тот факт, что элементы могут быть «больше», чтобы получить достойный ответ, не обязательно означает, что они лучше. Если они «сверхсложные», то время вычислений может быть больше, чем в случае с более мелкими, но «менее сложными» элементами!

Зная, что я решил протестировать QUAD4 против элементов QUAD8 для этой проблемы. Это очень маленькая задача, поэтому будет сложно измерить время. Большинство прогонов «значительно меньше 1 секунды», и в такие моменты трудно точно измерить время. Но мы все равно видим, как модель сходится!

Так как это не будет стоить мне много, я могу начать с одного элемента (!) и двигаться к все более и более мелкой сетке. Конечно, вам не нужно быть таким «точным» в исследованиях сходимости сетки. Вы можете удобно начать с размера сетки, который, по вашему мнению, «имеет смысл».

Сначала займемся элементами QUAD4. Я не буду показывать вам все модели, которые я сделал (это довольно скучно, если честно). Ниже вы можете увидеть некоторые из них:

Если мы поместим все эти результаты на простую диаграмму, она будет выглядеть так:

Вы можете ясно видеть, что ответ, который мы получаем, хорошо сходится. Под этим я подразумеваю, что с увеличением количества элементов ответ «стабилизируется». Глядя на график, мы также можем сказать, что он «похож» на то, что ответ составляет около 300 МПа.

Для меня этого достаточно. Но если нужно, вы можете «навредить» диаграмме математическими вычислениями, чтобы увидеть, к какому точному значению это сходится. Но так как я знаю, что разница между 297МПа (50 элементов) и 299,7МПа (500 элементов) всего 0,9%. Я просто «в порядке» с результатом модели с 50 элементами.

Лично я не стал бы копать глубже, разве что для анализа усталости. 1-2% точности меня всегда удовлетворяет. Черт! Можно утверждать, что результат модели с 10 элементами по длине (285 МПа), дающий ошибку около 5%, все еще является разумным! Это зависит только от того, насколько большая у вас модель. Ждать еще 3 недели, пока вычисления повысят точность с 5% до 1%, возможно, не лучшая идея. Но, конечно, это может быть и отличной идеей… это действительно зависит от того, что вы делаете!

Поделитесь этим постом с друзьями!

• Facebook
• LinkedIn

Конвергенция сетки: Возьми 2

Теперь это будет происходить быстрее, так как мы уже знаем, что происходит! Ниже вы можете увидеть результаты для элементов QUAD8. Это, конечно, те же условия и все.

Не уверен, заметили ли вы… но ответ всегда 300 МПа! Я имею в виду, начиная с 1 элемента, до 500 элементов по длине… это постоянно 300 МПа! Я думаю, нам не нужно строить график в этом случае, так как это было бы потрясающе горизонтально! Это ясно показывает, что ответ «сошелся» и что правильный результат равен 300 МПа.

Должен признаться, что даже зная это и понимая почему… 1-3 элемента по длине мне все равно было бы неудобно!

Проверяем то, что уже знаем!

Это место, где мы можем остановиться на секунду и задаться вопросом, что мы уже получили (и почему). Также хотелось бы прояснить, почему элементы QUAD8 «всегда знали» правильный ответ!

Сначала посчитаем напряжение вручную. Я думаю, вы уже знаете, что это должно быть 300 МПа, но никогда не помешает проверить, верно?

Отлично! Итак, теперь мы знаем, сколько стресса мы должны получить. И QUAD4, и QUAD8 пришли к правильному решению (да!). Но было совершенно ясно, что элементы QUAD8 сошлись моментально, а элементы QUAD4 немного потрудились.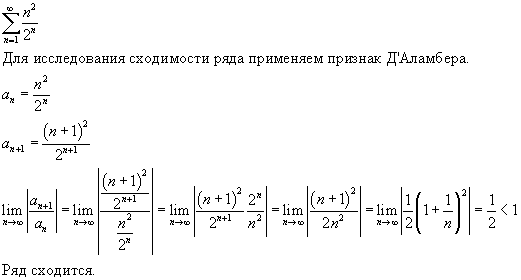 Давайте посмотрим поближе.

Видите ли, элементы QUAD8 могут «легко» выполнять линейное распределение напряжений по своей длине. Это благодаря дополнительным узлам, которые они имеют по краям. Вы можете думать о них как о «точках данных». Эти точки позволяют нам лучше рассчитать, что происходит внутри элемента (благодаря функциям формы). Если эта тема вас увлекает, вы можете прочитать больше здесь, а также посмотреть один из моих сеансов YouTube Live по этой теме. Это означает, что у элемента QUAD8 нет проблем с тем фактом, что изгиб вне плоскости вызывает линейные изменения в распределении напряжения на элементе.

С другой стороны, элементы QUAD4 «слепы» к таким действиям. Если есть изгиб вне плоскости, вызывающий напряжение, элемент QUAD4 хочет, чтобы это напряжение было «постоянным» на его поверхности. Это не всегда так для элементов QUAD4. Например, в своей плоскости они «разрешили бы» линейное распределение напряжений. Но это совсем другая тема (и не связанная с нашей проблемой).

Консоль настроена таким образом, чтобы обеспечить линейное изменение изгибающего момента. Это означает, что напряжение, вызванное этим изгибом, также будет «идеально» линейным. Вы можете увидеть это ниже:

Это означает, что даже один элемент QUAD8 может «с этим справиться». Проще говоря, он «хорошо подходит» для работы с линейным изменением напряжения в элементе. Элементы QUAD 4 на другой стороне боролись. Это потому, что они хотят иметь постоянное значение напряжения по всей ширине. Задачу легко показать так:

Как видите, каждый элемент QUAD4 просто «собирает» все напряжения со своей площади, и усредняет их. Или, по крайней мере, это то, что происходит в супер упрощенном виде. Вот почему уменьшение размера элемента изменило результаты. Чем меньше площадь элемента, который у вас есть, тем меньше влияние оказывает этот эффект. Вплоть до того, что если бы элемент был «бесконечно мал», усредненный результат по его минимальной площади был бы на самом деле точным.

Из этого примера видно, что использование элементов QUAD8 означает, что вам не нужно беспокоиться о сходимости сетки. Это, конечно, не так… и это также причина, по которой в этом посте есть второй пример!

И последнее, но не менее важное!

Итак, вы уже знаете, как решить задачу сходимости сетки! Так что, возможно, вы захотите попробовать сделать второй пример самостоятельно, прежде чем читать дальше? Это, безусловно, хорошая практика!

На этот раз наш кантилевер нагружен на поверхность. Казалось бы, небольшое изменение, но оно даст нам все эмоции, которые понадобятся для сегодняшнего поста! Смотри:

Я буду использовать те же граничные условия (вместе с предположением о симметрии), что и в предыдущем случае. И я буду использовать те же конечные элементы с той же настройкой. Так что я буду измерять, сколько элементов «по длине» в модели. Это будет индикатор размера сетки. Здесь нечего больше сказать, кроме этого:

Небольшое примечание:

В этом примере я использую количество элементов вдоль выбранного ребра в качестве «индикатора» того, насколько мелкая у меня сетка. Вы всегда можете использовать другие измерения. Признаюсь, я не фанат используемого для этого элемента «размер». Вы знаете «ширину края элемента» в миллиметрах. Но вы всегда можете использовать другое «количество элементов» для сходимости сетки. Вам даже не нужно измерять количество элементов во всей модели. Это может быть легко ограничено количеством элементов в любой конкретной части вашей модели. Просто используйте то, что в вашем уме красиво представляет, насколько маленькие элементы у вас есть. Желательно в том месте, где вы ищете результат, не обязательно во всей модели.

Это также означает, что вам не нужно везде иметь сетку одинакового размера. Совершенно нормально иметь большие элементы во многих местах и ​​маленькие элементы «там, где это важно»!

Схождение сетки: возьмем 3

Как и в предыдущем примере, мы начнем с элементов QUAD4. Опять же, ниже вы можете увидеть избранные случаи (я убрал деление на элементы для 500 FE, так что вы действительно можете что-то увидеть):

Если у вас потрясающая память (и вы внимательно слушаете!) вы можете заметить, что результаты действительно сходятся «помедленнее». Я имею в виду, что в предыдущем примере с 3 QUAD4 ответ был 250 МПа, а «всего» 216,7 МПа. Для 10 элементов разница все же есть (285 против 271,5 МПа). Черт! Даже для 500FE по длине разница все равно есть (299,7 против 299,4 МПа). Явно что-то в этой задаче более «сложное» для решения. И да… вы угадали. Окончательный ответ одинаков в обоих случаях.

Разницу хорошо видно на графике конвергенции. Синяя диаграмма — «старая» из предыдущего случая с нагрузкой на конце. Текущее дело отмечено оранжевым цветом.

Думаю, легко заметить, что оранжевая кривая сходится «медленнее» к правильному решению. Это все еще так, но это не так просто. Интересно, что в предыдущем случае 5 элементов QUAD4 были более или менее точными, чем 10 элементов QUAD4 сейчас (около 270 МПа). Ранее я упоминал, что 10 элементов по краю можно считать приличными (точность 5%). Сейчас это немыслимо, по крайней мере для меня. В этом случае точность 10 элементов по длинному краю составляет всего 10%. Это слишком много для меня. Это показывает нам, что размер сетки зависит не только от геометрии, но и от нагрузки. Или, если быть точнее, от напряженного состояния в рассчитываемой нами области.

Я очень надеюсь, что вам уже интересно, почему это так! Но сначала…

Конвергенция сетки: возьми 4

Прежде чем мы двинемся дальше, давайте взглянем на элементы QUAD8 в нашем небольшом испытании! На этот раз они не будут работать так круто, как раньше:

Понятно, что они хорошо сходятся, но это не то, что произошло «с самого начала», как в предыдущем примере. Здесь нам потребуется 3FE по длине для «приличия», что, очевидно, намного меньше, чем в случае элементов QUAD4. График сходимости можно увидеть ниже:

Грандиозный финал!

Как и в предыдущем случае, сначала давайте взглянем на фактический ответ:

Но знание максимального значения само по себе не является решением. Как и раньше, мы должны также обратить внимание на распределение напряжений. Здесь происходит вся магия. Видите ли, поскольку нагрузка распределена равномерно, распределение изгибающего момента будет параболическим, как вы можете видеть ниже:

Зная распределение напряжения, давайте проделаем трюк, который мы сделали в прошлый раз. Мы уже знаем, что эти элементы QUAD4 хотят иметь постоянное напряжение на своей поверхности. Ну… по крайней мере, в нашем случае, так как это вызвано изгибом вне плоскости элемента. Думаю, вы легко можете себе представить, что будет дальше!

Я думаю, что, увидев приведенную выше схему, вы уже знаете, что происходит. Элементы QUAD4 в нашем случае хотят иметь постоянное значение напряжения. Поэтому они работают таким образом, чтобы «сделать так, чтобы это произошло». Обратите внимание, что элемент QUAD4 не «знает» правильный ответ, а просто вычисляет свое значение в обратном порядке (как я показал вам выше). Вместо этого «внутренняя математика» элемента ограничена, и это ограничение привело к результатам в элементах. И так получилось, что эти результаты соотносятся с «действительными» результатами так, как я показал вам выше.

Это также объясняет, почему теперь ответ сходится сложнее. Квадратичную кривую сложнее аппроксимировать блоками «постоянных значений», чем линию из предыдущего примера. Некоторое количество элементов может быть «достаточно хорошим», чтобы аппроксимировать линейно распределенное напряжение. Но в той же модели, если напряжение «квадратичное», одних и тех же элементов может не хватить! Знаете, вот так:

Как ни странно, вы не будете знать, какое распределение напряжений будет в вашей модели. Я имею в виду, конечно… вы можете что-то подозревать. В простых случаях (таких как этот) вы даже можете быть уверены. Но обычно, особенно в больших и сложных моделях, вы просто не узнаете. Так что обычно лучше предположить «хуже», чем «лучше», и взять меньшие элементы «на всякий случай».

Остается только то, что «происходит» с элементами QUAD8! Конечно, это аналогичная проблема. Я уже говорил вам, что QUAD8 «хорошо подходит» для линейного изменения напряжения на их поверхности. Здесь изменение напряжения является «квадратичным», поэтому даже QUAD8 не получает «идеального» ответа с самого начала. Но у них есть огромное преимущество: они могут иметь линейное распределение напряжения (а не постоянное напряжение, как в QUAD4). Это позволяет им легче «вписаться» в фактическое распределение напряжений по сравнению с QUAD4.

В то время как напряжение изменялось линейно, QUAD8 предлагал «идеальное соответствие». При квадратичном распределении есть некоторые «ошибки», но, как вы понимаете, гораздо меньше, чем в случае с QUAD4. На самом деле, достаточно маленький, чтобы сделать рисунок ниже немного неуклюжим…

Вот почему QUAD8 было легче свести правильный ответ, даже при использовании очень небольшого количества элементов.

Это может говорить о том, что элементы QUAD8 просто лучше, но есть еще кое-что, что нужно учитывать…

Время важнее!

Когда все сказано и сделано, побеждает не «наименьшее количество необходимых элементов»! В конце концов, вы можете получить одинаковую точность между двумя моделями. В одном было бы меньше элементов QUAD8, в другом больше элементов QUAD4. Поскольку точность аналогична… вопрос в том, какой из них «лучше»?

Для меня победа за той моделью, которая вычисляет быстрее! Как я уже писал в начале, этот пример слишком мал для надежного измерения времени. Большинство моделей вычисляются менее чем за 1 с. Однако 500 FE по краю QUAD4 заняли 12 секунд… а для QUAD8 — 52 секунды. Значительно больше. Кроме того, эти вещи будут «составляться», а с более крупными моделями разница будет еще больше.

Я пытаюсь сказать, что простого ответа нет. К сожалению, здесь вы не узнаете, лучше ли вам использовать QUAD4 или QUAD8… проще говоря, я просто не знаю!

Проверка того, что лучше для вас:

Есть способ проверить, какие элементы лучше всего подходят для большинства ваших случаев!

Просто выберите модель, которая будет представлять «типичную проблему», с которой вам придется иметь дело в своей работе. Затем выполните проверку сходимости сетки как для элементов QUAD4, так и для элементов QUAD8. Черт! Вы даже можете добавить туда элементы TRI, если хотите.

Измерьте время, необходимое для вычисления при каждом запуске.

В конце концов, решите, какой уровень точности вам подходит… и просто проверьте, какой тип элементов обеспечивает требуемую точность с кратчайшим временем вычислений!

Допускаю, вам придется делать схождение сетки несколько раз для одной и той же задачи (для разных типов элементов). Это займет некоторое время и, безусловно, непрактично в вашей повседневной работе. Но делая это на 1-2 типичных примерах, вы можете показать, какие элементы лучше всего подходят для вас. Время, которое это сэкономит вам в будущем на вычислениях, стоит затраченных усилий!

Но я чувствую, что должен упомянуть еще кое-что. Необработанное время — отличный показатель, но не слишком зацикливайтесь на нем.

Есть и другие соображения, которые вы можете принять во внимание. Первое, что приходит мне на ум, это сколько мелких деталей в вашей модели. Обычно сетка имеет небольшой размер рядом с небольшими функциями, которые вы хотите иметь в своей модели. Но, с другой стороны, «более качественные» элементы (типа QUAD8) могут «позволить» использовать сверхбольшие элементы «вообще». В таком случае переход между мелкими элементами рядом с деталями и сверхбольшими элементами в других местах приведет к тому, что сетка будет «уродливой» с низким качеством. Я бы подумал об этом и при выборе типа элемента.

Резюме!

Вот оно! Я надеюсь, что вам понравился этот пример сходимости сетки, и он помог вам кое-что узнать о том, как работает FEA! Давайте попробуем резюмировать то, о чем мы говорили здесь:

• Имеет смысл проводить МКЭ для задач, которые можно решить вручную. Это поможет вам понять, что происходит, и увидеть, дает ли ваш подход к моделированию МКЭ правильные результаты!
• Размер сетки нельзя просто игнорировать. Было бы здорово, но даже такая простая задача показывает, что точность зависит от размера элемента. Я бы не стал сильно волноваться по этому поводу, но и игнорировать это тоже не стоит!
• На самом деле здорово понимать, как все работает. Я первый признаюсь, что мне не нравится изучать математику МКЭ. Для меня такие простые примеры — средство «понимания», как все работает. Без всех уравнений…
• Выполнение сходимости сетки для «типичной модели» для выбора наилучшего типа сетки — хорошая идея! Я сделал это давным-давно. Но когда я пишу это, я чувствую, что я должен вернуться к этому! За последние годы я многому научился, и мы немного изменили подход к решению проблем. Возможно, сейчас выводы из такого исследования были бы другими… кто знает!

Хотите узнать больше? Я тебя прикрыл!

Если вам нравится мой стиль преподавания, обязательно ознакомьтесь с моим БЕСПЛАТНЫМ курсом FEA ниже.

Важность сходимости сетки

 

В этой статье, состоящей из двух частей, описывается, возможно, одна из наиболее игнорируемых проблем, влияющих на точность, а именно; сходимость сетки. Это относится к малости элементов, необходимых в модели, чтобы гарантировать, что на результаты анализа не повлияет изменение размера сетки. Мы сталкивались со случаями, когда размер сетки просто принимался как историческое наследие, которое нельзя изменить, и не было никаких сведений о его влиянии на точность. Это плохая практика.

Эта статья непосредственно применима к анализу статического напряжения. Несмотря на то, что размер сетки важен для всех анализов, существуют и другие факторы, влияющие на выбор соответствующего размера элемента в более сложных анализах. Это относится к большинству программ «h element»; Программы «p-элемента» (например, Pro Mechanica) сходятся к результату в процессе решения и в значительной степени не зависят от размера элемента.

 

Как провести исследование конвергенции

Кривая сходимости

Формальный метод установления сходимости сетки требует построения кривой критического параметра результата (обычно какого-то напряжения) в определенном месте в зависимости от некоторой меры плотности сетки. По крайней мере, три прогона конвергенции потребуются для построения кривой, которую затем можно будет использовать для указания того, когда конвергенция достигнута или насколько далека самая точная сетка от полной сходимости. Однако, если два прогона с разной плотностью сетки дают одинаковый результат, сходимость уже должна быть достигнута, и кривая сходимости не нужна.

 

Рисунок 1 – кривая сходимости по 4 точкам

 

Локальное уточнение сетки

Теоретически, для каждого последующего уровня измельчения сетки в исследовании сходимости все элементы модели должны быть разделены во всех направлениях. Хотя последнее требование важно, нет необходимости выполнять его для всей модели: принцип Сен-Венана подразумевает, что локальные напряжения в одной области конструкции не влияют на напряжения в других местах. Таким образом, с физической точки зрения мы должны иметь возможность проверить сходимость модели, уточнив сетку только в интересующих областях и сохранив неочищенную (и, возможно, несходящуюся) сетку в других местах. У нас также должны быть переходные области от грубой сетки к мелкой, достаточно удаленные от интересующей области (не менее 3 элементов для линейных элементов).

Геометрия границы — сопутствующий эффект

Общее влияние на результаты напряжения при использовании линейных (прямосторонних) элементов для представления изогнутой поверхности или края заключается в том, что геометрия границы будет лучше представлена ​​по мере уточнения сетки. Это эффект моделирования или геометрии, отличный от конвергенции сетки, которая является численной. Стоит осознавать различие между этими двумя аффектами.

Стратегия создания сетки

Идея использования только локальных Уточнение сетки для исследования конвергенции может быть расширено. Если требуется, чтобы модель создавала точные напряжения только в определенных областях, представляющих интерес, роль всех элементов, удаленных от этих областей, заключается только в представлении геометрии и передаче нагрузки. Это требует гораздо более низкого уровня детализации сетки, чем для точного прогнозирования напряжения. Таким образом, эти элементы могут быть значительно больше, с учетом ограничений, связанных как с переходами разумного качества, так и с представлением геометрии.

Использование более крупных элементов вдали от областей интереса в модели является обычной практикой, но более тонкий момент заключается в том, что они не искажают геометрию и могут быть выполнены подходящие переходы сетки; эти элементы могут быть 90 287 значительно 90 288 больше, чем элементы в интересующих областях, без ущерба для точности. Сравните это как стратегию создания сетки с заполнением всей модели небольшими высококачественными элементами для повышения «общей» точности. Этот последний подход неэффективен и вряд ли повысит точность анализа статического напряжения с помощью неявного кода.

Резюме

• Каждый отдел должен иметь некоторые базовые данные о сходимости сетки для своих моделей.
  
• Для демонстрации сходимости сетки можно использовать ряд прогонов модели с возрастающими уровнями детализации сетки в интересующих областях.
  
• Размеры элементов, удаленных от области, не оказывают существенного влияния на результаты в этой области, при условии, что они не искажают геометрию отдаленных объектов.

 

 

Распространение исследования конвергенции на другие модели

Если одна модель подвергалась исследованию конвергенции, как описано в первой статье, то было бы логично утверждать, что соответствующая область в модели «похожей» структуры с тот же уровень детализации сетки будет иметь тот же уровень точности. Это верно при условии, что «сходство» моделей включает в себя сходство градиентов напряжения.

Часто усиление области конструкции может привлекать больше нагрузки и создавать более высокие напряжения в галтелях или других элементах, что требует тщательного детального проектирования и анализа. Усиленная конструкция в этом случае не «похожа» на предыдущую конструкцию в том смысле, что она будет иметь более высокие градиенты напряжения, что потребует увеличения плотности сетки в этой области, чтобы обеспечить сравнимую точность с анализом предыдущей конструкции. Это особенно важно, поскольку напряжения стремятся к предельной прочности материала и становятся критическими для принятия новой конструкции.

Даже без изменения конструкции конструкции простое увеличение величины нагрузки означает увеличение градиента напряжения в определенных областях. Хотя точность в процентах от пикового напряжения не изменится, точность относительно предела текучести материала будет снижена, если сетка не будет уточнена.

 

Примеры неправильной практики

Использование размера элемента в качестве меры сходимости

конвергентная сетка в непохожей модели или в другом месте аналогичной модели недействительна.

Точность измерения напряжения будет в некоторой степени зависеть от размера элемента, но важнее близость элемента к концентрации напряжения или изменение нагрузки в конструкции в интересующей области.

 

Распространенный случай игнорирования сходимости

На рисунке напротив показана область двухмерной или трехмерной сетки, представляющая внутренний угол. Радиус не моделируется. Такой внутренний угол с нулевым радиусом может иметь бесконечное теоретическое напряжение, если он сделан из абсолютно эластичного материала. Это связано не с какими-либо численными эффектами МКЭ, а с тем, что концентрация напряжений в большинстве ситуаций для этой геометрии бесконечна.

По мере уточнения сетки напряжение будет увеличиваться без ограничений. Таким образом, напряжения, предсказанные КЭ-анализом смоделированного таким образом галтеля, зависят только от размера элементов и не имеют ничего общего с какими-либо реальными значениями, которые могут там возникнуть.

Довольно часто ощутимые напряжения можно предсказать по представлению внутреннего скругления таким образом, но это не означает, что они действительны; фактический радиус, указанный на чертеже, должен быть представлен соответствующим количеством элементов, расположенных вокруг скругления, для достижения предсказуемого упругого напряжения. (Могут быть серьезные последствия, если чертеж, определяющий этот элемент, не включает минимальный радиус. )

Сводка

• Избегайте использования только размера элемента в качестве индикатора сходимости.
  

• Результаты исследования локальной конвергенции могут быть распространены только на соответствующие места в структурно подобных моделях с аналогичными нагрузками.
  

• При значительном увеличении величины нагрузки точность относительно фиксированного допустимого напряжения снижается.
  

• Не моделируйте критические внутренние скругления, как показано на рисунке выше, так как они не могут предсказать истинные напряжения.

 

Перейти к следующей статье базы знаний: Основы численных методов для статического, динамического и переходного анализа или вернуться к списку серий статей базы знаний

Конвергенция массового и межличностного общения пациентов на онлайн-форуме: гибрид Анализ методов

1. Бенсинг Дж., Верхаак П. Общение во время медицинских встреч. В: Каптейн А., Вайнман Дж., редакторы. Психология здоровья. Мальден: Издательство Блэквелл; 2004. стр. 261–287. [Академия Google]

2. Бландфорд А. HCI для здоровья и благополучия: проблемы и возможности. Int J Hum-Comput Stud. 2019 ноябрь; 131: 41–51. doi: 10.1016/j.ijhcs.2019.06.007. [CrossRef] [Google Scholar]

3. Крепс Г.Л. Информационные и коммуникационные онлайн-системы для улучшения результатов в отношении здоровья за счет конвергенции коммуникаций. Hum Commun Res. 2017 30 июня; 43 (4): 518–530. doi: 10.1111/hcre.12117. [CrossRef] [Google Scholar]

4. Воруганти Т., Грюнфельд Э., Макуваза Т., Бендер Дж.Л. Веб-инструменты для текстового общения между пациентом и поставщиком медицинских услуг при хронических заболеваниях: предварительный обзор. J Med Internet Res. 2017 27 октября; 19(10):e366. doi: 10.2196/jmir.7987. https://www.jmir.org/2017/10/e366/ [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

5. Walther JB, Valkenburg PM. Слияние массового и межличностного общения с помощью технологии интерактивной коммуникации: симпозиум. Hum Commun Res. 2017 30 июня; 43 (4): 415–423. doi: 10.1111/hcre.12120. [CrossRef] [Google Scholar]

6. van der Meij E, Huirne JA, Ten Cate AD, Stockmann HB, Scholten PC, Davids PH, Bonjer HJ, Anema JR. Периоперационная программа электронного здравоохранения для улучшения послеоперационного восстановления после операции на брюшной полости: оценка процесса рандомизированного контролируемого исследования. J Med Internet Res. 2018 02 января; 20(1):e1. дои: 10.2196/жмир.8338. https://www.jmir.org/2018/1/e1/ [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

7. van Eenbergen MC, van de Poll-Franse LV, Heine P, Mols F. Влияние участия в онлайн-сообществах по борьбе с раком на результаты, о которых сообщают пациенты: систематический обзор. JMIR Рак. 2017 сен 28;3(2):e15. doi: 10.2196/рак.7312. https://cancer.jmir.org/2017/2/e15/ [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

8. Лобчук М., Макклемент С., Ригни М., Коупленд А., Байрампур Х. Качественный анализ «натуралистических» бесед в онлайн-сообществе поддержки рака легких под руководством сверстников. Рак Нурс. 2015;38(5):E21–E31. дои: 10.1097/NCC.0000000000000207. [PubMed] [CrossRef] [Google Scholar]

9. Сил С., Зибланд С., Чартерис-Блэк Дж. Гендер, опыт лечения рака и использование Интернета: сравнительный анализ ключевых слов интервью и онлайн-групп поддержки рака. соц. мед. 2006 г., май; 62 (10): 2577–2590. doi: 10.1016/j.socscimed.2005.11.016. [PubMed] [CrossRef] [Google Scholar]

10. Eysenbach G, Powell J, Kuss O, Sa E. Эмпирические исследования по оценке качества медицинской информации для потребителей во всемирной паутине: систематический обзор. ДЖАМА. 2002;287(20):2691–700. дои: 10.1001/jama.287.20.2691. [PubMed] [CrossRef] [Google Scholar]

11. Батенбург А., Дас Э. Эмоциональный подход к преодолению трудностей и влияние онлайн-группы поддержки под руководством сверстников среди пациентов с раком молочной железы: лонгитюдное исследование. J Med Internet Res. 2014 28 ноября; 16 (11): e256. doi: 10.2196/jmir.3517. https://www.jmir.org/2014/11/e256/ [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

12. Nwosu CR, Cox BM. Влияние Интернета на отношения между врачом и пациентом. Health Informatics J. 2016 г., 25 июля; 6 (3): 156–161. doi: 10.1177/146045820000600308. [Перекрестная ссылка] [Академия Google]

13. Caiata-Zufferey M, Abraham A, Sommerhalder K, Schulz PJ. Онлайн-поиск медицинской информации в контексте медицинской консультации в Швейцарии. Качество здоровья Res. 2010 авг; 20 (8): 1050–1061. doi: 10.1177/1049732310368404. [PubMed] [CrossRef] [Google Scholar]

14. Rupert DJ, Gard Read J, Amoozegar JB, Moultrie RR, Taylor OM, O’Donogue AC, Sullivan HW. Информация о здоровье, созданная сверстниками: роль онлайн-сообществ в принятии решений о здоровье пациентов и лиц, осуществляющих уход. Сообщество здоровья J. 2016 ноябрь; 21 (11): 1187–1197. doi: 10.1080/10810730.2016.1237592. http://europepmc.org/abstract/MED/27805496. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

15. Shah DV, Cappella JN, Neuman WR. Большие данные, цифровые медиа и вычислительная социальная наука. Ann Am Acad Pol Soc Sci. 2015 09 апреля; 659 (1): 6–13. doi: 10.1177/0002716215572084. [CrossRef] [Google Scholar]

16. Abdul-Muhsin H, Tyson M, Raghu S, Humphreys M. Информированный пациент: анализ поведения при поиске информации и хирургических результатов среди мужчин с доброкачественной гиперплазией предстательной железы. Am J Mens Health. 2017 янв; 11 (1): 147–153. дои: 10.1177/1557988315617527. http://europepmc.org/abstract/MED/26614445. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

17. Leydon G, Boulton M, Moynihan C, Jones A, Mossman J, Boudioni M, McPherson K. Информационные потребности онкологических больных и поведение при поиске информации: подробное интервью. БМЖ. 01 апреля 2000 г .; 320 (7239): 909–913. doi: 10.1136/bmj.320.7239.909. http://europepmc.org/abstract/MED/10742000. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

18. Рахмани А., Фергюсон С., Джабарзаде Ф., Мохаммадпурасл А., Моради Н., Пакпур В. Потребности иранских больных раком в поддерживающей терапии. Индийский J Palliat Care. 2014 сен; 20 (3): 224–228. дои: 10.4103/0973-1075.138400. http://www.jpalliativecare.com/article.asp?issn=0973-1075;year=2014;volume=20;issue=3;spage=224;epage=228;aulast=Rahmani. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

19. Hong Y, Peña-Purcell NC, Ory MG. Результаты онлайн-поддержки и ресурсов для выживших после рака: систематический обзор литературы. Пациент Educ Couns. 2012 март; 86 (3): 288–296. doi: 10.1016/j.pec.2011.06.014. [PubMed] [CrossRef] [Google Scholar]

20. Shea-Budgell M, Kostaras X, Myhill K, Hagen N. Информационные потребности и источники информации для пациентов во время наблюдения за раком. Карр Онкол. 2014 авг; 21 (4): 165–173. дои: 10.3747/co.21.1932. http://www.current-oncology.com/index.php/oncology/article/view/1932/1555. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

21. Hesse BW, Nelson DE, Kreps GL, Croyle RT, Arora NK, Rimer BK, Viswanath K. Доверие и источники медицинской информации: влияние Интернет и его последствия для поставщиков медицинских услуг: результаты первого национального исследования тенденций в области медицинской информации. Arch Intern Med. 2005;165(22):2618–2624. doi: 10.1001/archinte.165.22.2618. [PubMed] [CrossRef] [Академия Google]

22. Престин А., Вьё С.Н., Чоу В.С. Онлайн-активность в области здравоохранения жива и здорова или остается на прежнем уровне? Результаты 10-летнего исследования национальных тенденций в области информации здравоохранения. Сообщество здоровья J. 2015;20(7):790–798. doi: 10.1080/10810730.2015.1018590. [PubMed] [CrossRef] [Google Scholar]

23. Xiao N, Sharman R, Rao H, Upadhyaya S. Факторы, влияющие на поиск медицинской информации в Интернете: эмпирический анализ национального исследования, связанного с раком. Система поддержки Decis. 2014 янв; 57: 417–427. doi: 10.1016/j.dss.2012.10.047. [Перекрестная ссылка] [Академия Google]

24. Путс МТЕ, Папуцис А., Спринголл Э., Туранжо А.Е. Систематический обзор неудовлетворенных потребностей недавно диагностированных пожилых больных раком, проходящих активное лечение рака. Поддержите уход за раком. 2012 июль; 20 (7): 1377–1394. doi: 10.1007/s00520-012-1450-7. [PubMed] [CrossRef] [Google Scholar]

25. Iconomou G, Vagenakis AG, Kalofonos HP. Информационные потребности, удовлетворенность общением и психологический статус основных лиц, осуществляющих уход за онкологическими больными, получающими химиотерапию. Поддержите уход за раком. 2001 ноябрь; 9(8): 591–596. doi: 10.1007/s005200100259. [PubMed] [CrossRef] [Google Scholar]

26. Brandes K, van der Goot MJ, Smit EG, van Weert JC, Linn AJ. Понимание взаимодействия инструментальных проблем и эмоций больных раком. Пациент Educ Couns. 2017 г., май; 100 (5): 839–845. doi: 10.1016/j.pec.2017.02.002. [PubMed] [CrossRef] [Google Scholar]

27. Hack TF, Degner LF, Parker PA, SCRN Communication Team Коммуникационные цели и потребности онкологических больных: обзор. Психоонкология. 2005 г., 14 октября (10): 831–845; обсуждение 846. doi: 10.1002/pon.949. [PubMed] [CrossRef] [Google Scholar]

28. Sommerhalder K, Abraham A, Zufferey MC, Barth J, Abel T. Интернет-информация и медицинские консультации: опыт с точки зрения пациентов и врачей. Пациент Educ Couns. 2009 ноябрь; 77 (2): 266–271. doi: 10.1016/j.pec.2009.03.028. [PubMed] [CrossRef] [Google Scholar]

29. Рейнгольд Х. Виртуальное сообщество: Homesteading на электронных границах. США: Addison-Wesley Longman Publishing Co, Inc.; 2000. [Google Академия]

30. Гуден Р.Дж., Уайнфилд Х.Р. Онлайн-дискуссионные форумы по раку молочной железы и простаты: тематический анализ гендерных различий и сходств. J Health Psychol. 2007 г., январь; 12 (1): 103–114. doi: 10.1177/1359105307071744. [PubMed] [CrossRef] [Google Scholar]

31. Sanders R, Linn AJ, Araujo TB, Vliegenthart R, van Eenbergen MC, van Weert JC. Различные платформы для разных потребностей пациентов: автоматический анализ контента различных онлайн-платформ медицинской информации. Int J Hum-Comput Stud. 2020 Май; 137:102386. doi: 10.1016/j.ijhcs.2019.102386. [CrossRef] [Google Scholar]

32. Синха А., Портер Т. , Уилсон А. Использование интернет-форумов по вопросам здоровья пациентами с хроническим кашлем: качественное исследование. J Med Internet Res. 2018 24 января; 20 (1): e19. doi: 10.2196/jmir.7975. https://www.jmir.org/2018/1/e19/ [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

33. Бендер Дж.Л., Фельдман-Стюарт Д., Тонг С., Ли К., Брандейдж М., Пай Х., Робинсон Дж., Панзарелла Т. Использование Интернета, связанное со здоровьем, среди мужчин с раком простаты в Канаде: исследование реестра рака. J Med Internet Res. 201919 ноября; 21(11):e14241. дои: 10.2196/14241. https://www.jmir.org/2019/11/e14241/ [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

34. van Eenbergen MCHJ, Vromans RD, Boll D, Kil PJM, Vos CM , Крамер Э.Дж., Молс Ф., ван де Полл-Франс Л.В. Изменения в использовании Интернета и пожелания выживших после рака: сравнение между 2005 и 2017 годами. Рак. 2020 15 января; 126 (2): 408–415. doi: 10.1002/cncr.32524. http://europepmc.org/abstract/MED/31580497. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

35. Сандерс Р., Линн А.Дж. Исследование смешанного метода, изучающее влияние разговоров об использовании Интернета пациентами на результаты, о которых сообщают пациенты. Сообщество здоровья J. 2018;23(9):815–823. doi: 10.1080/10810730.2018.1514443. [PubMed] [CrossRef] [Google Scholar]

36. Bylund CL, D’Agostino TA, Ostroff J, Heerdt A, Li Y, Dickler M. Воздействие и намерение обсуждать информацию о раке в Интернете среди пациентов с раком молочной железы. . Дж Онкол Практ. 2012 г., янв; 8 (1): 40–45. doi: 10.1200/JOP.2011.000271. http://europepmc.org/abstract/MED/22548010. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

37. Linn AJ, Schouten BC, Sanders R, van Weert JC, Bylund CL. Говоря о докторе Google: Коммуникационные стратегии, используемые практикующими медсестрами и пациентами с воспалительными заболеваниями кишечника в Нидерландах для обсуждения медицинской информации в Интернете. Пациент Educ Couns. 2020 июнь; 103 (6): 1216–1222. doi: 10.1016/j.pec.2020.01.011. [PubMed] [CrossRef] [Google Scholar]

38. Cutrona CE. Стресс и социальная поддержка — в поисках оптимального соответствия. J Soc Clin Psychol. 1990 март; 9 (1): 3–14. doi: 10.1521/jscp.1990.9.1.3. [CrossRef] [Google Scholar]

39. Chen Y, Li C, Liang J, Tsai C. Медицинская информация, полученная из Интернета, и изменения в принятии медицинских решений: разработка анкеты и кросс-секционное исследование. J Med Internet Res. 2018 12 февраля; 20(2):e47. doi: 10.2196/jmir.9370. https://www.jmir.org/2018/2/e47/ [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

40. Stafford TF, Stafford MR, Schkade LL. Определение видов использования и вознаграждений в Интернете. Решение наук. 2004 май; 35 (2): 259–288. doi: 10.1111/j.00117315.2004.02524.x. [CrossRef] [Google Scholar]

41. Рубин А. Перспектива использования и удовлетворения медиаэффектов. В: Брайант Дж., Зиллманн Д., редакторы. Серия сообщений LEA. Медиа-эффекты: достижения в теории и исследованиях. Нью-Джерси: Издательство Lawrence Erlbaum Associates; 2002. стр. 525–548. [Google Scholar]

42. Гейл Н.К., Хит Г., Кэмерон Э., Рашид С., Редвуд С. Использование рамочного метода для анализа качественных данных в междисциплинарных исследованиях в области здравоохранения. БМС Мед Рез Методол. 2013 18 сент.; 13:117. дои: 10.1186/1471-2288-13-117. https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/1471-2288-13-117. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

43. Kanker.nl. [2016-12-15]. www.kanker.nl.

44. Рак сегодня Всемирной организации здравоохранения. Международное агентство по изучению рака. 2019. [2019-10-19]. http://gco.iarc.fr/today/data/factsheets/cancers/39-All-cancers-fact-sheet.pdf.

45. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Duchesnay MPE. Scikit-learn: Машинное обучение в Python. J Машинное обучение Res. 2011 Июн; 19(1): 2825–2830. [Google Scholar]

46. Ранганатан П., Аггарвал Р., Прамеш К.С. Распространенные ловушки в статистическом анализе: шансы против риска. Перспект Клин Рез. 2015;6(4):222–224. doi: 10.4103/2229-3485.167092. http://www.picronline.org/article.asp?issn=2229-3485;year=2015;volume=6;issue=4;spage=222;epage=224;aulast=Ranganathan. [PMC бесплатная статья] [PubMed] [CrossRef] [Google Scholar]

47. Muusses LD, van Weert JCM, van Dulmen S, Jansen J. Химиотерапия и поведение при поиске информации: характеристики пациентов, использующих источники информации в СМИ. Психоонкология. 2012 Сентябрь;21(9)): 993–1002. doi: 10.1002/пон.1997. [PubMed] [CrossRef] [Google Scholar]

48. Bylund CL, Makoul G. Изучение эмпатии при медицинских встречах: наблюдательное исследование с использованием системы кодирования эмпатической коммуникации. Община здоровья. 2005;18(2):123–140. doi: 10.1207/s15327027hc1802_2. [PubMed] [CrossRef] [Google Scholar]

49. Луптон Д. Пациент, вовлеченный в цифровые технологии: самоконтроль и самопомощь в эпоху цифрового здравоохранения. Социальная теория здоровья. 2013 19 июня; 11 (3): 256–270. doi: 10.1057/sth.2013.10. [Перекрестная ссылка] [Академия Google]

50. Eysenbach G, Powell J, Englesakis M, Rizo C, Stern A. Виртуальные сообщества, связанные со здоровьем, и электронные группы поддержки: систематический обзор результатов онлайн-взаимодействий между равными. БМЖ. 2004 г., 15 мая; 328 (7449): 1166. doi: 10.1136/bmj.328.7449.1166. http://europepmc.org/abstract/MED/15142921. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

51. Эйзенбах Г. Медицина 2.0: социальные сети, сотрудничество, участие, посредничество и открытость. J Med Internet Res. 2008 г., 25 августа; 10 (3): e22. дои: 10.2196/жмир.1030. https://www.jmir.org/2008/3/e22/ [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

52. Бендер Дж.Л., Хименес-Маррокин М.