Примеры исследования несобственных интегралов на сходимость
Примеры исследования несобственных интегралов на сходимость
Пример 1 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a>1 и расходится при a£1.
Пример 2 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a<1 и расходится при a³1.
Пример 3 Исследовать на сходимость .
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два
.
Сходимость первого интеграла I1 исследуем с помощью эквивалентной функции: ( т. к. n>0), а интеграл сходится при m>-1 (пример 2). Аналогично, для интеграла I2 :
, а интеграл сходится при m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 и m+n<-1, и будет расходится при нарушении хотя бы одного из них.
Пример 4 Исследовать на сходимость .
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:
.
Так как arctgx »x при x®0, то интеграл I1 эквивалентен интегралу , который сходится при m+1>-1 т. е. при m>-2 (пример1).
Для подынтегральная функции в несобственном интеграле первого рода I2 подберем эквивалентную:
т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n<-1, и расходится в противном случае.
Объединяя условия сходимости интегралов I1 и I2 получим условия сходимости исходного интеграла: m>-2 и m+n<-1 одновременно.
Замечание. В примерах 2-4 использовался 2 признак сравнения, который обеспечивает необходимые и достаточные условия сходимости, что позволяет, установив сходимость при некотором условии на значения параметров, не доказывать расходимость интеграла при нарушении полученных условий сходимости.
Пример 5 Исследовать на сходимость .
Данный интеграл содержит особую точку 0, в которой подынтегральная функция может обращается в бесконечность при p<0, поэтому снова разобьем исходный интеграл на два:
.
Интеграл I1 является несобственным интегралом второго рода, и подынтегральная функция эквивалентна при x®0 функции xp (e-x ®1 при x®0), т. е. I1 сходится при p>-1 (пример 1).
Интеграл I2 является несобственным интегралом первого рода. Подобрать функцию, эквивалентную подынтегральной функции, такую, чтобы она не содержала показательной функции, не удается. Поэтому использовать признак сравнения 2, как в предыдущих примерах, нельзя. Применим первый признак сравнения, для чего используем следующий известный факт:
При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax < M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
,
Т.
е. интеграл I2 сходится при любом p.
Таким образом, исходный интеграл сходится при p>-1.
Пример 6 Исследовать на сходимость .
Проведем замену переменной: t = lnx, и получим
.
Разбиение интеграла на два произведено аналогично примеру 5. Интеграл I1 полностью эквивалентен интегралу I1 из примера 5 и, следовательно, сходится при q<1.
Рассмотрим интеграл I2 . При условии 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения и a=(1-p)/2. ).
Итак, I2 сходится при p>1. Однако, на этом исследование сходимости этого интеграла не закончено, так как использованный признак сходимости дает только достаточные условия сходимости. Поэтому нужно исследование сходимости при 1-p£0.
Рассмотрим случай p=1. Тогда интеграл I2 эквивалентен , который сходится при q>1 (заметим, что в этом случае интеграл I1 расходится) и расходится в противном случае.
При p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что При 1-p>0, и, следовательно, начиная с некоторого А>1 выполнено T—QE(1-P)T ³ M=const>0. Тогда для интеграла I2 справедлива оценка
,
Где интеграл в правой части расходится, что и доказывает расходимость интеграла I2 .
Суммируя полученные результаты, получаем что исходный интеграл сходится при q<1 и p>1, в противном случае интеграл расходится.
Пример 6 Исследовать на абсолютную и условную сходимость .
Разобьем исходный интеграл на два:
.
Сходимость. Интеграл I1 эквивалентен , т. е. сходится при p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
Интеграл I2 сходится про признаку Дирихле-Абеля при p>0 т. к. первообразная sin(x) ограничена, а функция 1/xp монотонно стремится к нулю при x стремящемся к бесконечности.
Покажем, что при p£0 интеграл расходится. Воспользуемся для этого критерием Коши, а точнее его отрицанием
.
Возьмем в качестве R1и R2 следующие величины: R1=2pk и R2=2pk+p/2, тогда
, при p>0.
Таким образом, интеграл сходится при 0<p<1.
Абсолютная сходимость Абсолютная сходимость интеграла I1 уже установлена, рассмотрим абсолютную сходимость I2 . Оценим интеграл сверху:
, т. е. интеграл сходится при p>1.
Для доказательства расходимости при p£1 оценим интеграл снизу
.
Разобьем последний интеграл от разности функций на разность интегралов
.
Если оба интеграла сходятся, то и интеграл от разности сходится, если один из интегралов расходится, а другой сходится — то интеграл от разности расходится. В случае расходимости обоих интегралов сходимость интеграла от разности подлежит дальнейшему исследованию. Нас интересует второй из описанных случаев.
расходится (пример 1) при p<1. сходится по признаку Дирихле-Абеля при 1>p>0 (см.
Сходимость), следовательно интеграл оценивается снизу расходящимся интегралом, т. е. расходится.
Случай p³1 нас не интересует, т. к. при этих значениях параметра интеграл расходится.
Таким образом, исходный интеграл сходится абсолютно при 0<p<1, сходится условно при 1£p<2.
| < Предыдущая | Следующая > |
|---|
Как вычислить несобственный интеграл и выяснить сходимость
- Понятие несобственного интеграла и его геометрический смысл
- Несобственные интегралы с бесконечными пределами и их сходимость
- Несобственные интегралы от неограниченных функций и их сходимость
Для вычисления несобственных интегралов требуются хорошие знания определенных интегралов. и пределов. По сути несобственный интеграл — особый случай определенного интеграла.
Как и при решении определенного интеграла, в результате решения несобственного интеграла
должно получиться некоторое число.
Но это лишь тогда, когда несобственный интеграл сходится. Если же он
расходится, то ответ так и записывается: несобственный интеграл расходится.
Несобственные интегралы первого рода. По сути это тот же определённый интеграл, но в случаях, когда интегралы имеют бесконечный верхний или нижний пределы интегрирования, или оба предела интегрирования бесконечны.
Несобственные интегралы второго рода. По сути это тот же определённый интеграл, но в случаях, когда интеграл берётся от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не имеет, обращаясь в бесконечность.
Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f(x) непрерывна на отрезке [a, b], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью.
Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f(x) находится выше оси Ox, определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f(x), осью абсцисс и ординатами x = a, x = b. В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f(x) (на рисунке ниже — красного цвета), x = a и осью абсцисс.
Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:
,
.
Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся.
Площадь может быть и бесконечностью и в этом случае несобственный
интеграл называется расходящимся.Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае — расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.
Несобственные интегралы с бесконечным верхним пределом
Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.
Определение. Несобственным интегралом с бесконечным верхним пределом
интегрирования от непрерывной функции f(x) на промежутке
от a до ∞ называется
предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел
интегрирования неограниченно растёт, т.
е.
.
Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся, а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.
Пример 1. Вычислить несобственный интеграл (если он сходится).
Решение. На основании определения несобственного интеграла находим
Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.
В следующем примере подынтегральная функция почти как в примере 1, только степень икса — не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?
Пример 2.
Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).
Решение. Предположим сначала, что , тогда
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при имеет место . Если , то и не существует.
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:
.
Это обобщённая формула Ньютона-Лейбница.
Пример 3. Вычислить несобственный интеграл (если он сходится).
Решение. С помощью метода замены переменной можно получить очень полезную формулу:
Доказывать эту формулу нет необходимости, но запомнить стоит — пригодится. Итак, применяя эту формулу для нахождения первообразной получим
Итак, несобственный интеграл сходится и равен 1.
Пример 4. Вычислить несобственный интеграл (если он сходится).
Решение. Находим
.
Но предел не существует, т. е. данный несобственный интеграл расходится.
Пример 5. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция непрерывна в каждой точке, поэтому определённый интеграл от неё на отрезке [0, b] существует при всяком b. Находим этот интеграл:
.
Находим предел этого интеграла:
.
По определению, значение данного несобственного интеграла:
.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Интеграл
Несобственные интегралы с бесконечным нижним пределом
Аналогично определяется несобственный интеграл от непрерывной функции с бесконечным нижним пределом интегрирования, обозначаемый символом , а именно
.
Если этот предел существует (и, значит, конечен, то есть, равен некоторому числу, а не бесконечности), то данный несобственный интеграл называется сходящимся.
Пример 6. Вычислить несобственный интеграл с бесконечным нижним пределом(если он сходится).
Решение. Находим предел данного интеграла:
Вывод: данный несобственный интеграл сходится, а его значение равно -1/2.
Несобственные интегралы с двумя бесконечными пределами
Несобственный интеграл с двумя бесконечными пределами интегрирования, обозначаемый символом , нужно предварительно представить в виде суммы двух несобственных интегралов, один из которых с конечным верхним пределом интегрирования, другой — с конечным нижним пределом интегрирования, т.е.
.
По определению,
,
причём этот несобственный интеграл считается сходящимся, если оба предела существуют, когда a и b независимо друг от друга неограниченно возрастают по абсолютной величине.
Пример 7. Вычислить несобственный интеграл с двумя бесконечными пределами (если он сходится).
Решение. На основании определения несобственного интеграла с двумя бесконечными пределами представляем данный интеграл как сумму двух несобственных интегралов:
.
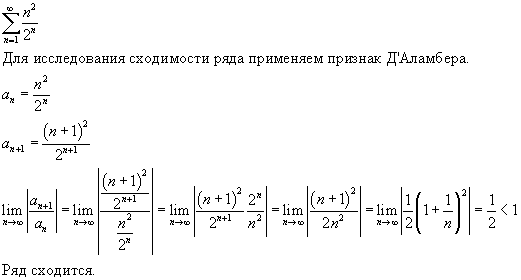
Преобразуем подынтегральное выражение к форме , с помощью выделения полного квадрата:
По формуле находим:
(Эта формула, которой мы воспользовались, а также другие формулы, пригодные для интегрирования дробей, приведены в уроке Интегрирование некоторых рациональных дробей и иррациональностей).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
.
Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:
.
Пусть функция f(x) задана на
отрезке от a до b и неограниченна на нём.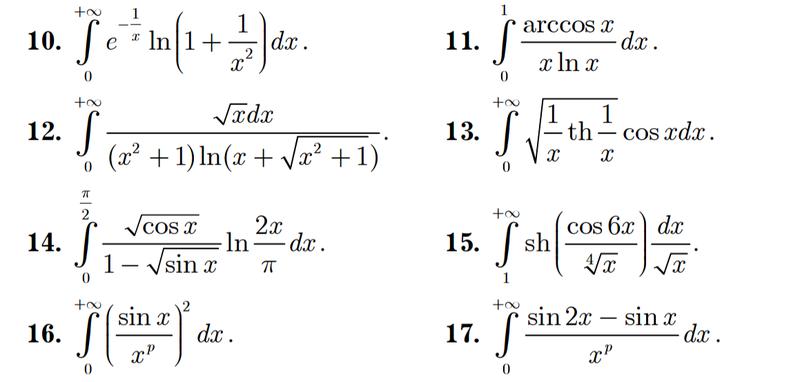
Предположим, что функция обращается в бесконечность в точке b,
в то время как во всех остальных точках отрезка она непрерывна.
Определение. Несобственным интегралом функции f(x) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c, если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена, т.е.
.
Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае — расходящимся.
Используя формулу Ньютона-Лейбница, выводим:
.
Это также обобщённая формула Ньютона-Лейбница. Именно она применяется в решении задач на вычисление несобственных интегралов от неограниченных функций.
Пример 8. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция при неограниченно возрастает, а в точке x = 0 функция не определена, то есть, не существует. Применяем обобщённую формулу Ньютона-Лейбница:
(так как при x = 0 первообразная непрерывна). Вывод: данный несобственный интеграл сходится и равен -3/2.
Пример 9. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция непрерывна в каждой точке полуотрезка [0, 1]. В точке x = 1 функция обращается в бесконечность. Если взять , то на [0, c] подынтегральная функция непрерывна и, следовательно, существует интеграл.
.
Найдём предел этого интеграла:
Результат предыдущих действий: несобственный интеграл сходится и его значение мы нашли.
Пример 10. Исследовать на сходимость несобственный интеграл (верхний предел интегрирования больше нижнего).
Решение. Подынтегральная функция обращается в бесконечность при x = b, в остальных точках она непрерывна. Предположим сначала, что , тогда для :
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при
.
Если , то
.
не существует.
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Интеграл
Начало темы «Интеграл»
Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов
Найти неопределённый интеграл: начала начал, примеры решений
Метод замены переменной в неопределённом интеграле
Интегрирование подведением под знак дифференциала
Метод интегрирования по частям
Интегрирование дробей
Интегрирование рациональных функций и метод неопределённых коэффициентов
Интегрирование некоторых иррациональных функций
Интегрирование тригонометрических функций
Определённый интеграл
Продолжение темы «Интеграл»
Площадь плоской фигуры с помощью интеграла
Объём тела вращения с помощью интеграла
Вычисление двойных интегралов
Длина дуги кривой с помощью интеграла
Площадь поверхности вращения с помощью интеграла
Определение работы силы с помощью интеграла
Поделиться с друзьями
Сходимость несобственных интегралов — справочник для студентов и школьников
Признаки сходимости несобственных интегралов первого рода
В некоторых задачах достаточно не рассчитать интеграл, а выяснить, сходится он или нет.
{1} \frac{d x}{\sin x}
\) расходится.
Интеграл расходится.
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Интегрирование по частям Интегрирование заменой переменной Внесение под знак дифференциала Метод непосредственного интегрирования
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
13.
3 Интегральный тестКак правило, довольно трудно, а часто и невозможно определить точное значение ряда. Во многих случаях возможно по крайней мере чтобы определить, сходится ряд или нет, и поэтому мы будем проводить большую часть нашего времени на этой проблеме.
Если все члены ряда $\ds a_n$ неотрицательны, то, очевидно,
последовательность частичных сумм $\ds s_n$ неубывающая. Это означает, что
если мы сможем показать, что последовательность частичных сумм ограничена, то
ряды должны сходиться. Мы знаем, что если ряд сходится, то члены
$\ds a_n$ стремятся к нулю, но это не означает, что $\ds a_n\ge a_{n+1}$ при
каждые $n$. Многие полезные и интересные ряды обладают этим свойством.
однако, и они являются одними из самых простых для понимания. Давайте посмотрим на
пример.
92$ и так далее — иными словами, в точности условия
серии. Частичная сумма $\ds s_n$ — это просто сумма площадей
первые $n$ прямоугольников. Поскольку все прямоугольники лежат между кривой
и оси $x$ любая сумма площадей прямоугольников меньше, чем
соответствующей площади под кривой, и поэтому, конечно, любая сумма
площадь прямоугольника меньше площади под всей кривой, т.
2/6\примерно 1,6$.
$\квадрат$
Мы уже знаем, что $\sum 1/n$ расходится. Что пойдет не так, если мы попытаемся применить эту технику к нему? Вот расчет: $$ s_n={1\более 1}+{1\более 2}+{1\более 3}+\cdots+{1\более n} не доказывать, что $\sum 1/n$ расходится, а просто это конкретное вычисление не может доказать, что оно сходится. Небольшой модификация, однако, позволяет нам доказать вторым способом, что $\sum 1/n$ расходится.
Пример 13.3.2 Рассмотрим слегка измененную версию рисунка 13.3.1, показанную на рисунке 13.3.2. 9\infty {1\over \sqrt{n}}$ — это $p$-ряд с $p=1/2
Поскольку обычно трудно вычислить значение ряда
именно, часто требуется хорошее приближение. В реальном смысле,
хорошее приближение настолько хорошо, насколько мы о нем знаем, т. е. пока
приближение на самом деле может быть хорошим, оно ценно только на практике
если мы можем гарантировать его точность до некоторой степени. Эта гарантия
обычно легко найти ряды с уменьшающимися положительными членами.
2$ до двух знаков после запятой.
92} + 0,005$.
(отвечать)
Репетитор по математике — Интеграл — Теория
Репетитор по математике — Интеграл — Теория — Неправильный интегралДовольно часто мы не заботимся о точном значении интеграла, мы просто нужно знать, сходится он или нет. Поскольку большинство интегралов довольно сложно оценить, обычно проще просто сравнить интегрированную функцию с другой, более простой функцией, а затем использовать это сравнение прийти к какому-то выводу. В этом разделе мы рассмотрим только основные неправильные интегралы — то есть с одной «проблемой». Более общие интегралы всегда оцениваются путем разбиения их на несколько основных интегралов (с одним задача), к каждому из которых мы применяем тесты сходимости. Из-за симметричности ситуации, мы сформулируем наши теоремы сравнения для случая, когда проблема появляется на правой конечной точке.
Сначала предположим, что задействованные функции положительны. Этот
сильно упрощает нашу ситуацию.
Как мы заметили
раньше было только два
альтернативы в этом случае: Либо площадь под графиком конечна, либо она
бесконечный.
Теорема (сравнительный тест).
Пусть b — действительное число или b = ∞, позволять a < b . Пусть f и g будут функции, непрерывные и неотрицательные на [ а , б ) и ж ≤ г на [ а , б ).Если сходится, то и сходится.
Если расходится, то и расходится.
Идея этого теста должна быть понятна из картинки:
Если площадь под графиком 90 115 г 90 116 конечна, то такой же должна быть и площадь меньшая площадь под графиком f . И наоборот, если область под график f имеет бесконечную площадь, тогда большая область под графиком из г тоже должно быть.
Картинка также дает понять, что сравнение может работать только в одном
направление, и два вышеупомянутых импликации не могут быть истинными как эквивалентности.
Например, предположим, что площадь под графиком f конечна.
Так как область под графиком г больше, вывод невозможен.
возможно: его площадь может быть конечной, но также и бесконечной. это главное
Недостаток сравнительного теста.
Пример:
Определите, сходится ли следующий интеграл:
Этот интеграл на самом деле можно вычислить с помощью частичных дробей, но он легче ответить на этот вопрос, используя тест сравнения. Отметим, что для положительный х , . Поскольку интеграл сходится (это мы помним, см. Свойства и примеры), Сравнительный тест, также рассматриваемый интеграл сходится.
Мы только что увидели основное преимущество сравнительного теста: очень часто он очень
легкий. Этот пример был типичным. Учитывая (сложную) функцию, мы находим
функция сравнения, как правило, степенная, потому что их поведение нам хорошо известно.
Затем мы пытаемся установить некоторое неравенство. Если нам повезет, мы получим
вывод довольно легко.
Если нам не повезет, мы увидим главное
недостаток этого теста в действии:
Пример:
Определите, сходится ли следующий интеграл:
Опять же, этот интеграл можно вычислить, используя неполные дроби, но мы пробуем это, используя тест сравнения. Отметим, что для положительных x , . Тестовый интеграл сходится (как и раньше), но на этот раз неравенство сравнения неверно так и нельзя сделать вывод. Сравнительный тест не прошел (как используется). Это Следует отметить, что эта проблема фактически может быть решена с помощью Сравнительный тест, но требует более тонкого выбора тестовой функции г . Обоснование задействованного неравенства требует некоторой работы, поэтому в конце концов, проще использовать другой тест. Любознательный читатель будет найти решение с помощью сравнительного теста здесь.
Этот пример показывает, что недостаточно просто провести сравнение. Данный
a function f , мы пытаемся найти подходящую (простую) тестовую функцию.
Если
существует естественный кандидат h , который меньше, чем f , он будет
быть полезным, только если его интеграл расходится; мы бы искали такие ч если
мы подозревали, что интеграл от f расходится, и хотели это доказать.
Если есть естественный кандидат g , который больше, чем f , он
будет полезен, только если его интеграл сходится; мы бы постарались найти такие g , если мы подозревали, что интеграл от f сходится.
Сравнительный тест также можно рассматривать как обобщение следующий факт ( ср. Свойства интеграла Римана):
Если f и g интегрируемы по Риману на [a,b] и ж ≤ г на [ a , b ], затем
Сравнительный тест, по сути, говорит, что то же самое верно и для
неотрицательные функции и несобственные интегралы. Однако тогда неравенство
между интегралами не является строго верным (поскольку они могут не существовать), скорее,
имеет следующий смысл: если «меньший интеграл» бесконечен, то
«большее» также, естественно, должно быть бесконечным, так как только бесконечность удовлетворяет
неравенство
∞ ≤ А .
С другой стороны, если «больший интеграл» конечен, то так и должно быть «меньший», и его значение должно быть меньше или равно. Это «неравенство подход» также прекрасно иллюстрирует, почему сравнительный тест работает только в одну сторону. Мы покажем это, вернувшись к нашим первым двум примерам.
В первом можно представить, что, интегрируя неравенство мы получаем неравенство
Теперь кажется естественным, что данный интеграл сходится, мы даже получаем верхняя граница его значения.
Во втором примере можно представить, что, интегрируя неравенство мы получаем неравенство
В этом неравенстве заданный интеграл может быть равен конечному числу, но также до бесконечности (как несомненно ∞ ≥ 1/3). Таким образом, вывод невозможен.
Теперь также должно быть яснее, почему мы требуем, чтобы функция f была
неотрицательный. Если бы мы позволили ему упасть ниже оси x , у нас было бы
нет контроля над тем, сколько площади он там накапливает.
Таким образом, сравнительный тест
для функций, которые меняют свой знак, должны быть задействованы две тестовые функции,
тот, который мешает f из-за того, что он слишком велик, и еще один, который мешает этому
для получения слишком большой области ниже оси x . Такой сложный тест
обычно не требуется, и мы можем обойтись более простым (но менее мощным) тестом,
сравнительный тест, который отслеживает f с использованием абсолютного значения:
Теорема (Сравнительный тест — версия абсолютного значения).
Пусть b — действительное число или b = ∞, позволять а < б . Пусть f и g будут функции, непрерывные на [ a , b ) и пусть | ф | ≤ г по [ a , b ).Если сходится, то и сходится.
Следующий тест является гораздо более сильным инструментом, чем сравнительный тест. В
в частности, его вывод формулируется как эквивалентность, поэтому он не разделяет
Основной недостаток сравнительного теста.
Его главный недостаток в том, что
его правильное применение требует дополнительной работы.
Теорема (критерий предельного сравнения).
Пусть b — действительное число или b = ∞, пусть a < b . Пусть f и g будут функции, непрерывные на [ a , b ), пусть f ≥ 0 там. Предположим, что предел существует конечный, но не равен нулю. Тогда интеграл сходится тогда и только тогда, когда интеграл сходится.
Этот тест работает несколько иначе. Учитывая функцию ф , мы
найти тестовую функцию g , которая не обязательно должна быть больше
или меньше f ; на самом деле, иногда она может быть выше, а иногда
опуститься ниже f . Важно то, что по мере приближения x к б (с соответствующей стороны, т.е. с а ), эти две функции
должны быть в основном равны (вплоть до кратности). Это проверяется с помощью «limit
сравнение на b «, что как раз и является предельным допущением в Предел
Сравнительный тест.
Таким образом, мы подтверждаем, что наше предположение о тестовой функции было
правильный. Обычно (для «правильного» предположения) предел должен быть равен 1.
Это означало бы, что когда x приближается к b , соотношение
это об одном.
Умножая получаем, что если x близко к b , то f ( x ) ~ г ( x )
(имеется в виду, что они примерно одинаковые). Тогда кажется естественным, что также
Так что эти интегралы должны получиться примерно одинаковыми, и вывод теорема кажется ясной. Если один из интегралов конечен, то и Другой. Если один из них расходится, то должен расходиться и другой.
Тест предельного сравнения также верен для функций, которые всегда
отрицательный. На самом деле его можно применять даже к функциям, которые не
обязательно сохраняют свои признаки. Но чтобы работали, изменения не должны
случаются «слишком часто». Поскольку точное указание этого условия не стоит
беда, люди обычно игнорируют это более общее представление и просто используют это
тест с неотрицательными функциями.
Пример:
Определите, сходится ли следующий интеграл:
Если x близко к бесконечности, то есть если это действительно большое число, то в знаменателе будет преобладать квадрат, а остальное можно не учитывать. Этот мотивирует наш выбор тестовой функции: г ( x ) = 1/x 2 . Теперь нам нужно обосновать правильность нашего выбора:
Предел существует и не равен нулю, поэтому данная функция и выбранная тестовая функция действительно очень похожа на бесконечность. Поскольку мы знаем что интеграл сходится, то сходится и данный интеграл.
Это была типичная тестовая задача предельного сравнения. Сначала мы нашли тест
функция. Затем мы использовали предел, чтобы обосновать правильность нашего выбора. Тогда мы
посмотрели на соответствующий интеграл с пробной функцией, исследовали его
сходимости, и, наконец, мы перенесли этот вывод на данный интеграл.
Краткое изложение стратегии выбора правильной тестовой функции и некоторых
важные примеры мы ссылаемся на
Обзор методов — Несобственные интегралы
а также
Решенные задачи — несобственные интегралы.
Следует отметить, что тест предельного сравнения не лучше (в смысле более общего), чем сравнительный тест. Есть проблемы, когда сравнение через неравенство может быть достигнуто, в то время как предельное сравнение принципиально невозможно. Одна такая проблема в Решенные проблемы — неправильно Интегралы.
Все три теста, указанные выше, имеют сопутствующую версию, которая обрабатывает случай когда есть проблема в левой конечной точке интервала. Поскольку модификации очевидны, мы предпочитаем показать его применение на одной задаче. Мы также используем эту возможность, чтобы показать, как это работает, когда «проблема» не бесконечность, а вертикальная асимптота.
Пример: Определите, сходится ли следующий интеграл:
Возникла проблема с разрешением 90 115 x 90 116 = 2. Мы утверждаем, что если x близко к 2 (справа), то данная функция ведет себя почти точно так же . Это требование должно быть обосновано:
Мы видим, что наше предположение было верным, так как предел дал ненулевое число.
Теперь мы должны
исследовать соответствующий несобственный интеграл для нашей тестовой функции:
Этот интеграл расходится, так как это одна из степеней, которые мы исследовали в Свойства и примеры и мы Запомни это. По критерию предельного сравнения также расходится данный интеграл.
Хотя вышеприведенное решение правильно соответствовало тесту сравнения пределов, оно может стоит посмотреть на смысл всей процедуры. Предел приводит к приведенное выше сравнение означает, что если x действительно близко к 2 (от прямо тогда . Отсюда следует также подобие между интегралами от 2 справа. квадратный корень из 2 является мультипликативной константой, поэтому мы можем разложить ее на множители и получить сравнение
Поскольку тестовый интеграл справа расходится и умножение на
ненулевое число не может это исправить, также интеграл слева должен быть
расходящийся. Мы также видим, что мультипликативная константа, которую мы получаем во время
предельным сравнением в наших рассуждениях можно пренебречь, так как оно не может
влияют на сходимость наших интегралов (но он должен быть ненулевым для
это).
Теперь читатель, вероятно, задается вопросом, как мы придумали тестовую функцию. Ведь это достаточно сложно и требует немалый опыт, даже тогда это может быть сложно. Это основная причина, по которой сравнительные тесты в основном используется для задач с бесконечностью, соответственно отрицательной бесконечностью. Там мы можем себе представить x — действительно большое число, и наша интуиция может помогите нам определить, какие части данной функции становятся неважными.
Назад к теории — несобственные интегралы
5.3 Тесты на дивергенцию и интегральные тесты. Исчисление, том 2
Цели обучения
- 5.3.1 Используйте тест дивергенции, чтобы определить, сходится ряд или расходится.
- 5.3.2 Используйте интегральный тест, чтобы определить сходимость ряда.
- 5.3.3 Оцените значение ряда, найдя границы его остаточного члена.
В предыдущем разделе мы определяли сходимость или расходимость нескольких рядов, явно вычисляя предел последовательности частичных сумм {Sk}.
{Sk}. На практике явное вычисление этого предела может быть затруднено или невозможно. К счастью, существует несколько тестов, которые позволяют нам определить сходимость или расхождение для многих типов рядов. В этом разделе мы обсудим два из этих тестов: тест дивергенции и интегральный тест. Мы рассмотрим несколько других тестов в оставшейся части этой главы, а затем подытожим, как и когда их использовать.
Тест на расхождение
Для сходимости ряда ∑n=1∞an∑n=1∞an n-й член anan должен удовлетворять условию an→0an→0 при n→∞.n→∞.
Следовательно, из алгебраических предельных свойств последовательностей
limk→∞ak=limk→∞(Sk−Sk−1)=limk→∞Sk−limk→∞Sk−1=S−S=0.limk→∞ak=limk→∞(Sk−Sk−1) =limk→∞Sk−limk→∞Sk−1=S−S=0.
Следовательно, если ∑n=1∞an∑n=1∞an сходится, то n-й член an→0an→0 при n→∞.n→∞. Важным следствием этого факта является следующее утверждение:
Ifan↛0asn→∞,∑n=1∞и расходится. Ifan↛0asn→∞,∑n=1∞и расходится.
(5.8)
Этот тест известен как тест на расхождение, потому что он позволяет доказать, что ряд расходится.
Теорема 5,8
Тест на расхождение
Если limn→∞an=c≠0limn→∞an=c≠0 или limn→∞anlimn→∞an не существует, то ряд ∑n=1∞an∑n=1∞an расходится.
Важно отметить, что обратная теорема неверна. То есть, если limn→∞an=0,limn→∞an=0, мы не можем сделать никакого заключения о сходимости ∑n=1∞an.∑n=1∞an. Например, limn→∞(1/n)=0,limn→∞(1/n)=0, но гармонический ряд ∑n=1∞1/n∑n=1∞1/n расходится. В этом разделе и остальных разделах этой главы мы покажем еще много примеров таких рядов. Следовательно, хотя мы можем использовать критерий расходимости, чтобы показать, что ряд расходится, мы не можем использовать его, чтобы доказать, что ряд сходится. В частности, если an→0,an→0, тест на расхождение неубедителен.
Пример 5.13
Использование теста на расхождение
Для каждой из следующих серий примените тест на расхождение.
Если тест на расходимость доказывает, что ряд расходится, укажите это. В противном случае укажите, что тест расхождения неубедителен.
- ∑n=1∞n3n−1∑n=1∞n3n−1
- ∑n=1∞1n3∑n=1∞1n3
- ∑n=1∞e1/n2∑n=1∞e1/n2
Решение
- Поскольку n/(3n−1)→1/3≠0,n/(3n−1)→1/3≠0, по критерию расходимости можно заключить, что
∑n=1∞n3n−1∑n=1∞n3n−1
расходится. - Так как 1/n3→0,1/n3→0, тест на дивергенцию неубедителен.
- Поскольку e1/n2→1≠0,e1/n2→1≠0, по признаку расходимости ряд
∑n=1∞e1/n2∑n=1∞e1/n2
расходится.
Контрольно-пропускной пункт 5.12
Что тест на дивергенцию говорит нам о ряде ∑n=1∞cos(1/n2)?∑n=1∞cos(1/n2)?
Интегральный тест
В предыдущем разделе мы доказали, что гармонический ряд расходится, рассмотрев последовательность частичных сумм {Sk}{Sk} и показав, что S2k>1+k/2S2k>1+k/2 для всех положительных целых чисел k.
k. В этом разделе мы используем другую технику для доказательства расходимости гармонического ряда. Этот метод важен, потому что он используется для доказательства расхождения или сходимости многих других рядов. Этот тест, называемый интегральным тестом, сравнивает бесконечную сумму с неправильным интегралом. Важно отметить, что этот тест можно применять только тогда, когда мы рассматриваем ряд, все члены которого положительны.
Чтобы проиллюстрировать, как работает интегральный тест, используйте гармонический ряд в качестве примера. На рис. 5.12 мы изобразили гармонический ряд, нарисовав последовательность прямоугольников с площадями 1, 1/2, 1/3, 1/4,… 1, 1/2, 1/3, 1/4,… вместе с функция f(x)=1/x.f(x)=1/x. Из графика мы видим, что
∑n=1k1n=1+12+13+⋯+1k>∫1k+11xdx.∑n=1k1n=1+12+13+⋯+1k>∫1k+11xdx.
Следовательно, для каждого k,k k-я частичная сумма SkSk удовлетворяет
Sk=∑n=1k1n>∫1k+11xdx=lnx|1k+1=ln(k+1)−ln(1)=ln(k+1).Sk=∑n=1k1n>∫1k+11xdx= lnx|1k+1=ln(k+1)−ln(1)=ln(k+1).
Поскольку limk→∞ln(k+1)=∞, limk→∞ln(k+1)=∞, мы видим, что последовательность частичных сумм {Sk}{Sk} неограничена. Следовательно, {Sk}{Sk} расходится, а, следовательно, расходится и ряд ∑n=1∞1n∑n=1∞1n.
Рисунок 5.12 Сумма площадей прямоугольников больше площади между кривой f(x)=1/xf(x)=1/x и осью xx для x≥1.x≥1. Поскольку площадь, ограниченная кривой, бесконечна (как вычислено несобственным интегралом), сумма площадей прямоугольников также бесконечна.
Теперь рассмотрим ряд ∑n=1∞1/n2.∑n=1∞1/n2. Мы покажем, как с помощью интеграла можно доказать, что этот ряд сходится. На рис. 5.13 мы нарисовали последовательность прямоугольников с площадями 1,1/22,1/32,…1,1/22,1/32,… вместе с функцией f(x)=1/x2.f(x )=1/x2. Из графика мы видим, что
∑n=1k1n2=1+122+132+⋯+1k2<1+∫1k1x2dx.∑n=1k1n2=1+122+132+⋯+1k2<1+∫1k1x2dx.
Следовательно, для каждого k,k k-я частичная сумма SkSk удовлетворяет
Sk=∑n=1k1n2<1+∫1k1x2dx=1−1x|1k=1−1k+1=2−1k<2.
Sk=∑n=1k1n2<1+∫1k1x2dx=1−1x|1k=1 −1k+1=2−1k<2.
Мы заключаем, что последовательность частичных сумм {Sk}{Sk} ограничена. Мы также видим, что {Sk}{Sk} является возрастающей последовательностью:
.Sk=Sk−1+1k2fork≥2.Sk=Sk−1+1k2fork≥2.
Поскольку {Sk}{Sk} возрастает и ограничено, по теореме о монотонной сходимости оно сходится. Следовательно, ряд ∑n=1∞1/n2∑n=1∞1/n2 сходится.
Рисунок 5.13 Сумма площадей прямоугольников меньше суммы площадей первого прямоугольника и площади между кривой f(x)=1/x2f(x)=1/x2 и осью xx для x≥1 .х≥1. Поскольку площадь, ограниченная кривой, конечна, сумма площадей прямоугольников также конечна.
Мы можем расширить эту идею, чтобы доказать сходимость или расхождение для многих различных рядов. Предположим, что ∑n=1∞an∑n=1∞an — это ряд с положительными членами anan, такой, что существует непрерывная положительная убывающая функция ff, где f(n)=anf(n)=an для всех натуральных чисел. Тогда, как показано на рис.
5.14(а), для любого целого числа k,k k-я частичная сумма SkSk удовлетворяет
Sk=a1+a2+a3+⋯+ak Следовательно, если ∫1∞f(x)dx∫1∞f(x)dx сходится, то последовательность частичных сумм {Sk}{Sk} ограничена. Поскольку {Sk}{Sk} — возрастающая последовательность, если она также является ограниченной последовательностью, то по теореме о монотонной сходимости она сходится. Делаем вывод, что если ∫1∞f(x)dx∫1∞f(x)dx сходится, то сходится и ряд ∑n=1∞an∑n=1∞an. С другой стороны, из рис. 5.14(b) для любого целого числа k,k k-я частичная сумма SkSk удовлетворяет Sk=a1+a2+a3+⋯+ak>∫1k+1f(x)dx. Sk=a1+a2+a3+⋯+ak>∫1k+1f(x)dx. Если limk→∞∫1k+1f(x)dx=∞,limk→∞∫1k+1f(x)dx=∞, то {Sk}{Sk} — неограниченная последовательность и, следовательно, расходится. В результате ряд ∑n=1∞an∑n=1∞an также расходится. Мы заключаем, что если ∫1∞f(x)dx∫1∞f(x)dx расходится, то ∑n=1∞an∑n=1∞an расходится. Рисунок
5. Предположим, что ∑n=1∞an∑n=1∞an ряд с положительными членами an.an. Предположим, что существуют функция ff и натуральное число NN такие, что выполняются следующие три условия: ∑n=1∞an и ∫N∞f(x)dx∑n=1∞an и ∫N∞f(x)dx Хотя из сходимости ∫N∞f(x)dx∫N∞f(x)dx следует сходимость связанного ряда ∑n=1∞an, ∑n=1∞an, из этого не следует, что значение интеграла и сериал тот же. ∑n=1∞(1e)n=1e+(1e)2+(1e)3+⋯∑n=1∞(1e)n=1e+(1e)2+(1e)3+⋯ — геометрический ряд с начальным членом a=1/ea=1/e и отношением r=1/e,r=1/e, который сходится к 1/e1-(1/e)=1/e(e-1)/e=1e-1.1/e1-(1/e)=1/e(e-1)/e=1e-1. Однако соответствующий интеграл ∫1∞(1/e)xdx∫1∞(1/e)xdx удовлетворяет ∫1∞(1e)xdx=∫1∞e-xdx=конечность→∞∫1be-xdx=конечность→∞-e-x|1b=конечность→∞[-e-b+e-1]=1e. ∫1∞(1e)xdx=∫1∞e−xdx=лимб→∞∫1be−xdx=лимб→∞−e−x|1b=лимб→∞[−e−b+e−1]=1e. Для каждого из следующих рядов используйте интегральный тест, чтобы определить, сходится ряд или расходится. Предположим, что все условия для интегрального теста выполнены. ∑n=1∞1n3и∫1∞1x3dx. ∫1∞1x3dx=limb→∞∫1b1x3dx=limb→∞[−12×2|1b]=limb→∞[−12b2+12]=12.∫1∞1x3dx=limb→∞∫1b1x3dx=limb →∞[−12×2|1b]=конечность→∞[−12b2+12]=12. ∑n=1∞1n3.∑n=1∞1n3. ∑n=1∞12n−1 и ∫1∞12x−1dx. ∑n=1∞12n−1 и ∫1∞12x−1dx. ∫1∞12x−1dx=limb→∞∫1b12x−1dx=limb→∞2x−1|1b=limb→∞[2b−1−1]=∞,∫1∞12x−1dx=limb→ ∞∫1b12x−1dx=limb→∞2x−1|1b=limb→∞[2b−1−1]=∞, ∑n=1∞12n−1∑n=1∞12n−1 Используйте интегральный тест, чтобы определить, сходится или расходится ряд ∑n=1∞n3n2+1∑n=1∞n3n2+1. Гармонический ряд ∑n=1∞1/n∑n=1∞1/n и ряд ∑n=1∞1/n2∑n=1∞1/n2 являются примерами ряда, называемого р -серия. Для любого действительного числа p,p ряд ∑n=1∞1np∑n=1∞1np называется p -рядом. Мы знаем, что p -ряд сходится, если p=2p=2, и расходится, если p=1.p=1. А как насчет других значений p?p? В общем, трудно, если вообще возможно, вычислить точное значение большинства pp-серий. Однако мы можем использовать тесты, представленные до сих пор, чтобы доказать, сходится или расходится pp-ряд. Если p<0,p<0, то 1/np→∞,1/np→∞, а если p=0,p=0, то 1/np→1,1/np→1. Следовательно, по тесту дивергенции ∑n=1∞1/np расходится, если p≤0.∑n=1∞1/np расходится, если p≤0. Если p>0,p>0, то f(x)=1/xpf(x)=1/xp — положительная, непрерывная, убывающая функция. Поэтому при p>0,p>0 используем интегральный критерий, сравнивая ∑n=1∞1nи∫1∞1xpdx.∑n=1∞1nи∫1∞1xpdx. Мы уже рассмотрели случай, когда p=1.p=1. Здесь мы рассматриваем случай, когда p>0,p≠1. ∫1∞1xpdx=конечность→∞∫1b1xpdx=конечность→∞11−px1−p|1b=конечность→∞11−p[b1−p−1].∫1∞1xpdx=конечность→∞∫1b1xpdx=конечность→ ∞11−px1−p|1b=лимб→∞11−p[b1−p−1]. Потому что b1-p→0ifp>1 и b1-p→∞ifp<1,b1-p→0ifp>1andb1-p→∞ifp<1, делаем вывод, что ∫1∞1xpdx={1p−1ifp>1∞ifp≤1.∫1∞1xpdx={1p−1ifp>1∞ifp≤1. Следовательно, ∑n=1∞1/np∑n=1∞1/np сходится, если p>1p>1, и расходится, если 0 Подводя итог, ∑n=1∞1np{сходится, еслиp>1 расходится, еслиp≤1.∑n=1∞1np{сходится, еслиp>1 расходится, еслиp≤1. (5.9) Для каждого из следующих рядов определите, сходится он или расходится. Сходится или расходится ряд ∑n=1∞1n5/4∑n=1∞1n5/4? Предположим, мы знаем, что ряд ∑n=1∞an∑n=1∞an сходится, и мы хотим оценить сумму этого ряда. Конечно, мы можем аппроксимировать эту сумму, используя любую конечную сумму ∑n=1Nan∑n=1Nan, где NN — любое натуральное число. Вопрос, который мы рассматриваем здесь, заключается в том, насколько хороша аппроксимация ∑n=1Nan?∑n=1Nan для сходящегося ряда ∑n=1∞an, ∑n=1∞an? Более конкретно, если мы позволим RN=∑n=1∞an-∑n=1NanRN=∑n=1∞an-∑n=1Nan будет остатком, когда сумма бесконечного ряда аппроксимируется NthNth частичной суммой, насколько велико RN?RN? Для некоторых типов рядов мы можем использовать идеи интегрального теста для оценки RN.RN. Предположим, что ∑n=1∞an∑n=1∞an — сходящийся ряд с положительными членами. Пусть SNSN будет N -й частичной суммой ∑n=1∞an.∑n=1∞an. Для всех натуральных чисел N,N, SN+∫N+1∞f(x)dx<∑n=1∞an Другими словами, остаток RN=∑n=1∞an−SN=∑n=N+1∞anRN=∑n=1∞an−SN=∑n=N+1∞an удовлетворяет следующей оценке: ∫N+1∞f(x)dx (5.10) Это известно как оценка остатка. Мы иллюстрируем оценку остатка из интегрального теста на рис. 5.15. В частности, представляя остаток RN=aN+1+aN+2+aN+3+⋯RN=aN+1+aN+2+aN+3+⋯ в виде суммы площадей прямоугольников, мы видим, что площадь из этих прямоугольников ограничен сверху ∫N∞f(x)dx∫N∞f(x)dx и ограничен снизу ∫N+1∞f(x)dx.∫N+1∞f(x)dx. RN=aN+1+aN+2+aN+3+⋯>∫N+1∞f(x)dxRN=aN+1+aN+2+aN+3+⋯>∫N+1∞f(x )дх и RN=aN+1+aN+2+aN+3+⋯<∫N∞f(x)dx.RN=aN+1+aN+2+aN+3+⋯<∫N∞f(x)dx . Делаем вывод, что ∫N+1∞f(x)dx С ∑n=1∞an=SN+RN, ∑n=1∞an=SN+RN, где SNSN — NthNth частичная сумма, заключаем, что SN+∫N+1∞f(x)dx<∑n=1∞an Рисунок
5.15
Для заданной непрерывной положительной убывающей функции ff и последовательности положительных членов anan, таких что an=f(n)an=f(n) для всех положительных целых чисел n,n, (a) площади aN+1+aN+2 +aN+3+⋯<∫N∞f(x)dx,aN+1+aN+2+aN+3+⋯<∫N∞f(x)dx, или (b) площади aN+1+aN +2+aN+3+⋯>∫N+1∞f(x)dx.aN+1+aN+2+aN+3+⋯>∫N+1∞f(x)dx. Следовательно, интеграл является либо завышенной, либо заниженной оценкой ошибки. Рассмотрим ряд ∑n=1∞1/n3. S10=1+123+133+143+⋯+1103≈1,19753.S10=1+123+133+143+⋯+1103≈1,19753. RN<∫N∞1x3dx.RN<∫N∞1x3dx. ∫10∞1x3dx=limb→∞∫10b1x3dx=limb→∞[−12×2]Nb=limb→∞[−12b2+12N2]=12N2.∫10∞1x3dx=limb→∞∫10b1x3dx=limb ∞[−12×2]Nb=конечность→∞[−12b2+12N2]=12N2. Для ∑n=1∞1n4,∑n=1∞1n4 вычислить S5S5 и оценить ошибку R5.R5. Для каждого из следующих рядов, если применяется критерий дивергенции, либо укажите, что limn→∞anlimn→∞an не существует, либо найдите limn→∞an.limn→∞an. Если тест на расхождение неприменим, укажите, почему. 138. an=nn+2an=nn+2 139. ан=n5n2−3an=n5n2−3 140. ан=n3n2+2n+1ан=n3n2+2n+1 141. an=(2n+1)(n−1)(n+1)2an=(2n+1)(n−1)(n+1)2 142. an=(2n+1)2n(3n2+1)nan=(2n+1)2n(3n2+1)n 143. ан=2n3n/2ан=2n3n/2 144. an=2n+3n10n/2an=2n+3n10n/2 145. ан=е-2/нан=е-2/n 146. ан=коснан=косн 147. ан=таннан=танн 148. an=1-cos2(1/n)sin2(2/n)an=1-cos2(1/n)sin2(2/n) 149. ан=(1−1n)2нан=(1−1n)2n 150. an=lnnnan=lnnn 151. an=(lnn)2nan=(lnn)2n Укажите, сходится ли данный pp-ряд. 152. ∑n=1∞1n∑n=1∞1n 153. ∑n=1∞1nn∑n=1∞1nn 154. ∑n=1∞1n23∑n=1∞1n23 155. ∑n=1∞1n43∑n=1∞1n43 156. ∑n=1∞nenπ∑n=1∞nenπ 157. ∑n=1∞nπn2e∑n=1∞nπn2e Используйте интегральный тест, чтобы определить, сходятся ли следующие суммы. 158. ∑n=1∞1n+5∑n=1∞1n+5 159. ∑n=1∞1n+53∑n=1∞1n+53 160. ∑n=2∞1nlnn∑n=2∞1nlnn 161. ∑n=1∞n1+n2∑n=1∞n1+n2 162. ∑n=1∞en1+e2n∑n=1∞en1+e2n 163. ∑n=1∞2n1+n4∑n=1∞2n1+n4 164. ∑n=2∞1nln2n∑n=2∞1nln2n Выразите следующие суммы в виде pp-рядов и определите, сходится ли каждый из них. 165. ∑n=1∞2−lnn∑n=1∞2−lnn ( Подсказка: 2−lnn=1/nln22−lnn=1/nln2. 166. ∑n=1∞3−lnn∑n=1∞3−lnn ( Подсказка: 3−lnn=1/nln33−lnn=1/nln3.) 167. ∑n=1∞n2−2lnn∑n=1∞n2−2lnn 168. ∑n=1∞n3−2lnn∑n=1∞n3−2lnn Используйте оценку RN≤∫N∞f(t)dtRN≤∫N∞f(t)dt, чтобы найти оценку остатка RN=∑n=1∞an−∑n=1NanRN=∑n=1∞an −∑n=1Nan, где an=f(n).an=f(n). 169. ∑n=110001n2∑n=110001n2 170. ∑n=110001n3∑n=110001n3 171. ∑n=1100011+n2∑n=1100011+n2 172. ∑n=1100n/2n∑n=1100n/2n [T] Найдите минимальное значение NN такое, что оценка остатка ∫N+1∞f 173. an=1n2,an=1n2, ошибка <10-4<10-4 174. an=1n1.1,an=1n1.1, ошибка <10-4<10-4 175. an=1n1.01,an=1n1.01, ошибка <10-4<10-4 176. an=1nln2n,an=1nln2n, ошибка <10-3<10-3 177. an=11+n2,an=11+n2, ошибка <10-3<10-3 В следующих упражнениях найдите такое значение NN, чтобы RNRN было меньше требуемой ошибки. Вычислите соответствующую сумму ∑n=1Nan∑n=1Nan и сравните ее с данной оценкой бесконечного ряда. 178. an=1n11,an=1n11, ошибка <10−4,<10−4,∑n=1∞1n11=1,000494…∑n=1∞1n11=1,000494… 179. an=1en,an=1en, ошибка <10−5,<10−5,∑n=1∞1en=1e−1=0,581976…∑n=1∞1en=1e−1=0,581976… 180. an=1en2,an=1en2, ошибка <10−5,<10−5,∑n=1∞n/en2=0,40488139857…∑n=1∞n/en2=0,40488139857… 181. an=1/n4,an=1/n4, ошибка <10−4,<10−4,∑n=1∞1/n4=π4/90=1,08232...∑n=1∞1/n4 =π4/90=1,08232... 182. an=1/n6,an=1/n6, ошибка <10−6,<10−6,∑n=1∞1/n4=π6/945=1,01734306...,∑n=1∞1/ n4=π6/945=1,01734306..., 183. Найдите предел n→∞n→∞ числа 1n+1n+1+⋯+12n.1n+1n+1+⋯+12n. ( Подсказка: Сравните с ∫n2n1tdt.)∫n2n1tdt.) 184. Найдите предел как n→∞n→∞ числа 1n+1n+1+⋯+13n1n+1n+1+⋯+13n Следующие несколько упражнений предназначены для того, чтобы дать представление о приложениях, в которых возникают частичные суммы гармонического ряда. 185. В некоторых приложениях вероятности, таких как так называемая оценка Уоттерсона для прогнозирования скорости мутаций в популяционной генетике, важно иметь точную оценку числа Hk=(1+12+13+⋯+1k).Hk =(1+12+13+⋯+1k). Напомним, что Tk=Hk-lnkTk=Hk-lnk убывает. 186. [T] Полная выборка с заменой, иногда называемая Проблема коллекционера купонов формулируется следующим образом: Предположим, что у вас есть NN уникальных предметов в корзине. На каждом этапе случайным образом выбирается предмет, идентифицируется и кладется обратно в корзину. Задача заключается в том, какое ожидаемое количество шагов E(N)E(N) потребуется для рисования каждого уникального элемента хотя бы один раз. Получается, что E(N)=NE(N)=N. HN=N(1+12+13+⋯+1N)HN=N(1+12+13+⋯+1N). Найдите E(N)E(N) для N=10,20 и 50N=10,20 и 50. 187. [T] Самый простой способ перетасовать карты — это взять верхнюю карту и вставить ее в случайное место в колоде, что называется случайной вставкой сверху, а затем повторить. 188. Предположим, скутер может проехать 100100 км на полном баке топлива. Предполагая, что топливо можно переливать с одного мотороллера на другой, но только в баке, представьте процедуру, позволяющую одному из мотороллеров проехать 100HN100HN км, где HN=1+1/2+⋯+1/N. HN=1+1/2+⋯+1/N. 189. Покажите, что для применения оценки остатка на [N,∞)[N,∞) достаточно, чтобы f(x)f(x) убывала на [N,∞),[N,∞), но ff не обязательно убывает на [1,∞).[1,∞). 190. [T] Используйте оценку остатка и интегрирование по частям, чтобы аппроксимировать ∑n=1∞n/en∑n=1∞n/en с погрешностью менее 0,0001,0,0001. 191. Сходится ли ∑n=2∞1n(lnn)p∑n=2∞1n(lnn)p, если pp достаточно велико? Если да, то для каких p?p? 192. [T] Предположим, что компьютер может суммировать один миллион членов в секунду расходящегося ряда ∑n=1N1n.
14
(a) Если мы можем вписать прямоугольники внутрь области, ограниченной кривой y=f(x)y=f(x) и осью xx, и площадь, ограниченная этими кривыми для x≥1x≥1, конечна, то сумма площадей прямоугольников также конечна. (b) Если набор прямоугольников описывает область, ограниченную y=f(x)y=f(x) и осью xx для x≥1x≥1, и область имеет бесконечную площадь, то сумма площадей прямоугольники также бесконечны. Теорема
5,9
Интегральный тест
Тогда
сходятся или расходятся (см. рис. 5.14).
Они могут быть разными, и часто таковыми являются. Например, Пример
5.14
Использование интегрального теста
Решение
∑n=1∞1n3и∫1∞1x3dx.
У нас есть
Таким образом, интеграл ∫1∞1/x3dx∫1∞1/x3dx сходится, а значит, сходится и ряд
Так как
интеграл ∫1∞1/2x−1dx∫1∞1/2x−1dx расходится, и поэтому
расходится. Контрольно-пропускной пункт
5.13
Определение
p>0,p≠1. Для этого случая Пример
5.15
Проверка сходимости ряда
p Решение
Контрольно-пропускной пункт
5.14
Оценка стоимости серии
Теорема
5.10
Оценка остатка от интегрального теста
Предположим, что существует функция ff, удовлетворяющая следующим трем условиям:
Другими словами, Пример
5.16
Оценка стоимости ряда
∑n=1∞1/n3. Решение
По оценке остатка мы знаем, что
У нас есть
Следовательно, ошибка R10<1/2(10)2=0,005.R10<1/2(10)2=0,005.
N>22,36. Чтобы убедиться, что остаток находится в пределах желаемой суммы, нам нужно округлить до ближайшего целого числа. Следовательно, минимально необходимое значение равно N=23.N=23. Контрольно-пропускной пункт
5.15
Раздел 5.3 Упражнения
)
Вычислите T=limk→∞TkT=limk→∞Tk с точностью до четырех знаков после запятой. ( Подсказка: 1k+1<∫kk+11xdx1k+1<∫kk+11xdx.)
Мы будем считать, что колода перетасована случайным образом, как только будет сделано достаточное количество случайных вставок вверх, чтобы карта, первоначально находившаяся внизу, достигла верха, а затем была вставлена случайным образом. Если в колоде n карт, то вероятность того, что вставка будет ниже карты, изначально находящейся внизу (назовем эту карту B)B), равна 1/n.1/n. Таким образом, ожидаемое количество случайных вставок сверху до того, как BB перестанет быть внизу, равно 9.0614 н . Как только одна карта находится ниже B, B, есть два места ниже BB, и вероятность того, что случайно вставленная карта окажется ниже BB, равна 2/n.2/n. Ожидаемое количество первых случайных вставок до того, как это произойдет, равно n/2.n/2. Две карты ниже BB теперь в случайном порядке. Продолжая в том же духе, найдите формулу для ожидаемого количества случайных вставок сверху, необходимых для того, чтобы колода считалась случайно перетасованной.
