Лучший ответ по мнению автора
| ||||||||||||||||
02.19
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
1)В воду объемом 1 л ,температура которой 20С°, бросают кусок железа массой 100г, нагретый до 500С°. При этом температура воды повышается до 24С° и некоторое количество её обращается в пар.
Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 5√3 см.
2+n-72)=1/(n+9)Результаты короткой программы у девушек на 6 этапе Гран-при среди юниоров по фигурному катанию 2022 в Гданьске, 6 октября
Японская фигуристка Ами Накаи лидирует после короткой программы на этапе Гран-при среди юниоров в Гданьске.
Гран-при среди юниоров
6-й этап
Гданьск, Польша
Девушки
Короткая программа
1. Ами Накаи (Япония) – 69,00
2. Мин Соль Квон (Южная Корея) – 66,81
3. Чжи А Син (Южная Корея) – 63,72
4. Джозефин Ли (США) – 61,72
5. Миа Калин (США) – 59,50
6. Си У Сон (Южная Корея) – 58,63
7. Мария Элийсе Кальювере (Эстония) – 57,92
8. Ноэлль Стреули (Польша) – 54,83
9. Никола Фомченкова (Латвия) – 53,94
10. Сарина Йоос (Швейцария) – 53,79
11. Элис Лин-Грейси (США) – 52,90
12. Аюми Шибаяма (Япония) – 52,31
Материалы по теме
Главные новости
- Finlandia Trophy. Губанова, Кийбус, Ким Йе Лим, Паганини, Торнгрен и Перейра выступят с короткими программами 5
- Japan Open. Малинин, Браун, Уно, Грассль, Сакамото, Куракова, Хендрикс и Кихира покажут произвольные программы 18
- Мемориал Панина. Коляда, Алиев, Мозалев, Игнатов и Даниелян выйдут на лед с произвольными программами 6
- Мемориал Панина. Туктамышева, Гущина, Садкова и Свириденко покажут произвольные программы 2
- Видео Японская фигуристка Ами Накаи исполнила тройной аксель на этапе юниорского Гран-при в Гданьске и одержала победу 5
- Гран-при среди юниоров. Накаи победила, Чжи А Син – 2-я, Мин Соль Квон – 3-я, Калин – 4-я 28
- Мемориал Панина. Бойкова и Козловский выиграли короткую программу, Мишина и Галлямов – 2-е, Кадырова и Колесов – 5-е 136
- Алексей Железняков: «Если Двоеглазова будет продолжать в том же духе, у нее хорошее будущее.
Я как хореограф ей доволен» 13
TopNews»> Бойкова и Козловский снялись с мемориала Панина из-за микротравмы партнера. Они лидировали после короткой программы 10
TopNews»> Козловский о кодексе этики ФФКР: «Сама задумка правильная. Главное, чтобы кодекс не стал орудием в сокрытии важных вещей» 5
Я как хореограф ей доволен» 13Новости моей команды
Выберите любимую команду
Выберите вид спортаФутболХоккейБаскетболБиатлонБокс/ммаФормула-1Теннис
ПОСЛЕДНИЕ НОВОСТИ
- Finlandia Trophy. Ташлерова и Ташлер, Грин и Парсонс, Фурнье Бодри и Соренсен покажут ритм-танцы
- Гран-при среди юниоров. Башинска и Бомон, Гримм и Савицкий, Льюис и Макмиллан покажут произвольные танцы
- Гран-при среди юниоров. Катайсэ, Ямпольски, Винокур, Наката, Со, Хагара и Пито выступят с произвольными программами
- Мемориал Панина. Мишина и Галлямов, Хабибуллина и Княжук выступят с произвольными программами, Бойкова и Козловский снялись 2
- «Мы откатали на 98% того, что хотели показать. Остальные 2% – чтобы компенсировать в произвольной завтра». Мишина и Галлямов о мемориале Панина 3
- Мемориал Панина. КМС. Шегай и Шамшуров выиграли короткую программу, Егорова и Маринский – 2-е 20
- «Мы утратили чувство безопасности. Решили последовать совету консула и уехать из России как можно скорее». Уртадо об уходе из группы Жулина 12
- Иван Букин и Екатерина Боброва выступят в ледовом шоу «Морозко» Ильи Авербуха 14
- Finlandia Trophy. Чха Чжун Хван одержал победу, Квителашвили – 2-й, Селевко – 4-й, Майоров – 7-й 53
- «Сегодня увидел, что сверкнула молния. Поскольку мне дали прозвище Повелитель молнии, на каток я ехал с облегчением». Алиев об участии в Мемориале Панина 4
- Мемориал Панина. КМС. Дикиджи одержал победу, Угожаев – 2-й, Лазарев – 3-й, Полянский – 4-й, Зонов – 5-й 29
- Реклама Скидка до 60% на любой курс от Нетологии по промокоду GOL5
- Татьяна Мишина: «Всегда ждем от Туктамышевой два акселя в произвольной. Она уже давно самостоятельный человек, и нам не приходится ее мотивировать» 39
- Даниелян о мемориале Панина: «Предложил рискнуть и попробовать четверной сальхов – где еще, если не здесь» 2
- Плющенко поздравил Путина с 70-летием: «Хочется пожелать ему сил и крепкого здоровья и чтобы все конфликтные ситуации им были разрешены как можно быстрее» 228
- «Квантовый скачок в фигурном катании». Плющенко о планах Малинина исполнить 7 четверных в произвольной на Japan Open 16
- Алиса Двоеглазова: «Мой кумир – Анна Щербакова. Нравилось на Олимпиаде, как она эмоционально погрустила, улыбнулась, очень интересно было» 52
- Мемориал Панина. КМС. Двоеглазова победила, Петрова – 2-я, Кравчина – 3-я, Гордеева – 4-я, Мазур – 9-я 176
- Загитова на вопрос Утяшевой, занято ли ее сердце: «Возможно» 179
- Илья Малинин планирует исполнить 7 четверных прыжков в произвольной программе на Japan Open 80
TopNews»> Мемориал Панина. КМС. Шегай и Шамшуров, Черемных и Бутенко, Егорова и Маринский покажут произвольные программы
TopNews»> Уртадо о завершении карьеры: «В Испании нет специалистов уровня Жулина. Ни льда, ни тренеров, никаких условий для эффективной работы» 18
TopNews»> Видео Камила Валиева исполнила четверной тулуп на тренировке 128
TopNews»> Finlandia Trophy. Хокке и Кункель одержали победу, Ефимова и Бломмарт – 2-е, Макинтош и Мимар – 3-и 3
TopNews»> Гран-при среди юниоров. Голубева и Мур победили, Серова и Хобта – 2-е, Барам и Тюменцев – 3-иАрхив новостей
Опрос
🥇 Наконец-то выиграет золото
29%
🥈🥉 Опять вторые и третьи места
71%
тригонометрия — Если $\sin\alpha + \cos\alpha = 0,2$, найдите числовое значение $\sin2\alpha$.
Задавать вопрос
Спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 1к раз
$\begingroup$
Если $\sin\alpha + \cos\alpha = 0,2$, найти числовое значение $\sin2\alpha$. Как найти значение для $\sin\alpha$ или $\cos\alpha$, чтобы использовать формулу двойного угла? 92 = \фракция{1}{4}$$ так $$\sin\alpha = \pm\frac{1}{2}$$ тогда достаточно просто подставить $\sin\alpha = \pm\frac{1}{2}$ и $\cos\alpha=\frac{\sqrt{3}}{2}$ в $$\sin2 \alpha = 2\sin\alpha\cos\alpha$$, чтобы получить $$\sin2\alpha = \pm\frac{\sqrt{3}}{2}$$
Где я не могу продвинуться с вопросом
«Если $\sin\alpha + \cos\alpha = 0,2$, найдите числовое значение $\sin2\alpha$».
Как найти значение для $\sin\alpha$ или $\cos\alpha$, чтобы использовать формулу двойного угла? 92 \alpha = 0,04, 2 \sin \alpha \cos \alpha=-0,96=\sin (2\alpha)$
$\endgroup$
3
$\begingroup$
$$\cos \alpha + \sin \alpha = \sqrt{2} (\frac{\cos \alpha}{\sqrt{2}} + \frac{\sin \alpha}{\sqrt{2} }) = \ sqrt {2} (\ sin \ frac {\ pi} {4} \ cos \ alpha + \ cos \ frac {\ pi} {4} \ sin \ alpha) = \sqrt{2}\sin(\frac{\pi}{4} + \alpha) = .2 $$
Взяв обратный грех каждой стороны, получаем $$ \alpha = 2.2143 + 2 \pi n_1 \mid n_1 \in \mathbb{Z} \,\,\,\text{or}\,\,\, \alpha = 2\pi n_2 — .643501 \mid n_2 \in \mathbb{Z}$$ 92 \alpha = 1.96$, откуда заключаем $\sin\alpha — \cos\alpha = \pm 1.4$
Из $\слева\{ \начать{массив}{л} \sin\альфа + \cos\альфа = 0,2\\ \sin\alpha — \cos\alpha = 1,4 \конец{массив} \право\}$ находим $(\sin\alpha, \cos\alpha) = (0,8, -0,6)$
Из $\слева\{ \начать{массив}{л} \sin\альфа + \cos\альфа = 0,2\\ \sin\alpha — \cos\alpha = -1.
Обратите внимание, что ни одно из этих решений не является посторонним. 92 \альфа + 2\sin \альфа \cos\альфа &= 0,04 \\ 1+\sin 2\альфа &= 0,04 \\ \sin 2\альфа &= -0,96 \end{align}
и было бы просто продолжить
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 9{2}}\alpha } \\
& LHS=RHS \\
\end{align}\]
Следовательно, доказано.Примечание: В этом вопросе высока вероятность того, что учащийся допустит ошибки в вычислениях. Также они могли ошибиться при применении алгебраических и тригонометрических формул. Таким образом, студенты должны быть осторожны при решении вопроса.
4.1 Редакция | Тригонометрия | Сиявула
4.1 Редакция (EMCG9)
Тригонометрические отношения
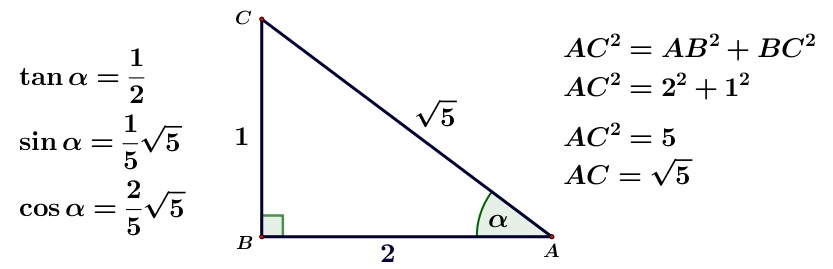
Мы определили основные тригонометрические соотношения, используя длины сторон прямоугольного треугольника.
\(\begin{массив}{[электронная почта защищена]{\;}[электронная почта защищена]{\;}[электронная почта защищена]{\;}[электронная почта защищена]{\;}[электронная почта защищена]{\;}[ электронная почта защищена]{\;}[электронная почта защищена]{\;}[электронная почта защищена]{\;}} \ sin \ hat {A} & = & \ frac {\ text {напротив}} {\ text {гипотенуза}} & = \ frac {a} {c} & \ qquad \ qquad & \qquad \sin \hat{B}&=&\frac{\text{напротив}}{\text{гипотенуза}} &= \frac{b}{c} \\ & & & & & & & \\ \cos \hat{A}&=&\frac{\text{смежный}}{\text{гипотенуза}} &= \frac{b}{c} &\qquad \qquad & \qquad \cos\шляпа{B}&=&\frac{\text{смежный}}{\text{гипотенуза}} &= \frac{a}{c} \\ & & & & & & & \\ \tan \hat{A}&=&\frac{\text{напротив}}{\text{смежный}} &= \frac{a}{b} & \qquad \qquad & \ qquad \ tan \ hat {B} & = & \ frac {\ text {напротив}} {\ text {смежный}} & = \ frac {b} {a} \конец{массив}\) 9{2}\).
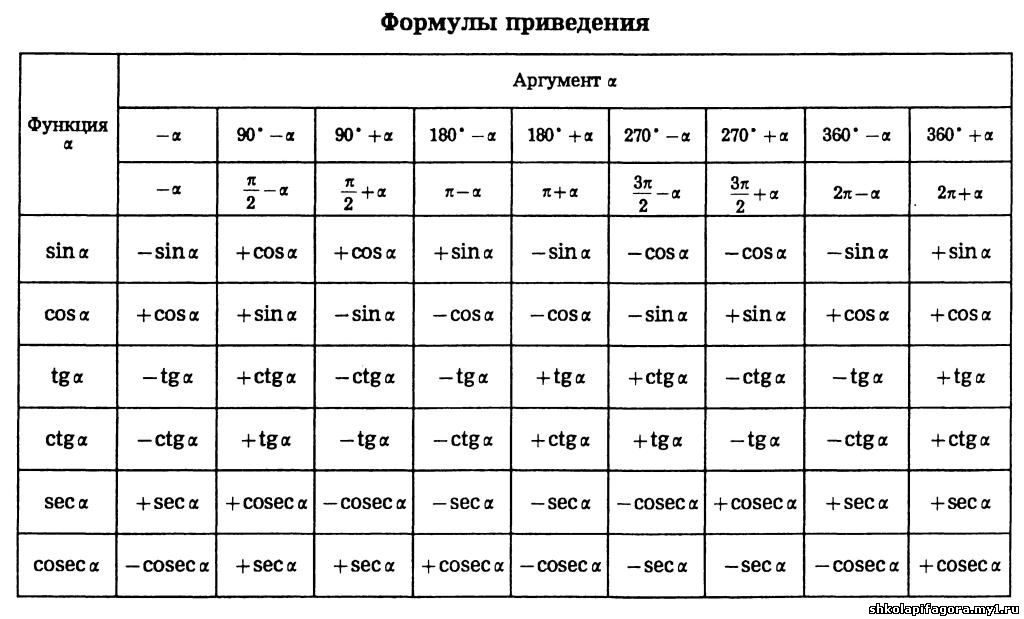
Схема CAST
Знак тригонометрического соотношения зависит от знаков \(x\) и \(y\):
Формулы приведения и кофункции:
Формулы приведения верны для любого угла \(\theta\). Для удобства мы предполагаем, что \(\theta\) является острый угол (\(\text{0}°<\theta <\text{90}°\)).
При определении значений функции (\(\text{180}°±\theta\)), (\(\text{360}°±\theta\)) и (\(-\theta\)) функция не меняется.
При определении значений функций (\(\text{90}°±\theta\)) и (\(\theta ±\text{90}°\)) функция переходит в свою кофункцию.
Отрицательные углы
\начать{выравнивать*} \sin (- \тета) &= — \sin \тета \\ \cos (- \тета) &= \cos \тета \\ \загар (- \тета) &= — \загар \тета \конец{выравнивание*}Специальные угловые треугольники
Эти значения полезны, когда нам нужно решить задачу с тригонометрическими функциями без использования калькулятор.
θ
\(\text{0}\)°
\(\text{30}\)°
\(\text{45}\)°
\(\text{60}\)°
\(\text{90}\)°
\(\cos θ\) \(\текст{1}\)
\(\ гидроразрыва {\ sqrt {3}} {2} \)
\(\frac{1}{\sqrt{2}}\)
\(\ гидроразрыва{1}{2}\)
\(\текст{0}\)
\(\sinθ\) \(\текст{0}\)
\(\ гидроразрыва{1}{2}\)
\(\frac{1}{\sqrt{2}}\)
\(\ гидроразрыва {\ sqrt {3}} {2} \)
\(\текст{1}\) \(\тангенс θ\) \(\текст{0}\)
\(\frac{1}{\sqrt{3}}\)
\(\текст{1}\)
\(\sqrt{3}\)
неопределенный
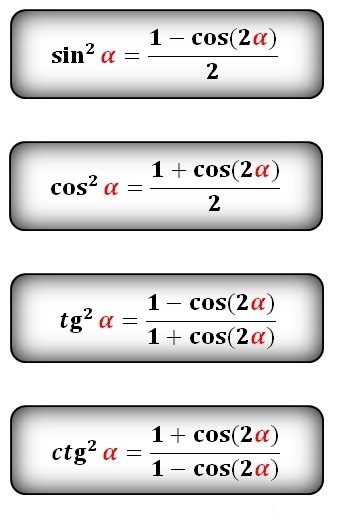
Тригонометрические тождества 92 \ тета} \конец{выравнивание*}
Все эти соотношения и тождества очень полезны для упрощения тригонометрических выражений.
Рабочий пример 1: Редакция
Определить значение выражения без использования калькулятора:
\[\frac{\cos \text{420} ° — \sin \text{225} ° \cos ( — \text{45} °)}{\tan \text{315} ° }\]
Используйте формулы приведения, чтобы выразить каждое тригонометрическое соотношение через острый угол
\начать{выравнивать*} &\frac{\cos \text{420} ° — \sin \text{225} ° \cos ( — \text{45} °)}{\tan \text{315} ° } \\ &= \frac{\cos ( \text{360} ° + \text{60} °) — \sin ( \text{180} ° + \text{45} °) \cos ( — \text{45} °)}{\tan ( \text{360} ° — \text{45} °) } \\ &= \frac{\cos\text{60} ° — ( — \sin \text{45} ° ) (\cos \text{45} °)}{- \tan \текст{45} ° } \\ &= \frac{ \cos \text{60} ° + \sin \text{45} ° \cos \text{45} ° }{- \tan \text{45} ° } \конец{выравнивание*}
Теперь используйте специальные углы для вычисления упрощенного выражения: \начать{выравнивать*} &= \frac{ \cos \text{60} ° + \sin \text{45} ° \cos \text{45} ° }{- \tan \text{45} ° } \\ &= \frac{ \frac{1}{2} + \left( \frac{1}{\sqrt{2}} \right)\left( \frac{1}{\sqrt{2}} \right) }{- 1} \\ &= — \left( \frac{1}{2} + \frac{1}{2} \right) \\ &= -1 \конец{выравнивание*} 9{2} \альфа\\ & \\ \поэтому \text{левый} &= \text{правый} \конец{выравнивание*}
Альтернативный метод: мы могли бы также начать с левой части тождества и подставил \(\tan \alpha = \frac{\sin \alpha}{\cos \alpha}\) и упростил, чтобы получить правую часть сторона.
Ограничения
Нам нужно определить значения \(\alpha\), для которых любой из терминов в тождестве будет не определено: 9{2} \альфа &= 0 \\ \поэтому \cos \alpha &= 0 \\ \поэтому \alpha &= \text{90} ° \text{ или } \text{270} ° \конец{выравнивание*}
Мы также должны учитывать значения \(\alpha\), для которых \(\tan \alpha\) не определено. Следовательно идентификатор не определен для \(\alpha = \text{90} ° + k \cdot \text{180} °\).
Полезные советы:
- Иногда полезно записывать \(\tan \theta\) в терминах \(\sin \theta\) и \(\cos \theta\).
- Никогда не пишите тригонометрическое соотношение без угла. Например, \(\tan = \frac{\sin}{\cos}\) не имеет значение.
- Для подтверждения личности упрощайте только одну сторону личности за раз.
- Как видно из рабочего примера выше, иногда необходимо упростить обе стороны удостоверения.
- Не забудьте записать ограничения:
- значения, для которых не определено ни одно из тригонометрических соотношений;
- значения переменной, при которых любой из знаменателей тождества равен нулю.
Ревизия – формулы приведения, кофункции и тождества
Учебник Упражнение 4.1
\(\sin\text{149} °\)
\begin{align*} \sin \text{149} ° &= \sin ( \text{180} ° — \text{31} °) \\ &= \sin \text{31} ° \\ &= А \end{выравнивание*}
\(\cos ( — \text{59} °)\)
\begin{align*} \cos ( — \text{59} °) &= \cos \text{59} ° \\ &= \cos ( \text{90} ° — \text{31} °) \\ &= \sin \text{31} ° \\ &= А \end{align*}
\(\cos \text{329} °\)
\begin{align*} \cos \text{329} ° &= \cos ( \text{360} ° — \text{31} °) \\ &= \cos\text{31} ° \\ &= \sqrt{1 — \sin^{2} \text{31} °} \\ &= \sqrt{1 — A^{2}} \end{выравнивание*}
\(\tan \text{211} ° \cos \text{211} °\)
\begin{align*} \tan \text{211} ° \cos \text{211} ° &= \left( \frac{\sin \text{211} °}{\cos \text{211} °} \right) \cos \text{211} ° \\ &= \sin \text{211} ° \\ &= \sin ( \text{180} ° + \text{31} °) \\ &= — \sin \text{31} ° \\ &= — А \end{выравнивание*} 9{2}}} \end{align*}
Упростить \(P\) до одного тригонометрического отношения:
\[P = \sin ( \text{360} ° + \theta) \cos ( \text{180} ° + \theta) \tan( \text{360} ° + \тета)\]
\begin{выравнивание*} P &= \sin ( \text{360} ° + \theta) \cos ( \text{180} ° + \theta) \tan( \text{360} ° + \тета) \\ &= \sin \theta (- \cos \theta) ( \tan \theta) \\ &= -\sin\theta\cos\theta\left(\frac{\sin\theta}{\cos\theta}\right) \\ &= -\sin^{2} \тета \end{выравнивание*}
Упростить \(Q\) до одного тригонометрического отношения:
\[Q = \frac{ \cos (\theta — \text{360} °) \sin ( \text{90} ° + \theta) \sin (- \theta)}{\sin (\theta + \text{180} °)}\]
\begin{выравнивание*} \text{Примечание: } & \cos (\theta — \text{360} °) \\ &=\cos [- ( \text{360} ° — \theta)] \\ &=\cos ( \text{360} ° — \theta) \\ &=\cos\тета\\ & \\ Q &= \frac{ \cos (\theta — \text{360} °) \sin ( \text{9{2}(\beta + \text{180} °) \cos(\beta — \text{90} °)}\]
\begin{align*} \text{Примечание: } & \tan (\beta — \text{360} °) \\ &= \tan [- ( \text{360} ° — \beta)] \\ &= — \tan ( \text{360} ° — \beta) \\ &= — ( — \загар \бета ) \\ &= \загар \бета\\ \text{И} & \cos (\beta — \text{90} °) \\ &= \cos [- ( \text{9{2} \бета \sin \бета } \\ &= — \frac{1}{\sin\beta} \\ &= — \фракция{1}{р} \end{align*}
\(\dfrac{\cos (- \text{120} °)}{\tan \text{150} °} + \cos \text{390} °\)
\begin{align*} & \dfrac{\cos ( \text{120} °)}{\tan \text{150} °} + \cos \text{390} ° \\ &= \frac{ \cos( \text{180} ° — \text{60} °)}{ \tan ( \text{180} ° — \text{30} °)} + \cos( \text{360} ° + \text{30} °) \\ &= \frac{ — \cos \text{60} °}{ — \tan \text{30} °} + \cos \text{30} ° \\ &= \frac{ \sin \text{30} °}{\frac{ \sin \text{30} °}{\cos \text{30} °}} + \cos \text{30} ° \\ &= \cos \text{30} ° + \cos \text{30} ° \\ &= 2 \cos \text{30} ° \\ &= 2 \влево(\frac{\sqrt{3}}{2} \вправо) \\ &= \sqrt{3} \end{выравнивание*}
\((1 — \sin \text{45} °)(1 — \sin \text{225} °)\)
\begin{align*} & (1 — \sin \text{45} °)(1 — \sin \text{225} °) \\ &= 1 — \sin \text{45} ° — \sin \text{225} ° + (\sin \text{45} °)(\sin \text{225} °) \\ &= 1 — \sin \text{45} ° — \sin ( \text{180} ° + \text{45} °) + (\sin \text{45} °)(\sin ( \text{180} ° + \text{45} °)) \\ &= 1 — \sin \text{45} ° + \sin \text{45} ° — \sin^{2} \text{45} ° \\ &= 1 — \sin^{2} \text{45} ° \\ &= 1 — \left( \frac{1}{\sqrt{2}} \right)^{2} \\ &= 1 — \фракция{1}{2} \\ &= \фракция{1}{2} \end{выравнивание*} 92 \тета\\ &= \текст{0} \end{align*}
Используйте формулы приведения и специальные углы, чтобы показать, что
\[\frac{\sin ( \text{180} ° + \theta) \tan ( \text{720} ° + \theta) \cos (- \theta)}{\cos ( \text{90} ° + \theta) }\]
можно упростить до \(\sin\theta\).
Используйте формулы приведения и кофункции для упрощения выражения
\начать{выравнивать*} & \frac{\sin (\text{180} ° + \theta) \tan (\text{720} ° + \theta) \cos (- \theta)}{\cos ( \text{90} ° + \theta) }\\ &= \frac{ — \sin \theta \tan \left( 2( \text{360} °) + \theta \right) \cos \theta}{ — \sin\тета} \\ &= \загар \тета \соз \тета \\ & = \ влево ( \ гидроразрыва {\ грех \ тета} {\ соз \ тета} \ справа) \ соз \ тета \\ &= \sin\тета \конец{выравнивание*}
Не используя калькулятор, определите значение \(\sin \text{570} °\).
Использование специальных углов для определения значения выражения
\начать{выравнивать*} \sin \text{570} ° &= \sin ( \text{360} ° + \text{210} °) \\ &= \sin ( \text{210} °) \\ &= \sin ( \text{180} ° + \text{30} °) \\ &= — \sin \text{30} ° \\ &= — \фракция{1}{2} \конец{выравнивание*}
Учитель математики Троя просит класс ответить на следующий вопрос.
Прокомментируйте ответ Троя и покажите правильный метод подтверждения личности.
Вопрос требует, чтобы Трой подтвердил личность. Однако работая с обеими сторонами личность в то же время, он признал, что это было правдой. Правильный метод доказательства идентичность состоит в том, чтобы работать только с одной стороной за раз и показывать, что одна сторона равна Другой. Иногда необходимо сначала упростить одну сторону тождества, а потом еще и упростить другую сторону, чтобы показать, что они равны. Троя тоже должна была заявленные ограничения. 9{2}\theta}{\cos\theta(1+\sin\theta)} \\ &= \dfrac{\cos\theta}{1+\sin\theta} \\ &= \текст{левый} \конец{выравнивание*}
Ограничения: не определено, где \(\cos \theta = \text{0}, \text{ и } \sin \theta = — \текст 1}\).
Тогда \(\theta \ne \text{90} + k \cdot \text{180} ° \text{ и } \theta \ne — \text{90} + k \cdot \text{360} °\). 92\тета}{\соз\тета}\\ &=\cos\тета\\ &= \текст{справа} \конец{выравнивание*}
Ограничения: не определено, где \(\cos \theta = \text{0}\) и где \(\tan \theta\) равно неопределенный.
Поэтому \(\theta \ne \text{90} °; \text{270} °\).
\(\dfrac{2\sin\theta\cos\theta}{\sin\theta +\cos\theta}=\sin\theta +\cos\theta -\dfrac{1}{\sin\theta +\cos\theta}\) 92\тета-1}{\sin\тета+\cos\тета} \\ &=\dfrac{1+2\sin\theta \cos\theta-1}{\sin\theta+\cos\theta} \\ &=\dfrac{2\sin\theta\cos\theta}{\sin\theta+\cos\theta} \\ &= \текст{левый} \конец{выравнивание*}
Ограничения: не определено, где \(\sin \theta = \text{0}, \enspace \cos \theta = \текст{0}\).
Поэтому \(\theta \ne \text{0} °; \text{92\beta}{\sin\beta\cos\beta} \right )\cos\beta\\ &=\dfrac{1}{\sin\beta}\\ &= \текст{справа} \конец{выравнивание*}
Ограничения: не определено, где \(\sin \beta = \text{0}, \enspace \cos \beta = \text{0}\) и где \(\tan\beta\) не определено.
Поэтому \(\beta \ne \text{0} °; \text{90} °; \text{180} °; \text{270} °; \text{360} °\). 92\тета} \\ \поэтому \text{левый } &= \text{правый } \конец{выравнивание*}
Ограничения: не определено, где \(\sin \theta = \pm \text{1}, \enspace \sin \theta = \text{0}, \enspace \cos \theta = \text{0}\).
Ограничения также включают значения \(\theta\), для которых \(\tan \theta\) неопределенный.
Поэтому \(\theta \ne \text{0} °; \text{9{2}\alpha} \times \cos\alpha \\ &=\dfrac{1}{\cos\alpha} \конец{выравнивание*} \начать{выравнивать*} \text{RHS} &= \dfrac{1 — \tan \alpha}{\cos \alpha — \sin \alpha} \\ &= \dfrac{1 — \frac{\sin \alpha}{\cos \alpha}}{\cos \alpha — \sin \alpha} \\ &= \dfrac{\frac{\cos \alpha — \sin \alpha}}{\cos \alpha}}{\cos \alpha — \sin \alpha} \\ &= \dfrac{\cos\alpha — \sin\alpha}{\cos\alpha(\cos\alpha — \sin\alpha)} \\ &= \dfrac{1}{\cos\alpha} \\ &= \текст{левый} \конец{выравнивание*}
Ограничения: где \(\sin\alpha = \cos\alpha\) и где \(\tan\alpha\) не определено.
Поэтому \(\alpha \ne \text{45} °; \text{90} °; \text{270} °; \text{225} °\).
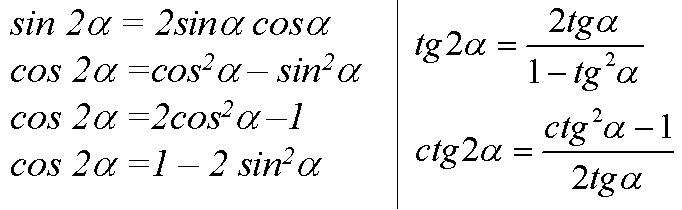
4
\конец{массив}
\право\}$
находим $(\sin\alpha, \cos\alpha) = (-0,6, 0,8)$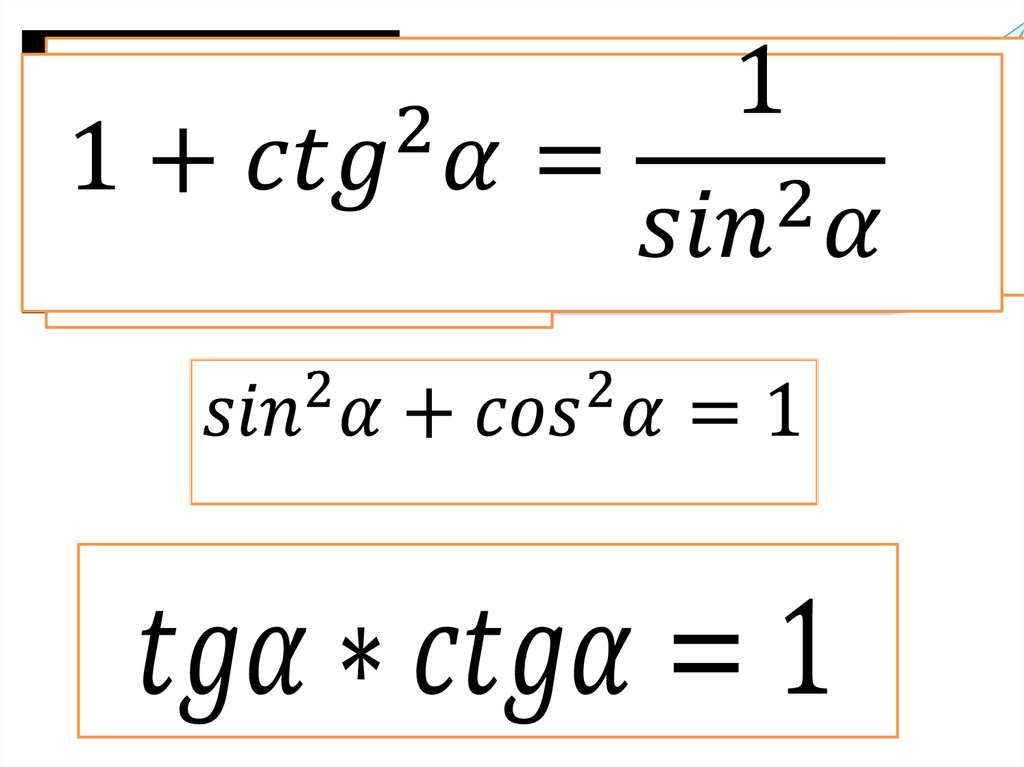
Помните, что длины сторон прямоугольного треугольника подчиняются теореме
Пифагор.
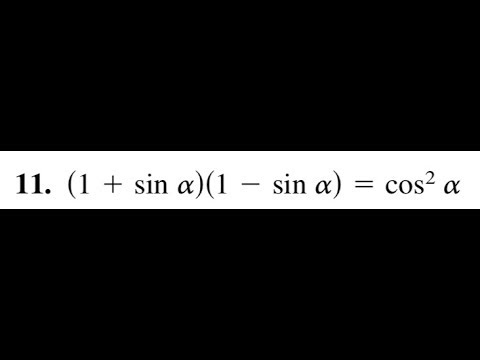
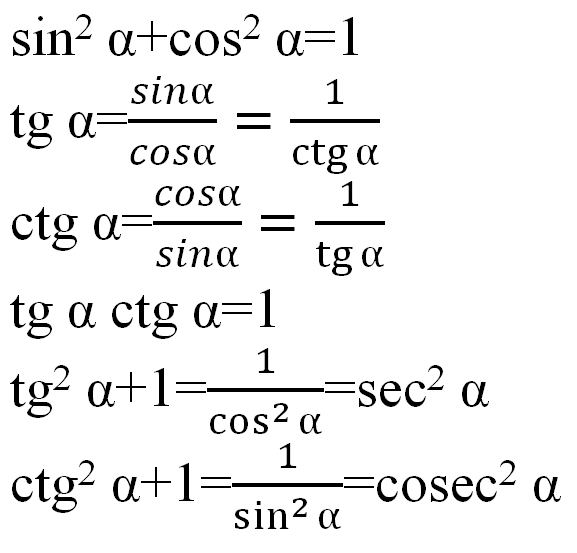
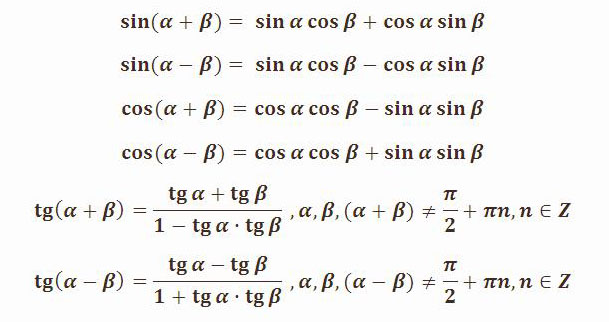{2} \тета \\
\поэтому \text{левый} &= \text{правый}
\конец{выравнивание*}
