Уравнения кривых второго порядка: Кривые второго порядка

2}=0, \] т.е. уравнение (8). Рассмотрим теперь варианты уравнения (12), соответствующие случаю $AC &nbsp

3.2 Кривые на плоскости 3.4 Прямая на плоскости

&nbsp

7.2. Общее уравнение кривых второго порядка, их классификация

Алгебраическая кривая второго порядка — это геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

(16)

в котором по крайней мере один из коэффициентов отличен от нуля. Это уравнение, путем определенных преобразований, а именно, — поворота и параллельного переноса осей координат может быть приведено к некоторому простейшему виду, называемомуканоническим.

Если исключить случаи вырождения, т.е. когда уравнение (16) распадается на уравнения первого порядка или описывает единственную точку, можно выделить три принципиально различных типа кривых, — это эллипс, гипербола и парабола.

К их числу относится и окружность, которая является частным случаем эллипса.

Изложим принципы классификации кривых второго порядка.

Определяющую роль в идентификации кривых играют некоторые выражения, называемые инвариантами, которые сохраняют знак при выполнении указанных преобразований. По этой причине тип кривой, с использованием инвариантов, может быть установлен по исходному уравнению.

Не рассматривая здесь вырожденные случаи, т.е. те из них, когда уравнение (16), описывают точку, мнимый эллипс или распадается на уравнения прямых, таких инварианта два, — это определитель уравнения (16)

(17)

и определитель его квадратичной части

. (18)

Тогда, в зависимости от сочетания их знаков уравнение (16) описывает:

— эллипс, если ;

— гиперболу, если ;

— параболу, если .

1. Определите вид кривой второго порядка, приведите её уравнение к каноническому виду и постройте её в декартовой системе координат:

а); б); в).

Решение:

а) Шаг 1. Для определения вида кривой второго порядка запишем определители и(см.формулы (17),(18)).Имеем

Так как а, то данная кривая — эллипс.

Шаг 2. Приведём уравнение к каноническому виду методом выделения полных квадратов (метод Лагранжа):

1)Сгруппируем слагаемые, содержащие одинаковые переменные:

2)Вынесем за скобку старшие коэффициенты

3)Выделим в скобках полные квадраты. Имеем

.

4)Раскроем внешние скобки.

.

и перенесём свободные члены в правую часть. После приведения подобных получим

5) Разделим теперь обе части уравнения на 36. Получим

Шаг 3. Построим кривую второго порядка в декартовой системе координат.

Из последнего уравнения видно, что центр эллипса находится в точке (-3;1), полуоси,.Используя эти данные построим график эллипса.

б) Аналогично примеру а), сначала определим вид кривой второго порядка по её уравнению.Имеем

,

.

Так как , то данная кривая является гиперболой.

Приведём уравнение к каноническому виду.

1)Сгруппируем слагаемые с одинаковыми переменными

.

2)Вынесем за скобку старшие коэффициенты.

.

3)Выделим в скобках полные квадраты.

,

4)Раскроем теперь внешние скобки

,

перенесём свободные члены в правую часть и приведём подобные

5) Разделив теперь обе части уравнения на 4,получим

Построим эту кривую в декартовой системе координат.

Из последнего уравнения видно, что полуоси гиперболы равны,. Центр симметрии гиперболы в точке (2;-1)- находится аналогично центру эллипса и окружности. Вершины гиперболы расположены в точках (3;-1) и (1;-1) — то есть, они расположены по левую и правую сторону от центра симметрии на расстояниипо осиОХ. Асимптоты гиперболы пересекают противоположные вершины прямоугольника нас центром в точке (2;-1). Используя это, строим график гиперболы

.

в) Определим вид кривой второго порядка. Для этого раскроем скобки и приведем подобные. Имеем

Разделив на 16, получим каноническое уравнение параболы

.

Построим кривую в декартовой системе координат.

Из последнего уравнения видно, что парабола проходит через точку (0;0), осью симметрии является

ОХ. Построим таблицу некоторых точек параболы

х	0	2	8	32
у	0

При помощи этих данных строим график параболы.

2. Найти площадь треугольника, две вершины которого находятся в фокусах данного эллипса, а третья в центре окружности

, .

Решение.

Приведём уравнения к каноническому виду.

После приведения становится понятным, что — уравнение окружности с центром в точке (1;-3), а — уравнение эллипса с центром в точке (0;0) и полуосями и. Найдём фокусы данного эллипса. По формуле (3):=. Тогда фокусы данного эллипса в точках (;0) и (-;0). Таким образом, вершины искомого треугольника в точках О(1;-3),(;0) и(-;0)

.

Площадь полученного треугольника вычислим по формуле , где- это высота, опущенная на сторону=2.Заметим, что высота равна модулю ординаты точки О, то есть, =3. Тогда

Ответ:

3. Найти уравнения гиперболы, вершины которой находятся в фокусах данного эллипса, а фокусы – в его вершинах

.

Решение.

Найдём вершины эллипса . Для этого приведём его уравнение к каноническому виду. Из полученного уравнения получим полуоси,. Тогда вершины эллипса (;0) и (-;0), (0;) и (0;-). Найдём фокусы этого эллипса по формуле (3). Заметим, что фокусы эллипса находятся на ОУ, , значит,и. По условию задачи вершины искомой гиперболы находятся в фокусах данного эллипса, значит вершины гиперболы,. Тогда фокусы искомой кривой тоже расположены наОУ:(0;) и (0;-).

Зная вершину гиперболы, можно найти одну из полуосей. Так как фокусы расположены на ОУ, то уравнение будет иметь вид: . Значит, . По формуле (11), откуда. По определению канонического уравнения гиперболы параметр. Значит вторая полуось гиперболы. Искомое уравнение гиперболы имеет вид:.

Ответ.

4. Составить канонические уравнения парабол, фокусы которых совпадают с фокусами данного эллипса.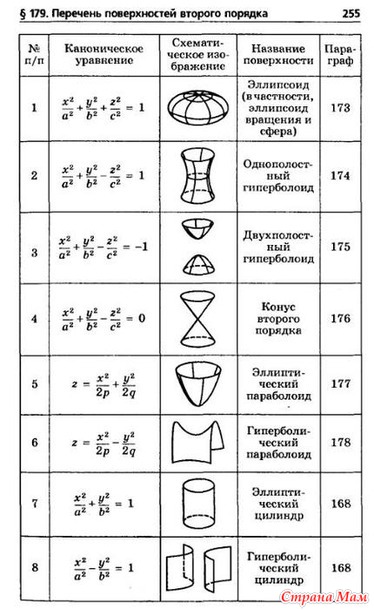

Написать для них уравнение директрисы.

Решение.

Приведём уравнение эллипса к каноническому виду.

Найдём фокусы эллипса (формула (3)).Имеем , тогда.

Построим каноническое уравнение параболы с фокусом . Так как для параболы, то. Тогда уравнение параболы имеет вид. Директрисой этой кривой является прямая.

Построим каноническое уравнение параболы с фокусом .

Для параболы с положительным значением координаты у фокуса,,. Тогда уравнение параболы. Директриса этой кривой второго порядка.

Ответ: ,или,.

Кривые второго порядка

Содержание

Введение

1.Кривые второго порядка

1.1 Эллипс

1.2 Гипербола

1.3 Парабола

2.Теоремы, связанные с кривыми второго порядка

Литература

Введение

Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.

Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.

1. Кривые второго порядка

Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением

ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0

где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .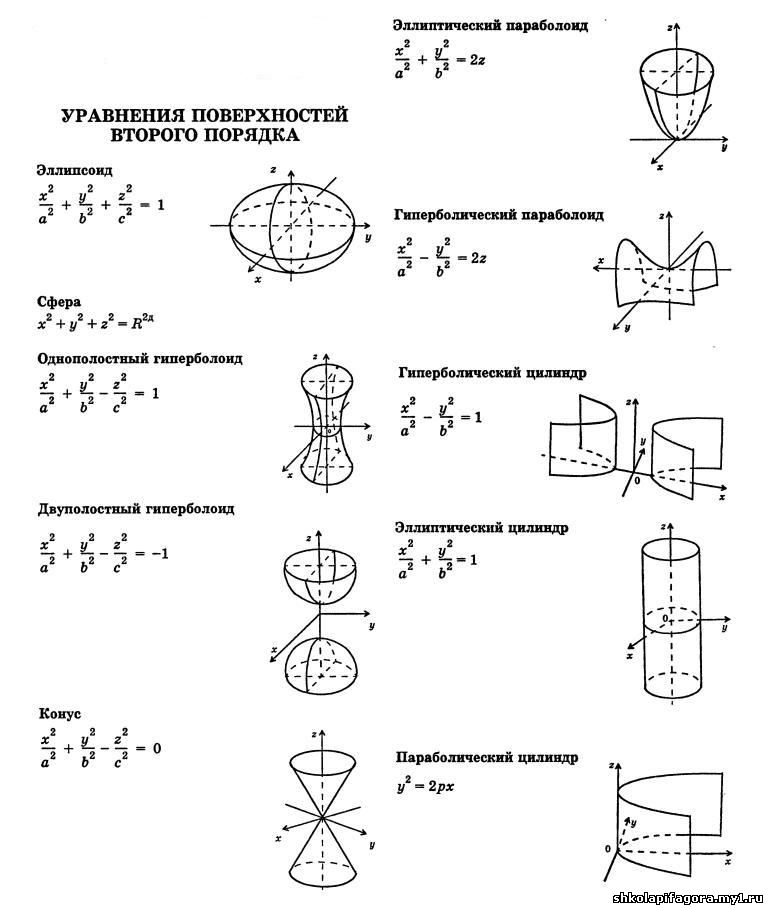

Вид кривой зависит от четырёх инвариантов:

инварианты относительно поворота и сдвига системы координат:

инвариант относительно поворота системы координат (полуинвариант):

Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:

Так, например, невырожденная кривая

оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли

положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:

Или

λ2 − Iλ + D = 0.

Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:

Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.

Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.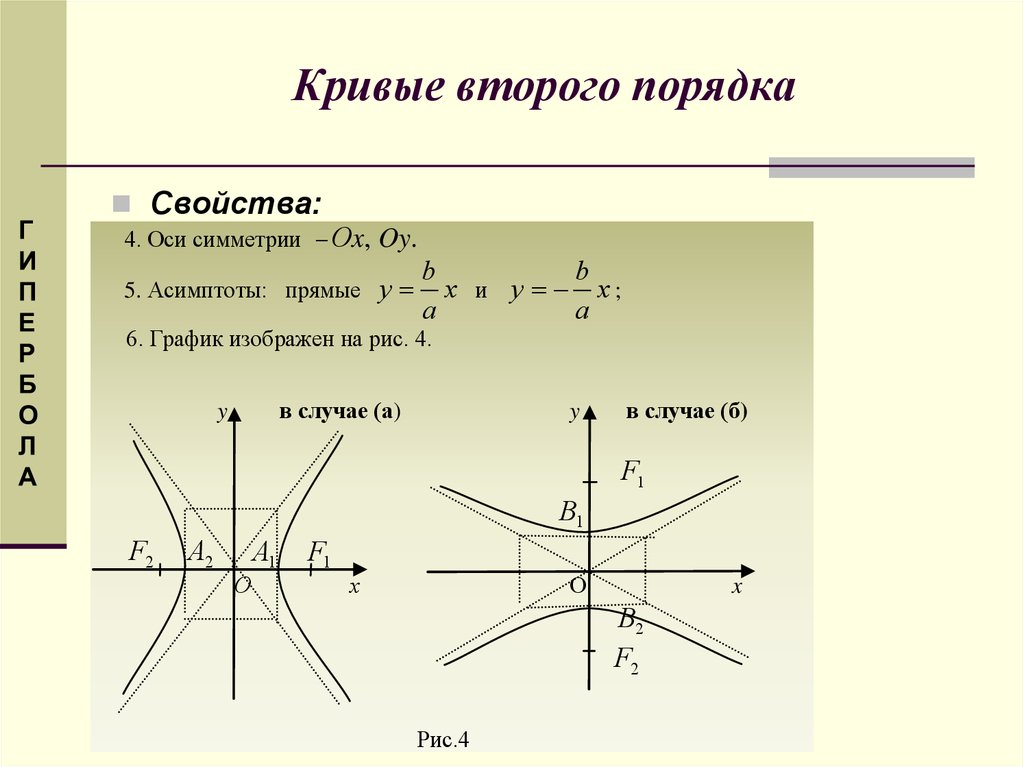

Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:

1.1 Эллипс

Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.

Если эллипс описывается каноническим уравнением

где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где

Величина e = c/a называется эксцентриситетом эллипса.

По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам

Если фокусы эллипса совпадают, то эллипс является окружностью.

1.2 Гипербола

Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением

где a > 0, b > 0 — параметры гиперболы.

Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.

В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.

Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.

С осью OY гипербола не пересекается.

Отрезки a и b называются полуосями гиперболы.

Рис.1

Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.

Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).

Рис.2

Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.

1.3 Парабола

Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением

y2 = 2 px

где p > 0 — параметр параболы.

Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.

В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.

Рис.3

Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы:

2. Теоремы, связанные с кривыми второго порядка

Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:

Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой.Теорема Паскаля двойственна к теореме Брианшона.

Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:

Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.

В частности, в вырожденном случае:

Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.

Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.

Литература

1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.

2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.

3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: «Наука», 1988.

5: Линейные уравнения второго порядка

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

30721

• Уильям Ф. Тренч
• Университет Тринити

В этой главе мы изучаем особенно важный класс уравнений второго порядка. Из-за их многочисленных приложений в науке и технике дифференциальные уравнения второго порядка исторически были наиболее тщательно изученным классом дифференциальных уравнений. Исследования по теории дифференциальных уравнений второго порядка продолжаются и по сей день. Эта глава посвящена уравнениям второго порядка, которые можно записать в виде $$ P_0(x)y»+P_1(x)y’+P_2(x)y=F(x). \nonumber $$ Говорят, что таких уравнений

линейный . Как и в случае линейных уравнений первого порядка, это дифференциальное уравнение называется однородным , если \(F\equiv0\), или неоднородным , если \(F \not \equiv 0\).

• 5.1: Однородные линейные уравнения

  Этот раздел посвящен теории однородных линейных уравнений.

  • 5.1.1: Однородные линейные уравнения (упражнения)

• 5. 2: Однородные уравнения с постоянными коэффициентами

  В этом разделе рассматриваются однородные уравнения специального вида $$ ay»+by’+cy=0, $$, где \(a\), \(b\) и \(c\) постоянны (\ (а\ne0\)). Когда вы закончите этот раздел, вы будете знать все, что нужно знать о решении таких уравнений.

  • 5.2.1: Однородные уравнения с постоянным коэффициентом (упражнения)

• 5.3: Неоднородные линейные уравнения

  В этом разделе представлена ​​теория линейных неоднородных уравнений.

  • 5.3.1: нежеские линейные уравнения (упражнения)

• 5.4: Метод неопределенных коэффициентов I

  Этот раздел представляет метод неиспользованных коэффициентов, которые могут использоваться для неэгровых уравнений. форма y»+by’+cy=F(x), где a, b и c являются константами, а F(x)  имеет особую форму, которая все еще является достаточно общей, чтобы встречаться во многих приложениях. В этом разделе широко используется идея изменения параметров, представленная ранее.

  • 5.4.1: Метод неопределенных коэффициентов I (упражнения)

• 5.5: Метод неопределенных коэффициентов II

  уравнение с постоянными коэффициентами Q — многочлены.

  • 5.5.1: Метод неопределенных коэффициентов II (упражнения)

• 5.6: Понижение порядка

  В этом разделе рассматривается понижение порядка, метод, основанный на идее изменения параметров, который позволяет нам найти общее решение неоднородного линейного уравнения второго порядка при условии что мы знаем одно нетривиальное (не тождественно нулевое) решение ассоциированного однородного уравнения.

  • 5.6.1: Сокращение заказа (учения)

• 5.7: Вариация параметров

  В этом разделе рассматривается метод, традиционно называемый вариацией параметров, который позволяет найти общее решение неоднородного линейного уравнения второго порядка при условии, что известны два нетривиальных решения (с непостоянным отношением) уравнения связанное однородное уравнение.

  • 5.7.1: Изменение параметров (упражнения)

---

/или куратор Уильям Ф. Тренч.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Глава

   Автор

   Уильям Ф. Тренч

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   3,0

   Показать страницу TOC

   да

2. Теги

   1. источник[1]-math-9424

COMP 200 и COMP 130

Система общего назначения

Примечание :  COMP 130 студентов НЕ должны знать, как сделать частичное методы дифференциальных уравнений, используемые в следующих выводах! Здесь важно увидеть форма математического результаты и иметь возможность использовать эти результаты. Выводы представлены просто для полноты и строгости.

Рассмотрим следующий обобщенный связанный дифференциал уравнение с участием x и y , где оба являются функциями времени и связаны двумя связями первого порядка функции, 𝜳 и 𝜱:

Эти уравнения первого порядка того типа, которые использовались для создания нашего существующий алгоритм Лотки-Вольтерра первого порядка:  

( т ₀ нижний индекс относится к значению этой производной или функции, оцениваемой в момент времени t ₀ .)  

Но уточнить это приближении, нам нужно вычислить вторые производные по времени с использованием частичного дифференциация:

Подставим исходные уравнения обратно в:

Расширение ряда Тейлора второго порядка из х(т) и у(т) около времени т ₀ таким образом:

Обратите внимание, что симметрия в  𝜳 и 𝜱 это было присутствующий в наших исходных парных производных выше, отражается в здесь мы имеем разложение в ряд Тейлора второго порядка.

Также обратите внимание, что в действительности представлено только 8 различных величин. приведенный выше результат:

• (2) Текущие значения х и у (т.е. оценивается в т ₀ )
• (2) Текущие значения 𝜳 и 𝜱 (т.е. оценивается в т ₀ )
• (4) Текущие значения производных от 𝜳 и 𝜱 с уважать x и у , оценивается в т ₀ .

Таким образом, для расчета следующего временного шага в х и у кривых со вторым порядком точности, так как нам заданы текущие ценности х и у , чтобы вычислить следующие значения, нам нужно только вычислить не более 6 отдельные количества.

 

2

^nd Заказать Модель Лотки-Вольтерры

В уравнении Лотки-Вольтерры для моделирование хищник-жертва, уравнения связи

Здесь х(т) это популяция добычи и y(t) — хищник населения и, таким образом, переменные определяются как:

Для выполнения расчета 2 ^-й -й порядок расширения ряда Тейлора четыре части должны быть рассчитано:

Вооружившись 4 расчетами выше плюс 2 расчетами для 𝜳 и 𝜱, которые производные первого порядка по времени для популяций жертвы и хищника соответственно один теперь можно построить ряд результатов Тейлора 2 ^и порядка для зайца и популяции рысей в соответствии с уравнениями из последнего раздела выше.

Следующий уровень?

Рассмотрим следующие понятия: 

• Если кривая, которую мы пытаемся аппроксимировать, представляет собой прямую линию, то Решение 2-го порядка невыгодно, потому что вторая производная всегда ноль.
• Вторая производная или, в более общем смысле, следующая более высокая производная всегда гораздо сложнее вычислить.
• Но если размер шага достаточно мал, всегда можно уменьшить погрешность до сколь угодно малого уровня.
• Равномерно маленькие шаги значительно увеличивают количество вычислений требуется.

Но почему бы нам просто не использовать маленькие размеры шага только там, где это необходимо ? Грубо говоря, если мы делаем приближение первого порядка, чем больше второе производная, тем меньше размер шага.

Эти методы сортировки называются методами «адаптивного размера шага». Примеры адаптивных решателей ступенчатых дифференциальных уравнений:

• Адаптивные методы Рунге-Кутты
• Метод Рунге-Кутта-Фельберга

К сожалению, они выходят за рамки этого класса. Пройдите курс CAAM (например, CAAM 353), чтобы узнать больше.

Больше эффектов?

Давайте продолжим и исследуем добавление некоторых новых эффектов к Модель Лотки-Вольтерры, такая как ограниченная пропускная способность окружающей среды, это означает, что животные могут умереть от голода, если их популяция станет слишком высокий:   Prey Голод в Лотка-Вольтерра

Эволюция нерастяжимых и упругих кривых с зажатыми концами по эволюционному уравнению второго порядка в ℝ2

Открытый доступ Опубликовано 24 марта 2018 г.

Chun-Chi Lin and Yang-Kai Lue

Из журнала Geometric Flows

https://doi. org/10.1515/geofl-2018-0002

Для любого заданного C ² — гладкая начальная открытая кривая с фиксированным положением и фиксированной касательной в граничных точках получаем длительное существование гладких решений при эволюции второго порядка плоских кривых. Более того, асимптотический предел сходящейся подпоследовательности является нерастяжимой эластикой.

Ключевые слова: параболическое уравнение второго порядка; зажатое граничное условие; Уиллмор функциональный; плоские кривые

MSC 2010: 35B65; 35К51; 53А04; 53C44

Ссылки

[1] Сигурд Ангенент. О формировании особенностей течения укорочения кривой. J. Diff erential Geom., 33(3):601-633, 1991.10.4310/jdg/1214446558Search in Google Scholar

[2] Анна Далл’Аква, Чун-Чи Лин и Паола Поцци. Эволюция открытых упругих кривых в Rn при фиксированной длине и естественных граничных условиях. Анализ (Берлин), 34(2):209-222, 2014.10.1515/anly-2014-1249Поиск в Google Scholar

[3] Анна Далл’Аква, Чун-Чи Лин и Паола Поцци. Градиентный поток для открытых упругих кривых с фиксированной длиной и зажатыми концами. Анна. SNS Pisa (5), 17:1031-1066, 2017.10.2422/2036-2145.201511_009Поиск в Google Scholar

[4] Анна Далл’Аква и Паола Поцци. L2-поток Уиллмора-Хелфриха кривых с естественными граничными условиями. Комм. Анальный. Geom., 22(4):617-669, 2014.10.4310/CAG.2014.v22.n4.a2Search in Google Scholar

[5] Gerhard Dziuk, Ernst Kuwert, and Reiner Schätzle. Эволюция упругих кривых в Rn: существование и вычисление. СИАМ Дж. Матем. Anal., 33(5):1228-1245 (электронный), 2002.10.1137/S0036141001383709Поиск в Google Scholar

[6] Норихито Койсо. О движении кривой к эластике. В Actes de la Table Ronde de Géométrie Diff érentielle (Luminy, 1992), том 1 Sémin. Congr., стр. 403-436. соц. Мат. Франция, Париж, 1996. Поиск в Google Scholar

[7] Chun-Chi Lin. L2-поток упругих кривых с зажатыми граничными условиями. J. Diff erential Equations, 252(12):6414-6428, 2012.10.1016/j.jde.2012.03.010Search in Google Scholar

[8] Chun-Chi Lin and Yang-Kai Lue. Эволюция нерастяжимой и упругой кривых с защемленными концами по эволюционному уравнению второго порядка в R2. Препринт 2017. Поиск в Google Scholar

[9] Чун-Чи Лин, Ян-Кай Лю и Хартмут Р. Шветлик. L2-поток второго порядка нерастяжимых упругих кривых с шарнирно закрепленными концами на плоскости. J. Elast, 119(2):263-291, 2015.10.1007/s10659-015-9518-5Поиск в Google Scholar

[10] Маттео Новага и Шинья Окабе. Поток укорочения-выпрямления кривых для незамкнутых плоских кривых бесконечной длины. J. Diff erential Equations, 256(3):1093-1132, 2014.10.1016/j.jde.2013.10.009Search in Google Scholar

[11] Александр Полден. Кривые и поверхности наименьшей полной кривизны и течения четвертого порядка. Кандидатская диссертация, Тюбингенский университет, 1996.Поиск в Google Scholar

[12] Yingzhong Wen. l2 поток выпрямления кривой в плоскости. Герцог Математика. J., 70(3):683-698, 1993.10.1215/S0012-7094-93-07016-0Поиск в Google Scholar

[13] Yingzhong Wen. Поток выпрямления кривых деформирует замкнутые плоские кривые с ненулевым числом вращения в окружности. J. Diff erential Equations, 120(1):89-107, 1995.10.1006/jdeq.1995.1106Поиск в Google Scholar

Получено: 2017-9-15

Принято: -91-2017 030170038

Опубликовано в Интернете: 24 марта 2018 г.

© 2018

Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 License.

Статья Эволюция нерастяжимых и упругих кривых с зажатыми концами по эволюционному уравнению второго порядка в ℝ

²

Chun-Chi Lin, Yang-Kai Lue 2018

• МДА
• АПА
• Гарвард
• Чикаго
• Ванкувер

Лин, Чун-Чи и Лу, Ян-Кай.

No related posts.