Как число умножить на матрицу: определение, свойства и примеры решения задач

Произведение матрицы на число | это… Что такое Произведение матрицы на число?

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.

Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.

Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями «||…||»).

Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.

У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов.

Содержание 1 История 2 Матрица как запись коэффициентов системы линейных уравнений 3 Операции над матрицами 4 Квадратная матрица и смежные определения 5 Свойства матриц 6 Элементарные преобразования матриц 7 Типы матриц 8 Матрица линейного оператора 9 См. также 10 Литература 11 Ссылки

История

Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.

Матрица как запись коэффициентов системы линейных уравнений

Систему из m уравнений с n неизвестными

можно представить в матричном виде

и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_i

j системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{— 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{— 1}AX = A ^{— 1}B

A ^{− 1}A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{— 1}B.

Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.

Операции над матрицами

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число λ (обозначение: λA

) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

c_ij = a_ij + b_ij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

c_ij = a_ij — b_ij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

cij =	∑	aikbkj
	k

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения

AB = C есть . Умножение матриц не коммутативно.

Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A — матрица размера , то A^T — матрица размера

Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = A

E = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A ^{— 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

AA ^{− 1} = E

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

Свойства матриц

1. A + (B + C) = (A + B) + C
2. A + B = B + A
3. A(BC) = (AB)C
4. A(B + C) = AB + AC
5. (B + C)A = BA + CA
9. (A^T)^T = A
10. (A * B)^T = B^T * A^T

Элементарные преобразования матриц

Основная статья: Элементарные преобразования матрицы

Элементарными преобразованиями строк матрицы называются следующие преобразования:

1. Умножение строки на число отличное от нуля
2. Прибавление одной строки к другой строке

Элементарные преобразование столбцов матрицы определяются аналогично.

Типы матриц

• Антиперестановочная: AB = − BA
• Единичная
• Блочно-диагональная
• Ганкелева
• Верхнетреугольная
• Вырожденная
• Диагональная
  • Трёхдиагональная
• Заполненная — в вычислительной математике матрица, которая практически не содержит нулей. Такую матрицу приходится хранить в памяти целиком. Антоним: разреженная.
• Квадратной называют матрицу, количество строк в которой равно количеству столбцов. Для квадратных матриц существует определитель.
• Кососимметрическая
• Нижнетреугольная
• Нормальная
• Нулевая
• Ортогональная
• Перестановочная: AB = BA
• Разреженная — в вычислительной математике матрица, содержащая много нулей. Организовав подходящую структуру данных, вычисления с разреженными матрицами можно проводить очень быстро. Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная.
• Симметричная
  1. Симметричная матрица A положительно определена (A > 0), если значения у всех ее главных угловых миноров A_k > 0
  2. Симметричная матрица A отрицательно определена (A < 0), если матрица ( − A) положительно определена, то есть если для любого k главный минор k-го порядка A_k имеет знак ( − 1)^k
• Теплицева
• Треугольная
• Эрмитова
• Циркулянт
• Унитарная
• Унимодулярная

Матрица линейного оператора

Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Выберем базис . Пусть  — произвольный вектор. Тогда его можно разложить по этому базису:

,

где x^k — координаты вектора в выбранном базисе.

Здесь и далее предполагается суммирование по немым индексам.

Пусть  — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим

.

Вектора также разложим в выбранном базисе, получим

,

где  — j-я координата k-го вектора из .

Подставим разложение в предыдущую формулу, получим

.

Выражение , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица при умножении на столбец x^k даёт в результате координаты вектора , возникшего от действия оператора на вектор , что и требовалось получить.

См. также

• Норма матрицы
• Определитель матрицы
• Массив — тип данных в программировании, соответствующий многомерной матрице.
• Разрежённый массив — компьютерная форма представления матриц со множеством нулей.
• Линейные матричные неравенства — аппарат для решения задач синтеза законов управления.

Литература

• Дж. Голуб, Ч.Ван Лоун Матричные вычисления. — М.: Мир, 1999 (djvu).
• Беллман Р. Введение в теорию матриц. — М.: Мир, 1969 (djvu).
• Гантмахер Ф. Р. Теория матриц (2-е издание). — М.: Наука, 1966 (djvu).
• Ланкастер П. Теория матриц. — М.: Наука, 1973 (djvu).
• Соколов Н. П. Пространственные матрицы и их приложения. — М.: ГИФМЛ, 1960 (djvu).

Ссылки

• Операции над матрицами онлайн

Как умножать матрицы? — GeeksforGeeks

Знание матриц необходимо для различных разделов математики. Матрицы — один из самых мощных инструментов в математике. В линейной алгебре умножение матриц — это одна из бинарных операций, которые можно выполнять над матрицами. Умножение любых двух матриц A и B возможно только в том случае, если обе матрицы совместимы. «Матрица» — это прямоугольный массив чисел, расположенных в строках и столбцах. Горизонтальные линии называются строками, а вертикальные — столбцами. Если матрица имеет «m» строк и «n» столбцов, то говорят, что это матрица «m на n» и записывается как матрица «m × n». Мы можем выполнять различные бинарные операции с матрицами, такие как сложение, вычитание, умножение и т. д. В этой статье мы подробно узнаем об умножении матриц.

Умножение матриц

Умножение матриц — очень простая вещь в математике. Если умножать на число, то просто умножайте число на все элементы, присутствующие в матрице. Но если мы умножим матрицу на другую матрицу, то должны увидеть некоторые правила. Умножение любых двух матриц дает одну матрицу, а это возможно только в том случае, если количество столбцов в 1-й матрице равно количеству строк во 2-й матрице. Если «A = [a _ij ] _m×n » и «B = [b _ij ] _n×p » — две матрицы, то произведение A и B обозначается как AB, порядок которых равен «m × p». Обычно умножение матриц не является коммутативным, т. е. AB ≠ BA, или, проще говоря, произведение матриц A и B равно AB, но не BA.

Условия умножения матриц

Обратите внимание, что умножение любых двух матриц возможно только в том случае, если обе матрицы совместимы. Мы можем перемножить две матрицы, если количество столбцов в 1-й матрице равно количеству строк во 2-й матрице, иначе данные матрицы нельзя перемножить.

1. Допустим, есть матрица размера 2×3 и другая матрица размера 3×2, тогда мы можем применить умножение между этими матрицами, потому что количество столбцов и строк одинаково в обеих матрицах. И результирующая матрица будет 2×2
2. . Допустим, матрица размера 3×3 и другая матрица размера 4×2, тогда мы не можем применить умножение между этими матрицами, потому что количество столбцов и строк не то же самое в обе матрицы.

Умножение матриц на матрицы

Рассмотрим две матрицы 3 × 3, содержащие элементы [a _ij ] и [b _ij ] соответственно. Умножение будет таким, как показано на рисунке ниже:

Существует некоторое правило,

1. Возьмите 1-ю строку первой матрицы и умножьте значения на 1-й столбец второй матрицы. Не умножайте строки на строки или столбцы на столбцы.
2. В первой итерации умножьте значение строки на значение столбца и просуммируйте эти значения. Вот на этой картинке [a ₀₀ ] умножается на [b ₀₀ ], то 2-е значение 1-го столбца 1-й матрицы [a ₁₀ ] умножается на 2-е значение 1-й строки 2-й матрицы [b ₀₁ ]. Точно так же все значения умножаются.
3. Затем после одной итерации все производственные значения суммируются и размещаются как элементы результирующей матрицы, как показано на рисунке.

Матрица Формула умножения для матриц «2 × 2»

Процесс умножения одинаков для матриц любого порядка. Мы должны умножить каждый элемент каждой строки первой матрицы на элементы каждого столбца второй матрицы и сложить все произведения, чтобы получить результирующую матрицу. Рассмотрим две матрицы «2 × 2» матрицы A и B.

Матрица Формула умножения для матриц «3 × 3»

Рассмотрим две матрицы «3 × 3» матрицы P и Q. Теперь формула умножения матриц для матриц «3 × 3» показаны следующим образом:

Пример: Перемножьте приведенные ниже матрицы.

Решение:

Умножение матрицы на скалярное значение

Матрица может быть умножена на скалярное значение, что называется скалярным умножением, а также на матрицу, что называется умножением матриц. Скалярное умножение — это умножение матрицы на скалярное значение. Когда матрица «A = [a _ij ]» умножается на скалярное значение «k», каждый элемент данной матрицы умножается на скалярное значение. Результирующая матрица выражается как kA, где kA = k[a _ij ] = [ka _ij ], для всех значений i и j.

Пример:

Свойства умножения матриц

Ниже приведены некоторые важные свойства мультипликации матриц:

• Коммуративное свойство: . Матиат. Если A и B — две матрицы, то AB ≠ BA.
• Ассоциативное свойство: Умножение матриц по своей природе ассоциативно. Если A, B и C — три матрицы, то A(BC) = (AB)C, если произведения A(BC) и (AB)C определены.
• Распределительное свойство: Если A, B и C — три матрицы, то, применяя распределительное свойство, мы получаем A (B + C) = AB + BC, если и только если A, B и C совместимы .
• Произведение со скаляром: Если A и B — две матрицы и AB определено, то k(AB) = (kA)B = A(Bk), где k — скалярное значение.
• Определитель: Если A и B — две матрицы и AB определено, то определитель матрицы «AB» равен произведению определителей матриц A и B, т. е. det (AB) = det A × дет Б.
• Транспонирование: Если A и B — две матрицы и AB определено, то (AB)T = BTAT, где T представляет собой транспонирование матрицы.
• Комплексное сопряжение: Если A и B две комплексные матрицы, то (AB)* = B*A*.
  Произведение любых двух ненулевых матриц может дать нулевую матрицу, т. е. если AB = O, то это не означает, что A = O или B = O.

Решенные примеры

Пример 1. Пусть и найти A×B?

Решение:

 

Пример 2. Пусть  и . Найти А×В?

Решение:

Пример 3. Пусть   ,   и . Найти (AB + AC)?

Решение:

Теперь рассчитайте (AB + AC)

9003

Пример 4.

.0082 Пусть  , и , тогда найдите значение p?

Solution:

First, calculate A ² ,

Given 

By placing the value of A ² in the equation, we get

Теперь мы можем написать:

8 = 2p и -8 = -2p

Итак, p = 4

Значение p равно 4.

Пример 5. Найдите значение 3P, если  .

Решение:

Часто задаваемые вопросы по умножению матриц

Вопрос 1: Что такое умножение матриц?

Ответ:

В линейной алгебре умножение матриц — это одна из бинарных операций, которые можно выполнять над матрицами. Умножение любых двух матриц возможно только тогда, когда количество столбцов в первой матрице равно количеству строк во второй матрице.

Вопрос 2: Можно ли матрицу «3 × 2» умножить на матрицу «3 × 3»?

Ответ:

Умножение любых двух матриц возможно только тогда, когда количество столбцов в первой матрице равно количеству строк во второй матрице. Здесь первая матрица имеет 2 столбца, а вторая матрица имеет 3 строки. Таким образом, матрицу «3 × 2» нельзя умножить на матрицу «3 × 3», поскольку обе они несовместимы.

Вопрос 3: Как мы можем перемножить две матрицы?

Ответ:

Перед умножением данных матриц нам нужно проверить, равно ли количество столбцов в первой матрице количеству строк во второй матрице. Если матрицы удовлетворяют указанному выше требованию, то умножьте каждый элемент каждой строки первой матрицы на элементы каждого столбца второй матрицы и сложите все произведения.

Умножение матриц Excel | Топ 2 Метод

В Excel есть встроенная функция умножения матриц. Это функция МУЛЬТИМЕТР. Он принимает два массива в качестве аргумента и возвращает произведение двух массивов, учитывая, что оба массива должны иметь одинаковое количество строк и столбцов.

Содержание

• Что такое умножение матриц в Excel?
  • Объяснение
  • Синтаксис
  • Как выполнить умножение матриц в Excel? (с примерами)
    • Пример №1 – Умножение матрицы на скалярное число.
    • Пример №2. Умножение матриц двух отдельных массивов
    • Пример №3
    • Пример №4. Умножение матриц между массивами с одним столбцом и одной строкой
    • Пример №5. Определение квадрата матрицы с помощью MMULT в ExcelMMULT В ExcelMMULT встроена функция математики и тригонометрии в Excel, которая выполняет матричное умножение двух массивов, где столбцы массива 1 эквивалентны строкам массива 2. читать далее
  • Что нужно помнить
  • Рекомендуемые статьи

Объяснение

Умножение матриц — одна из полезных функций excelПолезные функции ExcelГлавные функции MS excel: сочетания клавиш, суммирование значений, фильтрация данных, специальная вставка, вставка случайные числа, инструмент анализа поиска цели, вставка серийных номеров и т. д. читать далее представлены для выполнения математических операций. Это помогает получить произведение двух матриц. Матрицы, которые нужно умножить, имеют определенное количество строк и столбцов для представления данных. Результирующий размер матрицы берется из количества строк первого массива и количества столбцов второго массива. Однако есть условие умножения матриц. Количество столбцов в первой матрице должно равняться количеству строк во второй матрице.

Предопределенная функция МУМНОЖ, представленная в программе Excel, используется для выполнения матричного умножения. Умножение матриц в Excel сокращает много времени, затрачиваемого на ручное вычисление произведения матриц.

В общем, мы можем выполнять умножение матриц двумя способами. Во-первых, выполняется простое скалярное умножение с использованием основных арифметических операций. Во-вторых, расширенное умножение матриц управляется с помощью функции массива в excelArray. Функция ExcelArray – чрезвычайно полезные и мощные формулы, которые используются в Excel для выполнения некоторых из самых сложных вычислений. Существует два типа формул массива: один возвращает один результат, а другой возвращает несколько результатов.Подробнее.

Формула Excel, используемая для умноженияФормула Excel, используемая для умноженияУмножение в Excel выполняется путем ввода оператора сравнения «равно» (=), за которым следует первое число, «звездочка» (*) и второе число.Подробнее вводится двумя способами, включая ввод вручную функции МУМНОЖ после знака равенства или выбор библиотеки математических и триггерных функций, представленной на вкладке «Формулы». Математическая функция МУМНОЖ помогает вернуть произведение двух массивов. Это одна из предопределенных функций ExcelФункции ExcelФункции Excel помогают пользователям экономить время и вести обширные рабочие листы. Существует более 100 функций Excel, классифицированных как финансовые, логические, текстовые, даты и время, функции поиска и справки, математические, статистические и информационные функции. Подробнее, используемые в рабочих листах для выполнения вычислений за короткое время..

Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Excel Matrix Multiplication (wallstreetmojo.com)

Синтаксис

Необходимый синтаксис, которому мы должны следовать для умножения матриц:

• Параметры: Массив1 и массив2 — это два обязательных параметра для выполнения умножения.
• Правило: Столбцы массива1 должны быть равны строкам массива2, а размер произведения должен быть равен количеству строк в массиве1 и количеству столбцов в массиве2.
• Возвраты: Функция МУМНОЖ генерирует числа в матрице произведения. Он вставляется как формула или функция рабочего листа в расчеты Excel.

Давайте рассмотрим изображение ниже.

Тогда произведение A*B будет следующим:

Как выполнить умножение матриц в Excel? (с примерами)

Умножение матриц в Excel имеет некоторые приложения реального времени. Существует два способа умножения матриц. Ниже приведены некоторые примеры умножения матриц в Excel.

Вы можете скачать этот шаблон Excel для умножения матриц здесь — Шаблон Excel для умножения матриц

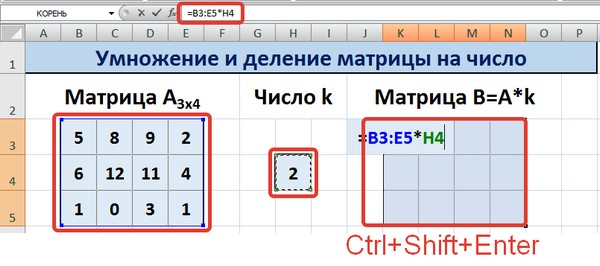
Пример № 1 — Умножение матрицы на скалярное число.

Начнем.

1. Во-первых, мы должны ввести данные в массив.

   
   

2. Затем мы должны выбрать скалярное значение, которое нам нужно умножить на массив, т. е. 3.

   
   

3. Оценить строки и столбцы результирующего массива. Здесь результирующий массив будет размером 3 х 3.
4. После этого мы должны выбрать диапазон ячеек, равный размеру результирующего массива, чтобы разместить результат и ввести нормальную формулу умножения.

   
   

5. При вводе формулы мы должны нажать Ctrl + Shift + Enter. Следовательно, будет получен результат, как показано ниже.

   
   

Пример #2. Умножение матриц двух отдельных массивов

• Шаг 1: Сначала мы должны ввести данные в массив A размером 3×3.

• Шаг 2:  Затем вставьте данные во второй массив с именем B размером 3 × 3.

• Шаг 3: Нам нужно убедиться, что столбцы первого массива имеют тот же размер, что и строки второго массива.
• Шаг 4: Оценка строк и столбцовСтроки и столбцыЯчейка представляет собой пересечение строк и столбцов. Строки и столбцы составляют программное обеспечение, которое называется Excel. Область рабочего листа Excel разделена на строки и столбцы, и в любой момент времени, если мы хотим сослаться на определенное место этой области, нам нужно сослаться на ячейку. Подробнее о результирующем массиве.
• Шаг 5: Выберите диапазон ячеек, равный размеру результирующего массива, чтобы поместить результат, и введите формулу умножения МУМНОЖ.

Далее мы должны вставить значения для расчета произведения A и B.

После того, как мы введем формулу, нажмите Ctrl + Shift + Enter , чтобы получить результат. Результаты, которые мы можем получить путем умножения двух массивов, следующие. Размер результирующего массива 3X3.

Пример #3

Умножение матриц между массивами с одной строкой и одним столбцом. Рассмотрим элементы матриц следующим образом:

Матрица A имеет размер 1×3, а матрица B имеет размер 3×1. Таким образом, размер матрицы продукта A * B [AB] равен 1 × 1. Итак, теперь мы должны вставить в ячейку формулу умножения матриц.

Нажмите клавишу «Ввод», чтобы получить результат.

Пример №4. Умножение матриц между массивами с одним столбцом и одной строкой

Матрица A имеет размер 3×1, а матрица B — 1×3. Размер произведения A*Матрица B [AB] равна 3×3.

Таким образом, ответ будет таким:

Пример 5. Определение квадрата матрицы с помощью MMULT в ExcelMMULT В ExcelMMULT — это встроенная функция математики и тригонометрии в Excel, которая выполняет матричное умножение двух массивов, где столбцы массива 1 эквивалентны строкам массива 2. читать далее

Квадрат матрицы A определяется путем умножения A на A.

Результирующая матрица получается как:

Что нужно помнить

• Количество столбцов в массиве1 и количество строк в массиве2 должны быть равны выполнить умножение матриц.
• Трудно изменить часть массива, так как массив представляет собой группу элементов.
• При выполнении умножения массива следует использовать CTRL+SHIFT+ENTER для получения всех элементов результирующей матрицы.

  No related posts.