Как делить двоичные числа столбиком
Для записи чисел в двоичной системе используются цифры 0 и 1. В таблице представлены целые числа записанные в двоичной системе счисления:. Для записи чисел в восьмеричной системе используются цифры от 0 до 7. В таблице представлены целые числа записанные в восьмеричной системе счисления:. Процесс преобразования в восьмеричную систему счисления аналогичен преобразованию в двоичную системы, изменяется только основание системы счисления, число на которое мы делим.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- 1.
15 Деление двоичных чисел
- Деление в двоичной системе счисления
- СЦЕНАРИЙ ВИДЕО-УРОКА «СИСТЕМЫ СЧИСЛЕНИЯ. ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (IV)»
- Please turn JavaScript on and reload the page.
- Количество информации. Основы логики: Методическое пособие
- Умножение двоичных чисел
- деление двоичных чисел столбиком
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Деление столбиком целых чисел — математика — all-audio.pro
1.15 Деление двоичных чисел
Подробное, пошаговое, решение задачи деления целых двоичных чисел прямо на сайте в режиме OnLine.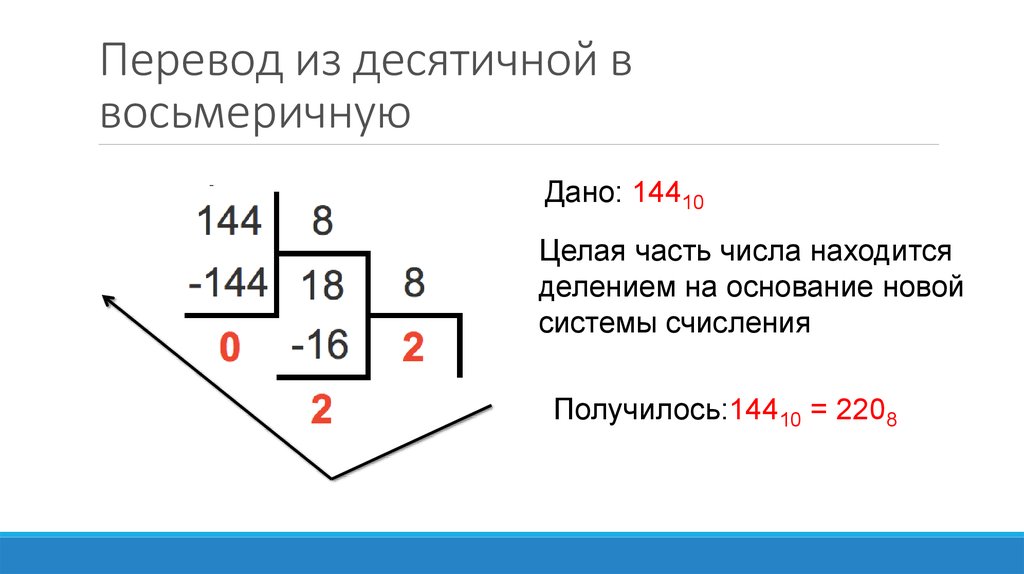
Перед умножением все числа будут переведены в двоичную ситему автоматически. Обратите внимание! Здесь будет показан машинный метод деления двоичных чисел — метод без восстановления остатка. Он используется в процессорах и других вычислительных устройствах. При этом у вас есть возможность выбрать разрядность арифметико-логического устройства разрядную сетку.
На этом шаге выберите, из выпадающего списка ниже, систему счисления, в которой вы будете вводить делимое и делитель, величину разряднойй сетки разрядность регистров сомножителей , и нажмите кнопку «Дальше». Если вы затрудняетесь с выбором разрядной сетки, то оставьте значение «Авто». Деление двоичных чисел OnLine с решением, бесплатно: машинный метод ШАГ-1, Выбор системы счисления и разрядной сетки Подробное, пошаговое, решение задачи деления целых двоичных чисел прямо на сайте в режиме OnLine.
Система счисления исходных операндов : Двоичная Восьмеричная Десятичная Шестнадцатеричная Разрядная сетка : Авто 8 — бит 16 — бит 24 — бит 32 — бит Поделитесь информацией с друзьями «В Контакте «, «Одноклассниках» и т. Copyright www. E-mail: mail reshinfo. Двоичная Восьмеричная Десятичная Шестнадцатеричная.
Деление в двоичной системе счисления
Дистанционное обучение. Тестирование on-line. Зачетная книжка. Вход для.
Для записи чисел в двоичной системе используются цифры 0 и 1. В таблице представлены целые числа записанные в двоичной системе счисления.
СЦЕНАРИЙ ВИДЕО-УРОКА «СИСТЕМЫ СЧИСЛЕНИЯ. ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (IV)»
Деление в двоичной системе Помогите пожалуйста поделить на , желательно с алгоритмом Помогите решить. Просьба расписать по действиям. Деление чисел в восьмеричной системе счисления Ребята, кто разбирается , help me! Разделите 22 в восьмеричной системе счисления на 15 в Как компьютер переводит из двоичной в десятичную систему счисления? Возможно вопрос поймут неправильно. Бинарная система счисления — деление Добрый вечер!
Бинарная система счисления — деление Добрый вечер!
Please turn JavaScript on and reload the page.
Арифметические действия в двоичной системе производятся по обычным для позиционных систем правилам, которые нам известны из десятичной арифметики, но при этом используются таблицы сложения и умножения двоичной системы:. Таблица сложения в двоичной системе очень проста. Надо только помнить, что прибавление нуля не меняет число, а один плюс один, будет два. Таблица умножения ещё проще.
Подробное, пошаговое, решение задачи деления целых двоичных чисел прямо на сайте в режиме OnLine.
Количество информации. Основы логики: Методическое пособие
На прошлом уроке мы научились складывать и вычитать двоичные числа. Сейчас мы с Вами рассмотрим их умножение и деление. Так же, как и в предыдущих уроках, правильность полученного результата мы будем проверять в десятичной системе счисления. Итак, начнем с умножения двоичных чисел. Для начала рассмотрим следующую простую таблицу, которая используется для этого.
Умножение двоичных чисел
Вход Регистрация. Поиск по сайту. Учебные заведения. Проверочные работы. Отправить отзыв. Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам. Эти правила применимы и ко всем другим позиционным системам счисления.
Вы искали деление двоичных чисел столбиком? двоичные числа,как делить двоичные числа столбиком,как делить столбиком двоичные числа.
деление двоичных чисел столбиком
Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт. Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор. Калькулятор справочный портал.
Информация от лат. Informatio — разъяснение, изложение — одно из основных понятий науки. Наряду с такими понятиями, как вещество, энергия, пространство и время, оно составляет основу современной научной картины мира. В просторечии может употребляться как синоним слова сообщение.
Привет, посетитель сайта ZametkiNaPolyah.
Компьютерные сети Системное программное обеспечение Информационные технологии Программирование. Все о программировании Обучение Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации Главная Тексты статей Добавить статьи Контакты Арифметические операции в двоичной системе.
В этой статье: Деление в столбик Дополнения 10 Источники. Двоичные числа можно делить в столбик, чтобы лучше понять сам процесс или написать простую компьютерную программу. Также можно применить метод дополнений, который довольно редко используется в программировании. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 25 человек а.
Двоичная система счисления
Содержание:
Что такое двоичная система счисления
Как перевести целое десятичное число в двоичную систему счисления
Как перевести десятичную дробь в двоичную систему счисления
Как перевести число из двоичной системы счисления в десятичную
Как перевести дробное двоичное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в двоичной системе счисления
Двоичная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа.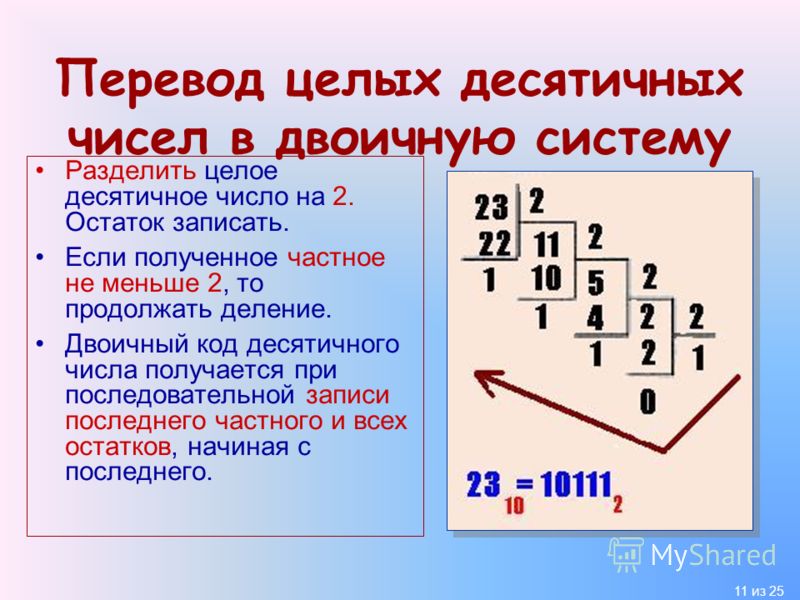
Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в двоичную систему счисления
Для того, чтобы перевести целое десятичное число в двоичную систему счисления нужно десятичное число делить на 2 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
Например, переведем число 17310 в двоичную систему счисления:
173 : 2 = 86 остаток: 1
86 : 2 = 43 остаток: 0
43 : 2 = 21 остаток: 1
21 : 2 = 10 остаток: 1
10 : 2 = 5 остаток: 0
5 : 2 = 2 остаток: 1
2 : 2 = 1 остаток: 0
1 : 2 = 0 остаток: 1
17310 = 101011012
Как перевести десятичную дробь в двоичную систему счисления
Для того чтобы перевести десятичную дробь в двоичную систему счисления необходимо сначала перевести целую часть десятичной дроби в двоичную систему счисления,
а затем дробную часть, последовательно умножать на 2, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число)
или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Например, переведем десятичное число 5.7410 в двоичную систему счисления:
Переведем целую часть
5 : 2 = 2 остаток: 1
2 : 2 = 1 остаток: 0
1 : 2 = 0 остаток: 1
510 = 1012
Переведем дробную часть
0.74 · 2 = 1.48
0.48 · 2 = 0.96
0.96 · 2 = 1.92
0.92 · 2 = 1.84
0.84 · 2 = 1.68
0.68 · 2 = 1.36
0.36 · 2 = 0.72
0.72 · 2 = 1.44
0.44 · 2 = 0.88
0.88 · 2 = 1.76
0.7410 = 0.10111101012
5.7410 = 101.10111101012
Двоичные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной двоичной.
Как перевести число из двоичной системы счисления в десятичную
Для того, чтобы перевести число из двоичной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля.
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число на 2 в
степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
| Позиция в числе | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Число | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
101011012 = 1 ⋅ 27 + 0 ⋅ 26 + 1 ⋅ 25 + 0 ⋅ 24 + 1 ⋅ 23 + 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 20 = 17310
Как перевести дробное двоичное число в десятичное
Для того, чтобы перевести дробное двоичное число в десятичное, необходимо записать дробное двоичное число, убрав точку и затем сверху расставить индексы.
Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число на
2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Каждая позиция цифры (индекс) будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число на
2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем дробное двоичное число 110.101 в десятичное:
| Позиция в числе | 2 | 1 | 0 | -1 | -2 | -3 |
| Число | 1 | 1 | 0 | 1 | 0 | 1 |
110.1012 = 1 ⋅ 22 + 1 ⋅ 21 + 0 ⋅ 20 + 1 ⋅ 2-1 + 0 ⋅ 2-2 + 1 ⋅ 2-3 = 6.62510
Таблица значений десятичных чисел от 0 до 100 в двоичной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в двоичной системе счисления |
| 010 | 02 |
| 110 | 12 |
| 210 | 102 |
| 310 | 112 |
| 410 | 1002 |
| 510 | 1012 |
| 610 | 1102 |
| 710 | 1112 |
| 810 | 10002 |
| 910 | 10012 |
| 1010 | 10102 |
| 1110 | 10112 |
| 1210 | 11002 |
| 1310 | 11012 |
| 1410 | 11102 |
| 1510 | 11112 |
| 1610 | 100002 |
| 1710 | 100012 |
| 1810 | 100102 |
| 1910 | 100112 |
| 2010 | 101002 |
| 2110 | 101012 |
| 2210 | 101102 |
| 2310 | 101112 |
| 2410 | 110002 |
| 2510 | 110012 |
| 2610 | 110102 |
| 2710 | 110112 |
| 2810 | 111002 |
| 2910 | 111012 |
| 3010 | 111102 |
| 3110 | 111112 |
| 3210 | 1000002 |
| 3310 | 1000012 |
| 3410 | 1000102 |
| 3510 | 1000112 |
| 3610 | 1001002 |
| 3710 | 1001012 |
| 3810 | 1001102 |
| 3910 | 1001112 |
| 4010 | 1010002 |
| 4110 | 1010012 |
| 4210 | 1010102 |
| 4310 | 1010112 |
| 4410 | 1011002 |
| 4510 | 1011012 |
| 4610 | 1011102 |
| 4710 | 1011112 |
| 4810 | 1100002 |
| 4910 | 1100012 |
| 5010 | 1100102 |
| Значение числа в десятичной системе счисления | Значение числа в двоичной системе счисления |
| 5110 | 1100112 |
| 5210 | 1101002 |
| 5310 | 1101012 |
| 5410 | 1101102 |
| 5510 | 1101112 |
| 5610 | 1110002 |
| 5710 | 1110012 |
| 5810 | 1110102 |
| 5910 | 1110112 |
| 6010 | 1111002 |
| 6110 | 1111012 |
| 6210 | 1111102 |
| 6310 | 1111112 |
| 6410 | 10000002 |
| 6510 | 10000012 |
| 6610 | 10000102 |
| 6710 | 10000112 |
| 6810 | 10001002 |
| 6910 | 10001012 |
| 7010 | 10001102 |
| 7110 | 10001112 |
| 7210 | 10010002 |
| 7310 | 10010012 |
| 7410 | 10010102 |
| 7510 | 10010112 |
| 7610 | 10011002 |
| 7710 | 10011012 |
| 7810 | 10011102 |
| 7910 | 10011112 |
| 8010 | 10100002 |
| 8110 | 10100012 |
| 8210 | 10100102 |
| 8310 | 10100112 |
| 8410 | 10101002 |
| 8510 | 10101012 |
| 8610 | 10101102 |
| 8710 | 10101112 |
| 8810 | 10110002 |
| 8910 | 10110012 |
| 9010 | 10110102 |
| 9110 | 10110112 |
| 9210 | 10111002 |
| 9310 | 10111012 |
| 9410 | 10111102 |
| 9510 | 10111112 |
| 9610 | 11000002 |
| 9710 | 11000012 |
| 9810 | 11000102 |
| 9910 | 11000112 |
| 10010 | 11001002 |
Калькулятор двоичного деления
Создано Филиппом Маусом
Отзыв Стивена Вудинга
Последнее обновление: 13 декабря 2022 г.
- Как делить двоичные числа?
- Каковы правила двоичного деления?
- Как рассчитать остаток от деления?
- Как выполнить двоичное деление для отрицательных значений?
- Как использовать калькулятор двоичного деления?
- Часто задаваемые вопросы
Калькулятор двоичного деления поясняет как делить двоичные числа . В этой статье изложены концепции двоичных и десятичных чисел и , а также даны пошаговые инструкции для выполнения деления двоичных чисел .
Как разделить двоичные числа?
С самого раннего возраста нас всех учат знакомиться с десятичной системой, числами по основанию. Мы умеем их понимать и выполнять с ними арифметические операции. Но вся коммуникация в нашем цифровом мире основана на двоичные числа, цифры которых могут иметь только два значения: 0 и 1 . Эти двоичные числа могут быть преобразованы в десятичную систему (как целые, так и двоичные дроби), но арифметические операции, такие как двоичное сложение, двоичное умножение или двоичное вычитание, также могут выполняться в двоичной системе.
Двоичное деление сильно следует десятичному длинному делению . Процедура состоит из повторяющихся шагов двоичного вычитания.
Каковы правила двоичного деления?
Начиная с левого (старшего) бита, проверяется, можно ли вычесть делитель из текущей цифры делимого . Если да, то в этом бите частного отмечается 1 ; если нет, то 0 . Переносится остаток от процесса деления, и к нему добавляется следующая цифра делимого . Вы повторяете эту процедуру до тех пор, пока не будет достигнут правый (наименее значащий) бит.
Как рассчитать остаток от деления?
Остаток от деления — это остаток после последнего процесса деления . Он меньше делителя и поэтому не может быть разделен дальше.
Давайте рассмотрим эту процедуру на примере ниже. Двоичное число 101010 делится на 110 (42 и 6 в десятичной системе):
Пройдем процесс деления шаг за шагом, по битам:
- Берем первый бит делимого , то есть
1. Это на меньше , чем делитель
Это на меньше , чем делитель 110, поэтому этот бит в частном равен0, а остаток от1сохраняется. - Добавляется следующая цифра делимого, но
10равно , все еще меньшему , чем делитель110, поэтому бит частного равен0. - Добавьте следующий бит делимого:
101. Это еще меньше , чем делитель110; следовательно, частный бит равен0. - Добавляется следующая цифра делимого:
1010. Это на больше , чем делитель, поэтому мы вычитаем110из1010, в результате чего остается100. Бит частного установлен на1. - Бит делимого добавляется к остатку, что дает
1001. Это больше, чем110; вычесть из него делитель, в результате чего останется110в остатке. Соответствующий частный бит равен
Соответствующий частный бит равен 1. - Добавляется последний бит делимого, и мы вычитаем
110из110, в результате чего остается0, а последний бит частного равен1. - Конечным результатом является частное
000111и остаток0.
Как выполнить двоичное деление для отрицательных значений?
Отрицательные двоичные значения можно обрабатывать с помощью представления с дополнением до двух со знаком . После этого преобразования двоичных чисел деление двоичных чисел может быть выполняется так же, как и для положительных значений .
Калькулятор двоичного деления использует представление с дополнением до двух. Это означает, что, например, для 8-битного представления первый бит ваших входных чисел будет битом со знаком. Учтите это в своих расчетах и, если необходимо, увеличьте битовое представление .
Помимо этих основных арифметических операций, двоичные числа также допускают побитовые операции, которые не могут быть выполнены в десятичной системе. К ним относятся битовые сдвиги, а также операции AND, OR и XOR.
Как использовать калькулятор двоичного деления?
Вы узнали о разнице между двоичной и десятичной системами и о том, как делить двоичные числа. Теперь давайте разберемся как работает этот калькулятор двоичного деления . Для этого посмотрим, все ли мы сделали правильно в пошаговой процедуре и воспользуемся теми же значениями: 101010 разделить на 110 .
- Выберите двоичное представление . Этот параметр определяет количество битов, которое могут иметь ваши входные делимое, делитель и частное.
- Наше делимое имеет 6 значащих битов, поэтому нам подходит 8-битное представление.
- Введите ваши цифры :
- Дивиденд:
101010- Делитель:
110
- Калькулятор двоичного деления представляет ваше частное и остаток в двоичной и десятичной системе .
 Это результаты вашего деления двоичных чисел.
Это результаты вашего деления двоичных чисел.
- Частное: двоичное:
111, десятичное:7- Остаток: двоичный и десятичный:
0
Если ваш двоичный результат имеет значение 1 в старшем разряде и может быть понят как положительный результат в записи без знака или отрицательный результат в записи со знаком, оба результата будут отображаться .
Часто задаваемые вопросы
Как выполнить двоичное деление с помощью сдвига?
Двоичное деление, особенно с делителями, являющимися степенью двойки, можно выполнить с помощью сдвига битов вправо . Деление на 2 — это сдвиг на один бит, 4 — 2 бита, 8 — 3-битный сдвиг и т. д. Благодаря своей математической эффективности этот метод обычно используется в цифровых приложениях.
Филип Маус
Двоичное представление
Вы можете записывать двоичные числа, содержащие не более 8 цифр. Вам не нужно вводить лидирующие нули.
Вам не нужно вводить лидирующие нули.
Дивиденд
Делитель
Посмотреть 10 похожих двоичных калькуляторов 1️0️
Двоичное сложениеДвоичная дробьДвоичное умножение… Еще 7 Я написал как дополнение к моему бинарному калькулятору. В первой статье обсуждается бинарное сложение; во второй статье обсуждается двоичное вычитание; в третьей статье обсуждается двоичное умножение; в этой статье обсуждается двоичное деление.
Пример двоичного деленияКарандашно-бумажный метод двоичного деления аналогичен карандашно-бумажному методу десятичного деления, за исключением того, что вместо него используются двоичные числа. Однако, как оказалось, двоичное деление проще. Нет необходимости угадывать, а затем проверять промежуточные частные; они либо 0, либо 1, и их легко определить на глаз.
Десятичное деление
Карандашно-бумажное деление, также известное как длинное деление, является самым сложным из четырех арифметических алгоритмов. Как и другие алгоритмы, он требует от вас решения более мелких подзадач того же типа. Но в отличие от других алгоритмов, здесь нет ограниченного набора «фактов», решающих все возможные подзадачи. Решение этих подзадач деления требует оценок, предположений и проверок. В дополнение к этим подзадачам деления также требуются умножение и вычитание.
Но в отличие от других алгоритмов, здесь нет ограниченного набора «фактов», решающих все возможные подзадачи. Решение этих подзадач деления требует оценок, предположений и проверок. В дополнение к этим подзадачам деления также требуются умножение и вычитание.
Давайте рассмотрим, как выполняется десятичное деление, чтобы мы могли подготовить почву для того, как деление выполняется в двоичном формате. Вот пример:
Пример десятичного деленияАлгоритм представляет собой серию шагов, каждый из которых состоит из следующих четырех подшагов:
- Разделить : Разделить рабочую часть делимого на делитель. (Дивидендом является число под чертой.)
- Умножение : Умножение частного (одна цифра) на делитель.
- Вычесть : Вычесть произведение из рабочей части делимого. (Минусы не пишу — они подразумеваются.)
- Вниз : Скопируйте следующую цифру делимого, чтобы сформировать новую рабочую часть.
Вот пример снова, шаг за шагом:
Шаги десятичного деления- Шаг 0
Входит ли 88 в 8? Нет, потому что оно больше 8.
 Входит ли 88 в 83? Нет, потому что оно больше 83. Входит ли 88 в 831? Да, потому что оно меньше или равно 831.
Входит ли 88 в 83? Нет, потому что оно больше 83. Входит ли 88 в 831? Да, потому что оно меньше или равно 831.(Первый шаг длинного деления, как обычно практикуется, объединяет несколько шагов и их подшагов в один. Вот почему я называю этот шаг 0. Технически 88 делится на 8 нулей, поэтому мы должны записать 0, умножить 88 на 0, вычтите 0 из 8, а затем запишите 3. Далее, мы должны записать 0, потому что 88 входит в число 83, умноженное на ноль, умножьте 88 на 0, вычтите 0 из 83 и запишите 1. Мы просто устраняя кучу вещей, которые производят лишние ведущие нули.)
- Шаг 1
- Разделить : 88 входит в 831? (Да, мы уже знаем это с шага 0.) Сколько раз он входит? 9 раз. (Обычно вы должны угадать ответ и выполнить умножение и вычитание, чтобы убедиться, что вы угадали правильно; я просто покажу правильный ответ, чтобы не запутаться.)
- Умножьте : 9 x 88 = 792. (Если бы 9 было догадкой, ваша первая проверка — увидеть, меньше ли 792, чем 831.
 Пока все хорошо.)
Пока все хорошо.) - Вычесть : 831 — 792 = 39. (Если 9 было предположением, ваша вторая проверка состоит в том, чтобы убедиться, что 39 меньше 88. Это так, значит, ваше предположение было правильным. На самом деле, в этом случае это должно проверить out, так как мы не можем подняться выше 9.)
- Сбить : Сбить 2, чтобы получилось 392.
- Шаг 2
- Разделить : 88 входит в 392? Да, 4 раза.
- Умножить : 4 x 88 = 352.
- Вычесть : 392 – 352 = 40.
- Уменьшить : Уменьшить подразумеваемый завершающий 0, чтобы получилось 400.
- Шаг 3
- Разделить : 88 входит в 400? Да, 4 раза.
- Умножить : 4 x 88 = 352.
- Вычесть : 400 – 352 = 48.
- Уменьшить : Уменьшить подразумеваемый завершающий 0, чтобы получилось 480.
- Шаг 4
- Разделить : 88 входит в 480? Да, 5 раз.

- Умножить : 5 x 88 = 440.
- Вычесть : 480 – 440 = 40.
- Уменьшить : Уменьшить подразумеваемый завершающий 0, чтобы получилось 400.
- Разделить : 88 входит в 480? Да, 5 раз.
- Шаг 5
Остановите прессы! Мы пытались разделить 400 на 88 раньше — два шага назад. Это означает, что с этого момента у нас есть двузначный цикл (45). Ответ 9,445.
Красные цифры — это переносы, возникающие во время подэтапов умножения (по соглашению умножение выполняется так, как если бы делитель — большее число — был сверху). Каждая красная цифра зачеркивается перед следующим умножением. Чтобы избежать беспорядка, я решил не отмечать заимствования, возникающие во время вычитания.
Я выбрал самый сложный тип примера
В моем примере есть многозначный делитель и ответ с остатком, который я записал в виде повторяющейся десятичной дроби. Мне нужен был один пример, который полностью демонстрировал длинное деление. Я мог бы выбрать задачу с одноразрядным делителем (что не требует угадывания, если вы знаете факты умножения), или задачу, которая дает целое частное, или задачу, которая дает частное с дробной частью, которая оканчивается. Я мог бы выразить дробную часть в виде целого остатка или в форме дроби.
Я мог бы выбрать задачу с одноразрядным делителем (что не требует угадывания, если вы знаете факты умножения), или задачу, которая дает целое частное, или задачу, которая дает частное с дробной частью, которая оканчивается. Я мог бы выразить дробную часть в виде целого остатка или в форме дроби.
Другие случаи
- Если делитель или делимое отрицательное, вы можете удалить знаки и поставить соответствующий знак к ответу в конце.
- Если делитель имеет десятичную точку, сдвиньте десятичную точку вправо, пока делитель не станет целым числом, и сдвиньте делимое на такое же количество знаков.
- Если делитель больше делимого, просто действуйте по алгоритму как есть. Замыкающие нули будут сведены вниз, чтобы сформировать соответствующие подзадачи.
Двоичное деление
Вернемся к примеру введения, 1011.11/11. Здесь он разбит на шаги по тому же алгоритму, который я использовал для десятичных чисел:
Шаги двоичного деления- Шаг 0
11 превращается в 1? Нет, потому что оно больше 1.
 Входит ли 11 в 10? Нет, потому что оно больше 10. Входит ли 11 в 101? Да, потому что оно меньше или равно 101. (Помните, это двоичные числа; произносите их «один-один», «один-ноль», «один-ноль-один» и т. д.)
Входит ли 11 в 10? Нет, потому что оно больше 10. Входит ли 11 в 101? Да, потому что оно меньше или равно 101. (Помните, это двоичные числа; произносите их «один-один», «один-ноль», «один-ноль-один» и т. д.) - Шаг 1
- Разделить : 11 входит в 101? (Да, мы уже знаем это с шага 0.) Сколько раз он входит? Один раз. Нет никаких догадок. Легко увидеть, что 11 меньше 101, поэтому мы знаем, что оно входит. А если оно входит, то только один раз.
- Умножить : 1 x 11 = 11. (Помните, как просто «умножить» двоичное число на одну цифру — просто скопируйте число вниз, если эта единственная цифра равна 1, или запишите 0, если эта единственная цифра 0.)
- Вычесть : 101 – 11 = 10.
- Сбить : Сбить 1, чтобы получилось 101.
- Шаг 2
- Разделить : 11 входит в 101? Да, 1 раз.
- Умножить : 1 x 11 = 11.
- Вычесть : 101 – 11 = 10.

- Сбить : Сбить 1, чтобы получилось 101.
- Шаг 3
- Разделить : 11 входит в 101? Да, 1 раз.
- Умножить : 1 x 11 = 11.
- Вычесть : 101 – 11 = 10.
- Сбить : Сбить 1, чтобы получилось 101.
- Шаг 4
- Разделить : 11 входит в 101? Да, 1 раз.
- Умножить : 1 x 11 = 11.
- Вычесть : 101 – 11 = 10.
- Сбить : Сбить 0, чтобы получилось 100.
- Шаг 5
- Разделить : 11 входит в 100? Да, 1 раз.
- Умножить : 1 x 11 = 11.
- Вычесть : 100 – 11 = 1.
- Сбить : Сбить 0, чтобы получилось 10.
- Шаг 6
- Разделить : 11 входит в 10? Нет (запишите 0).
- Умножение : (Нам не нужно записывать этот шаг, мы просто получим 0.
 )
) - Вычесть : (Нам не нужно записывать этот шаг, мы просто получим 10.)
- Сбить : Сбить 0, чтобы получилось 100.
- Шаг 7
Здесь мы останавливаемся, признавая, что мы разделили 100 на 11 два шага назад. Это означает, что с этого момента у нас есть двузначный цикл (10). Частное равно 11,1110.
Проверка ответа
Когда в ответе есть повторяющаяся дробная часть, ее проверка не так проста, как для других арифметических операций. Что мы можем сделать, так это аппроксимировать частное до конечного числа мест, а затем проверить, близко ли оно к ожидаемому ответу.
Проверить ответ можно несколькими способами. Один из способов — выполнить двоичное умножение вручную: вы проверяете, что приближенное частное (например, 11,11101011), умноженное на делитель (11), равно делимому (1011,11). (Я оставлю это как упражнение, но ответ будет 1011.11000001, что очень близко к 1011.11).
Другой способ проверки — преобразовать операнды в десятичные числа, выполнить десятичное деление, а затем преобразовать приблизительный десятичный ответ в двоичный. 1011,11 = 11,75 и 11 = 3. 11,75/3 = 3,916. Оценивая это как 3,91666666666666667, например, мой двоичный преобразователь говорит, что это равно 11,111010101010101010101010101010101010 при усечении до 36 знаков. Похоже, он хочет быть 11.1110, ответ, который мы получили, используя двоичное деление.
1011,11 = 11,75 и 11 = 3. 11,75/3 = 3,916. Оценивая это как 3,91666666666666667, например, мой двоичный преобразователь говорит, что это равно 11,111010101010101010101010101010101010 при усечении до 36 знаков. Похоже, он хочет быть 11.1110, ответ, который мы получили, используя двоичное деление.
Вы также можете проверить ответ, используя мой двоичный калькулятор. Он говорит, что 1011.11/11 — это 11.111010101010 (например, до 12 мест). Опять же, это выглядит как 11.1110.
Если вы хотите проверить повторяющуюся часть напрямую, вы можете использовать этот инструмент преобразования; вот что нужно ввести:
- Начальная база: 2
- Неотъемлемая часть: 11
- Неповторяющаяся дробная часть: 11
- Повторяющаяся дробная часть: 10
- Новая база: 10
Это дает ожидаемый десятичный ответ: 3,916. (На самом деле, более прямой способ использовать этот инструмент — ввести «2» для «Нового основания»; это дает дробь 101111/1100, что эквивалентно нашей задаче деления 1011,11/11. )
)
Вы также можете использовать этот инструмент для преобразования в обратном направлении, убедившись, что 3.916 преобразуется в 11.1110.
(Есть также аналитические способы точной проверки ответа: читайте мои статьи о методе вычитания, прямом методе и методе рядов.)
Обсуждение
Как и другие арифметические алгоритмы, я описал алгоритм деления в базисно-независимый способ. Я хотел подчеркнуть механическую процедуру, а не то, почему она работает (в десятичном или двоичном формате).
Когда вы выполняете длинное двоичное деление, вы можете обнаружить, что выполняете в уме некоторые подшаги в десятичной форме (например, 101 – 11 равно 5 – 3 = 2, что равно 10 в двоичной системе).
Хотя двоичное деление проще, чем десятичное деление (поскольку здесь нет угадывания и, по сути, нет умножения), вы обнаружите, что всегда имея одно и то же число (делитель) с вычитаемым, вы получите закономерность, которая начнет вас завораживать; легко заблудиться в этом море 1 и 0.

 15 Деление двоичных чисел
15 Деление двоичных чисел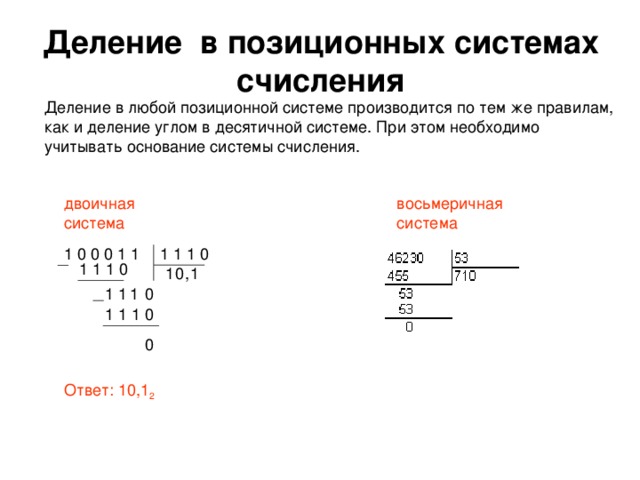 Это на меньше , чем делитель
Это на меньше , чем делитель  Соответствующий частный бит равен
Соответствующий частный бит равен  Это результаты вашего деления двоичных чисел.
Это результаты вашего деления двоичных чисел. Входит ли 88 в 83? Нет, потому что оно больше 83. Входит ли 88 в 831? Да, потому что оно меньше или равно 831.
Входит ли 88 в 83? Нет, потому что оно больше 83. Входит ли 88 в 831? Да, потому что оно меньше или равно 831. Пока все хорошо.)
Пока все хорошо.)
 Входит ли 11 в 10? Нет, потому что оно больше 10. Входит ли 11 в 101? Да, потому что оно меньше или равно 101. (Помните, это двоичные числа; произносите их «один-один», «один-ноль», «один-ноль-один» и т. д.)
Входит ли 11 в 10? Нет, потому что оно больше 10. Входит ли 11 в 101? Да, потому что оно меньше или равно 101. (Помните, это двоичные числа; произносите их «один-один», «один-ноль», «один-ноль-один» и т. д.)
 )
)