Умножение и деление чисел с разными знаками, отрицательных и положительных чисел
Умножение целых чисел
Правило умножения целых чисел звучит так:
Чтобы умножить целые числа, нужно перемножить их абсолютные величины и перед результатом поставить знак плюс, если оба сомножителя имеют одинаковые знаки или минус, если сомножители имеют разные знаки.
Например,
-4 ⋅ 5 = — (|-4|⋅|5|) = — (4 ⋅ 5) = -20
-4 ⋅ (-5) = |-4|⋅|-5|= 4 ⋅ 5 = 20
4 ⋅ 5 = |4|⋅|5|= 4 ⋅ 5 = 20
4 ⋅ (-5) = — (|4|⋅|-5|) = — (4 ⋅ 5) = -20
Умножение чисел с разными знаками
Чтобы умножить числа с разными знаками, нужно перемножить модули множителей и перед произведением поставить знак минус.
Например, 8 ⋅ (-7) = — (|8|⋅|-7|) = — (8 ⋅ 7) = -56
Как умножать отрицательные числа?
Чтобы умножить отрицательные числа, нужно перемножить их модули и перед произведением поставить знак плюс.
Например, -9 ⋅ (-10) = |-9|⋅|-10|= 9 ⋅ 10 = 90
Как умножать положительные числа?
О разных методах и правилах умножения натуральных чисел читайте в нашем уроке: Умножение натуральных чисел.
Умножение нескольких целых чисел
Как определить знак произведения, если множителей больше двух и они имеют разные знаки? Для нахождения произведения нескольких множителей целых чисел нужно перемножить модули множителей и перед результатом поставить знак:
– если количество отрицательных сомножителей четное число, то произведение будет положительным, перед результатом ставим знак «+»;
– если количество отрицательных сомножителей нечетное число, то произведение будет отрицательным, перед результатом ставим знак «-»;
Пример. Найти произведение: -5 ⋅ 2 ⋅3 ⋅ (-4) ⋅ (-10)
-5 ⋅ 2 ⋅3 ⋅ (-4) ⋅ (-20) = — 2400
Объяснение: вычислили произведение абсолютных величин множителей, перед произведением ставим знак минус, ведь количество отрицательных сомножителей составляет 3, нечетное число
Пример. Найти произведение: 8 ⋅ 4 ⋅ (-2) ⋅ (-10) ⋅ 6
8 ⋅ 4 ⋅ (-2) ⋅ (-10) ⋅ 6 = 3840
Объяснение: выполнили умножение абсолютных величин множителей, перед произведением ставим плюс или ничего не ставим, поскольку количество отрицательных сомножителей равно 2 — четное число
Свойства умножения целых чисел: переместительный, сочетательный, распределительный законы
Для умножения целых чисел характерными являются переместительный, сочетательный, распределительный законы:
Переставное свойство: от перестановки множителей местами произведение не изменится.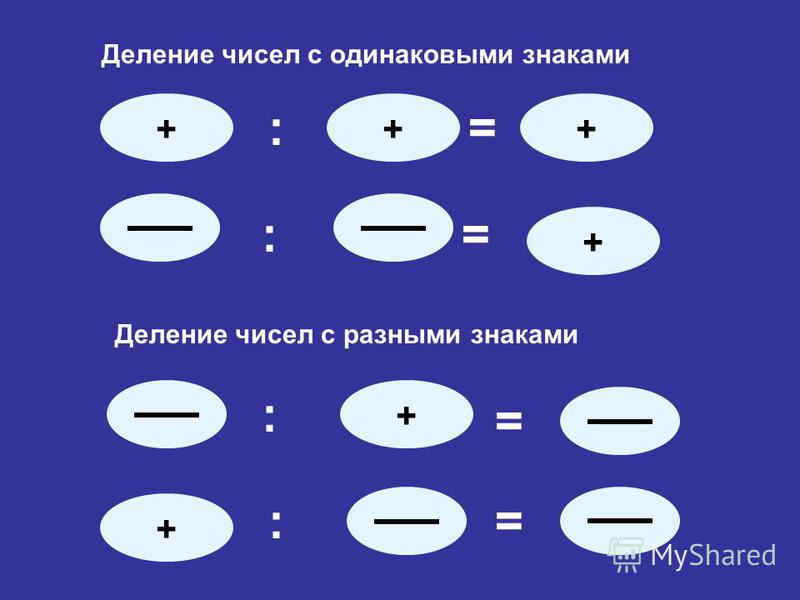
Для любых целых чисел выполняется равенство:
Проверим на примере:
-3 ⋅ (-9) = (-9) ⋅ (-3)
Ведь -3 ⋅ (-9) = 27 і (-9) ⋅ (-3) = 27
Сочетательное свойство:
Где a, b, c – любые целые числа
[–8 ⋅ (–3)] ⋅ 2 = 24 ⋅ 2 = 48
–8 × (–3 × 2) = -8 ⋅ (-6) = 48
Поэтому [–8 ⋅ (–3)] ⋅ 2 = –8 × (–3 × 2)
Распределительное свойство:
Для любых целых чисел a, b, c выполняется равенство:
Проверим распределительное свойство умножения целых чисел на примере:
(–5 + 9) ⋅ (–7) = 4 ⋅ (-7) = -28
(–5 + 9) ⋅ (–7) =- 5 ⋅ (-7) + 9 ⋅ (-7) = 35 – 63 = -28
Итак, (–5 + 9) ⋅ (–7) =- 5 ⋅ (-7) + 9 ⋅ (-7)
Умножение целых чисел на 0, 1 и -1
а ⋅ 0 = 0 , где а – любое целое число
Произведение целых чисел, хотя бы один множитель которых равен 0, равно нулю.
Для любых целых чисел выполняются следующие равенства:
Деление целых чисел
Деление двух отрицательных целых чисел и двух чисел с разными знаками имеет то же содержание, что и деление положительных чисел: по данному произведению и одному из множителей посредством деления определяют второй множитель.
Если (-4) ⋅ 6 = -24, то (-24) : (-4) = 6 и (-24) : 6 = -4
Рассмотрим подробнее равенство (-24) : (-4) = 6 – в ней делимое равно -24, делитель равен -4 и частное от деления равно 6
Найдем абсолютные величины каждого компонента:
|-24| = |24|, |-4| = |4|, |6|= |6|
Можно сделать вывод, что для нахождения модуля частного нужно поделить модуль делимого на модуль делителя. Если делимое и делитель являются отрицательными числами, то частное будет положительным числом.
Как правильно делить отрицательные числа?
Чтобы найти частное двух отрицательных целых чисел, нужно поделить модули этих чисел. Частное будет положительным числом.
Как правильно делить числа с разными знаками?
Чтобы разделить числа с разными знаками, нужно модуль делимого разделить на модуль делителя и перед результатом поставить знак минус.
–18 : 6 = –(|–18| : |6|) = – (18 : 6) = -3
Деление целых чисел, если делимое или делитель равно 0 или 1
а – любое целое число, но в первом и третьем равенствах а≠ 0.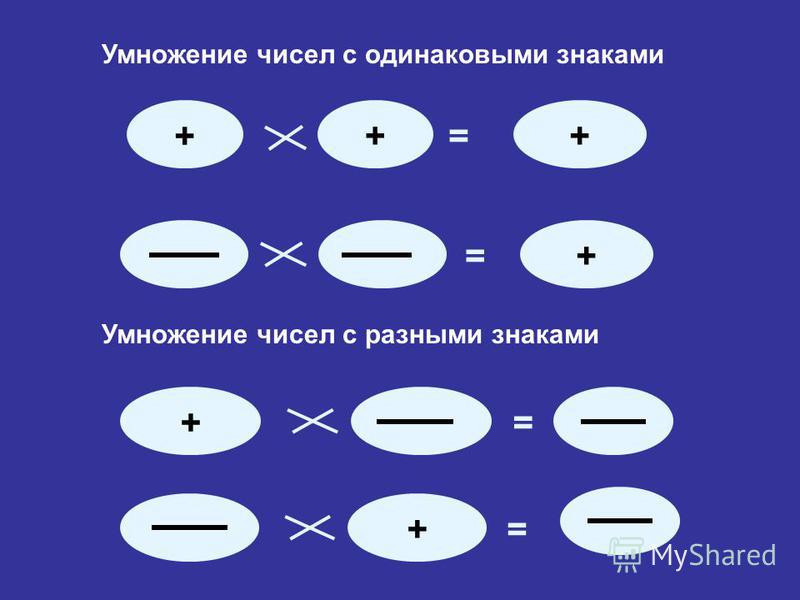
Ведь целые числа на 0 делить нельзя.
Умножение и деление рациональных чисел
В данном уроке рассматривается умножение и деление рациональных чисел.
Умножение рациональных чисел
Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь умножать целые числа.
Необходимо также знать основные законы умножения такие как переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и закон умножения на ноль.
Пример 1. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками
Модуль числа равен , а модуль числа равен .
Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Таким образом, значение выражения равно
Короткое решение выглядит следующим образом:
Пример 2. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус:
Решение для данного примера можно записать покороче:
Пример 3. Найти значение выражения
Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
Решение для данного примера можно записать покороче:
Пример 4. Найти значение выражения
Это умножение отрицательных рациональных чисел.
Перемножим модули этих чисел и перед полученным ответом поставим плюс
Решение для данного примера можно записать покороче:
Пример 5. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Короткое решение будет выглядеть значительно проще:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть
Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Решение для данного примера можно записать покороче
Пример 7. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Сначала в ответе получилась неправильная дробь , но мы выделили в ней цéлую часть.
Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.
Первое действие:
Второе действие:
Ответ: значение выражения равно −2.
Пример 9. Найти значение выражения:
Переведём смешанные числа в неправильные дроби:
Получили умножение отрицательных рациональных чисел.
Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Пример 10. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
Второе действие:
Третье действие:
Четвёртое действие:
Ответ: значение выражения равно
Пример 11. Найти значение выражения
Вспоминаем закон умножения на ноль.
Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 12. Найти значение выражения
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 13. Найти значение выражения
Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .
Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.
Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение.
Поэтому в получившемся новом выражении возьмём в скобки те дроби, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Далее вычисляем выражение по действиям. Сначала вычислим выражения в скобках, и полученные результаты сложим
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения равно
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.
Пример 14. Найти значение выражения −4,2 × 3,2
Это умножение рациональных чисел с разными знаками.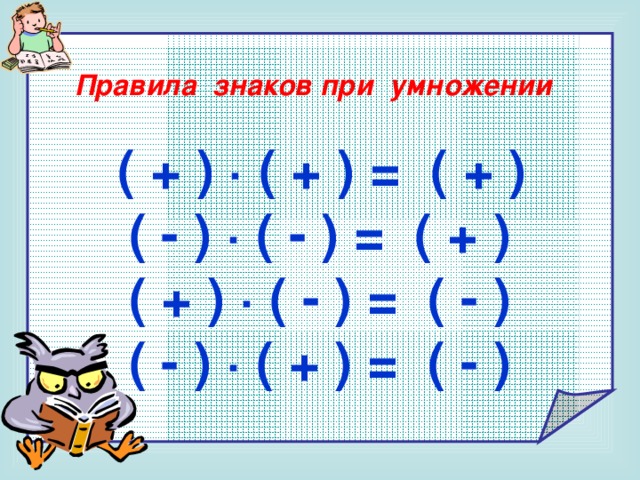
Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичные дроби.
Пример 15. Найти значение выражения −0,15 × 4
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичную дробь и целое число.
Пример 16. Найти значение выражения −4,2 × (−7,5)
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Деление рациональных чисел
Деление рациональных чисел свóдится к умножению этих же чисел. Для этого первую дробь умножают на дробь, обратную второй.
Затем применяются правила умножения рациональных чисел.
Пример 1. Выполнить деление:
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули данных рациональных чисел и перед полученным ответом поставить минус.
Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение
Таким образом, значение выражения равно
Подробное решение выглядит следующим образом:
Короткое решение можно записать так:
Пример 2. Выполнить деление
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Короткое решение можно записать так:
Пример 3. Выполнить деление
Умнóжим первую дробь на дробь, обратную второй.
Обратная для второй дроби это дробь
Получили умножение отрицательных рациональных чисел. Выполним данное умножение. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Пример 4. Выполнить деление
В данном случае нужно первое число −3 умножить на дробь, обратную дроби .
Обратная для дроби это дробь . Затем следует применить правило умножения рациональных чисел с разными знаками:
Пример 5. Выполнить деление
Умнóжим первую дробь на число, обратное числу 4.
Обратное числу 4 это дробь . На неё и умножим первую дробь
Пример 6. Выполнить деление
Умнóжим первую дробь на число, обратное числу −3
Обратное числу −3 это дробь
Пример 7. Найти значение выражение −14,4 : 1,8
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус
Обратите внимание, как модуль делимого был разделён на модуль делителя.
В данном случае потребовалось суметь разделить десятичную дробь на другую десятичную дробь.
Если нет желания работать с десятичными дробями (а это бывает часто), то эти десятичные дроби можно перевести в смешанные числа, затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.
Вычислим предыдущее выражение −14,4 : 1,8 этим способом. Переведём десятичные дроби в смешанные числа:
Теперь переведём полученные смешанные числа в неправильные дроби:
Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:
Пример 8. Найти значение выражения
Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:0
Пример 9. Найти значение выражения −7,2 : (−0,6)
Это деление отрицательных рациональных чисел.
Чтобы выполнить данное деление, нужно первую дробь умножить на дробь обратную второй.
Перенесём в обеих дробях запятую на одну цифру вправо, получим деление −72:(−6)
Многоэтажные дроби
Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:
В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:
В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной.
При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.
Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.
Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.
После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:
И далее можно воспользоваться методом деления дробей — умножить первую дробь на дробь, обратную второй.
Пример 2. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь
А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .
Пример 3. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2
А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.
Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.
Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.
Реализуется этот метод следующим образом:
Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж.
А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения ( × )
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!
Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:
С первого на четвёртый. Со второго на третий.
В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.
Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.
Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь пользуясь новой схемой.
Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть
В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.
Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:
В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:
Использование переменных
Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.
Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.
Использование переменных оправдано, при работе с многоэтажными дробями. Например:
Найти значение выражения
Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.
Выражение, находящееся в числителе можно занести в переменную с любым названием, например:
Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A
А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B
Теперь наше изначальное выражение принимает вид . То есть мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.
Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .
Найдём значение переменной A
Найдём значение переменной B
Теперь подставим в главное выражения вместо переменных A и B их значения:
Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:
Таким образом, значение выражения равно −1.
Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.
Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как
Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.
Задания для самостоятельного решения
Задание 1. Выполните умножение:
Решение:
Показать решение
Задание 2. Выполните умножение:
Решение:
Показать решение
Задание 3. Выполните умножение:
Решение:
Показать решение
Задание 4. Выполните умножение:
Решение:
Показать решение
Задание 5. Выполните умножение:
Решение:
Показать решение
Задание 6. Выполните умножение:
Решение:
Показать решение
Задание 7. Выполните умножение:
Решение:
Показать решение
Задание 8. Выполните умножение:
Решение:
Показать решение
Задание 9. Выполните деление:
Решение:
Показать решение
Задание 10. Выполните деление:
Решение:
Показать решение
Задание 11. Выполните деление:
Решение:
Показать решение
Задание 12. Выполните деление:
Решение:
Показать решение
Задание 13. Выполните деление:
Решение:
Показать решение
Задание 14.
Выполните деление:
Решение:
Показать решение
Задание 15. Выполните деление:
Решение:
Показать решение
Задание 16. Выполните деление:
Решение:
Показать решение
Задание 17. Выполните деление:
Решение:
Показать решение
Задание 18. Вычислите выражение:
Решение:
Показать решение
Задание 19. Вычислите выражение:
Решение:
Показать решение
Задание 20. Вычислите выражение:
Решение:
Показать решение
Задание 21. Вычислите выражение:
Решение:
Показать решение
Задание 22. Вычислите выражение:
Решение:
Показать решение
Задание 23. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Задание 24. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Показать решение
Задание 25. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Показать решение
Задание 26.
Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Показать решение
Задание 27. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Показать решение
Задание 28. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Показать решение
Задание 29. Используя метод «С первого на четвёртый, со второго на третий»
, запишите следующую дробь в виде умножения и вычислите:Решение:
Показать решение
Задание 30. Найдите значение выражения:
Решение:
Показать решение
Задание 31. Найдите значение выражения:
Решение:
Показать решение
Задание 32. Найдите значение выражения:
Решение:
Показать решение
Задание 33. Найдите значение выражения:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
10.
6: Умножение и деление чисел со знаком- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48897
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады через OpenStax CNX
Цели обучения
- уметь умножать и делить числа со знаком
- уметь умножать и делить числа со знаком с помощью калькулятора
Умножение чисел со знаком
Рассмотрим сначала произведение двух положительных чисел. Умножить: \(3\cdot 5\).
\(3 \cdot 5\) означает \(5 + 5 + 5 = 15\)
Это предполагает, что (В более поздних курсах математики слово «предполагает» превращается в слово «доказательство».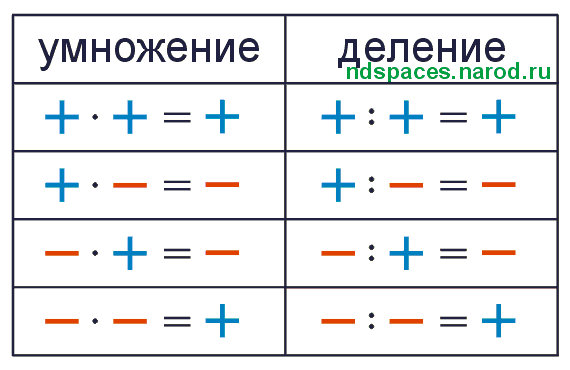
доказывать утверждение Математические доказательства строятся для проверки утверждения во всех возможных случаях.)
\(\text{(положительное число)} \cdot \text{(положительное число)} = \text{(положительное число)}\)
Короче говоря,
(+) (+) = (+)
Теперь рассмотрим произведение положительного числа на отрицательное. Умножьте: (3)(-5)
(3)(-5) означает (-5) + (-5) + (-5) = -15
Это предполагает, что
\(\text{(положительно число)} \cdot \text{(отрицательное число)} = \text{(отрицательное число)}\)
Более кратко,
(+) (-) = (-)
По коммутативному свойству умножения, мы получаем
\(\text{(отрицательное число)} \cdot \text{(положительное число)} = \text{(отрицательное число)}\)
Более кратко,
(-) (+) = (-)
Знак произведения двух отрицательных чисел можно предположить, рассмотрев следующую иллюстрацию.
Умножить -2 соответственно на 4, 3, 2, 1, 0, -1, -2, -3, -4.
У нас есть следующие правила умножения чисел со знаком.
Правила умножения подписанных Чисел
Умножение чисел со знаком:
- Чтобы умножить два действительных числа, имеющих одинаковый знак , умножьте их абсолютные значения. Продукт положительный.
(+) (+) = (+)
(-) (-) = (+) - Чтобы умножить два действительных числа, имеющих противоположных знаков , умножьте их абсолютные значения. Произведение отрицательное.
(+) (-) = (-)
(-) (+) = (-)
Набор образцов A
Найдите следующие продукты.
\(8 \cdot 6\)
Решение
\(\begin{array} {ccl} {|8|} & = & {8} \\ {|6|} & = & {6} \end{array} \big \} \) Умножьте эти абсолютные значения.
\(8 \cdot 6 = 48\)
Так как числа имеют одинаковый знак, произведение положительное.
Таким образом, \(8 \cdot 6 = +48\), или \(8 \cdot 6 = 48\).
Набор образцов A
(-8)(-6)
Решение
\(\begin{array} {ccl} {|-8|} & = & {8} \\ {|-6 |} & = & {6} \end{array} \big \}\) Умножьте эти абсолютные значения.
\(8 \cdot 6 = 48\)
Так как числа имеют одинаковый знак, произведение положительное.
Таким образом, \((-8)(-6) = +48\), или \((-8)(-6) = 48\).
Набор образцов A
(-4)(7)
Решение
\(\begin{array} {ccl} {|-4|} & = & {4} \\ {|7|} & = & {7} \end{array} \big \}\) Умножьте эти абсолютные значения.
\(4 \cdot 7 = 28\)
Поскольку числа имеют противоположные знаки, произведение отрицательное.
Таким образом, (-4)(7) = -28.
Набор образцов A
6(-3)
Решение
\(\begin{array} {ccl} {|6|} & = & {6} \\ {|-3|} & = & {3} \end{array} \big \}\) Умножьте эти абсолютные значения.
\(6 \cdot 3 = 18\)
Поскольку числа имеют противоположные знаки, произведение отрицательное.
Таким образом, 6(-3) = -18.
Тренировочный набор A
Найдите следующие продукты.
3(-8)
- Ответить
-24
Тренировочный набор A
4(16)
- Ответить
64
Тренировочный набор A
(-6)(-5)
- Ответить
30
Тренировочный набор A
(-7)(-2)
- Ответить
14
Тренировочный набор A
(-1)(4)
- Ответить
-4
Тренировочный набор A
(-7)7
- Ответить
-49
Деление чисел со знаком
Чтобы определить знаки в задаче на деление, вспомните, что
\(\dfrac{12}{3} = 4\), так как \(12 = 3 \cdot 4\)
Это предполагает что
\(\dfrac{(+)}{(+)} = (+)\)
\(\dfrac{(+)}{(+)} = (+)\), поскольку (+) = (+ ) (+)
Что такое \(\dfrac{12}{-3}\)?
12 = (-3)(-4) предполагает, что \(\dfrac{12}{-3} = -4\).
То есть
\(\dfrac{(+)}{(-)} = (-)\)
(+) = (-) (-) предполагает, что \(\dfrac{(+)}{( -)} = (-)\)
Что такое \(\dfrac{-12}{3}\)?
-12 = (3)(-4) предполагает, что \(\dfrac{-12}{3} = -4\). То есть
\(\dfrac{(-)}{(+)} = (-)\)
(-) = (+) (-) предполагает, что \(\dfrac{(-)}{( +)} = (-)\)
Что такое \(\dfrac{-12}{-3}\)?
-12 = (-3)(4) предполагает, что \(\dfrac{-12}{-3} = 4\). То есть
\(\dfrac{(-)}{(-)} = (+)\)
(-) = (-)(+) предполагает, что \(\dfrac{(-)}{( -)} = (+)\)
У нас есть следующие правила деления чисел со знаком.
Правила деления чисел со знаком
Деление чисел со знаком:
- Чтобы разделить два действительных числа, имеющих одинаковый знак , разделите их абсолютные значения. Коэффициент положительный.
\(\dfrac{(+)}{(+)} = (+)\dfrac{(-)}{(-)} = (+)\) - Чтобы разделить два действительных числа, которые имеют противоположных знаков , разделите их абсолютные значения.
Коэффициент отрицательный.
\(\dfrac{(-)}{(+)} = (-)\dfrac{(+)}{(-)} = (-)\)
Коэффициент отрицательный. Набор образцов B
Найдите следующие частные.
\(\dfrac{-10}{2}\)
Решение
\(\begin{array} {ccc} {|-10|} & = & {10} \\ {|2| } & = & {2} \end{array} \big \}\) Разделите эти абсолютные значения.
\(\dfrac{10}{2} = 5\)
Поскольку числа имеют противоположные знаки, частное отрицательно.
Таким образом, \(\dfrac{-10}{2} = -5\).
Набор образцов B
\(\dfrac{-35}{-7}\)
Решение
\(\begin{array} {ccc} {|-35|} & = & {35} \\ {|-7|} & = & {7} \end{массив} \big \}\) Разделите эти абсолютные значения.
\(\dfrac{35}{7} = 5\)
Поскольку числа имеют одинаковые знаки, частное положительно.
Таким образом, \(\dfrac{-35}{-7} = 5\).
Набор образцов B
\(\dfrac{18}{-9}\)
Решение
\(\begin{array} {ccc} {|18|} & = & {18} \\ {|-9|} & = & {9} \end{массив} \big \}\) Разделите эти абсолютные значения.
\(\dfrac{18}{9} = 2\)
Поскольку числа имеют противоположные знаки, частное отрицательно.
Таким образом, \(\dfrac{18}{-9} = -2\).
Практический набор B
Найдите следующие частные.
\(\dfrac{-24}{-6}\)
- Ответить
4
Практический набор B
\(\dfrac{30}{-5}\)
- Ответить
-6
Практический набор B
\(\dfrac{-54}{27}\)
- Ответить
-2
Практический набор B
\(\dfrac{51}{17}\)
- Ответить
3
Набор образцов C
Найдите значение \(\dfrac{-6(4 — 7) — 2(8 — 9)}{-(4 + 1) + 1}\).
Решение
Используя порядок операций и то, что мы знаем о числах со знаком, мы получаем,
\(\begin{array} {rcl} {\dfrac{-6(4 — 7) — 2(8 — 9)}{-(4 + 1) + 1}} & = & {\dfrac{-6(-3) — 2(-1)}{-(5) + 1}} \\ {} & = & {\dfrac{18 + 2}{-5 + 1}} \\ {} & = & {\dfrac{20}{-4}} \\ {} & = & {-5} \end{array} \)
Тренировочный набор C
Найдите значение \(\dfrac{-5(2-6)-4(-8-1)}{2(3-10)-9(-2)}\).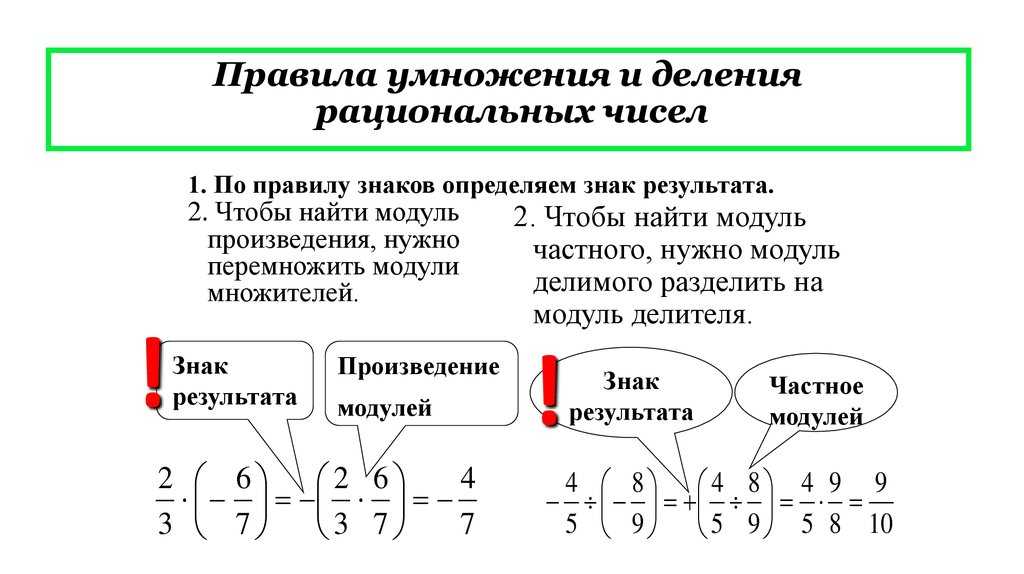
- Ответить
14
Калькуляторы
Калькуляторы с клавишей
можно использовать для умножения и деления чисел со знаком.
Набор образцов D
Используйте калькулятор, чтобы найти каждое частное или произведение.
\((-186) \cdot (-43)\)
Решение
Поскольку этот продукт содержит \(\text{(отрицательный)} \cdot \text{(отрицательный)}\), мы знаем, что результатом должно быть положительное число. Мы проиллюстрируем это на калькуляторе.
| Дисплей считывает | ||
| Тип | 186 | 186 |
| Пресс | -186 | |
| Пресса | \(\раз\) | -186 |
| Тип | 43 | 43 |
| Пресс | -43 | |
| Пресс | = | 7998 |
Таким образом, \((-186) \cdot (-43) = 7,998\)
Образец набора D
\(\dfrac{158.
64}{-54.3}\). Округлить до одного десятичного знака.
Решение
Так как этот продукт включает \(\text{(отрицательный)} \cdot \text{(отрицательный)}\), мы знаем, что результатом должно быть положительное число. Мы проиллюстрируем это на калькуляторе.
| Дисплей считывает | ||
| Тип | 158,64 | 158,64 |
| Пресса | \(\дел\) | 158,64 |
| Тип | 54,3 | 54,3 |
| Пресс | -54,3 | |
| Пресс | = | -2,921546961 |
Округляя до одного десятичного знака получаем -2,9.
Практический набор D
Используйте калькулятор, чтобы найти каждое значение.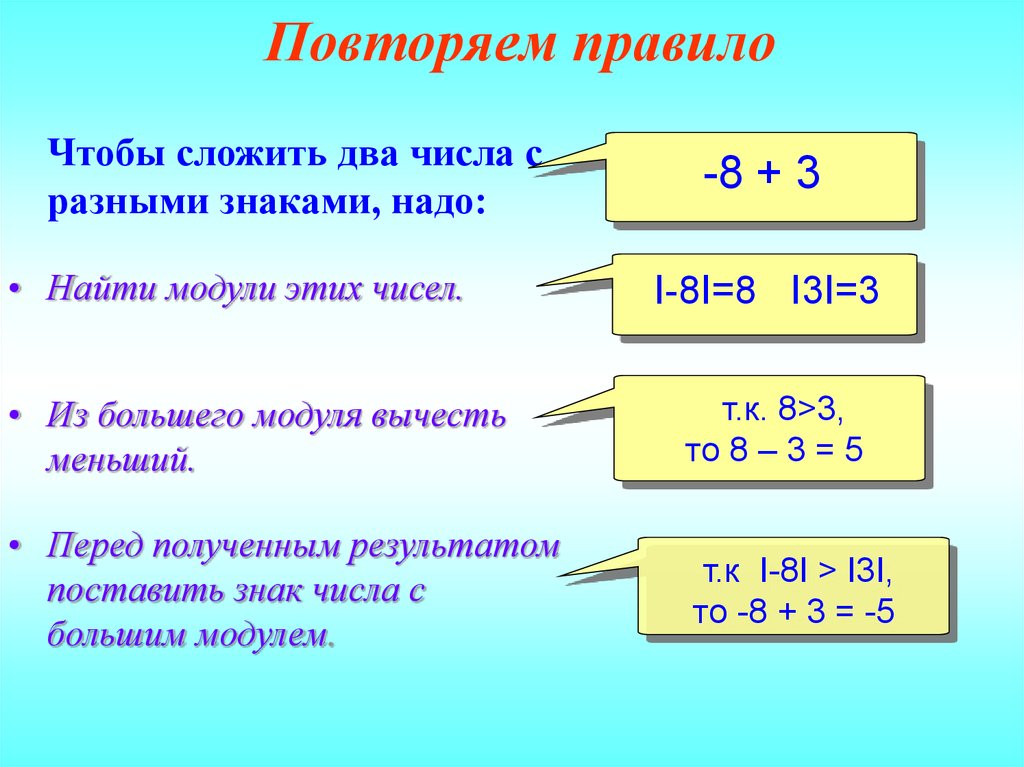
\((-51.3) \cdot (-21.6)\)
- Ответить
1 108,08
Тренировочный набор D
\(-2.5746 \дел -2.1\)
- Ответить
1,226
Тренировочный набор D
\((0,006) \cdot (-0,241)\). Округлить до трех знаков после запятой.
- Ответить
-0,001
Упражнения
Найдите значение каждого из следующих. Используйте калькулятор, чтобы проверить каждый результат.
Упражнение \(\PageIndex{1}\)
(-2)(-8)
- Ответить
16
Упражнение \(\PageIndex{2}\)
(-3)(-9)
Упражнение \(\PageIndex{3}\)
(-4)(-8)
- Ответить
32
Упражнение \(\PageIndex{4}\)
(-5)(-2)
Упражнение \(\PageIndex{5}\)
(3)(-12)
- Ответить
-36
Упражнение \(\PageIndex{6}\)
(4)(-18)
Упражнение \(\PageIndex{7}\)
(10)(-6)
- Ответить
-60
Упражнение \(\PageIndex{8}\)
(-6)(4)
Упражнение \(\PageIndex{9}\)
(-2)(6)
- Ответить
-12
Упражнение \(\PageIndex{10}\)
(-8)(7)
Упражнение \(\PageIndex{11}\)
\(\dfrac{21}{7}\)
- Ответить
3
Упражнение \(\PageIndex{12}\)
\(\dfrac{42}{6}\)
Упражнение \(\PageIndex{13}\)
\(\dfrac{-39}{3}\)
- Ответить
-13
Упражнение \(\PageIndex{14}\)
\(\dfrac{-20}{10}\)
Упражнение \(\PageIndex{15}\)
\(\dfrac{-45}{-5}\)
- Ответить
9
Упражнение \(\PageIndex{16}\)
\(\dfrac{-16}{-8}\)
Упражнение \(\PageIndex{17}\)
\(\dfrac{25}{-5}\)
- Ответить
-5
Упражнение \(\PageIndex{18}\)
\(\dfrac{36}{-4}\)
Упражнение \(\PageIndex{19}\)
8 — (-3)
- Ответить
11
Упражнение \(\PageIndex{20}\)
14 — (-20)
Упражнение \(\PageIndex{21}\)
20 — (-8)
- Ответить
28
Упражнение \(\PageIndex{22}\)
(-4) — (-1)
Упражнение \(\PageIndex{23}\)
0 — 4
- Ответить
-4
Упражнение \(\PageIndex{24}\)
0 — (-1)
Упражнение \(\PageIndex{25}\)
-6 + 1 — 7
- Ответить
-12
Упражнение \(\PageIndex{26}\)
15 — 12 — 20
Упражнение \(\PageIndex{27}\)
1 — 6 — 7 + 8
- Ответить
-4
Упражнение \(\PageIndex{28}\)
2 + 7 — 10 + 2
Упражнение \(\PageIndex{29}\)
3(4 — 6)
- Ответить
-6
Упражнение \(\PageIndex{30}\)
8(5 — 12)
Упражнение \(\PageIndex{31}\)
-3(1 — 6)
- Ответить
15
Упражнение \(\PageIndex{32}\)
-8(4 — 12) + 2
Упражнение \(\PageIndex{33}\)
-4(1-8) + 3(10-3)
- Ответить
49
Упражнение \(\PageIndex{34}\)
-9(0-2) + 4(8-9) + 0(-3)
Упражнение \(\PageIndex{35}\)
6(-2 — 9) — 6(2 + 9) + 4(-1 — 1)
- Ответить
-140
Упражнение \(\PageIndex{36}\)
\(\dfrac{3(4 + 1) — 2 (5)}{-2}\)
Упражнение \(\PageIndex{37}\)
\(\dfrac{4(8 + 1) — 3 (-2)}{-4 — 2}\)
- Ответить
-7
Упражнение \(\PageIndex{38}\)
\(\dfrac{-1(3 + 2) + 5}{-1}\)
Упражнение \(\PageIndex{39}\)
\(\dfrac{-3(4 — 2) + (-3)(-6)}{-4}\)
- Ответить
-3
Упражнение \(\PageIndex{40}\)
-1(4 + 2)
Упражнение \(\PageIndex{41}\)
-1(6 — 1)
- Ответить
-5
Упражнение \(\PageIndex{42}\)
92\).
Упражнение \(\PageIndex{45}\)
Найдите \(\dfrac{3}{8}\) из \(\dfrac{32}{9}\).
- Ответить
\(\dfrac{4}{3} = 1 \dfrac{1}{3}\)
Упражнение \(\PageIndex{46}\)
Запишите это число в десятичной форме, используя цифры: «пятьдесят две трехтысячных»
Упражнение \(\PageIndex{47}\)
Отношение хлора к воде в растворе составляет 2 к 7. Сколько мл воды содержится в растворе, содержащем 15 мл хлора?
- Ответить
\(52 \dfrac{1}{2}\)
Упражнение \(\PageIndex{48}\)
Выполнить вычитание -8 — (-20)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Денни Бурзински и Уэйд Эллис-младший
- Лицензия
- СС BY
- Показать страницу TOC
- нет
- Теги
Умножение и деление целых чисел
Умножение и деление целых чисел — две основные операции, выполняемые над целыми числами. Умножение целых чисел — это то же самое, что и повторяющееся сложение, которое означает добавление целого числа определенное количество раз. Например, 4 × 3 означает прибавление 4 три раза, т. е. 4 + 4 + 4 = 12. Деление целых чисел означает равное группирование или деление целого числа на определенное количество групп. Например, -6 ÷ 2 означает деление -6 на 2 равные части, что дает -3. Давайте узнаем больше об умножении и делении целых чисел в этой статье.
| 1. | Что такое умножение и деление целых чисел? |
| 2. | Умножение целых чисел |
| 3. | Деление целых чисел |
| 4. | Примеры умножения и деления целых чисел |
| 5. | Свойства умножения и деления целых чисел |
6. | Часто задаваемые вопросы об умножении и делении целых чисел |
Что такое умножение и деление целых чисел?
Четыре основные арифметические операции, связанные с целыми числами:
- Сложение целых чисел
- Вычитание целых чисел
- Умножение целых чисел
- Деление целых чисел
Умножение и деление целых чисел являются наиболее важными часто используемыми арифметическими операциями. Давайте подробно изучим умножение и деление целых чисел.
Умножение целых чисел
Умножение целых чисел — это процесс многократного сложения положительных и отрицательных чисел, или мы можем просто сказать целые числа. Когда мы подходим к случаю умножения целых чисел, необходимо учитывать следующие случаи:
- Умножение 2 положительных чисел
- Умножение 2 отрицательных чисел
- Умножение 1 положительного и 1 отрицательного числа
При умножении целых чисел с двумя положительными знаками Положительное x Положительное = Положительное = 2 × 5 = 10.
При умножении целых чисел с двумя отрицательными знаками Отрицательное x Отрицательное = Положительное = –2 × –3 = 6.
При умножении целых чисел с одним знаком минус и одним знаком плюс Отрицательное x Положительное = Отрицательное = –2 × 5 = –10.
Следующая таблица поможет вам запомнить правила умножения целых чисел:
| Типы целых чисел | Результат | Пример |
|---|---|---|
| Оба целых числа положительные | Положительный | 2 × 5 = 10 |
| Оба целых числа Отрицательные | Положительный | –2 × –3 = 6 |
| 1 положительный и 1 отрицательный | Отрицательный | –2 × 5 = –10 |
Пример: Анна съедает 4 печенья в день.
Сколько печенья она съест за 5 дней? ⇒ 5 × 4 = 20 печенек.
Умножение целых чисел Правила и шаги
Умножение целых чисел очень похоже на обычное умножение. Однако, поскольку целые числа имеют дело как с отрицательными, так и с положительными числами, у нас есть определенные правила или условия, которые следует помнить при умножении целых чисел, как мы видели в предыдущем разделе. Давайте посмотрим на шаги для умножения целых чисел.
- Шаг 1: Определите абсолютное значение чисел.
- Шаг 2: Найдите произведение абсолютных значений.
- Шаг 3: После получения продукта определите знак числа в соответствии с правилами или условиями.
Давайте рассмотрим пример, чтобы лучше понять шаги. Умножить — 7 × 8.
Шаг 1: Определить абсолютное значение — 7 и 8.
|-7| = 7 и |8| = 8.
Шаг 2: Найдите произведение абсолютных значений чисел 7 и 8.
7 × 8 = 56
Шаг 3: Определите знак произведения в соответствии с правилами умножения целых чисел.
Согласно правилу умножения целых чисел, если отрицательное число умножить на положительное число, то произведение будет отрицательным числом.
Следовательно, — 7 × 8 = — 56.
Деление целых чисел
Деление целых чисел включает группировку элементов. Он включает в себя как положительные числа, так и отрицательные числа. Точно так же, как и умножение, деление целых чисел связано с теми же случаями.
- Деление 2 положительных чисел
- Деление 2 отрицательных чисел
- Деление 1 положительного и 1 отрицательного числа
При делении целых чисел с двумя положительными знаками: Положительный ÷ Положительный = Положительный → 16 ÷ 8 = 2.
При делении целых чисел с двумя отрицательными знаками: Отрицательный ÷ Отрицательный = Положительный → –16 ÷ –8 = 2
При делении целых чисел с одним знаком минус и одним знаком плюс Отрицательный ÷ Положительный = Отрицательный → –16 ÷ 8 = –2.
Следующая таблица поможет вам запомнить правила деления целых чисел:
| Типы целых чисел | Результат | Пример |
|---|---|---|
| Оба целых числа положительные | Положительный | 16 ÷ 8 = 2 |
| Оба целых числа Отрицательные | Положительный | –16 ÷ –8 = 2 |
| 1 положительный и 1 отрицательный | Отрицательный | –16 ÷ 8 = –2 |
Чтобы подвести итог и упростить задачу, при умножении или делении целых чисел нужно помнить две вещи:
- Когда знаки разные, ответ всегда отрицательный.
- При одинаковых знаках ответ всегда положительный.
Примеры умножения и деления целых чисел
Несколько примеров умножения и деления целых чисел приведены в таблице ниже:
| Умножение | Подразделение |
|---|---|
| 4 × 2 = 8 | 15 ÷ 3 = 5 |
| 4 × -2 = -8 | 15 ÷ –3 = –5 |
| -4 × 2 = -8 | –15 ÷ 3 = –5 |
| -4 × -2 = 8 | –15 ÷ –3 = 5 |
Свойства умножения и деления целых чисел
Свойства умножения и деления целых чисел помогают нам определить отношения между двумя или более целыми числами, когда они связаны операцией умножения или деления между ними.
Есть несколько свойств, связанных с умножением и делением целых чисел.
Свойства, связанные с умножением и делением целых чисел, перечислены ниже:
- Свойство замыкания
- Коммутативное свойство
- Ассоциативное свойство
- Распределительная собственность
- Идентификационное свойство
Давайте подробно разберем каждое свойство, связанное с делением и умножением целых чисел.
Свойство замыкания умножения целых чисел
Свойство замыкания указывает, что множество замкнуто для любой конкретной математической операции. Целые числа замкнуты относительно сложения, вычитания и умножения. Однако они не закрываются при делении.
| Операция | Пример |
|---|---|
| a × b — целое число | 2 × –6= –12 |
| a ÷ b не всегда целое число | –3/4 это дробь |
Свойство перестановочности умножения целых чисел
Согласно свойству перестановочности перестановка операндов местами в операции не влияет на результат.
Сложение и умножение целых чисел следуют коммутативному свойству, в то время как деление целых чисел не обладает этим свойством.
| Операция | Пример |
|---|---|
| а × б = б × а | 5 × (–6) и (–6) × 5 = –30 |
| а ÷ б ≠ б ÷ а | 15 ÷ 3 = 5, но 3 ÷ 15 = 1/5 |
Ассоциативное свойство умножения целых чисел
Согласно ассоциативному свойству изменение группировки целых чисел не меняет результат операции. Ассоциативность применяется к сложению и умножению двух целых чисел, но не к делению целых чисел.
| Операция | Пример |
|---|---|
| (а × б) × с = а × (б × с) | (5 × –3) × 2 = –30 5 × (–3 × 2) = –30 |
| (а ÷ б) ÷ в ≠ а ÷ (б ÷ в) | (20 ÷ 5) ÷ 2 = 2, но 20 ÷ (5 ÷ 2)= 8 |
Распределительное свойство умножения целых чисел
Распределительное свойство утверждает, что для любого выражения формы a (b + c), что означает a × (b + c), операнд a может быть распределен между операндами b и c как (a × b + a × c), т.
е. a × (b + c) = a × b + a × c. Умножение целых чисел является распределительным над сложением и вычитанием. Распределительное свойство не выполняется для деления целых чисел.
| Операция | Пример |
|---|---|
| a × (b + c) = (a × b) + (a × c) | 4 × (–3 + 6) = 12 (4 × –3) + (4 × 6) = 12 |
| а × (б – в) = (а × б) – (а × в) | 2 × (5 – 3) = 4 (2 × 5) – (2 × 3) = 4 |
Свойство тождества умножения целых чисел
В случае умножения целых чисел 1 является мультипликативным тождеством. В случае деления целых чисел нет элемента идентичности.
| Добавляемый идентификатор: 0 | Идентичность при умножении равна 1 |
|---|---|
| Для любого целого числа a, a + 0 = 0 + a = a | Для любого целого числа a 1 × a = a × 1 = a |
| Например, 8 + 0 = 0 + 8 = 8 | Например, (– 4) × 1 = 1 × (– 4) = – 4 |
Умножение и деление целых чисел Советы и рекомендации:
- Не существует ни самого маленького, ни самого большого целого числа.
- Наименьшее положительное целое число равно 1, а наибольшее отрицательное целое число равно -1. Правило
- PEMDAS применяется для операций над целыми числами. «Операции» — это любые из следующих действий: скобки, квадраты, степени, квадратные корни, деление, умножение, сложение и вычитание.
Статьи по теме:
Ознакомьтесь с этими интересными статьями, посвященными концепции умножения и деления целых чисел.
- Таблица умножения целых чисел
- Умножение и деление целых чисел Рабочий лист
- Калькулятор деления целых чисел
- Калькулятор умножения целых чисел
Часто задаваемые вопросы об умножении и делении целых чисел
Что такое умножение целых чисел?
Умножение целых чисел — это повторяющееся сложение чисел, означающее, что число добавляется само к себе определенное количество раз. Например, 4 × 2 означает, что 4 добавляется два раза. Отсюда следует, что 4 + 4 = 4 × 2 = 8,
Каковы свойства умножения целых чисел с примерами?
Свойства умножения целых чисел приведены ниже:
- Свойство замыкания → -2 × 3 = -6, где -2, 3 и -6 — целые числа.
- Ассоциативное свойство → (2 × 3) × (-9) = 2 × (3 × -9) = -54.
- Коммутативное свойство → -4 × -7 = -7 × -4 = 28.
- Распределительное свойство → 3 × (-4 + 2) = (3 × -4) + (3 × 2) = -6.
- Элемент идентичности → 3 × 1 = 1 × 3 = 3. 1 — это элемент идентичности.
Каковы правила умножения и деления целых чисел?
Основные правила деления и умножения целых чисел приведены ниже:
- Умножение или деление двух чисел с одинаковым знаком дает положительное число.
- Умножение или деление двух чисел с противоположными знаками дает отрицательное число.
Каковы свойства деления целых чисел?
Свойства деления целых чисел приведены ниже:
- Если мы разделим 0 на любое ненулевое целое число, ответ всегда будет 0. Это может быть математически выражено как 0 ÷ a = 0.
- Любое целое число, деленное само на себя, дает 1. Отсюда следует, что a ÷ a = 1.
- Когда целое число делится на другое целое число, оно удовлетворяет алгоритму деления, который гласит: «делимое = делитель × частное + остаток».
- При делении целого числа на 1 результатом всегда является само целое число. Например, -5 ÷ 1 = -5.
Что такое правило деления целых чисел?
Ниже приведены правила деления целых чисел:
- Положительное ÷ положительное = положительное
- Отрицательный ÷ отрицательный = положительный
- Отрицательный ÷ положительный = отрицательный
Как умножать целые числа?
При умножении целых чисел следуйте этому трюку, чтобы легко получить ответ:
- Умножайте без отрицательного знака.
- Если оба целых числа отрицательные или оба положительные , произведение будет положительным .
- Если одно целое число положительное, а другое отрицательное, произведение будет отрицательное .
Как умножать несколько целых чисел?
Если целых чисел больше двух, выполните следующие простые действия, чтобы их умножить:
- Умножьте без отрицательного знака.
