Что такое треугольник: определение, классификация, свойства
В данной публикации мы рассмотрим определение, классификацию и свойства одной из основных геометрических фигур – треугольника. Также разберем примеры решения задач для закрепления представленного материала.
- Определение треугольника
- Классификация треугольников
- Свойства треугольника
- Примеры задач
Определение треугольника
Треугольник – это геометрическая фигура на плоскости, состоящая из трех сторон, которые образованы путем соединения трех точек, не лежащих на одной прямой. Для обозначения используется специальный символ – △.
- Точки A, B и C – вершины треугольника.
- Отрезки AB, BC и AC – стороны треугольника, которые часто обозначаются в виде одной латинской буквы. Например, AB = a, BC = b, AC = c.
- Внутренность треугольника – часть плоскости, ограниченная сторонами треугольника.
Стороны треугольника в вершинах образуют три угла, традиционно обозначающиеся греческими буквами – α, β, γ и т.д. Из-за этого треугольник еще называют многоугольником с тремя углами.
Углы можно, также, обозначать с помощью специального знака “∠“:
- α – ∠BAC или ∠CAB
- β – ∠ABC или ∠CBA
- γ – ∠ACB или ∠BCA
Классификация треугольников
В зависимости от величины углов или количества равных сторон выделяют следующие виды фигуры:
1. Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°.
2. Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
3. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°.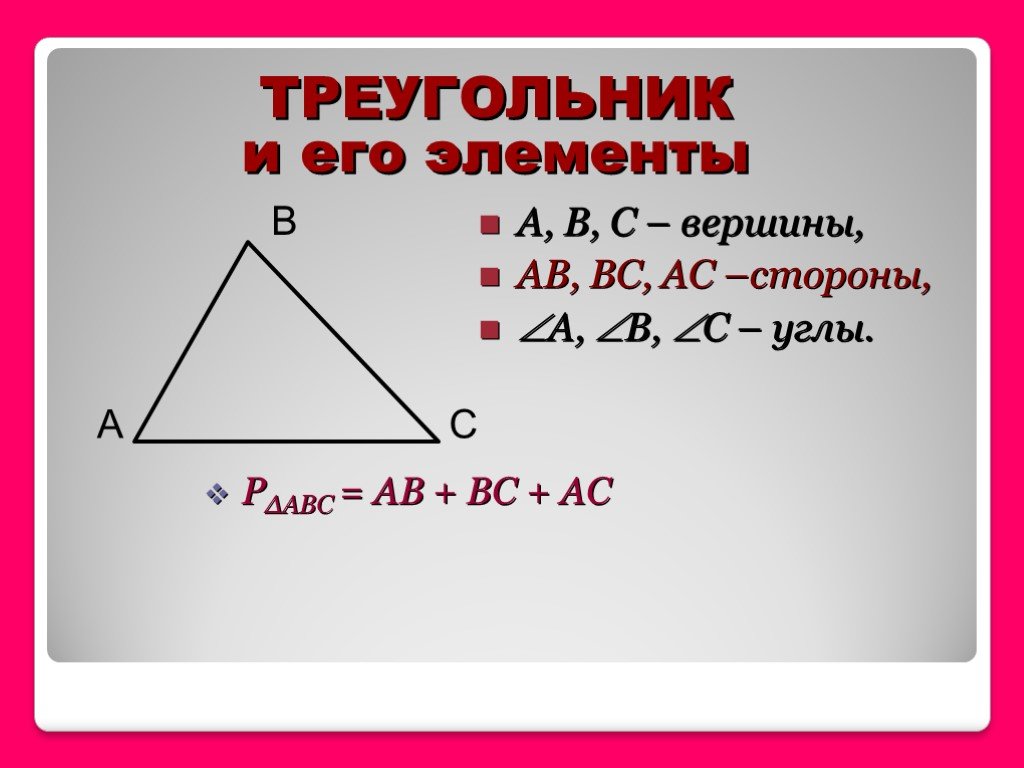
В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).
4. Разносторонний – треугольник, у которого все стороны имеют разную длину.
5. Равнобедренный – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).
6. Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
Свойства треугольника
1. Любая из сторон треугольника меньше двух оставшихся, но больше их разности. Для удобства примем стандартные обозначения сторон – a, b и с. Тогда:
b – c < a < b + c, при b > с
Это свойство применяется для проверки отрезков на предмет того, могут ли они образовывать треугольник.
2. Сумма углов любого треугольника равняется 180°. Из этого свойства следует, что в тупоугольном треугольнике два угла всегда являются острыми.
3. В любом треугольнике напротив большей стороны находится больший угол, и наоборот.
Примеры задач
Задание 1
В треугольнике известны два угла – 32° и 56°. Найдите значение третьего угла.
Решение
Примем известные углы за α (32°) и β (56°), а неизвестный – за γ.
Согласно свойству о сумме всех углов, α + β + γ = 180°.
Следовательно, γ = 180° – α – β = 180° – 32° – 56° = 92°.
Задание 2
Даны три отрезка длиной 4, 8 и 11. Выясните, могут ли они образовать треугольник.
Решение
Составим неравенства для каждого из заданных отрезков, исходя из свойства, рассмотренного выше:
11 – 4 < 8 < 11 + 4
8 – 4 < 11 < 8 + 4
11 – 8 < 4 < 11 + 8
Все они верны, следовательно, данные отрезки могут быть сторонами треугольника.
Треугольник (символ). История и значение в разных культурах
Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов. В Древнем Египте он был прямоугольным и являлся воплощением триады духовной воли, любви и высшего разума человека. Вертикальная сторона египетского треугольника составляла три единицы длины, основание— четыре, а гипотенуза — пять. Толковалась эта геометрическая фигура следующим образом: вертикальную сторону соотносили с мужским началом, основание — с женским, а гипотенуза символизировала плод их союза.
Треугольный нимб Бога Саваофа. Роспись в православном храме
Старший аркан «Повешенный» из колоды Таро герцога Висконти, XV в. Свободная нога повешенного изогнута так, что образует треугольник с прямой ногой
Ж.-Б. Рено. Свобода или смерть. На картине, созданной в эпоху Великой французской революции, масонский наугольник, как и фригийский колпак, является символами равенства
На Древнем Востоке почитали треугольник как символ природы всего сущего.
Треугольник с вершиной, соединенной с такой же геометрической фигурой, ацтеки использовали в качестве эмблемы временного цикла. Герменевтической традиции известно множество видов треугольников, имеющих различные толкования: например, данная геометрическая фигура с горизонтальной чертой почиталась ими пассивным символом, который означает воздух, а перевернутая является олицетворением чаши, которая готова принять воду, а также соответствует женскому началу.
Для средневековых алхимиков треугольник с вершиной, устремленной вверх, являлся знаком пламени, «мужского огня», а при его наложении на описанный выше знак женского начала мы получим индуистскую эмблему объединения созидающего и порождающего начал — гексаграмму. В индийской традиции такой символ толковался также и как знак любви богов ко всему земному.
В Европе же данная геометрическая фигура была известна как звезда Давида. Треугольник, вписанный в окружность, олицетворяет собой мир форм, заключенный в круге вечности. Плутарх, описывая эту геометрическую фигуру, называл пространство, ограниченное сторонами треугольника, равниной истины, на которой расположены образы всего, что было и будет.
Треугольники могут выступать и в качестве лунного символа, тогда они располагаются горизонтально и соприкасаются своими вершинами. Общая точка этих треугольников символически обозначает смерть и новолуние.
Магическая гексаграмма. Составляющие данную фигуру цифры не повторяются и при сочетании сумм вершин и сторон треугольника всегда дают число 26. В нумерологии целью создания подобных фигур было желание расширить и увеличить магическое воздействие цифр
Медаль НАСА за полет в космос. Космический корабль «Шатл» вписан в символ огня
Эзотерическое изображение пяти планет в звездах Давида: Венеры, Марса, Меркурия, Юпитера и Сатурна
В буддийской традиции два смыкающихся треугольника олицетворяют чистое пламя и Три Драгоценности Будды. Китайский символ восстановления изображается в виде треугольника с подвешенными к нему мечами, а у христиан — треугольника, образованного посредством трех пересекающихся окружностей. Это олицетворяет Троицу в единении и равенстве трех ее составляющих.
Два соединенных вершинами вертикальных треугольника разделяют символизм песочных часов, олицетворяя неумолимо идущее время и смертность. Также песочные часы часто используются для обозначения благочестивого, тихого образа жизни, краткости человеческой жизни, а также применяются как атрибут отца-времени и порой даже смерти.
Гексаграмма как оккультный символ
Два треугольника в петлицах — знаки различия отделённого командира в РККА с 1935 г.
Три треугольника под звездой на рукаве — знаки различия старшины в РККА с 1919 г.
Мандала Ваджраварахи. Средневековый тибетский свиток. Два наложенных друг на друга тре — уголь ника в форме гексаграммы символизируют единство мудрости и сострадания
Треугольники на сосудах
В эпоху неолита у ранних земледельческих народов треугольники в орнаментах символизировали воздух, землю и огонь. Они — одни из самых древних символов, связанных с сельскохозяйственными работами, природой и ее календарными циклами.
Керамический сосуд земледельцев натуфийской культуры, Египет
Троица и треугольник
Начиная с ранних христиан треугольник был символом Святой Троицы.
Равносторонний треугольник толковался как равенство и единая божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот символ составляли из трех переплетенных между собой рыб. Символ Троицы по католической традиции составлялся из трех малых треугольников, вписанных в один большой с кругами на вершинах. Три этих круга означают триединство, но каждый круг независим и совершенен сам по себе. Эта схема иллюстрировала принцип триединства и вместе с тем индивидуальности каждого составляющего Святой Троицы.
Схема Святой Троицы по католической традиции
Треугольники как символ Троицы в готической архитектуре
Треугольник в античной архитектуре
В античной традиции треугольник, обращенный вершиной вверх, символизировал стремление материи к духу. Поэтому фронтоны древнегреческих храмов в самой глубокой древности делали треугольными и всячески украшали. В отличие от поздних, более северных европейских построек наличие двускатной крыши не было вызвано климатическими условиями.
В Древней Греции был теплый климат и снега зимой не было.
Храм Зевса в Олимпии. Реконструкция
Треугольник Кеплера
В начале XVII в. знаменитый астроном Кеплер составил диаграмму соединения планет Сатурна и Юпитера. Так в астрономии называют расположение планет, при котором для земного наблюдателя эклиптические долготы равны нулю, а сами небесные тела находятся близко друг к другу или даже перекрываются. Кеплер представил это явление в виде треугольника, который вращается по зодиакальному кругу, совершая полный оборот за 2400 лет.
Великий треугольник соединения Сатурна и Юпитера
Треугольники в алхимииЧетыре стихии: Земля, Вода, Воздух и Огонь. Миниатюра из алхимического трактата XVII в.
Рождение Сына Солнца из Философского яйца. Миниатюра из алхимического трактата XVII в.
Король Земли поклоняется философской сере. Миниатюра из алхимического трактата XVII в.
Созвездие Треугольника
Точное происхождение названия этого созвездия неизвестно.
Свое название оно получило на Древнем Востоке, его знали и использовали в навигации финикийские мореходы. Для них оно символизировало священный камень пирамидальной формы. Треугольник входил в число 48 классических созвездий античности. Древние греки считали, что это — перенесенная на небо дельта Нила, что указывает на египетские корни названия созвездия. Уже в Новое время на звездном небе были выделены созвездия Южного Треугольника и Наугольника.
Созвездие Треугольника. Иллюстрация из астрономического атласа «Уранография» Я. Гевелия
Глаз в треугольнике
Символ, графически представляющий собой вписанный в треугольник глаз, называемый «глазом провидения» или «всевидящим оком», появился в Европе в XVII в. Считается, что он восходит к солярному глазу Гора древних египтян. Этот знак получил широкое распространение в барочной архитектуре, украшая фронтоны роскошных католических костелов.
В XIX в. он появился и на православных храмах, например, на фронтоне Казанского собора в Санкт-Петербурге.
Христианство рассматривало его как символ Святой Троицы. Одновременно этот символ использовался и масонами, которые трактовали его как символ абсолюта, просвещения и высшего знания. У масонов «глаз провидения» располагается над стулом мастера ложи, чтобы таким образом напоминать о всепроникающей во все тайны мудрости Творца.
Декларация прав человека и гражданина, Франция, конец XVIII в.
Герб белорусского города Браслав
Печать Соломона
Печать Соломона — другое название звезды Давида, образованной наложением друг на друга двух треугольников, т.е. гексаграммы. По преданию, царь Соломон с помощью этого знака управлял духами, заключенными в медный сосуд. Считается, что печать Соломона является мощным амулетом, способным защитить своего обладателя от влияния злых духов.
Эфиопский орден Соломоновой печати
Каббалистический амулет печать Соломона
Поделиться ссылкой
Обучение и поддержка — Программное обеспечение для записи
Привет! Как мы можем вам помочь?
ЗАГРУЗКИ И АКТИВАЦИЯ
Программное обеспечение Sibelius
Проблемы с активацией или регистрацией
5
ваш продукт?
Чат сейчас
ОБУЧЕНИЕ
Воспроизводите партии в унисон и улучшайте свою музыку с помощью этой опции.
Узнайте, как установить, запустить и настроить приложение.
Берите с собой Sibelius и все свои партитуры, куда бы вы ни отправились.
Просмотреть все руководства
ИЗДЕЛИЯ
{название статьи}
{описание статьи}
{Дата статьи}
Просмотреть все статьи
Учитесь у Avid и других
Задайте вопрос сообществу
Получите помощь и совет от других пользователей Avid
Присоединяйтесь к обсуждению
Получите информацию 09 Читайте статьи, блоги и т.
д.
Читать блоги
Пройти обучение
Совершенствовать свои навыки с помощью практического обучения
Найти курс
Получить сертификат 05z Расширить свою карьеру с отраслевой сертификацией
Сертификат пользователя Sibelius
Получить книгу
Расширьте свои знания в своем собственном темпе
Основы Sibelius
Партнеры по обучению Avid
Пройдите обучение рядом с вами через нашу сеть независимых обучающих компаний и учреждений
Найдите ALP
Станьте ALP
РЕСУРСЫ
Документация
Avid Link Documentation 9000 0002
Системные требования
Спецификации
Гарантия
Предложения поддержки
Варианты поддержки
Планы поддержки Avid Advantage
Код поддержки Avid
У вас нет плана поддержки? Получить один раз поддержку
Купить ASC для физических лиц
Купить ASC для организаций
Передача права собственности
Переназначить ваше оборудование или программное обеспечение другому лицу
Передать ваш продукт Sibelius
3 CONT 09
Служба поддержки
По вопросам с вашей учетной записью или лицензированием и активацией программного обеспечения Avid
Контакт
Поддержка учетной записи
По вопросам, связанным с вашей учетной записью или лицензированием и активацией программного обеспечения Avid.
Начать чат
Создать обращение >
Служба поддержки интернет-магазина
По вопросам размещения заказа, выставления счетов или возврата онлайн-заказа
Контакт
Служба поддержки интернет-магазина
При возникновении проблем с размещением заказа, выставлением счетов или возвратом онлайн-заказа.
Общаться сейчас
Создать обращение >
Техническая поддержка
При возникновении проблем с продуктом, решением или услугой Avid
Контакт
Техническая поддержка
Техническая поддержка Требуется контракт на активную поддержку, подписка или код поддержки Avid.
Создать кейс
Клиенты со стандартными планами поддержки должны приобрести код поддержки Avid (ASC) для поддержки по телефону в обычные рабочие часы.
Клиенты с планами поддержки ExpertPlus, Elite или Cloud могут звонить круглосуточно и без выходных по указанным ниже номерам.
Позвоните нам
Америка
1-800-800-2843 / +1 978-275-2476
9 Европа
Великобритания: +44 3308 085 382
Германия: +49180 132 4009
Франция: +33 141 494 040
Испания: +34 518 889 411
Финляндия: +35 892 290 1690
Швеция: +46 844 255 90
Дания: +45 39 8 55 909 9 8002843
Азия
Южная Корея: +822 3483 3226
Австралия: +612 8228 1456
Япония: +81 3 4565 4184
Остальная часть Азиатско-Тихоокеанского региона: +81 3 4565 4184
462
Если страна нет в списке, наберите: +44 3308 085 382
Живой звук — Avid VENUE / S3L / S6L — нажмите здесь 9\circ\,$ (угол),
может быть нет треугольника , ровно один треугольник или два треугольника которые соответствуют информации SSA.
Пусть $\,a\,$ и $\,b\,$ — положительные действительные числа, используемые для обозначения длин двух сторон треугольника.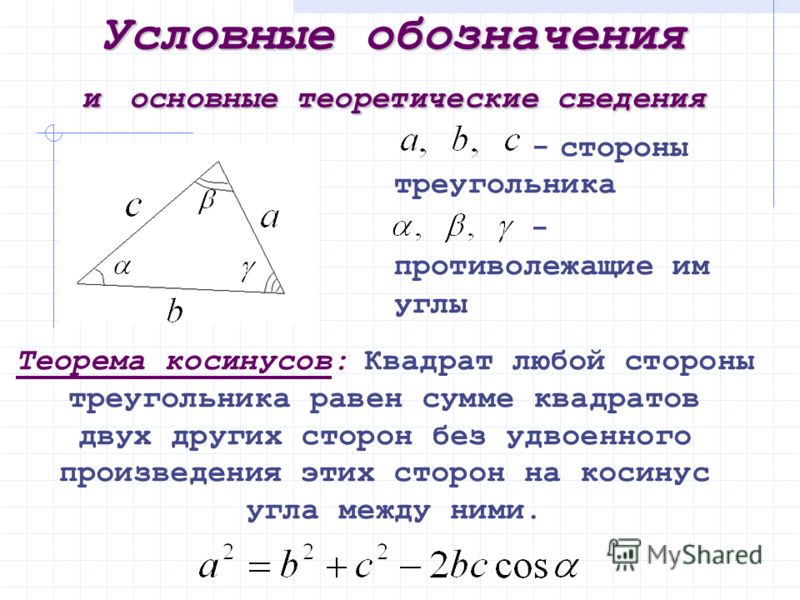 Пусть $\,\theta\,$ обозначает меру невключенного угла. Как показано справа, $\,a\,$ $\,b\,$ и $\,\theta\,$ образуют ситуацию SSA — две стороны и невключенный угол. Чтобы значительно сократить количество слов, я говорю что-то вроде:
|
В следующей последовательности эскизов $\,b\,$ и $\,\theta\,$ считаются постоянными, а $\,\theta\,$ является острым углом.
Сторона длины $\,a\,$ становится все больше и больше:
$0 Когда $\,a\,$ меньше $\,b\sin\theta\,$, это слишком мало, чтобы достичь пунктирной линии.Независимо от того, какой угол между $\,a\,$ и $\,b\,$ треугольник не может быть завершен. Для $\,0 нет треугольника | $0 нет треугольника, определяемого $\,a\,$ $\,b\,$ и $\,\theta\,$ | |||
$a = b\sin\theta$Когда $\,a\,$ достигает длины высоты ($\,a = b\sin\theta\,$), тогда ровно столько, чтобы попало в пунктирную линию и образовало (правильный) треугольник.  Для $\,a = b\sin\theta\,$ существует ровно один (прямоугольный) треугольник | $a = b\sin\theta$ ровно один (прямоугольный) треугольник, определяемый $\,a\,$ $\,b\,$ и $\,\theta\,$ | |||
$\,b\sin\тета Это самый интересный случай!Этот случай является причиной отсутствия теоремы о конгруэнтности SSA. Для значений $\,a\,$ строго между $\,b\sin\theta\,$ и $\,b\,$ Таким образом, имеются два разных треугольника , которые соответствуют информации SSA. Для $\,b\sin\theta двух различных треугольников |
два разных треугольника, определяемых $\,a\,$ $\,b\,$ и $\,\theta\,$ | |||
$а = б$Для $\,a = b\,$ существует ровно один равнобедренный треугольник, определяемый сторонами $\,a\,$ и $\,b\,$ и невключенным углом $\,\theta\,.  $ | $a = b$ ровно один равнобедренный треугольник | |||
$а > б$Когда $\,a\,$ больше, чем $\,b\,$, то окружность радиуса $\,a\,$ пересекает пунктирную линиюв двух разных точках. Однако, только одна из этих точек дает треугольник с внутренним углом $\,\theta\,.$ Для $\,a > b\,$ существует ровно один треугольник | $a > b$ ровно один треугольник |
Резюме: Границы для нулевого, одного, двух треугольников в конфигурации SSA
На этом рисунке показаны описанные выше ситуации SSA.
Сторона $\,b\,$ и угол $\,\theta
В числовой строке показаны значения $\,a\,$, соответствующие нет , один и два треугольника .
Красный (без $\,\треугольника\,$),
синий (два $\,\треугольника\,$s),
и черный (один $\,\треугольник\,$)
интервалы изменяются
в зависимости от значений $\,b\,$ и $\,\theta\,.$
Введите свои значения для $\,b\,$ и $\,\theta\,$ ниже — получайте удовольствие! 9\циркуляр
Примечание:
Если угол $\,\theta\,$ тупой (или прямой), то ситуация иная.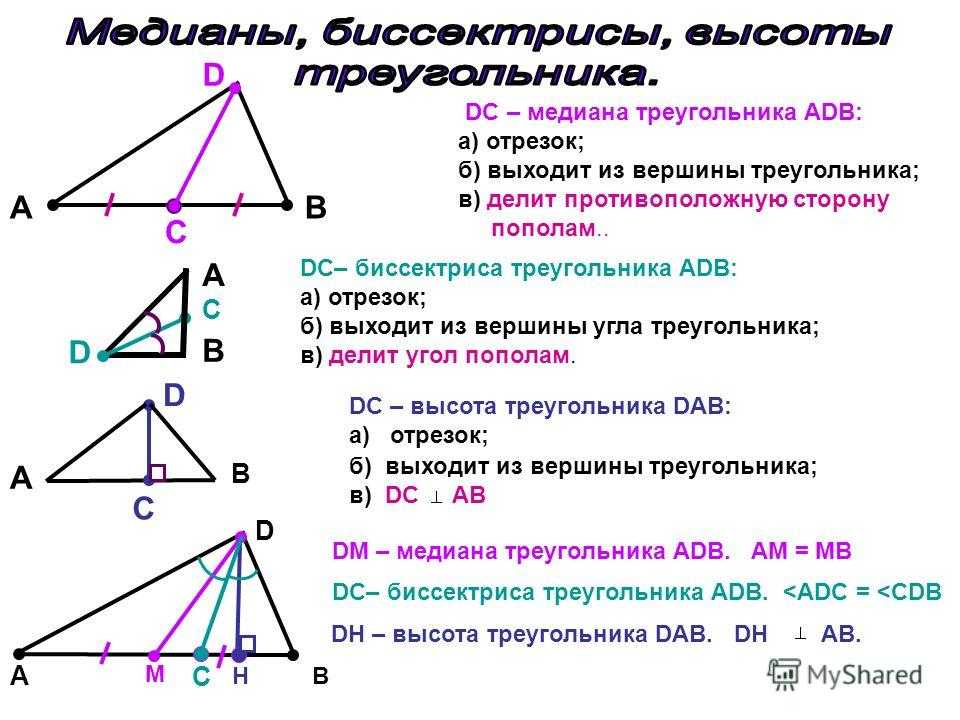
В этом случае треугольник не существует до $\,a > b\,$, в которой существует единственный треугольник:
Практика рисования кейсов SSA
| Получите случайную ситуацию SSA, нажав ниже. Зарисуйте данную ситуацию на листе бумаги — сделайте это примерно в масштабе, но на самом деле ничего не измеряйте. На основе вашего эскиза предположите, сколько треугольников соответствуют этой конфигурации SSA. Тогда проверьте свою догадку. |
Ваш браузер не поддерживает аудио элементы.
ПРОЧТЕНИЕ, ЧАСТЬ 2
Введение в функцию арксинуса и примеры
Возможно, вы сетуете:
Вот хорошие новости:
(ноль, один или два треугольника),
, если вы сделаете математику правильно!
Проиллюстрируем тремя подобными примерами.
В каждом из них вам дан угол и его противоположная сторона, а также вторая сторона.
Суть вот в чем: осознайте, что это ситуация SSA, и будьте осторожны !
Во всех этих примерах $\,\beta\,$ обозначает угол (изначально неизвестный) от второй стороны.
9\ circ \ приблизительно 1,34}
\конец{собрать}
$$ $
Следовательно, не существует углов $\,\beta\,$ с $\,\sin\beta = 1,34\,.$У нас могло бы быть отметил, что $\,a > b\,$ помещая нас в «один треугольник» категория. Нам не нужно было этого делать — математика сказала нам! |
Комментарии к обозначениям при решении треугольников
При именовании треугольников принято использовать:
 \circ — D\,$’,
тогда $\,D\,$ относится к мера угла при вершине $\,D\,.$ Обозначение треугольника в Precalculus проще, чем обозначение треугольника в Geometry.
Неудобно писать что-то вроде ‘$\,\sin(m\angle P)\,$’. Громоздкая нотация (без необходимости в ней) может сделать простые вещи сложными. Итак — в Precalculus — , когда нет возможной путаницы , |
Полный пример:
Использование закона синусов для исследования конфигурации «SSA» 9\circ\,$ угол с противоположной стороной длины $\,23\,.
$ Другая сторона имеет длину $\,30\,.$ Если возможно, решите треугольник.
Округление углов до одного десятичного знака и сторон до двух десятичных знаков.
Любое значение, используемое внутри арксинуса, должно быть округлено как минимум до четырех знаков после запятой.
РЕШЕНИЕ:
| Полезно сделать набросок для определения обозначений. (Попробуйте сделать примерно в масштабе, но обязательно ничего не меряй!) Обратите внимание, что это ситуация «SSA», и будьте осторожны! Сделайте предположение о количестве треугольников, определяемом информацией SSA. Похоже на ситуацию с двумя треугольниками! | Также полезно использовать таблицу (или таблицы) для организации результатов:
Таблица(и) будет заполняться по мере завершения вычислений.  В этом примере таблицы повторяются, При самостоятельном решении таких задач,
| Вы можете использовать
WolframAlpha для выполнения вычислений. |