Таблица котангенсов | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Котангенс, также как и тангенс, является отношением катетов друг к другу. Функция котангенса отличается от своего брата-близнеца только тем, что тангенс – это отношение противолежащего катета к прилежащему относительно угла α, а котангенс – отношение прилежащего к противолежащему. Таким образом, котангенс является функцией, обратной от тангенса, и зная одну из них можно с легкостью найти другую.
Чаще всего в одном решении применяется только одно из данных отношений. В случае если дан котангенс угла α, можно определить значение угла, соответствующее заданным числам, в таблице, приведенной ниже.
Найти котангенс угла ctg(α), зная угол
Угол α
Таблица котангенсов от 0° до 180°
|
|
|
|
|
Таблица котангенсов от 181° до 360°
|
|
|
|
|
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функции y=sin(x) и ее график.
График функции (синусоида)
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 8) наибольшее и наименьшее значения функции.
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).
Рис.1.
Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции — все действительные числа. Это можно записать так:
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции область значений: . Это можно записать так:.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при Наименьшее значение функции равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при.
Это можно записать так:.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при Наименьшее значение функции равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при.
Синус — нечетная функция: , поэтому ее график симметричен относительно начала координат.
Синус — периодическая функция с наименьшим положительным периодом : , таким образом, через промежутки длиной вид графика функции повторяется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной , а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние , где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение , то есть график функции проходит через начало координат.
На оси значение . Поэтому необходимо найти такие значения , при которых , то есть ордината соответствующей точки единичной окружности, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при (см. рис. 1).
Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, при всех , а также, учитывая период, при всех .
Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому при .
Промежутки возрастания и убывания. Учитывая периодичность функции с периодом , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .
Если (рис. 3, а), то при увеличении аргумента ордината соответствующей точки единичной окружности увеличивается (то есть , следовательно, на этом промежутке функция возрастает. Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков
Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков
Рис.2 Рис.3
Если (рис.3,б), то при увеличении аргумента ордината соответствующей точки единичной окружности уменьшается (то есть ), таким образом, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции . Учитывая периодичность этой функции (с периодом ), достаточно сначала построить график на любом промежутке длиной , например на промежутке . Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината соответствующей точки единичной окружности. На рисунке 4 показано построение графика функции на промежутке . Учитывая нечетность функции (ее график симметричен относительно начала координат), для построения графика на промежутке отображаем полученную кривую симметрично относительно начала координат (рис.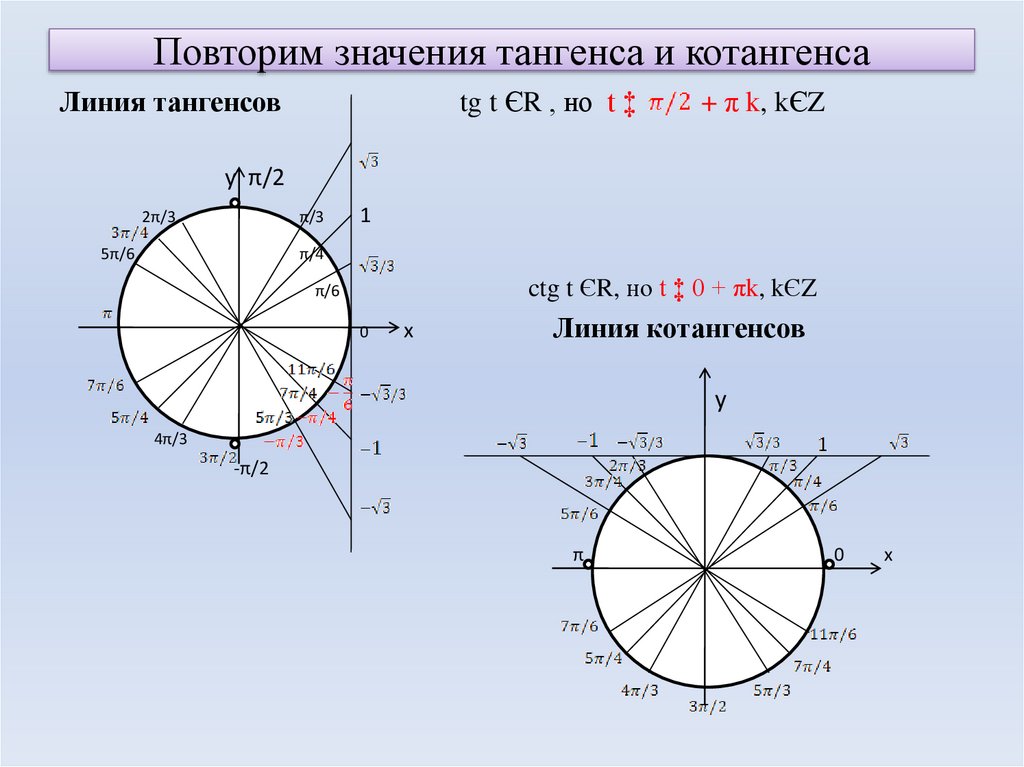 5).
5).
Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной , то, учитывая периодичность синуса (с периодом ), повторяем вид графика на каждом промежутке длиной (то есть переносим параллельно график вдоль оси на , где k — целое число). Получаем график, который называется синусоидой .(Рис.6)
Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой . Такие процессы называют гармоническими колебаниями.
График функции можно получить из синусоиды сжатием или растяжением ее вдоль координатных осей и параллельным переносом вдоль оси . Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой , где А — амплитуда
колебания, — частота, — начальная фаза, — период колебания.
СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число).
- Область значений:
-
Функция четная:
(график симметричен относительно оси ).
- Функция периодическая с периодом :
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции — все действительные числа. Это можно записать так:
.
Рис.7
Для точек единичной окружности абсциссы находятся в промежутке и принимают все значения от -1 до 1, поскольку через любую точку отрезка оси абсцисс (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции . Это можно записать так: .
Следовательно, область значений функции . Это можно записать так: .
Как видим, наибольшее значение функции равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при .
Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при .
Косинус — четная функция: , поэтому ее график симметричен относительно оси .
Косинус — периодическая функция с наименьшим положительным периодом : . Таким образом, через промежутки длиной вид графика функции повторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение . На оси значение . Поэтому необходимо найти такие значения , при которых , то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при .
Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 0 при , а также, учитывая период, при всех .
Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому при
Промежутки возрастания и убывания. Учитывая периодичность функции , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .
Если (рис. 9, а), то при увеличении аргумента абсцисса соответствующей точки единичной окружности уменьшается (то есть ), следовательно, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков .
Если (рис. 9, б), то при увеличении аргумента абсцисса соответствующей точки единичной окружности увеличивается (то есть ), таким образом, на этом промежутке функция возрастает. Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков .
Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков .
Рис.8 Рис.9
Проведенное исследование позволяет построить график функции аналогично тому, как был построен график функции . Но график функции можно также получить с помощью геометрических преобразований графика функции , используя формулу
Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки а также
абсциссы и ординаты этих точек. Так как , то при повороте
прямоугольника около точки на угол — против часовой стрелки он перейдет в прямоугольник . Но тогда . Следовательно, 00.
Укажем также формулы, которые нам понадобятся далее:.
Тогда,
Таким образом, .
Учитывая, что , график функции можно получить из графика функции его параллельным переносом вдоль оси на (рис. 11). Полученный график называется косинусоидой (рис. 12).
11). Полученный график называется косинусоидой (рис. 12).
Рис.11
Рис.12
График функции (тангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
Диаграммы тангенса и котангенса | Brilliant Math & Science Wiki
Из определения функций тангенса и котангенса мы имеем
\[ \tan(\theta)= \frac{\sin(\theta)}{\cos(\theta)},\ quad \cot( \theta)= \frac{\cos(\theta)}{\sin(\theta)}. \]
\]
Таким образом, \(\tan(\theta)\) не определено для значений \ (\theta\) такой, что \(\cos(\theta) = 0\). Теперь рассмотрим график \(\cos (\theta)\):
Из этого графика видно, что \(\cos(\theta) = 0\), когда \(\theta = \frac{\pi}{2} + k\pi\) для любого целого числа \(k\) . Это означает, что функция тангенса имеет вертикальные асимптоты при этих значениях \(\theta\).
Касательная функция стремится к положительной или отрицательной бесконечности в этих асимптотах? Поскольку \(\theta\) приближается к \(\frac{\pi}{2}\) снизу, \(\big(\theta\) принимает значения меньше, чем \(\frac{\pi}{2}\), а все ближе и ближе к \(\frac{\pi}{2}\big),\) \(\sin (\theta) \) принимает положительные значения, которые все ближе и ближе к \(1\), а \( \cos (\theta)\) принимает положительные значения, которые все ближе и ближе к \(0\). Это показывает, что \(\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\) положителен и стремится к бесконечности, поэтому \(\tan(\theta)\) имеет положительная вертикальная асимптота как \(\theta \rightarrow \frac{\pi}{2} \) снизу. С помощью аналогичного анализа, когда \(\theta\) приближается к \(\frac{\pi}{2}\) сверху, \(\big(\theta\) принимает значения больше, чем \(\frac{\pi}{ 2}\) по мере приближения к \(\frac{\pi}{2}\big),\) \(\sin (\theta) \) принимает положительные значения, которые все ближе и ближе к \(1\ ), а \(\cos (\theta)\) принимает отрицательные значения, которые все ближе и ближе к \(0\). Это показывает, что \(\tan(\theta)\) имеет отрицательную вертикальную асимптоту как \(\theta \rightarrow \frac{\pi}{2} \) сверху. Ниже показан график касательной для области \(0 \leq \theta \leq 2\pi\):
С помощью аналогичного анализа, когда \(\theta\) приближается к \(\frac{\pi}{2}\) сверху, \(\big(\theta\) принимает значения больше, чем \(\frac{\pi}{ 2}\) по мере приближения к \(\frac{\pi}{2}\big),\) \(\sin (\theta) \) принимает положительные значения, которые все ближе и ближе к \(1\ ), а \(\cos (\theta)\) принимает отрицательные значения, которые все ближе и ближе к \(0\). Это показывает, что \(\tan(\theta)\) имеет отрицательную вертикальную асимптоту как \(\theta \rightarrow \frac{\pi}{2} \) сверху. Ниже показан график касательной для области \(0 \leq \theta \leq 2\pi\):
График тангенса по всей его области выглядит следующим образом:
Аналогично, \(\cot(\theta)\) не определено для значений \(\theta\), таких что \(\sin(\theta) = 0\). Из графика \(\sin (\theta),\) мы видим, что \(\sin(\theta) = 0\), когда \(\theta = 0 + k\pi\) для любого целого числа \(k\ ), из чего следует, что функция котангенса имеет вертикальные асимптоты при этих значениях \(\theta:\)
Заметим, что из определения тангенса и котангенса мы получаем следующее соотношение между функциями тангенса и котангенса:
\[ \tan(\theta) = \frac{\sin (\theta)}{\cos (\ тета)} = \ гидроразрыва {1} {\ \ \ гидроразрыва {\ соз (\ тета)} {\ грех (\ тета)} \ \} = \ гидроразрыва {1} {\ кроватки (\ тета)}. \]
\]
Действительно, мы можем видеть, что на графиках тангенса и котангенса функция тангенса имеет вертикальные асимптоты, где функция котангенса имеет значение 0, а функция котангенса имеет вертикальные асимптоты, где функция тангенса имеет значение 0.
Графики тангенса и котангенса удовлетворяют следующим свойствам:
- диапазон: \((-\infty, \infty)\)
- период: \(\pi\)
- обе нечетные функции.
Из графиков функций тангенса и котангенса видно, что периоды тангенса и котангенса равны \(\pi\). В тригонометрических тождествах мы увидим, как доказать периодичность этих функций с помощью тригонометрических тождеств.
Какие значения \(\theta\) в интервале \([0, \pi]\) удовлетворяют \(\tan(\theta) = \cot(\theta)?\) Можно ли это увидеть из графиков функции тангенса и котангенса? 92 = 1\). Это выполняется для \(\tan \theta = \pm 1\) или \(\theta = \frac{\pi}{4}, \frac{3\pi}{4}\).
Из графиков тангенса и котангенса также видно, что точками пересечения двух графиков в области \([0,\pi]\) являются \( \big( \frac{\pi}{4}, 1 \big)\) и \( \big( \frac{3\pi}{4}, -1 \big).
\ _\square \)
Котангенс — Формула, График, Область, Диапазон
Котангенс — одна из 6 тригонометрических функций. Обычно его называют «кроваткой». Как и другие тригонометрические отношения, формула котангенса также определяется как отношение сторон прямоугольного треугольника. Формула cot x равна отношению основания и перпендикуляра прямоугольного треугольника. Вот 6 основных тригонометрических функций и их сокращения.
| Тригонометрическая функция | Аббревиатура |
|---|---|
| Синусоидальная функция | грех |
| Функция косинуса | потому что |
| Функция касания | желтовато-коричневый |
| Функция косеканса | КСК |
| Функция секущей | сек |
| Функция котангенса | детская кроватка |
Давайте узнаем больше о котангенсе, изучив его определение, формулу cot x, его область определения, диапазон, график, производную и интеграл. Также мы увидим, каковы значения котангенса на единичной окружности.
Также мы увидим, каковы значения котангенса на единичной окружности.
| 1. | Что такое котангенс? |
| 2. | Формула котангенса |
| 3. | Свойства котангенса |
| 4. | Закон котангенса |
| 5. | Период котангенса |
| 6. | Котангенс единичной окружности |
| 7. | Домен, диапазон и график котангенса |
| 8. | Производная и интеграл от котангенса |
| 9. | Часто задаваемые вопросы о котангенсе |
Что такое котангенс?
Котангенс — одно из основных тригонометрических соотношений. Фактически это одно из обратных тригонометрических соотношений csc, sec и cot. Обычно его обозначают как «кроватка х», где х — угол между основанием и гипотенузой прямоугольного треугольника. Альтернативные названия котангенса — котангенс и котангенс х. Котангенс угла в прямоугольном треугольнике определяется как отношение прилежащей стороны (стороны, прилежащей к углу) к противолежащей стороне (стороны, противолежащей углу).
Альтернативные названия котангенса — котангенс и котангенс х. Котангенс угла в прямоугольном треугольнике определяется как отношение прилежащей стороны (стороны, прилежащей к углу) к противолежащей стороне (стороны, противолежащей углу).
Котангенс Формула
Формула котангенса для угла θ: cot θ = (прилежащая сторона) / (противоположная сторона). . Рассмотрим прямоугольный треугольник ABC, образующий прямой угол в точке B. Тогда AB — сторона, примыкающая к A, а BC — сторона, противолежащая A. Тогда котангенс треугольника A (который записывается как детская кроватка A),
детская кроватка A = (прилегающая сторона A) / (противоположная сторона A) = (AB) / (BC).
Например, если AB = 3 и BC = 4, то кроватка A = 3/4.
Свойства котангенса
Мы уже знаем, что кроватка x = (Смежный) / (Противоположный). Помимо этого, существует несколько других формул отношения котангенса, в которых котангенс может быть записан через другие тригонометрические отношения.
Котангенс относительно Cos и Sin
Мы знаем, что sin θ = (Противоположный) / (Гипотенуза) и cos θ = (Смежный) / (Гипотенуза). Если мы разделим cos θ на sin θ , мы получим
(cos θ) / (sin θ) = (Смежный) / (Гипотенуза) × (Гипотенуза) / (Противоположный)
= (Смежный) / (Противоположный)
= кроватка θ
Следовательно, кроватка θ = (cos θ) / (sin θ) — это формула кроватки x с точки зрения cos и sin.
Котангенс через Tan
Мы знаем, что tan θ = (Противоположный)/(Смежный) и cot θ = (Смежный)/(Противоположный). Таким образом, cot и tan обратны друг другу. Таким образом, мы можем написать cot θ = 1/tan θ и tan θ = 1/cot θ. Таким образом, раскладушка с точки зрения загара есть. раскладушка θ = 1/тангенс θ. Существует еще одна формула для записи кроватки в терминах загара: cot θ = тангенс (π/2 — θ) (или) тангенс (90° — θ).
Котангенс через косек
Из одного из тождеств Пифагора csc 2 θ — ctg 2 θ = 1. Отсюда получаем cot 2 θ = csc 2, Если взять квадратный корень с обеих сторон, кроватка θ = √(csc 2 θ — 1). Следовательно, детская кроватка в терминах csc равна кроватка θ = √(csc 2 θ — 1)
Отсюда получаем cot 2 θ = csc 2, Если взять квадратный корень с обеих сторон, кроватка θ = √(csc 2 θ — 1). Следовательно, детская кроватка в терминах csc равна кроватка θ = √(csc 2 θ — 1)
Закон котангенса
Рассмотрим треугольник ABC, где AB = c, BC = a и CA = b. Закон котангенса похож на закон синусов, но включает половинные углы. Закон котангенса гласит: (cot A/2) / (s — a) = (cot B/2) / (s — b) = (cot C/2) / (s — c). Здесь s — полупериметр треугольника. т. е. s = (a + b + c)/2.
Знак котангенса
Отношение котангенса (разумеется, как tan, так и cot) положительно только в первом и третьем квадрантах. Он отрицателен во втором и четвертом квадрантах. Таким образом,
- раскладушка (π — θ) = — раскладушка θ (2 -й квадрант)
- раскладушка (π + θ) = раскладушка θ (3 -й -й квадрант)
- раскладушка (2π — θ) = — раскладушка θ (4 -й квадрант)
- раскладушка (2π + θ) = раскладушка θ (1 ст квадрант)
Период котангенса
Мы знаем, что все тригонометрические функции являются периодическими функциями. Кроме того, из предыдущего раздела мы знаем, что кроватка (2π + θ) = кроватка θ . Но функция котангенса может иметь меньший период π (поскольку функция котангенса положительна в первом и третьем квадранте, где углы в третьем квадранте равны π + угол в первом квадранте). Таким образом, период котангенса равен π. т. е. раскладушка (π + θ) = раскладушка θ .
Кроме того, из предыдущего раздела мы знаем, что кроватка (2π + θ) = кроватка θ . Но функция котангенса может иметь меньший период π (поскольку функция котангенса положительна в первом и третьем квадранте, где углы в третьем квадранте равны π + угол в первом квадранте). Таким образом, период котангенса равен π. т. е. раскладушка (π + θ) = раскладушка θ .
Котангенс отрицательного угла
Котангенс отрицательного угла равен отрицательному значению котангенса положительного угла. т. е. кроватка (-x) = -кроватка x для любого x в области. Отсюда можно сделать вывод, что котангенс является нечетной функцией.
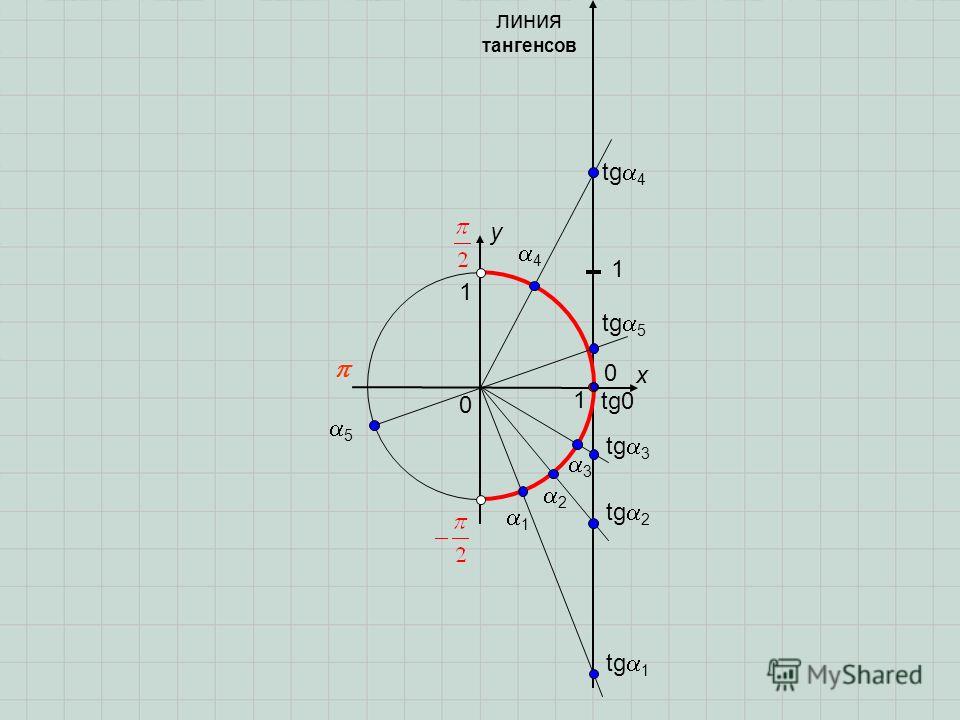
Котангенс единичной окружности
Мы знаем, что каждая точка на единичной окружности дает значения cos и sin соответствующего угла. Чтобы найти котангенс соответствующего угла, мы просто делим соответствующее значение cos на соответствующее значение sin, потому что у нас есть формула cot x, определяемая как cot x = (cos x) / (sin x).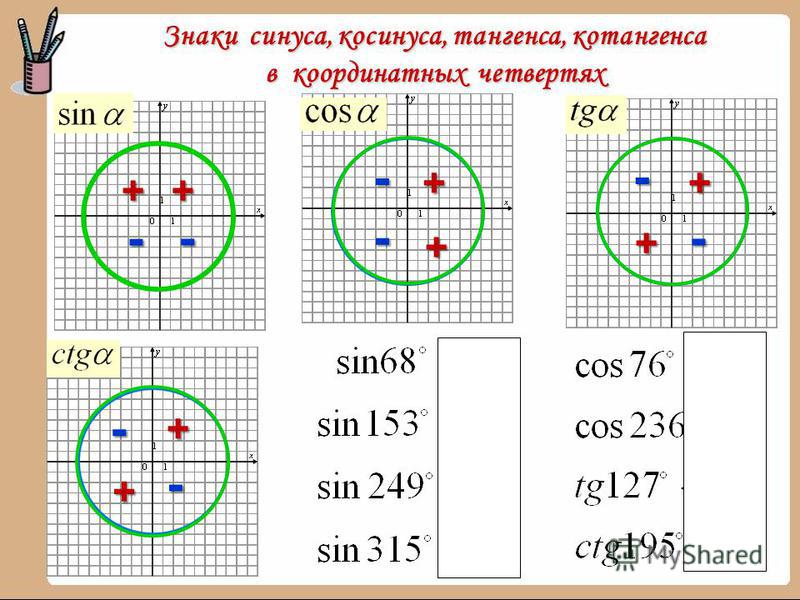 Здесь мы можем видеть значения cot θ для некоторых стандартных углов.
Здесь мы можем видеть значения cot θ для некоторых стандартных углов.
Таким же образом мы можем вычислить котангенс всех углов единичной окружности. Вот единичный круг с функцией котангенса.
Домен, диапазон и график котангенса
В этом разделе давайте посмотрим, как мы можем найти область определения и область значений функции котангенса. Кроме того, мы увидим процесс построения графика в своей области.
Область и диапазон котангенса
В предыдущем разделе мы видели, что кроватка не определена при 0° (0π), 180° (1π) и 360° (2π) (другими словами, котангенс не определен везде, где sin x равен нулю, потому что cot x = (cos x)/(sin x)). Мы знаем, что sin x равен нулю для целых чисел, кратных π, поэтому функция котангенса не определена для всех целых чисел, кратных π. Таким образом, кроватка nπ НЕ определена ни для какого целого числа n. Таким образом, областью определения котангенса является множество всех действительных чисел (R), кроме nπ (где n ∈ Z). Опять же, из единичного круга мы можем видеть, что функция котангенса может давать все действительные числа, и, следовательно, ее областью значений является множество всех действительных чисел (R). Таким образом,
Опять же, из единичного круга мы можем видеть, что функция котангенса может давать все действительные числа, и, следовательно, ее областью значений является множество всех действительных чисел (R). Таким образом,
- Область определения котангенса — это множество действительных чисел, кроме всех целых чисел, кратных π
- Областью котангенса является множество всех действительных чисел
т. е. cot x : R — {nπ / n ∈ Z} → R
График котангенса
Поскольку функция котангенса НЕ определена для целых чисел, кратных π, на графике есть вертикальные асимптоты для всех кратных π котангенса. Кроме того, из единичного круга (в одном из предыдущих разделов) мы можем видеть, что котангенс равен 0 во всех нечетных кратных π/2. Кроме того, из единичного круга мы можем видеть, что в интервале, скажем (0, π), значения кроватки уменьшаются по мере увеличения углов. Следовательно, ctg — убывающая функция. Таким образом, график функции котангенса выглядит так.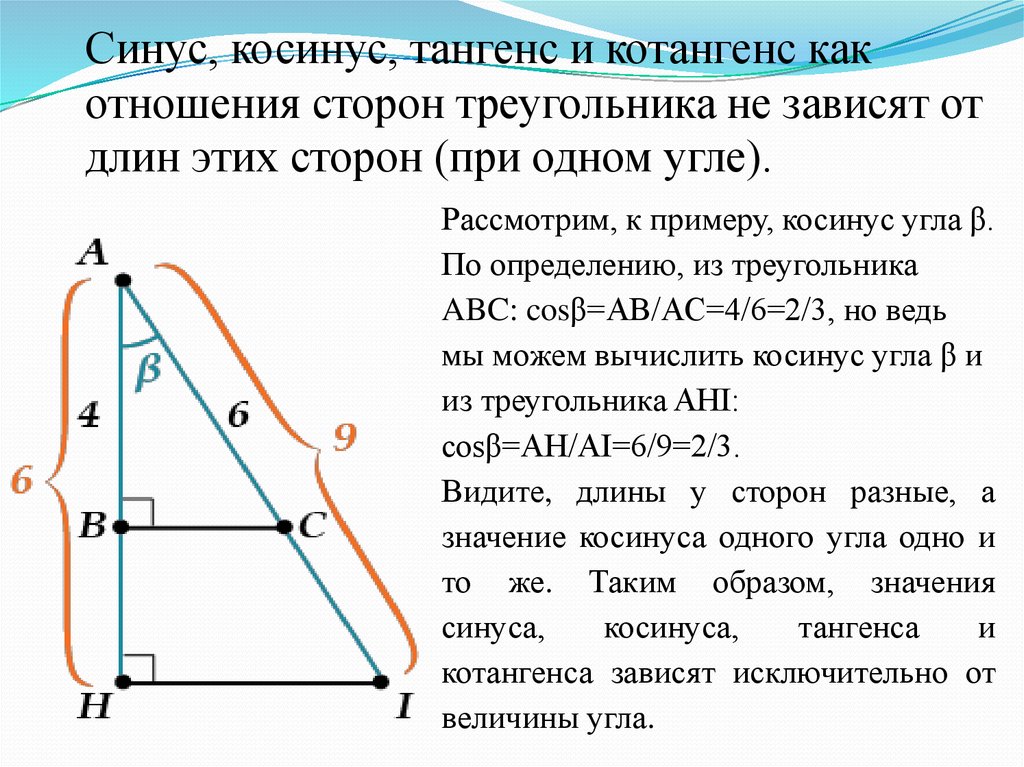
Производная и интеграл от котангенса
Чтобы найти производную и интеграл котангенса, мы используем формулу тождественного котангенса cot x = (cos x) / (sin x). Давайте посмотрим, как.
Производная котангенса
Пусть y = cot x = (cos x) / (sin x). Тогда по правилу частных
y’ = [sin x d/dx(cos x) — cos x d/dx(sin x)] / (sin x) 2
= [sin x (- sin x) — cos x (cos x)] / sin 2 x
= [-sin 2 x — cos 2 x] / sin 2 x
= — [sin 2 x + cos 2 x] / sin 909029 002 = — 1/sin 2 x — [Используя тригонометрическое тождество sin 2 x + cos 2 x = 1]
= -csc 2 x — [Поскольку sin x = 1/csc x и csc x = 1/sin x]
Таким образом, производная от cot x равна -csc 2 x.
Интеграл от котангенса
∫ cot x = ∫ (cos x) / (sin x) dx
Вычислим этот интеграл методом подстановки. Для этого пусть sin x = u. Тогда cos x dx = du.
Для этого пусть sin x = u. Тогда cos x dx = du.
Тогда, используя приведенный выше интеграл, получим
∫ (1/u) du = ln |u| + C, где C — постоянная интегрирования.
Замените u = sin x здесь,
∫ кроватка x dx = ln |sin x| + C
Таким образом, интеграл от cot x равен ln |sin x| + C.
Важные моменты по котангенсу:
- Cot x Формула: cot x = (cos x) / (sin x)
- Некоторые важные формулы котангенса:
детская кроватка x = (cos x)/(sin x)
детская кроватка х = 1/загар х
детская кроватка (-x) = — детская кроватка x
детская кроватка θ = √(csc 2 θ — 1) - Домен cot x равен R — {nπ}, а его диапазон равен R.
- Функция котангенса имеет вертикальные асимптоты при всех кратных π.
Темы по теме:
- Детская кроватка — Формула загара
- Тригонометрия
- Тригонометрический калькулятор
- Калькулятор арккотангенса
- Детская кроватка 53 градуса
- Детская кроватка 18 градусов
- Детская кроватка 1 градус
Часто задаваемые вопросы о котангенсе
Что такое котангенс в тригонометрии?
Котангенс является одним из тригонометрических отношений и определяется как cot x = (прилежащая сторона)/(противоположная сторона) для любого угла x между основанием и гипотенузой в прямоугольном треугольнике.
Что такое формулы котангенса?
Некоторые из важных формул кроватки x:.
- детская кроватка x = (смежный)/(напротив)
- раскладушка x = (cos x)/(sin x)
- детская кроватка х = 1/тан х
- детская кроватка (π/2 — x) = загар x
- детская кроватка (π + x) = детская кроватка x
- детская кроватка (2π + x) = детская кроватка x
- детская кроватка (-x) = — детская кроватка x
- раскладушка θ = √csc²θ — 1
Является ли котангенс обратным тангенсу?
Нет, обратным тангенсом является арктангенс. Пишется как загар -1 . Но (tan x) -1 = 1/tan x = кроватка x. (tan x) -1 и tan -1 x НЕ совпадают.
Что такое домен и диапазон котангенса?
Область определения котангенса равна R — {nπ, где n — целое число}, а диапазон значений котангенса равен R. Здесь R — множество всех действительных чисел.
Что является противоположностью формулы котангенса?
Мы не используем терминологию противоположности котангенса.

 804
804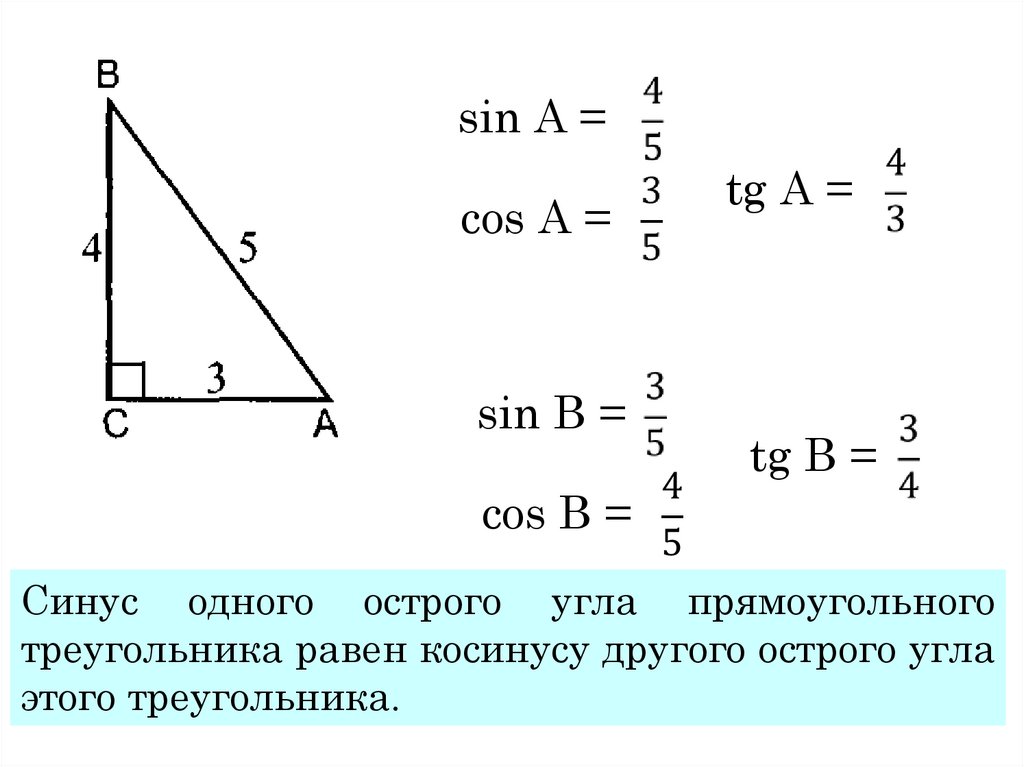 7536
7536 2309
2309 2126
2126 7002
7002 6003
6003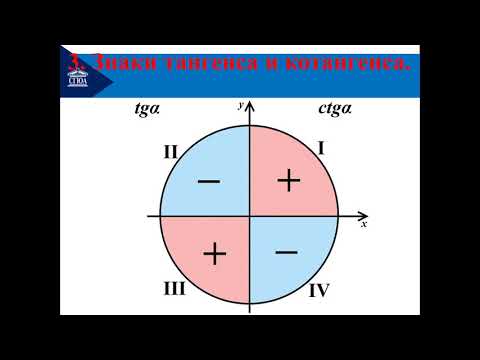 1154
1154 3315
3315 327
327 5543
5543 1051
1051 3249
3249 8693
8693 0503
0503 6363
6363 \ _\square \)
\ _\square \)