При $k=0$ получаем $x_{0} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4}{3} +i\cdot \sin \frac{\pi /4}{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)=\sqrt[{6}]{2} \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)$.
При $k=1$ получаем
\[\begin{array}{l} {x_{1} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4+2\pi }{3} +i\cdot \sin \frac{\pi /4+2\pi }{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right)=} \\ {=\sqrt[{6}]{2} \cdot \left(\cos \frac{3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right)} \end{array}\]При $k=2$ получаем
\[\begin{array}{l} {x_{2} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4+4\pi }{3} +i\cdot \sin \frac{\pi /4+4\pi }{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{17\pi }{12} +i\cdot \sin \frac{17\pi }{12} \right)=} \\ {=\sqrt[{6}]{2} \cdot \left(\cos \frac{17\pi }{12} +i\cdot \sin \frac{17\pi }{12} \right)} \end{array}\]Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами. {2} +4+4i=1-4+4=1.\]
{2} +4+4i=1-4+4=1.\]
Так как $D>0$, уравнение имеет два корня:
\[x_{1} =\frac{-(1-2i))-\sqrt{1} }{2} =\frac{-1+2i-1}{2} =\frac{-2+2i}{2} =-1+i.\] \[x_{2} =\frac{-(1-2i))+\sqrt{1} }{2} =\frac{-1+2i+1}{2} =\frac{2i}{2} =i.\]Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
Рис. 2
Примечание 4
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 13.11.2021
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Урок «Решение квадратных уравнений на множестве комплексных чисел» (углубленный уровень)
Конспект урока по теме: «Решение квадратных уравнений на множестве комплексных чисел»
Часть 1.
Дата 08.11.2020г. | Урок № 1 | Класс 11 | Предмет Алгебра и начала анализа | ||||||||||||
Тема урока: Решение квадратных уравнений на множестве комплексных чисел | УМК Никольский С.М. «Алгебра и начала анализа» | ||||||||||||||
Место урока в системе уроков по теме (всего уроков на тему/номер урока по теме): 1/2 | |||||||||||||||
Тип урока: урок открытия нового знания | |||||||||||||||
Дидактические единицы учебного материала, которыми ученик должен владеть для успешной работы на уроке | Дидактические единицы учебного материала, которые ученик изучит на уроке | ||||||||||||||
Представлять, понимать | Знать | Уметь | Понятия: квадратный корень из комплексного числа, корни квадратного уравнения на множестве комплексных чисел Утверждения (теоремы, аксиомы): основная теорема алгебры, теорема о количестве корней многочлена, теорема о сопряженных комплексных корнях Алгоритмы (правила): алгоритм нахождения квадратного корня из комплексного числа, алгоритм решения квадратных уравнений на множестве комплексных чисел Методы (рассуждений, решения задач): дедуктивный
| ||||||||||||
-развитие числовых множеств, -взаимное расположение множества комплексных чисел в ряду множеств, -множество решений квадратного уравнения на координатной плоскости | -определение квадратного корня из действительного числа, -разницу между арифметическим квадратным корнем и квадратным корнем, -что такое квадратное уравнение, -формулу нахождения действительных корней квадратного уравнения, -алгебраическую форму комплексного числа, — геометрический смысл комплексного числа на плоскости, — определение и смысл мнимой единицы, -определение корня из комплексного числа и его свойства, — теорему о корнях степени n из комплексного числа
| -находить корни квадратного уравнения на множестве действительных чисел, -выполнять операции над комплексными числами, -находить корни степени n из комплексного числа | |||||||||||||
Планируемые предметные результаты урока | |||||||||||||||
| Ученик должен знать | Ученик должен уметь | Ученик научится представлять и понимать | |||||||||||||
На 3 | На 4 | На 5 | На 3 | На 4 | На 5 | ||||||||||
-основную теорему алгебры, -алгоритм нахождения квадратного корня из комплексного числа, -алгоритм решения квадратных уравнений на множестве комплексных чисел
| -определение квадратного корня из комплексного числа, -основную теорему алгебры, -алгоритм нахождения квадратного корня из комплексного числа, -алгоритм решения квадратных уравнений на множестве комплексных чисел
| -определение квадратного корня из комплексного числа, -основную теорему алгебры, -теорему о количестве корней многочлена, -теорему о сопряженных комплексных корнях, -алгоритм нахождения квадратного корня из комплексного числа, -алгоритм решения квадратных уравнений на множестве комплексных чисел
| -используя алгоритм находить значение квадратного корня из комплексного числа, -решать квадратные уравнения на множестве комплексных чисел
| -производить операции над комплексными числами, -используя алгоритм находить значение квадратного корня из комплексного числа, -решать квадратные уравнения на множестве комплексных чисел | -производить операции над комплексными числами, -используя алгоритм находить значение квадратного корня из комплексного числа, -решать квадратные уравнения на множестве комплексных чисел, -решать квадратные уравнения с коэффициентами из множества комплексных чисел | Научится находить значение квадратного корня из комплексного числа, решать квадратные уравнения на множестве комплексных чисел | |||||||||
Метапредметная направленность урока заключается в возможности нахождения физических величин, характеризующих постоянный и переменный электрический ток | посредством решения задач в комплексных числах | ||||||||||||||
Личностная направленность урока заключается в приобретении знаний через выявление заинтересованности обучающихся в изучаемом материале | посредством включения учащихся в активную работу, поиск информации | ||||||||||||||
Технология обучения | Форма обучения | Метод обучения | |||||||||||||
проблемное обучение | лекция, беседа | объяснительно-иллюстративный | |||||||||||||
| Дидактические средства обучения | |||||||||||||||
компьютер, проектор, презентация Power Point | |||||||||||||||
Источники информации: | |||||||||||||||
1) для учителя | 2) для обучающихся | ||||||||||||||
Методические пособия для учителей по теме урока, справочники | Учебное пособие, презентация, конспект в тетради, справочные материалы | ||||||||||||||
Цель урока: (определяется планируемыми результатами и способами их достижения) | Задачи урока: (конкретизация цели) | ||||||||||||||
Овладение методами решения квадратные уравнения на множестве комплексных чисел | Сформировать систему новых понятий, ввести новые термины, алгоритмы, отработать формулы, применяемые для решения квадратного уравнения, научиться находить квадратные корни из комплексного числа | ||||||||||||||
Часть 2.
Характеристики этапов урока | |||||
1. | 2. | 3. | 4. | 5. | 6. |
Этап урока, время | Цели этапа | Предметные учебные действия, формируемые и/или актуализируемые на этапе | Универсальные учебные действия, формируемые и/или актуализированные на этапе | ФОУД | Используемые на этапе СО |
1. (1-2 мин) | Поприветствовать детей, создать благожелательную атмосферу урока, нацелить учащихся на работу | — | Личностные: — сформированность позитивной моральной самооценки и моральных чувств.
Коммуникативные: — умение слушать, — интегрироваться в группу сверстников и строить продуктивное взаимодействие и сотрудничество со сверстниками и взрослыми, — умение выражать свои мысли в соответствии с условиями коммуникации, — планирование учебного сотрудничества с учителем и сверстниками.
Регулятивные: —
предвосхищение результата и уровня усвоения знаний. | — | — |
2. Актуализация знаний (5-7 мин) | Актуализировать ранее изученные понятия, алгоритмы и навыки | Применение формул дискриминанта и нахождения корней квадратного уравнения для решения квадратных уравнений, выполнение операций над комплексными числами | Коммуникативные: — умение задавать вопросы, — формулирование собственного мнения,
Познавательные: — умение строить речевое высказывание, — анализ объектов с целью выделения признаков, — сравнение, — выбор оснований и критериев для сравнения, — классификация объектов.
Регулятивные: — планирование своих действий | Ф | Презентация, учебник |
3. Целеполагание, постановка проблемы (2-5 мин) | Подведение детей к формулировке и постановке задач урока. Составление плана работы Организовать анализ учащимися возникшей ситуации и на этой основе выявить места и причины затруднения, осознать то, в чем именно состоит недостаточность их знаний, умений или способностей. | — | Коммуникативные: — умение выражать свои мысли в соответствии с условиями коммуникации, —
планирование учебного сотрудничества с учителем и сверстниками. Познавательные: — структурирование знаний, — установление причинно-следственных связей, — построение рассуждения в форме связи простых суждений об объекте, — формулирование проблемы, — создание способов решения проблемы. | Ф | Доска, презентация |
4. Решение проблемы (15 мин) | Предложить сформулировать цель урока. Научить учащихся извлекать квадратный корень из комплексного числа Предложить
учащимся новый способ действий при решении квадратных уравнения, сформировать
умение его применять как при решении задачи, вызвавшей затруднение, так и при
решении других задач такого типа. | Находить значение квадратного корня из отрицательного числа, решать квадратные уравнения, находить его корни при отрицательном значении дискриминанта | Коммуникативные: -учёт разных мнений и стремление к координации различных позиций в сотрудничестве,
Регулятивные: — принятие и сохранение учебной задачи, — планирование своих действий в соответствии с поставленной задачей и условиями её реализации,
Познавательные: — выделение существенной информации, — формулирование проблемы, — поиск разнообразных способов решения задачи | Ф | Презентация, учебник |
5. Систематизация знаний (15 мин) | Усвоение
учащимися нового способа действия при решении типовых задач. Этап первичного закрепления и самостоятельного решения несколько типовых заданий на новый способ действия при этом проговаривали вслух выполненные шаги и их обоснование – определения, алгоритмы, свойства и т.д.
| Находить значение квадратного корня из отрицательного числа, решать квадратные уравнения, находить его корни при отрицательном значении дискриминанта | Личностные: — формирование мотивов достижения целей, Формирование границ «знания» и «незнания».
Регулятивные: — принятие и сохранение учебной задачи, — учёт правила в планировании и контроле способа решения, — различение способа и результата действия.
Познавательные: — структурирование знаний, — построение речевого высказывания в письменной форме, — установление причинно-следственных связей
| Ф И | Презентация |
6. (1-2 мин) | Соотнесение поставленных задач с достигнутым результатом, фиксация нового знания, постановка дальнейших целей | — | Личностные: — формирование самоидентификации, адекватной позитивной самооценки, самоуважения и самопринятия.
Регулятивные: — восприятие оценки учителя, — адекватная самооценка.
Познавательные: — построение речевого высказывания в устной и письменной форме. | Ф | Презентация |
Характеристики этапов урока | |||
1. | 7. | 8. | |
Этап урока, время | Деятельность учителя (с указанием конкретных методов и приемов, техник обучения, средств и форм контроля, учебно-познавательных и учебно-практических задач, решаемых на данном этапе) | Деятельность учащихся | Продукт деятельности учащихся |
1. Мотивирование на учебную деятельность (1-2 мин) | Организационный момент, приветствие, пожелание. Приветствует учащихся, проверяет их готовность к уроку | Приветствуют учителя, проверяют свою готовность к уроку | — |
2. (5-7 мин) | Задает учащимся вопросы по пройденным темам, актуализируя знания, необходимые для формулирования темы урока, представляет вниманию учащихся задания для отработки освоенных ранее навыков | Отвечают на вопросы учителя, решают квадратные уравнения на множестве действительных чисел, вспоминают такие понятия, как дискриминант, корни квадратного уравнения, а также мнимая единица и операции над комплексными числами | Конспект учащихся в тетради |
3. Выявление места и причины затруднения (2-5 мин) | Организует диалог с учащимися, в ходе которого конкретизирует понятия, формулирует некоторые задачи урока, помогает учащимся сформулировать возникшую проблему нахождения корней квадратного уравнения при отрицательном значении дискриминанта, составляет совместно с обучающимися план решения проблемы | На основе наводящих вопросов учителя самостоятельно формулируют проблему, с которой столкнулись | Конспект учащихся в тетради |
4. Решение проблемы (15 мин) | Дает определение квадратного корня из комплексного числа, формулирует необходимые теоремы, фиксирует алгоритм нахождения корня из комплексного числа и алгоритм решения квадратных уравнений на множестве комплексных чисел. | Выписывают выводы, доказательства. Учатся извлекать корни из комплексных чисел, применяют этот навык при решении квадратных уравнений на множестве комплексных чисел | Конспект в тетради |
5. Систематизация знаний (15 мин) | Возвращает
учащихся к исходному уравнению, вызвавшему трудность в нахождении корней,
показывает, что теперь они могут самостоятельно справиться с данной
проблемой. Предлагает учащимся выполнить самостоятельно ряд заданий на закрепление приобретенных навыков | Применяют полученные знания в решении поставленной в ходе урока проблемы, выполняют самостоятельно ряд заданий на закрепление изученной темы | Выполненные в тетради самостоятельные задания |
6. Подведение итогов (1-2 мин) | Задает вопросы о задачах урока. Рефлексия | Проговаривают по плану новые знания, высказывают свои впечатления от урока | Лист самооценки |
Часть 3.
Ход урока.
Этап 1. Мотивирование на учебную деятельность (1-2 мин)
Добрый день, дорогие ученики! Рада приветствовать вас на уроке алгебры. Как ваше настроение? Сегодня нас ждёт новая, но интересная тема. Я уверена, что к концу урока каждый из вас научится применять новые знания на практике. Запишите, пожалуйста в ваших тетрадях сегодняшнее число и «Классная работа». Начнём!
Этап 2. Актуализация знаний (5-7 мин)
До введения отрицательных чисел можно было говорить, что уравнение х+3=2 не имеет корней, так как не существовало неотрицательного числа, которое обращало бы это уравнение в верное равенство. Однако после введения отрицательных чисел это уравнение стало разрешимым.
Но уж про существование отрицательных чисел мы давно с вами знаем, так же, как и умеем решать простые линейные уравнения.
Вопрос. Поработаем с вами устно. Для начала попробуем вспомнить, что такое квадратное уравнение и какой оно имеет вид? (Квадратное уравнение – это уравнение вида ax2+bx+c=0 при a≠0)
На доске записывается квадратное уравнение 5x2−2x−3=0
Вопрос. Является ли это уравнение квадратным? (Да, является)
Является ли это уравнение квадратным? (Да, является)
Вопрос. Исходя из чего вы сделали такой вывод? (Потому что коэффициент при х2 отличен от нуля, значит перед нами многочлен второй степени)
Вопрос. Хорошо! А как называются коэффициенты квадратного уравнения и чему они равны в рассматриваемом нами уравнении? (Старший коэффициент – а, второй коэффициент – b и свободный член – c. В нашем уравнении они равны 5, -2 и -3 соответственно)
Вопрос. Молодцы! Значит, перед нами квадратное уравнение с коэффициентами 5, -2 и -3. Нам необходимо решить уравнение, что это значит? (Решить уравнение – значит найти все его корни или доказать, что корней нет)
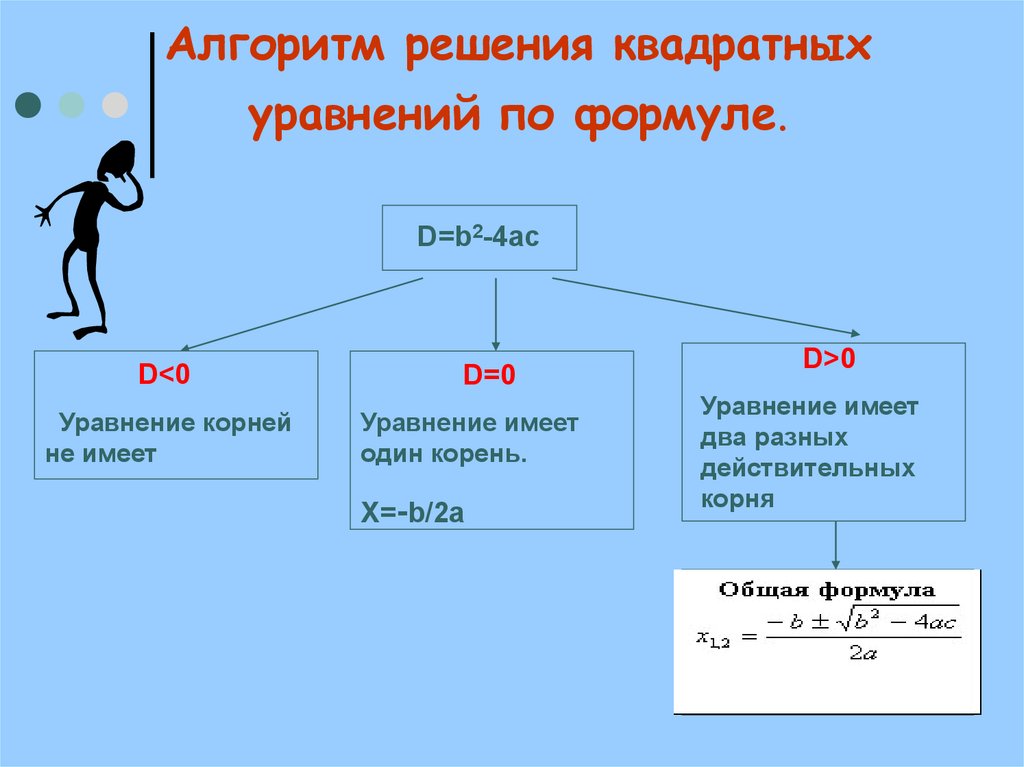
Вопрос. Получается, нам необходимо найти корни квадратного уравнения. Каков алгоритм нахождения корней квадратного уравнения? С чего начинаем? (Сначала находим дискриминант по формуле D=b2-4ас)
Вопрос. На доске записывается формула дискриминанта и предлагается ученикам устно проговорить, какие коэффициенты мы подставляем в эту формулу и какое значение получаем (Дискриминант данного квадратного уравнения равен 64)
Вопрос. Что же позволяет узнать нам значение дискриминанта? (Если дискриминант больше
0, то уравнение имеет два корня, равен нулю – один корень, меньше нуля –
уравнение не имеет корней. В нашем случае уравнение имеет два корня, так как
дискриминант положителен)
Что же позволяет узнать нам значение дискриминанта? (Если дискриминант больше
0, то уравнение имеет два корня, равен нулю – один корень, меньше нуля –
уравнение не имеет корней. В нашем случае уравнение имеет два корня, так как
дискриминант положителен)
Вопрос. В чем разница между арифметическим квадратным корнем из числа a и просто квадратным корнем из числа a? (Арифметический квадратный корень может быть только положительным. Просто квадратный корень может быть как положительным, так и отрицательным.)
Вопрос. С количеством корней определились, теперь осталось найти их. Как же нам это сделать? (Диктуют формулу нахождения корней квадратного уравнения)
Подставляем в формулу наши коэффициенты и получаем корни уравнения (-0,6; 1)
Вопрос. Замечательно! С задачей мы справились. Теперь давайте с вами приблизимся к
более обозримому прошлому и вспомним темы, которые изучили совсем недавно.
Скажите, пожалуйста, что такое мнимая единица? (Мнимая единица — это число,
квадрат которого равен −1. )
)
Вопрос. А для чего мы с вами вводили понятие мнимой единицы? (Чтобы научиться работать с комплексными числами, которые состоят как из действительной, так и из мнимой части)
Вопрос. Расскажите, какие операции мы научились производить над комплексными числами (Рассказывают изученный материал)
Этап 3. Выявление места и причины затруднения (2-5 мин)
Хорошо! Запишите в тетради такое уравнение . И давайте попробуем его решить.
Учащиеся сталкиваются с тем, что дискриминант приобретает отрицательное значение и говорят, что корней данное уравнение не имеет.
Да, решая квадратные уравнения на множестве действительных чисел мы с вами отмечали, что далеко не все квадратные уравнения имеют корни на данном множестве. Но как же хочется, чтобы все задачи были разрешимы, не так ли?
Получив отрицательный дискриминант, вы зашли в тупик, найти корни этого уравнения не представляется возможным. Как же нам быть?
Для решения такой
непростой задачи нам с вами как раз и потребуются знания о множестве
комплексных чисел и об операциях над этими числами. Вместе с учащимися пытаемся
сформулировать цель на сегодняшний урок: овладение методами решения квадратные
уравнения на множестве комплексных чисел
Вместе с учащимися пытаемся
сформулировать цель на сегодняшний урок: овладение методами решения квадратные
уравнения на множестве комплексных чисел
Этап 4. Решение проблемы (15 мин)
Вопрос. Что мы знаем об извлечении корня из отрицательных чисел? (что корень из отрицательных чисел не извлекается).
А что, если я докажу вам сегодня на уроке, что не так уж этот корень и нереален? А помогут мне в этом числа, с которыми мы познакомились на предыдущем занятии — комплексные числа!
Верно, что во множестве действительных чисел корней из отрицательных чисел быть не может. Но введение понятия «комплексное число» продвинуло вперед современную математику, а с ней и другие естественные науки.
Исследование алгебраических уравнений является одним из важнейших вопросов в математике. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение
.
Для того чтобы это уравнение имело решение, необходимо расширить множество действительных чисел путем присоединения к нему корня уравнения
.
Обозначим этот корень через . Таким образом, по определению
, или
,
следовательно,
.
Таким образом, действительных чисел явно недостаточно, чтобы построить такую теорию квадратных уравнений, в рамках которой каждое квадратное уравнение было бы разрешимо. Это приводит к необходимости расширять множество действительных чисел до множества, в котором было бы разрешимо любое квадратное уравнение. Такое множество называется множеством комплексных чисел и обозначается С.
Рассматривать будем на таком примере:
Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:
Выполним проверку того, что эти корни и права оказываются решением уравнения:
Что и требовалось доказать.
Как же извлечь
корень из комплексного числа? Так вот, квадратные корни из комплексного числа
определяются точно так же, как и квадратные корни из действительного
неотрицательного числа.
Сформулируем с вами в тетрадях такое определение
Определение. Квадратным корнем из комплексного числа w называется комплексное число z такое, что .
Например, числа i и –i являются значениями квадратного корня из числа –1, потому что по определению числа i, и .
Квадратные корни из числа w обозначаются как . Позже будет показано, что если , то w имеет только два различных значения, которые противоположны друг другу. С учетом этого для квадратного корня из числа –1 можем записать равенство
.
Получается, из любого числа мы умеем извлекать квадратный корень: как из действительного, так и из комплексного. Давайте сформулируем и запишем с вами основную теорему алгебры и следствия из нее.
Вопрос. Как показать, что значением квадратного корня из числа 0 является единственное число?
(По определению . Возведя в квадрат получим, что и .
Следовательно a =
0 и b =
0, т. е. z =
0.)
е. z =
0.)
Рассмотрим на примере, как можно находить значения квадратных корней из комплексного числа.
Пример 1. Найти .
Решение. Пусть комплексное число z = x+yi, где x и y – действительные числа, удовлетворяет равенству . Так как , то выполняется равенство , откуда
по определению равенства двух комплексных чисел. Из последнего равенства следует, что и y = 3x. Подставляя данное выражение для y в равенство , приходим к уравнению
.
Обозначим x2=m. Тогда , откуда . Решая это квадратное уравнение, находим m1 = –9, m2 = 1.
При m = –9 для x получаем уравнение , которое действительных корней не имеет.
При m = 1 для x получаем уравнение x2 = 1, откуда
.
Таким образом,
значениями квадратного корня из числа w = –8+6i являются два числа . Кратко это можно записать в
виде
Кратко это можно записать в
виде
Совместно с учащимися формулируется алгоритм нахождения квадратного корня из комплексного числа и записывается в тетради
Теорема (формула вычисления корня из комплексного числа) Пусть z = a + ib — отличное от нуля комплексное число. Тогда существуют два взаимно противоположных комплексных числа, квадраты которых равны z, а иных квадратных корней из z не существует.
Возможность извлечения квадратного корня из любого комплексного числа, в том числе и из любого действительного числа, приводит к тому, что каждое квадратное уравнение с действительными или комплексными коэффициентами имеет корни.
Пример 2. Решить уравнение .
Решение. Для нахождения корней сначала выделим полный квадрат в левой части:
.
В результате уравнение можно записать в виде
.
Так как , то далее возможны два случая.
I. , откуда
II. , откуда .
Ответ. .
Пример
3. Решить уравнение .
Решить уравнение .
Решение. Сначала разделим все коэффициенты на 1+i:
.
В результате приходим к уравнению . Затем, как и в предыдущем примере, выделим в левой части полный квадрат:
.
В итоге получим уравнение .
Для нахождения его корней сначала вычислим , как это было показано. Пусть . Тогда , откуда . Из последнего уравнения . Подставляя в уравнение , получаем . Отсюда, с учетом того, что , находим . Следовательно,
, .
Ответ. .
Вопрос. Сколько корней в множестве комплексных чисел имеет уравнение ? (Четыре. . Каждый из сомножителей имеет два корня.)
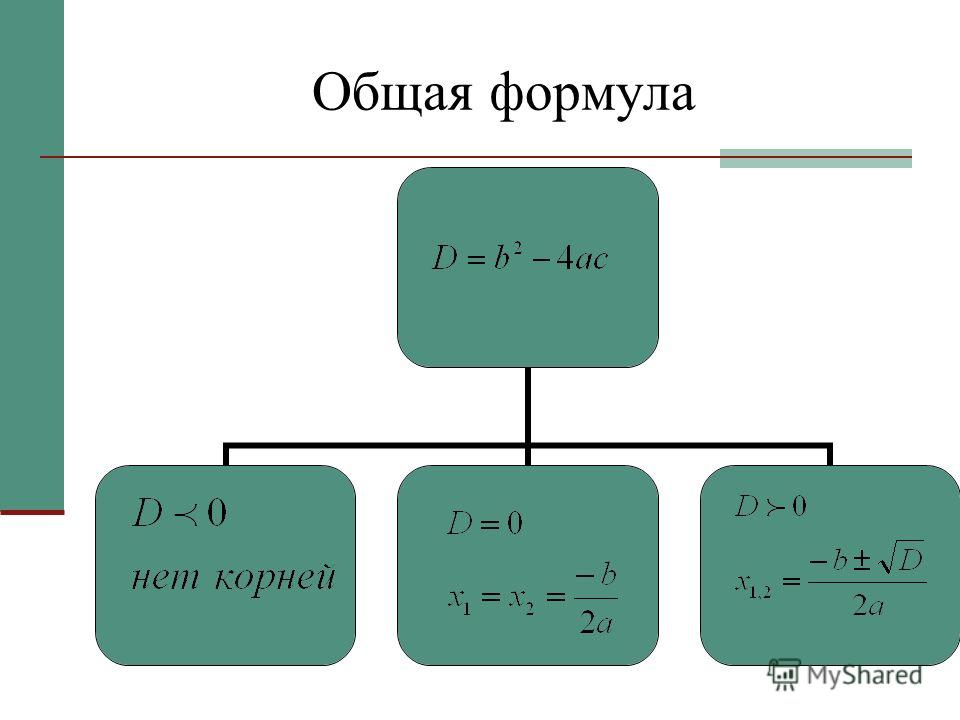
Преобразования, которые выполнялись на конкретных примерах, можно проделать и в общем виде для уравнения , где a, b, c – комплексные числа, причем . Итогом этой работы будет формула .
В
полученной формуле под знаком корня стоит хорошо знакомое выражение , которое является дискриминантом
квадратного уравнения. Так как в множестве комплексных чисел квадратный корень
из ненулевого числа принимает два значения, то при полученная
формула задает два различных корня квадратного уравнения.
Так как в множестве комплексных чисел квадратный корень
из ненулевого числа принимает два значения, то при полученная
формула задает два различных корня квадратного уравнения.
Совместно с учащимися формулируется алгоритм нахождения корней квадратного уравнения и записывается в тетради.
Открытие такого важного знания о комплексных числах, позволило применять его в анализе цепей переменного тока. Так, например, первый закон Кирхгофа в комплексной форме звучит так: алгебраическая сумма комплексных действующих значений токов в узле равна нулю:
.
Этап 5. Систематизация знаний (15 мин)
Давайте теперь вернемся к нашему уравнению, решить которое мы сначала не смогли и найдем его корни. (Учащиеся находят комплексные корни уравнения)
А теперь закрепим полученные знания выполнением небольшой самостоятельной работы.
Задание 1.
Выбрать из
предложенных вариантов ответов правильные. Правильных ответов может быть
несколько. В этом случае надо выбрать все правильные.
Сколько существует квадратных корней из 2 на множестве комплексных чисел?
1. 1 корень.
2. 2 корня.
3. 3 корня.
4. 4 корня.
Ответ: 2.
Какие из перечисленных чисел будут квадратными корнями из i?
1. .
2. .
3. .
4. .
Ответ: 3, 4.
Какие из перечисленных чисел будут квадратными корнями из ?
1. .
2. .
3. .
4. .
Ответ: 2, 4.
Сколько существует корней у уравнения
5. 1 корень.
6. 2 корня.
7. 3 корня.
8. 4 корня.
Ответ: 4.
Задание 2.
Выбрать правильные ответы.
Из предложенных чисел выбрать квадратный корень из .
1. .
2. .
3. .
4. .
Ответ: 2.
Из предложенных чисел выбрать решение уравнения .
1. .
.
2. .
3. .
4. .
Ответ: 3.
Из предложенных чисел выбрать решение уравнения .
1. –3.
2. –2.
3. 2.
4. 3.
Ответ: 3.
Из предложенных чисел выбрать решение уравнения .
1. 1+i.
2. .
3. .
4. .
Ответ: 3.
Этап 6. Подведение итогов (1-2 мин)
Трудным ли для вас было покорение этой математической вершины? Я бы хотела узнать, где вы находитесь:
· по-прежнему у подножия горы;
· на середине пути;
· на вершине;
· изобразите себя на этой горе.
(Учащимся раздаются карточки с домашним заданием)
1. Найдите
значения квадратного корня из числа:
а) –8; б) –3–4i; в)5–12i;
г) 15+8i; д) ; е) ;
ж) ; з) ; и) .
2. Решите
квадратное уравнение:
а) ; б) ;
в) ; г) ;
д) ; е) .
3. Решите
квадратное уравнение:
а) ;
б) ;
в) .
4. Найдите
четыре корня уравнения:
а) ; б) .
5. Решите уравнение .
СПАСИБО ЗА УРОК!
Корни кубического комплексного уравнения
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
IV. Действия с комплексными числами в тригонометрической форме.
При умножении комплексных чисел их модули перемножаются, а аргументы складываются:
z1z2= r1 r2 ( cos (φ1 + φ2) + i (sin (φ1 + φ2))
При делении комплексных чисел их модули делятся, а аргументы вычитаются:
(
cos (φ1 — φ2)
+ i (sin (φ1 — φ2)).
Формула Муавра.
zn= (r ( cos φ+ i sin φ))n= rn( cos nφ + i sin nφ),
Пример:
Частное комплексных чисел и равно …
Решение: Воспользуемся формулой: Получим:
Ответ:
2. Степень комплексного числа равна …
Решение: Согласно формуле Муавра находим:
Ответ:
Решите самостоятельно:
1. Произведение комплексных чисел и равно …
Ответ:
2. Произведение комплексных чисел и равно …
Ответ:
4. Дано комплексное число . Тогда значение равно …
Ответ:
V.
 Решение квадратных уравнений.
Решение квадратных уравнений.Любое уравнение n-ой степени на множестве комплексных чисел имеет ровно n корней, причём корни считаются столько раз, какова их кратность в данном уравнении.
Уравнения вида az2 + bz + c = 0 (где z- комплексное число) решаются по общей формуле:
z1,2=, где ,при этом:
если D=0, уравнение имеет один действительный корень,
если D>0, уравнение имеет два действительных корня,
если D<0, уравнение имеет два мнимых корня.
Пример:
Корни квадратного уравнения равны …
Решение: Учитывая равенство мы можем найти корни данного уравнения, принадлежащие множеству комплексных чисел; получим: Корнями уравнения являются комплексные числа и
Решите самостоятельно:
Корни квадратного уравнения равны …
Ответ:
Корни квадратного уравнения равны …
Ответ: Корнями
уравнения являются комплексные числа
и
.
Корни квадратного уравнения равны …
Ответ:
Корни квадратного уравнения равны …
Ответ:
Модуль числа.
Определение: Модулем комплексного числа z = a + bi называется числои обозначается , т.е. .
Пример:
Модуль комплексного числа равен …
Решение: Модуль комплексного числа вычисляется по формуле , где – действительная, а – мнимая часть комплексного числа. Тогда
Ответ:
Решите самостоятельно:
1. Модуль комплексного числа равен …
Ответ:
2. Модуль комплексного числа равен …
Ответ:
3. Модуль комплексного числа равен …
Ответ:
Р Я Д Ы
Ч
Ответа нет
исловые ряды:
1
Ответ ряд расходится
. Необходимое условие сходимости:
Необходимое условие сходимости:
нет
2.Достаточные условия:
P>1 – ряд расходится
I
P<1 – ряд сходится
.Признак Даламбера:
P=1 – нет ответа
II.Признак сравнения:
1) – сходится — сходится, т.к. сходится его мажорантный ряд
2) – расходится, — расходится как мажорантный для расходящегося
III.Эталонные ряды(г.п.):
-сходится |q|<1,
– расходится т.к. гармонический
,
IV. Знакопеременные ряды:
– ряд модулей
, сходится -абсолютно сходящийся
расходится — ответа нет
V. Знакочередующиеся ряды
по признаку Лейбница – сходится
Функциональные ряды:
1.Степенные:
(по степеням x)
(по степеням ).Область сходимости – множество всех точек сходимости.
2.Ряд Тейлора – Маклорена:
R сходимости =
интервал (-R;R)
3. Тригонометрические
ряды. Ряды Фурье.
Тригонометрические
ряды. Ряды Фурье.
опр:; слагаемое – гармоники, — амплитуды, 1,2,n-частоты
При
Коэффициенты Фурье
-частоты
Если функция чётная
Если разложить по cos чётным образом продолжить график
Если функция нечётная
Если разложить по sin нечётным образом продолжить
СУММА ЧИСЛОВОГО РЯДА |
1.Дан числовой ряд . Частичная сумма равна …
4.Дан числовой ряд: Его частичная сумма равна …
ТЕМА ЧИСЛОВЫЕ РЯДЫ.
……… и их четвертыми членами. 1. , 2. | …………и их пятыми членами. 1. , 2. |
……….их
четвертыми членами. | их пятыми членами. . 2. |
Для исследования вопроса о сходимости числового ряда используется необходимый признак сходимости числового ряда Тогда могут сходиться ряды …
1.
Решение 1) . Тогда . Достаточный признак сходимости выполняется, значит, данный ряд может сходиться. 2) . сходиться.(предел равен нулю т.к в знаменателе N в большей степени) 3) . . расходится. 4) . . расходится.
2.
3. ПРИМЕРЫ РЯДОВ
сходятся | сходятся | расходятся | расходятся |
ТЕМА
ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ
РЯДОВ. | |||||
Для исследования числового ряда на сходимость можно пользоваться признаком Даламбера и признаком Коши Тогда сходящимися являются ряды …
Решение: 1) Для ряда воспользуемся признаком Даламбера. Тогда получим: Так как , то данный ряд сходится. 2) Для ряда воспользуемся признаком Даламбера. Имеем: тогда получим: . Так как , то данный ряд расходится. 3) Для ряда воспользуемся признаком Коши. Имеем: тогда получим: Так как , то данный ряд сходится. 4) Для ряда воспользуемся признаком Коши. Имеем: тогда получим: Так как , то данный ряд расходится.
2. исследования числового ряда на сходимость можно пользоваться признаком Даламбера и признаком Коши Тогда сходящимися являются ряды …
Решение: 1)
Для ряда
воспользуемся
признаком Даламбера. Получим Тогда Так
как
,
то данный ряд сходится.
2) Для ряда
признак
Даламбера. Получим Тогда
расходится.
3)
Для ряда
признаком
Коши.
Получим
,
ряд сходится. 4) Для ряда
признак Коши.
Получим Тогда ряд расходится.
4) Для ряда
признак Коши.
Получим Тогда ряд расходится.
3.
Сходятся по Деламберу | Расходятся по Деламберу | |
Сходятся по Коши | Расходятся по Коши | |
| ||
1. Для
степенного ряда
радиус
сходимости R равен …1
Для
степенного ряда
радиус
сходимости R равен …1
Радиус сходимости R степенного ряда равен …10 | |
Для степенного ряда радиус сходимости R равен …2 | |
равен 1 | |
Радиус сходимости R степенного ряда равен …10 |
Решение: Радиус сходимости степенного ряда находится по формуле По условию задачи имеем, что примеры
1.Известно, что ряд Маклорена для функции имеет вид Тогда равняется …
Решение: Напоминаем, что нужно сделать подстановку – вместо x записать Получим
2.Известно, что ряд Маклорена для функции имеет вид Тогда равняется …
3.Известно, что ряд Маклорена для функции имеет вид Тогда …
4. Известно,
что ряд Маклорена для функции
имеет
вид Тогда
равняется …
Известно,
что ряд Маклорена для функции
имеет
вид Тогда
равняется …
Решение: Cделаем подстановку, вместо x запишем тогда получим:
Тогда равняется … | |||||
Тогда равняется …
| |||||
Тогда …
| |||||
Тогда равняется …
|
 ru 🎓
ru 🎓1
Первый слайд презентации: Комплексные числа и квадратные уравнения
-решение квадратных уравнений на множестве комплексных чисел; -алгоритм извлечения квадратного корня из комплексного числа; -полезные следствия для формулы корней квадратного уравнения
Изображение слайда
2
Слайд 2: Квадратное уравнение с действительными коэффициентами
?
Изображение слайда
3
Слайд 3: На множестве С можно находить корни любых квадратных уравнений!
Как извлечь квадратный корень из отрицательных действительных чисел?
Решение квадратных уравнений с действительными коэффициентами и D<0. Как извлечь квадратный корень из любого комплексного числа? (в алгебраической и тригонометрической форме записи).
Решение квадратных уравнений с комплексными коэффициентами.
Как извлечь квадратный корень из любого комплексного числа? (в алгебраической и тригонометрической форме записи).
Решение квадратных уравнений с комплексными коэффициентами.
Изображение слайда
4
Слайд 4: Как извлечь квадратный корень из отрицательных действительных чисел?
Определение: квадратным корнем(корнем второй степени) из комплексного числа z называют комплексное число, квадрат которого равен z.
Изображение слайда
5
Слайд 5: Формула извлечения квадратного корня из отрицательных действительных чисел
Изображение слайда
6
Слайд 6: Решение квадратных уравнений с действительными коэффициентами и D<0
Важно знать! Если у уравнения есть комплексный корень, то и сопряжённое ему число – тоже является корнем этого уравнения! Сопряжённые числа
Изображение слайда
7
Слайд 7: Как извлечь квадратный корень из любого комплексного числа? (в алгебраической и тригонометрической форме записи)
Теорема: Если b≠0, то Что равносильно системе условий:
Изображение слайда
8
Слайд 8
Например:
Изображение слайда
9
Слайд 9: Избежать громоздких вычислений позволяет тригонометрическая форма записи комплексного числа
Теорема: Доказательство: Всегда 2 корня!
Изображение слайда
10
Слайд 10
= = = Аналогично: Важно запомнить! При возведении комплексного числа в квадрат – его аргумент удваивается!!!
Изображение слайда
11
Слайд 11: Алгоритм извлечения квадратного корня из комплексного числа:
Найти модуль ρ и аргумент α этого числа;
Провести окружность радиусом √ ρ с центром в начале координат;
Провести через начало координат прямую под углом к положительному направлению оси абсцисс;
Две точки пересечения проведённых окружности и прямой – дают ответ.
Изображение слайда
12
Слайд 12
1). = = z 2 -2 1 -1 2)-4).
Изображение слайда
13
Слайд 13: Решение квадратных уравнений с комплексными коэффициентами
Так как множества и совпадают между собой, то для решения квадратных уравнений с комплексными коэффициентами можно сохранить привычную формулу корней квадратного уравнения:
Изображение слайда
14
Последний слайд презентации: Комплексные числа и квадратные уравнения: Полезные следствия для формулы корней квадратного уравнения:
(теорема Виета) Если Z 1 и Z 2 –корни квадратного уравнения то (формула разложения квадратного трёхчлена на линейные множители) Если Z 1 и Z 2 –корни квадратного уравнения то
Изображение слайда
Решение квадратных уравнений.
 2 + b*x + c = 0
,где x
—
переменная, a,b,c
– константы; a0
. Задача состоит в отыскании корней уравнения.
2 + b*x + c = 0
,где x
—
переменная, a,b,c
– константы; a0
. Задача состоит в отыскании корней уравнения.Геометрический смысл квадратного уравнения
Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х)
. Из этого следует, что есть три возможных случая:
1)
парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).
2) парабола имеет одну точку пересечения с осью Ох . Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).
3)
Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. 2
и осуществим преобразование
2
и осуществим преобразование
Отсюда находим
Формула дискриминанта и корней квадратного уравнения
Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0 При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле
Теорема Виета
Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p
, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q
. Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а
отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. 2+x-6=0
.
2+x-6=0
.
Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения
С второго условия получаем, что произведение должно быть равно -6
. Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2}
. С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны
Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см 2 .
Решение:
Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х
– большую сторону, тогда 18-x
меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
х 2 -18х+77=0.
Найдем дискриминант уравнения
Вычисляем корни уравнения
Если х=11
,
то 18-х=7
,
наоборот тоже справедливо (если х=7
, то 21-х=9
).
Задача 6. Разложить квадратное 10x 2 -11x+3=0 уравнения на множители.
Решение:
Вычислим корни уравнения, для этого находим дискриминант
Подставляем найденное значение в формулу корней и вычисляем
Применяем формулу разложения квадратного уравнения по корнями
Раскрыв скобки получим тождество. 2+(2а+6)х-3а-9=0
имеет более одного корня?
2+(2а+6)х-3а-9=0
имеет более одного корня?
Решение:
Рассмотрим сначала особые точки, ими будут значения а=0
и а=-3
. При а=0
уравнение упростится до вида 6х-9=0; х=3/2
и будет один корень. При а= -3
получим тождество 0=0
.
Вычислим дискриминант
и найдем значения а
при котором оно положительно
С первого условия получим а>3
. Для второго находим дискриминант и корни уравнения
Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0
получим 3>0
.
Итак, за пределами промежутка (-3;1/3)
функция отрицательная. Не стоит забывать о точке а=0
,
которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи
Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.
Важно! В корнях четной кратности функция знак не меняет.
Обратите внимание! Любое нелинейное неравенство школьного курса алгебры нужно решать с помощью метода интервалов.
Предлагаю вам подробный алгоритм решения неравенств методом интервалов , следуя которому вы сможете избежать ошибок прирешении нелинейных неравенств .
Решение квадратных уравнений с отрицательными дискриминантами
Как мы знаем,
i 2 = — 1.
Вместе с тем
(- i ) 2 = (- 1 i ) 2 = (- 1) 2 i 2 = -1.
Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i и — i . Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?
Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi равен — 1. Тогда
(а + bi ) 2 = — 1,
а 2 + 2аbi — b 2 = — 1
Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях.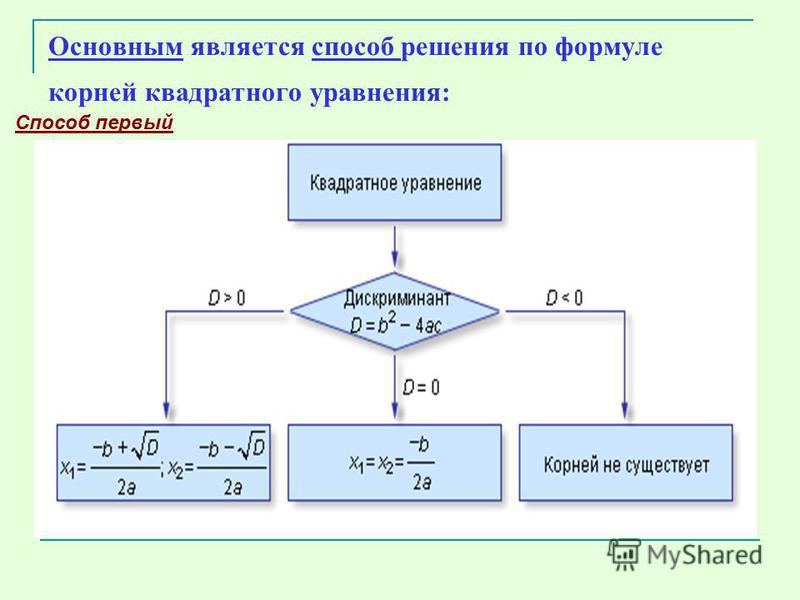 Поэтому
Поэтому
| { | а 2 — b 2 = — 1 ab = 0 (1) |
Согласно второму уравнению системы (1) хотя бы одно из чисел а и b должно равняться нулю. Если b = 0, то из первого уравнения получается а 2 = — 1. Число а действительное, и поэтому а 2 > 0. Неотрицательное число а 2 не может равняться отрицательному числу — 1. Поэтому равенство b = 0 в данном случае невозможно. Остается признать, что а = 0, но тогда из первого уравнения системы получаем: —b 2 = — 1, b = ± 1.
Следовательно, комплексными числами, квадраты которых равны -1, являются только числа i и —i , Условно это записывается в виде:
√-1 = ± i .
Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а . Такими числами являются √ai и -√ai . Условно это записывается так:
Такими числами являются √ai и -√ai . Условно это записывается так:
√— а = ± √ai .
Под √a здесь подразумевается арифметический, то есть положительный, корень. Например, √4 = 2, √9 =.3; поэтому
√-4 = + 2i , √-9= ± 3i
Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x 2 + 2х + 5 = 0; тогда
х 1,2 = — 1 ± √1 -5 = — 1 ± √-4 = — 1 ± 2i .
Итак, данное уравнение имеет два корня: х 1 = — 1 +2i , х 2 = — 1 — 2i . Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.
Понятие комплексного числа
Комплексным числом называется выражение вида a + ib , где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:
- Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
a = b и c = d . - Суммой двух комплексных чисел a + ib и c + id называется комплексное число
a + c + i (b + d). - Произведением двух комплексных чисел a + ib и c + id называется комплексное число
ac – bd + i (ad + bc).
Комплексные числа часто обозначают одной буквой, например, z = a + ib . Действительное число a называется действительной частью комплексного числа z , действительная часть обозначается a = Re z . Действительное число b называется мнимой частью комплексного числа z , мнимая часть обозначается b = Im z . Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,
Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что , а именно
В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi , например, 0 + i 3 = 3 i . Чисто мнимое число i1 = 1 i = i обладает удивительным свойством:
Таким образом,
№ 4 .1. В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множествавещественных чисел или множества комплексных чисел .
График функции
Фрагмент графика функции
Способы задания функции
[править]Аналитический способ
Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.
Возможно, кусочное задание, то есть различное для различных значений аргумента.
[править]Табличный способ
Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:
[править]Графический способ
Осциллограмма задаёт значение некоторой функции графически.
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
[править]Рекурсивный способ
Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.
- факториал;
- числа Фибоначчи;
- функция Аккермана.
[править]Словесный способ
Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.
- функция, возвращающая цифру в записи числа пи по её номеру;
- функция, возвращающая число атомов во вселенной в определённый момент времени;
- функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождени
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Виды квадратных уравнений
Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.
Говоря математическим языком, квадратное уравнение — это уравнение вида:
Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:
Здесь а =1; b = 3; c = -4
Здесь а =2; b = -0,5; c = 2,2
Здесь а =-3; b = 6; c = -18
Ну, вы поняли…
В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.
Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.
Такие квадратные уравнения называются полными.
А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:
5х 2 -25 = 0,
2х 2 -6х=0,
-х 2 +4х=0
И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:
2х 2 =0,
-0,3х 2 =0
Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.
Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…
Вот и все главные виды квадратных уравнений. Полные и неполные.
Решение квадратных уравнений.

Решение полных квадратных уравнений.
Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:
Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .
Формула для нахождения корней квадратного уравнения выглядит так:
Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:
а =1; b = 3; c = -4. Вот и записываем:
Пример практически решён:
Это ответ.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !
Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !
Предположим, надо вот такой примерчик решить:
Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:
Например, вот так:
Узнали?) Да! Это неполные квадратные уравнения .
Решение неполных квадратных уравнений.
Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .
Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !
Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:
Остаётся корень извлечь из 9, и всё. Получится:
Тоже два корня. х 1 = -3 , х 2 = 3 .
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
Дискриминант. Формула дискриминанта.
Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:
Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:
Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:
D = b 2 — 4ac
И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.
Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.
Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)
Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…
Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…
Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:
Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:
А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.
Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.
Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.
Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…
При работе с дробями ошибки, почему-то так и лезут…
Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.
Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:
Вот и всё! Решать – одно удовольствие!
Итак, подытожим тему.
Практические советы:
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.
3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.
4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!
Теперь можно и порешать.)
Решить уравнения:
8х 2 — 6x + 1 = 0
х 2 + 3x + 8 = 0
х 2 — 4x + 4 = 0
(х+1) 2 + x + 1 = (x+1)(x+2)
Ответы (в беспорядке):
х 1 = 0
х 2 = 5
х 1,2 = 2
х 1 = 2
х 2 = -0,5
х — любое число
х 1 = -3
х 2 = 3
решений нет
х 1 = 0,25
х 2 = 0,5
Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.
Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.
Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».
Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
D = b 2 – 4ас.
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .
Например. Решить уравнение х 2 – 4х + 4= 0.
D = 4 2 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х 2 + х + 3 = 0.
D = 1 2 – 4 · 2 · 3 = – 23
Ответ: корней нет .
Решить уравнение 2х 2 + 5х – 7 = 0 .
D = 5 2 – 4 · 2 · (–7) = 81
х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5
х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1 .
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .
На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
Пример. Решить уравнение
3х 2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3
х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27
Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27
√(D 1) = √27 = √(9 · 3) = 3√3
х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3
х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.
D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12
√(D 2) = √12 = √(4 · 3) = 2√3
х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3
х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax
2 + c
= 0 выполнено неравенство (−c
/a
) ≥ 0, корней будет два.
 Формула дана выше;
Формула дана выше; - Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7.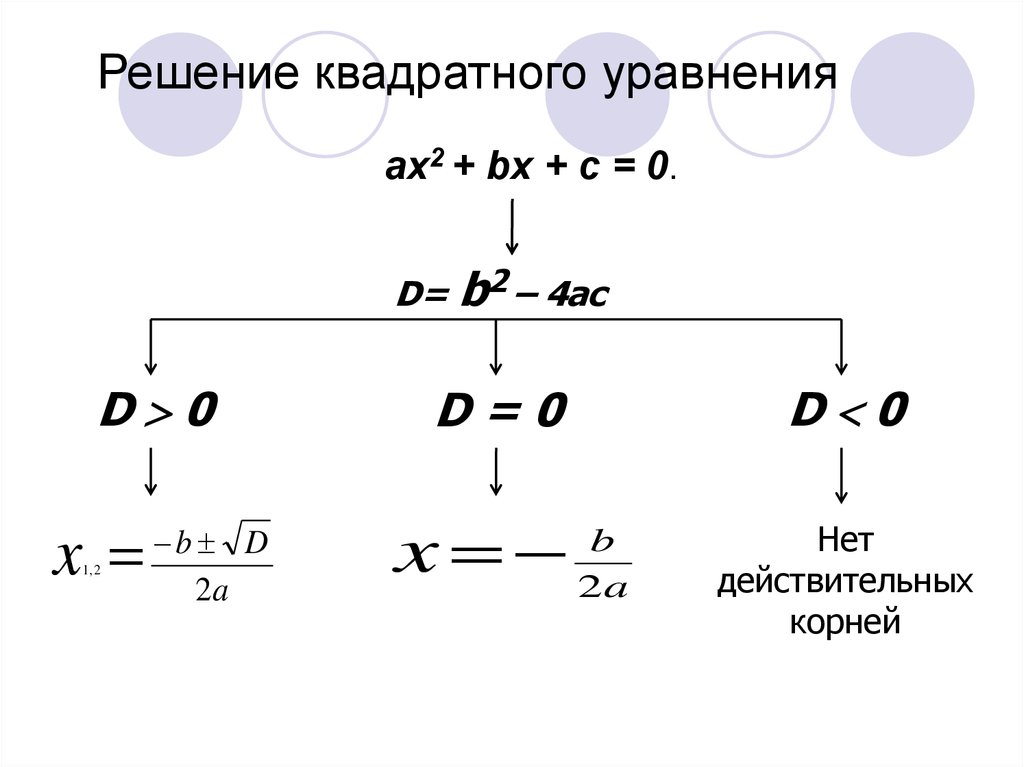 2+2x+3[/латекс] 9{2}-4ac<0[/latex], то число под радикалом будет отрицательным. Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений нет. Однако вы можете использовать мнимые числа. Тогда у вас будет два сложных решения: одно путем добавления мнимого квадратного корня, а другое путем его вычитания.
2+2x+3[/латекс] 9{2}-4ac<0[/latex], то число под радикалом будет отрицательным. Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений нет. Однако вы можете использовать мнимые числа. Тогда у вас будет два сложных решения: одно путем добавления мнимого квадратного корня, а другое путем его вычитания.
Попробуйте
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Комплексные корни — определение, формула, применение, примеры
Комплексные корни — это мнимые корни квадратичных или полиномиальных функций. Эти комплексные корни представляют собой форму комплексных чисел и представлены как α = a + ib и β = c + id. Квадратное уравнение, имеющее значение дискриминанта меньше нуля (D<0), имеет мнимые корни, которые представляются в виде комплексных чисел.
Комплексные корни имеют действительную и мнимую части, и формула i 2 = -1 полезно для вычисления комплексных корней. Давайте узнаем больше о свойствах и операциях сложных корней, с помощью примеров, часто задаваемых вопросов.
Давайте узнаем больше о свойствах и операциях сложных корней, с помощью примеров, часто задаваемых вопросов.
| 1. | Что такое комплексные корни? |
| 2. | Свойства комплексных корней |
| 3. | Операции над комплексными корнями |
| 4. | Примеры комплексных корней |
| 5. | Практические вопросы |
| 6. | Часто задаваемые вопросы о комплексных корнях |
Что такое комплексные корни?
Комплексные корни — это мнимые корни квадратных уравнений, представленные в виде комплексных чисел. Квадратный корень из отрицательного числа невозможен, поэтому мы преобразуем его в комплексное число. Квадратные уравнения со значениями дискриминанта меньше нуля b 2 — 4ac < 0, преобразуется с использованием i 2 = -1 для получения сложных корней. Здесь -D записывается как i 2 D.
Здесь -D записывается как i 2 D.
Комплексные корни выражаются как комплексные числа a + ib. Сложный корень состоит из действительной части и мнимой части. Комплексный корень часто представляется как Z = a + ib. Здесь «а» — действительная часть комплексного числа, обозначаемая Re(Z), а «b» — мнимая часть, обозначаемая как I’m(Z). Здесь ib — мнимое число.
В мнимой части комплексного числа буква «i» обозначается как йота. Йота — я очень полезен, чтобы найти квадратный корень из любого отрицательного числа. Здесь i 2 = -1, а отрицательное число -N представлено как i 2 N, и теперь оно превратилось в положительное число.
Свойства комплексных корней
Величина комплексных корней:
Комплексный корень α = a + ib представлен в виде точки (a, 92}\)|. Это легко понять с помощью теоремы Пифагора, и здесь модуль комплексного корня представлен гипотенузой прямоугольного треугольника, основанием является действительная часть, а высота — мнимая часть. {-1}\frac{b}{a}\ ). 9{-1}\).
{-1}\frac{b}{a}\ ). 9{-1}\).
Операции над комплексными корнями
Комплексные корни простых алгебраических выражений также можно складывать, вычитать, умножать или делить подобно обычным нормалям. Рассмотрим подробно каждую из операций.
Сложение комплексных корней
Комплексные корни также можно складывать аналогично сложению натуральных чисел. Для сложных корней к действительной части прибавляется действительная часть, а к мнимой — мнимая часть. Два комплексных корня α = a + ib и β = c + id при сложении имеют α + β = (a + c) + i(b + d) . Добавление комплексных корней следует закону замыкания, коммутативному закону, ассоциативному закону, аддитивному тождеству и аддитивному обратному закону, аналогичному нормальным числам.
Вычитание комплексных корней
Вычитание комплексных корней аналогично вычитанию нормальных чисел. Поскольку комплексные корни являются комплексными числами, действительная часть вычитается из действительной части, а мнимая часть вычитается из мнимой части, чтобы найти результирующий ответ. 2 = -1\). Два комплексных числа α = a + ib и β = c + id при умножении дают α × β = (ca — bd) + i(ad + bc). Умножение комплексных корней возможно и в полярной форме. Умножение комплексных чисел подчиняется всем свойствам замыкания, коммутативности, ассоциативности и дистрибутивности. 92)}\).
2 = -1\). Два комплексных числа α = a + ib и β = c + id при умножении дают α × β = (ca — bd) + i(ad + bc). Умножение комплексных корней возможно и в полярной форме. Умножение комплексных чисел подчиняется всем свойствам замыкания, коммутативности, ассоциативности и дистрибутивности. 92)}\).
☛ Похожие темы
- Аргумент комплексного числа
- Комплексный номер
- Умножение комплексных чисел
- Деление комплексных чисел
- Комплексное сопряжение
- Математическая индукция
Часто задаваемые вопросы о комплексных корнях
Что такое комплексные корни в уравнениях?
Комплексные корни — это мнимые корни уравнений, представленные в виде комплексных чисел. Квадратные уравнения со значением дискриминанта меньше нуля имеют мнимые или комплексные корни. Комплексные корни имеют вид α = a + ib и β = c + id и имеют действительную и мнимую части. 92 = —1\) при вычислении комплексных корней. 2 = -1 \). Квадратное уравнение, имеющее положительное или нулевое значение дискриминанта, имеет действительные корни, а при значении дискриминанта меньше нуля имеет комплексные корни.
2 = -1 \). Квадратное уравнение, имеющее положительное или нулевое значение дискриминанта, имеет действительные корни, а при значении дискриминанта меньше нуля имеет комплексные корни.
Многочлены с комплексными корнями
Горячая математикаОсновная теорема алгебры уверяет нас, что любой многочлен с настоящий номер коэффициенты можно полностью разложить по полю комплексные числа .
В случае квадратичные многочлены , корни комплексные, когда дискриминант отрицательный.
Пример 1:
Фактор полностью, используя комплексные числа.
Икс 3 + 10 Икс 2 + 169 Икс
Во-первых, Икс .
Икс 3 + 10 Икс 2 + 169 Икс знак равно Икс ( Икс 2 + 10 Икс + 169)
Теперь используйте
квадратичная формула
для выражения в скобках, чтобы найти значения
Икс
для которого
Икс
2
+
10
Икс
+
169
знак равно
0
.
Здесь а знак равно 1 , б знак равно 10 а также с знак равно 169 .
Икс знак равно − б ± б 2 − 4 а с 2 а
Икс знак равно − 10 ± 10 2 − 4 ( 1 ) ( 169) 2 ( 1 ) знак равно − 10 ± 100 − 676 2 знак равно − 10 ± − 576 2
Запишите квадратный корень, используя мнимые числа.
Икс знак равно − 10 ± 24 я 2 знак равно − 5 ± 12 я
Теперь мы знаем, что значения Икс для которого выражение
Икс 2 + 10 Икс + 169
равно 0 находятся Икс знак равно − 5 + 12 я а также Икс знак равно − 5 − 12 я .
Таким образом, исходный многочлен можно представить как
Икс 3 + 10 Икс 2 + 169Икс знак равно Икс ( Икс − [ − 5 + 12 я ] ) ( Икс − [ − 5 − 12 я ] )
Вы можете убедиться в этом, используя
ФОЛЬГА
.
Иногда вы можете разложить многочлен на множители, используя комплексные числа, не используя квадратную формулу. Например, разница квадратов правило:
Икс 2 − а 2 знак равно ( Икс + а ) ( Икс − а )
Это также может быть использовано с комплексными числами, когда а 2 отрицательно, следующим образом:
Икс 2 + 25 знак равно ( Икс + 5 я ) ( Икс − 5 я )
Пример 2:
Фактор полностью, используя комплексные числа.
9 Икс 2 у + 64 у
Во-первых, исключить
у
.
9 Икс 2 у + 64 у знак равно у ( 9 Икс 2 + 64 )
Теперь используйте разность правила квадратов, чтобы разложить 9 Икс 2 + 64 .
9 Икс 2 + 64 знак равно 9Икс 2 − ( − 64 ) знак равно ( 3 Икс ) 2 − ( 8 я ) 2 знак равно ( 3 Икс + 8 я ) ( 3 Икс − 8 я )
Следовательно,
9
Икс
2
у
+
64
у
знак равно
у
(
3
Икс
+
8
я
)
(
3
Икс
−
8
я
)
. 2 — 5x + 17. Есть предложения? Вот что у меня есть на данный момент:
2 — 5x + 17. Есть предложения? Вот что у меня есть на данный момент:
импорт математики
импортировать cmath
def quadSolver(a,b,c, tol = 1e-18):
print('Уравнение: {0}x**2 + {1}x + {2}'.format(a,b,c))
дискриминант = b**2 - 4 * a * c
если дискриминант > 0:
root1 = float(-b + math.sqrt(b**2 - 4 * a * c))/ (2 * a)
root2 = float(-b - math.sqrt(b**2 - 4 * a * c))/ (2 * a)
print('Имеет два корня:')
печать (корень1)
печать (корень2)
Элиф дискриминант == 0:
root1 = float(-b + math.sqrt(b**2 - 4 * a * c))/ (2 * a)
print('Имеет двойной корень:')
печать (корень1)
Элиф дискриминант < 0:
root1 = (-b + cmath.sqrt(b**2 - 4 * a * c))/ (2 * a)
root2 = (-b - cmath.sqrt(b**2 - 4 * a * c))/ (2 * a)
print('Имеет два сложных корня:')
печать (корень1)
печать (корень2)
** Это сработало, поэтому теперь он производит комплексные корни, но теперь у меня проблемы, когда a = 0, т. е. когда y = mx + b или y = константа. Итак, как я могу отредактировать его, чтобы охватить и их?
е. когда y = mx + b или y = константа. Итак, как я могу отредактировать его, чтобы охватить и их?
- python
Если ваш дискриминант < 0, вы, вероятно, хотите cmath.sqrt в своих вычислениях:
>>> import cmath >>> cmath.sqrt(-1) 1j
РЕДАКТИРОВАТЬ: Чтобы ответить на ваш второй вопрос, когда a == 0 ваше уравнение является линейным: bx + c = 0 и его единственное решение x = -c/b . (Очевидно, что если a==b==0 вам не нужно решать уравнение!)
Не проверено, но чтобы дать вам представление:
import math
импортировать cmath
def quadSolver(a,b,c, tol = 1e-18):
print('Уравнение: {0}x**2 + {1}x + {2}'.format(a,b,c))
если а==b==0:
если с!=0:
print('Недопустимое уравнение')
еще:
print('0=0 не интересное уравнение')
возвращаться
если а==0:
print('Единственное решение x =', -c/b)
возвращаться
дискриминант = b**2 - 4 * a * c
если дискриминант > 0:
root1 = (-b + math. sqrt(дискриминант))/ (2 * a)
root2 = (-b - math.sqrt(дискриминант))/ (2 * a)
print('Имеет два корня:')
печать (корень1)
печать (корень2)
Элиф дискриминант == 0:
root1 = float (-b + math.sqrt (дискриминант))/ (2 * a)
print('Имеет двойной корень:')
печать (корень1)
Элиф дискриминант < 0:
root1 = (-b + cmath.sqrt(дискриминант))/ (2 * a)
root2 = (-b - cmath.sqrt(дискриминант))/ (2 * a)
print('Имеет два сложных корня:')
печать (корень1)
печать (корень2)
sqrt(дискриминант))/ (2 * a)
root2 = (-b - math.sqrt(дискриминант))/ (2 * a)
print('Имеет два корня:')
печать (корень1)
печать (корень2)
Элиф дискриминант == 0:
root1 = float (-b + math.sqrt (дискриминант))/ (2 * a)
print('Имеет двойной корень:')
печать (корень1)
Элиф дискриминант < 0:
root1 = (-b + cmath.sqrt(дискриминант))/ (2 * a)
root2 = (-b - cmath.sqrt(дискриминант))/ (2 * a)
print('Имеет два сложных корня:')
печать (корень1)
печать (корень2)
(Обратите внимание, поскольку вы определяете дискриминант , вы также можете использовать его в своих последующих вычислениях).
4
импорт математики
импортировать cmath
деф основной():
a = int (ввод («введите a:»))
b = int (ввод («введите b:»))
c = int (ввод («введите c:»))
d=((math.pow(b,2))-(4*a*c))
если а!=0:
если д>0:
x1=(-b+math. sqrt(d))/(2*a)
x2=(-b-math.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("настоящий корень")
Элиф д==0:
х=-б/(2*а)
распечатать("х=",х)
print("равный корень")
Элиф д<0:
x1=(-b+cmath.sqrt(d))/(2*a)
x2=(-b-cmath.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("сложный корень")
еще:
print("это не квадратное уравнение")
главный()
########albany.cs######
sqrt(d))/(2*a)
x2=(-b-math.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("настоящий корень")
Элиф д==0:
х=-б/(2*а)
распечатать("х=",х)
print("равный корень")
Элиф д<0:
x1=(-b+cmath.sqrt(d))/(2*a)
x2=(-b-cmath.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("сложный корень")
еще:
print("это не квадратное уравнение")
главный()
########albany.cs######
2
импорт математики
импортировать cmath
деф основной():
a = int (ввод («введите a:»))
b = int (ввод («введите b:»))
c = int (ввод («введите c:»))
d=((math.pow(b,2))-(4*a*c))
если а!=0:
если д>0:
x1=(-b+math.sqrt(d))/(2*a)
x2=(-b-math.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("настоящий корень")
Элиф д==0:
х=-б/(2*а)
распечатать("х=",х)
print("равный корень")
Элиф д<0:
x1=(-b+cmath. sqrt(d))/(2*a)
x2=(-b-cmath.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("сложный корень")
еще:
print("это не квадратное уравнение")
главный()
########albany.cs######
sqrt(d))/(2*a)
x2=(-b-cmath.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("сложный корень")
еще:
print("это не квадратное уравнение")
главный()
########albany.cs######
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Комплексные корни квадратных уравнений
Воспоминания о квадратных уравнениях Из предыдущих классов
Квадратные уравнения
ax 2 +bx+c =0 где a≠0
Решение или корень квадратного уравнения
Вещественное число α называется корнем или решением квадратного уравнения, если
aα 2 +bα+c=0
мы можем узнать подробности по ссылкам ниже
- Квадратичный многочлен
- Графический квадратичный полином
- что такое квадратное уравнение
- Как решать квадратные уравнения
- Факторинг квадратных уравнений
- Решение квадратных уравнений путем заполнения квадрата
- Решение квадратных уравнений с помощью квадратной формулы
- Характер корней квадратного уравнения
- Задача на дискриминант квадратного уравнения
- Квадратичные задачи со словами
Некоторые другие моменты, которые следует помнить
- Корнем квадратного уравнения являются нули многочлена p(x).

- Из второй главы мы знаем, что многочлен степени может иметь не более двух нулей. Таким образом, квадратное уравнение может иметь не более двух корней
- Квадратное уравнение не имеет действительных корней, если b 2 - 4ac < 0
Решенные примеры
1. Найдите корни квадратного уравнения
x 2 -6x=0
Решение
В этом квадратном уравнении нет постоянного члена, мы можем использовать x как общий множитель
x(x-6)=0
Итак, корни равны х=0 и х=6
2. Решить квадратное уравнение0453 3. Решить квадратное уравнение методом факторизации
х 2 -х -20=0
Решение
1) Сначала надо умножить коэффициенты а и с. В этом случае =1Х-20=-20
Возможный кратные 4,5 ,2,10
2) Кратные 4,5 удовлетворяют уравнению
x 2 -5x+4x-20=0
x(x-5)+4(x-5)=0
(x+4)(x-5)=0
или x=-4 или 5
4. Решить квадратное уравнение квадратным методом
x 2 -3x-18=0
Решение
Для квадратного уравнения 9{2}-4ac}}{2a}$
Здесь a=1
b=-3
c=-18
Подставляя эти значения, мы получаем
x=6 и -3
Введение сложных корней
Мы уже изучили комплексное число в предыдущей главе. {2}}}{2a} $ 9{2}}}{2a}$
{2}}}{2a} $ 9{2}}}{2a}$
Комплексные корни встречаются в сопряженных парах, и это очень ясно из приведенных выше корней
Квадратные уравнения, содержащие комплексные корни, могут быть решены с использованием метода факторизации, метода квадратов и метода квадратичных уравнений, описанных выше
Комплексное квадратное уравнение
До сих пор мы читали о квадратном уравнении, где коэффициенты действительны. Комплексное квадратное уравнение – это уравнение, в котором коэффициентом являются комплексные числа.
Эти квадратные уравнения также могут быть решены с использованием метода факторизации, квадратного метода и квадратичного метода, описанных выше 9{2}}}{2}$=1-3i
(2) При каких значениях k многочлен x 2 +4x+k имеет два комплексно-сопряженных корня?
Решение:
, чтобы корни были сложными конъюгатом, мы должны иметь
B 2 -4AC <0
16-4K <0
или K> 4
также прочитайте
 Также
Также - 9005 9.
- Что такое комплексные числа
- Алгебра комплексных чисел
- Сопряжение комплексных чисел
- Модуль комплексных чисел
- Самолет Арганда
- Заполярье Представительство комплекса №
- Вращение комплексного номера
- Идентификаторы для комплексных чисел
- Формула Эйлера и теорема Де Муавра
- Кубический корень из единства
- Комплексные корни квадратных уравнений
- Решения и рабочие листы NCERT
- Решение NCERT Комплексные числа. Упражнение 5.1
- Задачи на комплексные числа
- Рабочий лист комплексных чисел
Графическое представление комплексных корней | Ресурсы IB по математике от Intermathematics
Графическое понимание комплексных корней
Если вы изучали комплексные числа, то вам должно быть известно, что многие многочлены имеют комплексные корни. Например, x 2 + 1 = 0 имеет решение x = i и -i. Мы знаем, что решение x 2 – 1 = 0 (x = 1 и -1) дает два значения x, при которых график пересекает ось x, но что графически представляет решение x = i или -i?
Например, x 2 + 1 = 0 имеет решение x = i и -i. Мы знаем, что решение x 2 – 1 = 0 (x = 1 и -1) дает два значения x, при которых график пересекает ось x, но что графически представляет решение x = i или -i?
На сайте Maths Fun Facts есть отличный пост, в котором рассматривается основная идея, лежащая в основе этого, и я расскажу об этом немного подробнее. Этот конкретный графический метод работает только с квадратичными уравнениями:
Шаг 1
У вас есть квадратичный граф с комплексными корнями, скажем, y = (x – 1) 2 + 4. Записав эту форму, мы можем увидеть минимальная точка графика находится в (1,4), поэтому она не пересекает ось x.
Шаг 2
Отразите этот граф вниз в точке его вершины. Мы делаем это путем преобразования y = (x – 1) 2 + 4 в y = - (x – 1) 2 + 4
Шаг 3
Мы находим корни этого нового уравнения, используя по формуле квадрата или путем перестановки с сохранением знака плюс или минус. центр (1,0) и радиус 2. Это коснется обоих корней.
центр (1,0) и радиус 2. Это коснется обоих корней.
Шаг 4
Теперь мы можем представить комплексные корни исходного уравнения, повернув два только что найденных действительных корня на 90 градусов против часовой стрелки с центром вращения в центре окружности.
Точки B и C на диаграмме представляют комплексные корни (если мы рассматриваем график как представляющий комплексную плоскость). Таким образом, комплексные корни исходного уравнения равны x = 1 ± 2i.
Общий случай
Сравнительно просто показать алгебраически, что происходит:
Если мы возьмем два общих уравнения:
1) y = (x-a) 2 + b
2) y = -(x-a) 2 + b (это отражение в вершине уравнения 1)
(b > 0). Тогда первое уравнение всегда будет иметь комплексные корни. Корни обоих уравнений будут иметь вид:
1) a ±i√b
2) a ±√b
Таким образом, мы можем думать о (2) как о круге радиуса √b с центром в (a ,0). Следовательно, умножение √b на i приводит к повороту точки (√b, 0 ) 90 градусов против часовой стрелки вокруг точки (a,0). Поэтому комплексные корни будут графически представлены точками вверху и внизу этого круга. (a, √b) и (a, -√b)
Следовательно, умножение √b на i приводит к повороту точки (√b, 0 ) 90 градусов против часовой стрелки вокруг точки (a,0). Поэтому комплексные корни будут графически представлены точками вверху и внизу этого круга. (a, √b) и (a, -√b)
Графическое нахождение сложных корней куба
Существует также способ графического вычисления комплексных корней куба с 1 действительным и 2 комплексными корнями. Этот метод описан с алгебраическим объяснением здесь
Шаг 1
Мы строим кубик с 1 действительным и 2 комплексными корнями, в этом случае y = x 3 – 9x 2 + 25x – 17.
Шаг 2
Находим прямую, проходящую через действительный корень (1,0) и являющуюся касательной к функции.
Шаг 3
Если координата x пересечения касательной с кубической равна a, а градиент касательной равен m, то комплексные корни равны a ± (√m)i. В этом случае пересечение касательной x находится в точке 4, а градиент касательной равен 1, поэтому комплексные корни равны 4 ± 1i.
В этом случае пересечение касательной x находится в точке 4, а градиент касательной равен 1, поэтому комплексные корни равны 4 ± 1i.
[второе последнее предложение отредактировано — спасибо за комментарии ниже!]
Важные ресурсы для студентов IB:
1) Revision Village
Revision Village был создан, чтобы помочь студентам IB с повторением темы как во время курса и по окончании школьных экзаменов в 12 классе и выпускных экзаменов в 13 классе. Я настоятельно рекомендую учащимся использовать его в качестве ресурса во время курса (а не только для окончательного пересмотра в 13-м классе!) Существуют специальные ресурсы для студентов HL и SL как по анализу, так и по приложениям.
В комплексном банке вопросов вы найдете разбивку по каждой основной предметной области (например, алгебре, математическому анализу и т. д.), а затем предоставит большой банк вопросов с оценками. Что мне нравится в этом, так это то, что вам дается рейтинг сложности, а также схема оценок, а также отработанный видеоурок. Действительно полезно!
Действительно полезно!
В разделе практических экзаменов вы найдете большое количество готовых викторин, экзаменов и контрольных работ. Все они имеют рабочие решения и позволяют вам сосредоточиться на конкретных темах или начать общий пересмотр. Здесь также есть несколько отличных сложных вопросов для тех учащихся, которые хотят получить 6 и 7 баллов.
Каждый курс также имеет специальный раздел видеоуроков, в котором представлены 5-15-минутные обучающие видеоролики по каждой отдельной части программы, удобно отсортированные по темам.
2) Руководства по исследованиям и материалы для Документа 3
Я собрал четыре подробных руководства в формате PDF, чтобы помочь учащимся подготовиться к исследовательской курсовой работе и исследованиям по Документу 3. Гиды по исследованию рассказывают о критериях выставления оценок, типичных ошибках учащихся, отличных идеях для исследований, технических советах, методах моделирования и различных статистических методах с подробными пояснениями.

 Мотивирование на учебную деятельность
Мотивирование на учебную деятельность 


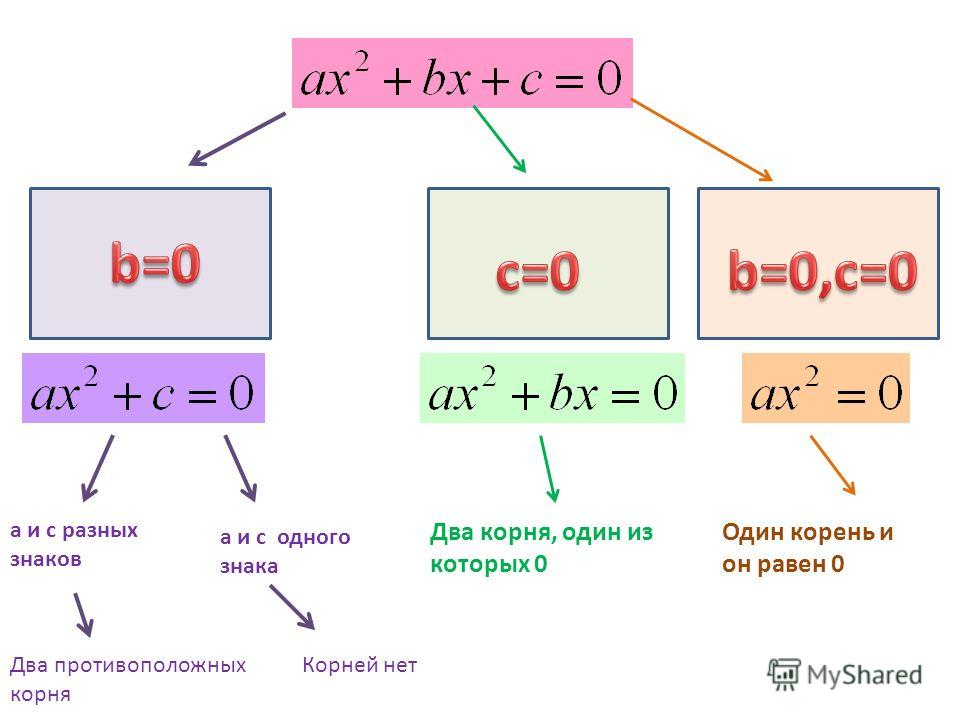

 Подведение итогов
Подведение итогов
 Актуализация знаний
Актуализация знаний

 Первые полторы тысяч разложений.
Первые полторы тысяч разложений.
 2n+B=0 >>
2n+B=0 >>
 Настройка.
Настройка. Подробно
Подробно 1.
2.
1.
2.
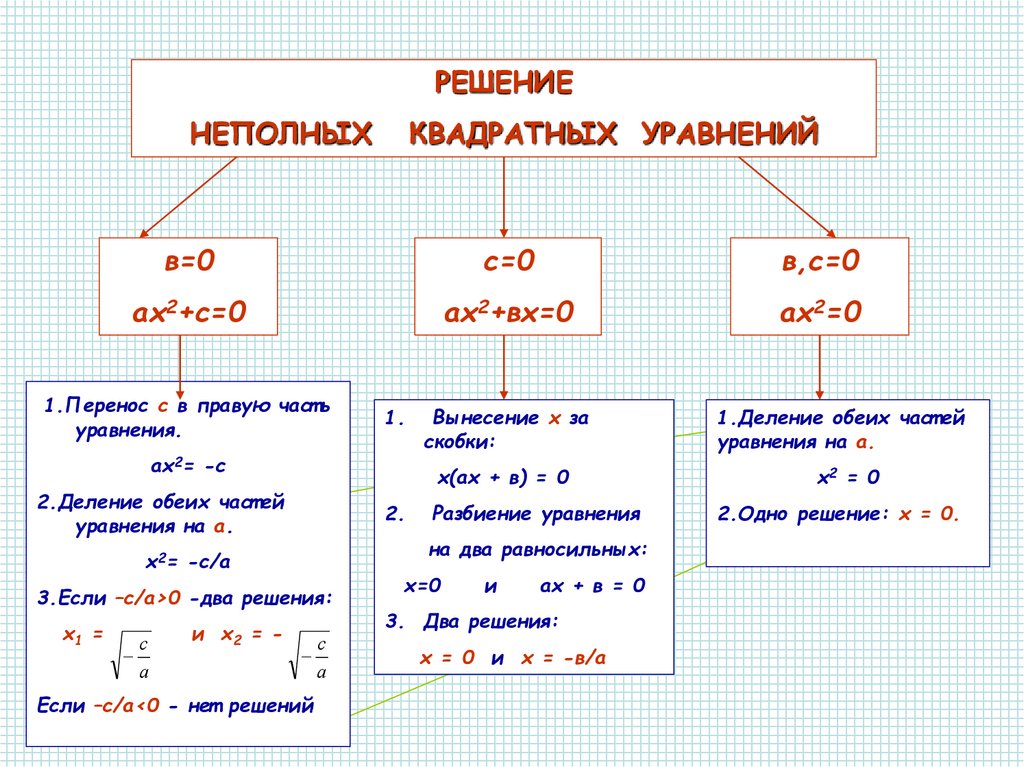 Формула дана выше;
Формула дана выше; sqrt(дискриминант))/ (2 * a)
root2 = (-b - math.sqrt(дискриминант))/ (2 * a)
print('Имеет два корня:')
печать (корень1)
печать (корень2)
Элиф дискриминант == 0:
root1 = float (-b + math.sqrt (дискриминант))/ (2 * a)
print('Имеет двойной корень:')
печать (корень1)
Элиф дискриминант < 0:
root1 = (-b + cmath.sqrt(дискриминант))/ (2 * a)
root2 = (-b - cmath.sqrt(дискриминант))/ (2 * a)
print('Имеет два сложных корня:')
печать (корень1)
печать (корень2)
sqrt(дискриминант))/ (2 * a)
root2 = (-b - math.sqrt(дискриминант))/ (2 * a)
print('Имеет два корня:')
печать (корень1)
печать (корень2)
Элиф дискриминант == 0:
root1 = float (-b + math.sqrt (дискриминант))/ (2 * a)
print('Имеет двойной корень:')
печать (корень1)
Элиф дискриминант < 0:
root1 = (-b + cmath.sqrt(дискриминант))/ (2 * a)
root2 = (-b - cmath.sqrt(дискриминант))/ (2 * a)
print('Имеет два сложных корня:')
печать (корень1)
печать (корень2)
 sqrt(d))/(2*a)
x2=(-b-math.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("настоящий корень")
Элиф д==0:
х=-б/(2*а)
распечатать("х=",х)
print("равный корень")
Элиф д<0:
x1=(-b+cmath.sqrt(d))/(2*a)
x2=(-b-cmath.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("сложный корень")
еще:
print("это не квадратное уравнение")
главный()
########albany.cs######
sqrt(d))/(2*a)
x2=(-b-math.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("настоящий корень")
Элиф д==0:
х=-б/(2*а)
распечатать("х=",х)
print("равный корень")
Элиф д<0:
x1=(-b+cmath.sqrt(d))/(2*a)
x2=(-b-cmath.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("сложный корень")
еще:
print("это не квадратное уравнение")
главный()
########albany.cs######
 sqrt(d))/(2*a)
x2=(-b-cmath.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("сложный корень")
еще:
print("это не квадратное уравнение")
главный()
########albany.cs######
sqrt(d))/(2*a)
x2=(-b-cmath.sqrt(d))/(2*a)
печать("x1=",x1" и x2=",x2)
print("сложный корень")
еще:
print("это не квадратное уравнение")
главный()
########albany.cs######
