Метод Гаусса
Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (быть несовместной).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений, который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.
Преобразования расширенной матрицы (это матрица системы — матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) строки матрицы можно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить.
4) строку матрицы можно умножить (разделить) на любое число, отличное от нуля.
5) к строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» — с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:
Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х1, стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0.
Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0.
2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную хn. Для этого решаем элементарное уравнение А*хn = В. В примере, приведенном выше, х3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной.
 Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по апробированной методике:
2 шаг. Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг. Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг. К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг. Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23), и, соответственно, 11x3 = 23, x3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x3
x2 = 3
x1 + x2 – x3 = 1, следовательно x1 + 3 – 1 = 1, x1 = –1
Ответ: x1 = –1, x2 = 3, x3 = 1.
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3. Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
Умножим второе и третье уравнения на 4, получим:
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х3 = 0,96 или приблизительно 1.
х2 = 3 и х1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Определители квадратных матриц.
Определитель матрицы – это число, характеризующее квадратную матрицу А и тесно связанное с решением систем линейных уравнений. Определитель матрицы А обозначается или . Любой квадратной матрице А порядка n ставится в соответствие по определенному закону вычисленное некоторое число, называемое определителем, или детерминантом, n-го порядка этой матрицы. Рассмотрим определители второго и третьего порядков.
Пусть дана матрица
,
тогда ее определитель второго порядка вычисляется по формуле
.
Пример. Вычислить определитель матрицы А:
Ответ: -10.
Определитель третьего порядка вычисляется по формуле
.
Пример. Вычислить определитель матрицы В
.
Ответ: 83.
Вычисление определителя n-го порядка производится на основании свойств определителя и следующей теоремы Лапласа: определитель равен сумме произведений элементов любой строки (столбца) матрицы на их алгебраические дополнения:
.
Алгебраическое дополнение элемента равно , где — минор элемента , получаемый путем вычеркивания в определителе i-ой строки и j-го столбца.
Минором порядка элемента матрицы А называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-ой строки и j-го столбца.
Пример. Найти алгебраические дополнения всех элементов матрицы А:
.
Ответ: .
Пример. Вычислить определитель матрицы треугольной матрицы:
.
Ответ: -15.
Свойства определителей:
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число , то ее определитель умножится на это число.
3. При транспонировании матрицы ее определитель не изменится.
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
7. Сумма произведения элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.
8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
9. Сумма произведений произвольных чисел на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа .
10. Определитель произведения двух квадратных матриц равен произведению их определителей.
Обратная матрица.
Определение. Матрица называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
.
Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка. Если определитель матрицы отличен от нуля, то такая квадратная матрица называется невырожденной.
Необходимое и достаточное условие существования обратной матрицы: Обратная матрица существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
Первый алгоритм вычисления обратной матрицы:
1. Находим определитель исходной матрицы. Если определитель не равен нулю, то исходная матрица невырожденная и обратная матрица существует.
2. Находим матрицу , транспонированную к А.
3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу .
4. Вычисляем обратную матрицу по формуле: .
5. Проверяем правильность вычисления обратной матрицы, исходя из ее определения .
Пример. Найти матрицу, обратную к данной:
.
Ответ: .
Второй алгоритм вычисления обратной матрицы:
Обратную матрицу можно вычислить на основании следующих элементарных преобразований над строками матрицы:
— перемена местами двух строк;
— умножение строки матрицы на любое число, отличное от нуля;
— прибавление к одной строке матрицы другой строки, умноженной на любое число, отличное от нуля.
Для того чтобы вычислить обратную матрицу для матрицы А, необходимо составить матрицу , затем путем элементарных преобразований привести матрицу А к виду единичной матрицы Е, тогда на месте единичной матрицы получим матрицу .
Пример. Вычислить обратную матрицу для матрицы А:
.
Составляем матрицу В вида:
.
Элемент = 1 и первую строку, содержащую данный элемент, назовем направляющими. Осуществим элементарные преобразования, в результате которых первый столбец преобразуется в единичный столбец с единицей в первой строке. Для этого ко второй и третьей строкам прибавим первую строку, соответственно умноженную на 1 и -2. В результате этих преобразований получим:
.
Окончательно получим
.
Откуда .
Ранг матрицы.Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы А обозначается rang(A) или r(A).
Из определения следует: а) ранг матрицы не превосходит меньшего из ее размеров, т.е. r(А) меньше или равен минимальному из чисел m или n; б) r(A)=0 тогда и только тогда, когда все элементы матрицы А равны нулю; в) для квадратной матрицы n-го порядка r(A)=n тогда и только тогда, когда матрица А — невырожденная.
Пример: вычислить ранги матриц:
.
Ответ: r(A)=1. Ответ: r(A)=2.
Назовем элементарными преобразованиями матрицы следующие:
1) Отбрасывание нулевой строки (столбца).
2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
3) Изменение порядка строк (столбцов) матрицы.
4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
5) Транспонирование матрицы.
Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Примеры: Вычислить матрицу , где
; ;
Ответ: .
Пример: Вычислить матрицу , где
; ; ; E – единичная матрица.
Ответ: .
Пример : Вычислить определитель матрицы
.
Ответ: 160.
Пример: Определить, имеет ли матрица А обратную, и если имеет, то вычислить ее:
.
Ответ: .
Пример : Найти ранг матрицы
.
Ответ: 2.
2.4.2. Системы линейных уравнений.
Система m линейных уравнений с n переменными имеет вид:
,
где , — произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений. Решением системы уравнений называется такая совокупность n чисел ( ), при подстановке которых каждое уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Теорема Крамера: Пусть — определитель матрицы А, составленной из коэффициентов при переменных “х”, а — определитель матрицы, получаемой из матрицы А заменой j-го столбца этой матрицы столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам: (j=1, 2, …, n). Эти уравнения получили названия формул Крамера.
Тогда, если , то система имеет единственное решение, определяемое по формулам: (j=1, 2, …, n). Эти уравнения получили названия формул Крамера.
Пример. Решить системы уравнений по формулам Крамера:
Ответы: (4, 2, 1). (1, 2, 3) (1, -2, 0)
Метод Гаусса – метод последовательного исключения переменных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних по номеру переменных, находятся все остальные переменные.
Пример: Решить системы уравнений методом Гаусса.
Ответы: (1, 1, 1). (1, -1, 2, 0). (1, 1, 1).
Для совместных систем линейных уравнений верны следующие утверждения:
· если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система уравнений имеет единственное решение;
· если ранг матрицы совместной системы меньше числа переменных, т. е. r<n, то система неопределенная и имеет бесконечное множество решений.
е. r<n, то система неопределенная и имеет бесконечное множество решений.
2.4.3. Технология выполнения операций над матрицами в среде EXCEL.
Рассмотрим некоторые аспекты работы с табличным процессором Excel, которые позволяют упростить расчеты, необходимые для решения оптимизационных задач. Табличный процессор – это программный продукт, предназначенный для автоматизации обработки данных табличной формы.
Работа с формулами.В программах электронных таблиц формулы служат для выполнения множества разнообразных расчетов. С помощью Excel можно быстро создать формулу. Формула состоит из трех основных частей:
— знак равенства;
— совокупность значений или ссылки на ячейки, с которыми выполняются расчеты;
— операторы.
Использование в формулах функций. Чтобы облегчить ввод формул, можно воспользоваться функциями Excel. Функции – это встроенные в Excel формулы. Для активизации той или иной формулы следует нажать кнопки Вставка, Функции. В появившемся окне Мастер функций слева содержится перечень типов функций. После выбора типа справа будет помещен список самих функций. Выбор функций осуществляется щелчком клавиши мыши на соответствующем названии.
Для активизации той или иной формулы следует нажать кнопки Вставка, Функции. В появившемся окне Мастер функций слева содержится перечень типов функций. После выбора типа справа будет помещен список самих функций. Выбор функций осуществляется щелчком клавиши мыши на соответствующем названии.
При выполнении операций над матрицами, решении систем линейных уравнений, решении оптимизационных задач можно применять следующие функции Excel:
— МУМНОЖ — умножение матриц;
— ТРАНСП — транспонирование матрицы;
— МОПРЕД — вычисление определителя матрицы;
— МОБР — вычисление обратной матрицы.
Кнопка находится на панели инструментов. Функции для выполнения операций с матрицами находятся в категории Математические.
Умножение матриц с помощью функции МУМНОЖ. Функция МУМНОЖ возвращает произведение матриц (матрицы хранятся в массивах 1 и 2). Результатом является массив с таким же числом строк, как массив 1, и с таким же числом столбцов, как массив 2.
Пример. Найти произведение двух матриц А и В в среде Excel (см. рис 2.9):
; .
— Введите матрицы А в ячейки А2:C3 и В в ячейки E2:F4.
— Выделите диапазон ячеек для результата умножения – h3:I2.
— Введите формулу умножения матриц =МУМНОЖ(A2:C3, E2:F4).
— Нажмите клавиши CTRL+SHIFT+ENTER.
Вычисления обратной матрицы с помощью функции МОБР.
Функция МОБР возвращает обратную матрицу для матрицы, хранящейся в массиве. Синтаксис: МОБР(массив). На рис. 2.10 приведено решение примера в среде Excel.
Пример. Найти матрицу, обратную к данной:
.
Рисунок 2.9. Исходные данные для умножения матриц.
Рисунок 2.10. Исходные данные для вычисления обратной матрицы.
Дата добавления: 2017-10-04; просмотров: 2353; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Решение высшей математики онлайн
‹— Назад
С понятием определителя мы уже сталкивались при изучении векторного произведения в разделе 10. Там были введены определители матриц второго и третьего порядка. В этом разделе мы дадим определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка . Такое рекуррентное определение и было использовано для введения определителя матрицы третьего порядка . Отметим также, что определитель существует только у квадратных матриц.
Там были введены определители матриц второго и третьего порядка. В этом разделе мы дадим определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка . Такое рекуррентное определение и было использовано для введения определителя матрицы третьего порядка . Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы будем обозначать или .
Определение 14.6 Определителем квадратной матрицы второго порядка называется число . Определителем квадратной матрицы порядка , , называется число
где — определитель матрицы порядка , полученной из матрицы вычеркиванием первой строки и столбца с номером .
Легко проверить, что это определение для определителей второго и третьего порядка совпадает с данным ранее в разделе 10.
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка:
Замечание 14.7 Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Замечание 14.8 В определении 14.6 было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядка и принимающая значения в множестве чисел.
Замечание 14.9 В литературе вместо термина «определитель» используется также термин «детерминант», имеющий тот же самый смысл. От слова «детерминант» и появилось обозначение .
Рассмотрим некоторые свойства определителей, которые сформулируем в виде предложений.
Предложение 14.6 При транспонировании матрицы определитель не меняется, то есть .
Предложение 14.7 Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть .
Предложение 14.8 Если в матрице поменять местами две строки, то ее определитель сменит знак.
Ввиду ограниченности курса доказательства этих трех свойств мы опускаем. Читатель может найти их в учебниках по линейной алгебре [3], [5] или же может без особых сложностей проверить их на матрицах второго и третьего порядков.
Предложение 14.9 Если матрица имеет две одинаковые строки, то ее определитель равен нулю.
Доказательство. Поменяем местами две одинаковые строки. В силу предложения 14.8 определитель сменит знак. С другой стороны, так как строки были одинаковыми, то матрица не изменилась и, следовательно, не изменился и ее определитель. Получим, что , откуда следует, что .
В дальнейшем нам потребуется складывать строки и умножать строку на число. Эти действия над строками (столбцами) мы будем выполнять так же, как действия над матрицами-строками (матрицами-столбцами), то есть поэлементно. Результатом будет служить строка (столбец), как правило, не совпадающая со строками исходной матрицы. При наличии операций сложения строк (столбцов) и умножения их на число мы можем говорить и о линейных комбинациях строк (столбцов), то есть суммах с числовыми коэффициентами.
Предложение 14.10 Если строку матрицы умножить на число , то ее определитель умножится на это число.
Доказательство. Пусть — исходная матрица, — матрица, полученная из умножением первой строки на число :
Тогда
где — определитель матрицы, полученной из матрицы или, что то же самое, из матрицы вычеркиванием первой строки и -ого столбца.
Вынесем множитель за знак суммы и получим
Пусть теперь матрица получается из матрицы умножением -ой строки на число . Поменяем местами первую и -ую строки в матрице и то же самое проделаем в матрице . Получим две новых матрицы и . По предложению 14.8
| (14.10) |
Очевидно, что матрица получается из матрицы умножением первой строки на число . Как только что было доказано, . Таким образом, из второго равенства (14.10) находим , отсюда с помощью первого равенства (14.10) получаем .
Как только что было доказано, . Таким образом, из второго равенства (14.10) находим , отсюда с помощью первого равенства (14.10) получаем .
Предложение 14.11 Если матрица содержит нулевую строку, то ее определитель равен нулю.
Доказательство. Нулевую строку можно рассматривать как строку из единиц, умноженную на число ноль. По предложению 14.10 определитель такой матрицы равен нулю, умноженному на определитель матрицы, содержащей строку из единиц. Результат такого умножения всегда будет ноль.
Предложение 14.12 Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю.
Доказательство. По предложению 14.10 определитель исходной матрицы равен числу , умноженному на определитель матрицы, у которой есть две одинаковые строки. По предложению 14.9 определитель последней матрицы равен нулю. Поэтому и определитель исходной матрицы равен нулю.
По предложению 14.9 определитель последней матрицы равен нулю. Поэтому и определитель исходной матрицы равен нулю.
Предложение 14.13 Пусть в матрице -ая строка имеет вид . Тогда , где матрица получается из матрицы заменой -ой строки на строку , а матрица — заменой -ой строки на строку .
Доказательство. Пусть первая строка матрицы имеет вид . Тогда
Для случая утверждение доказано.
Пусть . Обозначим через , , матрицы , , и , в которых поменяли местами первую и -ую строки. По только что доказанному (для ) утверждению . По предложению 14.8 , , . Следовательно, . Умножив обе части последнего равенства на , получим требуемое утверждение.
Следовательно, . Умножив обе части последнего равенства на , получим требуемое утверждение.
Предложение 14.14 Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.
Доказательство. Пусть к -ой строке матрицы прибавлена -ая строка, умноженная на число . Новую матрицу обозначим . В матрице элементы -ой строки имеют вид . По предложению 14.13 , где — матрица, полученная из матрицы заменой -ой строки на -ую строку, умноженную на число . По предложению 14.12 , то есть .
Предложение 14.15 Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.
Доказательство. По предложению 14.13 определитель исходной матрицы равен сумме определителей матриц, в каждой из которых есть пропорциональные строки. По предложению 14.12 все эти определители равны нулю. Следовательно, и определитель исходной матрицы тоже равен нулю.
По предложению 14.12 все эти определители равны нулю. Следовательно, и определитель исходной матрицы тоже равен нулю.
Определение 14.7 Алгебраическим дополнением к элементу матрицы называется число, равное , где — определитель матрицы, полученной из матрицы вычеркиванием -ой строки и -ого столбца.
Алгебраическое дополнение к элементу матрицы обозначается .
Пример 14.4 Пусть . Тогда
Замечание 14.10 Используя алгебраические дополнения, определение 14.6 определителя можно записать так:
Предложение 14.16 Разложение определителя по произвольной строке. Для определителя матрицы справедлива формула
Доказательство.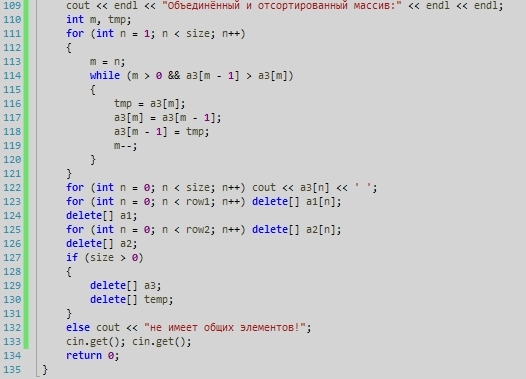 Если , положим . Пусть . Тогда -ую строку поменяем местами со строкой с номером . Определитель сменит знак. Затем строку с номером поменяем местами со строкой с номером . Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока -ая строка матрицы не станет первой строкой новой матрицы, которую мы обозначим . Отметим, что в матрице , начиная со второй строки, стоят строки матрицы , причем порядок их следования не изменился.
Если , положим . Пусть . Тогда -ую строку поменяем местами со строкой с номером . Определитель сменит знак. Затем строку с номером поменяем местами со строкой с номером . Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока -ая строка матрицы не станет первой строкой новой матрицы, которую мы обозначим . Отметим, что в матрице , начиная со второй строки, стоят строки матрицы , причем порядок их следования не изменился.
При переходе от матрицы к матрице определитель сменит знак раз (проверьте для случая ). Таким образом
| (14.11) |
Это соотношение верно и при . По определению 14.6 определителя,
где — определитель матрицы, полученной из матрицы вычеркиванием первой строки и -ого столбца. Первая строка матрицы совпадает с -ой строкой матрицы , поэтому . Результат вычеркивания в матрице первой строки и -ого столбца будет таким же, как при вычеркивании в матрице -ой строки и -ого столбца. Поэтому , где — определитель матрицы, полученной при вычеркивании в матрице -ой строки и -ого столбца. Следовательно,
Первая строка матрицы совпадает с -ой строкой матрицы , поэтому . Результат вычеркивания в матрице первой строки и -ого столбца будет таким же, как при вычеркивании в матрице -ой строки и -ого столбца. Поэтому , где — определитель матрицы, полученной при вычеркивании в матрице -ой строки и -ого столбца. Следовательно,
В силу равенства (14.11) получим
По определению 14.7 алгебраического дополнения получим . Тогда из предыдущего равенства вытекает
что и требовалось доказать.
Пример 14.5 Вычислите .
Решение. Воспользуемся разложением по третьей строке, так выгоднее, поскольку в третьей строке два числа из трех — нули. Получим
Предложение 14. 17 Для квадратной матрицы порядка при выполнено соотношение
17 Для квадратной матрицы порядка при выполнено соотношение
| (14.12) |
Доказательство. Пусть — матрица, полученная из матрицы , в которой -ая строка заменена -ой строкой этой же матрицы, а сама -ая строка осталась без изменения. Таким образом, в матрице есть две одинаковые строки и в силу предложения 14.9 .
С другой стороны, используя разложение определителя по -ой строке (предложение 14.16), получим
где — алгебраическое дополнение к элементу . Так как все строки матрицы , кроме -ой, совпадают со строками матрицы , то . Так как по построению матрицы , то
Так как , то равенство (14.12) доказано.
Предложение 14. 18 Все свойства определителя, сформулированные для строк ( предложения 14.8-14.17), справедливы и для столбцов, в частности, справедливо разложение определителя по -ому столбцу
18 Все свойства определителя, сформулированные для строк ( предложения 14.8-14.17), справедливы и для столбцов, в частности, справедливо разложение определителя по -ому столбцу
| (14.13) |
и равенство
при .
Доказательство. В силу предложения 14.6 определитель не меняется при транспонировании матрицы, а ее столбцы становятся строками транспонированной матрицы, для которой доказываемые свойства имеют место.
Предложение 14.19 Определитель треугольной матрицы равен произведению элементов ее главной диагонали.
Доказательство. Воспользуемся индукцией по порядку матрицы. Для :
Для :
утверждение верно. Предположим, что доказываемое утверждение верно для матриц порядка . Покажем, что оно верно для матрицы порядка .
Если — верхняя треугольная матрица, то используем разложение по первому столбцу (равенство (14.13) при ):
Справа стоит определитель треугольной марицы порядка . По предположению индукции этот определитель равен . Поэтому .
Если — нижняя треугольная матрицы, то нужно воспользоваться разложением по первой строке. В остальном рассуждения аналогичны.
Итак, утверждение верно для матрицы порядка . Предложение доказано.
Следствие 14.1 Определитель единичной матрицы равен единице, .
Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений. Алгоритм вычислений следующий.
Алгоритм вычислений следующий.
Алгоритм создания нулей в столбце.
Пусть требуется вычислить определитель матрицы порядка . Если , то поменяем местами первую строку и любую другую, в которой первый элемент не нуль. В результате определитель , будет равен определителю новой матрицы с противоположным знаком. Если же первый элемент каждой строки равен нулю, то матрица имеет нулевой столбец и по предложениям 14.11, 14.18 ее определитель равен нулю.
Итак, считаем, что уже в исходной матрице . Первую строку оставляем без изменений. Прибавим ко второй строке первую строку, умноженную на число . Тогда первый элемент второй строки будет равен
Остальные элементы новой второй строки обозначим , . Определитель новой матрицы по предложению 14.14 равен .
Первую строку умножим на число и прибавим к третьей. Первый элемент новой третьей строки будет равен
Первый элемент новой третьей строки будет равен
Остальные элементы новой третьей строки обозначим , . Определитель новой матрицы по предложению 14.14 равен .
Процесс получения нулей вместо первых элементов строк продолжим дальше. Наконец, первую строку умножим на число и прибавим к последней строке. В результате получается матрица, обозначим ее , которая имеет вид
причем . Для вычисления определителя матрицы используем разложение по первому столбцу
Так как , то
В правой части стоит определитель матрицы порядка . К нему применим тот же алгоритм, и вычисление определителя матрицы сведется к вычислению определителя матрицы порядка . Процесс повторяем до тех пор, пока не дойдем до определителя второго порядка, который вычисляется по определению.
Если матрица не обладает какими-то специфическими свойствами, то заметно уменьшить объем вычислений по сравнению с предложенным алгоритмом не удается. Еще одна хорошая сторона этого алгоритма — по нему легко составить программу для компьютера для вычисления определителей матриц больших порядков. В стандартных программах вычисления определителей используется этот алгоритм с не принципиальными изменениями, связанными с минимизацией влияния ошибок округления и погрешностей входных данных при вычислениях компьютера.
Пример 14.6 Вычислите определитель матрицы
.
Решение. Первую строку оставляем без изменения. Ко второй строке прибавляем первую, умноженную на число :
Определитель не меняется. К третьей строке прибавляем первую, умноженную на число :
Определитель не меняется. К четвертой строке прибавляем первую, умноженную на число :
К четвертой строке прибавляем первую, умноженную на число :
Определитель не меняется. В результате получаем
По тому же алгоритму считаем определитель матрицы порядка 3, стоящий справа. Первую строку оставляем без изменений, ко второй строке прибавляем первую, умноженную на число :
К третьей строке прибавляем первую, умноженную на число :
В результате получаем
Ответ. .
Замечание 14.11 Внимательный читатель, наверное, отметил, что хотя при вычислениях использовались дроби, результат оказался целым числом. Действительно, используя свойства определителей и то, что исходные числа — целые, операций с дробями можно было бы избежать. Но в инженерной практике числа крайне редко бывают целыми. Поэтому, как правило, элементы определителя будут десятичными дробями и применять какие-то ухищрения для упрощения вычислений нецелесообразно.
Поэтому, как правило, элементы определителя будут десятичными дробями и применять какие-то ухищрения для упрощения вычислений нецелесообразно.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
 ru 🎓
ru 🎓1
Первый слайд презентации
1 Лекция N 7 Тема: Метод Гаусса
Изображение слайда
2
Слайд 2
2 Решение систем линейных уравнений. Метод Гаусса Пример.
Изображение слайда
3
Слайд 3
3 1) Составим расширенную матрицы системы
Изображение слайда
4
Слайд 4
4 2) Приведем матрицу к ступенчатому виду -2 +
Изображение слайда
5
Слайд 5
5
Изображение слайда
6
Слайд 6
6
3) Составим новую систему
Система имеет единственное решение
Можно было продолжить преобразования, и привести систему к виду Гаусса.
Изображение слайда
7
Слайд 7
7 Теорема Кронекера-Капелли. 1) Если, то система не имеет решения 2) Если, где — число неизвестных, то система имеет единственное решение 3) Если, то система имеет бесконечное множество решений.
Изображение слайда
8
Слайд 8
8 Примеры Пример 1. Исследовать на совместность и решить систему методом Гаусса. -5
Изображение слайда
9
Слайд 9
9
Система имеет бесконечное множество решений. Найдем число свободных неизвестных
Базисная неизвестная, свободная. Обозначим свободную неизвестную
Получим
Ответ:, где
Обозначим свободную неизвестную
Получим
Ответ:, где
Изображение слайда
10
Слайд 10
10 В этом примере система имеет бесконечное множество решений. Запишем некоторые из них: Все решения являются точками прямой 4 2
Изображение слайда
11
Слайд 11
11 Пример 2. Исследовать на совместность и решить систему методом Гаусса. -1 -2
Изображение слайда
12
Слайд 12
12 Система несовместна (по теореме Кронекера-Капелли) -1
Изображение слайда
13
Слайд 13
13
Мы рассмотрели два метода решения систем линейных уравнений:
1) Метод Крамера
2) Метод Гаусса
Метод Крамера предполагает вычисление определителей. Мы вычисляли определители 3-его порядка разложением по элементам первой строки.
Мы вычисляли определители 3-его порядка разложением по элементам первой строки.
Изображение слайда
14
Слайд 14
14 Пример. Способ 1. -4 5
Изображение слайда
15
Слайд 15
15 Способ 2.
Изображение слайда
16
Слайд 16
16 1) Определитель не изменится, если поменять строки на соответствующие столбцы Свойства определителей 2) Если у определителя 2 одинаковые строки или столбца, то он равен нулю. 3) Если у определителя нулевая строка или столбец, то он равен нулю.
Изображение слайда
17
Слайд 17
17
4) Если две строки (столбца) поменять местами, то знак определителя изменится на противоположный. Свойства определителей
5) Общий множитель строки (столбца) можно выносить за знак определителя.
6) Определитель не изменится, если к элементам строки (столбца) прибавить элементы другой строки (столбца), умноженные на число.
Свойства определителей
5) Общий множитель строки (столбца) можно выносить за знак определителя.
6) Определитель не изменится, если к элементам строки (столбца) прибавить элементы другой строки (столбца), умноженные на число.
Изображение слайда
18
Слайд 18
18 Пример. Вычислить: (т.к. две одинаковые строки)
Изображение слайда
19
Слайд 19
Пусть дана матрица Определителем второго порядка, соответствующим данной матрице, называется число Определитель обозначают символом
Изображение слайда
20
Слайд 20
Таким образом, Числа называются элементами определителя Пример
Изображение слайда
21
Слайд 21
Приведем свойства определителя второго порядка
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами, т.е.
Определитель не изменится, если его строки поменять местами с соответствующими столбцами, т.е.
Изображение слайда
22
Слайд 22
2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, т.е.
Изображение слайда
23
Слайд 23
3. Определитель с двумя одинаковыми строками (или столбцами) равен нулю. 4. Общий множитель всех элементов строки (или столбца) можно выносить за знак определителя:
Изображение слайда
24
Слайд 24
5. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю
6. Если к элементам какой-либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины, т.е.
Если к элементам какой-либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины, т.е.
Изображение слайда
25
Слайд 25
Рассмотрим матрицу Определитель третьего порядка
Изображение слайда
26
Слайд 26
Определителем третьего порядка называют число
Изображение слайда
27
Слайд 27
Назовем минором, соответствующим данному элементу определителя третьего порядка, определитель второго порядка, полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Например, минор соответствующий элементу есть определитель
Например, минор соответствующий элементу есть определитель
Изображение слайда
28
Слайд 28
Назовем алгебраическим дополнением Например, Правило. Определитель третьего порядка равен сумме попарных произведений элементов какой-либо его строки (или столбца) на их алгебраические дополнения
Изображение слайда
29
Слайд 29
Пример Вычислить Разлагаем по 1-му столбцу
Изображение слайда
30
Слайд 30
Можно разлагать по 2-ой строке
Изображение слайда
31
Слайд 31
Все свойства определителей 2-ого порядка остаются справедливыми для определителей 3-его порядка. Свойства
Пример
Вычислить
т.к. совпадают первая и вторая строки.
Свойства
Пример
Вычислить
т.к. совпадают первая и вторая строки.
Изображение слайда
32
Слайд 32
Все свойства определителей 2-ого и 3-его порядков сохраняются для определителей высших порядков. Определители высших порядков Пример
Изображение слайда
33
Слайд 33
Понятие обратной матрицы вводится только для квадратных матриц. Обратная матрица Опр. Матрица называется обратной к матрице, если — единичная матрица
Изображение слайда
34
Слайд 34
Теорема. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы матрица A была невырожденной, т. е. чтобы её определитель был отличен от нуля.
Рассмотрим
е. чтобы её определитель был отличен от нуля.
Рассмотрим
Изображение слайда
35
Слайд 35
Составим матрицу из алгебраических дополнений Составим новую матрицу поменяв местами строки и столбцы (матрица называется транспонированной ).
Изображение слайда
36
Слайд 36
Изображение слайда
37
Слайд 37
Составим матрицу, обратную матрице второго порядка Здесь Тогда
Изображение слайда
38
Слайд 38
Пример. то A – невырожденная, и, следовательно, существует обратная матрица
то A – невырожденная, и, следовательно, существует обратная матрица
Изображение слайда
39
Слайд 39
Вычисляем алгебраические дополнения:
Изображение слайда
40
Слайд 40
Изображение слайда
41
Слайд 41
Изображение слайда
42
Слайд 42
Свойства Примеры Вычислить определитель произведения 1. 2.
Изображение слайда
43
Слайд 43
По свойству 1
Изображение слайда
44
Слайд 44
Домашнее задание
1. Проверить, что, действительно
Проверить, что, действительно
Изображение слайда
45
Последний слайд презентации: 1 Лекция N 7 Тема: Метод Гаусса
Домашнее задание 2. Вычислить
Изображение слайда
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
Стр 1 из 38Следующая ⇒ Свойство 1. Определитель квадратной матрицы не изменяется при её транспонировании: . Доказательство свойства 1 для квадратных матриц 2 и 3 порядков проводится по единой схеме. Приведём доказательство для квадратной матрицы 2-го порядка. Пусть Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её определитель равен нулю. Свойство 2 непосредственно вытекает из определения определителя. Свойство 3. При перестановке местами любых двух строк (столбцов) матрицы её определитель меняет знак. Доказательство свойства 3 приведём для квадратных матриц третьего порядка. Пусть
Пусть — матрица, полученная из матрицы перестановкой мест первых двух строк, т.е. Аналогично проходит доказательство свойства 3, при перестановке любых других строк (столбцов). Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число. Доказательство свойства 4 приведём для случая умножения элементов первой строки, квадратной матрицы третьего порядка, на произвольное число . Пусть Аналогично доказывается свойство 4 для всех остальных случаев. Свойство 5. Если каждый элемент i-й строки (столбца) матрицы представлен в виде суммы двух слагаемых, то определитель такой матрицы равен , где элементы матриц и , за исключением элементов -й строки (столбца), совпадают с соответствующими элементами матрицы . А в -х строках (столбцах) матриц и стоят упомянутые первые и вторые слагаемые соответственно. Доказательство свойства 5 приведём для случая, когда элементы первой строки квадратной матрицы второго порядка, представлены в виде двух слагаемых. Пусть . Аналогично доказывается свойство 5 и для квадратных матриц третьего порядка. Отметим некоторые следствия, непосредственно вытекающие из перечисленных 5 основных свойств определителя. Следствие 1. Определитель матрицы, имеющей две одинаковые строки (столбца) равен нулю. Доказательство. Пусть — квадратная матрица, имеющая две одинаковые строки (столбца). — матрица полученная в результате перестановки указанных одинаковых строк (столбцов) матрицы . Тогда, с одной стороны, , с другой стороны, в силу свойства 3, . Следовательно, . Из последнего равенства следует, что . Следствие 2. Если какие-либо две строки (столбца) матрицы пропорциональны, то её определитель равен нулю. Доказательство. Пусть — квадратная матрица третьего порядка, имеющая две пропорциональные строки. Будем считать, без ограничения общности, что в матрице пропорциональны две строки. Предположим, что элементы второй строки получены умножением соответствующих элементов первой строки на некоторое число . Следствие 3. Доказательство. Пусть — квадратная матрица третьего порядка В качестве иллюстрации доказательства, рассмотрим случай, когда к элементам первой строки матрицы прибавляются элементы второй строки, умноженные на произвольное число . Тогда, в силу свойства 5 и следствия 2 = Миноры и алгебраические дополнения. Пусть — произвольная квадратная матрица, – её элемент, стоящий в позиции . Вычеркивая из матрицы i-ю строку и -ый столбец, получим некоторую матрицу , порядка . Определитель матрицы называется минором элемента . Минор элемента будем обозначать символом . Число называется алгебраическим дополнением элемента . Для обозначения алгебраического дополнения элемента будем пользоваться символом . 12345678910Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Основные свойства определителей и их геометрический смысл. — Мегаобучалка
Свойство 1. Если А, В две квадратные матрицы, то .
Свойство 2. При транспонировании определитель не меняется: = .
Свойство 3. Если строка или столбец матрицы состоит из нулей, то .
Геометрический смысл: Если в системе векторов есть 0 — вектор, то объём параллелепипеда равен 0.
Свойство 4. Если поменять местами любые две строки (или два столбца), то сменит знак.
Это связано с тем, что при смене мест 2 элементов в перестановке меняется чётность: одна инверсия появится или наоборот, исчезнет.
Свойство 5. Если матрица содержит две одинаковых (или пропорциональных) строки или столбца, то .
Доказывается из предыдущего свойства: если в матрице две одинаковые строки, то меняя их местами, мы изменим знак, но они же одинаковы, поэтому не должен измениться. Тогда = , то есть . Для пропорциональных то же самое, так как можем сначала вынести коэффициент за знак определителя, и строки станут одинаковыми, а тогда .
Тогда = , то есть . Для пропорциональных то же самое, так как можем сначала вынести коэффициент за знак определителя, и строки станут одинаковыми, а тогда .
Геометрический смысл. Если два ребра параллелепипеда коллинеарны, то фигура станет плоской, объём = 0.
ЛЕКЦИЯ № 2. 10.09.2019
Свойство 6. Если любую строку (столбец) матрицы умножить коэффициент с, то увеличится в с раз.
Идея доказательства: если в каждом произведении элементов один из них умножен на с, то вся сумма, состоящая из таких слагаемых, также увеличится в с раз.
Это свойство даёт возможность выносить общий множитель за знак определителя из какой-либо строки. Геометрический смысл: Если умножить на коэффициент даже один из векторов, образующих параллелограмм, то площадь параллелограмма умножится на этот коэффициент.
Если умножить не один, а оба вектора, то площадь увеличится в раз. Для 3 векторов в пространстве и параллелепипеда, если умножить каждый вектор на , то объём вырастет в раз.
Следствие: 6а) .
Свойство 7. Если все элементы какой-либо строки представлены в виде сумм двух элементов:
= + .
то данный определитель равен сумме двух определителей, где в первом из них в этой строке — первые слагаемые, а во втором — вторые (все остальные строки в обоих определителях без изменения).
Доказательство проведём для произвольных матриц 2-го порядка.
(для n аналогично).
= + .
действительно: = = .
Для матриц большего порядка, аналогично, в любом из n! слагаемых по n элементов, какой-то один окажется суммой двух чисел, в итоге каждое слагаемое распадётся на два, и в сумме будет 2 n! слагаемых, где одни n! образуют 1-й определитель, а другое n! — второй.
Свойство 8. Если к любой строке прибавить другую строку, домноженную на число, не изменится.
Доказательство. Если в предыдущем свойстве в роли вторых элементов взяты элементы другой строки этой же самой матрицы, домноженные на коэффициент k, то:
= + тогда во 2-м определителе строки пропорциональны, он равен 0. То есть мы видим, что если к одной строке прибавить строку, кратную какой-то строке из этой же матрицы, определитель не изменится.
То есть мы видим, что если к одной строке прибавить строку, кратную какой-то строке из этой же матрицы, определитель не изменится.
Это важное свойство даёт возможность преобразовывать и упрощать матрицы в процессе вычисления определителей.
Замечание. Очевидно, что можно не только прибавить, но и отнять от строки строку, ведь мы можем домножить на коэффициент .
Геометрический смысл. Если к вектору b прибавить вектор a, умноженный на любой коэффициент, то площадь параллелограмма не изменится, основание и высота остались старыми, см. чертёж:
Здесь площадь параллелограмма, образованного векторами a,b такая же, как для образованного векторами a, b+2a.
Из свойства 8 следует, что строки можно складывать и вычитать, на этом основан метод Гаусса приведения к треугольной форме.
Важно! Определитель не меняется (св-во 8), если умножать строку в уме (в буфере обмена) и затем, уже кратную, прибавлять к какой-либо другой. Если же просто умножать строку, которая находится в матрице, то определитель умножится на коэффициент (свойство 6). Это совершенно разные операции, не надо их путать.
Это совершенно разные операции, не надо их путать.
Следствие 8 а). Если какая-либо строка матрицы является суммой других строк, то .
Идея доказательства: Если третья строка есть сумма первой и второй, то вычитая 1-ю и 2-ю из неё, получим строку из нулей.
Пример. Вычислить приведением к треугольной форме.
Заметим, что ниже углового элемента (1) число 2. Поэтому из 2-й строки вычтем 1-ю, умноженную на 2. Т.е.вычесть надо строку (2 6).
= = = 1.
Пример Вычислить определитель: методом Гаусса (приведением к треугольной форме).
Применим свойство 8. Постараемся обнулить все элементы ниже .
Из 2-й строки вычтем 1-ю строку: = .
Теперь из 3-й вычтем удвоенную 1-ю, будет .
Чтобы завершить приведение к треугольному виду, вычтем из 3-й строки удвоенную 2-ю, получится . А теперь просто найдём произведение чисел по диагонали, так как привели к треугольной форме. Определитель равен 2. Ответ: 2.
Определитель равен 2. Ответ: 2.
Этот метод особено будет нужен в теме «системы уравнений», но, как видим, помогает и при вычислении определителей.
Матрица
. Какие строки/столбцы являются дубликатами других в матрицах R?
TL;DR
Для целочисленных матриц одинакового размера, но разных форм ( 5e+06 -x2, 5e+05 -by-20, 5000-by-2000), содержащих целые числа от 1 до 10 , самым быстрым протестированным ответом с основанием был , группирующий / , соответствующий , предложенный в комментарии @alexis_laz. Самый быстрый ответ, отличный от base , был data.table::frank / соответствует , хотя группировка / соответствует во всех случаях, даже превосходя ответ data.table в случае 5000 на 2000.
Обратите внимание, что результаты могут различаться для двойных матриц или целочисленных матриц с большим диапазоном и в зависимости от количества потоков, доступных для data. . [TODO?]  table
table
Фон
@MikaelJagan’s asplit / match( ответ кажется «элегантным решением с использованием базы R». Однако ,
)
?match предупреждает:
Сопоставление списков потенциально очень медленное, и его лучше избегать, за исключением простых случаев.
Учитывая, что OP имеет «матрицу со многими строками и столбцами», мы хотели сравнить производительность asplit / match( с ответом другого ,
)
base ответы:
- @Onyambu’s
paste/match(answer;, ) - @ThomasIsCoding’s
взаимодействие/совпадение(ответ;, ) - @alexis_laz’s
grouping/match(ответ., )
Мы сравнили их с некоторыми ответами, отличными от базы , которые мы использовали в качестве ориентира (признавая, что ОП запросил только базу ):
- Ответ @MikaelJagan
Rcpp; - @Henrik’s
data.отвечает: table
table - Прохождение самосоединения
which = TRUEиmult = "first" отдо[.data.table; - Два подхода, основанные на ранжировании строк, различающиеся тем, как обрабатываются совпадения:
-
frank(ties.method = "average")/match(,, ) -
frank(ties.method = "dense")/match(., )
-
- Прохождение самосоединения
Настройка
библиотека (микробенчмарк)
библиотека (данные.таблица)
получитьDTthreads() # 4
f_asplit <- функция (х) {
л <- assplit(x, 1L)
совпадение(л, л) }
f_paste <- функция (x) {
s <- do.call(вставить, как.data.frame(x))
совпадение (ы, с) }
f_interaction <- функция (х) {
z <- as.integer (взаимодействие (as.data.frame (x)))
совпадение(г, г) }
f_grouping <- функция (x) {
g <- do.call(группировка, as.data.frame(x))
о <- порядок (g, метод = "основание")
e <- attr(g, "заканчивается")
z <- rep. int(seq_along(e), c(e[1L], e[-1L] - e[-length(e)]))[o]
совпадение(г, г) }
f_join <- функция (x) {
д <- as.data.table(x)
d[d, on = имена (d), mult = "первый", что = TRUE] }
f_frank_average <- функция(х) {
д <- as.data.table(x)
r <- frank(d, ties.method = "средний")
совпадение(г, г) }
f_frank_dense <- функция (х) {
д <- as.data.table(x)
r <- frank(d, ties.method = "плотный")
совпадение(г, г) }
Rcpp::sourceCpp('<скопировать исходный код из ответа @MikaelJagan\ здесь>')
int(seq_along(e), c(e[1L], e[-1L] - e[-length(e)]))[o]
совпадение(г, г) }
f_join <- функция (x) {
д <- as.data.table(x)
d[d, on = имена (d), mult = "первый", что = TRUE] }
f_frank_average <- функция(х) {
д <- as.data.table(x)
r <- frank(d, ties.method = "средний")
совпадение(г, г) }
f_frank_dense <- функция (х) {
д <- as.data.table(x)
r <- frank(d, ties.method = "плотный")
совпадение(г, г) }
Rcpp::sourceCpp('<скопировать исходный код из ответа @MikaelJagan\ здесь>')
Сравнительный анализ
Много строк, мало столбцов
Сначала мы оценили производительность, используя целочисленную матрицу 5e+06 2 на 2:
set.seed(1L) x <- матрица (выборка (10L, размер = 1e+07L, замена = TRUE), ncol = 2L) микробенчмарк( f_asplit (х), f_paste(х), f_interaction(x), f_группировка (х), f_join (х), f_frank_average(x), f_frank_dense(x), f_rcpp(х), раз = 10л, проверить = "идентично", настройка = gc(ЛОЖЬ) )
Единица: миллисекунды
expr min lq среднее медиана uq max neval
f_asplit(x) 17369. 93905 18861.
93905 18861. 19070.21298 19013.0180 19207.29194 22420.71085 10
f_paste(x) 502.63884 507.35077 509.01823 509.2443 511.72301 515.10083 10
f_interaction(x) 234,19311 236,52494 241,80098 238,7392 242,32923 259,75644 10
f_grouping(x) 182,25226 182,89358 187,09642 184,6124 187,10444 208,15532 10
f_join(x) 119,43460 120,86829 123,16607 122,9332 125,07169 128,44722 10
f_frank_average(x) 104,40150 107,53607 111,00268 108,5597 116,80375 121,83675 10
f_frank_dense(x) 86,60926 88,29555 91,42976 90,4716 92,32413 99,30659 10
f_rcpp(x) 459.02304 464.79855 472.43669 468.2492 470.25508 523.06734 10
f_asplit на два порядка медленнее, чем альтернативы base . f_grouping — самый быстрый ответ base , но f_frank_dense быстрее примерно в 2 раза (и самый быстрый в целом).
x содержит и уникальных элементов.
По этой причине мы выполнили второй тест, на этот раз рассматривая матрицу с меньшим количеством строк ( 5e+05 ) и большим количеством столбцов (20).
комплект.семян(1л) x <- матрица (выборка (10L, размер = 1e+07L, замена = TRUE), ncol = 20L)
Первоначальный тест f_interaction привел к ошибке выделения памяти, поэтому он был исключен из теста.
системное время (f_interaction (x))
Ошибка: невозможно выделить вектор размером 7,5 Гб Хронометраж остановился на: 173,2 6,05 200,4
микробенчмарк( f_asplit (х), f_paste(х), ## f_interaction(x), f_группировка (х), f_join (х), f_frank_average(x), f_frank_dense(x), f_rcpp(х), раз = 10л, проверить = "идентично", настройка = gc(ЛОЖЬ) )
Единица: миллисекунды
expr min lq среднее медиана uq max neval
f_asplit(x) 5416.08762 5681.23523 5731.89246 5732.31779 5905.44517 5913.77141 10
f_paste(x) 592. 92990 604.15083 629.31101 623.78679 637.81814 724.83871 10
f_grouping(x) 63,89522 64,14134 65,42723 65,11530 66,00557 68,06045 10
f_join(x) 340,73722 342,18096 353,35774 352,08861 359,88480 382,13480 10
f_frank_average(x) 69, 70,81840 72,29819 72,04409 73,11977 77,44347 10
f_frank_dense(x) 52,58033 53,33760 54,4202954,01672 55,63532 56,99664 10
f_rcpp(x) 184096.21999 184816.36584 185774.76817 186218.58335 186696.31674 186781.24972 10
92990 604.15083 629.31101 623.78679 637.81814 724.83871 10
f_grouping(x) 63,89522 64,14134 65,42723 65,11530 66,00557 68,06045 10
f_join(x) 340,73722 342,18096 353,35774 352,08861 359,88480 382,13480 10
f_frank_average(x) 69, 70,81840 72,29819 72,04409 73,11977 77,44347 10
f_frank_dense(x) 52,58033 53,33760 54,4202954,01672 55,63532 56,99664 10
f_rcpp(x) 184096.21999 184816.36584 185774.76817 186218.58335 186696.31674 186781.24972 10
f_grouping остается самым быстрым ответом base . Примечательно, что теперь он на порядок быстрее f_paste и лишь незначительно медленнее f_frank_dense .
Еще меньше строк, еще больше столбцов
Мы провели финальный тест, исключив самые медленные ответы в последнем раунде ( f_asplit и f_rcpp ), теперь с учетом целочисленной матрицы 5000 на 2000:
set.seed(1L) x <- матрица (выборка (10L, размер = 1e+07L, заменить = TRUE), ncol = 2000L)
микробенчмарк( ## f_asplit(x), f_paste(х), ## f_interaction(x), f_группировка (х), f_join (х), f_frank_average(x), f_frank_dense(x), ## f_rcpp(x), раз = 10л, проверить = "идентично", настройка = gc(ЛОЖЬ) )
Единица: миллисекунды
expr min lq среднее медиана uq max neval
f_paste(x) 1067,47994 1075. 45148 1083.17391 1080.72997 1089.74027 1102.45249 10
f_grouping(x) 19,24007 19,50026 19,86404 19,79002 20,25302 20,60127 10
f_join(x) 616.66706 621.29854 630.61460 628.16315 636.39097 650.16180 10
f_frank_average(x) 59,82007 61,41706 62,68610 62,99318 64,56520 64,88463 10
f_frank_dense(x) 58,03648 60,59857 63,50526 61,99278 66,03694 71,30638 10
45148 1083.17391 1080.72997 1089.74027 1102.45249 10
f_grouping(x) 19,24007 19,50026 19,86404 19,79002 20,25302 20,60127 10
f_join(x) 616.66706 621.29854 630.61460 628.16315 636.39097 650.16180 10
f_frank_average(x) 59,82007 61,41706 62,68610 62,99318 64,56520 64,88463 10
f_frank_dense(x) 58,03648 60,59857 63,50526 61,99278 66,03694 71,30638 10
Теперь f_grouping самый быстрый в целом и быстрее, чем f_frank_dense примерно в 3 раза.
Матрицы и системы уравнений
6.1 - Матрицы и системы уравненийОпределение матрицы
- Прямоугольный массив действительных чисел
- м рядов по n столбцов
- Названо с использованием заглавных букв
- Первый нижний индекс — строка, второй нижний индекс — столбец
Терминология
- Матрица с м строк и n столбцов называется матрицей порядка m x n .

- Квадратная матрица — это матрица с равным количеством строк и столбцов. Поскольку количество строки и столбцы одинаковы, говорят, что он имеет порядок n .
- Главной диагональю квадратной матрицы являются элементы от левого верхнего угла к правому нижнему матрица.
- Матрица-строка — это матрица, имеющая только одну строку.
- Матрица-столбец — это матрица, имеющая только один столбец.
- Матрица только с одной строкой или одним столбцом называется вектором.
Преобразование систем линейных уравнений в Матрицы
Каждое уравнение в системе становится строкой. Каждая переменная в система становится столбцом. Переменные удаляются, и коэффициенты помещаются в матрицу. Если включена правая сторона, это называется расширенной матрицей. Если правая сторона не включена, это называется матрицей коэффициентов.
Система линейных уравнений...
х + у - г = 1 3х - 2у + г = 3 4x + y - 2z = 9
становится расширенной матрицей. ..
..
| х | и | по | справа | ||
|---|---|---|---|---|---|
| 1 | 1 | -1 | 1 | ||
| 3 | -2 | 1 | 3 | ||
| 4 | 1 | -2 | 9 |
Элементарные операции с рядами
Элементарные операции со строками — это операции, которые могут быть выполнены с матрицей и будут производить эквивалентная строкам матрица. Если матрица является расширенной матрицей, построенной из системы линейных уравнений, то матрица, эквивалентная строкам, будет иметь тот же набор решений, что и исходная матрица.
При работе с системами линейных уравнений можно было выполнить три операции. что не изменит множество решений.
что не изменит множество решений.
- Поменять местами два уравнения.
- Умножение уравнения на ненулевую константу.
- Умножить уравнение на ненулевую константу и добавить его к другому уравнению, заменив это уравнение.
Когда система линейных уравнений преобразуется в расширенную матрицу, каждое уравнение становится строка. Итак, теперь есть три элементарные операции со строками, которые дадут эквивалент строки матрица.
- Поменять местами два ряда
- Умножить строку на ненулевую константу
- Умножить строку на ненулевую константу и добавить ее к другой строке, заменив эту строку.
Формы рядного эшелона и сокращенного рядного эшелона
Это строковые эквивалентные формы матрицы. Можно легко решить систему линейных уравнений когда матрицы находятся в одной из этих форм.
Ряд-Эшелон Форма
Матрица имеет форму строки-эшелона, если выполняются следующие условия.
- Если есть строка из всех нулей, то она находится внизу матрицы.
- Первый ненулевой элемент любой строки равен единице. Этот элемент называется ведущим.
- Начальный элемент любой строки находится справа от ведущего элемента предыдущего ряда.
- Ведущий в ряду не обязательно должен быть непосредственно справа от ведущего в ряду предыдущий ряд.
- Матрица в ступенчатой форме будет иметь нули ниже лидирующих единиц.
- Исключение по Гауссу переводит матрицу в эшелонированную форму, а затем выполняется обратная замена. требуется для завершения поиска решений системы.
- Строково-ступенчатая форма матрицы не обязательно уникальна.
Сокращенная форма рядного эшелона
Матрица находится в сокращенной форме строки-эшелона, когда выполняются все условия формы строки-эшелона
и все элементы выше, как и ниже, ведущие равны нулю.
- Если есть строка из всех нулей, то она находится внизу матрицы.
- Первый ненулевой элемент любой строки равен единице. Этот элемент называется ведущим.
- Начальный элемент любой строки находится справа от ведущего элемента предыдущего ряда.
- Все элементы выше и ниже ведущей единицы равны нулю.
- Ведущий в ряду не обязательно должен быть непосредственно справа от ведущего в ряду предыдущий ряд.
- Матрица в ступенчато-строковой форме будет иметь нули как над, так и под ведущими единицами.
- Исключение Гаусса-Жордана переводит матрицу в редуцированную ступенчато-строковую форму.
- Для завершения поиска решений системы не требуется обратной подстановки.
- Редуцированная строково-ступенчатая форма матрицы уникальна.
Исключение Гаусса
- Запишите систему линейных уравнений в виде расширенной матрицы
- Выполните элементарные операции со строками, чтобы преобразовать матрицу в эшелонированную форму строк
- Преобразование матрицы обратно в систему линейных уравнений
- Используйте обратную замену, чтобы получить все ответы
Исключение Гаусса-Джордана
- Запишите систему линейных уравнений в виде расширенной матрицы
- Выполните элементарные операции над строками, чтобы привести матрицу в сокращенную ступенчатую форму строк
- Преобразование матрицы обратно в систему линейных уравнений
- Обратная замена не требуется
Поворотный
- Поворот — это процесс, который автоматизирует операции со строками, необходимые для помещения матрицы в рядно-эшелонная или редуцированная рядно-эшелонная форма
- В частности, поворот превращает элементы выше или ниже ведущей единицы в нули
Типы растворов
Возможны три типа решений при решении системы линейных уравнений
Независимый- Согласованный
- Уникальное решение
- Матрица с уменьшенным числом строк имеет то же количество ненулевых строк, что и переменные
- Левая часть обычно представляет собой единичную матрицу, но не обязательно
- Чтобы получить независимое решение, уравнений должно быть не меньше числа переменных.

| х | и | по | справа | ||
|---|---|---|---|---|---|
| 1 | 0 | 0 | 3 | ||
| 0 | 1 | 0 | 1 | ||
| 0 | 0 | 1 | 2 |
Когда вы преобразуете расширенную матрицу обратно в форму уравнения, вы получаете x=3, у=1 и г=2.
Зависимый- Согласованный
- Много решений
- Запишите ответ в параметрической форме
- Матрица с уменьшенным числом строк содержит больше переменных, чем ненулевые строки
- Не обязательно должен быть ряд нулей, но обычно он есть.

- Это также может произойти, когда уравнений меньше, чем переменных.
| х | и | по | справа | ||
|---|---|---|---|---|---|
| 1 | 0 | 3 | 4 | ||
| 0 | 1 | -2 | 3 | ||
| 0 | 0 | 0 | 0 |
Первое уравнение будет x + 3z = 4. Решение для x дает x = 4 - 3z.
Второе уравнение будет y - 2z = 3. Решение для y дает y = 3 + 2z.
Столбец z не очищен (все нули, кроме одно число), поэтому другие переменные будут определены через z. Следовательно, г будет параметр т и решение ...
х = 4 - 3т, у = 3 + 2т, г = т
Несоответствие- Нет решения
- Матрица с уменьшенным числом строк имеет ряд нулей в левой части, но
правая часть не равна нулю.

| х | и | по | справа | ||
|---|---|---|---|---|---|
| 1 | 0 | 3 | 4 | ||
| 0 | 1 | -2 | 3 | ||
| 0 | 0 | 0 | 2 |
Здесь нет решения. Вы можете записать это как нулевое множество Ø, пустой набор {} или нет решения.
Операции со строками матрицы
Над строками используются 3 основные операции. матрица когда вы используете матрицу для решить систему линейных уравнений . Обычно цель состоит в том, чтобы левая часть матрицы выглядела как единичная матрица .
Три операции:
- Переключение строк
- Умножение строки на число
- Добавление строк
Переключение строк
Вы можете поменять местами строки матрицы, чтобы получить новую матрицу.
[ 2 3 − 2 6 0 0 3 − 6 1 0 2 − 3 ] → [ 1 0 2 − 3 2 3 − 2 6 0 0 3 − 6 ]
В примере, показанном выше, мы перемещаем строку
1
грести
2
, Строка
2
грести
3
, и Строка
3
грести
1
. (Причина для этого состоит в том, чтобы получить
1
в левом верхнем углу.)
(Причина для этого состоит в том, чтобы получить
1
в левом верхнем углу.)
Умножение строки на число
Вы можете умножить любую строку на число. (Это означает умножение каждой записи в строке на одно и то же число.)
[ 1 0 2 − 3 2 3 − 2 6 0 0 3 − 6 ] → р 3 : 1 3 р 3 [ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ]
В этом примере мы умножили строку
3
матрицы на
1
3
. (Это дает нам
1
нам нужно в строке
3
, Столбец
3
.)
(Это дает нам
1
нам нужно в строке
3
, Столбец
3
.)
Добавление строк
Вы также можете добавить две строки вместе и заменить строку результатом.
Например, в матрицу, полученную в последнем примере, мы можем добавить строки 2 а также 3 вместе, запись за записью:
[ 2 3 − 2 6 ] + [ 0 0 1 − 2 ] _ [ 2 3 − 1 4 ]
Затем мы заменяем строку
2
с результатом.
[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ] → р 2 : р 2 + р 3 [ 1 0 2 − 3 2 3 − 1 4 0 0 1 − 2 ]
Добавление нескольких строк
Мы сказали, что было всего три операции, и они есть. Но, используя последние две операции в сочетании, мы можем добавлять целые кратные строки к другим строкам, чтобы ускорить работу.
Но, используя последние две операции в сочетании, мы можем добавлять целые кратные строки к другим строкам, чтобы ускорить работу.
Шаг назад, поэтому у нас есть матрица:
[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ]
Теперь вместо того, чтобы просто добавить строку 2 + Строка 3 , Добавить ряд 2 + ( 2 × Строка 3 ) :
[ 2 3 − 2 6 ] + [ 0 0 2 − 4 ] _ [ 2 3 0 2 ]
Затем замените строку
2
с результатом.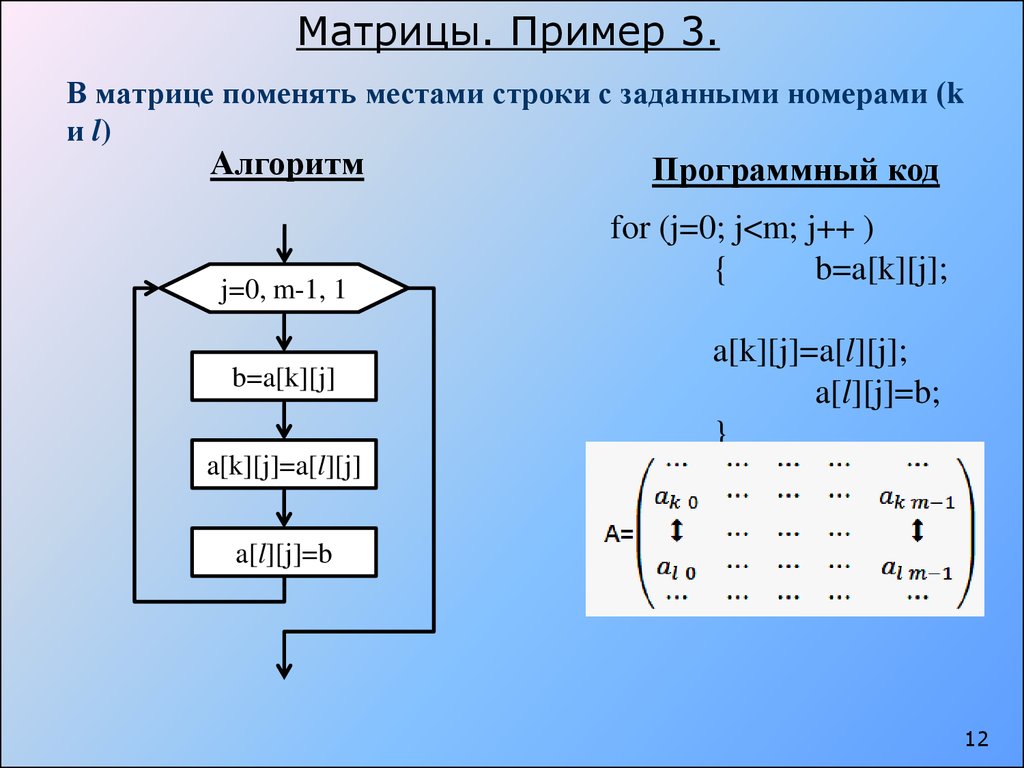
[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ] → р 2 : р 2 + 2 р 3 [ 1 0 2 − 3 2 3 0 2 0 0 1 − 2 ]
Таким образом, мы получаем
0
в строке
2
, Столбец
3
.
Мы можем сделать это снова, чтобы получить 0 в строке 2 , Столбец 1 . Здесь мы умножаем ряд 1 по − 2 , добавьте строку 2 и замените строку 2 с результатом.
[ 1 0 2 − 3 2 3 0 2 0 0 1 − 2 ] → р 2 : − 2 р 1 + р 2 [ 1 0 2 − 3 0 3 − 4 8 0 0 1 − 2 ]
Мы покажем еще несколько шагов, чтобы получить
3
×
3
единичная матрица слева (и, таким образом, решить систему).
Следующим шагом является добавление Строка 2 + ( 4 × Строка 3 ) чтобы получить 0 в строке 2 , Столбец 3 .
[ 1 0 2 − 3 0 3 − 4 8 0 0 1 − 2 ] → р 2 : р 2 + 4 р 3 [ 1 0 2 − 3 0 3 0 0 0 0 1 − 2 ]
Далее нам нужен ноль в строке
1
, Столбец
3
.
[ 1 0 2 − 3 0 3 0 0 0 0 1 − 2 ] → р 1 : р 1 − 2 р 3 [ 1 0 0 1 0 3 0 0 0 0 1 − 2 ]
Последний шаг — это просто применение второй операции, умножение строки на число.
[ 1 0 0 1 0 3 0 0 0 0 1 − 2 ] → 1 3 р 3 [ 1 0 0 1 0 1 0 0 0 0 1 − 2 ]
Теперь у нас есть решение в виде заказанной тройки ( 1 , 0 , − 2 ) .
Важная заметка: Если уравнения, представленные вашей исходной матрицей, представляют собой одинаковые или параллельные линии, вы не сможете получить единичную матрицу, используя эти операции со строками. В этом случае решения либо не существует, либо существует бесконечно много решений системы.
В этом случае решения либо не существует, либо существует бесконечно много решений системы.
17.1 Детерминанты
17.1 Детерминанты
| ||
Определитель матрицы или преобразования можно определить разными способами. Вот, пожалуй, самое простое определение:
1. Для диагональной матрицы это произведение диагональных элементов.
2. Неизменяется прибавлением кратности одной строки к другой.
Легко видеть, что эти два свойства являются общими для n-мерного
объем n-мерного параллелепипеда, определяемый строками (или столбцами)
считаются векторами, когда базисные векторы ортонормированы . (Они
взаимно ортогональны, и каждая имеет длину 1.) Такое добавление просто наклоняет
сторон параллелепипеда без изменения его толщины.
(Они
взаимно ортогональны, и каждая имеет длину 1.) Такое добавление просто наклоняет
сторон параллелепипеда без изменения его толщины.
Определитель также линеен в каждой строке и меняет знак, когда любые две строки
взаимозаменяемы.
Тот факт, что он линейный в каждой строке, означает, что вы можете выбрать любую строку, и
запишите определитель в виде суммы вкладов, каждый из которых линейен по одному элементу
того ряда. Коэффициенты этого элемента в этом выражении для определителя
называется кофактором элемента. Поскольку (i, j)-й
элемент матрицы уже линеен в i-й строке и j-м столбце, его кофактор
не может содержать никаких других вкладов из этой строки или столбца. это на самом деле г.
n-1-мерный определитель матрицы, полученный путем исключения этой строки и
столбец исходной матрицы, умноженный на (-1) i-j .
Получаем:
.
Если A имеет две одинаковые строки, то его определитель равен 0. Это означает, что подстановка элементов любой другой строки вместо a jk здесь (замена jk на sk для j, отличного от s в этом
уравнение) дает определитель матрицы с двумя одинаковыми строками, который равен
0. Все это означает, что у нас есть выражение для обратной матрицы
A с элементами a jk .
Это означает, что подстановка элементов любой другой строки вместо a jk здесь (замена jk на sk для j, отличного от s в этом
уравнение) дает определитель матрицы с двумя одинаковыми строками, который равен
0. Все это означает, что у нас есть выражение для обратной матрицы
A с элементами a jk .
Получаем, что A B = I , где B задано матрицей, где (k,
j)-й элемент - это кофактор (j, k), разделенный на определитель A .
Другими словами имеем:
Еще один интересный факт заключается в том, что если мы возьмем любой вектор v с компонентами v k и формой ,
это определитель матрицы, полученной заменой j-й строки
исходная матрица компонентами вектора v . По идентичным рассуждениям
— определитель матрицы, полученной заменой j-го столбца числа A компонентами v .
Но этот продукт, разделенный на А является j-й составляющей результата применения A -1 к v :
Это утверждение называется Правило Крамерса .
Если мы начнем с уравнений, представимых как A r = v , то решение
имеет вид r = A -1 v . Правило Крамерса говорит нам, что j-й
составляющая r , j-я неизвестная в наших уравнениях, есть отношение
определитель матрицы, полученной заменой j-го столбца А на v , деленное на определитель самого A .
Линейность определителя в каждой строке или столбце
отдельно подразумевает, что его можно записать в виде суммы терминов, каждый из которых
произведение, содержащее по одному множителю из каждой строки и столбца, умноженное на константу.
Поскольку определитель диагональной матрицы является произведением диагональных элементов,
эта константа равна 1, когда все элементы расположены по диагонали. Если мы переключим
две строки, определитель меняет знак; это означает, что константа всегда
1 или -1, равное -1, когда элементам требуется нечетное число переключателей строки для
поставить их все на главную диагональ, а 1 когда это можно сделать с четным
количество переключателей.
Отдельный член определителя может быть охарактеризован парами строк-столбцов
показатели различных факторов в нем. Поскольку индекс каждой строки и столбца должен встречаться
в каждом слагаемом определителя, мы можем описать его, перечислив по порядку
индексы строк в паре со столбцами 1,2,....
Таким образом, в трех измерениях есть шесть терминов, которые могут быть описаны
списки индексов строк: 123, 231, 312, 213, 132, 321. Подобные списки называются перестановками числа s от единицы до n, здесь для n = 3.
Мы можем представить себе каждую перестановку как отображение, которое принимает индексы 123...
соответственно его списку: таким образом, 132 можно представить как отображение от 1 до 1,
2 к 3 и 3 к 2. Это дает нам другое обозначение для описания перестановок:
мы можем записать циклы, которые проходят числа при перестановке
отображение: таким образом, при 132 1 остается фиксированным и находится в цикле сам по себе, а 2 идет
к 3, которое переходит в 2: мы описываем это обозначением (1)(23). Перестановка
231 соответствует циклу (123), а тождественное отображение 123 имеет цикл
представление (1)(2)(3).
Перестановка
231 соответствует циклу (123), а тождественное отображение 123 имеет цикл
представление (1)(2)(3).
Одна приятная особенность этих обозначений заключается в том, что из них сразу видно,
соответствующий член в определителе получает знак плюс или минус. Каждый цикл
четной длины (например, (23)) вызывает изменение знака, , поэтому знак положительный
если в этом представлении есть четное число циклов четной длины
перестановка индекса, соответствующая термину. Отрицательно, если есть
нечетное число циклов четной длины.
Матрица
Операции со строками (стр. "Операции" по-математики означает «процедуры». Четыре «основных операции над числами: сложение, вычитание, умножение, и деление. Для матриц есть три основных операции над строками; что есть три процедуры, которые вы можете проделать со строками матрицы. Первая операция переключение строк. Например, учитывая матрицу: ...вы можете переключать ряды вокруг, чтобы поместить матрицу в более удобное расположение строк, например: Частое переключение строк обозначено стрелками, например: При переключении рядов, Будьте осторожны, чтобы скопировать записи правильно. Вторая операция умножение строк. Например, учитывая следующую матрицу: . Это умножение строк часто обозначается стрелкой с умножением, указанным вверху из них, вот так: "1 R 1 " указывает фактическую операцию. "1" говорит, что мы умножили на минус один; " Р 1 " говорит, что мы работали с первой строкой. Обратите внимание, что второй и третьи строки были скопированы без изменений во вторую матрицу. Умножение применяется только к первой строке, поэтому записи для двух других строк были просто перенесено без изменений. Умножать можно на что угодно тебе нравится. Например, чтобы получить ведущую 1 в третьей строке предыдущей матрицы можно умножить третью строку минус половина: Так как вы не делали
что-либо с первой и второй строками, эти записи были просто скопированы
без изменений в новую матрицу. Вы можете сделать больше одного умножение строк в пределах одного и того же шага, так что вы могли бы сделать два вышеуказанные шаги всего за один шаг, например: Рекомендуется использовать какую-либо форму обозначения (например, стрелки и нижние индексы выше), чтобы вы может следить за вашей работой. Матрицы очень грязные, особенно если вы делая их вручную, а заметки могут облегчить проверку вашей работы позже. Это также произведет впечатление на вашего учителя. Операция последней строки добавление строки. Добавление строк аналогично методу «дополнения». для решения системы линейных уравнений. Предположим, у вас есть следующая система уравнений: Вы можете начать решать эту систему, сложив столбцы, чтобы получить 4 y = 4: Вы можете сделать что-то подобное
с матрицами. ...можно "уменьшить"
(добавьте больше начальных нулей) во вторую строку, добавив первую строку в
это (общая цель с матрицами на этом этапе состоит в том, чтобы получить «1»
или "0"
а потом "1"
в начале каждой строки матрицы). Когда вы сводили двойное уравнение
линейной системы, добавив, вы нарисовали полосу «равно» через
снизу и добавил вниз. Когда вы используете сложение на матрице, вы
нужно взять немного бумаги для заметок, потому что вы не хотите пытаться сделать
работать внутри матрицы. Итак, добавьте две строки на свой черновик: Это твоя новая секунда строка; вы напишете его вместо старого второго ряда. Результат будет выглядеть так: В данном случае " R 1 + Р 2 "
на стрелке означает "Я добавил первую строку ко второй, и вот результат
Я получил". Топ | 1 | 2 | Возвращаться к индексу Далее >>
|
|
|
7 способов найти и удалить повторяющиеся значения в Microsoft Excel
Повторяющиеся значения в ваших данных могут быть большой проблемой! Это может привести к существенным ошибкам и переоценке ваших результатов.
Но найти и удалить их из ваших данных в Excel довольно просто.
Загрузить примеры файлов
В этом руководстве мы рассмотрим 7 различных методов поиска и удаления повторяющихся значений из ваших данных.
Видеоруководство
Что такое повторяющееся значение?
Повторяющиеся значения возникают, когда в ваших данных появляется одно и то же значение или набор значений.
Для данного набора данных вы можете определять дубликаты разными способами.
В приведенном выше примере имеется простой набор данных с 3 столбцами для марки, модели и года выпуска для списка автомобилей.
- На первом изображении выделены все дубликаты, основанные только на марке автомобиля.
- Второе изображение выделяет все дубликаты в зависимости от марки и модели автомобиля. Это приводит к тому, что на один дубликат меньше.
- Второе изображение выделяет все дубликаты на основе всех столбцов в таблице. Это приводит к тому, что еще меньше значений считаются дубликатами.

Результаты дублирования на основе одного столбца и всей таблицы могут сильно отличаться. Вы всегда должны знать, какая версия вам нужна и что делает Excel.
Поиск и удаление повторяющихся значений с помощью команды «Удалить дубликаты»
Удаление повторяющихся значений в данных — очень распространенная задача. Это настолько распространено, что для этого есть специальная команда на ленте.
Выберите ячейку внутри данных, из которых вы хотите удалить дубликаты, и перейдите к Вкладка Data и щелкните команду Remove Duplicates .
Затем Excel выберет весь набор данных и откроет окно «Удалить дубликаты».
- Затем вам нужно сообщить Excel, если данные содержат заголовки столбцов в первой строке. Если этот флажок установлен, первая строка данных будет исключена при поиске и удалении повторяющихся значений.
- Затем вы можете выбрать, какие столбцы использовать для определения дубликатов.
 Есть также удобные Select All и Unselect All Кнопки выше, которые вы можете использовать, если у вас есть длинный список столбцов в ваших данных.
Есть также удобные Select All и Unselect All Кнопки выше, которые вы можете использовать, если у вас есть длинный список столбцов в ваших данных.
Когда вы нажмете OK , Excel удалит все найденные повторяющиеся значения и предоставит вам итоговый подсчет того, сколько значений было удалено и сколько значений осталось.
Эта команда изменит ваши данные, поэтому лучше всего выполнить команду на копии ваших данных, чтобы сохранить исходные данные нетронутыми.
Поиск и удаление повторяющихся значений с помощью расширенных фильтров
Существует еще один способ избавиться от повторяющихся значений в ваших данных с ленты. Это возможно благодаря расширенным фильтрам.
Выберите ячейку внутри данных и перейдите на вкладку Данные и щелкните команду фильтра Расширенный .
Откроется окно расширенного фильтра.
- Вы можете выбрать Фильтровать список на месте или Копировать в другое место .
 Фильтрация списка на месте скроет строки, содержащие дубликаты, а копирование в другое место создаст копию данных.
Фильтрация списка на месте скроет строки, содержащие дубликаты, а копирование в другое место создаст копию данных. - Excel будет угадывать диапазон данных, но вы можете настроить его в диапазоне списка . Диапазон критериев можно оставить пустым, а поле Копировать в необходимо будет заполнить, если был выбран параметр Копировать в другое место .
- Установите флажок для Только уникальные записи .
Нажмите OK , и вы удалите повторяющиеся значения.
Расширенные фильтры могут быть удобным вариантом для избавления от повторяющихся значений и одновременного создания копии ваших данных. Но расширенные фильтры смогут выполнять это только для всей таблицы.
Поиск и удаление повторяющихся значений с помощью сводной таблицы
Сводные таблицы предназначены только для анализа ваших данных, верно?
Вы также можете использовать их для удаления повторяющихся данных!
С помощью этого метода вы фактически не будете удалять повторяющиеся значения из своих данных, вы будете использовать сводную таблицу для отображения только уникальных значений из набора данных.
Сначала создайте сводную таблицу на основе ваших данных. Выберите ячейку внутри ваших данных или весь диапазон данных ➜ перейдите к Вставить вкладку ➜ выберите Сводная таблица ➜ нажмите OK в диалоговом окне Создать сводную таблицу.
С новой пустой сводной таблицей добавьте все поля в область Rows сводной таблицы.
Затем вам нужно будет изменить макет результирующей сводной таблицы, чтобы она имела табличный формат. Выбрав сводную таблицу, перейдите на вкладку Design и выберите Report Layout . Здесь вам нужно изменить две опции.
- Выберите параметр Показать в табличной форме .
- Выберите параметр Повторить все метки элементов .
Вам также потребуется удалить все промежуточные итоги из сводной таблицы. Перейдите на вкладку Design ➜ выберите Промежуточные итоги ➜ выберите Не показывать промежуточные итоги .
Теперь у вас есть сводная таблица, которая имитирует табличный набор данных!
В сводных таблицах перечислены только уникальные значения элементов в области «Строки», поэтому эта сводная таблица автоматически удалит все дубликаты в ваших данных.
Поиск и удаление повторяющихся значений с помощью Power Query
Power Query предназначен для преобразования данных, поэтому вы можете быть уверены, что он способен находить и удалять повторяющиеся значения.
Выберите таблицу значений, из которой вы хотите удалить дубликаты ➜ перейдите на вкладку Данные ➜ выберите запрос Из таблицы/диапазона .
Удаление дубликатов на основе одного или нескольких столбцов
С помощью Power Query вы можете удалять дубликаты на основе одного или нескольких столбцов в таблице.
Вам нужно выбрать, на основе каких столбцов удалять дубликаты. Вы можете удерживать Ctrl, чтобы выбрать несколько столбцов.
Щелкните правой кнопкой мыши заголовок выбранного столбца и выберите в меню Удалить дубликаты .
Вы также можете получить доступ к этой команде на вкладке Главная ➜ Удалить строки ➜ Удалить дубликаты .
= Table.Distinct(#"Предыдущий шаг", {"Сделать", "Модель"}) Если вы посмотрите на созданную формулу, она использует Функция Table.Distinct со вторым параметром, указывающим, какие столбцы использовать.
Удаление дубликатов на основе всей таблицы
Чтобы удалить дубликаты на основе всей таблицы, вы можете выбрать все столбцы в таблице, а затем удалить дубликаты. Но есть более быстрый метод, который не требует выбора всех столбцов.
В левом верхнем углу предварительного просмотра данных есть кнопка с выбором команд, которые можно применить ко всей таблице.
Нажмите кнопку таблицы в верхнем левом углу ➜, затем выберите Удалить дубликаты .
= Table.Distinct(#"Предыдущий шаг")
Если вы посмотрите на созданную формулу, то увидите, что она использует ту же функцию Table.Distinct без второго параметра. Без второго параметра функция будет действовать на всю таблицу.
Сохранять дубликаты на основе одного столбца или всей таблицы
В Power Query также есть команды для сохранения дубликатов для выбранных столбцов или для всей таблицы.
Выполните те же действия, что и при удалении дубликатов, но вместо этого используйте команду Сохранить строки ➜ Сохранить дубликаты . Это покажет вам все данные, которые имеют повторяющееся значение.
Поиск и удаление повторяющихся значений с помощью формулы
Вы можете использовать формулу, чтобы помочь вам найти повторяющиеся значения в ваших данных.
Сначала вам нужно будет добавить вспомогательный столбец, который объединяет данные из любых столбцов, на которых вы хотите основывать дублирующее определение.
= [@Make] & [@Model] & [@Year]
Приведенная выше формула объединит все три столбца в один столбец. Он использует оператор амперсанда для соединения каждого столбца.
= TEXTJOIN("", FALSE , CarList[@[Make]:[Year]]) Если у вас есть длинный список столбцов для объединения, вы можете использовать приведенную выше формулу. Таким образом, вы можете просто ссылаться на все столбцы как на один диапазон.
Затем вам нужно будет добавить еще один столбец для подсчета повторяющихся значений. Это будет использоваться позже для фильтрации строк данных, которые появляются более одного раза.
= СЧЁТЕСЛИМН($E$3:E3, E3)
Скопируйте приведенную выше формулу вниз по столбцу, и она подсчитает, сколько раз текущее значение появляется в списке значений выше.
Если счетчик равен 1, то значение появляется в данных впервые, и вы сохраните его в своем наборе уникальных значений. Если количество равно 2 или больше, то значение уже появилось в данных и является повторяющимся значением, которое можно удалить.
Добавьте фильтры в свой список данных.
- Перейдите на вкладку Данные и выберите команду Фильтр .
- Используйте сочетание клавиш Ctrl + Shift + L.
Теперь вы можете фильтровать столбец Count. Фильтрация по 1 приведет к получению всех уникальных значений и удалению всех дубликатов.
Затем вы можете выбрать видимые ячейки из результирующего фильтра, чтобы скопировать и вставить их в другое место. Используйте сочетание клавиш Alt + ; чтобы выбрать только видимые ячейки.
Поиск и удаление повторяющихся значений с помощью условного форматирования
С помощью условного форматирования можно выделить повторяющиеся значения в ваших данных.
Как и в случае с формулой, вам необходимо добавить вспомогательный столбец, объединяющий данные из столбцов. Условное форматирование не работает с данными в разных строках, поэтому вам понадобится этот комбинированный столбец, если вы хотите обнаруживать дубликаты на основе более чем одного столбца.
Затем нужно выбрать столбец объединенных данных.
Чтобы создать условное форматирование, перейдите на Главная вкладка ➜ выберите Условное форматирование ➜ Правила выделения ячеек ➜ Повторяющиеся значения .
Это откроет окно условного форматирования повторяющихся значений.
- Вы можете выбрать выделение Повторяющихся или Уникальных значений.
- Вы также можете выбрать один из предопределенных форматов ячеек, чтобы выделить значения или создать свой собственный формат.
Предупреждение . Предыдущие методы поиска и удаления дубликатов рассматривают первое вхождение значения как дубликат и оставляют его без изменений. Однако этот метод выделяет первое вхождение и не делает различий.
Теперь, когда значения выделены, вы можете фильтровать повторяющиеся или уникальные значения с помощью параметра фильтрации по цвету. Не забудьте добавить фильтры к своим данным. Перейдите на вкладку Data и выберите фильтр 9.0032 или используйте сочетание клавиш Ctrl + Shift + L.
Не забудьте добавить фильтры к своим данным. Перейдите на вкладку Data и выберите фильтр 9.0032 или используйте сочетание клавиш Ctrl + Shift + L.
- Щелкните переключатель фильтра.
- Выберите Фильтр по цвету в меню.
- Фильтрация по цвету, используемому в условном форматировании, для выбора повторяющихся значений или фильтрация по параметру «Без заливки», чтобы выбрать уникальные значения.
Затем вы можете выбрать только видимые ячейки с помощью сочетания клавиш Alt + ;.
Поиск и удаление повторяющихся значений с помощью VBA
В VBA есть встроенная команда для удаления дубликатов в объектах списка.
Sub RemoveDuplicates()Dim DuplicateValues As RangeУстановить DuplicateValues = ActiveSheet.ListObjects("CarList").RangeDuplicateValues.RemoveDuplicates Columns:=Array(1, 2, 3), Header:=xlYesEndSub
Описанная выше процедура удалит дубликаты из таблицы Excel с именем CarList .

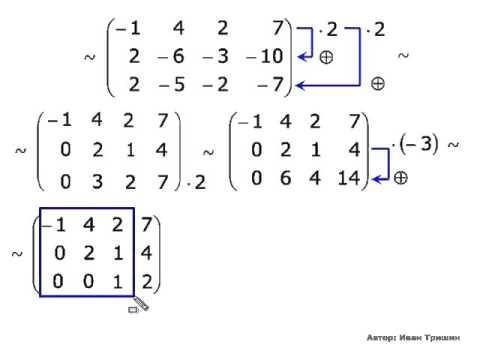 Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.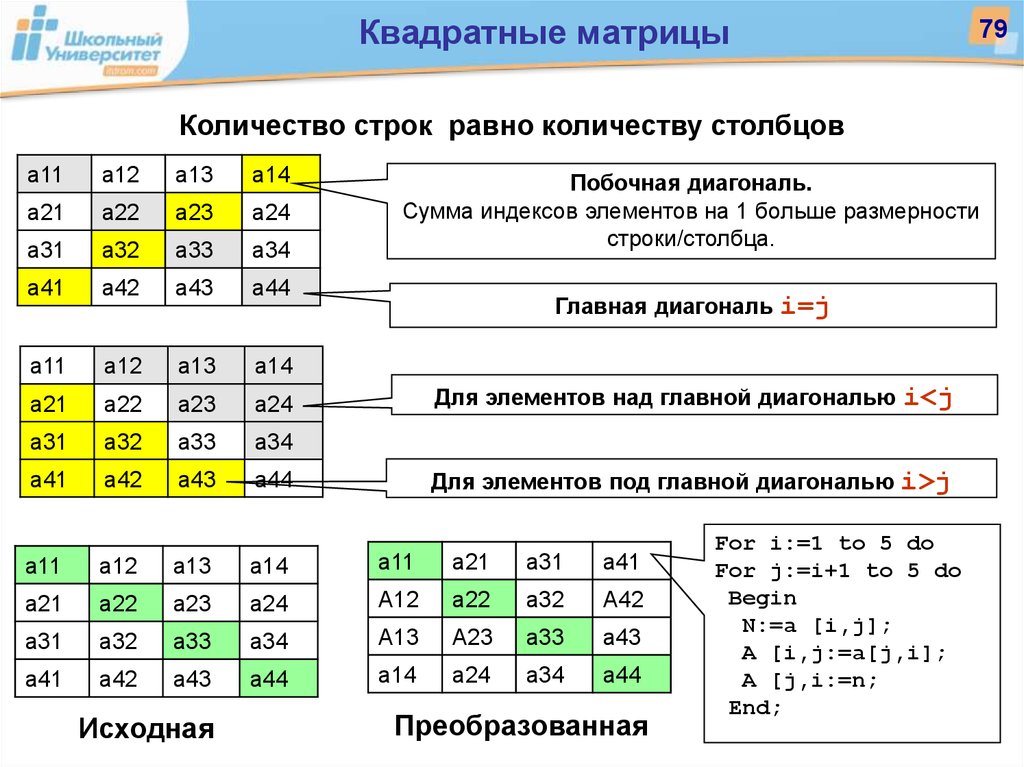
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления


 Если к элементам какой-либо строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженные на любое число , то определитель не изменится.
Если к элементам какой-либо строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженные на любое число , то определитель не изменится. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.015 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.015 с.) table
table  int(seq_along(e), c(e[1L], e[-1L] - e[-length(e)]))[o]
совпадение(г, г) }
f_join <- функция (x) {
д <- as.data.table(x)
d[d, on = имена (d), mult = "первый", что = TRUE] }
f_frank_average <- функция(х) {
д <- as.data.table(x)
r <- frank(d, ties.method = "средний")
совпадение(г, г) }
f_frank_dense <- функция (х) {
д <- as.data.table(x)
r <- frank(d, ties.method = "плотный")
совпадение(г, г) }
Rcpp::sourceCpp('<скопировать исходный код из ответа @MikaelJagan\ здесь>')
int(seq_along(e), c(e[1L], e[-1L] - e[-length(e)]))[o]
совпадение(г, г) }
f_join <- функция (x) {
д <- as.data.table(x)
d[d, on = имена (d), mult = "первый", что = TRUE] }
f_frank_average <- функция(х) {
д <- as.data.table(x)
r <- frank(d, ties.method = "средний")
совпадение(г, г) }
f_frank_dense <- функция (х) {
д <- as.data.table(x)
r <- frank(d, ties.method = "плотный")
совпадение(г, г) }
Rcpp::sourceCpp('<скопировать исходный код из ответа @MikaelJagan\ здесь>')
 93905 18861.
93905 18861. 92990 604.15083 629.31101 623.78679 637.81814 724.83871 10
f_grouping(x) 63,89522 64,14134 65,42723 65,11530 66,00557 68,06045 10
f_join(x) 340,73722 342,18096 353,35774 352,08861 359,88480 382,13480 10
f_frank_average(x) 69, 70,81840 72,29819 72,04409 73,11977 77,44347 10
f_frank_dense(x) 52,58033 53,33760 54,4202954,01672 55,63532 56,99664 10
f_rcpp(x) 184096.21999 184816.36584 185774.76817 186218.58335 186696.31674 186781.24972 10
92990 604.15083 629.31101 623.78679 637.81814 724.83871 10
f_grouping(x) 63,89522 64,14134 65,42723 65,11530 66,00557 68,06045 10
f_join(x) 340,73722 342,18096 353,35774 352,08861 359,88480 382,13480 10
f_frank_average(x) 69, 70,81840 72,29819 72,04409 73,11977 77,44347 10
f_frank_dense(x) 52,58033 53,33760 54,4202954,01672 55,63532 56,99664 10
f_rcpp(x) 184096.21999 184816.36584 185774.76817 186218.58335 186696.31674 186781.24972 10
 45148 1083.17391 1080.72997 1089.74027 1102.45249 10
f_grouping(x) 19,24007 19,50026 19,86404 19,79002 20,25302 20,60127 10
f_join(x) 616.66706 621.29854 630.61460 628.16315 636.39097 650.16180 10
f_frank_average(x) 59,82007 61,41706 62,68610 62,99318 64,56520 64,88463 10
f_frank_dense(x) 58,03648 60,59857 63,50526 61,99278 66,03694 71,30638 10
45148 1083.17391 1080.72997 1089.74027 1102.45249 10
f_grouping(x) 19,24007 19,50026 19,86404 19,79002 20,25302 20,60127 10
f_join(x) 616.66706 621.29854 630.61460 628.16315 636.39097 650.16180 10
f_frank_average(x) 59,82007 61,41706 62,68610 62,99318 64,56520 64,88463 10
f_frank_dense(x) 58,03648 60,59857 63,50526 61,99278 66,03694 71,30638 10




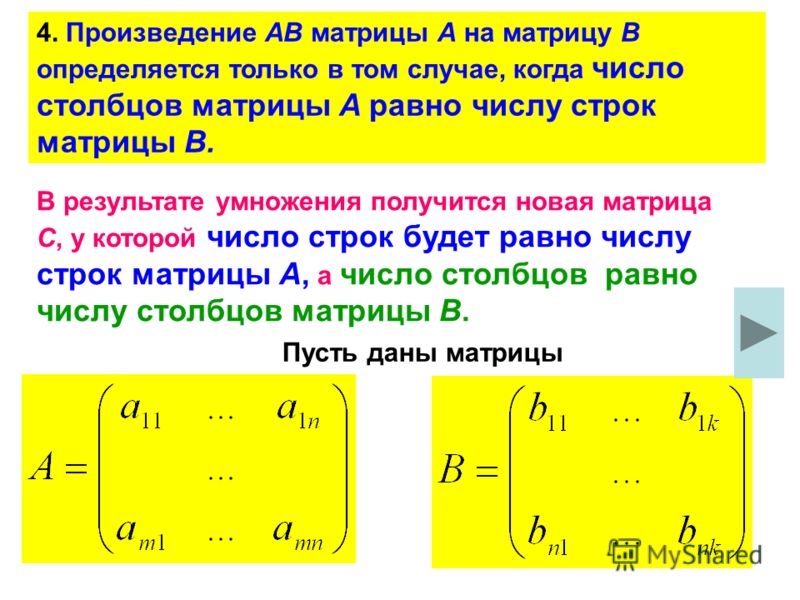 1 из 2)
1 из 2)  ..можно умножить
первый ряд на 1
получить положительную ведущую
значение в первой строке:
..можно умножить
первый ряд на 1
получить положительную ведущую
значение в первой строке:
 Например, учитывая следующую матрицу:
Например, учитывая следующую матрицу: Поскольку первая строка на самом деле не изменилась, и поскольку мы не изменили
делать что-либо с третьей строкой, эти строки копируются в новую матрицу
без изменений.
Поскольку первая строка на самом деле не изменилась, и поскольку мы не изменили
делать что-либо с третьей строкой, эти строки копируются в новую матрицу
без изменений.
 Есть также удобные Select All и Unselect All Кнопки выше, которые вы можете использовать, если у вас есть длинный список столбцов в ваших данных.
Есть также удобные Select All и Unselect All Кнопки выше, которые вы можете использовать, если у вас есть длинный список столбцов в ваших данных. Фильтрация списка на месте скроет строки, содержащие дубликаты, а копирование в другое место создаст копию данных.
Фильтрация списка на месте скроет строки, содержащие дубликаты, а копирование в другое место создаст копию данных.