Определение координат вектора заданного координатами его начальной и конечной точки.
Определение координат вектора заданного координатами его начальной и конечной точки.Навигация по странице:
- Основное соотношение
- Формулы для определение координат вектора заданного координатами его начальной и конечной точки
- для плоских задач
- для пространственных задач
- для n -мерного пространства
- Примеры задач
- плоская задача
- пространственных задача
- задача в n -мерным пространстве
Смотрите также онлайн калькулятор для определения координат вектора по двум точкам.
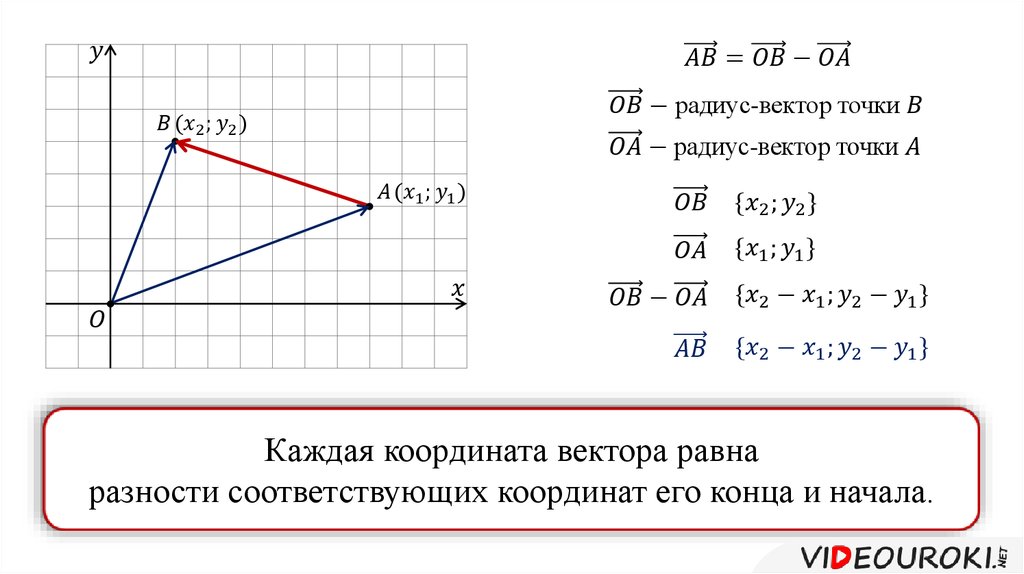
Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задач
В случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay}
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay ; Bz — Az}
Формула определения координат вектора для n -мерного пространства
В случае n-мерного пространства вектор AB заданный координатами точек A(A1 ; A2 ; . .. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
.. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
AB = {B1 — A1 ; B2 — A2 ; … ; Bn — An}
Примеры задач связанных с определением координат вектора по двум точкам
Примеры для плоских задач
Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).
Решение: AB = {3 — 1; 1 — 4} = {2; -3}.
Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).
Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8
Ответ: B(8; -3).
Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).
Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2
ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
Ответ: A(-2; -5).
Примеры для пространственных задач
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).
Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.
Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8
ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
ABz = Bz — Az => Bz = ABz + Az => Bz = 2 + 3 = 5
Ответ: B(8; -3; 5).
Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).
Решение:
ABx = B x — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2
ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
ABz = Bz — Az => Az = Bz — ABz => Az = 1 — 4 = -3
Ответ: A(-2; -5; -3).
Примеры для n -мерного пространства
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).
Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.
Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).
Решение:
AB1 = B
AB2 = B2 — A2 => B2 = AB2 + A2 => B2 = 1 + (-4) = -3
AB3 = B3 — A3 => B3 = AB3 + A3 => B3 = 2 + 3 = 5
AB4 = B4 — A4 => B4 = AB4 + A4 => B4 = 1 + 2 = 3
Ответ: B(8; -3; 5; 3).
Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).
Решение:
AB1 = B1 — A1 => A1 = B1 — AB1 => A1 = 3 — 5 = -2
AB2 = B2
AB3 = B3 — A3 => A3 = B3 — AB3 => A3 = 1 — 4 = -3
AB4 = B4 — A4 => A4 = B4 — AB4 => A4 = 8 — 5 = 3
Ответ: A(-2; -5; -3; 3).
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Как найти координаты вектора
Предварительные сведения
Здесь мы ограничимся двумерным случаем. Введение понятия для трехмерного случая проводится аналогично. Для того, чтобы ввести понятие координат вектора сначала введем и докажем следующие лемму и теорему.
Для того, чтобы ввести понятие координат вектора сначала введем и докажем следующие лемму и теорему.
Лемма 1: Если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ коллинеарны, и вектор $\overrightarrow{a}$ не является нулевым, то существует действительное число $k$, такое что выполняется равенство$\overrightarrow{b}=k\overrightarrow{a}$
Доказательство.
Возможны два случая:
$\overrightarrow{a}\uparrow \uparrow \overrightarrow{b}$
Обозначим число $k$ следующим образом: $k=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$. Так как векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены, а $k\ge 0$, то векторы $k\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены. Далее, имеем, что
\[\left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}|\]Из этого всего следует, что $\overrightarrow{b}=k\overrightarrow{a}$.

$\overrightarrow{a}\uparrow \downarrow \overrightarrow{b}$
Обозначим число $k$ следующим образом: $k=-\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$. Так как векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ противоположно направленные, а $k \[\left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}|\]
Из этого всего следует, что $\overrightarrow{b}=k\overrightarrow{a}$.
Лемма доказана.
Теорема 1
Любой вектор можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом:
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]
Доказательство.
Существование: Докажем, что такое разложение имеет место. Здесь возможны два случая:
Вектор $\overrightarrow{c}$ коллинеарен (к примеру) вектору $\overrightarrow{b}$.

По лемме 1, будем иметь
\[\overrightarrow{c}=n\overrightarrow{b}\]Значит, если число $m=0$, то получим
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]Вектор $\overrightarrow{c}$ не коллинеарен векторам $\overrightarrow{a}$ и $\overrightarrow{b}$.
Возьмем произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OB}=\overrightarrow{b},\ \overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OC}=\overrightarrow{c}$. Пусть Проведем прямую $CD||OB$ (рис. 1)
Рисунок 1. Иллюстрация теоремы 1
По правилу треугольника для сложения векторов, получим
\[\overrightarrow{c}=\overrightarrow{OD}+\overrightarrow{DC}\]По построению, получаем что векторы $\overrightarrow{OD}||\overrightarrow{a}$ и $\overrightarrow{DC}||\overrightarrow{b}$, следовательно, по лемме 1, имеем
\[\overrightarrow{OD}=m\overrightarrow{a},\ \overrightarrow{DC}=n\overrightarrow{b}\]Значит
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]
Единственность: Предположим противное, что помимо разложения$\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}$ существует разложение $\overrightarrow{c}=m’\overrightarrow{a}+n’\overrightarrow{b}$. Вычтем эти два равенства из друг друга:
Вычтем эти два равенства из друг друга:
Получаем систему:
Рисунок 2.
Следовательно, разложение единственно.
Теорема доказана.
Координаты вектора
Рассмотрим далее систему координат. От начала координат $O$ в направлении оси $Ox$ отложим вектор $\overrightarrow{i}$, а в направлении оси $Oy$ отложим вектор $\overrightarrow{j}$, длины которых равны единице.
Определение 1
Векторы $\overrightarrow{i}$ и $\overrightarrow{j}$ называются координатными векторами.
Так как векторы $\overrightarrow{i}$ и $\overrightarrow{j}$ не коллинеарны то, по теореме 1, любой вектор можно разложить в виде $\overrightarrow{c}=m\overrightarrow{i}+n\overrightarrow{j}$.
Определение 2
Коэффициенты разложения вектора $\overrightarrow{c}=m\overrightarrow{i}+n\overrightarrow{j}$ называются координатами данного вектора в данной системе координат, то есть
\[\overrightarrow{c}=\{m,\ n\}\]
Линейные операции над векторами
Теорема 2
Теорема о сумме векторов: Координаты суммы векторов равны сумме соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow{a}=\left\{x_1,\ y_1\right\}$, $\overrightarrow{b}=\{x_2,\ y_2\}$, тогда
Следовательно
Теорема доказана.
Теорема 3
Теорема о разности векторов: Координаты разности векторов равны разности соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow{a}=\left\{x_1,\ y_1\right\}$, $\overrightarrow{b}=\{x_2,\ y_2\}$, тогда
Следовательно
Теорема доказана.
Теорема 4
Теорема о произведении вектора на число: Координаты произведения вектора на число равны произведению соответствующих координат это число.
Доказательство.
Пусть $\overrightarrow{a}=\left\{x,\ y\right\}$, тогда $\overrightarrow{a}=x\overrightarrow{i}+\ y\overrightarrow{j}. $
$
Следовательно
Теорема доказана.
Пример задачи на нахождение координат вектора
Пример 1
Пусть $\overrightarrow{a}=\left\{3,\ 4\right\}$, $\overrightarrow{b}=\{2,\ -1\}$. Найти $\overrightarrow{a}+\overrightarrow{b}$, $\overrightarrow{a}-\overrightarrow{b}$ и $3\overrightarrow{a}$.
Решение.
\[\overrightarrow{a}+\overrightarrow{b}=\left\{3+2,\ 4-1\right\}=\{5,\ 3\}\] \[\overrightarrow{a}-\overrightarrow{b}=\left\{3-2,\ 4+1\right\}=\{1,\ 5\}\] \[3\overrightarrow{a}=\left\{3\cdot 3,3\cdot 4\right\}=\{9,12\}\]
Как определяются координаты вектора в пространстве. Координаты вектора. Направляющие косинусы. Свойства скалярного произведения векторов
Нахождение координат вектора довольно часто встречаемое условие многих задач в математике. Умение находить координаты вектора поможет вам в других, более сложных задачах со схожей тематикой. В данной статье мы рассмотрим формулу нахождения координат вектора и несколько задач.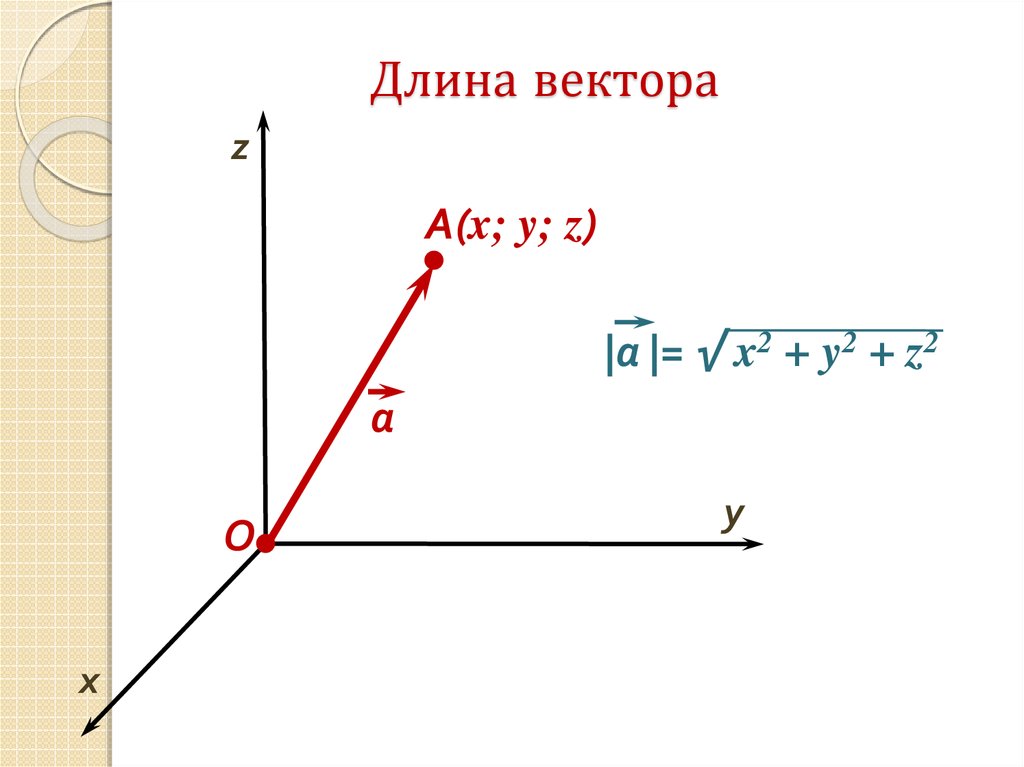
Нахождение координат вектора в плоскости
Что такое плоскость? Плоскостью считается двухмерное пространство, пространство с двумя измерениями (измерение x и измерение y). К примеру, бумага – плоскость. Поверхность стола – плоскость. Какая-нибудь необъемная фигура (квадрат, треугольник, трапеция) тоже является плоскостью. Таким образом, если в условии задачи нужно найти координаты вектора, который лежит на плоскости, сразу вспоминаем про x и y. Найти координаты такого вектора можно следующим образом: Координаты AB вектора = (xB – xA; yB – xA). Из формулы видно, что от координат конечной точки нужно отнять координаты начальной точки.
Пример:
- Вектор CD имеет начальные (5; 6) и конечные (7; 8) координаты.
- Найти координаты самого вектора.
- Используя вышеупомянутую формулу, получим следующее выражение: CD = (7-5; 8-6) = (2; 2).
- Таким образом, координаты CD вектора = (2; 2).
- Соответственно, x координата равна двум, y координата – тоже двум.

Нахождение координат вектора в пространстве
Что такое пространство? Пространство это уже трехмерное измерение, где даны 3 координаты: x, y, z. В случае, если нужно найти вектор, который лежит в пространстве, формула практически не меняется. Добавляется только одна координата. Для нахождения вектора нужно от координат конца отнять координаты начала. AB = (xB – xA; yB – yA; zB – zA)
Пример:
- Вектор DF имеет начальные (2; 3; 1) и конечные (1; 5; 2).
- Применяя вышеупомянутую формулу, получим: Координаты вектора DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Помните, значение координат может быть и отрицательным, в этом нет никакой проблемы.
Как найти координаты вектора онлайн?
Если по каким-то причинам вам не хочется находить координаты самостоятельно, можно воспользоваться онлайн калькулятором . Для начала, выберите размерность вектора. Размерность вектора отвечает за его измерения. Размерность 3 означает, что вектор находится в пространстве, размерность 2 – что на плоскости. Далее вставьте координаты точек в соответствующие поля и программа определит вам координаты самого вектора. Все очень просто.
Далее вставьте координаты точек в соответствующие поля и программа определит вам координаты самого вектора. Все очень просто.
Нажав на кнопку, страница автоматически прокрутится вниз и выдаст вам правильный ответ вместе с этапами решения.
Рекомендовано хорошо изучить данную тему, потому что понятие вектора встречается не только в математике, но и в физике. Студенты факультета Информационных Технологий тоже изучают тему векторов, но на более сложном уровне.
Необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.
Координаты вектора
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $\overline{a}$, начало которого совпадает с началом системы координат (рис. 1).
Определение
Координатами вектора $\overline{a}$ называются проекции $a_{x}$ и $a_{y}$ данного вектора на оси $O x$ и $O y$ соответственно:
Величина $a_{x}$ называется абсциссой вектора $\overline{a}$, а число $a_{y}$
— его ординатой . То, что вектор $\overline{a}$ имеет координаты
$a_{x}$ и $a_{y}$,
записывается следующим образом: $\overline{a}=\left(a_{x} ; a_{y}\right)$.
То, что вектор $\overline{a}$ имеет координаты
$a_{x}$ и $a_{y}$,
записывается следующим образом: $\overline{a}=\left(a_{x} ; a_{y}\right)$.
Пример
Запись $\overline{a}=(5 ;-2)$ означает, что вектор $\overline{a}$ имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Сумма двух векторов, заданных координатами
Пусть заданы $\overline{a}=\left(a_{x} ; a_{y}\right)$ и $\overline{b}=\left(b_{x} ; b_{y}\right)$, тогда вектор $\overline{c}=\overline{a}+\overline{b}$ имеет координаты $\left(a_{x}+b_{x} ; a_{y}+b_{y}\right)$ (рис. 2).
Определение
Чтобы найти сумму двух векторов , заданных своими координатами, надо сложить их соответствующие координаты.
Пример
Задание. Заданы $\overline{a}=(-3 ; 5)$ и $\overline{b}=(0 ;-1)$. Найти координаты вектора $\overline{c}=\overline{a}+\overline{b}$
Решение. $\overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$
Умножение вектора на число
Если задан $\overline{a}=\left(a_{x} ; a_{y}\right)$, то тогда вектор
$m \overline{a}$ имеет координаты
$m \overline{a}=\left(m a_{x} ; m a_{y}\right)$, здесь
$m$ — некоторое число (рис. 3).
3).
Пример
Задание. Вектор $\overline{a}=(3 ;-2)$. Найти координаты вектора 2$\overline{a}$
Решение. $2 \overline{a}=2 \cdot(3 ;-2)=(2 \cdot 3 ; 2 \cdot(-2))=(6 ;-4)$
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $A\left(a_{x} ; a_{y}\right)$ и $B\left(b_{x} ; b_{y}\right)$. Тогда координаты вектора $\overline{A B}=\left(x_{1} ; y_{1}\right)$ находятся по формулам (рис. 4):
$x_{1}=b_{x}-a_{x}, y_{1}=b_{y}-a_{y}$
Определение
Чтобы найти координаты вектора , заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.
Пример
Задание. Найти координаты вектора $\overline{A B}$, если $A(-4 ; 2), B(1 ;-3)$
Решение. $\overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$
Направляющие косинусы
Определение
Направляющими косинусами вектора называются косинусы углов, образованных вектором с
положительными направлениями осей координат. {2}}}$
{2}}}$
Здесь $\alpha$, $\beta$ и $\gamma$ — углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.
На оси абсцисс и ординат называются координатами вектора . Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).
Формула определения координат вектора для двухмерных задач.
В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:
= (x 2 — x 1 ; y 2 — y 1).
Формула определения координат вектора для пространственных задач.
В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:
= (x 2 — x 1 ; y 2 — y 1 ; z 2 — z 1 ).
Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты .
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат .
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов .
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.
Определение 1
Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.
С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.
Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач
Прямоугольная система координат на плоскости обычно обозначается O x y , где O x и O y – оси коорднат. Ось O x называют осью абсцисс, а ось O y – осью ординат (в пространстве появляется ещё одна ось O z , которая перпендикулярна и O x и O y).
Пример 1
Итак, нам дана прямоугольная декартова система координат O x y на плоскости если мы отложим от начала координат векторы i → и j → , направление которых соответственно совпадет с положительными направлениями осей O x и O y , и их длина будет равна условной единице, мы получим координатные векторы.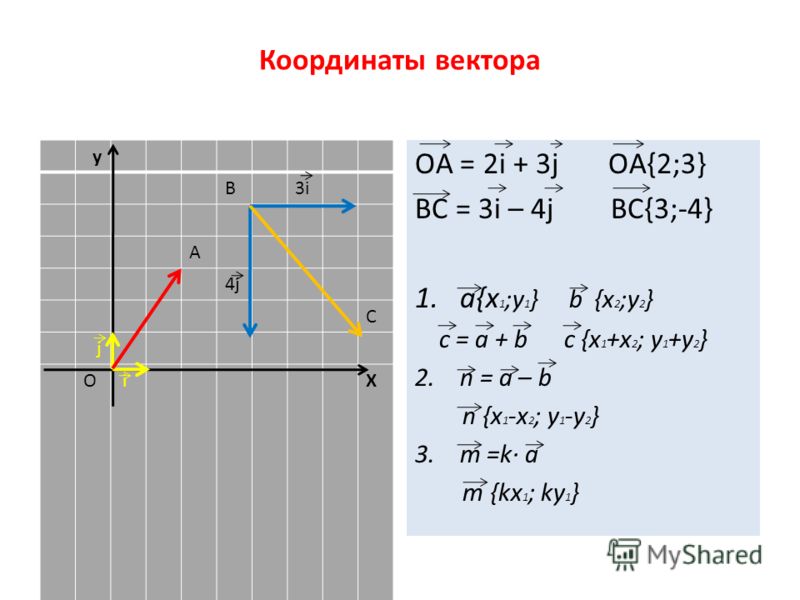 То есть в данном случае i → и j → являются координатными векторами.
То есть в данном случае i → и j → являются координатными векторами.
Координатные векторы
Определение 2Векторы i → и j → называются координатными векторами для заданной системы координат.
Пример 2
Откладываем от начала координат произвольный вектор a → . Опираясь на геометрическое определение операций над векторами, вектор a → может быть представлен в виде a → = a x · i → + a y · j → , где коэффициенты a x и a y — единственные в своем роде, их единственность достаточно просто доказать методом от противного.
Разложение вектора
Определение 3Разложением вектора a → по координатным векторам i → и j → на плоскости называется представление вида a → = a x · i → + a y · j → .
Определение 4
Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.
Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись a → = (2 ; — 3) означает, что вектор a → имеет координаты (2 ; — 3) в данной системе координат и может быть представлен в виде разложения по координатным векторам i → и j → как a → = 2 · i → — 3 · j → .
Замечание
Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.
Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы i → и j → имеют координаты (1 ; 0) и (0 ; 1) соответственно, и они могут быть представлены в виде следующих разложений i → = 1 · i → + 0 · j → ; j → = 0 · i → + 1 · j → .
Также имеет место быть нулевой вектор 0 → с координатами (0 ; 0) и разложением 0 → = 0 · i → + 0 · j → .
Равные и противоположные векторы
Определение 5Векторы a → и b → равны тогда, когда их соответствующие координаты равны.
Определение 6
Противоположным вектором называется вектор противоположный данному.
Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, — a → = (- a x ; — a y) .
Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов i → , j → , k → , а произвольный вектор a → раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид a → = a x · i → + a y · j → + a z · k → , а коэффициенты этого разложения (a x ; a y ; a z) называются координатами вектора в данной (трехмерной) системе координат.
Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты i → = (1 ; 0 ; 0) , j → = (0 ; 1 ; 0) , k → = (0 ; 0 ; 1) , координаты нулевого вектора также равны нулю 0 → = (0 ; 0 ; 0) , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равны a → = b → ⇔ a x = b x , a y = b y , a z = b z , и координаты противоположного вектора a → противоположны соответствующим координатам вектора a → , то есть, — a → = (- a x ; — a y ; — a z) .
Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.
Пусть нам дана некоторая прямоугольная декартова система координат O x y и на ней задана произвольная точка M с координатами M (x M ; y M) .
Определение 7
Вектор O M → называется радиус-вектором точки M .
Определим, какие координаты в данной системе координат имеет радиус-вектор точки
Вектор O M → имеет вид суммы O M → = O M x → + O M y → = x M · i → + y M · j → , где точки M x и M y это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а i → и j → — координатные векторы, следовательно, вектор O M → имеет координаты (x M ; y M) в данной системе координат.
Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.
Аналогично в трехмерном пространстве радиус-вектор точки M (x M ; y M ; z M) разлагается по координатным векторам как O M → = O M x → + O M y → + O M z → = x M · i → + y M · j → + z M · k → , следовательно, O M → = (x M ; y M ; z M) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
До сих пор считалось, что векторы
рассматриваются в пространстве. Начиная
с этого момента будим считать, что все
векторы рассматриваются на плоскости.
Будем также полагать, что на плоскости
задана Декартова система координат
(даже если об этом не говорится),
представляющая две взаимно перпендикулярные
числовые оси – горизонтальная ось
и
вертикальная ось.
Тогда каждой точке
на
плоскости ставится в соответствие пара
чисел
,
которые являются ее координатами.
Обратно, каждой паре чисел
соответствует точка плоскости такая,
что пара чисел
являются ее координатами.
Из элементарной геометрии известно,
что если на плоскости имеются две точки
и
,
то расстояние
между
этими точками выражается через их
координаты по формуле
Пусть на плоскости задана Декартова
система координат. Орт оси
будем обозначать символом,
а орт осисимволом.
Проекцию произвольноговекторана осьбудем обозначать символом
Орт оси
будем обозначать символом,
а орт осисимволом.
Проекцию произвольноговекторана осьбудем обозначать символом
,
а проекцию на осьсимволом
.
Пусть — произвольный вектор на плоскости. Имеет место следующая теорема.
Теорема 22.
Для любого вектора
на плоскости существует пара чисел
.
При этом
,
.
Доказательство.
Пусть дан вектор. Отложим векторот начала координат. Обозначим черезвектор-проекцию векторана ось, а черезвектор-проекцию векторана ось. Тогда, как видно из рисунка 21, имеет место равенство
.
Согласно теореме 9,
,
.
Обозначим
,
.
Тогда получаем
.
Итак, доказано, что для любого вектора
существует пара чисел
таких, что справедливо равенство
,
,
.
При другом расположении вектора относительно осей доказательство аналогично.
Определение.
Пара чисел
итаких, что
,
называются координатами вектора. Числоназывается иксовой координатой, а числоигрековой координатой.
Числоназывается иксовой координатой, а числоигрековой координатой.
Определение.
Пара ортов осей координат
называется ортонормированным базисом
на плоскости. Представление любого
векторав виде
называется разложением векторапо базису
.
Непосредственно из определения координат вектора следует, что если координаты векторов равны, то равны и сами векторы. Справедливо также и обратное утверждение.
Теорема.
Равные векторы имеют равные координаты.
Доказательство.
,
и
.
Докажем, что
,
.
Из равенства векторов следует, что
.
Допустим, что
,
а
.
Тогда
и значит
,
что не верно. Аналогично, если
,
но
,
то
.
Отсюда
,
что не верно. Наконец, если допустить,
что
и
,
то получаем, что
.
Это означает, что векторы
иколлинеареы. Но это не верно, так как
они перпендикулярны. Следовательно,
остается, что
,
,
что и требовалось доказать.
Таким образом, координаты вектора
полностью определяют сам вектор. Зная
координаты
ивектораможно построить сам вектор, построив векторы
и
и сложив их. Поэтому часто сам векторобозначают в виде пары его координат и
пишут
.
Такая запись означает, что
.
Непосредственно из определения координат вектора следует следующая теорема.
Теорема.
При сложении векторов их координаты складываются а при умножении вектора на число его координаты умножаются на это число. Записываются эти утверждения в виде
.
Доказательство.
,
Теорема.
Пусть
,
причем начало вектора точкаимеет координаты
,
а конец вектора есть точка
.
Тогда координаты вектора связаны с
координатами его концов следующими
соотношениями
,
.
Доказательство.
Пусть
и пусть вектор-проекция векторана осьсонаправлен с осью(см. рис. 22). Тогда
так
как длина отрезка на числовой осиравна координате правого конца минус
координата левого конца. Если вектор
Если вектор
противонаправлен оси(как на Рис. 23), то
Рис. 23.
Если
,
то в этом случае
и тогда получаем
.
Таким образом, при любом расположении
вектора
относительно
осей координат его координатаравна
.
Аналогично доказывается, что
.
Пример.
Даны координаты концов вектора
:
.
Найти координаты вектора
.
Решение.
В следующей теореме приводится выражение длины вектора через его координаты.
Теорема 15.
Пусть
.Тогда
.
Доказательство.
Пусть и- вектор-проекции векторана осии, соответственно. Тогда, как показано при доказательстве теоремы 9, имеет место равенство
.
При этом, векторы ивзаимно перпендикулярны. При сложении этих векторов по правилу треугольника получаем прямоугольный треугольник (см. Рис. 24).
По теореме Пифагора имеем
.
,
.
Следовательно
,
.
.
.
Пример.
.Найти.
Введем понятие направляющих косинусов вектора.
Определение.
Пусть вектор
составляет с осьюугол,
а с осьюугол(см. Рис. 25).
,
.
Следовательно,
Так как для любого вектора имеет место равенство
,
Где — орт вектора, то есть вектор единичной длины, сонаправленный с вектором, то
Вектор
определяет направление вектора.
Его координаты
и
называются направляющими косинусами
вектора.
Направляющие косинусы вектора можно
выразить через его координаты по формулам
,
.
Имеет место соотношение
.
До настоящего момента в этом параграфе считалось, что все векторы располагаются в одной и той же плоскости. Теперь сделаем обобщение для векторов в пространстве.
Будем считать, что в пространстве задана Декартова система координат с осями ,и.
Орты осей ,ибудем обозначать символами,и, соответственно (Рис. 26).
Можно показать, что все понятия и формулы, которые были получены для векторов на плоскости, обобщаются для
Рис. 26.
26.
векторов в пространстве. Тройка векторов
называется ортонормированным базисом
в пространстве.
Пусть ,и- вектор-проекции векторана оси,и, соответственно. Тогда
.
В свою очередь
,
,
.
Если обозначить
,
,
,
То получаем равенство
.
Коэффициенты перед базисными векторами ,иназываются координатами вектора. Таким образом, для любого векторав пространстве существует тройка чисел,,, называемых координатами векторатаких, что для этого вектора справедливо представление
.
Вектор
в этом случае также обозначают в виде
.
При этом, координаты вектора равны
проекциям этого вектора на координатные
оси
,
,
,
где — угол между вектороми осью,- угол между вектороми осью,- угол между вектороми осью.
Длина вектора выражается через его координаты по формуле
.
Справедливы утверждения о том, что
равные векторы имеют равные координаты,
при сложении векторов их координаты
складываются, а при умножении вектора
на число его координаты умножаются на
это число. 2\), откуда получаем требуемое равенство.
2\), откуда получаем требуемое равенство.
Утверждение
Если в прямоугольной системе координат точка \(M\) – середина отрезка \(PQ\), где \(P(x_1;y_1), \ Q(x_2;y_2)\), то
\[M\left(\dfrac{x_1 + x_2}{2}; \dfrac{y_1 + y_2}{2}\right)\]
Доказательство
Пусть \(M(a;b)\).
1) Пусть \(PQ\parallel Oy \Rightarrow x_1=x_2=a\). Значит, \(a=\dfrac{x_1+x_2}2=\dfrac{a+a}2\) – верно.
Т.к. \(PM=MQ\), следовательно, \(|y_2-b|=|y_1-b| \Rightarrow y_2-b=y_1-b\) или \(y_2-b=b-y_1\), что равносильно \(y_2=y_1\) или \(b=\dfrac{y_1+y_2}2\). Первое равенство невозможно (т.к. тогда точки \(P\) и \(Q\) совпадают).
2) Случай \(PQ\parallel Ox \Rightarrow y_1=y_2=b\) доказывается аналогично.
3) \(x_1\ne x_2, y_1\ne y_2\).
Тогда \(Ma=b\) – средняя линия трапеции \(x_1PQx_2\), следовательно, равна полусумме оснований, то есть \(b=\dfrac{y_1+y_2}2\).
Аналогично \(a=\dfrac{x_1+x_2}2\).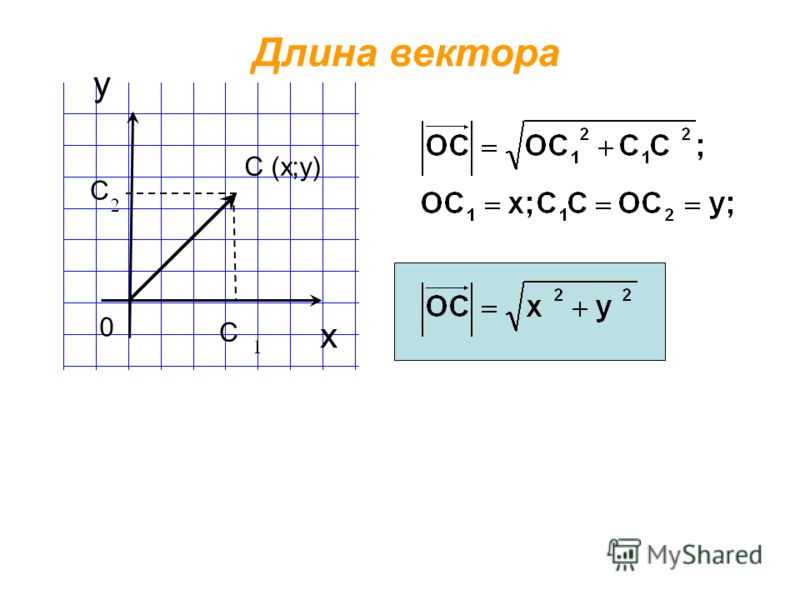
\[{\Large{\text{Векторы на координатной плоскости}}}\]
Лемма
Если векторы \(\overrightarrow a\) и \(\overrightarrow b\) коллинеарны, то существует такое число \(\lambda\ne 0\), что \(\overrightarrow a=\lambda\overrightarrow b\).
Доказательство
1) Если \(\overrightarrow a\uparrow \uparrow \overrightarrow b\).
Рассмотрим вектор \(\dfrac1{|\overrightarrow a|}\overrightarrow a\). Данный вектор сонавправлен с \(\overrightarrow a\), а его длина равна \(1\). Тогда вектор \(\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\) также сонаправлен с \(\overrightarrow a\), но его длина равна \(|\overrightarrow b|\). То есть равен вектору \(\overrightarrow b\).
2) Если \(\overrightarrow a\uparrow \downarrow \overrightarrow b\).
Аналогично доказывается, что \(\overrightarrow b=-\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\).
Определение
Если вектор \(\overrightarrow p\) представлен как линейная комбинация двух векторов: \(\overrightarrow p=\alpha\overrightarrow a+\beta
\overrightarrow b\), то говорят, что вектор \(\overrightarrow p\) разложен по векторам \(\overrightarrow a\) и \(\overrightarrow b\).
\(\alpha, \beta\) – коэффициенты разложения.
Пусть векторы \(\overrightarrow i\), \(\overrightarrow j\) – векторы, длины которых равны \(1\), а направление совпадает с направлением осей \(Ox\) и \(Oy\) соответственно. Такие векторы называются единичными векторами.
Тогда если \(\overrightarrow p=a\overrightarrow i+b\overrightarrow j\), то \(\{a;b\}\) – координаты вектора \(\overrightarrow p\).
Свойства координат вектора
1. Равные векторы имеют равные координаты.
2. Координаты суммы векторов равны сумме координат каждого вектора: если \(\overrightarrow a\{x_1;y_1\}, \ \overrightarrow b\{x_2;y_2\}\), то \(\overrightarrow a+\overrightarrow b=\{x_1+x_2;y_1+y_2\}\).
3. Каждая координата произведения вектора на число равна произведению соответствующей координаты данного вектора на это число: \(\overrightarrow a\{x;y\}, \ \lambda \) – число, то \(\lambda\overrightarrow a\{\lambda x;\lambda y\}\). 2}\).
2}\).
\[{\Large{\text{Скалярное произведение векторов}}}\]
Определение
Пусть от одной точки отложены два вектора \(\overrightarrow {AB}\) и \(\overrightarrow {AC}\). Тогда угол между этими векторами – это угол \(\angle BAC\), не превышающий развернутого угла.
Скалярное произведение векторов \(\overrightarrow a\) и \(\overrightarrow b\) – это число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение: \(\overrightarrow a\cdot \overrightarrow b\) или \((\overrightarrow a, \overrightarrow b)\). \[(\overrightarrow a, \overrightarrow b)=|\overrightarrow a|\cdot
|\overrightarrow b|\cdot \cos\widehat{(\overrightarrow a,
\overrightarrow b)}\]
Следствия
1. Если ненулевые векторы взаимно перпендикулярны, то косинус угла между ними равен нулю, следовательно, и их скалярное произведение равно нулю.
2. Если угол между ненулевыми векторами острый, то скалярное произведение положительно.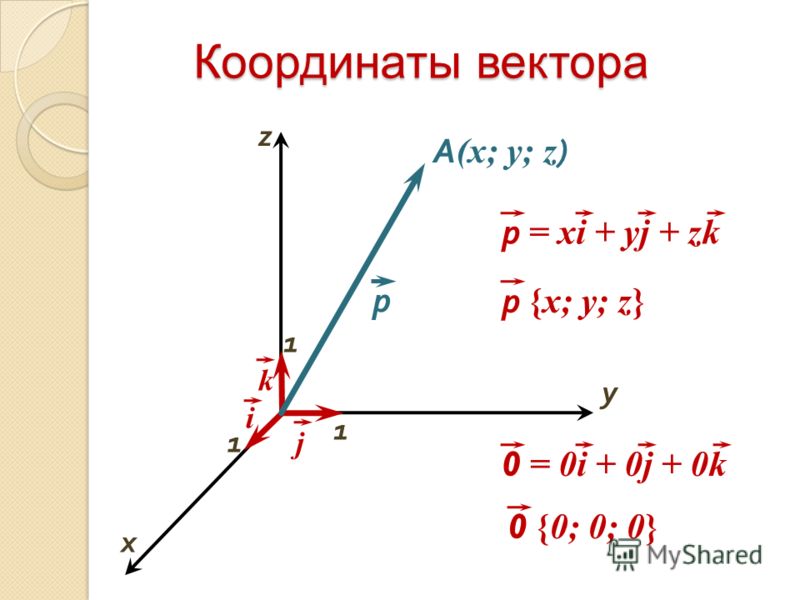 2=0
\Leftrightarrow |\overrightarrow a|=0\).
2=0
\Leftrightarrow |\overrightarrow a|=0\).
2. Переместительный закон: \(\overrightarrow a\cdot \overrightarrow b=\overrightarrow b\cdot \overrightarrow a\).
3. Распределительный закон: \(\overrightarrow a \cdot (\overrightarrow b+\overrightarrow c)=\overrightarrow a\cdot \overrightarrow b+\overrightarrow a\cdot \overrightarrow c\).
4. Сочетательный закон: \((\lambda\overrightarrow a)\cdot \overrightarrow b=\lambda (\overrightarrow a\cdot \overrightarrow b)\).
Как найти координаты вектора в трехмерном пространстве
Еще из школьного курса алгебры и геометрии мы знаем о понятии трехмерного пространства. Если разобраться, сам термин «трехмерное пространство» определяется как система координат с тремя измерениями (это знают все). По сути, описать любой объемный объект можно при помощи длины, ширины и высоты в классическом понимании. Однако давайте, как говорится, копнем несколько глубже.
Что такое трехмерное пространство
Как уже стало ясно, понимание трехмерного пространства и объектов, способных существовать внутри него, определяется тремя основными понятиями. Правда, в случае с точкой это именно три значения, а в случае с прямыми, кривыми, ломаными линиями или объемными объектами соответствующих координат может быть больше.
Правда, в случае с точкой это именно три значения, а в случае с прямыми, кривыми, ломаными линиями или объемными объектами соответствующих координат может быть больше.
В данном случае все зависит именно от типа объекта и применяемой системы координат. Сегодня наиболее распространенной (классической) считается Декартова система, которую иногда еще называют прямоугольной. Она и некоторые другие разновидности будут рассмотрены несколько позже.
Кроме всего прочего, здесь нужно разграничивать абстрактные понятия (если можно так сказать, бесформенные) вроде точек, прямых или плоскостей и фигуры, обладающие конечными размерами или даже объемом. Для каждого из таких определений существуют и свои уравнения, описывающие их возможное положение в трехмерном пространстве. Но сейчас не об этом.
Понятие точки в трехмерном пространстве
Для начала определимся, что представляет собой точка в трехмерном пространстве. В общем-то, ее можно назвать некой основной единицей, определяющей любую плоскую или объемную фигуру, прямую, отрезок, вектор, плоскость и т. д.
д.
Сама же точка характеризуется тремя основными координатами. Для них в прямоугольной системе применяются специальные направляющие, называемые осями X, Y и Z, причем первые две оси служат для выражения горизонтального положения объекта, а третья относится к вертикальному заданию координат. Естественно, для удобства выражения положения объекта относительно нулевых координат в системе приняты положительные и отрицательные значения. Однако же сегодня можно найти и другие системы.
Разновидности систем координат
Как уже говорилось, прямоугольная система координат, созданная Декартом, сегодня является основной. Тем не менее в некоторых методиках задания местоположения объекта в трехмерном пространстве применяются и некоторые другие разновидности.
Наиболее известными считаются цилиндрическая и сферическая системы. Отличие от классической состоит в том, что при задании тех же трех величин, определяющих местоположение точки в трехмерном пространстве, одно из значений является угловым. Иными словами, в таких системах используется окружность, соответствующая углу в 360 градусов. Отсюда и специфичное задание координат, включающее такие элементы, как радиус, угол и образующая. Координаты в трехмерном пространстве (системе) такого типа подчиняются несколько другим закономерностям. Их задание в данном случае контролируется правилом правой руки: если совместить большой и указательный палец с осями X и Y, соответственно, остальные пальцы в изогнутом положении укажут на направление оси Z.
Иными словами, в таких системах используется окружность, соответствующая углу в 360 градусов. Отсюда и специфичное задание координат, включающее такие элементы, как радиус, угол и образующая. Координаты в трехмерном пространстве (системе) такого типа подчиняются несколько другим закономерностям. Их задание в данном случае контролируется правилом правой руки: если совместить большой и указательный палец с осями X и Y, соответственно, остальные пальцы в изогнутом положении укажут на направление оси Z.
Понятие прямой в трехмерном пространстве
Теперь несколько слов о том, что представляет собой прямая в трехмерном пространстве. Исходя из основного понятия прямой, это некая бесконечная линия, проведенная через точку или две, не считая множества точек, расположенных в последовательности, не изменяющей прямое прохождение линии через них.
Если посмотреть на прямую, проведенную через две точки в трехмерном пространстве, придется учитывать по три координаты обеих точек. То же самое относится к отрезкам и векторам. Последние определяют базис трехмерного пространства и его размерность.
То же самое относится к отрезкам и векторам. Последние определяют базис трехмерного пространства и его размерность.
Определение векторов и базиса трехмерного пространства
Как принято считать, в трехмерной системе координат может существовать три основных вектора, которые определяют базис. При этом базисов с соответствующими независимыми тремя векторами может быть бесчисленное множество.
Заметьте, это могут быть только три вектора, но вот троек векторов можно определить сколько угодно. Размерность пространства определяется количеством линейно-независимых векторов (в нашем случае – три). И пространство, в котором имеется конечное число таких векторов, называется конечномерным.
Зависимые и независимые векторы
Что касается определения зависимых и независимых векторов, линейно-независимыми принято считать векторы, являющиеся проекциями (например, векторы оси X, спроецированные на ось Y).
Как уже понятно, любой четвертый вектор является зависимым (теория линейных пространств). А вот три независимых вектора в трехмерном пространстве в обязательном порядке не должны лежать в одной плоскости. Кроме того, если определять независимые векторы в трехмерном пространстве, они не могут являться, так сказать, один продолжением другого. Как уже понятно, в рассматриваемом нами случае с тремя измерениями, согласно общей теории, можно построить исключительно только тройки линейно-независимых векторов в определенной системе координат (без разницы, какого типа).
А вот три независимых вектора в трехмерном пространстве в обязательном порядке не должны лежать в одной плоскости. Кроме того, если определять независимые векторы в трехмерном пространстве, они не могут являться, так сказать, один продолжением другого. Как уже понятно, в рассматриваемом нами случае с тремя измерениями, согласно общей теории, можно построить исключительно только тройки линейно-независимых векторов в определенной системе координат (без разницы, какого типа).
Плоскость в трехмерном пространстве
Если рассматривать понятие плоскости, не вдаваясь в математические определения, для более простого понимания этого термина, такой объект можно рассматривать исключительно как двумерный. Иными словами, это бесконечная совокупность точек, у которых одна из координат является постоянной (константой).
К примеру, плоскостью можно назвать любое количество точек с разными координатами по осям X и Y, но одинаковыми координатами по оси Z. В любом случае одна из трехмерных координат остается неизменной. Однако это, так сказать, общий случай. В некоторых ситуациях трехмерное пространство может пересекаться плоскостью по всем осям.
Однако это, так сказать, общий случай. В некоторых ситуациях трехмерное пространство может пересекаться плоскостью по всем осям.
Существует ли более трех измерений
Вопрос о том, сколько может существовать измерений, достаточно интересен. Как считается, мы живем не в трехмерном с классической точки зрения пространстве, а в четырехмерном. Кроме известных всем длины, ширины и высоты, такое пространство включает в себя еще и время существования объекта, причем время и пространство между собой взаимосвязаны достаточно сильно. Это доказал еще Эйнштейн в своей теории относительности, хотя это больше относится к физике, нежели к алгебре и геометрии.
Интересен и тот факт, что сегодня ученые уже доказали существование как минимум двенадцати измерений. Конечно, понять, что они собой представляют, сможет далеко не каждый, поскольку это относится скорее к некой абстрактной области, которая находится вне человеческого восприятия мира. Тем не менее факт остается фактом. И не зря же многие антропологи и историки утверждают, что наши пращуры могли иметь некие специфичные развитые органы чувств вроде третьего глаза, которые помогали воспринимать многомерную действительность, а не исключительно трехмерное пространство.
Кстати сказать, сегодня существует достаточно много мнений по поводу того, что экстрасенсорика тоже является одним из проявлений восприятия многомерного мира, и тому можно найти достаточно много подтверждений.
Заметьте, что современными базовыми уравнениями и теоремами описать многомерные пространства, отличающиеся от нашего четырехмерного мира, тоже не всегда представляется возможным. Да и наука в этой области относится скорее к области теорий и предположений, нежели к тому, что можно явно ощутить или, так сказать, потрогать или увидеть воочию. Тем не менее косвенные доказательства существования многомерных миров, в которых может существовать четыре и более измерений, сегодня ни у кого не вызывают сомнений.
Заключение
В целом же, мы очень кратко рассмотрели основные понятия, относящиеся к трехмерному пространству и базовым определениям. Естественно, существует множество частных случаев, связанных с разными системами координат. К тому же мы постарались особо не лезть в математические дебри для объяснения основных терминов только для того, чтобы вопрос, связанный с ними, был понятен любому школьнику (так сказать, объяснение «на пальцах»).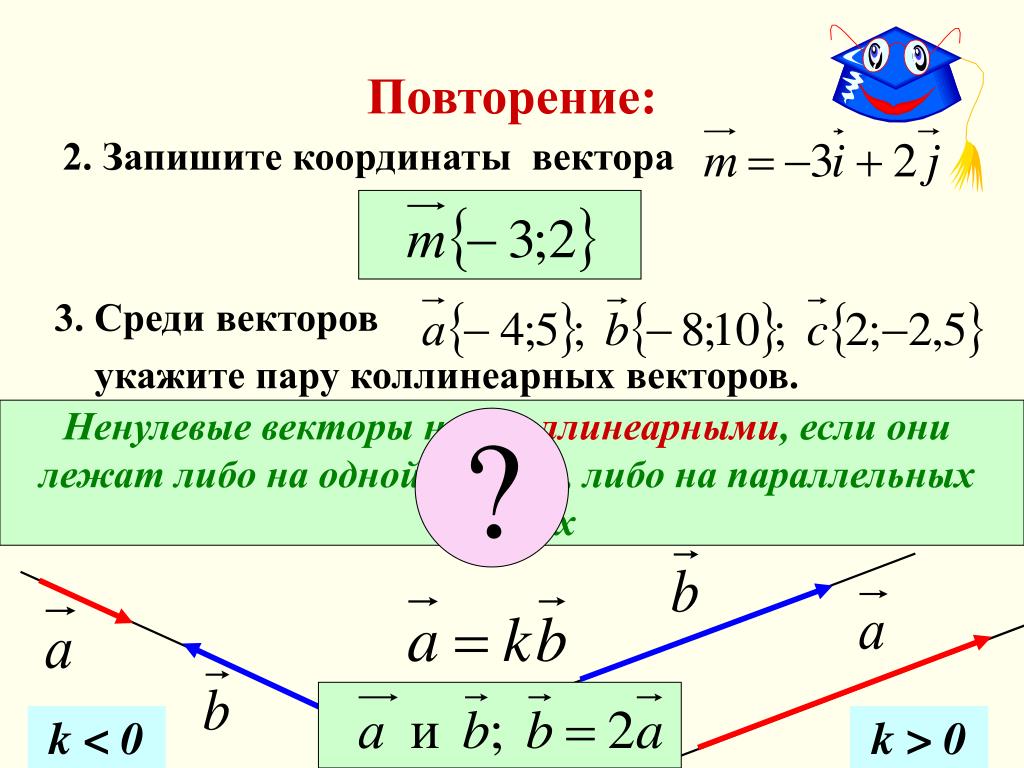
Тем не менее, думается, даже из таких простых трактовок можно сделать вывод о математическом аспекте всех составляющих, входящих в базовый школьный курс алгебры и геометрии.
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространствеВыберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Только координат не две, а три. Возьмем векторы и .
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и .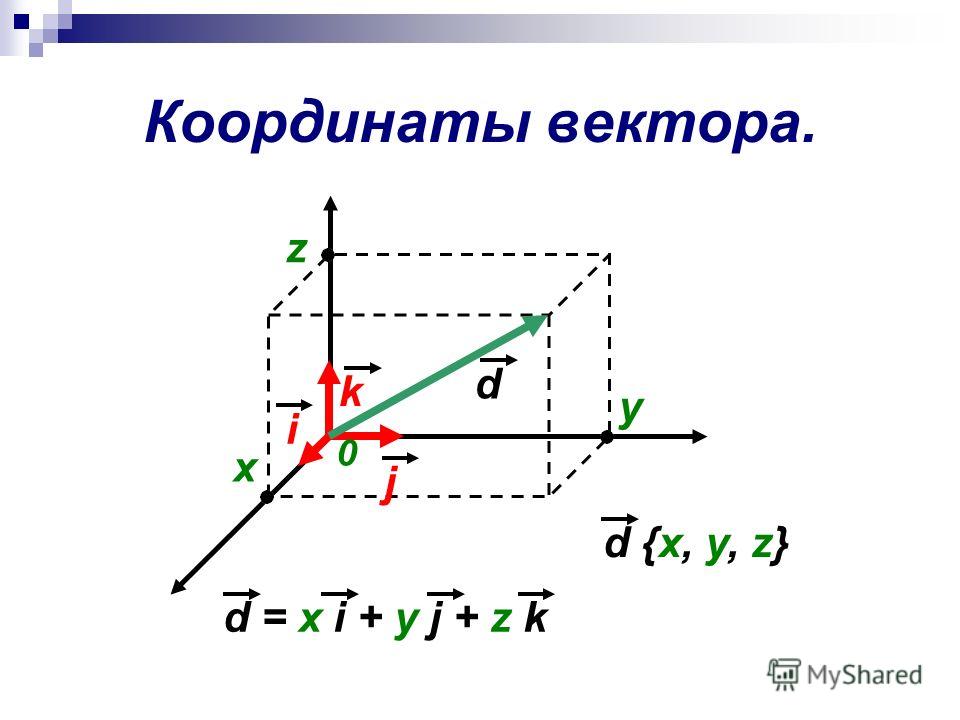 Для этого нужны их координаты.
Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1.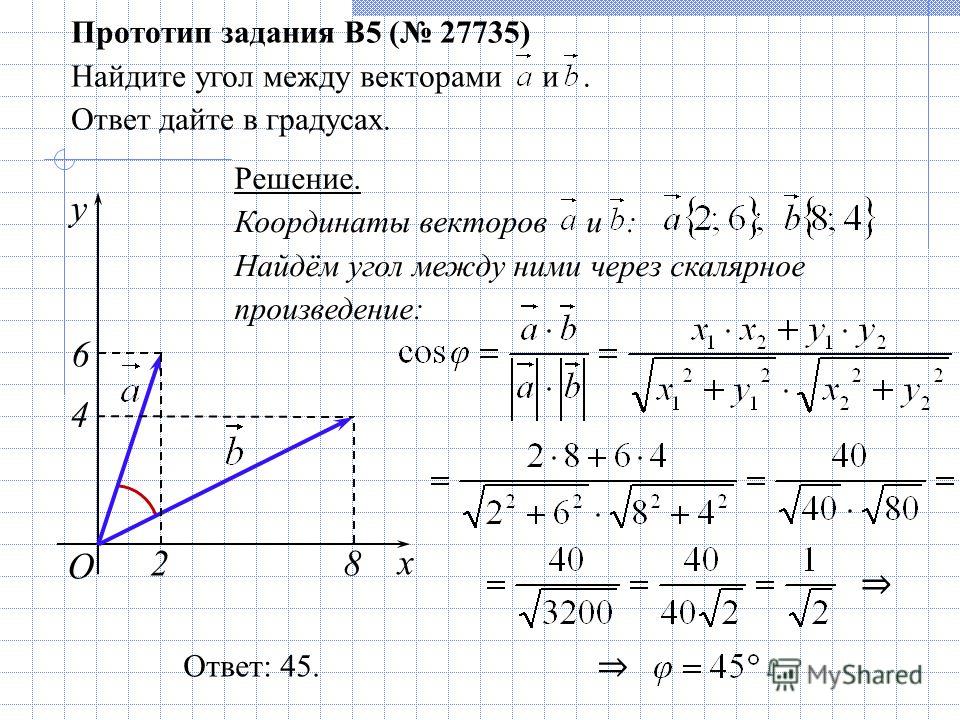 Найдите косинус угла между прямыми AD и BC1
Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает.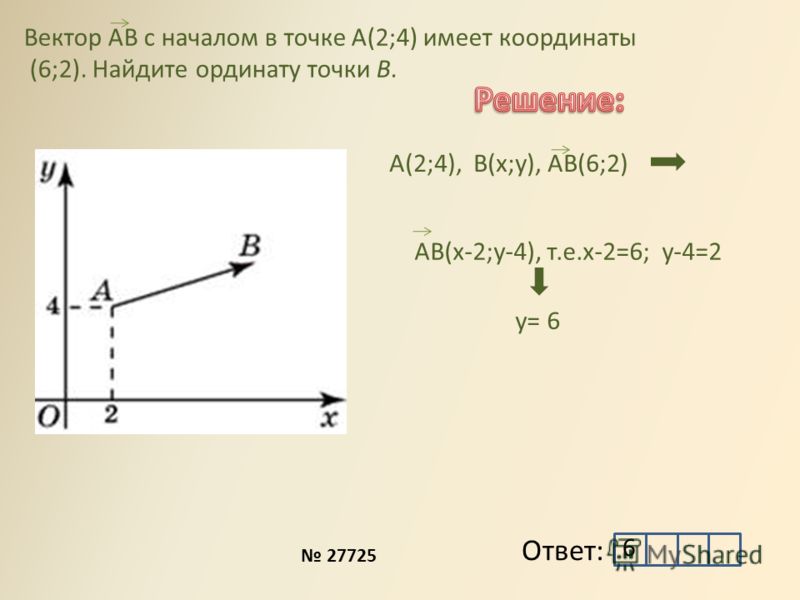 Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33.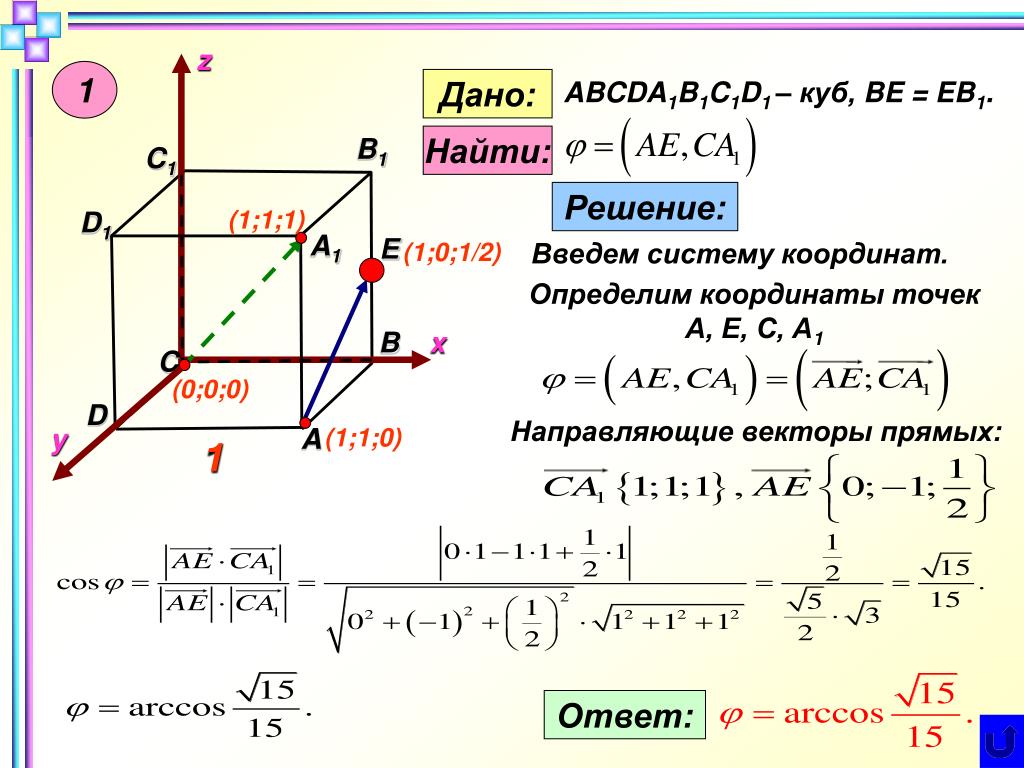 Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего.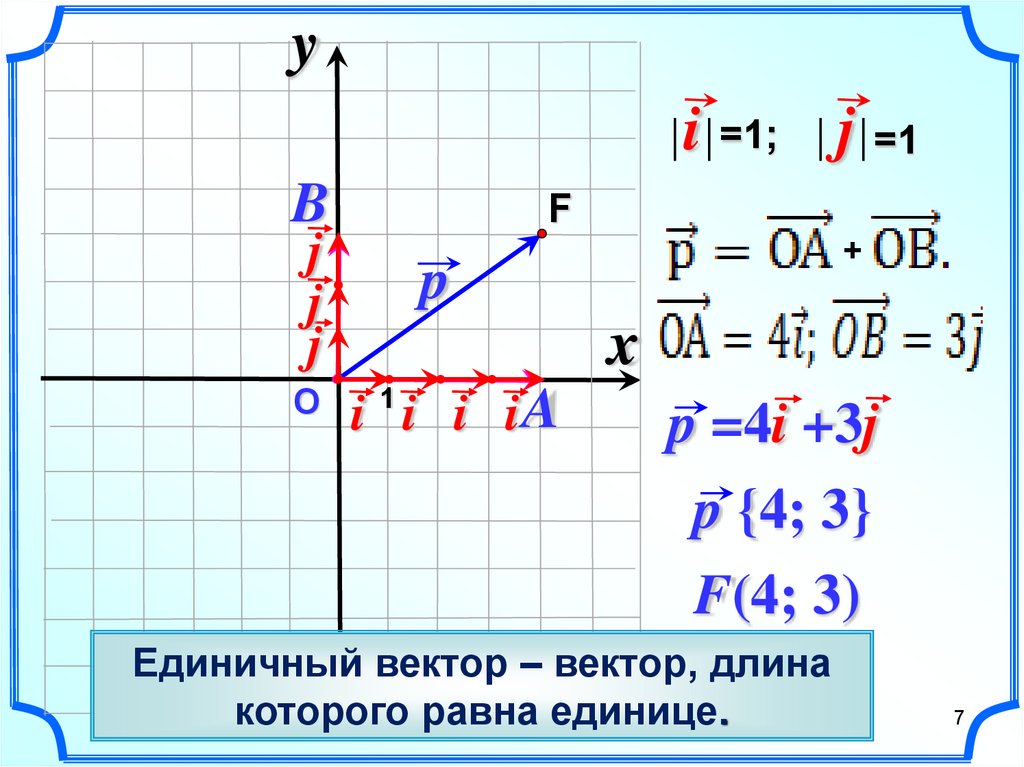 А отрезок OO1 и равен высоте параллелепипеда.
А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Калькулятор служит для вычисления длины вектора в трехмерном пространстве.
Длиной или модулем вектора мы называем длину отрезка, изображающего данный вектор.
Формула для определения длины вектора a в трехмерном пространстве через его координаты представлена ниже.
Чтобы произвести вычисление длины вектора в трехмерном пространстве, введите в соответствующих полях значение координаты x и координаты y и координаты z, после чего нажмите кнопку » ВЫЧИСЛИТЬ «.
Результатом работы программы будет значение длины вектора в трехмерном пространстве.
Зачетный урок по теме: «Метод координат»
- Елсукова Светлана Анатольевна
Разделы: Математика
Цели урока:
- подвести итог по изучению темы,
- проверить усвоенные знания,
- подготовка к контрольной работе.

Класс разбивается на 5 групп по 5 человек. Старшими в группе назначаются успевающие ученики (помощники учителя).
1 этап. Организационный момент. Постановка целей
2 этап. Ответы на вопросы с использование сигнальных карт (15 минут)
Каждой группе выдается путевой лист, в котором помощники будут отмечать знание/незнание ответа на вопрос. Каждому учащемуся выдаются две карточки: зеленая и красная. Как только вопрос сформулирован, ученики поднимают сигнальные карты (знаю ответ – зеленая карточка, не знаю ответ – красная карточка). Затем один ученик по просьбе учителя вслух дает ответ на поставленный вопрос.
Вопрос 1. Сформулируйте лемму о двух коллинеарных векторах.
(Если векторы и коллинеарны и , то существует такое число k, что ).
Вопрос 2. Сформулируйте теорему о разложении вектора по двум неколлинеарным векторам.
(Любой вектор можно разложить по двум данным
неколлинеарным векторам, причем коэффициенты
разложения определяются единственным образом).
Вопрос 3. Что такое координаты вектора?
(Это коэффициенты разложения вектора по координатным векторам).
Вопрос 4. Сформулируйте правило нахождения координат суммы векторов.
(Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов).
Вопрос 5. Сформулируйте правило нахождения координат разности векторов.
(Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов).
Вопрос 6. Сформулируйте правило нахождения координат произведения вектора на число.
(Каждая координата произведения вектора на число равна произведению соответствующих координат вектора на это число).
Вопрос 7. Напишите на доске формулу для вычисления координат вектора по координатам его начала и конца.
()
Вопрос 8. Напишите на доске формулу для
вычисления координат середины отрезка по
координатам его концов.
Напишите на доске формулу для
вычисления координат середины отрезка по
координатам его концов.
()
Вопрос 9. Напишите на доске формулу для вычисления длины вектора по его координатам.
()
Вопрос 10. Напишите на доске формулу для вычисления расстояния между двумя точками.
()
Вопрос 11. Напишите на доске уравнение окружности данного радиуса с центром в донной точке и уравнение окружности с центром в начале координат.
Вопрос 12. Напишите уравнение данной прямой в прямоугольной системе координат.
(ax+by+c=0).
3 этап. Выполнение индивидуального задания (10 минут)
Каждому ученику выдаются задания, которые они должны выполнить самостоятельно.
Примерные варианты карточек.
Карточка 1.
- Лежит ли точка A(2;-1) на окружности, заданной уравнением ?
- Найдите длину вектора .

- Найдите координаты середины отрезка PQ, если P(5;-3), Q(3;-7).
Карточка 2.
- Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 3.
- Найдите координаты вектора , если A(2;-5), B(-3;4).
- Напишите уравнение прямой, проходящей через точку M(3;-2) и параллельной оси ординат.
Карточка 3.
- Напишите уравнение окружности с центром в начале координат, если она проходит через точку C(2;-1).
- Найдите расстояние между точками A(-1; 3) и B(2; -1).
- Найдите координаты вектора , равного сумме векторов и , если .
Карточка 4.
- Лежит ли точка A(2;-1) на прямой, заданной уравнением 2x-3y-7=0.
- Напишите уравнение окружности, если ее центр –
точка (4;5), а радиус равен 2.

- Найдите координаты вектора , равного разности векторов и , если .
Карточка 5.
- Напишите уравнение окружности с центром в точке P(-2;-1), если она проходит через точку Q(1;3).
- Найдите координаты вектора , если C(-1; 6), D(3; -2).
- Найдите координаты вектора , если , а .
4 этап. Групповое решение задачи (15 минут)
Каждой группе дается задача.
Даны координаты трех вершин параллелограмма KLMN: K(-4; 2), L(0; 5), M(12; 0). Найдите координаты четвертой вершины и периметр данного параллелограмма.
Представитель группы, первой правильно решившей задачу, объясняет решение у доски.
5 этап. Домашнее задание
По учебнику Л. С. Атанасяна, №№ 996, 1001, 1005.
2$$ и задайте коэффициенты $a,b,c$ в виде координатного вектора вида $\langle a,b,c \rangle$ — координаты относительно нового базиса.
Помимо линейно-алгебраических методов смены базиса, можно переписать многочлен в требуемом виде судебным применением дополнения квадрата и разложения на множители, либо очень простым применением теоремы Тейлора для нахождения коэффициентов ряда Тейлора с центром в $t = 2$ (это, вероятно, самый эффективный метод). В качестве альтернативы вы можете разложить полином выше и решить систему уравнений для неопределенных коэффициентов. 92 — 4t + 4$ :
$${\bf T}= \left[\begin{array}{rrr} 1&-2&4\\ 0&1&-4\\ 0&0&1 \end{массив}\right]$$ Вы видите, какие числа должны быть помещены где? А затем решаем для $\bf v$ систему уравнений: $${\bf T}{\bf v} = \left[\begin{array}{r}2\\3\\-2\end{array }\right]$$
Это будет легко, когда вы научитесь решать системы матричных уравнений.
Чтобы расширить решение JnxF (чтобы избежать путаницы), матрица, используемая для умножения в его ответе, на самом деле является 92\}$, так что на самом деле это «перемещение» системы координат назад: $t\to t+2$, что отменяет предыдущее изменение $t \to t-2$.
$\endgroup$
4
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
линейная алгебра — Определение координат вектора относительно базиса
заданный вопрос
Изменено 7 лет, 2 месяца назад
Просмотрено 67 раз
$\begingroup$
Задача: Пусть $V = \mathbb{R}[X]_{\leq 4}$ — векторное пространство всех многочленов степени не выше $n$, и пусть $\alpha = \left\{1 , 1+x, (1+x)^2, (1+x)^3, (1+x)^4\right\}$ — базис для $V$.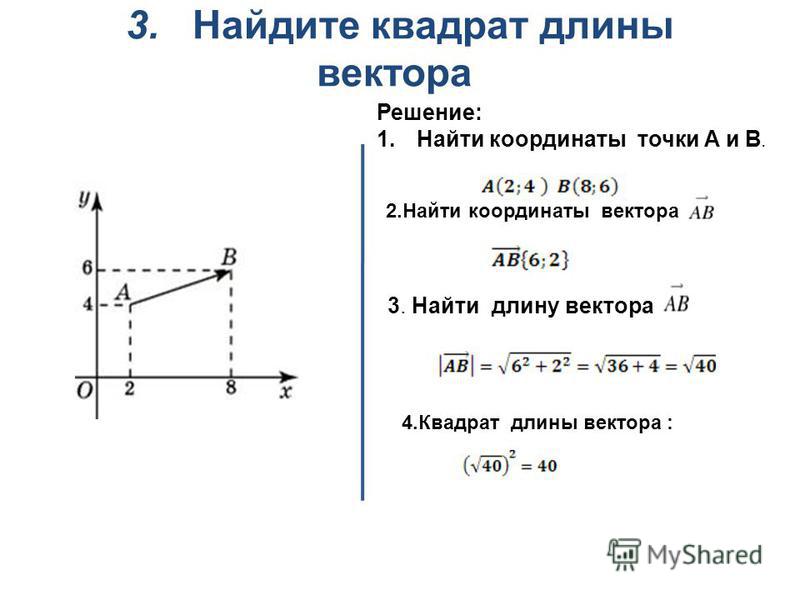 4$ относительно этого базиса. 94) \end{align*} где я расширил базисные векторы. При проверке соответствующих коэффициентов получается следующая система уравнений: \begin{align*} \begin{cases} \lambda_1 + \lambda_2 + \lambda_3 + \lambda_4 + \lambda_5 &= 0 \\ \lambda_2 + 2 \ lambda_3 + 3\lambda_4 + 4 \lambda_5 &= 1 \\ \lambda_3 + 3 \lambda_4 + 6 \lambda_5 &= 0 \\ \lambda_4 + 4 \lambda_5 &= 1 \\ \lambda_5 &= 1 \end{cases} \end{align*} Я поместил это в расширенную матрицу и уменьшил строку:
\begin{выравнивание*} и \left(\begin{массив}{ccccc|c}
1 и 1 и 1 и 1 и 1 и 0 \\
0 и 1 и 2 и 3 и 4 и 1 \\
0 и 0 и 1 и 3 и 6 и 0 \\
0 и 0 и 0 и 1 и 4 и 1 \\
0 и 0 и 0 и 0 и 1 и 1
\конец{массив}\справа)
\begin{matrix} \xrightarrow{R_4 \rightarrow R_4 — 4 R_5} \\ \xrightarrow{R_3 \rightarrow R_3 — 6 R_5} \\ \xrightarrow{R_2 \rightarrow R_2 — 4R_5} \\ \xrightarrow{R_1 \rightarrow R_1 — R_5} \end{matrix} \left(\begin{array}{ccccc|c}
1 и 1 и 1 и 1 и 0 и -1 \\
0 и 1 и 2 и 3 и 0 и -3 \\
0 и 0 и 1 и 3 и 0 и -6 \\
0 & 0 & 0 & 1 & 0 & -3 \\
0 и 0 и 0 и 0 и 1 и 1
\end{массив}\right) \\ \begin{matrix} \xrightarrow{R_3 \rightarrow R_3 — 3R_4} \\ \xrightarrow{R_2 \rightarrow R_2 — 3 R_4} \\ \xrightarrow{R_1 \rightarrow R_1 — R_4} \end{матрица} & \left(\begin{массив}{ccccc|c}
1 и 1 и 1 и 0 и 0 и -4 \\
0 и 1 и 2 и 0 и 0 и 6 \\
0 и 0 и 1 и 0 и 0 и 3 \\
0 и 0 и 0 и 1 и 0 и -3 \\
0 и 0 и 0 и 0 и 1 и 1
\конец{массив}\справа)
\end{align*} Затем с обратной заменой я обнаружил, что \begin{align*} \begin{cases} \lambda_5 &= 1 \\ \lambda_4 &= -3 \\ \lambda_3 &= 3 \\ \lambda_2 &= 0 \\ \lambda_1 &= -7 \end{cases} \end{align*} Но когда я подставляю это в уравнение выше, это не дает мне правильный вектор.
4$ относительно этого базиса. 94) \end{align*} где я расширил базисные векторы. При проверке соответствующих коэффициентов получается следующая система уравнений: \begin{align*} \begin{cases} \lambda_1 + \lambda_2 + \lambda_3 + \lambda_4 + \lambda_5 &= 0 \\ \lambda_2 + 2 \ lambda_3 + 3\lambda_4 + 4 \lambda_5 &= 1 \\ \lambda_3 + 3 \lambda_4 + 6 \lambda_5 &= 0 \\ \lambda_4 + 4 \lambda_5 &= 1 \\ \lambda_5 &= 1 \end{cases} \end{align*} Я поместил это в расширенную матрицу и уменьшил строку:
\begin{выравнивание*} и \left(\begin{массив}{ccccc|c}
1 и 1 и 1 и 1 и 1 и 0 \\
0 и 1 и 2 и 3 и 4 и 1 \\
0 и 0 и 1 и 3 и 6 и 0 \\
0 и 0 и 0 и 1 и 4 и 1 \\
0 и 0 и 0 и 0 и 1 и 1
\конец{массив}\справа)
\begin{matrix} \xrightarrow{R_4 \rightarrow R_4 — 4 R_5} \\ \xrightarrow{R_3 \rightarrow R_3 — 6 R_5} \\ \xrightarrow{R_2 \rightarrow R_2 — 4R_5} \\ \xrightarrow{R_1 \rightarrow R_1 — R_5} \end{matrix} \left(\begin{array}{ccccc|c}
1 и 1 и 1 и 1 и 0 и -1 \\
0 и 1 и 2 и 3 и 0 и -3 \\
0 и 0 и 1 и 3 и 0 и -6 \\
0 & 0 & 0 & 1 & 0 & -3 \\
0 и 0 и 0 и 0 и 1 и 1
\end{массив}\right) \\ \begin{matrix} \xrightarrow{R_3 \rightarrow R_3 — 3R_4} \\ \xrightarrow{R_2 \rightarrow R_2 — 3 R_4} \\ \xrightarrow{R_1 \rightarrow R_1 — R_4} \end{матрица} & \left(\begin{массив}{ccccc|c}
1 и 1 и 1 и 0 и 0 и -4 \\
0 и 1 и 2 и 0 и 0 и 6 \\
0 и 0 и 1 и 0 и 0 и 3 \\
0 и 0 и 0 и 1 и 0 и -3 \\
0 и 0 и 0 и 0 и 1 и 1
\конец{массив}\справа)
\end{align*} Затем с обратной заменой я обнаружил, что \begin{align*} \begin{cases} \lambda_5 &= 1 \\ \lambda_4 &= -3 \\ \lambda_3 &= 3 \\ \lambda_2 &= 0 \\ \lambda_1 &= -7 \end{cases} \end{align*} Но когда я подставляю это в уравнение выше, это не дает мне правильный вектор. Может кто-нибудь сказать мне, где я ошибся, пожалуйста?
Может кто-нибудь сказать мне, где я ошибся, пожалуйста?
- линейная алгебра
- векторные пространства
- системы уравнений
$\endgroup$
2
$\begingroup$
В сокращении последней строки, когда вы выполняете $R_1\leftarrow R_1-R_4$, последнее число в $R_1$ должно быть $-1-(-3)=-1+3=2$, но вы написали $-4 $. Это делает самую последнюю обратную замену $\lambda_1$ неправильной.
Я не понимаю, что вы делаете. Ваша исходная матрица была верхнетреугольной, поэтому оттуда можно было выполнить обратную подстановку, так что вообще не требовалось сокращения строк. И вы остановились до того, как дошли до формы эшелона с уменьшенным числом строк, где не потребовалась бы обратная замена. Какой у тебя был смысл делать несколько сокращений рядов, не переходя полностью к уменьшенной эшелонированной форме рядов?
$\endgroup$
$\begingroup$
Координаты: {$-7,12,-3,-3,1$} см. ваши операции
ваши операции
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Координаты точки, компоненты вектора и середины отрезка
Координаты точки на плоскости
Давайте посмотрим, как векторы используются для присвоения координат точкам на плоскости.
Рассмотрим фиксированную точку на плоскости $$O$$ (известную как начало координат) и базис $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$ $$V_2$ $ (пространственный вектор размерности $$2$$).
Напомним, что в основе $$V_2$$ лежат два линейно независимых вектора. Множество, образованное $$O$$ и $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$, образует систему отсчета на плоскости, поскольку позволяет определить положение любых других точки на плоскости.
Это связано с тем, что любые другие точки $$P$$ на плоскости вместе с точкой $$O$$ определяют вектор $$\overrightarrow{OP}$$. Пусть $$(p_1,p_2)$$ — компоненты вектора в базисе $$B$$. Тогда $$(p_1,p_2)$$ — это координаты точки $$P$$ в системе отсчета $$R=\{O;\overrightarrow{u}, \overrightarrow{v}\}$$, и мы пишем $$P=(p_1,p_2)$$.
Процедура нахождения координат точки $$P$$ в заданной системе отсчета следующая:
Из точек $$O$$ и $$P$$ определяем вектор $$\overrightarrow{OP}$$
Выразим вектор $$\overrightarrow{OP}$$ в виде линейной комбинации векторов базиса $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$, т.
 е. , $$\overrightarrow{OP}=p_1 \cdot \overrightarrow{u}+p_2 \cdot \overrightarrow{v}$$
е. , $$\overrightarrow{OP}=p_1 \cdot \overrightarrow{u}+p_2 \cdot \overrightarrow{v}$$- $$P=(p_1,p_2)$$
Выразите точку $$P$$ чертежа в системе отсчета $$R =\{O;\overrightarrow {u}, \overrightarrow{v}\}$$.
- Рисуем вектор $$\overrightarrow{OP}$$:
- Выразим вектор $$\overrightarrow{OP}$$ в виде линейной комбинации векторов базиса $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$:
- Получаем $$\overrightarrow{OP}=\overrightarrow{u}+2\overrightarrow{v}$$ и, следовательно, координаты точки $$P$$ равны $$P = (1 , 2 )$$
В дальнейшем в качестве системы отсчета $$R$$ будем рассматривать систему, образованную началом координат $$O = (0, 0)$$ и каноническим базисом $$V_2$$ $$B =\{\overrightarrow{i},\overrightarrow{j}\}$$.
Компоненты вектора, определяемого двумя точками
Теперь посмотрим, как определить компоненты вектора, если известны координаты его концов:
Пусть $$P =(p_1,p_2)$$ и $$ Q = (q_1,q_2)$$ — две точки плоскости, а $$\overrightarrow{PQ}$$ — вектор, идущий из $$P$$ в $$Q$$. Тогда компоненты вектора $$\overrightarrow{PQ}$$ равны $$\overrightarrow{PQ}=(q_1-p_1,q_2-p_2)$$.
Тогда компоненты вектора $$\overrightarrow{PQ}$$ равны $$\overrightarrow{PQ}=(q_1-p_1,q_2-p_2)$$.
Дано $$P = (2, 6)$$ и $$Q = (-3, 9)$$. Компоненты вектора $$\overrightarrow{PQ}$$ таковы: $$\overrightarrow{PQ}= (-3 — 2, 9- 6) = (-5, 3)$$
Применение вектора к точке
Для данной точки $$P$$ и вектора $$\overrightarrow{v}$$ результат применения вектора к точка — это новая точка $$Q$$, расположенная в направлении $$\overrightarrow{v}$$ и на расстоянии $$|\overrightarrow{v}|$$. (модуль вектора $$\overrightarrow{v}$$)
Координаты этой новой точки $$Q$$ вычисляются из координат $$P =(p_1,p_2)$$ и $$\overrightarrow{ v}=(v_1,v_2)$$ таким образом $$$Q = P +\overrightarrow{v}=(p_1+v_1,p_2+v_2)$$$
ПРИМЕЧАНИЕ. Очень важно помнить, что эта операция сложения имеет смысл только между точкой и вектором. Мы никогда не должны складывать две точки, а результатом сложения двух векторов будет другой вектор, а не точка!
Рассмотрев следующий рисунок, определите координаты точки $$P$$ рисунка, полученного приложением вектора $$\overrightarrow{v}$$ к точке $$A$$.
Начнем с вычисления компонент вектора $$\overrightarrow{v}$$:$$$\overrightarrow{v} = (2 — (-1), 4-2) = (3, 2) $$$ Поскольку $$P$$ является результатом применения вектора $$\overrightarrow{v}$$ к точке $$A$$, имеем $$$P=A+\overrightarrow{v}=(0,4) +(3,2)=(3,6)$$$
Середина отрезка
Рассмотрим теперь отрезок с концами $$A = (a_1,a_2)$$ и $$B = (b_1,b_2)$$. Пусть $$M =(m_1,m_2)$$ — середина указанного выше отрезка. Очевидно, что указанная выше точка удовлетворяет тому, что $$\overrightarrow{AB}=2\cdot \overrightarrow{AM}$$, или что $$(b_1-a_1,b_2-a_2)=2\cdot (m_1-a_1,m_2- a_2)$$
Разделяя покомпонентно получаем: $$$\begin{массив}{rcl} b_1-a_1 & = & 2 \cdot (m_1-a_1) \\ b_2-a_2 &=& 2\cdot (m_2-a_2) \end{массив}$$$ и изолируя имеем: $$$\begin{array}{rcl} m_1 & = & \displaystyle \frac{a_1+b_1}{2}\\ m_2 &=& \displaystyle \frac{a_2+b_2}{2} \end{array} $$$ Так что мы можем вычислить координаты середины отрезка по координатам его концов.
По точкам $$A = (-3, 7)$$ и $$B = (1, 2)$$ найдите середину отрезка, который они определяют.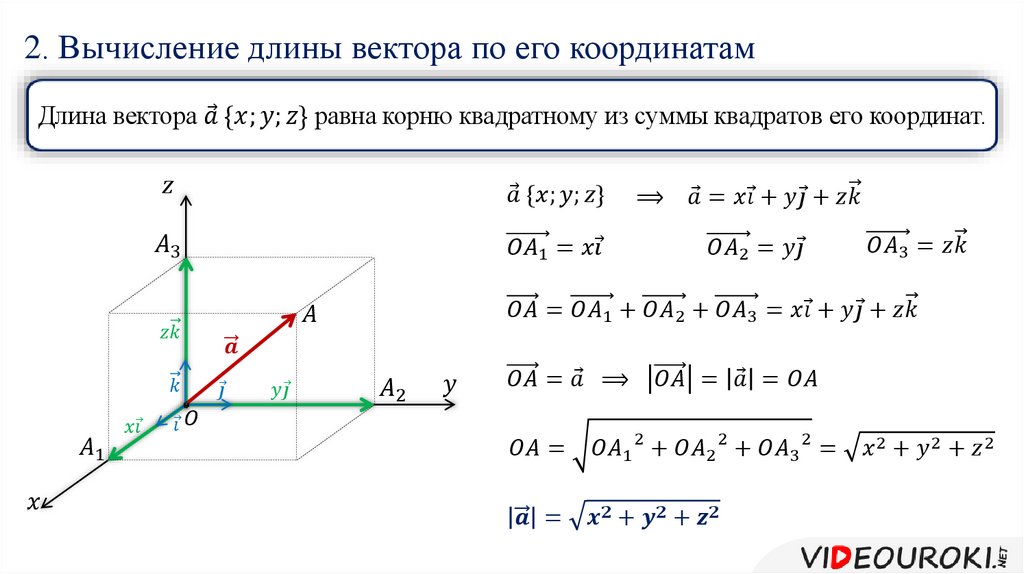
Применяя предыдущие формулы, имеем: $$$\begin{array}{rcl} m_1 & = & \displaystyle \frac{a_1+b_1}{2}= \frac{-3+2}{2}=-1\\ m_2 &=& \displaystyle \frac{a_2+b_2}{2}=\frac{7+2}{2}=\frac{9}{2} \end{array}$$$ Следовательно, середина отрезка $$AB$$ равна $$M = (-1, \displaystyle \frac{9}{2})$$
2.2 Системы координат и компоненты вектора — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Описывать вектора в двух и трех измерениях с точки зрения их компонентов, используя единичные векторы вдоль осей.
- Различать векторные компоненты вектора и скалярные компоненты вектора.
- Объясните, как величина вектора определяется через компоненты вектора.
- Определите угол направления вектора на плоскости.
- Объясните связь между полярными координатами и декартовыми координатами на плоскости.
Векторы обычно описываются их компонентами в системе координат. Даже в повседневной жизни мы естественным образом пользуемся понятием ортогональных проекций в прямоугольной системе координат. Например, если вы спросите у кого-нибудь направление к определенному месту, вам, скорее всего, скажут пройти 40 км на восток и 30 км на север, чем 50 км в направлении 37°37° к северу от востока.
Даже в повседневной жизни мы естественным образом пользуемся понятием ортогональных проекций в прямоугольной системе координат. Например, если вы спросите у кого-нибудь направление к определенному месту, вам, скорее всего, скажут пройти 40 км на восток и 30 км на север, чем 50 км в направлении 37°37° к северу от востока.
В прямоугольной (декартовой) xy -системе координат на плоскости точка на плоскости описывается парой координат ( x , y ). Аналогичным образом вектор A→A→ на плоскости описывается парой его векторных координат. Координата x вектора A→A→ называется его x -компонентой, а y -координата вектора A→A→ называется его y -компонентой. Компонента вектора x представляет собой вектор, обозначаемый A→xA→x. Вектор y -компонента представляет собой вектор, обозначаемый A→yA→y. В декартовой системе компоненты вектора x и y являются ортогональными проекциями этого вектора на оси x и y соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонентов:
Вектор y -компонента представляет собой вектор, обозначаемый A→yA→y. В декартовой системе компоненты вектора x и y являются ортогональными проекциями этого вектора на оси x и y соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонентов:
A→=A→x+A→y.A→=A→x+A→ у.
2.10
Как показано на рис. 2.16, вектор A→A→ является диагональю прямоугольника, где x -компонента A→xA→x является стороной, параллельной оси x , а y -компонента A→yA→y является стороной, параллельной оси y . Компонента вектора A→xA→x ортогональна компоненте вектора A→yA→y.
Рисунок 2.16 Вектор A→A→ на плоскости в декартовой системе координат представляет собой векторную сумму его векторных x — и y -компонент. Компонента вектора A→xA→x размером x является ортогональной проекцией вектора A→A→ на 9.
2.12
Если мы знаем координаты b(xb,yb)b(xb,yb) начальной точки вектора (где b означает «начало») и координаты e(xe,ye)e(xe,ye ) конечной точки вектора (где e означает «конец»), мы можем получить скалярные компоненты вектора, просто вычитая координаты исходной точки из координат конечной точки:
{Ax=xe−xbAy =ye-yb.{Ax=xe-xbAy=ye-yb.
2.13
Пример 2.3 9на
y — ось указывает вертикально вверх. Начало вектора смещения расположено в точке b(6.0, 1.6), а конец вектора смещения расположен в точке e(2. 0, 4.5). Подставьте координаты этих точек в уравнение 2.13, чтобы найти скалярные компоненты DxDx и DyDy вектора смещения D→D→. Наконец, подставьте координаты в уравнение 2.12, чтобы записать вектор смещения в форме компонента вектора.
0, 4.5). Подставьте координаты этих точек в уравнение 2.13, чтобы найти скалярные компоненты DxDx и DyDy вектора смещения D→D→. Наконец, подставьте координаты в уравнение 2.12, чтобы записать вектор смещения в форме компонента вектора.Раствор
Мы определяем xb=6,0xb=6,0, xe=2,0xe=2,0, yb=1,6yb=1,6 и ye=4,5ye=4,5, где физической единицей является 1 см. Скаляр 9)см.
2.14
Это решение показано на рис. 2.17.
Рисунок 2.17 График вектора смещения. Вектор указывает от начальной точки b до конечной точки e .
Значение
Обратите внимание, что физическая единица — здесь 1 см — может быть помещена либо с каждым компонентом непосредственно перед единичным вектором, либо глобально для обоих компонентов, как в уравнении 2.14. Часто последний способ удобнее, потому что он проще.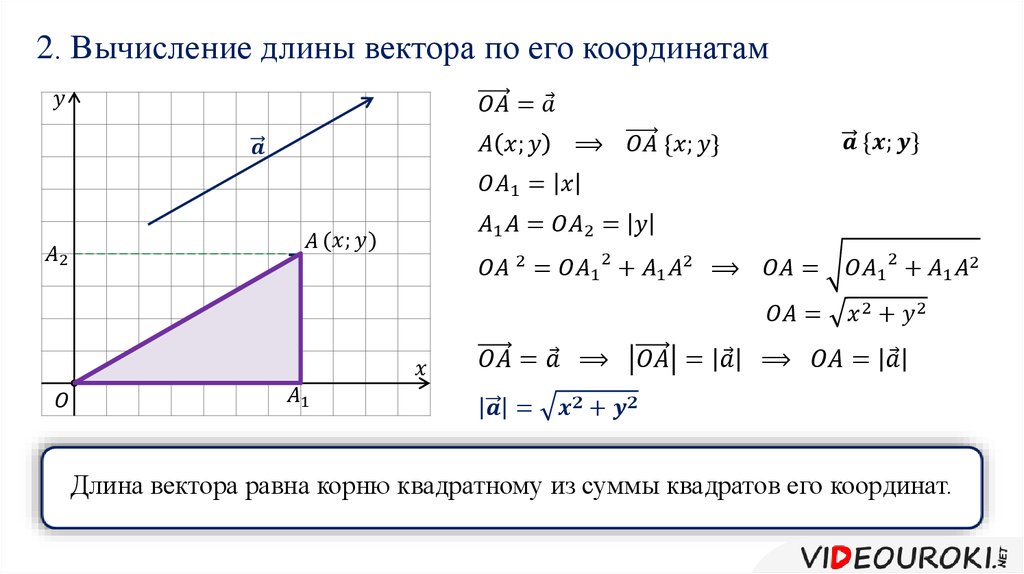 9, который параллелен направлению оси + y -. Следовательно, y -компонентный вектор D→yD→y указывает вверх, как показано на рис. 2.17. Скаляр y -компонента вектора D→D→ равен Dy=+2,9Dy=+2,9. Вектор смещения D→D→ является результатом двух его компонент вектора .
9, который параллелен направлению оси + y -. Следовательно, y -компонентный вектор D→yD→y указывает вверх, как показано на рис. 2.17. Скаляр y -компонента вектора D→D→ равен Dy=+2,9Dy=+2,9. Вектор смещения D→D→ является результатом двух его компонент вектора .
Форма векторной составляющей вектора смещения Уравнение 2.14 говорит нам, что указатель мыши переместился на мониторе на 4,0 см влево и на 2,9 см вверх от своего начального положения.
Проверьте свое понимание 2,4
Синяя муха приземляется на лист миллиметровой бумаги в точке, расположенной на 10,0 см правее его левого края и на 8,0 см выше его нижнего края, и медленно движется к точке, расположенной на расстоянии 5,0 см от левого края и 5,0 см от нижнего края нижний край. Выберите прямоугольную систему координат с началом в левом нижнем углу листа и найдите вектор смещения мухи. Проиллюстрируйте свое решение графиком.
Проиллюстрируйте свое решение графиком.
Зная скалярные компоненты AxAx и AyAy вектора A→A→, мы можем найти его величину A и его дирекционный угол θAθA. Угол направления — или, для краткости, направление — это угол, который вектор образует с положительным направлением на оси x . Угол θAθA измеряется в направлении против часовой стрелки от оси +x к вектору (рисунок 2.18). Поскольку длины A , AxAx и AyAy образуют прямоугольный треугольник, они связаны теоремой Пифагора:
A2=Ax2+Ay2⇔A=Ax2+Ay2.A2=Ax2+Ay2⇔A=Ax2+Ay2.
2,15
Это уравнение работает, даже если скалярные компоненты вектора отрицательны. Направляющий угол θAθA вектора определяется через тангенс функции угла θAθA в треугольнике, показанном на рисунке 2.18:
2.18
Когда вектор лежит либо в первом квадранте, либо в четвертом квадранте, где составляющая AxAxis положительна (рис. 2.19), угол направления θAθA в уравнении 2.16) идентичен углу θθ.
2.19), угол направления θAθA в уравнении 2.16) идентичен углу θθ.
Когда вектор лежит либо в первом квадранте, либо в четвертом квадранте, где составляющая AxAx положительна (рис. 2.19), угол θθ в уравнении 2.16 идентичен углу направления θAθA. Для векторов в четвертом квадранте угол θθ отрицателен, что означает, что для этих векторов угол направления θAθA измеряется на по часовой стрелке от положительной оси x . Точно так же для векторов во втором квадранте угол θθ отрицателен. Когда вектор лежит либо во втором, либо в третьем квадранте, где компонента AxAx отрицательна, угол направления равен θA=θ+180°, θA=θ+180° (рис. 2.19).).
Рисунок
2.19
Скалярные компоненты вектора могут быть положительными или отрицательными. Векторы в первом квадранте (I) имеют обе скалярные компоненты положительные, а векторы в третьем квадранте имеют обе скалярные компоненты отрицательные. Для векторов в квадрантах II и III угол направления вектора равен θA=θ+180°, θA=θ+180°.
Пример 2,4
Величина и направление вектора смещения
Вы перемещаете указатель мыши на мониторе из исходного положения в точке (6,0 см, 1,6 см) к значку, расположенному в точке (2,0 см, 4,5 см). Каковы величина и направление вектора смещения указателя?
Стратегия
В примере 2.3 мы нашли вектор смещения D→D→ указателя мыши (см. уравнение 2.14). Мы идентифицируем его скалярные компоненты Dx=-4,0 смDx=-4,0 см и Dy=+2,9 смDy=+2,9 см и подставляем в уравнения 2.15 и 2.16, чтобы найти звездную величину D и направление θDθD соответственно.
Раствор
Величина вектора D→D→ равна
D=Dx2+Dy2=(−4,0 см)2+(2,9 см)2=(4,0)2+(2,9)2 см=4,9 см. D=Dx2+Dy2=(−4,0 см)2+(2,9 см) )2=(4,0)2+(2,9)см, найти его величину и направление.
Во многих приложениях величины и направления векторных величин известны, и нам нужно найти равнодействующую многих векторов. Например, представьте, что 400 автомобилей движутся по мосту Золотые Ворота в Сан-Франциско при сильном ветре. Каждая машина дает мосту разные толчки в разных направлениях, и мы хотели бы знать, насколько большим может быть результирующий толчок. У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения равнодействующей путем рисования векторов и измерения их длин и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам. Подобного беспокойства не возникает, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе состоит в том, чтобы найти компоненты вектора, когда известны направление и величина вектора.
Например, представьте, что 400 автомобилей движутся по мосту Золотые Ворота в Сан-Франциско при сильном ветре. Каждая машина дает мосту разные толчки в разных направлениях, и мы хотели бы знать, насколько большим может быть результирующий толчок. У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения равнодействующей путем рисования векторов и измерения их длин и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам. Подобного беспокойства не возникает, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе состоит в том, чтобы найти компоненты вектора, когда известны направление и величина вектора.
Вернемся к прямоугольному треугольнику на рис. 2.18. Отношение противолежащего катета AxAx к гипотенузе A является функцией косинуса направляющего угла θAθA, Ax/A=cosθAAx/A=cosθA, а отношение противолежащего катета AyAy к гипотенузе A является функцией синуса θAθA, Ay/A=sinθAAy/A=sinθA.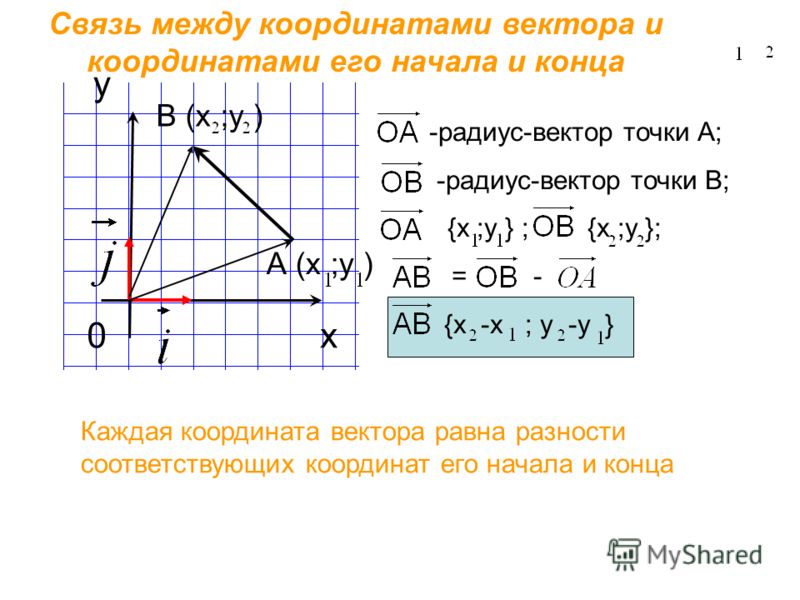 Когда известна величина A и направление θAθA, мы можем решить эти соотношения для скалярных составляющих:
Когда известна величина A и направление θAθA, мы можем решить эти соотношения для скалярных составляющих:
{Ax=AcosθAAy=AsinθA.{Ax=AcosθAAy=AsinθA.
2.17
При расчете компонентов вектора по уравнению 2.17 необходимо соблюдать осторожность при выборе угла. Угол направления θAθA вектора — это угол, измеренный на 90 289 против часовой стрелки на 90 150 от положительного направления по оси 90 289 x 90 150 до вектора. Измерение по часовой стрелке дает отрицательный угол.
Пример 2,5
Компоненты векторов смещения
Группа спасения пропавшего ребенка следует за поисковой собакой по кличке Солдат. Десантник много бродит и делает много пробных обнюхиваний по разным тропам. Солдат в конце концов находит ребенка, и у истории счастливый конец, но его перемещения на разных ногах кажутся действительно запутанными. На одной из ног он проходит 200,0 м на юго-восток, затем бежит на север около 300,0 м.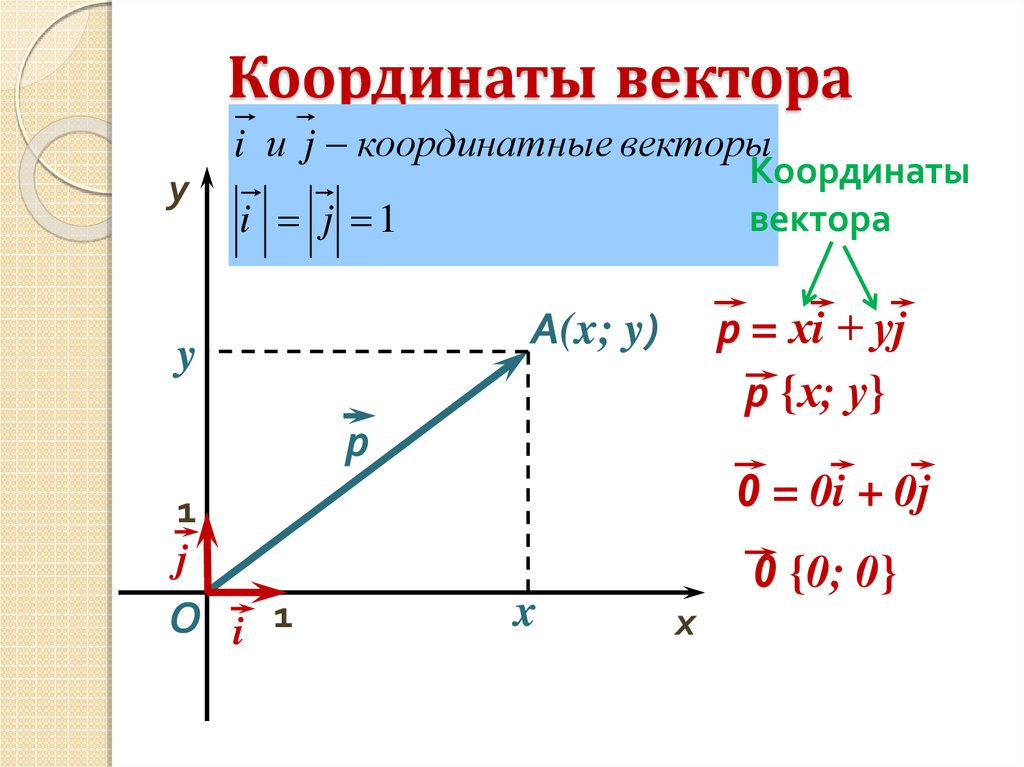 На третьем этапе внимательно исследует запахи на протяжении 50,0 м в направлении 30°30° к западу от севера. На четвертом этапе Trooper идет прямо на юг на 80,0 м, находит свежий запах и поворачивает на 23°23° к западу от юга на 150,0 м. Найдите скалярные компоненты векторов смещения Десантника и его векторов смещения в форме векторных компонент для каждой ноги.
9оси и указывает на север. Десантник делает пять ног, поэтому есть пять векторов смещения. Начнем с определения их величин и углов направления, затем воспользуемся уравнением 2.17, чтобы найти скалярные компоненты смещений, и уравнением 2.12, чтобы найти вектора смещения.
На третьем этапе внимательно исследует запахи на протяжении 50,0 м в направлении 30°30° к западу от севера. На четвертом этапе Trooper идет прямо на юг на 80,0 м, находит свежий запах и поворачивает на 23°23° к западу от юга на 150,0 м. Найдите скалярные компоненты векторов смещения Десантника и его векторов смещения в форме векторных компонент для каждой ноги.
9оси и указывает на север. Десантник делает пять ног, поэтому есть пять векторов смещения. Начнем с определения их величин и углов направления, затем воспользуемся уравнением 2.17, чтобы найти скалярные компоненты смещений, и уравнением 2.12, чтобы найти вектора смещения.
Раствор
На первом участке величина смещения L1=200,0мL1=200,0м и направление юго-восточное. В качестве дирекционного угла θ1θ1 мы можем принять либо 45°45°, измеренные по часовой стрелке с восточного направления, либо 45°+270°45°+270°, измеренные против часовой стрелки с востока. При первом выборе θ1=−45°θ1=−45°. При втором выборе θ1=+315°θ1=+315°. Мы можем использовать любой из этих двух углов. Компоненты
9вдоль оси x и оси y соответственно. Декартову систему координат очень удобно использовать при описании перемещений и скоростей тел и действующих на них сил. Однако это становится громоздким, когда нам нужно описать вращение объектов. При описании вращения мы обычно работаем в полярной системе координат.
При первом выборе θ1=−45°θ1=−45°. При втором выборе θ1=+315°θ1=+315°. Мы можем использовать любой из этих двух углов. Компоненты
9вдоль оси x и оси y соответственно. Декартову систему координат очень удобно использовать при описании перемещений и скоростей тел и действующих на них сил. Однако это становится громоздким, когда нам нужно описать вращение объектов. При описании вращения мы обычно работаем в полярной системе координат.
В полярной системе координат положение точки P на плоскости задается двумя полярными координатами (рис. 2.20). Первая полярная координата — это радиальная координата 9направление показывает, как угол φφ изменяется в направлении против часовой стрелки. Таким образом, точка P , имеющая координаты ( x , y ) в прямоугольной системе, может быть эквивалентно описана в полярной системе координат двумя полярными координатами (r,φ)(r,φ).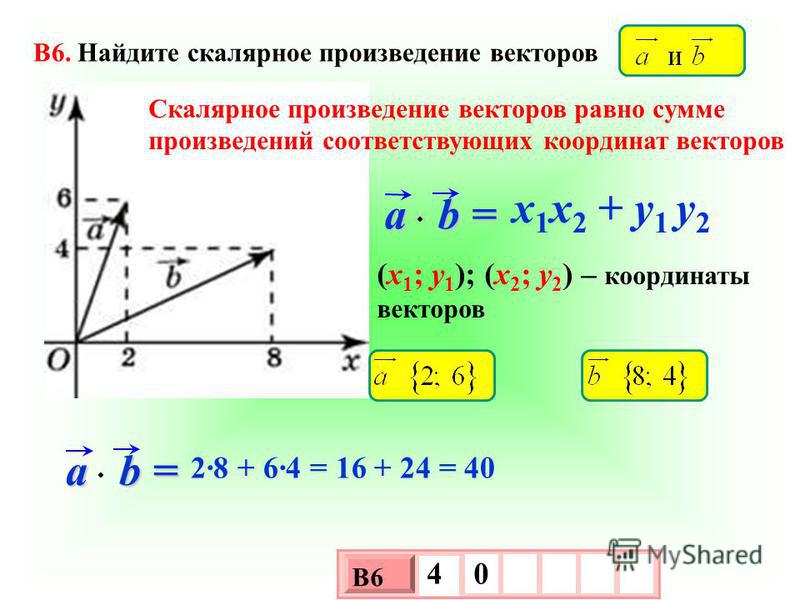 Уравнение 2.17 справедливо для любого вектора, поэтому мы можем использовать его для выражения координат x и y вектора r→r→. Таким образом, мы получаем связь между полярными координатами и прямоугольными координатами точки 9определяет положительное направление вращения углом φφ.
Уравнение 2.17 справедливо для любого вектора, поэтому мы можем использовать его для выражения координат x и y вектора r→r→. Таким образом, мы получаем связь между полярными координатами и прямоугольными координатами точки 9определяет положительное направление вращения углом φφ.
Пример 2,6
Полярные координаты
Кладоискатель находит одну серебряную монету на расстоянии 20,0 м от сухого колодца в направлении 20°20° северной востока и одну золотую монету на расстоянии 10,0 м от колодца в направлении 20°20° северной широты. запад. Каковы полярные и прямоугольные координаты этих находок относительно скважины?
Стратегия
Колодец отмечает начало системы координат, а восток — + 9.0289 x — направление. Мы определяем радиальные расстояния от местоположений до начала координат, которые составляют rS=20,0mrS=20,0м (для серебряной монеты) и rG=10,0mrG=10,0м (для золотой монеты). Чтобы найти угловые координаты, мы конвертируем 20°20° в радианы: 20°=π20/180=π/920°=π20/180=π/9. Мы используем уравнение 2.18, чтобы найти координаты x и y монет.
Чтобы найти угловые координаты, мы конвертируем 20°20° в радианы: 20°=π20/180=π/920°=π20/180=π/9. Мы используем уравнение 2.18, чтобы найти координаты x и y монет.
Раствор
Угловая координата серебряной монеты φS=π/9φS=π/9, тогда как угловая координата золотой монеты φG=π−π/9.=8π/9φG=π−π/9=8π/9. Следовательно, полярные координаты серебряной монеты равны (rS,φS)=(20,0m,π/9)(rS,φS)=(20,0m,π/9), а полярные координаты золотой монеты равны (rG,φG) =(10,0м,8π/9)(rG,φG)=(10,0м,8π/9). Мы подставляем эти координаты в уравнение 2.18, чтобы получить прямоугольные координаты. Для золотой монеты координаты
{xG=rGcosφG=(10,0m)cos8π/9=−9,4myG=rGsinφG=(10,0m)sin8π/9=3,4m⇒(xG,yG)=(−9,4m,3,4m).{xG= rGcosφG=(10,0m)cos8π/9=-9,4myG=rGsinφG=(10,0m)sin8π/9=3,4m⇒(xG,yG)=(-9,4m,3,4m).
Для серебряной монеты координаты
{xS=rScosφS=(20,0m)cosπ/9=18,9myS=rSsinφS=(20,0m)sinπ/9=6,8m⇒(xS,yS)=(18,9m,6,8m).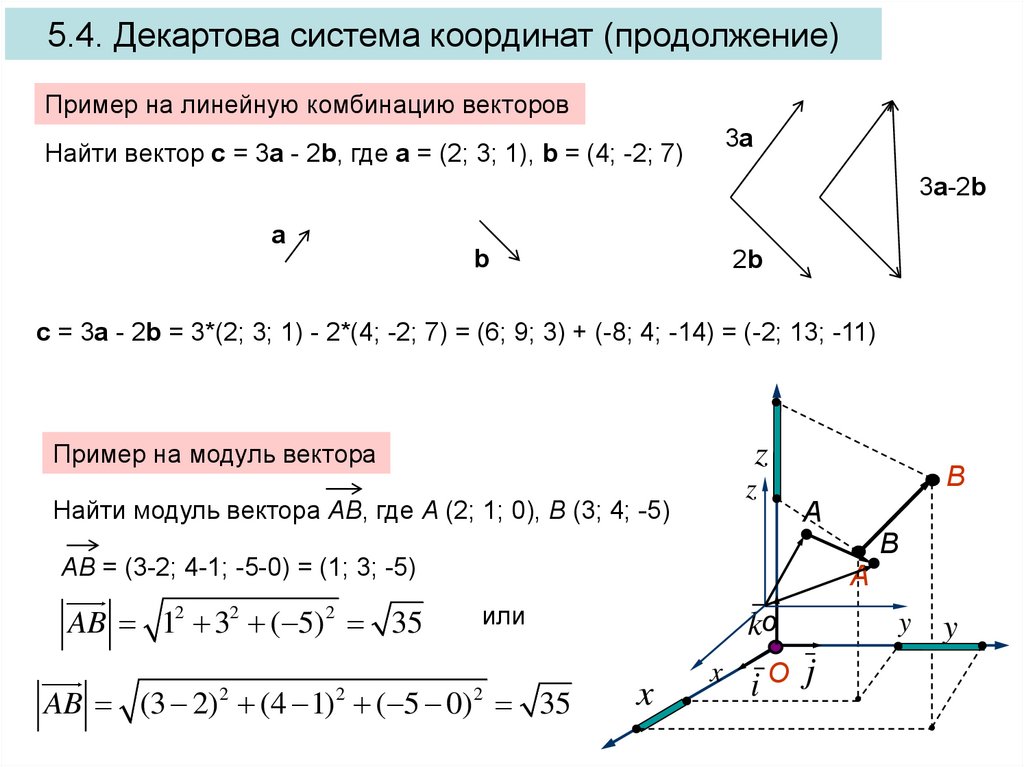 {xS=rScosφS= (20,0m)cosπ/9=18,9myS=rSsinφS=(20,0m)sinπ/9=6,8m⇒(xS,yS)=(18,9m,6,8m).
{xS=rScosφS= (20,0m)cosπ/9=18,9myS=rSsinφS=(20,0m)sinπ/9=6,8m⇒(xS,yS)=(18,9m,6,8m).
Векторы в трех измерениях
Чтобы задать положение точки в пространстве, нам нужны три координаты ( x , y , z ), где координаты x и y задают расположение на плоскости, а координата z дает вертикальное положение над или под плоскостью. Трехмерное пространство имеет три ортогональных направления, поэтому нам нужно не два, а 9.
2,19
Если известны координаты его начала b(xb,yb,zb)b(xb,yb,zb) и конца e(xe,ye,ze)e(xe,ye,ze), его скалярные компоненты равны получается путем взятия их разностей: AxAx и AyAy задаются уравнением 2.13, а z -компонента задается
Az=ze-zb.Az=ze-zb.
2,20
Величина A получается путем обобщения уравнения 2.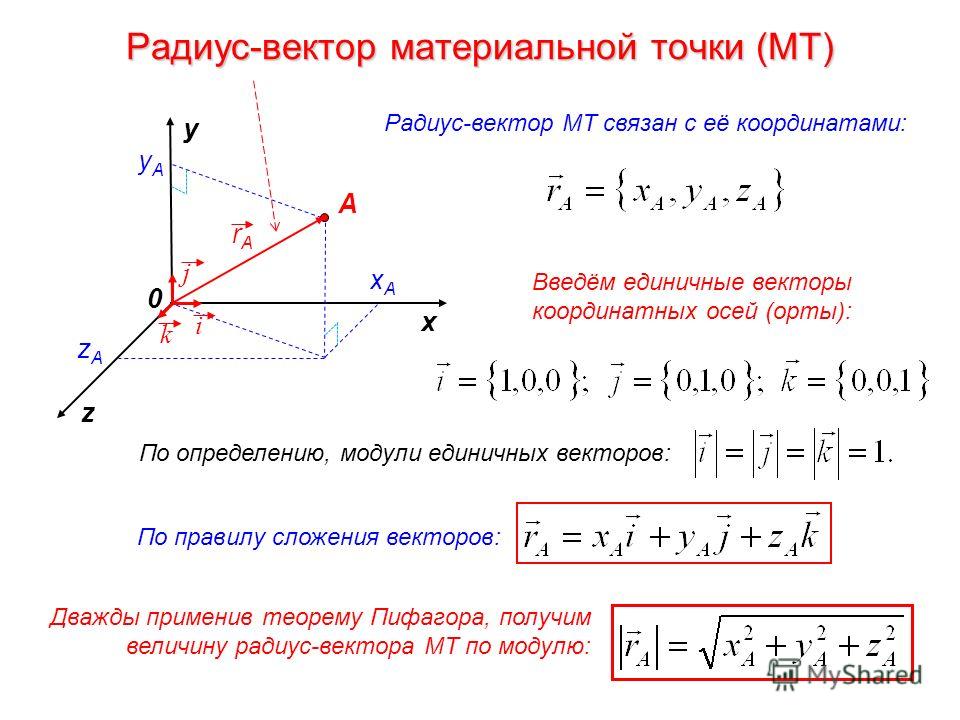 15 на три измерения:
15 на три измерения:
A=Ax2+Ay2+Az2.A=Ax2+Ay2+Az2.
2,21
Это выражение для величины вектора получается из двойного применения теоремы Пифагора. Как видно на рис. 2.22, диагональ в плоскости xy имеет длину Ax2+Ay2Ax2+Ay2, а ее квадрат в сумме с квадратом Az2Az2 дает A2A2. Обратите внимание, что когда z -компонента равна нулю, вектор полностью лежит в xy -плоскости и его описание сводится к двум измерениям.
Рисунок 2,22 Вектор в трехмерном пространстве представляет собой векторную сумму трех его векторных компонент.
Пример 2,7
Взлет дрона
При взлете IAI Heron (рис. 2.23) его положение относительно диспетчерской вышки составляет 100 м над землей, 300 м восточнее и 200 м севернее. Через одну минуту его положение 250 м над землей, 1200 м на восток и 2100 м на север. Каков вектор смещения дрона относительно диспетчерской? Какова величина его вектора смещения?
Каков вектор смещения дрона относительно диспетчерской? Какова величина его вектора смещения?
Рисунок 2,23 Дрон IAI Heron в полете. (кредит: сержант Рейнальдо Рамон, ВВС США) 9, который указывает вверх от земли. Первая позиция дрона — это начало (или, что то же самое, начало) вектора смещения, а его вторая позиция — конец вектора смещения.
Решение
Мы идентифицируем b (300,0 м, 200,0 м, 100,0 м) и e (1200 м, 2100 м, 250 м) и используем уравнения 2.13 и 2.20, чтобы найти скалярные компоненты дрона. вектор смещения:
{Dx=xe-xb=1200,0 м-300,0 м=900,0 м,Dy=ye-yb=2100,0 м-200,0 м=19) м/с, какова величина вектора скорости дрона?
Вектор положения — определение, формула, примеры, часто задаваемые вопросы
Вектор положения используется, чтобы помочь нам найти положение одного объекта относительно другого объекта. Векторы положения обычно начинаются в начале координат, а затем заканчиваются в любой другой произвольной точке. Таким образом, эти векторы используются для определения положения конкретной точки относительно ее начала.
Векторы положения обычно начинаются в начале координат, а затем заканчиваются в любой другой произвольной точке. Таким образом, эти векторы используются для определения положения конкретной точки относительно ее начала.
В этой статье давайте узнаем о векторах положения, их определении, формулах с решенными примерами.
| 1. | Что такое вектор положения? |
| 2. | Как найти вектор положения? |
| 3. | Формула вектора положения |
| 4. | Часто задаваемые вопросы о векторе положения |
Что такое вектор положения?
Вектор положения представляет собой прямую линию, один конец которой прикреплен к телу, а другой конец прикреплен к движущейся точке, и используется для описания положения точки относительно тела. По мере перемещения точки вектор положения будет изменяться по длине или по направлению, или по длине и по направлению одновременно.
Определение вектора положения
Вектор положения определяется как вектор, который указывает либо положение, либо положение любой заданной точки относительно любой произвольной контрольной точки, такой как начало координат. Направление вектора положения всегда указывает от начала этого вектора к заданной точке.
- В декартовой системе координат, если O является началом координат, а P(x 1 , y 1 ) является другой точкой, то вектор положения, направленный из точки O в точку P, может быть представлен как ОП.
- В трехмерном пространстве, если начало координат O = (0,0,0) и P = (x 1 , y 1 , z 1 ), то вектор положения v точки P может быть представлено как: v = x 1 i + y 1 j + z 1 k
Рассмотрим два вектора P и Q с векторами положения p = (2,4) и q = (3, 5) соответственно. Координаты векторов P и Q можно записать в виде: P = (2,4), Q = (3, 5). Давайте рассмотрим начало координат O, как показано на изображении ниже. Мы будем рассматривать частицу, которая движется из точки P в точку Q. Вектор положения частицы можно определить как вектор, который начинается от начала координат до точки, в которой находится частица.
Давайте рассмотрим начало координат O, как показано на изображении ниже. Мы будем рассматривать частицу, которая движется из точки P в точку Q. Вектор положения частицы можно определить как вектор, который начинается от начала координат до точки, в которой находится частица.
На приведенной выше диаграмме вектор положения частицы, когда она находится в точке P, является вектором OP, а когда она находится в точке Q, это вектор OQ.
Как найти вектор положения?
Очень важно сначала определить координаты точки, прежде чем найти вектор положения этой точки. Рассмотрим две точки, A и B, где A = (x 1 , y 1 ) и B = (x 2 , y 2 ).
- Далее найдем вектор положения из точки А в точку В, вектор АВ.
- Чтобы определить этот вектор положения, нам нужно вычесть соответствующие компоненты A из B: AB = (x 2 — x 1 , y 2 — y 1 ) = (x 2 — x 1 ) я + (у 2 — у 1 ) у
Формула вектора положения
Если мы знаем положение любой точки в плоскости xy, то мы можем использовать формулу для определения вектора положения между этими двумя точками. Например, рассмотрим точку A, которая имеет координаты (x k , y k ) в плоскости xy и еще одна точка B, имеющая координаты (x k+1 , y k+1 ).
Например, рассмотрим точку A, которая имеет координаты (x k , y k ) в плоскости xy и еще одна точка B, имеющая координаты (x k+1 , y k+1 ).
- Формула для определения вектора положения от A до B: AB = (x k+1 — x k , y k+1 — y k ).
- Вектор положения AB относится к вектору, который начинается в точке A и заканчивается в точке B.
- Аналогично, если мы хотим найти вектор положения из точки B в точку A, то мы можем использовать: BA = (x к — х к+1 , у к — у к+1 )
Похожие статьи о векторе положения
Ознакомьтесь со следующими страницами, связанными с вектором положения
- Добавление калькулятора векторов
- Калькулятор угла между двумя векторами
- Обработка векторов, указанных в форме i-j
- Неравенство треугольников в векторах
- Вычитание двух векторов
Важные примечания по вектору положения
Ниже приведен список нескольких точек, которые следует помнить при изучении вектора положения относительно любой произвольной точки отсчета, такой как начало координат.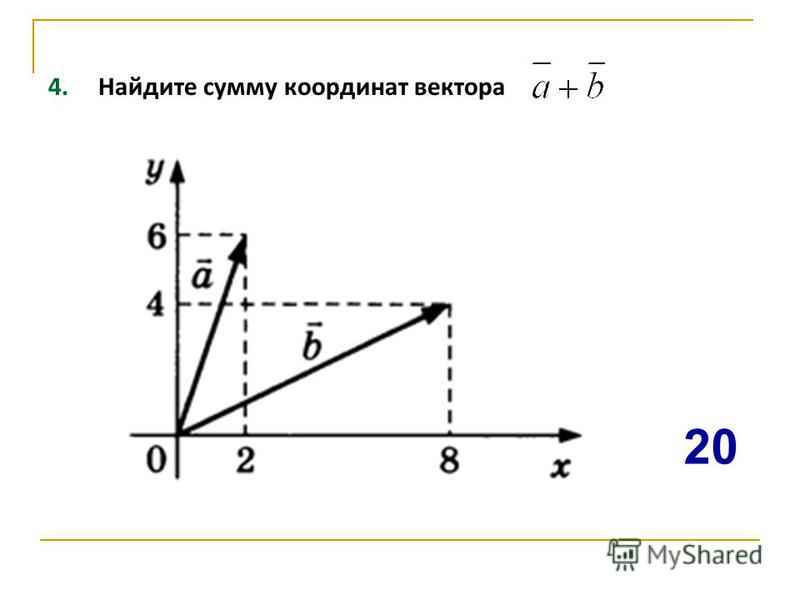
Примеры вектора положения
Пример 1: Для двух точек P = (-4, 6) и Q = (5, 11) определите вектор положения PQ.
Решение: Если в системе координат xy заданы две точки, то мы можем использовать следующую формулу для нахождения вектора положения PQ: — y 1 )Где (x 1 , y 1 ) представляет координаты точки P и (x 2 , y 2 ) представляет координаты точки Q. Таким образом, просто подставив значения точек P и Q в приведенное выше уравнение, мы можем найти вектор положения PQ:
PQ = (5-(-4), 11-6)
PQ = ((5+ 4 ), 11-6)
PQ = (9, 5) = 9 i + 5 j
Таким образом, вектор положения PQ эквивалентен вектору, который начинается в начале координат. Этот вектор направлен в точку на 9 единиц вправо по оси x и на 5 единиц вверх по оси y.

Пример 2: Для двух точек P = (-4, 6) и Q = (5, 11) определите вектор положения QP.
Решение: Если в системе координат xy заданы две точки, то мы можем использовать следующую формулу для нахождения вектора положения QP: — y 2 )
Где (x 1 , y 1 ) представляет координаты точки P и (x 2 , y 2 ) представляет координаты точки Q. Обратите внимание, что вектор положения QP представляет собой вектор, направленный от точки Q к точке P. Он отличается от вектора положения PQ, который направлен от P к Q. Таким образом, просто подставив значения точек P и Q в приведенное выше уравнение , мы можем найти вектор положения QP:
QP = (-4-5, 6-11)
QP = (-9, -5) = -9 i — 5 j
Таким образом, вектор положения QP равен эквивалентен вектору, который начинается в начале координат. Этот вектор направлен в точку 9единиц влево по оси x и на 5 единиц вниз по оси y.

перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по позиционному вектору
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о векторе положения
Что такое
вектор положения в математике?Вектор положения представляет собой прямую линию, один конец которой прикреплен к телу, а другой конец прикреплен к движущейся точке, и используется для описания положения точки относительно тела. Направление вектора положения всегда указывает от начала этого вектора к заданной точке.
Как найти вектор положения?
Очень важно сначала определить координаты точки, прежде чем найти вектор положения этой точки. Рассмотрим две точки, A и B, где A = (x 1 , y 1 ) и B = (x 2 , y 2 ).
Рассмотрим две точки, A и B, где A = (x 1 , y 1 ) и B = (x 2 , y 2 ).
- Далее найдем вектор положения из точки А в точку В, вектор АВ.
- Чтобы определить этот вектор положения, нам нужно вычесть соответствующие компоненты A из B: AB = (x 2 — x 1 , y 2 — у 1 )
В чем разница между вектором положения и вектором смещения?
Вектор положения определяется как вектор, указывающий либо положение, либо местоположение любой заданной точки относительно любой произвольной контрольной точки, такой как начало координат. Принимая во внимание, что вектор смещения помогает нам найти изменение вектора положения данного объекта.
Где всегда начинается вектор положения?
Вектор положения начинается в начале координат и заканчивается в любой другой произвольной точке. Они используются для определения положения точки относительно начала координат.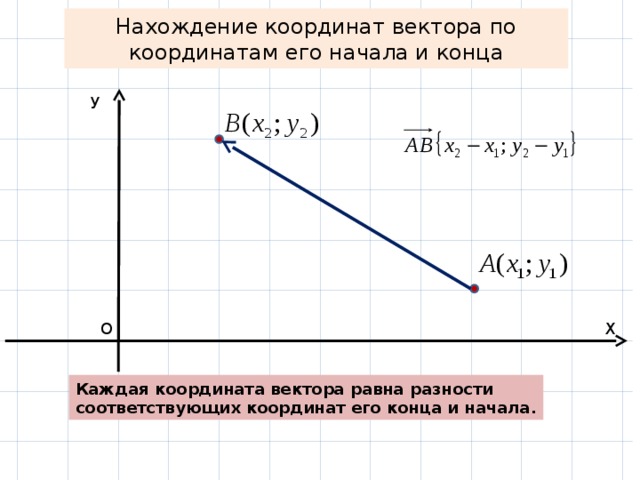
В чем разница между вектором положения и единичным вектором?
Вектор считается единичным вектором, если он используется для указания только направления и имеет величину, равную 1. Для направления не требуется величина, поэтому величина единичного вектора всегда равна 1. A вектор положения определяется как вектор, который указывает либо положение, либо местоположение любой заданной точки относительно любой произвольной опорной точки, такой как начало координат.
Какая формула для вектора положения?
Если мы знаем положение любой точки в плоскости xy, то мы можем использовать формулу для определения вектора положения между этими двумя точками. Например, рассмотрим точку A с координатами (x k , y k ) в плоскости xy и другую точку B с координатами (x k+1 , y k+ 1 ). Формула для определения вектора положения от A до B: AB = (x k+1 — x k , y к+1 — у к ).
Является ли смещение вектором положения?
Нет, смещение не является вектором положения. Вектор положения используется, чтобы помочь нам найти местоположение одного объекта относительно другого объекта. Важно знать положение тела, когда мы описываем его движение. Но тогда вектор смещения можно определить как изменение или вариацию заданного вектора положения.
Изменение базиса — Учебные пособия по расчету
Изменение базиса — Учебное пособие по расчету HMCПусть $V$ — векторное пространство, и пусть $S = \{{\bf v_1,v_2, \ldots, v_n}\}$ — множество векторов в $V$. Напомним, что $S$ образует базис для $V$, если выполняются следующие два условия: пусть $V$ — векторное пространство и пусть $S = \{{\bf v_1,v_2, \ldots, v_n}\} $ — набор векторов в $V$. Напомним, что $S$ образует базис для $V$, если выполняются следующие два условия:
Если $S = \{{\bf v_1,v_2, \ldots, v_n}\}$ является базисом для $V $, то каждый вектор ${\bf v} \in V$ может быть выражен однозначно как линейная комбинация ${\bf v_1,v_2, \ldots, v_n}$: $$ {\bf v} = c_1{\bf v_1} + c_2{\bf v_2} + \cdots + c_n{ \bf v_n}. $$ Думайте о $\left[\begin{array}{c} c_1\\ c_2\\ \vdots \\ c_n \end{array}\right]$ как о координатах относительного ${\bf v}$ к базе $S$. Если $V$ имеет размерность , это количество векторов, необходимых для формирования основы. $n$, то каждый набор из $n$ линейно независимых векторов в $V$ образует базис для $V$. В каждом приложении у нас есть выбор, какую основу мы используем. В этом уроке мы опишем преобразование координат векторов при смене базиса. 92$. Для вектора ${\bf v} \in V$ по заданным его координатам $[{\bf
v}]_B$ в базисе $B$ мы хотели бы иметь возможность выразить ${\bf v}$ в
его координат $[{\bf v}]_{B’}$ в базисе $B’$, и наоборот.
$$ Думайте о $\left[\begin{array}{c} c_1\\ c_2\\ \vdots \\ c_n \end{array}\right]$ как о координатах относительного ${\bf v}$ к базе $S$. Если $V$ имеет размерность , это количество векторов, необходимых для формирования основы. $n$, то каждый набор из $n$ линейно независимых векторов в $V$ образует базис для $V$. В каждом приложении у нас есть выбор, какую основу мы используем. В этом уроке мы опишем преобразование координат векторов при смене базиса. 92$. Для вектора ${\bf v} \in V$ по заданным его координатам $[{\bf
v}]_B$ в базисе $B$ мы хотели бы иметь возможность выразить ${\bf v}$ в
его координат $[{\bf v}]_{B’}$ в базисе $B’$, и наоборот.
Предположим, что базисные векторы ${\bf u’}$ и ${\bf w’}$ для $B’$ имеют следующие координаты относительно базиса $B$:
\begin{выравнивание*} ~[{\bf u’}]_B & = & \left[\begin{array}{c} a \\ b \end{массив}\right] \qquad \\ ~[{\bf w’}]_B & = & \left[\begin{array}{c} c \\ d \end{массив}\right]. \qquad \end{выравнивание*}
Это означает, что \begin{выравнивание*} {\bf u’} & = & a{\bf u} + b{\bf w} \\ {\bf ш’} & = & c{\bf u} + d{\bf ш} \end{выравнивание*}
изменение матрицы координат с $B’$ на $B$ $$ P = \left[\begin{array}{cc} a & c \\ b & d \\ \end{array} \right ] $$ определяет изменение координат ${\bf v} \in V$ при замене базиса с $B’$ на $B$. {-1} = \left[\begin{массив}{cc}
\frac{1}{5} & \frac{2}{5} \\
-\frac{1}{5} и \frac{3}{5}
\конец{массив}\справа],
$$
мы можем убедиться, что
$$
[{\bf v}]_{B’} = \left[\begin{массив}{cc}
\frac{1}{5} & \frac{2}{5} \\
-\frac{1}{5} и \frac{3}{5}
\end{массив}\right]\left[\begin{массив}{c}
4\3
\end{массив}\right] = \left[\begin{массив}{c}
2\1
\конец{массив}\справа]
$$
с чего мы начали.
{-1} = \left[\begin{массив}{cc}
\frac{1}{5} & \frac{2}{5} \\
-\frac{1}{5} и \frac{3}{5}
\конец{массив}\справа],
$$
мы можем убедиться, что
$$
[{\bf v}]_{B’} = \left[\begin{массив}{cc}
\frac{1}{5} & \frac{2}{5} \\
-\frac{1}{5} и \frac{3}{5}
\end{массив}\right]\left[\begin{массив}{c}
4\3
\end{массив}\right] = \left[\begin{массив}{c}
2\1
\конец{массив}\справа]
$$
с чего мы начали.
В следующем примере мы вводим третий базис, чтобы посмотреть на отношения между двумя нестандартными базами .
Пример
Пусть $B” = \left\{ \left[ {2 \top 1} \right],\left[ {1 \top 4} \right]\right\}$. Чтобы найти изменение матрицы координат из базиса $B’$ из предыдущего примера в $B”$, сначала выразим базисные векторы $\left[ {3 \atop 1} \right]$ и $\left[ { -2 \поверх 1} \справа]$ $B’$ как линейные комбинации базисных векторов $\left[ {2 \поверх 1} \справа]$ и $\left[ {1 \поверх 4} \справа] $ of $B”$: \begin{eqnarray*} \mbox{Set }\left[ \begin{array}{c} 3 \\ 1 \end{array}\right] & = & a\left[\begin {array}{c} 2 \\ 1 \end{массив}\right] + b\left[\begin{array}{c} 1 \\ 4 \end{массив}\right] \\ \left[\begin {array}{c} -2 \\ 1 \end{массив}\right] & = & c \left[\begin{array}{c} 2 \\ 1 \end{массив}\right] + d\left [\begin{array}{c} 1 \\ 4 \end{array}\right] \end{eqnarray*} и решить полученные системы r $a,b,c,$ и $d$: \begin{ eqnarray*} \left[ \begin{array}{c} 3 \\ 1 \end{массив}\right] & = & \frac{11}{7} \left[\begin{array}{c} 2 \ \ 1 \end{массив}\right] – \frac{1}{7}\left[\begin{array}{c} 1 \\ 4 \end{массив}\right] \\ \left[\begin{ array}{c} -2 \\ 1 \end{array}\right] & = & \frac{- 9}{7}\left[\begin{array}{c} 2 \\ 1 \end{массив}\right] + \frac{4}{7}\left[\begin{array}{c} 1 \\ 4 \end{array}\right] \end{eqnarray*} Таким образом, матричная форма перехода $B’$ в $B”$ равна $$ \left[\begin{array}{cc} \frac{11}{ 7} & \frac{-9}{7} \\ \frac{-1}{7} & \frac{4}{7} \end{массив}\right]. $$ Вектор ${\bf v}$ с координатами $\left[ {2 \atop 1} \right]$ относительно базиса $B’$ имеет координаты $$ \left[\begin{array}{cc} \frac{11}{7} & \frac{-9}{7} \\ \frac{-1}{9} & \frac{4}{7} \end{массив}\right]\left[\ begin{array}{c} 2 \\ 1 \end{array}\right] = \left[\begin{array}{c} \frac{13}{7} \\ \frac{2}{7} \ end{array}\right] $$ относительно базиса $B”$. Вернемся к стандартному базису: $$ [ {\bf v} ]_B = \frac{13}{7}\left[\begin{array}{c} 2 \\ 1 \end{array}\right ] + \frac{2}{7}\left[\begin{array}{c} 1 \\ 4 \end{array}\right] = \left[\begin{array}{c} 4 \\ 3 \ end{array}\right], $$, что согласуется с результатами предыдущего примера.
$$ Вектор ${\bf v}$ с координатами $\left[ {2 \atop 1} \right]$ относительно базиса $B’$ имеет координаты $$ \left[\begin{array}{cc} \frac{11}{7} & \frac{-9}{7} \\ \frac{-1}{9} & \frac{4}{7} \end{массив}\right]\left[\ begin{array}{c} 2 \\ 1 \end{array}\right] = \left[\begin{array}{c} \frac{13}{7} \\ \frac{2}{7} \ end{array}\right] $$ относительно базиса $B”$. Вернемся к стандартному базису: $$ [ {\bf v} ]_B = \frac{13}{7}\left[\begin{array}{c} 2 \\ 1 \end{array}\right ] + \frac{2}{7}\left[\begin{array}{c} 1 \\ 4 \end{array}\right] = \left[\begin{array}{c} 4 \\ 3 \ end{array}\right], $$, что согласуется с результатами предыдущего примера.
Вращение осей координат
Предположим, мы получаем новую систему координат из стандартной
прямоугольной системе координат, вращая оси против часовой стрелки на
угол $\theta$. Новый базис $B’ = \left\{{\bf u’, v’}\right\}$
единичных векторов вдоль осей $x’$ и $y’$ соответственно, имеет
координаты
\begin{выравнивание*}
~[{\bf u’}]_B & = & \left[\begin{массив}{c}
\cos\тета \\ \sin\тета
\конец{массив}\справа] \\
~[{\bf v’}]_B & = & \left[\begin{массив}{c}
-\sin\theta \\ \cos\theta
\end{массив} \right]
\end{выравнивание*}
в исходной системе координат.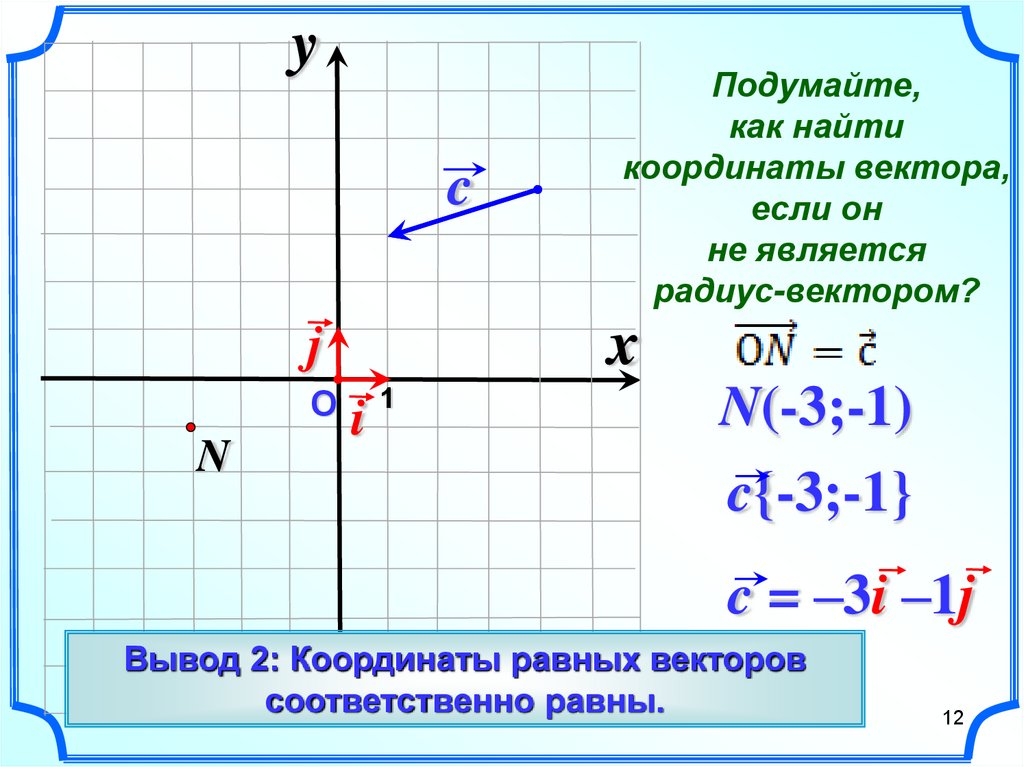

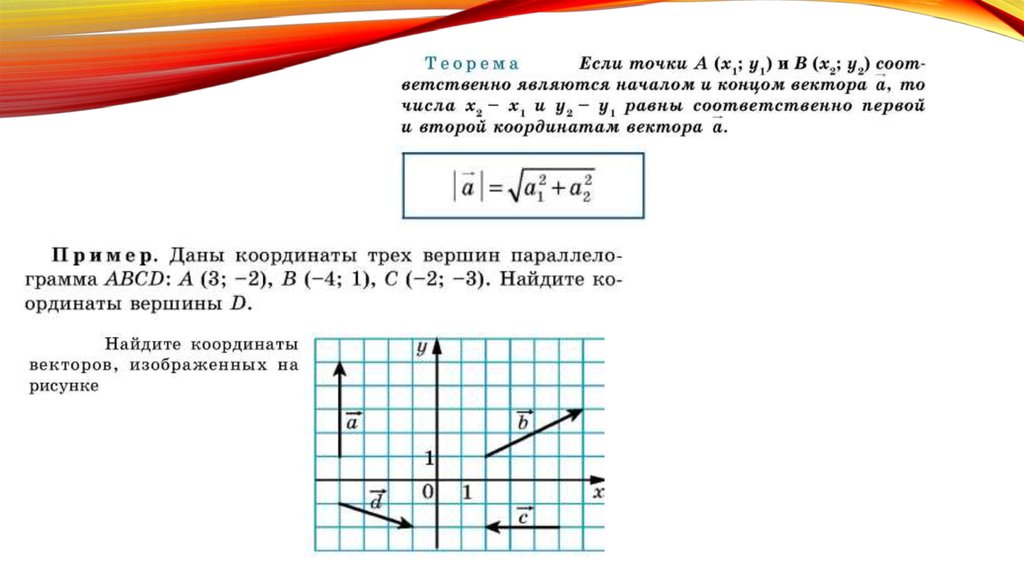




 е. , $$\overrightarrow{OP}=p_1 \cdot \overrightarrow{u}+p_2 \cdot \overrightarrow{v}$$
е. , $$\overrightarrow{OP}=p_1 \cdot \overrightarrow{u}+p_2 \cdot \overrightarrow{v}$$
