Касательная. Задачи на касательную | Статья в журнале «Молодой ученый»
Чтобы правильно и рационально решать задачи, связанные с уравнением касательной, нужно четко понимать, что такое касательная, владеть техникой составления уравнения касательной к графику функции и представлять себе, для решения каких задач (в том числе и задач с параметрами) можно использовать метод касательной.
Опр. 1. Касательной к графику функции у = f(x) называется предельное положение секущей MN при (рис. 1).
Рис. 1
Касательная к кривой может иметь с ней несколько общих точек или пересекать ее. Можно дать и другое определение касательной к кривой.
Опр. 2. Касательной к графику функции у = f(x) в точке A0(x0; f(x0)) называется прямая, проходящая через точку

Уравнение касательной к кривой у = f(x) в точке с абсциссой х0имеет вид: .
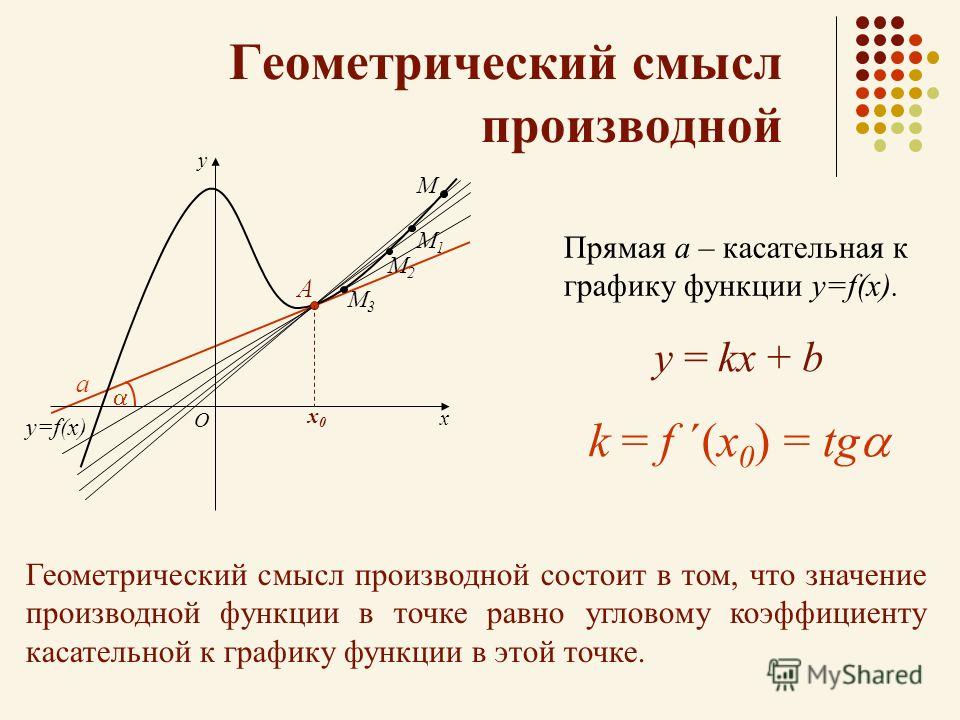
Между понятием касательной и понятие производной имеется тесная связь. Геометрический смысл производной можно выразить так: если функция у = f(x) в точке х0 имеет производную, то в точке с этой абсциссой определена касательная к графику функции , причем ее угловой коэффициент равен . Вывод: если в точке х0 есть производная функции ,
то в точке с этой абсциссой есть касательная к графику функции и наоборот; если в точке х0 нет производной функции , то в точке с этой абсциссой нет касательной к графику функции и наоборот.
Укажем
случаи, когда
функция не имеет в точке касательной, и, следовательно, не
имеет и производной. Таких случаев три: угловая точка, точка
возврата, узловая точка
(рис. 2 а, б, в). Особо
отметим случай, когда в точке функция имеет бесконечную
производную (рис. 2 г).
угловая точка точка возврата узловая точка
а) б) в) г)
Рис. 2
Рассмотрим решение некоторых задач.
Задачи, связанные с определением того, является ли прямая у
Находим общие точки графиков, т. е. решаем уравнение f(x) = kx + b, а затем для каждого из его решений вычисляем .
 В тех случаях, когда
= k,
имеет место касание, в других —
пересечение.
В тех случаях, когда
= k,
имеет место касание, в других —
пересечение.Находим корни уравнения = k и для каждого из них проверяем, выполняется ли равенство f(x) = kx + b. При его выполнении получаем абсциссы точек касания.
Обобщая оба способа, заметим, что для того чтобы прямая у = kx + b была касательной к графику функции у = f(x), необходимо и достаточно существование хотя бы одного числа х0, для которого выполняется система
При каких значениях b прямая у = 3х +b является касательной к графику функции у =?
Решение. Записав условие касания получим
Ответ:
.
При каких значениях а прямая у=ах+2 является касательной к графику функции
Указание.
Ответ: а = e-3
При каких значениях а прямая является касательной к графику функции
Указание.
Ответ: а = 7 или а = -1.
Является ли прямая касательной к графику функции ? Если является, то найти координаты точки касания.
Решение. Пусть . Из условия следует, что должны выполняться равенство , где - возможная абсцисса точки касания. Имеем:
Если теперь
составить уравнение касательной к графику заданной функции в каждой
из двух найденных точек, то окажется, что в точке
как раз и получится
. Значит, точка касания имеет координаты (1;-1).
Значит, точка касания имеет координаты (1;-1).
К графику функции проведена касательная, параллельная прямой . Найти ординату точки касания.
Решение. . Абсцисса интересующей нас точки касания удовлетворяет уравнению . Имеем:
Таким образом, . Значит, - абсцисса точки касания. Чтобы найти ординату точки касания преобразуем выражение, задающее функцию:
Ответ: 1.
Написать уравнение всех касательных к графику функции , параллельных прямой .
Решение.
Так как касательная должна быть параллельна прямой
,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
.
Отсюда
или
.
Ответ: ,.
Найти все значения , при каждом из которых касательная к графикам функций и в точках с абсциссой параллельны.
Решение. Известно, что тангенс угла наклона касательной к графику функций в точке с абсциссой равен . Следовательно, все искомые значения будут корнями уравнения , откуда . Используя формулу разности синусов углов, будем иметь . Решая полученное уравнение, получаем
Найти расстояние между касательными к графику функции , расположенными параллельно оси .
Решение. Найдем критические точки заданной функции:
Так как,
производная в точках
и
равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
.
Итак, расстояние d между касательными, параллельными оси , равно
С составлением уравнения касательной, параллельной данной прямой, связана задача о нахождении кратчайшего расстояния между графиком некоторой функции f(x) и прямой .
Во многих случаях удается найти касательную к графику , параллельную данной прямой и делящую плоскость на две части, в одной из которых расположен график функции, а в другой — заданная прямая. Тогда кратчайшим расстоянием между графиком функции и прямой является расстояние от точки М(х0; у
Найти кратчайшее расстояние между параболой и прямой
Решение. Убедившись, что графики не имеют общих
точек (уравнение
не имеет решений), запишем
уравнение такой касательной к графику функции
,
которая параллельна прямой
Уравнение касательной имеет
вид
касание происходит в точке
Прямая у =
х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
.
Убедившись, что графики не имеют общих
точек (уравнение
не имеет решений), запишем
уравнение такой касательной к графику функции
,
которая параллельна прямой
Уравнение касательной имеет
вид
касание происходит в точке
Прямая у =
х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
.
Ответ:
Довольно сложной является задача составления уравнения всех касательных к графику функции у = f(x), проходящих через заданную точку М(х0; у0), вообще говоря, не лежащую на графике. Приведем алгоритм решения этой задачи.
1. Составляем уравнение касательной к графику функции у = f(x) в произвольной точке графика с абсциссой t:
2. Решаем
относительно t
уравнение
и для каждого его
решения t
записываем
соответствующую
касательную в виде
.
Решаем
относительно t
уравнение
и для каждого его
решения t
записываем
соответствующую
касательную в виде
.
Написать уравнение всех касательных к графику функции , проходящих через точку
Указание.
Уравнение касательной в точке с абсциссой t
имеет вид
.
Так как эта
касательная проходит через точку
(2; -2), то
,
откуда
.
Ответ: .
Найти площадь треугольника, образованного касательными, проведенными к графику функции через точку и секущей, проходящей через точки касания.
Указание.
Уравнение
дает два
решения: t1
= 1, t2
= 4. Таким
образом, точки K1
(1;1) и
K2(4;2)
являются точками касания.
Ответ: 0,25.
Говорят, что
прямая
является общей касательной графиков функции
и
,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
является общей касательной графиков функций
(в точке М(2; 5) и
(в точке K(0,5;
-1)). Заметим, что графики функций
и
имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
.
Доказать, что параболы и имеют в их общей точке общую касательную. Найти уравнение этой общей касательной. Решение. Уравнение имеет единственный корень х=2, т. е. параболы имеют единственную общую точку М(2;0).
 Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
и
.
Далее составляем уравнение касательной.
Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
и
.
Далее составляем уравнение касательной.
Ответ:.
В завершении рассмотрим решение еще нескольких задач на касательную с параметром.
При каких значениях параметра касательная к графику функции в точке проходит через точку (2;3)?
Решение. Составим уравнение касательной к графику заданной функции в точке : Так как эта прямая проходит через точку (2;3), то имеет место равенство , откуда находим: .
Может ли касательная к кривой в какой-либо ее точке составлять острый угол с положительным направлением оси ?
Решение.
Найдем производную функции
.
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
Ответ: Не может.
Найти значение параметра , при котором касательная к графику функции в точке проходит через точку М(1;7).
Решение. Пусть тогда . Составим уравнение касательной:
По условию эта касательная проходит через точку М(1;7), значит, , откуда получаем:
При каких значениях параметра прямая является касательной к графику функции ?
Решение. Из условия следует, что должно выполнятся равенство где абсцисса точки касания. Значит, и связаны между собой равенством (1). Составим уравнение касательной к графику заданной функции в точке
Из условия
следует, что должно выполняться равенство
. Решив это уравнение, получим
.
Тогда из (1) получаем, что
.
Решив это уравнение, получим
.
Тогда из (1) получаем, что
.
При каком значении прямая является касательной у графику ?
Решение. Так как прямая является касательной к графику функции , то в точке касания угловой коэффициент касательной равен 3. Но угловой коэффициент касательной равен значению производной функции в этой точке, то есть , откуда , следовательно, - абсцисса точки касания. Найдем теперь из условия равенства значений функций и при . Имеем , откуда .
При каких значениях параметра а касательные к графику функции , проведенные в точках его пересечения с осью оx, образуют между собой угол 60о?
Решение.
В этой задаче, как и в предыдущих, речь идет о касательных к графику
функции. Составлять уравнение касательной не надо, достаточно
использовать геометрический смысл производной, то есть угловые
коэффициенты касательных. Графиком данной функции является парабола с
ветвями, направленными вверх, пересекающая ось оx
в двух точках (случай а=0
нас не устраивает):
и
учитываем,
что х2>0
(рис. 3)
Составлять уравнение касательной не надо, достаточно
использовать геометрический смысл производной, то есть угловые
коэффициенты касательных. Графиком данной функции является парабола с
ветвями, направленными вверх, пересекающая ось оx
в двух точках (случай а=0
нас не устраивает):
и
учитываем,
что х2>0
(рис. 3)
Рис. 3
Касательные АМ
и ВМ пересекаются под углом 60о
в точке М, лежащей на оси параболы, причем возможны два случая: либо
,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен
Далее имеем:
.
Таким образом, получаем, что
,
то
.
Во втором случае
,
поэтому угол между касательной АО и остью ох
равен 150о. Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
.
Таким образом, получаем, что
,
то есть
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
.
Таким образом, получаем, что
,
то есть
Ответ: .
Литература:
Далингер, В.А. Начала математического анализа в задачах [Текст]: учебное пособие / В.А. Далингер. – Омск: Изд-во ГОУ ОМГПУ, 2009. – 312 с.
Звавич, Л.И. Алгебра и начала анализа. 8-11 кл. [Текст]: пособие для школ и классов с углубл. изучением математики / Л. И. Звавич, Л.Я. Шляпочник, М.В. Чинкина.– М.: Дрофа, 1999. – 352 с.
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Определение 1Угол наклона прямой y=kx+b называется угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.
На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Определение 2Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
- Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
- Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
- Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
- Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.

Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α — красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.
Определение 4Получаем формулу для нахождения секущей вида:
k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) — это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Определение 5Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0), с наличием отрезка, который имеет множество значений х, близких к x0.
Пример 1Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y=2x сливается с прямой у=х+1.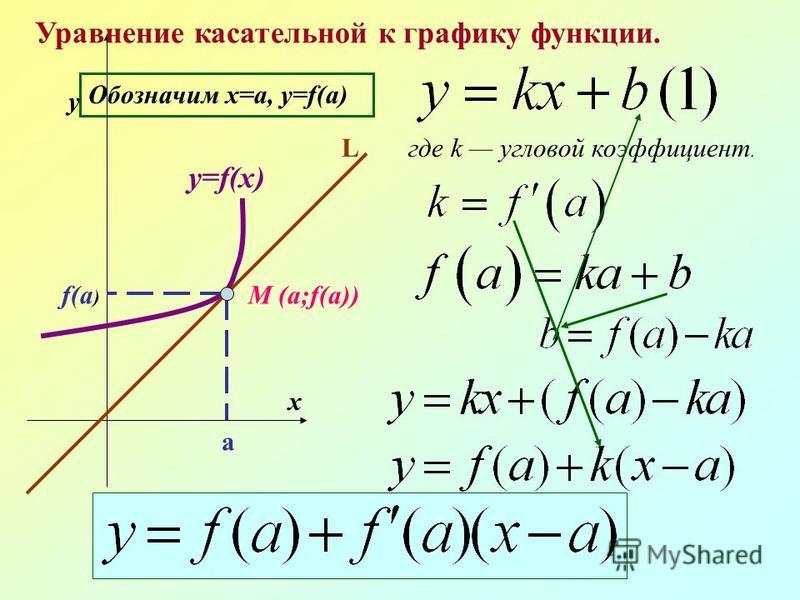
Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.
Определение 6Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.
То есть получаем, что f’(x) может существовать в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной в точке равняется производной в точке x0. Тогда получаем, что kx=f'(x0).
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.
Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).
Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).
Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу — kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
Пример 2Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке с координатами (1; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.
Необходимо найти производную в точке со значением -1. Получаем, что
y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33
Значение f’(x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.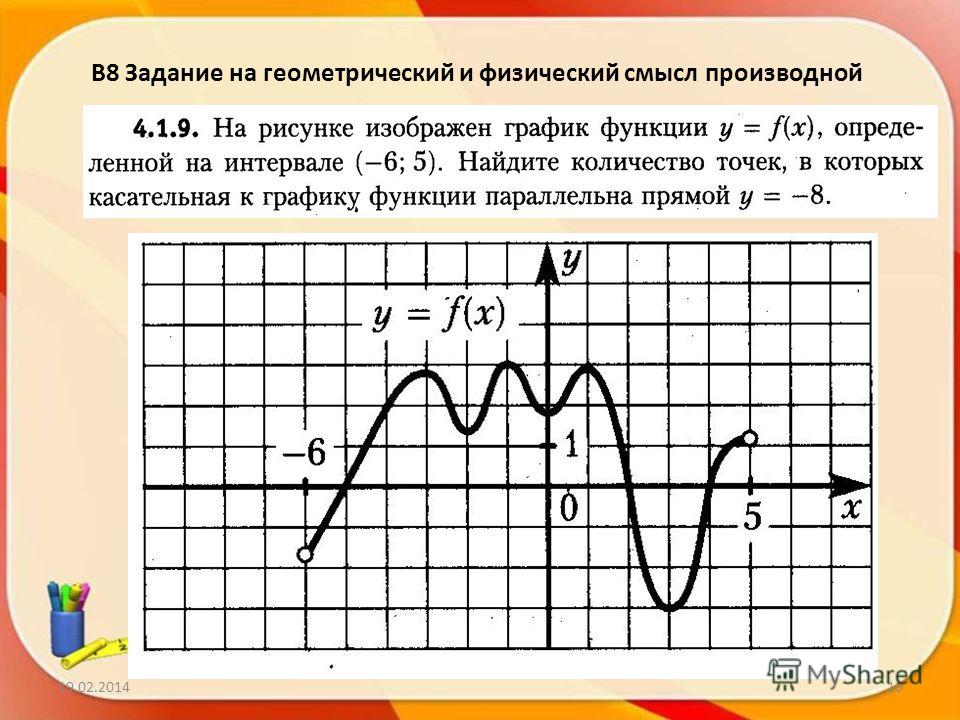
Тогда kx=tg αx=y'(x0)=33
Отсюда следует, что αx=arctg33=π6
Ответ: уравнение касательной приобретает вид
y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Пример 3Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45
Если x0=1, тогда f’(x) не определена, но пределы записываются как limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).
Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.
Для наглядности изобразим графически.
Пример 4Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где
- Касательная не существует;
- Касательная располагается параллельно ох;
- Касательная параллельна прямой y=85x+4.
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что
y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)
Необходимо продифференцировать функцию. Имеем, что
y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)
Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:
limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3
Вычисляем значение функции в точке х=-2, где получаем, что
- y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.

- Касательная параллельна ох, когда угловой коэффициент равняется нулю. Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.
Решим:
-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2 15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞
Вычисляем соответствующие значения функции
y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43
Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны.
 Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0
Другое уравнение имеет два действительных корня, тогда
15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞
Перейдем к нахождению значений функции. Получаем, что
y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83
Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.
Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные в точках -1; 415, 5; 83.
Возможно существование бесконечного количества касательных для заданных функций.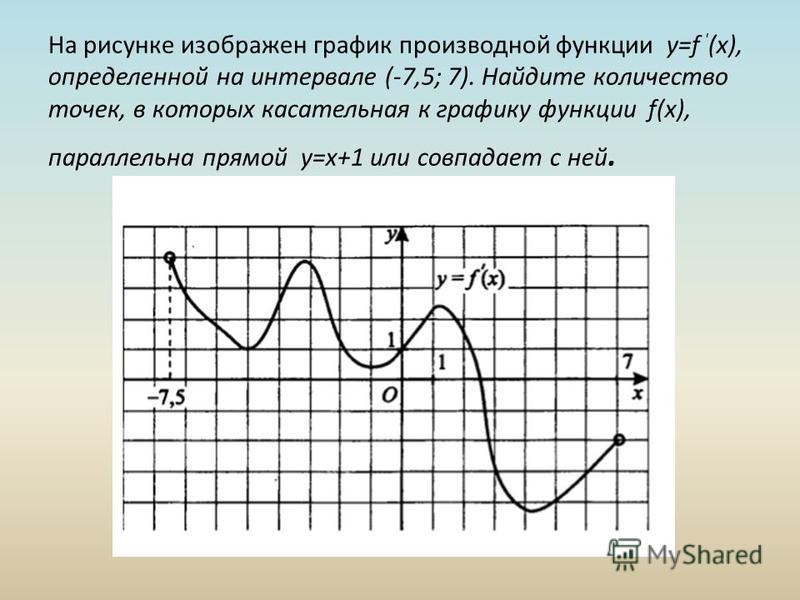
Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x0 получаем, что kx=y'(x0). Из данного равенства найдем значения х для точек касания.
Получаем, что
y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.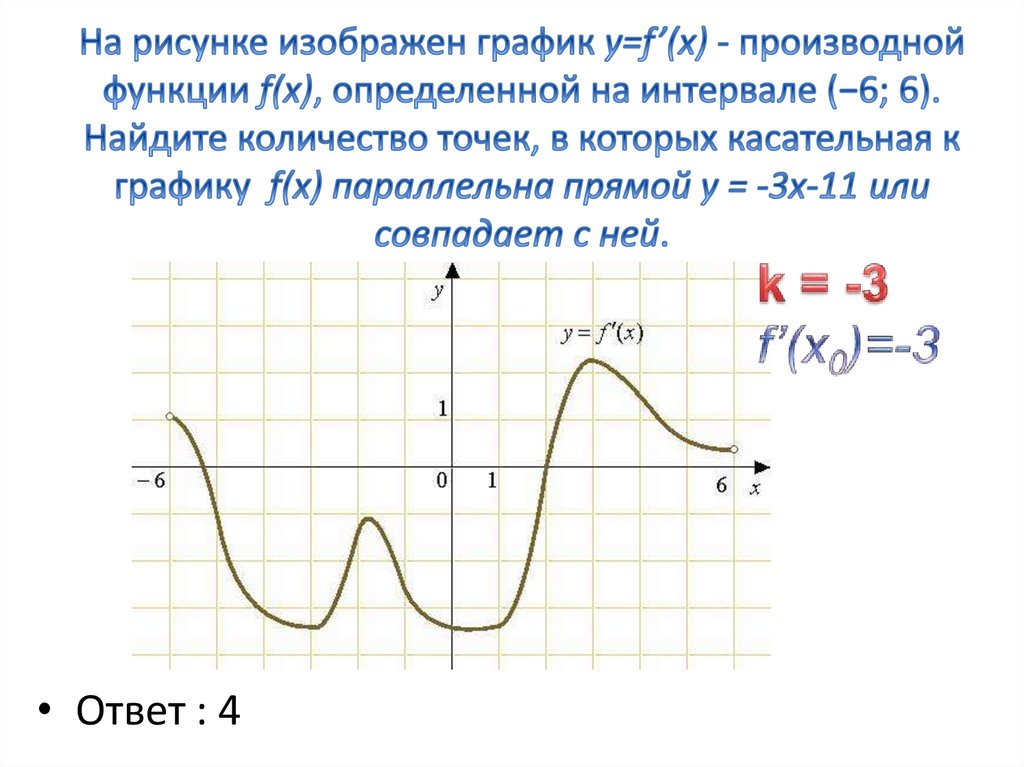
32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk
32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk
x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z
Z- множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y0=3cos32x0-π4-13
y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13
y0=3·1—192-13 или y0=3·-1—192-13
y0=45-13 или y0=-45+13
Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.
Ответ: необходимы уравнения запишутся как
y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.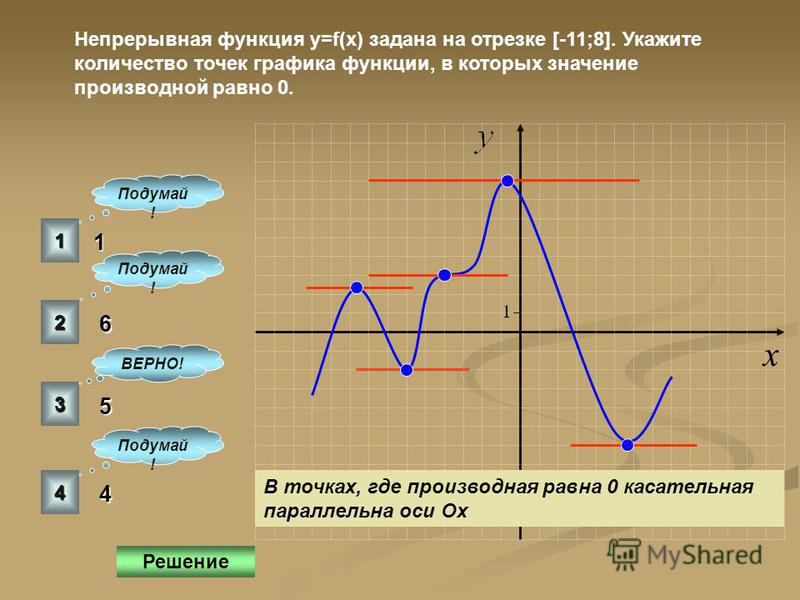
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.
Данное равенство может быть записано как объединение двух функций:
y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x0; y0, которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.
Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.
Касательная к эллипсу
Когда эллипс имеет центр в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter
Если касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.
Пример 6Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.
Решение
Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что
x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5
Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что
x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32
Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид
y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5
Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид
y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.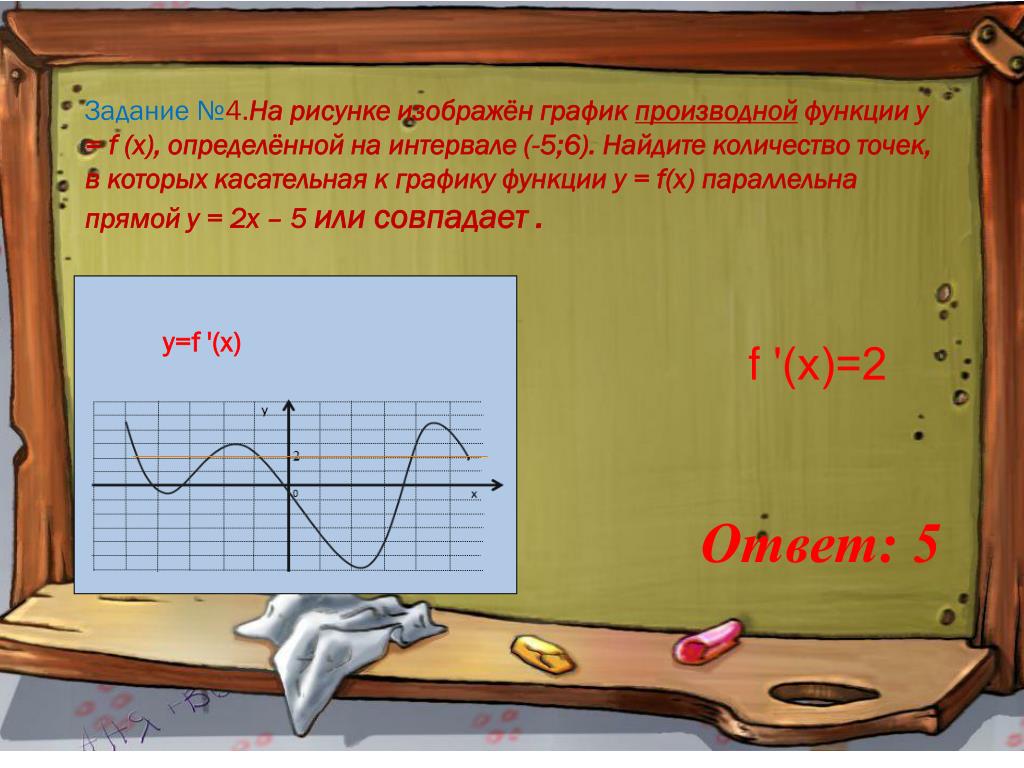
Гипербола может быть представлена в виде двух объединенных функций вида
y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter
В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Пример 7Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.
Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3
Ответ: уравнение касательной можно представить как
y=-3·x-7-33-3=-3·x+43-3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.
Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a
Графически изобразим как:
Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.
Такая касательная будет параллельна оу относительно параболы.
Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4
Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.
Получаем:
kx=y'(x0)=tg αx=tg 150°=-13
Отсюда определим значение х для точек касания.
Первая функция запишется как
y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.
Вторая функция запишется как
y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34
Имеем, что точки касания — 234; -5+34.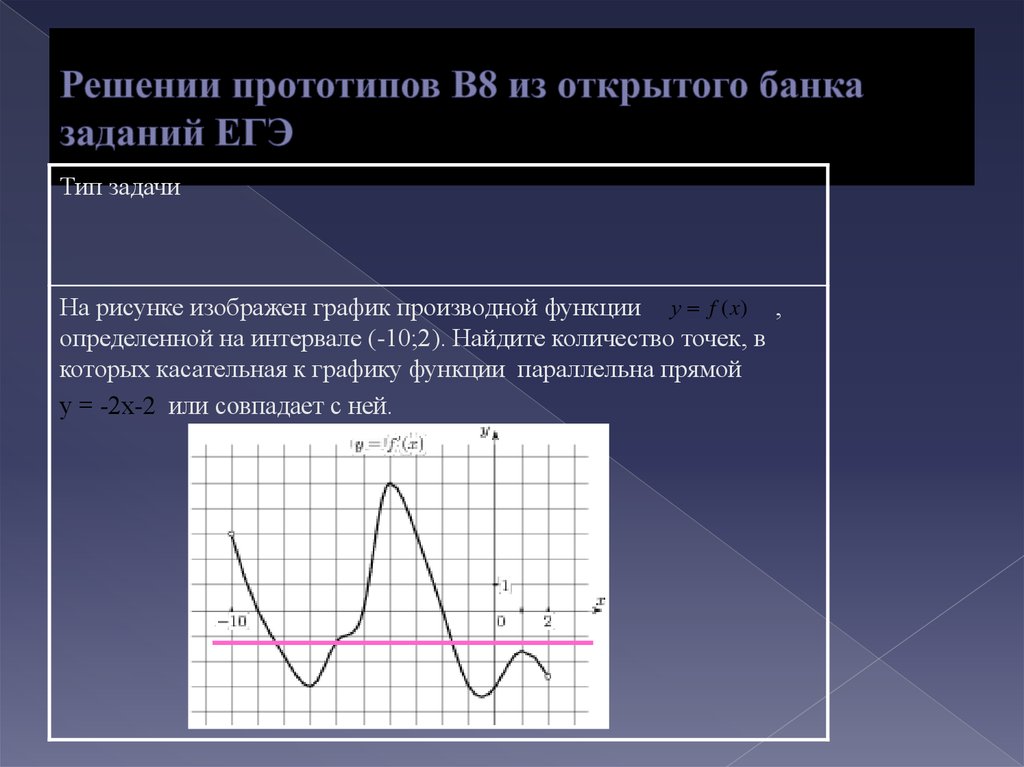
Ответ: уравнение касательной принимает вид
y=-13·x-234+-5+34
Графически изобразим это таким образом:
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Касательная к графику
Определения и понятия.
Определение.
Углом наклона прямой y=kx+b называют угол , отсчитываемый от положительного направления оси абсцисс до прямой y=kx+b в положительном направлении (то есть, против часовой стрелки).
На рисунке положительное
направление оси абсцисс
Определение.
Угловым
коэффициентом прямой y=kx+b на
Угловой коэффициент прямой равен тангенсу угла наклона прямой, то есть, .
- Угол наклона прямой равен нулю, когда прямая параллельна оси абсцисс. В этом случае нулю равен и угловой коэффициент, так как тангенс нуля есть ноль.
 Следовательно, уравнение прямой будет иметь вид y=b.
Следовательно, уравнение прямой будет иметь вид y=b. - Когда угол наклона прямой y=kx+b является острым ( или ), то угловой коэффициент k является положительным числом (так как тангенс острого угла принимает положительные значения ) и указывает на возрастание графика прямой.
- В случае, когда прямая располагается перпендикулярно оси абсцисс (параллельно оси ординат) и задается равенством x=c, где c — некоторое действительное число.
- Когда угол наклона прямой y=kx+b является тупым ( или ), то угловой коэффициент k является отрицательным числом и указывает на убывание графика прямой.
Определение.
Прямую AB, проведенную через две точки графика функции y=f(x), называют секущей. Другими словами, секущая – это прямая, проходящая через две точки графика функции.
На рисунке секущая
прямая AB изображена
синей линией, график функции y=f(x) — черной кривой,
угол наклона секущей
— красной дугой.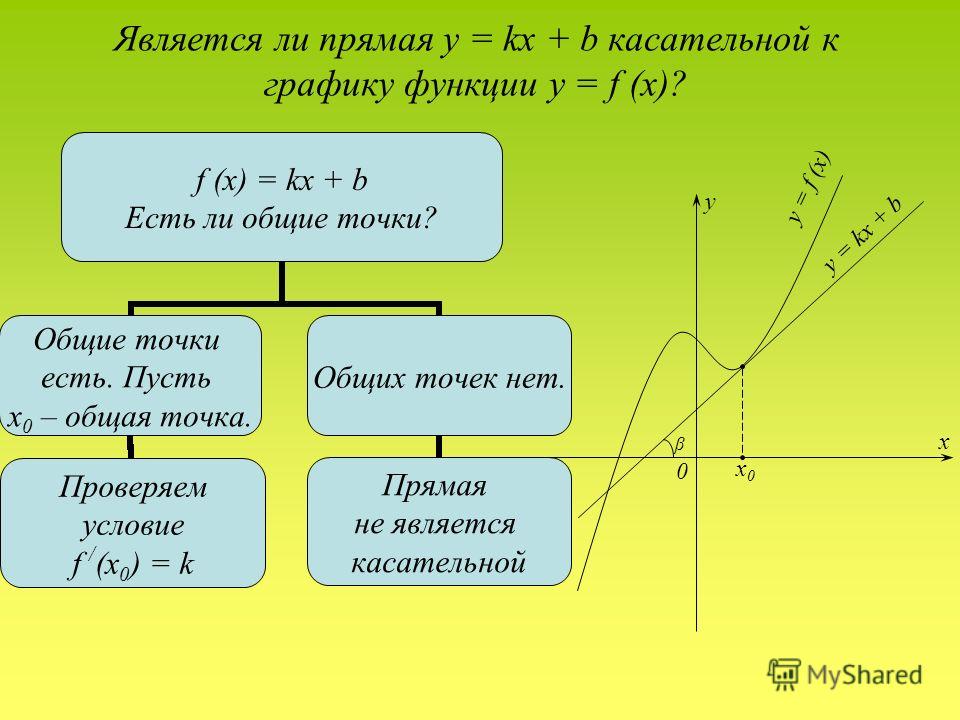
Если принимать
во внимание, что угловой коэффициент
прямой равен тангенсу угла наклона
(об этом говорили выше), и тангенс
угла в прямоугольном треугольнике A
То есть, угловой коэффициент секущей определяется равенством или , а уравнение секущей записывается в виде или (при необходимости обращайтесь к разделу уравнение прямой с угловым коэффициентом, проходящей через заданную точку).
Секущая прямая разбивает график функции на три части: слева от точки А, от А до В и справа от точки В, хотя может иметь более чем две общих точки с графиком функции.
На рисунке ниже приведены три фактически разных секущих (точки А и В различны), но они совпадают и задаются одним уравнением.
Нам ни разу не встречались
разговоры о секущей прямой для
прямой. Но все же, если отталкиваться
от определения, то прямая и ее секущая
прямая совпадают.
Но все же, если отталкиваться
от определения, то прямая и ее секущая
прямая совпадают.
В некоторых случаях
секущая может иметь с графиком
функции бесконечное число
Определение.
Касательной к графику функции y=f(x) в точке называют прямую, проходящую через точку , с отрезком которой практически сливается график функции при значениях х сколь угодно близких к .
Поясним это определение на примере. Покажем, что прямая y = x+1 является касательной к графику функции в точке (1; 2). Для этого покажем графики этих функций при приближении к точке касания (1; 2). Черным цветом показан график функции , касательная прямая показана синей линией, точка касания изображена красной точкой.
Каждый последующий рисунок является увеличенной областью предыдущего (эти области выделены красными квадратами).
Хорошо видно, что
вблизи точки касания график функции
практически сливается с касательной
прямой y=x+1.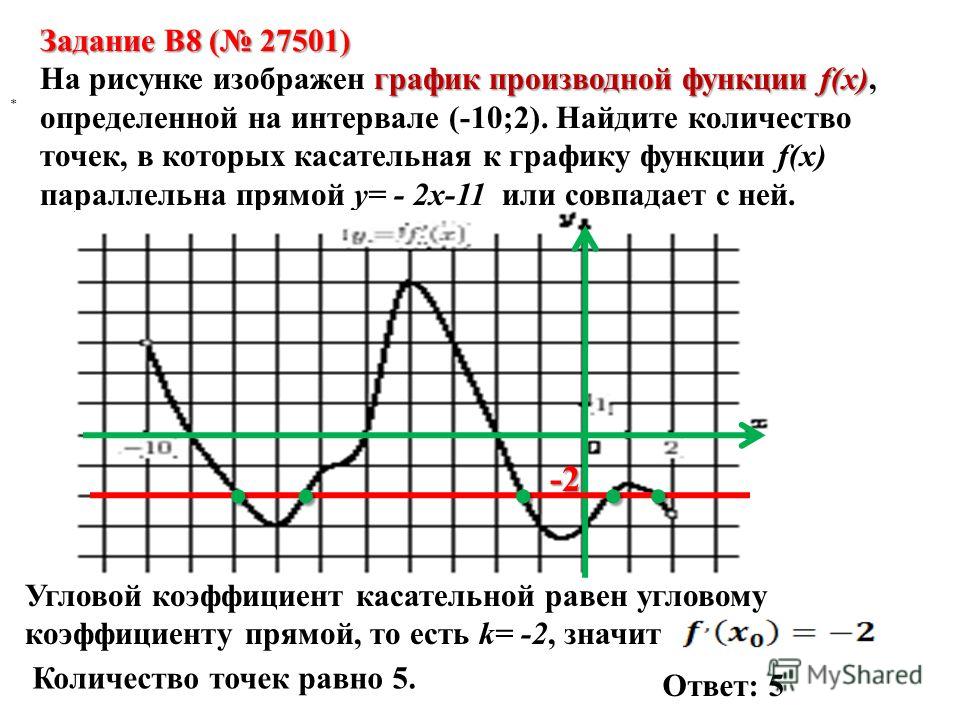
А сейчас перейдем к более значимому определению касательной.
Для этого покажем,
что будет происходить с
Рисунок ниже иллюстрирует этот процесс.
Секущая АВ (показана синей пунктирной прямой) будет стремиться занять положение касательной прямой (показана синей сплошной линией), угол наклона секущей (показан красной прерывистой дугой) будет стремиться к углу наклона касательной (изображен красной сплошной дугой).
Определение.
Таким образом, касательная к графику функции y=f(x) в точке А – это предельное положение секущей AB при .
Вот теперь можно переходить к оописанию геометрического смысла производной функции в точке.
К началу страницы
Геометрический смысл производной функции в точке.
Рассмотрим секущую АВ графика функции y=f(x) такую, что
точки А и В имеют соответственно
координаты
и
, где
— приращение аргумента. Обозначим через
приращение функции.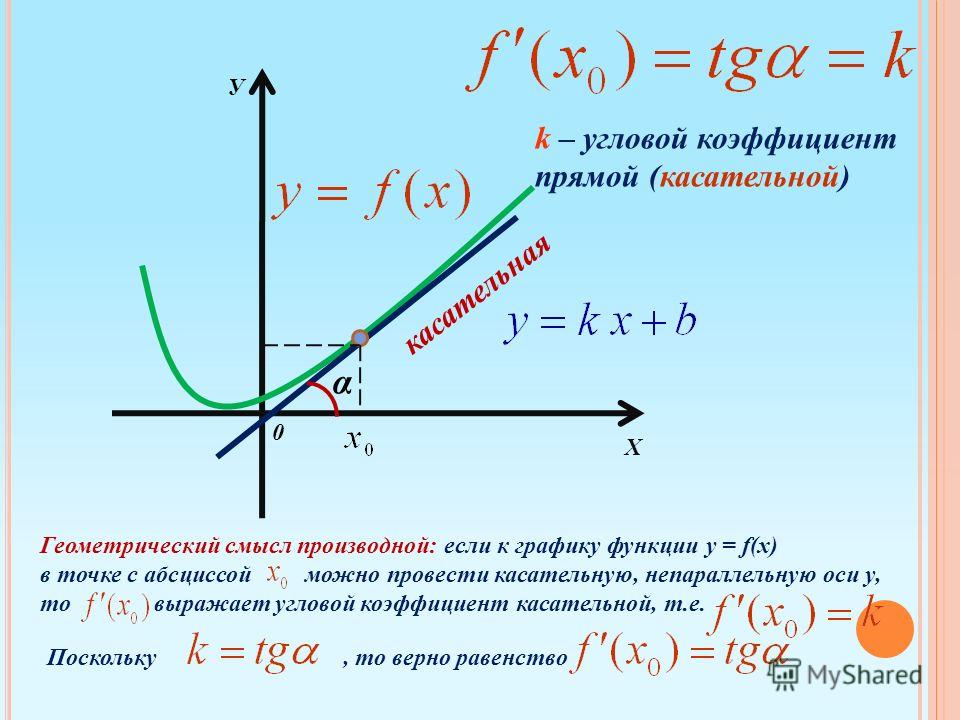 Отметим все на чертеже:
Отметим все на чертеже:
Из прямоугольного треугольника АВС имеем . Так как по определению касательная – это предельное положение секущей, то .
Вспомним определение производной функции в точке: производной функции y=f(x) в точке называется предел отношения приращения функции к приращению аргумента при , обозначается .
Следовательно, , где — угловой коэффициент касательной.
Таким образом, существование производной функции y=f(x) в точке эквивалентно существованию касательной к графику функции y=f(x) в точке касания , причемугловой коэффициент касательной равен значению производной в точке , то есть .
Заключаем: геометрический смысл производной функции в точке состоит в существовании касательной к графику функции в этой точке.
К началу страницы
Уравнение касательной прямой.
Для записи уравнения
любой прямой на плоскости достаточно
знать ее угловой коэффициент
и точку, через которую она
проходит. Касательная прямая проходит
через точку касания и ее угловой
коэффициент для
Касательная прямая проходит
через точку касания и ее угловой
коэффициент для
Уравнение
касательной к графику функции
Мы подразумеваем, что существует конечное значение производной , в противном случае касательная прямая либо вертикальна (если и ), либо не существует (если ).
В зависимости от углового коэффициента , касательная может быть параллельна оси абсцисс ( ), параллельна оси ординат ( в этом случае уравнение касательной будет иметь вид ), возрастать ( ) или убывать ( ).
Самое время привести несколько примеров для пояснения.
Пример.
Составить уравнение касательной к графику функции в точке (-1;-3) и определить угол наклона.
Решение.
Функция определена
для всех действительных чисел (при
необходимости обращайтесь к
статье область
определения функции). Так как (-1;-3) – точка
касания, то
.
Так как (-1;-3) – точка
касания, то
.
Находим производную
(для этого может пригодиться
материал статьидифференцирование
функции, нахождение производной) и вычисляем ее значение в точке
:
Так как значение
производной в точке касания
есть угловой коэффициент
Следовательно, угол
наклона касательной равен
, а уравнение касательной прямой имеет
вид
Графическая иллюстрация.
Черным цветом показан график исходной функции, касательная прямая изображена синей линией, точка касания — красной точкой. Рисунок справа представляет собой увеличенную область, обозначенную красным пунктирным квадратом на рисунке слева.
Пример.
Выяснить, существует ли касательная к графику функции в точке (1; 1), если да, то составить ее уравнение и определить угол ее наклона.
Решение.
Областью определения
функции является все множество
действительных чисел.
Находим производную:
При производная не определена, но и , следовательно, в точке (1;1) существует вертикальная касательная, ее уравнение имеет вид x = 1, а угол наклона равен .
Графическая иллюстрация.
Пример.
Найти все точки
графика функции
, в которых:
a) касательная не существует; b) касательная параллельна
оси абсцисс; c) касательная
параллельна прямой
.
Решение.
Как всегда начинаем
с области определения функции.
В нашем примере функция
Продифференцируем
функцию:
При x=-2 производная
не существует, так как односторонние
пределы в этой точке не равны:
Таким образом, вычислив значение функции при x=-2, мы можем дать ответ на пункта): , касательная к графику функции не существует в точке (-2;-2).
b) Касательная параллельна оси
абсцисс, если ее угловой коэффициент
равен нулю (тангенс угла наклона равен
нулю). Так как
, то нам нужно найти все значения х, при которых
производная функции обращается в ноль.
Эти значения и будут абсциссами точек
касания, в которых касательная параллельна
оси Ox.
Так как
, то нам нужно найти все значения х, при которых
производная функции обращается в ноль.
Эти значения и будут абсциссами точек
касания, в которых касательная параллельна
оси Ox.
При
решаем уравнение
, а при
— уравнение
:
Осталось вычислить
соответствующие значения функции:
Поэтому, — искомые точки графика функции.
Графическая иллюстрация.
График исходной функции изображен черной линией, красными точками отмечены найденные точки, в которых касательные параллельны оси абсцисс.
c) Если две прямые на плоскости параллельны, то их угловые коэффициенты равны (об этом написано в статье параллельные прямые, параллельность прямых). Исходя из этого утверждения, нам нужно найти все точки графика функции, в которых угловой коэффициент касательной равен восьми пятым. То есть, нам нужно решить уравнение . Таким образом, при решаем уравнение , а при — уравнение .
Дискриминант первого
уравнения отрицателен, следовательно,
оно не имеет действительных корней:
Второе уравнение
имеет два действительных корня:
Находим соответствующие
значения функции:
В точках
касательные к графику функции параллельны
прямой
.
Графическая иллюстрация.
График функции изображен черной линией, красной линией показан график прямой , синими линиями показаны касательные к графику функции в точках .
Для тригонометрических функций в силу их периодичности, может существовать бесконечно много касательных прямых, имеющих один угол наклона (одинаковый угловой коэффициент).
Пример.
Написать уравнения всех касательных к графику функции , которые перпендикулярны прямой .
Решение.
Чтобы составить
уравнение касательной к
Угловой коэффициент касательных найдем из условия перпендикулярности прямых: произведение угловых коэффициентов перпендикулярных прямых равно минус единице, то есть . Так как по условию угловой коэффициент перпендикулярной прямой равен , то .
Приступим к нахождению
координат точек касания. Для
начала найдем абсциссы, затем вычислим
соответствующие значения функции
– это будут ординаты точек
касания.
При описании геометрического
смысла производной функции в
точке
мы отметили, что
. Из этого равенства найдем абсциссы точек
касания.
Мы пришли к тригонометрическому
уравнению. Просим обратить на него внимание,
так как позже мы его используем
при вычислении ординат точек
касания. Решаем его (при затруднениях
обращайтесь к разделу решение тригонометрических
уравнений):
Абсциссы точек
касания найдены, вычислим соответствующие
ординаты (здесь используем равенство,
на которое мы просили обратить внимание
чуть выше):
Таким образом,
— все точки касания. Следовательно, искомые
уравнения касательных имеют вид:
Графическая иллюстрация.
На рисунке черной кривой показан график исходной функции на отрезке [-10;10], синими линиями изображены касательные прямые. Хорошо видно, что они перпендикулярны красной прямой . Точки касания отмечены красными точками.
К началу страницы
Касательная
к окружности, эллипсу, гиперболе, параболе.
До этого момента мы занимались нахождением уравнений касательных к графикам однозначных функций вида y = f(x) в различных точках. Канонические уравнения кривых второго порядка не являются однозначными функциями. Но окружность, эллипс, гиперболу и параболу мы можем представить комбинацией двух однозначных функций и уже после этого составлять уравнения касательных по известной схеме.
Касательная к окружности.
Окружность с центром в точке и радиусом R задается равенством .
Запишем это равенство
в виде объединения двух функций:
Здесь первая функция
соответствует верхней
Таким образом, чтобы
составить уравнение
Легко показать, что
в точках окружности с координатами
и
касательные параллельны оси абсцисс
и задаются уравнениями
и
соответственно (на рисунке ниже они показаны
синими точками и синими прямыми), а в точках
и
— параллельны оси ординат и имеют уравнения
и
соответственно (на рисунке ниже они отмечены
красными точками и красными прямыми).
Уравнение касательной. Уравнение касательной к графику функции
Пример 1. Дана функция f (x ) = 3x 2 + 4x – 5. Напишем уравнение касательной к графику функции f (x ) в точке графика с абсциссой x 0 = 1.
Решение. Производная функции f (x ) существует для любого x R . Найдем ее:
= (3x 2 + 4x – 5)′ = 6x + 4.
Тогда f (x 0) = f (1) = 2; (x 0) = = 10. Уравнение касательной имеет вид:
y = (x 0) (x – x 0) + f (x 0),
y = 10(x – 1) + 2,
y = 10x – 8.
Ответ. y = 10x – 8.
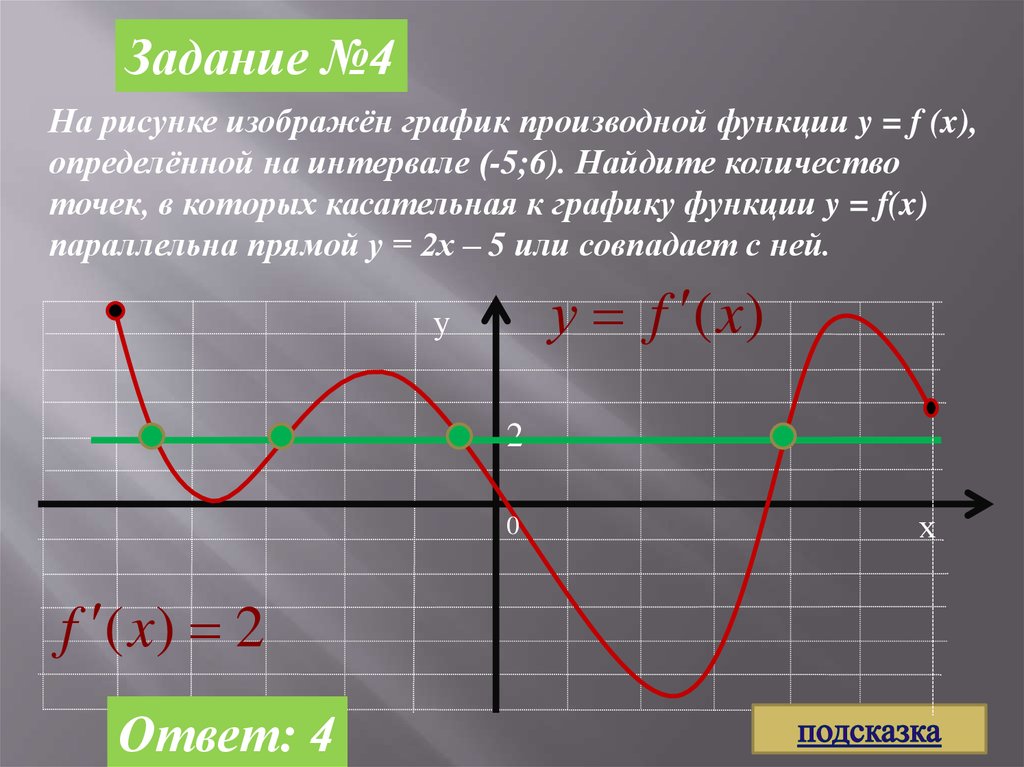
Пример 2. Дана функция f (x ) = x 3 – 3x 2 + 2x + 5. Напишем уравнение касательной к графику функции f (x ), параллельной прямой y = 2x – 11.
Решение. Производная функции f (x ) существует для любого x R . Найдем ее:
Производная функции f (x ) существует для любого x R . Найдем ее:
= (x 3 – 3x 2 + 2x + 5)′ = 3x 2 – 6x + 2.
Так как касательная к графику функции f (x ) в точке с абсциссой x 0 параллельна прямой y = 2x – 11, то ее угловой коэффициент равен 2, т. е. (x 0) = 2. Найдем эту абсциссу из условия, что 3x – 6x 0 + 2 = 2. Это равенство справедливо лишь при x 0 = 0 и при x 0 = 2. Так как в том и в другом случае f (x 0) = 5, то прямая y = 2x + b касается графика функции или в точке (0; 5), или в точке (2; 5).
В первом случае верно числовое равенство 5 = 2×0 + b , откуда b = 5, а во втором случае верно числовое равенство 5 = 2×2 + b , откуда b = 1.
Итак, существует две касательные y = 2x + 5 и y = 2x + 1 к графику функции f (x ), параллельные прямой y = 2x – 11.
Ответ. y = 2x + 5, y = 2x + 1.
Пример 3. Дана функция f (x ) = x 2 – 6x + 7. Напишем уравнение касательной к графику функции f (x ), проходящей через точку A (2; –5).
Решение. Так как f (2) –5, то точка A не принадлежит графику функции f (x ). Пусть x 0 — абсцисса точки касания.
Производная функции f (x ) существует для любого x R . Найдем ее:
= (x 2 – 6x + 1)′ = 2x – 6.
Тогда f (x 0) = x – 6x 0 + 7; (x 0) = 2x 0 – 6. Уравнение касательной имеет вид:
y = (2x 0 – 6)(x – x 0) + x – 6x + 7,
y = (2x 0 – 6)x – x + 7.
Так как точка A принадлежит касательной, то справедливо числовое равенство
–5 = (2x 0 – 6)×2– x + 7,
откуда x 0 = 0 или x 0 = 4. Это означает, что через точку A можно провести две касательные к графику функции f (x ).
Это означает, что через точку A можно провести две касательные к графику функции f (x ).
Если x 0 = 0, то уравнение касательной имеет вид y = –6x + 7. Если x 0 = 4, то уравнение касательной имеет вид y = 2x – 9.
Ответ. y = –6x + 7, y = 2x – 9.
Пример 4. Даны функции f (x ) = x 2 – 2x + 2 и g (x ) = –x 2 – 3. Напишем уравнение общей касательной к графикам этих функции.
Решение. Пусть x 1 — абсцисса точки касания искомой прямой с графиком функции f (x ), а x 2 — абсцисса точки касания той же прямой с графиком функции g (x ).
Производная функции f (x ) существует для любого x R . Найдем ее:
= (x 2 – 2x + 2)′ = 2x – 2.
Тогда f (x 1) = x – 2x 1 + 2; (x 1) = 2 x 1 – 2. Уравнение касательной имеет вид:
Уравнение касательной имеет вид:
y = (2x 1 – 2)(x – x 1) + x – 2x 1 + 2,
y = (2x 1 – 2)x – x + 2. (1)
Найдем производную функции g (x ):
= (–x 2 – 3)′ = –2x .
Пусть дана функция f , которая в некоторой точке x 0 имеет конечную производную f (x 0). Тогда прямая, проходящая через точку (x 0 ; f (x 0)), имеющая угловой коэффициент f ’(x 0), называется касательной.
А что будет, если производная в точке x 0 не существует? Возможны два варианта:
- Касательная к графику тоже не существует. Классический пример — функция y = |x | в точке (0; 0).
- Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π /2).
Уравнение касательной
Всякая невертикальная прямая задается уравнением вида y
= kx
+ b
, где k
— угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x
0 , достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f (x ), которая имеет производную y = f ’(x ) на отрезке . Тогда в любой точке x 0 ∈ (a ; b ) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x 0) · (x − x 0) + f (x 0)
Здесь f ’(x 0) — значение производной в точке x 0 , а f (x 0) — значение самой функции.
Задача. Дана функция y = x 3 . Составить уравнение касательной к графику этой функции в точке x 0 = 2.
Уравнение касательной: y = f ’(x 0) · (x − x 0) + f (x 0). Точка x 0 = 2 нам дана, а вот значения f (x 0) и f ’(x 0) придется вычислять.
Для начала найдем значение функции. Тут все легко: f
(x
0) = f
(2) = 2 3 = 8;
Теперь найдем производную: f
’(x
) = (x
3)’ = 3x
2 ;
Подставляем в производную x
0 = 2: f
’(x
0) = f
’(2) = 3 · 2 2 = 12;
Итого получаем: y
= 12 · (x
− 2) + 8 = 12x
− 24 + 8 = 12x
− 16.
Это и есть уравнение касательной.
Задача.
Составить уравнение касательной к графику функции f (x ) = 2sin x + 5 в точке x 0 = π /2.
В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:
f
(x
0) = f
(π
/2) = 2sin (π
/2) + 5 = 2 + 5 = 7;
f
’(x
) = (2sin x
+ 5)’ = 2cos x
;
f
’(x
0) = f
’(π
/2) = 2cos (π
/2) = 0;
Уравнение касательной:
y = 0 · (x − π /2) + 7 ⇒ y = 7
В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.
Рассмотрим следующий рисунок:
На нем изображена некоторая функция y = f(x), которая дифференцируема в точке a. Отмечена точка М с координатами (а; f(a)). Через произвольную точку Р(a + ∆x; f(a + ∆x)) графика проведена секущая МР.
Если теперь точку Р сдвигать по графику к точке М, то прямая МР будет поворачиваться вокруг точки М. При этом ∆х будет стремиться к нулю. Отсюда можно сформулировать определение касательной к графику функции.
Касательная к графику функции
Касательная к графику функции есть предельное положение секущей при стремлении приращения аргумента к нулю. Следует понимать, что существование производной функции f в точке х0, означает, что в этой точке графика существует касательная к нему.
При этом угловой коэффициент касательной будет равен производной этой функции в этой точке f’(x0). В этом заключается геометрический смысл производной. Касательная к графику дифференцируемой в точке х0 функции f — это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).
Уравнение касательной
Попытаемся получить уравнение касательной к графику некоторой функции f в точке А(x0; f(x0)). Уравнение прямой с угловым коэффициентом k имеет следующий вид:
Так как у нас угловой коэффициент равен производной f’(x0) , то уравнение примет следующий вид: y = f’(x0) *x + b.
Теперь вычислим значение b. Для этого используем тот факт, что функция проходит через точку А.
f(x0) = f’(x0)*x0 + b, отсюда выражаем b и получим b = f(x0) — f’(x0)*x0.
Подставляем полученное значение в уравнение касательной:
y = f’(x0)*x + b = f’(x0)*x + f(x0) — f’(x0)*x0 = f(x0) + f’(x0)*(x — x0).
y = f(x0) + f’(x0)*(x — x0).
Рассмотрим следующий пример: найти уравнение касательной к графику функции f(x) = x 3 — 2*x 2 + 1 в точке х = 2.
2. f(x0) = f(2) = 2 2 — 2*2 2 + 1 = 1.
3. f’(x) = 3*x 2 — 4*x.
4. f’(x0) = f’(2) = 3*2 2 — 4*2 = 4.
5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x — 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x — 7.
Ответ: y = 4*x — 7.
Общая схема составления уравнения касательной к графику функции y = f(x):
1. Определить х0.
2. Вычислить f(x0).
3. Вычислить f’(x)
Инструкция
Определяем угловой коэффициент касательной к кривой в точке М.
Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).
Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.
Найдите значение абсциссы точки касания, которую обозначаются буквой «а». Если она совпадает с заданной точкой касательной, то «а» будет ее х-координате. Определите значение функции f(a), подставив в уравнение функции величину абсциссы.
Определите первую производную уравнения функции f’(x) и подставьте в него значение точки «а».
Возьмите общее уравнение касательной, которое определяется как y = f(a) = f (a)(x – a), и подставьте в него найденные значения a, f(a), f «(a). В результате будет найдено решение графика и касательной.
Решите задачу иным способом, если заданная точка касательной не совпала с точкой касания. В этом случае необходимо в уравнение касательной вместо цифр подставить «а». После этого вместо букв «х» и «у» подставьте значение координат заданной точки. Решите получившееся уравнение, в котором «а» является неизвестной. Поставьте полученное значение в уравнение касательной.
Составьте уравнение касательной с буквой «а», если в условии задачи задано уравнение функции и уравнение параллельной линии относительно искомой касательной. После этого необходимо производную функции , чтобы координату у точки «а». Подставьте соответствующее значение в уравнение касательной и решите функцию.
В этой статье мы разберем все типы задач на нахождение
Вспомним геометрический смысл производной : если к графику функции в точке проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке .
Возьмем на касательной произвольную точку с координатами :
И рассмотрим прямоугольный треугольник :
В этом треугольнике
Отсюда
Это и есть уравнение касательной, проведенной к графику функции в точке .
Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти и .
Есть три основных типа задач на составление уравнения касательной.
1. Дана точка касания
2. Дан коэффициент наклона касательной, то есть значение производной функции в точке .
3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.
Рассмотрим каждый тип задач.
1 . Написать уравнение касательной к графику функции в точке .
.
б) Найдем значение производной в точке . Сначала найдем производную функции
Подставим найденные значения в уравнение касательной:
Раскроем скобки в правой части уравнения. Получим:
Получим:
Ответ: .
2 . Найти абсциссы точек, в которых касательные к графику функции параллельны оси абсцисс.
Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции в точках касания равно нулю.
а) Найдем производную функции .
б) Приравняем производную к нулю и найдем значения , в которых касательная параллельна оси :
Приравняем каждый множитель к нулю, получим:
Ответ: 0;3;5
3 . Написать уравнения касательных к графику функции , параллельных прямой .
Касательная параллельна прямой . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной , а, тем самым, значение производной в точке касания .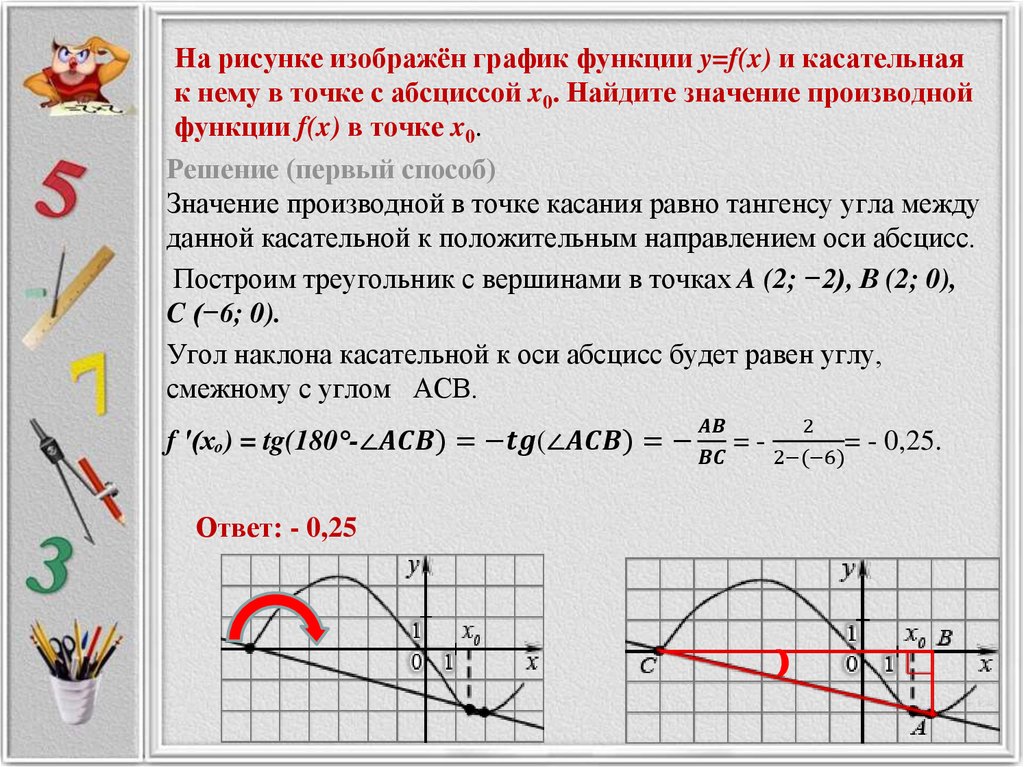 2}»>. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и не является точкой касания.
2}»>. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и не является точкой касания.
Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания .
Найдем значение .
Пусть — точка касания. Точка принадлежит касательной к графику функции . Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:
.
Значение функции в точке равно .
Найдем значение производной функции в точке .
Сначала найдем производную функции . Это .
Производная в точке равна .
Подставим выражения для и в уравнение касательной. Получим уравнение относительно :
Решим это уравнение.
Сократим числитель и знаменатель дроби на 2:
Приведем правую часть уравнения к общему знаменателю. Получим:
Упростим числитель дроби и умножим обе части на — это выражение строго больше нуля.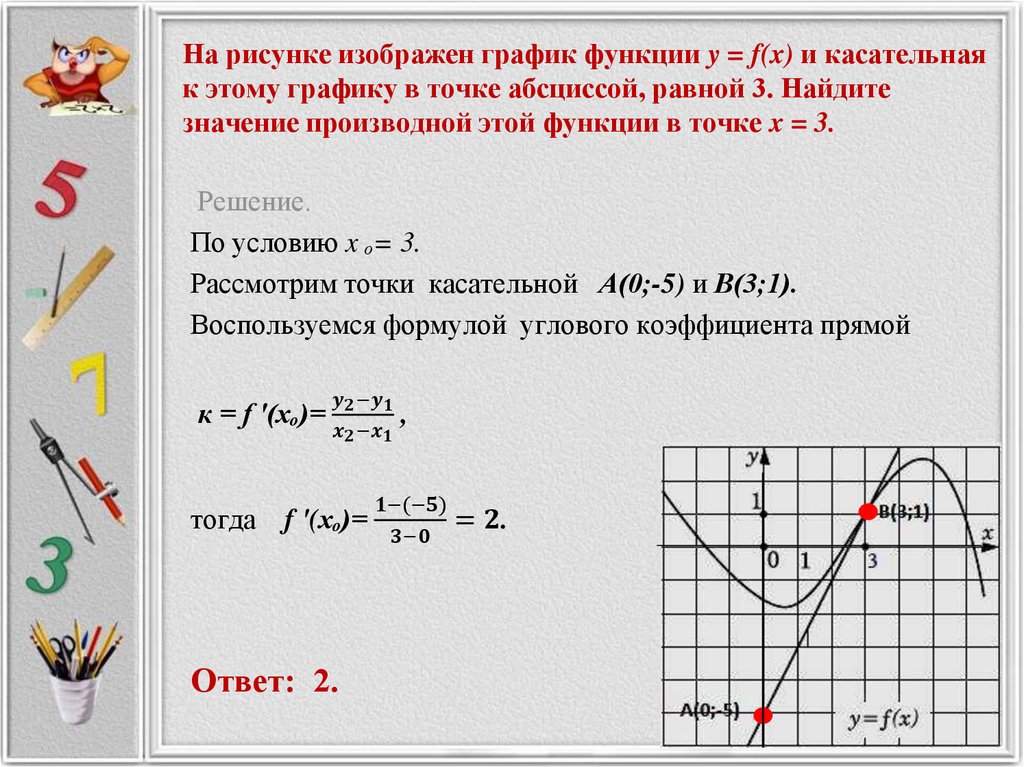 2} {8-3x_0>=0} }}{ }»>
2} {8-3x_0>=0} }}{ }»>
Решим первое уравнение.
Решим квадратное уравнение, получим
Второй корень не удовлетворяет условию title=»8-3x_0>=0″>, следовательно, у нас только одна точка касания и её абсцисса равна .
Напишем уравнение касательной к кривой в точке . Для этого подставим значение в уравнение — мы его уже записывали.
Ответ:
.
Уравнение касательной
В этой статье мы разберем все типы задач на нахождение уравнения касательной.
Вспомним геометрический смысл производной: если к графику функции в точке проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке .
Возьмем на касательной произвольную точку с координатами :
И рассмотрим прямоугольный треугольник :
В этом треугольнике
Отсюда
Или
Это и есть уравнение касательной, проведенной к графику функции в точке .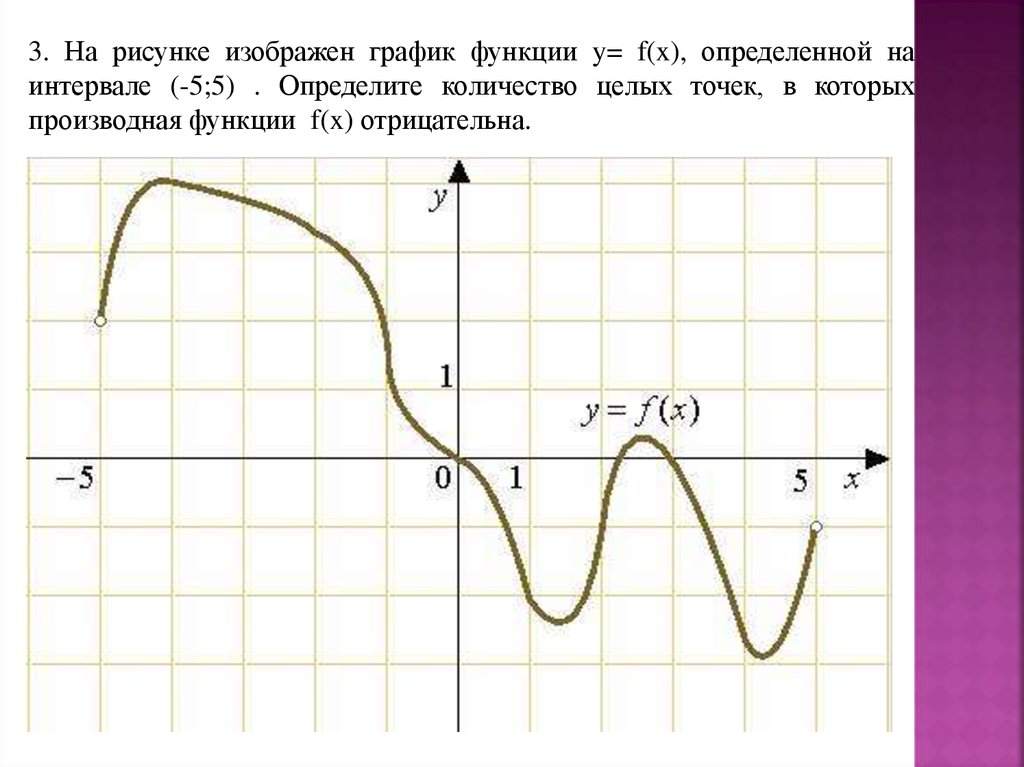
Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти и .
Есть три основных типа задач на составление уравнения касательной.
1. Дана точка касания
2. Дан коэффициент наклона касательной, то есть значение производной функции в точке .
3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.
Рассмотрим каждый тип задач.
1. Написать уравнение касательной к графику функции в точке .
а) Найдем значение функции в точке .
.
б) Найдем значение производной в точке . Сначала найдем производную функции
Подставим найденные значения в уравнение касательной:
Раскроем скобки в правой части уравнения. Получим:
Ответ: .
2. Найти абсциссы точек, в которых касательные к графику функции параллельны оси абсцисс.
Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции в точках касания равно нулю.
а) Найдем производную функции .
б) Приравняем производную к нулю и найдем значения , в которых касательная параллельна оси :
Приравняем каждый множитель к нулю, получим:
Ответ: 0;3;5
3. Написать уравнения касательных к графику функции , параллельных прямой .
Касательная параллельна прямой . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.
Это второй тип задач на нахождение уравнения касательной.
Итак, у нас дана функция и значение производной в точке касания.
а) Найдем точки, в которых производная функции равна -1.
Сначала найдем уравнение производной.
Нам нужно найти производную дроби.
Приравняем производную к числу -1.
или
или
б) Найдем уравнение касательной к графику функции в точке .
Найдем значение функции в точке .
(по условию)
Подставим эти значения в уравнение касательной:
.
б) Найдем уравнение касательной к графику функции в точке .
Найдем значение функции в точке .
(по условию).
Подставим эти значения в уравнение касательной:
.
Ответ:
4. Написать уравнение касательной к кривой , проходящей через точку
Сначала проверим, не является ли точка точкой касания. Если точка является точкой касания, то она принадлежит графику функции, и её координаты должны удовлетворять уравнению функции. Подставим координаты точки в уравнение функции.
Подставим координаты точки в уравнение функции.
. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и не является точкой касания.
Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания.
Найдем значение .
Пусть — точка касания. Точка принадлежит касательной к графику функции . Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:
.
Значение функции в точке равно .
Найдем значение производной функции в точке .
Сначала найдем производную функции . Это сложная функция.
Производная в точке равна .
Подставим выражения для и в уравнение касательной. Получим уравнение относительно :
Решим это уравнение.
Сократим числитель и знаменатель дроби на 2:
Приведем правую часть уравнения к общему знаменателю. Получим:
Упростим числитель дроби и умножим обе части на — это выражение строго больше нуля.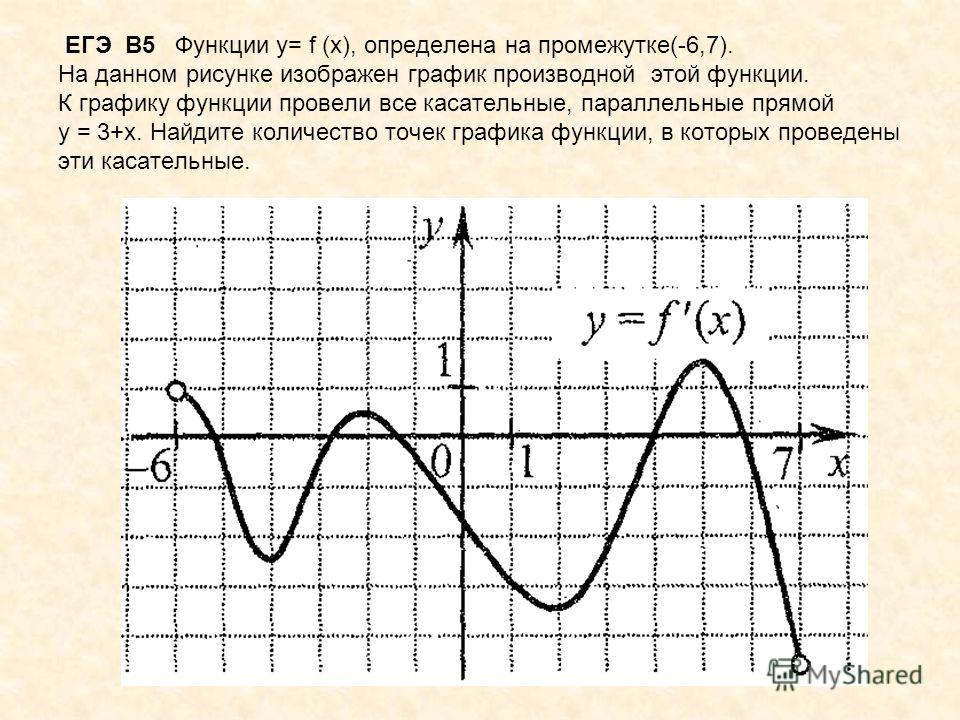
Получим уравнение
Это иррациональное уравнение.
Решим его. Для этого возведем обе части в квадрат и перейдем к системе.
Решим первое уравнение.
Решим квадратное уравнение, получим
или
Второй корень не удовлетворяет условию , следовательно, у нас только одна точка касания и её абсцисса равна .
Напишем уравнение касательной к кривой в точке . Для этого подставим значение в уравнение — мы его уже записывали.
Получим:
Ответ:
И.В. Фельдман, репетитор по математике.
Касательная к графику функции, как составить уравнение, свойства, угловой коэффициент касательной проведенной к графику функции, формула, примеры решения
На экзаменах по дисциплинам с физико-математическим уклоном или при расчетах встречается тип задач о касательной к графику функции.
Однако следует разобраться в основных терминах и соотношениях.
Специалисты рекомендуют пользоваться специальным алгоритмом, позволяющим правильно находить точку касания прямой с какой-либо фигурой.
- Общие сведения
- Определения и понятия
- Геометрический смысл
- Касательные к фигурам и графикам
- Одна и несколько окружностей
- Эллипс, гипербола и парабола
- Примеры решения
- Рекомендации специалистов
- Упражнения и ход вычислений
Общие сведения
Касательной называется прямая, имеющая с фигурой или графиком заданной функции одну общую точку. Однако иногда она проходит через 2 точки. В этом случае ее называют секущей. Прямая задается следующим уравнением: y = kx + b. Значение «k» — это угловой коэффициент.
Для решения задач следует разобрать основные понятия, определения, формулы и свойства касательной.
Кроме того, очень важно понять ее геометрический смысл, поскольку без него будет сложно разобраться в более сложных дисциплинах с физико-математическим уклоном.
Определения и понятия
У касательной есть определенный параметр — угол наклона (а).
Его необходимо отсчитывать от оси абсцисс (только положительное направление) к прямой, заданной графиком y = kx + b.
От него зависит ее расположение.
Коэффициент «к» равен значению тангенса угла наклона, т. е. tg(a).
Математики сделали некоторые выводы, которые основываются на значении углового коэффициента:
В первом, втором и третьем случаях коэффициент является положительным, а в последнем — отрицательным. Эти факты следует учитывать при решении задач. Касательная прямая может являться и секущей, т. е. соприкасаться с графиком функции сразу в двух и более точках. Следует отметить, что при параллельности прямой оси ОХ (y = b), она может пересекать функцию бесконечное число раз.
Существует еще одно определение: касательной к функции вида y = f(x) в точке (х0, f(x0)) является прямая, которая проходит через эту точку с тем условием, что отрезок имеет множество значений, близких к ней (х -> x0).
Геометрический смысл
Пусть дана некоторая функция y = f(x) и секущая АВ (рис. 1). Координаты последней в точках А и В следующие: А(х0;f(x0)) и В(х0+zx;f(x0+zx)). Величина «zx» — приращение аргумента по х, которое показано стрелками. Если подставить координаты в функцию, то она имеет такой вид: zy = zf(x) = f(x0+zx) — f(zx).
Рисунок 1. Геометрический смысл.
Соотношение, которое было получено выше, называется производной. Если к графику в точке проведена секущая или касательная, то тангенс угла будет равен самой производной заданной функции в точке с координатой х0.
Из этого определения можно сделать вывод о существовании производной.
Если значение последней равно 0, то, следовательно, не существует общих точек с заданной фигурой.
Касательные к фигурам и графикам
При решении задач следует обратить внимание на частные случаи. Нужно произвести расчеты уравнения прямой или найти точки соприкосновения с окружностью, эллипсом, гиперболой или параболой. Очень распространенная задача встречается также в механике о ременной передаче.
Частные случаи позволят найти оптимальное решение и метод расчета, поскольку экономия времени является важным элементом при научных исследованиях, написании контрольных работ и сдаче экзаменов. Важный этап — идентификация типа задачи. Касательная к вышеперечисленным фигурам — основной тип заданий, но существуют и более сложные функции.
Например, сложно составить уравнение прямой, которая имеет точки касания с какой-либо сложной функцией. 2] + yц.
2] + yц.
Две функции являются полукругами и вместе образуют окружность. Чтобы составить график круга в точке (х0;у0), нужно уравнение в этой точке. В точках с координатами (хц;yц+R) и (хц;yц-R) уравнения касательных к окружности задаются следующими уравнениями: y = yц + R и y = yц — R. Если взять точки (хц+R;yц) и (хц-R;yц), они будут иметь такую форму: x = xц + R и x = xц — R.
В случае для двух окружностей всего можно провести до 4 касательных (2 внешних и 2 внутренних). Это зависит от случая расположения фигур. Точкой пересечения внешних считается внешняя гомотетия (подобие), а внутренних — в центре внутреннего подобия. Внешними называются прямые, которые касаются внешних точек круга. Если касательные являются внутренними, то они пересекают линию, соединяющую центры окружностей.
Следует отметить, что внешний и внутренний центры гомотетии лежат на некоторой прямой. Она проходит через центры заданных окружностей. 2 — 4a(c — x).
2 — 4a(c — x).
В зависимости от его значения находятся корни:
Суть сводится к решению обыкновенного квадратного уравнения. Если коэффициент а=1, то корни можно найти по теореме Виета: x1 + x2 = — b и x1 * x2 = c.
Примеры решения
Существует несколько типов задач на нахождение уравнения прямой, которая соприкасается с заданным графиком функции. Самой простой является задача со следующей формулировкой: прямая является касательной к графику функции. Найдите все точки касания. В этом случае задается уравнение графика функции и прямой. Некоторые задания считаются более сложными. В них необходимо написать уравнение касательной или касательных.
Рекомендации специалистов
Для решения задачи нужно внимательно прочитать условие и выяснить величины, которые следует найти. Все построено на нахождении производной функции. После этого нужно подставить значение координат точки в выражение первообразной. В некоторых случаях функция задается параметрически. Для удобства ее рекомендуется перевести в каноническую форму.
Все построено на нахождении производной функции. После этого нужно подставить значение координат точки в выражение первообразной. В некоторых случаях функция задается параметрически. Для удобства ее рекомендуется перевести в каноническую форму.
Рекомендуется разбивать задачу на несколько подзадач, поскольку будет очень просто выполнить проверку и исправить найденные ошибки. Существует несколько способов нахождения уравнения касательной: автоматизированный и ручной. В первом случае нужно использовать программное обеспечение. Оптимальным решением проблемы является онлайн-калькулятор.
При ручном режиме нужно решать, а иногда выполнить построение графика. Для оптимизации вычислений можно использовать Excel. График должен быть качественно построен и предельно понятен. В некоторых случая нужно будет вычислять предельные значения используя границы (lim).
Упражнения и ход вычислений
Нужно написать уравнение прямой-касательной к y(x) = x^3 — 2x^2 + 3 в т. 2 — 4ac = 4 — 4 * 3 * (-3) = 40.
2 — 4ac = 4 — 4 * 3 * (-3) = 40.
Рекомендуется оставить в таком виде, поскольку при вычислении кубического корня появятся некоторые погрешности. В этих примерах необязательно составление графика.
Таким образом, геометрический смысл уравнения касательной к функции — производная. Следует изучить основные понятия, формулы и разобрать решение типовых задач. Также нужно повторить таблицу производных функций.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Найти уравнение прямой, касательной к кривой в заданной точке
Все ресурсы по предварительному исчислению
12 Диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Precalculus Help » Вводный расчет » Касательные к кривой » Найдите уравнение прямой, касательной к кривой в заданной точке
Найдите уравнение линии, касательной к графику
в точке , в форме пересечения наклона.
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с того, что вспомним, что одним из способов определения производной функции является наклон касательной функции в данной точке. Следовательно, нахождение производной нашего уравнения позволит нам найти наклон касательной. Поскольку две вещи, необходимые для нахождения уравнения прямой, — это наклон и точка, мы на полпути.
Мы вычисляем производную по степенному правилу.
Однако нам нужен наклон касательной не в любой точке, а именно в этой точке. Чтобы получить это, мы просто подставляем наше значение x 1 в производную.
Следовательно, наклон нашей касательной равен .
Теперь нам нужна точка на нашей касательной. Наш выбор довольно ограничен, так как единственная точка на касательной, которую мы знаем, — это точка, в которой она пересекает наш исходный график, а именно точка .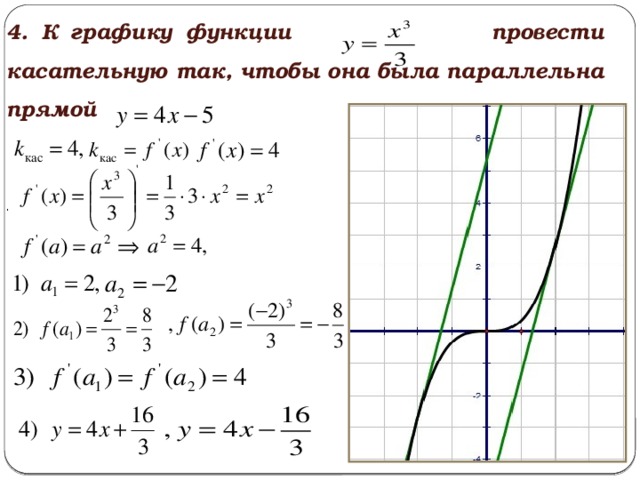
Таким образом, мы можем подставить эти координаты вместе с нашим наклоном в общую форму точка-наклон, чтобы найти уравнение.
Решение для даст нам форму пересечения наклона.
Сообщить об ошибке
Найти уравнение касательной прямой к функции
at .
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение касательной в точке зависит от производной в этой точке и значения функции.
Производная в этой точке равна
с использованием степенного правила
, что означает
Производная равна нулю, поэтому касательная будет горизонтальной.
Он пересекает ее в точке since , так что эта линия .
Сообщить об ошибке
По заданной функции найдите уравнение касательной в точке .
Возможные ответы:
Правильный ответ:
Объяснение:
Перепишите в форме пересечения наклона, , , чтобы определить наклон.
Наклон данной функции равен 2.
Подставьте наклон и заданную точку в форму наклона и точки пересечения, чтобы определить точку пересечения по оси y.
Подставьте это и наклон обратно в уравнение пересечения наклона.
Уравнение касательной:
Сообщить об ошибке
Используя предельное определение производной, найдите уравнение касательной к кривой в точке .
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с нахождения уравнения производной, используя предельное определение:
Определим и следующим образом:
Затем мы можем определить их разность:
Затем мы делим на h, чтобы подготовиться к пределу:
Тогда уравнение предела даст нам предел, производная .
Теперь мы должны понять, что наклон линии, касательной к кривой в данной точке, эквивалентен производной в этой точке. Итак, если мы определим нашу касательную линию как: , то это m определяется следующим образом:
Следовательно, уравнение касательной к кривой в данной точке:
Сообщить об ошибке
Напишите уравнение касательной к кривой в точке .
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала найдите наклон этой касательной, взяв производную:
Подставив 1 вместо x:
Итак, наклон равен 4
Теперь нам нужно найти координату y, когда x равен 1, поэтому подставьте 1 к исходному уравнению:
варианты ответа:
распределите 4
добавьте 2 к обеим сторонам
Сообщите об ошибке
Напишите уравнение для касательной к точке .
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала найдите наклон касательной, взяв первую производную:
Чтобы закончить определение наклона, подставьте значение x, 2:
, наклон равен 6
Теперь найдите y -координата, где x равно 2, подставив 2 к исходному уравнению:
Чтобы написать уравнение, начните в форме точки-наклона, а затем используйте алгебру, чтобы преобразовать его в наклон-пересечение, как варианты ответа.
распределите 6
прибавьте 8 к обеим сторонам
Сообщите об ошибке
Напишите уравнение касательной для точки .
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала возьмите первую производную, чтобы найти наклон:
Чтобы продолжить поиск наклона, подставьте значение x, -2:
Затем найдите координату y, подставив — 2 в исходное уравнение:
Координата y:
Теперь запишите уравнение в форме точки-наклона, а затем алгебраически обработайте его, чтобы оно соответствовало одной из форм пересечения наклона вариантов ответа.
распределить -5
добавить в обе стороны
Сообщить об ошибке
Напишите уравнение для касательной к точке .
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала распространите файл . Это облегчит получение производной:
Теперь возьмите производную уравнения:
Чтобы найти наклон, подставьте значение x -3:
Чтобы найти координату y точки, подставьте значение x в исходное уравнение:
Теперь напишите уравнение в виде точка-наклон, затем используйте алгебру, чтобы преобразовать его в наклон-пересечение, как варианты ответа: 9
Сообщить об ошибке
Уведомление об авторских правах 380 практических тестов Вопрос дня Карточки Learn by Concept
Видео с вопросами: нахождение точек на кривой кубической функции, в которых касательная к кривой параллельна заданной прямой
Стенограмма видео
Найдите точки на кривой 𝑦 равно трем 𝑥 в кубе минус пять 𝑥 плюс семь, в которых касательные параллельны прямой четыре 𝑥 плюс 𝑦 минус два равно нулю.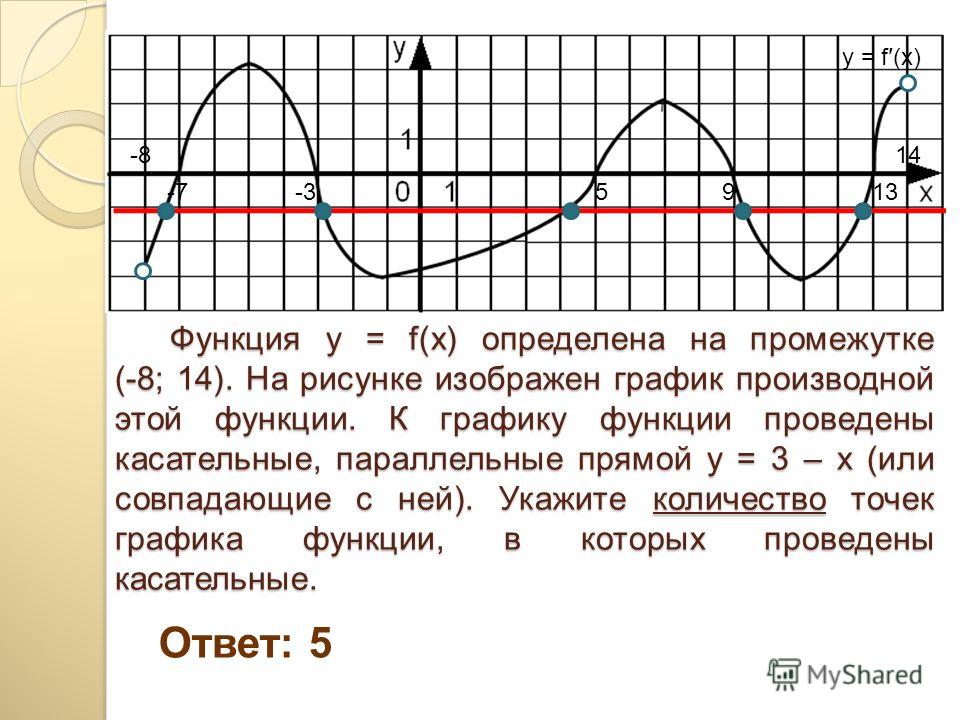
Во-первых, напомним, что две прямые параллельны, если они имеют одинаковый наклон. Мы можем вычислить наклон линии четыре 𝑥 плюс 𝑦 минус два равно нулю, сначала преобразовав ее уравнение в форму наклона и точки пересечения. Помните, что форма уравнения наклона и пересечения прямой линии: 𝑦 равно 𝑚𝑥 плюс 𝑏, где 𝑚, коэффициент при 𝑥, представляет собой наклон линии, а 𝑏, постоянный член, представляет 𝑦-отрезок. Чтобы преобразовать уравнение этой линии в форму наклона и пересечения, нам нужно вычесть четыре 𝑥 с каждой стороны, а также добавить два к каждой стороне уравнения. Это дает 𝑦 равно минус четырем 𝑥 плюс два. Теперь мы можем сравнить это с формой уравнения прямой линии с наклоном и точкой пересечения, и мы видим, что наклон этой линии, коэффициент при 𝑥, равен минус четырем.
Теперь мы знаем, что касательные, которые мы ищем к этой кривой 𝑦, равны трем 𝑥 в кубе минус пять 𝑥 плюс семь, также должны иметь отрицательный наклон четыре, если они должны быть параллельны прямой четыре 𝑥 плюс 𝑦 минус два равен нулю. Наклон кривой задается ее первой производной или функцией наклона, которую мы называем d𝑦 через d𝑥, и ее можно найти путем дифференцирования уравнения кривой по 𝑥. Наша функция 𝑦 является полиномом от 𝑥. Итак, мы вспоминаем общее степенное правило дифференцирования, которое говорит нам, что производная по 𝑥 от 𝑎𝑥 в 𝑛-й степени, где 𝑎 и 𝑛 — вещественные константы, равна 𝑎, умноженному на 𝑛, умноженному на 𝑥 в степени 𝑛 минус один. Умножаем на мощность и затем уменьшаем мощность на единицу.
Наклон кривой задается ее первой производной или функцией наклона, которую мы называем d𝑦 через d𝑥, и ее можно найти путем дифференцирования уравнения кривой по 𝑥. Наша функция 𝑦 является полиномом от 𝑥. Итак, мы вспоминаем общее степенное правило дифференцирования, которое говорит нам, что производная по 𝑥 от 𝑎𝑥 в 𝑛-й степени, где 𝑎 и 𝑛 — вещественные константы, равна 𝑎, умноженному на 𝑛, умноженному на 𝑥 в степени 𝑛 минус один. Умножаем на мощность и затем уменьшаем мощность на единицу.
Итак, давайте теперь применим это правило, чтобы найти выражение для d𝑦 с помощью d𝑥. Первый член в 𝑦 равен трем 𝑥 в кубе. Итак, дифференцируем, имеем три умножить на три. Затем мы уменьшаем степень 𝑥 на единицу, давая 𝑥 в квадрате. Итак, у нас есть три умножить на три 𝑥 в квадрате. Чтобы различать термин отрицательные пять 𝑥, мы можем думать об этом как о отрицательных пяти 𝑥 в первой степени. Таким образом, применяя степенное правило дифференцирования, мы имеем отрицательные пять, умноженные на единицу, умноженные на 𝑥 в нулевой степени.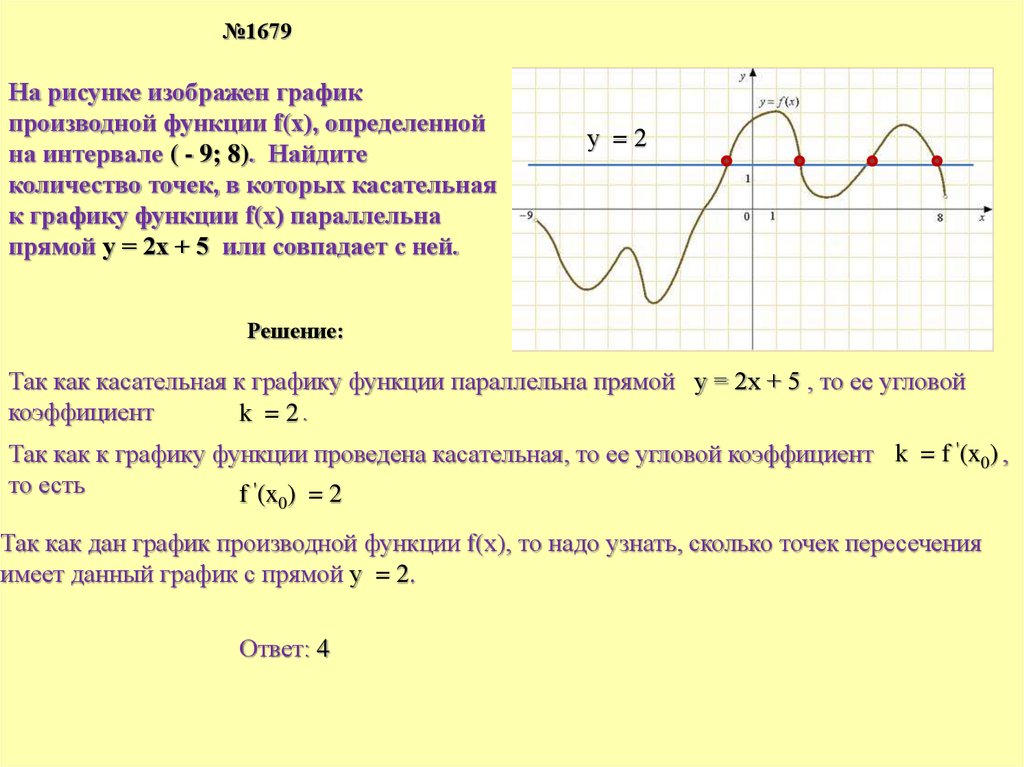 Но если вспомнить, что 𝑥 в нулевой степени равно единице, то эту часть записывать не нужно.
Но если вспомнить, что 𝑥 в нулевой степени равно единице, то эту часть записывать не нужно.
Наконец, дифференцируем положительную семерку и вспоминаем, что производная константы по 𝑥 равна нулю. Чтобы понять, почему это так, мы можем думать о константе семь как о семи, умноженных на 𝑥 в степени нуля. Как мы уже говорили, 𝑥 в нулевой степени равно единице. Если бы мы затем применили общее правило степени, у нас было бы семь, умноженное на ноль, умноженное на 𝑥 в отрицательной степени. Но, конечно, умножение чего-либо на ноль просто дает ноль. Таким образом, у нас остается три, умноженные на три 𝑥 в квадрате минус пять, умноженные на единицу, что упрощается до девяти 𝑥 в квадрате минус пять.
Теперь мы нашли выражение для функции наклона этой кривой. Помните, однако, что мы пытаемся определить точки, в которых касательные параллельны прямой четыре 𝑥 плюс 𝑦 минус два равно нулю, которые, как мы уже установили, являются точками, в которых наклон равен минус четырем. Чтобы найти 𝑥-координаты этих точек, мы можем взять наше выражение для функции наклона и установить его равным отрицательным четырем, что дает девять 𝑥 в квадрате минус пять равно отрицательным четырем. Теперь мы решим это уравнение, чтобы определить значения 𝑥. Во-первых, мы добавляем пять к каждой части уравнения, что дает девять 𝑥 в квадрате равно единице. Затем делим на девять, что дает 𝑥 в квадрате равно одной девятой.
Теперь мы решим это уравнение, чтобы определить значения 𝑥. Во-первых, мы добавляем пять к каждой части уравнения, что дает девять 𝑥 в квадрате равно единице. Затем делим на девять, что дает 𝑥 в квадрате равно одной девятой.
Чтобы найти 𝑥, мы берем квадратный корень, 𝑥 равно плюс или минус квадратный корень из одной девятой. Это эквивалентно плюс-минус квадратному корню из единицы на квадратный корень из девяти. И поскольку оба эти числа являются квадратными, это упрощается до плюс-минус один на три или плюс-минус треть. Теперь мы нашли 𝑥-координаты точек на этой кривой, где касательные параллельны данной прямой. Последний шаг — также найти их 𝑦-координаты, что мы можем сделать, подставив каждое из наших 𝑥-значений в уравнение кривой. Когда 𝑥 равно положительной трети, прежде всего, 𝑦 равно трем, умноженным на треть в кубе минус пять, умноженным на треть плюс семь. Это три на 27 минус пять на три плюс семь, что упрощается до 49.больше девяти.
Мы могли бы показать это, сократив дробь три больше 27 до единицы больше девяти, а затем записав каждый из двух других членов также как дроби со знаменателем девять. Когда 𝑥 равно отрицательной одной трети, 𝑦 равно трем, умноженным на отрицательную одну треть в кубе минус пять, умноженному на отрицательную одну треть плюс семь. Это равно минус три на 27 плюс пять на три плюс семь, что равно 77 на девять. Таким образом, мы нашли, что координаты двух точек на кривой 𝑦 равны трем 𝑥 в кубе минус пять 𝑥 плюс семь, в которых касательные параллельны прямой четыре 𝑥 плюс 𝑦 минус два равно нулю. Эти очки составляют одну треть, 49больше девяти и минус одна треть, 77 больше девяти.
Когда 𝑥 равно отрицательной одной трети, 𝑦 равно трем, умноженным на отрицательную одну треть в кубе минус пять, умноженному на отрицательную одну треть плюс семь. Это равно минус три на 27 плюс пять на три плюс семь, что равно 77 на девять. Таким образом, мы нашли, что координаты двух точек на кривой 𝑦 равны трем 𝑥 в кубе минус пять 𝑥 плюс семь, в которых касательные параллельны прямой четыре 𝑥 плюс 𝑦 минус два равно нулю. Эти очки составляют одну треть, 49больше девяти и минус одна треть, 77 больше девяти.
6.4 Уравнение касательной к кривой | Дифференциальное исчисление
Предыдущий 6.3 Правила дифференциации | Следующий 6,5 Вторая производная |
6.
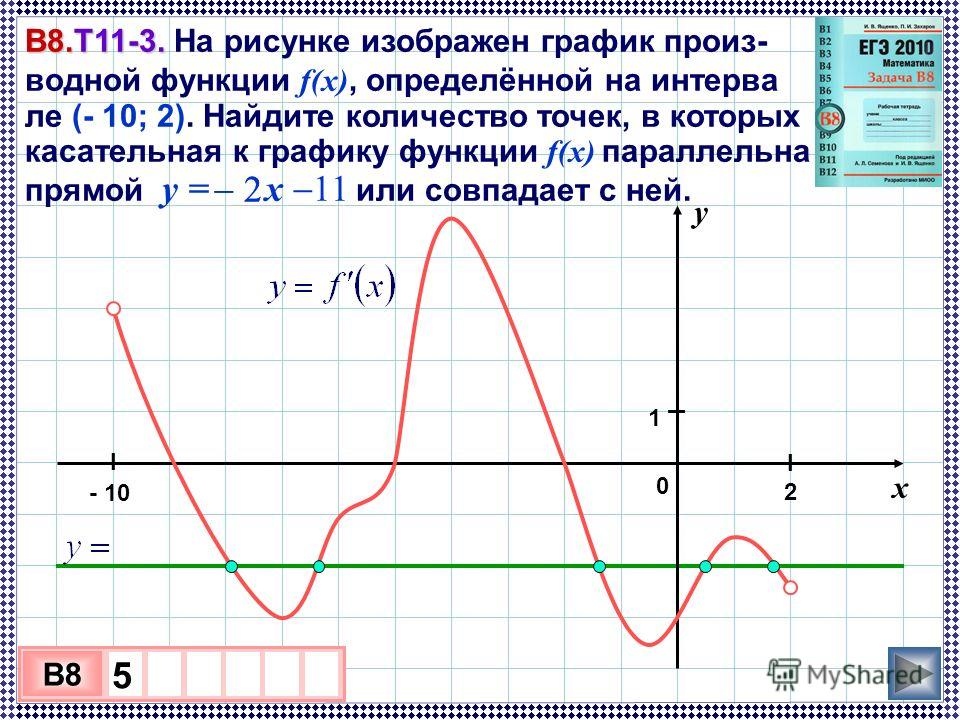 4 Уравнение касательной к кривой (EMCH8) temp text
4 Уравнение касательной к кривой (EMCH8) temp textВ данной точке кривой градиент кривой равен градиенту касательной к изгиб.
Производная (или функция градиента) описывает градиент кривой в любой точке кривой. Точно так же он также описывает градиент касательной к кривой в любой точке кривой.
Для определения уравнения касательной к кривой:
- Найдите производную по правилам дифференцирования.
- Подставьте \(x\)-координату данной точки в производную, чтобы вычислить градиент касательной.
- Подставить градиент касательной и координаты заданной точки в
соответствующую форму уравнения прямой. 9{2} \\
& \\
\поэтому \frac{dy}{dx} &= 3 \left( 2x \right) \\
&= 6x
\конец{выравнивание*}
Вычислить градиент касательной
Чтобы определить градиент касательной в точке \(\left(1;3\right)\), мы подставьте \(х\)-значение в уравнение для производной.

\начать{выравнивать*} \frac{dy}{dx} &= 6x \\ \поэтому m &= 6(1) \\ &= 6 \конец{выравнивание*}
Определить уравнение касательной
Подставить градиент касательной и координаты заданной точки в форма точки градиента уравнения прямой линии.
\начать{выравнивать*} y-{y}_{1} & = m\left(x-{x}_{1}\right) \\ у-3 & = 6\влево(х-1\вправо) \\ у & = 6х-6+3 \\ у & = 6x-3 \конец{выравнивание*}
Эскиз кривой и касательной
Рабочий пример 14: Нахождение уравнения касательной к кривой 9{2} + 24(-1) + 9 \\ \поэтому m &= 12 — 24 + 9 \\ &= -3 \конец{выравнивание*}
Определите уравнение касательной
Подставьте градиент касательной и координаты точки в уравнение градиентно-точечная форма уравнения прямой линии.

\начать{выравнивать*} y-{y}_{1} & = m\left(x-{x}_{1}\right) \\ y-1 & = -3\влево(x-(-1)\вправо) \\ у & = -3х — 3 + 1 \ у & = -3x — 2 \конец{выравнивание*}
Рабочий пример 15: Нахождение уравнения нормали к кривой
- Определить уравнение нормали к кривой \(xy = -4\) в точке \(\влево(-1;4\вправо)\).
- Нарисуйте грубый набросок.
Найдите производную
Сделайте \(y\) предметом формулы и продифференцируйте по \(x\): 9{2}} \\ \поэтому m &= 4 \конец{выравнивание*}
Используйте градиент касательной для расчета градиента нормали:
\начать{выравнивать*} m_{\text{тангенс}} \times m_{\text{нормаль}} &= -1 \\ 4 \times m_{\text{нормаль}} &= -1 \\ \поэтому m_{\text{нормаль}} &= -\frac{1}{4} \конец{выравнивание*}
Найти уравнение нормали
Подставить градиент нормали и координаты заданной точки в уравнение градиентно-точечная форма уравнения прямой линии.

\начать{выравнивать*} y-{y}_{1} & = m\left(x-{x}_{1}\right) \\ y-4 & = -\frac{1}{4}\left(x-(-1)\right) \\ y & = -\frac{1}{4}x — \frac{1}{4} + 4\\ y & = -\frac{1}{4}x + \frac{15}{4} \конец{выравнивание*} 9{2} + (4)(2) -7 \\ &=13 \\ \поэтому \text{Касательная: } y &=13x +c \конец{выравнивание*}
где \(c\) — это \(y\)-отрезок.
Касательная пересекает \(F(x)\) в точке \((2;F(2))\)
\начать{выравнивать*} F(2) &=(2)^{3} + 2(2)^{2} — 7(2) +1 \\ &=8+8-14+1\ &=3 \\ \text{Касательная: } 3 &=13(2) + c \\ \поэтому с &= — 23 \\ у & = 13x — 23 \конец{выравнивание*} 9{2}\) равно \(\text{5}\).
 {2} \\
&=1-3 \влево( \frac{25}{36} \вправо) \\
&=1 — \фракция{25}{12} \\
&= — \фракция{13}{12} \\
\поэтому & \left( — \frac{5}{6};- \frac{13}{12} \right)
\end{выравнивание*} 9{2}+2x+1\) равно \(\text{0}\).
{2} \\
&=1-3 \влево( \frac{25}{36} \вправо) \\
&=1 — \фракция{25}{12} \\
&= — \фракция{13}{12} \\
\поэтому & \left( — \frac{5}{6};- \frac{13}{12} \right)
\end{выравнивание*} 9{2}+2x+1\) равно \(\text{0}\).\begin{выравнивание*} \text{Градиент касательной } = g'(x) = \frac{2}{3}x+2 \\ \поэтому \frac{2}{3}x+2 &=0 \\ \frac{2}{3}x &= -2\\ \поэтому x&=-2 \times \frac{3}{2} \\ &=-3 \\ \text{И} g(-3) &= \frac{1}{3}(-3)^{2}+2(-3)+1 \\ &= \фракция{1}{3}(9)-6+1\ &= 3-6+1 \\ &= -2 \\ \поэтому & (-3;-2) \end{align*}
параллельно линии \(y=4x-2\).
 {2} \\
& = 1
\конец{выравнивание*}
{2} \\
& = 1
\конец{выравнивание*}Следовательно, касательная параллельна данной прямой в точке точка \((1;1)\).
перпендикулярно прямой \(2y+x-4=0\).
\начать{выравнивать*} \text{Перпендикулярно } 2y + x — 4 &= 0 \\ y&= -\frac{1}{2}x+2\\ \поэтому \text{ градиент } \perp \text{ линия } & = 2 \quad (m_1 \times m_2 = -1) \\ \поэтому f'(x) &= 8x-4 \\ \поэтому 8x-4 &=2\\ 8x&=6\\ х&=\фракция{3}{4} \\ \поэтому y&=\left[2\left(\frac{3}{4}\right)-1\right]^{2} \\ &=\фракция{1}{4} \\ \поэтому \влево(\frac{3}{4};\frac{1}{4}\right) \конец{выравнивание*}
Следовательно, касательная перпендикулярна данной прямой в точке точка \(\left(\frac{3}{4};\frac{1}{4}\right)\).
 {2} — 4х + 3 = 0 \\
(х-3)(х-1) = 0 \\
х=3 \текст{ или } х=1 \\
\text{Форма: «хмурый» } (a < 0) \\\)
{2} — 4х + 3 = 0 \\
(х-3)(х-1) = 0 \\
х=3 \текст{ или } х=1 \\
\text{Форма: «хмурый» } (a < 0) \\\)Найдите уравнения касательных к \(f\) в точке:
- \(y\)-пересечение \(f\).
- поворотный момент \(f\).
- точка, где \(x = \text{4,25}\).
- \begin{выравнивание*} у _ {\ текст {целое}}: (0; -3) \\ m _ {\ text {тангенс}} = f ‘(x) &= -2x + 4 \\ f'(0) &=-2(0) + 4 \\ \поэтому m &=4\\ \text{Касательная}y&=4x+c\\ \text{Через }(0;-3) \поэтому y&=4x-3 \end{выравнивание*}
- \begin{выравнивание*} \text{Поворотный момент: } (2;1) \\ m _ {\ text {тангенс}} = f ‘(2) &= -2 (2) + 4 \\ &=0\\ \text{Касательное уравнение } y &= 1 \end{выравнивание*} 9{2}+4(\текст{4,25})-3 \\ &= -\текст{4,0625} \\ m _ {\ text {тангенс}} \ text { в } x & = \текст{4,25} \\ m&=-2(\text{4,25})+4\\ &=-\текст{4,5} \\ \text{Касательная}y&=-\text{4,5}x+c\\ \text{Через}(\text{4,25};-\text{4,0625}) \\ -\text{4,0625}&=-\text{4,5}(\text{4,25})+c\\ \поэтому c&= \text{15,0625} \\ у&=-\текст{4,5}х+\текст{15,0625} \end{выравнивание*}
Нарисуйте три касательные выше на графике \(ф\).

Запишите все наблюдения о трех касательные к \(f\).
Тангенс в точке \(y_{\text{int}}\) (синяя линия): градиент равен положительна, функция в этой точке возрастает.
Касательная в точке поворота (зеленая линия): уклон равен нулю, касательная — это горизонтальная линия, параллельная оси \(x\).
Касательная в точке \(x=\text{4,25}\) (фиолетовая линия): градиент отрицательно, функция в этой точке убывает.
Предыдущий
6.3 Правила дифференциации
Оглавление Следующий
6,5 Вторая производная
Построение касательных к функциям и вычисление производной
Глава 11.
 Динамическая геометрия исчисления
Динамическая геометрия исчисленияВ главе 6 мы познакомили вас с блокнотами. возможности построения графиков функций. В В этой главе мы воспользуемся этими возможностями для изучения геометрии исчисление, начиная с отношения секущих к кривой, касательных той же кривой и производной функции, порождающей изгиб. Мы также представили в Глава 6 идея использования ползунков (переменных сегментов горизонтальной линии) для изменения параметры функции. следующий раздел проведет вас через шаги по созданию собственного инструмента слайдера который вы будете использовать для создания многих функций в этой главе.
Это довольно легко создать ползунки (динамические линейные сегменты) для предоставления значений, которые можно манипулировать, просто перемещая конечную точку ползунка.
- В новом эскизе перейдите в меню Graph и выберите Определить систему координат .
- Создайте на эскизе свободную точку и назовите ее A.

- Выберите точку A и ось x и постройте линию параллельно оси x через точку A.
- Поместите свободную точку B на этой линии.
- Скрыть линию через точки A и B.
- Построить сегмент между A и B.
- Выберите точки A и B и измерьте их абсциссу .
- Вычислите x B -x A и переименуйте это вычисление b .
- Скройте значения для x B и x A и отключите метку для точки A (нажмите на точку A с помощью текстового инструмента).
Теперь вы готовы создать слайдер из этой конструкции. Выполните следующие шаги:
- Выберите ось X, сегмент и две его конечные точки, и значение, помеченное b .
- Нажмите последнюю кнопку на панели инструментов и удерживайте кнопку мыши нажатой.
- Выберите Create Tool в появившемся подменю.
- Назовите инструмент slider_tool и установите флажок Show 9.
 1501 Script View коробка.
1501 Script View коробка.
Окно, подобное рис. 11.1. ниже должно появиться:
Рисунок 11.1: Окно просмотра сценария для Slider_Tool
- Двойной щелчок по первому заданному (1. Straight Object Икс).
- Установите флажок Автоматически сопоставлять объект эскиза в появившееся диалоговое окно. Straight Object x должен переместиться в часть Assassining окна Script View.
- Сохраните свой эскиз как Slider_tool в инструмент Папка.
Ваш slider_tool теперь будет доступен для использования при каждом открытии GSP 4.
Использовать ваш инструмент ползунка, чтобы создать четыре ползунка в новом эскизе. Оси координат будут созданы автоматически. Ваши слайдеры (сегменты) будут иметь только одну конечную точку. Появятся четыре меры. Перемаркируйте эти меры в соответствии с этикетками на вашем ползунки. Чтоб не путать какая конечная точка является подвижной, вы можете скрыть немаркированную конечную точку каждого слайдер.
 Используйте меры каждого
ползунок для создания и построения новой функции : f(x) = ax 3 +bx 2 +cx+d . Ты
должно иметь что-то вроде рисунка 11.2 ниже.
Используйте меры каждого
ползунок для создания и построения новой функции : f(x) = ax 3 +bx 2 +cx+d . Ты
должно иметь что-то вроде рисунка 11.2 ниже.Рисунок 11.2: График кубическая функция, использующая 4 ползунка в качестве параметров.
Узнать больше роли четырех параметров в кубической функции, регулируя каждый из ползунки. Создать новую кубическую используйте три ползунка в качестве корней функции: например. г(х) = а(х-б)(х-с)(х-d) . Узнайте, как эти две кубические функции отличаются и чем похожи.
В этом упражнении мы будем использовать наш ползунок . инструмент для создания контрольной точки, которая будет использоваться для измерения небольших изменений в разрешении x . Назовите эту контрольную точку d x . Место свободная точка на оси x графика вашей функции для кубической функции f(x) = ax 3 +bx 2 +cx+d .
 Назовите эту свободную точку x .
Измерьте абсциссу этой точки и обозначьте это измерение как x 9.1501 . В
калькулятор создает меру (x — d x/2) и (x
+ д х/2) . Использование калькулятора ВСП и каждого из этих показателей
и функция f(x) , создайте
значения f(x — d x/2) и f(x + d x/2) соответственно. Следующие шаги
отобразит эти значения f(x) в виде точек на графике и секущей между ними.
их.
Назовите эту свободную точку x .
Измерьте абсциссу этой точки и обозначьте это измерение как x 9.1501 . В
калькулятор создает меру (x — d x/2) и (x
+ д х/2) . Использование калькулятора ВСП и каждого из этих показателей
и функция f(x) , создайте
значения f(x — d x/2) и f(x + d x/2) соответственно. Следующие шаги
отобразит эти значения f(x) в виде точек на графике и секущей между ними.
их.1. Выберите меры (x — d x/2) и f(x — d x/2) в указанном порядке и Plot as ( x , y в меню Graph. Точка должна появится на вашем функциональном графике.
2. Сделайте то же самое для (x + d x/2) и f(x + d x/2) Секунда точка должна появиться на вашем функциональном графике.
3. Выделите эти две новые точки на графике и проведите через них линию .

4. Измените длину d x , чтобы увидеть, что происходит с этой секущей.
Поскольку d x становится очень маленьким, эта секущая линия кажется стать касательной к кривой, представляющей кубическую функцию. С д х очень маленький (<0,1) переместить бесплатно x точек вдоль оси x чтобы увидеть, как секущая проходит вдоль кривой (см. рис. 11.3).
Рисунок 11.3
Удлинить d x , чтобы вы могли четко видеть две точки на графике функция. Нанесите на график точки x , f(x) . Эта точка должен появиться между двумя точками, определяющими секущую линию. Выберите секущую и точку между двумя точками, определяющими линию. Постройте прямую, параллельную секущая через точку х , ф(х) . Измерьте наклон этой касательная линия. Когда вы делаете d x очень маленькими, секущая линия становится касательной.
 Если вы сделаете d x большими (d x > 2.0) и переместите свободную точку на x , станет очевидно, что линия, параллельная
секущая линия через f(x) не
всегда касается кубической функции. Снова сделайте d x маленькими. В настоящее время
постройте точку, определяемую мерой x и наклон линии через точку f(x) [Выберите меру x и наклон касательной в
этот порядок и Plot as ( x , y ) из меню Graph.] С этим новым
точка все еще выбрана, построить ее геометрическое место относительно свободной точки x на оси x . Теперь у вас должен быть эскиз, который выглядит
что-то вроде рисунка 11.4. Какой формы эта геометрическая кривая? Как эта кривая
относятся к производной кубической функции?
Если вы сделаете d x большими (d x > 2.0) и переместите свободную точку на x , станет очевидно, что линия, параллельная
секущая линия через f(x) не
всегда касается кубической функции. Снова сделайте d x маленькими. В настоящее время
постройте точку, определяемую мерой x и наклон линии через точку f(x) [Выберите меру x и наклон касательной в
этот порядок и Plot as ( x , y ) из меню Graph.] С этим новым
точка все еще выбрана, построить ее геометрическое место относительно свободной точки x на оси x . Теперь у вас должен быть эскиз, который выглядит
что-то вроде рисунка 11.4. Какой формы эта геометрическая кривая? Как эта кривая
относятся к производной кубической функции?Рисунок 11.4: Построение касательной к кубической функции и построение ее наклона
Создать выражение для производной вашей кубической функции, выбрав выражение для f(x) и выбрав Derivative в меню Graph.
 Должно получиться следующее выражение: f(x) = 3ax 2 +2bx+c . Используйте калькулятор, чтобы получить
значение этого выражения для точки x . Сделать d x очень
маленький. Что вы замечаете о
наклон касательной и значение этого выражения в точке x ? Переместите свободную точку x . Эти значения остаются прежними? Остаются ли они
равны друг другу?
Должно получиться следующее выражение: f(x) = 3ax 2 +2bx+c . Используйте калькулятор, чтобы получить
значение этого выражения для точки x . Сделать d x очень
маленький. Что вы замечаете о
наклон касательной и значение этого выражения в точке x ? Переместите свободную точку x . Эти значения остаются прежними? Остаются ли они
равны друг другу?значение производной меняется в зависимости от положения x , поэтому мы можем изобразить эту зависимость графически. Выберите выражение для производной ( f(x) = 3ax 2 +2bx+c ) и выберите Функция графика на графике меню. Какой формы график производной функции? Эта кривая совпадает внутри с геометрическим местом наклона касательной, проходящей через точку f(x)? Увеличивайте d x , пока не увидите некоторое разделение между этими двумя кривые. Остаются ли формы кривых одинаковыми, даже если они разделены? Уменьшить d x пока две кривые снова не совпадут.

Меняйте коэффициенты, а затем напишите три вещи о связи между графиками кубического функция и ее производная (см. рис. 11.5).
Рисунок 11.5: Графики кубической функции и ее производной
Исследование производной квадратного числа
Начать новый эскиз, создайте оси и поместите свободную точку на оси x . Переименуйте эту точку в x . Используйте свои 9Инструмент ползунка 1500 для создания трех контрольные точки а, б и в. Следовать метод, который вы использовали для кубической функции, чтобы создать функцию f(x) = x 2 +bx+c и построить ее график. Создайте ползунок dx и используйте его для построения секущей к вашему квадратичная функция. Нанесите на график точки x , f(x) . Построить прямую через f(x) параллельно вашей секущей. Переместите точку x , чтобы увидеть касательную и секущие линии движутся вокруг вашей параболы. Варьируйте дх.
 Сделайте его настолько большим, насколько сможете. Переместить х
опять таки. Появляется ли когда-нибудь касательная , а не , чтобы касаться
изгиб? Вернитесь к своему кубическому эскизу и попробуйте то же самое. Что кажется
специальные о квадратичной функции?
Сделайте его настолько большим, насколько сможете. Переместить х
опять таки. Появляется ли когда-нибудь касательная , а не , чтобы касаться
изгиб? Вернитесь к своему кубическому эскизу и попробуйте то же самое. Что кажется
специальные о квадратичной функции?Назначение 11.1 : Создайте выражение для производной вашего квадратичного f'(x)=2ax+b (или спросите GSP для производной вашей функции) и постройте ее график. Значение f'(x) равно наклону секущей для любого x?
Докажите (алгебраически) что секущая через точки ((x-dx/2), f(x-dx/2)) и ((x+dx/2), f(x+dx/2)) всегда будут параллельны касательной в точке (x, f(x)) для любой квадратичной функции!
Использование описанные выше методы построения создают график функции общего синуса: f(x)= asin(bx+c ) и постройте точки (x+ d x/2, f(x+ d x/2)) и (x- d , d 2 f(x- d x/2)) для построения секущей синусоиды.
 [Примечание. Вам потребуется изменить Preferences для измерения угла в меню Edit до радиан .] Сделайте d x очень маленьким и измерьте наклон
секущая-касательная линия. Участок х и
наклон как ( x , y ). Постройте геометрическое место этой новой точки на графике при изменении x . Чем эта новая кривая похожа на
Ваша синусоида? Варьируйте а и с. Как
влияют ли эти коэффициенты на две кривые? Варьировать б. Как этот коэффициент
влияет на две кривые? Сделайте b = 1,00. Что вы заметили в двух
кривые? Чем они отличаются и
чем они похожи? Измените a и c снова. Что ты заметил? Установите оба параметра a и b
равен 1; установить с равным нулю. Сделайте предположение о функции, которая
создал бы кривую, изображающую наклон касательной к синусу х .
[Примечание. Вам потребуется изменить Preferences для измерения угла в меню Edit до радиан .] Сделайте d x очень маленьким и измерьте наклон
секущая-касательная линия. Участок х и
наклон как ( x , y ). Постройте геометрическое место этой новой точки на графике при изменении x . Чем эта новая кривая похожа на
Ваша синусоида? Варьируйте а и с. Как
влияют ли эти коэффициенты на две кривые? Варьировать б. Как этот коэффициент
влияет на две кривые? Сделайте b = 1,00. Что вы заметили в двух
кривые? Чем они отличаются и
чем они похожи? Измените a и c снова. Что ты заметил? Установите оба параметра a и b
равен 1; установить с равным нулю. Сделайте предположение о функции, которая
создал бы кривую, изображающую наклон касательной к синусу х .Назначение 11.2 : Создайте производную функцию g(x) asin(bx+c) , используя измерения параметров и новую функцию . пункт меню «График».
 Сюжет
г(х). График вашей производной функции должен совпадать с графиком
наклон касательной к f(x) для
очень маленький d x . Если это
не изменяется коэффициент b. Какую роль играет b в наклоне
функция?
Сюжет
г(х). График вашей производной функции должен совпадать с графиком
наклон касательной к f(x) для
очень маленький d x . Если это
не изменяется коэффициент b. Какую роль играет b в наклоне
функция?Рисунок 11.6
Построение полигонов для Приблизительно Район
слово Интеграция несет в себе понятие , объединяющихся вместе. Если мы рассмотрим ситуацию вождения автомобиля в пути в течение двух часов, для Например, общее расстояние, пройденное за два часа, будет нашим средним скорость умножается на пройденное время. Если бы мы могли пройти весь путь с одной скоростью (скажем, 50 миль в час), то график зависимости скорости от времени будет представлять собой горизонтальную прямую линию, а пройденное расстояние будет равно площади прямоугольника, показанного на рис.
 11.7.
это 100 миль (50×2).
11.7.
это 100 миль (50×2).Возврат к квадратичная функция, управляемая вашими ползунками или параметрами для a, b и c. Построить отраженное изображение точки LL относительно вертикальной оси. Переместите точку UL в отражение LL с помощью кнопки движения. Теперь измените параметр (b) для коэффициент x -члена в вашем функция. Что вы заметили в прямоугольнике накопления или значении для площадь под кривой? Цифры 11.16 и 11.17 иллюстрируют ситуацию для двух различных значений b.
Рисунок 11.16: Площадь под квадратичным уравнением с нижней границей = -Верхняя граница
Касательные линии: уравнение, наклон и график
На латыни слово касательная означает «касаться». Итак, касательная — это линия, которая касается. Рассмотрим велосипед, движущийся по ровному тротуару. Дорога по существу касается велосипедного колеса, поскольку она касается колеса в одной точке. В этой статье мы дополнительно обсудим значение касательной, формулу касательной и значение наклона касательной.

Определение и формула касательной линии
Касательная линия — это линия, которая «просто касается» точки. Его также можно определить как линию, соединяющую две бесконечно близкие точки на кривой.
Касательная к кривой в точке с координатами , — это линия, проходящая через с наклоном
, если предел существует.
Уравнение касательной
Один наклон , уравнение касательной линии такое же, как и любая другая линия в форме точка-наклон через точку:
Касательные линии на графике
На приведенном ниже графике мы говорим, что является касательной линия к кривой в точке . Или мы можем сказать, что касается кривой в точке .
Касательная, выделенная зеленым цветом, просто касается кривой f в точке P — StudySmarter Original
Обратите внимание, как касательная «просто касается» кривой в точке P.

Наклон касательной
Геометрия
Наклон касательной в точке на кривой равен наклону кривой в таком случае. Предположение, касающееся касательных линий, заключается в том, что при просмотре графика кривой, если вы увеличите масштаб достаточно близко к сегменту кривой, кривая будет выглядеть неотличимой от касательной.
Например, давайте увеличим график выше.
Увеличение в точке, где касательная линия касается кривой — StudySmarter Original
Увеличение еще немного…
Здесь мы видим, что касательная и точка кривой, где касается касательная, неразличимы — StudySmarter Original
Обратите внимание на то, как линия касательной получается при соединении двух бесконечно близких точек на кривой.
Дополнительное уравнение наклона касательной
Существует еще одна версия уравнения для наклона касательной, с которой проще работать. Это уравнение говорит о том, что наклон касательной равно
Это уравнение устанавливает и .
 Поскольку приближается к , приближается к 0. Таким образом, формируется дополнительное уравнение касательной.
Поскольку приближается к , приближается к 0. Таким образом, формируется дополнительное уравнение касательной.Это уравнение для наклона касательной должно показаться вам знакомым… Это уравнение для производной функции в точке (a, f(a)). Итак, можно сказать, что наклон касательной к кривой в точке P равен производной кривой в точке P !
Примеры нахождения уравнения касательной
Пример 1
Найдите уравнение для касательной к в точке (2, 4).
Поскольку нам дана точка, все, что нам нужно, чтобы составить уравнение касательной, это наклон. Чтобы найти наклон, воспользуемся дополнительным уравнением касательной.
Наклон касательной в точках (2, 4) равен
Итак, уравнение касательной к f(x) в (2, 4) есть.
Вспомните, как наклон касательной совпадает с производной. Таким образом, мы также можем просто взять производную и подставить ее, чтобы найти наклон касательной в точке .

График функции f(x) и касательной к f(x) в точках (2, 4) — StudySmarter Original
Пример 2
точка (1, 0).
Опять же, поскольку нам даны и точка, все, что нам нужно, чтобы составить уравнение касательной линии, это наклон. Чтобы найти наклон, воспользуемся дополнительным уравнением касательной.
С , наклон касательной в точке (1, 0) равен:
Итак, уравнение касательной к f(x) в точке (1, 0) равно .
Опять же, вспомним, что наклон касательной совпадает с производной. Таким образом, мы также можем просто взять производную и подставить 1, чтобы найти наклон касательной в точке .
График f(x) и касательная к f(x) в точке (1, 0) — StudySmarter Original
Касательные линии в окружности
Говорят, что прямая касается окружности , если она касается окружности ровно в одной точке. Если линия касается окружности в точке, то касательная линия перпендикулярна радиусу, проведенному к точке.


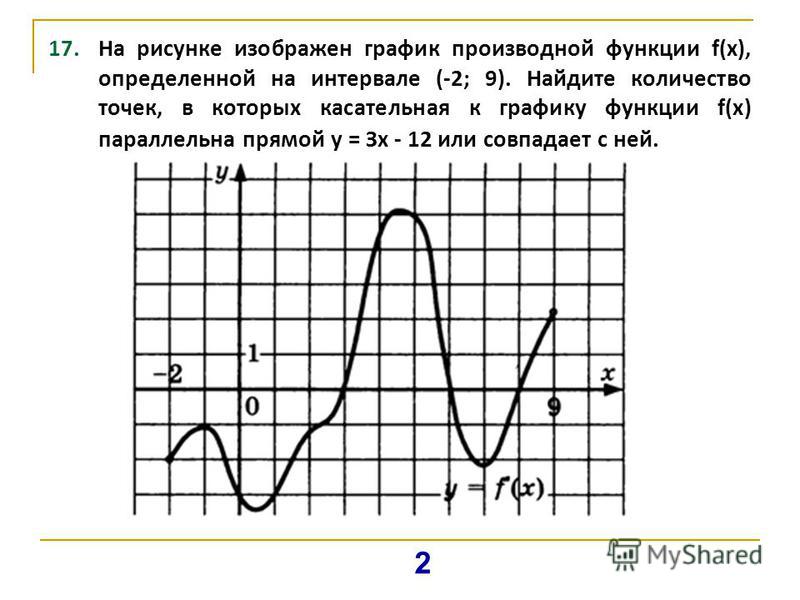 В тех случаях, когда
= k,
имеет место касание, в других —
пересечение.
В тех случаях, когда
= k,
имеет место касание, в других —
пересечение. Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
и
.
Далее составляем уравнение касательной.
Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
и
.
Далее составляем уравнение касательной.

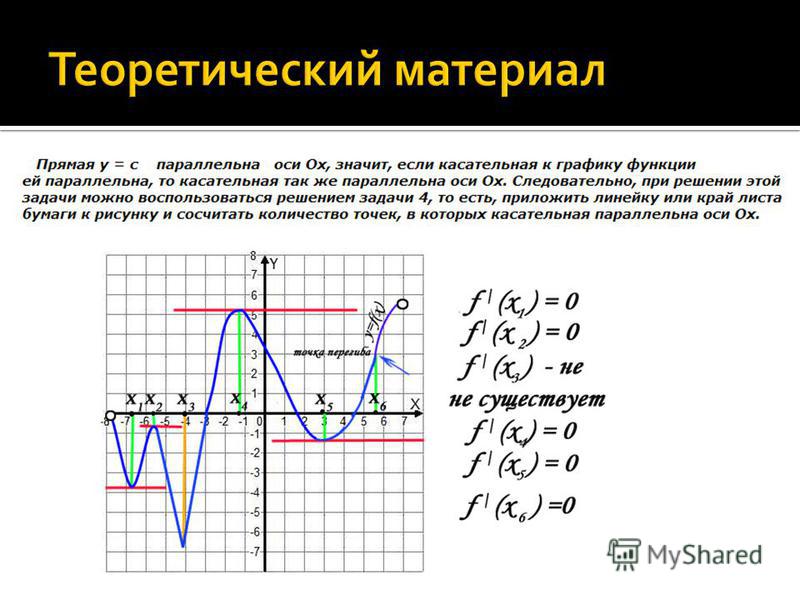 Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85. Следовательно, уравнение прямой будет иметь вид y=b.
Следовательно, уравнение прямой будет иметь вид y=b.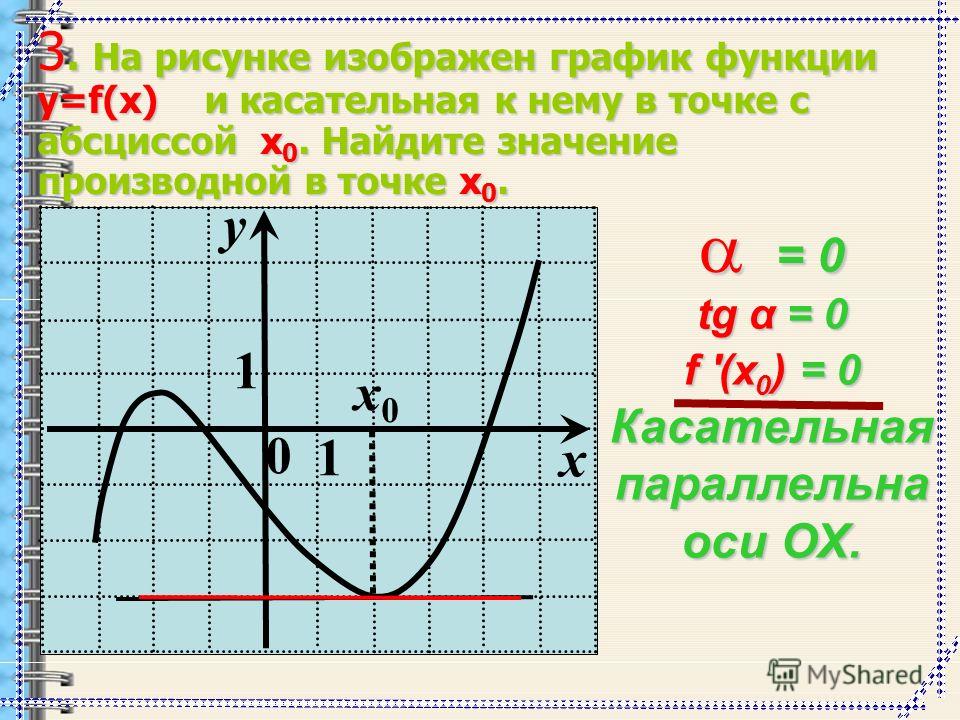 Составить уравнение касательной к графику функции f
(x
) = 2sin x
+ 5 в точке x
0 = π
/2.
Составить уравнение касательной к графику функции f
(x
) = 2sin x
+ 5 в точке x
0 = π
/2.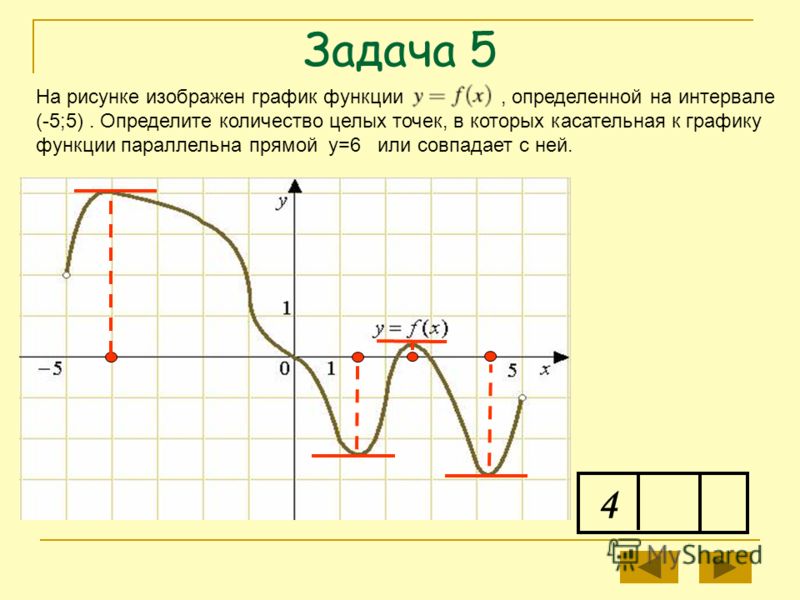 Если значение последней равно 0, то, следовательно, не существует общих точек с заданной фигурой.
Если значение последней равно 0, то, следовательно, не существует общих точек с заданной фигурой.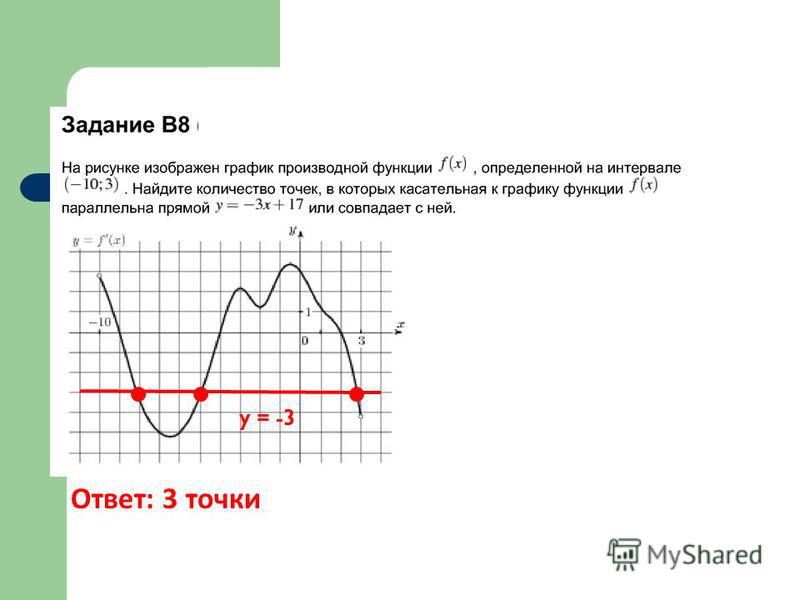
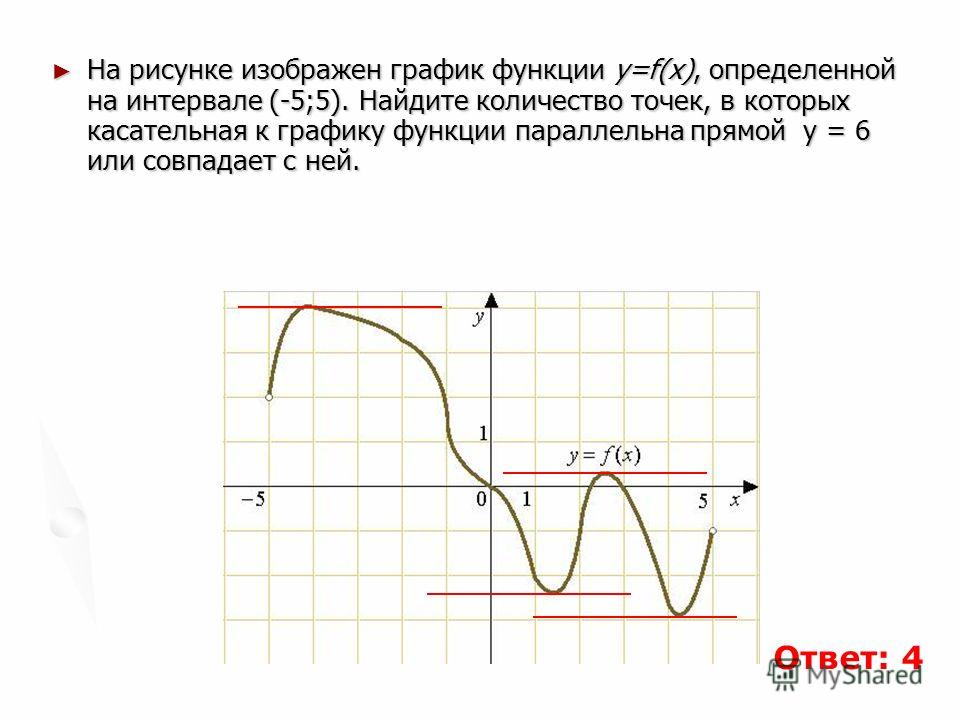
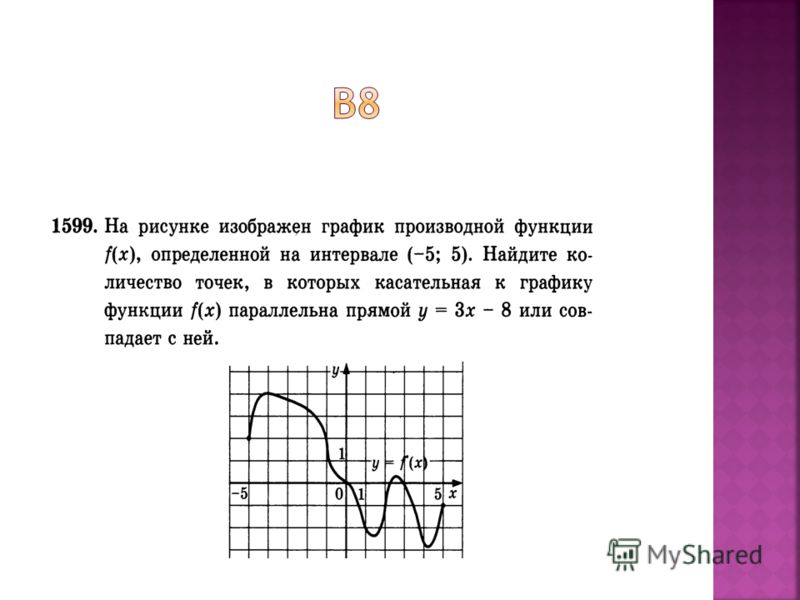
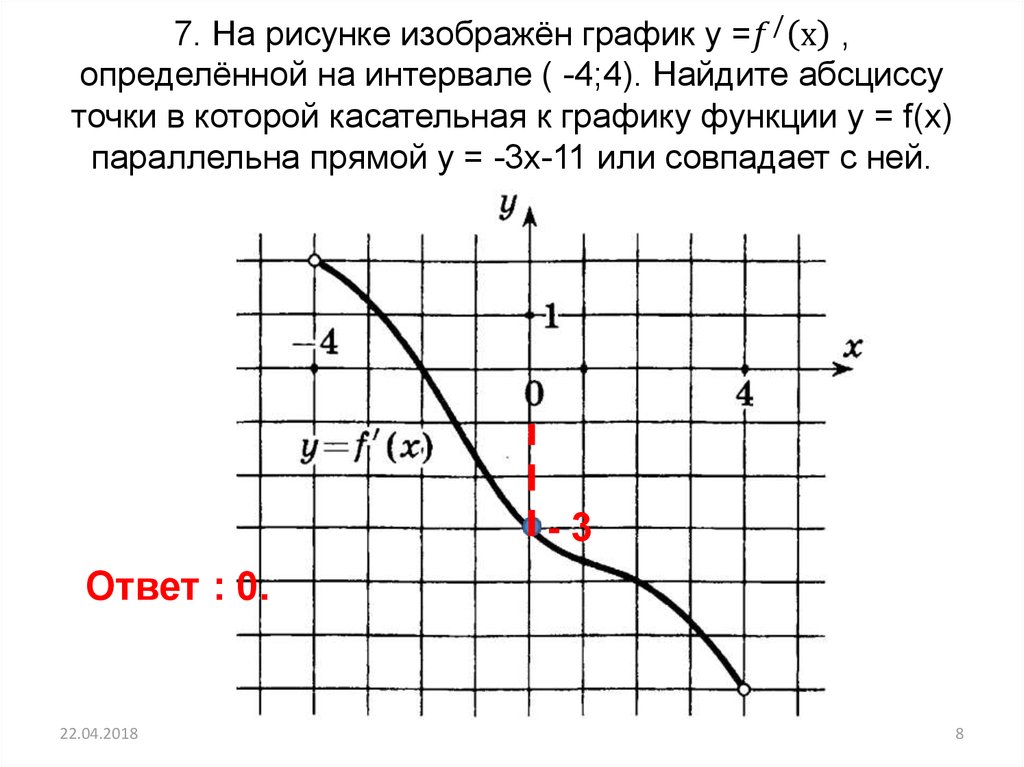 {2} \\
&=1-3 \влево( \frac{25}{36} \вправо) \\
&=1 — \фракция{25}{12} \\
&= — \фракция{13}{12} \\
\поэтому & \left( — \frac{5}{6};- \frac{13}{12} \right)
\end{выравнивание*} 9{2}+2x+1\) равно \(\text{0}\).
{2} \\
&=1-3 \влево( \frac{25}{36} \вправо) \\
&=1 — \фракция{25}{12} \\
&= — \фракция{13}{12} \\
\поэтому & \left( — \frac{5}{6};- \frac{13}{12} \right)
\end{выравнивание*} 9{2}+2x+1\) равно \(\text{0}\).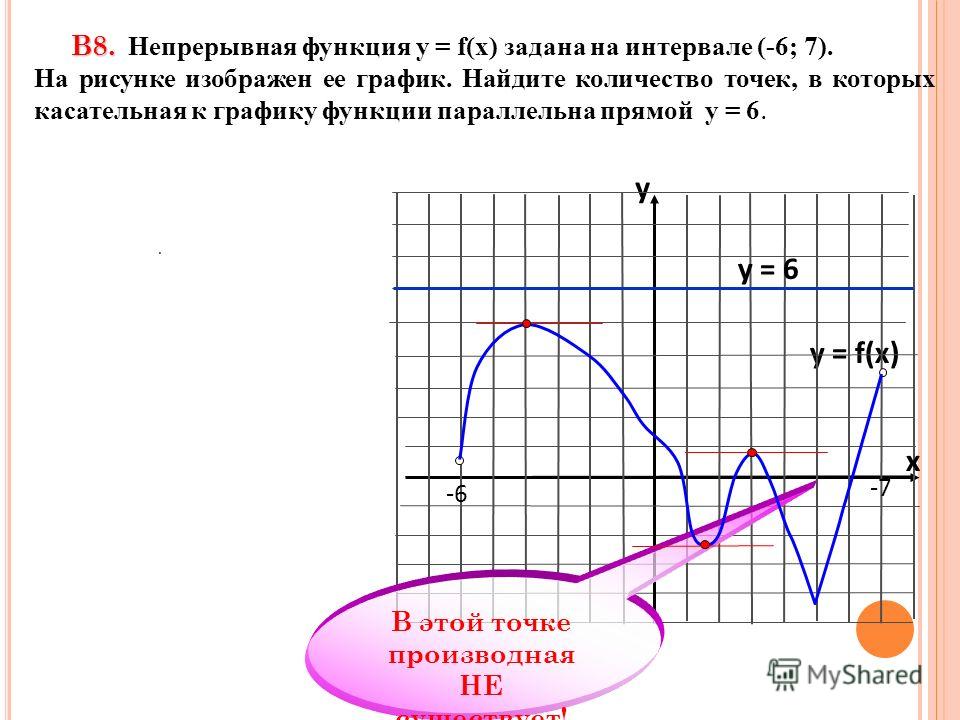 {2} \\
& = 1
\конец{выравнивание*}
{2} \\
& = 1
\конец{выравнивание*}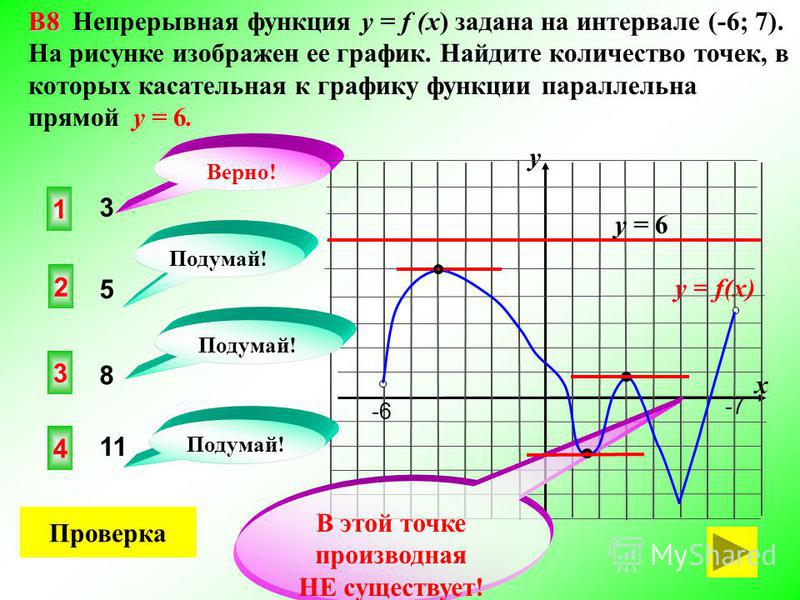 {2} — 4х + 3 = 0 \\
(х-3)(х-1) = 0 \\
х=3 \текст{ или } х=1 \\
\text{Форма: «хмурый» } (a < 0) \\\)
{2} — 4х + 3 = 0 \\
(х-3)(х-1) = 0 \\
х=3 \текст{ или } х=1 \\
\text{Форма: «хмурый» } (a < 0) \\\)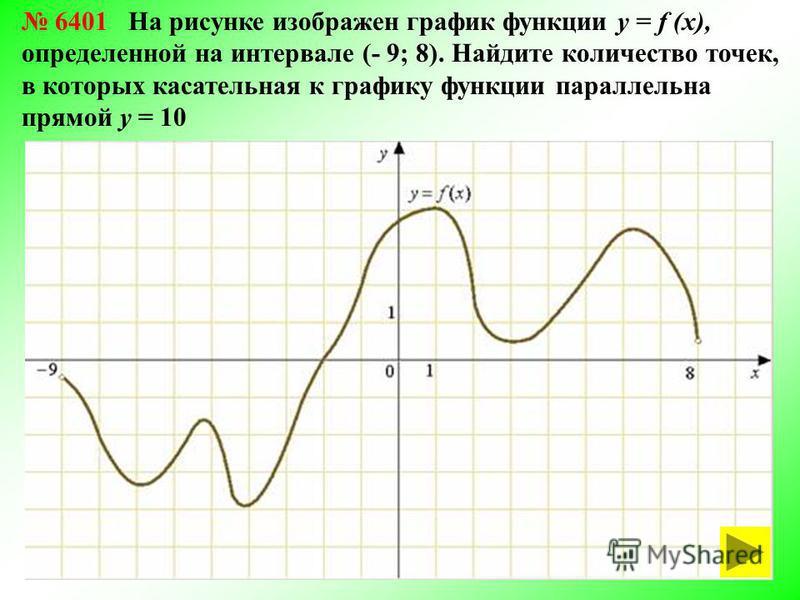
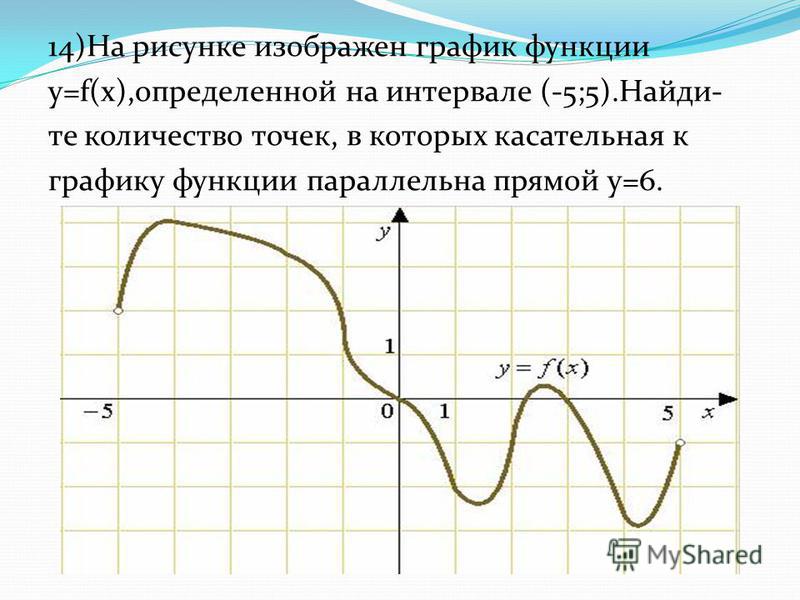 Динамическая геометрия исчисления
Динамическая геометрия исчисления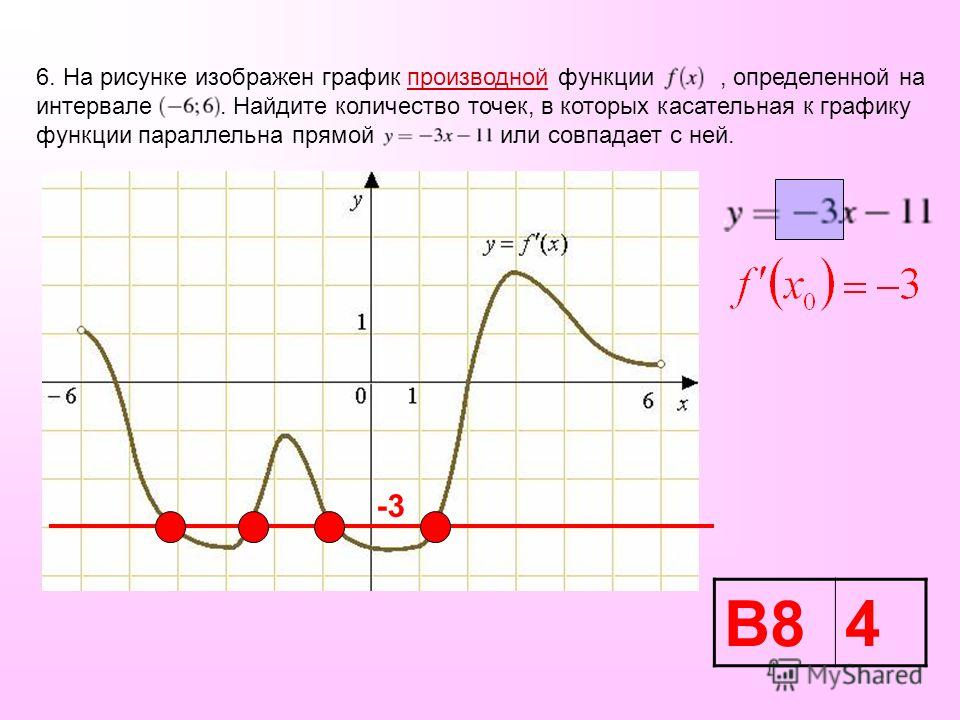
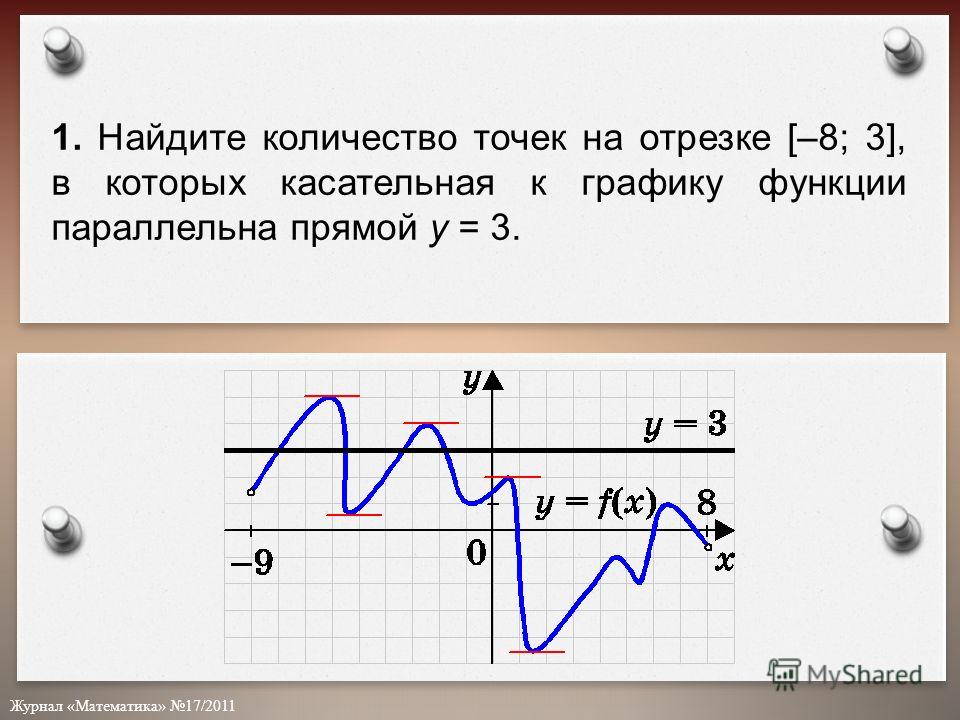 1501 Script View коробка.
1501 Script View коробка. Используйте меры каждого
ползунок для создания и построения новой функции : f(x) = ax 3 +bx 2 +cx+d . Ты
должно иметь что-то вроде рисунка 11.2 ниже.
Используйте меры каждого
ползунок для создания и построения новой функции : f(x) = ax 3 +bx 2 +cx+d . Ты
должно иметь что-то вроде рисунка 11.2 ниже.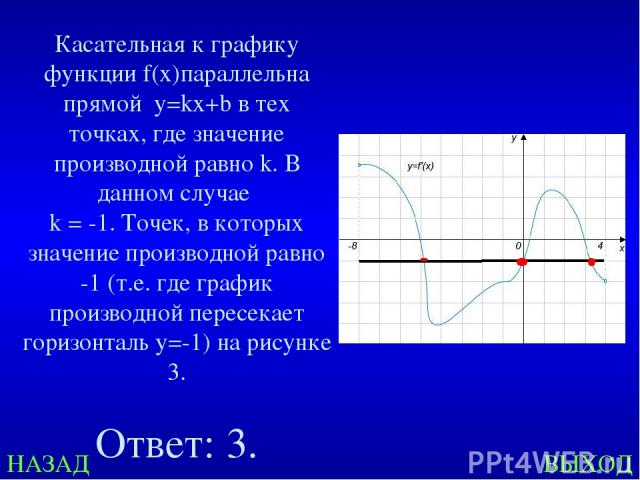 Назовите эту свободную точку x .
Измерьте абсциссу этой точки и обозначьте это измерение как x 9.1501 . В
калькулятор создает меру (x — d x/2) и (x
+ д х/2) . Использование калькулятора ВСП и каждого из этих показателей
и функция f(x) , создайте
значения f(x — d x/2) и f(x + d x/2) соответственно. Следующие шаги
отобразит эти значения f(x) в виде точек на графике и секущей между ними.
их.
Назовите эту свободную точку x .
Измерьте абсциссу этой точки и обозначьте это измерение как x 9.1501 . В
калькулятор создает меру (x — d x/2) и (x
+ д х/2) . Использование калькулятора ВСП и каждого из этих показателей
и функция f(x) , создайте
значения f(x — d x/2) и f(x + d x/2) соответственно. Следующие шаги
отобразит эти значения f(x) в виде точек на графике и секущей между ними.
их.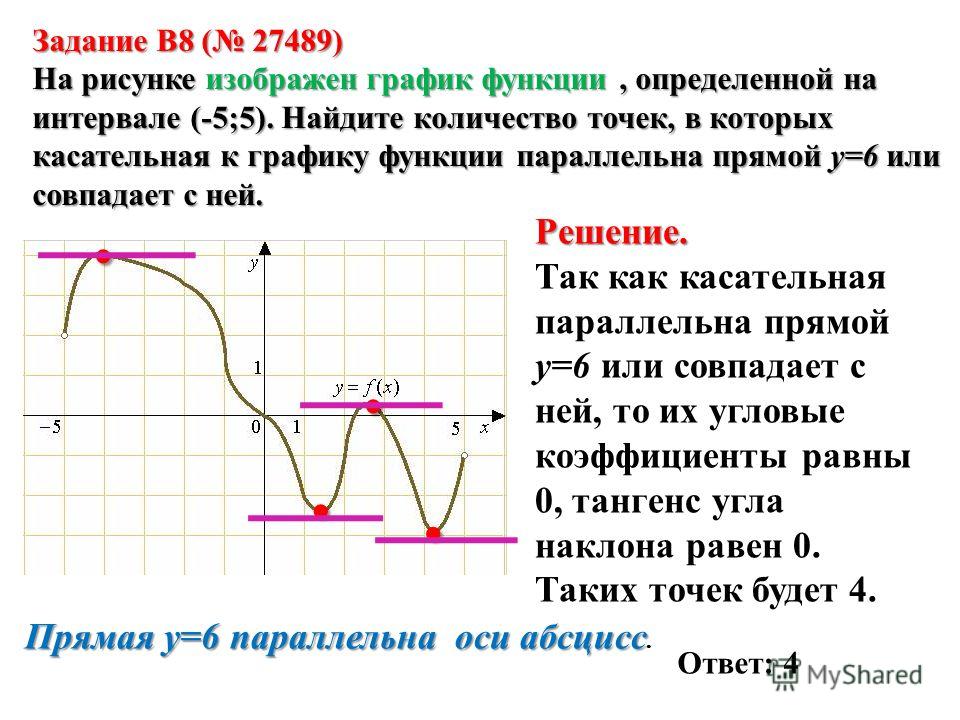
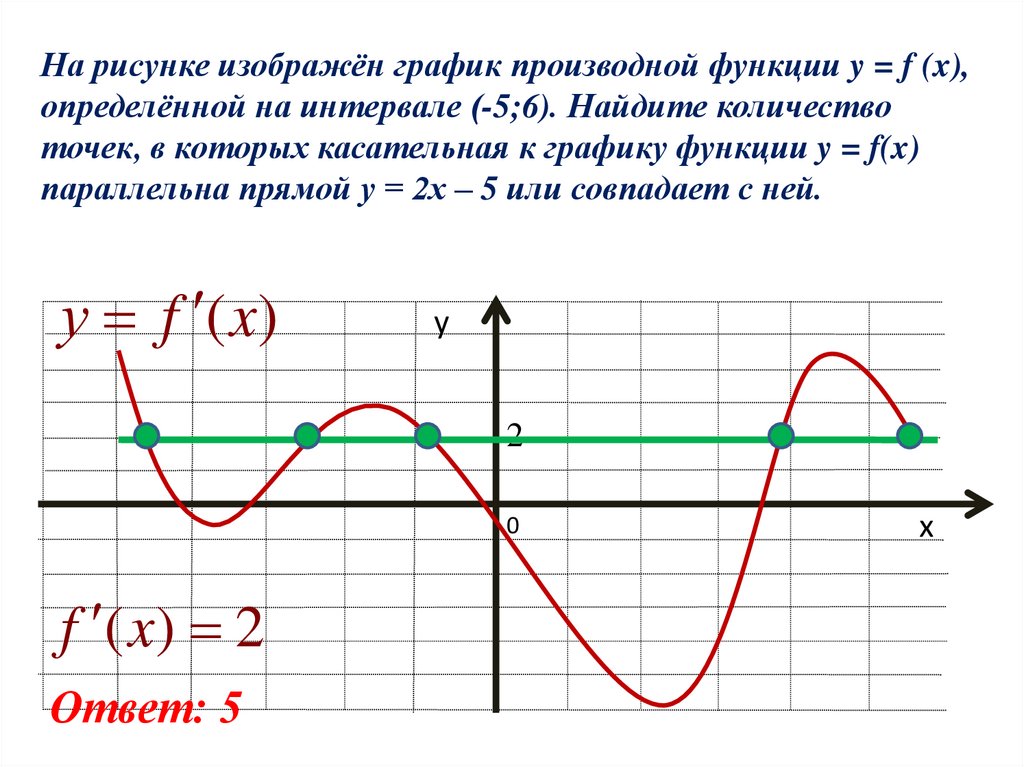 Если вы сделаете d x большими (d x > 2.0) и переместите свободную точку на x , станет очевидно, что линия, параллельная
секущая линия через f(x) не
всегда касается кубической функции. Снова сделайте d x маленькими. В настоящее время
постройте точку, определяемую мерой x и наклон линии через точку f(x) [Выберите меру x и наклон касательной в
этот порядок и Plot as ( x , y ) из меню Graph.] С этим новым
точка все еще выбрана, построить ее геометрическое место относительно свободной точки x на оси x . Теперь у вас должен быть эскиз, который выглядит
что-то вроде рисунка 11.4. Какой формы эта геометрическая кривая? Как эта кривая
относятся к производной кубической функции?
Если вы сделаете d x большими (d x > 2.0) и переместите свободную точку на x , станет очевидно, что линия, параллельная
секущая линия через f(x) не
всегда касается кубической функции. Снова сделайте d x маленькими. В настоящее время
постройте точку, определяемую мерой x и наклон линии через точку f(x) [Выберите меру x и наклон касательной в
этот порядок и Plot as ( x , y ) из меню Graph.] С этим новым
точка все еще выбрана, построить ее геометрическое место относительно свободной точки x на оси x . Теперь у вас должен быть эскиз, который выглядит
что-то вроде рисунка 11.4. Какой формы эта геометрическая кривая? Как эта кривая
относятся к производной кубической функции? Должно получиться следующее выражение: f(x) = 3ax 2 +2bx+c . Используйте калькулятор, чтобы получить
значение этого выражения для точки x . Сделать d x очень
маленький. Что вы замечаете о
наклон касательной и значение этого выражения в точке x ? Переместите свободную точку x . Эти значения остаются прежними? Остаются ли они
равны друг другу?
Должно получиться следующее выражение: f(x) = 3ax 2 +2bx+c . Используйте калькулятор, чтобы получить
значение этого выражения для точки x . Сделать d x очень
маленький. Что вы замечаете о
наклон касательной и значение этого выражения в точке x ? Переместите свободную точку x . Эти значения остаются прежними? Остаются ли они
равны друг другу?
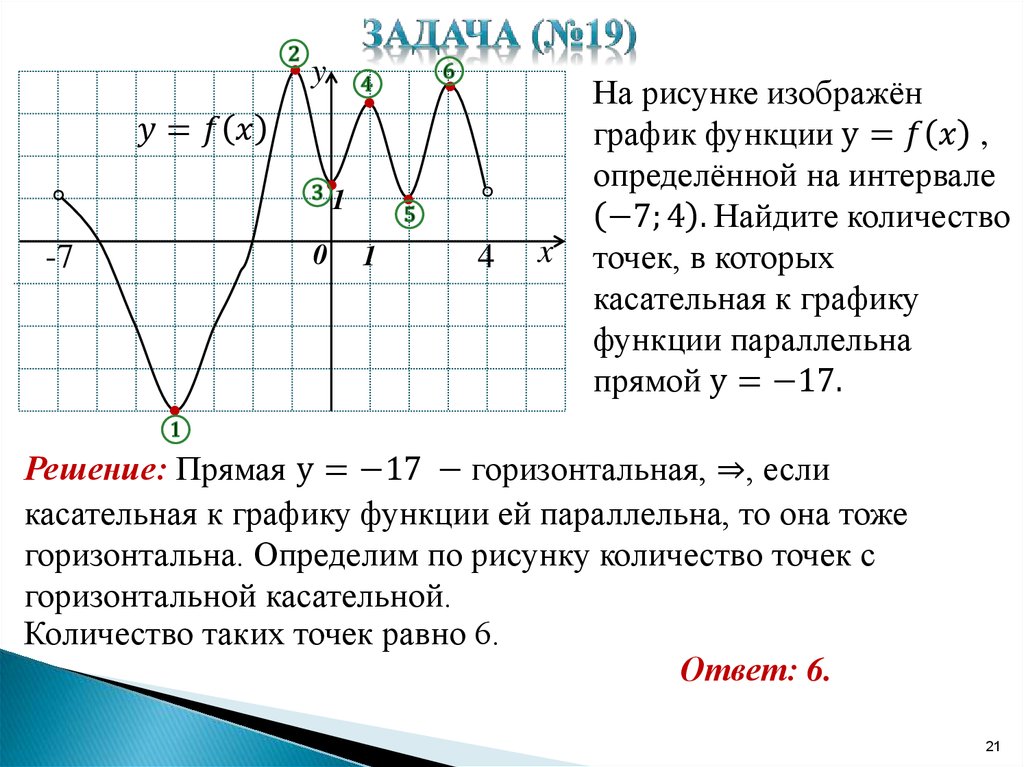 Сделайте его настолько большим, насколько сможете. Переместить х
опять таки. Появляется ли когда-нибудь касательная , а не , чтобы касаться
изгиб? Вернитесь к своему кубическому эскизу и попробуйте то же самое. Что кажется
специальные о квадратичной функции?
Сделайте его настолько большим, насколько сможете. Переместить х
опять таки. Появляется ли когда-нибудь касательная , а не , чтобы касаться
изгиб? Вернитесь к своему кубическому эскизу и попробуйте то же самое. Что кажется
специальные о квадратичной функции?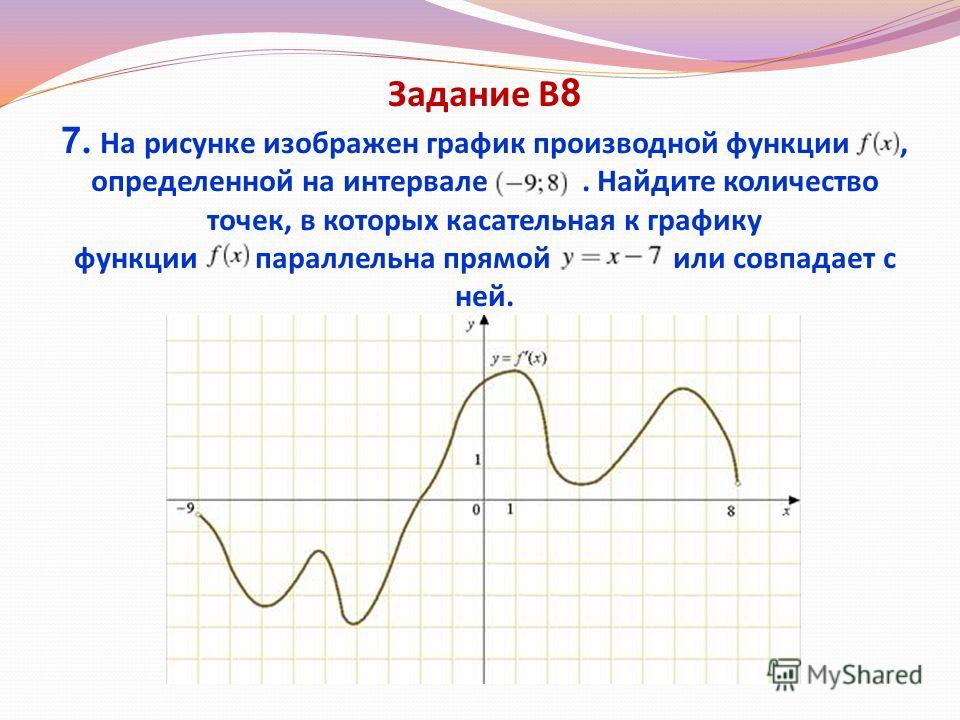 [Примечание. Вам потребуется изменить Preferences для измерения угла в меню Edit до радиан .] Сделайте d x очень маленьким и измерьте наклон
секущая-касательная линия. Участок х и
наклон как ( x , y ). Постройте геометрическое место этой новой точки на графике при изменении x . Чем эта новая кривая похожа на
Ваша синусоида? Варьируйте а и с. Как
влияют ли эти коэффициенты на две кривые? Варьировать б. Как этот коэффициент
влияет на две кривые? Сделайте b = 1,00. Что вы заметили в двух
кривые? Чем они отличаются и
чем они похожи? Измените a и c снова. Что ты заметил? Установите оба параметра a и b
равен 1; установить с равным нулю. Сделайте предположение о функции, которая
создал бы кривую, изображающую наклон касательной к синусу х .
[Примечание. Вам потребуется изменить Preferences для измерения угла в меню Edit до радиан .] Сделайте d x очень маленьким и измерьте наклон
секущая-касательная линия. Участок х и
наклон как ( x , y ). Постройте геометрическое место этой новой точки на графике при изменении x . Чем эта новая кривая похожа на
Ваша синусоида? Варьируйте а и с. Как
влияют ли эти коэффициенты на две кривые? Варьировать б. Как этот коэффициент
влияет на две кривые? Сделайте b = 1,00. Что вы заметили в двух
кривые? Чем они отличаются и
чем они похожи? Измените a и c снова. Что ты заметил? Установите оба параметра a и b
равен 1; установить с равным нулю. Сделайте предположение о функции, которая
создал бы кривую, изображающую наклон касательной к синусу х . Сюжет
г(х). График вашей производной функции должен совпадать с графиком
наклон касательной к f(x) для
очень маленький d x . Если это
не изменяется коэффициент b. Какую роль играет b в наклоне
функция?
Сюжет
г(х). График вашей производной функции должен совпадать с графиком
наклон касательной к f(x) для
очень маленький d x . Если это
не изменяется коэффициент b. Какую роль играет b в наклоне
функция?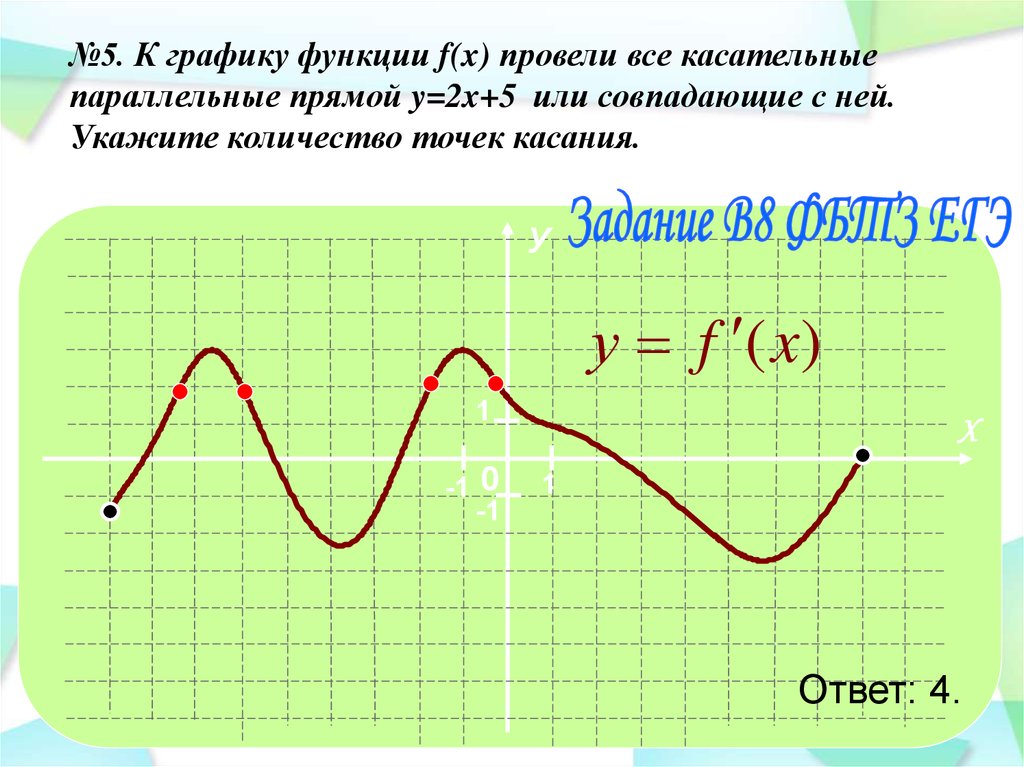 11.7.
это 100 миль (50×2).
11.7.
это 100 миль (50×2).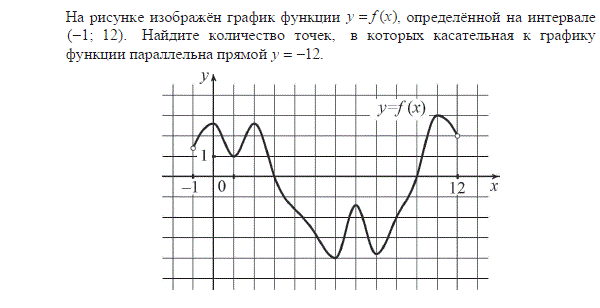
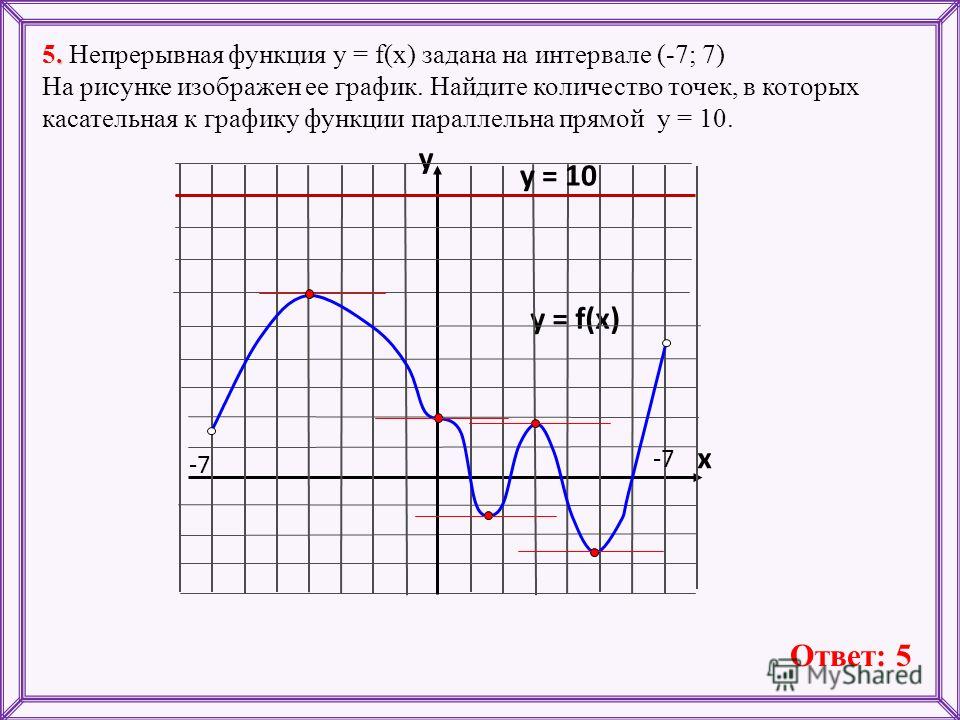
 Поскольку приближается к , приближается к 0. Таким образом, формируется дополнительное уравнение касательной.
Поскольку приближается к , приближается к 0. Таким образом, формируется дополнительное уравнение касательной.