Как найти косинус между двумя векторами: Как найти косинус угла между векторами? Ответ на webmath.ru

Угол между векторами и скалярное произведение векторов

Теоретический урок по предмету математики для решения задач по теме «Векторы».

Содержание данной страницы электронного справочника для школьников:

• – тема «Свойства векторов» рассматривается на примере решения задачи 86;
• – онлайн задания, как находить угол между векторами, в том числе в координатной форме, как определяется скалярное произведение векторов, скалярный квадрат, представлены в контрольных работах 87 — 107 учебника.

Подключиться к телеграм-каналу «Учи английский». Онлайн-курс английского языка для начинающих.

Свойства векторов

1) Вектор

коллинеарный с вектором

2)

↑↑

↑↑

3)

=

4)

=

—

5) Дано: система координат

модуль вектора

= 5

= 12

Найдите: OA

Решение:

OA=

= 13

OA =

= 13

Ответ: OA = 13

***

 

Пусть

и

— данные векторы.

1) Отложим от точки O векторы

=

и

=

2) Если

↑↓

— противоположно направленные векторы, то лучи OA и OB образуют угол

AOB

3) Если

↑↑

— сонаправленные векторы, то угол между векторами

и

равен 0°.

Угол между двумя векторами

и

обозначается так:

 

Определение:

Два вектора называются перпендикулярными, если угол между ними равен 90°.

***

 

Задача 86.

Дано:

ABCD — квадрат

AC ∩ BD = O

 

Найти: углы между векторами

BAC,

DAB = ?

Вычисление:

a) Т. к. AC — диагональ квадрата, то она делит угол

A пополам. Тогда угол между векторами

= 45°

б) Т.к. ABCD — квадрат, то градусная мера угла между векторами

=

= 90°, т.е. прямой угол.

***

 

Наверх

Скалярное произведение векторов

Задача 87.

Дано:

ABCD — ромб

BD = AB; AC ∩ BD = 0

 

Вычислите: угол, образованный векторами

и

,

и

,

и

= ?

Решение:

а) По определению ромба ΔABD — равносторонний (AB = AD = BD).

Значит, все углы в треугольнике равны 60°.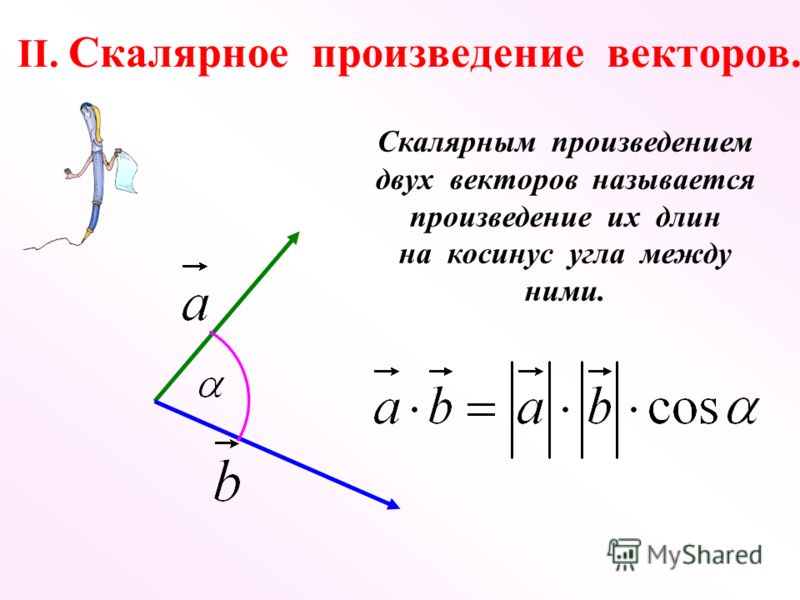 Тогда угол между векторами

= 60°

б) Т.к. векторы

↑↑

сонаправленные, то угол между векторами

= 0°

в) Т.к. векторы

↑↓

— противоположно направленные, то угол между векторами

= 180°

***

 

Определение:

Скалярным произведением двух векторов (формула 1) называется произведение длин этих векторов на косинус угла (Cos) между ними.

Обозначение:

или

=

*cos (a,b)     (1)

Из формулы скалярного произведения векторов через косинус угла (1) следует:

1) скалярное произведение векторов больше нуля, если угол между векторами меньше 90°, т. е.

>0, если

<90°

скалярное произведение векторов меньше нуля, если угол между векторами больше 90°, т.е.

<0, если

>90°

2) Если

↑↑

— сонаправленные векторы, то угол между векторами равен нулю градусов, т.е.

=0°

=

3) Если

— перпендикулярные векторы и

=90°

Cos 90° = 0, то

= 0

Верно и обратное, т.е. если

= 0

Вывод: = 0

***

 

Задача 88.

Дано:

Векторы

=2

=3

Угол α = 90°

Найти: скалярное произведение векторов

Решение:

Используя формулу скалярного произведения векторов через косинус угла, получаем

=

•

• Cos 90° = 2 • 3 • 0 = 0

Ответ:

= 0

***

 

Скалярный квадрат

***

 

Задача 89.

Дано:

ΔABC — равносторонний

AB = a

 

Найти: скалярное произведение векторов 1)

2)

Решение: В равностороннем треугольнике все углы равны 60°.

1)

=

•Cos (

) =

•

=

2)

=

•Cos (120°) = —

***

 

Задача 90.

Дано:

Векторы

=2;

=3

1) угол α = 45°

2) α = 135°

 

Найти: скалярное произведение векторов

Решение:

1)

=

•Cos 45° = 2 • 3 •

= 3

2)

=

•Cos 135° = 2 • 3 •

= -3

Ответ: 1) 3

; 2) -3

***

 

Задача 91.

Дано:

ΔABC — равносторонний

AB = a

BD — высота

 

Найти: скалярное произведение векторов

1)

2)

3)

Решение:

1)

=

•Cos 120° =

• (-Cos 60°) = —

2)

т.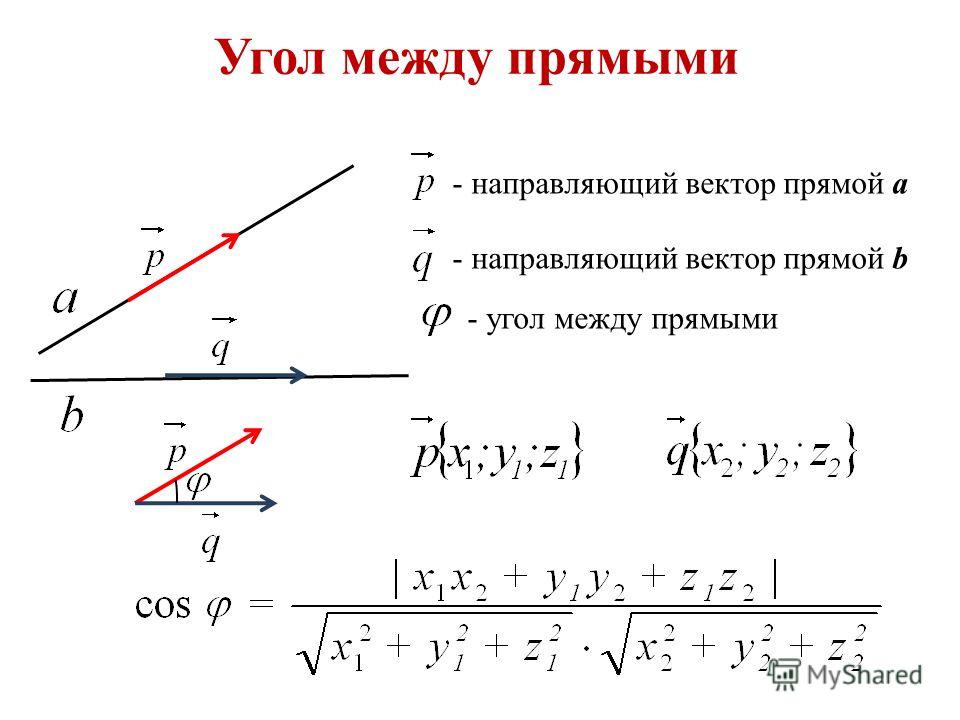 к. векторы перпендикулярны BD

AC

= 0

3)

=

=

Ответ:1) —

; 2) 0 ; 3)

 

Задача 92.

Дано:

ABCD — ромб

BD ∩ AC = 0

BD = AB

1)

;

2)

;

 

Найти: величину угла между векторами

1)

; 2)

Решение:

1) Рассмотрим ΔABC — равнобедренный, т.к. AB=BD.

Зная, что в ромбе все стороны равны, получаем ΔABD — равносторонний.

Тогда

DAB =

BDA = 60°

По свойству ромба следует, что

ADC = 120°

Тогда угол между векторами

=120°

 

2) Т.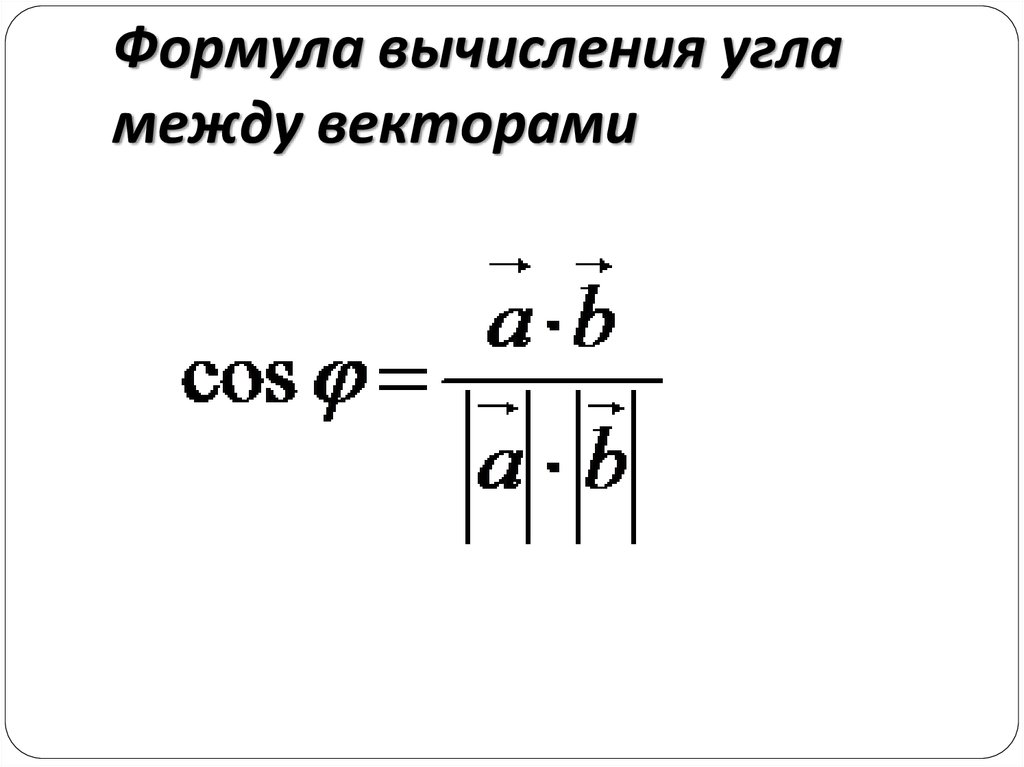 к. стороны параллельны и векторы сонаправлены:

BA || CD и

↑↑

, тогда векторы параллельны

||

, поэтому векторы равны

=

.

Рассмотрим треугольник ΔCBD — равнобедренный, т.к. две стороны равны: BD=BC.

По определению ромба ΔCBD — равносторонний.

Значит, угол

BDC = 60°

По свойству ромба угол

ADC = 120°.

Тогда угол между векторами

=120°.

Ответ: 1)

=120°; 2)

=120°.

***

 

Наверх

Скалярное произведение векторов в координатах

Теорема:

Если два вектора имеют координаты

{x₁; y₁};

{ x₂; y₂}, то скалярным произведением двух векторов (формула 2) называется произведение их координат:

(2)

 

Доказательство:

1 случай.

Если какой-нибудь вектор — нулевой, то равенство (2) выполняется очевидно.

2 случай.

Если векторы

и

— неколлинеарны.

Отложим векторы от произвольной точки O.

Рассмотрим треугольник ΔOBA.

Известно, что формула косинуса

c² = a² + b² — 2ab • Cos α, получаем равенство

AB­­² = OB² + OA² — 2 • OB • OA • Cos α (3)

Учитывая значения (*)

=

;

=

;

=

; а также, что OA = |

|; OB = |

| ; AB = |

|, подставив значения (*) в равенство (3), получаем

|

|² = |

|² + |

|² — 2

(4)

Используя формулу для вычисления длины вектора по его координатам, получаем

=

;

=

.

Т.к.

= {x₂ — x₁; y₂ – y₁}, то, используя формулу для вычисления расстояния между двумя точками

, получаем

|

| =

.

Тогда из равенства (4) следует

(x₂ — x₁)² + (y₂ – y₁)² = x₂² + y₂² + x₁² + y₁² — 2

x₂² -2 x₂ x₁ + x₁² + y₂² – 2 y₂y₁ + y₁² = x₂² + y₂² + x₁² + y₁² — 2

-2 x₂ x₁– 2 y₂y₁ = — 2

= x₂ x₁ + y₂ y₁

***

 

Следствия:

1) Если векторы перпендикулярны, т. е.

{x₁; y₁}

{ x₂; y₂}

x₁ x₂ + y₁ y₂ = 0

2) По определению скалярного произведения двух векторов (формула 1)

=

•

• Cos α

Cos α =

Формула для нахождения косинуса угла через координаты векторов:

 

Для вычисления синуса и тангенса угла между векторами через косинус угла используются формулы приведения и тригонометрические функции.

 

***

 

Наверх

Скалярное векторное произведение

Задача 93.

Если

{

; -1};

{2; 3}, то

= 0,5 + (-3) = -2,5

***

 

Задача 94.

Если

{x; -1};

{3; 2} и векторы перпендикулярны

, тогда

= 3x — 2

0 = 3x — 2

2 = 3x

x =

***

 

Задача 95.

Дано:

Координаты точек

A(2;8), B(-1;5), C(3;1)

 

Найти: косинус угла между векторами Cos A = ?

Решение:

Т.к. каждая координата вектора равна разности соответствующих координат его конца и начала

{b₁ – a₁; b₂ – a₂}, тогда

= {

} = {

}

= {

} = {

}

Используя формулу для нахождения углов через координаты векторов

Cos A =

, получаем

Cos A =

=

=

=

Ответ: Cos A =

***

 

Длина вектора

Задача 96.

Дано:

угол между векторами равен

=

=60° ,

длины векторов |

| = 1, |

| = |

| = 2

 

Найти: произведение векторов (

)

= ?

Решение:

(

)

=

+

= |

|•|

|•Cos 60° + |

|•|

|•Cos 60° = 1 + 2 = 3

Ответ: (

)

= 3

***

 

Задача 97.

Дано:

=

,

=

длина векторов |

|=|

|=1

— перпендикулярные векторы

Найти: произведение векторов

= ?

Решение:

= (

)•(

) = 3

² + 12

— 2

— 8

² =

= 3

² + 10

— 8

² = 3|

|² + 0 — 8|

|² = -5.

Ответ:

= -5.

***

 

Задача 98.

Дано:

{1,5 ; 2},

{4 ; -0,5}

 

Найти: произведение векторов

= ?

Решение:

= x₁ x₂ + y₁ y₂ = 6 + (-1) = 5

Ответ:

= 5.

***

 

Задача 99.

Дано:

{0 ; -3},

{5 ; x}

— перпендикулярные векторы

 

Найти: произведение векторов

= ?

Решение:

= x₁ x₂ + y₁ y₂

0 = 0 + (-3x)

3x = 0

x = 0

Ответ: при x=0,

.

***

 

Задача 100.

Дано:

Координаты точек

A(2;8), B(-1;5), C(3;1)

 

Найти: косинус угла векторов

1) Cos B = ?

2) Cos C = ?

Решение:

1)

Т.к. каждая координата вектора равна разности соответствующих координат его конца и начала

{b₁ – a₁; b₂ – a₂}, тогда

= {

} = {

}

= {

} = {

}

Используя формулу для нахождения углов через заданные координаты векторов

Cos B =

, получаем

Cos B =

=

= 0

2)

= {

} = {

}

= {

} = {

}

Cos C =

=

=

=

Ответ: Cos B =0, Cos C =

***

 

Задача 101.

Дано:

, где i и j – координатные векторы

 

Найти: длину вектора |

| = ?

Решение:

Найдем координаты вектора

.

{3; -4}

Т.к. длина вектора равна квадратному корню из суммы квадратов его координат |

| =

, тогда получаем

|

| =

=

= 5.

Ответ: |

| = 5.

***

 

Задача 102.

Дано:

ABCD — ромб

AB =

, AD =

 

Доказать: диагонали ромба в точке пересечения перпендикулярны

AC

BD или

=0

Доказательство:

Т. к. ABCD — ромб — параллелограмм, то векторы параллелограмма

,

=

—

= (

+

) (

—

) =

—

² +

² —

=

² —

² = =|

|² -|

|² = 0. Поэтому угол между векторами

= 90°. Значит, диагонали ромба в точке пересечения перпендикулярны AC

BD.

***

 

Задача 103.

Дано:

треугольник ΔABC — равнобедренный

AM — медиана

 

Доказать:

1) 4AM² = AB² + AC² + 2AB • AC • Cos A

2) CH = AM

Доказательство:

1) Т.к. точка M — середина BC, тогда

2

=

Значит, (2

) • (2

) = (

)(

) =

= AB² + 2AB + 2AB • AC • Cos A + AC² = AB² + AC² + 2AB • AC • Cos A

Получаем 4AM² = AB² + AC² + 2AB • AC • Cos A

 

2) По формуле, полученной выше, следует

4CH² = AC² + BC² + 2AC • BC • Cos C

Т.к. треугольник ΔABC — равнобедренный, тогда AB = BC,

A =

C

Cos

A = Cos

C

Получим, что 4CH² = AC² + BC²(=AB²) + 2AC • BC(=AB) • Cos C (= Cos A)

4CH² = AC² + AB² + 2AC • AB • Cos A

4CH² = 4AM²

=

2CH = 2AM | : 2

CH = AM

***

 

Задача 104.

Дано:

ABCD — выпуклый четырехугольник

BD = d₁ и AC = d₂ — диагонали

d₁ ∩ d₂ = O — точка пересечения диагоналей

 

Доказать:

Площадь четырехугольника равна половине произведения диагоналей на синус острого угла между ними

S_ABCD=

d₁ • d₂ • Sin α

Доказательство:

Площадь четырехугольника — сумма площадей четырех треугольников.

S_ABCD= S₁ + S₂ + S₃ + S₄ , где

S₁ = S_ΔAOB ; S₂ = S_ΔCOB ; S₃ = S_ΔCOD ; S₄ = S_ΔAOD

S₁ =

BO • OA • Sin α

S₂ =

BO • OC • Sin (180° — α) =

BO • OC • Sin α

S₃ =

CO • OD • Sin α

S₄ =

AO • OD • Sin (180° — α) =

AO • OD • Sin α

Сложив S₁ + S₂ + S₃ + S₄, получаем

S_ABCD=

BO • Sin α (OA+OC) +

+

OD • Sin α (CO+OA)

Т. к. OA+OC = AC, CO+OA = AC, BO + OD = BD тогда

S_ABCD=

BO • AC • Sin α +

OD • AC • Sin α =

BD • AC • Sin α

 

Формула площади выпуклого четырехугольника:

S_ABCD=

d₁ • d₂ • Sin α

 

 

***

 

Задача 105.

Дано:

два вектора образуют угол α = 150°,

длины векторов |

| = 2

, |

| = 2

 

Найти: длину вектора |2

—

| = ?

Решение:

BC² = AB² + AC² — 2 AB • AC • Cos 150°

BC² = 48 + 4 — 2 • 4

• 2 • (-

) = 52 + 24 = 76

BC =

= 2

Ответ: BC = |2

—

| = 2

***

 

Задача 106.

Дано:

Треугольник ΔABC

Угол

B = 45°,

C = 70°

a=24,6

 

Найти: Угол в градусах

A, стороны b, c

Решение:

A = 180° — (45° + 70°) = 75°

 

Используя теорему синусов

, получаем выражение

b =

≈ 19,2

c =

≈

≈ 25,5

Ответ:

A = 75°; b ≈ 19,2; c ≈ 25,5.

***

 

Задача 107.

Дано:

длины векторов |

| = 5, |

| = 8,

угол между 2 векторами

=60°

 

Найти: значение векторов

1) |

|= ?

2) |

|= ?

Решение: По теореме косинусов

1)

AC² = AB² + BC² — 2AB • BC • Cos 120°

AC² = 25 + 64 — 80 • (- 0,5) = 129

AC = ±

, но AC = —

не удовлетворяет решению задачи. Значит, AC =

.

 

2) BC² = AB² + AC² — 2AB • AC • Cos 60°

BC² = 89 — 80 • 0,5 = 49

BC = ±

, но BC = — 7 не удовлетворяет решению задачи. Значит, BC = 7.

Ответ: |

| =

; |

| = 7.

***

 

Между любыми двумя векторами можно найти угол. Нахождение угла между векторами

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. = a → , b → a → · b →

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

ωn = υ 2

Подставляя в это выражение υ из (10.9), находим, что

ωn = ω2 R

Модуль тангенциального ускорения в соответствии с (9.8) равен

опять уравнением (10.9), получаем:

(ω R)

t→ 0

t→ 0

t→ 0

t→ 0

ωτ = βR

(10. 10) d dt υ . Воспользовавшись

R β,

Таким образом, как нормальное, так и тангенциальное ускорение растет линейно с R — расстоянием точки от оси вращения.

Кроме рассмотренных ранее операций сложения и вычитания векторов, а также умножения вектора на скаляр (см. §2), существуют также операции перемножения векторов. Два вектора можно умножить друг на друга двумя способами: первый способ дает в результате некоторый новый вектор, второй — приводит к скалярной величине. Отметим, что операции деления вектора на вектор не существует.

Сейчас мы рассмотрим секторное произведение векторов. Скалярное произведение векторов мы введем позднее, когда оно нам понадобится.

Векторным произведением двух векторов А и В называется вектор С, обладающий следующими свойствами:

1) модуль вектора С равен произведению модулей перемножаемых векторов на синус угла α между ними (рис 35):

2) вектор С перпендикулярен к плоскости, в которой лежат векторы А и В, причем направление его связано с направлениями А и В по правилу правого винта: если смотреть вслед вектору С, го совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке.

Символически векторное произведение можно записать двумя способами: |AB| или A× B .

Мы будем пользоваться первым из этих способов, причем иногда для облегчения чтения формул будем ставить запятую между сомножителями. Не следует применять одновременно косой крест и квадратные скобки: [А× В], Недопустима запись такого вида: [АВ]=ABsinα. Слева здесь стоит вектор, справа — модуль этого вектора, т. е. скаляр. Справедливо следующее равенство:

| [ AB] |= ABsin α .

Поскольку направление векторного произведения определяется направлением вращения от первого сомножителя ко второму, результат векторного перемножения двух векторов зависит от порядка сомножителей. Изменение порядка сомножителей вызывает изменение направления результирующего вектора на противоположное (рис. 35)

= −

B× A = − (A × B).

Таким образом, векторное произведение не обладает свойством коммутативности. Можно доказать, что векторное произведение дистрибутивно, т.

е. что

[ A,(B1 + B2 + …+ BN )] = [ AB1 ] + [ AB2 ] + …+ [ ABN ] .

Векторное произведение двух полярных или двух аксиальных векторов есть аксиальный вектор. Векторное произведение аксиального вектора на полярный (или наоборот) будет, однако, вектором полярным. Изменение условия, определяющего направление аксиальных векторов, на обратное приведет в этом случае к изменению знака перед векторным произведением и одновременно к изменению знака перед одним из сомножителей, В итоге величина, выражаемая векторным произведением остается без изменений.

Модулю векторного произведения можно дать простую геометрическую интерпретацию: выражение ABsinα численно равно площади параллелограмма, построенного на векторах А и В (рис. 36; вектор С=[АВ] направлен в этом случае перпендикулярно к плоскости чертежа, за чертеж).

Пусть векторы А и В взаимно перпендикулярны (рис. 37).

1) , и образует с

Образуем двойное векторное произведение этих векторов:

D = A,[ BA] ,

т. е. умножим вектор В на А, а затем умножим вектор А на вектор, получившийся в результате первого умножения. Вектор [ВА] имеет модуль, равный BA(sin α = sin π 2

векторами А и B углы, равные π/2. Следовательно, модуль вектора D равен |A|*||=A*BA=A2 B. Направление же вектора D, как легко видеть из рис. 37, совпадает с направлением вектора В. Это дает нам основание написать следующее равенство:

Формулой (11.3) мы будем в дальнейшем пользоваться неодноктратно. Подчеркнем, что она справедлива только в том случае, когда векторы А и В взаимно перпендикулярны.

Уравнение (10.9) устанавливает связь между модулями векторов v и ω. С помощью векторного произведения может быть написано выражение, дающее cooтношение между самими векторами. Пусть тело вращает вокруг оси z с угловой скоростью ω (рис. 38). Jleгко видеть, что векторное произведение ω на радиус-вектор точки, скорость v которой мы хотим найти, представляет собой вектор, совпадающий по направлению с вектором v и имеющий модуль, равный ωr sinα=ωR, т. е. v [см. формулу (10.9)]. Таким образом, векторное произведение [ωR] и по направлению и по модулю равно вектору v.

Пусть V – n -мерное векторное пространство, в котором заданы два базиса: e 1 , e 2 , …, e n – старый базис, e » 1 , e » 2 , …, e « n – новый базис. У произвольного вектора a есть координаты в каждом из них:

a = a 1 e 1 + a 2 e 2 + … + a

n e n ;

a = a» 1 e » 1 + a» 2 e » 2 + … + a» n e « n .

Для того чтобы установить связь между столбцами координат вектора a в старом и новом базисах, надо разложить векторы нового базиса по векторам старого базиса:

e » 1 = a 11 e 1 + a 21 e 2 + … + a n 1 e n ,

e » 2 = a 12 e 1 + a 22 e 2 + … + a n 2 e n ,

………………………………..

e « n = a 1n e 1 + a 2n e 2 + … + a nn e n .

Определение 8.14. Матрицей перехода от старого базиса к новому базису называется матрица, составленная из координат векторов нового базиса относительно старого базиса, записанных в столбцы, т. е.

Столбцы матрицы T – это координаты базисных, а значит, линейно независимых, векторов, следовательно, эти столбцы линейно независимы. Матрица с линейно независимыми столбцами является невырожденной, ее определитель не равен нулю и для матрицы

T существует обратная матрица T –1 .

Обозначим столбцы координат вектора a в старом и новом базисах, соответственно, как [a ] и [a ]». С помощью матрицы перехода устанавливается связь между [a ] и [a ]».

Теорема 8.10. Столбец координат вектора a в старом базисе равен произведению матрицы перехода на столбец координат вектора a в новом базисе, то есть [a ] = T [a ]».

Следствие . Столбец координат вектора a в новом базисе равен произведению матрицы, обратной матрице перехода, на столбец координат вектора a в старом базисе, то есть [a ]» = T –1 [a ].

Пример 8.8. Составить матрицу перехода от базиса

e 1 , e 2 , к базису e » 1 , e » 2 , где e » 1 = 3e 1 + e 2 , e » 2 = 5e 1 + 2e 2 , и найти координаты вектора a = 2e » 1 – 4e » 2 в старом базисе.

Решение . Координатами новых базисных векторов относительно старого базиса являются строки (3, 1) и (5, 2), тогда матрица T примет вид . Так как [a ]» = , то [a ] = × = .

Пример 8.9. Даны два базиса e 1 , e 2 – старый базис, e » 1 , e » 2 – новый базис, причем e » 1 = 3e 1 + e 2 , e » 2 = 5e 1 + 2e 2 . Найти координаты вектора a = 2e 1 – e 2 в новом базисе.

Решение . 1 способ . По условию даны координаты вектора а в старом базисе: [a ] = . Найдем матрицу перехода от старого базиса e 1 , e 2 к новому базису e » 1 , e » 2 .

Получим матрицу Т = для нее найдем обратную матрицу T –1 = . Тогда согласно следствию из теоремы 8.10 имеем [a ]» = T –1 [a ] = × = .

2 способ. Так как e » 1 , e » 2 базис, то вектор а раскладывается по базисным векторам следующим образом a = k 1 e » 1 – k 2 e » 2 . Найдем числа k 1 и k 2 – это и будут координаты вектора а в новом базисе.

a = k 1 e » 1 – k 2 e » 2 = k 1 (3e 1 + e 2) – k 2 (5e 1 + 2e 2) =

= e 1 (3k 1 + 5k 2) + e 2 (k 1 + 2k 2) = 2e 1 – e 2 .

Так как координаты одного и того же вектора в данном базисе определяется однозначно, то имеем систему: Решая данную систему, получим k 1 = 9 и

k 2 = –5, т. о. [a ]» = .

Найдем связь между векторами j (вектор плотности тока) и Е (напряженность поля) в одной и той же точке проводника. Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Напряжение, приложенное концам проводника, равно Edl, а его сопротивление. Ток I это суммарный ток через S — площадь поперечного сечения проводника. Тогда ток dI ток через элементарную площадку dS. Подставив эти выражения в формулу. Запишем. .

Слайд 12 из презентации «Сопротивление проводника» к урокам физики на тему «Сопротивление»

Размеры: 720 х 540 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке физики, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…». Скачать всю презентацию «Сопротивление.ppt» можно в zip-архиве размером 66 КБ.

Скачать презентацию

«Наука физика» — Физика, как наука. Физика возникла еще во времена древних греков в V веке до н.э. Звуковые явления. Вещество. Материя. Электрические явления. Физические явления. Философия. Электрические явления — это взаимодействие электрических зарядов, сверкание молнии. Молекула воды. Связи физики настолько многообразны, что порой люди не видят их.

«Абрам Фёдорович Иоффе» — Иоффе на семинаре по физике полупроводников. Физико-технический институт. Физико-технический институт. Политехнический институт. Шокли и Иоффе. Здание Мюнхенского университета. Иоффе на строительстве циклотрона ФТИ. Одна из последних фотографий Иоффе. Капицы в Кембридже. Фото Капицы. А.Иоффе и его земляк С.Тимошенко — студенты петербургских институтов.

«История электричества» — XXI век — электрическая энергия окончательно стала неотъемлемой частью жизни. XIX век — Фарадей открывает электромагнитную индукцию и законы электролиза. Известно, что если некоторые вещества потереть о шерсть, они притягивают лёгкие предметы. XIX век — Максвелл формулирует свои уравнения. Работы Джоуля, Ленца, Ома по изучению электрического тока.

«Магнитная индукция» — Сила Ампера. Основные свойства магнитного поля. Взаимодействия между проводниками с током называют магнитными. Направление силы Ампера можно определить с помощью правила левой руки. Магнитное поле порождается электрическим током (движущимися зарядами). Магнитное поле существует реально независимо от нас, от наших знаний о нем.

«Рассеяние частиц» — Контраст в рассеянии рентгеновских лучей. Кошка Штурмана. Радиус инерции и константа поступательного трения. Радиус инерции однородной сферической частицы связан с ее радиусом r0. Радиус инерции и характеристическая вязкость. Вариация контраста методом h3O/D2O смесей. Плотность рассеяния растворителя.

Формула угла между векторами

Угол между двумя векторами

Рассмотрим понятие угла между двумя направлениями в пространстве.

Как и на плоскости, в пространстве направлением называется множество всех лучей, каждый из которых сонаправлен с данным. Таким образом, любой луч из данного множества сонаправленных лучей вполне определяет это направление (подобно тому, как любой направленный отрезок вполне определяет вектор, который он изображает). Поэтому направление в пространстве обычно задают при помощи только одного луча.

Углом между двумя направлениями называется величина наименьшего угла между любыми лучами этих направлений с общим началом.

Угол между лучами l₁ и l₂ обозначается \(\widehat{l_1; l_2}\). По определению угол между двумя направлениями находится в промежутке [0°; 180°].

Углом между двумя ненулевыми векторами называется угол между направлениями этих векторов. Угол между векторами а и b (рис. 21) обозначается \(\widehat{a; b}\)

Если угол между векторами а и b равен 90°, то эти векторы называют перпендикулярными (или ортогональными) и пишут: а ⊥ b.

Отметим, что если а\(\upuparrows\)b, то \(\widehat{a; b}\) = 0°, а если а\(\uparrow\downarrow\)b, то \(\widehat{a; b}\) =180°.

Рассмотрим некоторую прямую l, на которой выбрана единица измерения длины. Пусть А и В — некоторые точки прямой l такие, что |АВ| = 1.

Тогда векторы \(\overrightarrow{AB}\) и \(\overrightarrow{BA}\) называются единичными векторами прямой l (рис.22).

Единичные векторы прямой задают на ней два направления. Одно из них называется положительным, другое — отрицательным.

Прямая, на которой выбрана точка О (начало отсчета), задано положительное направление и задана единица измерения длины, называется осью. Вектор е (|е| = 1), задающий направление оси, называется единичным вектором оси (рис. 23).

Углом между вектором и осью, называется величина угла между направлением оси и направлением вектора (рис. 24).

Вычисление угла между двумя векторами.

По определению скалярного произведения

а • b = | а | • | b | cos\(\widehat{(a; b)}\).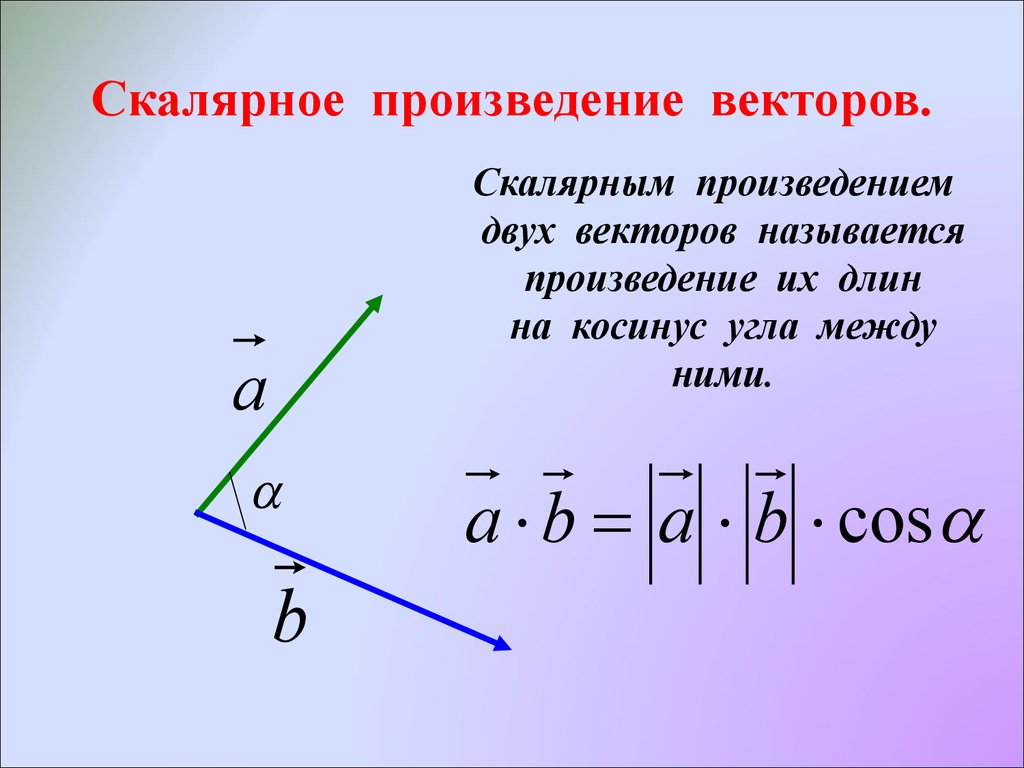 2}} = -\frac{4}{9} $$

Как найти угол между двумя векторами – mathsathome.com

Как найти угол между двумя векторами: Видеоурок

Калькулятор угла между двумя векторами

Калькулятор ниже вычисляет угол между 2D и 3D векторами. Просто введите компоненты каждого вектора в форму

Как найти угол между двумя векторами

Чтобы найти угол между двумя векторами:

1. Найдите скалярное произведение двух векторов.
2. Разделите это значение на величину первого вектора.
3. Разделите это значение на величину второго вектора.
4. Возьмите арккосинус этого значения, чтобы получить угол.

Например, найдите угол между и .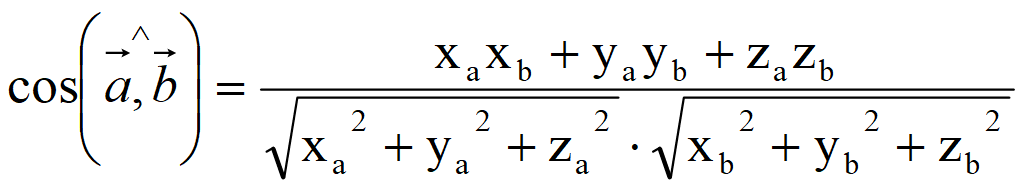

Шаг 1. Найдите скалярное произведение двух векторов

Чтобы найти скалярное произведение двух векторов, перемножьте соответствующие компоненты и сложите их.

Скалярное произведение двух двумерных векторов и находится с помощью .

Для векторов и скалярное произведение .

Поэтому

(3\-2)” role=”presentation” style=”font-size: 113%; position: relative;»>

Шаг 2. Разделите это на величину первого вектора

Чтобы вычислить величину вектора, используйте теорему Пифагора с компонентами 𝑥 и y вектора.

Величина любого вектора находится следующим образом: .

Следовательно, величина вектора равна .

Это становится который есть .

Величина первого вектора, a равна .

Мы делим скалярное произведение, рассчитанное ранее, на эту величину.

Получаем

Шаг 3. Разделим на величину второго вектора

Величина второго вектора b находится с помощью .

Для вектора величина равна .

Это становится который есть .

Делим предыдущий результат на эту величину, чтобы получить

Шаг 4. Возьмем арккосинус этого результата

Формула для нахождения угла между двумя векторами: .

Это можно преобразовать, взяв значение, обратное косинусу в обеих частях уравнения.

Угол между двумя векторами равен .

Как было рассчитано ранее:

Используя калькулятор, мы вводим, .

Это дает нам угол между двумя векторами как .

Формула угла между двумя векторами

Формула угла между двумя векторами, a и b равны θ=cos ^-1 ( ^a•b / _|a||b| ). Где вектор A IS (A _x A _Y ) и вектор B IS (B _x B _Y ), точка A • B = A _x B A • B = A _x B A • B = A _x B B A _x + а _у б _у .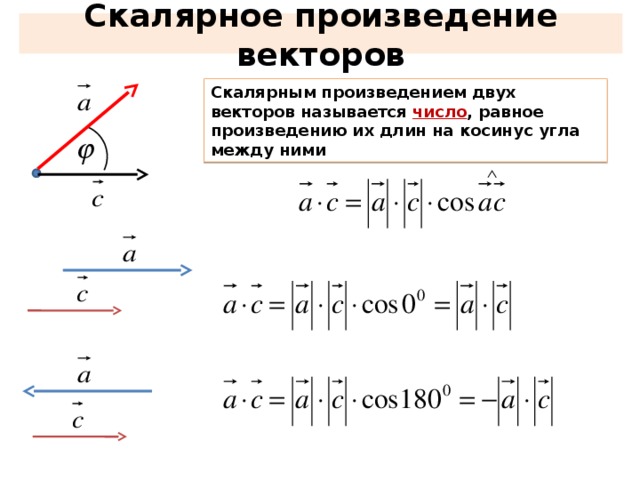 Величина вектора |a|=√ ( a _x ² + A _Y ² ) и величина вектора | B | = √ ( B _x ² + B _Y ² + B _Y ² 050505050505050505050505053 303030303030303. 33030305050505.

Наиболее распространенное отображение формулы для угла между двумя векторами показано ниже как .

Эту формулу можно преобразовать в более удобную формулу, взяв арккосинус обеих частей уравнения.

Это дает нам прямую формулу для угла между двумя векторами.

Угол между двумя векторами равен .

Мы можем использовать эту формулу, чтобы найти угол между двумя векторами в 2D.

Найдите угол между векторами и .

В этих двух векторах a _x = 2, a _y = 5, b _x = -4 и b _y = -1.

Скалярное произведение находится с помощью , которое для наших векторов становится и так .

Величина каждого вектора находится с помощью теоремы Пифагора с компонентами 𝑥 и y.

Для этих векторов и так далее. так что .

Теперь можно использовать формулу.

и это можно оценить прямо на калькуляторе, чтобы дать.

Как найти угол между двумя векторами в 3D

Чтобы найти угол между двумя векторами в 3D:

1. Найдите скалярное произведение векторов.
2. Разделите скалярное произведение на величину каждого вектора.
3. Используйте инверсию косинуса к этому результату.

Например, найдите угол между и .

Эти векторы содержат компоненты в трех измерениях: 𝑥, y и z.

Для вектора a _x =2, a _y = -1 и a _z = 3. z = 1.

Шаг 1. Найдите скалярное произведение векторов

Чтобы найти скалярное произведение двух векторов, умножьте соответствующие компоненты каждого вектора и сложите результаты.

Для трехмерного вектора .

Для наших векторов это становится .

Это упрощается до .

Шаг 2. Разделите это скалярное произведение на величину двух векторов

Чтобы найти величину вектора в 3D, используйте теорему Пифагора. Например, .

Для вектора , . Это упрощает до .

Для вектора , . Это упрощает до .

Мы делим скалярное произведение, найденное на шаге 1, на обе эти величины.

Получаем .

Шаг 4. Используйте обратный косинус для этого результата

Формула для угла между двумя векторами: . Эту формулу можно использовать для векторов в 2D или 3D.

Чтобы изменить эту формулу для угла, мы берем арккосинус обеих сторон.

Ранее мы рассчитали , и .

Поэтому .

Это можно оценить на калькуляторе, чтобы получить угол между двумя векторами как .

Что говорит нам знак cosθ о векторах?

Если значение cosθ положительное, угол между векторами острый. Если значение cosθ отрицательно, угол между векторами тупой.

Как определить, перпендикулярны ли два вектора

Два вектора перпендикулярны, если их скалярное произведение равно нулю. Для двух векторов (a _x a _y ) и (b _x b _y ) скалярное произведение равно A • B = A _x B _x + A _Y B _Y . Если a _x b _x + a _y b _y , то два вектора перпендикулярны. Это означает, что они встречаются под прямым углом.

Формула для угла между двумя векторами имеет вид .

Если , то эта формула принимает вид .

Если числитель дроби равен нулю, то и вся дробь равна нулю. Поэтому формула становится .

Решая это для угла, мы используем арккосинус нуля, .

Арккосинус нуля равен 90°.

Следовательно, если скалярное произведение двух векторов равно нулю, угол между двумя векторами всегда будет равен 90°.

Например, покажите, что и перпендикулярны.

Если два вектора перпендикулярны, это означает, что они пересекаются под прямым углом.

Чтобы показать, что два вектора перпендикулярны, вычислите скалярное произведение. Если скалярное произведение двух векторов равно нулю, векторы перпендикулярны.

Если скалярное произведение равно любому числу, отличному от нуля, векторы не перпендикулярны.

Скалярный продукт находится с помощью .

В векторах и , a _x = 3, a _y = 4, b _x = -8 и b _y = 6.

Следовательно, скалярное произведение становится .

Вычисляя это, мы получаем и так, .

Скалярное произведение равно нулю, поэтому векторы перпендикулярны.

Как найти угол между двумя векторами?

Угол между двумя векторами — это угол между их хвостами. Его можно найти либо с помощью скалярного произведения (скалярного произведения), либо с помощью перекрестного произведения (векторного произведения). Обратите внимание, что угол между двумя векторами всегда лежит в пределах от 0° до 180°.

Давайте узнаем больше об угле между двумя векторами как в 2D, так и в 3D вместе с формулой, выводом и примерами.

1.	Что такое угол между двумя векторами?
2.	Угол между двумя формулами векторов
3.	Как найти угол между двумя векторами?
4.	Часто задаваемые вопросы об угле между двумя векторами

Что такое угол между двумя векторами?

9Угол 0029 между двумя векторами — это угол, образованный при пересечении их хвостов. Если векторы НЕ соединены хвост-хвост, тогда мы должны соединить их от хвоста к хвосту, сдвинув один из векторов, используя параллельный сдвиг. Вот несколько примеров, чтобы увидеть, как найти угол между двумя векторами.

Здесь мы видим, что когда начало вектора соединяется с хвостом другого вектора, образующийся угол НЕ является углом между векторами. Вместо этого один из них должен быть сдвинут либо в том же направлении, либо параллельно самому себе так, чтобы хвосты векторов соединились друг с другом для измерения угла.

Формулы угла между двумя векторами

Есть две формулы для нахождения угла между двумя векторами: одна в терминах скалярного произведения, а другая в терминах перекрестного произведения. Но наиболее часто используемая формула нахождения угла между двумя векторами включает скалярное произведение (в следующем разделе мы увидим, в чем проблема с векторным произведением). Пусть a и b — два вектора, а θ — угол между ними. Тогда вот формулы, чтобы найти угол между ними, используя как скалярное произведение, так и перекрестное произведение:

• Угол между двумя векторами с использованием скалярного произведения, θ = cos ^-1 [ ( a · b ) / (| a | | b |) ]
• Угол между двумя векторами с использованием перекрестного произведения равен, θ = sin ^-1 [ | а × б | / (| а | | б |) ]

, где a · b — скалярное произведение, а a × b — перекрестное произведение a и б .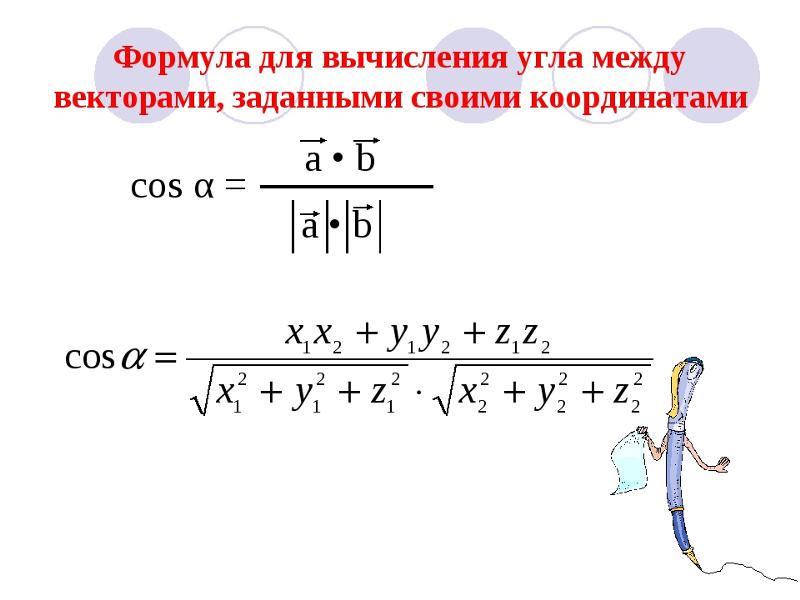 Обратите внимание, что формула перекрестного произведения также включает в себя величину в числителе, а формула скалярного произведения — нет.

Угол между двумя векторами с использованием скалярного произведения

По определению скалярного произведения a · b = | и | | б | cos θ . Решим это для cos θ. Разделив обе части на | и | | б |.

cos θ = ( a · b ) / (| A | | B |)

θ = COS ^-1 [( A · B ) / (| A | | B |)]

Это формула угла между двумя векторами в терминах скалярного произведения (скалярного произведения).

Угол между двумя векторами с помощью векторного произведения

По определению векторного произведения a × b = | и | | б | sin θ \(\шляпа{n}\). Чтобы решить это для θ, давайте возьмем величину с обеих сторон. Тогда мы получим

| а × б | = | и | | б | sin θ |\(\шляпа{n}\)|.

Мы знаем, что \(\hat{n}\) является единичным вектором и, следовательно, его величина равна 1. Итак,

| а × б | = | и | | б | sin θ

Разделив обе части на | и | | б |.

грех θ = | а × б | / (| a | | b |)

θ = sin ^-1 [ | а × б | / (| a | | b |) ]

Это формула угла между двумя векторами в терминах перекрестного произведения (векторного произведения).

Как найти угол между двумя векторами?

Давайте рассмотрим несколько примеров нахождения угла между двумя векторами с использованием скалярного произведения как в 2D, так и в 3D. Давайте также увидим неоднозначность использования формулы перекрестного произведения для нахождения угла между двумя векторами.

Угол между двумя векторами в 2D

Рассмотрим два вектора в 2D, скажем, a = <1, -2> и b = <-2, 1>. Пусть θ — угол между ними. Давайте найдем угол между векторами, используя как скалярное произведение, так и перекрестное произведение, и посмотрим, какую неоднозначность может вызвать перекрестное произведение.

Угол между двумя векторами в 2D с использованием скалярного произведения

Давайте вычислим скалярное произведение и величины обоих векторов.

• а · б = <1, -2> · <-2, 1> = 1(-2) + (-2)(1) = -2 — 2 = -4.
• | и | = √(1)² + (-2)² = √1 + 4 = √5
• | б | = √(-2)² + (1)² = √4 + 1 = √5

Используя формулу угла между двумя векторами с использованием скалярного произведения, θ = cos ^-1 [ ( a · b ) / (| a | | b |) ].

Тогда θ = cos ^-1 (-4 / √5 · √5) = cos ^-1 (-4/5)

Мы можем либо использовать калькулятор, чтобы оценить это непосредственно, либо мы можем использовать формулу cos ^-1 (-x) = 180° — cos ^-1 x и затем использовать калькулятор (всякий раз, когда скалярное произведение отрицательное, используйте формулу cos ^-1 (-x) = 180 ° — cos ^-1 x, это очень полезно, поскольку мы знаем, что угол между двумя векторами всегда лежит между 0 ° и 180 °). Тогда мы получим:

cos ^-1 (-4/5) ≈ 143,13°

Угол между двумя векторами в 2D с использованием векторного произведения

Давайте вычислим перекрестное произведение a и b .

a × b = \(\left|\begin{array}{ccc}
я&й&к\
1&-2&0\
-2 и 1 и 0
\end{array}\right|\) = <0, 0, -3>

Теперь найдем его величину.

| а × б | = √(0)² + (0)² + (-3)² = 3

Используя формулу угла между двумя векторами с использованием перекрестного произведения, θ = sin ^-1 [ | а × б | / (| а | | б |)].

Тогда θ = sin ^-1 (3 / √5 · √5) = sin ^-1 (3/5)

Если мы используем калькулятор для расчета, θ ≈ 36,87 (или) 180 — 36,87 (поскольку синус положителен и во втором квадранте). Итак,

θ ≈ 36,87 (или) 143,13°.

Таким образом, мы получили два угла и нет оснований выбирать один из них как угол между векторами a и b . Таким образом, формула перекрестного произведения может не всегда быть полезной для нахождения угла между двумя векторами.

Угол между двумя векторами в 3D

Давайте рассмотрим пример, чтобы найти угол между двумя векторами в 3D. Пусть a = i + 2 j + 3 k и b = 3 i — 2 j + k . Сначала мы вычислим скалярное произведение и величины:

• a · b = <1, 2, 3> · <3, -2, 1> = 1(3) + (-2)(- 2) + 3(1) = 3 — 4 + 3 = 2,
• | и | = √(1)² + (2)² + 3² = √1 + 4 +9 = √14
• | б | = √(3)² + (-2)² + 1² = √9 + 4 + 1 = √14

Имеем θ = cos ^-1 [( a · b ) / (| a | | b |)].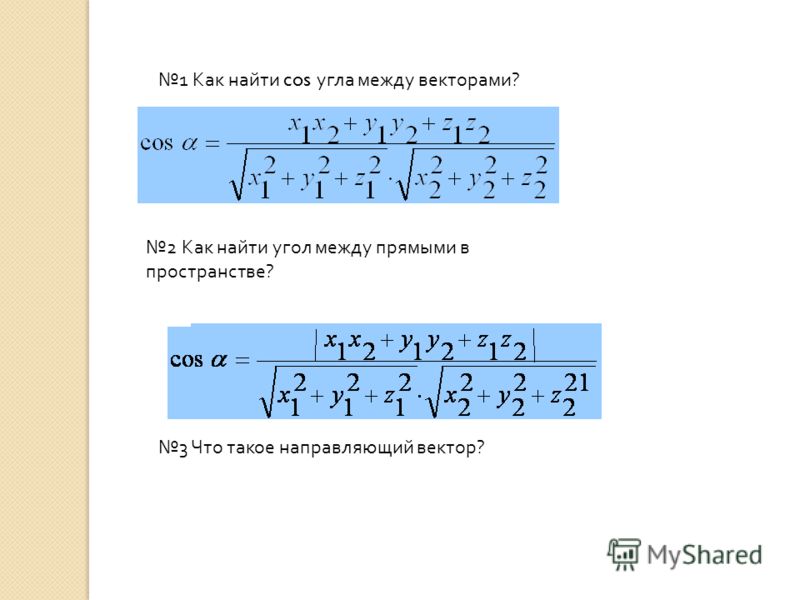

Тогда θ = cos ^-1 (2 / √14 · √14) = cos ^-1 (2 / 14) = cos ^-1 (1/7) ≈ 81,79°.

Важные моменты угла между двумя векторами:

• Угол (θ) между двумя векторами а и b находится по формуле |)].
• Угол между двумя равными векторами равен 0 градусов, как a | ² /| a | ² ) = cos ^-1 1 = 0°.
• Угол между двумя параллельными векторами равен 0 градусов, как (k| a | ² /k| a | ² ) = cos ^-1 1 = 0°.
• Угол (θ) между двумя векторами a и b с использованием перекрестного произведения равен θ = sin ^-1 [ | а × б | / (| а | | б |)].
• Для любых двух векторов a и b , если a · b положителен, то угол лежит между 0° и 90°;
  если a · b отрицательно, то угол лежит между 90° и 180°. ​​​
• Угол между каждым из двух векторов среди единичных векторов i , j и k равен 90°.

Связанные темы:

• Вектор положения
• Вычитание двух векторов
• Обработка векторов, указанных в форме i-j
• Неравенство треугольников в векторе

Часто задаваемые вопросы об угле между двумя векторами

Что означает угол между двумя векторами?

Угол между двумя векторами — это угол пересечения их хвостов, когда они присоединены хвост к хвосту. Если векторы не присоединены хвост к хвосту, то мы должны сделать параллельный сдвиг одного или обоих векторов, чтобы найти угол между ними.

Что такое формула угла между двумя векторами?

Угол (θ) между двумя векторами a и b можно найти с помощью скалярного произведения и перекрестного произведения. Вот угол между формулами двух векторов :

• Используя скалярное произведение: θ = cos ^-1 [ ( a · b ) / (| a | 0 8 b 90]
• Используя векторное произведение: θ = sin ^-1 [ | а × б | / (| и | | б |) ]

Как найти угол между двумя векторами?

Чтобы найти угол между двумя векторами a и b , мы можем использовать формулу скалярного произведения: a · b = | и | | б | cos θ . Если мы решим это для θ, мы получим θ = cos ^-1 [( a · b ) / (| a | | b |)].

Какой угол между двумя равными векторами?

Угол между двумя векторами a и b находится по формуле . Если два вектора равны, то подставляем в эту формулу b = a , тогда получаем |) ] = cos ^-1 (| a | ² /| a | ² ) = cos ^-1 1 = 0°. Таким образом, угол между двумя равными векторами равен 0.

Если угол между двумя векторами равен 90, то каково их скалярное произведение?

Скалярное произведение a и b равно a · b = | и | | б | cos θ. Если угол θ равен 90 градусов, то cos 90° = 0. Тогда a · b = | и | | б | (0) = 0. Таким образом, скалярное произведение двух перпендикулярных векторов равно 0,9.0009

Как найти угол между двумя векторами в 3D?

Чтобы найти угол между двумя векторами a и b , которые находятся в 3D:

• Вычислите их скалярное произведение a · b .
• Вычислить их величины | и | и | б |.
• Используйте формулу θ = cos ^-1 [( a · b ) / (| a | | b |)].

Чему равен угол между двумя векторами, если скалярное произведение равно 0?

Угол между двумя векторами равен θ = cos ^-1 [( a · b ) / (| a | | b |)]. Когда скалярное произведение равно 0, из приведенной выше формулы θ = cos ^-1 0 = 90°. Итак, когда скалярное произведение двух векторов равно 0, они перпендикулярны.

Объяснение урока: Угол между двумя прямыми в пространстве

В этом объяснении мы узнаем, как найти угол между двумя прямыми в трех измерениях с помощью формулы.

То есть, имея две линии в трехмерном пространстве, мы можем использовать формулу скалярного произведения их двух векторов направления, чтобы найти угол между двумя линиями. Мы преобразуем формулу, чтобы найти косинус угла между векторами направления, а затем возьмем арккосинус, чтобы найти угол между двумя линиями. Мы также увидим, как можно использовать направляющие косинусы двух прямых для нахождения одного и того же угла.

Для начала напомним, что одна прямая однозначно задается в пространстве либо в том случае, если она проходит через известную неподвижную точку и имеет известное направление, как на диаграмме 1 ниже, или если линия проходит через две известные фиксированные точки, как на диаграмме 2.

В первом случае прямая, имеющая вектор направления ⃑𝑑, проходит через точку 𝐴(𝑥,𝑦,𝑧), который имеет вектор положения ⃑𝑎. Если 𝑃(𝑥,𝑦,𝑧) — любая точка на этой прямой и ⃑𝑟 — вектор положения 𝑃, тогда ⃑𝑟=⃑𝑎+𝜆⃑𝑑 — векторное уравнение прямой. Здесь 𝜆 — скаляр, и каждое значение 𝜆 дает вектор положения одной уникальной точки на линии. Расширяя это, вспомним, что мы можем выразить уравнение линии в трех измерениях следующими способами.

Определение

В общем случае можно написать уравнение прямой, параллельной вектору направления Проходя через точку 𝐴 (𝑥, 𝑦, 𝑧)  как ⃑𝑟 = 𝑥⃑𝑖+𝑦⃑𝑗+𝑧⃑𝑘+𝜆𝑎⃑𝑖+𝑏⃑𝑗+𝑐⃑𝑘, 𝑥 = 𝑥+𝜆𝑎, 𝑦 = 𝑦+𝜆𝑏, 𝑧 = 𝑧+𝜆𝑐 ,𝑥−𝑥𝑎=𝑦−𝑦𝑏=𝑧−𝑧𝑐().(vectorform)(parametricform)Декартова форма

Точка с координатами (𝑥,𝑦,𝑧) бесконечно много точек на прямой, а 𝑎, 𝑏 и 𝑐 называются отношениями направлений .

Во втором случае (диаграмма 2) для прямой, проходящей через две известные неподвижные точки 𝐴(𝑥,𝑦,𝑧) и 𝐵(𝑥,𝑦,𝑧) с ассоциированными векторами ⃑𝑎 и ⃑𝑏, вектор направления этой линии определяется выражением ⃑𝑑=⃑𝑏−⃑𝑎. То есть ⃑𝑑=(𝑥−𝑥)⃑𝑖+(𝑦−𝑦)⃑𝑗+(𝑧−𝑧)⃑𝑘.

Тогда отношения направлений равны ∶(𝑧−𝑧), и используя либо 𝐴, либо 𝐵 в качестве фиксированной точки, мы можем снова записать линию в векторной , параметрической или декартовой форме.

Теперь предположим, что у нас есть две линии в пространстве, 𝐿 и 𝐿.

Если 𝐿 имеет направляющий вектор ⃑𝑑 и проходит через точку ⃑𝑎, а 𝐿 имеет направляющий вектор ⃑𝑑 и проходит через точку ⃑𝑎, то в векторной форме эти прямые имеют уравнения 𝐿∶⃑𝑟=⃑𝑎+𝜆⃑𝑑. 

Тогда угол между двумя прямыми равен углу между их направляющими векторами, ⃑𝑑 и ⃑𝑑. Это не зависит от их положения, так что на самом деле, если мы знаем векторы направления линий, мы можем найти угол между ними. Проводя каждый из ⃑𝑑 и ⃑𝑑 из общей точки, мы можем найти угол между ними, изменив формулу скалярного произведения двух векторов.

Определение: использование векторов направления для нахождения угла между двумя линиями в пространстве косинус угла 𝜃 между двумя линиями определяется выражением ⃑𝑑om⃑𝑑 = ‖⃑𝑑⃑𝑑⃑𝑑‖‖‖⃑𝑑⃑𝑑𝜃⟹𝜃𝜃⟹𝜃 = || ⃑𝑑⋅⃑𝑑 || ‖⃑𝑑⃑𝑑⃑𝑑‖‖⃑𝑑, coscos, где, по определению, мы вычисляем наименьший угол между двумя линиями, взяв абсолютное значение скалярного произведения (числитель). Возьмем арккосинус обеих сторон и найдем0.cos∘

На практике это означает, что для любых двух данных прямых в пространстве, если мы знаем вектор направления для каждой прямой, мы можем найти угол между двумя прямыми, используя эту формулу.

Мы также можем использовать направляющие косинусы двух прямых, чтобы найти угол между ними, где направляющие косинусы прямой в пространстве определяются следующим образом.

Определение: Направляющие косинусы

Для заданного вектора (𝑎,𝑏,𝑐) направляющие углы вектора, то есть (𝛼,𝛽,𝛾), представляют собой углы, которые вектор образует с положительными 𝑥, 𝑦 , и оси 𝑧 соответственно. Затем косинусы направления вектора задаются как 

Направляющие косинусы прямой обладают следующим свойством: coscoscos𝛼+𝛽+𝛾=1.

Используя следующее определение, мы можем найти угол между двумя прямыми в пространстве, используя их направляющие косинусы.

Определение: нахождение угла между двумя прямыми в пространстве с помощью их направляющих косинусов

𝐿 и 𝐿, то косинус острого угла 𝜃 между двумя прямыми равен cos𝜃=|𝑙𝑙+𝑚𝑚+𝑛𝑛|.

В следующих примерах показано, как работает наша переставленная формула скалярного произведения, когда у нас есть уравнения двух прямых в различных формах, а затем показано, как мы используем направляющие косинусы для нахождения угла между двумя прямыми. В нашем первом примере нам даны отношения направлений двух линий.

Пример 1: определение меры угла между двумя линиями с заданными отношениями направлений

Определите с точностью до секунды меру угла между двумя линиями, имеющими отношения направлений (−4,−3,−4 ) и (−3,−3,−1).

Ответ

Нам заданы отношения направлений двух линий, которые мы будем называть 𝐿 и 𝐿. Вспоминая, что отношения направлений являются коэффициентами компонентов 𝑥, 𝑦 и 𝑧 вектора направления, для 𝐿 и 𝐿 имеем векторы направлений , где ⃑𝑖, ⃑𝑗 и ⃑𝑘 — единичные векторы в направлениях 𝑥, 𝑦 и 𝑧.

Мы знаем, что угол между двумя линиями с векторами направления ⃑𝑑 и ⃑𝑑 определяется формулой cos𝜃 = || ⃑𝑑⋅⃑𝑑 || ‖⃑𝑑⃑𝑑⃑𝑑‖‖⃑𝑑, , где || ⃑𝑑⋅⃑𝑑|| обозначает модуль скалярного произведения векторов ⃑𝑑 и ⃑𝑑, ‖‖⃑𝑑‖‖ — модуль вектора ⃑𝑑, а ‖‖⃑𝑑

 — модуль вектор ⃑𝑑.

Для наших прямых 𝐿 и 𝐿 скалярное произведение их векторов направления есть −3×−3)+(−4×−1)=25.

Следовательно, абсолютное значение ||⃑𝑑⋅⃑𝑑|| равно 25. Величина ⃑𝑑 равна ‖‖⃑𝑑‖‖=(−4)+(−3)+(−4)=√41, и величина вектора ⃑𝑑 равна ‖‖⃑𝑑‖‖=(−3)+( −3)+(−1)=√19.

В нашей формуле для косинуса угла 𝜃 между направляющими векторами имеем cos𝜃=25√41√19.

Взяв арккосинус с обеих сторон, мы получим угол 𝜃=25√41√19≈26.39920173.cos∘

Нас просят найти меру угла с точностью до секунды, и для этого мы вспомним, что в одном градусе 60 минут, а в одной минуте 60 секунд. Поэтому мы умножаем десятичную часть наших градусов на 60: 0,39920173×60≈23,9521038. Итак, у нас есть 23,9521038′ (минуты) и умножение десятичной части нашего минут на 60: 0,9521038×60≈57,126≈57″ (секунд).

Тогда с точностью до секунды угол между двумя прямыми 𝐿 и 𝐿 равен 2623′57′′∘.

В нашем следующем примере мы увидим, как найти угол между двумя линиями, зная координаты двух точек на каждой линии.

Пример 2. Нахождение меры угла между двумя прямыми в трех измерениях по координатам четырех лежащих на них точек

Прямая 𝐿 проходит через две точки 𝐴(−2,2,−3) и 𝐵(−6,−4,−5), а прямая 𝐿 проходит через две точки 𝐶(1,4,1) и 𝐷(−9,−6,−9). Найдите величину угла между двумя прямыми, при необходимости давая ответ с точностью до двух знаков после запятой.

Ответ

Для нашей первой линии 𝐿 мы начинаем с нахождения ее отношений направлений, из которых мы можем сформировать ее вектор направления. Мы можем сделать это, вычитая коэффициенты для компонентов 𝑥, 𝑦 и 𝑧 первой точки 𝐴(−2,2,−3) из коэффициентов второй точки 𝐵(−6,−4,−5). Таким образом, вектор направления для 𝐿 имеет вид , ⃑𝑗 и ⃑𝑘 — единичные векторы в направлениях 𝑥, 𝑦 и 𝑧. Аналогично, используя точки 𝐶(1,4,1) и 𝐷(−9,−6,−9) на второй прямой 𝐿 имеем направляющий вектор найти угол между прямыми 𝐿 и 𝐿, мы можем использовать формулу для абсолютного значения скалярного произведения двух направляющих векторов, которая переставляется так, чтобы дать cos𝜃=||⃑𝑑⋅⃑𝑑||‖‖⃑𝑑‖‖ ‖‖⃑𝑑‖‖.

Это означает, что для нахождения нашего угла 𝜃 нам нужно найти скалярное произведение ⃑𝑑⋅⃑𝑑 векторов направления и их модулей ⃑𝑑‖‖. Скалярное произведение имеет вид )=120. 

Абсолютное значение ||⃑𝑑⋅⃑𝑑|| равно 120. Величина ⃑𝑑 равна ‖‖⃑𝑑‖‖=(−4)+(−6)+(−2)=√56 ,, а величина вектора ⃑𝑑 равна ‖‖⃑𝑑‖‖=(−10)+(−10)+(−10)=√300.

В нашей формуле для косинуса угла 𝜃 между направляющими векторами, тогда cos𝜃=120√56√300.

Вычисление арккосинуса с обеих сторон дает нам угол 𝜃=120√56√300≈22,2076.cos∘

Тогда с точностью до двух знаков после запятой угол между двумя прямыми 𝐿 и 𝐿 равен 22.21∘.

Стоит отметить, что взяв абсолютное значение скалярного произведения векторов направления в нашей формуле, мы гарантируем, что найдем острый угол между нашими двумя линиями. Однако между двумя прямыми линиями (которые не являются ни перпендикулярными, ни параллельными) на самом деле есть два угла, один острый (𝜃) и один тупой (𝛼):

Острый угол — это меньший угол, заключенный между положительными углами двух векторов направления, как на диаграмме 1 ниже.

Если наши векторы направления противоположны, как на диаграмме 2, то использование формулы без абсолютного значения скалярного произведения для вычисления угла между двумя линиями даст нам тупой угол 𝛼. Вот почему мы берем абсолютное значение, поскольку угол, который мы ищем, является меньшим из двух. Точно так же, хотя и требует немного больше работы, мы могли бы вычесть наш тупой угол из 180∶𝜃=180−𝛼∘∘, чтобы получить острый угол.

Эта идея проиллюстрирована в нашем следующем примере.

Пример 3. Нахождение меры угла между двумя прямыми по их уравнениям в трех измерениях

Нахождение меры угла между двумя прямыми линиями 𝐿∶𝑥=5−8𝑡,𝑦=−3−4𝑡,𝑧=5+6𝑡 и 𝐿∶𝑥−53=𝑦+5−6=𝑧−2−2 и округлить до ближайшей секунды.

Ответ

Чтобы найти угол между двумя прямыми в пространстве, поскольку угол между ними является углом между их направляющими векторами, мы сначала находим их направляющие векторы. Затем мы можем использовать приведенную ниже формулу, чтобы найти угол между двумя линиями:0009

В нашем случае у нас есть одна линия. 𝐿, заданный в параметрической форме: 𝑥=𝑥+𝜆𝑎,𝑦=𝑦+𝜆𝑏,𝑧=𝑧+𝜆𝑐, и другой, 𝐿, заданный в декартовой форме: 𝑥−𝑥𝑎=𝑦−𝑦 −𝑧𝑐,, где 𝜆 — скаляр, а прямая проходит через точку 𝐴(𝑥,𝑦,𝑧), с направляющим вектором ⃑𝑑=𝑎⃑𝑖+𝑏⃑𝑗+𝑐⃑𝑘.

Наша линия 𝐿 есть 𝐿∶𝑥=5−8𝑡,𝑦=−3−4𝑡,𝑧=5+6𝑡.

. Сравнивая с общей параметрической формой, мы видим, что если 𝜆 соответствует 𝑡, то 𝑎 =−8, 𝑏=−4 и 𝑐=6. Это наши отношения направлений, и поэтому наш вектор направления равен ⃑𝑑=−8⃑𝑖−4⃑𝑗+6⃑𝑘.

Обратите внимание, что для нахождения угла между двумя линиями нам не нужно указывать точки 𝐴 и 𝐴, через которые проходят линии. Хотя в этом случае мы можем просто прочитать это из нашего уравнения как 𝐴(5,−3,5).

Теперь рассмотрим нашу вторую строку 𝐿: 𝐿∶𝑥−53=𝑦+5−6=𝑧−2−2.

Поскольку в каждом из числителей коэффициенты при 𝑥, 𝑦 и 𝑧 равны 1, по сравнению с общей декартовой формой, мы можем снова просто считайте значения отношений направлений 𝑎, 𝑏 и 𝑐. Это 𝑎=3,𝑏=−6,𝑐=−2 и 9.0009

Наш вектор направления для линии 𝐿, таким образом, равен ⃑𝑑=3⃑𝑖−6⃑𝑗−2⃑𝑘.

Теперь мы можем вычислить скалярное произведение векторов направления, ⃑𝑑⋅⃑𝑑, и их величин ‑ и ‖‖⃑𝑑‖‖ для использования в формуле косинуса угла между двумя линиями.

Скалярное произведение равно 12.

Абсолютное значение этого, которое нам нужно для нашей формулы, равно ||⃑𝑑⋅⃑𝑑||=12. Величина ⃑𝑑 равна ‖‖⃑𝑑‖‖=(−8)+(−4)+6=2√29.,, а величина ⃑𝑑 равна ‖‖⃑𝑑‖‖=3+(−6)+(−2)=7.

С этими значениями в нашей формуле имеем cos𝜃= 1214√29.

Взяв арккосинус с обеих сторон, мы получим угол угол был бы отрицательным. Наше знание тригонометрии говорит нам, что арккосинус отрицательного числа даст тупой угол, то есть угол больше 90∘. Однако нам нужен острый угол между двумя прямыми, и именно поэтому мы берем абсолютное значение скалярного произведения. Альтернативой этому было бы сначала взять арккосинус нашего отрицательного результата, получив ∘: 𝜃=180−𝜃′=180−99,158574=80,841426.∘∘∘∘

Чтобы найти минуты и секунды этого угла, последовательно умножаем десятичную часть на 60 следующим образом: 0,84142565×60≈50,48553900′0,48553900×60≈29,13234000″.

Следовательно, угол между двумя прямыми 𝐿 и 𝐿 равен 8050′29′′∘.

В следующем примере мы покажем, как найти угол между двумя линиями в пространстве, зная их декартовы уравнения.

Пример 4. Нахождение меры угла между двумя прямыми

Найдите с точностью до секунды меру угла между двумя прямыми −2𝑥=4𝑦=−3𝑧 и −4𝑥=−5𝑦=2𝑧.

Ответ

Даны две прямые в пространстве, которые мы обозначим 𝐿 и 𝐿: 𝐿∶−2𝑥=4𝑦=−3𝑧,𝐿∶−4𝑥=−5𝑦=2𝑧.

Прямые заданы в декартовой форме, т. е. в виде 𝑏 и 𝑐 — отношения направлений, а линия имеет вектор направления ⃑𝑑=𝑎⃑𝑖+𝑏⃑𝑗+𝑐⃑𝑘 (где ⃑𝑖, ⃑𝑗 и ⃑𝑘 — единичные векторы в направлениях 𝑥, 𝑦 и 𝑧).

Чтобы найти угол между нашими двумя прямыми 𝐿 и 𝐿, мы будем использовать формулу cos𝜃=||⃑𝑑⋅⃑𝑑||‖‖⃑𝑑‖‖‖‖⃑𝑑‖‖.

 нужно знать отношения направлений (𝑎, 𝑏 и 𝑐) для наших двух линий, и мы можем найти их, сравнив три члена в общей декартовой форме, приведенной выше, с теми, что в каждой из наших двух линий.

Начиная с линии 𝐿, мы имеем 𝐿∶ -2𝑥 = 4𝑦 = −3𝑧, ∶𝑥 -𝑥𝑎 = 𝑦 -𝑦𝑏 = 𝑧 -𝑧𝑐.generalcartesianform

СПАСИТЬС 𝑥 Сначала: −2𝑥=𝑥−𝑥𝑎=𝑥𝑎−𝑥𝑎, и сравнивая коэффициенты, имеем 𝑥∶−2=1𝑎,∶0=−𝑥𝑎. константа

Если решить первое уравнение для 𝑎 мы находим, что 𝑎=−12. Далее, решая второе уравнение относительно постоянных членов, находим 𝑥=0. Следуя той же процедуре для членов 𝑦 и 𝑧, мы получаем 𝑥=𝑦=𝑧=0 и 𝑎=−12, 𝑏=14, 𝑐=−13.и

Поскольку 𝑥=𝑦=𝑧= 0, мы знаем, что прямая 𝐿 проходит через точку (0,0,0). А с нашими значениями 𝑎, 𝑏 и 𝑐 мы знаем, что 𝐿 имеет вектор направления ⃑𝑑=−12⃑𝑖+14⃑𝑗−13⃑𝑘.

Следуя точно такой же процедуре для нашей второй прямой 𝐿, мы находим, что эта прямая также проходит через точку (0,0,0) (поскольку 𝑥=𝑦=𝑧=0), и что 𝑎=− 14,𝑏=−15,𝑐=12.и𝐿 поэтому имеет вектор направления ⃑𝑑=−14⃑𝑖−15⃑𝑗+12⃑𝑘.

Теперь мы можем использовать наши векторы направления для определения угла между двумя линиями, используя приведенную выше формулу с абсолютным значением скалярного произведения и модулями наших двух векторов направления. Наше скалярное произведение равно .

Его абсолютное значение, ||⃑𝑑⋅⃑𝑑||, равно 11120. Величина ⃑𝑑 равна ‖‖⃑𝑑‖‖=−12+14+−13=√6112 , а модуль вектора ⃑𝑑 равен ‖‖⃑𝑑‖‖=−14+−15+12=√14120. 

С этими значениями в формуле мы тогда cos𝜃=×=22√61√141.√√

141≈76.27757930.cos∘

Однако мы еще не совсем закончили, так как нас просят найти угол с точностью до секунды. Для этого вспомним, что в одном градусе 60 минут и в одной минуте 60 секунд. Поэтому мы умножаем десятичную часть наших градусов на 60: 0,277579.30×60≈16,654758. Итак, у нас есть 16,654758′ (минуты), и умножение десятичной части наших минут на 60 дает нам 0,654758×60≈39,2855≈39′′ (секунд). Тогда с точностью до секунды угол между двумя прямыми 𝐿 и 𝐿 равен 7616′39∘.

В нашем последнем примере мы будем использовать направляющие косинусы, чтобы найти угол между двумя линиями в пространстве.

Пример 5. Нахождение меры угла между двумя прямыми с помощью их направляющих косинусов

Нахождение с точностью до секунды меры угла между прямой линией с отношением направлений (5,3,2) и прямой с направляющими углами (47,111,5023′30′′∘∘∘).

Ответ

Нам дано отношение направлений одной линии, которую мы назовем 𝐿, и углы направления второй линии, 𝐿. Чтобы найти меру угла между этими двумя прямыми, воспользуемся формулой cos𝜃=|𝑙𝑙+𝑚𝑚+𝑛𝑛|,, где (𝑙,𝑚,𝑛) и 𝑛) — это направляющие косинусы для наших двух линий, 𝐿 и 𝐿. Однако, прежде чем мы сможем это сделать, нам нужно найти направляющие косинусы для наших двух линий. Начиная с 𝐿, у нас есть отношение направлений (5,3,2). Направленный косинус для компонента 𝑥 задается формулой 𝑙=𝛼=𝑎√𝑎+𝑏+𝑐,cos, где 𝛼 — угол, который вектор направления линии составляет с осью 𝑥. В нашем случае 𝑙=𝛼=5√5+3+2=5√38.cos

Рационализируя знаменатель, мы имеем 𝑙=5√3838, и, следуя той же процедуре для наших компонентов 𝑦 и 𝑧, мы находим 𝑚=3√3838 и 𝑛=2√3838. Следовательно, для 𝐿 направляющие косинусы равны (𝑙,𝑚,𝑛)=5√3838,3√3838,2√3838.

. Для нашей второй прямой 𝐿 имеем направляющие углы (47,111,5023′30′′∘∘∘), поэтому мы просто берем косинусы этих углов, чтобы найти направляющие косинусы. Для простоты вычислений мы сначала преобразуем дирекционный угол в 𝑧-направлении в десятичную форму следующим образом: 5023′30′′=50+2360+303600≈50,39167. ∘∘

Тогда косинусы направления для 𝐿 равны (𝑙,𝑚,𝑛)=((47),(111),(50.39167)).∘∘∘coscoscos

Косинус угла между нашими двумя строками тогда дается coscoscoscos𝜃=|𝑙𝑙+𝑚𝑚+𝑛𝑛|=|||5√3838⋅(47)+3√3838⋅(111)+2√3838⋅(50,39167)|||≈0,585612835. ∘∘∘

Теперь, взяв арккосинус обеих частей нашего уравнения, мы находим 𝜃=(0,585612835)≈54,15370420.cos∘

Наконец, переводя в градусы, минуты и секунды последовательно умножая десятичные части на 60: 0,15370420×60≈90,222252 и 0,222252×60≈13,335. Следовательно, с точностью до секунды мера угла между двумя линиями равна 𝜃=549′13′′∘.

Мы завершим обсуждение угла между двумя линиями в пространстве, отметив некоторые ключевые моменты.

Ключевые точки

• Угол 𝜃 между двумя прямыми в пространстве — это угол между их направляющими векторами ⃑𝑑 и ⃑𝑑.
• Косинус угла равен cos𝜃=||⃑𝑑⋅⃑𝑑||‖‖⃑𝑑‖‖‖‖⃑𝑑‖‖.
• косинусы (𝑙,𝑚,𝑛) и (𝑙,𝑚,𝑛), косинус острого угла 𝜃 между двумя прямыми равен cos𝜃=|𝑙𝑙+𝑚𝑚+𝑛𝑛|.

  No related posts.